Abstract
The transmission of severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) occurs via contact with contaminated surfaces and inhalation of large airborne droplets and aerosols. As growing evidence of airborne SARS-CoV-2 transmission has been reported worldwide, ventilation is an effective method of reducing the infection probability of SARS-CoV-2. This leads to such questions as “What is a sufficient ventilation rate for avoiding the risk of COVID-19 infection?” Therefore, this study evaluates the critical ventilation rates according to room size and exposure time when a susceptible person is in the same room as an infector. The analytical results were based on data obtained from 70 confirmed COVID-19 cases transmitted in confined spaces without an operational ventilation system. The results reveal that even with active ventilation (20 h−1 air exchange rate), the critical exposure time for a susceptible person with a COVID-19 infector in a small space of 20 m3 is less than 1 h. For other cases (different space sizes), the estimated air exchange rates for avoiding the risk of infection are generally higher than various requirements for good indoor air quality. The findings of this study will provide guidelines for determining sufficient ventilation rates to protect against the highly contagious COVID-19.
Keywords: COVID-19, SARS-CoV-2, Airborne transmission, Air exchange rate, Ventilation
Introduction
Coronavirus disease 2019 (COVID-19) has become one of the worst infectious diseases and is caused by severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2). As of this writing (mid-December 2020), a year has passed, since the first cases of COVID-19 were reported in Wuhan, China, in December 2019. To date, over 71,000,000 confirmed cases and 1,610,000 deaths have been attributed to the COVID-19 pandemic worldwide [1].
Respiratory infectious disease transmission, such as the spread of COVID-19, occurs via the pathogens carried in droplets produced during human expiratory activities, such as coughing and sneezing, which produce relatively large droplets, and breathing and talking, which produce small droplets. Therefore, three host-to-host transmission infection routes for infectious respiratory diseases have been considered: (1) direct or indirect contact; (2) virus-laden droplets at close distances; and (3) virus aerosols at long distances [2–5]. SARS-CoV-2 is 70–120 nm in size [6–8] and can be emitted during talking and carried by the airflow. Small droplets or aerosols containing SARS-CoV-2 produced by talking and breathing may have a higher risk of transmission than larger droplets generated from sneezing and coughing. First, small particles can float in the air for a longer time without a specific cleaning process, such as ventilation or air purification [3, 7–10], and this longer residence time in the air significantly increases the probability of inhalation by a susceptible person [11]. Moreover, many studies have reported that talking and breathing produce a considerable number of particles, which can significantly influence airborne infections [12–17]. Papineni and Rosenthal [12] examined the size distribution of droplets generated from human expiratory activities, including breathing through the mouth and nose, coughing, and talking and reported that breathing tended to generate more small droplets than coughing, given the high frequency of breathing during human activity. Furthermore, more recent studies revealed that speaking generates comparable or greater numbers of particles than continuous coughing, exemplified by counting numbers [14, 16].
General precautions have been promoted to prevent the spread of COVID-19, such as hand hygiene, the use of face masks, and social distancing [18]. These precautions are highly effective for reducing the probability of COVID-19 infection via contact and large droplet contamination; however, the risk of airborne transmission remains high and should not be overlooked. Sufficient ventilation has been demonstrated to remove airborne infectious agents and pollutants effectively [6, 19]. Therefore, securing a sufficient ventilation rate is essential in indoor environments, particularly those where people spend over 90% of their time, such as offices, houses, public transportation, and classrooms. Therefore, many studies on measuring the ventilation or air exchange rates in indoor environments have been conducted. Stabile et al. [20] reported an average air exchange rate of 2.46 h−1 for the tested classrooms, which was lower than the US and European standards to achieve the required air quality. The minimum classroom ventilation rate recommended by the American Society of Heating, Refrigeration and Air-Conditioning Engineers Standard 62.1 (ASHRAE 62.1) is 6.7–7.4 L/s/person [21]. Furthermore, based on European standards, a ventilation rate of 20 L/s/person was set to achieve a “high” air quality level for non-smoking rooms [22]. In other studies, average air exchange rates of 7.3 and 12.7 h−1 were obtained for 19 houses in Texas and 20 residential buildings in the Mediterranean area of Italy, respectively [23, 24].
During the COVID-19 pandemic, owing to the highly contagious nature of SARS-CoV-2, much stricter regulation of ventilation rates should be applied; however, the level of regulation remains ambiguous. Dai and Zhao [25] estimated the relationship between the infection probability and ventilation rates in general scenarios, including buses, aircraft cabins, offices, and classrooms, by employing the Wells–Riley equation and achieved an infection probability less than 1% at ventilation rates of 100–350 and 1200–4000 m3/h for 0.25 and 3 h of exposure to an infector. However, limited studies have been conducted on the ventilation level required to minimize COVID-19 infection. In this study, on the basis of 70 confirmed cases of COVID-19 in South Korea suspected as airborne infection, an analytical study was conducted to predict the critical exposure time for a susceptible person to an infector before he or she is highly likely to be infected via the airborne transmission of SARS-CoV-2. This research is significant, as it will benefit regulatory agencies and research communities in determining a critical ventilation rate to prevent COVID-19 infection via airborne SARS-CoV-2. Moreover, the insight and the quantitative findings of this study will provide specific precautions for people and aid in preparing for the post-pandemic period with a high probability of resurgence.
Methods
A systematic analysis was conducted using the COVID-19 infection data (no mechanical ventilation, one infector in each space, and space volume less than 350 m3) provided for research on the cause of disease by the Korea Disease Control and Prevention Agency (KDCA) of the National Institute of South Korea. In this study, the critical exposure times of rooms with and without a mechanical ventilation system were evaluated. The analytical approach assumed a uniform spread of airborne virus particles in a room and a constant virus emission rate from a COVID-19 carrier.
Virus concentration and cumulated inhaled virus
The analysis was conducted based on a stay in a room with a COVID-19 carrier. The parameters used for analysis are shown in Fig. 1. In a room with a volume of V, the virus concentration at time t is defined as C(t). The emission rate of the virus from a COVID-19 carrier is defined by the number of virus particles emitted per unit time and is denoted by S.
Fig. 1.
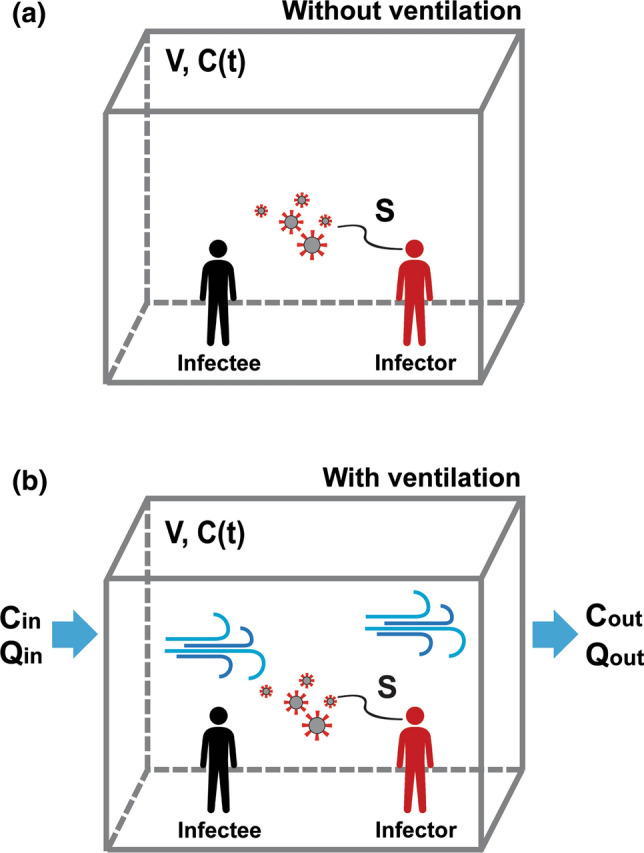
Schematic diagram of an infectee (susceptible person) and an infector in the same room a without and b with a ventilation system
Figure 1a presents a schematic for a room without a ventilation system, and the relationship between V, C(t), and S can be expressed as follows:
| 1 |
With an initial virus concentration of zero, i.e., C(0) = 0, the virus concentration C(t) in the room at time t can be obtained as follows:
| 2 |
The amount of virus inhaled D(T) during an exposure time of T can be evaluated as follows:
| 3 |
which gives
| 4 |
where Tw/o_vent is defined as the exposure time for a susceptible person to become infected in a room without a ventilation system, i.e., the critical dose of the virus for COVID-19 infection, and the amount of virus inhaled during this exposure time can be obtained as
| 5 |
indicating that the amount of virus inhaled is proportional to the second power of the exposure time due to the increasing virus concentration in the room as time elapses.
A similar analytical approach was followed to investigate virus inhalation in a room with a ventilation system operated with the inflow of clean air and outflow of contaminated air. The inflow and the outflow rates are denoted as Qin and Qout, and the virus concentrations in these two flows are denoted as Cin and Cout, respectively, as shown in Fig. 1b. Therefore, the temporal number concentration of virus particles in a room with a ventilation system can be expressed as follows:
| 6 |
The flowrates of these two flows (Qin and Qout) are assumed to be the same; hence, both can be denoted as Q. The virus concentration in the inflowing clean air, Cin, should be 0, and the concentration in the outflowing air, Cout, is assumed to be the same as that in the room at time t, i.e., Cout = C(t), assuming well-mixed air conditions in the room. Therefore, Eq. (6) becomes
| 7 |
With Eq. (7) and the initial condition of C(0) = 0, the virus concentration at time t can be determined as follows:
| 8 |
where n is the number of air exchanges per hour (i.e., the air exchange rate), which can be determined by Q/V. If Tw/_vent is defined as the exposure time for a person to become infected in a room with a ventilation system, the cumulative virus concentration rate inhaled by a person can be obtained from 0 to Tw/_vent by integrating Eq. (8) and is given by
| 9 |
Critical virus dose based on ventilation conditions
The cumulative inhaled virus concentration was obtained for two rooms, one with a ventilation system and one without. The critical dose for a person to become infected with COVID-19 is the same for both cases. Therefore, the relationship between Tw/o_vent and Tw/_vent can be derived assuming that D(Tw/o_vent) in Eq. (5) and D(Tw/_vent) in Eq. (9) are equal:
| 10 |
COVID-19 infection cases
Table 1 details the confirmed cases of COVID-19 during various activities held in enclosed spaces with a volume smaller than 350 m3 that satisfy the assumption of a spatially uniform virus distribution. Of note is that the space volumes were estimated using a constant height of 2.5 m. Seventy confirmed cases were provided by the KDCA, and the details on the cases were obtained from surveillance videos at the scenes and interviews with the people related to the cases. On the basis of that information, all seventy cases were suspected cases of infection caused by airborne virus transmission, as confirmed by the KDCA. Therefore, these data were used to develop an analytical approach for COVID-19 virus transmission patterns through air. As mentioned above, 70 people were reported as COVID-19 infectees in confined spaces, including accommodations for examiners (14 infectees), fitness centers (27 infectees), cellphone retail stores (seven infectees), army lectures (nine infectees), table tennis club activities (11 infectees), and taxis (two infectees). A mechanical ventilation system was not operated in these spaces, and the COVID-19 infection cases used in this study had one infector in each space.
Table 1.
Information regarding COVID-19 cases confirmed from July to September 2020 are reported by the Korea Centers for Disease Control and Prevention
| Case | Total number of infectees [–] | Exposure time to a carrier [h] | Space volume [m3] | Carrier wearing a face mask | Infectee wearing a face mask |
|---|---|---|---|---|---|
| Accommodation for examiners | 14 | 3 | 206.6 | N | Y |
| Fitness center 1 | 14 | 1–6 | 334.7 | N | N |
| Fitness center 2 | 13 | 1 | 175.3 | N | N |
| Cellphone retail store | 7 | 0.5–1 | 99.2 | Y | Y |
| Army lecture | 9 | 2.5 | 206.6 | N | Y |
| Table tennis club | 11 | 0.5–4 | 299.2 | N | N |
| Taxi 1 | 1 | 0.05 | 3.2 | Y | Y |
| Taxi 2 | 1 | 0.083 | 3.2 | Y | Y |
The space volume was estimated assuming a height of 2.5 m (excluding the taxi cases). The volume of a taxi was retrieved from the United States Environmental Protection Agency website [26]
Figure 2 presents the exposure time of the infectees as a function of the room size, and the size of the circles represents the number of people. The black, solid line represents the regression of the infection data (regression equation: log(Tw/o_vent) = 0.7774·log(V) − 1.5833, coefficient of determination: R2 > 0.783), and the figure also shows the 95% confidence intervals. The deviation of the data from the regression line could be due to whether the carriers (infectors) and infectees were wearing a face mask, their positions and activities, the amount of virus particles inhaled before infection (critical virus dose), the room/space structure, or furniture in the room. The COVID-19 carriers in the accommodations, fitness centers, army lectures, and table tennis clubs were not wearing face masks, while those in the cellphone retail stores and the taxi drivers were. Although both the infector and the infectee wore a face mask in the taxi, several factors facilitated infection: (1) a high concentration of SARS-CoV-2 due to the small space of the taxi; (2) the use of a loosely fitting face mask; and (3) the low filtration efficiency of a dental face mask. Despite the uncertainties, the trend of the graph in Fig. 2 indicates a proportional relationship between the room size and the duration of exposure to the carriers on a log-scale. On the basis of the regression line in Fig. 2, the critical exposure time to a COVID-19 carrier in the same room without a ventilation system, i.e., Tw/o_vent, is determined by the room size. Moreover, from Eq. (10), the required air exchange rate to prevent infection using a ventilation system can be determined based on the exposure time in the room under ventilation, i.e., Tw/_vent.
Fig. 2.
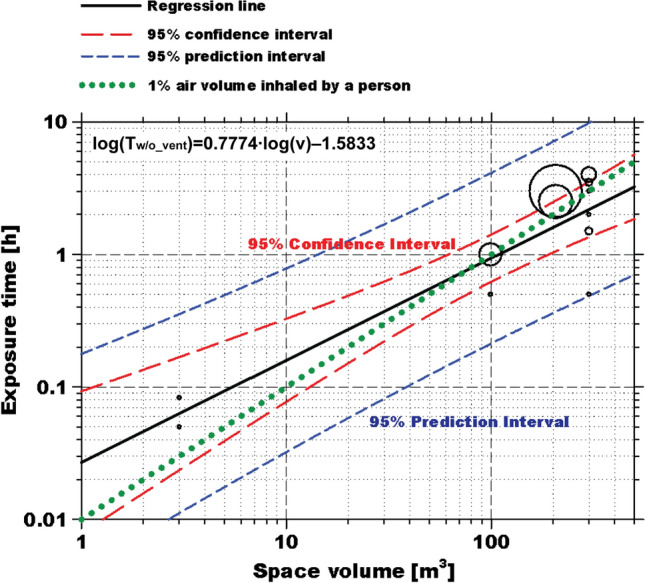
Reported exposure time of infectees to a COVID-19 carrier according to the volume of the space. The long and the medium dashed lines (red and blue color) are the 95% confidence and prediction intervals, respectively. The dotted line (green color) indicates the time spent for inhaling 1% of the air volume in a given space by a person with an assumed average breathing rate of 1 m3/h. This breathing rate is in the range of the sitting and the light exercise modes defined by the International Commission on Radiological Protection (ICRP, 1994) model [27]
Results and discussion
Air exchange rate and exposure time
Figures 3 and 4 show the estimated relationships between the ventilation (air exchange) rate, room size, and exposure time. As the results were obtained by applying the values from the black, solid regression line in Fig. 2 to the relationship in Eq. (10), the lines in Figs. 3 and 4 correspond to the 50% infection probability, which was a critical level for infection.
Fig. 3.
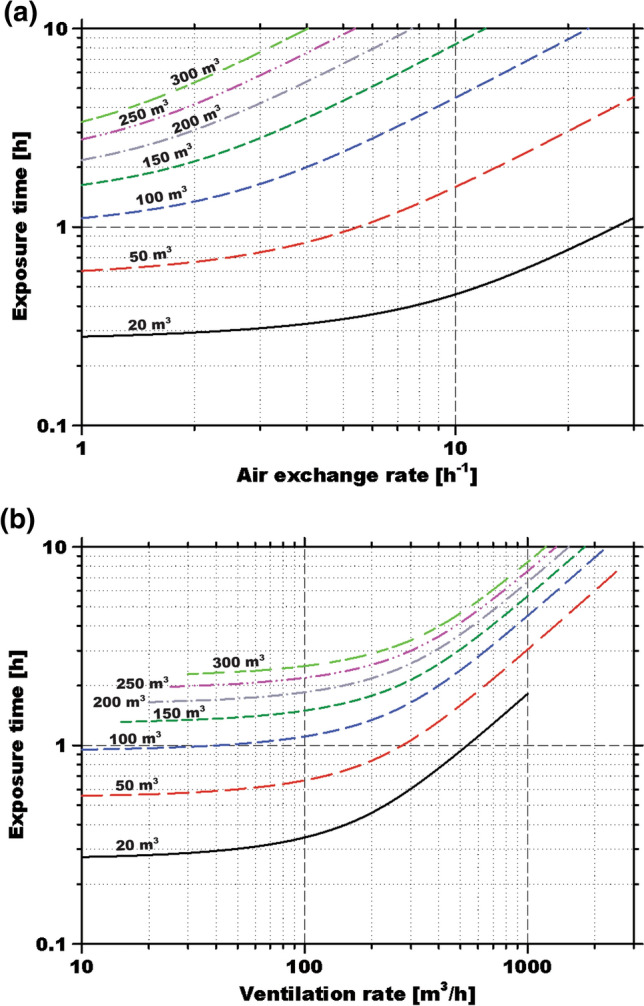
Estimated critical exposure time of a susceptible person to a COVID-19 carrier according to a air exchange and b ventilation rates for room sizes ranging from 20 to 300 m3. The increasing air exchange rate (ventilation rate) ensures a longer stay in the space
Fig. 4.
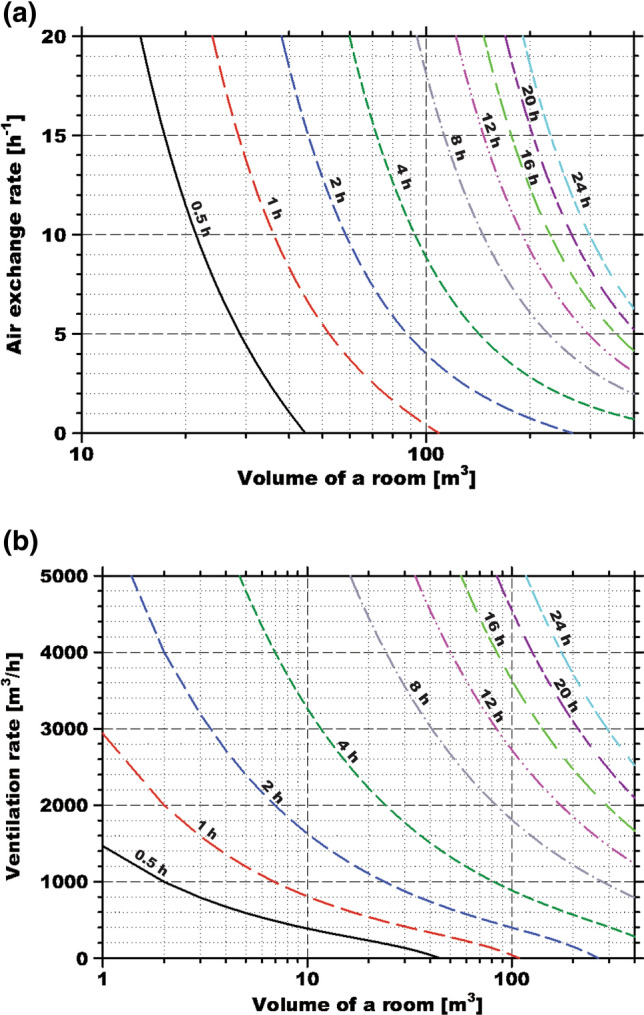
a Air exchange and b ventilation rates for critical exposure times ranging from 0.5 to 24 h according to room size. Small rooms require more active ventilation for avoiding the risk of infection
Typical examples with similar space volumes are presented in Fig. 3a. If one infector is assumed to be present in a confined space, the critical exposure time to an infector in the same room before infection increased as the air exchange rate increased. In a space smaller than 20 m3, an exposure time to an infector in the room of less than 1 h is guaranteed to cause a susceptible person to become infected, even under active ventilation of 20 h−1. Therefore, special precautions are required to prevent infection in a small space, such as a standard office. More importantly, preventing a COVID-19 carrier from entering such small public spaces (even those with a ventilation system) is crucial to suppress infection via airborne transmission.
The exposure times for different room sizes with the same air exchange rate (n = 1, 5, 10, 15, and 20 h−1) are summarized in Table 2. As the room size and the exchange rate increased, the exposure time greatly increased. For example, when the room size increased by five, ten, and fifteen times from 20 m3 to 100, 200, and 300 m3, the exposure times were 11.5, 33.6, and 63.1 h at an air exchange rate of 20 h−1, respectively. This is due to the lower virus concentration in larger rooms. However, more energy is required to produce a higher ventilation flowrate in a larger room with the same air exchange rate. Therefore, the relationship between the ventilation rate and the exposure time is presented in Fig. 3b, with the x-axis representing the ventilation rate (Q = n × V).
Table 2.
Summary of the estimated critical exposure times in hours at air exchange rates of 1, 5, 10, 15, and 20 h−1 in rooms ranging from 20 to 300 m3 in size
| Air exchange rate [h−1] | Space volume [m3] | ||||||
|---|---|---|---|---|---|---|---|
| 20 | 50 | 100 | 150 | 200 | 250 | 300 | |
| 1 | 0.28 | 0.60 | 1.11 | 1.63 | 2.17 | 2.76 | 3.39 |
| 5 | 0.34 | 0.94 | 2.39 | 4.32 | 6.64 | 9.31 | 12.30 |
| 10 | 0.46 | 1.59 | 4.49 | 8.34 | 12.98 | 18.33 | 24.30 |
| 15 | 0.61 | 2.31 | 6.64 | 12.42 | 19.39 | 27.41 | 36.37 |
| 20 | 0.77 | 3.04 | 8.82 | 16.52 | 25.82 | 36.50 | 48.45 |
Room size and air exchange rate
Figure 4 shows the relationship between the space volume and the ventilation rate required to achieve the critical exposure time for infection. As the room size decreased, the required air exchange rate to reach the same exposure time decreased exponentially. If the space volume of a school is assumed to range from approximately 150–300 m3 (as reported by Tanner [28]) and the stay in the school is assumed to be 8 h, air exchange rates exceeding 9.6 and 3.2 h−1 are required to avoid the risk of virus transmission in 150- and 300-m3 classrooms. The estimated exchange rate was much higher than that required to provide clean air in a classroom, which is typically less than 3 h−1 for a 150–200-m3 classroom [29]. Various requirements for indoor air quality have been set to achieve fresh air in North America, Europe, and other countries. Although setting an exact ventilation (air exchange) rate is difficult due to the different regulations for various conditions in classrooms, most of the stringent requirements for ventilation are more lenient than the ventilation rates obtained in this study. Moreover, the Ministry of Education of South Korea stipulates a required ventilation rate of 21.6 m3/h per person for classrooms, which corresponds to an exchange rate of 2–3 h−1 for typical classroom conditions (for example, a 2.7-h−1 exchange rate for a 200-m3 classroom with 25 students).
Conclusion
In this study, the critical ventilation rate and exposure time for a susceptible person to become infected by COVID-19 were examined following a unique analytical approach. First, we obtained from the KDCA information regarding 70 confirmed COVID-19 cases contracted during different activities and in different spaces, including accommodations, fitness centers, cellphone retail stores, lectures, sports clubs, and taxis. The analytical approach was developed assuming the following: (1) the virus concentration was uniform in a room, regardless of the presence of a ventilation system (well-mixed condition); (2) the virus generation rate of an infector was the same for all cases; and (3) the total number of virus particles inhaled before a susceptible person becomes infected by COVID-19 was the same for all individuals.
Based on these assumptions, the relationship between the exposure time and the ventilation rate according to the room size was investigated. The results show that, in a small space of 20 m3, such as an office, a susceptible person with an infector has a critical exposure time of less than 1 h, even with an active ventilation system providing an air exchange rate of 20 h−1. In classrooms, in which students generally spend 8 h per day, an air exchange rate much greater than 3.2 to 9.6 h−1 would be suitable for classrooms ranging from 300 to 150 m3 in size. These air exchange rates exceed the minimum ventilation rate recommended to ensure good air quality in classrooms. Of note is that the ventilation rates in this study were estimated by neglecting certain conditions, such as the ventilation’s flow direction and positions of the susceptible person and the infector. Therefore, the analytical approach loses validity as the room size increases, which is the reason we analyzed ventilation rates for a volume of space less than 350 m3. However, the results are significant for managing deadly diseases. Finally, this study provides the required or critical ventilation rates to suppress COVID-19 infection via airborne transmission and concludes that stricter ventilation regulations are needed.
Acknowledgements
The authors would like to thank KDCA for providing the valuable data. HDL is thankful for a research grant from Inha University.
Footnotes
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.World Health Organization, (n.d.). https://www.who.int/emergencies/diseases/novel-coronavirus-2019
- 2.Wang J, Du G. Irish J. Med. Sci. 2020;189:1143. doi: 10.1007/s11845-020-02218-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Patients L, Taylor D, Lindsay AC, Halcox JP, Engl N. J. Med. 2020;382:1564. [Google Scholar]
- 4.Asadi S, Bouvier N, Wexler AS, Ristenpart WD. Aerosol Sci. Technol. 2020;54:635. doi: 10.1080/02786826.2020.1749229. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Anderson EL, Turnham P, Griffin JR, Clarke CC. Risk Anal. 2020;40:902. doi: 10.1111/risa.13500. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Arshad Ali S, Baloch M, Ahmed N, Arshad Ali A, Iqbal A. J. Infect. Public Health. 2020;13:644. doi: 10.1016/j.jiph.2020.02.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Sohrabi C, Alsafi Z, O’Neill N, Khan M, Kerwan A, Al-Jabir A, Iosifidis C, Agha R. Int. J. Surg. 2020;76:71. doi: 10.1016/j.ijsu.2020.02.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.To KKW, Tsang OTY, Yip CCY, Chan KH, Wu TC, Chan JMC, Leung WS, Chik TSH, Choi CYC, Kandamby DH, Lung DC, Tam AR, Poon RWS, Fung AYF, Hung IFN, Cheng VCC, Chan JFW, Yuen KY. Clin. Infect. Dis. 2020;71:841. doi: 10.1093/cid/ciaa149. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Poirier C, Luo W, Majumder MS, Liu D, Mandl KD, Mooring TA, Santillana M. Sci. Rep. 2020;10:1. doi: 10.1038/s41598-019-56847-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Morawska L, Milton DK. Clin. Infect. Dis. 2020;71:2311. doi: 10.1093/cid/ciaa939. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Shaman J, Kohn M. Proc. Natl. Acad. Sci. U. S. A. 2009;106:3243. doi: 10.1073/pnas.0806852106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Papineni RS, Rosenthal FS. J. Aerosol Med. 1997;10:105. doi: 10.1089/jam.1997.10.105. [DOI] [PubMed] [Google Scholar]
- 13.Loudon RG, Roberts RM. Am. Rev. Respir. Dis. 1967;95:435. doi: 10.1164/arrd.1967.95.3.435. [DOI] [PubMed] [Google Scholar]
- 14.Johnson GR, Morawska L, Ristovski ZD, Hargreaves M, Mengersen K, Chao CYH, Wan MP, Li Y, Xie X, Katoshevski D, Corbett S. J. Aerosol Sci. 2011;42:839. doi: 10.1016/j.jaerosci.2011.07.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Chao CYH, Wan MP, Morawska L, Johnson GR, Ristovski ZD, Hargreaves M, Mengersen K, Corbett S, Li Y, Xie X, Katoshevski D. J. Aerosol Sci. 2009;40:122. doi: 10.1016/j.jaerosci.2008.10.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Morawska L, Johnson GR, Ristovski ZD, Hargreaves M, Mengersen K, Corbett S, Chao CYH, Li Y, Katoshevski D. J. Aerosol Sci. 2009;40:256. doi: 10.1016/j.jaerosci.2008.11.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Xie X, Li Y, Sun H, Liu L, Soc JR. Interface. 2009;6:S703. doi: 10.1098/rsif.2009.0388.focus. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.M.J. Evans, Avoiding Covid-19: Aerosol Guidelines. ArXiv. (2020)
- 19.Escombe AR, Oeser CC, Gilman RH, Navincopa M, Ticona E, Pan W, Martínez C, Chacaltana J, Rodríguez R, Moore DAJ, Friedland JS, Evans CA. PLoS Med. 2007;4:e68. doi: 10.1371/journal.pmed.0040068. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Stabile L, Dell’Isola M, Frattolillo A, Massimo A, Russi A. Build. Environ. 2016;98:180. doi: 10.1016/j.buildenv.2016.01.009. [DOI] [Google Scholar]
- 21.Ventilation for acceptable indoor air quality, ASHRAE Stand. 62.1. (2007)
- 22.Ventilation for non-residential buildings - Performance requirements for ventilation and room conditioning systems, Eur. Stand. EN 13779 (2006)
- 23.Stephens B, Siegel JA. Indoor Air. 2012;22:501. doi: 10.1111/j.1600-0668.2012.00779.x. [DOI] [PubMed] [Google Scholar]
- 24.Alfano DFR, Dell’Isola M, Ficco G, Tassini F. Build. Environ. 2012;53:16. doi: 10.1016/j.buildenv.2011.12.017. [DOI] [Google Scholar]
- 25.Dai H, Zhao B. Build. Simul. 2020;13:1321. doi: 10.1007/s12273-020-0703-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Vehicle size classes used in the fuel economy guide, (n.d.). https://www.fueleconomy.gov/feg/info.shtml#sizeclasses
- 27.ICRP, Human respiratory tract model for radiological protection, Ann. ICRP. 24 (1994) [PubMed]
- 28.C.K. Tanner, Minimum classroom size and number of students per classroom. https://www.scarsdaleschools.k12.ny.us/cms/lib/NY01001205/Centricity/Domain/1105/2014-11-19%20Meeting%20of%20Greenacres%20Building%20Committee%20Meeting%20Handout%203%20-%20Classroom%20Size%20Standards.pdf
- 29.Schibuola L, Scarpa M, Tambani C. Energy Procedia. 2016;101:257. doi: 10.1016/j.egypro.2016.11.033. [DOI] [Google Scholar]


