What Can We Learn from the Time Evolution of COVID‐19 Epidemic in Slovenia?

Abstract

A recent work indicates that temporarily splitting larger populations into smaller groups can efficiently mitigate the spread of SARS‐CoV‐2 virus. The fact that, soon afterward, the two million people Slovenia was the first European country proclaiming the end of COVID‐19 epidemic within national borders may be relevant from this perspective. Motivated by this evolution, in this paper the time dynamics of coronavirus cases in Slovenia is investigated with emphasis on how efficient various containment measures act to diminish the number of COVID‐19 infections. Noteworthily, the present analysis does not rely on any speculative theoretical assumption; it is solely based on raw epidemiological data. Out of the results presented here, the most important one is perhaps the finding that, while imposing drastic curfews and travel restrictions reduce the infection rate κ by a factor of four with respect to the unrestricted state, they only improve the κ‐value by ≈15% as compared to the much bearable state of social and economic life wherein wearing face masks and social distancing rules are enforced/followed. Significantly for behavioral and social science, our analysis may reveal an interesting self‐protection instinct of the population, which became manifest even before the official lockdown enforcement.

A novel method relying on raw epidemiologic data without speculative theoretical assumptions is proposed. Although based on the nonlinear logistic model, the analysis is amenable to linear regression. Applied to a specific case (Slovenia's COVID‐19 epidemic), this approach discourages too excessive curfews and travel restrictions, and unravels an interesting population's self‐protection instinct, which became manifest even before official lockdown enforcement.

1. Introduction

In the unprecedented difficulty created by the COVID‐19 pandemic outbreak,^{[ 1 ]} mathematical modeling (for recent efforts, see, e.g., refs. [2, 3, 4, 5, 6, 7, 8, 9, 10] and citations therein) developed by epidemiologists over many decades^{[ 11} , ¹² , ¹³ , ¹⁴ , ¹⁵ , ^{16 ]} may make an important contribution in helping politics to adopt adequate regulations to efficiently fight against the spread of SARS‐CoV‐2 virus while mitigating negative economic and social consequences. The latter aspect is of paramount importance^{[ 17 ]} also because, if not adequately considered by governments currently challenged to deciding possibly under dramatic circumstances and formidable tight schedule, it can jeopardize the health care system itself. As an effort in this direction, we drew recently attention^{[ 18 ]} to the general fact that the spread of the SARS‐CoV‐2 virus in smaller groups can be substantially slowed down as compared to the case of larger populations. In this vein, the time evolution of COVID‐19 disease in the two million people Slovenia certainly deserves special consideration, as on 15 May 2020, concluding that this country has the best epidemic situation in Europe, Prime Minister Janez Janška declared the end of the COVID‐19 epidemic within Slovenian borders.^{[ 19 ]} Subsequent developments (e.g., only four new cases between 15 and 24 May,^{[ 20 ]} cf. Table  1 and only 30 new cases between 15 May and 15 June 2020) have fortunately given further support to this declaration. Attempting to understand and learn from this sui generis circumstance is the very aim of the present paper.

Table 1.

Total confirmed cases and new confirmed cases per day of COVID‐19 epidemic in Slovenia reported by the National Institute of Public Health Data according to Wikipedia^{[ 20 ]}

Day of 2020	Date	Total confirmed	New confirmed per day
64	03‐04	1	1
65	03‐05	6	5
66	03‐06	8	2
67	03‐07	12	4
68	03‐08	16	4
69	03‐09	25	9
70	03‐10	34	9
71	03‐11	57	23
72	03‐12	89	32
73	03‐13	141	52
74	03‐14	181	40
75	03‐15	219	38
76	03‐16	253	34
77	03‐17	275	22
78	03‐18	286	11
79	03‐19	319	33
80	03‐20	341	22
81	03‐21	383	42
82	03‐22	414	31
83	03‐23	442	28
84	03‐24	480	38
85	03‐25	528	48
86	03‐26	562	34
87	03‐27	632	70
88	03‐28	684	52
89	03‐29	730	46
90	03‐30	756	26
91	03‐31	802	46
92	04‐01	841	39
93	04‐02	897	56
94	04‐03	934	37
95	04‐04	977	43
96	04‐05	997	20
97	04‐06	1021	24
98	04‐07	1056	35
99	04‐08	1092	36
100	04‐09	1125	33
101	04‐10	1161	36
102	04‐11	1188	27
103	04‐12	1205	17
104	04‐13	1212	7
105	04‐14	1220	8
106	04‐15	1248	28
107	04‐16	1269	21
108	04‐17	1305	36
109	04‐18	1318	13
110	04‐19	1331	13
111	04‐20	1336	5
112	04‐21	1345	9
113	04‐22	1354	9
114	04‐23	1367	13
115	04‐24	1374	7
116	04‐25	1389	15
117	04‐26	1396	7
118	04‐27	1402	6
119	04‐28	1408	6
120	04‐29	1418	10
121	04‐30	1429	11
122	05‐01	1434	5
123	05‐02	1439	5
124	05‐03	1439	0
125	05‐04	1439	0
126	05‐05	1445	6
127	05‐06	1448	3
128	05‐07	1449	1
129	05‐08	1450	1
130	05‐09	1454	4
131	05‐10	1457	3
132	05‐11	1460	3
133	05‐12	1461	1
134	05‐13	1463	2
135	05‐14	1464	1
136	05‐15	1465	1
137	05‐16	1465	0
138	05‐17	1466	1
139	05‐18	1466	0
140	05‐19	1467	1
141	05‐20	1468	0
142	05‐21	1468	0
143	05‐22	1468	0
144	05‐23	1468	0
145	05‐24	1468	0

Thanks to long standing efforts extending over many decades, a rich arsenal of theoretical methods of analyzing epidemics exists. Most of them trace back to the celebrated SIR model^{[ 11} , ¹² , ¹³ , ¹⁴ , ¹⁵ , ^{16 ]} wherein the time evolution of the numbers of individuals belonging to various epidemiological classes (susceptible (S), exposed (E), infected (I), recovered (R), etc.) is described by deterministic differential equations. Unfortunately, those approaches need many input parameters^{[ 21} , ^{22 ]} that can often be reliably estimated only after epidemics ended,^{[ 23 ]} which unavoidably compromises their ability of making predictions. As an aggravating circumstance, one should also add the difficulty not encountered in the vast majority of previous studies: how do the input parameters needed in model simulations change in time under so many restrictive measures (wearing face masks, social distancing, movement restrictions, isolation, and quarantine policies, etc.) unknown in the pre‐COVID‐19 era? Estimating model parameters from data fitting in a certain time interval to make predictions can easily run into a difficulty like that described in the first paragraph of Section 3.3.

As shown below, our approach obviates the aforementioned difficulty. We will adopt a logistic growth model in a form which is different from that often employed in the past^{[ 24} , ²⁵ , ²⁶ , ²⁷ , ^{28 ]} (see Sections 3.3 and 5 for technical details). This model is considerably simpler than SIR flavors, and already turned out to be an appealing framework in dealing with current COVID‐19 pandemic issues.^{[ 18} , ^{22 ]} Logistic functions (see Equation (2) below) were utilized for studying various problems.^{[ 29} , ³⁰ , ³¹ , ³² , ³³ , ^{34 ]} Studies on population dynamics of epidemic populations^{[ 35} , ³⁶ , ³⁷ , ³⁸ , ³⁹ , ⁴⁰ , ^{41 ]} were also frequently based on the logistic function.

Nevertheless, as anticipated, there is an important difference between the present approach (Section 3.3) and all the other approaches of which we are aware. The latter merely justify the logistic model by the fact that recorded disease numbers followed a nonlinear sigmoidal curve. Shortcomings of this standpoint are delineated in the beginning of Section 3.3. The strength of the approach presented in Section 3.3 is that we do not use any nonlinear fitting approach to analyze epidemiological data. Rather, we use raw epidemiological data to validate the logistic growth and straightforwardly extract the time dependent infection rate, which is the relevant model parameter for the specific case considered and makes it possible to compare how efficient different restrictive measures act to mitigate the COVID‐19 pandemic, and even to get insight significant for behavioral and social science.

2. Research Significance

Current (SIR, SEIR, SEIRS, etc.) modeling approaches to analyze epidemiological data are based on a series of hypotheses translated mathematically into a set of several (typically, three to five) of ordinary nonlinear differential equations. Neither these hypotheses made a priori nor the values of the pertaining (typically, three to five) model parameters are easy to validate; not even at epidemic's end, because their validation ultimately relies on nonlinear fitting models, for which notorious pitfalls are well documented in mathematical statistics.^{[ 42} , ⁴³ , ⁴⁴ , ⁴⁵ , ⁴⁶ , ⁴⁷ , ^{48 ]}

This state of affairs clearly justifies the need for a reliable methodology merely based on raw epidemiplogical data that obviates i) any a priori hypothesis difficult to control and ii) any nonlinear fitting model. Developing such a novel methodology and validating it against real epidemiological data of interest in the context of the ongoing COVID‐19 pandemic is the twofold goal of the present paper.

3. Results and Discussion

3.1. Standard Logistic Model

To briefly remind, standard logistical growth in time t of an infected population $n=n(t)$ follows an ordinary differential equation

$$\frac{\mathrm{d}}{\mathrm{d}t}n=\kappa n\left(1-\frac{n}{N}\right)$$ (1)

containing two constants (input model parameters): the (intrinsic) infection rate $\kappa (>0$) and the so called carrying capacity N. In a given environment, the latter has a fixed value to which the population saturates asymptotically (${\lim }_{t\to \infty }n(t)=N$) due to the Pauli‐type blocking factor^{[ 49} , ⁵⁰ , ^{51 ]} entering the parenthesis in the RHS of Equation (1). This can be seen by straightforwardly integrating Equation (1)

$$n(t)=\frac{N}{1+\left(\frac{N}{n_0}-1\right){\mathrm{e}}^{-\kappa \left(t-t_0\right)}}=\frac{N}{1+{\mathrm{e}}^{-\kappa \left(t-\tau \right)}}$$ (2)

with the initial condition ${n(t)|}_{t=t_0}=n_0$, which is often recast by using the half‐time $\tau \equiv t_0+\frac{1}{\kappa }\ln (\frac{N}{n_0}-1)$, $n{(t)}_{t=\tau }=N/2$. Noteworthily for the discussion that follows, Equation (2) assumes time‐independent model parameters.

In epidemiological language, $n(t)$ gives the cumulative number of cases at time t. Plotted as a function of t, the derivative with respect to time (throughout assumed a continuous variable) $\dot{n}(t)\equiv dn/dt$,

$$\dot{n}(t)=\frac{N\kappa }{4}{\mathrm{sech}}^2\frac{\kappa (t-\tau )}{2}$$ (3)

representing the “daily” number of new infections, is referred to as the epi(demiological) curve.

Figure  1a summarizes in graphical form the basic properties of logistic growth emerging the above equations. The importance of the result presented in Figure 1b will become apparent in Section 3.3.

Figure 1.

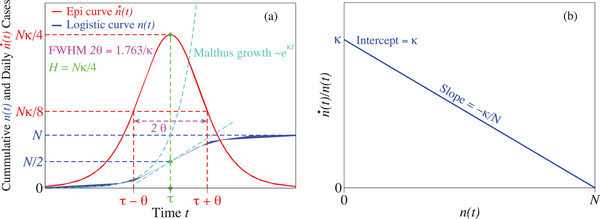
Panel (a) collects general properties of the standard logistic model. Panel (b) depicts a feature of the logistic growth whose importance is analyzed in Section 3.3.

3.2. Brief COVID‐19 Timeline in Slovenia

Before proceeding with the data analysis let us briefly summarize relevant public health measures, social distancing and movement restrictions imposed during the COVID‐19 crisis in Slovenia.^{[ 20} , ^{52 ]}

The first case of coronavirus was confirmed on March 4, 2020, imported via a returnee traveling from Morocco via Italy.^{[ 53 ]} On 10 March, the government banned all incoming flights from Italy, South Korea, Iran, and China; the land border with Italy was closed for all but freight transport; indoor public gatherings with more than 100 persons were prohibited, sporting and other events with more than 500 participants were allowed only without audience.

On 12 March, the nationwide COVID‐19 epidemic was proclaimed in Slovenia. On 14 March the Crisis Management Staff of the Republic of Slovenia established by the new government led by Prime Minister Janez Janša, confirmed on 13 March amidst the coronavirus outbreak, suspended unnecessary services. On 15 March all restaurants and bars as well as the Ljubljana Zoo were closed. On 16 March educational institutions, including kindergartens, primary and secondary schools were closed down, and public (bus, rail, air) transport was stopped. On 18 March public services (libraries, museums, cinemas, galleries were closed. On 19 March public gatherings were limited; gatherings in higher educational institutions and universities were prohibited; border checks (temperature, certificates of being healthy) were introduced. On 20 March de facto quarantine was established in Slovenia.

Significant easing occurred starting from 20 April. Border crossing gradually reopened (6, 22, and 24 April). Public transport resumed (27 April), some pupils returned to schools (27 April), all bars and restaurants as well as small hotels (up to 30 rooms) reopened for the first time since the shutdown was enforced in mid‐March. On 30 April, the general prohibition of movement was lifted.

Concluding that his country has the best epidemic situation in Europe, Prime Minister Janez Janška declared on 15 May the end of the COVID‐19 epidemic within Slovenian borders and allowed EU citizens free entrance.

3.3. Logistic Model with Time Dependent Parameters

The (blue) curve of Figure  2a depicting the evolution of total COVID‐19 infections in Slovenia (underlying data are collected in Table 1) has an appealing similarity to the logistic S‐shaped curve depicted in Figure 1. One would be therefore tempting to follow numerous previous authors,^{[ 35} , ³⁶ , ³⁷ , ³⁸ , ³⁹ , ⁴⁰ , ^{41 ]} who claimed that the logistic model applies merely because of the (apparently) good data fitting.

Figure 2.

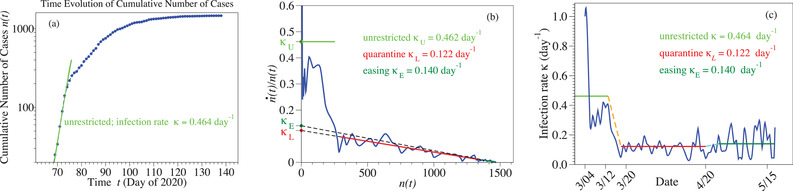
a) In the short initial phase of the epidemic, the number of infected individuals growths exponentially in time, which allows to estimate the initial value of the infection rate ($\kappa =0.464{\text{day}}^{-1}$). The curve of the logarithmic derivative $\mathrm{d}\ln n(t)/\mathrm{d}t=\dot{n}(t)/n(t)$ (blue line in panel (b)), which is merely obtained from epidemiological reports without any theoretical assumption, exhibits a linear trend that validates the description based on the logistic model. The carrying capacity $N(=1470$) is obtained from the intersection with the x‐axis. The curve of the time‐dependent infection rate $\kappa =\kappa (t)$ (blue line in panel (c)) deduced by means of Equation (5) suggests a piecewise linear approximation. Noteworthy, the infection rate ${\kappa }_E=0.140{\text{day}}^{-1}$ after lockdown easing is only slightly larger than the value ${\kappa }_L=0.122{\text{day}}^{-1}$ estimated for strict lockdown.

Still, to claim that a description based on a model like that of Equation (2) is valid, checking that the model parameters do not depend on the fitting range ($t_1,t_2$) is mandatory. For the specific case considered here, this means that fitting numbers of infected individuals in time range $t_1<t<t_2$ should yield, within inherent statistical errors, values of N and κ independent of t ₁ and t ₂. And, like in other known cases,^{[ 54} , ^{55 ]} this is just the stumbling block for the logistic function approach delineated in Section 3.1. In particular, the infection rate κ should not depend on how broad is the range ($t_1,t_2$); however, we checked by straightforward numerical calculations that it does.

Given the real epidemic timeline delineated in Section 3.2, the infection rate must indeed depend on time, $\kappa =\kappa (t)$. If the contrary was true, all containment measures would be useless. But when κ depends on t, Equations (2) and (3) no longer apply; they were deduced by integrating out Equation (1) assuming a time‐independent κ.

Fortunately, rather than merely inquiring how good the fitting curve based on Equation (2) is, we are able to directly check (and demonstrate, see below) the validity of a time‐dependent logistic model merely based on the real epidemiological reports. To this aim, we recast the differential Equation (1), which is the basic definition of the logistic growth (not to be confused with the logistic function of Equation (2)), as follows

$$\frac{\dot{n}}{n}=\kappa \left(1-\frac{n}{N}\right)$$ (4)

When put in this way, one can straightforwardly get insight in how to proceed. One should plot the ratio of the daily new cases to the cumulative number of cases (numerator and denominator in Equation (4), respectively) as a function of the cumulative number of cases and inspect whether the curve is linear or departs from linearity. Is the decrease linear (like anticipated in the ideal simulation presented in Figure 1b), we have the demonstration that the logistic growth model applies.

The curve constructed as described above using the COVID‐19 epidemic reports for Slovenia (Table 1, ref. [20]) is depicted in Figure 2a. As visible there, letting alone the strong fluctuations (possibly also due to the different methodology of reporting cases^{[ 20 ]}) in the initial stage, there is a transition from a high‐κ regime to a low‐κ regime. Definitely, the COVID‐19 restrictive measures worked. Interestingly (or, perhaps better, significantly), the low‐κ regime appears to set in on 17–18 March ($n=275-286$), suggesting a population's prudent reaction even prior the official lockdown enforcement (20 March). This is even more important given the fact that, in view of the finite incubation time (≈5 days), reported cases pertain to infections that occurred earlier.

An overall linear trend is clearly visible in the low‐κ regime of Figure 2a. Equation (4) makes it then possible to estimate the carrying capacity N from point where the (extrapolated) straight line intersects the x‐axis, while the intercept (or slope) can be used to deduce the infection rate κ.

Noteworthily, the low‐κ regime comprises two periods: lockdown and lockdown easing. To quantify the differences between these two periods, we used Equation (4) to analyze the epidemiological data from 18 March to 20 April ($78\le t\le 111$) and after 20 April ($t>111$) separately. We could not find any significant difference in N. With the value $N=1470$ (to be compared with the cumulative number of cases 1468 on 24 May) in hands we have computed via Equation (4) the time dependence of infection rate

$$\kappa (t)=\frac{\dot{n}(t)/n}{1-n(t)/N}$$ (5)

A slight difference could thus be obtained (${\kappa }_L\simeq 0.122{\text{day}}^{-1}$ vs ${\kappa }_E\simeq 0.140{\text{day}}^{-1}$), leading to the schematic representation depicted in Figure 2b.

We used the piecewise linear approximation of Figure 2b for the time dependent infection rate $\kappa \to \kappa (t)$ to numerically integrate the differential Equation (1).

Results of these numerical simulations for the total and daily number of cases are depicted by the green curves in Figure  3 along with the blue curves representing the epidemiological reports.

Figure 3.

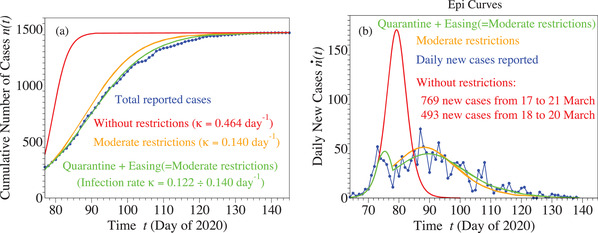
Curves for cumulative (panel (a)) and daily (panel (b)) number of cases based on epidemiological reports and simulated as described in the main text. Notice that the first peak around $t=73{\text{day}}^{-1}$ does not represent a spurious effect of fluctuations. It is a real effect reproduced by numerical simulation (green curve), which nicely demonstrates how restrictive measures enforced stopped the explosive (unrestricted) evolution depicted in red. The orange curves depict results that could have been achieved if, instead of severe lockdown, the much milder restrictions effective on 20 April were imposed starting 20 March.

In addition, we also show there simulations of how the Slovenian COVID‐19 epidemic would have evolved if:

• a)no restriction measure had been enforced. The (red) curves indicate that the result could have been grim: 769 new infections in 5 days or 493 new cases in 3 days. Again, restriction measures were definitely understandable;
• b)instead of severe lockdown, much more bearable restrictive measures as effective on 20 April would have been imposed on 20 March. The rather modest differences between the orange and green curves suggest that, unless the healthcare system capacity is overwhelmed, (justified) face masks and social distancing rules can be comparably efficient in mitigating the SARS‐CoV‐2 virus spread with draconian lockdown while obviating paralyzing economic and social life.

3.4. An Important Methodological Issue: Linear Regression versus Nonlinear Fitting Models

To better understand the important methodological advantage of the presently developed approach over other approaches utilized in the literature (mostly relying on SIR flavors), let us have a closer look at the intrinsic infection rate κ, which is the key parameter in the present description of the epidemic dynamics.

As depicted in Figure 2b, the present method allows to determine it by linear regression. All numerical data relevant for the present discussion (means, standard deviations, residuals, R ²‐, P‐, and T‐values) are collected in Figure  4 .

Figure 4.

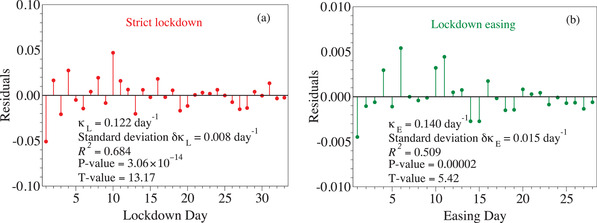
The values of the residuals uniformly scattered around zero and related statistical information for the a) strict lockdown and b) lockdown easing periods validate the linear regression analysis utilized in the present paper.

As usual in any statistical data analysis, let us start by focusing on the key quantity R ².^{[ 42} , ^{43 ]} The R ²‐values estimated by us (≈0.68 for strict lockdown and ≈0.51 for lockdown easing) would be sufficiently large to also validate the linear regression approach to physical and chemical systems, typically characterized by statistic fluctuations much weaker than the much less “deterministic” systems dealt with in pharmacology, medicine, and social sciences, where values $R^2\approx$0.1 are still “good” or at least acceptable. In the same vein, we should also mention both the small P‐values (≈3 × 10⁻¹⁴ for strict lockdown and ≈2 × 10⁻⁵), which are much smaller than the still “good” value of 0.05, and the large T‐values ($\approx +$13.2 for strict lockdown and ≈ +5.42 for lockdown easing), which again are substantially larger than the “good” value of +2.

Still, it is well known that a large R ² alone does not necessarily validate statistical data analysis. Unlike many commercial statistical software available in the market, MATHEMATICA 12.1.1 used for our statistical analysis allowed us to also interrogate this important issue. To this aim, we computed the residuals. The uniform, unbiased scattering around zero of their values visible in Figures 4a,b is a guarantee for the valid linear regression approach presently utilized. So, we arrived at an aspect worth to emphasize: linear regression is a self‐contained method whose validity can be assessed “internally”, without need of comparison with other methods, and this even more so if the validity of the latter cannot be unambiguously assessed (see below for more details).

Furthermore, the aforementioned results are based on our linear regression approach with intercept, the only method for which R ² has a sound mathematical foundation. R ² misses the adequate underlying mathematical basis not only for nonlinear fit models but even for linear fit without intercept. Pitfalls of using R ² for such cases are well documented in statistical mathematics.^{[ 44} , ⁴⁵ , ⁴⁶ , ^{47 ]} Notwithstanding this lack of foundation, quite unpleasantly, most commercial statistical software packages utilized in pharmacological and biochemical research run R ²‐calculations just for assessing the goodness‐of‐fit of nonlinear models.^{[ 48 ]} From this perspective, it is now easy to understand the challenge to uncritically applying SIR‐based models to quantify epidemic dynamics. As already noted in Section 2, these models generate nonlinear solutions, and the time evolution is obtained via numerical integration. To determine the phenomenological parameters (counterparts of κ, the single parameter governing dynamics in our approach) needed in SIR‐based simulations, fitting their nonlinear mathematical solution to epidemiological data is ubiquitous practice.

To end, the solution of the logistic model (Equation (2)) is also nonlinear, and attempting to directly using it for data fitting would run into the same formal difficulty (= questionable meaning of R ²) as SIR‐based treatments. The important methodological advantage of the approach proposed and applied in this paper is that the basic equation of the logistic model is amenable to a form (Equation (4)) that makes a linear regression analysis possible.

4. Additional Remarks

To avoid misunderstandings, we do not to end this paper before emphasizing that the foregoing analysis refers to the propagation of infection in a population strictly isolated from outside. While drawing attention on the advantage of (temporarily) suppressing intermingling in larger populations, our recent study^{[ 18 ]} (see Figure 4 there) also drew attention on the negative consequences on infection spread in cases where a smaller group can import infections from a larger group. Unfortunately, subsequent evolution of the Slovenian COVID‐19 epidemic also confirmed this prediction of ref. [18]. While new infection cases remained insignificant during the first month after calling official end to epidemic,^{[ 19 ]} with quarantine and travel restrictions to Slovenia lifted, the curve began to gradually rise (cf. Figure  5 ). Along with imported infections, cases of unknown origin may also be responsible for this post‐stabilization evolution which is beyond the scope of the present paper and deserves separate investigation.

Figure 5.

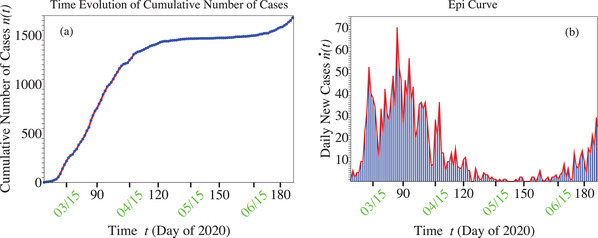
Curves for cumulative (panel (a)) and daily (panel (b)) number of cases^{[ 20} , ^{56 ]} depicting a gradual infection revival after travel restrictions to Slovenia were lifted.

5. Conclusion

We believe that especially the two results shown in Figure 2b — solely based on epidemiologically reported data without any extra (possibly speculative) theoretical supposition — are of extreme practical importance, as they could help setting adequate policies in the difficult period of the current COVID‐19 pandemic:

• i)Regarding the infection rate, it is worth emphasizing that, while substantially smaller than without imposing restrictions ($\kappa =0.464{\text{day}}^{-1}$), the value ${\kappa }_L=0.122{\text{day}}^{-1}$ during shutdown is only very slightly smaller than the value ${\kappa }_E=0.140{\text{day}}^{-1}$, after easing measures effective on 20 April. The important message conveyed by this finding is that the efficiency of hardly bearable unselective quarantine and remain‐isolated‐at‐home measures is very questionable. As one can intuitively expect, and what the present estimates do quantify, is that what really matters is not to keep everyone at home (as enforced, e.g., in Italy^{[ 57 ]}) but rather to impede virus transmission (as enforced, e.g., in Germany^{[ 58 ]}), for example, by wearing masks, adequate hygiene, and social distancing. Infection transmission does not strongly increase upon easing as long as face masks and social distancing prevent SARS‐CoV‐2 virus spreading. One should add at this point—an important fact that appears to be currently inadequately understood—that, along with a less pleasant effect of a short‐term slight increase of the daily new cases, a moderate increase in the infection rate also has a positive impact. It reduces epidemic duration; compare the right tail the green and orange curves in Figure 3b.
• ii)The fact that the carrying capacity N does not change upon lockdown easing is equally important. This is the maximum number of individuals that can be infected in a given environment. Rephrasing, the maximum number of infected individuals does not increase when the lockdown is released; the total carrying capacity of a given environment does not change.

From a methodological perspective, one should emphasize the important technical strength of the approach proposed above, which made it possible to arrive at the aforementioned conclusions. It is only the differential form, Equation (4), of logistic growth employed that obviates the need for any additional theoretical assumption and makes a linear regression analysis possible. Equally important from a pragmatic standpoint, the traditional approach of validating the logistic model by blind data fitting using its integral counterpart, Equation (2), does not work for COVID‐19 pandemic applications because the model parameter κ can and does depend on time. This time dependence $\kappa =\kappa (t)$ is essential to properly assess and make recommendations on the efficiency of the restriction measures to be enforced against SARS‐CoV‐2 virus spread.

And just because, in its differential form utilized here, the logistic model merely requires directly “measurable” epidemiological quantities (daily reports $\dot{n}(t)$ and cumulative number of cases $n(t)$, cf. Equation (4)) makes in the present unusual situation this model an alternative preferable to other more elaborate SIR‐based flavors. Even letting alone the formal objection related to the manner of statistically validating results obtained from nonlinear fitting (cf. Section 3.4), the latter models contain a series of phenomenological quantities that cannot be directly accessed “experimentally”. Governments confronted to taking decisions under unprecedented time pressure cannot await confirmation of often speculative theoretical hypotheses needed in data processing.

Before ending, let us also note that monitoring the $\kappa (t)$‐timeline allowed us to get insight also relevant for behavioral and social science; the self‐protection instinct of the population became manifest even before the official lockdown enforcement (cf. Section 3.3).

Conflict of Interest

The author declares no conflict of interest.

Data Availability Statement

The data that support the findings of this study are available in Wikipedia at https://urldefense.com/v3/__https://en.wikipedia.org/wiki/COVID-19_pandemic_in_Slovenia__;!!N11eV2iwtfs!6Z0DmVx_wMcLZyZGU-N-7WPuCV7c9BqeLAs-_13qcKs-ldpIkTbi7suaCCvVzisz7OYX$. These data were derived from the following resources available in the public domain: Slovenia's National Institute of Public Health “Dnevno spremljanje okužb s SARS‐CoV‐2 (COVID‐19) | https://urldefense.com/v3/__http://www.nijz.si__;!!N11eV2iwtfs!6Z0DmVx_wMcLZyZGU-N-7WPuCV7c9BqeLAs-_13qcKs-ldpIkTbi7suaCCvVzhj9gPBz$”. Retrieved 18 March 2020.