Abstract
Item response theory (IRT) has been recently adopted to successfully characterize the progression of Parkinson's disease using serial Unified Parkinson's Disease Rating Scale (UPDRS) measurements. However, it has yet to be applied in predicting the longitudinal changes of levodopa dose requirements in the real‐world setting. Here we use IRT to extract two latent variables that represent tremor and non‐tremor‐related symptoms from baseline assessments of UPDRS Part III scores. We show that relative magnitudes of the two latent variables are strong predictors of the progressive increase of levodopa equivalent dose (LED). Retrospectively collected item‐level UPDRS Part III scores and longitudinal records of prescribed medication doses of 128 patients with de novo PD extracted from the electronic medical records were used for model building. Supplementary analysis based on a subset of 36 patients with at least three serial assessments of UPDRS Part III scores suggested that the two latent variables progress at significantly different rates. A web application was developed to facilitate the use of our model in making individualized predictions of future LED and disease progression.
STUDY HIGHLIGHTS.
WHAT IS THE CURRENT KNOWLEDGE ON THE TOPIC?
The rate of disease progression and treatment responses differ substantially between rigidity and tremor‐dominant motor subtypes. Currently, little is known about how levodopa dose requirements change with disease progression in the real‐world setting.
WHAT QUESTION DID THIS STUDY ADDRESS?
By applying item response theory modeling framework, we investigated whether initial and future trajectories of levodopa equivalent dose (LED) could be predicted at the time of initial diagnosis using baseline UPDRS Part III measurements and patient covariates.
WHAT DOES THIS STUDY ADD TO OUR KNOWLEDGE?
The relative magnitudes of the two latent variables estimated from the baseline assessment of UPDRS Part III, in addition to patient age, provide crucial information to predict the adequate initial LED and its future trajectories in an individual patient.
HOW MIGHT THIS CHANGE CLINICAL PHARMACOLOGY OR TRANSLATIONAL SCIENCE?
Our study offers a novel method that allows effective prediction of future LED requirements based on a one‐time assessment of UDPRS Part III scores and patient covariates. The results of our work would be useful in determining the right LED based on a patient’s disease status and minimizing the need for empirical dose titrations.
INTRODUCTION
Parkinson's disease (PD) is widely assessed using the Unified Parkinson's Disease Rating Scale (UPDRS). 1 The UPDRS is composed of four parts with subscores of Part III assessing the motor symptoms. The sum of the item scores is generally used to track the progression of disease status. However, the implicit assumption of all items progressing at a more or less similar rate is being increasingly challenged. 2 To address the heterogeneous nature of the UPDRS score items, various methods have been used to identify distinct symptom clusters.
Item response theory (IRT) is a popular paradigm traditionally used in psychometrics to design, analyze, and score psychological tests and questionnaires. The core assumption is that each item score is a manifestation of the underlying latent ability or trait. Because certain items are easier to score than others, item difficulty is a core parameter of the IRT model. Items also differ in their discrimination, that is, some items more sensitively reflect the difference in the underlying ability than others.
Pharmaceutical and medical researchers are increasingly adopting IRT to analyze composite scores used for medical diagnosis, such as the Alzheimer's Disease Assessment Scale–Cognitive subscale 3 and others. 4 , 5 , 6 , 7 It has been successfully applied to modeling UPDRS progression in patients with PD as well. 8 , 9 , 10 When used in these contexts, latent ability or trait is often interpreted as latent disease severity. Item difficulty and discrimination then determine the probability of observing a particular symptom severity given the overall disease severity.
Levodopa remains the most effective drug for treating PD. 11 However, the progression of PD accompanies a concomitant increase in daily levodopa dose requirements. Because higher doses of levodopa lead to various motor complications 12 and a “wearing‐off” phenomenon, 13 accurately predicting the rate of such increase and elucidating the sources of its interindividual variability will help better optimize treatment and clinical trials targeting different stages of PD.
In practice, levodopa is only one of the possible treatment strategies. Alternative strategies include dopamine agonists, a monoamine oxidase type B inhibitor, and a catechol‐O methyl transferase inhibitor, calling for the need of a common scale to compare their effectiveness. The levodopa equivalent dose (LED) is defined as the dose yielding the same antiparkinsonian effects as 100 mg levodopa. Different formulae for calculating LEDs have been initially proposed that were subsequently standardized through meta‐analysis. 12 The most recent proposal of LED conversion factors includes opicapone and safinamide. 14
Here we apply IRT to baseline UPDRS Part III scores to extract two independent latent variables representative of tremor and nontremor symptoms. We then develop a model to predict the longitudinal trajectories of LED after treatment initiation under a nonlinear mixed effects framework. 15 We show how the rate of LED increase can be better predicted using these latent variables. As a supplementary analysis, we calculate the expected progression of the two latent variables over time based on a subset of patients with serial UPDRS Part III measurements. To facilitate the use of our model, we developed a web application that can be used to generate individualized predictions of LED and UPDRS Part III scores.
METHODS
Inclusion/exclusion criteria and study end points
This retrospective study included 128 patients with de novo PD who visited the outpatient clinic of the Neurology Department of Severance Hospital, Seoul, Korea, between March 2009 and October 2016. The institutional review board and hospital research ethics committee (Yonsei University Health system) approved this study and waived patient consent because of its retrospective character.
Information collected from the electronic medical record (EMR) included the following:
Basic demographic factors: age, sex
Medical history: hypertension, diabetes mellitus
Mini‐Mental Status Examination and Beck Depression Inventory assessed at the time of initial diagnosis
Item level UPDRS Part III scores assessed at the time of initial diagnosis and subsequent follow‐up visits
Dose amounts converted to LED prescribed during the observation period
Table 1 summarizes the collected data.
TABLE 1.
Descriptive statistics of collected data items
| Covariates | Mean (SD) or n (%) |
|---|---|
| Continuous | |
| Age, years | 61.07 (9.27) |
| Baseline UPDRS Part III score | 23.19 (10.56) |
| CCSIT | 7.10 (2.45) |
| MMSE | 26.48 (2.81) |
| Beck Depression Inventory | 14.81 (9.60) |
| Presence of diabetes mellitus | 18 (14.17%) |
| Presence of hypertension | 38 (29.92%) |
| Mean LED dose, mg | 567.87 (194.07) |
| Categorical | |
| Sex | |
| Male | 67 (52.76%) |
| Female | 60 (47.24%) |
| Number of UPDRS assessments | |
| 2 | 90 (70.87%) |
| 3 | 23 (18.11%) |
| 4 | 9 (7.09%) |
| 5 | 3 (2.36%) |
| >5 | 2 (1.57%) |
Abbreviations: CCSIT, Cross‐Cultural Smell Identification Test; LED, levodopa equivalent dose; MMSE, Mini‐Mental State Examination; UPDRS, Unified Parkinson's Disease Rating Scale.
The study end points were the subscores of the UPDRS Part III items and LEDs calculated from the prescription records, whose definitions are given in Table S1.
Modeling the increase of LED with time
To mimic the gradual increase in LED with disease progression, we fitted the following model to serial LED measurements:
| (1) |
where LED0 is the initial LED, LEDmax is the maximum LED allowed for prescription, and r is the rate of LED escalation.
An asymptotic exponential function (i.e., 1–e − rt) was used to describe the nonlinear increase of LED toward the maximum level. A simpler model assuming a linear increase of LED with time (i.e., rt) was not used because it allows boundless increases of LED.
Latent variables
Degeneration of dopamine neurons in the substantia nigra is known to be primarily responsible for the pathogenesis of PD. 16 The severity of bradykinesia and rigidity strongly correlates with the degree of dopamine depletion, but the severity of tremor does not show such correlation. 17 Based on this prior knowledge, we hypothesized that the variability associated with PD symptoms was caused by two independent dimensions, each of which represents tremor and nontremor symptoms.
To support this hypothesis, we performed principal components analysis and hierarchical clustering on the baseline UPDRS Part III items.
Item response models
Baseline model development
Let yj, j = 18,…, 31 denote the score of 14 items with j corresponding to the UPDRS Part III item, as shown in Table S1. The probability (P) of item score yj being greater than or equal to some integer n is expressed as follows:
| (2) |
| (3) |
where aj is the discrimination; bjn is the difficulty; j max = 20 for j = 20 and 22; j max = 8 for j = 21, 23–26 and j max = 4 otherwise; P(yj ≥0) = 1; and P(yj = j max) = P(yj ≥ j max).
Items associated with higher aj can better discriminate small differences in disease severity. Items with higher bjn require higher disease severity, S, to attain the same score. In this work, we did not estimate a separate difficulty parameter for each of the items because this would lead to a proliferation of parameters that far exceeds the data capacity. Instead, we introduced a threshold difficulty of achieving the minimum score of 1 and an incremental difficulty needed for each additional score. Denoting the threshold difficulty associated with item j as bj ,1 and incremental difficulty as bj ,inc, Equation ((1), (2)) can be modified to:
| (4) |
In accordance with the standard IRT modeling approach, we assumed that S follows a standard normal distribution. We then used baseline UPDRS Part III scores to fit the model. Hereafter, we use the notations S trem and S nontrem to represent the latent variables associated with tremor and nontremor symptom dimensions, respectively.
Covariate search
Covariate influence on the model parameter was tested using the following formulations:
| (5) |
| (6) |
| (7) |
Equation (5) imposes a linear relationship between the covariate and the parameter, whereas Equation (6) assumes a log‐linear relationship between the two. In both Equations (5) and (6), TVPar denotes the typical (or population) value of a parameter; COV and MED the covariate and median covariate, respectively; θ 1 the TVPar evaluated at the median covariate; and θ 2 the TVPar increment on the log scale for the unit increase of the covariate. Pari in Equation (7) denotes the parameter value for the ith individual and η i an interindividual random difference distributed as N(0, ω 2).
Covariate selection was based on a significant decline of residual sum of squares (p value <0.05).
Parameter estimation and model evaluation
NONMEM 7.4 18 , 19 was used for fitting the model and acquiring maximum likelihood estimates of the parameters.
Evaluation of the LED prediction model was done by generating goodness‐of‐fit plots of observed LED versus predicted LED and examining whether the scattered points fell around the line of unity. As a quantitative measure, we regressed the observed LED on the predicted LED and assessed the R 2 statistics.
To evaluate the IRT model performance, we generated a random number, u, from a uniform distribution and compared its value with P(yj ≥ n) (see Equation ((1), (2))) for n = 1, 2, 3, j max. If u > P(yj ≥ n) and u < P(yj ≥ n‐1), then = n, with denoting the simulated score. The distribution of was compared with that of the observed scores using mirror plots. 9 Scatterplots of observed versus median predicted proportions were additionally generated to help assist the overall goodness of fit.
To assess the correlation between residuals, we generated the expectations of the individual scores given the estimates of the latent variables, calculated as follows:
| (8) |
where yj, j = 18,..,31, denote the score of 14 items with j corresponding to the UPDRS Part III item, and j max = 20 for j = 20 and 22; j max = 8 for j = 21, 23–26; and j max = 4 otherwise. S = S trem for j = 20, 21 and S = S nontrem, otherwise. P(yj = i) was calculated based on Equation (3). We then generated a correlation matrix of the residuals, yj – E(yj).
Item characteristic curves were generated for each item and superimposed on the loess curves of the observed data.
Web application development
R/Shiny 20 was used to implement the developed model as an online web application. The UPDRS Part III scores may be either directly input using the application widgets or uploaded as a comma‐separated file. The estimated severities of tremor and nontremor symptoms and future LED trajectories are provided. The uncertainty associated with the estimated variables is also shown using profile likelihoods.
RESULTS
Modeling the longitudinal trajectories of LED
We fitted Equation (1) to the longitudinal measurements of LED under a nonlinear mixed effects modeling framework. The estimate of the rate of LED increase was 0.0025/month, suggesting that a typical patient would take about 92 years (= four half‐lives = 4 ) to reach the maximum LED of 2600 mg/day. The mean LED prescribed at the time of initial diagnosis was 440 mg/day. Although there was restricted interpatient variability associated with the initial LED, the rate of LED escalation showed significant differences among patients. The coefficients of variation (CV) of the initial LED and the rate of LED escalation were 32.35% and 74.17%, respectively. We hereafter denote the base model without covariates as Model 1.
Post hoc analysis using the empirical Bayesian estimates of the model parameters revealed a tendency of a higher initial LED in older age patients. On the other hand, the maximum LED seemed to negatively correlate with increasing age. The significance of these relationships was tested by incorporating age as covariates into both initial and maximum LEDs. Comparing the estimated −2‐log‐likelihoods, commonly referred to as the objective function values (OFVs), of the models with and without age as covariates returned a statistically significant difference (p = 1.78e‐07).
The following equations describe the relationship between age and LED0/ LEDmax:
| (9) |
| (10) |
We refer to the model incorporating age as covariates of LED0 and LEDmax as Model 2.
Principal components analysis and hierarchical clustering
Principal components analysis of baseline UPDRS Part III item scores showed that the first principal component, strongly correlated with nontremor items scores (all items except 20 and 21), explained 46.6% of total variability, whereas the second principal component, correlated with tremor items (items 20 and 21), explained 11.5% of the total variation (see Figure 1a).
FIGURE 1.
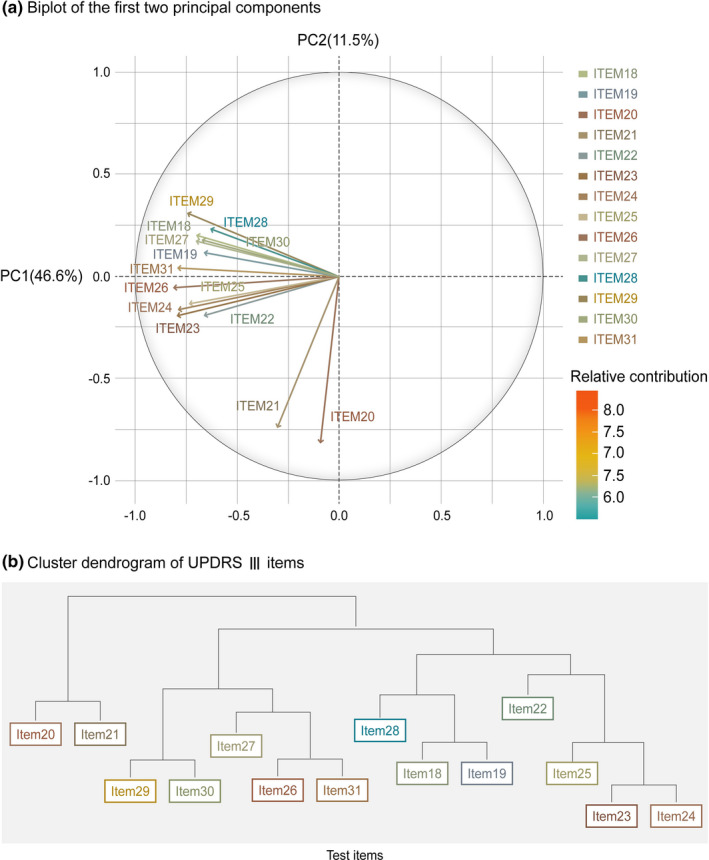
(a) Biplot generated by performing principal components analysis. (b) Dendrogram drawn by performing hierarchical clustering. PC1, principal component 1; PC2, principal component 2; UPDRS, Unified Parkinson's Disease Rating Scale
Hierarchical clustering returned a similar result where the highest branching point corresponded to the division of tremor (items 20/21) and nontremor symptoms (the rest of the items). Figure 1b depicts the dendrogram of the hierarchical clusters.
Item response model
IRT model was fitted using the pretreatment UPDRS Part III item scores from 126 patients, and the maximum likelihood estimates of the model parameters were acquired (Table 2a).
TABLE 2.
Maximum likelihood estimates of the models: (a) IRT model of baseline UPDRS Part III scores and (b) LED prediction model
| (a) IRT model of baseline UPDRS Part III scores | |||
|---|---|---|---|
| Item | Item‐related parameter (%RSE) | ||
| aj | bj ,1 | bj ,inc | |
| 18 | 1.14 (22.66) | −0.58 (37.09) | 2.95 (19.52) |
| 19 | 1.19 (19.57) | −1.07 (23.95) | 3.15 (16.44) |
| 20 | 1.43 (16.04) | −0.60 (32.89) | 0.65 (12.76) |
| 21 | 1.13 (24.22) | −1.17 (20.22) | 0.89 (22.27) |
| 22 | 1.26 (17.97) | −1.97 (13.94) | 0.50 (13.95) |
| 23 | 1.70 (18.12) | −1.76 (13.30) | 1.01 (13.45) |
| 24 | 2.06 (15.18) | −1.31 (12.5) | 1.05 (11.70) |
| 25 | 1.94 (14.58) | −1.84 (10.78) | 0.96 (10.39) |
| 26 | 2.27 (15.1) | −2.27 (15.10) | 0.84 (9.66) |
| 27 | 2.19 (16.18) | 0.32 (44.34) | 1.64 (16.67) |
| 28 | 1.10 (20.35) | −1.19 (27.67) | 2.16 (17.40) |
| 29 | 1.46 (21.96) | −1.42 (18.56) | 3.17 (15.55) |
| 30 | 1.24 (25.40) | 1.12 (23.8) | 1.75 (22.19) |
| 31 | 2.21 (18.20) | −1.86 (13.89) | 2.07 (12.26) |
| (b) LED prediction model | |
|---|---|
| Parameter | Estimate (%RSE) |
| Fixed effects | |
| LED0, mg | 438.4 (3.36) |
| LEDmax, mg | 2010 (14.49) |
| r, /month | 0.0038 (22.91) |
| Covariate coefficients | |
| Age on LED0, years | 8.31 (17.96) |
| Age on LEDmax, years | 45.8 (26.32) |
| S nontrem on LED0 | 51.84 (27.27) |
| S nontrem – S trem on r | 0.40 (23.14) |
| Random effects | |
| Interindividual variance of LED0, CV% | 25.69 (11.95) |
| Interindividual variance of r, CV% | 54.72 (13.75) |
| Residual variance, mg2 | 134.2 (8.07) |
Abbreviations: aj, discrimination for item j; bj ,inc, incremental difficulty for item j; bj ,1, threshold difficulty for item j; CV, coefficient of variation; IRT, item response theory; LED, levodopa equivalent dose; LED0, initial LED; LEDmax, maximum LED allowed for prescription; r, rate of LED escalation; RSE, relative standard error; S nontrem, severity of nontremor symptoms; S trem, severity of tremor symptoms; UPDRS, Unified Parkinson's Disease Rating Scale.
Among nontremor symptoms, items 25 (pronation‐supination movements of hands) and 31 (bradykinesia) were among those associated with the lowest threshold difficulty levels. On the other hand, item 30 (postural instability) showed the highest threshold difficulty, followed by item 27 (rising from chair). Among the tremor symptoms, item 21 (kinetic/postural tremor) was consistently associated with a lower threshold difficulty than item 20 (resting tremor).
Joint modeling of longitudinal LED trajectories and baseline UPDRS Part III
To assess how the two latent variables, S trem and S nontrem, are related to the rate of increase of LED (r) and the initial LED (LED0), we assessed the correlation of and , the estimated differences of individual r and LED0 from the population mean, respectively, with S trem, S nontrem, S nontrem – S trem, and the baseline total UPDRS III score. The results are shown in Table S2 and Figure S1. The Pearson correlation coefficient between and S nontrem – S trem was 0.38 (p = 9.77e‐06) and that between LED0 and S nontrem was 0.40 (p = 2.67e‐06).
Based on the previous results, we constructed a joint LED‐UPDRS model by incorporating S trem – S nontrem as a covariate of r and S nontrem as a covariate of LED0. The OFV drop relative to the model incorporating only age was statistically significant (p = 4.94e‐10). The following equations describe the incorporated covariate–parameter relationships:
| (11) |
| (12) |
The full covariate model incorporating both age and latent variables as covariates is defined as Model 3. The parameter estimates of Model 3 are shown in Table 2b.
Model evaluation
The observed time trajectories of LED are shown in Figure 2a. The goodness‐of‐fit plots of the Models 1, 2, and 3 are shown in Figure 2b–d. The R2 statistics of the three models were 0.24, 0.28, and 0.52, respectively.
FIGURE 2.
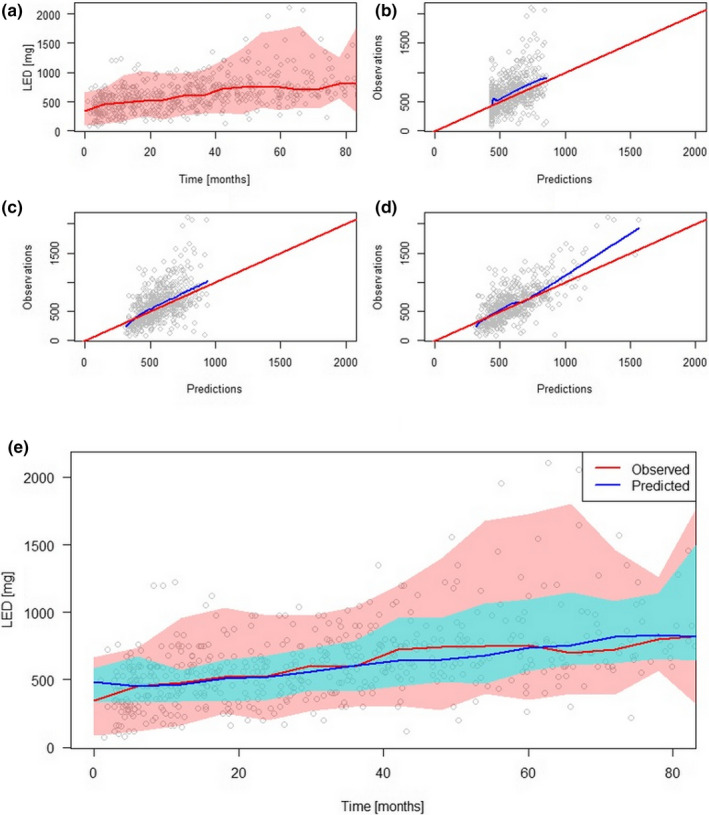
(a) Observed LED time trajectories. Red line represents the median, and the colored band represents the 2.5th to 97.5th percentiles. Observed versus predicted LEDs of (b) model without covariate (Model 1), (c) model incorporating age only (Model 2), and (d) model incorporating both age and latent variables (Model 3). (e) The median and 2.5th to 97.5th percentiles of observations (red) and predictions (blue) of Model 3 superimposed. LED, levodopa equivalent dose
Figure 3 shows the concordance of the observed and simulated scores using mirror plots. Most of the observed proportions fell within the 95% confidence intervals of the predicted proportions, with some items being better predicted than others. Item‐wise scatterplots of observed and predicted proportions (Figure S2) revealed a wider scatter around the line of unity for items 21, 22, and 26.
FIGURE 3.
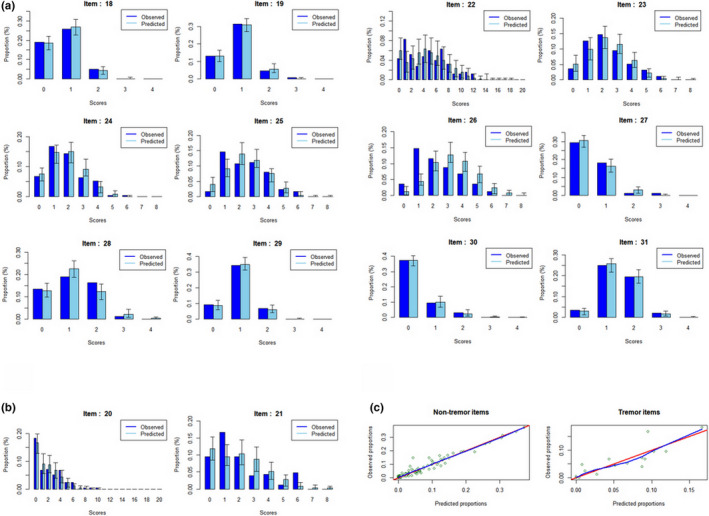
Item response theory model evaluations. Mirror plots of (a) nontremor and (b) tremor items illustrate the high concordance between the proportions of the observed and simulated scores. (c) Scatterplot showing the concordance of the observed and median predicted proportions of scores. The red line is the line of identity
Item characteristic curves of 14 UPDRS Part III items (Figure S3) showed an overall good fit with the observed trends, although tremor‐related items (items 20 and 21) showed a relatively poorer fit.
A Pearson correlation matrix (Figure S4), with correlation values ranging from −1 (indicated by blue) to +1 (indicated by red) revealed no distinct patterns, such as runs of positive or negative correlations or alternating positive and negative correlations.
The predicted trajectories of the latent variables
To understand the possible cause behind the significant effects S trem and S nontrem have on the rate of LED changes, we used a subset of 36 patients who underwent additional UPDRS assessments of at least three consecutive UPDRS Part III scores to generate the expected time trajectories of the latent variables. Figure 4 shows the results.
FIGURE 4.
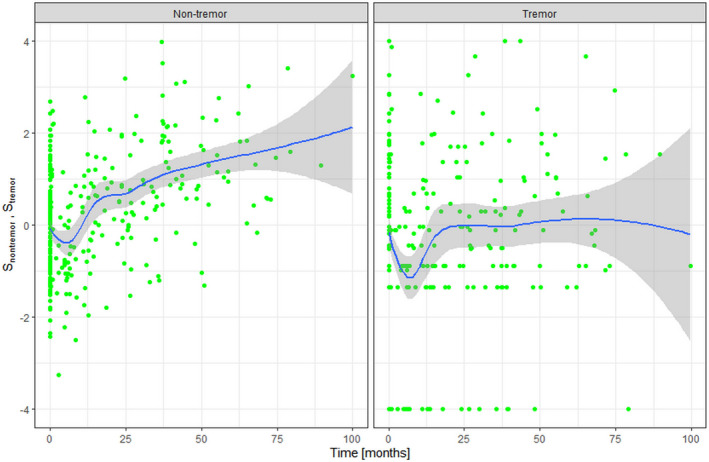
The predicted time trajectories of S nontrem (left) and S trem (right) based on the estimated item response theory model parameters of 36 patients with at least three serial Unified Parkinson's Disease Rating Scale Part III assessments. The rate of progression was significantly faster in S nontrem than S trem. S nontrem, severity of nontremor symptoms; S trem, severity of tremor symptoms
Visual inspection suggests that the progression of S nontrem is faster than S trem, whereas the initial treatment responses are similar between S nontrem and S trem. To check for statistical significance, we binned the time intervals to pretreatment, 0–1 year, 1–2 years, 2–3 years, 3–4 years, and 4 years and beyond. The difference of S nontrem between pretreatment (−0.097) and at 0–1 year (−0.137) was not statistically significant (p = 0.79). On the other hand, the difference of S trem at baseline (0.017) and 0–1 year (−0.159) showed a significant difference (p = 0.017). The difference of S nontrem between pretreatment (−0.097) and at 4 years and beyond (1.197) was highly significant (p = 3.22e‐05), whereas that of S trem was not (0.017 vs. 0.068; p = 0.73).
The previous results suggest that the initial treatment response is greater for S trem than S nontrem, whereas the rate of progression is faster in S nontrem than S trem.
Simulation based on the web application
We developed a web application to facilitate the implementation of our model, which is hosted at https://dongy.shinyapps.io/parkin. The application takes individual UPDRS Part III scores as inputs and outputs the estimates of S nontrem and S trem, their uncertainty, and the longitudinal predictions of LED. The scores can be directly supplied through application widgets or a file in .csv format. For the latter, the file should abide by a specific format to be properly parsed by the application. When a file consisting of serial UPDRS Part III assessments is uploaded, the application returns time series plots showing the changes of estimated S nontrem and S trem with time.
For illustrative purposes, three clinical scenarios were simulated using our web application. Figure S5 shows the setup details of scenarios 1 and 3.
Scenario 1: a 60‐year‐old patient with a UPDRS Part III tremor subscore of 14 and a nontremor subscore of 18 with a total score of 32 (tremor severity population percentile 83.66%, nontremor severity population percentile 39.29%)
Scenario 2: an 80‐year‐old patient with the same UPDRS Part III item scores as Scenario 1
Scenario 3: a 60‐year‐old patient with a UPDRS Part III tremor subscore of 3 and a nontremor subscore of 29 with a total score of 32 (tremor severity population percentile 49.31%, nontremor severity population percentile 69.03%)
Total UPDRS Part III scores of all patients were identical (i.e., 32) at baseline assessment. However, the predicted LED requirements of Scenarios 1, 2, and 3 were 424, 590, and 464 mg at baseline, and 807, 712, and 1127 mg, respectively, at 10 years after diagnosis (Figure S6).
A comparison of Scenarios 1 and 2 shows that given the same UPDRS Part III profiles, older age at initial diagnosis is associated with a higher initial LED but a slower rate of increase. Although Scenarios 1 and 3 have identical total UPDRS Part III scores, the predicted LED of Scenario 3 at 10 years after diagnosis is nearly 50% greater than that of Scenario 1.
DISCUSSION
We developed a model that extracts two latent variables that represent tremor and non‐tremor‐related symptoms from baseline UPDRS Part III measurements to predict the changes of LED requirements with disease progression. Our results suggested that the rate of LED increase is significantly faster in patients with dominant rigidity and postural instability/gait disorder symptoms.
To our knowledge, this is the first modeling study that attempts to predict the changes of LED with disease progression using real‐world data. Most previous studies concentrated on predicting disease progression based on changes of UPDRS. 15 UPDRS assessment, however, is time‐consuming and more suited to track disease progression in prospective clinical trials than in the clinician's office. LED, on the other hand, is easier to acquire. 14
Levodopa is commonly initiated at doses 50 mg four times daily or 100 mg three times daily, depending on the presence of motor fluctuations and the risk of developing dyskinesia. In elderly patients aged older than 65 years, levodopa is often used as first‐line therapy. In younger patients, dopamine agonists are predominantly used and levodopa is initiated only when symptom control becomes insufficient, except in cases where patients show severe adverse effects with dopamine agonists.
In our data, the initial LED was indeed positively correlated with age. Moreover, initial LED showed significant positive associations with both total baseline UPDRS Part III and the estimated severity of nontremor symptoms, with the latter showing a higher significance level. The finding of nontremor severity being a better predictor of estimated initial LED than total UPDRS Part III score suggests that IRT offers an improved method of dose selection. Based on our results, tremor symptoms play a minor role in determining the LED in the initial stages of treatment.
The rate of LED increase was faster in patients with dominant rigidity/bradykinesia, which is likely attributed to their faster disease progression as seen in Figure 4. However, the cause of differential progression rates between the two latent variables is uncertain. One possibility is that it is attributed to independent pathophysiological processes. Nevertheless, simulations based on our model suggest that the future LED trajectories diverge between patients with dominant rigidity/bradykinesia and patients with dominant tremor given the same baseline total UPDRS Part III score. This highlights the importance of analyzing UPDRS at the item level and supports the practical utility of the IRT framework in distinguishing patients showing similar total UPDRS Part III scores.
The core assumption of our IRT model was that two latent variables are sufficient to explain the totality of motor symptoms. We support this assumption based on both prior evidence and our data. First, a classification scheme of subtyping patients into either tremor dominant and postural instability and gait disorder dominant subtypes is widely in use and has been validated across a number of studies. 21 Second, analyses based on our data using principal components analysis showed that each of the first two principal components were highly correlated with nontremor and tremor items, respectively, and hierarchical clustering of item scores generated the highest level division between nontremor and tremor items.
Our method is in many ways superior to categorizing patients into different motor subtypes. The greatest advantage is in resolving the problem of dealing with patients in the gray area. Although a separate category of “mixed” type has traditionally been used to define these patients, drawing clear demarcations between different subtypes is difficult. IRT does not categorize patients but instead returns independent numbers to represent the severity of each symptom dimension.
From a clinical standpoint, the discrimination of an item reflects its sensitivity to changes in the underlying disease process, and difficulty parameter the relative order of its first appearance. Although discriminations of all items were roughly similar, a greater variability was observed in the threshold difficulties. Our results suggest that disability of pronation‐supination movements of hands (item 25) and bradykinesia (item 31) appear relatively early during the disease time course, whereas postural instability (item 30) and difficulty rising from chair (item 27) constitute hallmarks of late‐stage PD. Among tremor, kinetic/postural tremor (item 21) would appear before resting tremor (item 20). These interpretations fit well to that known from clinical experience.
IRT is a complex modeling framework, which can undermine its widespread use despite its usefulness. Our web application hides the technical details under the hood and only requires the users to input the UPDRS Part III measurements. The application then returns the recommended initial LED and its predicted increase with time. Furthermore, multiple assessments of UPDRS Part III scores can be fed into the application to acquire the time series plots of the estimated nontremor and tremor severities. We believe that these functionalities would greatly reduce the barrier for the practicing physicians and encourage them to actually use our model.
The greatest limitation of our study is in the limited scope of disease severity collected from a relatively small number of patients. The item scores rarely reached their maximum values. This aspect should be taken into account when trying to extrapolate our model to a larger population consisting of the full range of possible disease states. The limited number of patients with repeated UPDRS Part III measurements probably also led to an insufficient power to detect correlations between LED and UPDRS Part III changes. Finally, although nonmotor symptoms constitute a critical portion of PD manifestation, our work did not analyze them.
Notwithstanding these limitations, our study results were mostly concordant with that known from previous reports. The severity of nontremor symptoms reached approximately 1 standard deviation of the baseline severity by 50 months (see Figure 4), which is surprisingly close to that reported in a prior IRT‐based study. 8 The notion of negligible progression of tremor symptoms and the similar progression rates among the bradykinesia, rigidity, and gait and balance subscores are also supported by the literature. 22 The relative order of threshold difficulties, when interpreted as coinciding with the relative order of symptom appearance with disease progression, also agreed with clinical experience and prior research. 23
In conclusion, our study offers a novel method that allows effective prediction of future LED requirements based on a one‐time assessment of UDPRS part III scores. The web application that implements the developed model would significantly add to the practical value of our work. The idea of using LED changes acquired from real‐world data as an alternative disease progression marker, if validated through further studies, would open new ways to use the vast amount of observational data from electronic medical records. This would help acquire real‐world evidence of disease progression and treatment effectiveness under a variety of clinical settings.
CONFLICT OF INTEREST
All authors declared no competing interests for this work.
AUTHOR CONTRIBUTIONS
D.C., P.H.L., and K.P. wrote the manuscript. D.C., S.J.C., P.H.L., and K.P. designed the research. D.C., P.H.L., and K.P. performed the research. D.C. and K.P. analyzed the data.
Supporting information
Fig S1
Fig S2
Fig S3
Fig S4
Fig S5
Fig S6
Table S1
Table S2
Supplementary Material
Phil Hyu Lee and Kyungsoo Park contributed equally to this work.
Funding information
This study was supported by a new faculty grant of Yonsei University, Medical College, Seoul, Korea (6‐2019‐0073 to D.C.).
DATA AVAILABILITY STATEMENT
The data that support the findings of this study are available upon request from the corresponding authors. The data are not publicly available due to hospital policy regarding data security.
REFERENCES
- 1. Movement Disorder Society Task Force on Rating Scales for Parkinson's D . The unified parkinson's disease rating scale (UPDRS): status and recommendations. Mov Disord. 2003;18:738‐750. [DOI] [PubMed] [Google Scholar]
- 2. Vu TC, Nutt JG, Holford NH. Progression of motor and nonmotor features of Parkinson's disease and their response to treatment. Br J Clin Pharmacol. 2012;74:267‐283. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Ueckert S, Plan EL, Ito K, Karlsson MO, Corrigan B, Hooker AC. Improved utilization of ADAS‐cog assessment data through item response theory based pharmacometric modeling. Pharm Res. 2014;31:2152‐2165. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Vaccarino AL, Anderson K, Borowsky B, et al. An item response analysis of the motor and behavioral subscales of the unified Huntington's disease rating scale in huntington disease gene expansion carriers. Mov Disord. 2011;26:877‐884. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Toups M, Carmody T, Trivedi MH, Rush AJ, Hedayati SS. Performance of depression rating scales in patients with chronic kidney disease: an item response theory‐based analysis. Gen Hosp Psychiatry. 2016;42:60‐66. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Mielenz TJ, Callahan LF, Edwards MC. Item response theory analysis of centers for disease control and prevention health‐related quality of Life (CDC HRQOL) items in adults with arthritis. Health Qual Life Outcomes. 2016;14:43. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Chae D, Park K. An item response theory based integrated model of headache, nausea, photophobia, and phonophobia in migraine patients. J Pharmacokinet Pharmacodyn. 2018;45:721‐731. [DOI] [PubMed] [Google Scholar]
- 8. Gottipati G, Karlsson MO, Plan EL. Modeling a composite score in Parkinson's disease using item response theory. AAPS J. 2017;19:837‐845. [DOI] [PubMed] [Google Scholar]
- 9. Buatois S, Retout S, Frey N, Ueckert S. Item response theory as an efficient tool to describe a heterogeneous clinical rating scale in de novo idiopathic Parkinson's Disease patients. Pharm Res. 2017;34:2109‐2118. [DOI] [PubMed] [Google Scholar]
- 10. Gottipati G, Berges AC, Yang S, Chen C, Karlsson MO, Plan EL. Item response model adaptation for analyzing data from different versions of Parkinson's Disease rating scales. Pharm Res. 2019;36:135. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Nyholm D, Karlsson E, Lundberg M, Askmark H. Large differences in levodopa dose requirement in Parkinson's disease: men use higher doses than women. Eur J Neurol. 2010;17:260‐266. [DOI] [PubMed] [Google Scholar]
- 12. Tomlinson CL, Stowe R, Patel S, Rick C, Gray R, Clarke CE. Systematic review of levodopa dose equivalency reporting in Parkinson's disease. Mov Disord. 2010;25:2649‐2653. [DOI] [PubMed] [Google Scholar]
- 13. Bhidayasiri R, Hattori N, Jeon B, et al. Asian perspectives on the recognition and management of levodopa ‘wearing‐off’ in Parkinson's disease. Expert Rev Neurother. 2015;15:1285‐1297. [DOI] [PubMed] [Google Scholar]
- 14. Schade S, Mollenhauer B, Trenkwalder C. Levodopa equivalent dose conversion factors: An updated proposal including opicapone and safinamide. Mov Disord Clin Pract. 2020;7:343‐345. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Venuto CS, Potter NB, Dorsey ER, Kieburtz K. A review of disease progression models of Parkinson's disease and applications in clinical trials. Movement Disord. 2016;31:947‐956. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Magrinelli F, Picelli A, Tocco P, et al. Pathophysiology of motor dysfunction in Parkinson's disease as the rationale for drug treatment and rehabilitation. Parkinsons Dis. 2016;2016:9832839. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Antonini A, Vontobel P, Psylla M, et al. Complementary positron emission tomographic studies of the striatal dopaminergic system in Parkinson's disease. Arch Neurol. 1995;52:1183‐1190. [DOI] [PubMed] [Google Scholar]
- 18. Bauer RJ. NONMEM tutorial part I: Description of commands and options, with simple examples of population analysis. CPT Pharma Sys Pharmacol. 2019;8(8):525‐537. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Bauer RJ. NONMEM tutorial part II: Estimation methods and advanced examples. CPT Pharmacometrics Syst Pharmacol. 2019;8(8):538‐556. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Yu Y, Ouyang Y, Yao W. shinyCircos: an R/Shiny application for interactive creation of Circos plot. Bioinformatics. 2018;34:1229‐1231. [DOI] [PubMed] [Google Scholar]
- 21. Nutt JG. Motor subtype in Parkinson's disease: Different disorders or different stages of disease? Mov Disord. 2016;31:957‐961. [DOI] [PubMed] [Google Scholar]
- 22. Louis ED, Tang MX, Cote L, Alfaro B, Mejia H, Marder K. Progression of parkinsonian signs in Parkinson disease. Arch Neurol. 1999;56:334‐337. [DOI] [PubMed] [Google Scholar]
- 23. Jankovic J. Parkinson's disease: clinical features and diagnosis. J Neurol Neurosurg Psychiatry. 2008;79:368‐376. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Fig S1
Fig S2
Fig S3
Fig S4
Fig S5
Fig S6
Table S1
Table S2
Supplementary Material
Data Availability Statement
The data that support the findings of this study are available upon request from the corresponding authors. The data are not publicly available due to hospital policy regarding data security.


