Abstract
Objectives
A hospital-related cluster of 22 cases of coronavirus disease 2019 (COVID-19) occurred in Taiwan in January–February 2021. Rigorous control measures were introduced and could only be relaxed once the outbreak was declared over. Each day after the apparent outbreak end, we estimated the risk of future cases occurring in order to inform decision-making.
Methods
Probabilistic transmission networks were reconstructed, and transmission parameters (the reproduction number R and overdispersion parameter k) were estimated. The reporting delay during the outbreak was estimated (Scenario 1). In addition, a counterfactual scenario with less effective interventions characterized by a longer reporting delay was considered (Scenario 2). Each day, the risk of future cases was estimated under both scenarios.
Results
The values of R and k were estimated to be 1.30 ((95% credible interval (CI) 0.57–3.80) and 0.38 (95% CI 0.12–1.20), respectively. The mean reporting delays considered were 2.5 days (Scenario 1) and 7.8 days (Scenario 2). Following the final case, ttthe inferred probability of future cases occurring declined more quickly in Scenario 1 than Scenario 2.
Conclusions
Rigorous control measures allowed the outbreak to be declared over quickly following outbreak containment. This highlights the need for effective interventions, not only to reduce cases during outbreaks but also to allow outbreaks to be declared over with confidence.
Keywords: COVID-19, SARS-CoV-2, Epidemic modelling, End-of-outbreak declaration
Introduction
As of 9 March 2021, there have been fewer than 1,000 confirmed cases of severe acute respiratory syndrome coronavirus-2 (SARS-CoV-2) infection in Taiwan, of which only 77 were locally acquired (Taiwan Centres for Disease Control, 2021). Following stringent border control measures, proactive contact tracing and case isolation, Taiwan's largest individual outbreak to date has been a hospital-related outbreak that involved 22 cases and occurred in January–February 2021. Despite successful containment of that outbreak, some aspects were concerning. First, the custom of wearing face masks, especially in hospital, was unable to prevent transmission completely in several instances (Central Epidemic Command Centre, 2021b). Second, the source of infection for one of the infected inpatients was undetermined: that individual attended a hospital ward which was not included in a so-called ‘red zone’, and he did not interact with other confirmed cases (Central Epidemic Command Centre, 2021a). Third, having implemented control measures at the time of the first suspected cases, additional cases continued to be seen for severalseveral weeks afterwards. This led to further investigations into possible causes of the outbreak, and required an end-of-outbreak determination (i.e. assessment of the probability that the outbreak was over – or, conversely, the probability that additional reported cases would occur in future) after the last case was reported (Nishiura et al., 2016; Parag et al., 2020; Djaafara et al., 2021).
This article provides a descriptive analysis of the outbreak, and quantifies viral transmissibility during the outbreak. In addition, estimates of the probability that additional reported cases will occur in future are presented, as obtained in real-time after the final case had been observed. As the time since the last observed case increases, the certainty that the outbreak is over increases. Two distinct scenarios have been considered when estimating the probability of future cases. Scenario 1 describes containment of the outbreak under intensified contact tracing, as was the situation during this outbreak. Under Scenario 1, proactive testing and quarantine of all close contacts of confirmed cases (and suspected cases) after epidemiological investigations is considered, so that cases are found quickly, and transmission beyond individuals that attended hospital and their contacts is unlikely. Scenario 2 describes a situation with reduced contact tracing and testing, increasing the risk of transmission into the wider community, with some chains of transmission potentially remaining untraced. In this analysis, these scenarios are assessed by implementing two different reporting delays, which represent the time periods from symptom onset to case confirmation. The reporting delay under Scenario 1 is shorter than that under Scenario 2 due to efficient case identification, which is followed by isolation (Tian et al., 2021).
Materials and methods
Outbreak investigation
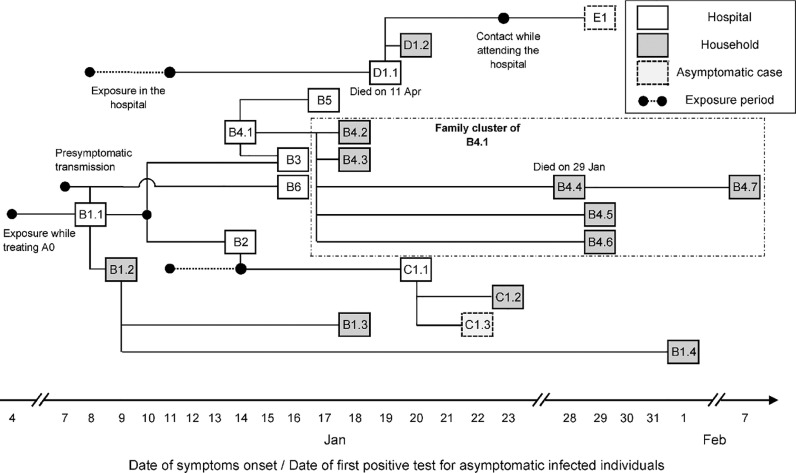
A cluster of locally acquired cases of SARS-CoV-2 infection occurred in Taiwan in January–February 2021. This cluster originated in a hospital and involved 22 reported cases (Figure 1 ). The first two cases to be detected, a doctor (B1.1) and his household and work contact (B1.2), were suspected positive and tested on 11 January 2021. They were confirmed positive the following day. The authorities acted proactively by testing their close contacts on 11 January 2021, ordering a two-week home isolation of all close contacts, restricting hospital admissions, and arranging for a second round of health inspections three days later. Regular press conferences raised public awareness and ensured that the local community remained vigilant throughout the outbreak.
Figure 1.
Timeline of exposure and possible connections between reported cases. Connections shown here were determined either by identifying the most probable infector via epidemiological investigation, or by the earliest time of symptom onset among all close contacts if the most likely pair could not be determined (such as in family clusters of B1.2, C1.1 and B4.1).
The index case (A0) was a Taiwanese female in her 60s who travelled to the USA in October 2020 and returned to Taiwan on 27 December 2020. Having tested negative for SARS-CoV-2 infection in the three days before her flight, she developed initial symptoms on 29 December 2020 while in quarantine. She was later hospitalized and placed on a ventilator. During her treatment, a doctor (B1.1) was exposed to the virus on 4 January 2021, and experienced initial mild symptoms on 8 January 2021. The virus further spread to his household contact (B1.2) and other medical personnel, most likely due to work-related interactions between B1.1, B2 and B3 on 10 January 2021. The chains of transmission that followed included three other work-related infections (B4–6), three infections of attending inpatients (C1.1, D1.1, E1), and transmission in their households. Household transmission accounted for 12 cases (57%), with the family cluster of B4.1 involving all seven family members including one death. In total, two deaths (B4.4, D1.1) occurred.
All cases were epidemiologically linked through contact tracing, except for an inpatient (D1.1) who had no record of contact with any known infected individual in the hospital. This suggests that his infection was likely due to either indirect transmission (e.g. via a contaminated surface from a known source) or from an undetected case. The same route of transmission could have occurred for infection of B2 by B1.1, as both individuals were wearing masks during their interaction (one of which was a highly effective surgical N95 mask).
One individual (C1.2) was pre-symptomatic when testing positive, with onset of symptoms two days later. Two infected individuals remained asymptomatic throughout infection. At least one pre-symptomatic transmission occurred: a foreign nurse (B6) was exposed to the virus on 7 January 2021 while interacting with B1.1, one day before B1.1 developed symptoms. Unlike the family cluster of B4.1, where the secondary attack rate was 100%, the employer of B6 and all of B6's family members tested negative despite their close contact with B6. Genetic sequencing of a subset of cases from the outbreak identified variant Epsilon (also known as Cal.20C, lineage B.1.429) which originated in Southern California in 2020 (GISAID, 2021; McCallum et al., 2021, Zhang et al., 2021).
Reconstruction of the transmission network and estimation of the transmission potential
The transmission potential of this novel variant was characterized by analysing the offspring distribution, which describes the number of secondary infections per primary case. A negative-binomial distribution was fitted with mean reproduction number and overdispersion parameter k (Riou and Althaus, 2020). The value of describes the average number of secondary infections per primary case, while measures variability in the number of secondary infections between primary cases and quantifies the potential for superspreading (which, for a fixed value of R, is more likely to occur for lower values of ).
First, the Wallinga–Teunis (WT) method (Wallinga and Teunis, 2004) was applied to resolve the uncertainty in transmission patterns in family clusters by incorporating the serial interval distribution (Nishiura et al., 2020). The serial interval distribution assumed here is similar to other reported estimates (Biggerstaff et al., 2020; Hart et al., 2021). The pairings of infectees to their infectors were known for 12 secondary cases as a result of epidemiological investigations: , , , , and . The infection of case D1.1, an inpatient who attended the hospital in the first week of the outbreak, was assigned to case B1.1 given the timing (B1.1 was the only symptomatic case at that time). All other potential infectors (B2, B3, B4.1, B5 and B6) developed initial symptoms more than two days after the visit of D1.1 to the hospital (Figure 1). The infectors of the other nine cases (excluding the index case A0) were uncertain, with the following possibilities: , , , , , , , , and . Almost all of these transmissions (except for infection of case B5) may have been due to household transmission, so exact determination of who infected whom is impossible. The infector of case B5 could not be identified precisely as that transmission likely occurred in the workplace, where case B5 contacted multiple possible infectors. Under the WT method, for each of those nine infectees , an infector was selected from their lists of potential infectors based on probabilistic sampling. The likelihood that case (with symptom onset at time ) infected case , relative to the likelihood that any other potential infector infected case , was given by:
| (1) |
where represents the serial interval distribution modelled by a Weibull distribution with mean days (i.e. ) and shape parameter (Nishiura et al., 2020).
Second, the number of transmissions from each primary case in any probabilistic realization of the transmission network was determined. A negative binomial probability mass function was fitted to each resulting distribution, with mean and overdispersion parameter k.
Generation-based reproduction number
The reconstructed transmission networks enabled a probabilistic assignment of generation membership to be made to cases, and derivation of the generation-based reproduction number, (Akhmetzhanov et al., 2018; Worden et al., 2020). Given a particular network, each node (i.e. each case) was assigned to a generation , where the value of represents the number of links from that node to the index case A0. The node A0 was placed at the root of the network and assigned to generation zero. To derive the generation-based reproduction number, , the number of transmissions generated by cases in generation was divided by the number of cases in that generation. Hence, the reproduction number for the final generation, (so that other generations ), was exactly zero. The reproduction number for generation zero was equal to one. As the transmission networks were generated probabilistically, each was also characterized by a posterior distribution.
Estimation of the reporting delay
Fitting the reporting delay distribution with a mixture of three shifted distributions (gamma, Weibull and lognormal), the mean reporting delay for this outbreak was estimated (under the intensive measures that were in place during this outbreak – Scenario 1). In addition, a counterfactual scenario (Scenario 2) in which public health measures are less rigorous was considered. Rather than attempting to model the wide range of possible effects of less rigorous contact tracing and case isolation, the reporting delay in Scenario 2 was simply set to be longer than in Scenario 1. In Scenario 2, the mean reporting delay was set by estimating its value using data for all local cases reported in Taiwan since the beginning of 2020.
Specifically, for each scenario, data describing dates of symptom onset and confirmation for all symptomatic cases were extracted. The number of extracted cases was for Scenario 1 and for Scenario 2. The likelihood was given by a mixture of three component likelihoods with respective weights (), and potential right truncation at the time of the latest update was accounted for:
| (2) |
| (3) |
where is the time difference between confirmation and symptom onset for case . As the extracted data contained only the dates of symptom onset and confirmation , it was assumed that the priors for the precise times of symptom onset and confirmation were uniformly distributed within those days: and . Some observed values of were negative, so the reporting delay distributions were modelled by shifted versions of the gamma, Weibull or lognormal distributions (). The function denoted the probability density function (PDF):
| (4) |
where is the shift of distribution (), and and are the mean and standard deviation of distribution . To improve the convergence of the mixture model, it was assumed that parameters were common to the three distributions, as has been proposed elsewhere for Bayesian model averaging (Keller and Kamary, 2018; Akhmetzhanov, 2021). The notation was used to denote the cumulative distribution function (CDF) of the reporting delay. The truncation time was set to correspond to the beginning of 12 April 2021.
The relative weightings of the different component distributions, , were defined using the formula:
| (5) |
End-of-outbreak probability
On a given day, a previously described method devised by Linton et al. (2021) was used to estimate whether or not the outbreak was over. First, the epidemic curve up to the time of report with dates of symptom onset for all symptomatic cases was considered. The probability that one or more new cases will be reported after day is given by the following expression:
| (6) |
In this expression, is the number of cases reported on day , and is the probability of transmissions occurring from a primary case , which follows a negative binomial distribution with mean and overdispersion parameter as described above. The function represents the probability that an individual infected by case reports infection by time . This function is therefore the CDF of a convolution of the serial interval and the reporting delay. For each potential infectee, the reporting delay was selected at random from the three distributions described above according to the probabilities (see Equation (5)).
Technical details
R 4.1.0 (R Development Core Team, 2021) and CmdStan 2.27.0 (Stan Development Team, 2021) were used to conduct the main analysis, and Python 3.6 was used for statistical inference of the generation-based reproduction number. Reproducible code for this study is available on GitHub at https://github.com/aakhmetz/Taiwan-COVID19-end-of-outbreak-JanFeb2021. All derived estimates of model parameters and the results of sensitivity analyses can be found in Tables S1–S2 and Figures S1–S3 (see online supplementary material).
Results
The statistical inference of the offspring distribution identified the median estimate of to be 1.30 (95% credible interval (CI) 0.57–3.80) and the median estimate of to be 0.38 (95% CI 0.12–1.20). The generation-based reproduction number (i.e. the expected number of transmissions arising from an infector in a specific generation of the transmission chain, where patient A0 represents generation zero) declined throughout the outbreak from generation one onwards. In generation one, the generation-based reproduction number was estimated to be six, falling below one by generation three (Figures S4 and S5, and Table S2, see online supplementary material). Inspection of probabilistic transmission networks (Figure S6, see online supplementary material) confirmed a high value of the case reproduction number R for B1.1, but also supported sequential transmission of the virus within households, resulting in a greater estimated value of compared with most earlier studies (Bi et al., 2020; Endo et al., 2020; Nakajo and Nishiura, 2021). A previous study by Ng et al. (2020) involved an analysis of data from Taiwan from 2020, and found an estimated value of that was substantially larger, in part due to the small sample size in their analysis (the posterior mean of was 19.20).
The mean reporting delay for the outbreak (under the intensive measures that were in place for this outbreak – Scenario 1) was estimated to be 2.5 days (95% CI 1.8–3.5) with a standard deviation (SD) of 1.6 days (95% CI 1.1–2.9). Under counterfactual Scenario 2, where the mean reporting delay was estimated for all local cases reported in Taiwan since the beginning of 2020, the mean reporting delay was 7.8 days (95% CI 6.2–10.1) with a SD of 7.8 days (95% CI 5.7–13.2). Due to a small number of negative delays (i.e. some individuals were detected prior to developing symptoms), the distributions were shifted approximately one day earlier as a result of the model fitting (1.0 day (95% CI 0.2–2.9) for Scenario 1 and 0.8 days (95% CI 0.1–2.0) for Scenario 2). The observed difference in mean reporting delays between Scenario 1 and Scenario 2 can be attributed to different ways in which cases were detected. Under Scenario 1, cases were detected quickly by rigorous contact tracing, whereas under Scenario 2, cases were detected by a combination of some contact tracing and symptom-based surveillance (Bi et al., 2020).
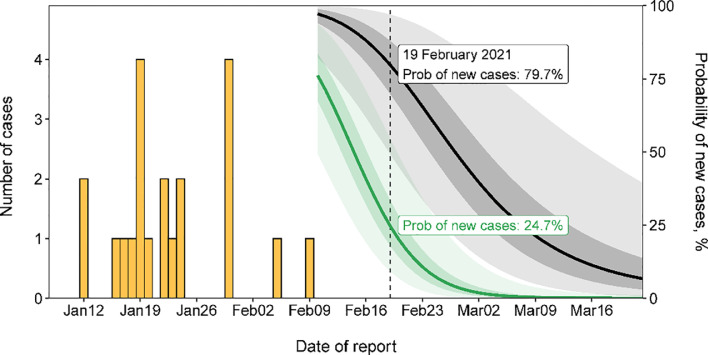
Incorporating the posterior distributions for the serial interval (Nishiura et al., 2020) and the reporting delay into the formula for the end-of-outbreak probability (Equation (6)), following the final case reported in this outbreak, a sharper decline in the estimated probability that new cases will be reported in future was observed under Scenario 1 than Scenario 2 (green and black lines and regions in Figure 2 ). Ten days after the last reported case, on 19 February 2021, this probability (reported here as a percentage) dropped to 24.7% under Scenario 1 compared with 79.7% under Scenario 2. Depending on the policy maker's ‘acceptable risk’, different thresholds in this probability could be chosen before declaring an outbreak over (Thompson et al., 2019). For instance, if a threshold of 10% is chosen, the outbreak could have been declared over on 24 February 2021 under Scenario 1 compared with a later date of 18 March 2021 under Scenario 2. Sensitivity analyses are presented for different values of and , as well as different reporting delay distributions for Scenario 2, in the online supplementary material, indicating qualitatively similar results. In each case, more rigorous control measures (characterized by a shorter reporting delay) allow policy makers to be confident that the outbreak is over sooner after the final reported case.
Figure 2.
The estimated risk of cases being reported in future for Scenario 1 (under intensified contact tracing; green) and Scenario 2 (less rigorous public health measures; black). Bars in orange indicate the incidence of SARS-CoV-2 infections by confirmation date.
Conclusions
In summary, these results suggest that the rigorous public health measures that were in place allowed the end of the outbreak to be declared approximately three weeks earlier than if these intensive measures had not been introduced. More generally, stringent control measures allow policy makers to be confident that outbreaks are over earlier compared to scenarios with less intense measures. However, in the outbreak considered here, even with strict control measures, public vigilance was required for several weeks after the final reported case, until total confidence that the outbreak was over was achieved (Figure 2).
To conclude, proactive countermeasures and high public compliance contributed to efficient containment and a high confidence that the hospital-related outbreak in Taiwan was over by late February 2021. Later identification of the outbreak could have led to a higher number of infections (Akhmetzhanov, 2020; Liu et al., 2020), and therefore potentially a later end-of-outbreak declaration.
Declaration of Competing Interest
None declared.
Acknowledgments
Acknowledgments
The authors thank the Taiwanese public health authorities and institutions for surveillance, laboratory testing, epidemiological investigations and data collection. In addition, the authors thank the two anonymous reviewers for their useful comments that helped us to improve the manuscript. ARA also thanks Yin-Chin Fan and Yun-Chun Wu (National Taiwan University) for discussions about this topic.
Funding source
S-mJ received funding from the Japan Society for the Promotion of Science via a KAKENHI grant (20J2135800).
Ethical approval
Not required.
Footnotes
Supplementary material associated with this article can be found, in the online version, at doi:10.1016/j.ijid.2021.06.028.
Appendix. Supplementary materials
References
- Akhmetzhanov AR. Large SARS-CoV-2 outbreak caused by asymptomatic traveler. China. Emerg Infect Dis. 2020;26:3106. doi: 10.3201/eid2612.203437. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Akhmetzhanov AR. Estimation of delay-adjusted allcause excess mortality in the USA: March–December 2020. Epidemiol Infect. 2021;149:e156. doi: 10.1017/S0950268821001527. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Akhmetzhanov AR, Lee H, S-m Jung, Kinoshita R, Shimizu K, Yoshi K, et al. Real time forecasting of measles using generation-dependent mathematical model in Japan, 2018. PLoS Curr Outbreaks. 2018;10 doi: 10.1371/currents.outbreaks.3cc277d133e2d6078912800748dbb492. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bi Q, Wu Y, Mei S, Ye C, Zou X, Zhang Z, et al. Epidemiology and transmission of COVID-19 in 391 cases and 1286 of their close contacts in Shenzhen, China: a retrospective cohort study. Lancet Infect Dis. 2020;20:911–919. doi: 10.1016/S1473-3099(20)30287-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Biggerstaff M, Cowling BJ, Cucunubá ZM, Dinh L, Ferguson NM, Gao H, et al. Early insights from statistical and mathematical modeling of key epidemiologic parameters of COVID-19. Emerg Infect Dis. 2020;26(11):11. doi: 10.3201/eid2611.201074. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Central Epidemic Command Centre. COVID-19 press conference of 5 February 2021 (in Chinese). 2021a. Available at: https://youtu.be/SLMJIV6ncBI (accessed 12 April 2021).
- Central Epidemic Command Centre. COVID-19 press conference of 17 January 2021 (in Chinese). 2021b. Available at: https://youtu.be/LvGoNhe2lXw (accessed 12 April 2021).
- Djaafara BA, Imai N, Hamblion E, Impouma B, Donnelly CA, Cori A. A quantitative framework for defining the end of an infectious disease outbreak: application to Ebola virus disease. Am J Epidemiol. 2021;190:642–651. doi: 10.1093/aje/kwaa212. [DOI] [PMC free article] [PubMed] [Google Scholar]
- GISAID. Accession numbers of first 3 samples: EPI_ISL_956329, EPI_ISL_956330, EPI_ISL_1020315. 2021.
- Endo A, Abbott S, Kucharski AJ, Funk S, CMMID COVID-19 Working Group Estimating the overdispersion in COVID-19 transmission using outbreak sizes outside China. Wellcome Open Res. 2020;5 doi: 10.12688/wellcomeopenres.15842.1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hart WS, Maini PK, Thompson RN. High infectiousness immediately before COVID-19 symptom onset highlights the importance of continued contact tracing. eLife. 2021;10:e65534. doi: 10.7554/eLife.65534. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keller M, Kamary K. Bayesian model averaging via mixture model estimation. arXiv 2017.
- Linton NM, Akhmetzhanov AR, Nishiura H. Localized end-of-outbreak determination for coronavirus disease 2019 (COVID-19): examples from clusters in Japan. Int J Infect Dis. 2021;105:286–292. doi: 10.1016/j.ijid.2021.02.106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu J, Huang J, Xiang D. Large SARS-CoV-2 outbreak caused by asymptomatic traveler. China. Emerg Infect Dis. 2020;26:2260–2263. doi: 10.3201/eid2609.201798. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCallum M, Bassi J, De Marco A, Chen A, Walls AC, Di Iulio J, et al. SARS-CoV-2 immune evasion by the B.1.427/B.1.429 variant of concern. Science. 2021 doi: 10.1126/science.abi7994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nakajo K, Nishiura H. Transmissibility of asymptomatic COVID-19: Data from Japanese clusters. Int J Infect Dis. 2021;105:236–238. doi: 10.1016/j.ijid.2021.02.065. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ng T, Cheng H, Chang H, Liu C, Yang C, Jian S, et al. Effects of case- and population-based COVID-19 interventions in Taiwan. medRrxiv. 2020 [Google Scholar]
- Nishiura H, Miyamatsu Y, Mizumoto K. Objective determination of end of MERS outbreak, South Korea, 2015. Emerg Infect Dis. 2016;22:146–148. doi: 10.3201/eid2201.151383. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nishiura H, Linton NM, Akhmetzhanov AR. Serial interval of novel coronavirus (COVID-19) infections. Int J Infect Dis. 2020;93:284–286. doi: 10.1016/j.ijid.2020.02.060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parag KV, Donnelly CA, Jha R, Thompson RN. An exact method for quantifying the reliability of end-of-epidemic declarations in real time. PLoS Comput Biol. 2020;16 doi: 10.1371/journal.pcbi.1008478. [DOI] [PMC free article] [PubMed] [Google Scholar]
- R Development Core Team. R: a language and environment for statistical computing; 2021. Available at: https://www.r-project.org (accessed 30 June 2021).
- Riou J, Althaus CL. Pattern of early human-to-human transmission of Wuhan 2019 novel coronavirus (2019-nCoV), December 2019 to January 2020. Euro Surveill. 2020;25:2000058. doi: 10.2807/1560-7917.ES.2020.25.4.2000058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stan Development Team. Stan modeling language users guide and reference manual, 2.27.0. 2021. Available at: https://mc-stan.org (accessed 3 June 2021).
- Taiwan Centres for Disease Control. 2021. Available at: https://www.cdc.gov.tw (accessed 12 April 2021).
- Thompson RN, Morgan OW, Jalava K. Rigorous surveillance is necessary for high confidence in end-of-outbreak declarations for Ebola and other infectious diseases. Phil Trans Roy Soc B. 2019;374:20180431. doi: 10.1098/rstb.2018.0431. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tian L, Li X, Qi F, Tang Q-Y, Tang V, Liu J, et al. Harnessing peak transmission around symptom onset for non-pharmaceutical intervention and containment of the COVID-19 pandemic. Nat Commun. 2021;12:1147. doi: 10.1038/s41467-021-21385-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wallinga J, Teunis P. Different epidemic curves for severe acute respiratory syndrome reveal similar impacts of control measures. Am J Epidemiol. 2004;160:509–516. doi: 10.1093/aje/kwh255. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Worden L, Ackley SF, Zipprich J, Harriman K, Enanoria WTA, Wannier R, et al. Measles transmission during a large outbreak in California. Epidemics. 2020;30:100375. doi: 10.1016/j.epidem.2019.100375. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang W, Davis BD, Chen SS, Sincuir Martinez JM, Plummer JT, Vail E. Emergence of a novel SARS-CoV-2 variant in Southern California. JAMA. 2021;325:1324–1326. doi: 10.1001/jama.2021.1612. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.