Asymmetric dynamics of dimeric SARS-CoV-2 and SARS-CoV main proteases in an apo form: Molecular dynamics study on fluctuations of active site, catalytic dyad, and hydration water

Abstract

Severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) has been widely spread around the world. It is necessary to examine the viral proteins that play a notorious role in the invasion of our body. The main protease (3CL^pro) facilitates the maturation of the coronavirus. It is thought that the dimerization of 3CL^pro leads to its catalytic activity; the detailed mechanism has, however, not been suggested. Furthermore, the structural differences between the predecessor SARS-CoV 3CL^pro and SARS-CoV-2 3CL^pro have not been fully understood. Here, we show the structural and dynamical differences between the two main proteases, and demonstrate the relationship between the dimerization and the activity via atomistic molecular dynamics simulations. Simulating monomeric and dimeric 3CL^pro systems for each protease, we show that (i) global dynamics between the two different proteases are not conserved, (ii) the dimerization stabilizes the catalytic dyad and hydration water molecules behind the dyad, and (iii) the substrate-binding site (active site) and hydration water molecules in each protomer fluctuate asymmetrically. We then speculate the roles of hydration water molecules in their catalytic activity.

1. Introduction

Severe Acute Respiratory Syndrome coronavirus (SARS-CoV) was originally identified in 2003 [1]. In 2019, the novel SARS coronavirus (SARS-CoV-2) emerged and has been spreading around the world. Both viruses cause severe pneumonia. The viruses encapsulate a single-stranded RNA in its viral envelope, and protrusions (i.e., spike proteins) project from the surface so that the virus can recognize certain receptors on cells.

The main protease (3-chymotrypsin like protease, 3CL^pro) plays an important role in the maturation of the SARS-CoV and SARS-CoV-2 coronaviruses. The protease is a cysteine protease and has a catalytic dyad formed by histidine (H41) and cysteine (C145), which are highly conserved among different coronaviruses (Fig. S1). The protease catalyzes the polyprotein translated from the viral RNA, breaking the polyprotein into functional pieces, which include the protease itself. In the present study, we called the protease “3CL^pro” and used the term “active site” as the one consisting of the physiological-ligand binding pocket and the hydrolysis-reaction catalytic site.

Because the SARS-CoV and SARS-CoV-2 3CL^pro are a protease, designing binders to the active site is a direct way to deactivate the catalytic activity. On the basis of this manner, many investigations have been attempted to identify novel binders to the active site [2], [3], [4], [5], [6]_^–[7]. For instance, a Michael acceptor inhibitor (N3) was originally designed to inhibit SARS-CoV 3CL^pro [2]. N3 also binds to the active site for SARS-CoV-2 3CL^pro (PDBID: 6LU7 and 7BQY) [3].

Another way to impair the catalytic activity can be to inhibit the dimerization of the protease [8]. For dimeric SARS-CoV 3CL^pro, an X-ray experiment suggested that the substrate pocket S1 in the active site of a protomer was collapsed and the other pocket wasn't, and hence one protomer is active, but the other is inactive [9]. The analysis of MD trajectories for dyad conformation suggested that one protomer in the dimeric SARS-CoV 3CL^pro was inactive and a monomeric SARS-CoV 3CL^pro was inactive [10]. However, for dimeric SARS-CoV-2 3CL^pro, room-temperature X-ray crystallography demonstrated that the collapse of S1 pocket in the dimer did not occur; the authors pointed out that previous crystal structures might have an artefact [11]. The dimer dissociation constant for both SARS-CoV and SARS-CoV-2 3CL^pro was estimated; also the catalytic efficiency of SARS-CoV-2 3CL^pro was slightly higher than SARS-CoV one [12]. Subsequently, the dissociation constant was revised by native mass spectrometry, the value of which was about 0.14$\pm$ 0.03$\mu \mathrm{M}$ [13]. The dimerization and the enzymatic activity was weakened by both the C- and N-terminal truncations of SARS-CoV 3CL^pro [14]. On the other hand, the C-terminal truncation, which ranged from 300 to 306, did not cause noticeable effects on the quaternary structure [15]. The stability of several known compounds on the active site was assessed for finding potent binding sites [16]. Their blind docking result implied that the dimer interface would be a potent target.

Although the relationship between the dimerization and the catalytic activity has been investigated so far [8], few studies demonstrate how they relate and why the dimerization matters for the catalytic activity. Furthermore, it is unclear whether the results of SARS-CoV 3CL^pro are reusable even for SARS-CoV-2 3CL^pro. It is thus necessary to investigate the relationship and the difference between the two proteases. It should be confirmed whether SARS-CoV-2 3CL^pro behaves in the same way as SARS-CoV 3CL^pro; and whether it is inactive in a monomeric form and is active in a dimeric form. No study revealed, from a statistical and structural viewpoint, the reason why the monomer is inactive, but the dimer is active. The present study aims to unveil the relationship between the protease's structure/dynamics and its catalytic activity.

In the present study, we demonstrate that the dimerization of the proteases stabilizes their catalytic dyad and hydration water behind the dyad. We apply atomistic molecular dynamics simulations to calculate the global dynamics, dyad stability, and hydration water dynamics. We find that the global dynamics of SARS-CoV-2 3CL^pro differ from those of SARS-CoV 3CL^pr. For both dimeric proteases, each active site complies with different structural probability distributions. The catalytic dyad is retained in a dimeric state but not in a monomeric state, and hydration water molecules behind the dyad stay longer in a dimeric state than in a monomeric state.

2. Materials and methods

2.1. Preparation of simulation systems

All the target proteases in the present study are shown in Table 1. One simulation system for a dimeric system of SARS-CoV-2 3CL^pro was constructed by homology modelling based on the structure of PDBID 1UJ1. The template sequence is shown in Table S1. Since the sequence identity is 96.3 %, the homology modelling approach would provide a reliable structural model. Furthermore, another dimeric system of SARS-CoV-2 3CL^pro was constructed from the X-ray structure of PDBID 6LU7. The structural data of the homodimer was downloaded from the “Biological Assembly” of the PDB 6LU7. Note that one protomer's conformation in the dimeric system is identical to the other protomer's because the asymmetric unit of the PDBID 6LU7 is monomeric (i.e., the root mean square displacement between the two protomers is zero). On the basis of the chain IDs, each chain was named “protomer A” and “protomer B”.

Table 1.

Summary of simulation. $N_{\mathrm{atoms}}$ is the number of atoms in a simulation system, $t_{\mathrm{each}}$ is the total simulation time of each run, and $N_{\mathrm{runs}}$ is the number of runs. All simulations were performed at $310\mathrm{K}$.

Target	State	No	Ref	PDB ID	$N_{\text{atoms}}$	$N_{\text{runs}}$	$t_{\text{each}},\mu s$
SASRS-CoV 3CLpro	Dimeric	1	[9]	1UK3a	87,554	5	1.0
		2	[9]	1UJ1b	79,123	5	1.0
	Monomeric	3	[9]	1UK3Ac	68,521	5	1.0
		4	[9]	1UK3Bd	70,073	5	1.0
SASRS-CoV-2 3CLpro	Dimeric	5	N/A	HMe	78,938	5	1.0
		6	[18]	6LU7f	79,466	10	1.0
	Monomeric	7	[18]	6LU7f	62,290	5	1.0
	Dimericg	8	[19]	6WQF	77,617	5	1.0
	Monomericg	9	[19]	6WQF	62,200	5	1.0

^aThis structure was determined at pH 7.6.⁹ MD simulations were performed for this in our previous study [20].

^bThis structure was determined at pH 6.0.⁹

^cProtomer A of 1UK3

^dProtomer B of 1UK3

^eA homology model (HM) derived from 1UJ1. This model was built by SWISS-MODEL [21],[22]. The query sequence is shown in Table S1 in the supporting information.

^fThe ligand was removed from 6LU7, and thus the systems from 6LU7 were an apo form.

^gThe dyad was ionized (i.e., H41⁺…C145⁻).

The protonation state of the histidine H41 would be crucial for the catalytic activity of 3CL^pro. For the careful assignment, the catalytic site in a known X-ray structure of 3CL^pro (PDBID: 1UJ1) was examined. The surroundings of the catalytic dyad (H41-C145) imply that ${\mathrm{N}}_{\epsilon }$ of H41 is protonated and ${\mathrm{N}}_{\mathrm{\delta }}$ of H41 is not (Fig. S2). Accordingly, ${\mathrm{N}}_{\epsilon }\left(\mathrm{H}41\right)$ was protonated and ${\mathrm{N}}_{\mathrm{\delta }}$ was not in No. 1-7 simulations. Nevertheless, because it is also plausible for 3CL^pro to form an ionized dyad $\mathrm{H}{41}^{+}\dots \mathrm{C}{145}^{-}$ [17], a dimeric system with two ionized dyad and a monomeric one with an ionized dyad were also constructed (No. 8-9 in Table 1). The computational results of the ionized systems are given in the Supporting Information.

For each structure prepared, the C- and N-terminus were capped by acetyl and amine groups, respectively. Then, each of the structures was immersed into a tetrahedron water box whose margin was 10 Å from each of the planes of the box to the structure. The salt concentration in the box was set to 0.1 M. Energy minimization was executed with all heavy atoms restrained and then without any restraints. Subsequently, five NVT simulations with different velocities were performed during 100 ps, and then five NPT simulations at 1 bar during 100 ps. From the five equilibrated structures, five independent NPT simulations at 1 bar at 310 K were performed. Only for the dimeric system of PDBID 6LU7, the number of simulations was 10. Production runs were performed for $1\mu \mathrm{s}\times 10$for the dimeric system and $1\mu \mathrm{s}\times 5$for the others (Table 1).

Computational setting are as follows: time step was set to 2 fs, an interaction table for cut-off scheme [23] was used whose list was updated every 20 fs. A leap-frog algorithm was used for an integrator, and LINCS [24] was for hydrogen-bond constraints (lincs_iter=1, lincs_order=4). V-rescale [25] was for temperature control for two groups, protein and non-protein (${\tau }_T=0.1$, compressibility=4.5$\times$10⁶). Berendsen coupling [26] was used for the first box equilibration, and Parrinelo-Rahman coupling for all production runs to control pressure [27],[28] (${\tau }_p^{\text{ref}}=1.0$, ${\tau }_p=2.0$). Short-range electrostatic and van der Waals interaction cut-off values were set to 12 Å. Amber ff99SB-ILDN was employed for protein force field [29] and TIP3P model [30] for water molecules. Reaction-field method [31] for long-range interaction calculation was used with the relative dielectric constant ${\epsilon }_{\text{rf}}$ set infinity. Note that, in Gromacs notation, the option epsilon-rf=0 means that ${\epsilon }_{\text{rf}}$ is infinity. Snapshots were stored for every 100 ps. Gromacs 2019.2 [32], [33], [34], [35], [36] was used for all simulations. The supercomputer TSUBAME 3.0 was used for all simulations. For analysis, MDAnalysis [37],[38] was used for parsing MD trajectory. All pictures for molecules were drawn by PyMOL 2.3.0 39. Every MD trajectory from $200\text{ns}$ to $1\mu \mathrm{s}$ was analyzed (see Fig.s S3 and S4).

2.2. Principal Component Analysis (PCA)

Cartesian-based PCA (cPCA) was used for description of global protein dynamics. The cPCA provides dynamic modes, i.e., eigenvectors ${\mathit{e}}_1^x,{\mathit{e}}_2^x,\dots ,{\mathit{e}}_n^x$, where $x$ is a system name and $n$ is the number of coordinates of interest. The eigenvectors ${\mathit{e}}_1^x,{\mathit{e}}_2^x,\dots ,{\mathit{e}}_n^x$ were arranged in a descending order of the eigenvalues. Correlations between ${\mathit{e}}_i^x$ and ${\mathit{e}}_j^y$ of different proteases were calculated (i.e., inner products ${\mathit{e}}_i^x·{\mathit{e}}_j^y\left(i,j=1,2,\dots ,n\right)$) [40]. Here, cPCA was applied to trajectories of the SARS-CoV 3CL^pro and SARS-CoV-2 3CL^pro systems. MD snapshot $i$ of a trajectory was expressed as ${\mathit{q}}^i=\left(q_1^i,q_2^i,\dots ,q_{3M}^i\right)$, where $M$ is the number of $\mathrm{C}\alpha$ atoms. Structural superimposition for every snapshot was carried out for all the $\mathrm{C}\alpha$ atoms. The variance-covariance matrix was defined as ${\left\{C_{mn}\right\}}_{m,n=1,\dots ,3M}={\langle q_m{q}_n\rangle }_T-{\langle q_m\rangle }_T{\langle q_n\rangle }_T$, where${\langle ·\rangle }_T$ is the ensemble average at temperature $T\left(=310\mathrm{K}\right)$. $C_{mn}$ was diagonalized, thereby generating eigenvectors ${\mathit{e}}_1^x,{\mathit{e}}_2^x,\dots ,{\mathit{e}}_M^x$ ($x=\text{SARSCoV},\text{SARSCoV}2$). Inner products ${\mathit{e}}_i^{\text{SARSCoV}}·{\mathit{e}}_j^{\text{SARSCoV}2}\left(i,j=1,2,3\right)$ were computed. Global modes were defined as the top-3 eigenvectors ${\mathit{e}}_1^x$, ${\mathit{e}}_2^x$, and ${\mathit{e}}_3^x$. The inner products indicate the correlation of global modes between of SARS-CoV-2 3CL^pro and SARS-CoV 3CL^pro.

Furthermore, distance-based PCA (dPCA) was also utilized to grasp a structural distribution [41]. In terms of a structural distribution, dPCA shows better performance (e.g., convergence of cumulative variances) than cPCA.[41] The dPCA was thus applied for the active site that was represented as a set of distances between $\mathrm{C}\alpha$ atoms (Table S2). The number of the selected $\mathrm{C}\alpha$ atoms was $N_{\mathrm{C}\alpha }=25$. The active site of MD snapshot $i$ was expressed as a set of distances ${\mathit{d}}^i=\left(d_1^i,d_2^i,\dots ,d_K^i\right)$, where $K$ was the number of distance pairs, i.e.,$K=N_{\mathrm{C}\alpha }\left(N_{\mathrm{C}\alpha }-1\right)/2$. The variance-covariance matric was defined as ${\left\{D_{mn}\right\}}_{m,n=1,\dots ,K}={\langle d_m{d}_n\rangle }_T-{\langle d_m\rangle }_T{\langle d_n\rangle }_T$. The matrix was diagonalized and then eigenvectors ${\mathit{a}}_1^x,{\mathit{a}}_2^x,\dots ,{\mathit{a}}_K^x$ ($x=\text{SARSCoV},\text{SARSCoV}2$) were generated. The active site ${\mathit{d}}^i$ of each snapshot $i$ was projected onto every eigenvector ${\mathit{a}}_j^x$by $x_{i,j}=\left({\mathit{d}}^i-\langle {\mathit{d}}^i\rangle \right)·{\mathit{a}}_j^x$, where $x_{i,j}$ is the position of each snapshot $i$ on $j^{\text{th}}$ eigenvector, i.e., $j^{\text{th}}$ principal component (PC$j$).

2.3. Statistical analysis of the catalytic dyad

The probability distribution of the catalytic dyad's distance was calculated (Fig. 1). On the basis of the probability distribution, the dyad was judged whether it was broken or not. The following procedure was used for the judgement: (i) The probability distribution of the dyad distance $d_{\text{dyad}}$ between ${\mathrm{N}}_{\epsilon }\left(\mathrm{H}41\right)$ and ${\mathrm{S}}_{\mathrm{\gamma }}\left(\mathrm{C}145\right)$ was calculated. The distribution was expressed as $P\left(d_{\text{dyad}}\right)$. (ii) The mode (the value that appears most frequently) of $P\left(d_{\text{dyad}}\right)$ was calculated, which was expressed as $D_{\text{dyad}}^{\text{mode}}$. (iii) The deviation of $D_{\text{dyad}}^{\text{mode}}$ from the reference distance $D_{\text{dyad}}^{\text{ref}}$ was calculated by

$$\Delta D=D_{\text{dyad}}^{\text{mode}}-D_{\text{dyad}}^{\text{ref}},$$ (1)

where $D_{\text{dyad}}^{\text{ref}}$ was the distance between ${\mathrm{N}}_{\epsilon }\left(\mathrm{H}41\right)$ and ${\mathrm{S}}_{\mathrm{\gamma }}\left(\mathrm{C}145\right)$ in the X-ray structure of PDBID 6LU7. The following condition was applied for the judgement of the dyad's state:

$$\begin{array}{c}\Delta D\ge 1.0\text{Å}\Rightarrow \text{the}\text{dyad}\text{is}\text{broken}\\ \Delta D<1.0\text{Å}\Rightarrow \text{the}\text{dyad}\text{is}\text{retained}\end{array}$$ (2)

Fig. 1.

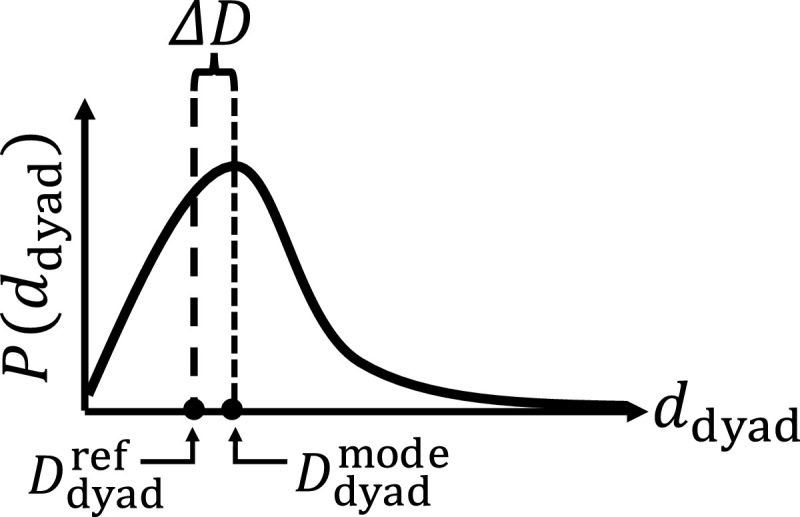
Probability distribution of the distance $d_{\mathrm{dyad}}$ between ${\mathrm{N}}_{\epsilon }\left(\mathrm{H}41\right)$ and ${\mathrm{S}}_{\gamma }\left(\mathrm{C}145\right)$. $D_{\mathrm{dyad}}^{\mathrm{ref}}$ was defined as the distance ($=3.9$ Å) between ${\mathrm{N}}_{\epsilon }\left(\mathrm{H}41\right)$ and ${\mathrm{S}}_{\mathrm{\gamma }}\left(\mathrm{C}145\right)$ in an X-ray structure (PDBID: 1UK3A). $D_{\mathrm{dyad}}^{\mathrm{mode}}$ was set to the most frequent value of $P\left(d_{\mathrm{dyad}}\right)$.

Using this condition, a confusion matrix was created (Table 3). This matrix was used for the evaluation of the structural difference of the dyad between the monomeric and the dimeric systems. Two-sided Fisher's exact test of independence was employed for the statistical assessment. The null hypothesis was that oligomeric states (i.e., monomeric or dimeric) are independent of the states of the dyad (i.e., broken or retained). Although this test is similar to ${\chi }^2$ test of independence, the use of Fisher's exact test is recommended if sample size is less than 1000 [42]. Matthew's correlation coefficient (MCC) of the matrix was also calculated for the assessment of the correlation between the two categories: monomeric/dimeric states and broken/retained dyad. MCC is considered a reliable statistical measure [43].

Table 3.

Confusion matrix for the dependency of monomeric/dimeric states on the dyad's conformation. “Monomeric” (first column) and “Dimeric” (second column) data were derived from the trajectories No. 3, 4, and 7 and No. 1, 2, and 6 (see Table 1).

	Monomeric	Dimeric	p-value= 0.0025
Broken dyad	10	8	MCC=0.48
Retained dyad	5	32

2.4. Residence time of water molecules

Survival probability (SP) [44] of water molecules within the defined sphere (Fig. 2) was calculated by the following procedure: The average coordinates $r_A$ of the triad (H41, H164, and D187) is calculated for each snapshot. The number of water molecules at time $t$ within the sphere of radius 5 Å centered at $r_A$ is expressed as $N\left(t\right)$. The number of water molecules within the sphere from $t$ to $t+\tau$ is represented as $N\left(t,t+\tau \right)$, where $\tau$ is called a lag time. The SP is then defined as:

$$SP\left(\tau \right)=\frac{1}{T}\sum _{t=1}^T\frac{N\left(t,t+\tau \right)}{N\left(t\right)}$$ (3)

where $T$ is the entire simulation time of interest and $0\le SP\left(\tau \right)\le 1$ . The SP tells us how fast water molecules within the sphere diffuse. Let us consider two extreme cases: if $SP\left(\tau \right)=1$ the number of water molecules within the sphere never decreases after time $\tau$, i.e., the water molecules stay in the sphere for the time $\tau$; if $SP\left(\tau \right)=0$, the number of water molecules within the sphere vanishes for the time $\tau$. Residence time ${\tau }_{0.5}^{\text{system}}$ was defined as the time $\tau$ when SP reaches 0.5. A python library, MDAnalysis, was used for the SP calculation [37], [38], [44].

Fig. 2.

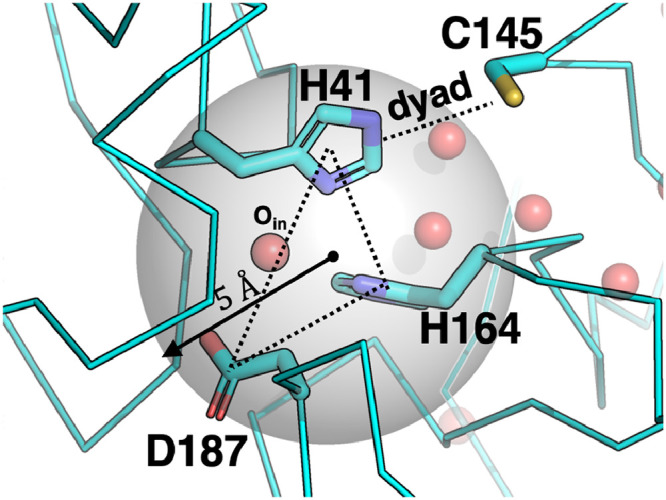
The definition of the spherical space used in the survival probability calculation. The transparent grey space was defined as the sphere whose center was positioned at the average coordinates of H41, H164, and D187 and whose radius was 5 Å. This depicted structure was taken from the PDB ID 6WQF [19]. The symbol O_in indicates an oxygen atom of a water molecule within the sphere. The water molecule is surrounded by H41, H164, and D187 and corresponds to the crystal water that are considered important for the catalytic activity [19],[45].

3. Results and discussion

This section presents results of the systems with neutral dyads mainly, whereas results of the systems with ionized dyads are given in the supporting information.

3.1. Correlation between major dynamic modes of the two proteases

Performing cPCA for the entire protein structure, we produced their dynamic modes (i.e., eigenvectors) for the dimeric SARS-CoV 3CL^pro and SARS-CoV-2 3CL^pro systems. Since it is unclear how much the two proteases' global motion is conserved, we examined dynamic modes’ correlations between the two proteases. Here, the correlation was defined as cosine similarity between a pair of eigenvectors, which were scaled to be unit vectors. Table 2 shows the correlation for each pair of eigenvectors. The highest correlation was 0.37 between ${\mathit{e}}_3^{\text{SARSCoV}}$and ${\mathit{e}}_3^{\text{SARSCoV}2}$, the second was 0.36 between ${\mathit{e}}_2^{\text{SARSCoV}}$and ${\mathit{e}}_3^{\text{SARSCoV}2}$, and the third was 0.35 between ${\mathit{e}}_2^{\text{SARSCoV}}$and ${\mathit{e}}_3^{\text{SARSCoV}2}$. The second mode ${\mathit{e}}_2^{\text{SARSCoV}}$ was distributed into ${\mathit{e}}_1^{\text{SARSCoV}2}$ and ${\mathit{e}}_3^{\text{SARSCoV}2}$. These results indicated that the major modes were not highly conserved, while the amino-acid sequence identity between two proteases was 96% that was very high value. The slight mutations on SARS-CoV-2 3CL^pro altered the structural dynamics of the previous SARS-CoV 3CL^pro. The alternation implied that the global dynamics were not a fundamental aspect for the proteases’ function.

Table 2.

Correlation coefficient between major eigenvectors.

		SARS-CoV-2 3CLpro (6LU7)
	Mode	${\mathit{e}}_1$	${\mathit{e}}_2$	${\mathit{e}}_3$
SARS-CoV 3CLpro (1UJ1&1UK3)a	${\mathit{e}}_1$	0.03	0.02	0.07
	${\mathit{e}}_2$	0.36	0.11	0.35
	${\mathit{e}}_3$	0.05	0.13	0.37

^aThe trajectories were initiated from two different initial structures 1UJ1 and 1UK3. Subsequently, they were merged into a single trajectory, which was analyzed via cPCA.

3.2. Structural Fluctuations of the Active Site

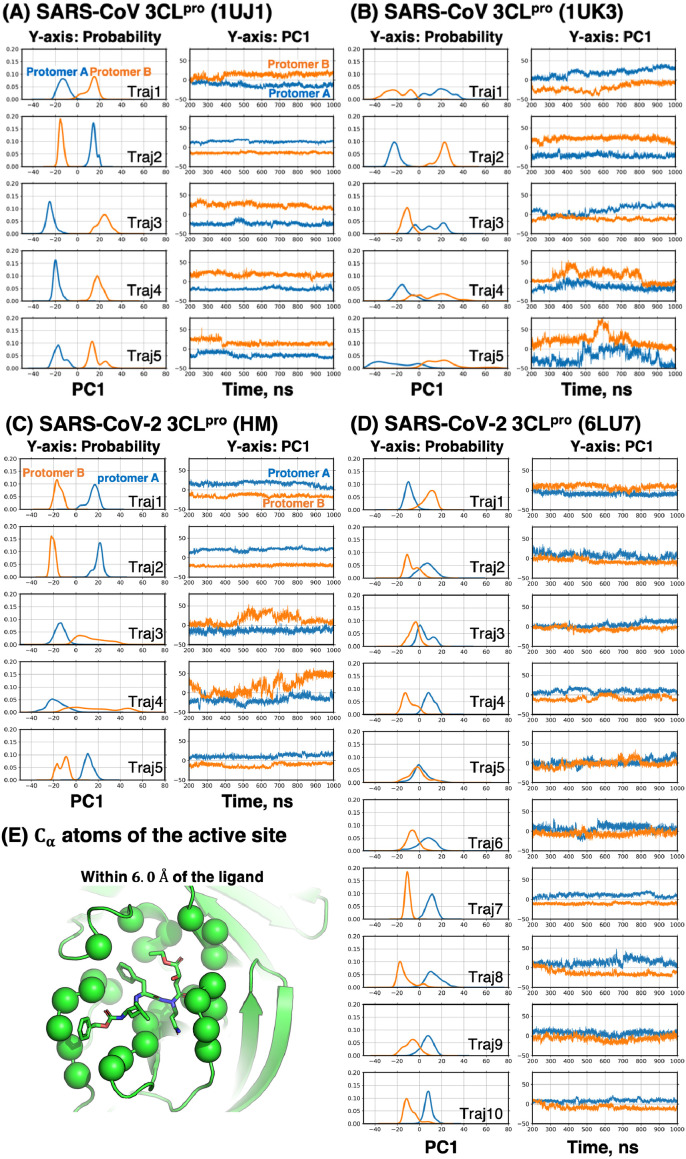
This section deals with structural fluctuations of the active site. For the analysis, we applied distance-based principal component analysis (dPCA) (Table S2 and Fig. 3E). Recall that the dimer has one active site in each protomer. We executed dPCA for each active site, obtaining the first principal component (PC1).

Fig. 3.

Probability distribution of the first principal component (PC1) and PC1’s trajectories along time evolution. PC1 was obtained from dPCA using $\mathrm{C}\alpha$ atoms of the active site. Blue and orange lines are for protomer A and B, respectively. (A) SARS-CoV 3CL^pro (1UJ1), (B) SARS-CoV 3CL^pro (1UK3), (C) SARS-CoV-2 CoV 3CL^pro (HM), and (D) SARS-CoV-2 3CL^pro (6LU7). (E) The $\mathrm{C}\alpha$ atoms of the active site that was used in dPCA. PC1 of each graph was not identical to each other, i.e., we analyzed each Traj i (i=1,2,…,10) individually in the dPCA, because merging multiple trajectories results in the expansion of conformational space, leading to the poor capability of dPCA to discriminate conformations.

For the dimeric systems with neutral dyads, the active site in a protomer fluctuated differently from the other protomer's (Fig. 3). For instance, Traj2 in Fig. 3A shows two distinguishable probability distributions of PC1. Although the undistinguished distribution in Traj5 of Fig. 3D also occurred, it appeared rarer than the separated distributions. At the beginning of the simulations for 6LU7, the two active sites were structurally identical. This eliminates the possibility that the separated distribution was attributed to the initial structures. The asymmetric fluctuations may imply that substrate specificity of a protomer differ from that of the other. This asymmetric fluctuations of the active site were supported by several crystal structures whose protomer has conformationally distinct active site (e.g., PDBID: 1UK3) [9] and by earlier computational studies [10],[47]. An earlier study also pointed out the structural heterogeneity of the active site on the basis of known crystal strucutres [46].

For the monomeric systems with a neutral dyad, we observed multimodal probability distributions along with PC1 (Fig. S5). For example, Traj5 in Fig. S5C shows a bimodal distribution, which indicated that the monomeric systems’ active site was unstable more than the dimeric systems. Keeping active site's conformation was thus likely to be a difficult task for the monomer; this can be one explanation of why the monomer is inactive. For both proteases, the dynamic modes were altered by the slight mutations (Table 2), but the distributions of the active site showed the same tendency: each active site fluctuated asymmetrically (Fig. 3).

3.3. Dyad stability

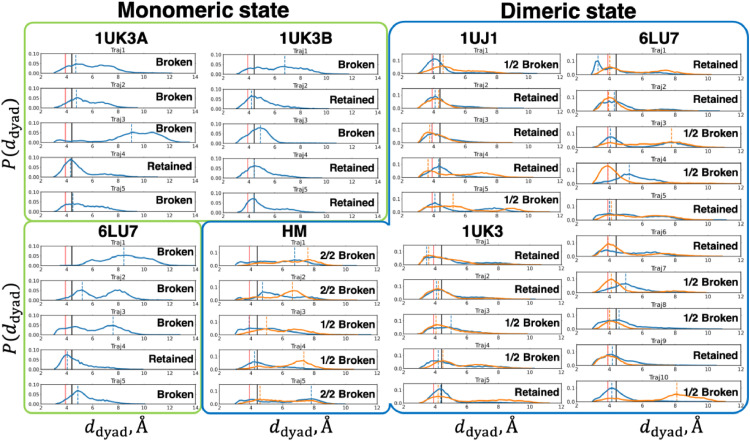
We investigated the distance fluctuations of the catalytic dyad in order to connect the dyad's fluctuations with the catalytic activity of the 3CL^pro. We calculated the distance $d_{\text{dyad}}$ between ${\mathrm{N}}_{\epsilon }\left(\mathrm{H}41\right)$ and ${\mathrm{S}}_{\mathrm{\gamma }}\left(\mathrm{C}145\right)$. For each trajectory, we computed a probability distribution of $d_{\text{dyad}}$ and obtained the mode $D_{\text{dyad}}^{\text{mode}}$ (i.e., the most frequent value). Using the mode and the reference distance $D_{\text{dyad}}^{\text{ref}}$, we judged whether the dyad was retained or broken (Table 3). Further details of this procedure are given in Materials and Methods.

We found that the dimeric systems tended to retain the active dyad's conformation more than the monomeric systems did (Fig. 4 and Table 3). To assess the difference between the monomeric and dimeric systems, we conducted Fisher's exact test and calculated Matthew's correlation coefficient (MCC). We have shown the statistical significance (p-value = 0.0025) if we employed the significance level of $\alpha =0.05$. Furthermore, MCC was 0.48, showing a positive correlation of broken dyad with the monomeric systems. Thus, from a statistical viewpoint, the dimeric systems are likely to retain the dyad, whereas the monomeric systems are less likely to do so. The dyad instability in the monomer was in agreement with the result that SARS-CoV 3CL^pro (not SARS-CoV-2 3CL^pro) at low concentration (corresponding to a monomeric state) did not show its enzymatic activity [10].

Fig. 4.

Probability distribution of $d_{\mathrm{dyad}}$ for each system (blue lines are for protomer A, and orange for protomer B). The green rectangle region is for monomeric systems; the blue region is for dimeric systems. Solid black lines indicate the upper bound for the judgement of whether the dyad is broken or retained. Red solid vertical lines are the distance between ${\mathrm{N}}_{\epsilon }\left(\mathrm{H}41\right)$ and ${\mathrm{S}}_{\mathrm{\gamma }}\left(\mathrm{C}145\right)$ in an X-ray structure (PDBID: 1UK3A). Orange and blue dotted lines are the mode (i.e., the most frequent value) of each probability distribution.

Table S3 shows that 20% dyad of one protomer in the dimeric systems tended to be broken. It implied that the dyad in each protomer kept its distance asymmetrically like the asymmetric conformation of the active sites in Fig. 3. We thus conjectured that the active site and the dyad in a protomer form conformations different from those in the other protomer and that each protomer has inhomogeneous catalytic activity. Although no study gave the direct evidence to this inhomogeneity, the structural heterogeneity of the active site has been pointed out from crystal structures [46].

It should be noted that the homology modelling structure could not retain the geometry of the dyad even though the template structure 1UJ1 retained its dyad geometry (Table S3). The entire dynamics seemed appropriate, but the probability distribution of the distance for the dyad might have been affected by the modelled initial structure. It suggested that a homology model should be handled carefully by examining not only the overall dynamics but also local structural fluctuations.

3.4. Consensus hydration sites of water molecules

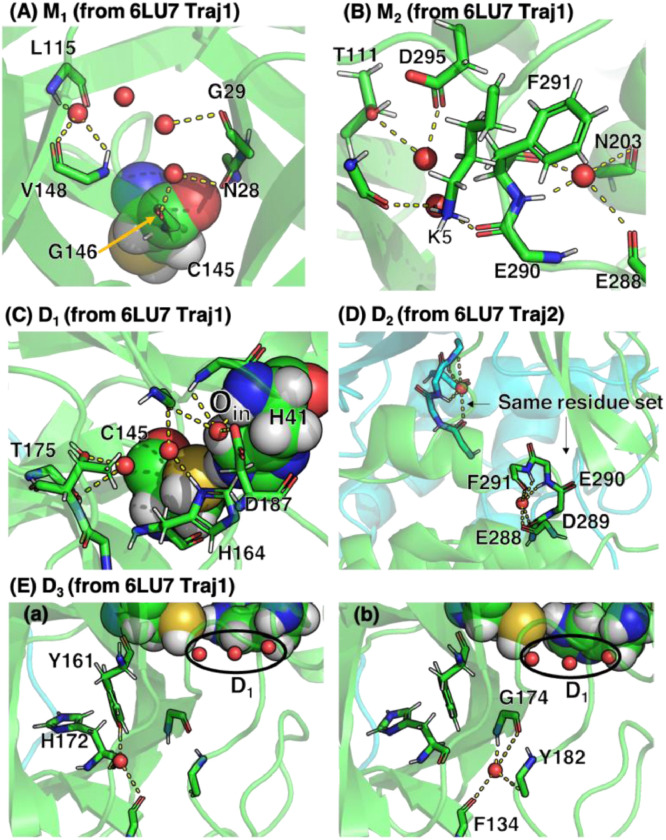
To investigate the role of hydration water in the catalytic activity, we identified sites in which water molecules stayed for more than 500 ns (Fig. S6 and S7). From the sites, we selected and studied three sites (M₁, M₂, and D₁, D₂, and D₃ in Fig. S6 and S7; M and D stands for Monomeric and Dimeric, respectively). Since these were found in most trajectories, we called the sites “consensus hydration sites”.

The consensus hydration sites had one noticeable feature: several water molecules were closely located and were stabilized mainly by the hydrogen bonds to N-H or C=O of the backbone (Fig. 5). For example, backbone's polar atoms in the site D₂ of both protomers interacted with a water molecule (Fig. 5D). The water molecule stabilized the loop in the site D₂. Interestingly, since some residues in the site D₂ (e.g., F291, E290, and E288) were seen even in the site M₂, this hydration site was likely to be conserved in both the monomeric and dimeric systems. The hydration site D₂ may play a crucial role in the dimerization: An earlier study suggested that the mutation E290A for SARS-CoV 3CL^pro led to a complete loss of the activity and dimerization because E290 in a protomer formed a salt bridge with R4 in the other protomer [48]. If the hydration water molecule does not stabilize the site D₂ containing E290, forming an appropriate orientation of E290 towards R4 can be difficult. The hydration water was also observed in crystal structures.

Fig. 5.

Consensus hydration sites obtained from representative snapshots of 6LU7. The sites are, respectively, shown in (A) M₁ (B) M₂, (C) D₁, (D) D₂, and (E) D₃. In (E), two representative structure (a) and (b) are shown. In (C), the water molecule O_in corresponds to the crystal water that are considered important for the catalytic activity [19],[45]. The sphere representation indicates the dyad H41 and C145. The small red spheres represent oxygen atoms of water molecules. Green and cyan cartoon representations show the protomer A and B, respectively. The dotted-yellow lines indicate hydrogen bonds of water molecules to amino-acid residues. The interactions were mainly from backbone atoms, except for the electrostatic interactions with the tips of following residues: K5 (Fig. 5B); T175, H164 and D187 (Fig. 5C); Y161 (Fig. 5E(a)).

The site D₁ in the dimeric systems contained three water molecules (Fig. 5C). This site accommodated the water molecule (dubbed ${\mathrm{O}}_{\text{in}}$) found in most crystal structures that is hydrogen-bonded to ${\mathrm{N}}_{\mathrm{\delta }}\left(\mathrm{H}41\right)$, ${\mathrm{N}}_{\epsilon }\left(\mathrm{Q}163\right)$, and ${\mathrm{O}}_{\mathrm{\delta }}\left(\mathrm{D}187\right)$ [19],[45]. The three water molecules were positioned behind the catalytic dyad, whereas water molecules in the site D₁ were not observed in the monomeric systems. Instead, the site M₁ appeared and was adjacent to D₁. M₁ was likely to be transformed into D₁ in the dimeric systems (Fig. S8)).

The site D₁ accommodating the three water molecules corresponds to the one where a single crystal water molecule is bound (e.g., PDB ID 6WQF, 6LU7, 1UK3, and 1UJ1) (Fig. 2). The difference between our MD trajectories and the crystal structures was the number of hydration water molecules. The crystal structures show the existence of a single crystal water molecule in the site D₁, whereas our trajectories indicated several water molecules in the site.

The site D₃ was observed in most of the trajectories, which was located near D₁ (Fig. 5E and the blue circles in Fig. S7). Thus, the site D₃ can be said to be the most agreed hydration site among the dimeric systems. Our result indicated that this site was conserved among the two different proteases (Fig. S7). Since the water molecule in the site D₃ stayed near D₁, it can contribute to the stability of the site D₁, and thus to the stability of the dyad. In the site D₃, a crystal water molecule is also seen in crystal structures (e.g., 6WQF, 6LU7, 1UK3, 1UJ1, 6M03); it corresponds to the water molecule in Fig. 5E(b). Our trajectories demonstrated that the water molecule in the site D₃ fluctuated between the following hydrogen-bond networks: Y182-G174-F134 and Y161-H172 (Fig. 5E(a) and 5E(b)). We noted that D₃ was not observed in all the trajectories of the monomeric systems (Fig. S6).

3.5. Residence time of water molecules in the hydration site D₁

In the previous section, we discussed the five hydration sites, and the site D₁ contained three water molecules, one of which corresponded to the catalytic water O_in. Here, we investigate the site D₁ further, using residence time ${\tau }_{0.5}^{\text{system}}$, which indicates how long water molecules stay in a site on average (see the definition Eqn. 3). We computed survival probability (SP) of water molecules within the spherical space defined in Fig. 2 (This space was the definition of the site D₁). We then estimated residence time ${\tau }_{0.5}^{\text{system}}$ for each system (Fig. 6 and S9, and Table S4).

Fig. 6.

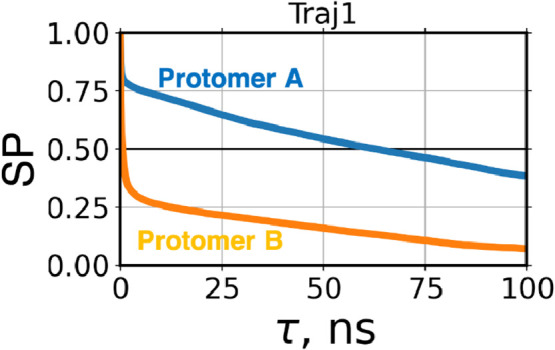
A representative of survival probability (SP) for water molecules in the site D₁, which was taken from Traj1 (1UJ1) in Fig. S9. The horizontal solid line indicates 0.5 of SP, by which ${\tau }_{0.5}^{\mathrm{system}}$ was defined. All of the results are given in Fig. S9.

For the monomeric systems, the residence time for 1UK3A and 1UK3B were shorter than the one for 6LU7 (left columns in Table S4). This showed that the ability of the monomeric SARS-CoV-2 3CL^pro to keep water molecules in the site D₁ was slightly higher than the monomeric SARS-CoV 3CL^pro. Also, since the site D₁ of the monomeric SARS-CoV-2 3CL^pro had the two distinctive values of the residence time (e.g., ${\tau }_{0.5}^{6\text{LU}7}=62.1\text{ns}$ and ${\tau }_{0.5}^{6\text{LU}7}=0.4$ in Table S4). The site D₁ appeared to form at least two water-bound modes. We referred to the two water-bound modes as “water-weakly-bound mode” (if ${\tau }_{0.5}^{\text{system}}<30\text{ns}$) and “water-strongly-bound mode” (${\tau }_{0.5}^{\text{system}}\ge 30\text{ns}$), respectively. On the other hand, the site D₁ in the monomeric SARS-CoV 3CL^pro appeared to form only water-weakly-bound mode, because of the short residence time (${\tau }_{0.5}^{\mathrm{s}}\approx 5.0\text{ns},\mathrm{s}=1\text{UK}3\mathrm{A}\text{or}1\text{UK}3\mathrm{B}$).

For dimeric systems, the site D₁ of one protomer was likely to hold water molecules for longer residence time than that of the other protomer (right columns in Table S4). For both SARS-CoV 3CL^pro and SARS-CoV-2 3CL^pro, the site D₁ of one protomer was capable of forming the water-strongly-bound mode, whereas the site D₁ of the other protomer formed the water-weakly-bound mode. Both protomers were unable to form the water-strongly-bound mode simultaneously (e.g., Fig. 6), but both were able to do the water-weakly-bound mode at the same time.

The comparison of the monomeric and dimeric systems demonstrated that the dimerization stabilized water molecules in the site D₁, because the residence time of the monomeric systems was at most $62.1\text{ns}$, whereas that of the dimeric systems was more than $100\text{ns}$. Indeed, several water molecules settled in the site D₁ for more than 800 ns (not residence time but simulation time). As further analysis, WaterMap method would also be useful to obtain insight into the hydration sites and drug design [49],[50].

It would be beneficial to reiterate the two features for the dimeric systems: (i) the longer residence time of water molecules in the site D₁ than the monomeric systems; (ii) more stable dyad than the monomeric systems. The two results showed that the dimerization stabilized the dyad and hydration water in the site D₁. Unexpectedly, the dyad stability appeared irrelevant to the residence time of the hydration water (Eqn S1 and Table S5), i.e., the hydration water was unlikely to stabilize the dyad. The hydration water molecules may have other roles in the catalytic activity, and we speculated the roles in the subsequent section.

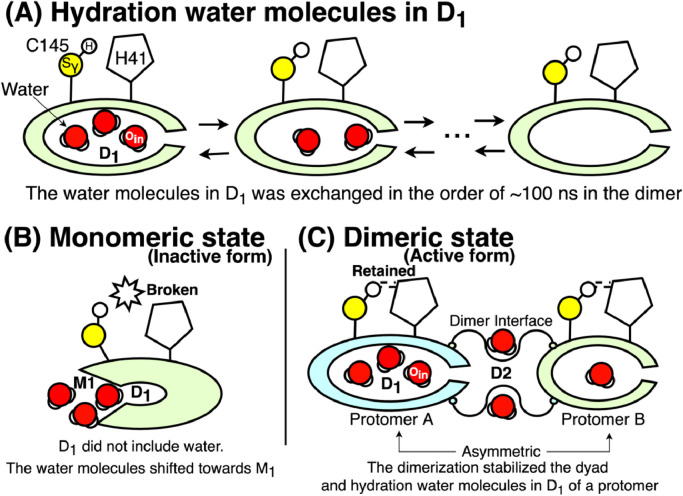
Fig. 7 summarizes the relationship between the water molecules, the dyad, and the oligomeric states. Fig. 7A illustrates the mobility of the hydration water molecules in D₁. The mobility depended on the oligomeric state of the proteases (Table S4 and Fig. S9). In a monomeric state, hydration water molecules did not stay in D₁, and the dyad tended to be broken (Fig. 7B). The dimerization stabilized the water molecules in D₁ and the dyad; the hydration water in D₂ appeared to contribute the dimerization (Fig. 7C).

Fig. 7.

The relation between hydration water molecules, the dyad, and oligomeric states. The red spheres with two white arcs indicate hydration water molecules, the red spheres labeled by O_in are the crystal water molecule observed in many crystal structures; In our simulations, the crystal water O_in was observed in the site D₁. The yellow and white spheres labeled by ${\mathrm{S}}_{\mathrm{\gamma }}$ and H, respectively, are sulfur atoms and hydrogen atoms of C145. (A) The mobility of hydration water molecules in the site D₁. (B) Hydration water molecules and the dyad in a monomeric state. (C) Hydration water molecules in the site D₁ and D₂ in a dimeric state. The molecules in D₁ of each protomer (cyan and light green) had different residence time.

3.6. Speculative roles of hydration water

For further consideration, we conjectured three roles of the hydration water molecules. The first possibility is that the water molecules stabilize the dyad, thereby keeping the activity. The water molecules, however, seemed irrelevant to the dyad stability because of the conditional probabilities calculated from Table S5. For the dyad stability, the dimerization did matter (Fig. 4 and Table 3).

The second possibility is that some of the water molecules in D₁ may transfer protons to C145 that is covalently bonded to a substrate, allowing the substrate to dissociate. It is thought that the catalytic process involves the hydrolysis of the covalent bond, which is attacked by a water molecule [51]. We speculated that a water molecule in D₁ can donate a proton to the covalent bond easier than bulk water molecules does because of the steric hinderance of the covalently-bonded substrate.

The third possibility is that the hydration water may prevent the active site from being denatured by accepting the heat generated by the catalytic reaction and dissipating it into bulk. The hydration water molecules in the site D₁ might act as a medium that gets and releases the heat into bulk. Earlier studies investigated the heat generated by a catalytic reaction of some enzymes: [52], [53], [54] The heat increased the enzyme's diffusivity [52],[53], and the energy of the heat was about 5 kcal/mol [54]. The results raise the question of why the resultant heat does not cause severe denaturation of the active site. We speculated that if the heat dissipates into the hydration water molecules in D₁, the active site may not be intensely perturbed. Since the water molecules in D₁ were mobile (Fig. 6 and S9), they were readily released into the bulk and stored again. In this way, the active site may be prevented from being overheated. For direct verification, future work will take the propagation of the heat into account. A computational method by Stock Gerhard group would be suitable, which applies local temperature jump and then keeps track of the energy propagation [55], [56], [57].

4. Conclusion

The investigation of SARS-CoV 3CL^pro and SARS-CoV-2 3CL^pro in an apo form provides fundamental insight into how they sustain their catalytic activity. In the present study, we simulated the two proteases. We revealed that major global modes were not conserved (Table 2). The changes in the modes would originate from the slight mutations on SARS-CoV-2 3CL^pro. We observed that each active site in the dimeric 3CL^pro obeyed different conformational distribution (Fig. 3). This may imply that each protomer has different substrate specificity. We found that the catalytic dyad in the dimeric systems tended to be retained more than that in the monomeric systems (Fig. 4 and Table 3), which indicated that the dimeric state is active.

Furthermore, we identified hydration water around the two proteases, the water which might be functionally relevant (Fig. 5). Hydration water molecules in the site D₁ of a dimeric state stayed longer than of a monomeric state (Fig. 6). Their residence time depended on the oligomeric states of the two proteases. Since it is thought that the dimer is an active form, these hydration water molecules might be functionally relevant. These tendencies above were also observed in the systems with ionized dyads.

Lastly, we point out unsolved problems. Although the dimerization is crucial for the catalytic activity, the dimerization interface has a large interaction surface, which causes difficulty in targeting the surface. For future work, we illustrated important residues on the interface in “Contact Residues on Dimer Interface” in the supporting information. Plus, even though the allostery cause by several mutations was investigated,[58] the knowledge of the effects on the protease's dynamics is still not adequate for application. Future work should describe more (e.g., by pointing out allosteric pathways) to allow us to manipulate the protease's function. SARS-CoV-2 can mutate readily because it is an RNA virus that mutates more quickly than DNA viruses.[59] The understanding of the mutation effects on the activity is indispensable to a fight for the viruses’ drug-resistance.

CRediT authorship contribution statement

Shinji Iida: Conceptualization, Methodology, Investigation, Validation, Formal analysis, Visualization, Writing – original draft, Data curation. Yoshifumi Fukunishi: Conceptualization, Project administration, Supervision, Funding acquisition, Writing – review & editing.

Declarations of Competing Interest

None.