Abstract
Motivation
Synapses are essential to neural signal transmission. Therefore, quantification of synapses and related neurites from images is vital to gain insights into the underlying pathways of brain functionality and diseases. Despite the wide availability of synaptic punctum imaging data, several issues are impeding satisfactory quantification of these structures by current tools. First, the antibodies used for labeling synapses are not perfectly specific to synapses. These antibodies may exist in neurites or other cell compartments. Second, the brightness of different neurites and synaptic puncta is heterogeneous due to the variation of antibody concentration and synapse-intrinsic differences. Third, images often have low signal to noise ratio due to constraints of experiment facilities and availability of sensitive antibodies. These issues make the detection of synapses challenging and necessitates developing a new tool to easily and accurately quantify synapses.
Results
We present an automatic probability-principled synapse detection algorithm and integrate it into our synapse quantification tool SynQuant. Derived from the theory of order statistics, our method controls the false discovery rate and improves the power of detecting synapses. SynQuant is unsupervised, works for both 2D and 3D data, and can handle multiple staining channels. Through extensive experiments on one synthetic and three real datasets with ground truth annotation or manually labeling, SynQuant was demonstrated to outperform peer specialized unsupervised synapse detection tools as well as generic spot detection methods.
Availability and implementation
Java source code, Fiji plug-in, and test data are available at https://github.com/yu-lab-vt/SynQuant.
Supplementary information
Supplementary data are available at Bioinformatics online.
1 Introduction
The synapse is a critical structure in the nervous system that enables communication and interaction between neurons. Cognitive functions hinge on proper wiring of synaptic connections within neural circuitry. With the help of microscopic fluorescence imaging of stained antibodies that co-localize with the underlying synaptic cleft, it becomes possible to measure the properties of synaptic puncta and neurites. This information enables researchers to gain insights into how brains function under normal and abnormal conditions. Therefore, automatic and accurate quantification of synaptic puncta is highly needed in today’s brain research. (Burette et al., 2015; Lin and Anthony, 2010; Ullian et al., 2011).
There are two main challenges in analyzing these fluorescence images of synaptic puncta (Fig. 1A–C). First, different neurites and puncta show significant variations in terms of morphology and brightness. Besides the heterogeneity of staining, another likely reason is the inherent variation among neurons and neurites according to the different roles they play and the discrepancies in maturity. Second, localization of proteins of interest within synaptic puncta is not typically perfect. One possible reason is that there is actually Synapsin I at low concentrations in the neurites, which results in a low level of positive staining. Another possibility is that staining procedures usually result in some degree of ‘non-specific’ staining. As a result, this diffuse, non-homogenous signal interferes with synaptic punctum detection. For example, even the signal to noise ratio is high for some puncta, it could be much lower for many others in the same dataset. The brighter puncta are more likely to be picked up, but this will introduce bias to the analysis. The non-specific antibodies make it hard to identify puncta purely based on intensity. Moreover, some diffused signals could be even stronger than some puncta. Therefore, the combination of punctum-intrinsic heterogeneity, imperfect protein localization to synapses, along with potentially low SNR, leads to great challenges in accurately and reliably detecting, segmenting and quantifying synaptic puncta.
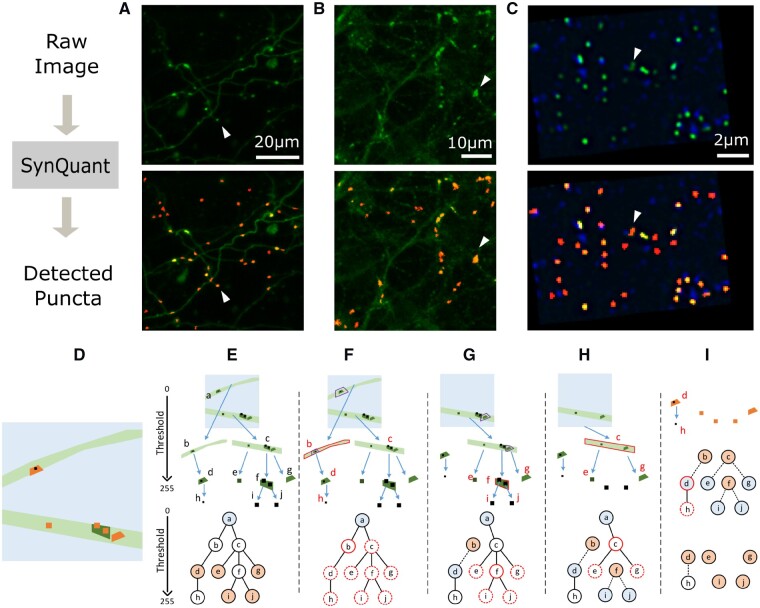
Fig. 1.
(A–C) Examples of raw data and detected puncta. First row images are the raw data and the second row overlaid the detected puncta by SynQuant (shown in red). In the first row, each white arrow points to an example punctum. In the second row, each arrow points to the detected punctum. (A) Bass’ 3D in vivo data (mean projected). (B) In house neuron-astrocyte co-cultured data. (C) Collman’s array tomography data (one z stack is shown). The pre-synaptic channel is shown in blue and the post-synaptic channel is shown in green. The detection results are based on the combination of these two channels. (D–I) Joint synaptic punctum detection and segmentation by iterative tree searching and updating. (D) Illustration for an image with neurites (light green) and puncta (orange). The light blue background and black dots are both noises from the perspective of synaptic punctum detection. (E) Tree structure based on thresholding. Top: the original image is the root node a (Thr = 0). Two branches (b and c) are the children of a with a higher Thr. Repeat this process, we get other nodes and edges. Bottom: tree representation. The light blue node is the root and orange ones are the puncta to be detected. (F) b is the current most significant node (red solid circle). The significance of all its descendants d and h, along with all nodes sharing the same ancestry with b are updated (red dashed circles). E.g. the neighborhood of d was originally chosen within a, but now they were chosen within b (purple boxes in a and b). (G) d becomes the root of a tree and b is the candidate punctum. As f is the most significant one now, e, i, j and g are chosen to be updated. (H) Now we have four trees with a, d, i and j as roots. Repeat this with node c. (I) Continue this process and we get the five significant puncta detected: d, e, g, i and j. Even though b, c and f are statistically significant regions, they are disqualified as puncta because they have children that are statistically significant. For the region d, it has a child h, but the region h is not statistically significant, so the region d remains as a synaptic punctum. (Color version of this figure is available at Bioinformatics online.)
Synapse detection has been an active research topic in recent years and quite a few methods were developed (Danielson and Sang, 2014; Feng et al., 2012; Kulikov et al., 2019; Schmitz et al., 2011; Simhal et al., 2017, 2018). In addition, many image analysis tools for subcellular localization and spot detection have the potential to be repurposed to detect synapses, among which Rezatofighi et al. (2012) and Zhang et al. (2007) are considered as the state of the art (Smal et al., 2010). We summarized these methods in Table 1 and present their main idea, pros and cons in Supplementary Table S1. Through experiments on multiple synthetic and real datasets and by comparison with ground truth or human perception, we found the performance of existing algorithms is far from satisfactory, with either high rates of errors or heavy user intervention. For thresholding-based methods, they do not work well under inhomogeneous background; lack of reliable training data makes it hard to use supervised methods. More importantly, most of them cannot provide a rigorous statistical foundation to assess their output regions and thus give no reliable method to distinguish puncta from noises. Besides, the inhomogeneity of synaptic puncta and neurites is not considered and the comparison between images under different conditions is not well calibrated.
Table 1.
Summary of synaptic punctum and spot detection methods
| Name | Reference | Training data needed | Pre- and post- synaptic channels | 3D | Complex back-ground | Manual intervention per image | GUI | Platform |
|---|---|---|---|---|---|---|---|---|
| SynQuant | This work | No | Yes | Yes | Yes | No | Yes | Fiji plug-in |
| PFSD | Simhal et al. (2018) | No | Yes | Yes | No | No | No | MATLAB, Python |
| SynD | Schmitz et al. (2011) | No | No | No | No | Yes | Yes | MATLAB |
| SynPAnal | Danielson and Sang (2014) | No | No | No | No | Yes | Yes | Java App |
| BGM3D | Feng et al. (2012) | No | No | Yes | No | No | No | MATLAB |
| MP-HD | Rezatofighi et al. (2012) | No | No | Yes | Yes | No | No | MATLAB |
| MS-VST | Zhang et al. (2007) | No | No | Yes | Yes | No | No | Binary file, C++ |
| DoGNet | Kulikov et al. (2019) | Yes | Yes | Yes | Yes | No | No | Python |
| Bouton | Bass et al. (2017) | Yes | No | Yes | Yes | No | Yes | MATLAB |
| U-Net | Ronneberger et al. (2015) | Yes | Yes | Yes | Yes | No | No | Python |
In this work, we develop a probability-principled synaptic punctum detection method that considers the signal non-specificity, heterogeneity and large noise. Then we integrate it into our software tool (SynQuant) that extracts neurites and puncta features (Fig. 1 and Supplementary Fig. S1B). To address the signal non-specificity and heterogeneity, we develop a model that is adaptive to localized region properties. If a region is a synaptic punctum, it is expected to be brighter than its surroundings, even though in the same image there may be brighter non-synaptic background regions. Here are two major analytical problems: (i) how to choose the neighborhood pixels for localized modeling and (ii) how to evaluate the difference between a candidate region and its surroundings, considering some differences may be purely due to noise. The choice of neighborhood pixels is crucial. For example, for a region inside the neurite, a low intensity pixel in the non-neurite background should not be used as a neighbor. A bright pixel in another punctum should not be used either. The difference cannot be solely evaluated based on intensity contrast, because it ignores the number of pixels participating in the comparison: the more pixels, the more reliable the contrast is. Further, although the conventional t-test between a group of pixels and their neighbors can integrate the intensity contrast and number of pixels, the model is severely biased. The operation of choosing a candidate region and its neighbors has already implied that the candidate region is brighter than its surroundings.
Based on the reasoning above, SynQuant contains two key components. First, we use order statistics (David and Nagaraja, 2003) to properly utilize the local information of puncta and fairly compare all synaptic punctum candidates (Fig. 2). For a given candidate punctum region, SynQuant integrates information from the average intensity inside the region, the average intensity of its neighbors, the sizes of the region and of its neighbors, the ranking of all pixels in these two parts and their noise variance. The theory of order statistics provides a powerful tool to correct the bias introduced by the candidate selection operation. To the best of our knowledge, this is the first time that the inherent bias for synaptic punctum detection has been rigorously modeled. Indeed, we suspect that the unawareness of the right model for the inherent bias was a major reason for the lack of rigorous statistical model in the field of synapse detection. Second, we propose an iterative updating strategy to identify appropriate neighbors of the synapse candidates for assessing their statistical significance. By this strategy, we will detect the smallest regions retaining statistical significance, which are more likely to be the synaptic puncta. In addition, our method uses the p-value/z-score reported by order statistics to control the false discovery rate (FDR), which can be pre-specified by the user.
Fig. 2.
Illustration of order-statistics based punctum significance evaluation. (A) A small patch of raw data. Brighter pixels have higher intensities. All pixels are contaminated by Gaussian noise , where is 0.005. (B) Binarize (A) with threshold 0.4. The pixels above the threshold is shown in red. (C) We remove isolated pixels in (B) and fill small holes. The resulting red part S is a candidate region. The blue pixels form its neighbor region . We create a sorted list of all pixels in region , where a pixel with higher intensity will appear earlier. In (C), most pixels in S appear earlier than most pixels in P in . (D) Under the null hypothesis, there is no true punctum and we obtain (along with S and P) by chance due to noise. In (D), we show an example when all pixels are gaussian noise and the intensity order given in is obeyed. The inner part is still brighter than the neighboring part, but the difference is much less obvious since there is no true punctum now. (E) Under the null hypothesis, we use order statistics to obtain the null distribution of (Eq. 1 to Eq. 4). The distribution of has a positive mean, which models the bias of thresholding operation. For the candidate found in (C), we calculate its test statistic and check it against the null distribution of . If it is in the position of the left red arrow, the punctum is not significant. If it is in the right red arrow, it is significant. Larger intensity difference between and larger size of and lower noise level will make the candidate more significant and more likely to be chosen. The creation of the null distribution also models the effect of filling small holes and considers the isolated higher intensity pixels in
Experiments show that our framework obtains a large accuracy gain of synaptic punctum detection on both simulated dataset and three annotated real datasets. In the rest of the paper, we will use synaptic puncta or puncta to refer the signals in fluorescence imaging to be detected. We use synapse or synaptic cleft to refer to manual annotation in the electron microscope.
2 Materials and methods
We first estimate the noise model parameters and stabilize the noise variance of the image (Supplementary Fig. S1B, left panel). After that, we create candidate punctum regions by binarizing the image with multiple intensity thresholds. These thresholds cover the whole range of signal intensities and do not require user intervention. Each threshold leads to some binary connected components, or regions (Fig. 1E). Clearly, regions can be overlapped. Indeed, we build a tree structure where each region becomes a node. The region corresponding to a child node is completely contained in the region of its parent node. Each region is assigned an initial significance score using order statistics. We iteratively search for candidate puncta in the tree and update the statistical significance for each candidate based on the search. The determination of a positive punctum is controlled by the user-specified threshold on the significance level. Neurite tracing, feature extraction, channel combining, 3D implementation and other details of the framework can be found in Supplementary S3.
2.1 Noise estimation and variance stabilization
Application of order statistics theory requires the noise statistics of the pixels in a candidate region and its neighborhood. Conventionally, the noise is modeled as following a Gaussian distribution which simplifies subsequent computations. However, the photon detector introduces noise whose variance is linearly dependent on the signal intensity. We apply the noise model proposed by Foi et al. (2008). The variance for pixel is modelled as . Here is the pixel noise variance. is the underlying signal intensity, which is unknown but can be well approximated by the observed pixel intensity. The term models the Poisson type noise and the term models the additive Gaussian noise. The model can be fit based on pixel data from a single image and the resulting and are used in the Anscombe transform to stabilize the noise (Foi et al., 2008), so that the noise variance associated with the new values after the transform is independent to the intensity itself and can be approximated by a single constant .
2.2 Puncta’s significance scores based on order statistics
In our adaptive tree search and updating algorithm, for each threshold, we get a set of isolated regions (nodes in the tree), each containing a set of pixels (Fig. 1D and E). These regions are potential candidates for synaptic puncta that need to be evaluated by statistical tests. The test for the individual region is based on the difference of this region and its neighbor pixels (Fig. 2E). A larger difference implies a larger possibility that this region is significantly different from the surroundings, which is a necessary (but not sufficient) condition for being a synaptic punctum. For each region, a group of neighbor pixels is selected. We assume there are pixels in the region and pixels in the neighbor, where is the intensity level of pixel . We may use a t-test to compare these two groups. However, due to the thresholding operation, almost all the pixels have higher intensities than the neighbors, though a few exceptions are allowed like isolated high-intensity pixels in the neighbors or low-intensity holes inside the region (Fig. 2B and C). Even if there is no true signal, due to the thresholding, positive difference usually exists between the means of the two groups for any candidate region considered (Fig. 2D and E). This positive difference is a bias and, if not corrected, will complicate the detection and result in a lot of false detections. Here, we are still interested in the difference between the candidate region and its neighbor pixels, and define the test statistic as the following,
| (1) |
Due to the thresholding, the intensities are almost always larger than any intensity of , even without a true signal. Thus, will almost always be positive. The theory of order statistics provides a formal approach to account for the bias by calculating the mean and variance of under the null hypothesis that there is no true signal among the candidate region and its neighbor pixels. Let , we can rewrite as in (David and Nagaraja, 2003):
| (2) |
Here, is a weight function corresponding to the coefficients for in Eq. 1. For , , and for , is the intensity order of among the samples. For instance, 3 if is the pixel with the third highest intensity in the pixels. Note that the order statistic theory requires a continuous function where . We linearly extrapolate the discrete values obtained here to the full range of . We define
| (3) |
and
| (4) |
Then we have and , when (David and Nagaraja, 2003). Here is the normal probability density function with zero mean and variance as the stabilized noise variance . is the corresponding inverse normal cumulative distribution function. The integration is computed by summation using all the samples. Then we define the order statistic score as a function :
| (5) |
where is asymptotically standard Gaussian and hence can be easily used to compute the statistical significance of any observed value of .
As mentioned above, in the presence of noise, the puncta from a certain threshold may contain holes (Fig. 2B). To make its shape more realistic, we may fill the holes (Fig. 2C). Besides, isolated pixels with higher intensity than the threshold might be included as neighbors (Fig. 2C). If we do not allow these exceptions, the pixels in the region is strictly brighter than all its neighbors. Then the null distribution of in Eq. 1 can be calculated simply by a truncated Gaussian model, which is computationally more efficient but less flexible in practice.
2.3 Correction for small sample in order statistics
We note that the statistical significance computed in Eq. 5 is a good approximation only when the sample size is large enough, which may not always be the case. With some typical image resolutions, one synaptic punctum may only contain about 10 or fewer pixels. Here we apply two corrections for the small sample size to improve the approximation. First, we notice for the double integration in , the integration space is a triangle defined by . Since we are using discrete samples, the boundary points will noticeably impact the integration results when the sample size is small. Therefore, half of the boundary points are incorporated in the integration and the other half are not.
Second, the integration over is based on a uniform grid, which corresponds to the values. However, the boundary points and (the largest and smallest values, respectively) strongly deviate from this uniform assumption and the results will be affected when the sample size is small. We would like the integration to mimic the summation. Therefore, we compute the distribution of the largest sample (or smallest) and use the mean to get a new grid. The mean value is computed by
| (6) |
Here should be densely sampled from 0 to 1. Then we get a new grid .
2.4 Iterative detection, FDR control and post-processing
Our iterative detection and segmentation scheme are driven by the statistical significance of each region as computed above (Fig. 1D–I and Supplementary S3.1). Assume the image is stored in 8 bits, we threshold it with all intensity values (0 to 255). For each threshold , we binarize the image and get all connected regions as foreground. Suppose we totally get regions with all thresholds, the set of all regions is denoted by . We denote as , then . We build a tree , whose nodes are . is the edge set describing the way to connect nodes in . Now each node is associated with a region , along with the threshold under which it is generated. Then the directed edge set is defined as , which links region to region that is completely within it (Fig. 1E). This structure shares the similar principle as Mattes et al. (1999).
Each node is also related to a neighbor pixel set and a score from order statistics. Since the computation of order statistics depends on the choice of neighbor pixels, depends on . Recalling Eq. 5, we have . On one hand, should include neighbor pixels of and thus will be within an ancestry node of , which is defined by the tree and denoted as . The number of pixels in needs to be carefully specified. If is too large, many pixels far away from the candidate region will be included and thus the comparison is not restricted to the local area. If is too small, we lose the statistical power to assess the significance of the candidate region. We find that requiring to have a similar size as the candidate region is a good balance. In practice, we specify the neighbor region by growing the candidate region layer by layer until is larger than . On the other hand, not all neighbor pixels of should be included in even though these pixels are close to , because these pixels may belong to another synaptic punctum region. Therefore, we require should not include any pixel of a significant region. Hence, also depends on as the significance of regions is determined by , which leads to the iterative scheme as described below.
Our algorithm iteratively updates and for each node on the tree . We initialize the root node (, whole image) as the candidate region. For all other nodes, we initialize . All the other nodes now choose neighbor pixels within the image (Fig. 1E) and do not avoid any pixels, because there is no significant region. Based on the choice of , we update for all nodes (except the root). Then we search for the most significant node and update for all the descendants of , except those that are already significant (Fig. 1F). After that, node is removed from the tree as a candidate punctum and its children will be new roots of new trees (Fig. 1G). Again, the updated will give us new . In later iterations, once any descendants of becomes a new candidate, is disqualified as a punctum. This drives the algorithm to avoid neurite-like structures (Fig. 1H–I).
FDR control is used during the iterations. In each iteration, we pick the candidate region with the highest score (Eq. 5) and determine whether we can add it to the list of significant regions. The decision is made such that we keep the FDR lower than a given threshold among all synaptic puncta detected. The threshold is a parameter specified by the user. Because overlapped regions may be correlated, we use the general case introduced by Benjamini and Yosef (1995). In each iteration, we test that whether adding the newly selected region to the list of existing significant regions can still keep the FDR lower than the threshold based on their p-values. If so, we add it as a new significant region and continue to new iteration. If not, the algorithm stops. The total number of iterations depends on the number of synaptic puncta (significant regions) in the image and the user-specified FDR threshold. More details can be found in Supplementary S3.2.
Three rules based on the prior knowledge of the puncta are applied to post-process the synaptic punctum candidates (Uijlings et al., 2013). First, we filter out candidates that are too small or too large. Second, we expect the puncta to be close to circles or ellipses and we enforce this by setting threshold on the aspect ratios of puncta. Third, we expect the detected puncta to be roughly convex shaped, so we compare the area of the bounding box of a punctum with its area and remove those with low filling rate. In the experiments, these rules are applied to all methods.
3 Results
We tested SynQuant on one simulated and three real datasets and compared it with four unsupervised methods and up to eleven variants of three supervised methods. The three real datasets include 2D cultured cells (Mizuno et al., 2018), 3D multi-channel array tomography on brain slices (Collman et al., 2015) and 3D in vivo data (Bass et al., 2017). We summarize the properties of each dataset in Supplementary Table S2. Among the methods, SynD, PFSD, Bouton and DoGNet were designed for synaptic punctum detection, MS-VST and MP-HD are spot detection tools, and U-Net is a deep learning model for semantic segmentation. DoGNet contains two shallow neural networks and two deeper models. Each model uses either an isotropic or anisotropic kernel to match the shape of puncta. For U-Net, we use the model provided in Kulikov et al., 2019. Here we did not include the two methods mentioned in Table 1: SynPAnal and BGM3D. SynPAnal needs user to crop the region of dendrite first. BGM3D is based on global thresholding like SynD. All the datasets, labels and code to generate the synthetic data are available on the GitHub website.
We evaluated the performance by precision, recall, F1-score and average precision (AP). We use Intersection-over-Union (IoU) to infer true positive (TP), which is more suitable when we want to jointly evaluate the detection and segmentation performance. If the overlap of ground truth and the detected punctum is larger than 50% of their union, the detected punctum is viewed as a TP. For real data, we do not have pixel-level annotations, so we set the threshold as 0%, that is, a TP is claimed as long as the detection has any overlap with the ground truth or annotation. Precision is defined as the TP/(TP+FP) and recall is TP/(TP+FN), where FP is the number of false positives and FN is the number of false negatives. The F1-score is . We report the best F1-score among all points in the precision-recall curve (see Supplementary S9.4 for z-score threshold setting of SynQuant). We also calculate the average precision based on the precision-recall curve (Everingham et al., 2010), which scans recall from 0.01 to 1, with step size 0.01. AP summarizes the information contained in the precision-recall curve and is a more comprehensive measure than the best F-score. Each method provides a score map with the same size as the input data. We threshold the score map from its minimum value to its maximum value with 100 thresholds. We calculate a precision-recall pair for the puncta above each threshold.
We use about 80% the data to train supervised methods. We use ‘trained’ to indicate that methods are trained from scratch. For Bouton, we also use its pre-trained model. For DoGNet, we also try to first train on the Collman’s data, which has the largest number of labels, and then fine tune it using the labeled data provided in each dataset. This allows us to train the deeper versions of models in DoGNet. These methods are put in the ‘tuned’ group. In all experiments and for all methods, post processing is applied. Other considerations and parameter settings are discussed in each experiment and in Supplementary S4. More details on training DoGNet and Un-Net can be found in Supplementary S5. The minimum size of a punctum is 8 voxels for real data and 4 for synthetic data; the maximum size is 300 voxels; the aspect ratio should be between 0.5 and 2; the ratio of voxels to bounding boxes should be larger than 0.5. We also investigated the relationship between synapse density and Down syndrome cell types as in Supplementary S10.
3.1 Results on synthetic data
Our simulated data consists of both synapse and neurite like signals to mimic real data (Supplementary S6), which simulates the punctum inhomogeneity and antibody non-specificity. We compared the F1-score of all methods with different simulation settings. We first simulated the impact of Poisson Gaussian noise on the performance (Supplementary S7). The SNR was calculated as the average SNR for each simulated punctum. For all SNRs, SynQuant performs always the best. For example, when IoU threshold is 0, the best F1-score of SynQuant outperforms the best performing peer method by 0.162 (0.981 versus 0.819) under 11.5 dB SNR. Then we studied the impact of the range of punctum size (Supplementary S7). SyQuant still performs the best in all experiments. When the range of punctum size is 9 to 150 pixels, the best F1-score from SynQuant outperforms the best peer method by 0.159 (0.962 versus 0.803) when the IoU threshold is 0.5 and SNR is 17.2 dB. With IoU threshold equals to 0.5, inaccurate segmentation of a puncta will be considered as a false positive. The experiments in the synthetic data show that SynQuant is robust to noises and punctum size changes. More details can be found in the Supplementary S7.
3.2 Results on Bass’ 3D in vivo data
We tested SynQuant on the in vivo 3D image data available in Bass et al. (2017). In this data, signals can be observed on both neurites and synaptic puncta (Fig 1A). The dataset contains 20 completely annotated images. We divide the 20 well annotated images into two groups. We randomly selected 16 images to train supervised methods and the remaining 4 were used to test all methods. We repeated this for 10 times and report the mean performance in Table 2. The results with standard error are given in Supplementary S9.1. Though the data is 3D, the annotations are 2D bounding boxes of the puncta. Besides, we find these labels are all oversized, which contain many redundant background pixels (Supplementary Fig. S3). Nearby puncta are easily overlapped with each other with these large labels. However, by examining the data, one punctum always occupies single isolated spatial location. Thus, we reduce the label size by taking the center of each punctum and put a square whose size is similar to the average actual size of puncta in the image. The shallow anisotropic version of DoGNet and the deep versions of DoGNet always fail if directly trained on this data. We do not include these methods here.
Table 2.
Results on Bass' in vivo 3D data
| Method | Precision | Recall | Best F1 | AP |
|---|---|---|---|---|
| Unsupervised | ||||
| SynQuant (proposed) | 0.912 | 0.862 | 0.882 | 0.895 |
| PFSD | 0.444 | 0.355 | 0.382 | 0.196 |
| SynD | 0.723 | 0.691 | 0.683 | 0.502 |
| MSVST | 0.906 | 0.757 | 0.818 | 0.779 |
| MP-HD | 0.898 | 0.717 | 0.789 | 0.738 |
| Supervised, trained | ||||
| DoGNet, shallow, isotropic | 0.882 | 0.785 | 0.823 | 0.800 |
| U-Net | 0.873 | 0.553 | 0.661 | 0.525 |
| Bouton | 0.806 | 0.851 | 0.823 | 0.746 |
| Supervised, pre-trained + tuned | ||||
| DoGNet, shallow, isotropic | 0.878 | 0.840 | 0.851 | 0.841 |
| DoGNet, shallow, anisotropic | 0.890 | 0.840 | 0.857 | 0.841 |
| DoGNet, deep, isotropic | 0.664 | 0.390 | 0.467 | 0.298 |
| DoGNet, deep, anisotropic | 0.642 | 0.412 | 0.484 | 0.324 |
| U-Net | 0.680 | 0.501 | 0.562 | 0.410 |
Note: Here Best F1 is the best F1 score among all points in the precision-recall curve. AP is the average precision. The experiments are repeated 10 times by randomly selecting training set and the average performance is shown here.
The bold faces were used to highlight these numbers. No statistical significance associated.
For Bouton, we used the pre-trained model based on the 80 partially labeled training images. In Bouton, the images are first mean-projected to 2D. For SynQuant and PFSD, we directly detected in 3D. For MS-VST and MP-HD, the performance of 3D version is comparable with 2D version, so we only show the 2D results. As we do not have 3D labeling, we apply DoGNet to mean-projected image as well. The 16 training images are not sufficient to train the deeper models in DoGNet and cannot make correct predictions. Therefore, other than directly training deeper models, we also used the 16 images to fine tune the deeper DoGNet/U-Net models that are pre-trained in Collman’s data. Results show that for both F1 score and average precision, SynQuant performs the best among all unsupervised methods compared (Table 2). DoGNet is the best performing supervised method. Bouton fails to detect the center of puncta accurately, which degrades its performance.
3.3 Results on Collman’s array tomography data
We tested SynQuant on the array tomography data in Collman et al., (2015). There are two datasets provided and each data is stained with multiple antibodies. We use the PSD stained post synaptic channel and the Synapsin labeled pre-synaptic channel. Each data is also imaged with electron microscopy (EM). The synaptic clefts in the EM images were annotated. The annotations are down-sampled to match the original resolution of the fluorescence staining (0.1 /pixel). We use Collman14 data to train all supervised methods and test on Collman15 data (the number of annotations on Collman14 is ∼5.5 times to that on Collman15.). The ground truth annotation is in EM channel, some of which do not correspond to the puncta in synaptic channels. This kind of inconsistency usually happens when the imaging field of view for fluorescence channels and EM channel are different. To correct it, we check each annotation. If it does not have any fluorescence staining co-localized, we remove that annotation.
The annotations on EM channel are not suitable for training the model from scratch for Bouton. SynD does not support 3D data, so we do not list it here. SynQuant and PFSD can be directly applied on 3D data. For other methods, we detect puncta stack by stack and combine the score maps afterwards. This is the default used by DoGNet and was shown to perform better than 3D version of DoGNet (Kulikov et al., 2019). The 3D version of MS-VST and MP-HD performs worse than their 2D version. Since the Collman14 data has large number of ground truth labels, we do not need to use other data to train first. Therefore, we do not have the ‘tuned’ models listed in Table 3. While DoGNet and PFSD are able to integrate information from two channels, other peer methods do not have this functionality. Therefore, for these methods, we apply the same method SynQuant uses to combine results from the pre-synaptic and the post-synaptic channels. We evaluate the performance on pre-synaptic channel, post-synaptic channel and combined results. Again, SynQuant performs best among all unsupervised methods and DoGNet is the best performing supervised methods.
Table 3.
Results on Collman's array tomography data
| Method | Precision | Recall | Best F1 | AP |
|---|---|---|---|---|
| Unsupervised | ||||
| SynQuant (proposed) | 0.882 | 0.699 | 0.780 | 0.754 |
| PFSD | 0.885 | 0.589 | 0.707 | 0.666 |
| MSVST | 0.905 | 0.648 | 0.756 | 0.715 |
| MP-HD | 0.876 | 0.648 | 0.745 | 0.680 |
| Supervised, trained | ||||
| DoGNet, shallow, isotropic | 0.795 | 0.691 | 0.739 | 0.638 |
| DoGNet, shallow, anisotropic | 0.868 | 0.636 | 0.734 | 0.621 |
| DoGNet, deep, isotropic | 0.880 | 0.708 | 0.784 | 0.704 |
| DoGNet, deep, anisotropic | 0.897 | 0.665 | 0.764 | 0.691 |
| U-Net | 0.823 | 0.631 | 0.715 | 0.626 |
| Supervised, pretrained | ||||
| Bouton | 0.602 | 0.224 | 0.327 | 0.229 |
The bold faces were used to highlight these numbers. No statistical significance associated.
3.4 Results on neuron-astrocyte co-cultured data
We tested SynQuant and other methods on our in-house neuron-astrocyte co-culture dataset, which contains 16 images. The size of each image is 256 by 256 pixels. Each image contains two channels: the synapse channel labeled by Synapsin I and the neurite channel labeled with Tuj1. We manually labeled puncta in the Synapsin I channels in these 16 images. Only the puncta that are clear enough to reach the consensus between two experts are considered as ground truth. The results based on other ways of combining the two annotators’ labels are given in Supplementary S9.2. We randomly selected 12 images to train DoGNet and U-Net. The remaining 4 are used for testing. This process was repeated for 10 times, and Table 4 shows the mean performance. For the results with standard error, please see Supplementary Table S6.
Table 4.
Results on neuron-astrocyte co-cultured data
| Method | Precision | Recall | Best F1 | AP |
|---|---|---|---|---|
| Unsupervised | ||||
| SynQuant (proposed) | 0.931 | 0.883 | 0.901 | 0.927 |
| PFSD | 0.448 | 0.677 | 0.529 | 0.321 |
| SynD | 0.524 | 0.934 | 0.664 | 0.484 |
| MSVST | 0.929 | 0.881 | 0.860 | 0.864 |
| MP-HD | 0.880 | 0.728 | 0.781 | 0.768 |
| Supervised, trained | ||||
| DoGNet, shallow, isotropic | 0.923 | 0.867 | 0.890 | 0.880 |
| DoGNet, shallow, anisotropic | 0.905 | 0.877 | 0.886 | 0.879 |
| U-Net | 0.924 | 0.786 | 0.841 | 0.806 |
| Supervised, pre-trained + tuned | ||||
| DoGNet, shallow, isotropic | 0.921 | 0.867 | 0.889 | 0.878 |
| DoGNet, shallow, anisotropic | 0.925 | 0.885 | 0.901 | 0.904 |
| DoGNet, deep, isotropic | 0.917 | 0.910 | 0.912 | 0.930 |
| DoGNet, deep, anisotropic | 0.913 | 0.899 | 0.902 | 0.919 |
| U-Net | 0.884 | 0.884 | 0.880 | 0.883 |
| Supervised, pre-trained | ||||
| Bouton | 0.561 | 0.527 | 0.530 | 0.429 |
The bold faces were used to highlight these numbers. No statistical significance associated.
For DoGNet and U-Net, directly using the model pre-trained on Collman’s data does not perform well, so we fine tune the model pre-trained on Collman’s data using 12 training images. We also directly train the DoGNet and U-Net models from scratch using the 12 training images. The deeper models in DoGNet cannot be successfully trained given limited training data, though they can be trained first with the larger Collman’s data and tuned after that. Even though U-Net is not designed for synaptic punctum detection, it works well in this data. Because the Bouton model that trained on this data performs similar with the pre-trained model, we directly use the pre-trained model here. We report the performance based on the average of the 8 test images and 10 repeated experiments. The precision and recall in Table 4 correspond to the best F1 score. SynQuant outperforms all unsupervised methods for this data.
3.5 Summary and remarks of the experimental results
In summary, tested on a large variety of experiment settings, including 2D versus 3D, single versus multiple channels, confocal, two-photon or array tomography, neurite contamination versus no contamination and manual labeling versus EM annotation, SynQuant always outperforms other unsupervised state-of-the-arts in terms of the average precision or the best F1 score. In the experiments, we directly apply the DoGNet package for neural-networks based methods. We note the performance of DoGNet and U-Net could be improved by extensively tuning the hyper parameters for each datasets. Since the datasets are all small, DoGNet and U-Net’s performance may also be improved by employing more sophisticated data augmentation, obtaining more labeled data and improving the accuracy of the labels.
4 Discussion
We have presented a new automatic synapse quantification framework (SynQuant) for detection and quantification of heterogeneous and noisy images of synapses and dendrites. SynQuant is able to detect synaptic puncta accurately and extract comprehensive features. The superior performance of SynQuant comes from the effective utilization of the local region-neighbor information. Enjoying the same principle as Hariharan et al. (2014), SynQuant uses the tree structure of regions to choose the correct neighborhood pixels. Order statistics provides an unbiased score to each candidate region. Compared with existing methods, SynQuant is able to extract accurate detection results, which allows access to important features for synapse studies.
Although supervised methods (like DoGNet) work well on the datasets we tested above and are likely to have better performance with more training data and more sophisticated deep learning structures, they have several limitations. First, the creation of training labels can be time consuming, especially if a lot of training samples are needed for better performance. Second, the model trained based on existing labels usually cannot be directly applied to another data, unless the datasets are obtained under very similar experiment setups. Therefore, more training labels on the new dataset are needed. Third, for datasets without ground truth, supervised models may be influenced by human bias unconsciously introduced in data labels. For example, we observed that in manually labelled real datasets, puncta with low intensities are much more likely to be missed in the labeling than those brighter ones. Under such biased labels, supervised models have a high risk of missing dimmer puncta. We note that SynQuant does not completely avoid users’ bias, because users need to choose a z-score threshold for SynQuant to balance the tradeoff between sensitivity and specificity, and this kind of balance can be viewed as user’s preference or bias. However, the sensitivity-specificity tradeoff is a necessity for any detection task and SynQuant makes it explicit.
SynQuant supports 3D data as well as multi-channel data with both the pre-synaptic puncta and post-synaptic puncta. Moreover, SynQuant is a general framework to analyze images with a high level of non-specificity. We can naturally adapt and apply it to bio-medical images beyond synapse staining, such as particle detection for the particle tracking problem.
In the future, SynQuant can be improved in two aspects. First, we did not study the optimal way of combining results from multiple channels; currently we simply adopted the approach used in Simhal et al., 2017. As multi-channel data are more and more prevalent, it is worthy to study how multiple channels can be best utilized to predict the synaptic cleft. Second, the order statistics step in SynQuant requires relatively high computational cost and memory usage on large images and could be unbearable for extremely large datasets. From our observation, most puncta are independent with each other. Thus, separating the field of view into sub-sections, parallelly handling them and optimally combining the results is likely to make SynQuant applicable to super-large scale datasets.
Supplementary Material
Acknowledgements
We thank the anonymous reviewers for their helpful suggestions.
Funding
This work was supported by funding to G.Y. (NIH R01MH110504 and NSF 1750931) and L.T. (NIH U01NS090604, DP2MH107056 and R21NS095325).
Conflict of Interest: none declared.
Contributor Information
Yizhi Wang, Bradley Department of Electrical and Computer Engineering, Virginia Polytechnic Institute and State University, Blacksburg, VA 22203, USA.
Congchao Wang, Bradley Department of Electrical and Computer Engineering, Virginia Polytechnic Institute and State University, Blacksburg, VA 22203, USA.
Petter Ranefall, Centre for Image Analysis and SciLifeLab, Department of Information Technology, Uppsala University, Uppsala, Sweden.
Gerard Joey Broussard, Department of Molecular Biology and Princeton Neuroscience Institute, Princeton University, Princeton, NJ 08544, USA.
Yinxue Wang, Bradley Department of Electrical and Computer Engineering, Virginia Polytechnic Institute and State University, Blacksburg, VA 22203, USA.
Guilai Shi, Department of Biochemistry and Molecular Medicine, University of California Davis School of Medicine, Sacramento, CA 95817, USA.
Boyu Lyu, Bradley Department of Electrical and Computer Engineering, Virginia Polytechnic Institute and State University, Blacksburg, VA 22203, USA.
Chiung-Ting Wu, Bradley Department of Electrical and Computer Engineering, Virginia Polytechnic Institute and State University, Blacksburg, VA 22203, USA.
Yue Wang, Bradley Department of Electrical and Computer Engineering, Virginia Polytechnic Institute and State University, Blacksburg, VA 22203, USA.
Lin Tian, Department of Biochemistry and Molecular Medicine, University of California Davis School of Medicine, Sacramento, CA 95817, USA.
Guoqiang Yu, Bradley Department of Electrical and Computer Engineering, Virginia Polytechnic Institute and State University, Blacksburg, VA 22203, USA.
References
- Bass C. et al. (2017) Detection of axonal synapses in 3d two-photon images. PLoS One, 12, e0183309. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Benjamini Y., Hochberg Y. (1995) Controlling the false discovery rate: a practical and powerful approach to multiple testing. J. R. Stat. Soc. B (Methodological), 57, 289–300. [Google Scholar]
- Burette A. et al. (2015) Knowing a synapse when you see one. Front. Neuroanat., 9, 100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Collman F. et al. (2015) Mapping synapses by conjugate light-electron array tomography. J. Neurosci., 35, 5792–5807. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Danielson E., Sang L. (2014) SynPAnal: software for rapid quantification of the density and intensity of protein puncta from fluorescence microscopy images of neurons. PLoS One, 9, e115298.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- David H.A., Nagaraja H.N. (2003) Order Statistics. 3rd edn. Wiley-Interscience, New York. [Google Scholar]
- Everingham M. et al. (2010) The pascal visual object classes (VOC) challenge. Int. J. Comput. Vis., 88, 303–338. [Google Scholar]
- Feng L. et al. (2012) Improved synapse detection for mGRASP assisted brain connectivity mapping. Bioinformatics, 28, i25–i3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Foi A. et al. (2008) Practical Poissonian-Gaussian noise modeling and fitting for single-image raw-data. IEEE Trans. Image Process., 17, 1737–1754. [DOI] [PubMed] [Google Scholar]
- Hariharan B. et al. (2014) Simultaneous detection and segmentation. In: Computer Vision–ECCV, Springer International Publishing, pp. 297–312. [Google Scholar]
- Kulikov V. et al. (2019) DoGNet: a deep architecture for synapse detection in multiplexed fluorescence images. PLoS Comput. Biol., 15, e1007012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin Y., Anthony K. (2010) Mechanisms of synapse and dendrite maintenance and their disruption in psychiatric and neurodegenerative disorders. Annu. Rev. Neurosci., 33, 349.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mattes J. et al. (1999) Tree representation for image matching and object recognition. In: Bertrand,G. et al. (eds.) Discrete Geometry for Computer Imagery, Springer, Berlin, Heidelberg, pp. 298–309. [Google Scholar]
- Meijering E. et al. (2004) Design and validation of a tool for neurite tracing and analysis in fluorescence microscopy images. Cytometry A, 58, 167–176. [DOI] [PubMed] [Google Scholar]
- Mizuno G.O. et al. (2018) Aberrant calcium signaling in astrocytes inhibits neuronal excitability in a human Down syndrome stem cell model. Cell Rep., 24, 355–365. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Najman L., Couprie M. (2006) Building the component tree in quasi-linear time. IEEE Trans. Image Process., 15, 3531–3539. [DOI] [PubMed] [Google Scholar]
- Ranefall P. et al. (2016) Fast Adaptive Local Thresholding Based on Ellipse Fit. In: Proceedings of the International Symposium on Biomedical Imaging (ISBI'16), Prague, Czech Republic.
- Rezatofighi S. et al. (2012) A new approach for spot detection in total internal reflection fluorescence microscopy. In: 2012 9th IEEE International Symposium on Biomedical Imaging (ISBI), pp. 860–863.
- Ronneberger O. et al. (2015) U-net: convolutional networks for biomedical image segmentation. In: International Conference on Medical Image Computing and Computer-Assisted Intervention. Springer, Cham. [Google Scholar]
- Smal I. et al. (2010) Quantitative comparison of spot detection methods in fluorescence microscopy. Med. Imaging IEEE Trans., 29, 282–301. [DOI] [PubMed] [Google Scholar]
- Schindelin J. et al. (2012) Fiji: an open-source platform for biological-image analysis. Nat. Methods, 9, 676–682. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schmitz S. et al. (2011) Automated analysis of neuronal morphology, synapse number and synaptic recruitment. J. Neurosci. Methods, 195, 185–193. [DOI] [PubMed] [Google Scholar]
- Simhal A.K. et al. (2017) Probabilistic fluorescence-based synapse detection. PLoS Comput. Biol., 13, e1005493. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Simhal A.K. et al. (2018) A computational synaptic antibody characterization tool for array tomography. Front. Neuroanat., 12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ullian E. et al. (2001) Control of synapse number by glia. Science, 291, 657–661. [DOI] [PubMed] [Google Scholar]
- Uijlings J. et al. (2013) Selective search for object recognition. Int. J. Comput. Vis., 104, 154–171. [Google Scholar]
- Zhang B. et al. (2007) Multiscale variance-stabilizing transform for mixed-Poisson-Gaussian processes and its applications in bioimaging. In: 2007 IEEE International Conference on Image Processing, pp. VI-233–VI-236.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.