Dynamic Time-Warping Correction for Shifts in Ultrahigh Resolving Power Ion Mobility Spectrometry and Structures for Lossless Ion Manipulations

Abstract

Detection of arrival time shifts between ion mobility spectrometry (IMS) separations can limit achievable resolving power (Rp), particularly when multiple separations are summed or averaged, as commonly practiced in IMS. Such variations can be apparent in higher Rp measurements and are particularly evident in long path length traveling wave structures for lossless ion manipulations (SLIM) IMS due to their typically much longer separation times. Here, we explore data processing approaches employing single value alignment (SVA) and nonlinear dynamic time warping (DTW) to correct for variations between IMS separations, such as due to pressure fluctuations, to enable more effective spectrum summation for improving Rp and detection of low-intensity species. For multipass SLIM IMS separations, where narrow mobility range measurements have arrival times that can extend to several seconds, the SVA approach effectively corrected for such variations and significantly improved Rp for summed separations. However, SVA was much less effective for broad mobility range separations, such as obtained with multilevel SLIM IMS. Changes in ions’ arrival times were observed to be correlated with small pressure changes, with approximately 0.6% relative arrival time shifts being common, sufficient to result in a loss of Rp for summed separations. Comparison of the approaches showed that DTW alignment performed similarly to SVA when used over a narrow mobility range but was significantly better (providing narrower peaks and higher signal intensities) for wide mobility range data. We found that the DTW approach increased Rp by as much as 115% for measurements in which 50 IMS separations over 2 s were summed. We conclude that DTW is superior to SVA for ultra-high-resolution broad mobility range SLIM IMS separations and leads to a large improvement in effective Rp, correcting for ion arrival time shifts regardless of the cause, as well as improving the detectability of low-abundance species. Our tool is publicly available for use with universal ion mobility format (.UIMF) and text (.txt) files.

Graphical Abstract

INTRODUCTION

Variations in analytical separations (e.g., achieved resolution, peak widths, limits of detection, and measurement dynamic range) not only limit measurement-to-measurement and lab-to-lab reproducibility and comparisons but can also impact the apparent resolution or resolving power (Rp) of separations. This is particularly the case for arrival time shifts between ion mobility spectrometry (IMS) separations, where multiple separations are typically summed or averaged to improve data qualities (most prominently, signal-to-noise ratios). This is in contrast to LC and GC where multiple separations are rarely summed or averaged, and interest is typically focused on the differences between the separations that can be attributed to analyte mixture differences. Such variations in IMS separations (e.g., for ions formed by ESI from a nominally identical sample) can be expected to become increasingly problematic with extended time scales or higher Rp measurements due to the higher probability of significant fluctuations in pressure, temperature, electric fields, etc.^1,2 In particular, lengthy separation times (often >1 s for an individual separation) allow ample opportunity for small pressure fluctuations (or other instabilities) to influence ion arrival times for individual separations. These instrumental fluctuations will lead to increased peak widths and peak asymmetry when multiple separations are summed, as well as decreased detectability for low-abundance species.

In previous work using structures for lossless ion manipulations (SLIM) multipass serpentine ultralong path with extended routing (SUPER) IMS,^3-5 we have found that a single value alignment (SVA) of the individual separations provided significant improvements in data quality, improving Rp in many cases. Such IMS separations are characterized by long separation times as well as narrow mobility ranges: situations where SVA should be most effective. We note that an SVA approach with IMS has also recently been applied by others. Caprioli and co-workers found that shifting all data points in a mobility spectrum by a single value was sufficient for correcting for arrival time fluctuations and variable surface features in MALDI-IMS.^6,7 Similarly, Meier et al. used an SVA tool to correct for collisional cross section (CCS) variations that they observed in their trapped ion mobility spectrometer (TIMS),⁸ which they attributed to small fluctuations in gas flow.

The limitations of the SVA approach can become significant when using ultra-high-resolution IMS separations with longer arrival times that also span wider mobility ranges. Perhaps the most extreme example is the recently developed multilevel SLIM IMS, which can separate ions of vastly different mobility over a single 43.2 m path (i.e., without the use of multipass approaches).⁹ In this case, the SVA approach would be expected to be effective over small mobility ranges (i.e., limited portions of the separation), but less effective over the whole separation because ion arrival times are nonlinearly dependent on mobility in traveling wave IMS (TWIMS).¹⁰

Ultrahigh Rp and broad mobility range IMS would benefit from the ability to account for nonlinear changes in arrival times between separations where the shifts change in magnitude differently for ions of much different mobility. One such method that can account for such nonlinear differences is dynamic time warping (DTW), which is a well-established time series classification technique used heavily in computer science and data mining for finding and matching similar features between spectra.^11-14 The premise of classical DTW is to find the minimum Euclidean distances (i.e., the smallest change in y-values) between two data sets and nonlinearly shift the corresponding time series to obtain the best fit.¹⁵ “Continuity” and “monotonicity” constraints are typically imposed in DTW algorithms to ensure that features are not ignored or repeated, respectively.¹⁵ Additionally, commonly used boundary conditions, such as the Sakoe–Chiba or Itakura parallelogram methods, place constraints on the time window during warping to prevent matching of features that are far apart.¹⁶ The combination of constraints provides more accurate and rapid analysis than without restrictions and also reduces the chances of obtaining a singularity,¹⁷ albeit at the expense of “optimal” alignment.

Although the DTW process was initially described by Bellman in 1953 (termed dynamic programming),¹⁸ it has since been applied to analytical separations that employ long separation times, including gas chromatography,¹⁹ liquid chromatography,²⁰ and capillary electrophoresis, and particularly 2-dimensional PAGE gel electrophoresis.²¹ These techniques generally employ DTW to find differences between separations rather than to improve resolution. It is rare to use data alignment techniques to increase the data qualities of presumably identical separations. However, data alignment in IMS often has a vital role in improving data quality and detectability of low-abundance species. Nonlinear data alignment, such as DTW, has not previously been recognized as useful in IMS, a view that can be largely attributed to its speed (generally <100 ms) and limited Rp.²² Although many more modern methods of times series analysis exist (e.g., decision trees,^23,24 hierarchical clustering,²⁵ support vector machines,^26,27 hidden Markov models,²⁸ etc.), several studies have shown that DTW outperforms many of these methods.^29-34 As the Rp and separation times of IMS continue to increase, we believe it will also be increasingly beneficial to correct for arrival time variations to optimize Rp and the sensitivity of summed separations.

Here, we report on the development and implementation of a DTW data alignment tool that corrects for arrival time shifts in IMS. An SVA tool was also developed and compared to DTW. We have found that the DTW performed similarly to SVA when used for a narrow range of mobilities but drastically outperformed SVA when used over a wide mobility range in measurements performed using a multilevel SLIM IMS-MS. The data aligners are combined into one easy-to-use package and are available for public use.

EXPERIMENTAL SECTION

Chemicals and Electrospray Ionization.

A low-concentration Agilent tuning mixture was purchased from Agilent Technologies (Santa Clara, CA). Heavy-labeled phosphopeptides and heavy-labeled Aβ peptide epimers were from New England Peptide, Inc. (Gardner, MA). The Agilent tuning mixture was used as received. Phosphopeptides were received as powders and were prepared to an equimolar concentration of 300 nM in 70:30 water acetonitrile with 0.5% formic acid. The components of the phosphopeptide mixture have been previously reported but are given in the Supporting Information for convenience (Table S1).⁹ The peptide epimers, also previously reported,³⁵ were prepared in a 250 nM mixture in 50:50 water:methanol with 0.5% acetic acid as well as individual solutions. Ions were generated by electrospray ionization using an HF-etched silica emitter³⁶ (20 μm i.d.) connected to a fused-silica capillary line (360 μm o.d., 100 μm i.d., Polymicro Technologies, Phoenix, AZ) and infused at a flow rate of 1 μL/min. A conductive microunion (Valco Instrument Co, Houston, TX) connected the electrospray tip to the fused-silica line.

Ion Optics, Ion Mobility, and Mass Spectrometry.

Experiments were performed using previously described multipass and multilevel SLIM systems.^4,9 Helium was the background gas for all experiments and was specifically used because wide m/z range ion transmission through the ion escalators in the multilevel SLIM system is presently more efficient than in nitrogen.⁹ The pressure in the multipass SLIM chamber was maintained at about 100 mTorr higher than in the IFT, while the pressure in the multilevel SLIM chamber was about 100 mTorr lower than the pressure in the second ion funnel. An MKS Baratron heated capacitance manometer (model 627F, 10 Torr range, MKS Instruments Inc., Andover MA) was installed on the multilevel SLIM chamber to measure the pressure. Readings were acquired at 10 Hz. The accuracy of the gauge was 0.12% of reading as specified by the manufacturer (e.g., accuracy at 3 Torr = ±3.6 mTorr).

Data Analysis.

Data were recorded in the universal ion mobility format (.UIMF) and visualized in the PNNL UIMF Viewer (https://github.com/PNNL-Comp-Mass-Spec/UIMF-Viewer/releases/). Figure plotting and resolving power calculations were performed in Matlab (Mathworks, Natick, MA). The IMS Drift Time Aligner loads and preprocesses data from both UIMF and tab-delimited text files, after which either an SVA is applied, or dynamic time warping is applied, using the NDtw library (https://www.nuget.org/packages/NDtw and https://github.com/doblak/ndtw). The aligners used in this study can be found as a single package on Github (https://github.com/PNNL-Comp-Mass-Spec/IMS-Drift-Time-Aligner/). The source code can be viewed using Microsoft Visual Studio (Microsoft Corporation, Redmond, WA), and the algorithms can be run using the Windows Powershell application. A README file associated with the algorithm describes the command line arguments that can be used and the syntax to include them.

RESULTS AND DISCUSSION

SLIM achieve high Rp IMS separations by sending ions through serpentine paths that are typically 13 m or more in length. Ions typically take between 100 ms and 1 s to traverse the path, depending on TW parameters. This time can increase if ions are routed back to the beginning of the ion track (i.e., multipass SLIM SUPER)⁴ or by the use of additional SLIM levels (in a multilevel SLIM design).⁹ Because of the relatively long separation IMS times and high Rp in SLIM, there is ample time for small changes in experimental parameters to occur, which will manifest as detectable changes in ion arrival time distributions (ATDs). Most prominently, small pressure fluctuations can and do occur. These fluctuations occur over time scales of milliseconds to seconds, which is too fast for both the pressure measurement and dynamic pressure compensation systems to correct for. Such pressure fluctuations result in artificial peak broadening when multiple separations are summed, and lower detectability for low-abundance species.

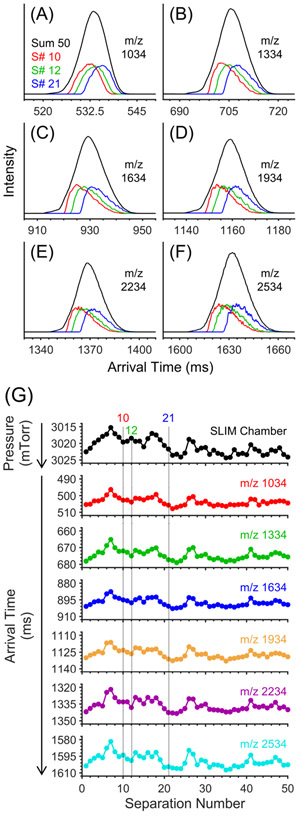
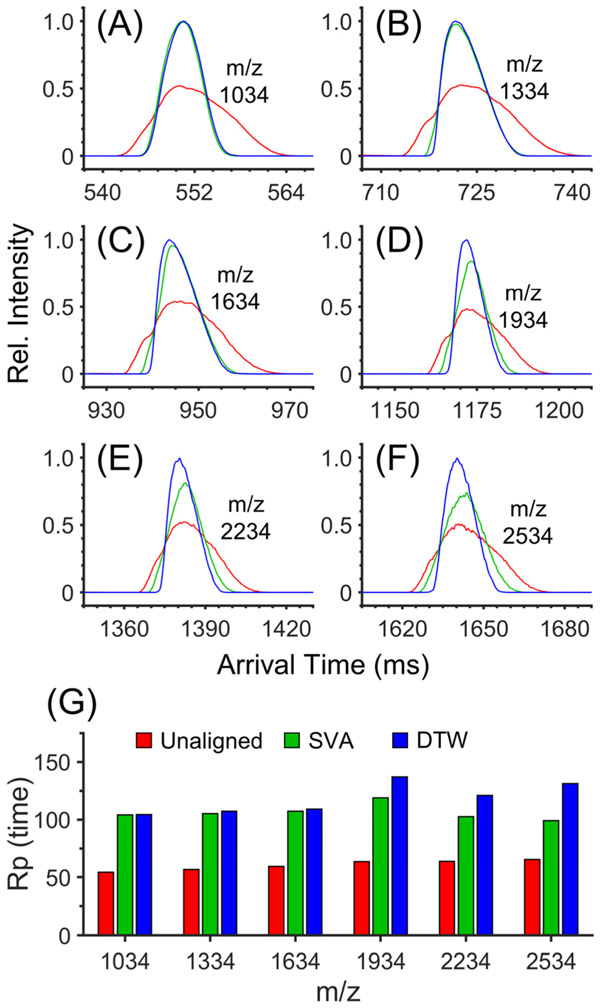
To initially investigate the effect of such pressure and IMS arrival time fluctuations, we separated negative Agilent tuning mixture ions using four ion levels of a multilevel SLIM module (~43 m) and summed 50 separations. Each separation took <2 s, and the sum of all 50 separations is shown in Figure 1A-F (black traces) for each of the six major peaks with m/z 1034–2534. Three individual separations out of the 50 are also shown (10 = red, 12 = green, 21 = blue) and highlight arrival time shifts for each ion. Note that the black traces were scaled for ease of visualization.

Figure 1.

Expanded views of negative Agilent tuning mixture ions acquired using 4 ion levels of a multilevel SLIM. (A) m/z 1034, (B) m/z 1334, (C) m/z 1634, (D) m/z 1934, (E) m/z 2234, and (F) m/z 2534. Each panel shows traces illustrating the sum of 50 separations (black) as well as three individual separations out of the set of 50 (red = 10, green = 12, blue = 21). (G) Average pressure fluctuations inside the SLIM chamber (black) and the associated shifts in arrival time distributions for ions with m/z 1034 (red), 1334 (green), 1634 (blue), 1934 (orange), 2234 (purple), and 2534 (light blue). Note that the y-axis is reversed in part G. Pressure measurements were performed at 10 Hz. Each point represents the average of all pressure measurements performed in single separation. TW_se speed =192 m/s. TW_sep amplitude = 25 V. TW_esc speed = 24 m/s. TW_esc amplitude = 20 V. Guard = −37 V. Injection time = 40 ms in-SLIM accumulation. Buffer gas = helium. Descriptions of typical SLIM operation and terminology can be found in refs 3, 4, 45, and 46.

The pressure inside the SLIM chamber was monitored during each separation at a frequency of 10 Hz (i.e., 20 readings per separation), although the delay between this measurement due to a pressure change is uncertain. Each set of 20 values was averaged, and the resulting averages were plotted as a function of separation number (Figure 1G, top black trace). The average pressure across all 50 separations was ~3.022 Torr. Note that lower pressures were recorded at the beginning of the experiment and higher pressures at the end (the y-axis is reversed). The pressure inside the SLIM chamber fluctuated between 3.014 and 3.025 Torr, or approximately ±5 mTorr (close to the stated accuracy of the Baratron pressure measurements).

The average ATDs of the six Agilent tuning mixture ions are also plotted in Figure 1G (bottom). As can be seen, the ATDs of all six ions shift in concert with the pressure change. For example, the average ATD of m/z 1034 (Figure 1G, red trace) decreases from 505 ms to about 496 ms during the first seven separations, which is also when pressure decreases from 3.022 to 3.014 Torr. After 24 separations, the average ATD of m/z 1034 slowly increases to about 509 ms and ends around 505 ms after 50 separations. The ATD shifts again follow the pressure fluctuations, which slowly increase to 3.025 Torr after 24 separations and end at a similar pressure after 50 separations. Other Agilent tuning mixture ions exhibit a similar trend. While the maximum percentage ATD shifts for each ion were similar (i.e., 0.5–0.8%), larger absolute ATD shifts occurred for low-mobility ions in SLIM and smaller absolute ATD shifts for higher-mobility ions. For instance, the ATDs for m/z 1034 range from 496 to 508 ms (i.e., 12 ms) while the ATDs for m/z 2534 (Figure 1B, light blue trace) range from 1582 to 1607 ms (i.e., 25 ms). The values for average ATD, standard deviation (std dev), maximum absolute ATD shift, and maximum percent ATD shift are shown in the Supporting Information (Table S2). This effect is expected as the impact of a pressure change will increase with arrival time for a given separation and will be discussed further in the context of dynamic time warping (DTW). The key point here is that small pressure fluctuations can have a measurable influence on ion ATDs in SLIM.

Single Value Alignment (SVA) of SLIM IMS Separations.

A relatively straightforward way to correct for arrival time fluctuations in SLIM SUPER IMS (and potentially other IMS techniques) is to use a postprocessing data alignment tool to shift all data points in a sample spectrum by some amount of time (i.e., single value alignment or SVA). We have previously applied such an approach for SLIM IMS and have found that it is effective for minimizing peak broadening and enhancing peak intensities, resulting in better resolution and detection limits.^1,35,37 We have not previously described the SVA approach in detail, but we include it as an option to DTW and will discuss it briefly here in comparison with DTW.

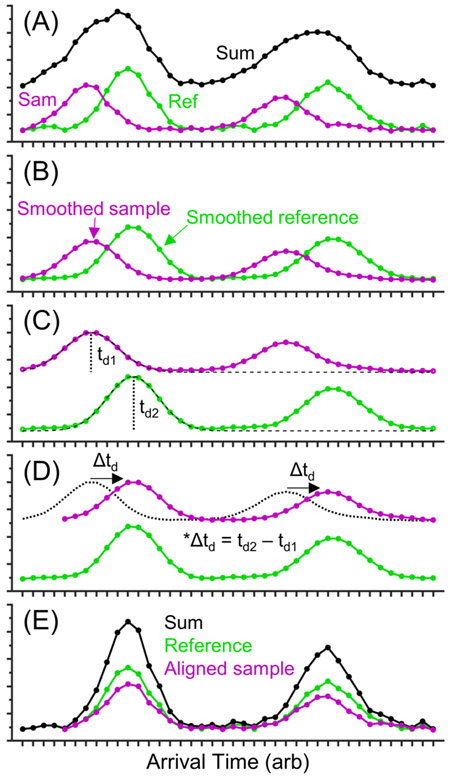
Figure 2 shows a pictorial workflow of the SVA tool that we have implemented for SLIM separations. In this example, an artificial sample spectrum (Figure 2A, pink trace) containing two Gaussian peaks with different intensities is compared to an artificial reference spectrum (Figure 2A, green trace) containing the same two Gaussian peaks, with a time offset between the two spectra. Both spectra are smoothed using a moving average to reduce contributions from noise (Figure 2B). Next, a single peak from an extracted ion chromatogram is detected by finding clustered points above an intensity threshold (Figure 2C). The highest intensity peak is normally chosen, but other peaks can be specified if desired. The average ATD of the chosen peak is extracted from the sample and reference data sets (i.e., peak apex). In this example, t_d1 and t_d2 are the average ATDs of the first peak in the sample and reference spectra, respectively. The difference between t_d2 and t_d1 is calculated and defined as Δt_d. SVA is performed by shifting all points in the sample spectrum by Δt_d (Figure 2D). The original reference spectrum and the shifted sample spectrum are reconstructed and summed to produce an alignment mobility spectrum with improved signal-to-noise and resolution (Figure 2E).

Figure 2.

Workflow of the SVA tool. (A) Examples of a sample [pink] and a selected reference [green] mobility spectrum containing two peaks and their sum [black]. Data processing involves (B) smoothing data with a 7 point moving average, (C) using a Gaussian fitting function to find peak centers, (D) finding the difference in peak centers between the sample and reference spectra and shifting the sample spectrum by the difference, and (E) summing the raw, aligned mobility spectra. In application, all spectra are individually shifted relative to the reference spectrum by the SVA tool. The improvement can be seen by comparing the “sum” spectra in panels A and E.

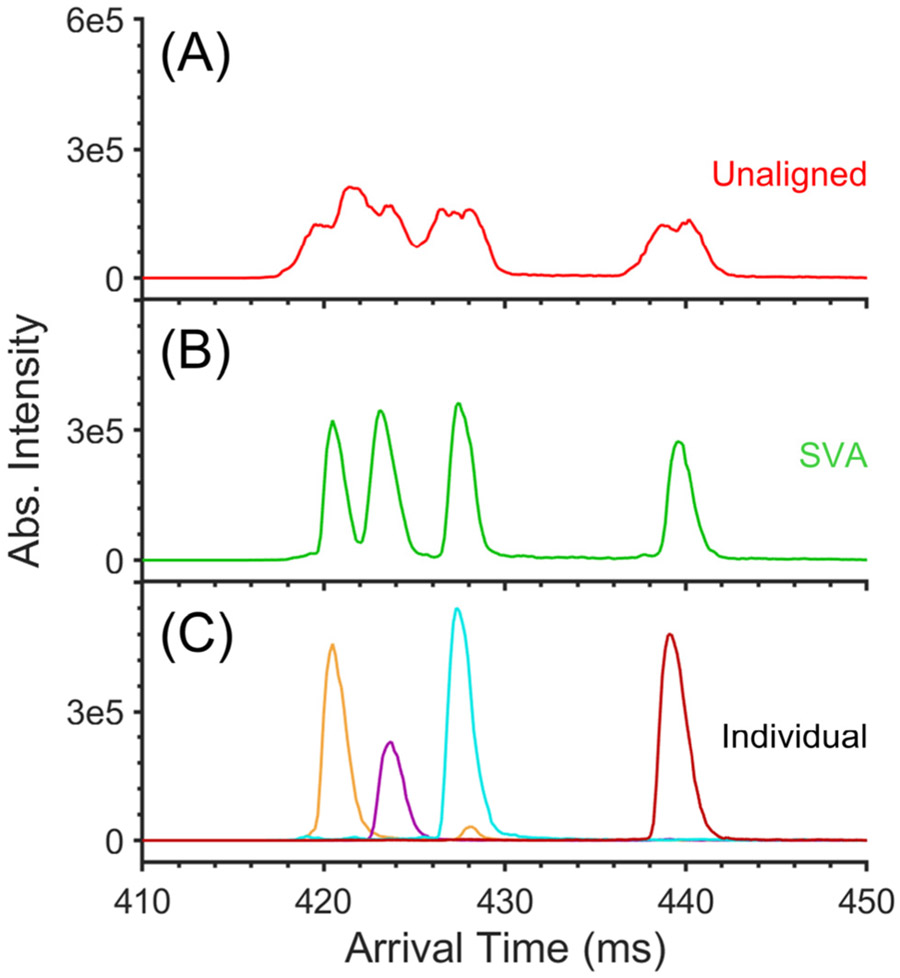
The performance of SVA was also evaluated by applying it to 25 mobility spectra of a mixture of four heavy-labeled peptide epimers.³⁵ Data were acquired using a multipass SLIM system (~81 m total separation path length) at ~4 Torr helium, and the sum of the unaligned separations is shown in Figure 3A. We note that all four epimers existed in the 3+ charge state, and the reduced mobilities of the epimers are similar. Three distinct peaks possessing multiple features were observed in the unaligned data. The first peak centered at approximately 422 ms was broader than the other two peaks at 428 and 440 ms, indicating the overlap of two epimer ATDs. Figure 3B shows the same 25 separations after SVA was performed, and Figure 3C shows 25 aligned and summed mobility spectra of individual epimers. As can be seen, all four peptide epimers were readily resolved after SVA. The wide peak formerly centered at 422 ms resolved into two peaks corresponding to LVFFAEDVGS[dD]K (orange trace) and LVFFAEDVGS-[dbD]K (purple trace). The latter two peaks corresponding to LVFFAEDVGSDK (light blue trace) and LVFFAEDVGS[bD] K (dark red trace) were also about 2.5 times higher in the aligned–summed mobility spectrum than in the unaligned–summed mobility spectrum. The calculated arrival time-based Rp for the LVFFAEDVGS[bD]K epimers was 122 for the unaligned and 296 for the aligned separations, respectively, showing a 2.4-fold increase. As can be seen, SVA can allow differentiation between ions with similar ATDs, otherwise overlapped in unaligned–summed mobility spectra, as well as making very low-abundance ions much more evident.

Figure 3.

(A) Unaligned and (B) SVA summed mobility spectra of a mixture of four heavy-labeled peptide epimers. (C) SVA spectra of individual peptide epimers: (orange) LVFFAEDVGS[dD]K, (purple) LVFFAEDVGS[dbD]K, (light blue) LVFFAEDVGSDK, (dark red) LVFFAEDVGS[bD]K. Each spectrum is the sum of 25 separations acquired using a multipass SLIM. Compression ratio ion mobility programming (CRIMP)⁴⁵ was performed after the 1st pass using a compression ratio of 50 000 to 1. TW_sep speed = 320 m/s. TW_sep amplitude = 40 V. Guard = 15 V. Injection time = 500 ms in-SLIM accumulation. Pressure ≈ 4.0 Torr helium.

Dynamic Time Warping (DTW) of SLIM IMS Separations.

As demonstrated in Figure 1, the pressure inside the multilevel SLIM chamber is generally quite stable (within the precision of pressure measurements). However, small pressure (or other) fluctuations can sporadically arise and cause shifts in ion ATDs. It is not entirely clear how or why such fluctuations occur, but we speculate that gas flows and entrained charged nanodroplets and clusters from the ion source contribute to such fluctuations. The multilevel SLIM system was designed to mitigate these fluctuations by incorporating an enclosure surrounding the atmospheric pressure interface and ion source, and two curved ion funnels prior to the SLIM entrance to prevent high mass cluster, droplet, or particle transmission. In addition, two needle valves are used for controlling gas flow into the SLIM chamber. Despite these efforts, small but detectable shifts in ion ATDs were still observed. While the SVA tool is useful for aligning mobility spectra composed of ions with a narrow range of mobilities, ions with larger mobility differences [e.g., Agilent tuning mixture negative ions,m/z 1034 (2.09 cm²/(V s)) to m/z 2534 (1.29 cm²/(V s))] will shift differently in response to pressure changes or other fluctuations. This issue can be effectively addressed using DTW.

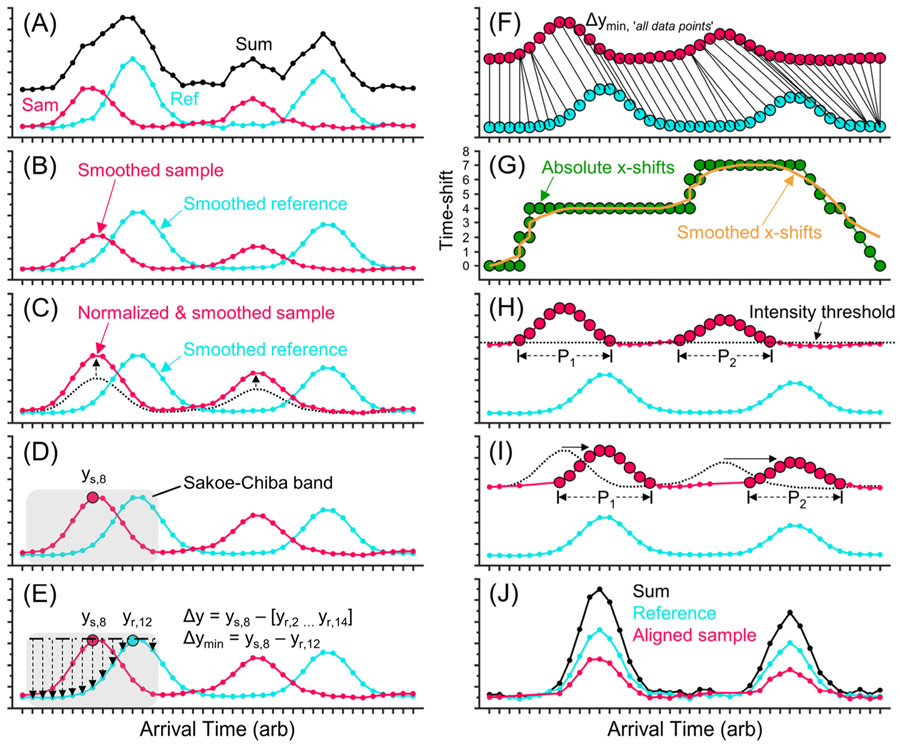
Figure 4 shows a pictorial workflow of DTW applied to two artificial IMS spectra. For simplicity, the spectra shown here are composed of 40 data points and contain two peaks. However, the DTW procedure is the same for spectra containing more data points and multiple peaks, with the caveat that the shifts applied vary for different regions of the same spectrum in a manner described below. The DTW process begins by comparing sample and reference spectra that are shifted in time (Figure 4A). As can be seen, the sum of the two spectra (black trace) yields a convoluted mobility spectrum that shows four discernible peaks, but there should only be two. The sample and reference data are first preprocessed using a moving average (Figure 4B). Then, the intensity of the sample data is normalized to the reference data (Figure 4C). A single data point from the sample data is selected for comparison (Figure 4D), depicted in this example as “y_s,8”, where “s” means sample, and “8” means the eighth point in the data set. A constraining range is set around the selected data point to ensure that only data points near the selected point will be compared while data points that are far away will not be considered. We used the Sakoe–Chiba method to create our constraining range, but other constraining methods exist (e.g., Itakura parallelogram).¹⁶ Next, the signal intensities of the reference data points residing inside the constraining range are subtracted from the intensity of y_s,8 (Figure 4E). The differences between these values (i.e., Euclidean distances, Δy) are stored in a matrix (i.e., cost matrix). The smallest Euclidean distance is then found (Δy_min), which identifies the reference data point that best matches the sample data point being compared. The smallest Euclidean distance in this example is from y_s,8 to y_r,12. The process of selecting a sample data point and finding the smallest Euclidean distance is performed for all data points in the sample spectrum (Figure 4F). Note that a single sample data point may be correlated to multiple reference data points, and vice versa. The program then finds the absolute time differences associated with each of the smallest Euclidean distances and plots the results (Figure 4G, green circles). As an example, the time difference between y_s,8 and y_r,12 is 4 units. A moving average of the time shifts is then performed (Figure 4G, yellow trace). The program then references the smoothed/normalized sample data set and performs a peak finding step (a.k.a. “data island”). A peak is defined as points that are (1) adjacent to each other and (2) above an intensity threshold (Figure 4H). The program then computes a moving average of the time shifts for the points in a peak and then averages the smoothed time shifts, yielding a single average time shift (Figure 4I). For example, the first peak (P₁) in the sample spectrum is composed of data points y_s,4 to y_s,13; the average time shift among these data points is 4 units, so all data points in P₁ are shifted by 4 units. The DTW process is performed for all detected peaks in a sample IMS spectrum. Data points that are not in a peak are shifted by the corresponding average time shift calculated in Figure 4G. For example, data point y_s,3 does not exist in a peak, so it will be shifted by the value extracted from the yellow trace in Figure 4G, which in this example is 1 unit (rounded up). After all data points are shifted, the aligned data are summed to provide a single IMS spectrum corrected for variations between separations (Figure 4J). Note that all coarriving ions (same ATD, different m/z) for a specific separation will be shifted by the same amount. A detailed description of DTW applied to an IMS spectrum possessing many more data points and peaks is provided in the Supporting Information along with a Supporting Figure (Figure S1).

Figure 4.

Workflow of the dynamic time warping (DTW) algorithm. (A) Examples of sample (red) and reference (light blue) mobility spectra composed of 40 points each and containing two Gaussian peaks. (black) Sum of the raw sample and reference spectra. Data processing first involves (B) smoothing data using a 7 point moving average and (C) normalizing the intensity of the sample data to the reference data. (D) An individual point in the sample data chosen and a constraining range (e.g., Sakoe–Chiba band) in the time domain is chosen (e.g., 6 points on either side, gray highlight). (E) The differences in intensity values are found (i.e., Euclidean distances), and the smallest difference out of the group is identified (e.g., y_s,8 → y_r,12). (F) Steps D and E are repeated for all data points in the sample spectrum. (G) The corresponding time domain shift is found for each of the smallest Euclidean distances (green), and a moving average of the time domain shifts (yellow trace) is performed. (H) Peaks in the sample spectrum are identified by setting an intensity threshold and defining all points above that threshold that are grouped as a peak. (I) The points defined as a peak are shifted using the average time domain shift of all points comprising the peak. All other points are shifted by the smoothed trace. (J) Aligned sample and reference spectra and their sum. In application, all spectra are individually shifted relative to the reference spectrum by the DTW tool. The improvement can be seen by comparing the “sum” spectra in panels A and J.

Comparison of the SVA and DTW Approaches.

To compare the performances of the SVA and DTW approaches, IMS spectra of negative Agilent tuning mixture ions were acquired using the four-level SLIM IMS. To illustrate the ability of DTW to correct for ATD shifts, the door to the ion source housing was opened twice and closed once to induce small pressure fluctuations. Unaligned ATDs while opening and closing the ion source housing are shown in Figure 5, red traces. Six Agilent tuning mixture ions were readily detected with high resolution (Figure 5A = m/z 1034, Figure 5B = m/z 1334, Figure 5C = m/z 1634, Figure 5D = m/z 1934, Figure 5E = m/z 2234, Figure 5F = m/z 2534). The measured pressure fluctuations and the Agilent tuning mixture ion ATDs over the course of 50 separations are shown in the Supporting Information (Figure S2). As can be seen, opening the door to the ion source housing caused the pressure inside the SLIM chamber to gradually increase by about 15 mTorr. Similarly, closing the door caused the pressure to gradually drop to its initial value. Figure S2 shows a strong correlation between pressure and the SLIM IMS ATDs, similar to that shown in Figure 1, and further illustrating the potential contribution of pressure fluctuations to ATD shifts.

Figure 5.

Expanded views of negative Agilent tuning mixture ions acquired using 4 ion levels of a multilevel SLIM. (A) m/z 1034, (B) m/z 1334, (C) m/z 1634, (D) m/z 1934, (E) m/z 2234, and (F) m/z 2534. Each panel shows spectra of unaligned (red), SVA (green), and DTW (blue) processed data. (G) Full width at half max measurements for negative Agilent tuning mixture ions in unaligned (red), SVA (green), and DTW aligned (blue) mobility spectra. Pressure fluctuations were induced by opening and closing the door to the ion source housing. Each mobility spectrum represents a sum of 50 separations. TW_sep speed = 192 m/s. TW_sep amplitude = 27 V. TW_esc speed = 24 m/s. TW_esc amplitude = 24 V. Guard = −35 V. Injection time = 40 ms in-SLIM accumulation. Pressure ≈ 3.6 Torr helium.

The raw mobility data were then subject to SVA, as previously illustrated in Figure 2, and the results (Figure 5, green traces) show that the peak widths became narrower, and peak intensities increased after SVA. We note that the peak widths of the low-mobility (higher-m/z) ions did not decrease as much as the higher-mobility ions, a result of a low-m/z (high-intensity) ion being used by the SVA process for alignment. The time-based resolving powers for the six Agilent tuning mixture ions are shown in Figure 5G. The Rp of m/z 1034 was ~54 in the unaligned mobility spectrum and ~104 in the SVA spectrum. This corresponds to a 92% increase in Rp. In contrast, the Rp of m/z 2534 was ~66 in the unaligned mobility spectrum and ~99 in the SVA spectrum. This represents a 51% increase in Rp, which is much less than the change obtained for m/z 1034. These data illustrate the shortcomings of SVA: ions with drastically different mobilities not being aligned as effectively, and the potential for further improvements by correction for such “nonlinear” shifts.

To overcome this SVA limitation, data were aligned using DTW (see Figure 4), and the results are shown in Figure 5, blue traces. Clearly, Rp’s in unaligned spectra are far smaller than those calculated after performing either SVA or DTW. Interestingly, there was little difference between the Rp’s calculated for high-mobility ions (e.g., m/z 1034) using SVA or DTW. An Rp of ~104 was calculated for m/z 1034 after DTW, which is the same as with SVA. However, the Rp increases and peak shape changes of lower-mobility ions are most evident in the DTW spectrum. For example, the m/z 2534 ATD appears broad using SVA, but much sharper with DTW. An Rp of ~131 was calculated for m/z 2534 using DTW, ~1.3-fold larger than calculated with SVA. The percent increase in Rp for all ions ranged from 84% to 115% after DTW, whereas the percent increase in Rp ranged from 51% to 92% after SVA. We note that our use of time-based Rp is reported here instead of CCS-based Rp, which would approximately double the indicated Rp.³⁸ DTW shifts for three individual separations are shown in the Supporting Information (Figures S3-S5). We conclude that DTW corrects for the nonlinear ATD shifts significantly better than SVA.

SVA and DTW were also performed on mobility spectra of negative Agilent tuning mixture ions possessing very large arrival time shifts. Full unaligned, SVA, and DTW aligned spectra are shown in the Supporting Information (Figure S6) along with DTW shifts for three individual separations (Figures S7-S9). A description of the data is also given preceding the figures, and the three txt files associated with Figure S6 (unaligned, SVA, DTW) are provided in the “TextFile” directory in the “Data” directory associated with the data aligner download for readers to verify the analysis using the aligner tools.

We note that both SVA and DTW typically use the middle separation as the reference because its pressure is usually in the middle of any gradual increases or decreases in pressure. However, other separations can be used as the alignment template and will produce very similar results. As an example, Rp’s are obtained for the Agilent tuning mixture mobility data acquired with large arrival time fluctuations using different separations as the reference separation. There are only very small differences in Rp depending on the reference spectrum chosen (Table S3).

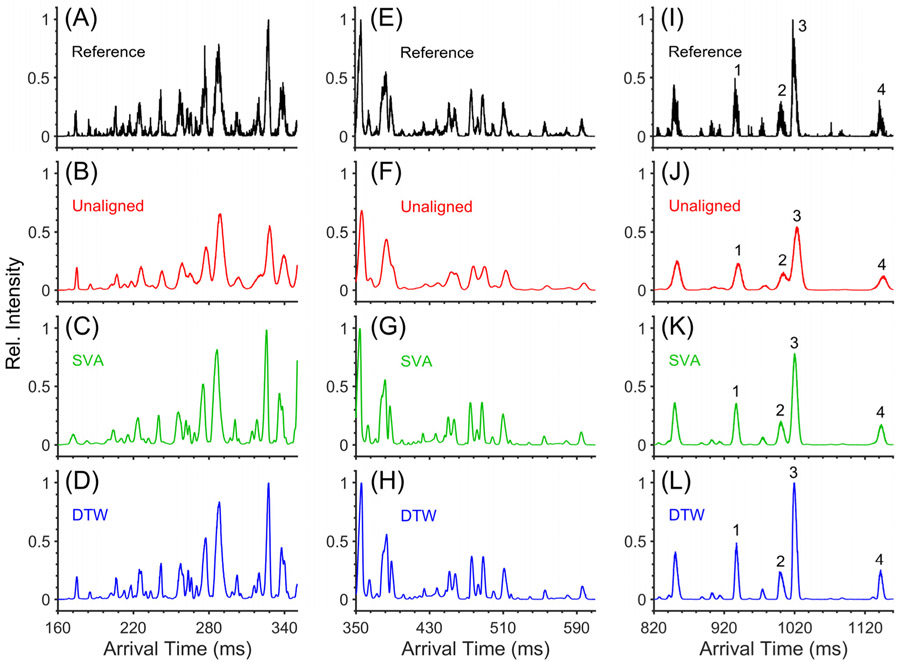
In further evaluation, DTW was applied to SLIM IMS data of a complex phosphopeptide mixture having a wide range of relative abundances. IMS spectra for three arrival time regions are shown in Figure 6, along with the corresponding portions of the single reference spectrum used for alignment (in black; Figure 6A,E,I). Comparisons of the unaligned (red), SVA (green), and DTW (blue) processed data show that both SVA and DTW result in narrower and more intense peaks compared to the unaligned data, with differences expected to depend on the details of the fluctuations, the choice of reference spectrum, and arrival times. While the peak widths, peak intensities, and resolution achieved using both aligners do not significantly differ in the higher-mobility region (i.e., lower arrival time; Figure 6B-D), several peaks in the middle-mobility region are partially resolved (Figure 6F-H). For example, the peak at about 385 ms in the unaligned data (Figure 6F) displays a small partially resolved feature on the tail side, but an additional feature on the front side becomes resolved after using SVA (Figure 6G). The first two peaks were identified and corresponded to two SSSPELVTHLK²⁺ isomers, and the last second peak corresponds to RCPTPEIQKK²⁺. A similar effect occurs for the DTW processed spectra (Figure 6H). Another example of resolution improvement occurs at about 480 ms where the unaligned data show two partially resolved peaks, but both SVA and DTW reveal a third low-intensity peak. However, the differences between SVA and DTW for these data are most apparent in the low-mobility region of the phosphopeptide mixture (Figure 6I-L). Four high-intensity peptides in this region are labeled 1–4, and their Rp’s using DTW were far larger than with SVA (Table 1). See the Supporting Information (Figures S10-S12) for DTW profiles for individual separations of the phosphopeptide mixture. We emphasize that DTW does not merge isomers (i.e., there is no loss of information, and multiple isomeric peaks do not collapse into a single peak), and a description and a figure (Figure S13) showing isomeric separation before and after SVA and DTW are provided in the Supporting Information. We also emphasize that in all cases the overall data quality with DTW is improved relative to the unaligned and SVA processed data and that the Rp achieved is essentially indistinguishable from that achieved in the single reference spectrum. Thus, DTW processing does not result in any significant loss of Rp compared to that for a single separation and where small pressure changes should not impact Rp. Furthermore, the absence of arrival time variations between separations obviously cannot result in any loss of Rp from the application of DTW.

Figure 6.

Expanded views of a mixture of phosphopeptide ions using 4 ion levels of a multilevel SLIM: (A–D) High-mobility region, (E–H) middle-mobility region, and (I–L) low-mobility region. From top to bottom, the 1st, 2nd, 3rd, and 4th panels show spectra of the individual reference separation SVA and DTW (black), unaligned (red), SVA (green), and DTW (blue) processed data, respectively. The unaligned, SVA, and DTW aligned data represent the sum of 100 separations. Numbered peaks in the low-mobility region for the unaligned, SVA, and DTW aligned data are identified in Table 1. TW_sep speed = 224 m/s. TW_sep amplitude = 32 V. TW_esc speed = 28 m/s. TW_esc amplitude = 27 V. Guard = −35 V. Injection time = 300 ms in-SLIM accumulation. Pressure ≈ 3.6 Torr helium.

Table 1.

Time-Based Resolving Powers of the Four Lowest-Mobility Phosphopeptides before and after SVA and DTW

			resolving power (time)
number	m/z	peptide sequence	unaligned	SVA	DTW
1	848.4/(1+)	LT(p)LQSAK*	90	136	170
2	937.4/(1+)	LS(p)MEIEK*	98	152	201
3	928.4/(1+)	MNS(p)LTFK*	99	124	154
4	1063.4/(1+)	LY(p)EEYTR*	93	132	181

A comparison of the unaligned, SVA, and DTW aligned data in Figure 6 shows that, in addition to Rp gains, S/N is drastically improved due to the summation of IMS spectra, which results in several additional peaks becoming evident after summation, compared to the unaligned data. For example, in the low-mobility region between peaks 3 and 4, there are many low-intensity peaks evident with DTW (Figure 6K), less evident with SVA (Figure 6L), and essentially unobserved for the unaligned data (Figure 6J). These low-intensity peaks are hinted at in the single reference spectrum (Figure 6I), but the more limited S/N here limits both the quality of the peak definition and the quantitative information related to the peak intensities (e.g., area). These observations highlight a considerable attribute associated with the use of DTW; the ability to effectively define and quantify peaks extending beyond a better measurement of peak areas to the very ability to even observe such peaks for their use in quantification.

Three general observations can be made regarding DTW: (1) It can be used to correct for large ATD shifts in sets of summed individual spectra. (2) It performs comparably to SVA when used over a small mobility range. (3) It significantly outperforms SVA when used over a broad mobility range. To expand on observation 3, the effects of using different Agilent tuning mixture ions as the reference peak for SVA using data with large arrival time shifts (Figure S14) show that ions farther away from the reference tend to show increasing peak widths. These results imply that SVA performs best when mobility differences are smaller but also can fail for ions with large mobility differences. For these reasons, SVA is appropriate and effective for multipass SLIM SUPER IMS separations that are inherently of limited mobility range but is less effective for the wide mobility range multilevel SLIM IMS separations.

Further improvements to the DTW alignment process can potentially be made using a weighted average instead of a normal average to calculate time offsets to shift peak islands, which could be useful for asymmetric peaks. It should also be possible to use a combination or variant of the Sakoe–Chiba and Itakura parallelogram constraining range methods to establish a narrow constraining range for high-mobility ions and a wider constraining range for lower-mobility ions, which would more closely resemble ion mobility data. Another established method is to employ the piecewise aggregate approximation to significantly speed up computation times (i.e., perform DTW using bins instead of individual data points). Additionally, the intensity threshold used to find peaks currently can define a peak based on a single arrival time data point, which potentially may be problematic. We allow this due to the relatively low intensities common to single IMS spectra, particularly for the generally narrower high-mobility ions. However, adapting this function to specify a set number of data points per peak will be considered in future versions of the DTW algorithm.

It is important when using DTW to optimize the width of the Sakoe–Chiba constraining range and the intensity threshold of the peak finder to avoid potential artifacts. One way to determine if an artifact is present after DTW is to examine the output spectrum to look for an intense, narrow band of ions somewhere in the ion heat map. For example, such a band can be seen in the high-mobility region of the phosphopeptide mixture when a low-intensity peak finding threshold is used to perform DTW, shown in the Supporting Information (Figure S15A,B). In such complex mixtures, many features are close together and have low intensities. The mobiligram associated with the heatmap also shows a sharp and intense peak, highlighted by a red arrow. In this case, a narrow band appears to have resulted from the DTW algorithm considering the edges of several peaks as separate from the main peak (due to the low intensity threshold). This results in the middle of the peaks shifting differently than the edges. It is possible to avoid this artifact by using a higher intensity threshold (Figure S15C). One can also see that the shifts of the narrow band are quite far away from the main body of the peak they came from. Therefore, we suggest using a narrower constraining range (Figure S15D). When using DTW, it is best to use the lowest intensity threshold and widest constraining range possible to obtain the best alignment possible while avoiding artifacts. As noted previously for SVA, it is better to choose a reference (i.e., template) spectrum for DTW whose pressure value is in the middle of the other separations and, in the absence of useful pressure information, a template spectrum from the middle of the set. This will allow a narrower constraining range to be used whereas the use of a different reference spectrum may require wider constraining ranges. An attraction of this approach is that such choices are readily automated and thus can speed overall data processing times.

DTW is also advantageous compared to aligning data based on curve fitting because it is independent of data type (e.g., ion class). To illustrate this advantage, a plot of CCS vs the drift times of negative Agilent tuning mixture ions from Figure 1 was generated and is shown in the Supporting Information (Figure S16). CCS values were obtained from Stow et al.,³⁹ and data were fitted using linear (red trace) and power (blue trace) functions. The linear function clearly deviates from the data trend, with the largest differences occurring at the smallest and largest CCS values. This indicates that a true linear alignment method (i.e., shifting data points in an IMS spectrum by incrementally larger values based on a linear regression analysis) is not a good choice for aligning data from TW-SLIM because CCS and drift time are not linearly correlated. On the other hand, a much better fit is obtained using the power function. Several studies exploring CCS calibration in TW-IMS and TW-SLIM have shown that power function fits are preferable because drift time and CCS are nonlinearly correlated.^40-44 However, these studies also show that different ion classes require different fitting parameters (i.e., slopes, intercepts, functions) to obtain accurate CCS measurements. Thus, an analyst needs knowledge of the compounds present in a mobility spectrum, and it will be difficult to generate a single curve to fit a mobility spectrum containing different compound classes. Since DTW is data-independent, it does not suffer from problems associated with curve fitting.

We finally note that DTW should not affect CCS calibration when using internal calibrants. Every mobility spectrum contains CCS information about each ion, including the reference spectrum. Aligning sample spectra to a reference spectrum does not change the CCS information already present in the reference spectrum, which itself remains unwarped. The composite spectrum generated after DTW (i.e., the summation of DTW aligned spectra) still contains the original CCS information from the reference spectrum, including any internal calibrants used for CCS determination.

CONCLUSIONS

IMS separation ATD alignment approaches based on SVA and DTW were described and successfully used to correct for shifts due to instrumental fluctuations (emphasizing pressure fluctuations) observed in very long path length traveling wave SLIM IMS separations, resulting in significant gains in effective Rp and S/N. Often the improvements were dramatic: peak widths narrowed, increasing effective Rp by as much as 115% after DTW, allowing peaks indistinguishable in the unaligned data to become partially or even fully resolved. Alignment also provided increased peak intensities for improved peak definition and detection. DTW was much more effective for wide mobility range data compared to SVA and can be used to align data regardless of the cause of the ion ATD shifts (pressure shifts or otherwise) or the details of the sample composition (e.g., mixture complexity). The improvements include not only better Rp, but also the ability to detect low level peaks that would otherwise become obscured due to variations in ion ATDs.

While all data presented here were collected via direct injection (i.e., invariant sample composition), it is also possible to use DTW with LC separations using peaks consistently present throughout the LC separation (e.g., using ions from a second electrospray source containing a reference mixture or always present ESI-specific peaks). It should also be feasible to apply DTW to such dynamic data (e.g., from LC separation) for complex samples by utilizing sets of ions that are common to small subsets of adjacent IMS separations and providing a smooth transition between such subsets. Finally, we recommend the use of SVA, and particularly DTW, for the averaging or summation of multiple IMS separations, and where extended IMS ATD data are most likely to display shifts due to minor pressure fluctuations or other experimental variables.