Deciphering the Allosteric Process of Phaeodactylum tricornutum Aureochrome 1a LOV Domain

Abstract

The conformational-driven allosteric protein diatom Phaeodactylum tricornutum aureochrome 1a (PtAu1a) differs from other light-oxygen-voltage (LOV) proteins for its uncommon structural topology. The mechanism of signaling transduction in PtAu1a LOV domain (AuLOV) including flanking helices remains unclear because of this dissimilarity, which hinders the study of PtAu1a as an optogenetic tool. To clarify this mechanism, we employed a combination of tree-based machine learning models, Markov state models, machine learning based community analysis, and transition path theory to quantitatively analyze the allosteric process. Our results are in good agreement with the reported experimental findings and reveal a previously overlooked Cα helix and protein linkers as important in promoting the protein conformational changes. This integrated approach can be considered as a general workflow and applied on other allosteric proteins to provide detailed information about their allosteric mechanisms.

Graphical Abstract

Introduction

Light, oxygen or voltage (LOV) domains are a subdivision of the Per-Arnt-Sim (PAS) superfamily that are sensitive to blue light and undergo conformational as well as dynamical changes upon light activation.^1,2 This activation begins with the formation of a covalent bond between a cofactor and a conserved cysteine residue. Possible cofactors include flavin adenine dinucleotide (FAD), flavin mononucleotide (FMN) or riboflavin.³ This covalent bond further promotes the overall structural changes, resulting in the alteration of the protein-protein interactions and thus signal transduction.⁴

Phaeodactylum tricornutum aureochrome 1a (PtAu1a) is a recently discovered LOV protein that consists of an unstructured N-terminal region, and a basic region leucine zipper (bZIP) DNA-binding domain connected to a C-terminal LOV core.⁵ The LOV domain, together with two flanking helices (A’α and Jα) is usually referred to as AuLOV.⁶ The protein is dynamically stable in the dark state due to the interaction between the LOV core and bZIP.⁷ This interaction prohibits the protein binding with DNA.⁸ A photo-induced covalent bond is formed between the C4a position of the cofactor FMN and a nearby sulfur in Cys287. This covalent bond triggers a series of conformational changes, including the undocking and unfolding of Jα helix from the LOV core surface, the release of A’α helix from the hydrophobic site on LOV domain surface, and dimerization of the LOV domains.⁷

These events lead to the increase of PtAu1a affinity for DNA binding and are proposed to be allosteric.⁹ Recent research has revealed that a combination of structural changes in the LOV core and the undocking of Jα helix is essential for the release of A’α helix and LOV domain dimerization.⁷ The allosteric mechanism in PtAu1a is considered to be different from other LOV proteins since the location of the LOV domain is in the C-terminus in PtAu1a, while in the N-terminus in others.^10,11 This structural difference raises the question on allosteric transmission in PtAu1a.

Various computational methods have been applied to explore protein allosteric mechanisms at atomic level.^12–14 Molecular dynamics (MD) simulations are capable of providing atomic-scale information, as well as structure-function relationships^15,16, and are widely used in sampling protein motions and structure landscapes.¹⁷ The significant computational power provided by graphical processing units (GPUs) has promoted the timescale of MD simulations from nanoseconds to milliseconds.^18,19 To obtain more biologically meaningful information from trajectories, Markov state models (MSMs) are often used to extract asymptotic kinetic information based on limited simulations.^20,21 Kinetically separate macrostates can be obtained from MSMs in the reduced dimension. Differences among these subspaces can then be quantified to gain insight into protein structure and function relations.

The success of MSMs depends on appropriate dimensionality reduction methods that can preserve global distances while retaining the most structural information.²² New dimensionality reduction methods have been developed to project the high-dimensional trajectories to lower dimensions for thorough study. However, many methods, such as principal component analysis (PCA)²³, time-structure based independent component analysis (t-ICA)²⁴ and t-distributed stochastic neighbor embedding (t-SNE) method²⁵, suffer from problems including maintaining the similarity between high dimensional space and low dimensional space, and are not resistant to system noise.²⁶ In the current study, MD simulations were projected onto a 2D space via the ivis framework²⁷, which is a nonlinear method based on Siamese neural networks (SNNs) and has been shown powerful in interpreting biological systems.²⁸

Machine learning has recently achieved great accomplishments in chemistry and biology. Raccuglia et al. applied machine learning algorithms trained on failed experimental data to predict reaction results with high accuracy.²⁹ Faber et al. employed machine learning techniques for feature vector representations of crystal structures.³⁰ Botu et al. integrated machine learning framework to accelerate ab initio molecular dynamics simulation.³¹ The broad applications of machine learning stem from the ability to process large datasets and, more importantly, provide explanatory details.^32,33 These favorable metrics offer a new prospective direction for the research on protein allostery. In this study, two tree-based machine learning models, random forest (RF) and one-vs-one random forest (OvO RF), were used to study the structural differences between macrostates and determine the contribution of residues to the allosteric process. In combination with machine learning and dynamic community analysis, Zhou et al. developed a new approach, known as machine learning based community analysis³⁴, to identify important structural features in dynamically-driven protein allostery. Here we applied this method on AuLOV and demonstrated the feasibility of this method in analyzing conformational-driven protein allostery.

The AuLOV is investigated in this study through the MD simulations, tree-based machine learning models, machine learning based community analysis and transition path theory. Our results identified key residues that are consistent with experimental discoveries and suggested the importance of Cα helix, overlooked thus far. Moreover, we quantified the important role of N- and C-terminal linkers in modulating AuLOV allostery. The integrated methods determined the importance of each residue in the allosteric process, and therefore provided new insights into the allosteric mechanisms, which may promote future research on PtAu1a as an optogenetic tool.

Methods

Molecular Dynamics (MD) simulations

The initial structures of native dark state monomer and native light state of AuLOV dimer were taken from the Protein DataBank (PDB)³⁵ with the PDB ID being 5dkk for the native dark state and 5dkl for the native light state. To keep the same number of residues in all structures, the longest common residue sequences (from Ser240 to Glu367) were modeled. Both the native dark and light structures contain FMN as a cofactor. The force field for the cofactor FMN was used from a previous study³⁶. In order to fully explore the protein dynamics with regard to the formation of the covalent bond between cysteine 287 and FMN, two new transient states, referred to as transient dark state and transient light state, were generated. Specifically, the transient dark state was generated by forming the Cysteinyl-Flavin C4a adduct bond in the native dark state structure. The transient light state was generated by removing the Cysteinyl-Flavin C4a adduct bond and constructing the dark state configuration in the native light state structure. These transient structures facilitate analysis of allosteric interconversion between the light- and dark-state structures.

The crystal structures were added with hydrogen atoms and were further solvated in a water box with the TIP3P water molecules³⁷. Sodium cations and chloride anions were added for charge neutralization. For each structure, energy minimization was done with the steep descent method and the adopted basis Newton-Raphson minimization. System temperature was raised to 300K through a 20 picoseconds (ps) MD simulations. Another 20ps simulations were done for equilibrium. 10 nanoseconds (ns) of isothermal-isobaric ensemble (NPT) followed by 1.1 microseconds (μs) of canonical ensemble (NVT) Langevin MD simulations were carried out at 300K. The first 0.1μs NVT simulations was considered as an equilibration stage and was discarded. Three NVT MD simulations were conducted independently for each protein structure. Therefore, a total of 12μs simulations were generated for analysis. SHAKE method was used to constrain all bonds associated with hydrogen atoms. 2 femtoseconds (fs) step size was used for all MD simulations. Trajectories were saved for every 100ps. Periodic boundary condition (PBC) was applied in simulations. Particle mesh Ewald (PME) algorithm³⁸ was used to calculate the electrostatic interactions. MD simulations were conducted using GPU accelerated OpenMM³⁹ and CHARMM27 force field.⁴⁰

Analysis of Simulation Trajectories

Root-Mean-Square Deviation (RMSD) and Root-Mean-Square Fluctuation (RMSF)

The dynamics stability of a MD simulation trajectory is measured by the root-mean-square deviation, which is calculated as:

$$\text{RMSD}=\sqrt{\frac{{\sum }_{i=1}^N{(r_i^0-U{r}_i)}^2}{N}}$$ (1)

where $r_i^0$ represents the coordinate of an atom i in Cartesian coordinate system and U is the most appropriate alignment transformation matrix between two structures. For each trajectory, the first frame was treated as the reference structure.

The root-mean-square fluctuation is used to measure the fluctuation of atoms in each frame with regard to the first frame in a MD simulation trajectory. Specifically, Cα atoms were considered important in representing the protein motions and the corresponding RMSFs of each Cα were calculated as:

$${\text{RMSF}}_i=\sqrt{\frac{1}{T}\sum _{j=1}^T{\left(r_i(t)-{\overline{r}}_i\right)}^2}$$ (2)

where T is the number of frames and ${\overline{r}}_i$ is the averaged Cartesian coordinate of the i^th Cα in the given trajectory.

Feature Processing

The 3N degrees of freedom in the Cartesian coordinate system hinders a thorough analysis of MD simulations in biological systems. Pairwise Cα distances are usually extracted to represent the structural characteristics of protein configurations.⁴¹ In the current study, a feature vector of each structure was constructed by calculating the distance pairs between one α carbon atom and another α carbon atoms in amino acids following the order of residue sequence. This feature vector was further encoded by a previously proposed transformation method⁴² with a cutoff of 10Å.

ivis Dimensionality Reduction Method

ivis is a machine learning based dimensionality reduction method that is originally developed for single cell technology.²⁷ The ivis framework applies the Siamese neural networks architectures that is composed of three identical base neural networks. For each base neural network, there are three dense layers consisting of 500, 500, and 2000 neurons with a final embedding layer of 2 neurons. A novel triplet loss function is implemented in the training process:

$$L_{\text{tri }}(\theta )={\left[\sum _{a,p,n}{D}_{a,p}-\text{min}\left(D_{a,n},D_{p,n}\right)+m\right]}_{+}$$ (3)

The symbol a represents the point of interest, often referred to as anchor point. The symbol p represents a positive point that is selected based on the k-nearest neighbors (KNNs) algorithm. The symbol n represents a negative point that is randomly selected from the rest of data samples. The similarity between two points is calculated as the Euclidean distance (D). The margin (m) is defined as the minimum distance between any pair of points and was set to default value of one. The advantage of ivis method lies in the triplet loss function, which aims to minimize the distance between the anchor points and the positive points while maximizing the distance between the anchor points and the negative points.

Adam optimizer with a learning rate of 0.001 was applied to train the neural network. To prevent overfitting, early stopping of 5 was used to terminate the training iteration if the triplet loss function does not decrease with 5 consecutive epochs.

Machine Learning Methods

Random Forest (RF) and One-vs-one (OvO) Random Forest Models

Random forest as a tree-based machine learning technique^43,44 was applied to learn the structural differences among macrostates in this study. Each random forest model is composed of 50 decision trees. Decision trees were trained individually and the final result of a random forest model is formed by a voting algorithm. Scikit-learn⁴⁵ version 0.20.1 was used to implement the random forest model.

The random forest model overcomes the problem of overfitting by employing several decision trees. However, in multi-task classification jobs, one-vs-one random forest model is more common and superior than the random forest model by constructing one classifier for each pair of classes.⁴⁶ The overall output is the weighted sum of all base classifiers. In the current study, 10 macrostates were trained with 45 random forest models. One-vs-one random forest model provides weighted sum of overall feature importance with specific feature importance regarding two given classes.

Feature Importance

The feature importance in a random forest model is calculated using the Gini impurity, which is calculated as:

$$\text{ Gini impurity }=\sum _{i=1}^C-f_i\left(1-f_i\right)$$ (4)

where f_i and C are the frequency of one label at a node that are chosen to divide the data set and the number of labels, respectively. A random forest model consists of multiple decision tree models. The importance of feature i in each decision tree is calculated as:

$$f_i=\frac{{\sum }_i^s{n}_j}{{\sum }_{k\in \text{all nodes}}{n}_k}$$ (5)

where s is the frequency of node j split on feature i. The importance of feature i in a random forest model is calculated by averaging its importances among decision tree models:

$$F_i=\frac{{\sum }_{j\in \text{all decision trees}}\text{norm}{f}_i}{N}$$ (6)

where norm f_i and N are the normalized feature importance of one decision tree and the number of decision trees, respectively.⁴⁷

Pairwise Cα distances were extracted as the input features and the corresponding feature importances were calculated. For each Cα distance, the importance was added to the related two residues. The accumulated feature importance of residues implies their contributions in the allosteric process.

Markov State Model

The long timescale protein dynamics is tracked by the Markov state model.⁴⁸ Each simulation frame is assigned to different microstates through MiniBatch k-means clustering method. Compared with microstates, macrostates are more biologically meaningful as they are considered as kinetically-separate equilibrium states. 10 macrostates were generated by Perron-cluster cluster analysis (PCCA).⁴⁹ Lag time is needed to build a MSM and was determined as 40ns based on the implied relaxation timescale. Transition matrix and corresponding transition probabilities were estimated based on this MSM. MSMBuilder⁵⁰ package (version 3.8.0) was used to build MSMs.

Machine Learning based Community Analysis

Machine learning based community analysis³⁴ is a newly proposed method by Zhou et al., which groups residues into communities. The main idea of this analysis is maximizing the overall feature importances across different communities while minimizing the total feature importances within each community. For an undirected graph characterizing the protein, nodes can be used to represent residues, and edges can be used to represent weighted Cα distances. For node i in community C_m, the inner edges of i are defined as the summation of edge values between node i and any other node in C_m, whereas the external edges of i are defined as the summation of edge values between node i and any other node in other communities. For each iteration of ML communities partition, node i can be moved to another community or swapped with another node in different communities. The benefit of these two explorative moves can be calculated as the external edges subtracted by the inner edges. The algorithm of this community analysis method is listed below.

1. ML communities are randomly partitioned;

2. The benefits of moving one node into another community and swapping one node with another between different communities are estimated to search for the maximum moving and swapping strategy, respectively;

3. One moving or swapping strategy with the highest benefit is chosen;

4. Repeat steps 2 and 3 with new ML community configuration until the highest benefit of all moving and swapping strategy is less than 0;

5. ML communities construction is completed if any strategy will increase the number of inner edges for each ML community.

The Kernighan-Lin algorithm⁵¹ has been implemented⁵² to search for local minimum values in graph theory. In the current research, the feature importances of Cα distances from the one-vs-one random forest model based on AuLOV dimer simulations were used. In order to apply ML based community analysis on monomer, the averaged importance for each Cα distance in monomer was calculated based on the dimer feature importance results.

Transition Path Theory

Transition path theory (TPT)^53,54 is used to identify the most probable routes from one macrostate to another. Dark state and light state were chosen based on the transition probability estimated in MSMs as initial and final states, respectively. All other states are considered as intermediate states. Possible transition paths from the dark state to the light state were simulated. The definition of the committor probability $q_i^{+}$ is the probability from one state to a target state. Based on this definition, $q_i^{+}$ is equal to zero for all microstates in initial state and $q_i^{+}$ is equal to one for all microstates in final state. The committor probability of other microstates is calculated as:

$$-q_i^{+}+\sum _{k\in I}{T}_{ik}{q}_k^{+}=-\sum _{k\in \text{target state }}{T}_{ik}$$ (7)

where T is the transition probability matrix and T_ik represents the transition probability from state i to state k.

$$f_{ij}={\pi }_i{q}_i^{-}{T}_{ij}{q}_j^{+}$$ (8)

where π is the stationary probability of T and π_iT_ij is the absolute probability of finding the system at the transition from i to j. $q_i^{-}$ is the backward committor probability calculated as $q_i^{-}=1-q_i^{+}$. The backward flux f_ji were also considered and subtracted in calculating the net flux $f_{ij}^{+}=\text{max}\left(0,f_{ij}-f_{ji}\right)$.

The flux from the initial state to the final state can be decomposed to individual pathways p_i, which can be calculated as:

$$p_i=\frac{f_i}{{\sum }_j{f}_j}$$ (9)

Results

MD simulations analysis

The native dark and light structures of AuLOV are illustrated in Figure 1. In the native light state, a covalent bond is formed between the C4a atom in FMN and the sulfur atom in residue Cys287 upon light excitation (Figure 1C). This covalent bond triggers a global conformational change and protein dimerization. To explore this effect and the protein response, the covalent bond between FMN and Cys287 is constructed in the dark state structure to construct a transient dark state. On the other hand, the covalent bond between FMN and Cys287 is removed in the light state structure to construct the transient light state. Both transient dark and transient light states are subjected to the simulation and analysis to aid in mapping allosteric trajectories in response to blue-light activation and thermal reversion to the dark state.

Figure 1: The native dark and light structures of AuLOV monomer.

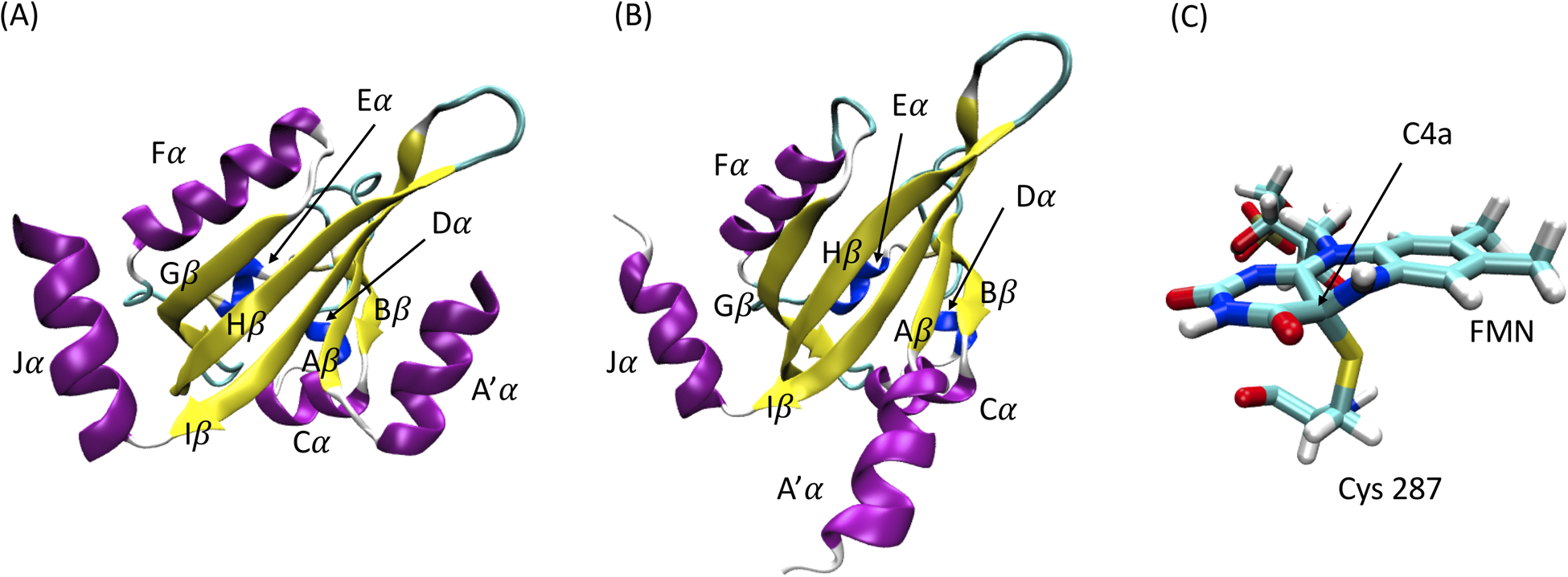
(A) Native dark structure; (B) Native light structure; (C) A covalent bond is formed between C4a position of FMN and sulfur atom in Cys 287 upon light excitation.

The time evolution of the RMSD in four trajectories is plotted in Figure 2. All RMSD values were calculated with reference to the first frame of each trajectory. The average RMSDs in native dark, native light, transient dark and transient light states are 1.75Å, 2.04Å, 2.39Å and 2.08Å, respectively. The plots show that each simulation is stable with low RMSD fluctuation values. The transient dark state is more dynamically active than the native dark state, indicating that the formation of covalent bond increases the flexibility of the protein. The RMSD results also imply the stability of the native dark state compared with the native light state.

Figure 2: The RMSDs of AuLOV MD simulation trajectories.

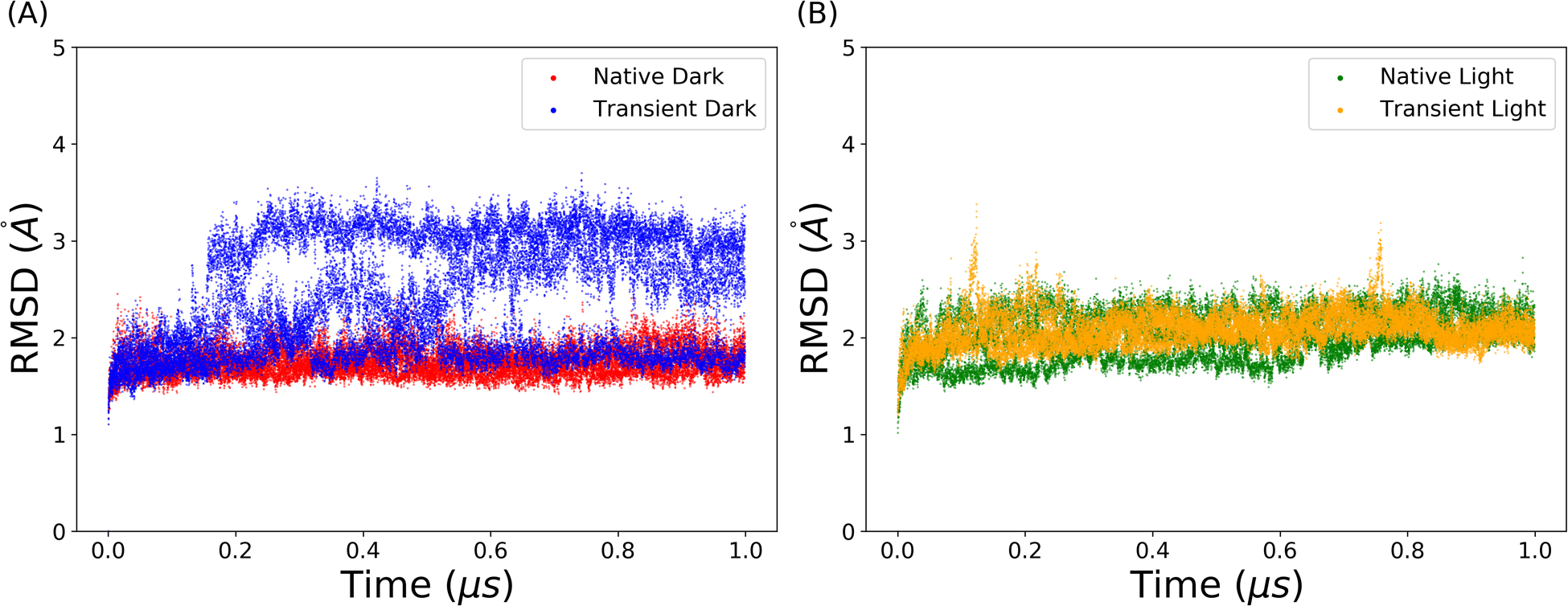
(A) Native dark and transient dark states; (B) Native light and transient light states.

As the allosteric process of AuLOV is characterized by conformational changes in the secondary structures, the backbone Cα is selected to measure the influence of light absorption on the protein structure. The RMSFs of the Cα atoms in AuLOV simulations are calculated and plotted in Figure 3. Both A’α and Jα helices were found to be dynamically active in all four states with increased dynamics in the two transient states. Differences between the two chains can be further quantified by comparing the RMSF values. In the native dark state, chains A and B showed no difference. In the native light state, the A’α in chain A is more flexible than that in chain B. Through the formation of the covalent bond in the transient dark state, both A’α and Jα helices in chain A showed enhanced flexibility.

Figure 3: The RMSFs of AuLOV Cα atoms in simulations.

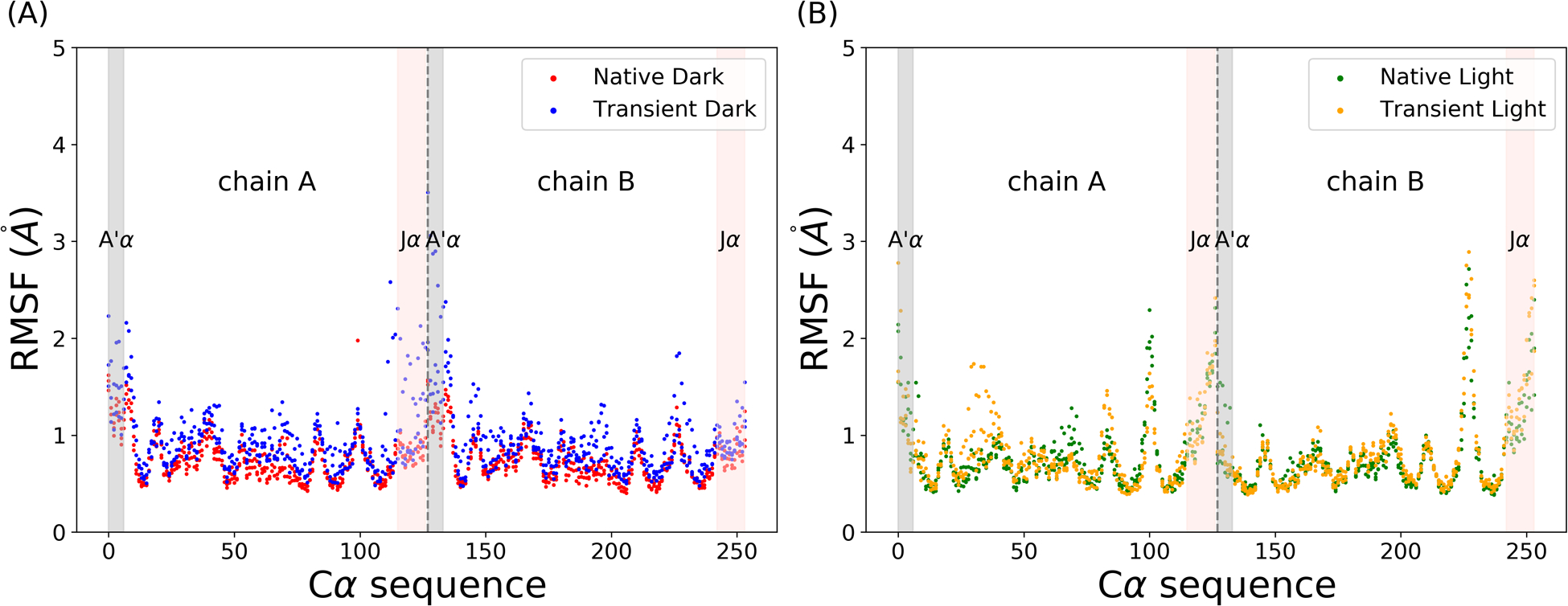
(A) Native dark and transient dark states; (B) Native light and transient light states. Grey dashed lines separate two chains.

Markov state model partitions kinetically separate macrostates

To represent the protein structure and movements, pairwise Cα distances were calculated as the representation of protein configurations. A total of 32131 Cα distances were extracted from the AuLOV dimer, composed of 254 residues. For each Cα distance, the value was further encoded through the feature preprocessing method outlined in the methods. For feature transformation, 10.0Åwas chosen as the threshold. The ivis dimensionality reduction method was applied to extract the collective variables and project the embedding layer onto a 2D surface. The distribution of four states in the ivis result is plotted in Figure 4A. The plot revealed that the transient dark state partially overlaps with the native dark state and the transient light state. The large region of transient dark state distribution is mainly because of the enhanced dynamics caused by the formation of the covalent bond. The distribution of the native light state is divided into two separate regions. The distribution of the transient light state covers a large area, and overlaps with the both regions of the native light state distribution.

Figure 4: ivis dimensionality reduction result and the implied timescales with regard to different lag times.

(A) The distribution of four protein states onto the 2-dimensional space; (B) Estimated relaxation timescale with different lag times calculated by MSMs.

Markov state model is based on the clustering results on the reduced dimension projected by ivis framework. To construct MSMs, MiniBatch k-means clustering method was applied to partition the distribution of protein simulations in the 2D region into 300 microstates. The top 20 relaxation timescales calculated by different MSMs with different lag times are plotted in Figure 4B. The implied timescale converges after 40ns, which was chosen as the lag time for MSM. The number of macrostates depends on the gap between the timescales, and a total of 10 macrostates were chosen to divide the reduced protein distribution into kinetically separated macrospaces. For each microstate, the corresponding labels of macrostates were determined by the PCCA method, which is based on the eigenfunction of the transition probability matrix in MSM. The resulting macrostates with their associated transition probabilities are illustrated in Figure 5. Two dark states and two light states are divided into 4 and 6 macrostates, respectively. Macrostates (states 1, 2, 3 and 10) are in the area of the native dark state and the transient dark state. Based on the similarity to the crystal dark state structure, macrostate 2 was considered as the native dark state. State 9 was recognized as the native light state using the same method. Other macrostates were considered as intermediate states. The low transition possibilities starting from macrostate 2 and 9 to adjacent macrostates indicate the stability of both the dark and light states. On the contrary, it is more likely for protein to shift between intermediate states. Two representative structures in the transient dark and transient light states are illustrated in Figure 6. Both A’α and Jα helices in the representative conformation of macrostate 3 (transient dark state, Figure 6A) move further from the LOV domain comparing to the native dark state (transparent grey structure in Figure 6A). These differences agree with the experimental finding that Jα helix interacts with the LOV core through hydrogen bonding between Gln365 and Cys316 as well as Tyr357 and Gln330 in the native dark state.⁸ In the light state, the hydrogen bond between Gln365 and Cys316 is broken after the formation of photo-induced covalent bond between FMN and Cys287, leading to the release of Jα helix from the LOV core. The A’α helix also interacts with the LOV core via a hinge region (Ala248, Glu249, Glu250 and Gln251) and covers a hydrophobic patch (as the back of A’α helix) in the native dark state. Due to the change of A’α helix orientation, the back of this helical structure as the hydrophobic patch is exposed in the light state. The protein structure of macrostate 5 (transient light state, Figure 6B) is similar to the structure of native light state due to the stabilizing interaction within the dimer structure.

Figure 5: Macrostates in MSM with transition probability.

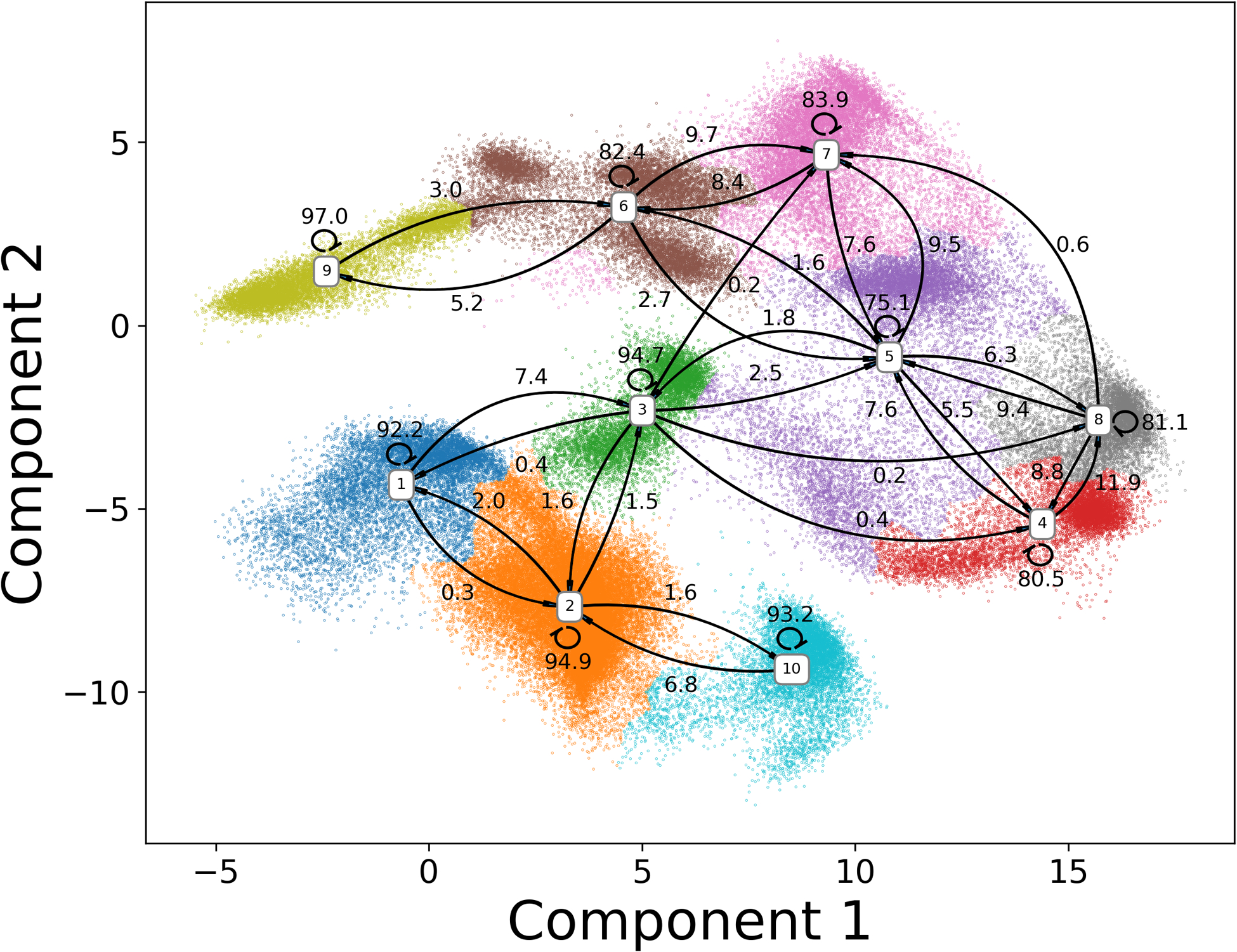
Based on the transition probabilities, states 2 and 9 were considered as the native dark and native light states among macrostates, respectively. Other macrostates were treated as intermediate states.

Figure 6: Representative conformations in the transient dark and light states.

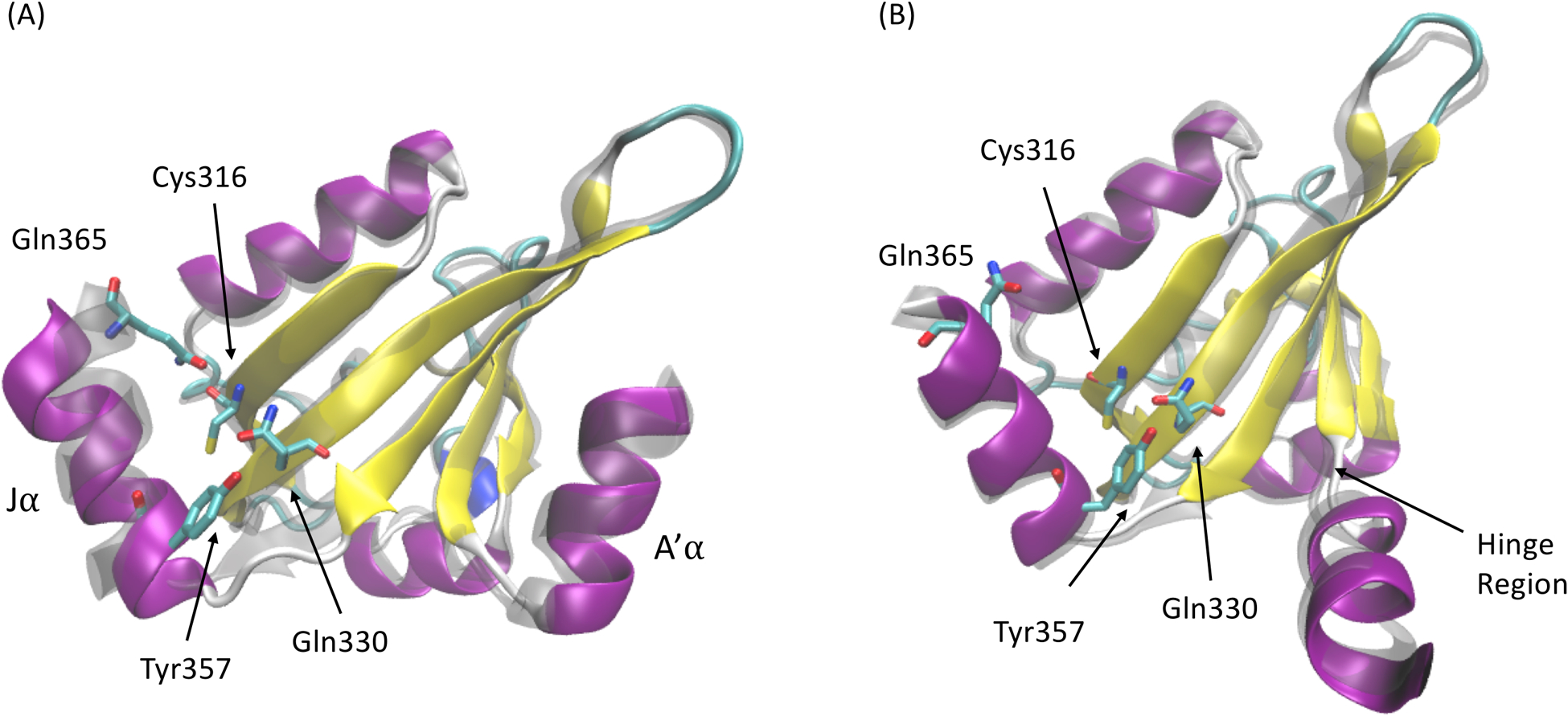
Monomer structures in (A) macrostate 3 from the transient dark state, and (B) macrostate 5 from the transient light state. Corresponding structures in native dark and native light states are shown in transparent grey color.

One-vs-one random forest model extracts key residues

In order to extract the key residues that play a vital role in AuLOV allostery, supervised machine learning models were applied to explore the structural differences among macrostates. Here, pairwise Cα distances were chosen as the translation and rotation invariant collective variables for the description of protein structures in the simulations. For each simulation, frames were saved for every 100 picoseconds (ps), resulting in 10000 frames for every 1 μs MD trajectory. Accordingly, 120000 samples with 32131 features were extracted from the simulated trajectories. Each frame was labeled based on the macrostate results. Random forest and one-vs-one random forest models were applied to distinguish the intrinsic conformational differences among macrostates. Training scores and testing scores were plotted in Figure 7. The testing accuracy was 93.5% in the random forest model at depth 9 and 94.5% in the OvO random forest model at depth 8. The high classification accuracy indicated that the two tree-based models were able to capture the characteristics of protein configuration of each macrostate using pairwise Cα distances.

Figure 7: Tree-based models for macrostate classification.

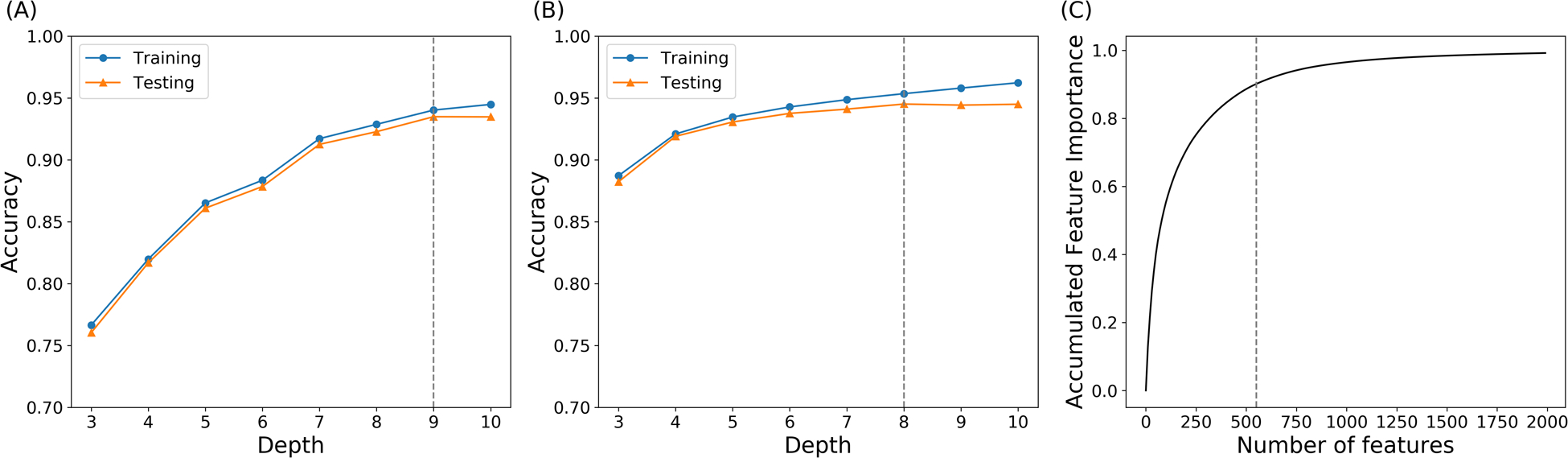
(A) Prediction accuracy of the random forest model with different tree depths; (B) Prediction accuracy of the one-vs-one random forest model with different tree depths; (C) Accumulated explained importance of the OvO random forest model in 8 tree depth with regard to the number of features. The top 550 features account for 90.2% of the overall importance.

The advantage of the tree-based models comes from the ability to quantitatively evaluate the contribution of each feature in classification model through the value of feature importance. Superior than random forest model, one-vs-one random forest model was applied to compute the feature importance for any two different macrostate pairs by conducting a random forest classification between these two specific macrostates. Therefore, for any two different macrostates, one distinct random forest estimator was built. A combination of 10 * 9/2 = 45 basic random forest classifiers were constructed for the pairwise macrostates classifications. Accumulated feature importance of one-vs-one random forest at depth 8 was plotted in Figure 7C. Overall, this method is an effective model, in which the top 550 features out of 32131 features account for 90.2% of the overall feature importance.

Those Cα distances related to two residues located on different chains are named as cross-monomer features. These cross-monomer features accounts for 59.77% of the overall importance. Therefore, the Cα distances within the same chain accounts for 40.23% of the overall importance. This shows that the OvO random forest can capture the structural changes within each monomer, as well as the relative motions between monomers.

In order to identify key residues based on the results of the OvO random forest model, the feature importance value of each Cα distance was added and accumulated to the two related individual residues. The top 20 residues are listed in Table 1. Among the identified residues, several have been experimentally confirmed to be important to AuLOV allostery and are shown in bold font. Residues Met313, Phe331, and Cys351 are found to undergo changes in orientation. Ala248, Gln249, Gln250, and Asn251 are residues linking the A’α helix to the Aβ strand that are important for signal transduction.⁸ Gln350 was also identified as essential for signal transduction in LOV domains, where it either undergoes a Gln-flip process in response to N5 protonation⁵⁵ or undergoes rotation between exposed and buried conformations⁵⁶ to relay the signal from the flavin active site to N- or C-terminal components. We also identify Phe252 as important for allostery. Notably, Phe252 was found by HDX-MS to be important in the destabilization of the A’α helix that is coupled to conformational changes in Bβ strand and Cα helix.⁸ Therefore, the OvO random forest can successfully identify important residues reported in experimental results. The residue importance can be accumulated to the protein’s secondary structures and the results were shown in Table 2. A’α and Jα helices account for 15.17% and 8.04% of the overall importance, respectively. The importance of Cα helix and linkers in AuLOV are also significant at 9.12% and 21.36%, respectively.

Table 1:

Top 20 residues identified by OvO random forest.

Residue ID	Residue Type	Residue ID	Residue Type
250a	GLN	349	VAL
245	LEU	247	THR
252	PHE	248	ALA
351	CYS	249	GLN
244	ALA	331	PHE
312	ASP	314	SER
246	GLN	334	ALA
268	SER	313	MET
350	GLN	336	LEU
335	ALA	251	ASN

^aExperimentally confirmed important residues are shown in bold font.

Table 2:

Accumulated feature importance of secondary structures in AuLOV.

Secondary structure	Importance percentage
A’α	15.17%
Aβ	7.12%
Bβ	2.28%
Cα	9.12%
Dα	0.70%
Eα	0.05%
Fα	2.14%
Gβ	6.43%
Hβ	14.13%
Iβ	13.46%
Jα	8.04%
Linkers	21.36%

Machine learning based community analysis splits protein structure into four communities

To explore the significance of different protein secondary structures, machine learning based community analysis was applied to split the protein structure into communities. This analysis was developed to divide residues into several communities (referred to as ML communities) so that the feature importance for pairwise Cα distances across different communities is maximum, while the feature importance within each community is minimum.

The relationship between the feature importance for pairwise Cα distances within ML communities and the number of ML communities are plotted in Figure 8A. Applying an elbow criterion, four ML communities were selected with the total feature importance within each ML community accounting for 0.50% and the total feature importance among ML communities accounting for 99.50%. Therefore, the changes among ML communities account for the dominant majority of the overall feature importance and are able to explain the changes between different communities. The changes within each ML community are ignored due to the negligible importance. By applying ML based community analysis, dynamics in each protein structure can be attributed to the changes among partitioned ML communities.

Figure 8: ML based Community analysis results of AuLOV.

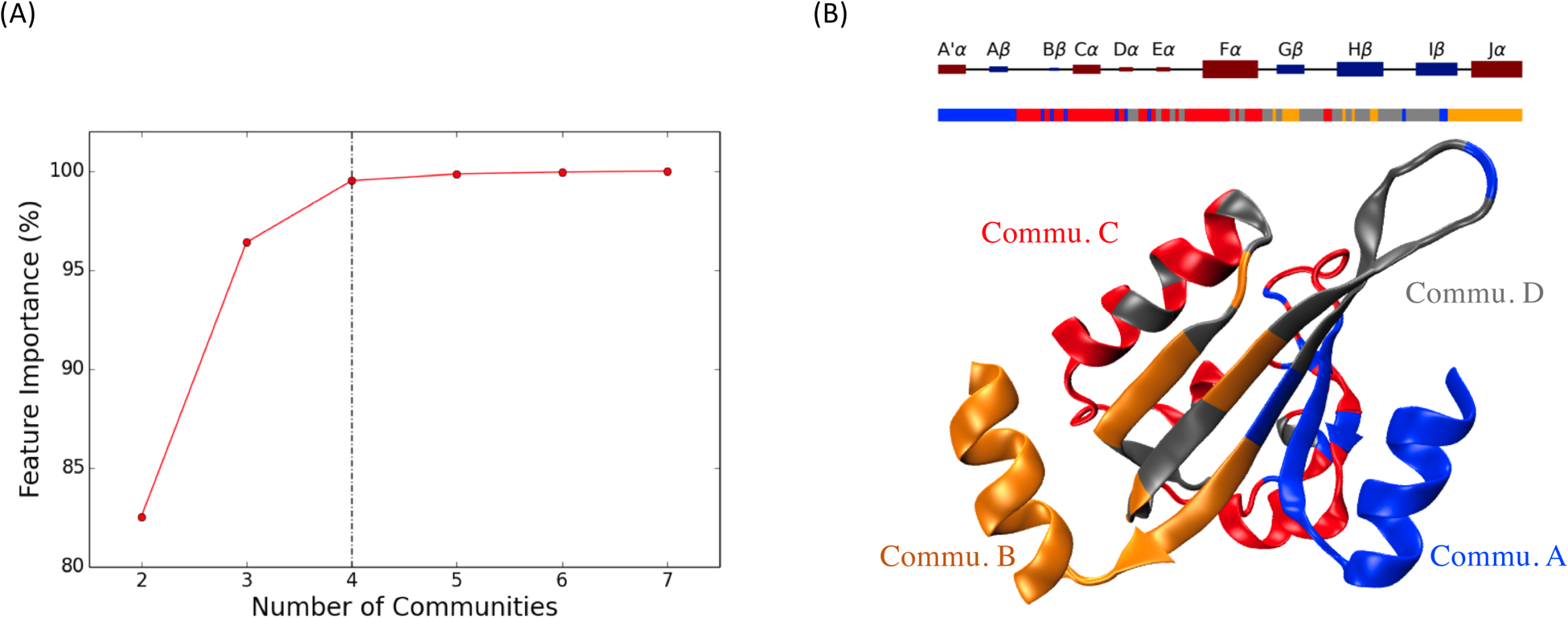
(A) Total feature importance among ML communities with regard to different number of communities; (B) Four ML communities named as Commu. A, Commu. B, Commu. C and Commu. D are illustrated in blue, orange, red and grey colors, respectively.

The distribution of different communities, with a complete partition result corresponding to protein secondary structure, is shown in Figure 8B. Commu. A (blue) includes most of A’α helix and Aβ strand, Commu. B (orange) includes Jα helix with part of Gβ and Hβ strands on the LOV core, Commu. C (red) includes Cα helix, part of Fα helix and linkers. Commu. D (gray) includes part of Fα helix, Gβ, Hβ and Iβ strands.

The machine learning based community analysis offered additional information based on the selected four ML communities and the corresponding different regions in the protein structure during simulation. The accumulated overall feature importance among each ML community pair is listed in Table 3. Correlations between Commu. A, Commu. B and the rest of the protein accounted for 82.99% of the total feature importance. This is not surprising since the A’α helix in Commu. A and Jα helix in Commu. B are the most distinguishing structures, which undergo significant conformational changes from the native dark state to the native light state. Through the accumulated feature importance of ML communities, A’α and Jα helices are confirmed to convey significant allostery characteristics. Unexpectedly, the correlation between Commu. C and Commu. D accounts for 16.57% of the total feature importance. Several transitions between adjacent macrostate pairs have significant contribution from Commu. C (Table 4). However, for transitions between nonadjacent macrostates, Commu. C accounts for less importance which explains the difference between macrostate pairs.

Table 3:

Accumulated feature importance between each ML community pair.

Features	Commu. A	Commu. B	Commu. C	Commu. D
Commu. A	0.12%	13.58%	25.87%	13.87%
Commu. B		0.03%	13.17%	16.44%
Commu. C			0.15%	16.57%
Commu. D				0.20%

Table 4:

The changes of Commu. A, Commu. B and Commu. C during transitions between macrostates.

Adjacent macrostates	Commu. A	Commu. B	Commu. C
State 2 (Dark) → State 3a	7.26%	26.69%	4.01%
State 2 → State 10	6.05%	18.51%	3.03%
State 3 → State 5	16.91%	12.74%	7.68%
State 5 → State 7	7.44%	2.04%	18.41%
State 5 → State 4	9.55%	6.40%	3.64%
State 5 → State 6	10.96%	6.98%	16.27%
State 7 → State 6	11.22%	3.97%	8.86%
State 6 → State 9 (Light)	12.35%	10.56%	19.13%
Non-Adjacent macrostates
State 10 → State 9	21.39%	23.63%	0.23%
State 10 → State 6	26.97%	15.11%	2.26%

^aState-transitions with large Commu. C component are shown in bold font.

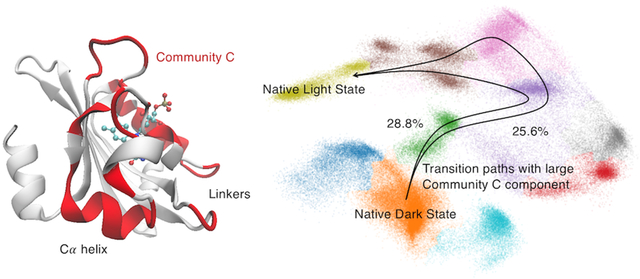
For those transitions between macrostates where Commu. C accounts for a large component, two promising routes from the dark state to the light state can be identified as: 1) State 2 → 3 → 5 → 7 → 6 → 9 and 2) State 2 → 3 → 5 → 6 → 9. These two proposed pathways lead to a hypothesis that Commu. C is important in propagating allosteric perturbations.

To estimate the probability of the two identified channels which include significant Comm. C contribution, the transition path theory was employed to generate an ensemble of pathways to estimate the probability of every pathway from State 2 (native dark state) to State 9 (native light state). A total of 3151 pathways were generated and divided as 212 distinct channels connecting these two states. The probability of each channel was calculated based on the net flux from the initial state to the target state. Overall, the probability of top 10 channels is listed in the Table 5. The population of these 10 channels account for 80.0% of the total pathway population.

Table 5:

The probability of top 10 channels simulated using transition path theory.

Channels	Probability
2, 3, 5, 7, 6, 9	28.8%
2, 3, 5, 6, 9	25.6%
2, 10, 5, 7, 6, 9	5.4%
2, 3, 7, 6, 9	4.7%
2, 3, 5, 8, 5, 7, 6, 9	3.9%
2, 3, 4, 8, 5, 7, 6, 9	3.0%
2, 3, 8, 5, 7, 6, 9	2.9%
2, 10, 5, 6, 9	2.3%
2, 1, 3, 5, 7, 6, 9	2.1%
2, 10, 5, 8, 5, 7, 6, 9	1.3%
Top 10 channels	80.0%

Among all 212 channels, the two identified channels 2-3-5-7-6-9 and 2-3-5-6-9 are the top 2 populated channels with 28.8% and 25.6% of overall probability, respectively. The sum of contributions from these top two channels accounts for 54.4% contributions, which is significant compared to all other pathways, suggesting the importance of Commu. C movement during the allosteric process. The first channel is more probable than the second one. This agrees with the observation that the transition probability from 5 to 7 (9.5%) as one step in the first channel is greater than that from 5 to 6 (1.6%) as one step in the second channel. Interestingly, the ML based community analysis reveals higher contribution from the Commu. C to the transition between states 5 and 7 than that between states 5 and 6.

Different communities account for different importance in each macrostate transition. To better show the trend of components in Commu. A, Commu. B and Commu. C with regard to Commu. D, the change of importance along the two proposed paths is plotted in Figure 9. Two paths share similar characteristics: 1) Commu. A accounts for little importance at the beginning of allostery process while the contribution goes up in later transitions; 2) Commu. B starts with high importance and decreases drastically after the first transition; 3) Commu. C is more important at the end of allostery process.

Figure 9: Change of community importance along transitions.

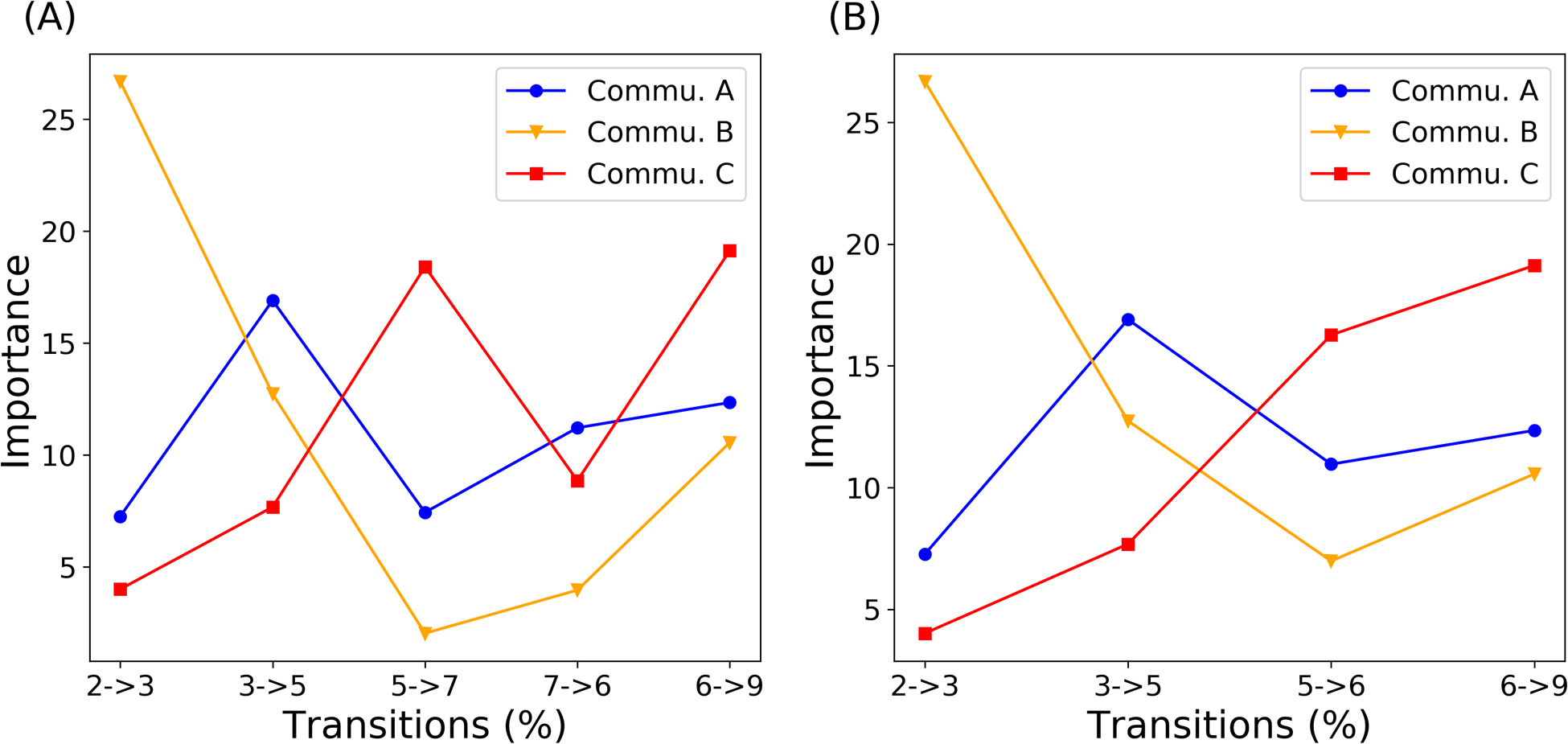
Community importance change along two identified paths from the native dark state to the native light state. (A) 2 (native dark) - 3 – 5 - 7 – 6 - 9 (native light); (B) 2 (native dark) - 3 – 5 - 6 – 9 (native light).

Discussion

PtAu1a is an allosteric protein that undergoes a series of conformational changes upon light activation beginning with the formation of covalent bond between Cys287 and FMN.⁵⁷ This computational study of AuLOV is integrated with MD simulations and other computational methods to provide quantitative analysis of the dynamics and importance of residues with regard to the overall allosteric process. While there is extensive research on the regulatory role of Jα helix and dimerization controlling A’α helix, a detailed mechanism of allostery with signal transmission route still needs scrutinization.

Signal transduction in LOV domain containing proteins typically involves coupling of adduct formation to conformational changes in the N- and C-termini via propagation across a central β-sheet.^58–61 Central to this signal transduction are key residues within the Iβ strand that enables its coupling with the Jα helix and interaction with A’α helix in the dark state, specifically the residue equivalent to Gln350 that is essential for LOV signal transduction.^55,56 In AuLOV, several additional light-induced rotamers (Met313, Leu317, Leu331, Leu333, and Cys351) were observed on the β-sheet surface⁸. Here, through the accumulated residue importance in the one-vs-one random forest model, we successfully identified Met313, Leu331, and Leu351 as being important in differentiating allosteric changes in AuLOV. In our models, these residues contribute to conformational changes linking the β-sheet surface to A’α helix through Gln350. We note that our computational methods mirror those identified experimentally where A’α helix contributes to the dynamic stability of the dark state by the interaction with LOV core through a hinge region. The hinge region consists of four conserved residues (Ala248, Gln249, Gln250, and Asn251), which were also found to be important via our approach (Table 1). Overall, the strong correlations between previous experimental results, and our Markov state model and OvO random forest analysis, confirm our methodology as being able to discern allosteric pathways in AuLOV.

Most proteins undergo allosteric process within a long timescale from milliseconds to seconds, including AuLOV, making it difficult to collect sufficiently long trajectories. Markov state model addresses this difficulty by extracting the slowest motion and long timescale information from limited simulations. However, while the slowest dynamical processes are often involved in protein allostery and are assumed to be the process of interest,⁶² fast-moving flanking helices or side chain rotations could play significant role in protein allostery. Due to their short timescales, these motions may not be represented well in the MSM. Although there are some studies focusing on fast protein motions and their relations with slow motions,^63,64 the functions of fast motions in protein allostery remains elusive and requires more studies. Regarding the allostery of AuLOV, the kinetics between dark- and light-states are beyond scale of minutes.⁸ Therefore, sub-ns protein local motions are unlikely to be determinant factors in AuLOV allosteric mechanism and are not the focus of the present study.

Although chain A and chain B in AuLOV are dynamically identical in the dark state, the A’α helices of the two chains differ in conformations upon dimerization.⁸ Our simulation results confirmed the differences between these two chains through a comparison of RMSF values. The RMSF results reflect that A’α helix in chain A is more dynamically active than that in chain B. The asymmetrical property in A’α helix could originate from either the interaction between A’α and Jα helices on different chains or the asymmetrical conformational change⁸, thus requiring further detailed study.

ML based community analysis used in this study provided an approach to partition protein conformation into communities based on the feature importance of pairwise Cα distances. Through this analysis, three important communities were identified. Commu. A containing A’α helix and Commu. B containing Jα helix were expected to account for great contribution, since these two helices undergo notably conformational changes upon light activation (Table 2). The Cα and Fα helices stand out as Commu. C, and surprisingly provided additional information for allosteric process. Commu. C accounts for great importance in adjacent transitions between macrostates and accounts for less importance in nonadjacent transitions compared with Commu. A and B.

Transition path simulations further validated the important allosteric function of Commu. C. For all possible transition pathways found by TPT, the top 2 channels are those with large Commu. C components and together constitute over 50% of the overall possibility. Although Commu. C consists of two helices as Cα and Fα, these two helices are not equally important. The allosteric role of Fα helix should be evaluated with caution since its accumulated feature importance is relatively low (Table 2), and the importance in Commu. D, which also includes part of Fα helix, is the least important community. Because Cα helix is important in both OvO random forest result and ML based community analysis, it is reasonable to conclude that Cα helix may play an important role in controlling AuLOV allostery. Moreover, Commu. C also includes several linking residues that account for a large portion of the overall importance, indicating the indispensable role of linkers in the allosteric process as reported in previous studies.^24,65

Examination of the two most probable channels linking conformational changes through the identified communities can allow construction of allosteric paths (Figure 9). In this study we identify that the Jα helix is fundamental in the early stage of AuLOV allostery, followed by changes in the A’α helix in later stages. In the first transition step from macrostate 2 → macrostate 3, Commu. B accounts for a large component compared with Commu. A, indicating the importance of Jα helix in the initial stage of allostery. As the allosteric perturbation propagates, the importance of Commu. B decreases and Commu. A becomes the more significant region. This important shift implied and confirmed the experimental finding that, after initial Cys287-FMN covalent bond formation, the first response of the protein structure is the undocking of the Jα helix, which is essential to the release of A’α helix.^56,66,67 The rising importance of Commu. C, together with the transition path theory results, suggests that Commu. C, especially Cα helix and linkers, is vital in the allosteric process and should be investigated further.

Conclusion

The LOV protein PtAu1a is a member of Aureochrome family that binds DNA upon blue light activation.⁵ Studies of the LOV domain with N- and C-teriminal helices indicate that in the absence of light it exists as monomeric units; upon blue light absorption, cysteinyl-flavin bond formation triggers a global conformational change which ultimately results in the dimerization of the LOV domains. In the present study, the protein dynamics of AuLOV with N- and C-terminal helices were simulated using MD simulations and analyzed using a series of computational methods. We quantified the differences of A’α and Jα helices dynamics in four functional states and the importance of each residue in the two chains with regard to the protein allosteric process. Key residues in overall structural changes identified by one-vs-one random forest agree with the results reported in other experimental work. Markov state model, combined with transition path theory, studied the importance of protein structures by a machine learning based community analysis. The functional role of key Community C, which includes the Cα helix and linkers, is revealed through in-depth analysis as propagating the allosteric perturbation. Overall, this study quantitatively analyzed the allostery process of AuLOV and linked the macroscopic conformational change to residue level importance. Our results provided new opportunities for a detailed mechanism explanation and offered further opportunities for the research of PtAu1a as an optogenetic tool. Future studies can facilitate our understanding of global protein conformational changes in the context of full-length PtAu1a.