Abstract
Background:
The past decade has seen a multitude of new in vivo functional imaging methodologies. However, the lack of ground-truth comparisons or evaluation metrics makes the large-scale, systematic validation vital to the continued development and use of optical microscopy impossible.
New-method:
We provide a new framework for evaluating two-photon microscopy methods via in silico Neural Anatomy and Optical Microscopy (NAOMi) simulation. Our computationally efficient model generates large anatomical volumes of mouse cortex, simulates neural activity, and incorporates optical propagation and scanning to create realistic calcium imaging datasets.
Results:
We verify NAOMi simulations against in vivo two-photon recordings from mouse cortex. We leverage this in silico ground truth to directly compare different segmentation algorithms and optical designs. We find modern segmentation algorithms extract strong neural time-courses comparable to estimation using oracle spatial information, but with an increase in the false positive rate. Comparison between optical setups demonstrate improved resilience to motion artifacts in sparsely labeled samples using Bessel beams, increased signal-to-noise ratio and cell-count using low numerical aperture Gaussian beams and nuclear GCaMP, and more uniform spatial sampling with temporal focusing versus multi-plane imaging.
Comparison with existing methods:
NAOMi is a first-of-its kind framework for assessing optical imaging modalities. Existing methods are either anatomical simulations or do not address functional imaging. Thus there is no competing method for simulating realistic functional optical microscopy data.
Conclusions:
By leveraging the rich accumulated knowledge of neural anatomy and optical physics, we provide a powerful new tool to assess and develop important methods in neural imaging.
Keywords: neural data analysis, two-photon microscopy, large-scale recordings, neural simulation
1. Introduction
The endeavor to understand neural systems has spurred rapid development of technology that can record brain activity at ever larger scales [1, 2, 3] and higher precision [4, 5, 6]. One such class of technology, functional optical microscopy, has empowered researchers to explore neural dynamics from synapse [7, 8] to large brain regions [9, 10]. Specifically, two-photon microscopy (TPM) combined with in vivo calcium imaging [11, 12, 13, 14, 15, 16] has enabled the simultaneous recording of unprecedented numbers of neurons (over 9000) at cellular resolution [17, 18].
Although TPM has found widespread use [19, 20, 21], many available experimental techniques and data processing algorithms lack appropriate, systematic assessment [22, 23]. This deficit can result in inaccurate interpretation of neural data [24]. A systematic comparison of techniques would allow researchers to make better informed decisions about equipment and data-processing.
For instance, while imaging deeper into scattering tissue with TPM can benefit from decreasing the excitation numerical aperture (NA) [15], it is unknown how this benefit interacts with other optical or experimental design choices, such as adaptive optics [25, 26] or dendritic imaging [27, 28]. Additionally, while many algorithms have been designed to extract the neural activity traces and spatial profiles from TPM data [29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43], few options exist to assess the fidelity of the inferred segmentation beyond comparisons to manually annotated data [44, 45, 24].
In both cases assessment suffers from a lack of ground truth data, the gold standard of which requires simultaneous intracellular electrophysiological and TPM recordings [46, 47]. Such experiments are both difficult to perform and limited to only a few neurons and imaging conditions. The small number of neurons from such experiments limits the assessment scope by biasing towards cells that are in focus, fire often, and fluoresce brightly. This problem is further exacerbated as assessing multiple imaging parameters requires recordings under each imaging condition, greatly increasing the cost of collecting such data.
Alternatively, subjective ground truth can be obtained from TPM recordings via manual annotation [48]. Human labels, however, do not provide access to the underlying neural spiking, are limited by the same signal-to-noise ratio (SNR) that limit demixing algorithms, and may also bias analysis against dim or sparsely firing neurons. These same issues also affect comparisons using simultaneous conventional TPM recordings to test novel imaging conditions [49, 50].
In place of collecting ground truth data, simulations can provide rich, controlled testing data. Such approaches have benefited other imaging modalities, such as fMRI [51]. Simulation-based approaches, however, often suffer from being either too simple or too complex. While simple simulations are computationally efficient, they often only create realizations of the model being tested rather than the actual underlying phenomenon [52, 53]. In contrast, complex simulations are instead limited in computation or have a different scope. Some existing simulations capture too much detail and are severely limited computationally, requiring high-performance computing to simulate more than small volumes with a handful of neurons [54, 55]. Others aim to answer different scientific questions, for example understanding neural connectivity [56, 57], and include some details that are not relevant to TPM, but not other important aspects that are relevant, such as vasculature. For these reasons, existing methods do not provide plausible and computationally efficient simulations useful for large-scale functional imaging.
To assess TPM methods with realistic and computationally efficient simulations, we present the Neural Anatomy and Optical Microscopy (NAOMi) simulator. Our framework leverages simple, but flexible, models of neural tissue to efficiently create large volumes with thousands of neurons on standard workstations (Fig. 1). Arbitrary patterns of spiking activity can be generated for this population, which our framework then transforms into realistic fluorescence traces separately for somas as well as processes. A light model approximates laser propagation and scattering throughout different locations of the simulated tissue. These components are combined in a simulated scanning procedure that incorporates important imaging effects, such as sample motion. We describe the simulation model, which has a publicly available software implementation1, and provide parameters for simulating two-photon GCaMP [46] recordings in layer 2/3 of mouse visual cortex. We used these simulated datasets to evaluate several automated calcium imaging demixing algorithms. Finally, we generated several more datasets to compare the performance of standard and specialized TPM experimental setups under a variety of sample conditions.
Figure 1:
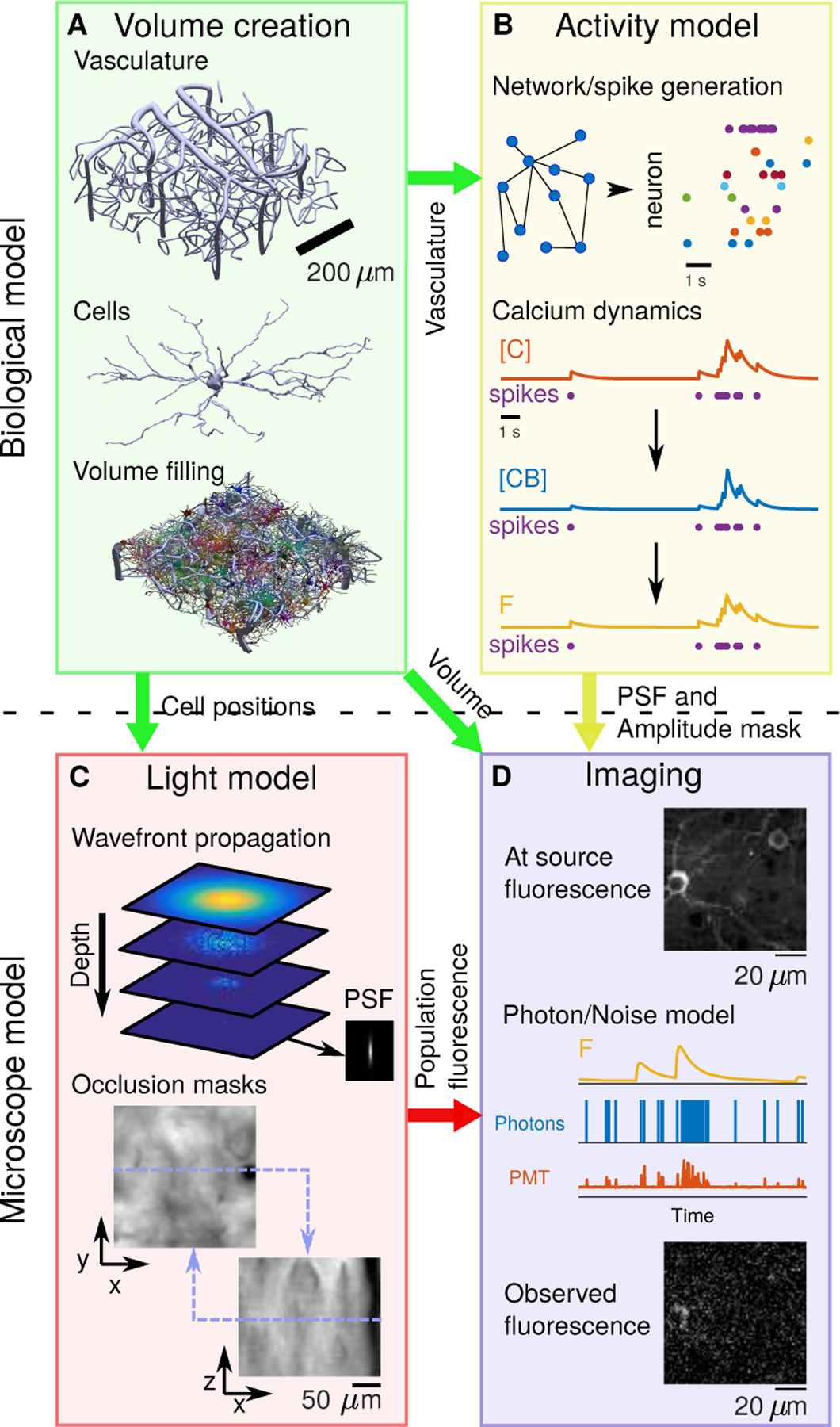
Block diagram of NAOMi simulator. A: Neural volume generation process. Vasculature is generated throughout the volume, followed by cell bodies and finally dendrites and axons are grown. B: Network activity generation. The spiking activity for each neuron is simulated and converted into calcium ([C]), bound calcium ([CB]), and fluorescence (F) for a chosen indicator. C: Light propagation model. An optical wavefront corresponding to particular microscope optics is propagated through a simulated scattering volume, generating a spatially changing scattered point-spread function (top, See Sup. Fig. 13) for creating relative intensity masks (bottom). D: Scanning and image formation. The volume, modulated by the simulated activity, is scanned using the output of the light model with motion and noise sources from a model of the light collection, amplification, and digitization process.
2. Results
2.1. Simulation design
Generating realistic imaging data useful for honest assessment of a spectrum of techniques hinges on accurate, efficient simulations of anatomical volumes at the scale of optical imaging (Fig. 1A). Our anatomical simulation starts by constructing a scaffolding of vasculature with three parts: surface vessels, diving vessels, and capillaries [58] (Tab. 1, Sup. Fig. 1, 2, 3, See Methods). Next, neurons are placed throughout the volume. Somas are placed first, and then dendrites and axons [59] are grown from the cell bodies (Sup. Fig. 4, 5, 6, 7, See Methods). Statistical models of neurons and process paths ensure variation in cell shapes and were tuned using morphological data from electron microscopy (EM) data [60] and optical microscopy [61, 62, 63] (Tab. 1, See Methods).
The next step in simulating TPM data is to augment each generated neuron with realistic fluorescence activity (Fig. 1B). Spiking activity for each neuron is either pre-defined or is generated using models that output correlated, bursting population activity based on models of neural connectivity [64, 65, 66, 67, 68] (Sup. Fig. 8, see Methods). Next, the known nonlinear calcium decay process simulates the dynamic concentration of calcium ions [69, 70]. This two compartment model describes separate dynamics for the cell bodies and the neurites, both driven by the same spike trains. As in related work, a protein-specific double exponential model modulates the calcium concentrations to create bound calcium concentrations with appropriate onset and offset time-constants [70, 71]. Finally, the bound calcium concentrations are converted to fluorescence values using the Hill-equation fit to fluorescence measurements [72, 73] (Tab. 1, Sup. Fig. 9, 10 see Methods).
The next step in the simulation is to estimate the optical properties of the specified microscope configuration within the generated tissue (Fig. 1C). The scattering nature of brain tissue substantially affects light propagation through it, resulting in an abberated point-spread function (PSF) and decreased optical performance. We approximate these complex effects by performing wavefront propagation of a specified beam shape (i.e. Gaussian or Bessel beams [74, 75]) through a generated volume of refractive index shifts (Sup. Fig. 11, 12, See Methods), generating simulated PSFs across the volume (e.g., Sup. Fig. 13). Comparisons of axial spread in simulated and real vasculature imaging of mouse neocortex validate the PSF abberation spreads (Sup. Fig. 14, see Methods). We find the axial spread 330 µm deep into tissue of simulated capillaries (9.98±3.8 µm) and real (11.19±2.31 µm) capillaries with 830 nm excitation light to be comparable and have similar distributions. These results are consistent with another estimate using capillary sources for estimating the axial spread of the PSF with 1280 nm excitation light [76].
The weight of the simulated PSF across different locations of the simulated volume forms an occlusion mask, representing inhomogeneity of optical performance across the sample. This occlusion mask is also modulated by an estimate of the absorption of emitted light through blood vessels and the neural volume as a function of position.
The final scanning module combines the outputs of the anatomical, light, and activity modules to produce images on a frame-by-frame basis (Fig. 1D). The fluorescence activity and occlusion mask modulate the anatomical volume, which is convolved with the simulated PSF to produce raw, noiseless, illumination images. Sub-pixel line-by-line offsets, representing brain motion, are applied prior to spatially resampling to the desired image resolution and applying the measurement noise model, modulated by the power level (Sup. Fig. 15). Measurement noise is simulated by per-pixel Poisson sampling of photons counts at the photo-multiplier tube (PMT) and converting these counts into electrical measurements via PMT photon and electronics amplification distributions (Sup. Fig. 11, see Methods). This process includes bleed-through across pixels from the amplifier’s temporal response kernel (Sup. Fig. 16, see Methods). This procedure is performed independently for each frame, and captures the complex, non-Gaussian noise profile inherent in TPM data.
2.2. Comparison of simulated data to real data
To validate the simulator holistically, we evaluated the overall simulation output against recordings from mouse V1 (Fig. 2). We generated a 500 µm x 500 µm x 100 µm volume and scanned a single plane in the volume with a 0.6-NA Gaussian point-spread function over 20,000 frames at 30 Hz sampling and 40 mW laser power, comparable to parameters in a recorded dataset obtained from mice expressing GCaMP6f being exposed to a set of visual stimuli (see Methods).
Figure 2:
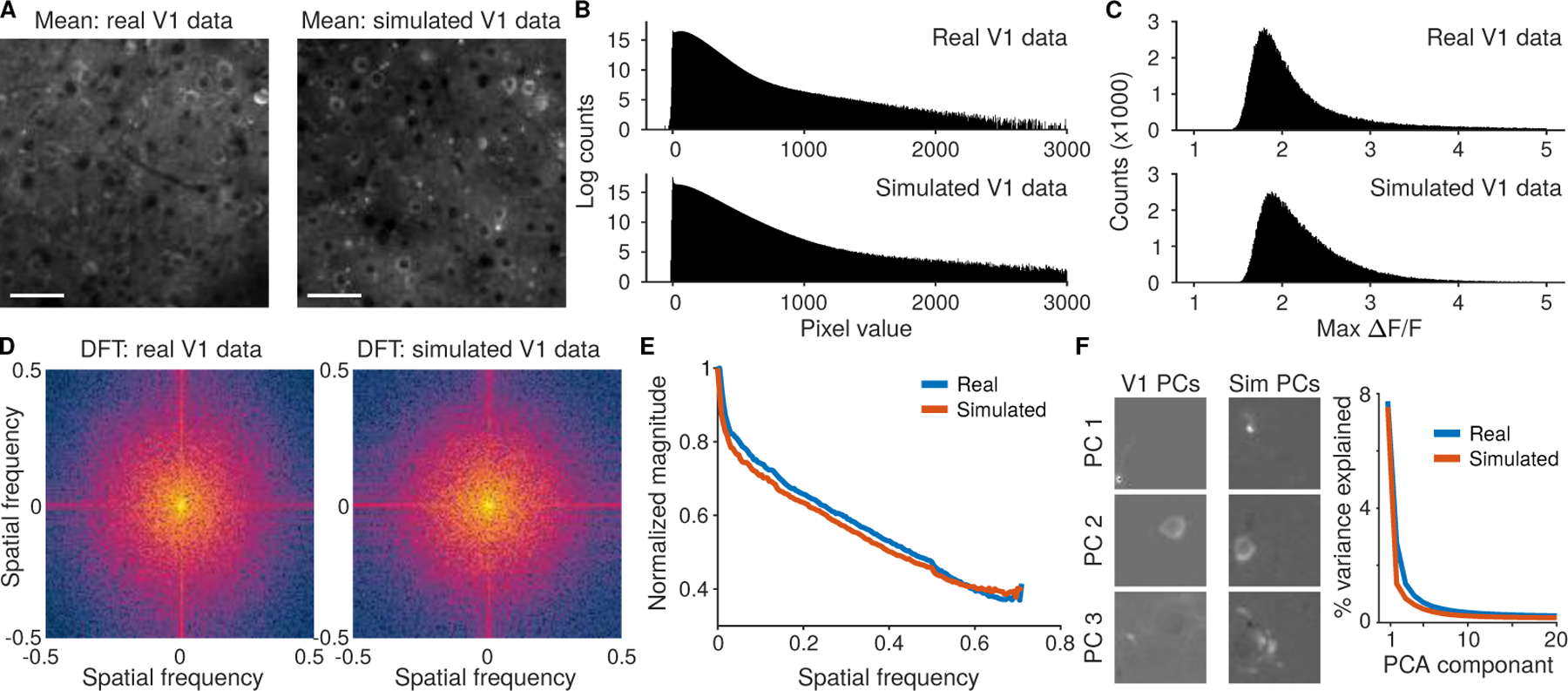
Comparison of simulated data to recordings of mouse V1 L2/3 using GCaMP6f. A: The mean image for mouse V1 recordings and simulated data. B: Pixel value distributions across the full videos display bimodal peaks and a right log-linear tail. C: Distribution of the maximum ∆F/F values across all pixels in the FOV match between the simulated and real V1 data. D: The spatial frequency content in the mean simulated image captures the qualities of the real data. Both the spread of frequencies and the tendency for high-frequency components in the fast- and slow- scan directions that result from line-by-line motion and pixel bleed-through are captured. E: The overall contributions at different spatial frequencies to the mean activity matches between the recording and simulation. F: Principal component decompositions for both the real and simulated data exhibit similar decays in the variance explained per component. The resulting spatial principal components are qualitatively similar.
The simulated videos and recorded videos visually share many of the same features (Sup. Video 1), including bright, sparse transients of fluorescence across the whole image. The overall mean images (average of frames across time; Fig. 2A) both show distinct cell bodies along with muted processes that have their intensity modulated by scattering from blood vessels and other tissue elements. Histograms of video pixel values (Fig. 2A,B) feature heavy right tails corresponding to neural activity and contain peaks at zero corresponding to zero-photon pixels.
The neural activity distribution for individual pixels was explored by comparing the relative strength of firing activity across the field of view (FOV). The distribution of maximum activity (maximum ∆F/F over 20,000 frames) for all pixels (Fig. 2C) for each of the two videos peaks at 2 with a slight heavy right tail, which corresponds to neurons that fired large transients within the videos. Other statistics, such as the distribution of values in the mean image, the standard deviations over all pixels, and measures of activity such as the ratios of maximum to median fluorescence values also match well (Sup. Fig. 17, 18).
The global frequency content of the two videos was estimated with the 2D discrete Fourier transforms of the mean images (Fig. 2D). The Fourier transforms of both videos depict very similar features, such as increased frequency content along the fast- and slow-scanning axes resulting from the sequential pixel bleed-through and residual line-by-line motion artifacts. Additionally, the frequency fall-off (Fig. 2E) for both the real and simulated data display the same decay. Finally, a plot of the effective dimensionality of both videos via Principal Component Analysis (PCA; Fig. 2F) shows both qualitative similarities between the spatial principal components (PCs) and quantitative similarities between the distribution of variance explained for the leading PCs on small patches of videos.
All analyses were repeated for a second dataset from a transgenic Thy1-GCaMP6f GP5.3 mouse, which demonstrated similar fits across the same comparison metrics (Sup. Fig. 19). Another metric of interest is the spatial decay of temporal correlations to neural activity from individual fluorescing components [18]. Comparisons between visual cortical data and NAOMi simulations show similar decays and long-scale correlations (Sup. Fig. 20). We also tested the robustness of time-traces to dendritic spikes under these simulated conditions (Sup. Fig. 21). Finally, we analyzed the robustness of the simulation to the anatomical parameters. Specifically we perturbed two main anatomical parameters: the cell size and cell density. We found that in terms of mean image statistics and imaging pixel histograms, cell size had a more pronounced effect with cell density minimally affecting the overall simulation output (Sup. Fig. 22,23). The primary reason for the increased effect of cell size as compared to cell density is due to the higher average fluorescence levels in larger cells with realistic PSFs. This effect greatly increases the maximum levels of fluorescence in a way that two smaller cells does not achieve.
2.3. Evaluation of automated segmentation
We evaluated TPM techniques using NAOMi by analyzing the performance of automated demixing algorithms and leveraging the ground truth information available. We applied three common algorithms — PCA/ICA [29], constrained non-negative matrix factorization (CNMF) [38], and Suite2p [18] — to 20,000 frames simulated from a 500 µm x 500 µm x 100 µm volume with 1 µm sampling at 30Hz scanning using a 0.6-NA Gaussian excitation numerical aperture (NA) at 40 mW average power. For both the CNMF and Suite2p algorithms there exist multiple versions. Here, we ran the 2017 releases of each code-base and all references to these algorithms indicate the 2017 versions. The ground truth consisted of the spatial profiles of each individual neuron and component within the volume and their individual fluorescence traces.
Each algorithm returned a set of demixed time traces and corresponding spatial profiles (Tab. 6–8, Sup. Fig. 24–27). Overall CNMF, Suite2p and PCA/ICA isolated 1091, 661, and 265 components, respectively, out of a total of 8,117 possible fluorescing components. Comparisons to the ground truth traces, based on a combined Pearson’s correlation cut-off of 0.1 on the time-traces and a 50% pixel overlap, reveal which components represented actual cells in the volume (Tab. 6). A pairing is considered to be a “strong pairing” if the correlation exceeded 0.5 (Fig. 3A,B, Sup. Fig. 28, 29). These correlation values account for all aspects of how well the estimated traces match the true time-courses, including missed transients and false transients from other components (e.g., neuropil; Fig. 3C).
Figure 3:
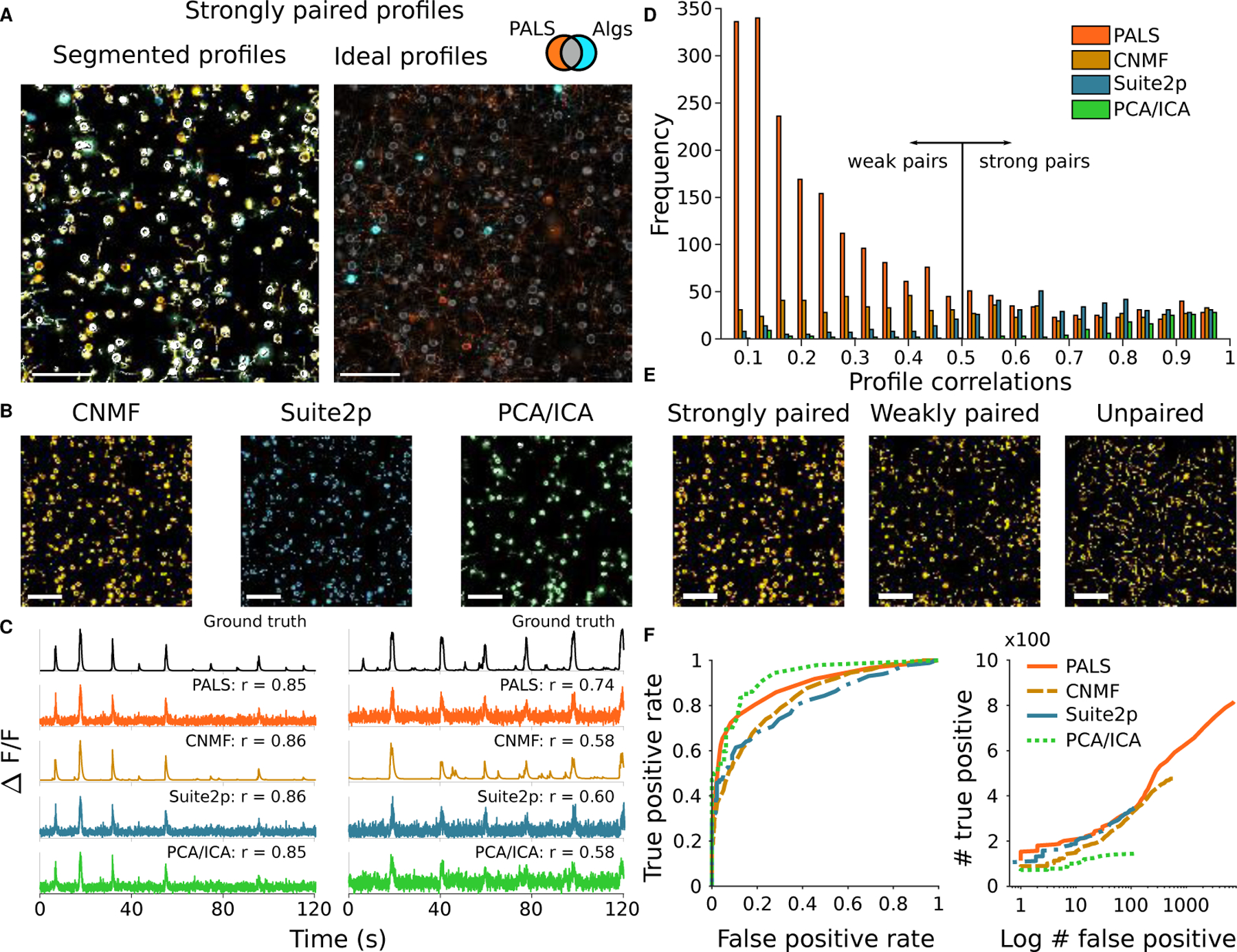
Comparison of popular calcium imaging segmentation algorithms using synthetic data generated using NAOMI. A: Left: Overlapped spatial profiles from CNMF (yellow), Suite2p (blue), and PCA/ICA (green) with a high (r⩾0.5) Pearson’s correlation. White profiles correspond to profiles found by all three algorithms. Right: Simulation-derived profiles with highly correlated PALS time traces (r⩾0.5, orange) are compared to profiles found by any automated algorithm (cyan). Spatial profiles found by both any algorithm and with highly correlated PALS time traces are depicted in gray. B: Strongly paired (r⩾0.5) spatial profiles from each algorithm displayed separately. C: Example timecourses estimated by each of the segmentation algorithms as compared to the ideal profile assisted least-squares (PALS) estimated timecourse and the ground truth timecourse. D: Histogram of correlation values of estimated timecourses to the ground truth timecourses for each match spatial profile. E: Spatial profiles from CNMF separated into strongly paired (r⩾0.5), weakly paired (r<0.5) or unpaired. F: ROC curves for strongly paired (r⩾0.5) spatial profiles sorted by their peak fluorescence and profile weight.
Of the paired profiles, some were doubled, i.e. multiple algorithmically discovered profiles matched to different portions of the same simulated cell (Sup. Fig. 30, Tab. 6). Accounting for doubling, CNMF, Suite2p, and PCA/ICA found 303, 292, and 137 unique cells at the ⩾ 0.5 correlation level. Interestingly, while CNMF found the most distinct components (i.e., before accounting for cells found with multiplicity), it only found approximately the same number of unique cells as Suite2p, and both have a lower rate of found true cells than PCA/ICA (Fig. 3D). Furthermore, comparisons of individual cells found (Tab. 7, 8) show that different methods found non-overlapping sets of cells (Sup. Fig. 31). For example, CNMF and Suite2p only agreed on 273 of the ≈ 300 cells (Fig. 3A, Tab. 7).
While these figures may seem small compared to the 8,117 total sources, not all fluorescence sources are visible above the noise level. The vast majority of sources within the simulation do not have somas that intersect the imaging plane, and the signal is primarily dendritic or axonal. To explore this effect with NAOMi, we computed auxiliary time-traces from the raw, noisy video using the “ideal” ground-truth spatial profiles to obtain the profile-aware least-squares (PALS) time trace estimates (see Methods). Due to the video signal-to-noise ratio (SNR), these estimates yielded only 415 time-courses accurately matched at the ⩾ 0.5 correlation level (Fig. 3D, Tab. 8) indicating that the gap induced by simultaneous estimation of spatial profiles is not overly large. In fact, the inherent denoising in some algorithms allows some cells’ time courses to be estimated with even higher fidelity than the traces derived from the ideal spatial profiles (e.g. CNMF identified 8 cells at the r > 0.5 level that the ideal profiles produced lower correlation values for; Tab. 8). To further explore the abilities of algorithms to extract the stronger somatic traces, we restricted the above analysis to include only components with somas close to the imaging plane and found similar relative perfomances between the three algorithms (Sup. Tab. 12–17).
One challenge in interpreting the results of automated demixing is that, sans ground-truth, it is difficult to determine if a source is a true cell or an artifact. Instead, sorting components based on metrics such as overall fluorescence levels can be used. Varying one such criterion — a threshold on the maximum fluorescence — to classify true and artifact sources results in receiver-operator characteristic (ROC) curves that compare the number of strongly paired components kept (true positives), to the number of weakly paired or unpaired components kept (false positives). These curves show that while PCA/ICA obtained the fewest components overall, CNMF and Suite2p found bright artifacts at much higher rates (Fig. 3E, Sup. Fig. 32).
One benefit of the NAOMi simulator is that we can easily explore how optical parameters effect algorithmic performance. We replicated the above analysis with a 2x increase in laser power (80 mW), keeping the volume and neural activity constant. Ideally this power boost would illuminate additional cells, as weaker and more sparsely firing cells would be more distinguishable. We found that all algorithms returned more unique components at the r ⩾ 0.5 level, with 424 for CNMF, 358 with Suite2p and 264 for PCA/ICA: a 39.93%, 22.6%, and 92.7% improvement (Sup. Tab. 9), respectively. Interestingly, despite the gain in absolute numbers of cells found, there was negligible improvement in rate of correctly found cells (true positive rate), and some ROC curves reduced in area, indicating that fluorescence magnitudes became less sufficient to differentiate true cells from artifacts (Sup. Fig. 32).
We note that in addition to laser power, other factors such as the sampling resolution, numerical aperture and neuropil strength also influence the ability to detect neural activity. NAOMi enables exploration of all these aspects. For example we find 1) a sharp cut-off in the ability to accurately detect components when sampling at intervals larger than 3 µm (Sup. Fig. 33) 2) an improvement in the ability to detect smaller burst sizes in the ∆F/F values with neuropil correction as in Suite2P [18] (Sup. Fig. 34), 3) a steady decay in signal strength per component as a function of NA, reaching a critical reduction of signal at NA ≈ 0.4 (Sup. Fig. 35), 4) a strongly limited ability to extracting activity traces at deep cortical layers (650 µm) with TPM with GCaMP (Sup. Fig. 36), and 5) evidence of increased contamination from dendrites and other cells at a lower imaging NA for a densely labeled sample (Sup. Fig. 37). While we focused on demixing alogrithms here, we note that NAOMi can be used to assess other algorithmic methods, such as baseline estimation (Sup. Fig. 38, See Methods).
2.4. Evaluation of TPM optical configurations
The ability to modify optical parameters and sample expression patterns allowed for direct assessment of the trade-offs between microscope configurations across sample conditions. We applied this new mode of assessment to perform three head-to-head comparisons: 1) imaging of sparsely labeled tissue using Bessel [8] vs. high-NA Gaussian beams (Fig. 4A–C), 2) imaging of nuclear labeled tissue using high-NA vs. low-NA (axially extended) Gaussian beams (Fig. 4D–F), and 3) volumetric imaging of densely labeled tissue using multiplane Gaussian [90] vs. temporally-focused beams [91] (Fig. 4G–I). In all experiments power levels were tuned to equalize total signal integrated over a neuronal volume.
Figure 4:
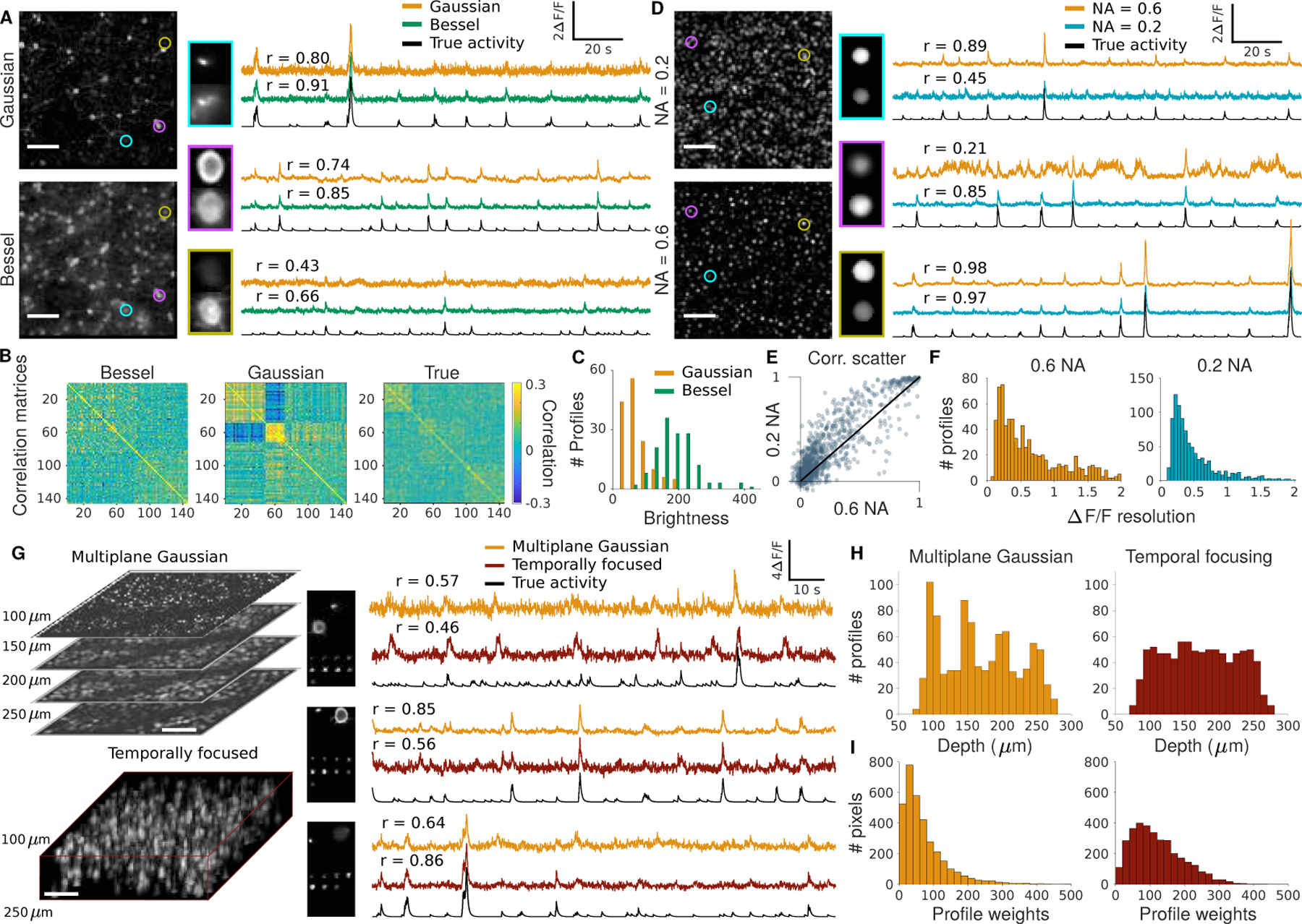
Comparison of specialized imaging modalities to standard high NA Gaussian TPM for a sparsely labeled volume (A-C), nuclear labeled volume (D-F), and volumetric imaging (G-I). A: Mean image (left) and example time traces (right) of a sparsely labeled volume with Bessel beam (top) and high NA Gaussian (bottom) illumination. B: Correlation matrices of extracted time traces for each method sorted by clustering into 3 groups using k-means. C: Histograms of spatial profile weights of cells in the volume using Gaussian and Bessel PSFs. D: Mean image (left) and example time traces (right) of a nuclear labeled volume with low NA Gaussian (top) and high NA Gaussian (bottom) illumination. E: Scatterplot of correlation values for low and high NA extracted timecourses against the true timecourse. F: Estimated ∆F F resolution of cells based on their spatial profile and the mean image. G: Mean image (left) and example time traces (right) of volumetric TPM with 4 high NA Gaussian planes (top) and 16 temporally focused planes (bottom) illumination. H: Histogram of axial positions of highly correlated (r ¿ 0.5) cells using a scanned high NA Gaussian or temporally focused illumination. I: Histograms of profile weights using high NA Gaussian or temporally focused illumination.
In our first comparison we simulated TPM recordings of a sparsely labeled (10% neurons expressing GCaMP6f) 500 µm x 500 µm FOV of mouse cortex using both conventional high-resolution TPM with a Gaussian PSF (0.6 NA) and extended depth-of-field TPM using a Bessel beam (0.4 NA, 60 µm long) [8]. As shown previously, Bessel beam imaging resulted in excitation throughout the whole volume, resulting in more uniform excitation of neurons (Fig. 4C) and more neurons recorded with high signal fidelity. Another consequence of the uniform excitation observed using Bessel beams is an increased robustness to axial motion. To verify that NAOMi captures this aspect, we clustered the extracted time-traces from Bessel and Gaussian imaging into three groups (Fig. 4B). The sorted correlation matrices show a strong motion-induced artifact only for Gaussian imaging, suggesting a reduced influence of motion artifacts on time-trace estimation using Bessel beams.
Our second comparison tested the performance of nuclear labeled TPM, which has been extensively used for larval zebrafish and C. elegans TPM [92, 93] but not in mouse brain imaging, in a 500 µm x 500 µm FOV of mouse cortex. We imaged this simulated tissue using Gaussian beams of two excitation NAs: 0.2 and 0.6 (Fig. 4D) and assumed equal brightness for nuclear indicators. Similar to the extended depth-of-field Bessel beam, the 0.2 NA excitation resulted in sampling more neurons from the volume and improved overall imaging performance (Fig. 4E,F). As the imaging volume is mostly non-fluorescing with nuclear-labeling, distinguishing individual cells is straightforward even with an extended depth-of-field. Because nuclei are several times larger than the lateral resolution of the 0.2 NA excitation beam, there are fewer advantages to switching to a Bessel beam setup and low NA imaging is more power efficient. A recently developed technique for soma-targeting of GCaMP [94] provides an alternative means to nuclear-labeling for improving labeling in an animal for somatic imaging. We generated a somatically labeled volume and simulated datasets at two excitation NAs similarly to the nuclear labeled case (Sup. Fig. 39) and found similar advantages to using a low excitation NA for TPM.
In addition to comparing NA values across nuclearly labeled samples, we also compared signal levels across a variety imaging NA values for cytosolically labeled TPM in L2/3 mouse cortex (Sup. Fig. 35). This analysis shows constant total overall integrated value (i.e., signal level) across a number of NA, which suggests little loss of power efficiency by reducing the excitation NA. While higher NA beams are more strongly affected by scattering in tissue, lower NA beams suffer from longer excitation tails, resulting in a decreased signal-background ratio. Surprisingly, these two effects roughly cancel out for the scattering and sample brightness levels found in two-photon GCaMP6f imaging.
Last, we compared multiplane TPM [90] to scanned temporal focused (s-TeFo) TPM [91] in a 500µm x 500 µm x 200 µm volume of the mouse cortex layers 2–4 (Fig. 4G). Comparing these two fast axial scanning TPM techniques that image large volumes with very different spatial sampling conditions permits us to understand optimal sampling strategies for the expanding area of high-throughput volumetric TPM. For multiplane Gaussian TPM, we scanned four planes, separated by 50 µm at 1 µm lateral sampling, at 10 Hz and for s-TeFo TPM, we scanned 16 planes, separated by 10 µm at 4 µm lateral sampling, at 10 Hz. Given a similar amount of excitation within the volume, both techniques performed comparably in extracting fluorescence traces with high fidelity. The axial distribution of highly correlated (r⩾0.5) cells in the multiplane TPM is multimodal, set at the focal positions of the four planes, while the s-TeFo distribution is much more uniform (Fig. 4H), as is reflected in the profile weight histograms (Fig. 4I). These simulations suggest that while s-TeFo as a technique may not drastically increase the number of recorded neurons, the more consistent spatio-temporal sampling of neurons may decrease sampling bias and provide robustness to motion-induced artifacts and signal crosstalk.
3. Discussion
We presented here the NAOMi simulation framework that generates detailed TPM data. This framework captures a variety of existing imaging principles using only anatomical and optical simulation blocks. NAOMi thus has the potential to 1) yield new insights into TPM technology and enables the testing and 2) validate existing and novel TPM methods, allowing for assessment and methodological optimization not currently possible. Toward this end, we have developed the ability to generate realistic synthetic neural volumes, transient calcium activity, and two-photon calcium imaging videos. We further increase the simulation efficiency by simplifying statistical models of the processes involved, reducing the computational burden and making this tool more broadly applicable.
We have demonstrated two important use cases of NAOMi: assessment of calcium imaging demixing methods and comparing optical configurations across imaging conditions. In both cases, useful large-scale ground truth is difficult to obtain experimentally. NAOMi leverages the accumulated knowledge of neuroanatomy, optical physics, and neuroscience to bypass these difficulties through simulation. The simulation software, along with the data from this paper, is made freely available to promote the assessment and development of TPM methods. Moreover, we have created a suite of publicly available datasets simulating additional experimental conditions, including various power levels, indicators, imaging depths, anatomical parameters, and optical configurations as an extended community resource.
Several groups have already begun to use NAOMi to test new algorithmic methodologies, including new denoising algorithms [95] and testing the effect of negative transients on algorithmic demising [96]. Other uses for algorithm development include testing motion correction algorithms, field-of-view alignment and registration, biophysical parameter learning, and filtering out artifactual profiles in the found components.
Beyond algorithms, NAOMi can also help optimize experimental designs, for example by testing which combination of indicators, NA, excitation power, and other microscope/experimental techniques best combine with the ensuing analysis to accurately reflect the underlying activity, i.e., via accuracy metrics based on the traces used to generate the simulated video. Thus NAOMi can help adapt experimental designs towards the scientific questions of interest. For example, fast indicators might be critical when analyzing short-time responses to environmental stimuli, however global activity manifolds guiding longer-term behavior might be better fit using data collected with slower, brighter indicators. This choice of indicator then influences the choice of microscopy technique and imaging rate: a slower, brighter indicator may be better suited for volumetric imaging at low frame rates, a trade-off frequently acceptable for manifold inference. This represents a potential shift in experimental design that enables experimentalists to think globally about the apparatus, data processing and analysis in a testable way.
To assess demixing algorithms, we generated a calcium imaging dataset typical of TPM in mouse neocortex and analyzed the performance of sev eral popular methods: CNMF [52], Suite2p [34], and PCA/ICA [29]. The available input cell shapes and timecourses enabled direct comparisons of the algorithm decompositions to ground truth, which revealed that methods with the highest number of found neurons also had much higher instances of artifactual components. This indicates the potential for many false positives in automated demixing (Sup. Fig. 28, Tab. 6). Using NAOMi data as a testing ground, more advanced detection metrics can be developed, to find better ways to filter out true cells from the full set of returned components.
Using NAOMi, we explored particular combinations of optics and samples in silico and illustrated the advantages three specialized techniques under specific sample conditions. We rapidly assessed how appropriate a particular technique is for the sample and optimized imaging parameters to maximize the quantity and quality of the data. Of particular note is the ability to make side-by-side comparisons of different techniques on identical sample conditions, which is only possible in simulation. Additionally, we explored the interaction of different components of in vivo calcium imaging and their effects on performance. For instance, we quantified how axial brain motion can effect estimated cell activity correlations as a function of sample type and optical configuration. The ability to directly compare and test out techniques allows experimenters to evaluate in silico the utility of a given technique for their experimental conditions.
Despite these results, there are several aspects of the simulation that were simplified for speed or simplicity. More realistic anatomically-constrained synaptic connectivity between simulated neurons [57] can be used to generate improved spatial distribution to neural activity. Additionally, while we provide a spike-train simulation to drive the fluorescence models, future iterations of NAOMi can leverage a number of other complex packages that specialize in realistic simulations of such activity for neural populations (e.g. [97]). In these cases, rather than replicate these methods, we encourage their use and integration into the NAOMi framework.
In the development of NAOMi we aimed to create a tool accessible to the community at large that is easily expandable in its scope and abilities. To this end, our software was designed to be modular so that as better anatomical models, optical descriptions of tissue, and TPM statistics become available, they can be easily incorporated into the existing framework. Additionally, single modules can be modified in order to simulate different setups. For example, changing the anatomical structure (e.g., blood-vessel size and cell body statistics) can allow for bench-marking imaging techniques in rats, rather than mice. These changes and extensions will allow NAOMi to be a useful tool for a wide variety of applications for experimentalists and methods developers.
The modular nature of the simulation also creates an opportunity to create new simulations for other brain areas. While in this work we focused on the well-studied visual cortex in mice, new EM data, for example in hippocampus [98] and medial entorhinal cortex [99] provide an opportunity to data mine the required anatomical parameters needed to adjust cell distribution functions, neural cell shape parameters, vasculature creation parameters, and dendritic and axonal properties. We expect that as EM data becomes cheaper to obtain and thus more widely available, such datasets will become available for many brain areas across species.
Work in other fields has shown the great utility of developing strong simulation-based models of experimental data (see [100] and references therein). NAOMi is a tool that fills part of this gap for neuroscience data. As neuroscience continues maturing, better models of data must be developed, especially for data that is as diverse and complex as two-photon calcium imaging. This and other work will allow researchers to not only more quantitatively judge the quality of their data, but also make better predictions on the data they will need for their experiments.
4. Materials and Methods
Our TPM simulator is designed to permit testing of many different aspects of the calcium imaging process. To achieve this flexibility, our simulator is divided into five distinct modules, each focused on a portion of either the tissue or scanning simulation (Fig. 1). The five modules are: 1) the neuron module responsible for generating single neurons, 2) the volume module responsible for assembling the neurons into a tissue volume that includes neuropil and vasculature, 3) the activity module that generates the temporal calcium traces for each neuron and the neuropil, 4) the optics module that simulates the point-spread function and occlusion due to the optical mask, and 5) the imaging module that simulates the TPM noise model and object motion.
4.1. Neuron model
The first module creates simple, yet plausible models of neurons that can be placed throughout a volume and scanned in simulation. We model the neural shape via a probability distribution over smooth deformation of a sphere, followed by a nonlinearity. This model allows for fast sampling of unique neurons, meaning that each simulated volume will contain a completely new set of neurons. Additionally, we provide for each neuron a nucleus modeled as a shrunken and smoothed version of the soma shape. This model captures the relationship observed in detailed field emission scanning electron microscopes (FESEM) [101]. Finally, we simulate for each neuron a number of dendrites, one of which is created thicker and at a downward orientation, as to model the apical dendrites.
The model of the smoothly deformed cell body is an isotropic Gaussian process [102] defined over a sphere. To sample from this distribution and create the cell body, we sample uniformly over a sphere [103], sample i.i.d. a Gaussian random variable for each point, and smooth the points according to the process covariance. Denoting the sample points , the height (distance from center of the sphere) can be sampled from
where l is the length-scale that controls the smoothness of the cell body, and d(·, ·) is the geodesic distance between any two points. For the unit sphere (radius one), this distance is the arc length along the great circle connecting the two points
When unconstrained, the radial height of this function can, at times, exceed the maximum and minimum realistic deformations rmax = maxi |ri| and rmin = mini |ri|. We thus rescale the radii values as
The resulting points ripi form the points for a mesh that define the interior of the cell body. To account for the non-spherical shape found in pyramidal neurons, we can modify the radii values by making the base radius at each point dependent on a function of its location on the sphere. Specifically, we use the equation for a tear-drop that is defined parametrically by the azimuth and elevation angles ϕ, and θ as
| (1) |
The final step in creating the cell body is to create the nucleus, which is accomplished by shrinking and smoothing the cell wall shape as defined by ripi as
Dendrites are added to each neuron via a stochastic growing process [59]. The process generates start and end points for each dendrite, and iteratively grows the dendrite through the volume while avoiding any obstacles (i.e. other cell’s somas, dendrites, or blood vessels). Apical and basal dendrite endpoints are separately set within the volume and the grown dendrites are dilated to widths consistent with measured anatomy (Tab. 1, Sup. Fig. 7).
4.2. Volume generation
To create the tissue volume, we initialize an empty volume and begin by placing blood vessels throughout the volume. For computational feasibility, the volume is modeled as a 3-D grid of points with sub-micron sampling (we typically use 0.5 µm distances). The blood vessels are grown in three parts: surface vasculature, diving arterioles, and capillaries. Surface vasculature is grown by connecting nodes randomly placed upon the surface of the volume. The connected paths are smoothly varied and dilated. Diving arterioles are set at endpoints of surface vasculature and connected to the bottom of the simulated volume. Capillaries are connected to the diving arterioles and pseudo-randomly placed within the volume in a space-filling fashion. Vessel diameters, concentration, branching frequency, and orientation were compared and fit to two-photon microscopy data of mouse vasculature (Schaffer-Nishimura lab, unpublished data).
Once initialized, the volume is then filled with the neuron somas. We sequentially place the neurons randomly throughout the empty space in the volume, with a minimum distance that allows cell bodies, but not nuclei, to overlap. The random placement can be modified to encourage neurons to be more spread out, or more cluttered. When an overlap occurs, the overlapping region is given to the latest cell to be placed. This allows our volume to contain touching cell bodies. Once all the cell somas are placed, dendrites are grown for each neuron sequentially, such as to avoid location conflicts with other cells. Apical dendrites are grown in the same fashion, only thicker, axially oriented, and having fewer transversal deviations. Separate apical dendrites corresponding to neurons in deeper cell layers are grown in a similar fashion from the bottom of the volume to the top.
As a final step, axons fill up the remaining empty space, up to the typical 0.7 fill fraction of layer 2/3 in mouse V1. The same dendrite growing algorithm [59] is used to create millions of short axon segments throughout the entire volume. To obtain the global correlated background components, axon segments are locally grouped together. The axon groups are assigned to individual cells by minimizing their centroid distance to cell bodies, and then all remaining axons groups are randomly assigned.
4.3. Time-trace generation
To simulate temporal activity, we provide a number of options to generate time-traces for each neuron. We provide both statistical models that generate stereotypical activity as well as more detailed [Ca2+] dynamics model. The statistical model provides a simple way to input basic behaviors of various fluorescent proteins (i.e. rise-time and decay). The [Ca2+] dynamics model simulates the molecular kinetics over time, and provides a way to test the time-trace assumptions made in calcium imaging analysis algorithms.
4.3.1. Spike-time generation
We provide two methods to generate spike trains to drive the fluorescence activity simulation. The first method creates independent activity for each neuron, including bursting behavior. The second model simulates a Hawkes process which accounts both for self-excitation, driving busting behavior, as well as inter-neuron spiking correlations [104].
To generate independent spike trains, we model each neuron as a bursting neuron, where bursts occur at independent, exponential intervals
| (2) |
for ∆tburst > 0. The rate of bursting λburst is chosen differently for each neuron. The rates can be given to the simulator, or the simulator can automatically draw burst rates from a Gamma distribution with a provided mean rate and parameter α = 1. For each burst, the number of spikes are chosen as
| (3) |
where the parameter λN controls the length of the bursting. The inter-spike times between spikes in a burst were modeled as uniformly random between 5 ms and 7 ms. Alternative distributions of spiking activities can easily be implemented by passing different λburst, α, or λN values to the simulator, or by direct modification to the code to implement different distributions that better reflect activity in other cortical areas.
For the Hawkes model simulation, we first generate a connectivity matrix that encodes how each neuron’s firing excites other neurons. We model this connectivity with a Watts-Strogatz small-world network model [64]. To correlate the processes to the network activity, we allow for all neurons to influence the background processes, while not allowing many return connections. To stabilize the point-process, we normalize the resulting connectivity matrix to have maximum eigenvalue magnitude of 0.98. We then run the Hawkes process using Lewis’ method [105], with an exponential distribution over the neuron’s base firing rates and a higher base firing rate for the background components. Finally, we bin the resulting continuous-time spike events into 1 ms bins to create the discretized spikes that are then fed into the calcium dynamics simulation.
4.3.2. AR-p dynamics
For each cell, we generate a baseline fluorescence, where is a Gaussian random variable. The variance σ2 controls the distribution of baselines, and we set a default value to σ2 = 0.04. The next step is to simulate the spike or “event” times for each neuron. As most neurons are sparsely active, we draw the firing rate of each neuron as λi ~ Gamma (a, θ). The parameter θ gives the average inter-spike distance in time and should be set according to the temporal sampling rate set in the simulation. The parameter a is the shape parameter and modulates the distribution of the firing rates. We find that a =1 (where the Gamma distribution collapses to an exponential distribution) yields realistic distributions of neuron activity levels. The actual event times are then sampled for each neuron according to a Poisson process with rate λi. To model the different calcium levels at each event (e.g. due to multiple spikes or to adaptation [106]), we sample the overall concentration as coming from a unit log-normal distribution (i.e. an exponentiated Normal distribution ).
Once the spike times are obtained, an auto-regressive model with p degrees of freedom (AR-p) is used to simulate the calcium and fluorescence impulse response. As a difference equation, AR-p models can be written as
where the ai’s are the AR coefficients and b is a scalar multiple of the input. The impulse response can be obtained by solving the inverse Laplace transform
Standard linear systems theory shows that h[n] will be composed of the exponentiated roots of the characteristic polynomial and therefore will be an exponentially decaying function. Higher order polynomials can result in a rise time as well. For this work we find that an AR-2 model (p = 2) sufficiently models the rise and fall of observed GCAMP responses. The filter h is convolved with the spike-time vector to create the temporal activity per neuron.
4.3.3. [Ca2+] dynamics
The fluorescence of a cell is dependent on the number of calcium ions bound to the indicator. if we denote [Ca2+] as the amount of free calcium in the cell and [B] as the number of proteins in the cell, we can use the binding/unbinding dynamics, coupled with the entry/exit dynamics of [Ca2+] in the cell to determine the fluorescence level at any given time. Specifically, we use the nonlinear diffusion of [Ca2+]
where [Ca2+]rest represents the baseline free [Ca2+] , γ is the [Ca2+] diffusion constant, κs is the endogenous [Ca2+] binding ratio, and Kd is the protein binding affinity constant [69, 70]. As γ is a function of the volume-to-surface area, we use a different γ value for dendrite dynamics as for dynamics in the soma [107]. While this model permits simulation of the [Ca2+] concentration over time, the model does not include the on/off time constants τon and τoff that describe how long it takes for the bound proteins to become active. We can model this effect, as in [70], by convolving with a double-exponential function
| (4) |
where the amplitude A and the time constants τon and τoff can be fit to the particular protein kinetics. The final step in simulating the fluorescence time-traces is to convert the calcium concentrations to fluorescence levels. For this task, we use the Hill equation
| (5) |
where the parameters KD and nH have been measured in the literature (specifically [72], Table 1), and the absolute florescence is
| (6) |
where the baseline fluorescence F0 can be tuned to the protein statistics.
Table 1:
Parameters used for in-silico simulation of neural activity in layer II/III of mouse primary visual area V1. Values for each parameter were either directly found in the literature or estimated from published data (entries with a †). The third column indicates whether these parameters were set directly in NAOMi, or were fit indirectly by setting other simulation parameters. In the latter cases, the measured values from a simulated NAOMi volume are shown for comparison, indicating that the simulated anatomy matches measured anatomical statistics.
| Parameter | Lit. Val. | Fit type | NAOMi Val. | Unit | Refs |
|---|---|---|---|---|---|
| Anatomical parameters: | |||||
| Neural density | 9.20E+04 | Direct | – | mm−3 | [60] |
| Fraction vasculature | 0.01–0.04 | Indirect | 0.032 | – | [60, 77, 78] |
| Fraction cell bodies | 0.12 | Indirect | 0.135 | – | [60] |
| Fraction neuropil | 0.84 | Indirect | 0.833 | – | [60] |
| Fraction dendrites* | 0.294 | Indirect | 0.223 | – | [60] |
| Fraction other (fluorescing)* | 0.401 | Indirect | 0.33 | – | [60] |
| Fraction other (not fluorescing)* | 0.293 | Indirect | 0.28 | – | [60, 79] |
| Vessel radius (capillary) | 2.00E+00 | Direct | – | µm | [58] |
| Vessel radius (penetrating) | 10 (9,11) | Direct | – | µm | [58] |
| Vascular density | 1–3 | Indirect | 2 | % | [77, 60, 58, 78] |
| Penetrating vessel density | 30† | Direct | – | mm−2 | [58] |
| Somatic volume* | 1.80E+03† | Indirect | 1.80E+03 | µm3 | [80] |
| Nuclear volume* | 800† | Indirect | 800 | µm3 | [80] |
| Cytoplasm volume* | 1000† | Indirect | 1000 | µm3 | [80] |
| Basal dendrite diameter | 0.7 | Direct | – | µm | [81] |
| Basal dendrite length | 100–160† | Indirect | 105 | µm | [61, 62, 63] |
| Apical dendrite diameter | 1–2 | Direct | – | µm | [82] |
| Axonal diameter | 0.3 | Direct | – | µm | [60] |
| Fluorescence parameters: | |||||
| GCaMP6f binding affinity Kd | 290 | Direct | – | nMol | [72] |
| Baseline Ca2+ concentration | 50.00 | Direct | – | nMol | [70] |
| Ca2+ binding ratio ks | 100,110 | Direct | 110 | AU | [69, 83, 84, 85] |
| Ca2+ diffusion constant γ | 1800 | Data fit | 292.3 | s−1 | [69, 83, 86] |
| Ca2+ axon diffusion constant γ | 2800 | Direct | – | s−1 | [69, 83, 84] |
| GCaMP6f Hill eqn. exponent nh | 2.7 | Direct | – | AU | [72] |
| GCaMP6f Hill eqn. amplitude | 25.2 | Direct | – | F | [72] |
| Indicator concentration | 10–200 | Direct | 10 | µM | [70, 87, 88] |
Adjusted for shrinkage: 31% [89]
Value estimated from data in the literature
4.4. Optics simulation
The optics module consists of modeling the shape and intensity of the point-spread function (PSF) within the scanned tissue. For computational purposes, we assume the shape of the PSF is constant across the scanned volume and only the amplitude is modulated. We estimate the PSF within the scanned tissue by propagating a specified field through the simulated tissue across the field of view.
We describe the scalar field at the front aperture of the objective lens as a Gaussian with a circular aperture and spherical phase:
| (7) |
where U0 is the scalar field, is the polar position, k is the wavenumber, ρ0 is the radius of the objective lens, ρe is the radius of the excitation beam, and f is the focal length of the objective lens. The wavefront is multiplied by any additional specified aberrations due to the microscope or the sample:
| (8) |
where θ is the polar angle, ai are the Zernike coefficients, and Zi are the Zernike polynomials. By default, only spherical aberration approximating the contribution of the refractive index mismatch of the sample and astigmatism approximating the contribution of offset scanning galvanometers are included.
The field U (ρ, θ) is propagated through the sample to the focal plane along a 2D grid of positions within a simulated refractive index volume δn. The volume δn is generated from the simulated vasculature and a 3D Gaussian process with a weight distribution approximating the refractive index distribution of mouse cortical tissue (see Supp Fig. 11) [108]:
| (9) |
where V is the vasculature and GP is the smooth Gaussian Process representing the optical properties in the non-vasculature areas. The vasculature provides the bulk of the long range refractive index shifts in the simulation, while the Gaussian process approximates the local shifts.
The Fresnel diffraction integral is used to estimate the field throughout the volume, and the split-step beam propagation method [109] is used to apply the effects of inhomogeneity within the volume. The simulated phase-difference volume is summed into optical phase masks corresponding to each propagation step:
| (10) |
This quantity is multiplied after each optical propgation step as
| (11) |
where ϕi = ϕ (xi, yi, zi) is the optical phase mask and Ui = U (xi, yi, zi) is the scalar field at each position. The resultant 3D field generated by the propagation is then used to calculate the two-photon PSF:
| (12) |
The aberrations caused by the phase differences approximate the effects of wavefront distortions caused by refractive index inhomogeneity within the imaged sample [110, 111]. The two-photon PSFs at each location across the field of view are averaged to obtain the PSF to be scanned through the simulation, and the summed intensity of the PSFs across the field are used to generate an intensity scaling mask for scanning. For runtime considerations, the PSF near the focal plane is sampled at the resolution of the volume while the out of focus PSF and scaling mask is sampled at a reduced resolution.
For alternative optical setups, we adjust the input field U0 accordingly. For a low numerical aperture excitation beam, ρe is reduced, and for a Bessel beam excitation U0 is replaced with an excitation ring. See supplementary information for more details.
An additional optical mask is also calculated by estimating the reduction in signal from absorption of the collected light by the vasculature. The collected light at each scanned position is reduced by a collection cone corresponding to the simulated collection objective numerical aperture:
| (13) |
where r(z) is the collected cone radius as a function of depth, and:
| (14) |
where C is fraction of light collected, d is the tissue depth, and A is the adjusted light absorbance of light emitted from GFP normalized by the arterial blood absorbance factor. This absorbance mask is multiplied to the optical excitation mask to give the combined spatial signal scaling mask.
4.5. Scanning in silico
The final module takes the generated volume, the generated PSF and time-traces, and generates the TPM output frames. The first step here is to use the time-traces and fluorescence distribution for each neuron to “color in” the corresponding volume with the current fluorescence level for that neuron. Similarly, the background level is set by repeating this process with the neuropil. The PSF is then convolved with the current volume, and the result is masked with the optical path mask to create an initial image.
To simulate motion in the movie, we select a portion of this initial frame to treat as the entire image. The starting position (upper left corner) for the with-motion frame is moved according to a small ± 0.5 µm jitter with occasional larger jumps (up to 2–3 µm). Options to include per-line motion and shearing are also implemented by choosing different sub-sections of each row as the with-motion frame is extracted from the larger motionless frame. This frame represents the fluorescence level at each point in the sampled image. To obtain the actual electrical signals sampled by the TPM device, we apply a noise model that simulates the number of photons incident on the array (modeled as Poisson) followed by an electrical noise model that is Gaussian, with increasing mean and variance with larger numbers of incident photons. If λ is the true florescence for a pixel, x is the number of incident photons, and y is the measured electrical signal, the noise model can be expressed as
where µ0 and are the baseline noise mean and variance (with no photons), and µ and σ2 are the parameters controlling how the measurement mean and variance grow with increased incident photons.
As a final step, we simulate the analog-to-digital accumulators’ property where photons arriving in one pixel’s accumulation time can cause an analog shape that bleeds through to the accumulation for the next pixel (Fig. 16). We simulate this effect by noting that if a photon arrives early in the sample period, then the analog PMT response g (t) is completely inside of the sample period and no bleed-through occurs. On the other hand, if the photon arrives within ∆ of the end of the sampling period, where ∆ is the temporal extent of g (t) (Fig. 16), then the tail end of g (t) that continues beyond the end of the period is integrated into the next sample. The probability of a given bleed-through level for one photon can thus be quantified as
| (15) |
where τ(b) represents the delay τ that is needed to result in a given bleed-through b. Since the relationship between b and τ,
is monotonically increasing when g (t) ⩾ for all t, τ (b) is a well defined function. Since photon arrivals are approximately independent, the bleed-through probability distribution for multiple photons is the convolution of the distribution for a single photon. The resulting statistical model then takes a random fraction (uniformly chosen between zero and 50%) of each pixel with probability 0.2, and adds that amount to the next pixel,
| (16) |
Vasculature scanning
To compare the axial spread of the PSF in deep volumes, we simulated datasets comparable to deep z-stacks of blood vessels [112]. The real z-stacks were taken in mouse neocortex at 830 nm excitation wavelength and a numerical aperture of 1.0 with 1 µm spatial sampling at depths up to 450 µm. For our analyses we generated local vasculature z-stacks (60 µm) at a depth of 330 µm by using the scanning module to iteratively scan a uniformly labeled simulated blood vessel volume. To adjust for the scattering at the new imaging wavelength, we used the equation provided in [108] along with a quadratic relationship between scattering length and refractive index. These values reasonably approximated values provided in [113] for nearby wavelengths. Additionally, we generated simulated datasets with randomly placed point sources (0.5 µm in size) that were scanned in a local z-stack.
We considered the axial and lateral spread of point sources (point source volumes) and line sources (capillaries in blood vessel volume) around 330 µm in depth for this analysis. For point sources we isolated a 7×7 pixel subregion centered around a point source, background subtracted the isolated values and estimated the axial full-width half-max (FWHM) of each source. For line sources capillaries were isolated into 30 × 30 pixel subregions, rotated, and a 5 µm central region of the brightest slice was used to estimate the lateral spread (FWHM). The central 5 µm subvolume was background subtracted and used to estimate the axial spread (FWHM). The axial PSF was estimated as the difference between the axial spread and half the lateral spread, an estimate which assumes the width of the lateral PSF and the line sources are roughly comparable.
Hemoglobin absorption
To calculate the absorption due to hemoglobin, we assumed default concentrations of 150mg/ml Hemoglobin (Hb), 64500 g/mol Hb, and 2.9 (abs/µm)/(mol/L) in units of abs/µm. The absorbance was then calculated using Scott Prahl’s Hb curve [114] and eGFP emission spectrum [115].
Estimation of per-trace noise variance
To estimate the noise variance for each time-trace, we begin with the basic per-pixel noise model
| (17) |
where the noise is heteroskedastic in that the variance is proportional to the mean
| (18) |
The least-squares estimate of the activations under the imperfect spatial profiles is
| (19) |
| (20) |
| (21) |
The covariance of this estimate is then
| (22) |
| (23) |
| (24) |
| (25) |
| (26) |
Calcium analysis algorithms
All analyses were computed with the 2017 versions of CNMF [52] and Suite2p [18]. Parameters were adjusted manually for each algorithm to optimize the output. For CNMF we used fr = 30, tsub = 5, patch size = [40,40], overlap = [8,8], K = 7, tau = 6, p = 0, and nu_bg = 1. For Suite2P we used diameter = 12, DeleteBin = 1, sig = 0.5, nSVDforROI = 1000, NavgFramesSVD = 5000, signalExtraction = ‘surround’, innerNeuropil = 1, outerNeuropil = Inf, minNeuropilPixels = 400, ratioNeuropil = 5, imageRate = 30, sensorTau = 0.5, maxNeurop = 1, sensorTau = 0.5, and redmax = 1. For PCA/ICA we used fr = 30, ssub = 2, tsub = 10, nPCs = 1000, smwidth = 3, thresh = 2, arealims = 10, mu = 0.5, dt = tsub/fr, deconvtau = 0, spike_th = 2, norm = 1. While figures displayed typical outputs (i.e., denoised traces from CNMF), all quantitative comparisons were computed using the raw DF/F traces returned by each algorithm.
Local correlation calculation
To calculate the local correlations, V1 two-photon recordings and simulations were motion corrected using correlation-based rigid motion correction [116]. A 1500-frame subsection of each dataset over a 250 × 250 pixel area was extracted. For each pixel, the Pearson correlation between its fluorescence activity and that of each of the neighboring pixels in a 51 × 51 pixel square neighborhood (up to 25 pixels away in each direction) were calculated. The results were averaged over all pixels (to create the mean images) and histograms were created to depict the spread for correlations along the fast-scan direction.
Computation of the ideal spatial profiles
The ground-truth template for each cell was obtained from NAOMi by lighting up that individual cell and zeroing out all other cells, and then scanning the volume at the simulated imaging depth plane. We further refined this profile to the ‘visible’ pixels by removing any pixel whose estimated noise variance was larger than the signal. Such a ‘binary mask’ is common, for example, in increasing intelligibility for speech data by applying the binary mask in the time-frequency domain.
Calculation of auxiliary time-traces
To calculate the auxiliary, noisy “ground truth” time traces, we used Profile assisted least squares (PALS), which uses the ground truth ideal profiles in a least-squares estimation. We considered the movie frames yt for t = 1…T and the calculated ground-truth spatial profiles X = [x1, …, xN]. The noisy time trace estimates were then calculated via the least-squares estimation procedure at each time-step t
| (27) |
Fitting GCaMP parameters
Fitting GCaMP6f and GCaMP6s parameters was accomplished by using either constrained optimization (interior-point implementation in MATALB) or BayesOpt [117]. Data used to fit these models were downloaded from [118] and are available on the Collaborative Research in Computational Neurosciences (CRCNS) web portal at https://crcns.org/data-sets/methods/cai-1/?searchterm=chen%20gcamp.
Baseline estimation
Baseline fluorescence estimation is critical for assessing how much of the total acquired signal originates from each individual cell, which in turn permits more accurate ∆F/F estimates. More accurate estimates both reduce both reduce the expected noise level, and also produce time traces that are more meaningful in that they directly relate to the actual intracellular calcium levels and spike rates. This is especially true in preperations with variable expression levels. Accurate baseline estimation is challenging with no clear present solution. Analyzing current methods for baseline estimation, however, can provide an approximate error range of this measure, which is vital for establishing error bars in the scaling of spike rate estimates and other factors for detemining data quality for ensuing analyses.
We analyzed ∆F/F distributions and estimates per pixel (pixelwise estimation) to obtain a range for the values that this ratio can take (Sup. Fig. 38). To estimate the baseline fluorescence level for each neuron we first calculated its spatial profile S(k) and the modal image M(k) for each pixel k. We assumed M(k) = c * S(k) + B(k) , where B(k) is the contribution to the fluorescence from all other sources and the baseline fluorescence level is given by c * S(k) . When the neuron was active, the pixel values were approximated as F(k) = (dF/F) * c S(k) + B(k), in the absence of background activity, which we assumed for this estimate.
We estimated c * S(k) by plotting a scatter-plot of S(k) against M(k) and noting that for a given S value, there exist a range of possible M values with a minimum value that increases as S increases. These minimum values correspond to the case where the contribution by B is minimal and approximately uniform, corresponding to fluorescence from the tails of the PSF. By fitting the line of these minimum values, we used this slope to approximate the value of c. Care may be taken to estimate this minimum B contribution by examining the values of pixels immediately outside the spatial profile. We used PCA to locally estimate S(k) , which better approximates these values immediately outside of the neuron, improving estimation accuracy.
For each pixel k, we note that B(k) must be positive. Therefore, for each pixel k, c <= M(k)/S(k), which set a upper bound for c. Second, we required that the maximum dF/F value for the indicator is not exceeded. By using the maximum fluorescence image, we set a lower bound for c. These give a physically allowable range of c for each neuron.
Robustness to dendritic arbor stimulation
The NAOMi simulation software allowed us to estimate the effect of dendritic specific signals on the estimation of overall activity traces. We explored this by generating a 100 µm x 100 µm x 100 µm volume and scanned it with a 40 mW diffraction-limited Gaussian beam. We then perturbed only the dendritic spike trains to include additional spikes, recomputed the time traces, and simulated a second video from the same volume. The ground-truth spatial components were used in conjunction with the movies to estimate the activity traces for each neuron from both videos (Sup. Fig. 21). To remove the confounding effect of noise, a post-processing wavelet denoising step was run on all time-traces. We found minimal differences in the time-traces due to this additional source of potential time-trace contamination.
Neuropil estimation and comparison
Neuropil is a vital characteristic of calcium imaging data. Moreover, the correlation between the activity present in the surrounding axons and dendrites may impact signal estimation. We compared correlations across the field-of-view for a simulated dataset with a 50 µm x 50 µm field-of-view from the V1 dataset used in Figure 2. In particular we calculated the correlation of individual pixels at increasing distances from the center pixel of a given component (as found via CNMF [52]), and then plotted the average correlations as a function of distance (Sup. Fig/ 20). While this analysis is similar to the analysis in [18], the imaging conditions of these datasets (both real and simulated) are different. We find NAOMi produces a qualitatively similar drop-off with a similar steady-state correlation (Sup. Fig. 20).
Impact of anatomical values on NAOMi
NAOMi leverages a large literature of measured anatomical properties. These properties impact the simulated videos and can change the quality of the simulation. We tested the robustness of NAOMi to two important properties here: cell size and cell density. We varied both values by ±20% and observed changes in the mean images (Sup. Fig. 22) and pixel value histograms (Sup. Fig. 23). For consistent comparisons of other statistics, we retained all other parameters, including the exact same vasculature, across all simulated volumes and videos. We found that while changes in density resulted in minimal qualitative changes to the mean images and histograms, changes in cell sizes had a more significant impact.
Real two-photon datasets used for comparison
All experimental procedures were approved by the Princeton University Institutional Animal Care and Use Committee. Two datasets were used for the comparisons: one recorded from a transgenic Ai93-Emx1 mouse (Emx1-IRES-Cre;Camk2a-tTA;Ai93(TITL-GCaMP6f) [119]) in Fig. 2 and a second from a Thy1 GP5.3 mouse (C57BL/6J-Tg(Thy1-GCaMP6f)GP5.3Dkim/J [120]) in Sup. Fig. 19. Animals were prepared and recorded in a manner similar to described in [49] and [121] from primary visual cortex.
Supplementary Material
Highlights.
We present a new method for generating realistic simulations of two-photon calcium imaging data
two-photon imaging simulations are used to evaluate the performance of automated segmentation algorithms
Datasets for a variety of customized two-photon microscopy techniques and sample conditions are generated and analyzed
Acknowledgements
The authors would like to thank Thomas Macrina and Sebastian Seung for helpful discussions of anatomy and electron microscopy data, and Chris Schaffer and Mohammad Haft-Javaherian for the use of and helpful discussions pertaining to their vasculature data. Moreover, the authors would like to thank Ben Scott, Sam Wang, Sue Ann Koay, Brian DePasquale and Dylan Rich For their insightful thoughts and comments throughout this project. A.S.C. and J.W.P. were supported by Simons Collaboration on the Global Brain (SCGB AWD543027), and a U19 NIH-NINDS BRAIN Initiative Award (5U19NS104648). A.S. was supported by NIH grant 1U19NS104648. D.W.T. was supported by NIH grants R01MH083868 and 1U19NS104648, and the Simons Collaboration on the Global Brain (SCGB 543051).
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Competing Financial Interests
The authors declare no competing financial interests.
Code Availability
The NAOMi simulation was coded in MATLAB and will be available via the following GIT repository: https://bitbucket.org/adamshch/naomi_sim/
Included are example scripts to demonstrate to users how to generate and explore simulated two-photon imaging movies. The code will also be made available on CodeOcean https://codeocean.com/ for additional accessibility.
Code available at https://bitbucket.org/adamshch/naomi_sim/src/master/.
Data Availability
A number of datasets were used to validate the NAOMi simulation. These data are available from different sources with different restrictions:
Two-photon images from mouse V1 (Fig. 2): This data was taken at the Princeton Neuroscience Institute by the laboratory of David Tank, and is available upon request to the authors.
Simulated videos (Fig. 2–4, Sup. Fig. 1–35): All simulated videos are available on an Open Science Framework repository https://osf.io/863j9/. A handful of volume files are too large to deposit at OSF and can be made available upon request from the authors.
Vasculature data (Sup. Fig. 1–3): Vasculature data was generously provided by the laboratory of Chris Schaffer [112].
Electron microscopy (EM) data (Sup. Fig. 4–6): The EM data is available from the Open Connectome project at https://neurodata.io/. Manual annotation used for somatic comparisons were performed by the authors and are available on the above Open Science Framework repository.
Dendrite morphology data (Sup. Fig. 7): The data used to compare dendritic morphology is freely available from the Allen Institute via the Cell Types database: https://celltypes.brain-map.org/.
Simultaneous spiking and fluorescence activity (Sup. Fig. 9): The data used to fit and compare the fluorescence model was collected by Chen et al. [46] and are available online at https://crcns.org/data-sets/methods/cai-1/about-cai-1.
References
- [1].Ogawa S, Lee T-M, Kay AR, Tank DW, Brain magnetic resonance imaging with contrast dependent on blood oxygenation, Proceedings of the National Academy of Sciences 87 (24) (1990) 9868–9872. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].Jun JJ, Steinmetz NA, Siegle JH, Denman DJ, Bauza M, Barbarits B, Lee AK, Anastassiou CA, Andrei A, Aydın Ç, et al. , Fully integrated silicon probes for high-density recording of neural activity, Nature 551 (7679) (2017) 232. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Mace E, Montaldo G, Cohen I, Baulac M, Fink M, Tanter M, Functional ultrasound imaging of the brain, Nature Methods 8 (8) (2011) 662. [DOI] [PubMed] [Google Scholar]
- [4].Kodandaramaiah SB, Franzesi GT, Chow BY, Boyden ES, Forest CR, Automated whole-cell patch-clamp electrophysiology of neurons in vivo, Nature methods 9 (6) (2012) 585. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Briggman KL, Helmstaedter M, Denk W, Wiring specificity in the direction-selectivity circuit of the retina, Nature 471 (7337) (2011) 183. [DOI] [PubMed] [Google Scholar]
- [6].Bock DD, Lee W-CA, Kerlin AM, Andermann ML, Hood G, Wetzel AW, Yurgenson S, Soucy ER, Kim HS, Reid RC, Network anatomy and in vivo physiology of visual cortical neurons, Nature 471 (7337) (2011) 177. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Yuste R, Denk W, Dendritic spines as basic functional units of neuronal integration, Nature 375 (6533) (1995) 682. [DOI] [PubMed] [Google Scholar]
- [8].Lu R, Sun W, Liang Y, Kerlin A, Bierfeld J, Seelig JD, Wilson DE, Scholl B, Mohar B, Tanimoto M, et al. , Video-rate volumetric functional imaging of the brain at synaptic resolution, Nature neuroscience 20 (4) (2017) 620. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Grinvald A, Lieke E, Frostig RD, Gilbert CD, Wiesel TN, Functional architecture of cortex revealed by optical imaging of intrinsic signals, Nature 324 (6095) (1986) 361. [DOI] [PubMed] [Google Scholar]
- [10].Scott BB, Thiberge SY, Guo C, Tervo DGR, Brody CD, Karpova AY, Tank DW, Imaging cortical dynamics in gcamp transgenic rats with a head-mounted widefield macroscope, Neuron 100 (5) (2018) 1045–1058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Grienberger C, Konnerth A, Imaging calcium in neurons, Neuron 73 (5) (2015) 862–885. [DOI] [PubMed] [Google Scholar]
- [12].Denk W, Strickler JH, Webb WW, Two-photon laser scanning fluorescence microscopy, Science 248 (4951) (1990) 73–6.URL http://www.ncbi.nlm.nih.gov/pubmed/2321027 [DOI] [PubMed] [Google Scholar]
- [13].Botcherby EJ, Juskaitis R, Wilson T, Scanning two photon fluorescence microscopy with extended depth of field, Optics Communications 268 (2) (2006) 253–260. URL <GotoISI>://WOS:000242302100011 [Google Scholar]
- [14].Tian L, Akerboom J, Schreiter ER, Looger LL, Neural activity imaging with genetically encoded calcium indicators, Progress in Brain Research 196 (2012) 79–94. URL http://www.ncbi.nlm.nih.gov/pubmed/22341322 [DOI] [PubMed] [Google Scholar]
- [15].Helmchen F, Denk W, Deep tissue two-photon microscopy, Nature Methods 2 (12) (2005) 932–940. [DOI] [PubMed] [Google Scholar]
- [16].Stosiek C, Garaschuk O, Holthoff K, Konnerth A, In vivo two-photon calcium imaging of neuronal networks, Proceedings of the National Academy of Sciences 100 (12) (2003) 7319–7324. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Weisenburger S, Tejera F, Demas J, Chen B, Manley J, Sparks FT, Traub FM, Daigle T, Zeng H, Losonczy A, et al. , Volumetric ca2+ imaging in the mouse brain using hybrid multiplexed sculpted light microscopy, Cell 177 (4) (2019) 1050–1066. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Pachitariu M, Stringer C, Dipoppa M, Schroder S, Rossi LF, Dalgleish H, Carandini M, Harris KD, Suite2p: beyond 10,000 neurons with standard two-photon microscopy, bioRxiv (2017). arXiv:https://www.biorxiv.org/content/early/2017/07/20/061507.full.pdf, doi: 10.1101/061507. [DOI]
- [19].Harvey CD, Collman F, Dombeck DA, Tank DW, Intracellular dynamics of hippocampal place cells during virtual navigation, Nature 461 (7266) (2009) 941–6. doi: 10.1038/nature08499. URL http://www.ncbi.nlm.nih.gov/pubmed/19829374 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Rickgauer JP, Deisseroth K, Tank DW, Simultaneous cellular-resolution optical perturbation and imaging of place cell firing fields, Nat Neurosci 17 (12) (2014) 1816–24. doi: 10.1038/nn.3866. URL http://www.ncbi.nlm.nih.gov/pubmed/25402854 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21].Dombeck DA, Khabbaz AN, Collman F, Adelman TL, Tank DW, Imaging large-scale neural activity with cellular resolution in awake, mobile mice, Neuron 56 (1) (2007) 43–57. doi: 10.1016/j.neuron.2007.08.003. URL http://www.ncbi.nlm.nih.gov/pubmed/17920014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22].Pnevmatikakis EA, Analysis pipelines for calcium imaging data, Current opinion in neurobiology 55 (2019) 15–21. [DOI] [PubMed] [Google Scholar]
- [23].Stringer C, Pachitariu M, Computational processing of neural recordings from calcium imaging data, Current opinion in neurobiology 55 (2019) 22–31. [DOI] [PubMed] [Google Scholar]
- [24].Gauthier JL, Tank DW, Pillow JW, Charles AS, Detecting and correcting false transients in calcium time-trace inferenceSubmitted (2018). URL https://www.biorxiv.org/content/early/2018/11/19/473470 [DOI] [PMC free article] [PubMed]
- [25].Rueckel M, Mack-Bucher JA, Denk W, Adaptive wavefront correction in two-photon microscopy using coherence-gated wavefront sensing, Proceedings of the National Academy of Sciences 103 (46) (2006) 17137–17142. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26].Ji N, Sato TR, Betzig E, Characterization and adaptive optical correction of aberrations during in vivo imaging in the mouse cortex, Proceedings of the National Academy of Sciences 109 (1) (2012) 22–27. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27].Svoboda K, Denk W, Kleinfeld D, Tank DW, In vivo dendritic calcium dynamics in neocortical pyramidal neurons, Nature 385 (6612) (1997) 161. [DOI] [PubMed] [Google Scholar]
- [28].Murayama M, Perez-Garci E, Nevian T, Bock T, Senn W, Larkum ME, Dendritic encoding of sensory stimuli controlled by deep cortical interneurons, Nature 457 (7233) (2009) 1137. [DOI] [PubMed] [Google Scholar]
- [29].Mukamel EA, Nimmerjahn A, Schnitzer MJ, Automated analysis of cellular signals from large-scale calcium imaging data, Neuron 63 (6) (2009) 747–760. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [30].Maruyama R, Maeda K, Moroda H, Kato I, Inoue M, Miyakawa H, Aonishi T, Detecting cells using non-negative matrix factorization on calcium imaging data, Neural Networks 55 (2014) 11–19. [DOI] [PubMed] [Google Scholar]
- [31].Pnevmatikakis E, Merel J, Pakman A, Paninski L, Bayesian spike inference from calcium imaging data, Asilomar Conference on Signals, Systems and Computers (2013) 349–353. [Google Scholar]
- [32].Vogelstein JT, Watson BO, Packer AM, Yuste R, Jedynak B, Paninski L, Spike inference from calcium imaging using sequential monte carlo methods, Biophysical journal 97 (2) (2009) 636–655. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [33].Yaksi E, Friedrich RW, Reconstruction of firing rate changes across neuronal populations by temporally deconvolved ca2+ imaging, Nature Methods 3 (5) (2006) 377–383. [DOI] [PubMed] [Google Scholar]
- [34].Pachitariu M, Packer AM, Pettit N, Dalgleish H, Hausser M, Sahani M, Extracting regions of interest from biological images with convolutional sparse block coding, Advances in Neural Information Processing Systems (2013) 1745–1753.
- [35].Apthorpe N, Riordan A, Aguilar R, Homann J, Gu Y, Tank D, Seung HS, Automatic neuron detection in calcium imaging data using convolutional networks, in: Advances in Neural Information Processing Systems, 2016, pp. 3270–3278.
- [36].Jon O, Schultz SR, Dragotti PL, et al. , A finite rate of innovation algorithm for fast and accurate spike detection from two-photon calcium imaging, Journal of neural engineering 10 (4) (2013) 046017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [37].Pnevmatikakis E, Paninski L, Sparse nonnegative deconvolution for compressive calcium imaging: algorithms and phase transitions, Advances in Neural Information Processing Systems (2013) 1250–1258.
- [38].Pnevmatikakis E, Gao Y, Soudry D, Pfau D, Lacefield C, Poskanzer K, Bruno R, Yuste R, Paninski L, A structured matrix factorization framework for large scale calcium imaging data analysis, arXiv preprint arXiv:1409.2903 (2014).
- [39].Petersen A, Simon N, Witten D, Scalpel: Extracting neurons from calcium imaging data, arXiv preprint arXiv:1703.06946 (2017). [DOI] [PMC free article] [PubMed]
- [40].Reynolds S, Abrahamsson T, Schuck R, Sjostrom PJ, Schultz SR, Dragotti PL, Able: an activity-based level set segmentation algorithm for two-photon calcium imaging data, ENeuro 4 (5) (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [41].Inan H, Erdogdu MA, Schnitzer M, Robust estimation of neural signals in calcium imaging, in: Advances in Neural Information Processing Systems, 2017, pp. 2901–2910.
- [42].Mishne G, Coifman RR, Lavzin M, Schiller J, Automated cellular structure extraction in biological images with applications to calcium imaging data, bioRxiv (2018) 313981.
- [43].Mishne G, Charles AS, Learning spatially-corellated temporal dictionaries for calcium imaging, Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP), Brighton, UK (May 2019). [Google Scholar]
- [44].Theis L, Berens P, Froudarakis E, Reimer J, Roson MR, Baden T, Euler T, Tolias A, Bethge M, Supervised learning sets benchmark for robust spike detection from calcium imaging signals, arXiv preprint arXiv:1503.00135 (2015).
- [45].Prada J, Sasi M, Martin C, Jablonka S, Dandekar T, Blum R, An open source tool for automatic spatiotemporal assessment of calcium transients and local ‘signal-close-to-noise’activity in calcium imaging data, PLoS computational biology 14 (3) (2018) e1006054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [46].Chen T-W, Wardill TJ, Sun Y, Pulver SR, Renninger SL, Baohan A, Schreiter ER, Kerr RA, Orger MB, Jayaraman V, et al. , Ultrasensitive fluorescent proteins for imaging neuronal activity, Nature 499 (7458) (2013) 295–300. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [47].Theis L, Berens P, Froudarakis E, Reimer J, Roson MR, Baden T, Euler T, Tolias AS, Bethge M, Benchmarking spike rate inference in population calcium imaging, Neuron 90 (3) (2016) 471–482. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [48].Berens P, Theis L, Stone JS, Sofroniew N, Tolias A, Bethge M, Freeman J, Standardizing and benchmarking data analysis for calcium imaging, Computational and Systems Neuroscience (2017).
- [49].Song A, Charles AS, Koay SA, Gauthier JL, Thiberge SY, Pillow JW, Tank DW, Volumetric two-photon imaging of neurons using stereoscopy (vtwins), Nature methods 14 (4) (2017) 420. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [50].Nobauer T, Skocek O, Pernıa-Andrade AJ, Weilguny L, Traub FM, Molodtsov MI, Vaziri A, Video rate volumetric ca 2+ imaging across cortex using seeded iterative demixing (sid) microscopy, Nature Methods 14 (8) (2017) 811. [DOI] [PubMed] [Google Scholar]
- [51].Welvaert M, Durnez J, Moerkerke B, Verdoolaege G, Rosseel Y, neurosim: An r package for generating fmri data, Journal of Statistical Software 44 (10) (2011) 1–18. [Google Scholar]
- [52].Pnevmatikakis EA, Soudry D, Gao Y, Machado TA, Merel J, Pfau D, Reardon T, Mu Y, Lacefield C, Yang W, et al. , Simultaneous denoising, deconvolution, and demixing of calcium imaging data, Neuron 89 (2) (2016) 285–299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [53].Weisenburger S, Prevedel R, Vaziri A, Quantitative evaluation of two-photon calcium imaging modalities for high-speed volumetric calcium imaging in scattering brain tissue, bioRxiv (2017) 115659.
- [54].Abdellah M, Bilgili A, Eilemann S, Shillcock J, Markram H, Schurmann F, Bio-physically plausible visualization of highly scattering fluorescent neocortical models for in silico experimentation, BMC bioinformatics 18 (2) (2017) 62. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [55].Markram H, Muller E, Ramaswamy S, Reimann MW, Abdellah M, Sanchez CA, Ailamaki A, Alonso-Nanclares L, Antille N, Arsever S, et al. , Reconstruction and simulation of neocortical microcircuitry, Cell 163 (2) (2015) 456–492. [DOI] [PubMed] [Google Scholar]
- [56].Egger R, Narayanan RT, Helmstaedter M, de Kock CP, Oberlaender M, 3d reconstruction and standardization of the rat vibrissal cortex for precise registration of single neuron morphology, PLoS computational biology 8 (12) (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [57].Egger R, Dercksen VJ, Udvary D, Hege H-C, Oberlaender M, Generation of dense statistical connectomes from sparse morphological data, Frontiers in neuroanatomy 8 (2014) 129. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [58].Blinder P, Tsai PS, Kaufhold JP, Knutsen PM, Suhl H, Kleinfeld D, The cortical angiome: an interconnected vascular network with noncolumnar patterns of blood flow, Nature neuroscience 16 (7) (2013) 889–897. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [59].Xu L, Mould D, Constructive path planning for natural phenomena modeling, in: Artificial Intelligence Techniques for Computer Graphics, 2009, pp. 83–102.
- [60].Braitenberg V, Schuz A, Cortex: Statistics and Geometry of Neuronal Connectivity, Studies Brain Function Series, Springer, 1998. [Google Scholar]
- [61].Jiang X, Shen S, Cadwell CR, Berens P, Sinz F, Ecker AS, Patel S, Tolias AS, Principles of connectivity among morphologically defined cell types in adult neocortex, Science 350 (6264) (2015) aac9462. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [62].Allen cell types database - overview. technical report, Allen Brain Institute (2015). URL http://help.brain-map.org/download/attachments/8323525/CellTypesOverview.pdf?version=1&modificationDate=1456188760121
- [63].Benavides-Piccione R, Ballesteros-Yanez I, De Lagran MM, Elston G, Estivill X, Fillat C, DeFelipe J, Dierssen M, On dendrites in down syndrome and ds murine models: a spiny way to learn, Progress in neurobiology 74 (2) (2004) 111–126. [DOI] [PubMed] [Google Scholar]
- [64].Watts DJ, Strogatz SH, Collective dynamics of ‘small-world’networks, nature 393 (6684) (1998) 440. [DOI] [PubMed] [Google Scholar]
- [65].Downes JH, Hammond MW, Xydas D, Spencer MC, Becerra VM, Warwick K, Whalley BJ, Nasuto SJ, Emergence of a small-world functional network in cultured neurons, PLoS computational biology 8 (5) (2012) e1002522. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [66].Guzman SJ, Schlogl A, Frotscher M, Jonas P, Synaptic mechanisms of pattern completion in the hippocampal ca3 network, Science 353 (6304) (2016) 1117–1123. [DOI] [PubMed] [Google Scholar]
- [67].Schroeter MS, Charlesworth P, Kitzbichler MG, Paulsen O, Bullmore ET, Emergence of rich-club topology and coordinated dynamics in development of hippocampal functional networks in vitro, Journal of Neuroscience 35 (14) (2015) 5459–5470. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [68].Greenberg DS, Wallace DJ, Voit K-M, Wuertenberger S, Czubayko U, Monsees A, Handa T, Vogelstein JT, Seifert R,Groemping Y, et al. , Accurate action potential inference from a calcium sensor protein through biophysical modeling, BioRxiv (2018) 479055.
- [69].Helmchen F, Tank DW, A single-compartment model of calcium dynamics in nerve terminals and dendrites, Cold Spring Harbor Protocols 2015 (2) (2015) pdb–top085910. [DOI] [PubMed] [Google Scholar]
- [70].Lutcke H, Gerhard F, Zenke F, Gerstner W, Helmchen F, Inference of neuronal network spike dynamics and topology from calcium imaging data, Frontiers in Neural Circuits 7 (2013) 201. doi: 10.3389/fncir.2013.00201. URL 10.3389/fncir.2013.00201 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [71].Deneux T, Kaszas A, Szalay G, Katona G, Lakner T, Grinvald A, Rozsa B, Vanzetta I, Accurate spike estimation from noisy calcium signals for ultrafast three-dimensional imaging of large neuronal populations in vivo, Nature communications 7 (2016) 12190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [72].Badura A, Sun XR, Giovannucci A, Lynch LA, Wang SS-H, Fast calcium sensor proteins for monitoring neural activity, Neurophotonics 1 (2) (2014) 025008–025008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [73].Sun XR, Badura A, Pacheco DA, Lynch LA, Schneider ER, Taylor MP, Hogue IB, Enquist LW, Murthy M, Wang SS-H, Fast gcamps for improved tracking of neuronal activity, Nature communications 4 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [74].Zipfel WR, Williams RM, Webb WW, Nonlinear magic: multiphoton microscopy in the biosciences, Nature biotechnology 21 (11) (2003) 1369. [DOI] [PubMed] [Google Scholar]
- [75].Theriault G, Cottet M, Castonguay A, McCarthy N, De Koninck Y, Extended two-photon microscopy in live samples with bessel beams: steadier focus, faster volume scans, and simpler stereoscopic imaging, Frontiers in cellular neuroscience 8 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [76].Kobat D, Horton NG, Xu C, In vivo two-photon microscopy to 1.6-mm depth in mouse cortex, Journal of biomedical optics 16 (10) (2011) 106014. [DOI] [PubMed] [Google Scholar]
- [77].Tsai PS, Kaufhold JP, Blinder P, Friedman B, Drew PJ, Karten HJ, Lyden PD, Kleinfeld D, Correlations of neuronal and microvascular densities in murine cortex revealed by direct counting and colocalization of nuclei and vessels, Journal of Neuroscience 29 (46) (2009) 14553–14570. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [78].Pathak AP, Kim E, Zhang J, Jones MV, Three-dimensional imaging of the mouse neurovasculature with magnetic resonance microscopy, PloS one 6 (7) (2011) e22643. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [79].Hraetova S, Nicholson C, Biophysical properties of brain extracellular space explored with ion-selective microelectrodes, integrative optical imaging and related techniques (2007). [PubMed]
- [80].Lee W-CA, Bonin V, Reed M, Graham BJ, Hood G, Glattfelder K, Reid RC, Anatomy and function of an excitatory network in the visual cortex, Nature 532 (7599) (2016) 370. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [81].Stuart G, Spruston N, Hausser M, Dendrites, Oxford University Press, 2016. [Google Scholar]
- [82].Louth EL, Luctkar HD, Heney KA, Bailey CD, Developmental ethanol exposure alters the morphology of mouse prefrontal neurons in a layer-specific manner, Brain research 1678 (2018) 94–105. [DOI] [PubMed] [Google Scholar]
- [83].Koester HJ, Sakmann B, Calcium dynamics associated with action potentials in single nerve terminals of pyramidal cells in layer 2/3 of the young rat neocortex, The Journal of Physiology 529 (3) (2000) 625–646. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [84].Kaiser KM, Zilberter Y, Sakmann B, Back-propagating action potentials mediate calcium signalling in dendrites of bitufted interneurons in layer 2/3 of rat somatosensory cortex, The Journal of Physiology 535 (1) (2001) 17–31. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [85].Helmchen F, Imoto K, Sakmann B, Ca2+ buffering and action potential-evoked ca2+ signaling in dendrites of pyramidal neurons, Biophysical Journal 70 (2) (1996) 1069–1081. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [86].Cox CL, Denk W, Tank DW, Svoboda K, Action potentials reliably invade axonal arbors of rat neocortical neurons, Proceedings of the National Academy of Sciences 97 (17) (2000) 9724–9728. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [87].Zariwala HA, Borghuis BG, Hoogland TM, Madisen L, Tian L, De Zeeuw CI, Zeng H, Looger LL, Svoboda K, Chen T-W, A cre-dependent gcamp3 reporter mouse for neuronal imaging in vivo, Journal of Neuroscience 32 (9) (2012) 3131–3141. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [88].Huber D, Gutnisky D, Peron S, O’connor D, Wiegert J, Tian L, Oertner T, Looger L, Svoboda K, Multiple dynamic representations in the motor cortex during sensorimotor learning, Nature 484 (7395) (2012) 473. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [89].Korogod N, Petersen CC, Knott GW, Ultrastructural analysis of adult mouse neocortex comparing aldehyde perfusion with cryo fixation, Elife 4 (2015) e05793. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [90].Grewe BF, Voigt FF, van’t Hoff M, Helmchen F, Fast two-layer two-photon imaging of neuronal cell populations using an electrically tunable lens, Biomedical Optics Express 2 (7) (2011) 2035–2046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [91].Prevedel R, Verhoef AJ, Pernia-Andrade AJ, Weisenburger S, Huang BS, Nobauer T, Fernandez A, Delcour JE, Golshani P, Baltuska A, et al. , Fast volumetric calcium imaging across multiple cortical layers using sculpted light, Nature Methods 13 (12) (2016) 1021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [92].Nguyen JP, Shipley FB, Linder AN, Plummer GS, Liu M, Setru SU, Shaevitz JW, Leifer AM, Whole-brain calcium imaging with cellular resolution in freely behaving caenorhabditis elegans, Proceedings of the National Academy of Sciences 113 (8) (2016) E1074–E1081. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [93].Akerboom J, Chen T-W, Wardill TJ, Tian L, Marvin JS, Mutlu S, Calderon NC, Esposti F, Borghuis BG, Sun XR, et al. , Optimization of a gcamp calcium indicator for neural activity imaging, Journal of Neuroscience 32 (40) (2012) 13819–13840. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [94].Chen Y, Jang H, Spratt PW, Kosar S, Taylor DE, Essner RA, Bai L, Leib DE, Kuo T-W, Lin Y-C, et al. , Soma-targeted imaging of neural circuits by ribosome tethering, Neuron 107 (3) (2020) 454–469. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [95].Lecoq J, Oliver M, Siegle JH, Orlova N, Koch C, Removing independent noise in systems neuroscience data using deepinterpolation, bioRxiv (2020). [DOI] [PMC free article] [PubMed]
- [96].Vanwalleghem GC, Constantin L, Scott EK, Calcium imaging and the curse of negativity, bioRxiv (2020). [DOI] [PMC free article] [PubMed]
- [97].A. Institute, The brain modeling toolkit (BMTK), https://github.com/AllenInstitute/bmtk (2017).
- [98].Harris KM, Spacek J, Bell ME, Parker PH, Lindsey LF, Baden AD, Vogelstein JT, Burns R, A resource from 3d electron microscopy of hippocampal neuropil for user training and tool development, Scientific data 2 (1) (2015) 1–19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [99].Schmidt H, Gour A, Straehle J, Boergens KM, Brecht M, Helmstaedter M, Axonal synapse sorting in medial entorhinal cortex, Nature 549 (7673) (2017) 469–475. [DOI] [PubMed] [Google Scholar]
- [100].Greenwald M, Beyond benchmarking—how experiments and simulations can work together in plasma physics, Computer physics communications 164 (1–3) (2004) 1–8. [Google Scholar]
- [101].Kasthuri N, Hayworth KJ, Berger DR, Schalek RL, Conchello JA, Knowles-Barley S, Lee D, Vazquez-Reina A, Kaynig V, Jones TR, et al. , Saturated reconstruction of a volume of neocortex, Cell 162 (3) (2015) 648–661. [DOI] [PubMed] [Google Scholar]
- [102].Rasmussen CE, Williams CKI, Gaussian Processes for Machine Learning (Adaptive Computation and Machine Learning), The MIT Press, 2005. [Google Scholar]
- [103].Carlson C, How I made wine glasses from sunflowers (2011). URL http://blog.wolfram.com/2011/07/28/how-i-made-wine-glasses-from-sunflowers/
- [104].Hawkes AG, Spectra of some self-exciting and mutually exciting point processes, Biometrika 58 (1) (1971) 83–90. [Google Scholar]
- [105].Ogata Y, On lewis’ simulation method for point processes, IEEE Transactions on Information Theory 27 (1) (1981) 23–31. [Google Scholar]
- [106].Roxin A, Brunel N, Hansel D, Mongillo G, van Vreeswijk C, On the distribution of firing rates in networks of cortical neurons, Journal of Neuroscience 31 (45) (2011) 16217–16226. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [107].Holthoff K, Tsay D, Yuste R, Calcium dynamics of spines depend on their dendritic location, Neuron 33 (3) (2002) 425–437. [DOI] [PubMed] [Google Scholar]
- [108].Jacques SL, Optical properties of biological tissues: a review, Physics in Medicine & Biology 58 (11) (2013) R37. [DOI] [PubMed] [Google Scholar]
- [109].Schmidt JD, Numerical simulation of optical wave propagation with examples in MATLAB, SPIE Bellingham, Washington, USA, 2010. [Google Scholar]
- [110].Chaigneau E, Wright AJ, Poland SP, Girkin JM, Silver RA, Impact of wavefront distortion and scattering on 2-photon microscopy in mammalian brain tissue, Optics express 19 (23) (2011) 22755–22774. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [111].Wang C, Ji N, Pupil-segmentation-based adaptive optical correction of a high-numerical-aperture gradient refractive index lens for two-photon fluorescence endoscopy, Optics letters 37 (11) (2012) 2001–2003. [DOI] [PubMed] [Google Scholar]
- [112].Haft-Javaherian M, Fang L, Muse V, Schaffer CB, Nishimura N, Sabuncu MR, Deep convolutional neural networks for segmenting 3d in vivo multiphoton images of vasculature in alzheimer disease mouse models, PloS one 14 (3) (2019) e0213539. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [113].Johansson JD, Spectroscopic method for determination of the absorption coefficient in brain tissue, Journal of biomedical optics 15 (5) (2010) 057005. [DOI] [PubMed] [Google Scholar]
- [114].Prahl S, Optical absorption of hemoglobin, http://omlc.ogi.edu/spectra/hemoglobin (1999).
- [115].Spectrum of egfp, http://www.tsienlab.ucsd.edu/Documents.htm, accessed: 2019-02-04.
- [116].Giovannucci A, Friedrich J, Gunn P, Kalfon J, Koay SA, Taxidis J, Najafi F, Gauthier JL, Zhou P, Tank DW, et al. , Caiman: An open source tool for scalable calcium imaging data analysis, bioRxiv (2018) 339564. [DOI] [PMC free article] [PubMed]
- [117].Martinez-Cantin R, Bayesopt: A bayesian optimization library for nonlinear optimization, experimental design and bandits, The Journal of Machine Learning Research 15 (1) (2014) 3735–3739. [Google Scholar]
- [118].Chen TW, Wardill TJ, Sun Y, Pulver SR, Renninger SL, Baohan A, Schreiter ER, Kerr RA, Orger MB, Jayaraman V, Looger LL, Svoboda K, Kim DS, Ultrasensitive fluorescent proteins for imaging neuronal activity, Nature 499 (7458) (2013) 295–300. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [119].Madisen L, Garner AR, Shimaoka D, Chuong AS, Klapoetke NC, Li L, van der Bourg A, Niino Y, Egolf L, Monetti C, Gu H, Mills M, Cheng A, Tasic B, Nguyen TN, Sunkin SM, Benucci A, Nagy A, Miyawaki A, Helmchen F, Empson RM, Knopfel T, Boyden ES, Reid RC, Carandini M, Zeng H, Transgenic mice for intersectional targeting of neural sensors and effectors with high specificity and performance, Neuron 85 (5) (2015) 942–58. doi: 10.1016/j.neuron.2015.02.022. URL http://www.ncbi.nlm.nih.gov/pubmed/25741722 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [120].Dana H, Chen T-W, Hu A, Shields BC, Guo C, Looger LL, Kim DS, Svoboda K, Thy1-gcamp6 transgenic mice for neuronal population imaging in vivo, PLoS One 9 (9) (2014) e108697. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [121].Koay SA, Thiberge SY, Brody C, Tank DW, Neural correlates of cognition in primary visual versus neighboring posterior cortices during visual evidence-accumulation-based navigation, bioRxiv (2019) 568766.
- [122].Rall W, Branching dendritic trees and motoneuron membrane resistivity, Experimental neurology 1 (5) (1959) 491–527. [DOI] [PubMed] [Google Scholar]
- [123].Sun J, Lee SJ, Wu L, Sarntinoranont M, Xie H, Refractive index measurement of acute rat brain tissue slices using optical coherence tomography, Optics express 20 (2) (2012) 1084–1095. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [124].Mutze J, Iyer V, Macklin JJ, Colonell J, Karsh B, Petrasek Z, Schwille P, Looger LL, Lavis LD, Harris TD, Excitation spectra and brightness optimization of two-photon excited probes, Biophysical journal 102 (4) (2012) 934–944. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [125].Watanabe K. NC., Microscope objective lens, Japanese Patent No. 2005–189732 (2005).
- [126].Hamamatsu, Metal Package PMT with Cooler, accessed Feb. 5, 2019.
- [127].Coherent, Chameleon Ultra Family Widely Tunable, Hands-Free, Modelocked Ti:Sapphire Lasers (2013).
- [128].Rademacker J, An exact formula to describe the amplification process in a photomultiplier tube, Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment 484 (1–3) (2002) 432–443. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
A number of datasets were used to validate the NAOMi simulation. These data are available from different sources with different restrictions:
Two-photon images from mouse V1 (Fig. 2): This data was taken at the Princeton Neuroscience Institute by the laboratory of David Tank, and is available upon request to the authors.
Simulated videos (Fig. 2–4, Sup. Fig. 1–35): All simulated videos are available on an Open Science Framework repository https://osf.io/863j9/. A handful of volume files are too large to deposit at OSF and can be made available upon request from the authors.
Vasculature data (Sup. Fig. 1–3): Vasculature data was generously provided by the laboratory of Chris Schaffer [112].
Electron microscopy (EM) data (Sup. Fig. 4–6): The EM data is available from the Open Connectome project at https://neurodata.io/. Manual annotation used for somatic comparisons were performed by the authors and are available on the above Open Science Framework repository.
Dendrite morphology data (Sup. Fig. 7): The data used to compare dendritic morphology is freely available from the Allen Institute via the Cell Types database: https://celltypes.brain-map.org/.
Simultaneous spiking and fluorescence activity (Sup. Fig. 9): The data used to fit and compare the fluorescence model was collected by Chen et al. [46] and are available online at https://crcns.org/data-sets/methods/cai-1/about-cai-1.


