Abstract
Background:
Data-driven methods such as independent component analysis (ICA) makes very few assumptions on the data and the relationships of multiple datasets, and hence, are attractive for the fusion of medical imaging data. Two important extensions of ICA for multiset fusion are the joint ICA (jICA) and the multiset canonical correlation analysis and joint ICA (MCCA-jICA) techniques. Both approaches assume identical mixing matrices, emphasizing components that are common across the multiple datasets. However, in general, one would expect to have components that are both common across the datasets and distinct to each dataset.
New method:
We propose a general framework, disjoint subspace analysis using ICA (DS-ICA), which identifies and extracts not only the common but also the distinct components across multiple datasets. A key component of the method is the identification of these subspaces and their separation before subsequent analyses, which helps establish better model match and provides flexibility in algorithm and order choice.
Comparison:
We compare DS-ICA with jICA and MCCA-jICA through both simulations and application to multiset functional magnetic resonance imaging (fMRI) task data collected from healthy controls as well as patients with schizophrenia.
Results:
The results show DS-ICA estimates more components discriminative between healthy controls and patients than jICA and MCCA-jICA, and with higher discriminatory power showing activation differences in meaningful regions. When applied to a classification framework, components estimated by DS-ICA results in higher classification performance for different dataset combinations than the other two methods.
Conclusion:
These results demonstrate that DS-ICA is an effective method for fusion of multiple datasets.
Keywords: Data fusion, fMRI, ICA, IVA, Common, distinct components
1. Introduction
Joint analysis, or fusion, of multiple datasets is becoming increasingly important in multiple fields and medical imaging is a very important one among those (Lahat et al., 2015; Mijović et al., 2014; Adalı et al., 2015a; Leeb et al., 2010). The goal of data fusion is to maximally use joint information available across datasets by letting them fully influence each other, hence making the best use of available information for the underlying problem (Adalı et al., 2018; Calhoun and Sui, 2016; James and Dasarathy, 2014; Savopol and Armenakis, 2002). Matrix and tensor decomposition-based methods are based on a latent variable model and enable such interaction among the datasets. An important strength of these methods is that they are directly interpretable, i.e., one can attach physical meaning to the output latent variables, or components (Smilde et al., 2017; Lahat et al., 2015; Adalı et al., 2018). Among these methods those based on independent component analysis (ICA) have proven especially useful for data fusion since they minimize the assumptions on the data and allow full interaction among the datasets (Calhoun and Adalı, 2012; Adalı et al., 2015b). However, ICA formulation is originally formulated for one dataset. This has led to the development of different extensions of ICA for the fusion of multiple datasets. These extensions rely on the model used to explain the underlying relationship of the components across the datasets and are successful when there is a good model match, i.e., the assumptions of the model are satisfied, which is key to better interpretability. In this paper, we introduce a powerful framework, disjoint subspaces for multiple datasets to leverage the strength of two popular fusion methods such that a better model match can be achieved.
In a latent variable model-based fusion, certain latent variables—or components—can be either highly correlated across the datasets or might have weak or no correlation. The main goal when fusing datasets is to make full use of those that are correlated. We define the highly correlated components as common across datasets and unique or low correlated ones as distinct. When the components are identified as common and distinct among the datasets, one obtains a more complete and realistic picture of the underlying relationship across the datasets (Smilde et al., 2017; Lock et al., 2013; Schouteden et al., 2014). A number of ICA-based fusion methods have focused on this very aspect, either taking advantage of only the common components or both common and the distinct components to explain the underlying relationship across multiple datasets. One such method, joint ICA (jICA) introduced in (Calhoun et al., 2006c), has been used for fusion of different medical imaging modalities such as functional magnetic resonance imaging (fMRI) and Electroencephalography (EEG) (Mangalathu-Arumana et al., 2012, 2018; Jacob et al., 2017), fMRI, structural MRI (sMRI) and EEG (Adalı et al., 2015b), fMRI data of multiple tasks (Calhoun et al., 2006a) and many others. Though widely used, jICA assumes a common shared mixing matrix for all datasets, thus treating all the estimated components as common and aligned across the datasets. While it is a strong assumption, when it is satisfied it provides much needed robustness in the estimation. Another method, MCCA-jICA (Sui et al., 2010, 2013a,b), uses a prior multiset canonical correlation analysis (MCCA) step. MCCA, an extension of canonical correlation analysis (CCA) for multiple datasets (Kettenring, 1971), to maximize the linear correlation between the datasets prior to the jICA step. This scheme aligns components more likely to be common across datasets and thus provides a better model match for the following jICA step. MCCA-jICA has been successfully applied for fusion of fMRI, diffusion tensor imaging (DTI) and sMRI (Sui et al., 2013a; Hirjak et al., 2020), fMRI, EEG and sMRI data (Sui et al., 2014) and 4-way fusion of MRI data (Liu et al., 2019). However, MCCA-jICA like jICA inherently assumes that most underlying components—or sources—in the decompositions are common across the datasets. As expected, the performance of both approaches suffers when not all components are shared. A more general extension of ICA to multiple datasets, independent vector analysis (IVA) (Adalı et al., 2014) alleviates this assumption but requires significant number of samples for reliable performance (Bhinge et al., 2019).
An effective approach would be to break the problem into two to achieve a desired trade-off in model match and robustness. We can first identify disjoint subspaces, those that are common across all the datasets along with those that are unique to each dataset in the fusion. We can then perform joint analysis on the common subspaces where strong assumptions of fusion methods are justified and perform separate analyses on the distinct subspaces. These separate analyses of disjoints subspaces thus ensure a better model match, and hence provide better interpretability of the estimated components. This is the main idea behind disjoint subspaces using ICA (DS-ICA), which we introduce in this paper. We present DS-ICA as an effective method for the fusion of multiple datasets, through the identification of common and distinct subspaces across more than two datasets. We propose solutions for the estimation and identification of common and distinct subspaces in multiple datasets using independent vector analysis with multivariate Gaussian distribution (IVA-G) (Anderson et al., 2012) and then use ICA to estimate joint independent components from common subspaces and distinct independent components from each distinct subspace separately. IVA-G generalizes ICA to multiple datasets, and through the use of Gaussian model takes only second-order statistics into account like CCA and its multiset generalization, MCCA (Kettenring, 1971). The strong identifiability condition of IVA—i.e., the ability to uniquely identify the underlying latent variables under very general conditions (Adalı et al., 2014; Anderson et al., 2012)—allows IVA-G to better capture the exact subspace structure across the datasets compared with MCCA as we show in the paper. Separation of the common and distinct subspaces as a first step reduces the dimensionality of the datasets, which in turn reduces the complexity and offers flexibility in the following analyses and enables better estimation of both the common and distinct components. For example, the assumption of a common mixing matrix becomes more flexible in DS-ICA than other methods due to the better estimation of subspace structure and separate analyses of common and distinct subspaces. A preliminary version of this approach is introduced in (Akhonda et al., 2019), for only two datasets. In this paper, we introduce the general method for fusion of multiple datasets (K ≥ 2), and study its properties demonstrating the trade-offs, and present its successful application to multitask fMRI data.
We first compare the performance of DS-ICA with the two closely related methods of jICA and MCCA-jICA through simulations and highlight its advantages. We then demonstrate its successful application to fusion of multitask fMRI data collected from 138 healthy subjects and 109 patients with schizophrenia. The three tasks in this study involves an auditory odd ball (AOD) task, a Sternberg item recognition paradigm (SIRP) task, and a sensorimotor (SM) task (Gollub et al., 2013). We show that DS-ICA can simultaneously estimate not only the common components that are shared across all datasets, but also the distinct ones unique to each task dataset. The common components estimated by DS-ICA primarily show activation in the motor, sensory motor, default mode network (DMN), visual and frontal parietal regions while the distinct ones show significant activations in part of the auditory and motor regions for AOD, visual region for SIRP and sensory motor region for SM task. These regions are indeed those that are expected to be common and distinct in terms of activation for these tasks, and have been previously shown to differentiate patients with schizophrenia from healthy controls (Kiehl and Liddle, 2001; Kiehl et al., 2005; Demirci et al., 2009; Öngür et al., 2010; Whitfield-Gabrieli et al., 2009; Hu et al., 2017), thus increasing our confidence in the results. Overall, DS-ICA estimates more components that can differentiate between healthy controls and patients with relatively higher discrimination level compared with jICA and MCCA-jICA. This, coupled with the meaningful activation areas of the estimated components show the advantage of using common and distinct components in fusion analysis. We use classification rate to compare the performances of different multiset fusion techniques across various combinations of datasets as an unambiguous and natural way to assess the relative performance of methods and to evaluate how informative the components are for the discrimination of healthy controls and patients. We show that DS-ICA achieves higher classification performance than other techniques for various combinations of the datasets, suggesting that it enables higher interaction among the datasets which results in better use of the available information. The study also guides us about the degree to which there exists complementary information across the datasets. We also test the stability of the group discriminant components across different subject groups and show that DS-ICA can consistently estimate these components across different subgroups.
The paper is organized as follows. In Section 2, we discuss about the existing ICA based algorithms. In Section 3, we introduce our new method and in Section 4, we discuss about implementation and results. We provide conclusions in the final section.
2. ICA-based approaches for fusion
Data-driven fusion of multiset medical imaging data collected from a group of subjects is challenging due to multiple factors. An important one among those is the high dimensionality of the datasets. Therefore, it is desirable to reduce each dataset into a feature and obtain a lower dimensional representation of the data, for each subject (Calhoun and Adalı, 2009) while keeping as much variability in the data as possible. Consider as a grouping of K feature datasets from M subjects, where the mth row of each dataset is formed by one multivariate feature for each subject. Such reductions alleviate the high dimensionality problem and offer a natural way to discover association across these feature datasets, i.e., the variations across subjects. The basic ICA model on kth dataset is formulated by
| (1) |
where each dataset is a linear mixture of M components— referred to as sources and given by the rows of matrix —through an invertible mixing matrix, . ICA estimates a demixing matrix Wk such that the maximally independent source components can be computed using . The columns of the estimated mixing matrices, , k = 1, …, K are referred to as the subject covariations, or profiles as they quantify the contributions to the overall mixtures Xk. The goal here is, given Xk, to estimate independent sources and their associated subject covariations or profiles, which we can interpret, i.e., attach a physical meaning to them. Note that both profiles and the estimated components, together or individually, can be used to establish connection across datasets (Adalı et al., 2018). However, ICA can only analyze a single dataset at a time by generating a decomposition on each dataset independent of other datasets (Levin-Schwartz et al., 2017). In the next section, we discuss different extensions of ICA to jointly analyze multiple datasets.
Joint ICA, the most popular extension of ICA for fusion, enables joint analysis by concatenating the datasets horizontally such that each dataset is stacked next to each other (Calhoun et al., 2006b). Given K ≥ 2 datasets that have a common row dimension of M, jICA performs a single ICA on the horizontally concatenated ‘joint’ dataset as follows:
| (2) |
where represents the joint source matrix and is the common mixing matrix shared by all K datasets. Since a single density function is used to estimate components from all the datasets, jICA requires all the datasets to have almost equal number of samples to ensure unbiased estimation of the results (Adalı et al., 2015a; Akhonda et al., 2018). Moreover, as the associations across the datasets are determined through the columns of shared mixing matrix, i.e., profiles, this automatically implies that the model assumes all the estimated components are common across concatenated datasets. One way to reduce the strong model assumption of jICA is by using MCCA (Kettenring, 1971), an extension of CCA for multiple datasets, prior to jICA, leading to MCCA-jICA (Sui et al., 2010).
MCCA-jICA aligns the components prior to jICA by maximizing the linear correlation among the datasets. MCCA as a preprocessing step estimates weighting vectors , k = 1,2, …, K and j = 1,2, …, M known as canonical coefficient vectors, such that the normalized correlation within is maximized. Here, uk’s are known as canonical variates and can be written in matrix form as
| (3) |
In MCCA, this is achieved through a deflationary approach where one first estimates the first set of canonical correlation coefficient vectors, , k = 1,2, … ,K using
| (4) |
and then proceeds to the next , k = 1,2, … ,K vectors such that is orthogonal to , resulting in orthogonal Wk, k = 1, 2, … ,K. Here, is the correlation between the jth canonical variates from k1 and k2 datasets and J(·) is the cost function needed to be optimized. A number of MCCA cost function are proposed in (Kettenring, 1971) and can be optimized to obtain the canonical correlation values. Estimated canonical variates are then decomposed using a jICA approach as follows,
| (5) |
The concatenation of canonical variates ensures that components are aligned across the datasets—i.e., same index components are correlated across datasets—and can be estimated by using a single density function in jICA (Sui et al., 2010). However, similar to the jICA technique, MCCA-jICA also assumes mixing parameters are the same for all estimated components. Moreover, maximization of correlation at the first step encourages only the available common information, which further minimizes the individual features available in each dataset, thus limits its application to common and distinct component analysis.
Another popular ICA-based method, parallel ICA (p-ICA) (Liu et al., 2009), consists of applying separate ICAs on each dataset, such that the correlation among the common subject covariations is maximized in each iteration. This method identifies the subject profiles that are correlated across datasets and maximizes the correlation only between those in later runs by using the cost function
| (6) |
where the linking term, f(·), introduces correlation across datasets through profiles and λ is dynamically adjusted to balance independence and the dataset correlation. Unlike jICA and MCCA-jICA, p-ICA can estimate both common and distinct components from the datasets. However, the application of p-ICA is few in practice due to its many limitations (Akhonda et al., 2018). Since f(·) is defined for only two datasets, p-ICA applies to only two datasets at a time. An extension of p-ICA, proposed in (Vergara et al., 2014), can be used for fusion of three datasets. However, similar to the two datasets case, the method again considers pair-wise correlations for maximizing correlation across more than two datasets. Moreover, the performance of p-ICA degrades with lower number of subjects in the analysis due to errors in correlation estimation. Finally, the optimization of the algorithm depends on fine-tuning of several user-defined parameters (Akhonda et al., 2019).
Since most ICA-based fusion methods assume some degree of commonality across the datasets, a practical approach would be to identify and split common and distinct subspaces from the datasets and perform separate analyses to achieve a better model match. Identifying and performing joint analysis only on the common subspace and individual analyses on distinct subspaces alleviates the potential model mismatch of jICA and MCCA-jICA, and exploits both common and distinct information available in each dataset. A preliminary version of this approach using CCA and ICA is introduced in (Adalı et al., 2018), but only for two datasets. In the next section, we introduce a new technique for the fusion of more than two datasets that can preserve the subspace structure and estimate components that reliably represent the common and distinct nature of the data.
3. Disjoint subspace analysis using ICA (DS-ICA) for K ≥ 2 datasets
In this section, we propose a new method, disjoint subspace analysis using ICA (DS-ICA), for the fusion of K ≥ 2 datasets by identifying and employing separate analyses on disjoint common and distinct subspaces. Consider the datasets Xk, k = 1,2, … ,K given in (1). Identifying the common and the distinct subspaces across multiple datasets is not straightforward due to the many possible correlation structures available across all K datasets. We propose to utilize three definite steps to identify and estimate common and distinct components. A general framework of DS-ICA performing all three steps is shown in Fig. 1. Details about the steps and options to perform those are discussed below.
Figure 1:
General framework of DS-ICA for common and distinct component estimation
3.1. Common order estimation
The first step of DS-ICA is to estimate the order of the common signal subspace C across K ≥ 2 datasets. Given K = 2, several techniques can be used to estimate C (Chen et al., 1996; Fujikoshi and Veitch, 1979; Seghouane and Shokouhi, 2019; Song et al., 2015). Among those, we use PCA-CCA introduced in (Song et al., 2015) since it is equally effective for both sample rich and sample poor scenarios, and provides robust performance when applied to fMRI analysis (Levin-Schwartz et al., 2016). PCA-CCA makes use of the strength of CCA to maximize the linear correlation between the reduced dimensional datasets obtained from an initial PCA step. The estimated canonical correlation values are then used to identify the order of the correlated signal subspace by using minimum description length (MDL) criterion given as
| (7) |
where n is the PCA rank, m = 1, …, M and r1(n), …, rM(n) denote the canonical correlation coefficient estimates using the PCA rank, n. However, since the method is limited to only two datasets, it cannot be used to identify the common signal subspace order for K > 2 datasets. One practical way to alleviate this issue is to apply PCA-CCA on pairwise datasets and use information-theoretic criterion to estimate the common order (Song et al., 2016). Other notable techniques include using maximum likelihood statistics on sample correlation values (Y. Wu et al., 2002), MCCA along with knee point detection (Bhinge et al., 2017) and rank-reduced hypothesis test on multiple datasets (Hasija et al., 2016). Among those, MCCA before knee point detection (MCCA-KPD), estimates common order C by using MCCA to maximize linear correlation across K > 2 datasets and provides robust performance when applied to simulated and real fMRI data (Bhinge et al., 2017). Since IVA-G generalizes MCCA, IVA-G can also replace the MCCA step in MCCA-KPD to estimate the common order across K > 2 datasets. It is, however, important to note that joint order selection methods such as MCCA-KPD only gives us a general direction about the common subspace order. In our study, we do not simply use the order estimated with the selected method but also evaluate the stability and the quality of the estimated components to choose the final C. Given the signal subspace order M and common order C, distinct signal subspace order can be estimated as D = M − C. Next, the common and distinct signal subspace orders C and D are used to identify and separate the common and distinct signal subspaces from the datasets.
3.2. Subspace Identification and Separation
The next step in DS-ICA is the identification and estimation of the common and distinct subspaces. Given the common order C for K ≥ 2 datasets, DS-ICA uses IVA to identify and split each Xk dataset into respective common and distinct parts such that
| (8) |
where rank(·) represents rank of the matrix and XkC and XkD are the common and distinct parts estimated from each K dataset. IVA generalizes ICA to multiple datasets and intimately related to both CCA and MCCA (Adalı et al., 2014). Given the model formulation in (1), IVA jointly estimates the demixing matrices Wk, k = 1,2, …, K such that estimated source components within are independent while maximally dependent with the corresponding components across the multiple datasets. This is done my modelling the source component vector (SCV), where jth SCV s(j) can be defined as
| (9) |
i.e., by concatenating the jth source component from each of the K dataset. Since SCV is defined using corresponding components across all datasets, it is where dependencies across the datasets are taken into account. This additional diversity, dependencies among the sources inside an SCV, is also what aligns the sources estimated across datasets, and thus helps with the resolution of permutation ambiguity for ICA across datasets. This is important for DS-ICA formulation as well since it assumes that the common sources are aligned and dependent across datasets. When a multivariate Gaussian distribution is used to model the SCV, thus taking only the second order statistics (SOS) into account, the resultant method is called independent vector analysis with multivariate Gaussian distribution (IVA-G) (Anderson et al., 2012). In our formulation, we use IVA-G to identify and estimate the common and distinct subspaces. We use the estimated components that are maximally correlated across the datasets to form the common subspaces and use the rest of the components that are not correlated across datasets to form distinct subspaces. This is done by using the estimated common and distinct order C and D on the estimated components as
| (10) |
| (11) |
such that (8) is satisfied. These common and distinct subspaces are then used in step 3 to estimate the common and distinct components through separate decompositions.
It is important to note here that other methods such as CCA, its extension to multiple datasets, MCCA, and joint and individual variation explained (JIVE) [12] that can also be used to identify and estimate the common and distinct subspaces across multiple datasets. Both MCCA and IVA-G use SOS to maximize the correlation between the datasets, and IVA-G solves the exactly equivalent cost function as MCCA with generalized variance method (GENVAR) when the demixing matrices are constrained to be orthogonal in IVA-G. However, the lack of orthogonality constraint in IVA-G provides more flexibility, allowing for a bigger solution space for the demixing matrices (Anderson et al., 2012). This also yields a strong identifiability condition—i.e., enables identification of a wide range of signals under very general conditions. This is the reason IVA-G can better preserve the subspace structure than MCCA, a really important feature as the subspace structure gets more complicated with the increase of number of datasets (Long et al., 2020; Anderson et al., 2014). This advantage is demonstrated with examples that involve rich covariance structures in (Long et al., 2020). JIVE, on the other hand, fails to identify components, especially the ones common across datasets, if the components are weak, hence making it less practical to the fusion of real fMRI data.
3.3. Common and Distinct Component Estimation
In the final step of DS-ICA, after extracting the common and distinct subspaces from each dataset using SOS, both subspaces can be analyzed separately using models that can take higher order statistics (HOS) or other statistical properties of the data into account. For example, the common or shared parts can be concatenated together and jointly analyzed by using jICA, while the distinct parts can be analyzed separately by using individual ICAs:
Concatenating only the common parts satisfies the strong assumptions of jICA model and results strongly associated underlying sources. On the other hand, separate analyses on the distinct parts provide sources that are distinct to each dataset. Thus, DS-ICA only enables fusion to common parts where it is suitable while analyzing distinct parts separately, minimizing the influence of distinct components in the common component analysis and vice versa. It is, however, important to note that other fusion techniques and decomposition methods can be used instead of jICA and ICA based of the nature of the data to estimate the common and distinct components. Since the number of variables to be estimated increases with the number of datasets, fusion methods such as jICA and MCCA-jICA become more constrained with added datasets due to their assumption of a common mixing matrix. On the other hand, DS-ICA alleviates this issue to some extent by splitting the datasets into parts, thus significantly reducing the dimension of the datasets under joint analysis , i.e., common parts. Performing separate analyses on the common and distinct subspaces reduces the number of variables to be estimated in fusion, reducing algorithmic complexities and providing flexibility to choose an algorithm suitable for each subspace analysis.
Algorithm.
DS-ICA with IVA-G
| Input: Xk, k = 1,2, …, K |
| Output: SC = Common components |
| SkC = Distinct components |
| AC, AkD = Subject covariation/profiles |
| 1: C = MCCA−KPD(Xk), 1 ≤ k ≤ K |
| 2: , where Wk = IVA–G(Xk), 1 ≤ k ≤ K, |
| 3: and |
| 4: , 1 ≤ k ≤ K, |
| where rank(Xk) = rank(XkC) + rank(XkD) |
| 5: XC = [X1C, X2C, …, XkC] = AC[S1C, S2C, …, SkC] = ACSC |
| 6: XkD = AkDSkD, 1 ≤ k ≤ K |
| 7: return AC, SC, AkD and SkD |
4. Implementation and results
4.1. Simulation setup and results
In this study, we compare the performance of three ICA-based fusion methods, namely, jICA, MCCA-jICA and DS-ICA as this is the set most closely related in terms of their goals and models. To ensure a fair comparison, we use the same ICA algorithm, ICA by entropy bound minimization (ICA-EBM), for all three methods. ICA-EBM uses a flexible density matching mechanism based on entropy maximization (Li and Adalı, 2009) and provides better estimation performance for neurological data compare to the other ICA algorithms (Long et al., 2019). We generate simulation examples for two datasets, and then extend it to three datasets using similar setups. The generative model for the simulations is given in Fig. 2. For each dataset, we generate N = 10 sources from Laplacian distribution with T = 1000 independent and identically distributed (i.i.d.) samples. We select Laplacian distribution since it is a good match to fMRI data (Long et al., 2019). We introduce correlation to C = 3 sources from each dataset with correlation values 0.9,0.7 and 0.5, which means that across all datasets there are 3 common components and rest of the components are distinct. In our simulation results, we let 0.3 be the minimum correlation value to be satisfied for defining common components. This is a value that will be specific for each application and is expected to be determined by the user. These latent sources are then linearly mixed with mixing matrices with elements from a standard Gaussian distribution N(0, 1), where M is the even number of subjects from two groups—a healthy control group and a patient group—each with M/2 samples (subjects).
Figure 2:
Simulation model for two datasets to compare the relative performance of DS-ICA, MCCA-jICA, and jICA. Here, the datasets are designed in a way that a fixed number of components across the two datasets are common, and the rest of the components are distinct. In addition, one common and one distinct component are designed to be discriminative across the two groups, , i.e., healthy controls and patients.
To simulate group difference in the subjects, a step type response with step height 1.5 is added to the columns of the mixing matrices or profiles such that one profile from each dataset associated with a common component and a single profile from the second dataset associated with a distinct component show group differences. Thus, we have profiles a1(m) = v1(m) + 1.5u(m), m = 1,2, …, M for the first dataset and ai(m) = vi(m) + 1.5u(m), i = 1,4 and m = 1,2, …, M for the second dataset to discriminate between the two subject groups. Here, M is the even number of subjects, vi(m)’s are generated using standard Gaussian distribution and u(m) is the step response with . The standard deviation of other profiles are adjusted such that they match the standard deviation of the discriminant profiles for each case we consider. We refer to the components corresponding to these group discriminant profiles as discriminative components since they can be identified through a two sample t-test. We use true order 10 for dimensionality reduction resulting in for MCCA-jICA and DS-ICA, while for jICA. In addition to DS-ICA, we use MCCA-KPD to estimate the final common order of 3 for both two and three datasets. We evaluate the performance of each method by either changing the number of subjects or the step-height used to distinguish two subject groups. In the first case, the number of subjects is changed from 20 to 200 with step-height fixed to 1.5, while in the second case, the step-height is changed from 0.2 to 2—resulting in correlation values in the range [0.1 1]—with subject number fixed to 50. Since the datasets are generated assuming there are two subject groups, it is the column of the estimated mixing matrices (profiles) that report on the subjects’ covariations and can be used to identify the discriminative profiles. We use a two-sample t-test on the estimated profiles between the loadings of the two groups and use p < 0.05 as the threshold to identify the discriminative profiles. The components associated with these profiles are the estimated components that show differences between the healthy controls and the patients. We estimate the correlation values between the true and estimated discriminative components and use these correlation values to evaluate each method’s performance.
Fig. 3 compares the performance of DS-ICA with MCCA-jICA and jICA for (a) 2 datasets as well as (b) 3 datasets case. In both simulations, estimation performance improves as the number of subjects and step height increases. Additionally, as expected, we can see that two variations of DS-ICA, DS-ICA (MCCA) and DS-ICA (IVA-G), outperform the other two methods for estimation of both common and distinct discriminative components. From Fig. 3(a), jICA being the most conservative approach suffers most, especially for the estimation of common discriminative components. On the other hand, MCCA-jICA provides much better results for the common components but suffers in the estimation of the distinct ones because of the maximization of association in the prior MCCA step. DS-ICA makes the most efficient use of the available data by performing separate analyses and outperforms the other two methods for both common and distinct discriminative components. DS-ICA (IVA-G) slightly outperforms DS-ICA (MCCA) as IVA-G estimates association structure better than the MCCA. Similar patterns are present in the second set of simulation for 3 datasets shown in Fig. 3(b). As the number of datasets increase the problem gets even more challenging for all the methods. Nevertheless, both DS-ICA (MCCA) and DS-ICA (IVA-G) show performance similar to the 2 dataset case and outperforms the other two methods. Estimation performance of jICA and MCCA-jICA decreases even more for the distinct components as the model becomes more constrained with the increase of datasets in fusion.
Figure 3:
Estimation performance of discriminative components with different subject numbers and step-heights for (a) 2 datasets and (b) 3 datasets. Here, component correlation is the average correlation between the true and estimated components averaged over 100 independent runs.
4.2. Task fMRI data and features
The fMRI datasets used in this study are from the Mind Research Network Clinical Imaging Consortium Collection (Gollub et al., 2013) (publicly available at https://coins.trendscenter.org/). These datasets were collected from 247 subjects, 138 healthy individuals and 109 schizophrenia patients, while performing auditory oddball (AOD), Sternberg item recognition paradigm (SIRP) and sensory motor (SM) tasks. We introduce the tasks and extracted multivariate features next.
4.2.1. Auditory oddball task (AOD)
The AOD task required subjects to listen to three different types of auditory stimuli, standard (1 kHz tones with a probability of 0.82), novel (complex sounds with probability 0.09) and target (1.2 kHz tones with probability 0.09), coming in a pseudo random order and press a button only when the target stimuli arrive. A regressor was created to model the target related stimuli as a delta function convolved with the default SPM HRF and subject averaged contrast images of target tones were used as a feature for this task.
4.2.2. Sternberg item recognition paradigm task(SIRP)
The SIRP is a visual task that required subjects to memorize a set of 1, 3, or 5 integer digits randomly selected from 0 to 9. The task paradigm lasts for a total of 46 seconds including 1.5 seconds of learning, 0.5 seconds of blank screen, 6 seconds of encoding where the whole sequence of digits was presented together, and finally 38 seconds of probing where the subjects were shown a sequence of integers and then required to press a button whenever a digit from the memorized set arrives. For this task, regressor was created by convolving three-digit probe response block with SPM HRF and average map of both runs was used as a feature.
4.2.3. Sensory motor task(SM)
The SM tasks required subjects to listen to a series of 16 different auditory tones and to press a button every time the pitch of the tones changed. Each tone lasts for 200 ms and within the frequency range of 236 Hz to 1318 Hz. There was a 500 ms inter-stimulus interval between the tones. Each run consisted of 15 increase-and-decrease blocks, alternated with 15 fixation blocks, with each lasted for 16 seconds. For this task, regressor was created by convolving entire increaseand-decrease block with SPM HRF, and average map of both runs was used as a feature.
4.2.4. Algorithm and order selection
After extracting the features from each subject’s data, all 245 subjects data are concatenated vertically to form the feature dataset resulting , k = 1, 2, 3 for each task. To avoid overfitting due to the high noise level of medical imaging data, it is critical to determine the order of the signal subspace. Using entropy based method proposed in (Fu et al., 2014), which can take sample dependency in the data into account, the order of the signal subspace is estimated for each task feature dataset. We use an order N = 25 for all three datasets resulting , k = 1, 2, 3 for DS-ICA and MCCA-jICA and for jICA. Here, N = max(N1, N2, N3) and N1, N2 and N3 are the estimated orders of the feature datasets, selected to retain the maximum joint information across datasets. A practical way to test the stability of the estimated order is to check the stability of the estimated components for different orders around that number. We check the performance of the methods for a set of orders [15, 20, 25, 30, 35], in the range of ±10 of the estimated order. It is observed that the results are quite similar in terms of activation areas for 20 and 30, whereas the activation areas started to change for order 15 and 35. DS-ICA then further divide the datasets into common and distinct parts by using the order of the common signal subspace C. We use multiple techniques mentioned in Section 3.1 to estimate the common order, and all of them give us similar results in the range [7, 12]. In this study, we use a common order C = 10 resulting 10 common and 15 distinct components in each dataset. Since there is no ground truth, we select the final order using the guidance of the selection methods and the quality and the stability of the estimated results. Here, we use the statistical significance of the profiles and the interpretability of the estimated components as evaluation criteria to select the final order.
To be fair to all three methods, we use the same ICA algorithm, ICA-EBM, to estimate the final components (Li and Adalı, 2009). ICA-EBM has been shown to provide superior performance with both simulation and brain imaging data compare to the other popular ICA algorithms (Adalı et al., 2015a). This is due to the fact that ICA-EBM doesn’t assume a fix form of distribution for the underlying sources and rather try to achieve upper bound of the entropy by using some measuring functions (Li and Adalı, 2009). This provides ICA-EBM the flexibility to estimate components from a wide verity of distributions, improving the estimation performance of the method. To enable better reproducibility of the results, we run the algorithm multiple times and select a run that is most consistent and hence will lead to a reproducible decomposition. We run the algorithms 10 times and select the most consistent run using cross intersymbol interference (Cross-ISI) presented in (Long et al., 2018).
4.3. Results
A two sample t-test is used on the subject covariations or profiles to test for significant group difference (p < 0.05) between two subject groups. The associated components of those profiles that pass the tests are referred to as discriminative components or putative biomarkers of disease. Components showing group difference are then thresholded at Z = 2.7 and shown in Figs. 4 and 5. DS-ICA estimates both common and distinct components shown in Fig. 4. Due to the high number (75) of the estimated components, here we are only showing the discriminative components and their associated ones across datasets. Across all three datasets, common components estimated by DS-ICA show higher group differences between healthy controls and patients than the estimated distinct components. This is because all three tasks are closely related to each other, collected from the same group of subjects and collected using the same fMRI modality. Therefore, it is natural to estimate more common components that show higher significant group difference than distinct ones. The discriminative components in DS-ICA, in general, show higher activation in visual, motor, and sensory-motor areas for patients while showing higher activation in default mode network (DMN), auditory, and frontal-parietal region for healthy controls. All these areas are known to be associated with schizophrenia (Hu et al., 2017; Du et al., 2012) and therefore indicate meaningful decomposition results.
Figure 4:
Estimated common and distinct components by DS-ICA for AOD, SIRP and SM. We only show the components showing significant group differences and their common components across datasets due to the high number (75) of the estimated components. The color red, orange and yellow means higher activation in controls and blue means higher activation in patients. The discriminative components in DS-ICA, in general, show higher activation in visual, motor, and sensory-motor areas for patients while in default mode network (DMN), auditory, and frontal-parietal region for healthy controls.
Figure 5:
Estimated components by jICA and MCCA-jICA. Note that each column in the figure represents the components that are correlated across datasets. We are only showing the ones that are showing group difference (p < 0:05) or part of a set where at least a single component of that set is showing group difference.
AOD is known to be the more favorable task for identifying schizophrenia (Kiehl and Liddle, 2001; Kiehl et al., 2005; Demirci et al., 2009), resulting in a higher number of discriminant components than the other two tasks. For AOD, the common components in Fig. 4(a) show significant activations in auditory, motor, DMN, sensory-motor and frontal-parietal regions, whereas the distinct ones in Fig. 4(b) show activation in mostly auditory and motor regions. SIRP being the visual task, both common and distinct components show significant activations mostly on the visual and DMN regions. Common and distinct components in SM show significant activations in motor, sensory-motor, DMN and frontal-parietal regions. Being more similar tasks, AOD and SM share a higher number of common components showing group difference between healthy controls and patients (C#2, C#3, C#4, C#5, C#6, C#8), though the discrimination level (p-value) in most of the components is higher in AOD than SM, as observed in Fig. 4(a). For example, motor (C#5) and auditory (C#8) components show very high group differences (lower p-values) in AOD compared with the SM. On the other hand, the visual component (C#1) responsible for receiving, integrating, and processing visual information shows very high activations in SIRP compared with the other two tasks. This is because the SIRP task is designed to extract more visual features than the other two tasks. Only the DMN component (C#3), which is found to be associated with schizophrenia more often than any other components in many prior studies (Öngür et al., 2010; Whitfield-Gabrieli et al., 2009; Hu et al., 2017), is showing discrimination across all three task datasets.
In Fig. 4(b), distinct components in AOD are showing significant activations in part of the motor and auditory regions, whereas for SIRP and SM discriminative components show activations mostly in the visual and motor regions. Since AOD is an auditory task that requires motor movement from the subjects, estimating distinct components that show significant activations in the auditory and motor regions reflects on the background on which the task was performed. This is true for SIRP and SM datasets also. Note that these are the components that carry unique information about the tasks, and in classification problem can be used as features to identify one task from another.
Fig. 5 shows the components estimated by jICA and MCCA-jICA. Rather than finding the common and distinct components separately, both jICA and MCCA-jICA estimate components by assuming commonality across datasets, and thus neither method is optimized to capture the distinct information. From Fig. 5(a), activation patterns of the associated components in jICA are well formed and focal in one dataset, while distorted and less focal in the other two datasets. For example, the first set of components in jICA (#1) show well-formed activation in visual areas for SIRP task but scattered activations for AOD and SM tasks. That is also true for other estimated components that are showing activations in auditory, motor and DMN regions. This is due to the fact that jICA uses a single density function to estimate components and assumes a common mixing matrix across the datasets. MCCA-jICA on the other hand, relaxes the shared mixing matrix assumption by applying a prior MCCA step. MCCA maximizes the correlation across the datasets, thus align the components before jICA analysis. Components estimated by MCCA-jICA are therefore well formed and showing activations in meaningful areas in all three datasets as shown in Fig. 5(b). Similar to the common components in DS-ICA, components estimated in MCCA-jICA are showing activations in motor, sensory-motor and DMN regions for AOD, visual region for SIRP and sensory-motor and auditory regions for SM. However, because of the maximization of correlation of the datasets and joint analyses of all the components at the same time, MCCA-jICA loses the individual variations available in the data and estimates components showing activations in similar areas across all datasets. This also affects the p-values of the estimated components. Compared with the DS-ICA, where common and distinct components are estimated separately, p-values are much higher in MCCA-jICA for estimated components that are showing activation in similar areas, i.e., visual in SIRP or motor in AOD.
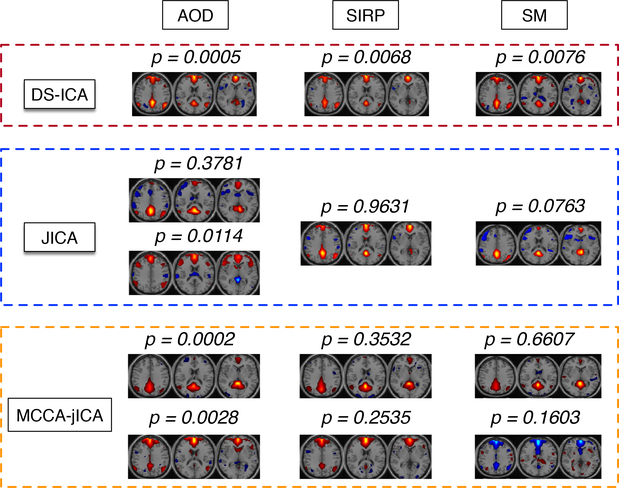
Fig. 6 shows a comparison of three fusion methods with respect to the estimated DMN components. Given the importance of the DMN as an important putative biomarker for schizophrenia (Öngür et al., 2010; Whitfield-Gabrieli et al., 2009; Hu et al., 2017), its robust estimation in all three datasets with more focal areas and higher group differences increases our confidence in the proposed method. On the other hand, most of the DMN components in jICA and MCCA-jICA are split into two components and do not show significant group difference. This example further shows the advantage of fully leveraging the statistical power of the data in the analysis using DS-ICA.
Figure 6:
Estimated DMN components by all three methods. Note that DMN components are more focal and show higher group difference in DS-ICA compared with the other two methods. In jICA and MCCA-jICA, most of the DMN components split into two components.
4.4. Classification procedure and results
We use the classification rate to evaluate the relative performance of different methods for different combination of datasets in a similar way given in (Levin-Schwartz et al., 2017). Since there is no ground truth for the underlying sources or profiles, using classification rate provides a natural way to compare the efficiency of each method to discriminate between healthy controls and patients. Note that our goal here is not to obtain a perfect classification rate, but instead to show performance advantage of fusion techniques over individual analysis for multitask fMRI data in the way they make use of joint information. Since all three methods we discuss here are based on ICA, we discuss the classification procedure for ICA first, and later extend it to multidataset fusion techniques. Considering , k = 1,2, …, K from (1), where K is the number of datasets and mth row of the each dataset is formed by extracting one multivariate feature from the mth subject. We randomly select 70% of subjects’ data to train and the rest 30% of the data to test the network. We keep a similar proportion of healthy controls and patients in all X, Xtrain, and Xtest datasets. Next, we reduce the Xtrain dataset dimension using PCA into an order specified in the previous section. We perform ICA-EBM on the reduced dimensional train datasets and perform a two sample t-test on each column of the estimated profile matrix to identify the profiles that shows significant group difference (p < 0.05). These profiles and their corresponding spatial maps are then formed into and respectively. We estimate by regressing onto to test the classifier. We train a radial basis kernel support vector machine (KSVM) (Cortes and Vapnik, 1995) using the columns of . The value of kernel parameters is selected by computing the average classification rate of 500 independent Monte-Carlo subsamplings of the data for different values and choosing the ones with the highest average classification rate. We perform a grid search of (C, γ) values from 10−3 to 103 and ended up selecting (1, 10). After finalizing the parameters, we perform the classification procedure on 300 independent Monte-Carlo samplings and report the average classification rate. A flow chart of the process is given in Fig. 7.
Figure 7:
Classification process for a single feature dataset. Training features are generated by selecting discriminatory features from ICA decomposition. is generated using linear regression of onto to test the classifier. The entire process is repeated N times and the average value of the classification rate is evaluated.
The process is similar for both jICA and MCCA-jICA, except the data matrix X is formed differently for these two, as described in the background section. For DS-ICA, computing the common and distinct components are done separately. We compute the group significant profiles separately and then concatenate them vertically to form . The associated brain spatial maps are concatenated horizontally to form . The rest of the process is similar to ICA. Note that the value of kernel parameter is selected for each method individually.
Fig. 8 shows the classification performance for each task dataset as well as their combinations. Fig. 8(a) shows the comparative results of different methods, while Fig. 8(b) compares the performance of the estimated common and distinct components in DS-ICA. There are many important messages to take away from Fig. 8. First, when analyzed separately, AOD obtains the highest classification score among the three task datasets. This indicates that AOD dataset carries information with more discriminatory power than the other two datasets.
Figure 8:
Average classification results using KSVM for individual datasets and their combinations using data fusion techniques. Fig. 8(a) compares the performance of jICA, MCCA-jICA and DS-ICA, while Fig. 8(b) compares the performance of DS-ICA using common and distinct components. Note that DS-ICA provides better classification performance compared with other two methods for different dataset combinations.
Second, from Fig. 8(a), classification rate improves as we move from single dataset to multidataset analyses. This is due to the fact that there is more discriminative power available in multi dataset combinations than any individual dataset. For example, when analyzing separately, the SM dataset results in the lowest classification performance, but combining SM with other two datasets, particularly with AOD, significantly improves the classification rate.
Third, among the three fusion techniques we consider in this study, DS-ICA provides better classification performance than the other two techniques. From Fig. 8(a), with DS-ICA being the most flexible method, it makes the best use of available information and achieves higher classification rate compared with jICA and MCCA-jICA for all possible dataset combinations. MCCA-jICA achieves better classification rate than jICA in almost all the scenarios except SIRP+SM, where jICA outperforms MCCA-jICA.
Finally, if the tasks are comparable with each other and the datasets share more common information, all three techniques show improvement in classification performance, which supports the advantage of multi dataset analysis. For example, combination of AOD and SM results in higher classification score than other combinations for all three techniques, whereas classification performance drops for SIRP+SM combination, especially for MCCA-jICA which prioritizes common information over distinct information.
Results shown in Fig. 8(b), which compares the performance of estimated common and distinct components in DS-ICA, also agree with this conclusion. Common components in DS-ICA lead to higher classification rates than distinct components in almost all dataset combinations except SIRP+SM, whereas distinct components yield better classification performance. This indicates that SIRP and SM datasets are more distinct in nature and when analyzed jointly provide less common information than other combinations. The similar classification performance of MCCA-jICA and jICA with common components in DS-ICA indicates the fact that both methods only take the common information in the datasets into account. DS-ICA, on the other hand, takes advantage of both common and distinct information and provides better classification performance than the other two methods, especially for the SIRP+SM combination where distinct information dominates.
5. Discussion
Multiple datasets collected for study of a given problem using different experimental conditions or modalities are expected to contain features that are common across datasets as well as features that are unique to each individual dataset. While fusing these connected datasets, traditional ICA-based methods typically emphasize the common or the shared information, disregarding the individual information available in the datasets. In this paper, we propose a new fusion method, DS-ICA, that can take advantage of not only of the common but also the distinct information available in the datasets. In addition, separating the common and the distinct subspaces prior to analysis allows a better model match to methods such as jICA, and also helps to reduce the dimensionality of the problem, allowing for more efficient estimation compared with methods like IVA. We show the performance advantages of DS-ICA over other ICA-based methods in simulations as well as in real multitask fMRI data collected from both healthy controls and patients with schizophrenia. Even though the focus of the current work is on the fusion of multitask fMRI data, DS-ICA model can be also used for the fusion of multimodal data, where datasets come from different modalities and hence are different in nature. Mathematical formulation of DS-ICA addressing multimodal data is given in Section 3.2.
Since DS-ICA separately estimates the common and distinct components and performs joint analysis only on the common subspace, it reduces the number of parameters to be estimated in the fusion analysis. Compared with jICA and MCCA-jICA, which estimate an N × N mixing matrix common to all, DS-ICA estimates a C ×C mixing matrix where C ≤ N. This reduced size single mixing matrix also helps DS-ICA with the interpretability of the estimated components, i.e., attaching physical meaning to the output results as common components. In a fusion scenario, where subjects’ data come from different experimental conditions or modalities, it is the variation across the subjects that connects the feature datasets across modalities (Adalı et al., 2018). Therefore, estimating a single mixing matrix only for the common components indicates that the subjects share a similar response to these components across the datasets. However, additional steps of order selection and subspace identification does make the DS-ICA computationally more expensive than both jICA and MCCA-jICA. DS-ICA uses IVA-G, which takes the SOS of the data into account, to identify and estimate the common and the distinct subspaces. It is important to note here that IVA, alone, can be also used to estimate the common and the distinct independent components. This is achievable by post processing the covariance matrices of the estimated SCVs (Long et al., 2020). However, IVA algorithms, especially the ones that use the higher or all order statistics (AOS), are computationally expensive and the number of parameters to be estimated increases proportionally with the number of datasets (Bhinge et al., 2019). For K datasets each with N sources, IVA jointly estimates K number of N ×N mixing matrices, a much greater number compared with the methods that use jICA for fusion where a single mixing matrix is estimated. Individual mixing matrices also make the IVA components harder to interpret, as there is no guarantee that components will share similar subject responses across the datasets.
While estimating the common subspace, it is possible to have sources that are correlated across all datasets as well as sources that are correlated in subsets of datasets. Depending on the common order used in the analysis, DS-ICA can identify partially correlated subspaces as well. However, it is important to note that identifying the complete correlation structure is a very difficult problem and the complexity level of the problem increases rapidly as the number of dataset increases. In this work, we only consider the subspace common to all to keep the problem simple. Here, we introduce DS-ICA as a general framework, and by extending the work to identify complete correlation structure such that multiple jICA can be performed in multiple common subsets is a useful and important future work.
6. Acknowledgement
This work was supported in part by NSF-CCF 1618551, NSF-NCS 1631838, and NIH R01 MH118695.
Footnotes
Declaration of competing interest
The authors declare no conflict of interest.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Adalı T, Akhonda MABS, Calhoun VD, 2018. ICA and IVA for data fusion: An overview and a new approach based on disjoint subspaces. IEEE Sensors Letters, 1–1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Adalı T, Anderson M, Fu G, 2014. Diversity in independent component and vector analyses: Identifiability, algorithms, and applications in medical imaging. IEEE Signal Processing Magazine 31, 18–33. [Google Scholar]
- Adalı T, Levin-Schwartz Y, Calhoun VD, 2015a. Multi-modal data fusion using source separation: Application to medical imaging. Proceedings of the IEEE 103, 1494–1506. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Adalı T, Levin-Schwartz Y, Calhoun VD, 2015b. Multi-modal data fusion using source separation: Two effective models based on ICA and IVA and their properties. Proceedings of the IEEE 103, 1478–1493. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Akhonda MABS, Levin-Schwartz Y, Bhinge S, Calhoun VD, Adalı T, 2018. Consecutive independence and correlation transform for multimodal fusion: Application to EEG and fMRI data, in: 2018 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), pp. 2311–2315. [Google Scholar]
- Akhonda MABS, Long Q, Bhinge S, Calhoun VD, Adalı T, 2019. Disjoint subspaces for common and distinct component analysis: Application to task FMRI data, in: 2019 53rd Annual Conference on Information Sciences and Systems (CISS), pp. 1–6. [Google Scholar]
- Anderson M, Adalı T, Li X, 2012. Joint blind source separation with multivariate Gaussian model: Algorithms and performance analysis. IEEE Transactions on Signal Processing 60, 1672–1683. [Google Scholar]
- Anderson M, Fu G, Phlypo R, Adalı T, 2014. Independent vector analysis: Identification conditions and performance bounds. IEEE Transactions on Signal Processing 62, 4399–4410. [Google Scholar]
- Bhinge S, Levin-Schwartz Y, Adalı T, 2017. Estimation of common subspace order across multiple datasets: Application to multi-subject fMRI data, in: 2017 51st Annual Conference on Information Sciences and Systems (CISS), pp. 1–5. doi: 10.1109/CISS.2017.7926123. [DOI] [Google Scholar]
- Bhinge S, Mowakeaa R, Calhoun VD, Adalı T, 2019. Extraction of time-varying spatiotemporal networks using parameter-tuned constrained iva. IEEE Transactions on Medical Imaging 38, 1715–1725. doi: 10.1109/TMI.2019.2893651. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Calhoun VD, Adalı T, Kiehl KA, Astur R, Pekar JJ, Pearlson GD, 2006a. A method for multitask fMRI data fusion applied to schizophrenia. Human Brain Mapping 27, 598–610. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Calhoun VD, Adalı T, 2009. Feature-based fusion of medical imaging data. IEEE Trans. Inf. Technol. Biomed. 13, 711–720. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Calhoun VD, Adalı T, 2012. Multisubject independent component analysis of fMRI: A decade of intrinsic networks, default mode, and neurodiagnostic discovery. IEEE Reviews in Biomedical Engineering 5, 60–73. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Calhoun VD, Adalı T, Giuliani NR, Pekar JJ, Kiehl KA, Pearlson GD, 2006b. Method for multimodal analysis of independent source differences in schizophrenia: Combining gray matter structural and auditory oddball functional data. Human Brain Mapping 27, 47–62. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Calhoun VD, Adalı T, Pearlson G, Kiehl K, 2006c. Neuronal chronometry of target detection: Fusion of hemodynamic and event related potential data. NeuroImage 30, 544–553. [DOI] [PubMed] [Google Scholar]
- Calhoun VD, Sui J, 2016. Multimodal fusion of brain imaging data: a key to finding the missing link (s) in complex mental illness. Biological psychiatry: cognitive neuroscience and neuroimaging 1, 230–244. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen W, Reilly JP, Wong KM, 1996. Detection of the number of signals in noise with banded covariance matrices. IEE Proceedings - Radar, Sonar and Navigation 143, 289–294. [Google Scholar]
- Cortes C, Vapnik V, 1995. Support-vector networks. Machine Learning 20, 273–297. [Google Scholar]
- Demirci O, Stevens MC, Andreasen NC, Michael A, Liu J, White T, Pearlson GD, Clark VP, Calhoun VD, 2009. Investigation of relationships between fMRI brain networks in the spectral domain using ICA and granger causality reveals distinct differences between schizophrenia patients and healthy controls. NeuroImage 46, 419–431. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Du W, Calhoun V, Li H, Ma S, Eichele T, Kiehl K, Pearlson G, Adalı T, 2012. High classification accuracy for schizophrenia with rest and task fMRI data. Frontiers in Human Neuroscience 6, 145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fu G, Anderson M, Adalı T, 2014. Likelihood estimators for dependent samples and their application to order detection. IEEE Transactions on Signal Processing 62, 4237–4244. [Google Scholar]
- Fujikoshi Y, Veitch LG, 1979. Estimation of dimensionality in canonical correlation analysis. Biometrika 66, 345–351. [Google Scholar]
- Gollub RL, Shoemaker JM, King MD, White T, Ehrlich S, Sponheim SR, Clark VP, Turner JA, Mueller BA, Magnotta V, O’Leary D, Ho BC, Brauns S, Manoach DS, Seidman L, Bustillo JR, Lauriello J, Bockholt J, Lim KO, Rosen BR, Schulz SC, Calhoun VD, Andreasen NC, 2013. The MCIC collection: a shared repository of multi-modal, multi-site brain image data from a clinical investigation of schizophrenia. Neuroinformatics 11, 367–388. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hasija T, Song Y, Schreier PJ, Ramírez D, 2016. Detecting the dimension of the subspace correlated across multiple data sets in the sample poor regime, in: 2016 IEEE Statistical Signal Processing Workshop (SSP), pp. 1–5. doi: 10.1109/SSP.2016.7551708. [DOI] [Google Scholar]
- Hirjak D, Rashidi M, Kubera KM, Northoff G, Fritze S, Schmitgen MM, Sambataro F, Calhoun VD, Wolf RC, 2020. Multimodal magnetic resonance imaging data fusion reveals distinct patterns of abnormal brain structure and function in catatonia. Schizophrenia bulletin 46, 202–210. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hu M, Zong X, Mann JJ, Zheng J, Liao Y, Li Z, He Y, Chen X, Tang J, 2017. A review of the functional and anatomical default mode network in schizophrenia. Neuroscience Bulletin 33, 73–84. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jacob M, Ford J, Roach B, Calhoun V, Mathalon D, 2017. 145. semantic priming abnormalities in schizophrenia: An ERP-fMRI fusion study. Schizophrenia bulletin 43, S76. [Google Scholar]
- James AP, Dasarathy BV, 2014. Medical image fusion: A survey of the state of the art. Information Fusion 19, 4–19. [Google Scholar]
- Kettenring JR, 1971. Canonical analysis of several sets of variables. Biometrika 58, 433–451. [Google Scholar]
- Kiehl KA, Liddle PF, 2001. An event-related functional magnetic resonance imaging study of an auditory oddball task in schizophrenia. Schizophrenia Research 48, 159–171. doi: 10.1016/S0920-9964(00)00117-1. [DOI] [PubMed] [Google Scholar]
- Kiehl KA, Stevens MC, Celone K, Kurtz M, Krystal JH, 2005. Abnormal hemodynamics in schizophrenia during an auditory oddball task. Biological Psychiatry 57, 1029–1040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lahat D, Adalı T, Jutten C, 2015. Multimodal data fusion: An overview of methods, challenges, and prospects. Proceedings of the IEEE 103, 1449–1477. [Google Scholar]
- Leeb R, Sagha H, Chavarriaga R, del. R. Millon J, 2010. Multimodal fusion of muscle and brain signals for a hybrid-BCI, in: 2010 Annual International Conference of the IEEE Engineering in Medicine and Biology, pp. 4343–4346. [DOI] [PubMed] [Google Scholar]
- Levin-Schwartz Y, Calhoun VD, Adalı T, 2017. Quantifying the interaction and contribution of multiple datasets in fusion: Application to the detection of schizophrenia. IEEE Transactions on Medical Imaging 36, 1385–1395. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Levin-Schwartz Y, Song Y, Schreier PJ, Calhoun VD, Adalı T, 2016. Sample-poor estimation of order and common signal subspace with application to fusion of medical imaging data. NeuroImage 134, 486–493. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li X, Adalı T, 2009. A novel entropy estimator and its application to ICA, in: IEEE International Workshop on Machine Learning for Signal Processing (MLSP), pp. 1–6. [Google Scholar]
- Liu J, Pearlson G, Windemuth A, Ruano G, Perrone-Bizzozero NI, Calhoun VD, 2009. Combining fMRI and SNP data to investigate connections between brain function and genetics using parallel ICA. Human Brain Mapping 30, 241–255. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu S, Wang H, Song M, Lv L, Cui Y, Liu Y, Fan L, Zuo N, Xu K, Du Y, Yu Q, Luo N, Qi S, Yang J, Xie S, Li J, Chen J, Chen Y, Wang H, Guo H, Wan P, Yang Y, Li P, Lu L, Yan H, Yan J, Wang H, Zhang H, Zhang D, Calhoun VD, Jiang T, Sui J, 2019. Linked 4-way multimodal brain differences in schizophrenia in a large chinese han population. Schizophrenia bulletin 45, 436–449. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lock EF, Hoadley KA, Marron JS, Nobel AB, 2013. Joint and individual variation explained (JIVE) for integrated analysis of multiple data types. The annals of applied statistics 7, 523. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Long Q, Bhinge S, Calhoun VD, Adalı T, 2020. Independent vector analysis for common subspace analysis: Application to multi-subject fmri data yields meaningful subgroups of schizophrenia. NeuroImage, 116872. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Long Q, Bhinge S, Levin-Schwartz Y, Boukouvalas Z, Calhoun VD, Adalı T, 2019. The role of diversity in data-driven analysis of multi-subject fMRI data: Comparison of approaches based on independence and sparsity using global performance metrics. Human brain mapping 40, 489–504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Long Q, Jia C, Boukouvalas Z, Gabrielson B, Emge D, Adalı T, 2018. Consistent run selection for independent component analysis: Application to fMRI analysis, in: 2018 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), pp. 2581–2585. [Google Scholar]
- Mangalathu-Arumana J, Beardsley S, Liebenthal E, 2012. Within-subject joint independent component analysis of simultaneous fMRI/ERP in an auditory oddball paradigm. NeuroImage 60, 2247–2257. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mangalathu-Arumana J, Liebenthal E, Beardsley SA, 2018. Optimizing within-subject experimental designs for jICA of multi-channel ERP and fMRI. Frontiers in neuroscience 12, 13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mijović B, De Vos M, Vanderperren K, Machilsen B, Sunaert S, Van Huffel S, Wagemans J, 2014. The dynamics of contour integration: A simultaneous EEG–fMRI study. NeuroImage 88, 10–21. [DOI] [PubMed] [Google Scholar]
- Öngür D, Lundy M, Greenhouse I, Shinn AK, Menon V, Cohen BM, Renshaw PF, 2010. Default mode network abnormalities in bipolar disorder and schizophrenia. Psychiatry Research: Neuroimaging 183, 59–68. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Savopol F, Armenakis C, 2002. Merging of heterogeneous data for emergengy mapping: Data integration or data fusion?, in: International Archives of Photogrammetry Remote Sensing and Spatial Information Sciences, Presented at 34th Conference for International Society for Photogrammetry and Remote Sensing (ISPRS), Ottawa, Canada. pp. 668–674. [Google Scholar]
- Schouteden M, Van-Deun K, Wilderjans TF, Van-Mechelen I, 2014. Performing DISCO-SCA to search for distinctive and common information in linked data. Behavior Research Methods 46, 576–587. [DOI] [PubMed] [Google Scholar]
- Seghouane A, Shokouhi N, 2019. Estimating the number of significant canonical coordinates. IEEE Access 7, 108806–108817. [Google Scholar]
- Smilde AK, Måge I, Naes T, Hankemeier T, Lips MA, Kiers HA, Acar E, Bro R, 2017. Common and distinct components in data fusion. Journal of Chemometrics 31, e2900. [Google Scholar]
- Song Y, Hasija T, Schreier PJ, Ramírez D, 2016. Determining the number of signals correlated across multiple data sets for small sample support, in: 2016 24th European Signal Processing Conference (EUSIPCO), pp. 1528–1532. [Google Scholar]
- Song Y, Schreier PJ, Roseveare NJ, 2015. Determining the number of correlated signals between two data sets using PCA-CCA when sample support is extremely small, in: 2015 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), pp. 3452–3456. [Google Scholar]
- Sui J, Adalı T, Pearlson G, Yang H, Sponheim SR, White T, Calhoun VD, 2010. A CCA+ICA based model for multi-task brain imaging data fusion and its application to schizophrenia. NeuroImage 51, 123–134. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sui J, Castro E, He H, Bridwell D, Du Y, Pearlson GD, Jiang T, Calhoun VD, 2014. Combination of FMRI-SMRI-EEG data improves discrimination of schizophrenia patients by ensemble feature selection, in: 2014 36th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, pp. 3889–3892. [DOI] [PubMed] [Google Scholar]
- Sui J, He H, Pearlson GD, Adali T, Kiehl KA, Yu Q, Clark VP, Castro E, White T, Mueller BA, Ho BC, Andreasen NC, Calhoun VD, 2013a. Three-way (n-way) fusion of brain imaging data based on mCCA+jICA and its application to discriminating schizophrenia. NeuroImage 66, 119–132. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sui J, He H, Yu Q, chen J, Rogers J, Pearlson G, Mayer A, Bustillo J, Canive J, Calhoun V, 2013b. Combination of resting state fMRI, DTI, and sMRI data to discriminate schizophrenia by n-way MCCA+jICA. Frontiers in Human Neuroscience 7, 235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vergara VM, Ulloa A, Calhoun VD, Boutte D, Chen J, Liu J, 2014. A three-way parallel ica approach to analyze links among genetics, brain structure and brain function. Neuroimage 98, 386–394. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Whitfield-Gabrieli S, Thermenos HW, Milanovic S, Tsuang MT, Faraone SV, McCarley RW, Shenton ME, Green AI, Nieto-Castanon A, LaViolette P, Wojcik J, Gabrieli JDE, Seidman LJ, 2009. Hyperactivity and hyperconnectivity of the default network in schizophrenia and in first-degree relatives of persons with schizophrenia. Proceedings of the National Academy of Sciences 106, 1279–1284. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu Y, Tam K, Li F, 2002. Determination of number of sources with multiple arrays in correlated noise fields. IEEE Transactions on Signal Processing 50, 1257–1260. doi: 10.1109/TSP.2002.1003051. [DOI] [Google Scholar]