Leveraging item accuracy and reaction time to improve measurement of child executive function ability

Abstract

Traditionally, executive function tasks (EF) have been scored using either accuracy or reaction time (RT) metrics. The current study, which includes 1015 1^st grade children from the Family Life Project, demonstrates a new scoring approach for the Hearts and Flowers (HF) task that uses both item-level accuracy and RT data to estimate latent EF ability. Our primary aim was to compare scores derived from this approach to standard scores often reported in the HF literature. A second aim was to test whether item-level accuracy and RT data were differentially related to latent EF ability, depending on children’s overall level of task performance. Our results indicated that item-level accuracy and RT data both convey unique information related to latent EF ability but that the relative contributions of each source of data vary across children. Accuracy was comparatively more informative of latent ability in children with lower HF task performance, while RT was comparatively more informative of latent ability in children with higher overall performance. Moreover, item-level RT was differentially related to latent EF ability for children in lower versus higher performing groups. Whereas faster responding was associated with higher ability in the higher performing group, slower responding was associated with higher ability for the lower performing group. Latent EF ability was related to criterion measures in ways comparable to traditional scores. Results are discussed in relation to the broader EF assessment literature.

Executive functions (EF) refers to a set of higher-order cognitive abilities that enable individuals to engage in planful, goal-directed behavior (Blair & Ursache, 2011). EF follows a protracted developmental time course, with a rapid period of development in the preschool years followed by more modest gains throughout childhood and into adulthood (Garon, Bryson, & Smith, 2008). Researchers are increasingly interested in the contributions of childhood EF to other domains of child functioning, including school readiness (Willoughby, Magnus, Blair, & Vernon-Feagans, 2016), academic achievement (Blair & Razza, 2007), and internalizing and externalizing behavior problems (Snyder, Miyake, & Hankin, 2015). Despite this wide interest, there are methodological concerns regarding the use of performance-based measures of EF ability, which may limit our ability to estimate the true role of EF in children’s development.

A primary problem concerns a lack of consensus across studies on preferred metrics of task performance (Camerota, Willoughby, & Blair, 2019). With the introduction of computerized EF assessments, both accuracy and reaction time (RT) data are now available for researchers to use to summarize an individual’s performance. Some common EF task scores include mean accuracy (e.g., proportion or percent correct) or mean RT (e.g., average RT across all correct items). Within RT metrics, some researchers use RT difference scores (ΔRT), which represent changes in speed in response to items that make executive demands (e.g., on a task block that requires cognitive flexibility or inhibitory control), compared to speed on items that do not make those demands (e.g., on a familiarization or baseline block). Although some studies report findings using both accuracy and RT metrics (e.g., Blair & Raver, 2014; Lakes et al., 2013; Schonert-Reichl et al., 2015), other studies use either accuracy (e.g., Diamond, Barnett, Thomas, & Munro, 2007) or RT (e.g., Ursache & Raver, 2015). However, both of these approaches have their limitations. Using accuracy and RT separately as independent or dependent variables raises the issue of how to reconcile divergent patterns of findings. For example, if significant associations are found for either accuracy or RT, but not both, it may be difficult to draw conclusions about the relationship of EF to other substantive variables. One might circumvent this problem by using either accuracy or RT, but this strategy requires researchers to make a-priori or post-hoc decisions about which metric of performance to use. Although some have postulated (Diamond et al., 2007; Diamond & Kirkham, 2005) that RT is the preferred metric of performance in older children or adults, or once accuracy exceeds a certain threshold or lacks variability, this recommendation has yet to be empirically tested or adopted.

Joint Models for EF Task Scoring

An alternative approach, which has the potential to reduce the issue of arbitrary task score selection, involves yoking together speed and accuracy data to create a single measure of child EF ability. Some applied researchers have taken an informal approach to creating single task scores from accuracy and RT data. One noteworthy example comes from the NIH Toolbox Cognitive Battery (comprised of Dimensional Change Card Sort [DCCS] and Flanker tasks), which takes a “two-vector approach” to task scoring (Zelazo et al., 2013). Individuals are first assigned a score of 0 to 5 based on their accuracy (i.e., by applying a fixed-point value to each correct response). Then, individuals demonstrating a high level of accuracy (≥ 80%) receive a second score that also ranges from 0 to 5, based on their median, log-transformed, and windsorized RT across items. These two scores are added together to yield a score ranging from 0 to 10 for highly accurate individuals. For less accurate individuals (< 80%), their total task scores range from 0 to 5, and only incorporate information about their accuracy.¹ Although this approach jointly makes use of accuracy and RT data, it is based on a series of untested assumptions, such as the threshold of accuracy above which RT is informative, the equal weighting of each item, and the equal weighting of accuracy and RT information. Recent work calls into question some of these assumptions (Camerota et al., 2019; Magnus, Willoughby, Blair, & Kuhn, 2017), necessitating a more sophisticated approach.

In the psychometric literature, there are a number of models that have been proposed for analyzing response accuracy, RT, or both (for recent reviews, see De Boeck & Jeon, 2019; Kyllonen & Zu, 2016). These modeling techniques fall into two broad categories: one that estimates separate models for response accuracy and response time (e.g., Maris, 1993; Rasch, 1960; Scheiblechner, 1979) and another that estimates joint models to simultaneously account for parallel accuracy and RT data (e.g., Roskam, 1987; Thissen, 1983; van der Linden, 2007). For example, Thissen’s (1983) model incorporates an item response model for accuracy into a regression model for (log) response time. Using a somewhat different approach, van der Linden (2007) jointly models response accuracy and response time within a multilevel modeling framework, in which separate measurement models for latent ability and latent speed are specified at the lower level and then integrated into a higher-level model that accounts for the correlation between these latent variables. It is this latter class of models – the joint modeling of accuracy and speed – that is the focus of the current investigation, as it more closely aligns with our goal of combining accuracy and RT data to create a single EF task score.

We are aware of only one study that has applied a joint model to EF task data (Magnus et al., 2017). In this study, researchers fit a “bi-factor-like” model (Cai, Yang, & Hansen, 2011) to accuracy and RT data from a number of inhibitory control (IC) tasks in a preschool-aged sample. Their model is a bi-factor confirmatory factor analysis (CFA) model that can be fit within traditional structural equation modeling (SEM) software. The model (Figure 1a) includes two orthogonal factors: an EF ability factor that is defined by item accuracy and a general speed factor that is defined by item RT. Importantly, item RT additionally loads onto the EF ability factor. This factor structure effectively parcels the variance in RT into that which is indicative of speed, and that which is indicative of ability. The authors found that their enhanced scores (e.g., those that made use of both accuracy and RT) increased the measurement precision of child IC ability and reduced floor and ceiling effects, as compared to task scores that were based solely on accuracy (Magnus et al., 2017).

Figure 1.

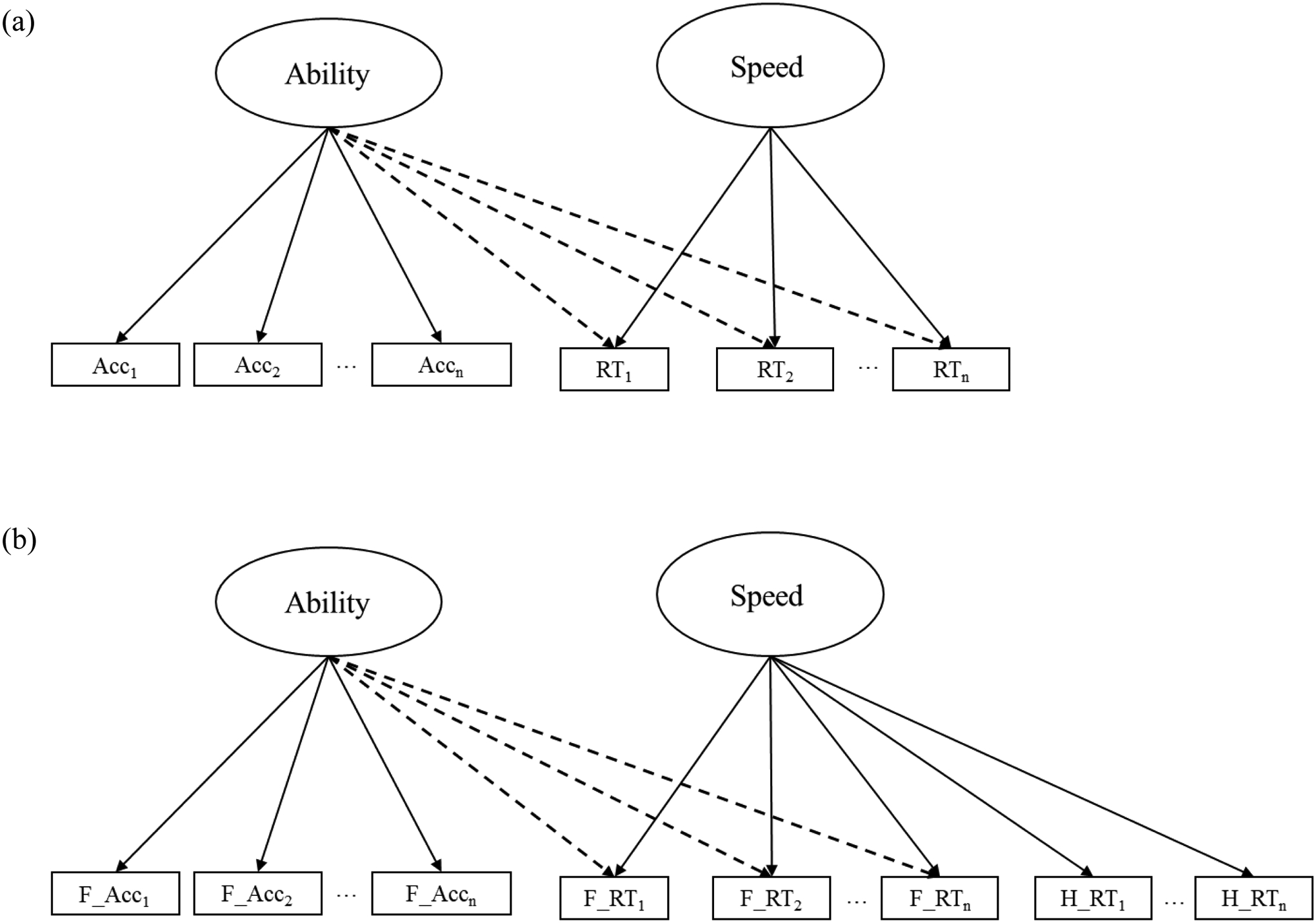
The bi-factor-like model (a) as previously estimated in studies of child EF (adapted from Magnus, Willoughby, Blair, & Kuhn, 2017) and (b) as estimated in the current study. RT = reaction time; Acc = accuracy; F = flowers block; H = hearts block;

The bi-factor-like model (henceforth referred to as the bi-factor model) therefore represents a novel scoring approach for EF task data that has demonstrated benefits over traditional scoring approaches. From a psychometric perspective, there are additional reasons to prefer the bi-factor model over other scoring approaches (e.g., mean accuracy or RT scores). For one, the factor loadings of each accuracy and RT item are freely estimated, rather than assumed to be equal. Given that different items are likely to be differentially informative of child speed and ability, this modeling approach appropriately captures this heterogeneity. Additionally, the degree to which accuracy and RT are indicative of ability can be empirically estimated and compared, rather than assumed to be equal, as in other approaches that have attempted to combine speed and accuracy (e.g., Zelazo et al., 2013). Finally, the CFA framework affords additional precision to task scoring, as latent estimates of speed and ability are purged of measurement error, an advantage that traditional mean scores (e.g., mean of accuracy items) do not have.

Despite these strengths, the bi-factor model has not been widely adopted as a scoring approach for EF data in children. One reason for this may be that the approach has yet to be replicated and extended to other EF tasks, or to older children. Therefore, our first aim is to fit a bi-factor model to data from a popular EF task collected in elementary-aged children. The Hearts and Flowers (HF) task is an adaptation of the Dots task that has been shown to be appropriate for use with children, adolescents, and adults (Davidson, Amso, Anderson, & Diamond, 2006). The task requires participants to press a spatially-congruent button (i.e., on same side of screen) when they see a heart stimulus, but to press a spatially-incongruent button (i.e., on opposite side of screen) when they see a flower stimulus. There are three blocks of items: congruent-only (i.e., hearts), incongruent-only (i.e., flowers), and mixed (i.e., hearts and flowers). The hearts block is often used as a baseline measure of response time due to its lack of executive demands. The flowers block is thought to more strongly tax inhibitory control, whereas the mixed block is thought to tap cognitive flexibility (Wright & Diamond, 2014). Working memory is inherently involved in all blocks, due to the need to hold the different rules in mind (Diamond, 2013). Although the HF task generates scores for both accuracy and RT, an unanswered question is the extent to which these two metrics are informative of underlying EF ability in children. Thus, we will fit the bi-factor model to HF task data and compare the contributions (e.g., factor loadings) of accuracy and RT to latent EF ability.

An important difference between the HF task used in this study and the IC tasks used in previous studies (e.g., Magnus et al., 2017) is that the HF task contains a baseline block of items (i.e., the hearts block) which similarly generates RT data. One traditional scoring approach involves subtracting hearts RT from flowers or mixed block RT to generate ΔRT scores. These ΔRT scores therefore represent the slowing down that occurs between baseline and EF-demanding blocks. In the current study, we will use RT from hearts items as additional indicators of our latent speed factor (Figure 1b). We hypothesize that the inclusion of additional reference items for latent speed will enhance our ability to parse EF-related variance from flowers and mixed RT.

Heterogeneity in Model Parameters Based on Child Ability

A related aim of this study is to determine whether accuracy and RT data are equally informative for children of different ability levels. As discussed earlier, a commonly-held assumption is that accuracy is the preferred metric of performance for younger children, or any group of individuals for whom average accuracy is low and variable (Diamond et al., 2007). Once the mean accuracy of a group approaches ceiling level, or fails to demonstrate variability, then RT (or RT difference scores) become the preferred metric of performance (e.g., Ursache & Raver, 2015). Users of these scoring guidelines implicitly assume that RT only becomes informative above a certain level of accuracy. This assumption has found some empirical support. For example, in our previous work, we established that accuracy and RT on the HF task interact to predict child academic and behavioral outcomes, such that RT is only informative when child accuracy exceeds a certain threshold (i.e., approximately 75%; Camerota et al., 2019). Given this finding, we might expect to see differential associations of item-level accuracy and RT to latent EF ability for children who perform better or worse on the HF task, compared to their peers. For example, children who find the HF task particularly challenging may differentially allocate cognitive resources to responding accurately versus responding quickly, whereas children who find the HF task easier may be able to maintain a high level of accuracy and respond quickly.

This distinction is supported by research showing that children of different ages and abilities use different strategies to maximize performance on EF tasks (Chevalier, James, Wiebe, Nelson, & Espy, 2014; Chevalier, Martis, Curran, & Munakata, 2015; Chevalier, Wiebe, Huber, & Espy, 2013). For example, researchers who study cognitive control make a distinction between the use of proactive (i.e., in anticipation of a stimulus) and reactive (i.e., responding after presentation of a stimulus) control strategies. Although the former is more efficient, young children are rarely able to demonstrate proactive control due to their more limited cognitive resources (Chevalier et al., 2015). However, children tend to shift from using reactive to proactive control around 6 years of age (e.g., Chevalier et al., 2014), suggesting that quantitative increases in EF across the early years may give rise to later qualitative shifts in EF strategy use, beginning around the transition to first grade. Given that the current study also includes children in this age group, a second aim is to test whether there are differences in the contributions of accuracy and RT to ability for children who perform relatively better or worse on the HF task. Consistent with our previous research (Camerota et al., 2019), we hypothesize that RT will be a stronger indicator of ability for children who perform with higher accuracy on the HF task.

Comparison of Enhanced and Traditional Task Scores

Finally, an overarching hypothesis is that incorporating information from both accuracy and RT will increase the precision by which we measure children’s EF ability. Using latent ability estimates derived from the bi-factor scoring models, we will test this hypothesis by descriptively and visually comparing our new ability scores to traditional scores (i.e., percent correct, ΔRT scores). We will also compare the predictive ability of new and traditional scores using several established criterion measures. These include child academic ability (Blair & Razza, 2007; Brock, Rimm-Kaufman, Nathanson, & Grimm, 2009; Bull & Scerif, 2001; Espy et al., 2004; Willoughby, Kupersmidt, Voegler-Lee, & Bryant, 2011) and ADHD symptomatology (Pauli-Pott & Becker, 2011), given that their relationship with EF has been well-documented.

The Current Study

The current study is therefore motivated by three aims. First, we will test an alternative scoring approach for the HF task, one which we believe has psychometric benefits over traditional scoring approaches. Although there is some preliminary evidence that joint accuracy and RT models have benefits for EF task scoring (Magnus et al., 2017), we will test this assertion in a large sample of children, using a task that is popular in the EF literature. We will interpret model coefficients regarding the contributions of accuracy and RT to latent estimates of child ability. We will also compare traditional (i.e., accuracy, ΔRT) and enhanced (i.e., bi-factor model factor scores) task scores to one other and to criterion measures, to determine whether our new scoring approach has advantages over traditional task scores. Finally, we will repeat these analyses separately for children who exhibit high versus low performance on the HF task, in order to compare the relative contributions of accuracy and RT to EF ability in these two groups.

Methods

Participants

The Family Life Project (FLP) is a longitudinal investigation of children and families residing in two regions with high rural poverty rates in North Carolina (NC) and Pennsylvania (PA). Families residing in target counties were recruited using a stratified random sampling approach yielding a representative sample of 1,292 families recruited over a one-year period (September 2003 through September 2004). Low-income families in both states and African-American families in NC were oversampled to ensure adequate power to test central research questions. Additional details about study sampling and recruitment procedures can be found elsewhere (Vernon-Feagans, Cox, Willoughby, Burchinal, & Garrett-Peters, 2013).

The current analyses were conducted using a subsample of children who had data from the Hearts and Flowers (HF) task at first-grade (N = 1015; M_age = 87.4 months, SD = 4.0 months). 51% of children in this subsample were male, 44% were African-American, and 78% of families were poor (< 200% of the poverty level) at the time of recruitment. This subsample does not differ from the full FLP sample in terms of child race, gender, research site (NC or PA), or poverty status at recruitment. All data collection activities were approved by the appropriate ethical review boards, and informed consent and assent were obtained from all study participants.

Measures

Focal data for these analyses are drawn from one home visit and one school visit conducted when children were in their second year of formal schooling. For the majority (93%) of children, this visit corresponded to the first grade and is therefore referred to as the first-grade visit. At the home visit, parents and children completed individual and dyadic activities, including parent-child interaction tasks and a computerized assessment of child EF ability. At the school visit, children completed assessments of their math and reading ability and teachers provided ratings of children’s Attention Deficit/Hyperactivity Disorder (ADHD) symptoms.

Executive Function

Executive function was measured using the Hearts and Flowers task (Davidson et al., 2006). On each trial, children were presented with a picture of a heart or a flower on one side of a laptop screen. They were instructed to press the keyboard button on the same side as the picture when the picture was a heart (congruent), but to press the keyboard button on the opposite side as the picture when the picture was a flower (incongruent). Children completed instructional and practice trials, which were repeatable up to three times to ensure they understood task demands. Practice trials were followed by 12 hearts-only trials, 12 flower-only trials, and 33 mixed trials. Stimuli were presented for up to 2500 ms (depending on whether a response was made) and advanced to the next trial following an interstimulus interval of 1000 ms. Accuracy and RT were measured for each individual trial. Consistent with previous studies (e.g., Davidson et al., 2006; Ursache & Raver, 2015), anticipatory responses (RT < 200 ms) were set to missing for both accuracy and RT metrics, as these responses occurred too fast to be in response to the stimulus. In addition, RT for incorrect responses was set to missing. Children who responded to at least 75% of trials were considered to have valid HF data.

Individual item accuracy and RT data were retained for use in latent scoring models. In addition, we calculated ‘traditional’ summary scores representing mean accuracy and RT difference (ΔRT) for each block, using conventions from the HF literature. Accuracy scores represented the proportion of correct responses (e.g., correct responses divided by sum of correct and incorrect responses). Similarly, the mean reaction time (RT) of correct responses was calculated for each block. Subsequently, we calculated two RT difference scores (ΔRT) by subtracting individuals’ mean RT on the heart-only block from their mean RT on the flower-only block (i.e., RT_flower – RT_heart) and mixed block (i.e., RT_mixed – RT_heart). These ΔRT scores represented the slowing due to increased inhibitory control and cognitive flexibility demands, respectively. Four summary measures (accuracy and ΔRT for flower-only and mixed blocks) were retained.

ADHD Symptom Ratings

Teachers rated child ADHD symptoms at the first-grade visit. Each of the 18 DSM-IV symptoms for ADHD were rated on a 4-point scale: 0 (not at all), 1 (just a little), 2 (pretty much), and 3 (very much). Following convention for use of this measure (Pelham, Gnagy, Greenslade, & Milich, 1992), items that were rated as either “pretty much” or “very much” (i.e., scores of 2 or 3) were considered an approximation for symptom endorsement. The total ADHD symptom score was used.

Math and Reading Ability

Child math and reading ability were assessed using the Woodcock-Johnson III (WJ III) Tests of Achievement, a normed set of tests measuring cognitive abilities, scholastic aptitude, and academic achievement. Math ability was indexed using the Applied Problems (AP) subtest in which children are asked to solve mathematical word problems. Reading ability was assessed using the Letter–Word Identification (LW) subtest, in which children are asked to identify letters and read words of increasing difficulty. We used standard scores for each subtest as outcome measures. All WJ III subtests have been shown to demonstrate high levels of reliability and validity (Woodcock, McGrews, & Mather, 2001).

Analytic Plan

Data analysis proceeded in four steps. First, we applied a bi-factor model to item-level accuracy and RT data, separately for the flowers and mixed blocks of the HF task (see Figure 1b for a schematic representation of the flowers model). Models were run separately in order to derive estimates of inhibitory control and cognitive flexibility, respectively. We used item-level logged RTs as continuous indicators of latent speed, and dichotomous accuracy as indicators of latent ability. Consistent with the parameterization of the bi-factor model, item-level RT also loaded on latent EF ability. As mentioned previously, this cross-loading enables accuracy and RT data to jointly inform estimates of latent ability. Finally, given that additional RT data were available from the hearts-only block (12 items), a baseline block that does not rely on executive ability, hearts RT items were included in all models as additional indicators of the latent speed variable.² In all models, EF ability and speed were constrained to be orthogonal, and the means and variances of both factors were set to 0 and 1, respectively, to enable model identification.

Mplus scripts for the flowers and mixed models are provided in Appendix A. All models were estimated using maximum likelihood (ML) with robust standard errors (Muthén & Muthén, 2017). ML was chosen over alternative estimators (e.g., weighted least squares) because it provides more stable estimates in models with many items, and unlike other estimators, it makes use of all information available in the response pattern (Wirth & Edwards, 2007). Because ML is a full information estimator, it is also better-equipped to handle missing data, which was particularly relevant to the current investigation, as there were varying levels of systematic missingness for both responses (e.g., due to skipped items or RT < 200ms) and RT (e.g., due to incorrect responses or RT < 200ms).

We first estimated bi-factor scoring models for the flowers and mixed blocks, using data from the entire sample. We provide and interpret the results from these two models. Next, we compared traditional scores to the enhanced EF scores that resulted from the bi-factor models. To do this, we first exported factor scores from the flowers and mixed models. For categorical variables and the ML estimator, Mplus estimates factor scores as the mean of the posterior distribution of the likelihood for each response pattern, assuming that the latent variable is normally distributed in the population. This is known as the expected a posteriori (EAP) method. We analytically and visually compared our enhanced ability scores (i.e., latent ability from flowers and mixed models) to traditional scores (i.e., accuracy and ΔRT from flowers and mixed blocks) using correlations and scatterplots. We also related task scores to our set of criterion measures (ADHD symptoms, math and reading ability) and used Fisher’s r-to-z transformations (Lee & Preacher, 2013) to compare the magnitude of correlations (|r|) of enhanced and traditional scores with criterion measures. These comparisons were conducted in SAS 9.4.

Finally, to determine whether the contributions of accuracy and RT to ability change depending on child EF performance, we re-estimated the two models separately for high and low performing children and compared their factor loadings. Our definition of high and low performing was based on a median split of accuracy on all test (i.e., flowers and mixed) trials (median = 87%; N_low = 517; N_high = 498). We repeat all analyses described above in these two subgroups, including exporting and comparing factor scores to traditional scores.

Results

Descriptive Statistics

Overall, accuracy was highest on the hearts items (M = .97; range = .94 to .99) and lowest on the mixed items (M = .80; range = .63 to .90), with flower accuracy falling in the middle (M = .87; range = .75 to .91). Mean RT showed a similar trend, with children tending to be fastest in responding to the hearts items (M = 611 ms; range = 519 to 717 ms) and slowest in responding to mixed items (M = 1161 ms; range = 942 to 1269 ms), with flowers RT falling in the middle (M = 849 ms; range = 715 to 1056 ms). These findings suggest that hearts items do not tap executive abilities, since children scored nearly at ceiling for all items, and tended to respond quickly. Item-level accuracy and RT for all blocks are presented in Appendix B.

Latent Variable Models (Full Sample)

First, we estimated the bi-factor model for the flowers and mixed blocks in the total sample. Descriptive statistics summarizing factor loadings from these models are displayed in the left hand columns of Table 1.

Table 1.

Summary of standardized factor loadings from group-based scoring models

	Full sample N = 1015				Low performing N = 517				High performing N = 498
Factor Loading (β)	Mean	SD	Min	Max	Mean	SD	Min	Max	Mean	SD	Min	Max
Flowers
EF by Accuracy	.66	.09	.50	.81	.63	.13	.40	.84	.20	.17	−.11	.44
EF by RT	−.40	.06	−.51	−.33	−.34	.12	−.56	−.19	−.43	.07	−.53	−.31
SPEED by RT (F)	.50	.06	.35	.58	.51	.07	.40	.61	.50	.07	.29	.56
SPEED by RT (H)	.70	.06	.58	.76	.70	.06	.57	.75	.71	.06	.60	.77
Mixed
EF by Accuracy	.39	.14	.02	.60	.55	.42	−.35	1.23	.07	.17	−.35	.38
EF by RT	.47	.08	.34	.66	.23	.05	.14	.35	−.46	.05	−.57	−.34
SPEED by RT (X)	.50	.04	.42	.58	.18	.03	.12	.24	.37	.04	.29	.45
SPEED by RT (H)	.69	.06	.57	.76	.25	.02	.22	.28	.71	.06	.60	.76

Note. F = flowers; H = hearts; X = mixed; RT = reaction time.

Flowers Block.

In the full sample, all accuracy items loaded strongly and significantly onto latent EF ability (λ_Acc = .50 to .81, p < .001), while RT from both flowers (λ_RT = .35 to .58, p < .001) and hearts (λ_RT= .58 to .76, p < .001) items loaded positively onto the latent Speed factor. Because of these positive factor loadings of RT on Speed in this and later models, we interpret this factor as representing person slowness. The mean loading for hearts RT (λ_RT= .70) was higher than that of flowers RT (λ_RT = .50), suggesting that hearts items were a stronger indicator of speed than flowers items. The cross-loadings of flowers RT on EF ability were significant and ranged from −.33 to −.51 (p < .001), indicating that faster responses (i.e., smaller RT) were indicative of better EF ability.

Mixed Block.

Similar to our findings in the flowers block, 32 of 33 accuracy items loaded significantly onto latent EF ability (λ_Acc = .13 to .60, p < .01).³ The loadings of mixed (λ_{RT_i} = .42 to .58, p < .001) and hearts RT (λ_{RT_i} = .57 to .76, p < .001) onto latent Speed were similar to those observed in the flowers block, with hearts RT again loading more strongly than mixed RT. However, unlike in the flowers block, mixed RT was positively related to EF ability, with factor loadings ranging from .34 to .66 (p < .001). Thus, unlike in the flowers block, slower responses (i.e., larger RT) were indicative of better EF ability in the full sample.

Comparison of Enhanced and Traditional EF Scores (Full Sample)

Descriptive Comparison.

Next, we estimated factor scores from the above models and compared them to traditional HF scores (i.e., accuracy and ΔRT scores). Descriptive statistics for all scores appear in Table 1. Latent EF ability from the flowers block was strongly correlated with both accuracy (r = .80, p < .001) and ΔRT (r = −.78, p < .001), in the expected directions. Similarly, latent EF ability from the mixed block was strongly, positively correlated with both accuracy (r = .73, p < .001) and ΔRT (r = .83, p < .001). It is worth noting that the direction of the correlation between EF ability and ΔRT is different in the two blocks, and maps onto the differences we observed in factor loadings in the two models. Whereas faster RT denotes better EF ability in the flowers block (e.g., negative correlation), slower RT denotes better EF ability in the mixed block (e.g., positive correlation). EF ability on the flowers and mixed blocks were modestly, positively correlated (r = .25, p < .001).

Visual Comparison.

Figure 2 represents a visual comparison between latent EF ability scores and accuracy and ΔRT scores in the flowers (top) and mixed (bottom) blocks. The y-axis for all panels represents the latent EF ability score, whereas the x-axis either represents accuracy (left panels) or ΔRT (right panels). In the top-left panel of Figure 2, we can see that the distribution of accuracy scores for the flowers block spans the entire theoretical range of scores (0 to 1). While there is a positive, linear relationship between EF ability and accuracy scores, at each value of accuracy, there is a range of EF ability scores observed. This ‘spreading’ of scores becomes more apparent at higher levels of accuracy. For example, there were 127 children who received an accuracy score of .83. Despite identical accuracy scores, their EF ability scores ranged from approximately −1.5 to 1.0. A similar trend is observed in the bottom-left panel. While the discrete nature of accuracy scores is less apparent in the mixed block (due to a greater number of items), we still observe a range of EF ability scores at each level of accuracy. Thus, incorporating RT data into the latent EF scores provides additional information that allows us to differentiate children’s EF ability.

Figure 2.

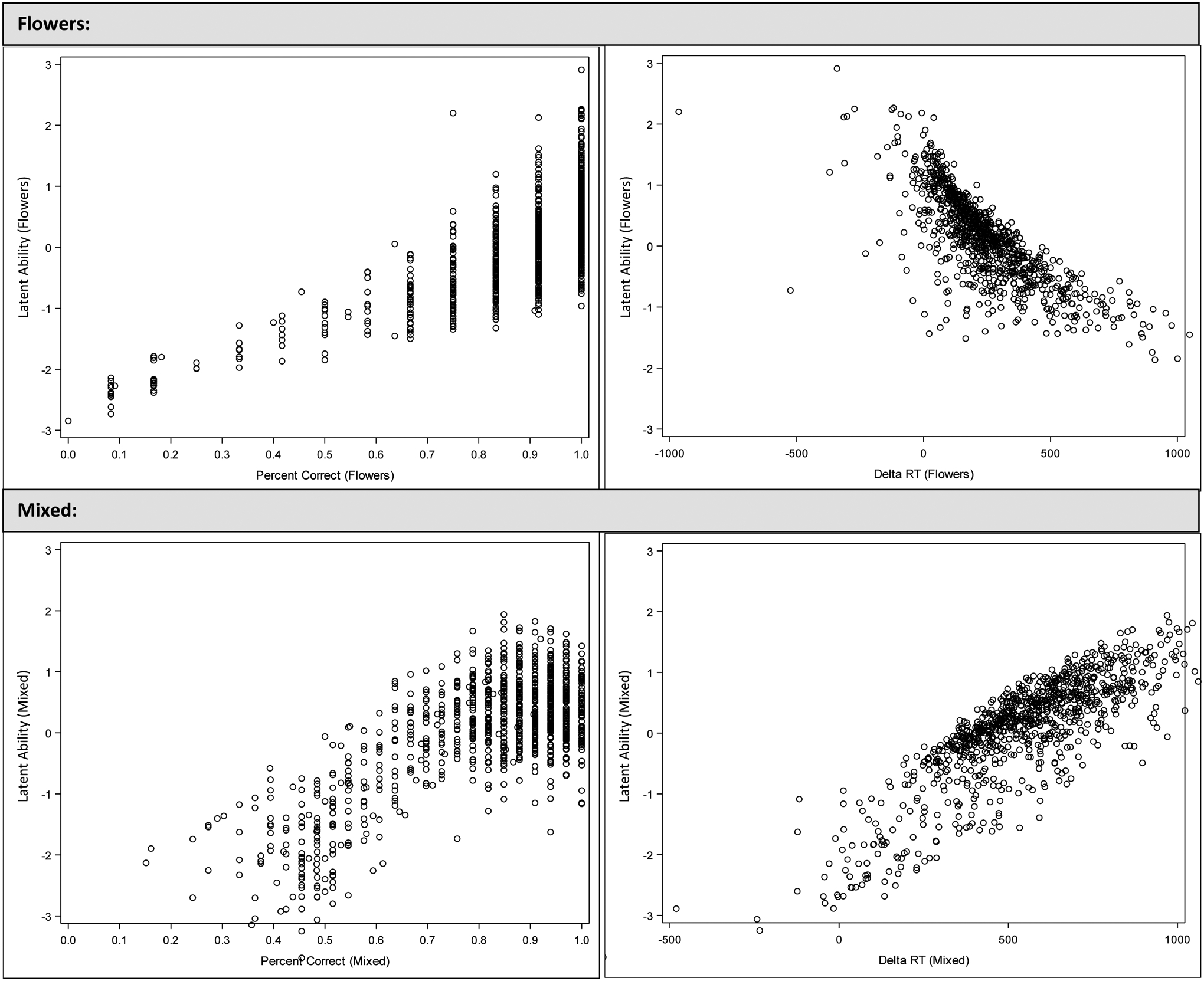
Comparison of traditional and enhanced EF scores in full sample

In the right panels of Figure 2, we see that the relationship between children’s ΔRT scores and their EF ability scores varies as a function of task block. Consistent with bi-factor model results, larger ΔRT indicated poorer EF ability in the flowers block (top right), whereas larger ΔRT indicated better EF ability in the mixed block (bottom right).

Relation with Criterion Measures.

Finally, we examined the correlations between the three HF scores and three criterion measures. Results for the full sample are presented in the left-most columns of Table 4. Considering scores from the flowers block, we found that our EF ability score performed similarly to accuracy scores for two of three criterion measures (child math and reading ability). Using Fisher’s r-to-z transformations, we determined that these correlation coefficients (r = .34 vs. r = .33; r = .20 vs r = .18) were not significantly different from one another (z < 1.03, p > .30). For one criterion measure (ADHD symptoms), accuracy scores were more predictive than EF ability. For all criterion measures, EF ability was more predictive than ΔRT. For the mixed block, we found that EF ability was more predictive of outcomes than ΔRT, but not as predictive as accuracy scores. Thus, across all comparisons, our enhanced score performed as well or worse than accuracy scores, but better than ΔRT scores.

Table 4.

Descriptive statistics and bivariate correlations among enhanced and traditional scores by performance group

Score	1	2	3	4	5	6	M	SD
1. EF Ability (F)	-	.34***	−.94***	.56***	−.03	−.56***	0.00	0.87
2. % Correct (F)	.87***	-	−.24***	.11*	−.05	−.11*	0.96	0.06
3. ΔRT (F)	−.66***	−.11*	-	−.54***	.01	.58***	210.9	155.0
4. EF Ability (X)	.34***	.51***	.30***	-	.17***	−.96***	0.00	0.94
5. % Correct (X)	.34***	.40***	−.02	.72***	-	−.14**	0.93	0.04
6. ΔRT (X)	.13**	.36***	.48***	.91***	.54***	-	543.5	176.3
M	0.00	0.77	280.1	0.00	0.67	542.7
SD	0.91	0.26	234.3	0.96	0.16	269.5

Note. Values above the diagonal represent statistics in the high-performing group, whereas values below the diagonal represent statistics in the low-performing group. Sample sizes for correlations range from 419 to 517 in the low-performing group, and from 492 to 498 in the high-performing group. F = flowers; X = mixed; RT = reaction time.

^*p < .05,

^**p < .01,

^***p < .001

Latent Variable Models (Subgroups)

Next, we re-estimated latent scoring models for the flowers and mixed blocks, separately for children in the high- and low-performing groups. To reiterate, children in the high-performing group were those whose combined accuracy on all test trials (i.e., both flowers and mixed trials) was 87% or greater, whereas children in the low-performing group had combined accuracy below 87%. Descriptive statistics summarizing factor loadings from subgroup models are presented in the right hand columns of Table 3.

Table 3.

Correlations between enhanced and traditional scores and criterion measures

	Full Sample N = 1015			Low Performing N = 517			High Performing N = 498
Flowers	% Correct	ΔRT	EF Ability	% Correct	ΔRT	EF Ability	% Correct	ΔRT	EF Ability
ADHD	−.20*** a	.01 b	−.16*** c	−.14** a	−.05 a	−.10* a	−.06 a	.02 a	−.04 a
WJ AP	.34*** a	−.14*** b	.33*** a	.26*** a	−.06 b	.23*** a	.11* a	−.15*** a	.16*** a
WJ LW	.20*** a	−.07* b	.18*** a	.12** a	.02 a	.09 a	.07 a	−.11* a	.10* a
Mixed				% Correct	ΔRT	EF Ability	% Correct	ΔRT	EF Ability
ADHD	−.25*** a	−.02 b	−.17*** c	−.15** ab	−.09 a	−.14** b	−.19*** a	.09 a	−.12** a
WJ AP	.40*** a	.02 b	.26*** c	.28*** a	.16*** b	.24*** a	.11* a	−.19*** a	.19*** a
WJ LW	.28*** a	.00 b	.17*** c	.20*** a	.08 b	.15*** a	.09* a	−.14** a	.15** a

Note. Values sharing the same superscript are not statistically different from one another (p > .05). ADHD = Attention Deficit/Hyperactivity Disorder symptoms; RT = reaction time; WJ = Woodcock Johnson; AP = Applied problems subtest; LW = Letter word subtest.

^*p < .05,

^**p < .01,

^***p < .001.

Flowers Block.

For children in the low-performing group, the pattern of factor loadings was very similar to what was reported in the full sample. All accuracy items loaded strongly and significantly onto latent EF ability (λ_Acc = .40 to .84, p < .001). RT from both flowers (λ_RT = .40 to .61, p < .001) and hearts (λ_RT = .57 to .75, p < .001) loaded positively onto latent Speed. All but one of the cross-loadings of RT on EF ability were significant (λ_RT = −.20 to −.56, p < .05). The one exception was RT from item 8 (λ_RT = −.19, p = .11).

For children in the high-performing group, only four of 12 accuracy items loaded significantly onto latent EF ability (λ_Acc = .32 to .44, p < .02). This finding indicates that accuracy was less strongly and inconsistently related to EF ability for high-performing children, compared to low-performing children. RT items for flowers (λ_RT = .29 to .56, p < .001) and hearts (λ_RT= .60 to .77, p < .001) items loaded onto latent Speed in a similar manner to that described in the low-performing group. In contrast to accuracy items, which did not consistently load onto EF ability, all factor loadings of flowers RT on EF ability were significant (λ_RT = −.31 to −.53, p < .001). The average loading of RT on EF ability was larger in magnitude in the high performing group (λ_RT = −.43) compared to the low-performing group (λ_RT = −.34), indicating that RT was more strongly related to EF ability in the high-performing group, compared to the low-performing group. The cross-loadings of RT on EF ability were negative in both groups, as in the full sample, suggesting that faster responses indicated better EF ability for all children.

Mixed Block.

We estimated a parallel set of models using items from the mixed block. For children in the low-performing group, 22 of 33 accuracy items loaded significantly and positively onto the EF ability latent factor (λ_Acc = .31 to 1.23, p < .02).⁴ RT items from mixed (λ_RT = .12 to .24, p < .001) and hearts (λ_RT = .22 to .28, p < .001) items loaded positively and significantly onto the latent Speed variable. Similar to the findings in the full sample, all factor loadings of RT on EF ability were significant and positive (λ_RT = .14 to .35, p < .001). These findings are therefore similar to those reported in the full sample, and indicate that accuracy and RT both inform EF ability, with slower responses (i.e., larger RT) indicating better EF ability.

In the high-performing group, the majority (24 of 33) of loadings of accuracy on EF ability were not significant (λ_Acc = −.26 to .24, p > .07). Of the nine significant accuracy loadings, seven were positive (λ_Acc = .19 to .38, p < .05) and two were negative (λ_Acc = −.25 to −.35, p < .03). Therefore, compared to the low-performing and full models, accuracy was less consistently related to latent EF ability in the high-performing model. Mixed (λ_{RT_i} = .29 to .45, p < .001) and hearts RT (λ_{RT_i} = .60 to .76, p < .001) loaded positively onto latent Speed. Unlike in the full and low-performing models, there was a negative relationship between RT and EF ability, as indicated by negative factor loadings of RT on EF ability (λ_{RT_i} = −.34 to −.57, p < .001). Thus, in the high-performing group, faster responses (i.e., smaller RT) were indicative of better EF ability, which is the opposite of what was found in the low-performing group and in the full sample.

Comparison of Enhanced and Traditional EF Scores

Because there were non-trivial differences in model parameters between low- and high-performing groups, we estimated factor scores separately for each group for use in subsequent score comparisons. That is, EF ability scores for children in the low-performing group came from the model that only included children who scored below the median, and vice versa. This strategy was considered appropriate given that factor loadings differed in significance, direction, and magnitude in the low- and high-performing models, suggesting measurement invariance between these two groups of children.

Descriptive Comparison.

As previously described in the full sample results, we compared latent EF ability estimated from the bi-factor model to traditional task scores (i.e., accuracy and ΔRT scores). Descriptive statistics for these scores, separated by low and high-performing groups, appear in Table 2. Accuracy scores were higher for the flowers block compared to the mixed block, and this was true for children in the low- (0.77 v. 0.67) and high-performing (0.96 v. 0.93) groups. On average, children slowed down in both the flowers and mixed blocks, as indicative by positive ΔRT scores. Children tended to slow down more in the mixed block as compared to the flowers block, as indicated by higher ΔRT scores, and this was true for both low-performing (542.7 ms vs. 280.1 ms) and high-performing (543.5 vs. 210.9) children.

Table 2.

Descriptive statistics and bivariate correlations among enhanced and traditional scores in full sample

Score	1	2	3	4	5	6
1. EF Ability (F)	-
2. % Correct (F)	.80***	-
3. ΔRT (F)	−.78***	−.20***	-
4. EF Ability (X)	.25***	.52***	.24***	-
5. % Correct (X)	.48***	.57***	−.14***	.73***	-
6. ΔRT (X)	−.09**	.25***	.52***	.83***	.26***	-
M	0.00	0.87	243.8	0.00	0.80	543.1
SD	0.90	0.21	199.6	0.95	0.18	226.1

Note. Sample sizes for correlations range from 911 to 1015. F = flowers; X = mixed; RT = reaction time.

^*p < .05,

^**p < .01,

^***p < .001

Table 2 also depicts correlations among different scores for children in the low- and high-performing groups. In the flowers block, latent EF ability was strongly correlated with both accuracy (r = .87, p < .001) and ΔRT (r = −.66, p < .001) in the low-performing group, which is similar to what was reported in the full sample (Table 1). Supporting the pattern of factor loadings observed in the scoring models, the negative correlation between latent EF ability and ΔRT scores indicate that faster responses (i.e., less slowing or smaller ΔRT) indicated better EF ability. In the high-performing group, EF ability was modestly correlated with accuracy (r = .34, p < .001), and strongly, negatively correlated with ΔRT (r = −.94, p < .001).⁵ These findings confirm that accuracy was less predictive of ability in the high-performing group, whereas RT was more predictive, compared to in the low-performing group.

For the mixed block, latent EF ability was strongly correlated with accuracy (r = .72, p < .001) and ΔRT (r = .91, p < .001) in the low-performing group, similar to what was reported in the full sample. In the high-performing group, latent EF ability was weakly correlated with accuracy (r = .17, p < .001), and strongly, negatively associated with ΔRT (r = −.96, p < .001). This pattern of findings again show a trend towards accuracy being less informative of ability for children with high task performance. Additionally, faster responding on mixed items (i.e. less slowing or smaller ΔRT) was indicative of better EF ability for the high-performing group. This finding was similar to what was reported in the flowers block, where faster responding was uniformly indicative of better EF ability, yet contrasts with the findings described above for the low-performing group, where slower responding on mixed items indicated better EF ability.

Visual Comparison.

Next, we visually compared latent EF ability scores with accuracy and ΔRT scores. Graphical comparisons between latent EF ability and traditional scores (i.e., % correct, ΔRT) for flowers and mixed blocks are depicted in Figures 3 and 4. In each figure, relations for low-performing and high-performing groups are presented in the top and bottom panels, respectively. Like in Figure 2, the y-axis for all panels represents the latent EF ability score, whereas the x-axis either represents accuracy (left panels) or ΔRT (right panels).

Figure 3.

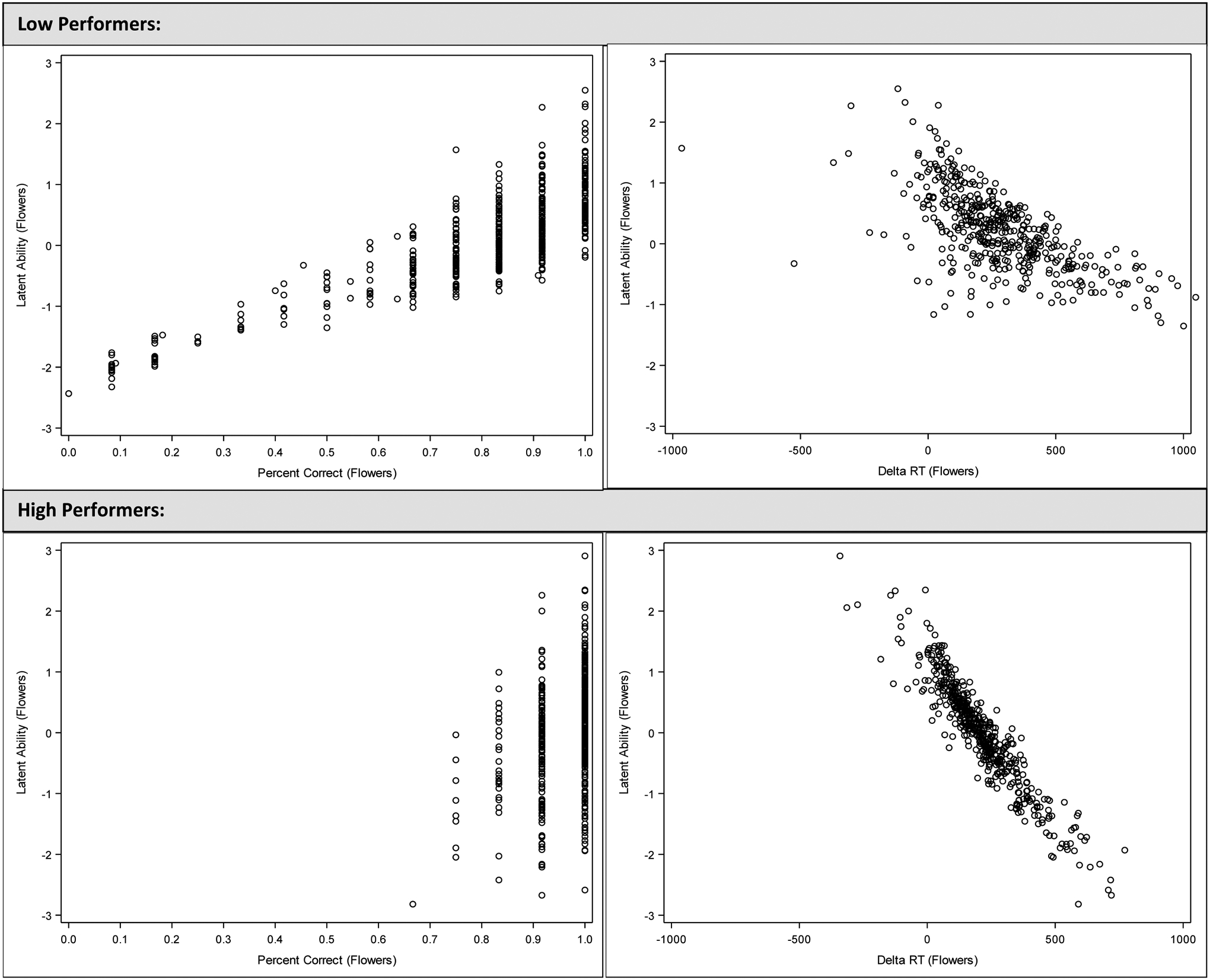
Comparison of traditional and enhanced EF scores by performance group (Flowers block)

Figure 4.

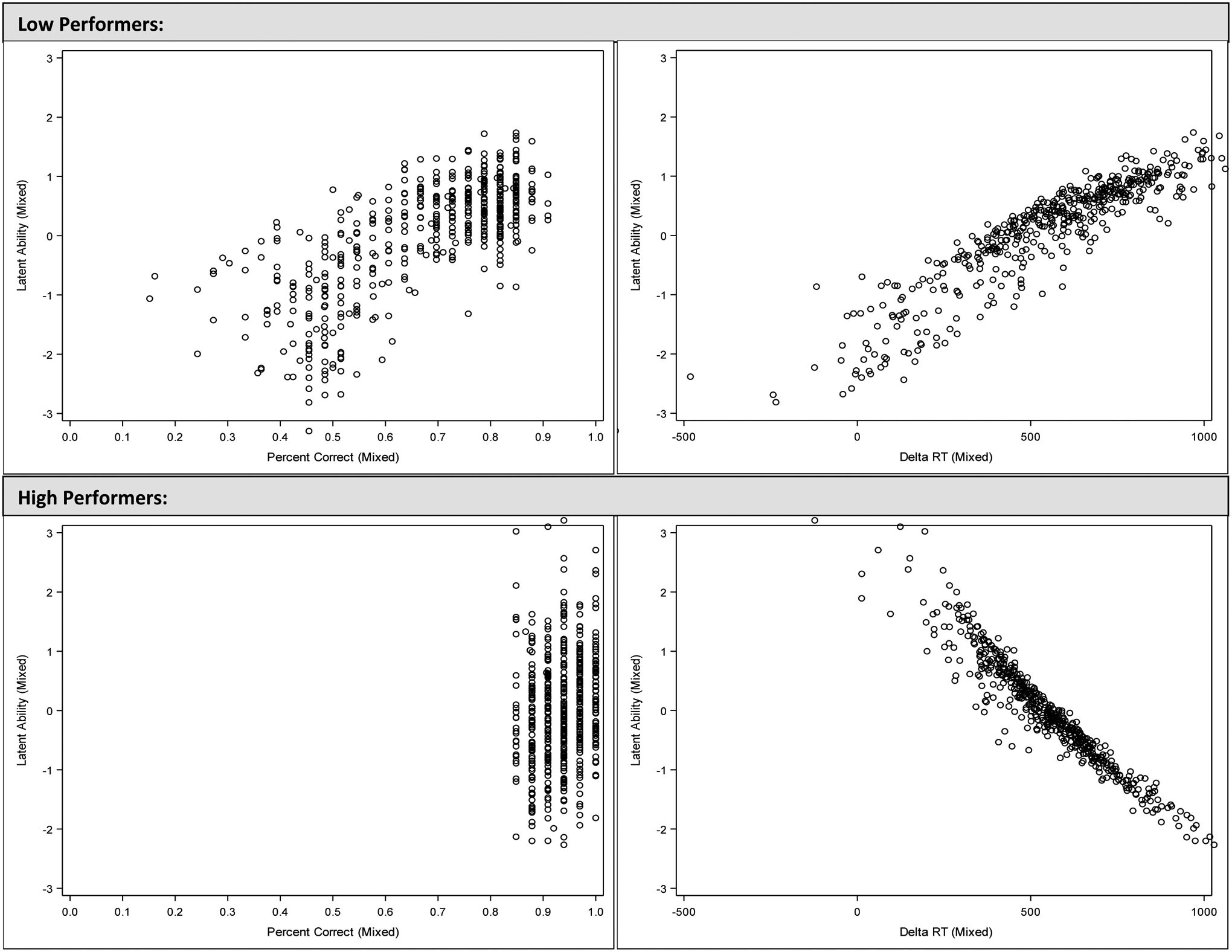
Comparison of traditional and enhanced EF scores by performance group (Mixed block)

In the left panels of both Figures 3 and 4, we can see the spreading of scores that occurs at each level of accuracy, which is similar to what was seen in the full sample (Figure 2). Thus, incorporating both accuracy and RT information into our EF ability score provides additional information that differentiates children who have the same accuracy score. In the right panels of Figure 3, we can see that the relationship between EF ability and ΔRT is negative for both low- and high-performing groups, but that ΔRT more strongly maps onto EF ability for the high-performing group (bottom-right panel). In Figure 4, the differing relationships between EF ability and ΔRT in the low- and high-performing groups is striking; in the top-right panel, there is a strong positive relationship, whereas in the bottom-right panel, there is a strong negative relationship.

Relation with Criterion Measures.

Finally, we examined the correlations between the three HF scores and three criterion measures (right columns of Table 4). Similar to the results from the full sample, accuracy and EF ability from the flowers block were similarly related to all criterion measures for children in both the low- and high-performing group. EF ability also performed as well or better than ΔRT for all criterion measures.

Moving to the mixed block, we found that EF ability performed as well as accuracy scores in both low- and high-performing groups. In the low-performing group, EF ability was more predictive of all three criterion measures compared to ΔRT, whereas in the high-performing group, EF ability performed as well as ΔRT. Thus, unlike in the full sample, our EF ability score performed as well or better than traditional scores in group-specific comparisons.

Discussion

The current study tested whether a scoring model that made joint use of accuracy and RT data could be applied to a commonly-used, performance-based EF task in a sample of first grade children. Our results showed that a bi-factor model could be applied to children’s HF data to yield interpretable model coefficients that provide information about the relationship of accuracy and RT to EF ability. In all models estimated, we found that accuracy and RT information were both informative of latent EF ability, although the relative contributions of accuracy and RT differed across task block and groups of children.

Currently, there is a precedent in the EF literature for using accuracy scores (i.e., percent correct) with young children, or with groups for whom mean levels of accuracy are low and variable (e.g., Diamond et al., 2007). On the other hand, there is a preference for using RT-based scores for older children and adults, or when mean levels of accuracy are high and unvarying (e.g., Ursache & Raver, 2015). We tested this assumption in a previous study and found that when children’s accuracy was high (at least above 70%, although exact values varied based on task block and outcome assessed), both accuracy and RT were significant predictors of child outcomes (Camerota et al., 2019). This previous study was one of the first to demonstrate the joint utility of accuracy and RT data as indicators of child EF ability, but its conclusions are mainly applicable to studies where EF is a predictor. In contrast, the current study particularly focuses on what to do with accuracy and RT data when EF is the outcome of interest.

The current investigation demonstrates the use of a latent variable scoring model that yokes accuracy and RT data into a single measure of child EF ability. The current study supports our previous findings in that item-level accuracy and RT data both contributed to the latent EF ability variable. Although the relative contributions of accuracy and RT to ability varied as a function of task block and child overall task performance, our results show that there is useful information about EF ability conveyed by both types of data. Thus, studies that arbitrarily choose one metric over another may be casting aside useful data that could serve to further differentiate individuals’ EF ability. We visually conveyed this idea by plotting accuracy scores against EF ability scores in Figure 2. The spreading out of scores at each level of accuracy clearly demonstrates that there is heterogeneity in children’s ability that can only be parsed out when RT is jointly considered alongside accuracy.

The second goal of our study was to test whether accuracy and RT were equally informative indicators of EF ability for children who performed better or worse on the task as a whole. By re-estimating the bi-factor model separately for children with low- and high-performance, we found marked differences in the contributions of accuracy and RT to latent EF ability. First, we found that accuracy was a stronger, more consistent indicator of EF ability for children who performed worse on the HF task as a whole. Whereas the majority of factor loadings of item accuracy on ability were significant in the low-performing group, the majority of these loadings were not significant in the high-performing group. This finding should cause researchers to think carefully about using accuracy as a sole indicator of HF task performance, even among relatively young children.

Second, we found that RT was a better indicator of ability for children in the high-performing group, as compared to children in the low-performing group. This finding was apparent when we compared the magnitude of factor loadings of RT on EF ability across the groups. In addition, one wholly unexpected finding was that the direction of the relationship between RT and EF ability was different for different groups of children. As opposed to the flowers only block, where faster RT universally indicated better EF ability, the relationship between RT and ability in the mixed block varied depending on children’s overall performance on the HF task. For children whose accuracy was low (i.e., below the median), RT was positively related to ability, meaning that slower responding indicated better EF. For children whose task accuracy was high (i.e., above the median), RT was negatively related to ability, meaning that faster responding was indicative of better EF ability. These differences in how RT relates to ability, even within a narrow range of same-aged children, would not have been apparent had we not tested an alternative scoring approach. As such, these results seriously call into question the use of traditional HF scores (e.g., % correct, ΔRT scores). An implicit assumption is that traditional composite scores work equally well as an index of performance for all individuals within the same study. However, our work now demonstrates that ΔRT is a better index of performance for children with high accuracy (Camerota et al., 2019), and that either longer or shorter ΔRT may indicate better EF ability, depending on accuracy. Thus, further attention to scoring approaches that simultaneously consider accuracy and RT is clearly needed.

When we compared the correlations between our enhanced EF ability scores, traditional HF scores, and a number of criterion measures, we did not find overwhelming evidence that our new score was any more predictive of child outcomes. In the full sample, this was likely because our estimated factor scores did not account for the heterogeneity in the relationship of accuracy and RT to latent ability. In subgroup analyses, we found that our EF ability score performed as well as traditional accuracy (i.e., % correct) scores, and as well or better than traditional RT (i.e., ΔRT) scores. Thus, by jointly accounting for accuracy and RT, our single, enhanced score performed as well as two other, more traditional scores.

There are practical and empirical reasons why one might prefer a single EF score for analyses. As discussed earlier, there are loose conventions regarding when researchers should use accuracy or RT scores, but these are far from universal guidelines. Thus, having a single score that jointly captures accuracy and RT circumvents the need to choose one metric over another a-priori, or having to reconcile potentially divergent patterns of findings when both metrics are considered separately. In addition to simplifying analyses, a single score may also be useful in studies examining change in EF ability over time. In the current literature, accuracy scores are eventually replaced with RT scores as a metric of EF ability when accuracy reaches a certain threshold. However, it would be difficult, if not impossible, to model change over time in EF if the metric of EF ability changes over the same timeframe. Therefore, having a single EF ability score that can be used with all ages opens up the possibility of modeling change over wide expanses of time, using techniques such as latent growth curve modeling. Additionally, although our new EF score did not show markedly stronger associations with contemporaneous criterion measures, it is possible that these enhanced scores may do a better job at detecting change in EF, either over time (e.g., Hughes, Ensor, Wilson, & Graham, 2010) or in response to intervention (e.g., Diamond et al., 2007). Therefore, there may be both practical and empirical merits to the new scoring approach demonstrated here.

Changes in the Relationship of Accuracy and RT to EF Ability

What does it mean for the construct of EF that there are shifts in the relationship of accuracy and RT to EF ability? Certainly, this finding calls into question the premise that EF development consists solely of quantitative increases in executive ability (Chevalier et al., 2013). Instead, there may be qualitative shifts in the strategies children use to complete EF tasks. Among children with relatively low accuracy scores, approaching the mixed block slowly was indicative of better EF ability, whereas among children with high accuracy scores, completing the mixed block quickly indicated better EF ability. Other studies have similarly reported differences in children’s approaches to EF tasks, such as differences in the utilization of proactive and reactive strategies for completing cognitive flexibility tasks (Chevalier et al., 2014, 2015, 2013). Interestingly, these previous studies have found that a transition in strategy use occurs around age 6, a similar age to the children tested in the current study. Additionally, we found evidence for this shift in the mixed block, which primarily measures cognitive flexibility. Thus, is possible that the different relationships between RT and EF ability observed in the current study are reflective of the shift from reactive to proactive control that occurs around this time. Children in the low-performing group may have responded slower because they were relying on reactive control (a less efficient type of control), whereas children in the high-performing group may have been able to maintain faster speeds because they were proficiently engaging proactive control. Although this hypothesis should be tested in future, our findings suggest that there may be a transition point in the development of EF around the late kindergarten/early elementary school years. This transition means that researchers should take care to examine heterogeneity in task scores, even when sampling children within a narrow age range, such as the current study.

Besides child-level processes, changes in task parameters, such as item presentation rate, might also change the relative contributions of accuracy and RT to EF ability. The distinction between speeded and non-speeded tests is one that has received attention in the psychological assessment literature more broadly (Goldhammer, 2015; Kyllonen & Zu, 2016), but has yet to be considered as it specifically relates to EF. However, it is relevant to the EF literature as well, where changes to stimulus presentation rate are one way in which EF tasks are made more difficult for children and adults (Davidson et al., 2006). Understanding the ways in which child and task characteristics alter the relationships of accuracy and RT to EF ability will enhance our understanding of the construct of EF, including how it is related to domain-general constructs such as processing speed (e.g., Hendry, Jones, & Charman, 2016). This knowledge will also contribute to a practical understanding of how EF tasks should be administered and scored.

Future Directions

Although the current study uses the Hearts and Flowers task as an exemplar to test a new scoring model, many other EF tasks also produce item-level accuracy and RT data. One future application of this work is determining whether the same type of scoring models can be applied to diverse types of EF tasks. Compared to a previous study that also demonstrated the use of a bi-factor scoring model with a number of inhibitory control tasks (Magnus et al., 2017), we found relatively stronger loadings of RT items onto latent EF ability, which is likely due to our use of baseline RT data (i.e., RT from hearts items). Therefore, future studies interested in applying these models to other EF tasks might consider whether baseline RT is also available, either from the same task or from a simple reaction time task (Willoughby, Blair, Kuhn, & Magnus, 2018).

Future studies should also investigate the different types of models that are available for yoking together accuracy and RT data. In the current study, we chose to apply a “bi-factor-like” model (Cai et al., 2011) because it was a relatively simple model that has previously been used with EF data in children (Magnus et al., 2017). However, there are a number of other models that have been developed for this purpose, many of which are derived from the item-response theory (IRT) framework (a more detailed review is provided by Van Der Linden, 2009). Within the IRT framework, accuracy and RT can be yoked together in several ways, either by incorporating RT information into the model for response accuracy, or vice versa. For example, Thissen’s (1983) model is an example of the latter, where parameters of the response accuracy model are incorporated into the RT model. Recently, Molenaar and colleagues (2015) described a general framework for joint accuracy and RT models, the bivariate linear item response theory (BGLIRT) model, which subsumes a number of specific models, including Thissen’s (1983) and van der Linden’s (2007). The BGLIRT approach is promising for applied researchers, as it is general enough to allow different parameterizations for the response and RT models (including non-linearity) and can be fit using common latent variable modeling software. Future studies might endeavor to fit various types of joint models to child EF data, and compare model fit and interpretation.

Study Limitations

Several limitations of the current manuscript are worth mentioning. Although the models estimated here parse variability in RT into that which is related to EF ability, and that which is related to speed, they do not address impurity in the accuracy measures. To the extent that child accuracy on HF items involves some non-executive ability, our EF ability latent variable is not necessarily a ‘pure’ measure of child EF. Future work might apply other parameterizations of the bi-factor model to understand whether variability in accuracy items might be parsed into executive and non-executive ability.

Next, we chose to divide children into low- and high-performance groups based on a median split of their accuracy on test trials. While this was a convenient strategy for testing the contributions of accuracy and RT to EF ability in two equal sized groups of children, it does not necessarily result in groups that are maximally different from one another (e.g., children whose scores were slightly above or below the median were put into different groups despite having very similar scores). Additionally, our strategy of estimating the bi-factor models in these groups separately, although warranted given the lack of measurement invariance, means that the scores from these two groups are not directly comparable. Future research might investigate whether partial measurement invariance can be established, in order to allow direct score comparisons across children with different task performance. Finally, our sample of children came from a study that oversampled for poverty and is therefore not generalizable to all first-grade children. Repeating these analyses in both low- and high-SES children, as well as in slightly younger and older children, may shed light on possible transitions in the relationship of accuracy and RT to EF ability during the transition to formal schooling. Future studies might also apply this scoring approach to EF data collected from representative samples, to create normed-reference and/or clinically-relevant scores that make joint use of accuracy and RT data.

Conclusions

In sum, the current manuscript presents a new scoring model that makes joint use of accuracy and RT data as indicators of child EF ability. With the provided Mplus code, we hope to make this approach accessible to applied researchers, as there are still many unanswered questions regarding the use of these types of scoring approaches. Although there are practical reasons to prefer a single score that yokes together accuracy and RT data, future applications of this work should investigate whether there are empirical benefits as well.

Public Significance Statement:

This study applies a new scoring model to a popular executive function (EF) task, which results in a single score that makes use of both accuracy and reaction time (RT) data. Using this scoring model, we find that accuracy and RT are differentially related to EF ability, depending on how well children performed on the task as a whole.

Appendix A. Mplus scripts for scoring models

Title: Flowers Model

Data: File is HF.dat;

Variable:

NAMES= H_Acc_1-H_Acc_12 H_RT_1- H_RT_12

F_Acc_1-F_Acc_12 F_RT_1-F_RT_12

M_Acc_1-M_Acc_33 M_RT_1-M_RT_33;

USEVARIABLES=F_Acc_1-F_Acc_12 F_RT_1-F_RT_12 H_RT_1- H_RT_12;

CATEGORICAL=F_Acc_1-F_Acc_12;

Analysis:

ESTIMATOR=MLR;

Model:

EF_F by F_Acc_1-F_Acc_12*;	! Link accuracy to EF Ability;
SPEED by F_RT_1-F_RT_12* H_RT_1- H_RT_12*;	! Link RT to Speed;
EF_F by F_RT_1-F_RT_12*;	! Link RT to EF Ability;
EF_F with SPEED@0;	! No covariance between EF Ability and Speed;
[F_Acc_1$1-F_Acc_12$1] (bi1-bi12);	! Define thresholds for accuracy;
[F_RT_1-F_RT_12](icept1-icept12);	! Define Intercepts for RT;
EF_F@1; [EF_F@0];	! Identify latent variables by setting
SPEED@1; [SPEED@0];	! mean= 0 and variance=1;
Output: stdyx;	! Request standardized results;
Savedata:
FILE is Flowers_Scores.txt;	! Save factor scores;
SAVE is fscores;

Title: Mixed Model

Data: File is HF.dat;

Variable:

NAMES= H_Acc_1-H_Acc_12 H_RT_1- H_RT_12

F_Acc_1-F_Acc_12 F_RT_1-F_RT_12

M_Acc_1-M_Acc_33 M_RT_1-M_RT_33;

USEVARIABLES= M_Acc_1-M_Acc_33 M_RT_1-M_RT_33 H_RT_1- H_RT_12;

CATEGORICAL= M_Acc_1-M_Acc_33;

Analysis:

ESTIMATOR=MLR;

Model:

EF_X by M_Acc_1-M_Acc_33*;	! Link accuracy to EF Ability;
SPEED by M_RT_1-M_RT_33* H_RT_1- H_RT_12*;	! Link RT to Speed;
EF_X by M_RT_1-M_RT_33*;	! Link RT to EF Ability;
EF_X with SPEED@0;	! No covariance between EF Ability and Speed;
[M_Acc_1$1-M_Acc_33$1];	! Define thresholds for accuracy;
[M_RT_1-M_RT_33];	! Define Intercepts for RT;
EF_X@1; [EF_X@0];	! Identify latent variables by setting
SPEED@1; [SPEED@0];	! mean= 0 and variance=1;
Output: stdyx;	! Request standardized results;
Savedata:
FILE is Mixed_Scores.txt;	! Save factor scores;
SAVE is fscores;

Appendix B. Item-level descriptive statistics for whole sample and subgroups.

	OVERALL (N = 1015)				LOW (N = 517)				HIGH (N = 498)
	Accuracy (%)		RT (ms)		Accuracy (%)		RT (ms)		Accuracy (%)		RT (ms)
	M	SD	M	SD	M	SD	M	SD	M	SD	M	SD
Flowers
1	0.75	0.43	1056.24	448.00	0.63	0.48	1190.82	484.78	0.88	0.32	956.00	389.91
2	0.88	0.32	714.93	329.95	0.80	0.40	742.00	371.51	0.97	0.17	691.90	288.33
3	0.86	0.35	888.29	342.05	0.75	0.43	956.73	391.99	0.97	0.18	832.80	283.97
4	0.88	0.32	748.45	345.03	0.79	0.41	782.00	403.03	0.98	0.14	720.47	285.30
5	0.86	0.35	893.35	349.92	0.76	0.43	942.11	400.34	0.95	0.21	853.11	296.49
6	0.89	0.31	771.59	367.70	0.80	0.40	820.89	425.01	0.98	0.15	729.41	304.57
7	0.91	0.29	781.03	371.24	0.83	0.38	826.27	437.84	0.99	0.12	741.59	296.31
8	0.86	0.35	919.80	344.96	0.76	0.43	965.00	392.23	0.97	0.18	882.87	296.22
9	0.89	0.31	794.13	358.13	0.82	0.39	841.84	421.82	0.98	0.15	752.71	285.84
10	0.85	0.36	923.40	365.80	0.74	0.44	979.73	420.04	0.96	0.20	878.61	309.33
11	0.87	0.34	835.09	356.89	0.77	0.42	884.07	391.77	0.97	0.16	794.91	320.35
12	0.88	0.32	857.40	396.02	0.79	0.41	907.30	458.97	0.98	0.13	816.26	330.22
Mixed
1	0.81	0.39	1252.57	489.01	0.67	0.47	1344.80	517.76	0.95	0.22	1185.11	455.73
2	0.90	0.31	942.45	327.66	0.81	0.39	952.35	358.00	0.99	0.12	934.02	299.52
3	0.80	0.40	1118.53	406.83	0.68	0.47	1085.66	447.94	0.93	0.26	1143.63	370.93
4	0.77	0.42	1266.15	430.22	0.64	0.48	1330.26	488.22	0.91	0.29	1219.24	375.95
5	0.78	0.41	1262.05	428.71	0.67	0.47	1278.85	478.79	0.90	0.30	1249.29	386.43
6	0.79	0.41	1174.98	437.73	0.66	0.47	1166.12	476.13	0.92	0.27	1181.51	407.55
7	0.87	0.33	963.35	330.66	0.77	0.42	965.03	354.37	0.98	0.13	961.99	310.54
8	0.63	0.48	1310.74	446.55	0.50	0.50	1257.86	529.35	0.76	0.43	1346.56	376.95
9	0.79	0.41	1197.07	366.56	0.65	0.48	1225.32	420.08	0.94	0.24	1177.05	322.29
10	0.80	0.40	1168.20	440.29	0.67	0.47	1181.24	514.73	0.93	0.26	1158.49	375.65
11	0.73	0.44	1190.41	424.58	0.61	0.49	1161.25	489.47	0.86	0.35	1211.91	368.67
12	0.68	0.46	1269.26	436.39	0.51	0.50	1270.27	515.14	0.87	0.34	1268.65	381.76
13	0.86	0.34	1051.63	390.10	0.75	0.43	1079.39	438.48	0.97	0.17	1029.56	345.71
14	0.74	0.44	1207.36	419.66	0.60	0.49	1237.82	486.71	0.89	0.32	1186.23	365.10
15	0.82	0.38	1159.83	422.98	0.71	0.46	1164.66	466.23	0.94	0.24	1156.07	386.53
16	0.89	0.32	1025.85	380.24	0.80	0.40	1060.89	433.06	0.98	0.14	996.64	327.44
17	0.75	0.43	1265.14	439.19	0.60	0.49	1324.96	472.77	0.91	0.28	1224.04	410.03
18	0.81	0.39	1123.75	400.23	0.68	0.47	1202.89	451.63	0.94	0.23	1064.18	345.42
19	0.85	0.36	1072.20	421.05	0.74	0.44	1108.82	463.00	0.97	0.17	1043.45	382.98
20	0.87	0.33	1009.82	355.17	0.77	0.42	1046.05	375.84	0.98	0.15	980.28	295.06
21	0.76	0.43	1220.38	408.83	0.63	0.48	1246.50	454.71	0.89	0.32	1201.18	370.90
22	0.86	0.34	1064.92	371.41	0.75	0.43	1102.68	420.68	0.98	0.13	1035.18	324.79
23	0.80	0.40	1197.69	380.34	0.68	0.47	1277.88	433.19	0.92	0.27	1136.33	321.55
24	0.77	0.42	1264.19	412.09	0.60	0.49	1324.19	450.53	0.95	0.23	1224.84	380.17
25	0.82	0.38	1174.10	416.92	0.70	0.46	1196.73	440.48	0.95	0.21	1157.04	397.89
26	0.85	0.35	1073.20	358.46	0.75	0.44	1087.20	377.76	0.96	0.19	1062.03	342.26
27	0.77	0.42	1238.64	410.94	0.63	0.48	1285.37	435.02	0.93	0.26	1206.27	390.61
28	0.79	0.41	1233.60	411.58	0.65	0.48	1317.55	464.10	0.94	0.24	1173.87	358.42
29	0.81	0.39	1151.20	375.47	0.67	0.47	1228.83	433.14	0.96	0.21	1094.82	316.00
30	0.83	0.38	1177.59	419.12	0.69	0.46	1192.01	449.85	0.97	0.17	1166.94	395.04
31	0.76	0.42	1209.14	409.20	0.61	0.49	1248.55	448.84	0.93	0.26	1182.44	378.18
32	0.81	0.39	1136.33	440.82	0.66	0.47	1191.93	488.02	0.96	0.19	1096.90	399.89
33	0.82	0.38	1145.99	418.93	0.68	0.47	1186.13	453.19	0.98	0.15	1117.53	390.81
Hearts
1	0.98	0.15	716.92	333.5	0.96	0.19	744.06	360.96	0.99	0.09	689.63	301.19
2	0.99	0.12	530.61	247.8	0.98	0.15	535.33	272.20	0.99	0.08	525.79	220.40
3	0.94	0.23	662.86	249.3	0.92	0.27	691.14	268.69	0.97	0.18	634.94	225.25
4	0.99	0.10	519.65	218.9	0.99	0.12	526.85	236.61	0.99	0.08	512.24	199.08
5	0.94	0.24	625.69	220	0.91	0.28	644.00	240.20	0.96	0.19	607.65	196.75
6	0.98	0.14	559.18	263.7	0.97	0.17	570.00	280.94	0.99	0.11	548.16	244.60
7	0.99	0.11	538.36	236.4	0.98	0.13	554.72	278.03	0.99	0.08	521.53	182.88
8	0.94	0.24	644.07	245.9	0.91	0.29	669.30	283.05	0.97	0.18	619.52	200.57
9	0.98	0.15	576.84	256.7	0.96	0.19	588.35	284.98	0.99	0.10	565.22	224.34
10	0.94	0.24	685.56	251.1	0.91	0.28	706.75	275.90	0.96	0.19	664.72	222.47
11	0.96	0.20	681.67	256.3	0.95	0.22	706.55	284.51	0.97	0.17	656.48	221.52
12	0.98	0.15	589.96	233.2	0.96	0.20	601.73	239.70	1.00	0.06	578.19	226.16

Note. Low and high groups refer to low- and high-performing children, respectively. A median split (median = 87%) based on test trial accuracy was used to distinguish the two groups.