Abstract
We theoretically investigate methods of controlling pulse generation in normal-dispersion fiber optical parametric chirped-pulse amplifiers. We focus on high-energy, ultrashort pulses at wavelengths widely separated from that of the pump, and find that within this regime, a number of simple properties describe the essential phase and gain dynamics. Of primary importance are the relationships between the chirps of the pump, seed, and parametric gain, which we theoretically predict and then experimentally validate. By properly arranging these parameters, the signal and idler waves can be widely customized to fulfill a remarkable range of application requirements, spanning from narrowband to few-cycle.
I. INTRODUCTION
Numerous fields throughout science and industry benefit from lasers generating femtosecond-scale pulses and high peak powers. Traditionally, this role has been filled by solid-state lasers due to their excellent performance and mature engineering. Recently, however, the capabilities of ultrafast fiber lasers have begun to rival those of their solid-state counterparts. Much of this progress has been motivated by the practical advantages of fiber sources: their compact form factors, alignment-insensitivity, and potentially lower costs offer prospects for broad impact, while their waveguide architecture greatly reduces thermal issues and beam quality considerations. While fiber lasers operating near the wavelengths of 1 μm, 1.55 μm, and 1.9 μm are now widespread thanks to the availability of ytterbium-, erbium-, and thulium-based gain media, respectively, pulsed fiber lasers emitting outside those spectral regions are much less impressive. This lack of spectral freedom hinders the impact of fiber lasers on applications such as deep bio-imaging and nonlinear spectroscopy, where a laser’s wavelength can be crucial [1]. Research is underway on fiber gain media operating at novel wavelengths [2-6], but such systems have yet to produce ultrafast pulses at the high (~many-nJ) energies that are demanded by emerging applications.
To fill this need, various methods have been developed for wavelength-converting ultrafast pulses while maintaining the advantages of fiber. The best-established technique is the soliton self-frequency shift, in which a short pulse in anomalous dispersion continuously redshifts due to stimulated Raman scattering [7, 8]. While this approach is fundamentally limited by the soliton area theorem [9], the use of large-mode- area rods has enabled it to reach megawatt-scale peak powers [10]. Furthermore, although solitons only exist in anomalous group-velocity dispersion, recent work using dispersion engineering in photonic bandgap fibers [11] and higher-order mode fibers [12, 13] has managed to extend soliton propagation to wavelengths that typically feature normal dispersion. SPM-enabled spectral shifting, whereby self-phase modulation of a short pulse is followed by filtering one of the nonlinearly-generated spectral fringes, has also led to impressive performance levels, with the added advantage that both redshifts and blueshifts can be obtained [14, 15]. A limitation common to both of these techniques, however, is the high peak intensity required: generating megawatt-scale pulses requires similarly high-power pump sources, which entails free-space coupling and operation near the thresholds for component damage and critical self-focusing.
Greater potential for scalability can be obtained from approaches utilizing stretched pulses. For instance, synchronously-pumped Raman lasers in silica [16-18] or phosphosilicate-based [19, 20] fibers have produced pulses at the multi-nanojoule level in the ~1.08-1.24 μm spectral region, with theory predicting order-of-magnitude improvements to come [21]. Interestingly from the standpoint of applications, the more modest peak powers and stretched pulses involved mean fully-spliced systems can be realized to take better advantage of the benefits of fiber. Nevertheless, while Raman gain is present in all fibers, wavelength conversion using this effect is limited to a single Stokes shift (or, in the case of cascaded processes, a few Stokes shifts) exclusively towards longer wavelengths, restricting the purview of this technique.
Four-wave-mixing provides a more versatile alternative. In a fiber with appropriate dispersion characteristics, phase-matching can be obtained over a broad spectral range, enabling efficient conversion to wavelengths either blueshifted or redshifted from the pump. Two major regimes exist, depending on the sign of the fiber’s group-velocity dispersion at the pump wavelength. With weakly-anomalous dispersion, extremely broadband gain can be obtained [22, 23], but only in spectral regions near that of the pump, making this regime less applicable to the generation of brand new colors. If, on the other hand, a fiber has weakly-normal group-velocity dispersion, phase-matched regions may exist at larger frequency separations from the pump [24]. To achieve this regime, the slight, positive group-velocity dispersion at the pump wavelength must be overwhelmed at larger frequency separations by significantly negative fourth-order dispersion. The small-signal, total wavevector mismatch Δβtot as a function of the offset from the pump angular frequency Ω is shown schematically for these two regimes in Figure 1, calculated in the typical manner as Δβtot = β2Ω2 + (1/12)β4Ω4 + 2γP where β2 is the group-velocity dispersion, β4 is the fourth-order dispersion, γ is the Kerr nonlinearity coefficient, and P is the pump power. For the normally-dispersive case (β2 > 0, β4 < 0), the standard analysis [24] yields phase-matching at:
| (1) |
FIG. 1:

Wavevector mismatch for negative group-velocity dispersion and zero fourth-order dispersion (solid red), and for positive group-velocity dispersion and negative fourth-order dispersion (dashed blue). Phase-matching is obtained at the marked points.
It should be noted that the wavevector mismatch varies more rapidly at the phase-matched points for the normal-dispersion case (see Fig. 1); thus, while the normal-dispersion regime allows phase-matching at frequencies significantly offset from the pump, the resulting parametric gain is typically less broadband than in the anomalous-dispersion case. Nevertheless, this regime has been used to realize picosecond- and femtosecond-scale fiber optical parametric oscillators (FOPOs) and amplifiers (FOPAs) at a variety of new and useful wavelengths [25-32].
The phase-matching characteristics in a fiber parametric system can be engineered by performing four- wave-mixing in an appropriate dispersion-shifted fiber or, more commonly, in a photonic crystal fiber (PCF) [33]. While the small mode areas endemic to such fibers would at first glance seem to limit the achievable pulse energies, this can be solved by scaling in the time domain. This tactic is exemplified by fiber optical parametric chirped-pulse amplification (FOPCPA), in which the pump pulses are dispersively stretched prior to parametric amplification, and the signal/idler are subsequently dechirped to ultrashort durations [34]. A handful of FOPCPA systems have been demonstrated to-date [35-41], most recently at microjoule-level energies [42] and in the normally-dispersive regime [43, 44]. Although such sources have the potential to perform on par with their bulky and costly solid-state counterparts, broadly-applicable design guidelines are currently lacking, which motivates further study into the dynamics, operation, and limits of FOPCPA systems.
Here, we present theoretical and experimental results on nonlinear pulse propagation in FOPCPA systems. Our analysis focuses on the generation of femtosecond pulses with nanojoule- to microjoule-scale energies, reflecting our interest in deep-tissue bio-imaging. We consider systems seeded by either narrowband or broadband sources, and explore how the pump characteristics are transformed and transferred during parametric conversion. A major result of this work is the recognition of the importance of the parametric gain chirp factor. Properly matching this parameter to the chirps of the pump and seed pulses allows a much broader range of pulses to be generated, spanning transform-limited durations of many picoseconds to a few optical cycles without loss of efficiency. The promise of achieving such versatility across much of the visible and near-infrared spectral regions makes FOPCPA an attractive candidate for all-fiber systems with unprecedented capabilities.
The paper is organized as follows. We begin by briefly describing two distinct regimes of FOPCPA: that seeded by an effectively continuous-wave (CW) beam, and that seeded by a broadband continuum. The CW-seeded case is discussed first, and the means by which the pump’s phase can be fully or partially transferred to the idler are explored. We then turn our attention to the spectro-temporal behavior of the parametric gain, and how it influences the conversion efficiency. These results are next extended to the case of a continuum seed, and experimental results are given to support the major conclusions. Finally, we summarize the major conclusions.
II. TYPES OF FOPCPAS
Here, we identify several variants of FOPCPA, distinguished by the relative bandwidths of the pump and seed. In the first case, both the pump and the seed are narrowband or quasi-CW; this regime does not generally produce ultrashort pulses, and therefore falls outside the scope of this work. In a second case, the pump is broadband (say, ≳1 THz) while the seed is CW or quasi-CW; for brevity, we will refer to this as the CW-seeded case. Finally, the seed may be broadband while the pump might be either broadband or relatively narrowband; we will refer to both of these as continuum-seeded. These two broad approaches—CW-seeded and continuum-seeded FOPCPA—each come with their own set of advantages and disadvantages. CW-seeded FOPCPA involves a simpler system due to the lack of a separate continuum-generation stage and the CW seed not requiring synchronization with the pump. On the other hand, an external laser is required to generate the CW seed, and for reasons that will be elaborated on below, such systems only generate a single useful four-wave-mixing product. By contrast, in a continuum-seeded FOPCPA, not only must a broadband seed be stably generated, but it must also be synchronized with the pump pulses. While this adds complexity, it can be done without resorting to a second laser, which may give continuum-seeded FOPCPA an advantage. As will be discussed, the additional degree of freedom provided through the seed can also enable levels of performance beyond the capabilities of CW-seeded FOPCPA.
III. CW-SEEDED FOPCPA
A. Overview
In this form of FOPCPA, a broadband, highly-chirped pump pulse interacts with a nearly monochromatic seed, which we take to be the signal. Four-wave-mixing between these two waves can be phase-matched using an appropriately-chosen fiber. If the pump and seed frequencies are widely-separated, as is often desired for applications, the group-velocity dispersion evaluated at the pump wavelength must be weakly normal, implying only a small group-velocity mismatch between the waves. This assumption of negligible group-velocity mismatch can be reinforced by using a relatively short fiber and a pump with a moderate (e.g., kW-scale) peak power and a highly-chirped (e.g., ≳100× transform limited) duration, as is readily obtainable using standard amplification techniques. Under these conditions, four-wave-mixing occurs to a good approximation independently at each point in time: different temporal/spectral components of the pump drive separate, quasi-CW four-wave-mixing processes seeded by the fixed-wavelength seed. These interactions can be described by the time-resolved energy conservation equation:
| (2) |
where the time-dependence of the pump frequency ωp reflects the chirped pump, and the CW nature of the seed (i.e., its linewidth being much narrower than the inverse of the pump’s chirped duration) will eliminate the time-dependence of the signal frequency ωs. This separation of different pulse components can be likened to frequency-domain nonlinear optics [45, 46], where the spatial rather than the temporal domain is used to maintain the independence of the components.
It is clear that for equation 2 to hold with a CW seed, the idler frequency ωi must also vary in time in a manner that mirrors ωp up to a factor of two [47, 48]. Thus, this mixing of a broadband pump and a CW signal produces not only a broadband, coherent idler, but one that is chirped in the same way as the pump. Provided that the pump is linearly-chirped, this implies a linearly-chirped idler that can subsequently be dechirped to its transform limit. The generation of this idler is accompanied by the amplification of the seed; however, because the latter retains both its narrowband nature and an interstitial pedestal of unamplified, CW light, it is typically of limited use. Modulating the seed intensity in tandem with the pump pulses may provide a way to circumvent this restriction, allowing CW-seeded FOPCPA systems to generate dualwavelength, femtosecond-picosecond pulse trains for applications like coherent Raman spectroscopy [49]. For more general uses, though, the CW seed wave acts merely as a facilitator of the desired nonlinear process: it coherently stimulates frequency conversion to the idler, while the pump drives the process and supplies the idler’s energy and bandwidth.
B. Phase dynamics
The analysis of fiber optical parametric systems is complicated by the presence of multiple waves and the large number of nonlinear interaction terms between them. Solid-state parametric systems often avoid this issue by taking advantage of the undepleted pump approximation, which takes the pump to be static and permits solution of the reduced-dimensionality system [50]. This regime likewise plays a role in reducing beam distortions and back-conversion. It is therefore perhaps surprising that not only can FOPCPA systems perform well under significant pump depletion, but they can in fact continue to be modeled well without accounting for signal-/idler-induced phase modulations.
To demonstrate this, numerical simulations are performed with the generalized nonlinear Schrodinger equation using the split-step method. Dispersive terms up through the sixth order are included, as is self-steepening. In keeping with experiments, the PCF is modeled after a commercially-available one (NKT Photonics SC-5.0-1040 [51]) with a length of 6.5 cm, a nonlinear coefficient of γ = 11.1/(kW · m), and dispersion coefficients β2 = 0.132 fs2/mm, β3 = 69.2 fs3/mm, β4 = −100.9 fs4/mm, β5 = 244.5 fs5/mm, and β6 = −839.7 fs6/mm, all evaluated at the 1030-nm central pump wavelength. In this example, a pump pulse of the form exp (− x2m) with supergaussian parameter 2m = 8 is constructed with an energy of 130 nJ, a full-width-at-half-maximum (FWHM) duration of 12.5 ps, and a linear up-chirp such that its transform-limited FWHM duration is 240 fs. The CW seed is modeled as another supergaussian pulse with a duration far exceeding that of the pump, a single wavelength of 850 nm, and a peak power of 40 mW. In all simulations, initial shot noise of one photon per frequency bin is included, and the simulation resolution is increased until the results no longer depend on it. At the output, the well-separated pump, signal, and idler waves are easily isolated in the Fourier domain. Various filter shapes such as rectangular, gaussian, or supergaussian are found to produce no significant differences. Based on our experiences in building CW-seeded FOPCPA systems (e.g., [43]), this numerical setup and the experimental analog discussed below are representative systems in this performance regime. As a first example, Figure 2 depicts the pump pulse at output of the simulated PCF. The pump’s intensity (solid lines) and instantaneous frequency (dashed lines) are shown for the case where a seed is provided (red), as well as the case where no such seed exists and no significant four-wave-mixing occurs (blue). Notably, the two cases are nearly identical apart from the noticeable pump depletion in the former. The signal and idler locally reduce the pump intensity, but do not appear to affect the pump’s phase.
FIG. 2:

Simulated pump power (solid) and frequency (dashed; spurious oscillations at low powers are masked) at the output of an FOPCPA that is either unseeded (blue) or CW-seeded (red).
Experiments confirm these findings. As in [43], pulses from a 1030-nm modelocked laser are stretched, amplified, and then combined via a dichroic mirror with a monochromatic, 852-nm signal beam from a distributed feedback (DFB) diode operated in CW. The combined beams are then coupled into a piece of PCF to produce a system analogous to that simulated above. At the output of the PCF, the light is collimated, and the pump, signal, and idler are separated using a series of dichroic mirrors. In particular, the remaining pump light is characterized using frequency-resolved optical gating (FROG) in order to provide a direct comparison to Figure 2, with the signal beam either present or blocked. The results are shown in Figure 3. By and large, introducing the seed (and thereby allowing the signal/idler to grow) only carves a noticeable hole out of the pump’s spectral and temporal center, leaving it otherwise unaffected. This lack of phase distortions from the signal and idler back to the pump, despite the latter being more than 60% depleted at its temporal center, is underlaid by the rapid, exponential growth of the signal and idler waves by as much as 60 dB. Because the signal and idler only become intense over a brief distance near the system output, it appears that cross-phase modulation effects from these waves remain negligible overall, even when their final peak powers are comparable to that of the pump.
FIG. 3:
Measured FROG reconstructions of residual pump pulses at the output of a FOPCPA system with and without a seed present. (a) Temporal intensity and instantaneous frequency. (b) Spectral intensity. (c) Measured and retrieved FROG traces for the unseeded and seeded cases.
A well-known feature of solid-state optical parametric amplifiers is the transfer of the pump’s phase onto the idler, while leaving the signal phase largely undistorted [52]. A similar phenomenon occurs in FOPCPA systems, with the phase dynamics being primarily dictated by the energy conservation equation (Eqn. 2). Figure 4 illustrates the quantitative accuracy of this effect. The simulated intensity profiles of the pump, signal, and idler for the seeded simulation discussed above are shown in panel (a), while panel (b) shows the instantaneous frequencies in the time domain. With the visual aids of offsetting the signal and idler frequencies and doubling the pump frequency, the behavior predicted by equation 2 for constant ωs is evident. It can be readily seen that this phase-mirroring effect will be applicable to other phase profiles as well, opening possibilities for nonlinear amplifiers where preserving a nonlinear chirp plays a role in improving dechirping [53-56] or advanced applications that can benefit from pulse-shaping at disparate wavelengths [57].
FIG. 4:
(a) Powers and (b) instantaneous frequencies of the pump, seed, and idler at the output of the CW-seeded FOPCPA system described in the text. The frequencies have been transformed as labeled to visually show their adherence to equation 2.
Our discussion of the pump phase transferring onto the idler has thus far largely assumed a supergaussian-like pump pulse, where the temporal intensity profile is relatively flat. Under these conditions, the FOPCPA behavior is largely driven by the phase dynamics: the temporal components are initially uniformly pumped, and the differences in their rates of evolution stem almost entirely from frequency-domain gain shaping. While this model has proven a useful aid for understanding these underlying phase dynamics, it is of practical relevance to also consider Gaussian-like pump pulses. In particular, we explore the dynamics of a Gaussian pump pulse that has been nonlinearly chirped by self-phase modulation prior to the FOPCPA. This is a scenario which might easily arise when pumping an FOPCPA with a chirped-pulse amplification (CPA) system, in which self-phase modulation is often a key impediment to compressibility. Separately, as will be elaborated on in section IIIC, high pump powers can be intrinsically useful for optimizing the performance of a FOPCPA systems. Finally, in contrast with standard large-mode-area amplifiers, pump amplifiers with smaller cores can couple more efficiently to the small mode of a PCF due to the reduced modal mismatch. Since such amplifiers will necessarily impose stronger self-phase modulation in advance of the FOPCPA, it is important to consider how this will affect the output of the FOPCPA. Motivated by these various factors, we next investigate the effect of a nonlinearly-chirped pump on a CW-seeded FOPCPA system, and find that the generated idler is surprisingly robust to even large amounts of pump nonlinearity.
It is well-known that self-phase modulation produces a phase that is proportional to the temporal intensity of a pulse; thus, a Gaussian pulse will acquire a nonlinear chirp on the whole, and a locally linear chirp only near its temporal center. A potential concern is that, because CW-FOPCPA can map the pump’s chirp onto the generated wave, the output of a CW-FOPCPA might feature a similarly nonlinear chirp, making the idler difficult to compress. To assess the extent of these distortions, we simulate a series of CW-seeded FOPCPAs under various pumping conditions. All of the launched pump pulses begin as 330-nJ, 1030-nm, Gaussian pulses with transform-limited FWHM durations of 120 fs, linearly up-chirped to FWHM durations of 24 ps. In each different simulation, the pump is additionally pre-conditioned with some amount of self-phase modulation, with the peak nonlinear phase shift in radians denoted by B. To isolate the effect of the chirp nonlinearity from the accompanying change in bandwidth, we repeat this battery of simulations with equivalent pump pulses that are purely linearly-chirped, but where the chirp rates are chosen to locally match those of the nonlinearly chirped pulses at t = 0. Mathematically, the nonlinear and equivalent linear cases correspond respectively to instantaneous angular frequencies of:
| (3) |
| (4) |
where α is a linear chirp parameter and P(t) = P0 exp(−t2/τ2) is the pump power. A graphical example, for B = 30π, is shown in Figure 5. A supergaussian (2m = 6) seed with a peak power of 40 mW at 850 nm is introduced, and propagation is simulated through 6.6 cm of the same PCF modeled in Figure 2.
FIG. 5:

Illustration comparing a launched, nonlinearly-chirped pulse (solid red) to one with an equivalent, linear chirp (dashed blue) for a Gaussian intensity (solid black). B = 30π is used for the nonlinear case.
At the output of these simulations, we characterize the generated idlers by their dechirped and transform-limited durations (Figure 6). Dechirping is performed in each case by maximizing the peak power with an ideal, second-order compressor, while the transform-limited pulse is calculated in the usual way using a zero-phase Fourier transform of the spectral field. The durations of both pulses are defined using the FWHM. It can be seen that increasing the pump’s chirp (whether linearly or nonlinearly) reduces both the compressed duration and the energy of the idler. This can be understood intuitively: with a larger pump bandwidth, a greater number of spectral components will experience some degree of conversion, yet those experiencing highly-efficient conversion will comprise a smaller fraction of the pump. More striking are the scant differences between the results using the nonlinearly- and linearly-chirped pumps. The corresponding idlers’ energies and transform-limited durations are almost indistinguishable, and the only notable sign of the pump’s nonlinear chirp is an increase in the dechirped idler duration of no more than 11%.
FIG. 6:
Simulated idler (a) energy and (b) duration (dechirped and transform-limited) as a function of nonlinear phase pre-applied to the pump.
We further illustrate this robustness by confining our attention to the case of the nonlinearly-chirped pump. Figure 7 depicts the temporal Strehl ratios (defined as the ratio of the dechirped peak power to the transform-limited peak power) of the launched pump pulses and the generated idler pulses. As expected, imposing a nonlinear chirp where B exceeds ≈ π causes the Strehl ratio of the launched pump to degrade sharply, reflecting the expected loss of compressibility. In spite of this, the idler’s Strehl ratio never drops below 85%. The idler remains highly compressible even up to B ≈ 90π; that this is an unrealistically high number far beyond the Raman threshold in a typical amplifier only serves to underscore the degree to which FOPCPA can preserve the idler’s compressibility even in the face of strong nonlinear phase distortions.
FIG. 7:

Temporal Strehl ratios of the dechirped (green) initial pump and (violet) generated idler pulses as a function of nonlinear phase pre-applied to the pump.
This pulse-cleaning effect is a direct consequence of the temporally peaked pump pulse, and can be explained by a simplified, analytic model. Previously, we showed that a temporally flat pump will cause the pump’s phase to map onto that of the idler. While that transfer is still in effect here, it is largely masked by the differential gain from the pump’s temporal profile. Differentiating equation 3 and Taylor expanding about t = 0 gives:
| (5) |
Deviations from a linear chirp become apparent near , at which point Pp ≈ P0 exp (−1/3). In the undepleted pump approximation, the parametric gain is exponential with a gain coefficient proportional to Pp [9]; therefore, considering that the peak gain in CW-FOPCPA systems can be on the order of 60 dB, the local conversion at can be more than 17 dB below that at the peak. While a more complete analysis requires accounting for pump depletion, simulations indicate that the conclusion remains largely unchanged: strong gain shaping in the time domain means the nonlinearly chirped regions of an SPM-pre- chirped, Gaussian-like pump never experience strong conversion, resulting in an effective pulse cleaning of the idler. Thus, even pump pulses that are too severely nonlinearly distorted to be directly useful in applications can drive FOPCPA systems that generate cleanly-compressible, ultrashort pulses.
C. Parametric gain chirp
Much of the interest in FOPCPA stems from its potential scalability, unique among fiber wavelength conversion methods. This follows directly from the independence of the various spectral/temporal pulse components previously discussed. Once an FOPCPA system has been successfully designed for a given pump pulse, its performance can be improved by stretching the pump pulses further before amplifying them to the original peak power, as demonstrated in [43, 44]. Having thereby discussed scaling in the time domain at constant pump peak power, it is natural to wonder whether FOPCPA systems might be similarly scalable in time at constant pump energy, with the goal of, e.g., reducing peak power requirements. One issue immediately presents itself: when pumping near the zero-dispersion wavelength, the nonlinear contribution to phase-matching is non-negligible, leading to the gain spectrum shifting with the pump power. That said, regimes can be found where this effect is minimal (e.g., when pumping deeper in the normally-dispersive regime, such that the power-containing term in equation 1 becomes small), or where wavelength-tunable sources can compensate for this effect. It is therefore of interest to consider the pulse dynamics of constant-energy scaling in the absence of this shift. As we will see, this line of inquiry will ultimately help clarify an important aspect of optimizing FOPCPA systems in general.
We begin by simulating a CW-seeded FOPCPA system with varying pump parameters. The pump is centered at 1030 nm, while the seed is placed at 950 nm. The pump’s energy and transform-limited duration are held constant at 20 μJ and 140 fs, respectively, while its linearly-chirped duration and peak power are allowed to vary. A high-order supergaussian pump shape (2m = 16) is used to ensure that XPM effects are uniform across most of the pulse. The fiber length is set to 1 cm for a pump with 75 kW of peak power, and is scaled inversely with the pump power so as to compare like stages in the conversion process. At the pump’s center wavelength, the PCF has a nonlinear parameter of γ = 11.1/(kW · m), a group-velocity dispersion of 200 fs2/mm, and a third-order dispersion of −7475 fs3/mm in all cases, while the fourth-order dispersion is varied to keep the peak gain at 950 nm at different pump powers (see Table I). We emphasize that these parameters are not intended to be realistic; rather, they are chosen so as to isolate and clearly illustrate a facet of the underlying pulse propagation dynamics. In the same vein, Raman scattering and self-steepening are neglected here.
TABLE I:
Simulation parameters corresponding to Figure 8. The pump’s center wavelength is used for evaluating β4.
| Pump Power (kW) |
Fiber Length (cm) |
β4 (fs4/mm) |
Idler Energy (nJ) |
Gain Chirp Factor |
|---|---|---|---|---|
| 50 | 1.5 | −1.249×105 | 1790 | −0.96 |
| 75 | 1.0 | −1.368×105 | 3320 | −0.69 |
| 100 | 0.75 | −1.487×105 | 4400 | −0.48 |
| 200 | 0.38 | −1.962×105 | 4910 | 0.00 |
| 400 | 0.19 | −2.912×105 | 4790 | 0.39 |
| 1600 | 0.047 | −8.613×105 | 4480 | 0.82 |
The results of these simulations are shown in Figure 8. As the pump power increases from 50 kW to 200 kW, the efficiency of the conversion to the idler at 1125 nm initially improves. There are several reasonable-sounding explanations for this, such as the increase of the four-wave-mixing bandwidth with power [9] or the lessening of walk-off effects as the fiber length is decreased (with the total walk-off falling from 2 ps to 0.3 ps over the range of conditions shown). However, none of these hypotheses can explain what happens next: as the power continues to increase beyond 200 kW, the converted energy reaches a maximum and then begins to wane. In the process, the locus of conversion shifts towards the trailing edge of the pulse. Clearly, the peak pump power has a non-trivial effect on the underlying pulse dynamics.
FIG. 8:
Scaling CW-seeded FOPCPA simulations in the time domain at constant pump energy. The resulting pump (solid green) and idler (dashed red) pulses are shown, while the labels give the initial pump peak powers and the output idler energies. Note the changing axis scales.
To clarify this mechanism, we note that broadband FOPCPA seeded by a CW seed fundamentally differs from typical amplification schemes in that the desired wave is not seeded. Rather, a signal is seeded at some other wavelength, and it is the amplification of that wave that causes the desired pulse to be generated as a byproduct. This is, in a sense, the inverse of the typical broadband amplification problem: instead of using one pump wavelength to amplify an array of different signal wavelengths, CW-seeded FOPCPA involves many different pump wavelengths amplifying a single, common signal wavelength. The more pump wavelengths that participate in this process, the more broadband the generated byproduct will be, up to an idler bandwidth of twice the pump bandwidth (as per Eqn. 2). The effective gain spectrum obtained in the idler region is determined by a sum over the pump frequencies, weighted not by their individual four-wave-mixing gain spectra as one might intuitively expect, but by the overlap of those spectra with the seed wavelength.
We can further our understanding of this effect by considering the parametric gain chirp. Our treatment of this parameter systematically extends that presented in [37]. The CW analysis of four-wave-mixing [9, 24] gives the offset between the pump and signal/idler frequencies as a function of the dispersion coefficients as evaluated at the pump frequency. If we allow the pump frequency to vary slightly, not only will the reference point for that offset change, but so will the offset’s magnitude as the dispersion coefficients are reevaluated at the new pump frequency. Thus, varying the pump frequency will produce some different sweep in the peak gain frequency. We define the gain chirp factor as this rate of change of the peak parametric gain frequency with respect to the pump frequency. If the gain chirp factor were identically zero, then every spectral component of a broadband pump would produce peak parametric gain at the same signal wavelength, leading to the maximally efficient scenario for CW-seeded FOPCPA. For a CW seed, this is the chirp-matched case. This idea of chirp-matching has been explored in fiber optical parametric amplifiers [22, 35-37, 44, 58], optical parametric oscillators [59] and Raman fiber amplifiers [21]; here, we formalize it in terms of the pump and fiber parameters for the case of four-wave-mixing with a fixed sideband frequency.
Mathematically, let a fiber have second-, third-, and fourth-order dispersion coefficients β2, β3, and β4, defined at some fixed frequency ω0. We will implicitly assume that β2 > 0 and β4 < 0, so as to realize phase-matching at large frequency offsets. We define the pump, signal, and idler frequencies respectively as:
| (6) |
| (7) |
| (8) |
Bearing in mind that the dispersion coefficients relevant to phase-matching will vary as a function of Ωp, the linear wavevector mismatch can be written as:
| (9) |
| (10) |
where βs,i,p denotes the wavevector magnitude of the signal, idler, or pump frequency, respectively, and assuming that ∣Ωp∣ ⪡ ∣Ω∣, we have neglected terms higher than first-order in Ωp. It is well-known that maximal parametric gain occurs at values of Ω that satisfy Δβ + 2γP = 0 [9]; by differentiating this expression with respect to Ωp, we arrive at an expression for the gain chirp factor, ρ:
| (11) |
Alternatively, rewriting β4 in terms of the peak power for a fixed value of Ω:
| (12) |
Given some (linear) pump chirp ∂ωp/∂t = αp, the peak of the parametric gain will be chirped as ∂ωgain/∂t = ραp in the vicinity of the signal band. Equation 12 makes clear the role of the peak power, and the trend observed in Figure 8. As shown in Table I, the gain chirp factor vanishes for a peak power of 200 kW in the simulated system. Hence, this is the gain chirp matched case mentioned previously, where all of the pump components amplify the same seed wavelength. It is this peak power that gives the maximally efficient, uniform conversion shown in Figure 8d, while for other values of the peak power, the non-zero gain chirp leads to some pump components contributing imperfectly to the amplification process.
An interesting feature of equation 12, which has been observed previously [37], is the appearance of the third-order dispersion coefficient. In the standard, CW analysis of four-wave-mixing, the third-order dispersion is dismissed as irrelevant to four-wave-mixing: the dispersion coefficients are defined about some fixed pump wavelength, causing the odd-order dispersive terms to cancel without affecting the phase-matching relation [9, 60]. However, defining the dispersion coefficients instead about some reference frequency and allowing the pump to vary shows that the third-order dispersion in fact controls the leading-order correction to the gain chirp factor. While the importance of the third-order dispersion is implicitly contained within the standard formulation (e.g., by letting the dispersion coefficients vary as functions of the pump frequency), we find it insightful to show it explicitly because it plays a marked role in the analysis below.
A useful consequence of this behavior is that the third-order dispersion can be used to vary the gain chirp factor independently of the other system parameters. Figure 9 depicts the simulated output of several FOPCPA systems which are identical but for the third-order dispersion, which is chosen to obtain gain chirp factors between 0 and 1.8. In all cases, a 1030-nm supergaussian pump (2m = 8) with a peak power of 10 kW, a transform-limited FWHM duration of 220 fs, and a linearly up-chirped FWHM duration of 70 ps is launched alongside a 850-nm CW seed with a 40-mW peak power, and propagation is simulated through 6.5 cm of the fiber used in Figure 11c (with β3 varied as needed). At ρ = 0, conversion to the idler takes place nearly uniformly over a broad duration (and therefore, due to the chirped pump, a broad bandwidth). As ρ increases, different temporal and spectral components experience different degrees of conversion, reducing the chirped duration, bandwidth, and energy of the generated idler. Similar results are observed for ρ < 0, with the time axis simply being reversed. It can be seen in Figure 10 that the energy and chirped duration (and consequently, the bandwidth) of the idler are approximately Lorentzian in ρ. Note that for a CW seed, the gain chirp factor has no direct effect on the idler’s chirp; rather, it helps determine the temporal/spectral window over which parametric conversion occurs, with the idler’s chirp always obeying equation 2 within that window.
FIG. 9:
Pump and idler pulses at the output of simulated FOPCPAs with different gain chirp factors obtained by varying β3.
FIG. 11:
Simulations of FOPCPAs with the dispersion coefficients at the pump wavelength given. Left: output pump (green) and idler (red) in the time domain. Right: corresponding spectra. The CW parametric gain spectra (dashed violet) calculated at the central pump frequencies vary widely in bandwidth, while the resulting pump and idler pulses remain largely unchanged.
FIG. 10:
Idler energies and chirped (FWHM) durations obtained from simulated FOPCPAs with different gain chirp factors.
The widths of the Lorentzians shown in Figure 10—i.e., the sensitivity of a system to the gain chirp factor—depend on the phase-matching bandwidth of a given, quasi-CW component. Provided that the gain chirp is perfectly matched, however, the phase-matching bandwidth is essentially irrelevant. For instance, Figure 11 depicts simulations of three different FOPCPA systems, with β2 and β4 adjusted to vary the phase-matching bandwidth at a constant frequency offset and β3 tuned to maintain perfect gain chirp matching (ρ = 0). The undepleted parametric gain spectra for the central pump frequency (calculated using the CW approach [9]) are shown in violet in panels (a.ii), (b.ii), and (c.ii), with bandwidths of roughly thrice, half, and 1/7th the idler bandwidths, respectively, measured at the −3 dB points relative to the maximum gain or idler intensities. Nevertheless, because all of the pump frequencies are contributing in each case, the generated idlers are almost identical in energy and bandwidth, evincing the central importance of gain chirp matching in FOPCPA systems.
Although varying the third-order dispersion is a convenient tool for isolating fundamental, gain-chirp-related dynamics, it is rarely a degree of freedom accessible in experiments. In practice, the wavelength and peak power of the pump are much more readily adjustable parameters. While practical or physical considerations may prevent perfect gain chirp matching from being achieved, a proper choice of these parameters (e.g., by prechirping the pump) can still help reduce the gain chirp mismatch and improve the efficiency of an FOPCPA system. Another feature that may affect the system performance is the sign asymmetry inherent to equation 12: if the output wavelength is flexible, choosing to seed the Stokes vs. the anti-Stokes wavelength (i.e., changing the sign of Ω) will flip the sign of the second term in equation 12, potentially bringing the gain chirp for that process closer to zero.
We have thus far neglected the shift in the gain spectrum as the pump depletes, and as the signal/idler powers become comparable to the remaining pump power. A full analysis that includes this phenomenon is quite complicated, and has been discussed both in general terms [61, 62] and as a source of undesirable structure in FOPCPA systems [63, 64] elsewhere. Furthermore, pump depletion effects are clearly relevant to the experimental and numerical results presented above, which exhibit local pump depletions of 50% or more. It is therefore noteworthy that the trends predicted from our small-signal analysis are borne out in Figures 8-11, as well as in the results that follow in section IV. No implicit assumptions about the relative pump, signal, and idler powers are made in the presented simulations. These findings suggest that pump depletion has only a small effect on the chirp-matching dynamics of the FOPCPA systems discussed here. Additional work may shed light on the reasons for this surprising conclusion, and whether pump depletion can be incorporated into a more rigorous theoretical framework.
IV. CONTINUUM-SEEDED FOPCPA
A. Overview
A second class of FOPCPA systems involves replacing the narrowband, CW seed with a broadband, stretched pulse. From a practical point of view, this approach has much to recommend it: in contrast with the CW-seeded case, the system can be entirely driven by a single oscillator, with no second, narrowband source needed. Broadband seed generation can be accomplished through any number of standard fiber techniques, such as the soliton self-frequency shift [7, 8], dispersive wave generation [65], or coherent supercontinuum generation [66, 67], with the FOPCPA conveniently compensating for the inherently low-energy nature of these fiber processes. Nevertheless, seeding with a broadband pulse adds its own set of complications. The generated seed must be coherent and highly stable, with low jitter in its energy, wavelength, and phase. The pump and seed pulses must also be both synchronized and roughly matched in duration, a process which can become technically involved when pulses at widely-separated wavelengths are involved. The degree to which these challenges will yield a net advantage over the CW-seeded case will depend on the needs of individual systems and applications. Provided these conditions can be fulfilled, however, continuum-seeded FOPCPA systems can exhibit impressive performance [42, 44], motivating a closer look at the underlying pulse propagation dynamics. Here, we consider continuum-seeded FOPCPA as a logical extension of the CW-seeded case. We find that under optimal conditions, continuum-seeded FOPCPA has the potential to significantly outperform its CW-seeded counterpart, producing pulses with a broad range of colors and bandwidths.
B. Gain chirp revisited
In section IIIC, we investigated how the parametric gain chirp affects the pulse dynamics in a CW-seeded FOPCPA. Here, we extend that analysis to the continuum-seeded case. Recall that when the seed is CW, a gain chirp factor near zero is desirable so that many pump frequencies can collectively amplify the same, fixed wavelength; this allows each pump frequency to contribute to the conversion process and efficiently generate an idler component at a different frequency. With a chirped seed, however, this is no longer necessary: even if the gain chirp is far from zero, the seed wavelength can vary in time to follow the shifting gain peak, maintaining optimal conversion.
A simple, analytical model serves to illustrate the modified situation. Let the pump and seed pulses both be linearly chirped:
| (13) |
| (14) |
where we have now lifted the CW assumption of αs = 0. The idler frequency follows accordingly:
| (15) |
We define the gain chirp factor ρ ≡ ∂ωs/∂ωp as before. The shifting gain peak in the region of the seed can then be written:
| (16) |
Matching the seed to the gain chirp implies ωs = ωgain at all times, from which we obtain the seed and idler chirps:
| (17) |
| (18) |
Since the signal and idler will have comparable durations, αs and αi are furthermore proportional to the two pulses’ bandwidths. Thus, we see that under perfect gain chirp matching, the fiber magnifies the pump bandwidth by a factor of ρ during transfer to the signal and (2–ρ) during transfer to the idler (less some factor related to the imperfect conversion in the lower-intensity wings of the pump). If both of these magnification factors are far from zero, highly broadband pulses can be generated from even a narrowband pump, provided that a sufficiently broadband seed can be supplied. This stands in contrast with the CW-seeded case, where the idler’s maximum bandwidth is limited to twice that of the pump—not surprising in light of equation 18, when the CW chirp-matching condition ρ = 0 is applied. Note that a matched seed might be chirped with either the same sign or the opposite sign as the pump, depending on the sign of ρ. It is furthermore worth observing that, provided the gain chirp is matched, the idler’s bandwidth is entirely determined by ρ and the pump bandwidth.
To verify this result numerically, we simulate a series of FOPCPAs using a linearly-chirped pump and seed. A supergaussian pump (2m = 4), a peak power of 10 kW, a linearly-chirped FWHM duration of 50 ps, and a transform-limited FWHM duration of 200 fs is launched. The supergaussian (2m = 6) seed has a 40-mW peak power and a fixed duration that greatly exceeds that of the pump, while its bandwidth is allowed to vary to produce various linear chirps. This amounts to varying as in equations 13-18 while leaving the signal and pump temporal intensities unchanged. Readers will note that this is not a situation easily achieved in experiments: more commonly, a seed is generated with some fixed bandwidth and then dispersively stretched to adjust its chirp, duration, and peak power simultaneously. Rather, our choice of varying the bandwidth under an invariant temporal intensity envelope is a convenient numerical approach that helps isolate the effect of chirp-matching alone. In each case, we vary the gain chirp factor via the third-order dispersion as in section IIIC while adjusting the seed chirp to match the gain chirp. Propagation is simulated through 4.3 cm of fiber with β2 = 4 fs2/mm, β4 = −439 fs4/mm, β5 = β6 = 0, and γ = 11/(kW · m) at the 1030-nm pump wavelength, with self-steepening effects included.
Figure 12 summarizes the results of these simulations. As expected, the gain chirp matching means the pump always experiences efficient, uniform conversion, with the energies and chirped durations of the signal and idler remaining approximately constant (Fig. 12a). This is in spite of pump being locally depleted by more than 50% (see inset, e.g.), supporting our neglect of pump depletion effects in our analysis. Indeed, if the output is observed at an earlier point in the propagation, the slight curvature visible in panel 12a becomes greatly flattened, reducing the range of energies from 6% to 0.2% relative to the mean.
FIG. 12:
Signal and idler parameters for different gain chirp factors. In each case, the seed chirp is perfectly matched to the gain chirp. In all cases, durations are measured using the full-width-at-half-maximum. TL: transform limit. Inset: initial pump and output pump, signal, and idler powers for ρ = 3.
The signal and idler bandwidths follow absolute-value trends centered at ρ = 0 and ρ = 2, respectively. This follows naturally from equations 17-18, both in the functional form and in the particular values of ρ at which the signal or idler bandwidth vanishes. In Figure 12, these bandwidths have been plotted as the reciprocals of the signal and idler’s FWHM transform-limited durations; note that this definition of spectral bandwidth differs from others such as the root-mean-square or FWHM by only a shape-dependent constant, leaving that conversion extraneous to the qualitative behavior discussed here. The ρ = 2 case, yielding a narrowband idler, can be viewed as a parametric analogue to coherent Raman scattering with spectral focusing [68, 69]. This use of chirp-matched pump and signal pulses to produce efficient four-wave-mixing with spectral magnification or compression has also been previously studied in the context of optical signal processing [70, 71], although the role of the fiber properties and the implications for high-energy amplification have not yet been systematically explored. Note that even when one pulse’s bandwidth goes to zero, the other’s can remain appreciable, offering the possibility of generating synchronized pairs of femtosecond and picosecond pulses.
To gain a fuller picture of these gain dynamics, we consider two cases in greater depth: one with a moderate gain chirp factor (ρ = 1), and another with a large one (ρ = 10). For each of these gain chirp factors, we vary the seed chirp relative to the pump chirp (αs/αp) while holding the pulse durations fixed. The stretched seed duration is always much longer than the pump, making this functionally equivalent to fine-tuning the stretching factor of an arbitrarily broadband seed at constant peak power.
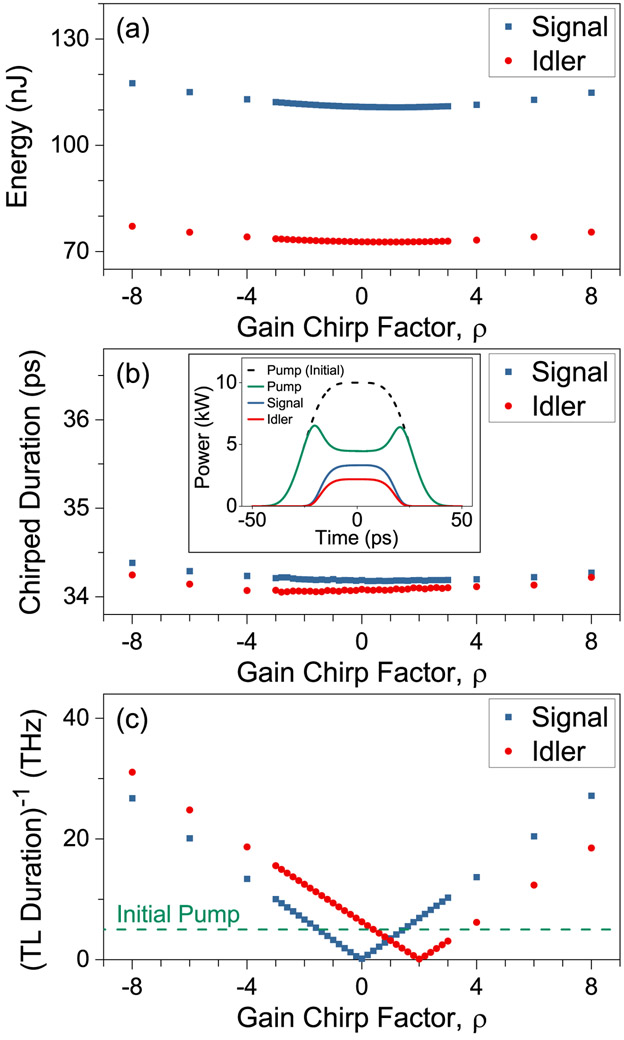
The energies and bandwidths of the signal and idler pulses for ρ = 1 are shown in Figure 13. The converted energy reaches a peak at a relative seed chirp of 1, indicating the perfect gain chirp matching at this point. Meanwhile, the generated signal and idler bandwidths decrease to zero at relative seed chirps of 0 and 2, respectively. While the lack of perfect gain chirp matching at these points means equations 17 and 18 do not strictly hold, the same qualitative behavior is apparent: a relative seed chirp of 0 means there is no signal bandwidth to begin with (i.e., the CW-seeded case), whereas a relative seed chirp of 2 results in spectral focusing to a narrowband idler. Importantly, these two zero-bandwidth points occur near the relative gain chirp that maximizes the converted energy. Thus, this value of ρ is well-suited for generating narrowband pulses, but cannot be used to obtain pulses that are simultaneously energetic and broadband.
FIG. 13:
Signal and idler parameters for different relative seed chirps, αs/αp, and a constant gain chirp factor of ρ = 1. The point where the seed is matched to the gain chirp is shown as a dashed line. Durations are measured using the full-width-at-half-maximum.
A different picture emerges when ρ is increased to 10 (Figure 14). The generated bandwidths behave qualitatively the same as before, with the signal and idler becoming narrowband at relative seed chirps of 0 and 2, respectively. In this case, however, the gain chirp is perfectly matched at a relative seed chirp of 10. As a result, the maximum energy point shifts to a higher relative seed chirp, away from the narrowband regions. The resulting pulses boast both high conversion efficiencies and short durations, with simulations producing ~30-40-fs signal and idler pulses despite the pump’s transform limited duration being only 200 fs. Even larger gain chirp factors serve to enhance this effect by further magnifying the pump bandwidth: provided that a seed with the requisite chirp can be generated, ultrashort continuum-seeded FOPCPA sources benefit from ρ being far from 0 and 2, such that ∣αs∣, ∣αi∣ ⪢ ∣αp∣ (Eqs. 17-18). As discussed in section IIIC, this holds even if the phase-matching bandwidth of any given pump component is narrow, as long as the gain-chirp-matching condition is satisfied. This conclusion should be compared to the CW-seeded case, where the lack of freedom in the seed chirp pins the optimal gain chirp factor to ρ = 0, with more modest performance. Once broadband and efficient amplification is achieved, the energy can be scaled as usual by stretching the pump and seed in tandem, taking care to preserve the relative chirp between them. These results are consistent with those presented in recent numerical work [44], which demonstrates an optimally-efficient pump/seed chirp ratio that produces a constant idler bandwidth, although the fixed fiber length and the unknown gain chirp factor preclude more direct comparisons to this work.
FIG. 14:
Signal and idler parameters for different relative seed chirps, αs/αp, and a constant gain chirp factor of ρ = 10. The point where the seed is matched to the gain chirp is shown as a dashed line. Durations are measured using the full-width-at-half-maximum.
In principle, each part of the FOPCPA system need only fulfill one role well: the pump supplies energy, the seed provides bandwidth, and the fiber properties magnify or shrink the available bandwidth as needed. With only a singular demand on each individual component, the potential exists for such systems to be optimized modularly, facilitating their engineering. This division of labor underlies the possibility of continuum-seeded FOPCPA sources with unprecedented performance. Continued research into coherent, broadband seed generation [72, 73] and the design of photonic crystal fibers with large gain chirp factors will be important for taking advantage of this capability.
C. Experimental results
To test these predictions, we perform experiments using the system depicted in Figure 15. A modelocked oscillator generates femtosecond pulses at 1560 nm and a repetition rate of 80 MHz, and the output is subsequently split between two branches. One beam is frequency-converted to 1060 nm using dispersive wave generation [65] and subsequently amplified in a Yb-doped fiber amplifier, while the other is used to generate a coherent supercontinuum spanning ~27 THz (FWHM) about 1300 nm. Both pulses naturally emerge from these processes positively chirped; a dispersion-shifted fiber (OFS PM Raman, 2.5 m) is used to further positively stretch the supercontinuum seed to ~11 ps (FWHM, calculated using the fiber dispersion), while a grating compressor is placed after the Yb-doped fiber amplifier in order to give it a tunable, negative chirp. The resulting, 1060-nm pump has an average power of up to 3 W, a bandwidth of 3.7 THz, and a duration that can be varied from ≈5 ps to ≈21 ps (Fig. 15).
FIG. 15:
(a) Schematic of an experimental FOPCPA system. EDFA: Er-doped fiber amplifier. YDFA: Yb-doped fiber amplifier. HNLF: highly-nonlinear fiber. DSF: dispersion-shifted fiber. TBPF: tunable bandpass filter. ODL: optical delay line. PCF: photonic crystal fiber. (b) Input spectra of the pump (solid black) and seed (dashed red), and (c) autocorrelation of the pump pulses before the grating compressor.
The pump and seed pulses are synchronized and coupled into 30 cm of PCF (NKT Photonics LMA-PM-5). Typical dispersion characteristics for this fiber are available from the manufacturer [74]; given the uncertainty involved in drawing such small-core fibers, we use the measured spontaneous parametric fluorescence spectrum to fine-tune the nominal parameters, arriving at β2 = 0.85 fs2/mm, β3 = 68.9 fs3/mm, and β4 = −116 fs4/mm about the 1060-nm pump. The nonlinear coefficient γ is taken to be 9/(kW · m) at the pump wavelength. Dispersive orders fifth and higher are assumed to be zero, as they amount to only small correction terms. Finally, for each pump duration, the pump-seed delay is adjusted to maximize the anti-Stokes power observed at the PCF output.
We measure the FOPCPA output across the full range of obtainable pump durations, varying the pump energy in each case to maintain a constant peak power of 0.9 kW. The resulting (anti-Stokes) idler and (Stokes) signal spectra are shown in Figures 16a and 16b, respectively. These results are further summarized in Figure 17, which illustrates (a) the bandwidth of the signal and idler, and (b) the efficiency of power conversion to the idler. Note that these plots cannot be directly compared to Figures 13 and 14: the latter two effectively vary the seed duration with a constant pump, whereas here, it is the seed that is fixed while the pump duration is swept. The plots also differ in that, because the pump energy is not held constant in experiments, it is more useful to plot the idler conversion efficiency rather than the absolute idler power. Nevertheless, the same qualitative trends are visible: as the pump increases in duration, it overlaps with more of the chirped seed’s frequency components, resulting in a general increase in the signal and idler bandwidths. Deviations from this trend, as well as the appearance of spectral structures, may be linked to the pump’s own spectral modulations mapping onto the time domain as it becomes more highly-chirped. The transfer of the seed’s bandwidth to the idler in spite of the relatively narrowband pump is evident in these plots, with the most broadband signal and idler pulses supporting FWHM transform-limited durations of 17 fs (4 cycles) and 24 fs (8 cycles), respectively. Dechirping such broadband, few-cycle pulses is a daunting task, but one that may benefit from pre-shaping of the pump phase as per section III B.
FIG. 16:
Experimental (a) idler and (b) signal spectra measured as a function of the pump duration. Pump autocorrelation FWHM durations are given in the legend.
FIG. 17:
(a) Bandwidths of the spectra shown in Figure 16. (b) Idler power conversion efficiency as a function of the pump duration.
In addition to the observed trends, these results furthermore show quantitative agreement with theory. Theoretically perfect gain chirp matching with linearly-chirped pulses would correspond to:
| (19) |
where Ωs,p and τs,p are the bandwidths and chirped durations of the seed and pump, respectively. Using equation 12, we calculate the gain chirp factor to be ρ = −8.6. For the measured pump and seed bandwidths, and the estimated seed duration, we arrive at an ideal pump duration of −13 ps (i.e., 13 ps with a chirp opposite that of the seed). Given a reasonable pulse shape, such a duration would manifest as a FWHM autocorrelation duration of ≈18-20 ps, in excellent agreement with the observed conversion efficiency maximum. In addition to validating the theoretical framework presented here, these results also suggest a strategy for scaling up the performance of such systems, by stretching the pump and seed in tandem so as to remain at the maximally efficient gain chirp matching point.
V. CONCLUSION
In summary, we have investigated the propagation dynamics of FOPCPA systems by analytical, numerical, and experimental means. We have studied the interactions between the pump, seed, and idler pulses, as well as how these are mediated by the properties of the fiber itself. A uniform pump can cleanly transfer its phase onto the idler, while a peaked pump can thwart this mirroring, providing opportunities for pre-shaping or pulse-cleaning as desired. We have also developed a framework for understanding the parametric gain chirp and its effect on both CW-seeded and continuum-seeded FOPCPAs. In the CW-seeded case, the system depends on an inversion of the standard amplification problem: rather than trying to directly amplify a multitude of seed frequencies, the goal is for all of the pump frequencies to amplify a single seed frequency, yielding a vanishing gain chirp and an energetic idler with up to twice the pump’s bandwidth. Although the amplified signal is not typically usable, this approach stands to be the simplest for femtosecond applications that require only a single wavelength. On the other hand, more demanding applications can benefit from the additional degree of freedom unlocked by using a continuum seed. In this case, the gain chirp factor modifies how the pump bandwidth transfers to the signal and idler, allowing combinations of broad or narrow signal and idler bandwidths to be achieved with a given pump without sacrificing power. Taking these dynamics into account will help enable the design of FOPCPA systems with a wide-ranging set of parameters, each tailor-made for a given application.
Acknowledgments
FUNDING
National Institutes of Health (NIH) (EB002019).
Footnotes
DISCLOSURES
WF: (P). RH: TOPTICA Photonics AG (E,I,P). FWW: (P).
References
- [1].Xu C and Wise FW, “Recent advances in fibre lasers for nonlinear microscopy,” Nat. Photonics 7, 875–882 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].Hofer R, Hofer M, Reider GA, Cernusca M, and Ober MH, “Modelocking of a Nd-fiber laser at 920 nm,” Opt. Commun 140, 242–244 (1997). [Google Scholar]
- [3].Qian K, Wang H, Laroche M, and Hideur A, “Mode-locked Nd-doped fiber laser at 930 nm,” Opt. Lett 39, 267–270 (2014). [DOI] [PubMed] [Google Scholar]
- [4].Daniel JMO, Simakov N, Tokurakawa M, Ibsen M, and Clarkson WA, “Ultra-short wavelength operation of a thulium fibre laser in the 1660–1750 nm wavelength band,” Opt. Express 23, 18269–18276 (2015). [DOI] [PubMed] [Google Scholar]
- [5].Dianov EM, “Bismuth-doped optical fibers: a challenging active medium for near-IR lasers and optical amplifiers,” Light Sci. & Appl 1, e12 (2012). [Google Scholar]
- [6].Duval S, Gauthier J-C, Robichaud L-R, Paradis P, Olivier M, Fortin V, Bernier M, Piché M, and Vallée R, “Watt-level fiber-based femtosecond laser source tunable from 2.8 to 3.6 μm,” Opt. Lett 41, 5294–5297 (2016). [DOI] [PubMed] [Google Scholar]
- [7].Mitschke FM and Mollenauer LF, “Discovery of the soliton self-frequency shift,” Opt. Lett 11, 659–661 (1986). [DOI] [PubMed] [Google Scholar]
- [8].Gordon JP, “Theory of the soliton self-frequency shift,” Opt. Lett 11, 662–664 (1986). [DOI] [PubMed] [Google Scholar]
- [9].Agrawal GP, Nonlinear Fiber Optics (Academic Press, New York, 2001), 3rd ed. [Google Scholar]
- [10].Horton NG, Wang K, Kobat D, Clark CG, Wise FW, Schaffer CB, and Xu C, “In vivo three-photon microscopy of subcortical structures within an intact mouse brain,” Nat. Photonics 7, 205–209 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Gérôme F, Cook K, George AK, Wadsworth WJ, and Knight JC, “Delivery of sub-100fs pulses through 8m of hollow-core fiber using soliton compression,” Opt. Express 15, 7126–7131 (2007). [DOI] [PubMed] [Google Scholar]
- [12].Rishøj L, Prabhakar G, Demas J, and Ramachandran S, “30 nJ, ~50 fs All-Fiber Source at 1300 nm using Soliton Shifting in LMA HOM Fiber,” in Conference on Lasers and Electro-Optics, (OSA, San Jose 2016), p. STh3O.3. [Google Scholar]
- [13].Rishøj L, Tai B, Kristensen P, and Ramachandran S, “Discovery of Soliton Self-Mode Conversion in Multimode Optical Fibers,” arXiv preprint arXiv:1805.06037 (2018). [Google Scholar]
- [14].Liu W, Li C, Zhang Z, Kärtner FX, and Chang G, “Self-phase modulation enabled, wavelength-tunable ultrafast fiber laser sources: an energy scalable approach,” Opt. Express 24, 15328–15340 (2016). [DOI] [PubMed] [Google Scholar]
- [15].Chung H-Y, Liu W, Cao Q, Song L, Kärtner FX, and Chang G, “Megawatt peak power tunable femtosecond source based on self-phase modulation enabled spectral selection,” Opt. Express 26, 3684–3695 (2018). [DOI] [PubMed] [Google Scholar]
- [16].Kharenko DS, Bednyakova AE, Podivilov EV, Fedoruk MP, Apolonski A, and Babin SA, “Feedback-controlled Raman dissipative solitons in a fiber laser,” Opt. Express 23, 1857–1862 (2015). [DOI] [PubMed] [Google Scholar]
- [17].Churin D, Olson J, Norwood RA, Peyghambarian N, and Kieu K, “High-power synchronously pumped femtosecond Raman fiber laser,” Opt. Lett 40, 2529–2532 (2015). [DOI] [PubMed] [Google Scholar]
- [18].Kharenko DS, Bednyakova AE, Podivilov EV, Fedoruk MP, Apolonski A, and Babin SA, “Cascaded generation of coherent Raman dissipative solitons,” Opt. Lett 41, 175–178 (2016). [DOI] [PubMed] [Google Scholar]
- [19].Kharenko DS, Efremov VD, Evmenova EA, and Babin SA, “Generation of Raman dissipative solitons near 1.3 microns in a phosphosilicate-fiber cavity,” Opt. Express 26, 15084–15089 (2018). [DOI] [PubMed] [Google Scholar]
- [20].Batjargal O, Ou Y-H, Keikens K, Barton JK, and Kieu K, “All-Fiber Dissipative Soliton Raman Laser Based on Phosphosilicate Fiber,” IEEE Photonics Technol. Lett 30, 1846–1849 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21].Hardy M, Olivier M, and Piché M, “Analytical model for synchronous Raman amplification of high-energy ultrashort pulses in optical fibers,” J. Opt. Soc. Am. B 32, 1593–1603 (2015). [Google Scholar]
- [22].Fourcade-Dutin C, Vanvincq O, Mussot A, Hugonnot E, and Bigourd D, “Ultrabroadband fiber optical parametric amplifier pumped by chirped pulses. Part 2: sub-30-fs pulse amplification at high gain,” J. Opt. Soc. Am. B 32, 1488–1493 (2015). [Google Scholar]
- [23].Wei X, Tan S, Mussot A, Kudlinski A, Tsia KK, and Wong KKY, “110 nm versatile fiber optical parametric amplifier at 1.0 μm,” Opt. Lett 40, 4090–4093 (2015). [DOI] [PubMed] [Google Scholar]
- [24].Pitois S and Millot G, “Experimental observation of a new modulational instability spectral window induced by fourth-order dispersion in a normally dispersive single-mode optical fiber,” Opt. Commun 226, 415–422 (2003). [Google Scholar]
- [25].Chemnitz M, Baumgartl M, Meyer T, Jauregui C, Dietzek B, Popp J, Limpert J, and Tünnermann A, “Widely tuneable fiber optical parametric amplifier for coherent anti-Stokes Raman scattering microscopy,” Opt. Express 20, 26583–26595 (2012). [DOI] [PubMed] [Google Scholar]
- [26].Gottschall T, Meyer T, Baumgartl M, Dietzek B, Popp J, Limpert J, and Tünnermann A, “Fiber-based optical parametric oscillator for high resolution coherent anti-Stokes Raman scattering (CARS) microscopy,” Opt. Express 22, 21921–21928 (2014). [DOI] [PubMed] [Google Scholar]
- [27].Gottschall T, Meyer T, Schmitt M, Popp J, Limpert J, and Tünnermann A, “Four-wave-mixing-based optical parametric oscillator delivering energetic, tunable, chirped femtosecond pulses for non-linear biomedical applications,” Opt. Express 23, 23968–23977 (2015). [DOI] [PubMed] [Google Scholar]
- [28].Demas J, Prabhakar G, He T, and Ramachandran S, “Wavelength-agile high-power sources via four-wave mixing in higher-order fiber modes,” Opt. Express 25, 7455–7464 (2017). [DOI] [PubMed] [Google Scholar]
- [29].Sharping JE, Pailo C, Gu C, Kiani L, and Sanborn JR, “Microstructure fiber optical parametric oscillator with femtosecond output in the 1200 to 1350 nm wavelength range,” Opt. Express 18, 3911–3916 (2010). [DOI] [PubMed] [Google Scholar]
- [30].Nguyen TN, Kieu K, Maslov AV, Miyawaki M, and Peyghambarian N, “Normal dispersion femtosecond fiber optical parametric oscillator,” Opt. Lett 38, 3616–3619 (2013). [DOI] [PubMed] [Google Scholar]
- [31].Gottschall T, Limpert J, and Tünnermann A, “Ultra-short pulse fiber optical parametric oscillator,” Opt. Lett 42, 3423–3426 (2017). [DOI] [PubMed] [Google Scholar]
- [32].Herda R, “Fiber-Optical Parametric Amplifier pumped by Chirped-Femtosecond Pulses,” in Laser Congress 2017 (ASSL, LAC), (OSA, Nagoya: 2017), p. JTu2A.49. [Google Scholar]
- [33].Sharping JE, “Microstructure Fiber Based Optical Parametric Oscillators,” J. Light. Technol 26, 2184–2191 (2008). [Google Scholar]
- [34].Hanna M, Druon F, and Georges P, “Fiber optical parametric chirped-pulse amplification in the femtosecond regime,” Opt. Express 14, 2783–2790 (2006). [DOI] [PubMed] [Google Scholar]
- [35].Bigourd D, Lago L, Kudlinski A, Hugonnot E, and Mussot A, “Dynamics of fiber optical parametric chirped pulse amplifiers,” J. Opt. Soc. Am. B 28, 2848–2854 (2011). [Google Scholar]
- [36].Bigourd D, d’Augerès PB, Dubertrand J, Hugonnot E, and Mussot A, “Ultra-broadband fiber optical parametric amplifier pumped by chirped pulses,” Opt. Lett 39, 3782–3785 (2014). [DOI] [PubMed] [Google Scholar]
- [37].Vanvincq O, Fourcade-Dutin C, Mussot A, Hugonnot E, and Bigourd D, “Ultrabroadband fiber optical parametric amplifiers pumped by chirped pulses. Part 1: analytical model,” J. Opt. Soc. Am. B 32, 1479–1487 (2015). [Google Scholar]
- [38].Caucheteur C, Bigourd D, Hugonnot E, Szriftgiser P, Kudlinski A, Gonzalez-Herraez M, and Mussot A, “Experimental demonstration of optical parametric chirped pulse amplification in optical fiber,” Opt. Lett 35, 1786–1788 (2010). [DOI] [PubMed] [Google Scholar]
- [39].Zhou Y, Li Q, Cheung KKY, Yang S, Chui PC, and Wong KKY, “All-Fiber-Based Ultrashort Pulse Generation and Chirped Pulse Amplification Through Parametric Processes,” IEEE Photonics Technol. Lett 22, 1330–1332 (2010). [Google Scholar]
- [40].Bigourd D, Lago L, Mussot A, Kudlinski A, Gleyze J-F, and Hugonnot E, “High-gain fiber, optical-parametric, chirped-pulse amplification of femtosecond pulses at 1 μm,” Opt. Lett 35, 3480–3482 (2010). [DOI] [PubMed] [Google Scholar]
- [41].Cristofori V, Lali-Dastjerdi Z, Rishøj LS, Galili M, Peucheret C, and Rottwitt K, “Dynamic characterization and amplification of sub-picosecond pulses in fiber optical parametric chirped pulse amplifiers,” Opt. Express 21, 26044–26051 (2013). [DOI] [PubMed] [Google Scholar]
- [42].Morin P, Dubertrand J, d’Augeres PB, Quiquempois Y, Bouwmans G, Mussot A, and Hugonnot E, “μJ-level Raman-assisted fiber optical parametric chirped-pulse amplification,” Opt. Lett 43, 4683–4686 (2018). [DOI] [PubMed] [Google Scholar]
- [43].Fu W and Wise FW, “Normal-dispersion fiber optical parametric chirped-pulse amplification,” Opt. Lett 43, 5331–5334 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [44].Qin Y, Batjargal O, Cromey B, and Kieu K, “All-fiber high-power 1700 nm femtosecond laser based on optical parametric chirped-pulse amplification,” Opt. Express 28, 2317–2325 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [45].Schmidt BE, Thiré N, Boivin M, Larameé A, Poitras F, Lebrun G, Ozaki T, Ibrahim H, and Légaré F, “Frequency domain optical parametric amplification,” Nat. Communications 5, 3643 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [46].Schmidt BE, Lassonde P, Ernotte G, Clerici M, Morandotti R, Ibrahim H, and Légaré F “Decoupling Frequencies, Amplitudes and Phases in Nonlinear Optics,” Sci. Reports 7, 7861 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [47].Kuo BP-P and Radic S, “Fast wideband source tuning by extra-cavity parametric process,” Opt. Express 18, 19930–19940 (2010). [DOI] [PubMed] [Google Scholar]
- [48].Zhang C, Cheung KKY, Chui PC, Tsia KK, and Wong KKY, “Fiber-Optical Parametric Amplifier With High-Speed Swept Pump,” IEEE Photonics Technol. Lett 23, 1022–1024 (2011). [Google Scholar]
- [49].Cheng J-X, Volkmer A, Book LD, and Xie XS, “Multiplex Coherent Anti-Stokes Raman Scattering Microspectroscopy and Study of Lipid Vesicles,” J. Phys. Chem. B 106, 8493–8498 (2002). [Google Scholar]
- [50].Boyd RW, Nonlinear Optics (Academic, 2008). [Google Scholar]
- [51].NKT Photonics, “SC-5.0–1040,” https://www.nktphotonics.eom/wp-content/uploads/sites/3/2015/02/nonlinear-fibers.pdf?1585674422, accessed March 31, 2019.
- [52].Ross IN, Matousek P, New GHC, and Osvay K, “Analysis and optimization of optical parametric chirped pulse amplification,” J. Opt. Soc. Am. B 19, 2945–2956 (2002). [Google Scholar]
- [53].Shah L, Liu Z, Hartl I, Imeshev G, Cho GC, and Fermann ME, “High energy femtosecond Yb cubicon fiber amplifier,” Opt. Express 13, 4717–4722 (2005). [DOI] [PubMed] [Google Scholar]
- [54].Zhou S, Kuznetsova L, Chong A, and Wise FW, “Compensation of nonlinear phase shifts with third-order dispersion in short-pulse fiber amplifiers,” Opt. Express 13, 4869–4877 (2005). [DOI] [PubMed] [Google Scholar]
- [55].Kuznetsova LP and Wise FW, “Scaling of femtosecond Yb-doped fiber amplifiers to tens of microjoule pulse energy via nonlinear chirped pulse amplification,” Opt. Lett 32, 2671–2673 (2007). [DOI] [PubMed] [Google Scholar]
- [56].Sidorenko P, Fu W, and Wise FW, “Nonlinear ultrafast fiber amplifiers beyond the gain-narrowing limit,” Optica 6, 1328–1333 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [57].Krogen P, Suchowski H, Liang H, Flemens N, Hong K-H, Kärtner FX, and Moses J, “Generation and multi-octave shaping of mid-infrared intense single-cycle pulses,” Nat. Photonics 11, 222–226 (2017). [Google Scholar]
- [58].Podivilov EV, Kharenko DS, Bednyakova AE, Fedoruk MP, and Babin SA, “Spectral comb of highly chirped pulses generated via cascaded FWM of two frequency-shifted dissipative solitons,” Sci. Reports 7, 2905 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [59].Brinkmann M, Hellwig T, and Fallnich C, “Optical parametric chirped pulse oscillation,” Opt. Express 25, 12884–12895 (2017). [DOI] [PubMed] [Google Scholar]
- [60].Michel ME, Fiber Optical Parametric Amplifiers, Oscillators and Related Devices (Cambridge University Press, Cambridge, 2008). [Google Scholar]
- [61].Cappellini G and Trillo S, “Third-order three-wave mixing in single-mode fibers: exact solutions and spatial instability effects,” J. Opt. Soc. Am. B 8, 824–838 (1991). [Google Scholar]
- [62].Trillo S, Millot G, Seve E, and Wabnitz S, “Failure of phase-matching concept in large-signal parametric frequency conversion,” Appl. Phys. Lett 72, 150–162 (1998). [Google Scholar]
- [63].Bigourd D, Morin P, Dubertrand J, Fourcade-Dutin C, Maillotte H, Quiquempois Y, Bouwmans G, and Hugonnot E, “Parametric gain shaping from a structured pump pulse,” IEEE Photonics Technol. Lett 31, 214–217 (2019). [Google Scholar]
- [64].Fourcade-Dutin C, Imperio A, Dauliat R, Jamier R, Muñoz-Marco H, Pérez-Millán P, Maillotte H, Roy P, and Bigourd D, “Temporal Distribution Measurement of the Parametric Spectral Gain in a Photonic Crystal Fiber Pumped by a Chirped Pulse,” Photonics 6, 20–28 (2019). [Google Scholar]
- [65].Akhmediev N and Karlsson M, “Cherenkov radiation emitted by solitons in optical fibers,” Phys. Rev. A 51, 2602–2607 (1995). [DOI] [PubMed] [Google Scholar]
- [66].Liu Y, Zhao Y, Lyngsø J, You S, Wilson WL, Tu H, and Boppart SA, “Suppressing Short-Term Polarization Noise and Related Spectral Decoherence in All-Normal Dispersion Fiber Supercontinuum Generation,” J. Light. Technol 33, 1814–1820 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [67].Heidt AM, Feehan JS, Price JHV, and Feurer T, “Limits of coherent supercontinuum generation in normal dispersion fibers,” J. Opt. Soc. Am. B 34, 764–775 (2017). [Google Scholar]
- [68].Hellerer T, Enejder AM, and Zumbusch A, “Spectral focusing: High spectral resolution spectroscopy with broad-bandwidth laser pulses,” Appl. Phys. Lett 85, 25–27 (2004). [Google Scholar]
- [69].Fu D, Holtom G, Freudiger C, Zhang X, and Xie XS, “Hyperspectral Imaging with Stimulated Raman Scattering by Chirped Femtosecond Lasers,” J. Phys. Chem. B 117, 4634–4640 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [70].Salem R, Foster MA, and Gaeta AL, “Application of space-time duality to ultrahigh-speed optical signal processing,” Adv. Opt. Photonics 5, 274–317 (2013). [Google Scholar]
- [71].Guan P, Røge KM, Lillieholm M, Galili M, Hu H, Morioka T, and Oxenløwe LK, “Time Lens-Based Optical Fourier Transformation for All-Optical Signal Processing of Spectrally-Efficient Data,” J. Light. Technol 35, 799–806 (2017). [Google Scholar]
- [72].Tu H, Liu Y, Turchinovich D, Marjanovic M, Lyngsø JK, Lægsgaard J, Chaney EJ, Zhao Y, You S, Wilson WL, Xu B, Dantus M, and Boppart SA, “Stain-free histopathology by programmable supercontinuum pulses,” Nat. Photonics 10, 534–540 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [73].Fourcade-Dutin C and Bigourd D, “Near infrared tunable source delivering ultra-short pulses based on an all normal dispersion fiber and a zero dispersion line,” Appl. Phys. B 124, 154 (2018). [Google Scholar]
- [74].ThorLabs, Inc., “LMA-PM-5,” https://www.thorlabs.com/thorproduct.cfm?partnumber=LMA-PM-5, 2019.