Defining Spatial Relationships Between Spinal Cord Axons and Blood Vessels in Hydrogel Scaffolds

Abstract

Positively charged oligo(poly(ethylene glycol) fumarate) (OPF+) hydrogel scaffolds, implanted into a complete transection spinal cord injury (SCI), facilitate a permissive regenerative environment and provide a platform for controlled observation of repair mechanisms. Axonal regeneration after SCI is critically dependent upon nutrients and oxygen from a newly formed blood supply. Our objective was to investigate fundamental characteristics of revascularization in association with the ingrowth of axons into hydrogel scaffolds, thereby defining spatial relationships between axons and the neovasculature. A novel combination of stereologic estimates and precision image analysis techniques quantitate neurovascular regeneration in rats. Multichannel hydrogel scaffolds containing Matrigel-only (MG), Schwann cells (SCs), or SCs with rapamycin-eluting poly(lactic co-glycolic acid) microspheres (RAPA) were implanted for 6 weeks following complete spinal cord transection. Image analysis of 72 scaffold channels identified a total of 2494 myelinated and 4173 unmyelinated axons at 10 μm circumferential intervals centered around 708 individual blood vessel profiles. Blood vessel number, density, volume, diameter, intervessel distances, total vessel surface and cross-sectional areas, and radial diffusion distances were compared. Axon number and density, blood vessel surface area, and vessel cross-sectional areas in the SC group exceeded that in the MG and RAPA groups. Individual axons were concentrated within a concentric radius of 200–250 μm from blood vessel walls, in Gaussian distributions, which identified a peak axonal number (Mean Peak Amplitude) corresponding to defined distances (Mean Peak Distance) from each vessel, the highest concentrations of axons were relatively excluded from a 25–30 μm zone immediately adjacent to the vessel, and from vessel distances >150 μm. Higher axonal densities correlated with smaller vessel cross-sectional areas. A statistical spatial algorithm was used to generate cumulative distribution F- and G-functions of axonal distribution in the reference channel space. Axons located around blood vessels were definitively organized as clusters and were not randomly distributed. A scoring system stratifies 5 direct measurements and 12 derivative parameters influencing regeneration outcomes. By providing methods to quantify the axonal-vessel relationships, these results may refine spinal cord tissue engineering strategies to optimize the regeneration of complete neurovascular bundles in their relevant spatial relationships after SCI.

Impact statement

Vascular disruption and impaired neovascularization contribute critically to the poor regenerative capacity of the spinal cord after injury. In this study, hydrogel scaffolds provide a detailed model system to investigate the regeneration of spinal cord axons as they directly associate with individual blood vessels, using novel methods to define their spatial relationships and the physiologic implications of that organization. These results refine future tissue engineering strategies for spinal cord repair to optimize the re-development of complete neurovascular bundles in their relevant spatial architectures.

Introduction

Traumatic spinal cord injury (SCI) results in motor, sensory, and autonomic dysfunction due to neuronal and vascular disruption.¹ Multichannel hydrogel scaffolds, implanted into a complete spinal cord transection model, allow for experimental manipulation of the local injury conditions. Hydrogels are a platform for the quantification^2–5 of repair mechanisms⁶ in regenerating spinal cord tissue. Positively charged hydrogel scaffolds fabricated from oligo(poly(ethylene glycol) fumarate) (OPF+) produce a permissive microenvironment for axonal regeneration,⁷ and enhance neuron outgrowth density and directionality.^8,9 Seeding OPF+ scaffolds with Schwann cells (SCs) provides neurotrophic and vasogenic signals, as well as a peripheral nerve myelination structure around central nervous system (CNS) axons.¹⁰

Multichannel scaffold adjoins specific anatomical tracts of the rat spinal cord, and enables independent measurements within scaffold channels as structurally separated areas.^11,12 OPF+ scaffolds containing SCs and embedded with rapamycin-releasing poly(lactic co-glycolic acid) (PLGA) microspheres reduced the foreign body response and promoted functional recovery after spinal cord transection.¹³ Rapamycin decreases inflammatory cell infiltration and activation in an SCI lesion environment.^14,15 The drug also reduces fibrosis in reaction to various implanted synthetic materials.^16,17 Rapamycin itself may enhance vascularization of regenerating tissue by normalizing blood vessel distribution^13,18–21

The availability of nutrients and oxygen from the regenerating blood supply is a critically important factor for axonal regrowth.^22,23 Vascular injury causes ischemia, hemorrhage, and increased permeability of vessels for the influx of inflammatory cells.²⁴ Blood vessel beds that form after SCI are disorganized and function inefficiently.²² The relationships between regenerating axons and blood vessels as neurovascular bundles that form within hydrogel biomaterials are not well understood. A correlation between blood vessel diffusion distances, as a function of the distribution of small caliber blood vessels, and the number of regenerating axons, has been shown.²⁵ The formation of a dense capillary structure with overlapping diffusion supply supported higher numbers of regenerating axons. A correlation between blood vessel formation and improvement of functional recovery after SCI has also been described.^26–28

In this study, our objective was to quantify spatial relationships between the neovasculature and regenerating axons within hydrogel scaffolds using stereologic estimates and precision measurements by image quantification.

Materials and Methods

OPF+ hydrogel scaffolds were implanted for 6 weeks into a complete transection injury with and without concomitant SC delivery and treatment with rapamycin. Materials and methods relating to PGLA microsphere and OPF+ hydrogel fabrication, SC culture, animal surgeries, scaffold implantation, tissue sectioning, antibodies, and immunohistochemistry have been published,¹³ and may be found in the Supplementary Data section. All procedures were approved by the Mayo Clinic Institutional Animal Care and Use Committee (IACUC), and were in accordance guidelines from the National Institutes of Health, Institute for Laboratory Animal Research and United States Public Health Policy on the Humane Care and Use of Laboratory Animals.

Primary antibodies were used against Tuj-1/βIII-tubulin (mouse anti-rat, 1:300, MAB1637; MilliporeSigma, Burlington, MA); myelin basic protein (MPB, goat anti-rat, 1:400, sc-31527; Santa Cruz Biotechnology, Dallas, TX); and collagen IV (rabbit anti-rat, 1:800, Ab6586; Abcam, Cambridge, MA). Secondary antibodies (each from Jackson ImmunoResearch Laboratories, West Grove, PA) included Cy™3-conjugated AffiniPure donkey anti-mouse IgG (1:200, #715-165-151, Tuj-1); AlexaFluor™ 647-conjugated AffiniPure donkey-anti goat IgG (1:200, #705-605-147, MBP); and Cy™2-conjugated AffiniPure donkey anti-rabbit IgG (1:200, #711-255-152, Collagen IV).

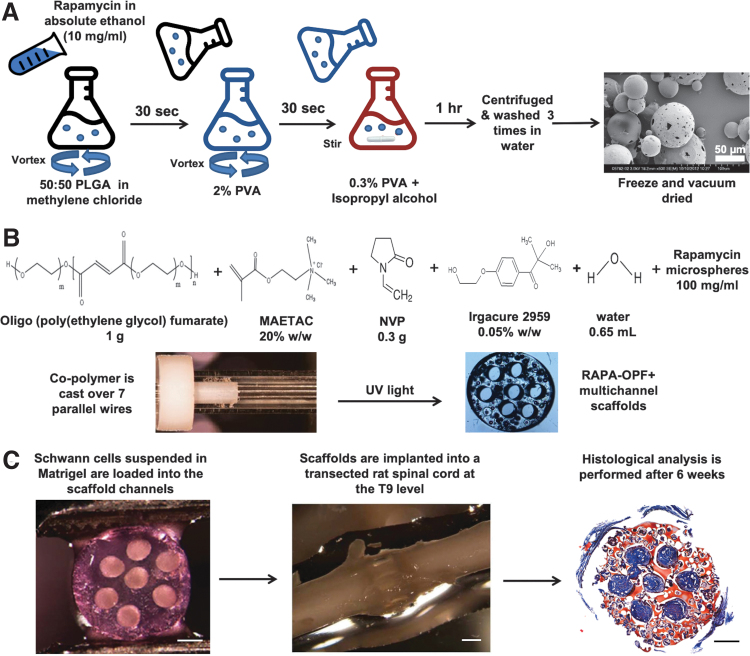
A schematic summary of microsphere and OPF synthesis, scaffold loading and implantation, and a representative histological cross-section through the scaffold midpoint is shown in Figure 1A–C. The mean diameter of individual PLGA microspheres, as measured by the NIH ImageJ (National Institutes of Health, Bethesda, MD²⁹) line measurement tool calibrated to the scale bar in scanning electron micrographs (Fig. 1A), was 57.42 ± 17.63 μm (mean ± SD), ranging from 18.11 to 99.19 μm (n = 199 rapamycin [RAPA] microspheres).

FIG. 1.

Schematic depiction of the experimental methods and design. (A) PLGA microspheres with rapamycin were fabricated using a water-in-oil-in-water double emulsion and solvent evaporation technique.¹³ Two hundred fifty milligrams 50:50 PLGA dissolved in 1 mL of methylene chloride and 100 μL of a 10 mg/mL solution of rapamycin in absolute ethanol, or ethanol vehicle (empty microspheres), were emulsified by vortexing. Two milliliters of 2% PVA was added dropwise while vortexing to produce the microsphere suspension, which was poured into 100 mL of 0.3% PVA under gentle stirring. One hundred milliliters of 2% isopropyl alcohol was added and the suspension stirred to evaporate off the methylene chloride. The microspheres were washed and freeze-dried under high vacuum. A scanning electron micrograph of the rapamycin microspheres is shown (scale bar = 50 μm). (B) One gram of OPF powder was dissolved in 650 μL of deionized water, 0.05% (w/w) of photoinitiator (Irgacure 2959), and 0.3 g of N-vinyl pyrrolidinone, a cross-linking reagent. Chemical modification with the positively charged monomer MAETAC (80% wt in water) followed at 20% w/w,⁸ producing OPF+ polymer solution. Twenty-five milligrams of PLGA microspheres was added to 250 μL OPF+ liquid polymer thereafter. Scaffolds were fabricated⁹ by injection of the liquid polymer with microspheres into a glass mold containing seven parallel aligned wires as placeholders for the channel spaces and polymerization by 365 nm UV light exposure for 1 h. Upon rehydration in PBS, cylindrical segments were cut to lengths of 2 mm, yielding scaffolds that were 2.6 mm in diameter and had seven longitudinal channels of 450 μm diameter. Scaffolds were sterilized by immersion in serial dilutions of ethanol. (C) SC and RAPA scaffolds contained SCs resuspended in 8 μL of prechilled Matrigel at a density of 10⁵ cells/μL.^6,10 Loading was performed using a gel-loading pipette tip under microscopic view at 4°C temperature, followed by 3 min at 37°C. Laminectomy through the T8–T10 level was followed by complete T9 spinal cord transection⁸ and OPF+ scaffold implantation within a 2 mm gap between the retracted spinal cord stumps. Immunohistochemical analysis of individual scaffold channels was performed after implantation for 6 weeks.¹³ (Scale bar = 500 microns). MAETAC, 2-(methacryloyloxy)ethyl]-trimethylammonium chloride; NVP, N-vinyl pyrrolidinone; OPF+, oligo(poly(ethylene glycol) fumarate); PLGA, poly(lactic co-glycolic acid); PVA, poly(vinyl alcohol); RAPA, rapamycin; SC, Schwann cell. Color images are available online.

The loading dosage of 4 μg rapamycin per mg PGLA had an encapsulation efficiency of 107% ± 8% as determined by extracting the drug by sonication of 5 mg of RAPA-PLGA microspheres in 1 mL of acetonitrile, and quantitating the concentration against a free rapamycin standard curve.¹³ The release kinetics of rapamycin microspheres embedded in OPF+ scaffolds, and the in vitro and in vivo physiologic effect of drug release, have been characterized in our model.¹³

OPF+ hydrogel has a zeta potential of 3.7 ± 1.1 mV, conductivity of 0.15 ± 0.02 mS cm⁻¹, pH of 4.09 ± 0.08, and sol fraction of 3.78% ± 1.87% in deionized water.³⁰ The compression and flexural moduli of scaffolds made from OPF+ (0.13 ± 0.03 and 1.87 ± 1.03 MPa, respectively) are similar to rat spinal cord tissue (0.19 ± 0.09 and 0.74 ± 0.14 MPa, respectively).⁹ OPF+ swelling ratios measured 13.32 ± 0.53 in distilled water.³⁰ Our unpublished data show a weight loss of 14% for OPF+ in PBS after 5 weeks. This slow degradation rate was attributed to a highly cross-linked network.

Image processing

Individual scaffold channels were imaged using a LSM510 laser scanning confocal microscope (Carl Zeiss, Inc., Oberkochen, Germany) at 20 × magnification. Seventy-two channels were imaged in OPF+ scaffolds with Matrigel and empty PLGA microspheres (n = 5 animals, 16 channels); OPF+ scaffold with SCs and empty PLGA microspheres (n = 6 animals, 34 channels); and OPF+ scaffolds with SCs and rapamycin-eluting PLGA microspheres (n = 6 animals, 22 channels).

Estimation of axons and blood vessel number, density, and physiologic measures

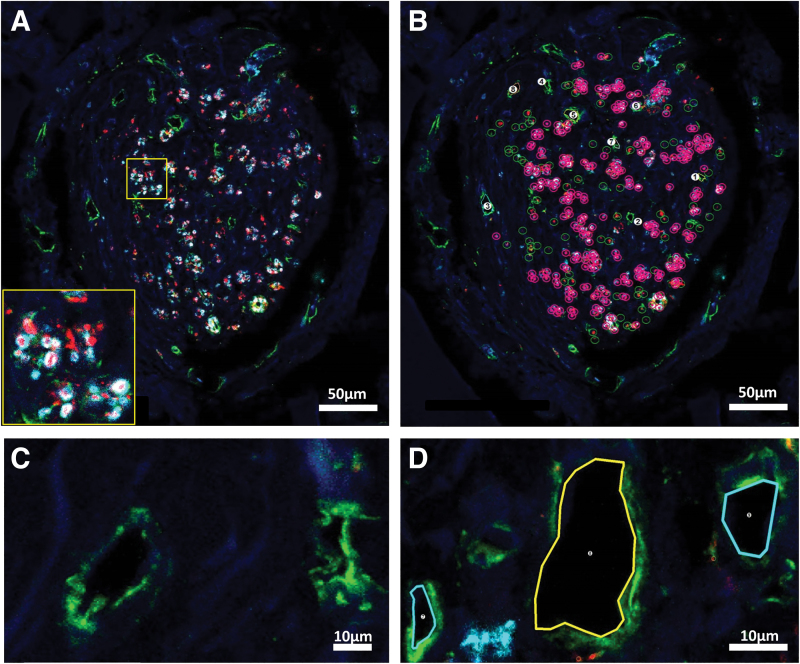
Image analysis was performed by an investigator who was blinded to the animal group using Neurolucida software (version 11.062; MBF Bioscience, Williston, VT). Core channel areas²⁵ were calculated from two orthogonal diameter measurements using the “Quick Measurement” Tool. Axons staining either with Tuj-1 (unmyelinated) or Tuj-1 co-localizing with MBP (myelinated) were digitally marked with separate symbols (Fig. 2A, B). The large majority of axons in the transverse tissue sections were punctate in appearance. Individual axons were marked when they appeared as discrete points of Tuj-1 positivity that could be distinguished clearly from the dark background or from an adjacent point. Axon diameters in cross-section ranged from ∼0.5 to 2 μm for unmyelinated axons and up to ∼5 μm in diameter if the central axon was circumscribed by positive MBP staining. More rarely, axons cut by the microtome at an obtuse angle, and of lengths typically less than 10 μm, were counted, provided that the staining borders were unbroken and linear.

FIG. 2.

Image processing and marking strategies to identify and count axons and vessels in OPF+ scaffold channels. (A) Confocal imaging of an SC channel within an OPF+ scaffold without rapamycin before marking. Scaffold channels were composed of an interior core of tissue containing regenerating axons and blood vessels, and a laminar, fibrotic outer layer adjacent to the scaffold channel, which was relatively devoid of axons and vessel structures. Axons were labeled in transverse tissue sections with immunostaining for Tuj-1 (βIII-tubulin) (red) and myelin basic protein (cyan). Unmyelinated axons appeared as punctate Tuj-1 staining, while myelinated axons appeared as positive myelin basic protein immunostaining circumscribed around central axonal Tuj-1 staining (insert). (B) Using Neurolucida software, markings designated unmyelinated axons with open green circles, myelinated axons with open pink circles and a central point, and blood vessels with numerical marks. Scale bar (A, B) = 50 μm. (C) Collagen IV staining outlined blood vessel walls (green). Vessels could be distinguished from cystic structures by the presence of a multilayered wall containing identifiable endothelial cell nuclei and subendothelial collagen IV staining around an open lumen. (D) Vessels were outlined and numbered by the software. Scale bar (C, D) = 10 μm. DAPI staining (blue) identifies cell nuclei in all panels. Color images are available online.

The manual neuron-tracing tool was repurposed to outline blood vessels along their innermost surface after collagen IV staining. Vessels could be distinguished from cystic structures by the presence of a multilayered wall containing identifiable endothelial cell nuclei by DAPI staining, and subendothelial collagen IV staining around an open lumen. Blood vessel perimeter lengths range from ∼14.0 to 148.4 μm. Numerical markers were assigned to each vessel (Fig. 2C, D). Blood vessel cross-sectional areas were calculated by the Neurolucida Explorer software. Total surface area of vessels was calculated as the summation of cross-sectional areas for all vessels within a given channel. A total of 708 blood vessel profiles and 6667 axons (2494 myelinated and 4173 unmyelinated axons) were analyzed (Table 1).

Table 1.

Numbers of Vessels and Axons Under Analysis

Marked structures	Vessels	um axons	m axons	Total axons
MG	133	495	207	702
SC	346	2796	2218	5014
RAPA	229	882	69	951
Total	708	4173	2494	6667

m, myelinated; MG, Matrigel only; RAPA, rapamycin; SC, Schwann cell; um, unmyelinated.

All measurements were made in single tissue sections taken from the scaffold midpoint. The midpoint was determined by counting the number of slides from the spinal cord stump borders, and thus comprising the scaffold span. A single tissue section was selected from the median slide number or closest available slide. Estimates for blood vessel length density (Lv) were derived according to the formula Lv = 2Q_A, where Q_A was the number of marked vessel profiles intersecting with tissue section plane within the measured area of the inner tissue channel core.^30–32 Estimates for surface area density (Sv) of blood vessels were derived from direct measurement of each vessel luminal area. Estimates for blood vessel volume (Vv) were derived from luminal surface area measurements multiplied by the tissue section thickness (10 μm). Mean blood vessel diameter was calculated from the ratio of surface area to length densities, according to the following equation:

$$\overline{d}=\frac{Sv}{Lv\pi }$$

Radial diffusion distances were derived as an inverse proportion of the length density, according to the following equation^31–33:

$$r\left(diff\right)=\frac{1}{\sqrt{\pi \bullet Lv}}$$

Sholl analysis

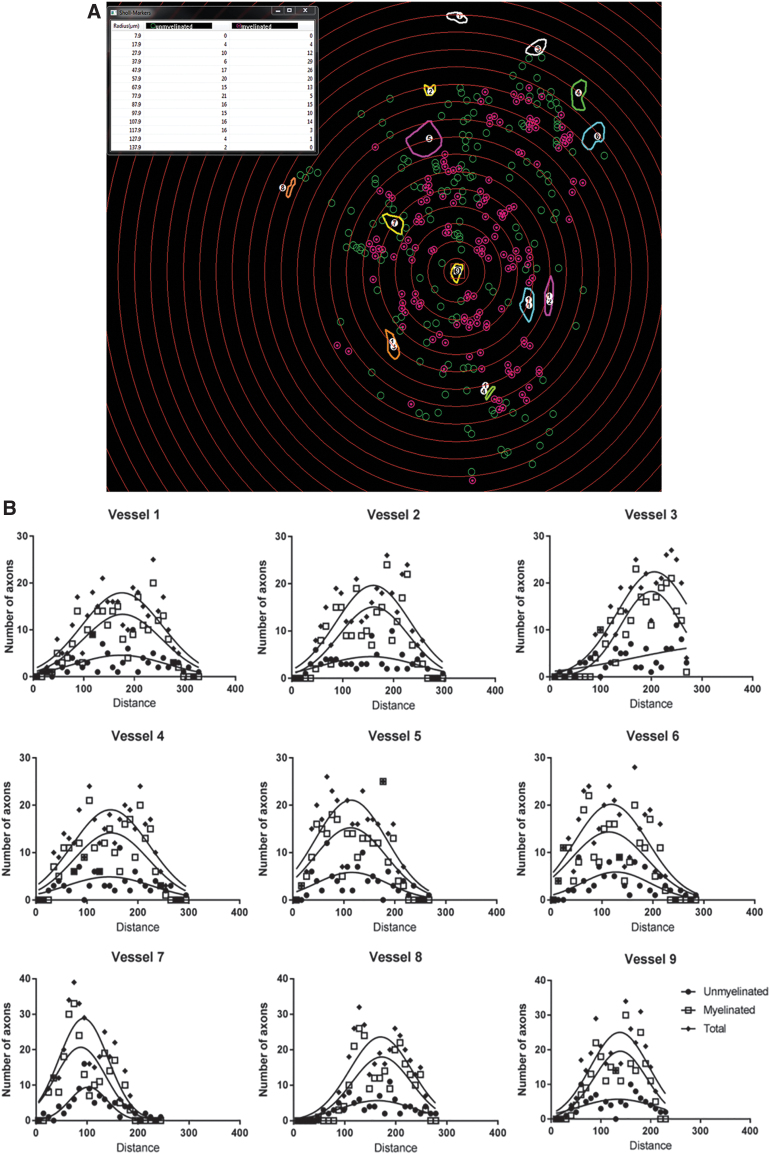
Sholl analysis assessed the relationship between axon number and distance from blood vessels. A starting radius was defined for each vessel by manual measurement of its maximal diameter using “Quick Measurement” tool. The software then generated a series of concentric circles at interval distances of 10 μm. All myelinated and unmyelinated axons falling between the bounds of adjacent concentric circles were counted and their distance from the vessel center was recorded within a 10 μm bin. Manual measurement of the distances between all blood vessels was performed in replicate. The mean value of all intervessel distances was used as a cutoff to exclude axons that were expected to be too far away from the central blood vessel to be supplied by that vessel.

Axon counts were plotted for each radius interval using Prism's GraphPad software (La Jolla, CA). Each vessel was represented by an individual graph depicting unmyelinated, myelinated, and total axon counts. A Gaussian function was fitted to each curve. Fifty-five Matrigel-only (MG), 71 SC, and 65 RAPA channel vessels surrounded by respective totals of 59, 98, and 82 axons were excluded due to low axon numbers prohibiting an accurate Gaussian curve. High cumulative axon counts over the remaining vessels required a strategy to condense the datasets. Values for Mean Peak Amplitude for each blood vessel were derived as the y-axis number of axons at each Gaussian curve apex, and the Mean Peak Distance as the distance value on the x-axis corresponding to the amplitude apex. Peak densities of axons were calculated as the Mean Peak Amplitude divided by πr², where r was defined as corresponding Mean Peak Distance.

Cumulative frequency distribution analysis

Immunofluorescence images of each channel were imported into Image J²⁹ using the Bio-Formats Importer to split the images into separate colors. The channel core area of reference was defined for the software by creating a manually outlined mask. A threshold was set to optimize contrast between the β-tubulin-positive axon background. Thresholding parameters were held constant for each image undergoing analysis. The image was converted into a binary format. Cumulative Frequency Distributions of axon spatial relationships were generated using the Spatial Statistics two-dimensional/three-dimensional (2D/3D) Plug-in for Image J.^34,35 The plug-in generates curves of the percent frequency of points in an image (y-axis), which are located within defined distance of each other, from shortest to longest distance along the x-axis.

The three statistical functions included the cumulative frequencies of the distances (1) between an axon and its nearest neighboring axon, termed the “G Function”; (2) between an axon and a randomly generated point in the reference space, termed the “F Function”; and (3) between two randomly generated points in the reference space, each with confidence intervals (CIs) calculated. Seven channels in each animal group were analyzed by the algorithm. The plug-in generated x-y pairs at accumulating frequency intervals of 0.1% (1000 data points) for the F or G function, and at 0.001% intervals (100,000 data points) for the random curve generation. An Excel macro was therefore written to scan the dataset and pull each x-y value and CI data at 1% cumulative frequency intervals, generating 100 data points per curve. Mean values of the x-values for each 1% frequency increment were calculated and plotted with CIs.

Statistics

Data are presented as mean value ± standard error of the mean, and CIs are calculated for cumulative frequency distribution curves. One-way analysis of variance with Tukey's post hoc multiple comparisons test determined statistical significance between groups of means. Correlation analysis determined significance of paired relationships with two-tailed p-values and Spearman r coefficients. p-Values of <0.05 were considered to be significant.

Experiment

Following complete spinal cord transection, we investigated the spatial relationships of regenerating axons to the neovasculature through OPF+ scaffolds containing MG (n = 5 animals per group), SCs only ( n = 6), or SCs with sustained release of rapamycin (RAPA; n = 6). Sixteen Matrigel, 34 SC, and 22 RAPA channels were available for analysis, with differences between groups accounted for by animal number and histologic preservation of intact channels for measurements after sectioning.

Relationship of core area to axon numbers and density

Scaffold channels were seen to be composed of two compartments. An interior core of tissue contained regenerating axons and blood vessels. A densely laminar, fibrotic outer layer adjacent to the scaffold channel wall was devoid of axons and vessel structures (Fig. 2A). Unmyelinated and myelinated axons were identified by immunohistochemical staining, and marked using the Neurolucida software (Fig. 2A, B). Unmyelinated axons appeared as discrete points staining positively for β-tubulin (red), while myelinated axons appeared as points of β-tubulin circumscribed by myelin basic protein immunostaining (cyan). Blood vessels were identified by positive immunostaining for collagen IV (green; Fig. 2C). The internal lamina borders of each vessel were outlined (Fig. 2D) to derive both vessel counts and lumen areas.

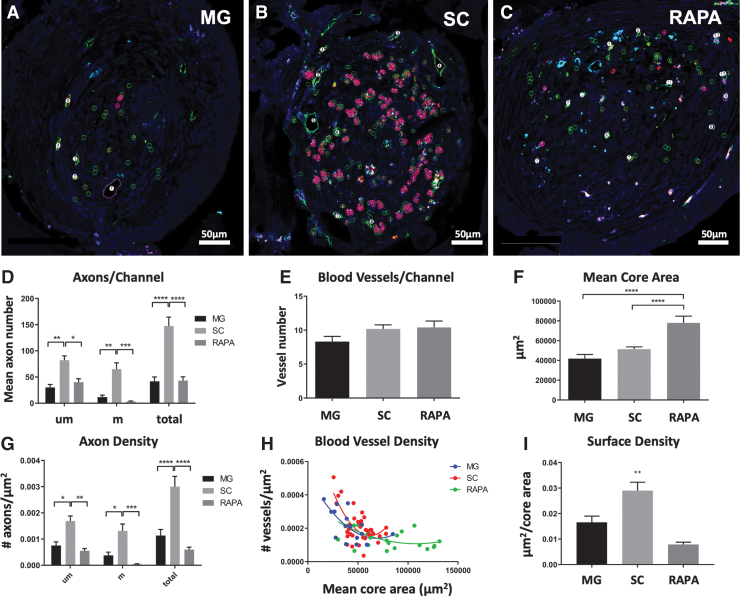
Myelinated and unmyelinated axons in MG, SC, and RAPA channels were organized in small clusters (Fig. 3A–C). The mean total number of axons in SC channels (147.50 ± 17.03 axons/channel; n = 34 channels) was greater than that observed in MG (41.78 ± 8.35 axons/channel; p < 0.0001; n = 16) (Fig. 3D) or RAPA scaffold channels (43.23 ± 7.2 axons/channel; p = < 0.0001; n = 22) (Fig. 3D). SC channels supported higher numbers of both myelinated and unmyelinated axon subtypes. The mean percentage of myelinated axons per channel in the RAPA group, 5.07% ± 1.6%, was lower than the 25.69% ± 6.0% observed in the MG group (p = 0.006) and 32.86% ± 4.0% in the SC group (p < 0.0001).

FIG. 3.

Axon and blood vessel number and density in relationship to core area. The core area, axon number, and blood vessel numbers were measured using Neurolucida software for rats implanted with OPF+ scaffold channels containing (A) Matrigel with sham PLGA microspheres (MG), (B) SCs with sham microspheres (SC), or (C) SCs with rapamycin microspheres (RAPA). Representative images of axonal densities with software markings are shown. Scale bar (A–C) = 50 μm. Unmyelinated and myelinated axons are marked with open green circles and open pink circles with a central point, as in Figure 2. Numerical markings sequentially label blood vessels. (D) Axon counts per scaffold channel (mean ± SEM) in each group were calculated for unmyelinated (um), myelinated (m), and total axons. (E) Vessel number (mean ± SEM) per channel in each animal group. (F) Interior core area mean ± SEM of MG, SC, and RAPA channels. (G) Axonal densities were defined as the number of axons per core area (μm²), and were calculated as mean ± SEM for unmyelinated (um), myelinated (m), and total axons. (H) Blood vessel densities demonstrated a negative correlation between mean core area and vessel density for all groups (MG: Spearman r = −0.5795, p = 0.0186; SC: Spearman r = −0.5129, p = 0.0019; RAPA: Spearman r = −0.4884, p = 0.0211). (I) Surface densities (Sv) of blood vessels as mean ± SEM per channel. *p < 0.05, **p < 0.01, ***p < 0.001, ****p < 0.0001 (n = 16 MG, 34 SC and 22 RAPA channels for each parameter). SCs, Schwann cells. Color images are available online.

There were no differences in the mean number of blood vessels per channel between groups, which measured 8.31 ± 0.78 vessels in MG channels (n = 16 channels), 10.18 ± 0.62 vessels in SC channels (n = 34), and 10.41 ± 0.95 vessels in the RAPA group (n = 22) (Fig. 3E).

Axons and blood vessels in the RAPA group were distributed across a larger mean core channel inner surface area (78,042 ± 6817 μm²; n = 22 channels) than the MG (41,829 ± 4175 μm²; n = 16; p = < 0.0001) and SC (51,407 ± 2272 μm²; n = 34; p = 0.0013) group (Fig. 3F). This observation was consistent with an antifibrotic effect of rapamycin in scaffold channels in allowing for an expansion of inner tissue lumen.¹³ The mean density of total, myelinated, and unmyelinated axons, as the number of axons per μm² of core surface area, was more concentrated (0.0030 ± 0.0004 total axons/μm²) in SC-seeded channels (n = 34 channels) than in MG (n = 16; 0.0012 ± 0.0002 total axons/μm²; p = < 0.0001) or RAPA groups (n = 22; 0.0006 ± 0.0001 axons/μm²; p = < 0.0001; Fig. 3G).

Greater core tissue areas in the RAPA group produced longer distances between individual blood vessel profiles. The mean intervessel distance in the RAPA group (146.1 ± 8.65 μm; n = 22 channels) was higher than vessel distances in the MG group (96.94 ± 5.66 μm; p = < 0.0001; n = 16) and SC (116.5 ± 3.947 μm; p = 0.0013; n = 34). There was a negative correlation between vessel density and core area in all three groups (MG: Spearman r = −0.5795, p = 0.0186, n = 16 XY pairs; SC: Spearman r = −0.5129, p = 0.0019, n = 34; and RAPA: Spearman r = −0.4884, p = 0.0211, n = 22) (Fig. 3H). Blood vessel densities as a function of mean core area were lowest in the RAPA group, as shown by the rightward shift of the RAPA correlation curve. The surface area densities (Sv) of blood vessels in SC channels averaged 0.029 ± 0.003 μm² per core area (n = 34 channels) greater than in MG (0.017 ± 0.002 μm² per core area; p < 0.01; n = 16) and RAPA channels (0.008 ± 0.001 μm² per core area; p < 0.01; n = 22) (Fig. 3I).

Analysis of blood vessel formation in OPF+ scaffold channels

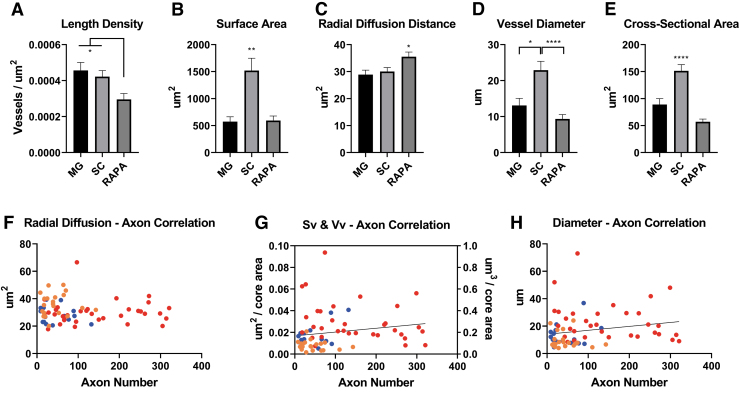
Analysis of blood vessels quantitated vessel distribution, morphology, and radial diffusion distance. The length density of vessels is a value that represents the combined length of all vessel profiles within a channel section plane. The mean length density (Lv) of blood vessels was calculated to be lower in RAPA channels (3.0 × 10⁻⁴ vessels/μm²; n = 22 channels) than MG (4.5 × 10⁻⁴ vessels/μm²; p < 0.05; n = 16) and SC (4.2 × 10⁻⁴ vessels/μm²; p < 0.05; n = 34) (Fig. 4A).

FIG. 4.

Blood vessel physiologic parameters in relation to axon number. (A) Length density (Lv) of blood vessels as a value that represents the combined length of all vessel profiles within a channel section plane was calculated as mean ± SEM for each group. (B) The surface area coverage of blood vessels per channel was the summation of each individual cross-sectional area measurement (mean ± SEM). (C) The radial diffusion distance was calculated as the inverse proportion of the Lv measurements per channel. Radial diffusion distance defines a cylindrical zone of nutrient and blood gas diffusion around the vessel wall.^30,31 (D) Blood vessel diameters were derived from stereologic estimates of the ratio of Lv and Sv (n = 16 MG, 34 SC, and 22 RAPA channels for parameter measurements in [A–D]). (E) Mean ± SEM cross-sectional areas of blood vessels in each channel type, by direct measurement of lumen area (n = 133 MG, 346 SC, and 229 RAPA vessel profiles). (F) Mean radial diffusion distances did not correlate with total channel axonal number for a given channel, but ranged consistently between 20 and 40 μm² with increasing axon numbers supported (n = 72). (G) Positive correlations between axonal number are shown between Sv and the volume densities (Vv, which equals Sv multiplied by the thickness of the tissue section, 10 μm) (Spearman coefficient = 0.3217, p = 0.006; n = 72). (H) Positive correlations were also observed between axon number and increasing blood vessel diameters (n = 72; Spearman coefficient = 0.2716, p = 0.022). *p < 0.05, **p < 0.01, ****p < 0.0001. Color images are available online.

The blood vessel surface area was larger in the SC group, with vessels occupying a mean area of 1519.0 ± 229.0 μm² per channel (n = 34 channels), than in MG (572.0 ± 89.8 μm² (n = 16) or RAPA channels (594.3 ± 83.90 μm²; n = 22) (Fig. 4B). Blood vessel volume measurement followed the same trends, with far larger mean vessel volumes of 1.519 × 10⁵ ± 0.230 × 10⁵ μm³ per channel in the SC group (n = 34 channels) compared with 5.720 × 10⁴ ± 8.98 × 10⁴ μm³ in MG (p < 0.01; n = 16) and 5.943 × 10⁴ ± 0.84 × 10⁴ in RAPA channels (p < 0.01; n = 22).

Additional physiologic parameters were derived from measurements of the Lv and Sv. The radial diffusion coefficient, a measure of a cylindrical zone of diffusion around a blood vessel, was calculated as the inverse function of the length density.^31,32 The mean diffusion distance for SC vessels was 30.00 ± 1.48 μm² (n = 34 channels), 28.89 ± 1.64 μm² in MG vessels (n = 16), and 35.52 ± 1.72 μm² (p < 0.05) in RAPA channels (n = 22) (Fig. 4C).

Mean blood vessel diameters per channel were calculated from the ratio of Lv to Sv. The mean diameter of blood vessels in SC channels was 22.90 ± 2.46 μm (n = 34) greater than the mean vessel diameters in MG vessels (13.10 ± 2.00; p < 0.05; n = 16) and RAPA vessels (9.36 ± 1.21 μm; p < 0.0001; n = 22) (Fig. 4D). This stereologic calculation of diameter was consistent with direct measurements of cross-sectional areas of individual blood vessels in channels. The mean cross-sectional area per blood vessel in SC channels was 151.40 ± 11.45 (n = 346 vessels) larger than that measured in MG (88.90 ± 11.08 μm²; n = 133) and RAPA vessels (74.57 ± 4.93 μm²) (both p < 0.0001; n = 229) (Fig. 4E).

Axon counts trended to be lower in the RAPA group channels with higher diffusion distances (Fig. 4F), but correlations were not statistically significant (n = 22 XY pairs). Diffusion distances consistently ranged between 20 μm and 50 μm with increasing axon number. The number of axons regenerating had positive correlations to the surface and volume area densities of vessels (Spearman coefficient = 0.3217, p = 0.006; n = 72 XY pairs) (Fig. 4G) and to the diameter of blood vessels (Spearman coefficient = 0.2716, p = 0.022; n = 72) (Fig. 4H).

Spatial relationships of regenerating axons to blood vessels in scaffold channels

To quantitate the spatial distribution of single myelinated and unmyelinated axons around individual blood vessels, a novel methodology was developed around a Sholl subanalysis. Concentric rings were centered upon each blood vessel increased in diameter by 10 μm intervals. Myelinated and unmyelinated axons were counted within the boundaries of each concentric ring interval (Fig. 5A, centering on Vessel 9, for example). The axonal number in each ring interval was plotted as a distribution function against their distances from the blood vessel.

FIG. 5.

Sholl analysis and Gaussian distributions of axon number with distance around blood vessels. (A) Measurement of axon distribution was done using a Sholl analysis. Concentric rings were generated by the software in 10 μm intervals around each vessel, in this example, Vessel 9. The rings were centered following determination of the vessel diameter as the innermost ring. Measured diameters ranged from 3.3 to 67.3 μm. Counts for unmyelinated (open circles) and myelinated axons (encircled points), which were located between two adjacent rings, were tabulated by the software. (B) The number of unmyelinated, myelinated, and total axons within each 10 μm radial increment was plotted as a function of the distance from each blood vessel, and consistently demonstrated a Gaussian distribution. These data were compressed by using the value of Mean Peak Amplitude to sample axon number at the maximal height of the distribution curve, and Mean Peak Distance as the corresponding distance from the vessel at which the distribution was maximal. Color images are available online.

Axonal distributions around blood vessels were observed to be Gaussian (Fig. 5B). Since the number of individual axons counted around each vessel within a given channel was cumulatively high, the dataset was condensed into values for Mean Peak Amplitude, as the number of axons on the y-axis represented by the peak of each Gaussian curve. The Mean Peak Distance was the distance on the x-axis at which the axonal number/amplitude was at its peak.

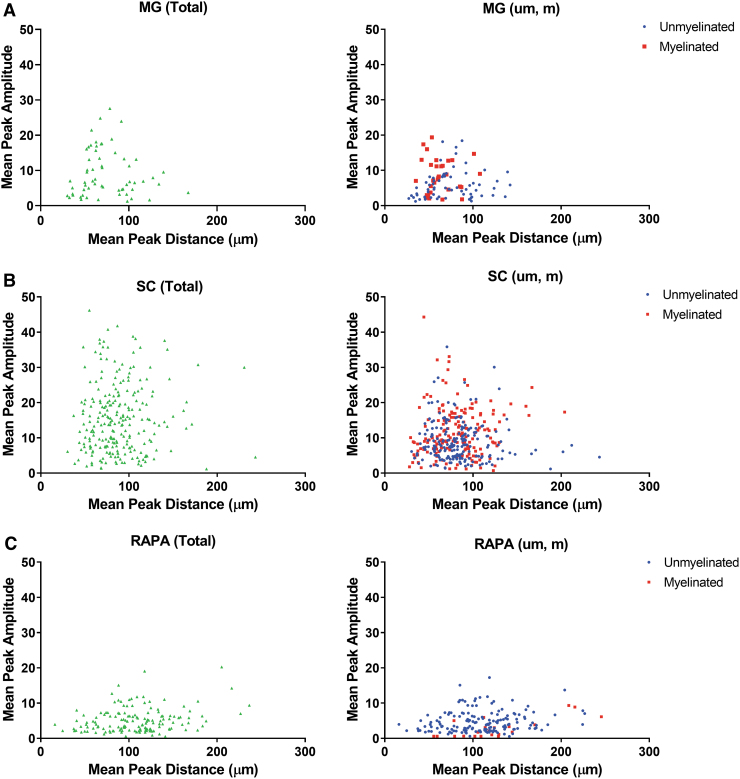
Plotting Mean Peak Amplitude against Mean Peak Distance (Fig. 6) identified that the distance of maximal axonal number from a vessel was located within a radius of less than 200 μm from the vessel wall in the MG (Fig. 6A). The averaged Mean Peak Distance was sequentially increased from 70.33 ± 3.56 μm around MG vessels (n = 78) to 89.28 ± 2.00 μm around SC vessels (n = 275), and to 106.06 ± 3.32 μm around RAPA vessels (n = 164; p > 0.0002 for each comparison) (Supplementary Fig. S1A). Similarly, a histogram analysis demonstrated a shift in the peak concentration of axon counts in bins centered on 60 μm from vessels for MG channels, 80 μm from vessels for the SC group, and 120 μm distances for the RAPA group (Supplementary Fig. S1B). The radius for maximal axonal number extended to 250 μm in the SC group and RAPA group (Fig. 6B–C).

FIG. 6.

Mean Peak Amplitude and Mean Peak Distance of axons compared to blood vessel cross-sectional area. Total, unmyelinated (um), and myelinated (m) counts at Mean Peak Amplitude were plotted against their respective Mean Peak Distances in (A) MG channels, (B) SC channels, and (C) RAPA channels. These relationships identified a zone of exclusion of 25–30 μm immediately adjacent to the blood vessel wall where axons were not located at their Mean Peak Amplitudes (n = 78 MG, 275 SC, and 164 RAPA axon distributions). Color images are available online.

The maximal number of axons was essentially excluded from a 25–30 μm radius immediately adjacent to a blood vessel, as observed in each animal group and whether the axons were myelinated or unmyelinated (Fig. 6). This effect was slightly less pronounced in the RAPA group, where two peak amplitudes representing <4 unmyelinated axons were located within the exclusion zone. The Mean Peak Amplitudes had a higher range in the SC group, from 1.18 to 54.88 (average 15.80 ± 0.66) axons (n = 275), than in the MG (range 1.27 to 27.59, average 8.16 ± 0.80; n = 78) or RAPA groups (range 0.55 to 20.25, average 5.09 ± 0.30; n = 164; p = 0.0085 for MG vs. RAPA averages, and <0.0001 for each SC comparison).

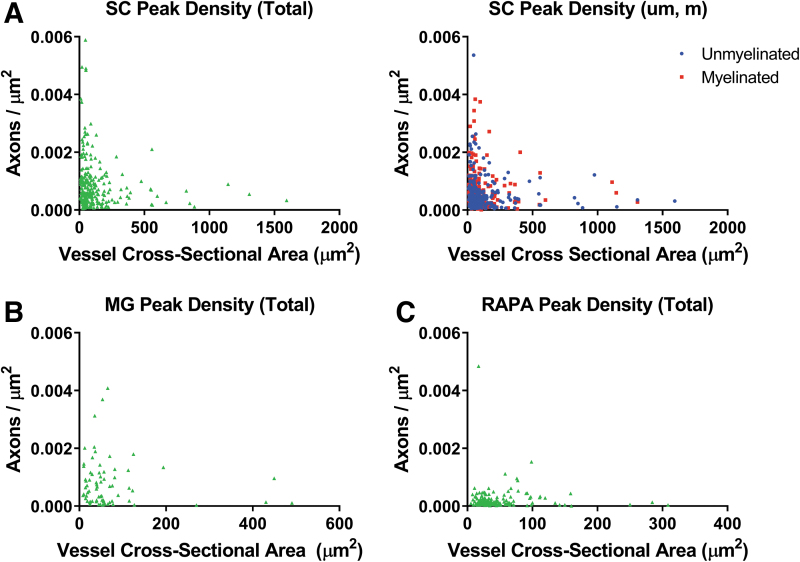
For each blood vessel, the Mean Peak Amplitudes for axonal concentrations were described as a function of the cross-sectional areas of the blood vessel around which the axons were distributed. Peak axonal density represented the peak amplitude of axons with respect to the circular area of intervening tissue determined by the Mean Peak Distance as the radius from the vessel wall. For SC channels (Fig. 7A), significant negative correlations were shown between peak axonal density of total axon amplitudes and vessel cross-sectional area for total (Spearman r = −0.1864, p = 0.0035; n = 243 density-vessel pairs), unmyelinated (Spearman r = −0.1473, p = 0.0252; n = 231), and myelinated axons (Spearman r = −0.1975, p = 0.0092; n = 173) (Fig. 7A). Correlations were not identified in MG or RAPA channels where the axonal densities were lower (Fig. 7B, C).

FIG. 7.

Relationships of axonal density to vessel cross-sectional area. Peak axonal density was derived as the Mean Peak Amplitude within the surface area defined by the Mean Peak Distance as the radius. Peak axonal density for each vessel was plotted to correlate with the vessel cross-sectional area of the reference vessel in (A) SC, (B) MG, and (C) RAPA group channels. A negative correlation was observed in SC channels, total (Spearman r = −0.1864, p = 0.0035; n = 243 density-vessel pairs), unmyelinated (Spearman r = −0.1473, p = 0.0252; n = 231), and myelinated axons (Spearman r = −0.1975, p = 0.0092; n = 173). Density—vessel area correlations were not identified in MG or RAPA channels. Color images are available online.

Distribution and relationship of regenerating axons to each other

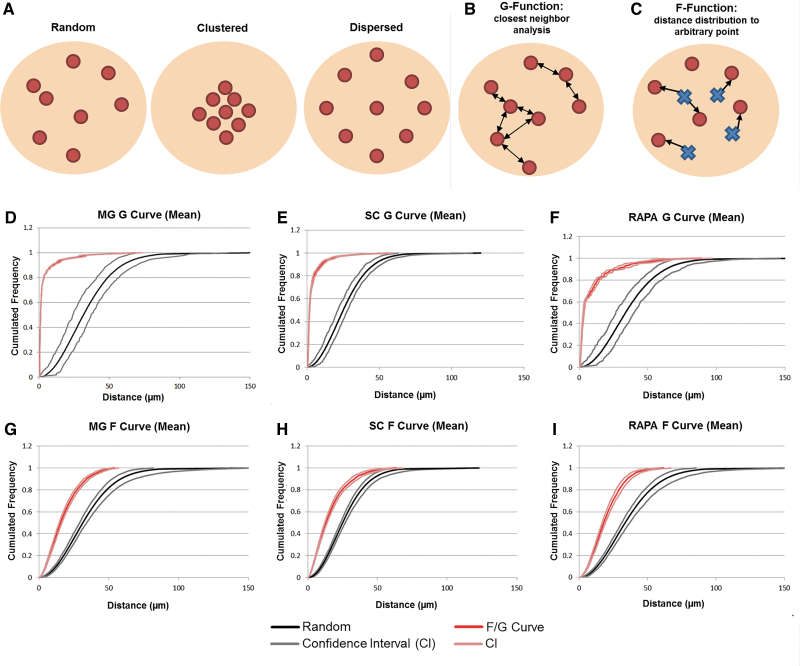
Cumulative distribution functions of inter-axon distances were generated using the Spatial Statistics 2D/3D Plug-in for NIH Image J^34,35 (Fig. 8). The distribution of axons within regenerating tissue could be considered to be random, clustered, or dispersed points in space (Fig. 7A–C). Cumulative frequencies of the percentage of axons located within a given distance from another axon defined the G-function, or a nearest neighbor analysis. The G-function assessed whether axons were distributed in clusters or were dispersed relative to the nearest neighbor analysis of randomly generated points. In each animal group, the shift in the cumulative distribution G-curves of axon distances far to the left of the random point distribution curve signified a grouped relationship between axons (n = 7 channels analyzed per group) (Fig. 8D–F).

FIG. 8.

Analysis of axon clustering. (A) Axon distributions can be classified as random, clustered, or dispersed. (B) The closest neighbor analysis (G-function) measures the cumulative distance distributions between axons. (C) The F-function measures the distance distributions between an axon and a randomly generated point within the reference space. (A–C) are adapted from reference.³⁵ The cumulative frequency of the percentage of axons or points (y-axis) at increasing distances from each other (x-axis) is depicted as G-curves, F-curves, and random point curves confidence intervals for MG (D, G), SC (E, H), and RAPA (F, I) channels. A grouped or clustered distribution of axons is demonstrated by the leftward shift of the F- or G- curve from the reference curves of random point distances (n = 7 channels analyzed per group). Color images are available online.

The closest neighbor analysis also demonstrated that 90% of axons in the MG or SC groups were each located under 10.1 μm from the next closest axon (Fig. 8D, E). The RAPA group (Fig. 8F) was slightly more dispersed with 90% of the axons being located within 20.6 μm (CI 24.2–32.4 μm) from the next closest axon.

Cumulative frequencies of the distances between an axon and a randomly generated point in the reference space were defined as the F-function. This analysis determined whether axons were distributed randomly, in definitive clusters, or in a dispersed organization. The shift in each F-function curve to the left of a curve of distances between random points demonstrated that the relationship between regenerating axons in each animal group was in a definitely clustered and nonrandom distribution (n = 7 channels analyzed per group) (Fig. 8G–I). The F-curve shift signified that the distance between an axon and a random point was consistently shorter than the distance between two randomly generated points, indicating that axons lie closer together than if they were mathematically distributed in a random pattern. For example, 90% of MG channel axons would be located within 34.0 μm of a random point (CI 30.6–34.5 μm), compared to 90% of random points being at within a distance of 58.5 μm (CI 52.4–68.3 μm).

Discussion

In this study, novel methods are described by which axonal regeneration and revascularization can be quantified in their innate spatial relationships. This approach adds to and can validate methods of stereologic estimation^31,33 by means of systematic and detailed measurements of the distribution of single axons in relation to individual blood vessels. In contrast to differential support of axonal regeneration between groups, blood vessel neovascularization occurred with similar numbers of vessels over time in each condition. Blood vessels in channel areas that were less fibrotic following rapamycin treatment needed to influence larger areas of core tissue, with implications for vessel morphology, tissue oxygenation, and nutrient distribution. SC channel blood vessel coverage was more extensive, and the vessel caliber larger, than MG and RAPA groups. Smaller vessels within that neovasculature supported improved regeneration of axonal densities.

By multiple measures, including surface area coverage, vessel volume, and blood vessel diameter, significantly more blood could be delivered to SC channels in association with improved radial diffusion distances and higher axonal counts. Axonal growth was seen to observe a given distance from the vessel wall as opposed to regenerating in very close approximation to the vessel wall. This finding may relate to radial diffusion physiology with peak axon numbers at optimal positions in nutrient and gas diffusion gradients. Plotting the peak axonal density values against vessel cross-sectional area confirmed a correlation between vascular caliber and support of axonal regeneration. This result supports our previous observations that improved axonal regeneration correlated with smaller radial diffusion distances and redundancy of vessel diffusion overlap.²⁵

We have proposed a methodology in which five simplified measurements can be easily and reproducibly made through image analysis software. Both the Neurolucida and NIH Image J platforms would have the capabilities to readily perform each of the proposed measurements. Point markers identified axon number and proportions of myelinated and unmyelinated profiles and blood vessel number, and enabled the Sholl analysis. Outline tracing identified blood vessel cross-sectional areas and core tissue areas. From these five direct measurements, an additional 12 parameters were derived that associated with a positive or negative influence neurovascular regeneration (Table 2), based upon the outcomes of three study conditions compared.

Table 2.

Direct Measurements, and Derivative Parameters of Positive or Negative Influence on Neurovascular Regeneration

Direct measurement	Derivative parameters	Positive parameter influence	Negative parameter influence
Point markers
Axon number, myelination	• Axonal density • Cumulative frequency distributions (F- and G-function)	• Higher axonal numbers, densities, and % myelination • Clustered distribution
Sholl analysis	• Gaussian fit, mean peak number and distance • Mean Peak Density	• Higher Mean Peak Amplitudes • Higher Mean Peak Densities	• Higher Mean Peak Distances
Blood vessel number	• Vessel length density (Lv) • Radial diffusion distance		• Low vessel number and length density • High radial diffusion distances
Outline tracing
Blood vessel cross-sectional area	• Vessel surface (Sv) and volume (Vv) Density vessel diameter (Sv/Lv)	• Higher vessel surface and volume densities • Increased vessel diameters • Higher summated vessel cross-sectional areas	• Higher individual vessel cross-sectional areas
Core tissue area	• Reference volume		• Increased core areas

Matrigel was used to suspend SCs in OPF+ scaffolds in uniform dispersion throughout the channel. In our early unpublished work to develop the technology, cells were suspended in saline, but settled against the inferior wall of the channels in a crescent shape in a gravity-dependent manner, leaving most of the channel empty.

We have extensively characterized the outcome of implanting OPF+ scaffolds loaded with Matrigel alone, compared to primary SCs suspended in Matrigel.^8,12,13,25 Matrigel scaffolds minimally supported axonal regeneration at an efficiency of less than 20% of that seen with scaffold-embedded SCs. Astrocyte and inflammatory infiltration into Matrigel-only channels occurred at a higher rate than in channels with cells already present at the time of implantation.²⁵ Blood vessel number and surface area were reduced in Matrigel-only scaffolds.^13,25 For each of these reasons, Matrigel with empty microspheres was selected as negative control condition, as a baseline or “blank slate” intervention with a regenerative capacity for axons and vessels, which is known to be poor.^8,12,25

Two conditions with suspended SCs in channels (SC and RAPA) were hypothesized to provide a therapeutic intervention that would improve neurovascular regeneration over that baseline. However, only one intervention (SC) was comparatively successful, allowing for a three-way analysis of the parameters that differentiated the SC outcome from the other two conditions. Positive regenerative outcomes in the SC group associated with (i) higher axonal numbers, densities, and myelination rates; (ii) higher blood vessel surface and volume densities; and (iii) higher Mean Peak Amplitudes and Mean Peak Densities. Relatively negative outcomes in MG or RAPA associated with (i) low vessel length densities; (ii) higher radial diffusion distances; (iii) higher Mean Peak Distances; and (iv) increased core area that would reduce axonal and vessel densities.

There were also some nuances. For vessel cross-sectional area measures, improved regeneration associated with higher vessel diameter and summated cross-sectional vessel areas, but axonal regeneration around individual vessels negatively correlated to increasing large cross-sectional areas. Larger vessels would physiologically have slower blood flow. Axonal numbers were lowest when Mean Peak Distances were either very close to the vessel or went beyond 150 μm, which supported the idea of an optimal spacing range.

The direct and derivative parameter measurements also provide for values of core area, axon or vessel number, density, and surface areas, and Sholl analysis outcomes that may be used to stratify neurovascular regeneration through a proposed scoring system (Table 3). In this study, the system proposed compares mean measurements for each parameter on a zero to four numerical ranking. The scoring is based upon outcomes within a multichannel scaffold in each of this study's experimental system. The conceptual framework, however, can readily be applied to other scaffold architectures in which values for the five basic measurement and 12 derivative parameters are determined, particularly because many of the parameters are density measurements.

Table 3.

Proposed Scoring System for Neurovascular Regeneration Parameters Based Upon the Multichannel OPF+ Dataset

Parameter	Value	Score	MG	SC	RAPA	Parameter	Value	Score	MG	SC	RAPA
Core area (μm2)						Blood vessels
						(Number per channel)
	>100,000	0					<5	0
	75,000–100,000	1			✓		6–10	1	✓
	50,000–75,000	2	✓	✓			11–15	2		✓	✓
	25,000–50,000	3					16–20	3
	<25,000	4					>20	4
Axons
Number per channel						Surface density (Sv; μm2/area)	<0.01	0			✓
	<10	0					0.01–0.02	1	✓
	20–50	1	✓		✓		0.021–0.03	2		✓
	51–100	2		✓			0.031–0.004	3
	101–200	3					>0.004	4
	>200	4
Myelination (%)	<10	0			✓	Length density (Lv; vessels/μm2)	<0.002	0
	11–20	1	✓				0.0021–0.004	1			✓
	21–30	2		✓			0.0041–0.006	2	✓	✓
	31–40	3					0.0061–0.007	3
	>40	4					>0.007	4
Sholl
Mean Peak Amplitude (number)						Surface area (μm2)	<500	0
	<5	0			✓		501–1000	1	✓		✓
	5–10	1	✓				1001–1500	2		✓
	11–15	2					1501–2000	3
	15–20	3		✓			>2000	4
	>20	4
Mean Peak Distance (μm)	<25 or >200	0				Radial diffusion distance (μm2)	>40	0
	26–50	1	✓				31–40	1			✓
	51–75	2		✓			21–30	2	✓	✓
	76–100	3			✓		11–20	3
	101–150	2					<10	4
	>150	1
Mean Peak Density (number/μm2 × 103)	<0.25	0				Diameter (Lv/Sv; μm)	<10	0			✓
	0.26–0.5	1			✓		11–20	1	✓
	0.51–1.0	2	✓	✓			21–30	2		✓
	1.1–1.5	3					31–40	3
	>1.5	4
						Cross-sectional area (μm2)	>2000	0
							1501–2000	1
							1001–1500	2
							501–1000	3
							<500	4	✓	✓	✓
			MG	SC	RAPA				MG	SC	RAPA
		Neural	10	16	5			Vessel	12	17	9
			MG	SC	RAPA
		Total neurovascular score	22	33	14

OPF+, oligo(poly(ethylene glycol) fumarate).

Administration of rapamycin resulted in improved functional recovery following spinal cord transection in our previous study.¹³ Rapamycin is an allosteric mTOR inhibitor, which has been shown to aid axonal regeneration following CNS and peripheral nervous system (PNS) injuries.^36–39 Treatment with rapamycin and SCs in this study produced fewer regenerating axons than SCs alone. Our study importantly identified this phenomenon, but its scope was limited, in that, an explanation for this was not explored.

Improved motor function recovery does not solely depend on axon density, but may be associated with reduced fibrosis and inflammation.^40–42 Rapamycin treatment has decreased cytokine production, and activation of microglia with functional improvements after SCI.^13,41 Rapamycin may have directly reduced the number of supporting SCs in our scaffold channels due to an antiproliferative effect. Rapamycin inhibits the proliferation of fibroblasts and increases apoptosis.⁴³ Reduction in the number of SCs relative may in turn impair their angiogenic and neurotrophic support. Additional studies using rapamycin in SCI have identified an antiangiogenic effect.^18,44,45

Microvessels in the CNS provide trophic support,^46–48 and regenerating axons have been shown to grow along blood vessels.⁴⁹ Strategies to limit vascular damage and restore blood flow to the injured cord could enhance spinal cord repair.^50,51 Increased blood vessel density correlates with improvements in neurologic function after SCI.^26–28 The anatomic distribution of axons and blood vessels is critical in neurodevelopment, and “re-development” of the spinal cord after injury is an important tissue engineering goal. Neuropilin 1 (Nrp1) knockout in endothelial cells in a mouse model produced abnormal formation of both blood vessels and axonal distribution.⁵² Vessel diameter was larger in the Nrp1^fl/−;Tie2-Cre mutants than in normal control animals, suggesting that smaller blood vessels facilitate normal axon formation.

Axons around blood vessels regenerated in defined clusters in OPF+ channels, which may represent axonal sprouting or multiple individual axons in parallel groups. In development, axons distributing from lateral geniculate nucleus follow chemical and electrical cues,⁵³ in that, axons that are the nearest to each other are electrically active at the same time. This synchrony of activity may help axons navigate to a target in groups. Blocking this electrical activity with tetrodotoxin led to abnormal patterning of connections to the visual cortex.⁵⁴ The closer proximity and greater number of axons could aid in pathfinding of spinal axons in OPF+ scaffolds.

Conclusion

Hydrogel scaffolds have provided a detailed model system to investigate the regeneration of axons and blood vessels after SCI, using novel methods to define their spatial relationships. Key observations include that SCs within hydrogel channels supported superior neurovascular bundle regeneration than in the MG or RAPA groups, in axon and vessel density, and in physiologic parameters of vessel diameter, and radial diffusion distances. Neurovascular bundles are represented spatially by a Gaussian distributions of axons around centralized vessels, with an area of relative exclusion of axonal regeneration in 25–30 μm immediately adjacent to the vessel wall or >150 μm in distance.

Important correlations for improving axonal growth include surface area densities of vessels and smaller vessel cross-sectional areas. Axons regenerate in spatial clusters defined mathematically by cumulative distribution functions. These results, including stratification of parameter outcomes into a proposed scoring system, may refine future tissue engineering strategies for SCI repair to optimize the regeneration of complete neurovascular bundles in their relevant spatial architectures.

Authors' Contribution

A.M.S., D.O., J.H., B.C., M.J.Y., A.J.W., and N.N.M.: major role in the acquisition of data; designed and conceptualized study; analyzed the data; and drafted and revised the article and figures for intellectual content. S.P.: major role in the acquisition of data; interpreted the data; revised the article for intellectual content; image acquisition, and analysis. D.K.: major role in the acquisition of data; interpreted the data; revised the article for intellectual content; excel macro generation; and cumulative frequency distribution analysis. P.S. and M.P.: major role in analyzing and interpreting the data and drafted and revised the article and figures for intellectual content. A.M.S.: major role in the acquisition, analysis, and interpretation of the data and revised the article and figures for intellectual content.

Disclosure Statement

No competing financial interests exist.

Funding Information

This work was generously funded by grants from the National Institute of Biomedical Imagining and Bioengineering (EB02390), National Institute of Biomedical Imagining and Bioengineering (TL1 TR002380), Morton Cure Paralysis Fund, and Craig H. Nielsen Foundation.

Supplementary Material

Supplementary Data

Supplementary Figure S1