Quality assurance tool for organ at risk delineation in radiation therapy using a parametric statistical approach

Abstract

Purpose

To develop a quality assurance (QA) tool that identifies inaccurate organ at risk (OAR) delineations.

Methods

The QA tool computed volumetric features from prior OAR delineation data from 73 thoracic patients to construct a reference database. All volumetric features of the OAR delineation are computed in three‐dimensional space. Volumetric features of a new OAR are compared with respect to those in the reference database to discern delineation outliers. A multicriteria outlier detection system warns users of specific delineation outliers based on combinations of deviant features. Fifteen independent experimental sets including automatic, propagated, and clinically approved manual delineation sets were used for verification. The verification OARs included manipulations to mimic common errors. Three experts reviewed the experimental sets to identify and classify errors, first without; and then 1 week after with the QA tool.

Results

In the cohort of manual delineations with manual manipulations, the QA tool detected 94% of the mimicked errors. Overall, it detected 37% of the minor and 85% of the major errors. The QA tool improved reviewer error detection sensitivity from 61% to 68% for minor errors (P = 0.17), and from 78% to 87% for major errors (P = 0.02).

Conclusions

The QA tool assists users to detect potential delineation errors. QA tool integration into clinical procedures may reduce the frequency of inaccurate OAR delineation, and potentially improve safety and quality of radiation treatment planning.

1. Introduction

Volume delineation is widely regarded as a large source of systematic uncertainty in radiation therapy.^{1, 2, 3} While traditional two‐ and three‐dimensional (3D) treatment delivery depends primarily on target delineation, modern treatment planning using, for example, intensity‐modulated radiotherapy relies heavily on organ at risk (OAR) objectives to tailor the dose distribution to maximize the therapeutic ratio. Inaccurate and inconsistent OAR delineation can mislead the planning team with respect to the quality of a treatment plan, resulting in suboptimal treatment delivery with an increased probability of adverse normal tissue complications. Avoidance of OAR delineation errors and uncertainty are paramount for treatments designed to conformally avoid OARs.

The OAR delineation is subject to (a) inherent inter‐ and intradelineator variability, in which repeated delineations result in minor variations in an agreed upon definition of the anatomic characteristics of the OAR boundary; (b) differences in the OAR definition in which different observers consider different anatomic characteristics of the OAR boundary; and (c) errors, in which the OAR mistakenly has additional or missing components. This work primarily focuses on reducing occurrences of (b) and (c).

Discrepancy in the anatomic characteristics of an OAR definition between different delineators can be a result of unclear instructions and/or insufficient training. Different approaches have been investigated to reduce this type of variability in OAR delineation.⁴ For example, studies have shown that the introduction of written guidelines reduced interobserver variability.^{3, 5} Breunig et al. showed that standardized training with individual feedback mechanism decreased interobserver delineation variability.⁶ Automatic OAR delineation can potentially improve consistency,⁷ however, at least some automatic delineated structures required user intervention.^{8, 9}

Delineation error is a result of an unintentional mistake made by a delineator. Human examination/review is the most common approach to detect delineation errors, although, due to various human factors such as fatigue and vigilance, human examination can leave behind detectable errors.¹⁰ Inclusion of quality assurance (QA) programs such as peer review and consensus meeting within the delineation workflow increased the OAR delineation error detection rate.^{11, 12} However, the inefficiency of peer review limits its incorporation into most clinical workflows, and when it is utilized, its effectiveness is prone to the same human factors. Alternatively, an automated QA tool for OAR delineation can objectively identify inaccurate delineations, and alert users to make appropriate modifications. A recent study by Altman et al. proposed a knowledge‐based QA program to assess contour integrity and reported a 95% sensitivity to detect “engineered” errors.¹³ A study by McIntosh et al. also demonstrated the possibility to apply classification approach to infer delineation errors.¹⁴

In this study, we introduce an automated QA tool for OAR delineation. The QA algorithm computes volumetric features of the OAR delineation and uses a statistical anomaly detection technique¹⁵ to detect features which deviate from the historic distribution. In contrast to the approach used in Altman et al.¹³ where many features were computed in 2D space, all volumetric features implemented in our QA algorithm are computed in 3D space. Furthermore, we developed a multicriteria outlier detection system to warn users of specific delineation outliers, based on combination of deviated features. The QA algorithm initially requires only a small amount of clinical delineation data as reference. The reference data can be suboptimal with some delineation errors. With use, the amount of clinical reference data will increase, and the added data will be specifically reviewed prior to addition to the reference set. With increased numbers, errors in the initial reference dataset will be diluted. The QA tool was tested on OAR structures in the thorax and its ability to detect delineation errors was assessed.

2. Materials and methods

2.A. OAR delineation QA tool

Figure 1 depicts the flowchart of the generation and operation of the QA tool. The OAR delineation QA procedure is as follows: For each OAR, the algorithm computes the 3D volumetric features of the delineation. Then, it performs a statistical inference test on the feature with respect to its historic distribution. Finally, the system reports if a specific delineation outlier is found, based on the combination of features which deviate from the historic distribution. The delineator can then adjust the OAR delineation accordingly. A feedback loop is integrated to update the historic distribution with the newly approved delineation.

Figure 1.

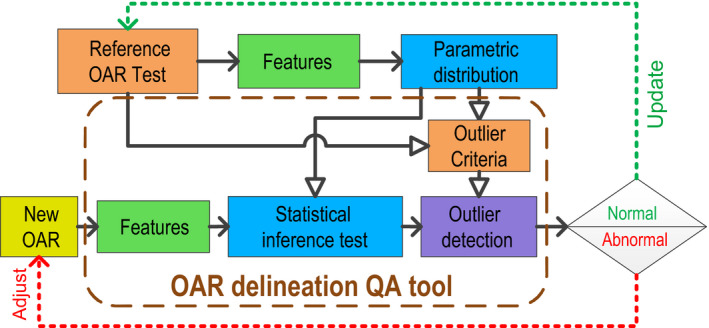
Flow of the OAR delineation QA tool. The open arrowhead (⇾) represents preparation and generation of the QA tool, the solid arrowhead (→) represents the QA procedure of a new OAR delineation. The reference OAR set is initialized with historic OAR delineations. A parameterized distribution of each volumetric feature is used to establish the statistical inference test. The multicriteria outlier detection system is developed from the parametric distributions in the initial reference. The QA procedure starts with calculation of the volumetric features, followed by the inference test to identify deviated features. The outlier detection system reports delineation abnormalities if detected. After finalizing, the newly approved OAR delineation will be included in the OAR reference for future QA procedures. [Color figure can be viewed at wileyonlinelibrary.com]

The QA tool was developed using the Pinnacle³ scripting environment (Philips, Fitchburg, WI, USA) and the Enthought Python distribution (Enthought, Austin, TX, USA) and was fully integrated into Pinnacle³ treatment planning system (tested with v9.10 and 9.14).

To create the historic feature distribution, OAR delineations from prior radiotherapy plans were used as reference and their 3D volumetric features were computed. Twenty‐five 3D volumetric features of the OAR delineation were computed by the QA algorithm. Because organs are 3D objects, none of the features were computed in 2D space; instead, all features were computed in 3D space. Table 1 summarizes the features used by the QA algorithm. The four computed tomography (CT) number features ($\overline{\rho }$, ${\sigma }_{\rho }$, ${\rho }_{\mathit{max}}$, and ${\rho }_{\mathit{min}}$) were obtained from Pinnacle³. All other parameters were computed from the binary OAR structure mask, which was exported from Pinnacle³ at the resolution of the image dataset. Computation of the surface area was implemented based on the Minkowski method with 13 directions.¹⁶ The number of disconnected volumes was calculated via a morphological label function.¹⁷ For computation of relative features $V/V_{\mathit{ext}}$ and $\mathrm{\Delta }{\stackrel{\rightharpoonup }{C}}_{A-ext}$, the volume and centroid coordinate of the External structure were extracted from only image slices that contained the corresponding OAR structure.

Table 1.

Summary of the volumetric features calculated for the OAR delineation

Features	Symbols	Descriptions
Volume, surface area, mass and density
Voxel volume (cm3)	$V$	As titled
Surface area (cm2)	$A$	As titled
Mass (g)	$m$	$\overline{\rho }\times V$
Mean CT number	$\overline{\rho }$.	As titled
Standard deviation CT number	${\sigma }_{\rho }$	As titled
Max CT number	${\rho }_{\mathit{max}}$	As titled
Min CT number	${\rho }_{\mathit{min}}$	As titled
Area to volume ratio (cm−1)	$A/V$	As titled
Specific surface area (cm2 g−1)	A/m	As titled
Ellipsoid features
For each of major axis $\stackrel{\rightharpoonup }{a}$, equatorial major axis $\stackrel{\rightharpoonup }{b}$, and equatorial minor axis $\stackrel{\rightharpoonup }{c}$
‐distance (cm)	$|\stackrel{\rightharpoonup }{a}|,|\stackrel{\rightharpoonup }{b}|,|\stackrel{\rightharpoonup }{c}|$	Distances between boundary, along the three axes
‐directional unit vector	$\widehat{a},\widehat{b},\widehat{c}$	Orthogonal unit vectors of the three axes (evaluate by dot product to statistical unit vector)
Meridional eccentricity	${\epsilon }_{\mathit{me}}$	Eccentricity of conic section formed by equatorial minor distance to major distance: $\sqrt{1-{|\stackrel{\rightharpoonup }{c}|}^2/{|\stackrel{\rightharpoonup }{a}|}^2}$
Equatorial eccentricity	${\epsilon }_{\mathit{eq}}$	Eccentricity of conic section formed by equatorial minor distance to equatorial major distance: $\sqrt{1-{|\stackrel{\rightharpoonup }{c}|}^2/{|\stackrel{\rightharpoonup }{b}|}^2}$
Relative features
Relative volume to External	$V/V_{\mathit{ext}}$	Ratio of OAR volume to External volume
Relative centroid displacement vector to External (cm)	$\mathrm{\Delta }{\stackrel{\rightharpoonup }{C}}_{A-ext}$	Centroid of OARA minus centroid of External (three dimensions are treated independently)
Relative centroid displacement vector between A and B (cm)	$\mathrm{\Delta }{\stackrel{\rightharpoonup }{C}}_{A-B}$	Centroid of OARA minus centroid of OARB (three dimensions are treated independently)
Others
Number of disconnected volumes	$N_V$	As titled

The distribution of each feature was parameterized to a best‐fit distribution using the allfitdist algorithm.¹⁸ From the parameterized feature distribution, the 95% confidence interval was computed to obtain the statistical bound. If the value of a feature was outside of its statistical bound, it would be considered a deviation from normal. Assuming all 25 features were independent, the probability that at least one normal feature being outside of the 95% confidence interval would be $1-0.{95}^{25}=72\%$. In order to reduce the number of outlier warnings and to generate relevant warning messages, a multicriteria outlier detection system was implemented, in which a warning message was only issued if an OAR contained a combination of deviant features. Table 2 describes the combination of deviant features required to trigger a warning. The link between outlier and feature combinations was determined from the reference delineation sets: After the feature distributions were derived, OARs with deviant features were identified from the distribution tails. Cross‐correlation between deviant features was then identified. In this study, a heuristic method was used to identify the correlations between abnormality from the list of OARs and deviant features. Assume the deviant features associated with the outlier were independent, the probability, P, that at least n of them being outside of the 95% confidence interval would be:

$$P=\sum _{k=n}^{N_a}\left(\begin{array}{c}{N}_a\\ k\end{array}\right){0.95}^{N_a-k}{0.05}^k,$$

where $N_a$ is the number of deviant features associated with the outlier and $\left(\begin{array}{c}n\\ k\end{array}\right)$ is the binomial coefficient. From this, we derived the minimum number of combinations of deviant features required to prompt a warning for 5% or less of the OARs examined. The heuristic method was sufficient to obtain the feature combinations required to prompt a warning for less than 5% due of the cases; statistical methods could alternatively have been used.

Table 2.

Summary of delineation outlier, the associated deviant features as defined in Table 1, and the minimum number of deviated features to trigger warning. + indicates value of feature above statistical upper bound, −indicates value of feature below statistical lower bound

Outliers	Relevant OARs	Deviant features	N to Trigger
Large volume	All OARs	$+V$, $+A$, $+m$, $-A/V$, $-A/m$, $+|\stackrel{\rightharpoonup }{a}|$, $+|\stackrel{\rightharpoonup }{b}|$, $+|\stackrel{\rightharpoonup }{c}|$, V/V ext	3
Small volume	All OARs	$-V$, $-A$, $-m$, $+A/V$, $+A/m$, $-|\stackrel{\rightharpoonup }{a}|$, $-|\stackrel{\rightharpoonup }{b}|$, $-|\stackrel{\rightharpoonup }{c}|$, $-V/V_{\mathit{ext}}$	3
Overextended boundary	Soft tissue OARs: for example, Heart	$-\overline{\rho }$, $+{\sigma }_{\rho }$, $-{\rho }_{\mathit{min}}$, $+{\rho }_{\mathit{max}}$	2
Retracted boundary	Soft tissue OARs: for example, Heart	$+\overline{\rho }$, $-{\sigma }_{\rho }$, $+{\rho }_{\mathit{min}}$, $-{\rho }_{\mathit{max}}$	2
Overextended boundary	Air bearing OARs: for example, Lung	$+\overline{\rho }$, $+{\sigma }_{\rho }$, $+{\rho }_{\mathit{max}}$, $+m$	2
Retracted boundary	Air bearing OARs: for example, Lung	$-\overline{\rho }$, $-{\sigma }_{\rho }$, $-{\rho }_{\mathit{max}}$, $-m$	2
Rough boundary	All OARs	$+A/V$, $+A/m$	2
Shape (usually extra segment)	All OARs	$+A/V$, $+A/m$, $+|\stackrel{\rightharpoonup }{a}|$, $+|\stackrel{\rightharpoonup }{b}|$, $+|\stackrel{\rightharpoonup }{c}|$, $-\widehat{a},-\widehat{b},-\widehat{c}$, $\pm {\epsilon }_{\mathit{me}}$, $\pm {\epsilon }_{\mathit{eq}}$	3
Position (x, y, z)	All OARs	$\pm \mathrm{\Delta }{\stackrel{\rightharpoonup }{C}}_{A-ext}$, $\pm \mathrm{\Delta }{\stackrel{\rightharpoonup }{C}}_{A-B}$ (must be same sign)	3
Disconnection (missing slice, ditzels)	All OARs	$+N_V$	1
Unknown	All OARs	Not the above combination	4

2.B. Tool evaluation

The QA algorithm was tested using a historic reference built from prior radiation therapy treatment plans from 73 lung cancer patients (exempted from institutional review board). CT datasets acquired on a Brilliance CT big bore simulator (Philips, Cleveland, OH, USA) were used for the study. The reconstruction in‐plane matrix size was 512 × 512 in 60 × 60 cm² field‐of‐view, slice thickness was 3 mm. Nine OARs were selected: BrachialPlexus_L, BrachialPlexus_R, Carina, Esophagus, Heart, Lung_L, Lung_R, SpinalCord, and Trachea.¹⁹ Not all datasets had all nine structures delineated. Thoracic volume was used because the definition of thoracic OAR structure was well understood within our clinic. The historical OAR structures were delineated by a medical resident or an experienced dosimetrist and approved by attending physician as a part of routine clinical treatment planning. Structures were delineated on Velocity (Varian Medical Systems, Palo Alto, CA, USA) and Pinnacle³. Structures delineated on Velocity were subsequently imported to Pinnacle³. The reference set was based purely on clinically utilized historical OAR delineations, without any modifications.

The QA tool was evaluated utilizing OARs from three different sources. These experimental OARs were from 15 independent CT datasets not in the reference population. The first cohort consisted of nine clinically approved manually delineated structure sets which contained 71 OAR delineations in total. To ensure common delineation errors existed in this cohort, we simulated errors by applying 34 manipulations to these OARs (some structures received two manipulations). The resultant OAR structures had an added ditzel (four total, at least 0.6 cm² in single slice), a missing slice (seven total), expansion/contraction (12 total, at most 0.5 cm in each direction), extra segment (four total, lung delineation extended to contralateral side in a slice), and structure mislabeling errors (seven total, three pairs of swapped OAR names and one structure with empty delineation). The nonmanipulated structures served as control of the sensitivity study. The second cohort consisted of three structure sets generated by the Auto‐Segmentation routine in Pinnacle³, and contained 18 OAR delineations in total. The third cohort of three structure sets consisted of 18 OAR delineations obtained by propagating the delineations by deformable mapping. Deformable registration was done between two CT datasets acquired at different time points for the same patient. Both registration and delineation propagation were performed on Velocity. Delineations from the second and third cohorts were not manually modified. The name and color of the OAR structures were standardized for consistency.

For the experiment, three experienced radiation oncology residents reviewed the experimental structure sets and identified delineation errors in two sessions. During the first session, the reviewers examined the delineations and identified errors without the QA tool. The second session was conducted at least 1 week after the initial session, in which the reviewers examined and identified errors in the same experimental sets (scrambled order) with the aid of the QA tool. For each delineation, they identified if they thought error(s) existed and categorized the type(s) of error. In addition, they classified their findings as minor or major errors based on their opinion of the presumed impacts on treatment planning and dosimetry. For analysis, a reviewer identified error was considered a true (consensus) error if two or more individuals identified the same error during either session. Classification of the error severity followed the same majority rule. If an error was consensually identified as major error in one session and minor error in the other, it was identified as a major error. During the experiment, reviewers did not make corrections on the delineations and the feedback feature of the QA tool was not used to update the reference OAR set.

3. Results

Overall, there were 11 boundary and 17 volume outlier warnings, six outlier warnings of rough boundary, 14 shape, 17 disconnection, 18 position outlier warnings. Some of these outlier warnings appear together for a single delineation, for example, volume and boundary warnings appeared together in eight delineations. In general, the occurrences of deviant features were directly correlated with the occurrences of the outlier warnings according to Table 2. Table 3 shows the top three features and their appearance rates of each warning for the experimental delineations. From the table, new associations between a deviant feature and the associated outlier warning can be seen, for example, $A/m$ appeared the most for a boundary outlier warning, even though it is not one of the required deviant features.

Table 3.

Outlier warnings and their top three most appearing corresponding deviant features

Warning (total number)	Most appearing feature (rate)	Second most appearing feature (rate)	Third most appearing feature (rate)
Boundary (11)	A/m (82%)	$\overline{\rho }$ , ${\rho }_{\mathit{max}}$ , $m$ (73%)	${\sigma }_{\rho }$(64%)
Volume (17)	$m$ (88%)	$A/m$ (82%)	$A/V$ (76%)
Roughness (6)	$A/V$ , $A/m$ (100%)	${\sigma }_{\rho }$ , $V/V_{\mathit{ext}}$ (67%)	$|\stackrel{\rightharpoonup }{b}|,|\stackrel{\rightharpoonup }{c}|$ , $\overline{\rho }$ , m (50%)
Shape (14)	${\epsilon }_{\mathit{eq}}$ (71%)	$\widehat{c}$ (57%)	$\widehat{b}$ , ${\epsilon }_{\mathit{me}}$ (43%)
Disconnection (17)	$N_V$ (100%)	${\epsilon }_{\mathit{eq}}$ (29%)	$\mathrm{\Delta }{\stackrel{\rightharpoonup }{x}}_{A-B}$ (24%)
Position (18)	$\mathrm{\Delta }{\stackrel{\rightharpoonup }{z}}_{A-B}$ (61%)	$\mathrm{\Delta }{\stackrel{\rightharpoonup }{x}}_{A-B}$ (56%)	$|\stackrel{\rightharpoonup }{b}|,|\stackrel{\rightharpoonup }{c}|$, $\mathrm{\Delta }{\stackrel{\rightharpoonup }{z}}_{A-ext}$ , $\mathrm{\Delta }{\stackrel{\rightharpoonup }{x}}_{A-ext}$, $\mathrm{\Delta }{\stackrel{\rightharpoonup }{y}}_{A-B}$ (33%)
No warning (51)	$\widehat{a}$ (16%)	$\widehat{b}$ , $\mathrm{\Delta }{\stackrel{\rightharpoonup }{z}}_{A-ext}$ , $\mathrm{\Delta }{\stackrel{\rightharpoonup }{x}}_{A-B}$ (8%)	$\widehat{c}$ , $\mathrm{\Delta }{\stackrel{\rightharpoonup }{y}}_{A-ext}$ , $\mathrm{\Delta }{\stackrel{\rightharpoonup }{z}}_{A-B}$ (6%)

$\mathrm{\Delta }\stackrel{\rightharpoonup }{x}$ is centroid displacement along x direction, and so forth.

Table 4 summarizes the (consensus) errors identified by the reviewers. During analysis, multiple errors on the same OAR were considered as multiple errors. Of the 34 manipulations, reviewer consensus identified eight as minor and 23 as major errors based on the predefined criteria. The remaining three manipulations (two ditzels and one contraction) were not defined as errors based on the majority rule. It was initially expected that the control group of clinically approved manual delineation would contain no major error. However, reviewers also identified 10 minor and two major errors in this control group. Over all cohorts, reviewers identified 43 no errors, 38 minor errors and 34 major errors, corresponding with 115 decisions from the 107 OAR delineations (eight OARs had two errors). Figure 2 presents some examples of delineations with identified errors.

Table 4.

Summary of identified errors. A majority rule was used to classify if an error existed and the error severity. During review, images were ungrouped and scrambled

	Minor errors	Major errors	No errors
Error categories
Boundary in transverse plane	27	11	‐
Slice extent	7	5	‐
Ditzel	2	0	‐
Extra segment	0	4	‐
Missing slice	2	7	‐
Mislabel	0	7	‐
Delineation groups
Manipulated manual delineation	8	23	3
Control manual delineation	10	2	33
Automatic delineation	6	5	7
Propagated delineation	14	4	0
OARs
Brachial Plexuses	3	3	4
Carina	6	2	4
Esophagus	3	3	6
Heart	4	6	5
Lungs	7	11	18
SpinalCord	8	6	2
Trachea	7	3	4
Total
	38	34	43

Figure 2.

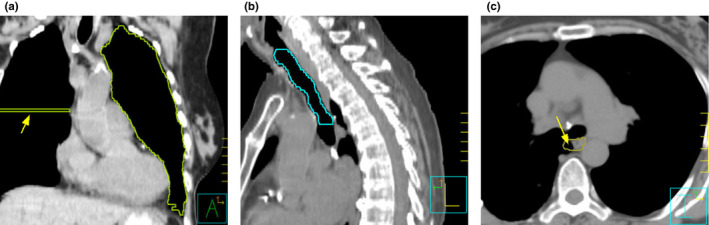
Examples of erroneous delineations from the experimental data. (a) Delineation of left lung from the manual delineation group with simulated error. An extra segment (arrowed) was extended to the contralateral side and was classified as major error. The OAR QA tool issued a shape warning for this delineation. (b) Delineation of trachea from the automatic delineation group. The automatic algorithm failed to include the tracheal cartilage within the delineation. As a result, it was classified as major boundary error in the transverse plane. The OAR QA tool issued a retracted boundary warning for this delineation. (c) Delineation of esophagus from the propagated delineation group. A minor boundary error in the transverse plane was classified because part of lung was included in the delineation (arrowed). The OAR QA tool did not issue any warning for this delineation. [Color figure can be viewed at wileyonlinelibrary.com]

When used alone (without human review), the QA tool error detection sensitivity was 37% (14 of 38) for minor errors and 85% (29 of 34) for major errors. Table 5, 6, 7 summarize the reviewers and QA tool error detection rate in different categories. Of the 31 manual manipulations identified as errors, the QA tool detected 29 of 31 (94%) of them, with 6 of 8 (75%) of them minor and 23 of 23 (100%) of them major errors. The QA tool also detected outliers in the three manipulated delineations that were not identified as errors using the reviewer consensus criteria. Over all error categories, the QA tool identified 22 of 22 (100%) of mistake type errors (ditzel, extra segment, missing slice and mislabel), but only 21 of 50 (42%) of the boundary type errors (transverse boundary and slice extent). The QA tool was particularly poor in identifying boundary errors in the propagated delineation sets (e.g., Fig 2c), finding 0 of 14 (0%) minor errors and 1 of 4 (25%) major errors in this cohort. This is because the volumetric features of the propagated delineation always remained similar to those of the original delineation. Therefore, reasonably propagated delineations would likely pass the QA algorithm. The QA tool also had difficulty identifying some of the major errors in Heart and Esophagus delineations. These five cases that the QA tool missed (false negative) were all transverse boundary or slice extent type errors (one automatic, one manual, three propagated). Major boundary errors for these delineations may be more difficult to detect because delineations of the Heart and Esophagus contain tissues in a wide range of CT numbers both within and among patients. As a result, boundary errors perceived by the reviewers might not be able to drive the corresponding features out of their 5% threshold.

Table 5.

Error detection rate by the QA tool and reviewers, categorized into the different error types

	QA tool		Reviewers – first session w/o QA tool		Reviewers – second session w/QA tool
	Minor errors	Major errors	Minor errors	Major errors	Minor errors	Major errors
Boundary in transverse plane	10/27	8/11	50/81	32/33	56/81	30/33
Slice extent	0/7	3/5	14/21	13/15	15/21	14/15
Ditzel	2/2	‐	4/6	‐	2/6	‐
Extra segment	‐	4/4	‐	12/12	‐	12/12
Missing slice	2/2	7/7	2/6	14/21	6/6	15/21
Mislabel	‐	7/7	‐	9/21	‐	17/21

Table 6.

Error detection rate by the QA tool and reviewers, categorized by the delineation cohorts

	QA tool		Reviewers – first session w/o QA tool		Reviewers – second session w/QA tool
	Minor errors	Major errors	Minor errors	Major errors	Minor errors	Major errors
Manipulated manual delineation	6/8	23/23	14/24	49/69	16/24	60/69
Control manual delineation	4/10	1/2	10/30	5/6	19/30	4/6
Automatic delineation	4/6	4/5	12/28	14/15	16/18	14/15
Propagated delineation	0/14	1/4	34/42	12/12	27/42	11/12

Table 7.

Error detection rate by the QA tool and reviewers, categorized into different OARs

	QA tool		Reviewers – first session w/o QA tool		Reviewers – second session w/QA tool
	Minor errors	Major errors	Minor errors	Major errors	Minor errors	Major errors
Brachial Plexuses	1/3	3/3	5/9	5/9	2/9	7/9
Carina	6/6	2/2	11/18	5/6	11/18	6/6
Esophagus	0/3	1/3	4/9	7/9	6/9	7/9
Heart	2/4	3/6	7/12	16/18	8/12	16/18
Lungs	0/7	11/11	18/21	24/33	14/21	28/33
SpinalCord	1/8	6/6	11/24	16/18	18/24	17/18
Trachea	4/7	3/3	14/21	7/9	19/21	8/9

Overall, with the help of the QA tool, reviewers improved their error detection sensitivity from 61% (70 of 114) to 68% (78 of 114) for minor errors, and from 78% (80 of 102) to 87% (89 of 102) for major errors. Using the asymptotic McNemar's test, the improvement in error detection was insignificant for minor errors (P = 0.17) and was significant for major errors (P = 0.02).

Among the OARs with no errors (based on majority rule), there were cases in which a single reviewer identified an error within an OAR in either or both experiment sessions. Overall, one of the three reviewers identified an error in 23 of 43 (53%) of the no error OARs in the first experiment session, and 20 of 43 (47%) in the second experiment session. The QA tool identified outliers in 11 of 43 (26%) of the OARs in this cohort. The most frequent warnings in this cohort were position outlier and disconnection, both occurred three times. With respect to organ type, five Lung_L delineations triggered warnings in this cohort (three disconnections, one shape, one position). While disconnection warnings were ditzels in which reviewers failed to identify as an error, the other identified outliers were most likely unusual patient anatomies, for example: the QA tool found that the size of one patient's heart was much larger than normal.

Between the two experiment sessions, the three reviewers changed their decisions 124 of 345 (36%) of time (33 from no to minor, 28 from minor to no, 19 from no to major, 9 from major to no, 28 from minor to major, and 7 from major to minor). Among the identifications that changed between minor and no error and vice versa, 34 of 61 (56%) of them aligned with and 27 of 61 (44%) of them contradicted the QA tool outlier/nonoutlier suggestions. Among the identifications that changed between major and no error and vice versa, 23 of 28 (82%) of them aligned with vs 5 of 28 (18%) of them contradicted the QA tool outlier/nonoutlier suggestions. Out of the 57 changed identifications that aligned with the QA tool suggestions, 13 were changed from no to minor error, 21 were changed from minor to no errors, 17 were changed from no to major error, and six were changed from major to no error.

4. Discussion

The OAR delineation QA tool is easy to implement. The algorithm uses a reasonable set of volumetric features and detects their outliers by observing the feature probability distributions. These features are easy to compute or basic features inherent to any 3D structure; thus in principal, the features would be applicable to any OAR delineation. No attempt was made to find the optimized set of features, either globally, or for an individual OAR structure. Additional features (perhaps even 2D features) can be added to the tool with little penalty. If one of our utilized features, or an added feature, is a poor discriminator for structure R, the feature's probability distribution for structure R would be wide, therefore the feature would have a negligible role in the outlier selection decision. The important features for an individual structure are thus auto‐identified. Analyzing the entire feature set for each structure improves the likelihood of finding a discriminatory feature combination for an arbitrary structure.

Intuitively, one might expect that hundreds of datasets are required to develop a reliable statistical model for anomaly detection; and thus might consider the use of a 73‐patient cohort insufficient. However, this study and some prior studies^{13, 20} have shown that, inspite of using a limited dataset to derive the statistical reference, the resultant models improved detection of delineation errors. This suggests that the benefits of statistical anomaly detection can be extended to mid to small clinics with limited resources. In addition, no pre‐reviewing or correction of the reference datasets is necessary. This approach eliminated the extensive amount of time required to pre‐review the delineations, and it eliminated the bias generated by the pre‐reviewers. For this study, we found that the initial reference delineations from the 73 patient cohort contained major errors such as missing slice and extra segment during the process of developing the outlier detection system. These errors were not corrected; instead, their features were included in the reference distribution. These erroneous delineations might expand the 95% confidence interval of the feature as we expected that most errors would be outliers in the statistical model. As the subsequent experiment showed, the statistical approach was robust enough to maintain high sensitivity in major error detection inspite of known errors in the reference distribution. Although not tested, removal of the erroneous reference delineations would likely improve the error detection sensitivity. Similarly, continued QA tool use, with reference set updating enabled, will likely reduce the frequency of major errors in the reference data, thereby also improve the sensitivity of error detection. As the reference delineations become more accurate, one might consider increasing the confidence interval to, for example, 99% for deviant feature warning if the number of false positive warning becomes tiresome.

The sensitivity for a QA algorithm to detect delineation error depends on the OAR dataset, and types and severity of the error. Therefore, it is difficult to assess the effectiveness of the QA algorithm by sensitivity alone. Instead, our experiment used a two‐session approach to assess how much the QA tool can improve user sensitivity in detecting delineation error. From our experiment, the error detection sensitivity of the QA algorithm was 37% and 85% for minor and major errors, respectively. The number is lower than some other QA algorithms reported by previous literatures: 95% from Altman et al.¹³ and 95% from Chen et al..²⁰ However, the aforementioned studies used strictly datasets with simulated errors. If only simulated errors were accounted in the analysis, the QA algorithm would have picked up 29 of 31 (94%) of errors, where three manipulations were not counted due to the majority rule. Nevertheless, comparison among different studies would not be meaningful unless the exact same dataset were to be used for the analysis.

There were only a small number of major errors in the control group of manual nonmanipulated structures because these structures were clinically utilized, therefore had previously been reviewed. This control group was expected to have no major errors. However, within this cohort, reviewers identified two major errors: a missing slice error which the QA tool detected and a boundary error which the QA tool did not detect. During the first session, two of three reviewers identified the missing slice error, and all three reviewers identified the boundary error. During the second session, still only two of three reviewers identified the missing slice error even though the QA tool warned them that this error existed. The boundary error detection decreased, being identified by only two of three reviewers. The apparent reduced detectability with the QA tool for the manual nonmanipulated cohort was due to a singular decision on an error in which the decision tool made no recommendation. This reduced detectability was likely an artifact of the few errors in the clinical data.

In our experiment, 89% of the minor errors were identified as transverse planes boundary errors or incorrect slice extent. The QA tool was insensitive in detecting these minor errors. This is due in part to the fact that the volumetric features are mostly shape related and are not currently equipped to analyze contrast features within the OAR or near the OAR boundary. Another reason for the low sensitivity was the inconsistency in minor error classification, as reviewers identified no error in one session and minor error in another 18% of the time among all decisions. Furthermore, 26% of the identified minor boundary or slice extent errors came from unperturbed clinical OAR delineations, which were previously approved by physician for patient treatment. This highlights the subjectivity of error definition, particularly for minor errors. For the minor boundary type errors, it is likely that many of them fell in the “inherent inter‐and intra‐delineator variability” and “OAR definition discrepancy between different delineators” categories. As the reference data also contain this inherent variability, it would be difficult for the QA tool to identify these boundary variations as outliers.

The current group of features was not very effective to detect errors in deformable registered delineations, which were found to be mostly boundary‐type errors. Boundary‐related error detection could potentially be improved by using intensity‐based features. Image‐based features are generally more complex and take longer to process compared with volumetric features. The volume‐based features used here provide potential clinical benefit and are simple to calculate. The identification of such features and resultant detectability improvements is left for future study.

In the current experiment, there was virtually no difference in reviewing time between the two experiment sessions. This is because reviewers were instructed to look for all possible errors. As a result, they kept looking for additional errors even after they found the errors suggested by the QA tool. A different study design resembling to common clinical workflow is needed to determine the time advantage of using the QA tool.

The reviewers were informed of the types of manipulations that were introduced, and that the manipulations mimicked common clinical delineation errors. The instructions ensured that all reviewers had a common understanding of their role in the study. The reviewers, however, were not informed of the frequency in which the manipulations happened. Therefore, the explicit instruction did not differ from the standard instruction that would be implicitly understood for clinical delineation review. The instructions provided might introduce minor systematic bias. However, without instruction, the definition of an error by the reviewers could become even more arbitrary and subjective.

One weakness of this and any delineation error experiment is the subjectivity of error identification. To achieve fairness in error definition, we used the majority rule approach to identify and classify error. However, the majority rule approach can be affected by reviewer's vigilance and could potentially misidentify even objective errors like OAR mislabeling. The reviewer's performance in our experiment was satisfactory, as only two ditzels and one contraction from the 34 manipulations were not classified as errors based on the majority rule.

Another weakness of our experiment was that the QA tool might skew a reviewer's perception of error. We found that decisions that changed between minor and no error and vice versa were 56%–44% in favor of the QA tool outlier/nonoutlier suggestions, but 82% of decisions that changed between major and no error and vice versa aligned with the QA tool outlier/non‐outlier suggestions. This suggests that decisions involving a minor error may be more subjective in nature. These decisions may be slightly skewed by the QA tool, but the reviewers went against the suggestions almost as often as with them. The decisions involving a major error, however, may involve more objective assessment in which reviewers was less likely to disagree after inspection. Intuitively, the order of the experiment sessions might give an advantage to the QA tool, however, the reverse order might bias against it by tipping reviewers off to specific findings in the images. The 1‐week interval and the scrambled data order should reduce reviewer's memory of specific errors, hence reduce the bias.

The results presented intentionally omitted the notion of specificity due to limitations of the experimental design. The majority rule for error identification guaranteed that the reviewer's “specificity” to be always more than 66% in both experiment sessions. Therefore, reviewer specificity might not be appropriate. As for the QA tool, it was designed to detect delineation outliers statistically. This includes both delineation errors and anatomic abnormalities. Since detection of an anatomical abnormality could potentially assist in clinical decision‐making, we would not consider its identification as false positive.

5. Conclusions

This work developed an automated OAR delineation QA tool to assist reviewers in the identification of inaccurate OAR delineations and demonstrated its effectiveness in detecting delineation errors. Unlike previous methods, our QA algorithm uses features that are strictly volumetric. Another unique feature is the multicriteria outlier detection system to help identify specific type of delineation outlier. The tool is fully integrated into Pinnacle³ treatment planning system. Our experiment showed that the QA tool detected major delineation errors effectively, and it significantly improved user's ability to detect these errors.

Conflict of interest

Jeffrey V. Siebers has a research agreement with Varian Medical Systems regarding EPID‐based dosimetry.