Scaling of lipid membrane rigidity with domain area fraction

Abstract

Biological membranes are highly heterogeneous in composition which in turn leads to local variations in the physical properties. Here we quantify how heterogeneity in stiffness determines the effective bending modulus, k_eff, of model phase-separated membranes with coexisting soft fluid and rigid gel domains. We find that the temperature- and composition- dependent trends in membrane rigidity collapse onto a single curve, such that k_eff directly scales with the area fraction of the rigid gel domains. Using no adjustable parameters, the measurements are found to agree with theoretical predictions for inhomogenous membranes and indicate that k_eff is sensitive to the lateral distribution of the rigid phase within the membrane. This key finding confirms that the properties of heterogeneous membranes can be quantitatively predicted if the area fraction and properties of the individual phases are known.

1. Introduction

The dynamics of soft membranes have attracted considerable theoretical and experimental attention for more than four decades. Much of this work has focused on lipid membranes as models for biological membranes, in which the underlying membrane dynamics and associated elastic properties influence both protein and cell functions. While significant advances have been made in quantifying the elastic properties of homogeneous membranes, much less is known about how the heterogeneity inherent in biological membranes affects their dynamics.

Biological membranes are a highly heterogeneous and crowded environment. Membranes contain rigid proteins and domains that are stiffer than the surrounding lipid matrix by a factor of 2 to 400.^1–8 Theoretical works that consider the effects of such rigid bodies, often referred to as inclusions or additives, show that the dynamics of heterogeneous membranes are governed by an effective bending modulus, k_eff. The predicted deviations of k_eff from the properties of homogeneous membranes are highly sensitive to the concentration, shape, and location of the inclusions, as well as whether the inclusions are inserted or absorbed.^9–16 Further adding to the complexity, there are limited experimental data to compare with existing theories, and conflicting results show the inclusions can increase, decrease, or have a negligible effect on the membrane stiffness.^16–25

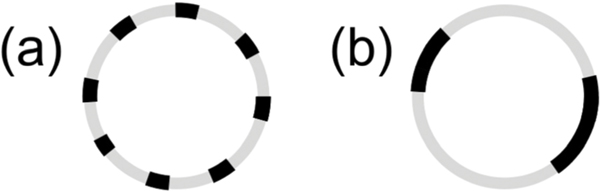
Here, we study the particular case in which the rigid inclusions are embedded with the same average number density in each leaflet. In this case, simple mixing models predict that adding rigid inclusions will stiffen the membrane and that k_eff will scale with ϕ, the area fraction of the rigid phase.^9–11 However, theoretical work by Netz and Pincus also considers how the inclusions are organized within the membrane and predicts that the functional form of the k_eff scaling with ϕ will depend on whether the domains are dispersed (Fig. 1a) or aggregated (Fig. 1b).¹¹ To the best of our knowledge, no experimental data span a wide enough concentration range of inclusions to compare with these differing theories. Comparisons between measurements and predictions at high ϕ, where the effects of the rigid phase on k_eff are most pronounced, will reveal the importance of membrane lateral organization.

Fig. 1.

Cartoon illustrations of lipid vesicle cross sections with (a) dispersed versus (b) aggregated domains.

To test these predictions, we systematically quantify k_eff in model heterogeneous membranes for a wide range of ϕ. We measure the bending undulations in phase-separated dimyristoylphosphocholine (DMPC, 14:0 PC) and distearylphosphocholine (DSPC, 18:0 C) membranes using neutron spin echo (NSE) spectroscopy. To vary ϕ from 0 to 1, we take advantage of the wide temperature range of two-phase coexistence by simply changing temperature in the phase coexistence region of the phase diagram (Fig. 2). Using no adjustable parameters, measurements of k_eff as a function of ϕ show better agreement with the theory of Netz and Pincus for inhomogeneous membranes, demonstrating that the functional form of the scaling does indeed depend on the membrane lateral organization.

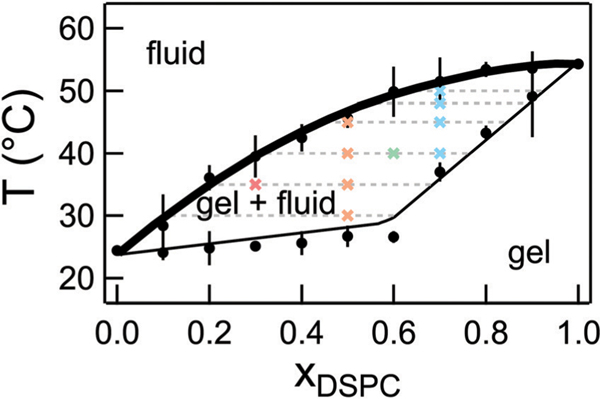
Fig. 2.

Phase diagram for mixtures of DMPC/DSPC in D₂O constructed from densitometry and DSC experiments. The solid lines are the published phase diagram for DMPC/DSPC in H₂O shifted by +0.2 °C.³³ The bold line is referred to as the fluidus line and the dotted lines are the tie lines at the respective temperature. Crosses represent the temperatures measured with NSE for the different lipid mixtures. Error bars on the transition temperatures represent one standard deviation of measurements from different samples and different techniques. Error bars represent one standard deviation throughout the text and in some cases are smaller than the symbol.

2. Experimental section

2.1. Materials

Lipids were purchased from Avanti Polar Lipids and used without further purification. Deuterium oxide (D₂O, 99.9% D) was purchased from Cambridge Isotopes. Relatively monodisperse unilameller vesicles with ≈100 nm diameter were prepared at the desired DMPC/DSPC ratios according to established extrusion protocols.^26,27 Lipids were mixed at the desired ratio in chloroform, dried under nitrogen, and then under vacuum overnight. The lipid film was rehydrated with D₂O at 55 °C to form multilayer vesicles. The multilayer vesicles then were sequentially extruded through 400 nm (15×), 200 nm (15×) and 100 nm (41×) and stored at 55 °C until measurement. The final solutions contained 100 mg mL⁻¹ lipid in D₂O and were homogeneous by eye. Solutions were measured within 3 days of preparation. The sample stability was checked with dynamic light scattering (DLS) and small angle neutron scattering (SANS). SANS measurements were also used to confirm that >95% of the vesicles were unilameller (Fig. S1, ESI†).

2.2. Differential scanning calorimetry (DSC)

DSC experiments were performed using a Microcal VP-DSC calorimeter. Samples were equilibrated at temperatures corresponding to the fluid phase, and at least 2 cooling and heating cycles were measured using a scan rate of 0.5 °C min⁻¹. The solvent background and baseline corrections were performed in the software package provided with the instrument, and the transition temperatures were determined using the tangent method (Fig. S2, ESI†).²⁸ Samples for DSC experiments had a lipid concentration of 5 mg mL⁻¹.

2.3. Density measurements

Density measurements were made using an Anton Paar DMA 500 density meter. The lipid volume was calculated from the measured density following procedures in literature.²⁹ The phase transition temperatures were determined from the derivative of the measured density versus temperature curve using the tangent method (Fig. S2, ESI†).^28,30 Lipid samples for density measurements were diluted to 20 mg mL⁻¹.

2.4. Neutron spin echo spectroscopy (NSE)

Data were collected on the NGA-NSE Spectrometer at the National Institute of Standards and Technology (NIST) Center for Neutron Research (NCNR) using neutron wavelengths (λ) of 0.8 nm and 1.1 nm with a wavelength spread of Δλ/λ≈0.2 to access a q-range of 0.45 nm⁻¹ < q < 1.2 nm⁻¹ and Fourier times, t, ranging from 0.01 ns to 100 ns corresponding to the bending undulations.³¹ The magnitude of the scattering vector, q, is defined as q = 4π/ λ sin(θ/2) in which θ is the scattering angle. The temperature was controlled within ±0.5 °C and the samples were equilibrated for 30 min before starting the measurements. All data were collected on cooling. The NSE data were corrected for instrument resolution and D₂O solvent background to give the normalized intermediate scattering function I(q,t)/I(q,0) using the DAVE software package.³²

3. Results and discussion

DMPC/DSPC mixtures are widely used as model systems to understand lipid membrane phase behavior and properties.^27,33–39 Our previous work measured the effects of the 4 carbon tail length mismatch on the dynamics of DMPC/DSPC mixtures in the fluid phase where the lipids are homogeneously mixed.²⁷ Here we focus on the membrane dynamics in the phase coexistence region. The phase behavior for DMPC/DSPC mixtures is well documented in literature; however, the NSE experiments required that the lipid mixtures be prepared in D₂O which is known to increase the melting transition temperature of pure lipids.⁴⁰ As seen in Fig. 2, our measurements of the lipid phase behavior using densitometry and differential scanning calorimetry (DSC) indicate that replacing H₂O with D₂O shifts the phase boundaries by ≈0.2 °C compared to the phase behavior reported for the mixtures in H₂O, but does not affect the shape of the boundaries. We refer to temperatures on the fluidus line as T_m, corresponding to the miscibility transition temperature.

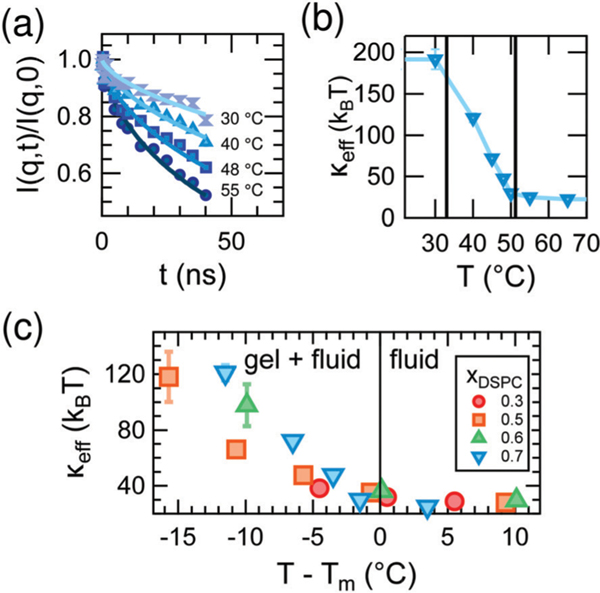
The equilibrium bending undulations of the phase-separated membrane are governed by the effective elasticity, k_eff. By directly measuring these thermal fluctuations with NSE, we are thus able to study changes in k_eff in the DMPC/DSPC bilayers as the mixtures are cooled from the fluid phase into the two-phase coexistence region and gel domains form. Shown in Fig. 3a are measured normalized intermediate scattering functions, I(q,t)/I(q,0), for bilayers containing a DSPC mole fraction (x_DSPC) of 0.7 at temperatures corresponding to the fluid (55 °C), gel + fluid coexistence (48 °C and 40 °C), and gel phases (30 °C). As seen in the I(q,t)/I(q,0) data in Fig. 3a, the relaxation time increases (curves decay less) with decreasing temperature, indicating that the membranes are becoming less dynamic (i.e. stiffer). All compositions exhibit this same behavior.

Fig. 3.

(a) I(q,t)/I(q,0) data (points) and fits to a stretched exponential (lines) at q = 1.1 nm⁻¹ for indicated temperature and (b) corresponding values of k_eff for mixed DMPC/DSPC membranes containing DSPC mole fraction (x_DSPC) of 0.7. The vertical lines in (b) demarcate the gel-fluid coexistence region. (c) Effective bending modulus, k_eff, of mixed DMPC/DSPC lipid bilayers for the compositions given in the legend as a function of relative temperature, T – T_m, in which T_m corresponds to the temperatures on the fluidus line of the phase diagram.

The I(q,t)/I(q,0) data for all temperatures are well fit by a stretched exponential decay as expected for single membrane bending undulations described by Zilman and Granek,

$$I(q,t)/I(q,0)=\exp \left[-{(\mathit{\Gamma }(q)t)}^{2/3}\right]$$ (1)

in which Γ(q) is the relaxation rate.⁴¹ The corresponding relaxation rates were used to determine the effective bending modulus, k_eff, using refinements to the Zilman–Granek model made by Watson and Brown to account for the intermonolayer friction between leaflets according to

$$\mathit{\Gamma }=0.0069\frac{k_{\text{B}}T}{\eta }\sqrt{\frac{k_{\text{B}}T}{{\kappa }_{\text{eff}}}}{q}^3$$ (2)

in which k_B is the Boltzman constant, T is the temperature, η is the viscosity of the D₂O solvent.^42,43

The changes in the membrane stiffness as a function of temperature for x_DSPC = 0.7 are quantified as k_eff in Fig. 3b. k_eff increases from ≈ 30 k_BT in the fluid phase to ≈ 200 k_BT in the gel phase of the mixed bilayers, consistent with the order of magnitude increase in bending moduli seen upon gelation of single component lipid bilayers.^30,44,45 However, the increase in modulus occurs over a much wider temperature range for the mixed DMPC/DSPC membranes than reported for single component bilayers. The bending modulus typically increases sharply at the melting temperature of the lipid as expected for a first order transition in a single component membrane.^44,46,47 Here we see a gradual increase in k_eff in all mixtures across the gel-fluid coexistence region of the phase diagram which can be up to 15° wide (Fig. 3c). Moreover, the gradual increase in k_eff is not linear with temperature and its shape changes with composition in a non-intuitive fashion as evident from Fig. 3c.

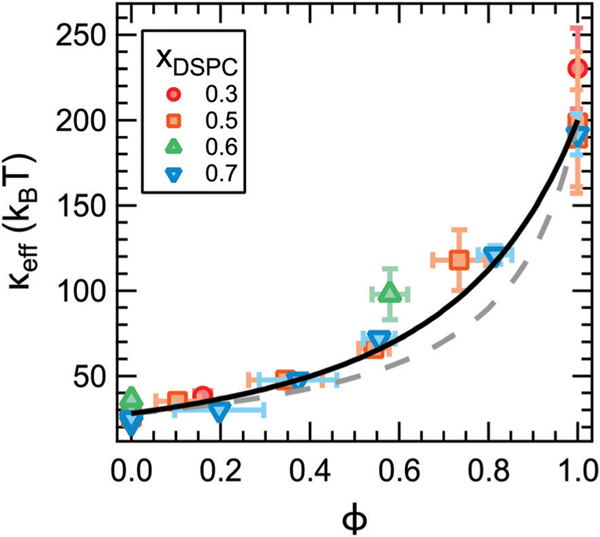
According to theoretical works on heterogeneous membranes, the trends in k_eff should scale in some way with the properties of the individual phases and their relative area fractions.^9–11 For a given lipid composition, the fraction of gel phase (f_gel) increases with decreasing temperature as the mixture is cooled into the coexistence region of the phase diagram. For a given temperature, f_gel will increase with increasing x_DSPC along the tieline. These trends in f_gel are qualitatively consistent with the changes in k_eff with temperature and x_DSPC in Fig. 3c. The mole fraction of gel phase can be quantified from the phase diagram in Fig. 2 according to the lever rule and converted to the area fraction, ϕ, using published values for the area per lipid of phosphatidylcholine lipids in the fluid and gel phases. Here we take A_fluid = 0.64 nm² and A_gel = 0.47 nm², respectively.^48,49 We note that A_fluid and A_gel have a temperature dependence; however, these effects are expected to be at most a 5% change and within the experimental uncertainty in the calculated ϕ value.^48–50 Replotting k_eff as a function of ϕ (Fig. 4) collapses the data for all compositions onto a single master curve. In other words, the effective rigidity scales directly with the area fraction of gel phase as theoretically predicted.

Fig. 4.

Effective bending modulus, k_eff, as a function of the gel phase area fraction, ϕ, measured by NSE (points) and calculated from the gel and fluid phase moduli (lines). k_eff was calculated using the averaged values of k_gel = 202 k_BT and k_fluid = 28 k_BT according to a weighted harmonic average (eqn (3), dotted line, χ² = 18.7) and theory by Netz and Pincus (eqn (4), solid line, χ² = 11.8) described in the text. Values in the legend refer to the membrane composition.

The simplest expression for the effective rigidity was first given in works by Markin⁹ and Helfrich and Kozlov¹⁰ and predicts that k_eff should follow a harmonic average of the fluid membrane and rigid inclusion moduli weighted by their respective area fractions,

$$\frac{1}{k_{\text{eff }}}=\frac{\varphi }{{\kappa }_{\text{gel }}}+\frac{1-\varphi }{{\kappa }_{\text{fluid }}}$$ (3)

in which k_gel and k_fluid are the bending moduli of the gel and fluid phases. Previous studies of both macroscopic and nanoscale phase separated membranes have shown that the coexisting phases have different moduli.^4–7 Assuming this behavior also holds in our systems, the bending moduli of the gel and fluid domains in a phase separated membrane are expected to be on the order of k_fluid ≈ 30 k_BT and k_gel ≈ 200 k_BT, respectively. Corresponding values for k_eff calculated using eqn (3) are shown as the dotted line in Fig. 4. As seen in the plot, eqn (3) systematically underestimates k_eff for ϕ > 0.4. Capturing the high ϕ data would require an unphysically large value of k_gel on the order of 10⁵ k_BT.

More recent theoretical work by Netz and Pincus also predict that k_eff should follow eqn (3) for membranes containing disordered and randomly mixed rigid inclusions as depicted schematically in Fig. 1a. However, in the limit of an aggregated phase in which the membrane separates into a phase of close packed rigid inclusions and a phase of the pure fluid membrane such as in Fig. 1b, they instead predict

$$\frac{1}{{\kappa }_{\text{eff}}}={\left(\frac{\varphi }{\sqrt{{\kappa }_{\text{gel}}}}+\frac{1-\varphi }{\sqrt{{\kappa }_{\text{fluid}}}}\right)}^2$$ (4)

Studies of phase-separated DMPC/DSPC mixtures indicate that the domains can be on the order of ≈ 100 nm in diameter and coarsen over time, and some works suggest that the gel phase can percolate forming a continuous phase.^{37–39,51,52} Accordingly, eqn (4) is expected to be a more appropriate model for the DMPC/DSPC membranes. Corresponding k_eff values are plotted as the solid line in Fig. 4. Considering the solid line is not a fit, our experimental results are in remarkably good agreement with this prediction.

While the theories discussed here should apply to any rigid inclusions embedded in a soft surfactant or lipid membrane, how k_eff scales with ϕ has direct implications for understanding the effects of transmembrane proteins on the stiffness of biological membranes. Red blood cells,⁵³ synaptic vesicles,⁵⁴ and viral membranes⁵⁵ have a transmembrane protein area occupancy on the order of ≈20% to 30%. Fig. 4 suggests that the rigid proteins may only have a small effect on k_eff at physiological concentrations regardless of how the proteins are distributed in the membrane (solid versus dashed line). At ϕ = 0.2, the inhomogeneous membranes are ≈1.2 to 1.3 times stiffer than the bare fluid membrane from eqn (3) and (4), respectively. These calculated values are for an ≈8x difference in moduli between the gel and fluid domains. Recent experimental results by Rosholm et al. suggest that proteins are ≈1.6 times stiffer than the cell membrane, and the resulting k_eff would be even smaller for this difference in moduli.³ The predicted small increase in k_eff is consistent with measurements of the mechanical properties of lipid extracts from the plasma membrane of red blood cells that showed the ≈20% area occupancy of transmembrane proteins had no appreciable effect on the membrane flexibility.²¹ However, incorporating more and/or stiffer protein would have a more significant effect. For example, Halobacterium halobium can incorporate as much as 75% by mass of the protein bacteriorhodopsin into its purple membrane which would have a much greater effect on the membrane elasticity.⁵⁵

The measured increase in k_eff for phase-separated membranes at high ϕ is in good agreement with the scaling predicted by Netz and Pincus for inhomogeneous membranes with an aggregated rigid phase and shows that k_eff does indeed depend on how the rigid phase is distributed in the membrane. The differences in the predicted scaling for aggregated versus dispersed rigid phases are most evident for ϕ > 0.4 in Fig. 4. Our data follow eqn (4) predicted for aggregated rigid inclusions, which is consistent with the formation of large gel domains reported in phase-separated DMPC/DSPC membranes. At the other limit of dispersed nanodomains or proteins, the theory predicts that k_eff will instead follow a weighted harmonic average (eqn (3)). Work by Sigurdsson et al. found good agreement between k_eff values from their simulations and calculated by eqn (3) for proteins dispersed in a lipid bilayer for ϕ < 0.3; however, the simulated values deviated from the theory for 0.3 < ϕ < 0.5, and simulations were not performed at higher ϕ.² While more experimental data are needed to validate the predictions for dispersed rigid phases, ongoing investigations into the effects of domain size, lipid chemistry, and other additives such as nanoparticles and proteins, will further elucidate the role of membrane composition and organization in determining k_eff.

4. Conclusions

In summary, we quantified the effective elasticity of phase-separated DMPC/DSPC membranes and validated the theoretically predicted effects of rigid domains on k_eff of inhomogeneous membranes. We showed that the data for different lipid mixing ratios and temperatures collapse onto a single master curve in which k_eff directly scales with the area fraction of gel phase and properties of the fluid and gel phases in phase-separated membranes. Our data agreed with theoretical predictions of Netz and Pincus with no adjustable parameters and provide a framework for quantitatively understanding the effects of rigid inclusions, such as lipid domains and integral membrane proteins, on the membrane elasticity based on their number density and relative stiffness.

This work was designed to experimentally measure the effective rigidity for a specific case of inhomogenous membranes described by theory. As stated at the outset, biological membranes are highly complex and there are likely many contributions to k_eff. For example, asymmetrically shaped inclusions, such as conical proteins like nicotinic acetylcholine receptors or potassium channels,^56,57 are predicted to couple to local curvature and lead to membrane softening.^12–16 Moreover, several studies have shown that adding proteins can modify the local membrane structure which in turn influences the membrane rigidity.^17,25 Of course many proteins also are not perfectly rigid and their dynamics must also couple to the membrane dynamics. Nevertheless, we hope that the insights provided by these simple model systems will inform and inspire future measurements of the effects of compositional heterogeneity on the elasticity of more biologically-relevant lipid membranes and the interplay between the membrane mechanics and biological function.

Highlighting research from the NIST Center for Neutron Research led by Elizabeth G. Kelley.

Biological membranes are a heterogeneous mixture containing rigid bodies dispersed in a soft lipid matrix. Kelley et al. measure the effective stiffness of model heterogeneous membranes using neutron spin echo (NSE) spectroscopy and show that the properties can be quantitatively predicted by theory.