Abstract
The photoacoustic effect relies on optical transmission, which causes thermal expansion and generates acoustic signals. Coherence-based photoacoustic signal processing is often preferred over more traditional signal processing methods due to improved signal-to-noise ratios, imaging depth, and resolution in applications such as cell tracking, blood flow estimation, and imaging. However, these applications lack a theoretical spatial coherence model to support their implementation. In this paper, photoacoustic spatial coherence theory is derived to generate theoretical spatial coherence functions. These theoretical spatial coherence functions are compared to k-Wave simulated data and experimental data from point and circular targets (0.1 to 12 mm in diameter) with generally good agreement, particularly in the shorter spatial lag region. The derived theory was used to hypothesize and test previously unexplored principles for optimizing photoacoustic short-lag spatial coherence (SLSC) images, including the influence of the incident light profile on photoacoustic spatial coherence functions and associated SLSC image contrast and resolution. Results also confirm previous trends from experimental observations, including changes in SLSC image resolution and contrast as a function of the first M lags summed to create SLSC images. For example, small targets (e.g., <1–4 mm in diameter) can be imaged with larger M values to boost target contrast and resolution, and contrast can be further improved by reducing the illuminating beam to a size that is smaller than the target size. Overall, the presented theory provides a promising foundation to support a variety of coherence-based photoacoustic signal processing methods, and the associated theory-based simulation methods are more straightforward than existing k-Wave simulations methods for SLSC images.
I. Introduction
PHOTOACOUSTIC imaging techniques rely on the photoacoustic effect to generate acoustic signals. To achieve the photoacoustic effect, pulsed light is transmitted and an acoustic wave is generated from the thermal expansion and contraction of an optically absorbing target. By tuning the wavelength of the incident light, techniques using this effect exploit the optical absorption spectrum of biologic chromophores to achieve high target sensitivity [1]. Common clinical targets include hemoglobin, nerves, and metal with major application areas in blood flow measurement [2], flow cytometry [3], vascular imaging [4], [5], surgical navigation and guidance [6]–[12], and implant placement [13], [14].
Coherence-based photoacoustic techniques are increasingly popular due to their ability to improve resolution and imaging depth. For example, changes in the volume of red blood cells flowing through an artery tend to generate fluctuations in the resulting photoacoustic pressure signal. The temporal coherence of these pressure signals can be used to implement photoacoustic correlation spectroscopy to estimate blood flow with better resolution and higher imaging depth than Doppler imaging methods [2].
Similarly, when imaging deep structures, conventional amplitude-based photoacoustic imaging is often challenged by low signal-to-noise ratios due to insufficient fluence at the target depth, optical scattering in tissues, and depth-dependent acoustic attenuation. Lateral resolution also suffers due to the depth-dependent acoustic beam widths. As a result, coherence-based imaging techniques have been introduced, primarily to reduce side-lobes and acoustic clutter. One example of a spatial coherence technique to improve image quality is coherence factor (CF) weighting, which improves spatial resolution and contrast [15]. CF weighting has been combined with other methods, such as synthetic aperture focusing [16] and an adaptive minimum variance method [17] to achieve additional improvements in spatial resolution and contrast. SNR-dependent CF weighting was also introduced to preserve contrast in high-noise scenarios [18]. Similar success was achieved when weighting traditional amplitude-based images with other types of coherence-based metrics, including coherence weighting to improve resolution in the elevation dimension [19] and short-lag spatial coherence (SLSC) weighting to reduce clutter in amplitude-based images [20].
Initial implementations of SLSC imaging to photoacoustic data demonstrate that weighting with amplitude-based images is not a requirement to achieve the benefits of reduced clutter and improved contrast and resolution [14], [21]–[24]. SLSC images directly display measured coherence values, and these measurements are independent of signal amplitude. As a result, SLSC images are particularly beneficial for photoacoustic imaging in high-noise environments, which can be caused by insufficient laser fluence incident on a target of interest. Insufficient laser fluence often results from low-energy sources (e.g., when using pulsed laser diodes [23], [25] or light emitting diodes [26]–[28]) or when imaging structures that are far away from the light source (e.g., when imaging brachytherapy seeds with an interstitial or transurethral approach [14], [21], [22], [29]). In these cases, photoacoustic SLSC images demonstrate considerable improvements in border delineations, contrast, contrast-to-noise ratios, and signal-to-noise ratios when compared to traditional delay-and-sum (DAS) beamforming and Fourier-based reconstruction techniques.
Although these benefits of coherence-based signal processing are based on experimental observations, a well-developed theory to describe expected spatial coherence has multiple additional benefits. For example, this theory can be used to study a wide range of potential optimizations that would otherwise require lengthy experimental testing, which is not always feasible. This theory may also be used to gain insight into potential unexpected and counterintuitive optimizations. We derived an initial narrowband photoacoustic spatial coherence theory in our associated conference paper [30] and updated this narrowband theory to consider frequencies within the bandwidth of an ultrasound probe [31]. In addition, we derived and tested additive noise models to further improve our initial theory [32]. This journal paper presents a complete mathematical description of our theory in the presence of noise, including validation with experimental data from multiple target sizes. We also discuss how our photoacoustic spatial coherence theory can be applied to optimize photoacoustic SLSC image display.
The remainder of paper is organized as follows: Section II provides a complete description of our theory for photoacoustic spatial coherence and details how it can be used to create theoretical photoacoustic SLSC images. Section III lists our validation methods using SLSC images that are derived from theoretical equations, k-Wave simulations [33], and experimental data consisting of thread, ink-filled tubes, and an in vivo hepatic blood vessel. Section IV shows the results of our validation methods and demonstrates the utility of our theory when selecting photoacoustic-based parameters to optimize the contrast and resolution of SLSC images. Finally, Section V discusses the major insights and implications derived from this work, and Section VI contains our concluding remarks.
II. Theory
A. Photoacoustic Spatial Coherence
A linear systems approach is used to describe the measured photoacoustic pressure field, P. The first component of the linear system is χ, which is the random, nonuniform distribution of moderately dense, spatially incoherent absorbers (also known as the source function or source distribution function) at source location X0 = (x, y, z). The moderately dense requirement (with moderate defined as 3.18 absorbers per mm2 and dense defined as 318.3 absorbers per mm2 in [34]) is introduced based on our observations that photoacoustic absorbers generally respond as an incoherent source function when the absorbers are moderately dense and as coherent source functions when the absorbers are dense. Guo et al. [35] similarly observed a coherent photoacoustic source when visualizing a dense ensemble of photoacoustic absorbers.
The second component of the linear system is AN, the initial pressure distribution of absorbers located at position Xo in the presence of noise [32]:
| (1) |
where Nsc scales zero-mean, Gaussian distributed, additive noise, NA, by the expected value of the amplitude of the initial pressure distribution, A, as described by the equation:
| (2) |
where ⟨·⟩ represents the expected value, and ⟨A⟩ may be interpreted as an average over uncorrelated pressure signals generated from a microscopic distribution of moderately dense photoacoustic absorbers. To avoid confusion with the description provided in [32], we clarify here that Nsc in Eq. (1) is equivalent to the NA term introduced in Eq. 8 of [32]. Although NA has the same definition in both manuscripts, the scaling term ⟨A⟩ is introduced in this manuscript in order for us to relate noise amplitudes to pressure amplitudes.
A is a function of the fluence, F, at depth z and two tissue properties (i.e., the Grüneisen parameter, Γ, and the optical absorption coefficient, μa), as defined by the following equation:
| (3) |
Based on the definitions provided in Eqs. (1)-(3), AN takes the following form:
| (4) |
The uncorrelated source-related noise, NA, originates from random fluctuations in the source distribution (e.g., variations in fluence at the absorber surface [32] and variations in the optical absorption within the absorber). This additive noise model is based on our observations of experimental data (as described in detail in our previous publication [32]). Note that Ref. [32] also describes an additional noise term related to the channel noise-to-signal ratio, which we assume to be negligible throughout this paper.
The third component of the linear system is Hrx, which is the spherical propagation of the sound wave from the source to a point, n, on the transducer:
| (5) |
where Xn is a point on the aperture (e.g., Xn = (xn, yn, 0)), c is the speed of sound, rn is the travel distance from the source to the aperture, and f is the acoustic frequency, which is related to the bandwidth of the ultrasound transducer.
The acoustic pressure measured from a single absorber is therefore defined as:
| (6) |
The total received pressure at a point on the aperture, Xn, is found by integrating the pressure field over X0, as described by:
| (7) |
To relate this derivation to previous derivations of photoacoustic pressure, note that Eq. (7) is similar to Eq. (2) in Ref. [36].
The photoacoustic spatial covariance, Rp, is the correlation of the pressure field at two lateral receiving positions X1 and X2:
| (8) |
where P∗ represents the complex conjugate of P. Expansion of Eq. (8) yields:
| (9) |
where and are independent variables over which the pressure field is integrated to determine the total received pressure at aperture positions X1 and X2, respectively.
Insertion of Eqs. (1) and (2) into Eq. (9) yields:
| (10) |
Because the source function, χ, has a random, nonuniform, moderately dense, spatially incoherent distribution, note that:
| (11) |
where χo represents the average power of the absorber distribution. Similarly, because NA is also a random variable,
| (12) |
where No is the variance of the Gaussian distribution of NA. According to Eqs. (11) and (12), the expected value of the source distribution and the associated noise within the source term are equal to zero except when .
The expressions in Eqs. (11) and (12) reduce the expression for spatial covariance in Eq. (10) to a single volume integral:
| (13) |
The initial photoacoustic response is assumed to reside within an isochronous volume, thus the spatial covariance over a short depth, z, within this volume is taken to be constant, which reduces the volume integral in Eq. (13) to a surface integral [37]–[39]. This assumption is satisfied in photoacoustic imaging for multiple reasons (e.g., short nanosecond duration laser pulses, laser pulse repetition frequencies on the order of several Hz as opposed to hundreds of kHz [23], acoustic temporal frequencies limited by the transducer bandwidth). We then apply the paraxial and Fresnel approximations to the amplitude and phase terms, respectively. The paraxial approximation assumes that we are primarily interested in the received response near the axis of each transducer element:
| (14) |
The Fresnel approximation assumes that the axial distance between the aperture and source (i.e., z) is orders of magnitude larger than the lateral and elevation distances between a position on the aperture and a source, as illustrated in Fig. 1 for the lateral dimension. This approximation also supports the separability of the lateral and elevation dimensions and yields the following approximations in the lateral dimension:
| (15) |
| (16) |
Fig. 1.
Illustration of the Fresnel approximation for an aperture (rectangle) and source (circle) located at the aperture center Xo. The distance from the source to a point on the aperture is rn The lateral distance X1 – X2 << z where z is the axial position of the source. Therefore, r ≈ z.
Using the approximations described in Eqs. (14)-(16) yields an equation for photoacoustic spatial covariance that only depends on lateral position:
| (17) |
where λ = c/f. Because broadband photoacoustic signals are sensed and filtered by a transducer with finite bandwidth, the λ term is primarily related to the acoustic frequency of the transducer [1], [40]. To evaluate Eq. (17) and obtain a spatial covariance, λ can be approximated as the wavelength corresponding to the center frequency of the transducer, λc. Note that Eq. (17) represents the product of a constant term, a phase term, and a Fourier transform that depends on both the initial pressure distribution (i.e., A) and scaled noise terms. The spatial frequencies in this Fourier transform are given by u = (x1 − x2)/λz.
There are two options to eliminate the phase term in Eq. (17) [41], [42] (i.e., the two points x1 and x2 are symmetric with respect to the lateral center of the transducer when receiving unfocused data, or delays were applied to focus the received channel data and align responses at one point of interest in the image field). With either option, the new expression for spatial covariance in the lateral dimension depends only on spatial frequency u:
| (18) |
where represents the spatial covariance in the spatial frequency domain.
Eq. (18) is similar to the equation describing the van Cittert-Zernike (VCZ) theorem applied to pulse-echo measurements [41], with the optics-related terms (i.e., Γ, μa, and F) replacing the term that would describe an acoustic transmit pressure amplitude (or acoustic receive pressure amplitude when the equation is derived using acoustic reciprocity [43]). The VCZ theorem requires incoherent source distributions, therefore this analogy for our photoacoustic spatial coherence theory applies to moderately dense absorber distributions.
A similar equation applies to the elevation dimension, considering that the lateral and elevation dimensions are separable. Therefore, a spatial covariance equation that includes both dimensions can be written as follows:
| (19) |
where y is the elevation dimension and v is the spatial frequency in the elevation dimension. Let y1 and y2 be defined as the equivalent terms to x1 and x2, respectively, in the elevation dimension rather than lateral dimension. Then, the spatial frequency in the elevation dimension is defined as v = (y1 − y2)/λz. Note that Eq. (19) uses one of the two assumptions for phase term elimination described above (i.e., either y1 and y2 are symmetric about the center of the transducer in the elevation dimension or the data are focused in the elevation plane of the transducer, which can typically be accomplished with a transducer lens). Although spatial covariance is inherently two dimensional, as described by Eq. (19), throughout this manuscript, we evaluate our theory in the separable lateral dimension of the transducer using Eqs. (17) and (18).
B. Photoacoustic Short-Lag Spatial Coherence Imaging
To make photoacoustic SLSC images, we consider the array steering vector, which encodes the steering direction from the aperture center to a focal point of interest, (xk, z), in the photoacoustic image. Shifting the focal point along the lateral image dimension changes the steering direction, as illustrated in Fig. 2. Alternatively, with a fixed steering direction, the image target may be laterally shifted relative to a fixed aperture to build lateral image pixels. This alternative is mathematically described using the shifting property of Fourier transforms, which states that a shift in space by xk corresponds to multiplication by a phase term in the spatial frequency domain, resulting in our final photoacoustic spatial covariance equation:
| (20) |
where the additional dependencies on x and z (shown in Eq. (17)) are omitted for simplicity. The lag in Eq. (20) is defined in units of distance as:
| (21) |
and m is related to spatial frequency as defined by:
| (22) |
where λ depends on the bandwidth of the probe, as described in Section II-A.
Fig. 2.
Steering direction from the aperture center to a focal point (xk, z) in the image, illustrated with the assumption that Eq. (17) represents an initial focus located at lateral position xk = 0.
Eq. (20) may be expressed in terms of spatial frequency as:
| (23) |
Note that the phase term in Eqs. (20) and (23) is generalizable because the definition of lag is represented in spatial units (i.e., m) rather than units of element number (i.e., m, as in previous derivations for ultrasound spatial coherence [41], [43], [44]), which makes this definition independent of the transducer pitch. An additional benefit of this independence includes applicability to transducers with variable pitch. The relationship between m and m is:
| (24) |
where pitch is the transducer pitch.
To obtain a theoretical SLSC image, the dependency on the entire bandwidth of the transducer was included by integrating Eq. (20) over wavelengths that correspond to the highest and lowest acoustic frequencies within the −6 dB bandwidth of the trasnducer frequency response (i.e., λH and λL, respectively, approximating equal weights for each wavelength), normalizing the result by the value obtained at lag zero (i.e., K(xk, z)), then integrating over the first M lags to obtain each pixel in the theoretical SLSC image, as defined by the equation:
| (25) |
The dependence on transducer pitch is introduced in Eq. (25) in order to maintain consistency with previous descriptions of the integration process. As an aside, if transducer pitch is variable, the relationship between m and m described in Eq. (24) would need to be updated, but this update would not change the format of Eq. (25).
C. Modeling Point Targets
Considering that point targets are defined as any target smaller than the resolution of the imaging system, we modify Eq. (6) to model point targets by first defining the source function as a delta function:
| (26) |
The correlation of the source function in Eq. (26) is defined as:
| (27) |
which states that the expected value of the point source is equal to zero except when . Next, Eq. (12) can be implemented to demonstrate that the noise associated with this point source is also equal to zero except when . Using a similar derivation and the same assumptions that follow after Eq. (12), we arrive at a mathematical expression for the spatial covariance of a point target:
| (28) |
Eq. (28) may also be expressed in terms of spatial frequency:
| (29) |
Eqs. (28) and (29) each represent a Fourier transform multiplied by a phase term, similar to Eqs. (20) and (23), respectively. To create theoretical SLSC images of point targets, the Rp in Eq. (25) was replaced with Eq. (28).
III. Methods
A. Theory-Based Simulations
A 2D phantom was simulated in MATLAB with its lateral dimension corresponding to the lateral dimension of an ultrasound transducer and axial dimension corresponding to the depth of the imaging plane. An ultrasound transducer was modeled with most properties similar to the Alpinion L3–8 transducer (i.e., 128 elements, 0.3 mm pitch, and 3.84 cm total length) with the exception of the kerf being equal to 0 mm. This transducer was placed at depth, z = 0 cm. The simulated targets for theoretical testing included a point target and circular targets with diameters ranging from 0.2 mm to 12 mm. The circular targets were modeled as a distribution of randomly positioned absorbers, as illustrated in Fig. 3(a) for a simulated blood vessel surrounded by tissue.
Fig. 3.
(a) Optical absorption (μa) distribution for a circular cross-section of a simulated 6 mm-diameter blood vessel with high optical absorption surrounded by tissue of low optical absorption, (b) Grüniesen parameter (Γ) distribution, (c) corresponding photoacoustic pressure distribution (AN), and (d) a lateral profile of AN taken from the axial depth indicated by the dashed white line.
Two types of fluence profiles were simulated to obtain F. The first profile was a light sheet with a uniform fluence value of F = 5 mJ/cm2 illuminating the entire phantom. The second profile was a Gaussian beam with an initial diameter, wo, of 1 mm or 5 mm, initial depth z = 6.8 mm, and a beam width that increased with depth. This Gaussian beam profile was simulated using the light propagation model defined as [45]:
| (30) |
where Fo is the initial fluence (set to 5 mJ/cm2) and zr is the Rayleigh length (set to 1.2 mm and 6.2 mm for the 1 mm and 5 mm initial beam diameters, respectively).
Unless otherwise stated, the following values were used to define μa, χ, Γ, No, and NA in Eqs. (20) and (28). The mean magnitude of μa was 111 cm−1 inside the photoacoustic target (to model hemoglobin in blood), 0.1 cm−1 outside the target (to model tissue), and 0 cm−1 when no absorbers were present [46]. The total number of absorbers, Nμ, for the phantom with the circular targets was determined by the density of absorbers, which was fixed at 40 absorbers per mm2. Because the Grüniesen parameter is known to vary locally due to the composite nature of biological tissue [46], Γ was modeled as random values ranging 0–0.81 and 0–0.144 in tissue and in blood, respectively [46], as illustrated in Fig. 3(b). The average power of the absorber distribution, χo was modeled as an arbitrary constant. The variance (No) of the added noise (NA) was empirically determined, resulting in the values reported in Table I. This combination of parameters produced a photoacoustic pressure distribution (AN), as illustrated in Figs. 3(c) and 3(d).
TABLE I.
σN (MEAN ± ONE STANDARD DEVIATION OF TEN MEASUREMENTS) FOR THE RESULTS REPORTED IN FIGS. 5, 7–11, AND 14
| Target Diameter (mm) | Theory | k-Wave | Experiment |
|---|---|---|---|
| Point | 0.044 ± 0.005 | 0.037 ± 0.008 | 0.056 ± 0.011 |
| 1.3 | 0.017 ± 0.005 | 0.014 ± 0.004 | 0.016 ± 0.005 |
| 4.5 | 0.014 ± 0.002 | 0.012 ± 0.004 | – |
| 8 | 0.002 ± 0.000 | 0.004 ± 0.003 | – |
| 12 | 0.084 ± 0.004 | 0.082 ± 0.008 | 0.080 ± 0.000 |
To obtain theoretical spatial coherence functions, Eqs. (20) and (28) were evaluated with an acoustic wavelength, λ ≈ λc = 269μm (which corresponds to a transducer with center frequency, fc = 5.5 MHz). This result was then normalized by the value obtained at lag zero. For each target size, Eqs. (20) and (28) were evaluated with ten unique μa, Γ, and NA distributions (with constant No) in order to provide statistical measurements summarizing the mean and standard deviation of presented results.
To implement theoretical SLSC imaging, Eq. (25) (including the point source simplification described in Section II-C) was evaluated over a discrete set of wavelengths that correspond to the −6 dB bandwidth of the frequency response of the Alpinion L3–8 ultrasound transducer (i.e., λL = 211 μm to λH = 395 μm for multiple lateral positions (i.e., xk) and for a specific M value. The wavelengths were incremented using a fixed Δf = 0.25 MHz, which resulted in a variable .
B. k-Wave Simulations
In order to compare our theoretical model to existing simulation methods for studying coherence-based beamformers, photoacoustic data were additionally simulated using the k-Wave software package [33]. The k-Wave acoustic receiver was modeled with most properties similar to the Alpinion L3–8 transducer (i.e., 128 elements, 3.84 cm total length, 0.3 mm pitch, 5.5 center frequency) with the exception of 0 mm kerf and 49 MHz sampling frequency. The targets were circular regions of moderately dense absorbers with diameters ranging from 0.1 mm (i.e. a point source) to 12 mm. Absorber locations within the circular region were randomly chosen (with the exception of the point source). These locations were constant between k-Wave and theoretical simulations of equally sized targets.
After creating ten unique absorber maps for each target size, each absorber map was combined with one of ten randomly generated Gaussian noise distributions created with the empirically determined standard deviations reported in Table I (in order to model the randomness of the initial pressure distribution associated with variations in fluence). In particular, each zero-mean Gaussian noise profile was added to the initial pressure distribution created with k-Wave simulations to create ten initial pressure distributions for each target size. For each pressure distribution, a time domain simulation was performed to generate 2D photoacoustic channel data, which was subsequently bandpass filtered to model the band-limiting effects of an Alpinion L3–8 ultrasound transducer with a center frequency of 5.5 MHz.
Spatial coherence functions and SLSC images were calculated from k-Wave data as described by the following equations from previous publications [6], [14], [47]:
| (31) |
| (32) |
where represents the normalized spatial correlation measured from received signals, m and N are defined in Section II-B, is the time-delayed acoustic signal received by the ith element, n is the sample depth in units of samples, to is the correlation kernel length, which was chosen to be 2.4λc (with some numerical implementation differences due to rounding), and SLSCpixel is one pixel in the short-lag spatial coherence image. The actual correlation kernel length (after rounding) was 23 samples. Unless otherwise stated, the value of M was set to 14, which corresponds to 11% of the number of elements in the receive aperture.
C. India Ink and Point Target Experiments
Two photoacoustic phantoms were used to validate the theoretical predictions of our model, particularly with regard to the effects of the illuminating beam diameter, target diameter, and varying M. The first photoacoustic phantom consisted of tubing of inner diameters ranging from 1.3 mm to 10 mm submerged in a water bath, as illustrated in Fig. 4. This tubing was rigidly fixed in an acrylic plate and initially filled with water to obtain the photoacoustic signal of the tubing alone. The water was aspirated and subsequently replaced with a 0.067 % India ink solution without altering the tubing position, enabling discrimination of signals from the tubing walls relative to signals from the India ink. The second photoacoustic phantom was a black thread of diameter 0.2 mm was suspended in a water bath.
Fig. 4.
Experimental set-up showing tubing of inner diameters 4.5 mm, 6 mm, 8 mm, and 10 mm (1.3 mm-, 2 mm-, and 4 mm-diameter tubing not shown) fixed in an acrylic scaffold and suspended in a water bath. The light source shown is the 1 mm-core-diameter optical fiber which was later interchanged with the 5 mm-diameter fiber bundle in the same position relative to the ultrasound transducer. An Alpinion L3–8 transducer is placed with its imaging plane viewing a circular cross-section of the tubing.
Ten frames of photoacoustic channel data of each target were acquired with an Alpinion (Bothell, WA) E-Cube 12R ultrasound scanner connected to an Alpinion L3–8 linear array transducer. The sampling frequency of the ultrasound system was 40 MHz. The transducer was positioned to visualize the circular cross section of the thread or tubing diameter in the image plane. In this transducer orientation, the thread was considered to be a point target.
Two different light delivery methods were coupled to the output port of a Phocus Mobile laser (Opotek, Inc., Carlsbad, CA) and independently used to acquire photoacoustic images with an optical wavelength of 760 nm. The first light delivery method was a 1-mm-core-diameter, multimode optical fiber with 0.5 numerical aperture (shown in Fig. 4). The laser output energy was 1.5 mJ per pulse. The second light delivery method was a larger 5 mm-diameter fiber bundle. The laser output energy was 125 mJ per pulse. Both light delivery methods were approximated to produce Gaussian-shaped beams.
Spatial coherence functions and SLSC images of the experimental data were calculated using Eqs. (31) and (32), respectively. The actual correlation kernel length (after rounding) was 17 samples. Unless otherwise stated, the value of M was set to 14, which corresponds to 11% of the number of elements in the receive aperture.
D. In Vivo Experiment
In vivo photoacoustic data were used to assess the performance of our theoretical framework in a more complex environment that represents a clinical or surgical scenario of interest. These data were acquired from a major vein in a porcine liver study approved by the Johns Hopkins Animal Care and Use Committee, as described in our previous publications [11], [32]. To briefly summarize the imaging procedure, a laparotomy was performed to gain access to the liver, and the same photoacoustic imaging system described in Section III-C was utilized. The Alpinion L3–8 linear array transducer and 5 mm-diameter fiber bundle were both in direct contact with the liver tissue to visualize a circular cross section of the hepatic vein. The laser was operated at 750 nm with an incident energy of 40.5 mJ per pulse on the tissue surface. The vein was approximately 12 mm in diameter in the cross-sectional view of the ultrasound image.
Spatial coherence functions and SLSC images of the in vivo data were calculated using Eqs. (31) and (32), respectively. The actual correlation kernel length (after rounding) was 17 samples. Unless otherwise stated, the value of M was set to 14, which corresponds to 11% of the number of elements in the receive aperture.
E. Empirical Methods to Add Noise to Simulated Datasets
The magnitude of the noise added to the theoretical and k-Wave simulated datasets was empirically determined based on the definition of σN reported in [32], which describes a phenomenological model of the deviation from a mean value at each lag in a coherence function. To determine the value of σN, theoretical and k-Wave datasets were first simulated with the SNR of the initial pressure distribution, SNRp, varied from 10 dB to 45 dB in 5 dB increments. SNRp is related to No (i.e., the variance of the Gaussian distribution of the additive noise in the initial pressure distribution, as introduced in Eq. (12)) based on the following definition:
| (33) |
where At is the mean amplitude of the initial pressure distribution inside the target in the absence of noise (i.e., A in Eq. (1)).
The following equation was then evaluated to calculate σN for the theoretical datasets:
| (34) |
where is the normalized coherence function generated by evaluating and normalizing the result of Eq. (28) or Eq. (20) for a theoretical point target or for theoretical targets larger than a point target, respectively. Otherwise, was obtained by evaluating Eq. (32) for k-Wave and experimental results. is the least-squares best fit polynomial for the first 35 lags of the coherence function at the center of the target and k is the number of lags used in the fit.
For each target size with multiple theoretical and k-Wave SNRp values simulated, the SNRp chosen for the σN values reported in Table I was the SNRp which generated a coherence function with the closest σN match to the σN measured from experimental data. The σN values measured from experimental data and chosen for theoretical and k-Wave simulations are reported in Table I. The blank entries in Table I indicate experimental coherence functions that contained noise less consistent with the associated phenomenological model (likely due to the presence of strong coherent reverberations from the tubing in the experimental data). Therefore, the SNRp value chosen for each simulated dataset in these cases was the SNRp which generated coherence functions with the most similar σN values between the theoretical and k-Wave simulations.
In addition to the σN values reported in Table I and due to notable differences between k-Wave and theoretical results, we were additionally interested in comparing theoretical results directly to experimental data. For these cases, σN values ranging 0.002 to 0.020 (which corresponded to SNRp ranging 40 dB to 20 dB, respectively) were compared. These ranges were consistent with the range of σN values reported in Table I.
For completeness, we note that the theoretical value of σN is related to NA (i.e., the additive noise in the initial pressure distribution) and No (i.e., the variance of the Gaussian distribution of NA) by relating Eqs. (34) and (20) (or Eqs. (34) and (28) for the point target case).
F. Exploring Theoretical Implications for SLSC Imaging
To explore notable trends derived from our photoacoustic spatial coherence theory, SLSC image contrast and resolution were characterized as functions of the light beam profile diameter and the target size, for various M values using Eq. (25). Contrast was defined as:
| (35) |
where st and so are the mean amplitude of signals within the a target and background region, respectively, of the SLSC image. Resolution trends were quantified by measuring the full width at half maximum (FWHM) of lateral profiles created with multiple target sizes and illumination profile diameters. These theoretical results were compared to the controlled phantom results from the experiments described in Section III-C.
IV. Results
A. Comparison of Delay-and-Sum and SLSC Images
Fig. 5 compares traditional DAS beamforming with coherence-based SLSC images of experimental 1.3 mm- and 8 mm-diameter targets comprised of India ink. The 1 mm-diameter optical fiber was used to acquire the photoacoustic image of the 1.3 mm target. The 5 mm-diameter fiber bundle was used to acquire the photoacoustic image of the 8 mm target. Theoretical SLSC data was simulated with a Gaussian beam fluence profile with 1 mm and 5 mm initial beam diameters for the 1.3 mm- and 8 mm-diameter targets, respectively.
Fig. 5.
(a) Experimental delay-and-sum (DAS) image, (b) experimental short-lag spatial coherence (SLSC) image, (c) theoretical SLSC simulation (with added noise), and (d) k-Wave simulation (with added noise) of 1.3 mm- and 8 mm-diameter targets. The circles in the experimental DAS and SLSC images denote the inner (solid line) and outer (dotted line) diameters of the Tygon tubing filled with India ink. SLSC images are normalized to the brightest pixel and limited to display a minimum value of zero for M = 11% of the aperture. DAS images are displayed with a 25 dB dynamic range.
SLSC beamforming more clearly delineates the target content and boundaries farthest from the light source when compared to DAS beamforming. The DAS photoacoustic images of the targets may appear smaller than their actual sizes due to the depth-dependent fluence distribution that is known to impact a majority of photoacoustic images reconstructed with DAS beamforming. However, although the amplitude decreases with depth, the boundaries are better delineated in the SLSC images because the spatial coherence of the received signals is independent of amplitude, which is one of the known benefits of the SLSC beamformer applied to photoacoustic data. As the tubing surrounding the experimental targets produces spatially coherent signals, the proximal and distal tubing and structural boundaries are more clearly visualized in the SLSC images, while signals above above the tubing are possibly due to a photoacoustic effect generated by the laser beam from the 1 mm-diameter optical fiber (1.3 mm target) or the 5 mm-diameter fiber bundle (8 mm target) interacting with the water surrounding the tubing.
Boundary delineation is a known benefit of SLSC imaging (compared to DAS and similar amplitude-based beamformers) applied to photoacoustic data, particularly when the target boundary is located at a considerable distance from the light source [8], [14], [21]. This enhanced target boundary delineation emphasizes the usefulness of coherence-based beamformers and highlights the importance of developing photoacoustic-specific spatial coherence theory to support their implementation.
B. Theoretical Photoacoustic Spatial Coherence Functions
Although experimental spatial coherence functions are expected to have some level of noise [32], theoretical spatial coherence functions were first simulated in the absence of noise (i.e., NA = 0), to better understand expected trends. When a light sheet profile is used in theoretical simulations, the width of the coherence function continuously decreases from constant across the aperture for a point target to a significantly shorter coherence length for the 10 mm target, as shown in Fig. 6(a). In comparison, when a narrow-beam Gaussian profile is used (1 mm initial beam diameter), the width of the coherence function follows the same trend as a light sheet until the target size exceeds the maximum beam diameter, as shown in Fig. 6(b), where the 2–10 mm targets have coherence functions that are similar to (and in some cases overlapping) each other. These noiseless theoretical results indicate that both the target size and the fluence profile of the illuminating light source affect photoacoustic spatial coherence.
Fig. 6.
Noiseless theoretical coherence functions of at the center of targets ranging in size from a point to 10 mm in diameter using (a) light sheet and (b 1 mm Gaussian beam profiles as the illuminating sources. The x-axis represents lag (i.e., m or m) as a percentage of the receive aperture.
Theoretical photoacoustic spatial coherence functions (simulated with a Gaussian beam fluence profile with 5 mm initial beam diameter) were compared to k-Wave simulated and experimental photoacoustic coherence functions created from multiple targets sizes. The light source for the experimental data was the 5 mm-diameter fiber bundle. Fig. 7(a) shows the agreement between coherence functions for point targets created with theory and k-Wave in the absence of noise. Both results have relatively constant coherence across the aperture.
Fig. 7.
Coherence functions from a point target center. (a) Simulated point target data without noise (NA = 0) shows coherence functions that are relatively constant across the aperture. (b) Simulated point target data with noise is compared to experimental point target data, demonstrating that point targets are partially coherent sources in the presence of noise. The x-axis represents lag (i.e., m or m) as a percentage of the receive aperture.
Fig. 7(b) demonstrates that the addition of noise yields a point target coherence function that decays as a function of lag. The theoretical, k-Wave, and experimental photoacoustic spatial coherence functions decrease at a similar rate as a function of lag and have qualitatively similar σN (i.e., deviation from a mean value at each lag in the coherence function).
The short-lag region was previously defined as the region of the coherence function extending to a fixed percentage the receive aperture. However, when comparing results from targets larger than a point target, we define the short-lag region as the region from lag 0 to the lag defined by the first zero-crossing of the theoretical coherence function. This new definition is introduced to account for the dependence of photoacoustic spatial coherence on both target size and the width of the light profile (demonstrated in Fig. 6). Our following results focus on the short-lag region.
Fig. 8 shows coherence functions from theoretical simulated datasets in the presence of noise compared with experimental and k-Wave results for targets with diameters of 1.3 mm and 4.5 mm. Theoretical data was simulated with a Gaussian beam fluence profile with 1 mm and 5 mm initial beam diameters, for the 1.3 mm- and 4.5 mm-diameter targets, respectively. The experimental light source was the 1 mm-diameter optical fiber and 5 mm-diameter fiber bundle for the 1.3 mm and 4.5 mm targets, respectively.
Fig. 8.
Comparison of theoretical, k-Wave, and experimental coherence functions at the location corresponding to the center of (a) 1.3 mm-diameter and (b) 4.5 mm-diameter targets. The x-axis represents lag (i.e., m or ) as a percentage of the receive aperture.
In Fig. 8(a), the theoretical, k-Wave, and experimental photoacoustic spatial coherence functions have general qualitative agreement (i.e., similar rate of decrease with increasing lag and similar σN). Fig. 8(b) shows a similar result for the the 4.5 mm-diameter target, as the three coherence functions generally agree in the short-lag region. However, values outside of the short-lag region, which should ideally have zero coherence in the absence of noise (as demonstrated in Fig. 6), produce significant deviations between datasets with values that seem to hover near zero. In addition, the experimental coherence function demonstrates what appears to be coherent reverberations artifacts at higher lags, which are not modeled in theoretical or k-Wave simulations and appear to dominate the noise described by σN.
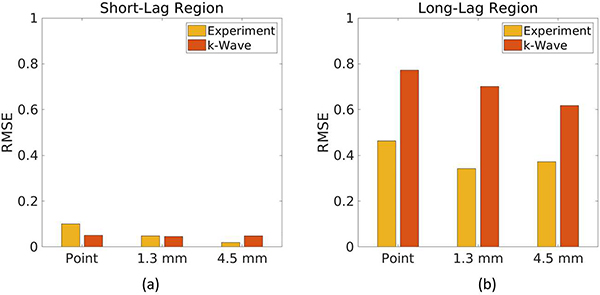
The agreement between theoretical results and k-Wave or experimental results was quantified with the root mean square error (RMSE) of coherence function differences measured at each lag value. This RMSE was calculated separately for the short-lag region (defined as 30% of the receive aperture for the point target and the first zero-crossing for larger targets) and the long-lag region (defined as all results outside of the short-lag region), as displayed in Fig. 9.
Fig. 9.
Root mean square error (RMSE) comparing both k-Wave data with noise and experimental data to theoretical coherence functions with noise in the (a) short-lag and (b) long-lag regions.
Figs. 9(a) and 9(b) confirm the qualitative observation that RMSE is consistently lower in the short-lag region (RMSE <0.05 when theory is compared to k-Wave and RMSE <0.1 when theory is compared to experiment) than in the long-lag region.
C. Comparison of SLSC Lateral Profiles
Fig. 10 shows photoacoustic SLSC images and corresponding lateral profiles for a point target and 12 mm-diameter target. For the theoretical simulations, the light profiles were a Gaussian with 5 mm initial beam diameter when simulating the point target and a light sheet when simulating the 12 mm target. The experimental results for the point target and the 12 mm target were derived from the thread and in vivo data, respectively. The inclusion of in vivo data enables the comparison of images without the effects of the tubing and surrounding water previously shown in Fig. 5. The theoretical, k-Wave, and experimental images in Fig. 10 generally show comparable lateral resolution for the 12 mm target. However, the k-Wave image has better resolution than the theoretical and experimental images for the point target. These similarities and differences are particularly evident with the alignment of the lateral profiles through each target center.
Fig. 10.
(a,e) Theoretical, (b,f) k-Wave, and (c,g) experimental photoacoustic SLSC images of a point target and 12 mm-diameter target. The experimental image of the 12 mm-diameter target is derived from the in vivo hepatic blood vessel data. Images are displayed with M = 11% of the aperture, with the exception of the 12 mm in vivo experimental target, which is displayed with M = 1% of the aperture. Images were normalized and thresholded to a minimum value of 0.3 in (a)-(c) and (g) and 0 in (e) and (f). (d,h) The corresponding lateral profiles demonstrate comparable resolution, target width, and coherence.
Fig. 11 shows lateral profiles for three target sizes and multiple M values. The experimental results for the point target, 4.5 mm target, and 12 mm target were derived from SLSC images of the thread, India ink, and in vivo hepatic blood vessel, respectively. For the point target and 4.5 mm target, theoretical data was simulated with a Gaussian beam fluence profile with 5 mm initial beam diameter. A light sheet fluence profile was used for theoretical simulations of the 12 mm target.
Fig. 11.
Lateral SLSC profiles at axial depths corresponding to the target center of (a) theoretical, (b) k-Wave, and (c) experimental SLSC images of the point, 4.5 mm, and 12 mm targets, each displayed with three different values of M represented as a percentage of the receive aperture. The experimental profiles are derived from SLSC images of the thread (point target), India ink (4.5 mm target), and in vivo vessel (12 mm target). The 12 mm in vivo target lateral SLSC profiles were normalized to the maximum value in each line plot.
Some differences were required to make comparisons across theory, k-Wave, and experimental datasets in Figs. 10 and 11. For example, dynamic range was adjusted to best display amplitudes within these targets. M values were different for the 12 mm in vivo target likely due to differences in the absorber distribution in the experimental data. Lateral profiles for this target were normalized because of the large amplitude differences within the target that dominate without normalization. In addition, lateral axes were adjusted to place the target at the center. There are also differences in the absorber appearances across the three datasets in Fig. 10.
Despite differences in display methods and appearance, the following two trends were nonetheless observed when comparing these datasets in Fig. 11. First, the contrast of the point target increases with an increase in M for both simulated data with noise and experimental data. Second, a low M value (i.e., 1 – 3 % of the aperture) generally excludes high spatial frequency content from the SLSC image and results in blurred target boundaries. As M increases, more high spatial frequency content is included in the SLSC image and target boundary delineation improves.
D. Effect of the Light Beam Profile on SLSC Image Contrast
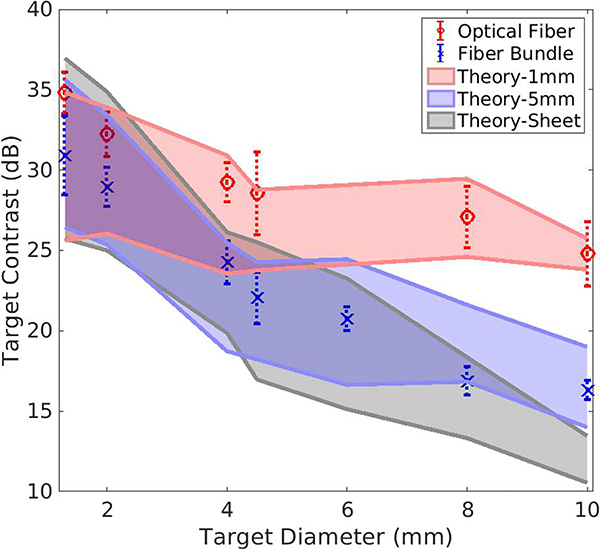
Fig. 6 indicates that the light beam profile affects the spatial coherence function, as the narrower light profile increases the coherence length of larger targets. This trend suggests that we can improve the SLSC image contrast of larger targets by using a narrow laser beam. To explore this effect that is based on our newly derived theory, the contrast of targets in theoretical and experimental SLSC images was measured as a function of diameter, resulting in Fig. 12.
Fig. 12.
Theoretical measurements of contrast in SLSC images as a function of target diameter for three illuminating beam profiles (light sheet, 1 mm-and 5 mm-diameter Gaussian beam). These theoretical predictions in the presence of noise are compared to experimental India ink data acquired with the fiber bundle (×) and the optical fiber (o). For the larger targets, theory and experimental data show improved contrast with the narrower illumination beam profile. All SLSC images are computed with M = 11% of the aperture.
For the theoretical results in Fig. 12, the upper and lower bounds of each illumination profile width (i.e., 1 mm, 5 mm, and light sheet) correspond to the mean contrast measurements of ten theoretical simulation results with SNRp = 20 dB and SNRp = 40 dB, respectively. The target contrast with the 1 mm Gaussian beam illumination profile decreased from 25.6–35.0 dB at a target diameter of 1.3 mm to 23.8–25.2 dB as target diameter increased to 10 mm. For the 5 mm Gaussian beam illumination profile, target contrast decreased from 26.5– 36.2 dB to 14.0–19.0 dB as target diameter increased. For the light sheet illumination profile, target contrast decreased from 25.7–35.4 dB to 10.5–13.7 dB as target diameter increased.
The theoretical results in Fig. 12 were compared to experimental photoacoustic SLSC images acquired with a 1 mm-core-diameter optical fiber (for comparison with the 1 mm narrow-beam Gaussian profile) and a 5 mm-diameter fiber bundle (for comparison with the 5 mm broader Gaussian profile). The experimental data (shown as data points in Fig. 12) generally agree with the theoretical results, as the smaller light beam profiles generate images with higher contrast for the same targets. In addition, the mean contrasts for experimental datasets are within the range of the theoretical prediction for the corresponding light source. The results in Fig. 12 demonstrate that the SLSC image contrast of targets can be improved by limiting the illuminating beam to a size that is smaller than the target size.
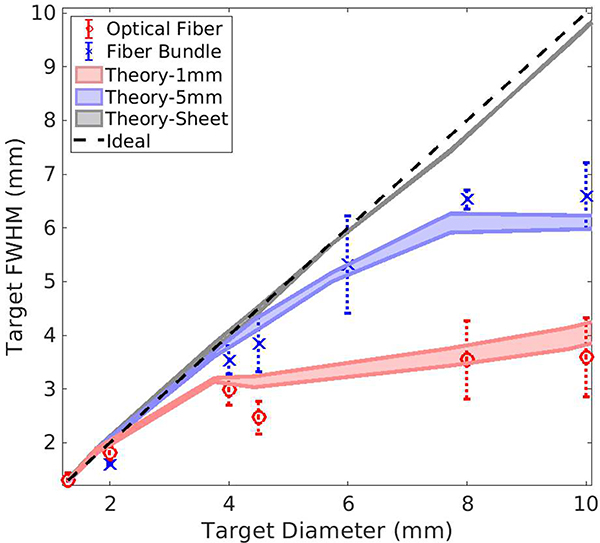
E. Effect of the Light Beam Profile on SLSC Image FWHM
Although SLSC image contrast can be increased by narrowing the width of the light beam profile (see Fig. 12), intuition suggests that only the portion of a large target that is illuminated with the narrow beam will be visible in the SLSC image. Fig. 13 explores this expectation with FWHM measurements of SLSC lateral profiles (M = 11%) created with target sizes ranging from 1.3 mm to 11 mm in diameter. Ideally, a one-to-one relationship would exist between these two measurements as indicated by the dashed line in Fig. 13. The upper and lower bounds of each illumination profile correspond to the mean FWHM measurements for ten theoretical simulations with SNRp = 20 dB and SNRp = 40 dB, respectively. With the light sheet illumination, the theoretical result in Fig. 13 generally follows the ideal expectation. When the light beam diameter is decreased to 5 mm, the measured FWHM no longer follows this ideal trend for targets ≥ 4.5 mm. Similarly, when the light beam diameter is further decreased to 1 mm, the theory shows more of a deviation from the ideal result. The data points in Fig. 13 show our experimental measurements for comparison with theoretical predictions. The experimental measurements generally follow the predicted trends.
Fig. 13.
Theoretical full width at half maximum (FWHM) measurements of SLSC lateral profiles as a function of target diameter for three illuminating beam profiles (light sheet, 1 mm-, and 5 mm-diameter Gaussian beams). These theoretical predictions in the presence of noise are compared to India ink experimental data acquired with the fiber bundle (×) and the optical fiber (o). The ideal 1:1 relationship is shown as a dashed line. SLSC lateral profiles were computed with M = 11% of the aperture.
F. Optimal M Value for Photoacoustic SLSC Images
The optimal choice for the number of lags summed to create SLSC images (i.e., M) is known to be correlated with the photoacoustic image lateral resolution (as shown in Fig. 11). To quantify this resolution, Fig. 14 shows the mean FWHM of SLSC lateral profiles of theoretical, k-Wave, and experimental point targets as a function of M with ± one standard deviation of the mean shown as shaded error bars. A 5 mm Gaussian fluence profile was used for theoretical simulations and the 5 mm-diameter fiber bundle was used as the experimental light source. Lateral resolution generally decays as a function of the M value used to create the SLSC images. As noted in Section IV-C, because coherence functions are a function of spatial frequency, they encode higher frequency content at higher M values resulting in SLSC images created with higher M values having improved target boundary delineation and resolution.
Fig. 14.
Lateral resolution calculated with theoretical, k-Wave, and experimental point target data sets as a function of M, which is represented as a percentage of the receive aperture.
In Fig. 14, the mean lateral resolution measured with theoretical and experimental data overlap when M ≥31%, and the best mean lateral resolution measurements were 0.6 mm for both theoretical and experimental data, which occurred when M ≥ 35% of the aperture. Consistent with the results in Fig. 10, the best resolution was generally achieved with k-Wave simulations, which is true regardless of the M value, although the reason for this lower resolution with k-Wave results is unclear. The fundamental reason for the theoretical deviation from experimental results in the short-lag region is also unclear. However, when comparing mean theoretical results to mean experimental and k-Wave results, these deviations were ≤1.1 mm and ≤1.9 mm, respectively. Despite these differences across the three datasets, there is a general trend of higher M values providing the best lateral resolution within each dataset, which is consistent with previous results [14].
The contrast of photoacoustic SLSC images was previously shown to be relatively constant as a function of M (albeit with a large standard deviation of measurements from multiple laser firings to image the same target) [14], [32]. However, lateral profiles from images of point targets (see Fig. 11) indicate that the optimal choice of M may depend on target size, as the smaller point target benefits from higher M values to improve target contrast. This dependence is also shown in our previous publication for multiple simulated noise levels [32].
Fig. 15 shows contrast as a function of target diameter for four M values (expressed as a percentage of the receive aperture) in order to compare theoretical simulations relating SLSC image contrast, M, and target size with experimental data. Theoretical predictions using a 5 mm Gaussian fluence profile are shown with solid lines, which represent the mean contrast of simulations with SNRp values ranging 20 dB to 40 dB. Experimental results obtained with a 5 mm fiber bundle as a light source are shown as the data points with the same colors as the corresponding theoretical predictions. The 1.3 mm target achieves higher contrast at M = 11% when compared to its contrast at M = 4% and M = 8%. This difference is less apparent for the 4 mm-diameter target. Discrepancies between the contrast predictions and the experimental results in Fig. 15 likely exist because the specific noise and absorber characteristics needed to match experimental data are unknown. Despite this discrepancy, the overall trends (i.e., higher contrast with smaller targets and larger M values) are generally consistent across either theoretical or experimental data. Thus, the presented theory can be used to predict the optimal choice of M values, based on target size, light profile diameter, and desired resolution. In general, smaller targets can be imaged with larger M values in order to boost target contrast and resolution.
Fig. 15.
Theoretical measurements of contrast in SLSC images as a function of target diameter for four M values (2%, 4%, 8%, and 11% of the receive aperture). These theoretical predictions in the presence of noise are compared to experimental data of SLSC images displayed with the same four M values (×, o, ∗, and △, respectively).
V. Discussion
This work is the first to present a complete photoacoustic spatial coherence theory for point targets and moderately dense optical absorbers. We developed and validated our theory with experimental and k-Wave data, then explored applications of this theory to optimize photoacoustic SLSC image contrast and resolution. Due to the lower accuracy of theory-based simulations in the long-lag region than the short-lag region as shown in Fig. 9, we propose the use of this theoretical method primarily for predictions within the short-lag region of the acoustic receiver aperture.
The inclusion of both k-Wave and experimental data in our analyses were critical to the validation of our theoretical models for five reasons. First, the controlled phantom experiment with varied illuminating beam diameters and target diameters enabled us to gain insights into the effects of these variables on SLSC image quality, as described in Sections IV-D through IV-F. Second, including k-Wave data enabled us to compare theoretical simulation results to an existing simulation method for studying coherence-based beamformers for photoacoustics. Third, support for our theoretical approach was achieved by showing that we can arrive at similar conclusions with k-Wave simulations (e.g., for the short-lag region of spatial coherence functions in Figs. 7 and 8 and for SLSC lateral profiles in Figs. 10 and 11), particularly in cases where we suffered from experiment-related artifacts (such as reverberations from tubing in Fig. 5 or the the large amplitude differences within the in vivo target, which required normalization of the associated line profiles in Fig. 11). Fourth, the similarities achieved with k-Wave data in cases where experimental similarity was not completely achieved (e.g., Fig. 5) enabled us to confirm that our theoretical derivation is a viable method to study photoacoustic spatial coherence. Fifth, the inclusion of in vivo data enabled us to introduce more complexity than capable with our phantom setup (e.g., optical scattering, acoustic scattering, absorbers and noise sources of clinical interest) without including confounding effects from experimental tubing. This inclusion of in vivo data also enabled us to determine if our major conclusions would be altered for this more realistic surgical scenario. Although there were some differences (such as in the appearance of the final SLSC images in Figs. 5 and 10), these differences did not affect the theory-based insights provided in Sections IV-D through IV-F.
Based on these insights, we conclude that there are two primary advantages of this photoacoustic spatial coherence theory. First, with the introduction of this theory, experiments are no longer necessary to explore how light profile designs will affect SLSC image contrast and resolution. A summary of the various effects that are supported by this theory include observations that SLSC image contrast can be improved by limiting the size of the illumination beam, the lateral width of the illumination beam limits visualization of the full lateral extent of target sizes larger than the illumination beam, and smaller targets can be imaged with higher M values to improve target contrast and resolution.
The second advantage is that our theory-based method is a more direct route to create SLSC simulation images without requiring simulations of channel data received by the acoustic aperture. Based on Eq. 25 and with consideration that λ is related to temporal frequency, m is related to spatial frequency, and integration is a linear filter, the SLSC image pixel can be interpreted as a joint spatial and temporal frequency filter applied to a scaled, noisy version of the square of the traditional initial pressure distribution expression in photoacoustic imaging. Using this implementation, our theory-based methods combine the simulations of a light profile and associated pressure distribution in one straightforward step. Implementation of this theory does not require Monte Carlo simulations to model the light profile incident on the target and the associated fluence distribution within the target in order to create a custom initial pressure distribution based on the incident light profile [48].
The presented theory was derived for a moderately dense distribution of absorbers, which enabled an analagous mathematical representation to the VCZ theorem applied to pulse-echo measurements [41]. This mathematical relationship can be considered as the VCZ theorem applied to photoacoustic imaging of moderately dense absorbers, and it appropriately explains the inverse relationship between target size and coherence length, which ultimately affects SLSC image contrast as a function of the number of lags summed. Thus, based on this theory, it is evident that larger targets, which produce shorter coherence lengths, will have the best contrast when SLSC images are created with lower M values.
Similarly, there is an inverse relationship between the lateral width of the light profile and the coherence length, which explains why limiting the size of an illumination beam will provide higher-contrast SLSC images of targets that are larger than the beam profile. This light profile adjustment is one potential method to compensate for our inability to control target sizes in most imaging cases of interest (e.g., in vivo imaging) in order to produce optimal-contrast SLSC images.
Alternatively, this theory also supports an adaptive pixelwise approach to choosing the optimal M value, which may be based on known regional target sizes and illumination profiles. For example, in photoacoustic-guided surgery, locally changing the M value with the known position of a tool tip has the potential to optimize visualization of the tool tip relative to larger anatomical structures [6]–[9]. An additional perspective is to potentially utilize the measured spatial coherence properties to predict target sizes based on the presented theory, which will be the focus of future work.
While it was previously shown that large targets containing a higher density of individual absorbers produce photoacoustic images with strong boundary contrast and minimal signal inside the target [35], [49], this representation is not shown in our theoretical and k-Wave simulation images, because the associated data sets are based on a moderately dense distribution of absorbers. In this moderately dense case, boundary signals do not dominate interior speckle and the entire target can be visualized with similar intensity throughout the target interior, as demonstrated with India ink in a 8 mm-diameter tube (Fig. 5) and with the 12 mm-diameter in vivo blood vessel (Fig. 10). These examples demonstrate that photoacoustic targets of interest can realistically contain a moderately dense distribution of absorbers and will not always produce signals only at the target boundaries.
As indicated by theory and confirmed with experimental measurements, there is a trade-off between target contrast and target boundary detection when optimizing the fluence profile incident on the target (see Figs. 12 and 13, respectively, which show better contrast with smaller optical beam widths and better FWHM measurements with larger optical beam widths). This trade-off can be resolved by raster scanning a narrow light beam and combining resulting images to improve both SLSC contrast and resolution. There is also a limit to the narrowness of the light profile based on laser safety limits and the incident laser fluence (which is inversely proportional to the diameter of the incident light profile). As noted above, the presented theoretical expressions are advantageous as they provide a new method to explore these potential tradeoffs prior to conducting experiments. One example of an application that will benefit from this exploration of tradeoffs is the design of specialized light delivery systems that attach to surgical tools, where there is a wide range of possible configurations that are more efficient to test in silico when compared to designing and building prototypes for experimental testing [7], [50], [51].
VI. Conclusion
This paper describes a theoretical photoacoustic spatial coherence framework that generally agrees with experimental data from target sizes spanning point targets to a 12 mm-diameter in vivo target. The proposed theory and associated theory-based simulation methods offer benefits over previously available methods, including the ability to predict SLSC image contrast, lateral resolution, and lateral FWHM values based on target size and the incident light beam profile. In addition, this theory provides insights into optimizing photoacoustic SLSC image display based on light profile width, contrast, and resolution measurements. This theory also establishes a foundation for future explorations to optimize other coherence-based photoacoustic techniques.
Acknowledgments
This work is supported by NSF CAREER Award ECCS-1751522, NIH R00 EB018994, and NSF GRF DGE1746891. The authors thank Kelley Kempski and Dr. Jin He for assistance with in vivo data collection, and Nicholas Louloudis, Sue Eller, and Ivan George for animal care and surgery support.
Biography

Michelle Graham (S’16) received the B.S. degree in biophysics (minor in electrical engineering) from the University of Scranton, Scranton, PA, USA in 2015, and the M.S.E. degree in electrical and computer engineering from Johns Hopkins University, Baltimore, MD, USA in 2018. She is currently pursuing the Ph.D. degree in electrical and computer engineering at Johns Hopkins University. She received the NSF Graduate Research Fellowship in 2018. Her research interests include photoacoustics, intraoperative photoacoustic imaging, and translational research.

Muyinatu A. Lediju Bell (S’08-M’14-SM’19) received the B.S. degree in mechanical engineering (minor in biomedical engineering) from the Massachusetts Institute of Technology, Cambridge, MA, USA, in 2006, and the Ph.D. degree in biomedical engineering from Duke University, Durham, NC, USA, in 2012. From 2009 to 2010, she conducted research abroad as a Whitaker International Fellow at The Institute of Cancer Research and Royal Marsden Hospital, Sutton, Surrey, U.K. From 2012 to 2016, she was a postdoctoral fellow with the Engineering Research Center for Computer-Integrated Surgical Systems and Technology, Johns Hopkins University, Baltimore, MD, USA.
Dr. Bell is currently an Assistant Professor in the Department Electrical and Computer Engineering with a joint appointment in the Department of Biomedical Engineering at Johns Hopkins University, where she founded and directs the Photoacoustic and Ultrasonic Systems Engineering Laboratory. Her research interests include ultrasound and photoacoustic imaging, coherence-based beamforming, deep learning for ultrasound and photoacoustic image formation, image-guided surgery, robotics, and medical device design.
Dr. Bell received the NSF CAREER Award in 2018, the NIH Trailblazer Award in 2018, MIT Technology Review’s Innovator Under 35 Award in 2016, and the NIH K99/R00 Pathway to Independence Award in 2015. She currently serves as Associate Editor of IEEE TRANSACTIONS ON ULTRASONICS, FER-ROELECTRICS, AND FREQUENCY CONTROL and of IEEE TRANSACTIONS ON MEDICAL IMAGING.
References
- [1].Beard P, “Biomedical photoacoustics,” Interface Focus, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].Chen SL, Ling T, Huang SW, Baac HW, and Guo J, “Photoacoustic correlation spectroscopy and its application to low-speed flow measurement,” Optics Letters, vol. 72, no. 2, pp. 181–204, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Galanzha EI and Zharov VP, “Photoacoustic flow cytometry,” Methods, vol. 57, no. 3, pp. 280–296, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Zhang EZ, Laufer JG, Pedley RB, and Beard PC, “In vivo high-resolution 3d photoacoustic imaging of superficial vascular anatomy,” Physics in Medicine and Biology, vol. 54, no. 4, 2009. [DOI] [PubMed] [Google Scholar]
- [5].Lao Y, Xing D, Yang S, and Xiang L, “Noninvasive photoacoustic imaging of the developing vasculature during early tumor growth,” Physics in Medicine and Biology, vol. 53, no. 15, 2008. [DOI] [PubMed] [Google Scholar]
- [6].Gandhi N, Allard M, Kim S, Kazanzides P, and Bell MAL, “Photoacoustic-based approach to surgical guidance performed with and without a da vinci robot,” Journal of Biomedical Optics, vol. 22, no. 12, p. 121606, 2017. [Google Scholar]
- [7].Allard M, Shubert J, and Bell MAL, “Feasibility of photoacoustic-guided teleoperated hysterectomies,” Journal of Medical Imaging, vol. 5, no. 2, p. 021213, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Bell MAL, Ostrowski AK, Kazanzides P, and Boctor EM, “Localization of transcranial targets for photoacoustic-guided endonasal surgeries,” Photoacoustics, vol. 3, no. 2, pp. 78–87, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Piras D, Grijsen C, Schtte P, Steenbergen W, and Manohar S, “Photoacoustic needle: minimally invasive guidance to biopsy,” Journal of Biomedical Optics, vol. 18, no. 7, p. 070502, 2013. [DOI] [PubMed] [Google Scholar]
- [10].Mari JM, Xia W, West SJ, and Desjardins AE, “Interventional multispectral photoacoustic imaging with a clinical ultrasound probe for discriminating nerves and tendons: an ex vivo pilot study,” Journal of Biomedical Optics, vol. 20, no. 11, p. 110503, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Kempski K, Wiacek A, Graham M, Gonxalez E, Goodson B, Allman D, Palmer J, Beck HHS, He J, and Bell MAL, “In vivo photoacoustic imaging of major blood vessels in the pancreas and liver during surgery,” Journal of biomedical optics, vol. 24, no. 12, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Graham M, Assis F, Allman D, Wiacek A, ad Mardava Gubbi EG, Dong J, Hou H, Beck S, Chrispin J, and Bell MAL, “In vivo demonstration of photoacoustic image guidance and robotic visual servoing for cardiac catheter-based interventions,” IEEE Transactions on Medical Imaging, vol. 39, no. 4, pp. 1015–1029, 2020. [DOI] [PubMed] [Google Scholar]
- [13].Su JL, Wang B, and Emelianov SY, “Photoacoustic imaging of coronary artery stents,” Optics Express, vol. 17, no. 2, pp. 19 894–19 901, 2009. [DOI] [PubMed] [Google Scholar]
- [14].Bell MAL, Kuo N, Song DY, and Boctor EM, “Short-lag spatial coherence beamforming of photoacoustic images for enhanced visualization of prostate brachytherapy seeds,” Biomedical Optics Express, vol. 4, no. 10, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].Hollman KW, Rigby KW, and O’Donnell M, “Coherence factor of speckle from a multi-row probe,” IEEE Ultrasonics Symposium, 1999. [Google Scholar]
- [16].Liao CK, Li ML, and Li PC, “Optoacoustic imaging with synthetic aperture focusing and coherence weighting,” Optics Letters, vol. 29, no. 21, pp. 2506–2508, 2004. [DOI] [PubMed] [Google Scholar]
- [17].Park S, Karpiouk AB, Aglyamov SR, and Emelianov SY, “Adaptive beamforming for photoacoustic imaging,” Optics letters, vol. 33, no. 12, pp. 1291–1293, 2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Wang YH and Li PC, “Snr-dependent coherence-based adaptive imaging for high-frame-rate ultrasonic and photoacoustic imaging,” IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, vol. 61, no. 8, pp. 1419–1432, 2014. [DOI] [PubMed] [Google Scholar]
- [19].Wang D, Wang Y, Zhou Y, Lovell J, and J. X, “Coherent-weighted three-dimensional image reconstruction in linear-array-based photoacoustic tomography,” Biomedical Optics Express, vol. 7, pp. 1957–1965, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Alles EJ, Jaeger M, and Bamber JC, “Photoacoustic clutter reduction using short-lag spatial coherence weighted imaging,” 2014 IEEE International Ultrasonics Symposium, pp. 41–44, 2014. [Google Scholar]
- [21].Bell MAL, Kuo N, Song D, Kang J, and Boctor EM, “In vivo visualization of prostate brachytherapy seeds with photoacoustic imaging,” Journal of Biomedical Optics, vol. 19, no. 12, p. 126011, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22].Bell MAL, Song DY, and Boctor EM, “Coherence-based photoacoustic imaging of brachytherapy seeds implanted in a canine prostate,” Proceedings of SPIE, vol. 9040, no. 90400Q, 2014. [Google Scholar]
- [23].Bell MAL, Guo X, Kang HJ, and Boctor EM, “Improved contrast in laser-diode-based photoacoustic images with short-lag spatial coherence beamforming,” 2014 IEEE International Ultrasonics Symposium, 2014. [Google Scholar]
- [24].Pourebrahimi B, Yoon S, Dopsa D, and Kolios MC, “Improving the quality of photoacoustic images using the short-lag spatial coherence imaging technique,” Proceedings of SPIE Photonics West - Photons Plus Ultrasound: Imaging and Sensing 2013, vol. 8581, 2013. [Google Scholar]
- [25].Kolkman R, Steenbergen W, and van Leeuwen T, “In vivo photoacoustic imaging of blood vessels with a pulsed laser diode,” Lasers in Medical Science, 2006. [DOI] [PubMed] [Google Scholar]
- [26].Hansen RS, “Using high-power light emitting diodes for photoacoustic imaging,” Proc. SPIE 7968 Medical Imaging:Ultrasonic Imaging, Tomography, and Therapy, 2011. [Google Scholar]
- [27].Allen TJ and Beard PC, “High power visible light emitting diodes as pulsed excitation sources for biomedical photoacoustics,” Biomedical Optics Express, vol. 7, pp. 1260–1270, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [28].Hariri A, Lemaster J, Wang J, Jeevarathinam A, Chao D, and Jokerst J, “The characterization of an economic and portable ledbased photoacoustic imaging system to facilitate molecular imaging,” Photoacoustics, vol. 9, pp. 10–20, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [29].Bell MAL, Guo X, Song DY, and Boctor EM, “Transurethral light delivery for prostate photoacoustic imaging,” Journal of biomedical optics, vol. 20, no. 3, p. 036002, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [30].Graham MT and Bell MAL, “Theoretical application of short-lag spatial coherence to photoacoustic imaging,” IEEE International Ultrasonics Symposium 2017, 2017. [Google Scholar]
- [31].Graham MT and Bell MAL., “Development and validation of a short-lag spatial coherence theory for photoacoustic imaging,” Proc. SPIE 10494, Photons Plus Ultrasound: Imaging and Sensing, 2018. [Google Scholar]
- [32].Stephanian B, Graham MT, Hou H, and Bell MAL., “Additive noise models for photoacoustic spatial coherence theory,” Biomedical Optics Express, vol. 9, no. 11, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [33].Treeby BE and Cox BT, “k-wave: Matlab toolbox for the simulation and reconstruction of photoacoustic wave-fields,” J. Biomed. Opt, vol. 15, no. 2, p. 021314, 2010. [DOI] [PubMed] [Google Scholar]
- [34].Dean-Bean J and Razansky D, “On the link between the speckle free nature of optoacoustics and visibility of structures in limited-view tomography,” Photoacoustics, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [35].Zijian Guo LVW, Li Li, “On the speckle-free nature of photoacoustic tomography,” Medical Physics, vol. 36, no. 9, pp. 4084–4088, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [36].Xu M and Wang LV, “Universal back-projection algorithm for photoacoustic computed tomography,” Physical Review, 2005. [DOI] [PubMed] [Google Scholar]
- [37].Cardoso J and Fink M, “Echographic diffraction filters and the diffraction function for random media through an instantaneous timefrequency approach,” The Journal of the Acoustical Society of America, vol. 90, no. 2, pp. 1074–1084, 1991. [Google Scholar]
- [38].Derode A and Fink M, “The notion of coherence in optics and its application to acoustics,” European Journal of Physics, vol. 15, no. 2, pp. 81–90, 1994. [Google Scholar]
- [39].Fink M and Cardoso JC, “Diffraction effects in pulse-echo measurement,” IEEE Transactions on Sonics and Ultrasonics, vol. 31, no. 4, pp. 313–329, 1984. [Google Scholar]
- [40].Irisawa K, Hirasawa T, Hirota K, Tsujita K, and Ishihara M, “Influence of laser pulse width to the photoacoustic temporal waveform and the image resolution with a solid state excitation laser,” Proceedings on SPIE, p. 8223, 2012. [Google Scholar]
- [41].Mallart R and Fink M, “The van cittert-zernike theorem in pulse echo measurements,” Journal of the Acoustical Society of America, 1991. [Google Scholar]
- [42].Goodman J, Statistical Optics. John Wiley & Sons, 2015. [Google Scholar]
- [43].Bottenus N and Ustuner KF, “Acoustic reciprocity of spatial coherence in ultrasound imaging,” IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [44].Liu D and Waag R, “About the application of the van cittert-zernike theorem in ultrasonic imaging,” IEEE Trans Ultrason Ferroelectr Freq Control, vol. 42, no. 4, pp. 590–601, 1995. [Google Scholar]
- [45].Fischer R, Tadic-Galeb B, and Yoder P, Optical System Design, Second Edition, 2008. [Google Scholar]
- [46].Yao DK, Yang C, Maslov K, and Wang LV, “Photoacoustic measurement of the grneisen parameter of tissue,” Journal of Biomedical Optics, vol. 19, no. 1, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [47].Lediju MA, Trahey GE, Byram BC, and Dhal JJ, “Short-lag spatial coherence of backscattered echose: Imaging characteristics,” IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [48].Jacques SL, “Coupling 3d monte carlo light transport in optically heterogeneous tissues to photoacoustic signal generation,” Photoacoustics, vol. 2, no. 4, pp. 137–142, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [49].Dean-Ben XL and Razansky D, “On the link between the speckle free nature of optoacoustics and visibility of structures in limited-view tomography,” Photoacoustics, vol. 4, no. 4, pp. 133–140, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [50].Eddins B and Bell MAL, “Design of a multifiber light delivery system for photoacoustic-guided surgery,” Journal of Biomedical Optics, vol. 22, no. 4, p. 041011, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [51].Shubert J and Bell MAL, “A novel drill design for photoacoustic guided surgeries,” Proc. of SPIE, Photons Plus Ultrasound: Imaging and Sensing, vol. 10494, 2018. [Google Scholar]