Dynamic piezoelectric MEMS-based optical metasurfaces

Combining piezoelectric MEMS with optical gap-plasmon metasurfaces enables electrically driven dynamic 2D wavefront shaping.

Abstract

Optical metasurfaces (OMSs) have shown unprecedented capabilities for versatile wavefront manipulations at the subwavelength scale. However, most well-established OMSs are static, featuring well-defined optical responses determined by OMS configurations set during their fabrication, whereas dynamic OMS configurations investigated so far often exhibit specific limitations and reduced reconfigurability. Here, by combining a thin-film piezoelectric microelectromechanical system (MEMS) with a gap-surface plasmon–based OMS, we develop an electrically driven dynamic MEMS-OMS platform that offers controllable phase and amplitude modulation of the reflected light by finely actuating the MEMS mirror. Using this platform, we demonstrate MEMS-OMS components for polarization-independent beam steering and two-dimensional (2D) focusing with high modulation efficiencies (~50%), broadband operation (~20% near the operating wavelength of 800 nanometers), and fast responses (<0.4 milliseconds). The developed MEMS-OMS platform offers flexible solutions for realizing complex dynamic 2D wavefront manipulations that could be used in reconfigurable and adaptive optical networks and systems.

INTRODUCTION

Optical metasurfaces (OMSs) represent subwavelength-dense planar arrays of nanostructured elements (often called meta-atoms) designed to control local phases and amplitudes of scattered optical fields, thus being able to manipulate radiation wavefronts at a subwavelength scale (1–5). Numerous applications have already been demonstrated in the past decade, including free-space wavefront shaping (6–9), versatile polarization transformations (10–13), optical vortex generation (14–16), and optical holography (17–20), to name a few. However, to date, most reported OMSs are static, featuring well-defined optical responses determined by OMS configurations that are set during fabrication. For more intelligent and adaptive systems, such as light detection and ranging (LIDAR), free-space optical tracking/communications, and dynamic display/holography (21–23), it would be highly desirable to develop dynamic OMSs with externally controlled reconfigurable functionalities.

Realization of dynamic OMSs is very challenging because of the high density of array elements that are also arranged in nanometer-thin planar configurations. One of the currently investigated approaches relies on using dynamically controlled constituents, whose optical properties can be adjusted by external stimuli, thereby tuning their optical responses and reconfiguring the OMS functionalities. A variety of dynamic OMSs have been demonstrated by using such materials, including liquid crystals (LCs) (24–26), phase-change materials (27–31), two-dimensional (2D) materials (32–37), and others (38–41). For example, by integrating the OMS into an LC cell, reconfigurable beam steering was realized through electrically rotating the LCs in an addressable manner (25). Phase-change materials such as Ge₂Sb₂Te₅ (27–30) or VO₂ (31) were also used to construct dynamic OMSs due to their reversible amorphous-crystalline or metal-insulator transitions. Furthermore, 2D materials, especially graphene, can be also used to implement dynamic OMSs since their optical properties can be remarkably adjusted through electrical gating/chemical doping with ultrafast switching speed, thus enabling dynamic OMSs with potentially ultrafast response (32, 34). Despite certain progress achieved with these configurations, there are still unresolved critical issues. Thus, LCs inherently require the polarization-resolved operation (24–26), phase-change materials feature relatively slow response times (29–31), while OMSs based on 2D materials suffer from relatively low modulation efficiencies (35, 36).

Another approach for realizing dynamic OMSs relies on direct modifying their geometrical parameters via mechanical actuations (42–52). Initial attempts include OMSs fabricated on elastomeric substrates with dynamic functionalities enabled by OMS stretching (45, 46). Faster and more accurate actuation can be achieved with microelectromechanical systems (MEMS) that allow for electrically controlled actuation with nanometer precision and resolution, featuring also mature design and fabrication techniques (42–44, 47–52). For example, varifocal lenses were realized with MEMS-actuated metasurface doublets, whose relative positions were controlled by MEMS actuators, resulting in continuous focal length tuning (50). In this configuration, however, the two OMSs and their individual responses are not modified, making it difficult to use for dynamic wavefront manipulation in general. Very recently, through directly structuring OMSs on a movable silicon membrane of a silicon-on-insulator (SOI) wafer, dynamic 1D wavefront shaping with fast response speed (~1 MHz) was demonstrated (51). In this case, direct OMS integration into the MEMS-actuated membrane leads to certain design limitations, resulting in polarization-dependent performance and impeding implementation of 2D wavefront shaping.

Here, by combining a thin-film piezoelectric MEMS (53–56) with the gap-surface plasmon (GSP)–based OMS (6–8, 57), we develop an electrically driven dynamic MEMS-OMS platform for realizing efficient, broadband, and fast 2D wavefront shaping in reflection. The main idea is to split the conventional GSP-based OMS (6–8, 57), so that an OMS layer containing metal nanobricks and a back reflector is physically separated by an electrically controlled air gap, with an ultraflat MEMS mirror serving as a moveable back reflector (Fig. 1A). OMSs and MEMS mirrors are designed and fabricated in separate processing paths and then combined, ensuring thereby the design freedom on both sides and reducing the fabrication complexity. The choice of the piezoelectric MEMS to be combined with the GSP-based OMS is dictated by specific advantages of the former, including continuous out-of-plane actuation capability and low voltage/power operation (53), which enable the development of continuously tunable/reconfigurable MEMS-OMS components with ultracompact sizes and low power consumption.

Fig. 1. 2D wavefront shaping with the MEMS-OMS.

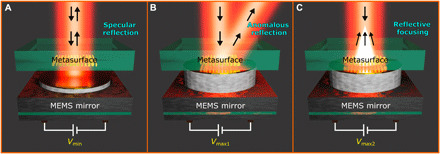
(A) Schematic of mirror-like light reflection by the MEMS-OMS before the actuation, i.e., with the initial gap of ~350 nm between the OMS nanobrick arrays and MEMS mirror. Incident light is specularly reflected by the MEMS-OMS regardless the OMS design. (B and C) Schematic of demonstrated functionalities, (B) anomalous reflection and (C) focusing (depending on the OMS design), activated by bringing the MEMS mirror close to the OMS surface, i.e., by decreasing the air gap to ~20 nm.

With this platform, we experimentally demonstrate dynamic polarization-independent beam steering (Fig. 1B) and reflective 2D focusing (Fig. 1C). By electrically actuating the MEMS mirror and thus modulating the MEMS-OMS distance, polarization-independent dynamic responses with large modulation efficiencies are demonstrated. Specifically, when operating at a wavelength of 800 nm, the beam steering efficiency (in the +1st diffraction order) reaches 40 and 46% for the respective transverse magnetic (TM) and transverse electric (TE) polarizations (electric field parallel/perpendicular to the reflection plane, respectively), where 76 and 78% are expected from simulations, while the beam focusing efficiency reaches 56 and 53% (64 and 66% expected from simulations). Furthermore, the dynamic response of the investigated MEMS-OMSs is characterized with the respective rise/fall times of ~0.4/0.3 ms, characteristics that can be further improved by using MEMS mirrors optimized for bandwidth in the megahertz range. For example, by using MEMS actuated membranes to ensure ~30 MHz of switching speeds (54–56).

RESULTS

Operational principle

Similar to the conventional GSP-based OMSs (6–8, 57), the proposed MEMS-OMS configuration represents a metal-insulator-metal (MIM) structure composed of a bottom thick gold layer atop a silicon substrate (MEMS mirror), an air spacer, and a top layer with 2D arrays of gold nanobricks on a glass substrate (OMS structure). The air spacer gap t_a can be finely adjusted by actuating the MEMS mirror (Fig. 2A). When the air gap is small (t_a < 200 nm), the optical responses of OMS unit cells are determined by the GSP excitation and resonance in the MIM configuration (57, 58) and thus by nanobrick dimensions (8, 57). To progress further toward the design of dynamically controlled MEMS-OMSs, several geometrical OMS parameters must be determined. First, we set the operating wavelength at 800 nm and choose the OMS unit cell size of 250 nm that should be substantially smaller than the operating wavelength (8, 57). Assuming the smallest achievable air gap is between 20 and 50 nm, the nanobrick thickness t_m is then optimized to achieve a wide phase coverage with large reflection amplitudes, resulting in the choice of t_m = 50 nm (fig. S1). The nanobrick lateral dimensions, side lengths, are chosen to be equal to ensure the polarization-independent optical response. Analysis of the complex reflection coefficients of the OMS conducted for increased air gaps reveals that the phase gradient for different nanobrick side lengths progressively decreases, with the reflection phase and amplitude becoming independent on the nanobrick length at an air gap of t_a = 350 nm (Fig. 2, B and C). This drastic transformation in the optical response is related to strong dependencies of the GSP excitation (at normal incidence) and GSP reflection at nanobrick terminations on the air gap: Both decrease rapidly for increased air gaps, thereby attenuating and eventually eliminating the GSP resonance. The observed transformation of the reflection phase response (Fig. 2C) implies a simple and straightforward approach to realize dynamically controlled MEMS-OMSs: For a given smallest air gap (for example, 20 nm), one can design any conceivable GSP-based OMS (59), whose functionality can then be switched on and off by moving the MEMS mirror. Hereafter, we demonstrate this approach by realizing dynamically controlled polarization-independent beam steering and reflective 2D focusing.

Fig. 2. Polarization-independent dynamic beam steering: Design.

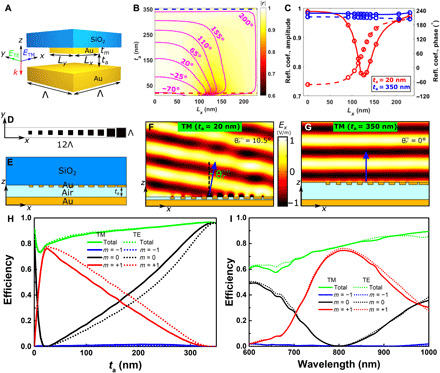
(A) Schematic of the OMS unit cell including the air gap and gold mirror. (B) The complex reflection coefficient r calculated as a function of the nanobrick side length L_x and air gap t_a with other parameters being as follows: λ = 800 nm, t_m = 50 nm, Λ = 250 nm, and L_y = L_x. Coloration is related to the reflection amplitude, while the magenta lines represent constant reflection phase contours. (C) Reflection phase (dashed lines) and amplitude (solid lines) dependencies on the nanobrick length L_x for two extreme air gaps: t_a = 20 nm (red) and 350 nm (blue). Circles represent the nanobrick sizes selected for the OMS supercell designed for dynamic beam steering. (D) Top view and (E) cross section of the designed MEMS-OMS supercell. (F and G) Distributions of the reflected TM electric field (x component) at 800-nm wavelength for air gaps of t_a = 20 and 350 nm, respectively. (H) Diffraction efficiencies of different orders (|m| ≤ 1) calculated as a function of the air gap t_a for TM/TE incident light with 800-nm wavelength. (I) Diffraction efficiencies of different orders (|m| ≤ 1) calculated at the air gap t_a = 20 nm as a function of the wavelength for TM/TE incident light.

Polarization-independent dynamic beam steering: Design

The MEMS-OMS design for realizing dynamically controlled polarization-independent beam steering requires the choice of the number N of unit cells in the OMS supercell that, in turn, determines the steering angle θ for the given unit cell size Λ = 250 nm, refractive index of silica glass n = 1.46, and light wavelength λ = 800 nm: sin θ = λ/nNΛ (6, 8, 57). Bearing in mind experimental conditions, we chose an OMS supercell consisting of 12 cells so that the steering angle is θ = 10.5° in glass (corresponding to 15.5° in air), facilitating the characterization of well-separated 0th/±1st diffraction orders with a 20×/0.42 objective. Following the approach described above, the phase response calculated with the air gap t_a = 20 nm for different nanobrick lengths is used to select the 12 nanobricks (Fig. 2C, red circles) and arrange them into an array along the x direction (Fig. 2, D and E) to mimic the reflection coefficient of an ideal blazed grating: r(x) = Aexp(i2πx/Λ_sc) (6, 8, 57), where A ≤ 1 is the reflection amplitude, and Λ_sc = 12Λ is the grating (supercell) period. The available phase range at t_a = 20 nm is slightly more than 270° (the red dashed line in Fig. 2C), implying that it is impossible to design a supercell with 12 different unit cells ensuring a constant phase gradient (the latter requires the phase range of 11 × 30° = 330°). One possible approach to deal with this problem is to increase the phase (discretization) steps to 90° (fig. S2, A to E), so that the required phase range would decrease to 3 × 90° = 270°, resulting in the possibility to compose the supercell from duplicated (Λ_sc = 4Λ × 2 = 8Λ) or triplicated (Λ_sc = 4Λ × 3 = 12Λ) cells (8). Our simulations suggested another approach, in which two unit cells were left out empty, i.e., without nanobricks, while the other 10 nanobricks cover the available phase range of 270°, thus ensuring better sampling of the phase profile and improving the efficiency of diffraction to the desired +1st order (fig. S2, F to L). Note that, in the absence of absorption, one might opt for another approach, such as doubling only the cells with extreme (minimum and maximum) phase responses (60).

The reflected electric field (x/y components) calculated for thus designed MEMS-OMS under the TM/TE incident light at 800-nm wavelength with t_a = 20 nm manifests smooth wavefronts traveling in the direction of the +1st diffraction order (Fig. 2F and fig. S2J, left). For increased air gaps, the phase gradients produced by the supercell nanobricks progressively decrease as expected (Fig. 2, B and C), with the phase gradient becoming zero and the reflected field returning to the specular reflection at an air gap of t_a = 350 nm (Fig. 2G and fig. S2J, right). Here, we remark that our simulations presented hereafter are concerned with the air gaps limited by 350 nm since, for larger air gaps, a MEMS-OMS would function in a completely different regime determined by multiple and periodic positions of Fabry-Pérot resonances (see Discussion). The associated decrease in the +1st order diffraction efficiency and increase in the 0th order one as a function of the air gap, are practically linear, promising large modulation efficiencies available with the actuated MEMS-OMS (Fig. 2H). Thus, +1st/0th-order diffraction efficiencies are expected to change from ~77/0 to 0/96% (for both TM and TE polarizations) when changing the air gap from 20 to 350 nm. Redistributions of the power between diffracted orders for gradually varying air gaps are interconnected with the corresponding modifications in the reflected fields, undergoing gradual transition (fig. S3) between those primarily diffracted (at t_a = 20 nm) and those primarily reflected (at t_a = 350 nm). The designed MEMS-OMS is expected to exhibit the broadband operation similar to that known for conventional GSP-based OMSs (7, 8, 57). We note that the MEMS-OMS performance at large air gaps is equivalent to that of a mirror, with the value of a suitably large air gap being proportional to the operating wavelength (see the consideration of the Fabry-Pérot–based operation in Discussion). With this caveat in mind, the MEMS-OMS overall performance is determined by that at the smaller air gap of t_a = 20 nm, suggesting a 1-dB bandwidth of ~150 nm near the operating wavelength of 800 nm (Fig. 2I). Note that, while the reflected field distribution for the air gap of 20 nm (Fig. 2F and fig. S2J, left) is not ideal for a number of reasons: insufficient phase range, unequal amplitude reflection coefficients, etc. (7, 8, 57), the performance of the MEMS-OMS at the design wavelength of 800 nm is practically ideal with only the +1st diffraction order being nonzero (Fig. 2I and fig. S2, H and I), i.e., this nonideal wavefront formation is of no practical importance for the device operation. As a final comment, it should be mentioned that, given the possibility of small air gap adjustments around the designed air gap of t_a = 20 nm, the diffraction efficiencies for different wavelengths could be enhanced, thus improving the effective bandwidth of the MEMS-OMS device (fig. S2, K and L).

Polarization-independent dynamic beam steering: Characterization

The MEMS-OMS for polarization-independent dynamic beam steering designed above (Fig. 2) was assembled from a separately fabricated OMS, an ultraflat MEMS mirror (53), and a printed circuit board (Fig. 3A; for details, see Materials and Methods along with fig. S4, A to D). The possibility of fabricating the MEMS mirror and OMS separately simplifies the design and fabrication processes, for example, by allowing the two components to be produced in separate processing lines with different minimum linewidth capabilities. The fabricated MEMS mirror and OMS were characterized individually using an optical microscope and scanning electron microscope (SEM) (Fig. 3, B and C). When joining the MEMS mirror and OMS, it is important to avoid any particles that can obstruct the mirror from getting close enough to the OMS. Because the mirror (i.e., 3 mm in diameter) was much larger than the OMS (i.e., 30 μm by 30 μm in size), the OMS was fabricated on top of a 10-μm-high pedestal, the idea being that any particles smaller than 10 μm outside the pedestal will not prevent the OMS and MEMS mirror from coming into contact. This pedestal did not affect the fabrication of the nanobricks, featuring overall consistency with the design apart from slightly rounded corners and minor size deviations (Fig. 3C) that are not expected to produce noticeable deterioration in the OMS performance (8). After assembling the MEMS-OMS, the MEMS-OMS separation was estimated using white light interferometry (Zygo NewView 6000) to be ~2 μm (fig. S4E), which is well within the ~6-μm-large moving range of the MEMS mirror (see Materials and Methods along with fig. S4F). Following that, we estimated the smallest achievable separation between the MEMS mirror and OMS substrate surface (crucial for efficient modulation) by using a multiwavelength interferometry (fig. S5). We found by actuating the MEMS mirror that, for several assemblies, this gap (t_m + t_a) can be as small as ~100 nm (fig. S5), corresponding to t_a ~ 50 nm, and these samples were then selected for further optical characterizations.

Fig. 3. MEMS-OMS assembly.

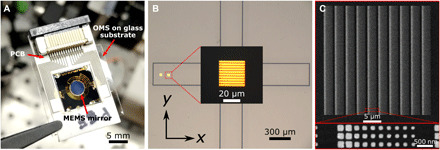
(A) Typical photo of the MEMS-OMS assembly consisting of the OMS patterned on a glass substrate, an ultraflat thin-film MEMS mirror, and a printed circuit board (PCB) for electrical connection. (B) Optical microscopy and (C) SEM images of the OMS representing the 30 μm by 30 μm and 250-nm-period array of differently sized gold nanobricks designed for dynamic beam steering, fabricated atop a 10-μm-high pedestal on the glass substrate, and used in the MEMS-OMS assembly. Photo credit: Chao Meng, University of Southern Denmark.

To characterize the MEMS-OMS performance, we used a wavelength-tunable (~700 to 1000 nm) laser with the corresponding optical, polarization, and imaging components (see Materials and Methods along with fig. S6). The MEMS mirror is electrically actuated to modulate the optical response of the MEMS-OMS observed visually in both direct object (OMS surface) and Fourier image planes (Fig. 4A). In the direct object images, this effect of power redistribution is seen in the appearance (at nonzero actuation voltages) of well-pronounced interference fringes formed due to the interference between the residual specular reflection and the +1st-order diffracted beam. For both polarizations, the redistribution of radiation power between the 0th and +1st diffraction orders are well pronounced, reaching the maximum contrast at 3.75 V with the diffraction efficiencies of 40/46% for the respective TM/TE polarizations (Fig. 4, A and B). The experimentally obtained diffraction efficiencies (Fig. 4B) are noticeably smaller than those expected from the simulations (Fig. 2H), discrepancies that are somewhat expected and attributed to additional absorption in gold nanobricks because of surface scattering and grain boundary effects as well as increased damping associated with a nanometer-thin titanium adhesion layer between gold-glass interfaces (8). Note that there is also a minor difference to be expected because of different media considered when determining the theoretical and experimental efficiencies (see Materials and Methods). The high-contrast dynamic beam steering, induced by actuating the MEMS mirror with the alternating voltages of 0 and 3.75 V at a slow switching speed, is clearly seen in the movie captured by the charge-coupled device (CCD) camera (movie S1). The MEMS-OMS operation is found to be polarization independent and broadband, exhibiting the 1-dB bandwidth of ~150 nm (Fig. 4C). By actuating the MEMS mirror with a periodic rectangle signal and detecting the spatially separated 0th/+1st order of diffraction fields, one observes relatively fast switching with the rise/fall times of ~0.4/0.3 ms, respectively (Fig. 4D). The response speed is related to the intrinsic oscillation frequency of the MEMS mirror, thus being dependent on the MEMS design parameters such as geometry, weight, stiffness, and so on (53–56). Note that the standard thin-film MEMS mirror used is rather large (~3 mm in diameter; Fig. 3A), with its surface area orders of magnitude larger than that of the OMS area (~30 μm by 30 μm in size; Fig. 3B), considerably slowing down the dynamic response. Bearing in mind the possibility of optimizing the MEMS mirror for fast switching speeds, one should expect that reaching operation bandwidths in the megahertz range, indeed, current state of the art in thin-film piezoelectric MEMS, can achieve ~30 MHz of switching frequencies (54–56). In terms of stability and repeatability of operation, thin-film piezoelectric MEMS can survive more than 10¹¹ cycles at full 20 V of ac cycles for standard operating conditions (23°C, 35% relative humidity), drifting by ~10% during its lifetime (61), although the repeatability within ~1 nm is feasible with accurate position feedback by, e.g., optical, capacitive, or piezoresistive sensing. As far as the vibration instability is concerned, it is important that the MEMS device and glass plate resonances are not excited, which is usually the case once resonance frequencies are above 1 kHz. The current MEMS device has a resonance frequency of ~4 kHz and that of the glass plate is much higher. Consequently, no vibration is expected under normal circumstances and no instability was observed.

Fig. 4. Polarization-independent dynamic beam steering: Characterization.

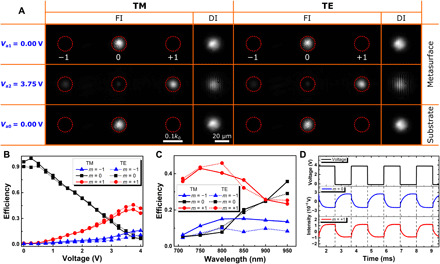
(A) Optical images at the direct object (DI) and Fourier image (FI) planes of the reflected light from MEMS-OMS under actuation voltages of V_a1 = 0.00 V (top) and V_a2 = 3.75 V (middle) for TM/TE normally incident light with 800-nm wavelength. Reflected light from unstructured substrate (bottom) in the MEMS-OMS device is also recorded as a reference. (B) Diffraction efficiencies of different orders (|m| ≤ 1) measured as a function of the actuation voltage for TM/TE incident light with 800-nm wavelength. (C) Diffraction efficiencies of different orders (|m| ≤ 1) measured as a function of the wavelength for TM/TE incident light. (D) Response time of the different diffraction orders (m = 0/+1) measured by actuating the MEMS mirror with a periodic rectangle signal.

Concluding the presentation of the demonstrated MEMS-OMS for polarization-independent dynamic beam steering, we would like to note that, although the experimentally observed performance (Fig. 4) is somewhat inferior to that expected from our simulations (Fig. 2), the experimental performance can be improved. The deterioration can be attributed partly to fabrication imperfections and to the smallest air gap t_a that was achieved in practice. It seems that the air gap decreases with applying the actuation voltage only up to ~3.75 V, resulting thereby in increasing +1st and decreasing 0th order diffraction efficiencies, whereas for larger voltages, the MEMS mirror starts to move slightly away from the OMS, probably because of the residual contaminants on the substrate or bending at the pedestal edges that prevent the MEMS mirror from moving further closer to the OMS surface. Both better fabrication accuracy and smaller air gaps are feasible and expected to be realized in further experiments.

Polarization-independent dynamic 2D focusing: Design

The MEMS-OMS design for realizing dynamically controlled polarization-independent 2D beam focusing in reflection requires the choice of diameter D and focal length f of the OMS lens that, in turn, determines the numerical aperture (NA) for the given refractive index in the image space n = 1.46 at an incident wavelength of λ = 800 nm: NA = nsin[tan⁻¹(D/2f)]. To realize strong focusing, we chose D = 14 μm and f = 15 μm, so that NA ≈ 0.62 is expected, which should be adequate to enable high-efficiency reflective 2D focusing (7). Following the same design approach used in demonstrating MEMS-OMS for dynamic beam steering, we use the phase response calculated with air gap t_a = 20 nm for different nanobrick lengths (the red dashed line in Fig. 2C) to extract the proper unit cells and arrange them into a circular region with D = 14 μm (Fig. 5A), approximating a hyperboloidal phase profile (7, 9) ${\mathrm{\varphi }}_{2D}=\frac{2\mathrm{\pi }}{\mathrm{\lambda }}n(f-\sqrt{x^2+y^2+f^2})$ in the xy plane (Fig. 5B). The above phase profile is also discretized with the step size Λ = 250 nm along both x and y directions, matching the unit cell size (Λ = 250 nm). In contrast to the previous work, we do not limit the choice of unit cells to a discrete design space [i.e., unit cells with discrete phase steps of 45° (7)]. Instead, appropriate lengths of the nanobricks are chosen from the entire space of simulation results (the red dashed line in Fig. 2C), thus ensuring better sampling of the 2D phase profile with minor deviations (fig. S7, A and B) from the required one (Fig. 5B). The deviation between the required and available phase profiles results mostly from the achievable phase coverage of ~270°, a limitation that could be circumvented by including more complex unit cell elements such as detuned GSP resonators (62) that can also be constructed square-like to ensure the polarization-independent operation or by using cross-like nanobricks, allowing for a wider phase coverage (57).

Fig. 5. Polarization-independent dynamic 2D focusing: Design.

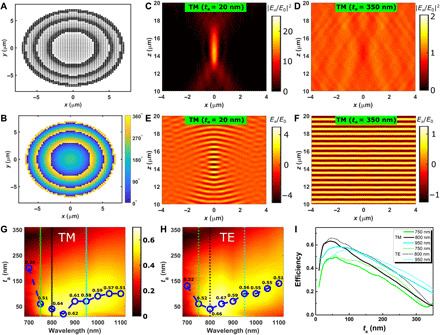
(A) Top view of the OMS designed for dynamic 2D focusing. (B) The phase profile required to focus radiation with focal length of 15 μm at 800-nm wavelength. (C and D) Distributions of the reflected intensity for TM incident light with 800-nm wavelength at air gaps of t_a = 20 and 350 nm, respectively. (E and F) Distributions of the reflected TM electric field (x component) at 800-nm wavelength for air gaps of t_a = 20 and 350 nm, respectively. (G and H) Focusing efficiencies calculated as a function of the operating wavelength λ and air gap t_a for TM/TE polarizations. The green, black, and cyan lines indicate the cases of λ = 750, 800, and 950 nm, respectively. (I) Focusing efficiencies calculated as a function of the air gap t_a for TM/TE polarizations with respective 750-, 800-, and 950-nm wavelengths.

Bearing in mind high computational demands when simulating 2D focusing (and thus aperiodic) OMSs, we estimate the focusing performance by simulating the corresponding (reduced to a 1D aperiodic configuration) OMS (fig. S7, C and D), which is designed to provide a 1D hyperboloidal phase profile ${\mathrm{\varphi }}_{1D}=\frac{2\mathrm{\pi }}{\mathrm{\lambda }}n(f-\sqrt{x^2+f^2})$, while the D, f, and λ are the same as that of the above-designed OMS with the 2D phase profile. The reflected intensity distributions calculated for this simplified MEMS-OMS under TM/TE incident light at 800-nm wavelength with t_a = 20 nm manifest high focusing quality with a diffraction-limited spot situated at the focal length of ~15 μm (Fig. 5C and fig. S7E). For increased air gaps, the phase gradients produced by nanobricks with different lengths progressively decrease (Fig. 2, B and C), approaching zero at an air gap of 350 nm, with the reflection transformed into specular reflection (Fig. 5D and fig. S7F). The associated reflected electric fields calculated near the focus display smoothly converging and planar wavefronts at air gaps t_a = 20 nm (Fig. 5E and fig. S7G) and 350 nm (Fig. 5F and fig. S7H), respectively, implying a high-efficiency operation of the actuated MEMS-OMS. Taking into account the possibility of adjusting the air gap to maximize the focusing efficiency at other (than the design) wavelengths, we evaluated the focusing efficiencies achievable at different wavelengths with varied air gaps (Fig. 5, G and H). The maximum achievable focusing efficiencies at the design wavelength of 800 nm are estimated to be ~64/66% (TM/TE) for the air gap of ~20 nm as expected. For other wavelengths, the polarization-independent focusing behavior is well maintained, while the corresponding maximal focusing efficiencies are expected to achieve at slightly different air gaps. To better visualize this feature, the focusing efficiency as a function of the air gap is explicitly plotted for distinct wavelengths of 750, 800, and 950 nm (Fig. 5I), showing for all wavelengths a nearly linear decrease of the efficiency for increasing air gaps without noticeable changes in the reflected field distributions (fig. S7, I to L).

Polarization-independent dynamic 2D focusing: Characterization

The MEMS-OMS for polarization-independent dynamic reflective 2D focusing designed as described above (Fig. 5) was assembled following the fabrication and precharacterization processes similar to those used when assembling the dynamic beam steering MEMS-OMS. Optical microscopy and SEM are used for monitoring the possible contaminants on the OMS surface and the fabrication quality (the upper-left inset of Fig. 6A and fig. S8).

Fig. 6. Polarization-independent dynamic 2D focusing: Characterization.

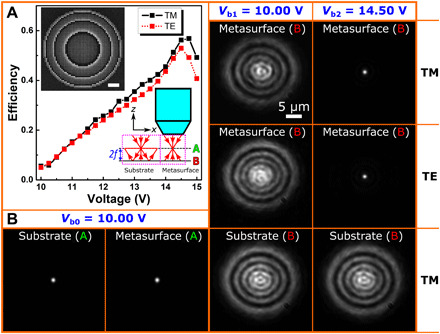
(A) Focusing efficiencies measured as a function of the actuation voltage for TM/TE incident light with 800-nm wavelength. The upper-left inset is a typical SEM image of the OMS representing 14-μm-diameter and 250-nm-period array of differently sized gold nanobricks designed for dynamic 2D focusing. Scale bar, 2 μm. The bottom-right inset illustrate the measurement method in which the incident beam is focused at plane A (focal plane of the objective) and impinging on the unstructured substrate or OMS area of the MEMS-OMS at plane B (2f distance away from the focal plane of the objective), resulting in respective divergent or focused reflected fields. (B) Optical images of the reflected light from the unstructured substrate and OMS area of the MEMS-OMS positioned at plane B with actuation voltages of V_b1 = 10.00 V and V_b2 = 14.50 V for TM/TE incident light at 800-nm wavelength. The reflected light from the unstructured substrate and OMS area of the MEMS-OMS positioned at plane A was also recorded as a reference.

To characterize the dynamic focusing MEMS-OMS, we electrically actuated the MEMS mirror and observed corresponding optical responses in the direct object plane (Fig. 6B). Since the MEMS-OMS was designed to exhibit a very short focal length of ~15 μm, it was not possible to directly access the focal plane using a beam splitter (BS) and a low-divergent incident laser beam. Instead, the focusing effect was verified by illuminating the MEMS-OMS with a focused incident beam and placing the MEMS-OMS surface plane B at a distance of ~2f (the double focal length of the MEMS-OMS) away from the incident beam focal plane A (see inset in Fig. 6A). According to the ray optics, the beam reflected by the OMS (when close to the MEMS mirror) will then be focused again at the focal plane of the objective (plane A in the bottom-right inset of Fig. 6A). At the same time, the reflection from the unstructured substrate surface (outside the OMS area) would be strong diverging (see the bottom-right inset in Fig. 6A). If one moves the MEMS-OMS surface to plane A, then the reflection behavior will be reversed: The reflection by the OMS will be diverging (after the objective) and the reflection by the unstructured surface collimated. This procedure was successfully used and described in detail in the previous experiment conducted with the static focusing OMS (7). In the current case with the dynamic focusing MEMS-OMS, it is expected for the MEMS-OMS arrangement to switch between the focusing configuration, when the applied voltage would bring the OMS very close to the MEMS mirror, and the mirror reflecting configuration for relatively small applied voltages that would correspond to sufficient large OMS and MEMS mirror separations.

To observe this transformation, we monitored the reflected light from the MEMS-OMS positioned at plane B while actuating the MEMS mirror. For both polarizations, the switching of the reflected light between the mirror (at V_b1 = 10.00 V) and focusing (at V_b2 = 14.50 V) cases was clearly visualized (Fig. 6B), with the focusing efficiencies reaching their maxima of ~56/53% at V_b2 = 14.50 V for the respective TM/TE light incidence at the wavelength of 800 nm (Fig. 6A). At the same time, the reflection from the unstructured substrate surface was not influenced with the applied voltages, revealing, however, that the reflection from the substrate at plane A is notably similar to the TM/TE reflection from the OMS at plane B, with the applied voltage being V_b2 = 14.50 V (Fig. 6B). The latter evidences a rather high efficiency and excellent quality of polarization-independent focusing by the MEMS-OMS at V_b2 = 14.50 V. The dynamic evolution of the reflected field from the MEMS-OMS positioned at plane B, induced by actuating the MEMS mirror with stepwise increased voltages from 10.00 to 14.50 V, is clearly observed with a CCD camera (movie S2). Because of the usage of the same MEMS component as that in the dynamic beam steering MEMS-OMS, similar response time of ~0.4 ms is expected. It is lastly worth noting that, according to the current state of the art in thin-film piezoelectric MEMS techniques (54–56), MEMS-OMS components with a few megahertz of switching bandwidth should be feasible and expected for further developments.

DISCUSSION

We have developed the electrically driven dynamic MEMS-OMS platform by combining a thin-film piezoelectric MEMS mirror with a GSP-based OMS. This platform offers controllable phase and amplitude modulation of the reflected light by finely actuating the MEMS mirror. We have designed and experimentally demonstrated MEMS-OMS devices operating in the near-infrared wavelength range for dynamic polarization-independent beam steering and reflective 2D focusing, both exhibiting efficient (~50%), broadband (~20% near the operating wavelength of 800 nm), and fast (<0.4 ms) operation. Note that the operation bandwidth can be markedly increased when using the circularly polarized light whose transformation relies on the OMS, making use of the geometrical (Pancharatnam-Berry) phase (17). The operation of both devices relies on the phase response transformation when changing the MEMS-OMS separation by adjusting the applied voltage within the range of ~4 V. The same operation principle can be used to design a MEMS-OMS for dynamically controlling any functionality available for conventional GSP-based OMSs, from polarization control/detection to vector/vortex beam generation (59): For a given smallest air gap, one designs the GSP-based OMS exhibiting a required functionality that can then be switched on and off by moving the MEMS mirror toward and away from the OMS surface.

Moreover, the nontrivial modification of the size-dependent phase response with the MEMS-OMS separation (Fig. 2B), which can accurately be adjusted by electrical MEMS actuation, suggests a possibility of realizing more sophisticated dynamic functionalities. One functionality of particular interest to commercial applications is the possibility of switching between multiple diffraction orders to allow for quasi-continuous beam steering (for use in, e.g., LIDAR applications). Thus, we have also designed and experimentally demonstrated the MEMS-OMS device for polarization-independent dynamic beam steering between three (0th, 1st, and 2nd) diffraction orders, corresponding to reflection angles of 0°, 5.2°, and 10.5° in glass (i.e., 0°, 7.7°, and 15.5° in air) under normally incident light with 800-nm wavelength. The OMS configuration (fig. S9) consisted of two OMSs with different supercells with Λ_sc1 = 12Λ and Λ_sc2 = 24Λ optimized at two distinct air gaps and interleaved by adopting a random-interleaving strategy (63). The experimental characterization (fig. S10) has confirmed the intended dynamic MEMS-OMS response: With the actuation voltage increasing, the +1st and +2nd diffraction orders became visible, succeeding one another, in accordance with our simulations (fig. S9, K and L).

Another promising direction for further research and development is to circumvent the necessity of bringing the MEMS mirror very close (~100 nm) to the OMS surface. For large MEMS-OMS separations, one can make use of localized plasmon resonances because of excitation of short-range surface plasmon polaritons (SR-SPPs) in thin metal films (58). Our preliminary simulations showed that the SR-SPP resonances hybridize with the Fabry-Pérot resonances (supported with wavelength-large air gaps) (64, 65) and open a similar to the considered above route to modify the OMS phase response by controlling the air gap (fig. S11, A to C). Note that at certain air gaps (separated by half of the wavelength), the reflected phase becomes independent on the nanobrick size (fig. S11, A and B), resulting thereby in the mirror-like behavior (fig. S11, D and E). In between these air gaps, there are gaps at which the phase does depend on the nanobrick size (see a dashed line at the gap of 1250 nm in fig. S11B). At these gaps, the nanobrick sizes can be chosen in a manner enabling one to realize a phase-gradient metasurface (fig. S11, F and G). Switching between these two distinct air gaps results therefore in switching between the mirror-like and gradient metasurface behavior, which is similar to switching between the same types of responses of the dynamic GSP-based metasurfaces. With this approach, the MEMS-OMS can be operated near the air gap of ~1 μm or more, as demonstrated with our simulations of dynamic beam steering (fig. S11, D to L), thus avoiding the problem of realizing nanometer-sized air gaps. Overall, we believe that diverse functionalities with dynamically reconfigurable performances can be realized using the developed MEMS-OMS platform, thus opening fascinating perspectives for successful realization of high-performance dynamically controlled devices with potential applications in future reconfigurable/adaptive optical systems.

MATERIALS AND METHODS

Simulation methods

All numerical simulations were performed using COMSOL Multiphysics 5.5. We modeled one individual glass-Au-air-Au unit cell (Fig. 2A), where periodic boundary conditions were applied in both x and y directions, and linearly x-polarized light at the design wavelength of 800 nm was normally incident onto the unit cell from the upper glass layer. The permittivity of Au is described by the interpolated experimental values (66), and the glass layer is taken as a lossless dielectric with a constant refractive index of 1.46. Then, the complex reflection coefficients (Fig. 2B) were calculated as a function of nanobrick lengths L_x, and air gap t_a with other parameters being as follows: λ = 800 nm, t_m = 50 nm, Λ = 250 nm, and L_y = L_x to ensure the polarization-independent optical responses.

To design the MEMS-OMS for dynamic beam steering, the phase response calculated with the air gap t_a = 20 nm for different nanobrick lengths is used to select the lengths of 12 nanobricks (Fig. 2C) for approximating the reflection coefficient of an ideal blazed grating: r(x) = Aexp(i2πx/Λ_sc) (6, 8, 57), where A ≤ 1 is the reflection amplitude, and Λ_sc = 12Λ is the grating (supercell) period. Reflected light directed to different diffraction orders are monitored, with different air gaps t_a and incident wavelengths λ for estimating the dynamic diffraction efficiencies and operation optical bandwidths, respectively (Fig. 2, D to I, and fig. S2, F to L). Here, the diffraction efficiencies are defined as the ratios of the light intensities (in glass) in the corresponding diffraction orders to the incident (in glass) light intensity.

MEMS-OMS for dynamic beam focusing is designed and simulated in a similar fashion. Nanobricks from the phase response calculated with the air gap t_a = 20 nm for different nanobrick lengths (Fig. 2C) are selected to approximate a 1D hyperboloidal phase profile of ${\mathrm{\varphi }}_{1D}=\frac{2\mathrm{\pi }}{\mathrm{\lambda }}n(f-\sqrt{x^2+f^2})$ (7, 9) within a 14-μm-diameter region in the xy plane (fig. S7, C and D). Reflected fields are monitored to visualize the dynamic beam focusing and estimate corresponding focusing efficiencies as a function of the gap sizes t_a and incident wavelengths λ, for both TM and TE polarizations (Fig. 5, C to I, and fig. S7, E to L). Here, the focusing efficiencies are defined as the ratio of the light power from the corresponding focal spot (in glass) to the incident (in glass) light power. Note that both diffraction and focusing efficiencies obtained in our simulations should not be directly compared to the experimental values that were measured in air because of the reflections at the glass-air interface. Considering the fact that all optical fields propagate at directions close to the normal to the OMS surface and disregarding multiple reflections, one can estimate the expected difference between the quantities obtained for the fields in air and in glass as η_air ≈ 0.93η_glass, i.e., the difference amounts to ~7%.

Fabrication and assembly of the MEMS-OMS devices

The OMSs for developing MEMS-OMS for dynamic beam steering/focusing were fabricated using standard electron beam lithography (EBL), thin-film deposition, and lift-off techniques. First, a 100-nm-thick poly(methyl methacrylate) (2% in anisole; MicroChem) layer and a 40-nm-thick conductive polymer layer (AR-PC 5090, Allresist) were successively spin-coated on a 16 mm by 16 mm glass substrate (Borofloat 33 wafer, Wafer Universe). Note that the glass substrate was preprocessed to have a 10-μm-high circular/cross-shaped pedestal on one side using optical lithography and wet etching. The OMSs were then defined on the pedestal of the glass substrate using EBL (JEOL JSM-6500F field-emission SEM with a Raith Elphy Quantum lithography system) and subsequently developed in 1:3 solution of methyl isobutyl ketone and isopropyl alcohol. After development, a 1-nm Ti adhesion layer and a 50-nm Au layer were deposited using thermal evaporation. The Au nanobricks were lastly formed atop the pedestal on the glass substrate after a lift-off process (Fig. 3 and fig. S8). Owing to the large size of the MEMS mirror (~3 mm in diameter) in comparison to the OMS (30 μm by 30 μm in size), the pedestal on the glass substrate is very practical for reducing the possible contaminants between the MEMS mirror and OMS surface, thus promising high-efficiency modulation of the MEMS-OMS devices.

The MEMS mirror, which is very similar to the previously reported ultraplanar, long-stroke, and low-voltage piezoelectric micromirror (53), is fabricated using standard semiconductor manufacturing processes (fig. S4A) and incorporating thin-film lead zirconate titanate (PZT) for actuation. First, a platinum-bottom electrode, a 2-μm-thick PZT film, and a top electrode consisting of TiW/Au were deposited on a SOI wafer (fig. S4A, first panel). Then, a central circular aperture of 3 mm was opened by using deep reactive ion etching of silicon and etching of the buried oxide (fig. S4A, second panel). An annulus trench is etched into the backside of the wafer, thereby releasing the circular plate. Last, the wafer backside is sputtered with Au (fig. S4A, third panel) for acting as the ultraflat MEMS mirror that is of vital importance in developing dynamic MEMS-OMS.

After the fabrication of both OMS and MEMS mirror, we move to the assembly and packaging processes for making MEMS-OMS devices (fig. S4A, fourth panel). Before assembly, the surface topography of the MEMS mirror and glass substrate were measured by a white light interferometry (Zygo NewView 6000), so as to select favorable areas on both sides with the least amount of contaminants and surface roughness that might obstruct the MEMS mirror from getting close enough to the OMS. Then, the MEMS mirror was glued to the glass substrate upon which the OMS has been structured (fig. S4, B to D). Getting the mirror and OMS parallel was done by adjusting the tilt of the MEMS mirror using the piezoelectric electrodes. The spacing between the MEMS mirror and the glass substrate (t_a + t_m) was measured to be commonly ~2 μm after mounting (fig. S4E), well within the 6-μm moving range of the MEMS mirrors (fig. S4F). Last, the MEMS-OMS was glued to a printed circuitry board, and gold wire bonding is used to connect electrically to the MEMS electrodes for enabling simple connection to a voltage controller used to actuate the MEMS mirror.

After the MEMS-OMS assembly, we applied multiwavelength interferometry to estimate the smallest achievable separation between the MEMS mirror and OMS surface (fig. S5). We found by actuating the MEMS mirror that, for several assemblies, this gap (t_m + t_a) can be as small as ~100 nm corresponding to t_a ~ 50 nm, and these samples were then selected for further optical characterizations.

Optical characterization of MEMS-OMS

To characterize the performances of the MEMS-OMS for dynamic 2D wavefront shaping, we used a fiber-coupled wavelength-tunable Ti:sapphire laser (Spectra-Physics 3900S; wavelength range, 700 to 1000 nm), whose light was directed through a half-wave plate (AHWP05M-980, Thorlabs), a Glan-Thompson polarizer and a first BS (BS₁; BS014, Thorlabs) successively, and then focused by an objective (Obj, M Plan Apo, ×20/×50 magnifications; Mitutoyo) onto the MEMS-OMSs. The reflected light was collected by the same objective and directed via BS₁ and a second BS (BS₂; BS014, Thorlabs) to two optical paths terminated with two CCD cameras (DCC1545M, Thorlabs) for visualizing respective direct object and Fourier plane images (fig. S6). Note that the objective of ×20/0.42 and ×50/0.55 are used for measuring respective MEMS-OMS for dynamic beam steering and focusing.

During the measurement, the MEMS mirror was electrically actuated to modulate the optical responses of the MEMS-OMS devices. To characterize the MEMS-OMS for dynamic beam steering, we measured both diffraction efficiencies and response time with the experimental setup shown in fig. S6. For estimating the diffraction efficiencies, we recorded the intensity of spatially separated 0th/±1st diffraction orders using a CCD camera at the Fourier plane for the laser beam being on the OMS area, which is then normalized with the reflection intensity from an unstructured substrate in the MEMS-OMS components. The response time of the MEMS-OMS was evaluated by actuating the MEMS mirror with a periodic rectangle signal from a function generator (TOE 7402, TOELLNER). The spatially separated diffraction orders at the Fourier plane could be selected by an iris and then projected to a photodetector (PDA20CS-EC, Thorlabs), which was connected to an oscilloscope (DSOX2024A, Keysight) for visualizing and recording the corresponding modulated signals. In the response time measurement, we recorded the 0th/+1st diffraction orders of the MEMS-OMS components, showing overall good repeatability and stability of the actuated MEMS-OMS components with the periodically electrical signals (Fig. 4D).

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/7/26/eabg5639/DC1