East Antarctic cooling induced by decadal changes in Madden-Julian oscillation during austral summer

About 20 to 40% of the recent summer cooling in the East Antarctic was forced by decadal changes in the Madden-Julian oscillation.

Abstract

While West Antarctica has experienced the most significant warming in the world, a profound cooling trend in austral summer was observed over East Antarctica (30°W to 150°E, 70° to 90°S) from 1979 to 2014. Previous studies attributed these changes to high-latitude atmospheric dynamics, stratospheric ozone change, and tropical sea surface temperature anomalies. We show that up to 20 to 40% of the observed summer cooling trend in East Antarctica was forced by decadal changes of the Madden-Julian oscillation (MJO). Both observational analysis and climate model experiments indicate that the decadal changes in the MJO, characterized by less (more) atmospheric deep convection in the Indian Ocean (western Pacific) during the recent two decades, led to the net cooling trend over East Antarctica through modifying atmospheric circulations linked to poleward-propagating Rossby wave trains. This study highlights that changes in intraseasonal tropical climate patterns may result in important climate change over Antarctica.

INTRODUCTION

Along with global warming over recent decades, the surface air temperature (SAT) in West Antarctica, in particular the Antarctic Peninsula, has warmed up rapidly, inducing an accelerated rate of ice-sheet melting (1–4). Different from the SAT in West Antarctica, the SAT in East Antarctica revealed a cooling trend during the austral warm season (December to May) (5–8) since the late 1970s (Fig. 1A). Understanding what controls the changes in Antarctic SAT, which is directly associated with ice-sheet melting and thus sea-level change, is of great importance to meteorology, ecology, and economy on a global scale.

Fig. 1. Changes in the Antarctic SAT in austral summer (DJF) from 1979 to 2014.

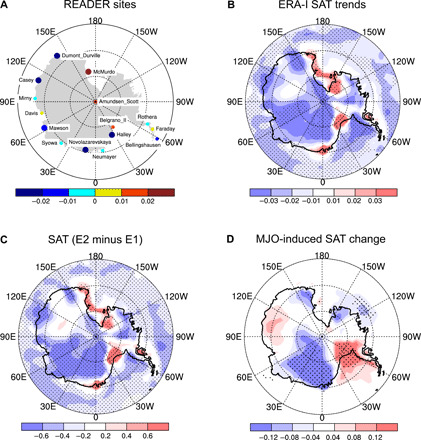
Antarctic SAT trends (K year⁻¹) based on (A) station observations and (B) ERA-I. (C) Differences in SAT (K) between the two epochs of 1997–2014 (E2) and 1979–1996 (E1). (D) SAT changes (E2 minus E1) induced by MJO-related variability estimated by the diagnostic equation, which incorporates the effects of decadal changes in MJO occurrence frequency with the intraseasonal SAT anomaly associated with the MJO (Eq. 1 in Materials and Methods). A large circle in (A) and stippling in (B) to (D) mark the regions with statistically significant changes at the 95% confidence level using the Mann-Kendall test [for the trend test in (A) and (B)], the Wilcoxon-Mann-Whitney test [for (C)], and the Monte Carlo method [for (D)], in which E1 and E2 years were randomly assigned and repeated 1000 times.

Both local and remote effects exert influences on the SAT changes over Antarctica (9–15). Atmospheric internal dynamics at higher latitude, such as variability of the Southern Annular Mode and related westerly jet, affects the local large-scale circulations over Antarctica and results in changes in Antarctic SAT (9, 10). Through radiative and dynamic effects, the ozone hole in the Antarctic stratosphere has also been identified as a driver of changes in the Antarctic surface climate (11). The Antarctic terrain also acts as an internal effect to determine the patterns of local climate change (12).

More remote mechanisms, with their roots in regions far from the poles, can also affect the Arctic Ocean and Antarctica. One such example is the atmospheric heating over the tropics, whose influence takes place through the excitation of Rossby wave trains (13, 14). This tropical heating may be induced by slow varying sea surface temperature (SST) anomalies (2, 8, 10, 13–15) or, even in the absence of SST anomalies, by the intraseasonal oscillation at the equator, e.g., the Madden-Julian oscillation (MJO) (16). The changes in the location and strength of MJO convection have been found to play a role in the Arctic amplification (17, 18), but the influences of these changes on Antarctic SAT trends are not well explored (19). Owing to the profound warming and changes in the large-scale circulation over the Indo-Pacific warm pool, the MJO activity over that location has strengthened in the past few decades (20). It has not been addressed, however, whether and how the MJO convection affects the East Antarctic cooling in austral summer [December-January-February (DJF)], when the MJO is the most vigorous.

Here, we elucidate a physical mechanism linking the temperature trend over East Antarctica to decadal changes in MJO by analyzing observational data and performing climate model experiments.

RESULTS

Changes in Antarctic SAT during austral summer

Over the recent three decades of 1979–2014, the DJF mean SAT showed a profound decreasing trend at most of the stations along the East Antarctic coast (30°W to 150°E), in contrast with an increasing trend at some stations on the western coast of Antarctica (Fig. 1A). To further reveal the geographical pattern of SAT changes over the entire Antarctic area and related processes that cause the Antarctic SAT changes, we analyze reliable reanalysis data (21). Among the reanalysis datasets (see Materials and Methods), the European Centre for Medium-Range Weather Forecasts interim reanalysis (ERA-I) demonstrates superior performance in capturing the SAT trends over Antarctica (fig. S1). The probability that ERA-I shows the same SAT trend in terms of sign as that derived from the station data over Antarctica is 0.73, although it fails to capture the weak warming trend at the South Pole (15). The root mean square error of the SAT linear trend derived from ERA-I against the observation is 0.02 K year⁻¹. The patterns of austral summer SAT changes over Antarctica using ERA-I are displayed in Fig. 1 (B and C). They show that the surface cooling appears over most of East Antarctica, including the coastal and interior areas. The most significant cooling can be seen over the eastern sector of East Antarctica (30°W to 90°E), while insignificant SAT change and very weak warming are evident in some areas over the western sector of East Antarctica (Fig. 1B). The pattern of SAT trends is highly consistent with the decadal differences in ERA-I SAT between the earlier epoch (E1; 1979–1996) and the recent epoch (E2; 1997–2014) over Antarctica (Fig. 1C). The SAT trends derived from the Antarctic reconstructed data based on three analyses (7) for 1979–2012 display a similar pattern but with weaker amplitude (fig. S2) compared to those from ERA-I, suggesting that the East Antarctic cooling is a robust signal, but its amplitude has some uncertainty, depending on the dataset used.

To understand whether and to what extent the tropical MJO-related effects contributed to SAT cooling over East Antarctica, we quantitatively estimate the MJO-induced SAT change at the decadal time scale. Because the MJO convection at the equator (fig. S3) may induce anomalous Rossby wave trains propagating toward high latitudes (17–19), the changes in the frequency of MJO convection over different regions at the equator and the changes in the intraseasonal SAT over high latitudes, and their nonlinear interaction could have led to the SAT changes over Antarctica (see Materials and Methods). The decadal changes in SAT induced by all three MJO-related effects discussed above (Fig. 1D) roughly resemble the pattern of epochal difference in the Antarctic SAT (Fig. 1C), with a remarkable cooling tendency over the eastern part of East Antarctica. Comparing the anomalous SAT amplitude shown in Fig. 1 (C and D), we find that the MJO-induced SAT changes account for 20 to 40% of the East Antarctic cooling from 1979 to 2014. The remaining (60 to 80%) contribution may arise from the climate noise of processes with intrinsic time scales less than 10 days such as synoptic-scale disturbances, as well as from processes with intrinsic time scales greater than 90 days such as decadal-to-multidecadal variability. Further diagnosis suggests that both the decadal changes in the occurrence of equatorial MJO convection over different regions and the decadal changes in intraseasonal SAT and circulation anomalies contribute to the East Antarctic cooling, while the nonlinear effect is relatively small (fig. S4).

MJO-related physical processes responsible for East Antarctic cooling

According to the result presented in Fig. 1D, the decadal changes in equatorial MJO activities have contributed substantially to the East Antarctic cooling. To explain how these MJO activities lowered the East Antarctic SAT, we examined the distributions of MJO convection anomalies and their remote effects on East Antarctic SAT (Fig. 2). We first compared the locations of MJO convection by calculating the numbers of active MJO days in each of the eight phases that define the MJO life cycle (see Materials and Methods and fig. S3) during the earlier epoch (E1; orange bars) and recent epoch (E2; blue bars). Figure 2A shows that the frequency of enhanced MJO convection over the equatorial Indian Ocean (phases 1 to 4) decreased during the recent decades. In contrast, the tropical western Pacific MJO convection (phases 5 to 8) occurred more frequently in E2. Among these phases, phases 1 and 6 reveal the largest changes in frequency between the two epochs. This finding of decreased Indian Ocean MJO convection but increased western Pacific MJO convection in E2 is confirmed when different MJO indices or criteria are used (see Materials and Methods and fig. S5). These changes are attributable to the recent expansion of the Indo-Pacific warm pool and anomalous circulations there (20). Through a teleconnection to polar latitudes, the changes in equatorial MJO convection related to the changes in MJO phase frequency would further induce changes in SAT at high latitudes (17–19). The pink and green bars in Fig. 2B display the temporal evolutions of SAT anomalies over East Antarctica after the occurrence of phases 1 and 6, respectively. After the occurrence of equatorial MJO phase 1 (6), and as the MJO propagates eastward, East Antarctic warming (cooling) appears. The positive (negative) SAT anomalies become obvious during the period of lag +3 to +11 days, which is the time frame for the Rossby wave moving from the tropics to the high-latitude area (22). The evolution of positive and negative SAT anomalies is consistently shown after the occurrence of MJO convective anomalies over the tropical Indian Ocean (phases 1 to 4) and western Pacific (phases 5 to 8), respectively (curves in Fig. 2B). These results suggest that the MJO heating over different locations at the equator leads to distinct SAT changes over East Antarctica.

Fig. 2. Decadal changes in MJO activity and their association with East Antarctic SAT change in austral summer for 1979–2014.

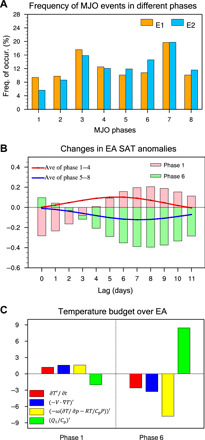
(A) Frequency (%) of active MJO days for each MJO phase in the austral summer (DJF) of 1979–1996 (E1; orange bars) and 1997–2014 (E2; blue bars). (B) Evolution of 10- to 90-day bandpass-filtered SAT anomalies (K) over East Antarctica (EA; 30°W to 150°E, 66.5° to 90°S) as a function of lag days after the occurrence of MJO phase 1 (pink bars) and phase 6 (green bars). The superposed is the average of MJO phases 1 to 4 (red curve) and that of phases 5 to 8 (blue curve), respectively. (C) Ten- to 90-day SAT budget terms in EA integrated over days 3 to 11 after the occurrence of MJO phase 1 (left) and phase 6 (right). Red, blue, yellow, and green bars represent the temperature tendency (10⁻⁷ K s⁻¹), the effects of horizontal advection, vertical adiabatic heating, and diabatic heating, respectively. An active MJO day is defined when the amplitude of the RMM index is greater than 1.5.

Diagnosis of temperature budget terms (see Materials and Methods) helps to elucidate the key processes responsible for the East Antarctic SAT changes (Fig. 2C). MJO phase 1 (6) induces a positive (negative) SAT tendency (∂T′/∂t), indicating a warming (cooling) tendency from lag +3 to +11 days. Both horizontal advection [(−V ∙ ∇T)′] and adiabatic heating [(−ωσ)′] associated with anomalous large-scale circulations account for the anomalous SAT tendency. After 3 to 11 days of MJO phase 1 (6), when the convective heating anomaly appears over the tropical Indian Ocean (western Pacific), a subsidence (ascent) anomaly associated with a positive (negative) anomaly of geopotential height at 500 hPa (H500) over East Antarctica, as shown in Fig. 3 (A and D), contributes to the adiabatic heating (cooling). Near the surface, the anomalous warm (cold) advection (Fig. 2C and fig. S6, A and B) is caused mainly by the interaction between the mean flow and perturbation temperature anomalies (fig. S6, C and D).

Fig. 3. Responses of large-scale circulation to tropical heating anomalies associated with MJO.

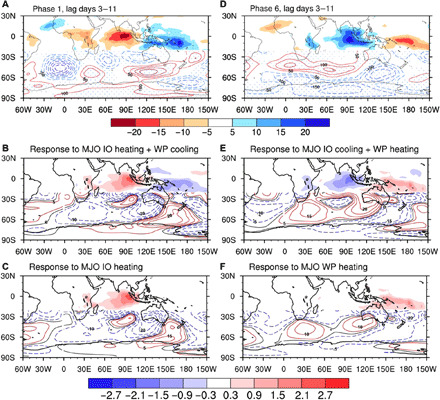
Observed 10- to 90-day bandpass-filtered perturbations of NOAA OLR (shading; W m⁻²) and 500-hPa geopotential height (contour; m) averaged over days 3 to 11 after the occurrence of MJO (A) phase 1 and (D) phase 6. (B, C, E, and F) Simulated 500-hPa geopotential height (contour; m) in an AGCM forced by mid-tropospheric heating anomalies (shading; K day⁻¹): (B) MJO phase 1–like heating over the Indian Ocean and cooling over the western Pacific, (C) MJO phase 1–like heating over the Indian Ocean only, (E) MJO phase 6–like cooling over the Indian Ocean and heating over the western Pacific, and (F) MJO phase 6–like heating over the western Pacific only. The heating and cooling fields represent the intraseasonal diabatic heating term in the temperature budget equation averaged over MJO phases 1 to 4 for (B) and (C) and phases 5 to 8 for (E) and (F). Stippling in (A) and (D) indicates the regions with statistically significant changes in circulation at the 5% significance level relative to the climatological state.

The results above indicate that during E2 the occurrence of MJO convection was less frequent in the Indian Ocean but more frequent in the western Pacific, which led to more frequent occurrence of intraseasonal cooling and hence contributed to the cooling trend over East Antarctica. Note that although the East Antarctic cooling leveled off slightly after 2014 (fig. S7A), the decadal changes in the MJO (fig. S7, B, C, and F) and their influences on the East Antarctic cooling were still evident when we extended the study period to 1979–2018 (fig. S7, D and E).

Model response to tropical MJO forcing during austral summer

To support the finding that the anomalous circulations over Antarctica are forced by the convective heating associated with the equatorial MJO, we performed numerical experiments using an atmospheric general circulation model (AGCM) forced by anomalous heating that mimicked the climatological MJO heating over the tropical Indian Ocean and western Pacific (see Materials and Methods). The MJO-related heating was maximized around 80°E and 160°E, over which the heating sources and background winds are effective in driving the extratropical circulation anomalies (23). The model shows a well-organized wave train response to the equatorial heating dipoles (Fig. 3, B and E), similar to observations (Fig. 3, A and D). The high-pressure (low-pressure) anomaly over East Antarctica remains clear when only a positive heating is prescribed over the equatorial Indian Ocean (western Pacific), as shown in Fig. 3 (C and F). This indicates that the high-latitude circulation anomalies that affect the SAT change over East Antarctica can be induced by the equatorial heating anomalies, consistent with previous findings regarding low- and high-latitude teleconnection (17–19). The underestimate of simulated circulation anomalies may be ascribed to the lack of dynamic feedbacks from transient eddies and the interaction between mean state and perturbations in the model.

The results of the AGCM experiment forced by climatological heating and mean states (Fig. 3) explain the effect of MJO frequency change on the East Antarctic cooling (the second term on the right-hand side of Eq. 1 in Materials and Methods). To unravel the relative effects of decadal differences (E1 versus E2) in MJO intensity and mean state, all of which can modulate the MJO-related SAT (the first term on the right-hand side of Eq. 1), we conducted additional experiments by prescribing one of the fields for E1 and E2, respectively, but keeping the other fields using the climatological mean values (Materials and Methods). We found that all the decadal changes in MJO intensity, mean winds, and mean temperature (related to background static stability) contributed to the changes in MJO-related teleconnection and the subsequent SAT cooling over East Antarctica (fig. S8).

The prescribed heating in the AGCM does not vary with time. To further confirm that the contributions of tropical MJO to the East Antarctic SAT changes, we conducted a suite of coupled GCM experiments in which the subseasonal signals were either retained or removed (see Materials and Methods). In the 70-year free-running simulation, referred to as the control experiment, the coupled GCM shows good skill in capturing the intraseasonal variability over the tropics (Fig. 4B). The eastward-propagating MJO signals with a periodicity of around 20 to 90 days are identified in the coupled model (Fig. 4B), similar to the observed (Fig. 4A). Although the model tends to overestimate the MJO amplitude, the geographical distribution of the intraseasonal variability in the control experiment (Fig. 4E) resembles that in the observation (Fig. 4D). To identify the active MJO days over the Indian Ocean and western Pacific, as in the observational analysis, the 20- to 90-day outgoing longwave radiation (OLR) and 200- and 850-hPa zonal winds in the control experiment are subjected to a multivariate empirical orthogonal function analysis. Then, the eight phases of the MJO life cycle were constructed (right panels in fig. S3). Note that the coupled model simulates reasonably well the observed MJO-Antarctica teleconnection, with a high-pressure (low-pressure) anomaly over Antarctica after the occurrence of Indian Ocean (western Pacific) MJO convection (fig. S9), giving us confidence in the model results.

Fig. 4. Sensitivity experiments of coupled GCM for verifying MJO effects on East Antarctic SAT changes.

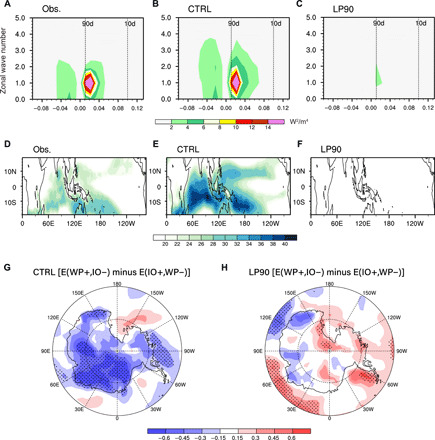
(A to C) Frequency–wave number analysis of austral summer OLR (W² m⁻⁴) over the tropical Indian Ocean and western Pacific (50°E to 160°W, 10°S to 10°N) derived from (A) observed NOAA OLR data in 1979–2014 and 70-year simulations of (B) free-running control experiment (CTRL) and (C) sensitivity experiment (LP90), in which MJO-related variability is suppressed by nudging the prognostic variables toward 90-day lowpass-filtered components in the CTRL. (D to F) SDs of 10- to 90-day filtered OLR (W m⁻²) from (D) NOAA OLR observation, (E) control experiment (CTRL), and (F) sensitivity experiment (LP90). (G and H) Differences in austral summer Antarctic SAT (K) between the decades with frequency of MJO days increased in western Pacific but decreased in Indian Ocean [E(WP+,IO−)] and the decades with the opposite MJO activity condition [E(IO+,WP−)] in (G) control experiment (CTRL) and (H) sensitivity experiment (LP90). Stippling marks the region with statistically significant SAT changes at the 99% confidence level.

To mimic the MJO conditions in E1 (E2), we selected 17-year-running windows in which the frequency of active MJO convection in the Indian Ocean is increased (decreased) but that in the western Pacific is decreased (increased), from the 70-year control experiment. There were seven cases similar to the observed E1 [i.e., increased/decreased strong-MJO events over the Indian Ocean/western Pacific in a 17-year window, referred to as E(IO+,WP−)] and three cases resembling E2 [i.e., increased/decreased strong-MJO events over the western Pacific/Indian Ocean in a 17-year window, represented by E(WP+,IO−)]. The difference in simulated Antarctic SAT between the two conditions [E(WP+,IO−) minus E(IO+,WP−)] shows the East Antarctic cooling (Fig. 4G), consistent with the observation (Fig. 1C). To ensure the robustness of the MJO–Antarctic SAT teleconnection, we repeated the same analysis using more cases like the observed E1/E2 in a 200-year control experiment (33 cases were identified) using the same coupled model. The East Antarctic cooling is still clearly seen when the western Pacific MJO convection occurs more frequently than the Indian Ocean MJO convection (fig. S10A). We repeated the same analysis using large samples of preindustrial (PI) simulations from the CMIP6 (Coupled Model Intercomparison Project Phase 6) models (see Materials and Methods) that show good capability in representing the tropical MJO variability and related teleconnection patterns (fig. S10B), and found a consistent result as revealed by the Geophysical Fluid Dynamics Laboratory (GFDL)–coupled GCM (fig. S10C). These model results of the control and PI experiments confirm that the linkage between equatorial MJO activities and Antarctic SAT changes at multidecadal time scales.

The sensitivity experiment (EXP_LP90), with the prognostic variables nudged toward the 90-day lowpass-filtered components derived from the control experiment, shows the effect of artificially removing MJO-related variability from the model integrations (Fig. 4, C and F). The composite analysis of the Antarctic SAT anomaly in EXP_LP90 using the same E(IO+,WP−)/E(WP+,IO−) (17-year window) periods identified from the control run clearly shows that the signals related to the East Antarctic cooling largely disappeared in the absence of MJO convection (Fig. 4H). The model results provide evidence of the MJO effect on the East Antarctic cooling and support the observational finding, namely, the more (less) frequent occurrence of western Pacific (Indian Ocean) MJO convection anomalies contributed to the East Antarctic cooling during austral summer in the recent decades of the study period.

DISCUSSION

This study provides evidence that decadal changes in MJO convection can contribute to East Antarctic cooling during austral summer. Our observational analysis first indicates that the MJO convection over the equatorial Indian Ocean (western Pacific) centered around 80°E (160°E) warms (cools) East Antarctica through the adiabatic warming (cooling) and thermal warm (cold) advection associated with tropically forced Rossby wave trains. We further reveal that the occurrence of MJO convection has been significantly decreased over the Indian Ocean but considerably increased over the western Pacific; together, they contributed to the East Antarctic cooling trend. We estimate that the MJO-induced SAT change can account for 20 to 40% of the East Antarctic cooling trend from 1979 to 2014. An idealized AGCM experiment supports the MJO forcing of Antarctic surface temperature changes. The linkage between MJO heating anomalies and East Antarctic cooling on decadal time scales is also supported by the long-term simulations of CMIP6 PI runs. Last, we show that the modulation by the decadal changes in the MJO disappears when the MJO is suppressed in coupled climate model simulations.

In a warmer climate, most of the models have predicted that the MJO convection will strengthen and propagate further eastward in the equatorial Pacific, while a few models simulate the opposite or weak responses to anthropogenic warming (24–26). Together with this projection, our results imply that the intensified MJO convection over the western Pacific is likely to accelerate the cooling over East Antarctica in the future, although this effect would be superimposed on other radiatively forced temperature changes. These findings underscore that the changes in frequency of intraseasonally varying tropical climate patterns may result in significant decadal-to-multidecadal remote climate changes, particularly in the polar regions.

The conclusions of this study also infer that, for a coupled GCM or an Earth system model, a realistic representation of tropical variability such as the MJO and its teleconnection is important for simulating and predicting the Antarctic climate change. Using the historical simulation data from 30 CMIP6 models, our preliminary assessments show that most of the models reproduce neither the summer cooling trend over East Antarctica nor the decadal changes in MJO heating feature over the Indian Ocean and western Pacific observed in the recent decades. Future studies should investigate whether the observed changes are internally generated or radiatively forced and to what extent the uncertainty in the simulated Antarctic SAT change can be ascribed to the biases of MJO simulation (and other remote and local processes) at the multidecadal time scale.

MATERIALS AND METHODS

Observational data

The monthly mean SAT data from Antarctic stations provided by the British Antarctic Survey Reference Antarctic Data for Environmental Research (READER) project (27) were used to analyze the SAT trend. For better understanding of the geographical distributions of Antarctic SAT changes, we used the Antarctic SAT reconstruction based on three reanalysis datasets (7) and the reanalysis from ERA-I (21), which shows higher reliability over the Antarctic area (28) compared to other reanalysis datasets (MERRA, NCEP-DOE, and JRA-55) (29–31). To diagnose the MJO-related effects on the East Antarctic SAT change, the long-term (1979 to 2014) daily near-surface temperature, surface pressure, wind field, vertical motion, and geopotential height were obtained from ERA-I. The MJO-related convection and heating patterns were analyzed using the OLR on 2.5° × 2.5° grid from the National Oceanic and Atmospheric Administration (NOAA) (32) and derived from the temperature budget equation using ERA-I, respectively.

Diagnostic methods

We used the real-time multivariate MJO (RMM) index (33) to describe the MJO activity over the equatorial regions. On the basis of this RMM index, the life cycle of equatorial MJO can be split into eight distinct phases: the initiation stage over the western Indian Ocean (phases 1 and 2), the mature phases in the eastern Indian Ocean (phases 3 and 4) and western Pacific (phases 5 and 6), and the weakened stage over the central-eastern Pacific (phases 7 and 8) (see fig. S2). The active MJO days were selected when the RMM amplitude was greater than 1.5. Other widely used MJO indices, such as the velocity potential MJO (VPM) index (34), OLR-based MJO index (OMI) (35), and original OLR MJO index (36), which were derived from only circulation or OLR alone, were also collected to confirm the robustness of epochal changes in the frequency of MJO convection occurrence measured by the RMM index.

To quantify the contributions of tropical MJO activity on the SAT changes over Antarctica, we used the diagnostic method proposed by Yoo et al. (19). The MJO-induced SAT trend at the decadal time scale (decadal difference) (the terms on the left-hand side of Eq. 1) can be retrieved from the combined effects of intraseasonal SAT variation associated with the MJO and MJO occurrence frequency. Thus, the decadal changes in all the intraseasonal SAT associated with the MJO (the first term on the right-hand side of Eq. 1), the frequency of MJO occurrence (the second term on the right-hand side of Eq. 1)), and their nonlinear effect (the third term on the right-hand side of Eq. 1) may lead to MJO-related SAT changes. The SAT changes for different lag (τ) days’ response to the occurrence of MJO events in different RMM phases (i) can be formulated as follows

$$\begin{array}{c}{\displaystyle \sum _{\mathit{i}=1}^8}{\mathit{T}}_{2,\mathit{i}}^{\prime }(\mathrm{\tau })\times {\mathit{N}}_{2,\mathit{i}}-{\displaystyle \sum _{\mathit{i}=1}^8}{\mathit{T}}_{1,\mathit{i}}^{\prime }(\mathrm{\tau })\times {\mathit{N}}_{1,\mathit{i}}=[{\displaystyle \sum _{\mathit{i}=1}^8}{\tilde{\mathit{T}}}_{2,\mathit{i}}^{\prime }(\mathrm{\tau })\times {\overline{\mathit{N}}}_{\mathit{i}}-{\displaystyle \sum _{\mathit{i}=1}^8}{\tilde{\mathit{T}}}_{1,\mathit{i}}^{\prime }(\mathrm{\tau })\times {\overline{\mathit{N}}}_{\mathit{i}}]\\ +[{\displaystyle \sum _{\mathit{i}=1}^8}{\overline{\mathit{T}}}_{\mathit{i}}^{\prime }(\mathrm{\tau })\times {\tilde{\mathit{N}}}_{2,\mathit{i}}-{\displaystyle \sum _{\mathit{i}=1}^8}{\overline{\mathit{T}}}_{\mathit{i}}^{\prime }(\mathrm{\tau })\times {\tilde{\mathit{N}}}_{1,\mathit{i}}]\\ +[{\displaystyle \sum _{\mathit{i}=1}^8}{\tilde{\mathit{T}}}_{2,\mathit{i}}^{\prime }(\mathrm{\tau })\times {\tilde{\mathit{N}}}_{2,\mathit{i}}-{\displaystyle \sum _{\mathit{i}=1}^8}{\tilde{\mathit{T}}}_{1,\mathit{i}}^{\prime }(\mathrm{\tau })\times {\tilde{\mathit{N}}}_{1,\mathit{i}}]\end{array}$$ (1)

where the prime means the intraseasonal (10- to 90-day) component, T is SAT, and the subscripts 1 and 2 denote the averages over the earlier epoch (E1; 1979–1996) and recent epoch (E2; 1997–2014), respectively. The overbar represents the climatological mean over the period 1979–2014, while a tilde is the deviation from the climatological mean state (i.e., $\tilde{\mathit{A}}=\mathit{A}-\overline{\mathit{A}}$). N is the occurrence frequency of active MJO events (RMM amplitude greater than 1.5). In this study, the Lanczos bandpass filter (36) was adopted to extract the intraseasonal (10- to 90-day) components.

To understand the physical processes responsible for the SAT changes, the temperature budget equation was diagnosed. The changes in temperature at each pressure level are controlled by the horizontal temperature advection, adiabatic process associated with vertical motion and statistic stability, and diabatic heating, which can be written as follows

$$\frac{\mathrm{\partial } \mathit{T}\prime }{\mathrm{\partial } \mathit{t}}=-(\mathbf{V}·\nabla \mathit{T})\prime +(\mathrm{\omega }\mathrm{\sigma })\prime +\frac{\mathit{Q}\prime }{{\mathit{C}}_{\mathrm{p}}}$$ (2)

where t is the time, V is the horizontal velocity vector, and ∇ is the horizontal gradient operator. σ represents the static stability (σ = ∂T/∂P − RT/C_pP), where R is the gas constant, P is the pressure, and C_p is the specific heat at constant pressure. Considering the topography of Antarctica, these SAT budget terms were calculated at the lowest layer above the surface pressure (P_s) level at individual grids.

To further understand the contributions of specific horizontal advection processes induced by different time scale components to the SAT change, air temperature and wind fields were decomposed into three components: the low-frequency background state with a period longer than 90 days (denoted by an overbar), the 10- to 90-day intraseasonal component (denoted by a prime), and the high-frequency component with a period less than 10 days (denoted by an asterisk). Thus, the intraseasonal temperature advection may come from various processes, such as the MJO–mean-flow interaction (the second and fourth terms on the right-hand side of Eq. 3), the eddy–mean-flow interaction (the third and seventh terms), the MJO-eddy interaction (the sixth and eighth terms), and/or the nonlinear MJO-MJO or eddy-eddy interaction (the fifth and last terms)

$$\begin{array}{c}-(\mathrm{V}·\nabla \mathit{T})\prime =-(\overline{\mathrm{V}}·\nabla \overline{\mathit{T}})\prime -(\overline{\mathrm{V}}·\nabla \mathit{T}\prime )\prime -(\overline{\mathrm{V}}·\nabla {\mathit{T}}^{*})\prime -(\mathrm{V}\prime ·\nabla \overline{\mathit{T}})\prime -(\mathrm{V}\prime ·\nabla \mathit{T}\prime )\prime \\ -(\mathrm{V}\prime ·\nabla {\mathit{T}}^{*})\prime -({\mathrm{V}}^{*}·\nabla \overline{\mathit{T}})\prime -({\mathrm{V}}^{*}·\nabla \mathit{T}\prime )\prime -({\mathrm{V}}^{*}·\nabla {\mathit{T}}^{*})\prime \end{array}$$ (3)

Experiments using an anomaly AGCM

The dynamical core of the GFDL AGCM (23), linearized by a three-dimensional climatological basic state, was used to investigate extratropical responses to tropical heating. The model was run at the resolution of triangular 42 (T42), with five levels in the sigma (= p/p_s) coordinate and biharmonic diffusion in the temperature and momentum equations. To mimic the planetary boundary layer, Rayleigh friction was applied to the lowest model level (sigma = 0.9), with a damping scale of 1 day⁻¹ that decayed linearly to 0.1 day⁻¹ at the level of sigma = 0.7. Newtonian cooling with an e-folding time scale of 10 days was applied to all levels in the temperature equation. For the climatological experiment, the basic mean states (zonal wind field, temperature, and surface pressure) in austral summer (DJF) were prescribed using the ERA-I fields averaged over 1979–2014. The geographical distributions of tropical heating associated with the MJO were constructed by the phase-composited diabatic heating derived from the temperature budget equation (Eq. 2).

To test the effects from each of MJO intensity, background wind, and static stability on the teleconnection at the decadal time scale, additional experiments were conducted by prescribing one of the fields for E1 and E2, respectively, but the other fields were prescribed by the climatological (1979–2014) states. For example, the differences in Antarctic circulation anomalies between simulations forced by the MJO states in E1 and E2 (but climatological mean states for the background fields) may explain the effect of MJO intensity. Likely, the comparison between the experiments prescribed by mean winds (temperature) in E1 and E2 and forced by climatological MJO thermal forcing could identify the role of wind (static stability) changes in teleconnection.

Experiments using GFDL coupled GCM

The AGCM introduced above was used to examine the extratropical response to equatorial heating, which mimicked the distribution of MJO convection, while its amplitude was invariant with time. To identify the influences of tropical heating at the subseasonal time scale on the SAT and circulation changes over Antarctica, we performed experiments using the GFDL Low Ocean Atmosphere Resolution (LOAR) version of Coupled Model 2.5 (37), which has high capability in simulating the MJO (38). The atmospheric component of the LOAR model has a C48 grid horizontal resolution (2° × 2°) with 32 vertical levels. The ocean model has 1° × 1° horizontal grid. With a focus on natural variability, the control experiment was integrated for 200 years with constant radiative forcing set at the 1990 level. Using the same radiative forcing, the sensitivity experiment was also integrated for 70 years but the model prognostic variables (e.g., u, v, q, and T) over the tropical regions (15°S to 15°N) were nudged toward their 90-day lowpass (LP90)–filtered components derived from the control experiment. In this case, the equatorial subseasonal variability with a periodicity shorter than 90 days was removed artificially, while other tropical variations with periodicities longer than 90 days were retained in the model. The sensitivity experiment is referred to as EXP_LP90. Comparing the large-scale circulation and SAT over East Antarctica simulated from the control experiment and EXP_LP90, we can verify the effects of tropical subseasonal heating on the atmospheric conditions in the high-latitude regions.

CMIP6 model outputs and assessments

The PI-control simulations of 13 coupled GCMs participated the CMIP6 (39), which provide long-term (>200-year) integration outputs with only the natural forcing (without anthropogenic influences), were used to support the linkage between the tropical intraseasonal variability and East Antarctic SAT changes at the decadal time scale. To select the models with reasonable MJO signals and associated teleconnection with East Antarctic SAT, the wave number–frequency analysis along with the ratio between the intraseasonal eastward- and westward-propagating powers (E/W ratio) (40) was analyzed. Moreover, the model skill in capturing the remote influences of MJO on East Antarctic SAT was also assessed by comparing the East Antarctic SAT tendency during lag 1 to 7 days of MJO phases 1 to 4 and 5 to 8 (Fig. 2B), respectively. Seven of the 13 models representing the basic features of MJO (E/W ratio ~ 2 to 2.5) and its teleconnection were selected to further examine the decadal relationship between MJO heating pattern and East Antarctic SAT trend. The selected models are able to capture decreases (increases) in the East Antarctic SAT after the occurrence of MJO heating over the western Pacific (Indian Ocean), as shown in fig. S10B. These models are as follows: CESM2, CESM2-FV2, CESM2-WACCM, CESM2-WACCM-FV2, EC-Earth3, EC-Earth3-AerChem, and TaiESM1.

The historical simulations (1980–2010) from 30 CMIP6 models were used to assess the uncertainty in East Antarctic summer cooling simulations and its association with the modeled MJO. The 30 models are ACCESS-CM2, ACCESS-ESM1-5, BCC-CSM2-MR, BCC-ESM1, CanESM5, CESM2, CESM2-FV2, CESM2-WACCM, CESM2-WACCM-FV2, CNRM-CM6-1, CNRM-CM6-1-HR, CNRM-ESM2-1, EC-Earth3-AerChem, EC-Earth3-Veg, EC-Earth3-Veg-LR, FGOALS-g3, GFDL-CM4, GISS-E2-1-G, HadGEM3-GC31-LL, HadGEM3-GC31-MM, INM-CM4-8, INM-CM5-0, IPSL-CM6A-LR, MIROC6, MIROC-ES2L, MPI-ESM1-2-HR, MRI-ESM2-0, NESM3, SAM0-UNICON, and UKESM1-0-LL.

For both the PI-control and historical simulations, daily OLR, 850- and 200-hPa zonal winds were used to obtain the MJO phase evolution and intensity, as in the observation based on multivariate empirical orthogonal function (EOF) analysis and RMM (33). Monthly 2-m temperature data were collected for trend analysis of Antarctic SAT, while daily SAT data were used to evaluate models’ capability in simulating the intraseasonal SAT variability modulated by MJO teleconnection. All the CMIP6 data were interpolated to a common grid of 2.5° × 2.5° resolution.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/7/26/eabf9903/DC1