Characterization and quantification of necrotic tissues and morphology in multicellular ovarian cancer tumor spheroids using optical coherence tomography

Abstract

The three-dimensional (3D) tumor spheroid model is a critical tool for high-throughput ovarian cancer research and anticancer drug development in vitro. However, the 3D structure prevents high-resolution imaging of the inner side of the spheroids. We aim to visualize and characterize 3D morphological and physiological information of the contact multicellular ovarian tumor spheroids growing over time. We intend to further evaluate the distinctive evolutions of the tumor spheroid and necrotic tissue volumes in different cell numbers and determine the most appropriate mathematical model for fitting the growth of tumor spheroids and necrotic tissues. A label-free and noninvasive swept-source optical coherence tomography (SS-OCT) imaging platform was applied to obtain two-dimensional (2D) and 3D morphologies of ovarian tumor spheroids over 18 days. Ovarian tumor spheroids of two different initial cell numbers (5,000- and 50,000- cells) were cultured and imaged (each day) over the time of growth in 18 days. Four mathematical models (Exponential-Linear, Gompertz, logistic, and Boltzmann) were employed to describe the growth kinetics of the tumor spheroids volume and necrotic tissues. Ovarian tumor spheroids have different growth curves with different initial cell numbers and their growths contain different stages with various growth rates over 18 days. The volumes of 50,000-cells spheroids and the corresponding necrotic tissues are larger than that of the 5,000-cells spheroids. The formation of necrotic tissue in 5,000-cells numbers is slower than that in the 50,000-cells ones. Moreover, the Boltzmann model exhibits the best fitting performance for the growth of tumor spheroids and necrotic tissues. Optical coherence tomography (OCT) can serve as a promising imaging modality to visualize and characterize morphological and physiological features of multicellular ovarian tumor spheroids. The Boltzmann model integrating with 3D OCT data of ovarian tumor spheroids provides great potential for high-throughput cancer research in vitro and aiding in drug development.

1. Introduction

Cell culture in vitro is a widely used tool to evaluate the biological performance of bioactive molecules, tissue morphology, drug action, protein production, and mechanism of diseases out of the living organism [1–3]. Recent developments in 3D cell culture indicates stronger similarities than monolayer cell cultures to in vivo conditions, therefore, offering promising platforms to study biological phenomena in vitro with high throughput. 3D tumor spheroids provide cell to cell as well as cell to extracellular matrix (ECM) interactions, which present similar cytoarchitecturally with in vivo tumors. The 3D tumor spheroid models have been developed to provide an immediate and long-lasting impact in shortening drug discovery and screening timelines, reducing costs of investment for bringing new anticancer medicines into the clinic [4–6]. Not only small drug, but also radiation and thermal therapies can be studied on spheroids, as they represent a more complex model than monolayers [7].

3D tumor spheroids composed of micro-size cellular aggregates have been broadly utilized to assemble models of different cancer types in vitro including breast [8–11], cervical [10,12], colon [13], lung [14,15], pancreas [16,17], and prostate [18–20]. These in vitro tumor spheroid models can mimic various feature of solid tumors: (i) Morphology and growth kinetics, which are critical factors for the quantitative assessment to predict cancer progression, recurrence, and metastasis [21,22]; (ii) Internal structure, including the formation of proliferative, senescence and necrotic zone due to absence of oxygen and nutrient transfer, which influences the therapeutic effects of drugs [23–26]; (iii) Mathematical modeling for growth kinetics, which can serve as personalized prognostic tools in the clinical application or potential therapies in preclinical drug development [27–29].

To study 3D tumor spheroids characteristics, fluorescence imaging techniques including confocal microscopy and multiphoton microscopy (MPM), are widely employed to characterize the morphology of tumor spheroids [30–34]. However, the limited penetration of light in tumor spheroids significantly hinders the understanding of the morphology and physiology of tumor spheroids. Additionally, light sheet fluorescence microscopy (LSFM) and single plane illumination microscopy (SPIM) are proposed as novel alternatives to provide a high-resolution 3D structural imaging of entire tumor spheroids [35–38]. Whereas these techniques require extensive steps for samples preparation including transferring, staining, mounting, and/or clearing of tumor spheroids, which impede longitudinal imaging and high-throughput screening [36].

Optical coherence tomography (OCT), as a well-established optical imaging modality, can obtain subsurface images of biological tissues noninvasively with a high-resolution and several millimeters penetration depth [39–44]. Compared to fluorescence imaging techniques, OCT detects backscattered signals and therefore does not require tissue labeling. In the field of tumor-detecting, OCT has been applied to recognize tumor margins ex vivo and analyze pathological characteristics of tumor lesions [45–49]. Additionally, OCT has also been utilized to detect the morphology, microenvironment, and vascular dynamics of tumors in vivo [50–52]. Previous studies showed OCT was able to detect 3D tumor spheroids and analyze the response and effectiveness of photodynamic therapy [53–55]. Recently, OCT was applied to obtain the volume of 3D glioblastoma and colorectal carcinoma tumor spheroids [56]. While the growth pattern of necrotic tissues within tumor spheroids has not been studied and growth kinetics of tumor spheroids has not been systematically described by mathematic models. Particularly, there was no study that reported the growth pattern of ovarian cancer tumor spheroids and the necrotic tissues within the spheroid. OVCAR-8 cells have been proposed as a representative model for high-grade serous ovarian cancer [57] and readily form spheroids that are drug resistant [58,59].

In this study, OCT was used to visualize and quantify the 3D structures of ovarian cancer tumor spheroids, and reconstruct necrotic regions within the tumor spheroids. Spheroids initiated with two different cell numbers (5,000 cells and 50,000 cells) were visualized for 18 days. Four different mathematical models were applied to describe the growth of tumor spheroid and the necrotic regions. The performance of these four different models was further evaluated using Akaike’s information criterion (AIC) and the root mean square error (RMSE). Our results demonstrated that OCT was a promising imaging modality for characterization and quantification of multicellular ovarian tumor spheroid in morphology, growth kinetics, and the formation of the necrotic core.

2. Materials and methods

2.1. Cell culture

Epithelial ovarian cancer cell line OVCAR-8 (NCI-Vial Designation 0507715) was cultured in a humidified incubator at 37 °C supplied with 5% CO₂. Cell line authentication and mycoplasma testing were performed by the University of Arizona, Genetics Core. OVCAR-8 cells were cultured in Roswell Park Memorial Institute (RPMI) media (SIGMA R8758) supplemented with 10% FBS (Hyclone SH30910.03) and 1% antibiotics, penicillin (100 U/mL), and streptomycin (100 µg/mL) (Thermo Fisher 15240062) according to the manufacturer’s instructions. T75 flask (TPP 90076) was used for culturing the cells and cells were passaged by using trypsin (Sigma 59418C) upon 85% confluency. The media was changed every two days.

2.2. Spheroid formation

Spheroid formation was induced by the ultra-low attachment technique as described before [58,59]. Briefly, round-bottom 96-well plates (CELLTREAT 229590) were treated with anti-adherence rinsing solution (STEMCELL 07010) by centrifuging the plates 1300 g for 5 min. The solution was aspirated, and wells were washed with the basal medium. OVCAR-8 cells were seeded in 200 mL of media containing either 5000 cells/well or 50000 cells/well and centrifuged at 100 g for 3 min. After 2 days of culture, 100 mL of medium was replaced with fresh medium every day for a total of 18 days.

2.3. OCT imaging system

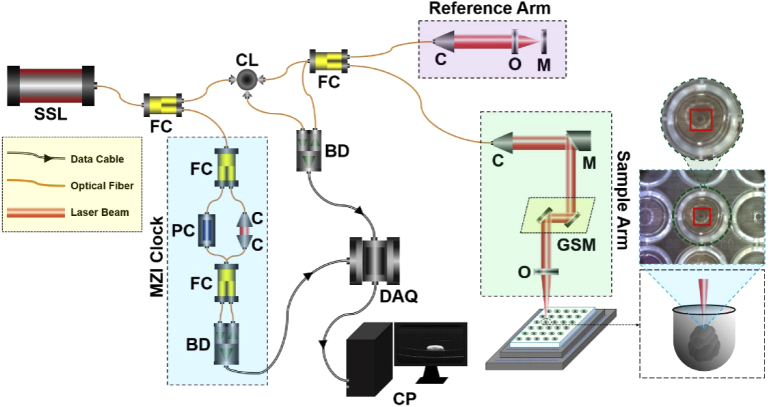
The swept-source optical coherence tomography (SS-OCT) system was applied for 3D tumor spheroid imaging (Fig. 1). A wavelength-swept laser was used as the light source with a central wavelength of 1310 nm and a broadband spectrum of 100 nm full-width at half-maximum (FWHM). The system had a 200 kHz wavelength-swept frequency with 25 mW average output power [60–63]. In this system, 97% of the laser output power was equally divided into the sample and reference arms of an OCT Michaelson interferometer and 3% of the output was distributed to a Mach-Zehnder interferometer (MZI) with a fixed difference to trigger the data acquisition board (DAQ) through generating a frequency-clock signal [60,63,64]. In the sample arm, the light was collimated and steered by a pair of galvanometer scanning mirrors (GSM, X by Y), and then focused on a 96-well plate through an objective lens to scan tumor spheroid samples. Afterward, the reference signal and the signal reflected from the sample arm interfered at the fiber coupler (FC) to form the interference fringes which was then recorded via a balanced photodetector (BD). The interference fringes from different depths were encoded according to the different optical frequencies. Finally, the fast Fourier transform (FFT) was employed on the interference fringes to generate the depth-resolved tomographic profiles. This system provided approximately a maximum depth detection field of ∼8.0 mm in the air and ∼6.0 mm in tissue. The axial and lateral resolutions of the SS-OCT system were approximate ∼10 µm and ∼12 µm respectively in tissues with a refractive index of tumor spheroids of 1.37 [55,65].

Fig. 1.

Schematic of the SS-OCT system for 3D imaging of tumor spheroids. SSL, swept-source laser. FC, fiber coupler. CL, circulator, DAQ, data acquisition board. BD, balance photodetector. PC, polarization controller. MZI, Mach-Zehnder interferometer. C, collimator. CP, computer. O, optical lens. M, mirror. GSM, galvanometer scanning mirror. The red square indicates the area our OCT system scanned for each tumor spheroid at each well.

2.4. OCT image acquisition and processing

The 3D OCT images of ovarian tumor spheroids were acquired from ∼1 to ∼18 days after the spheroid initiation of both cell lines. 10 tumor spheroids were imaged each day from OVCAR-8 spheroids at the same time point (24 h). During the imaging process, the OCT scanning range was fixed at a specific imaging field of 2.0 × 2.0 × 6.0 mm³ (X by Y by Z) with 3.0 × 3.0 × 6.25 µm³ (X by Y by Z) pixel size to cover the entire tumor spheroid. The 3D dataset of each tumor spheroid was acquired in ∼1.2 seconds.

2.5. Tumor spheroid histology

Tumor spheroids (n=3) at fixed time points (∼5d, ∼7d, ∼10d) were processed for histology to compare with corresponding OCT results. Spheroids were washed in PBS and fixed with 4% PFA then paraffin embedded. Sections with 4 µm were taken and stained with hematoxylin and eosin (H & E). Images were taken by Keyence Microscope BZ-X800. Sectioning and H & E staining is carried out by Tissue Pathology Shared Resource, Stephenson Cancer Center (SCC), University of Oklahoma Health Sciences Center. The Hematoxylin (cat#3801571) and Eosin (cat#3801616) were purchased from Leica biosystems and the staining was performed utilizing Leica ST5020 Automated Multistainer following the Hematoxylin-Eosin (HE) staining protocol at the SCC Tissue Pathology core.

2.6. Volumetric quantification of 3D tumor spheroids

The conventional diameter-based measurements of tumor volumes were calculated as $\pi d^3/6$ and $\pi w^{2}l/6$ [54]. Here d was the lateral-diameter, which was the average diameter of the tumor spheroid in X and Y directions in the en face OCT images (XY); w was the smallest diameter and l was the largest diameter in the axial- and lateral-diameter of the tumor spheroid. Axial-diameter was the average diameter of the tumor spheroid in-depth directions in two cross-sectional OCT images (XZ and YZ). A voxel-counting method was used in this study. Firstly, a mean filter (with a 7 × 7 kernel size) was employed to remove speckles within tumor spheroids in OCT images. Secondly, OCT images were segmented frame by frame along XZ image planes. Then, an automatic image processing method was utilized in each frame of OCT images (Section 2.7). Finally, the number of voxels within tumor regions was summed and the total volume of the spheroid was yielded via multiplying the actual volume of each individual voxel. All the imaging processing was carried out using MATLAB R2020b (Mathworks, Inc., Natick, MA, USA) software.

2.7. Automatic image processing and calculating

Figure 2 shows a flow chart and schematic diagram of this image processing procedure. First, the regions of interest (ROIs) were cropped automatically using an interactive cropping tool for each tumor spheroid. The ROIs were selected based on the largest area the tumor spheroid occupied in all the 2D OCT images (i.e., the cross-sectional image which contains the spherical center of the tumor spheroid). Second, a Sobel operator filter was used to identify the edge of the tumor regions. Third, a disk-shaped structuring element was utilized to dilate the areas which were recognized by edge detection. Next, the areas were filled to obtain the actual region of tumor spheroids. Finally, a spherical structuring element was used to smooth the border of the spheroid.

Fig. 2.

Flow chart of image processing method. ROI Selection was achieved by an interactive cropping tool. Edge Detection was implemented with a threshold of 0.07. Dilation was achieved using disk-shaped structuring element (radius-3, lines to create the disk-8). Filling was applied using “holes” function. Erosion was achieved using spherical structuring element (radius-3).

To figure out the parameters for the algorithm, four manually traced images were taken as gold standards to compare with the segmented images through Sørensen–Dice coefficient calculations. The Sørensen–Dice coefficient is mostly used in image segmentation, and this value represents the similarity between ground truth and segmented images. The parameters for the automatic image processing algorithm were selected by comparing the Sørensen–Dice coefficient from different combination of edge detection thresholds and morphological operations. The following values for sensitivity (edge detection threshold) were tested: 0.04, 0.05, 0.06, 0.07, 0.08, and 0.09. With regards to morphological operations application, methods with only dilation and methods with a combination of dilation and erosion were tested. For these operations, two structuring elements were used: disk structuring element and spherical structuring element. Table 1 shows the Dice coefficients after using a specific combination of edge detection threshold and morphological operation sequence. Application of 0.07 edge detection sensitivity while dilating and eroding the images with spherical structuring element resulted in the best Dice coefficient, 0.9449, and therefore, these parameters were further applied to the rest of the images.

Table 1. Dice coefficients after difference combination of edge detection threshold and morphological operations sequence.

	0.04	0.05	0.06	0.07	0.08	0.09
S	0.9118	0.9293	0.9340	0.9359	0.9375	0.9354
D	0.9174	0.9326	0.9365	0.9381	0.9386	0.9174
S-D	0.9393	0.9435	0.9445	0.9447	0.9432	0.9352
D-S	0.9433	0.9447	0.9448	0.9443	0.9400	0.8873
D-D	0.9402	0.9436	0.9444	0.9442	0.9408	0.8931
S-S	0.9408	0.9441	0.9448	0.9449	0.9429	0.9342

2.8. Necrotic tissue detection in 3D tumor spheroid

To identify the necrotic region of 3D tumor spheroids, the intrinsic optical attenuation measurement was used to recognize the necrotic tissues. The OCT intensity that originated from the backscattering signals at different depth could be described by the Beer-Lambert law as:

$$I_{(z)}=I_0{e}^{-2\mu z}$$

where, z was the depth in tumor spheroid sample, $\mu$ was the attenuation coefficient of intensity, and $I_0$ was the light intensity at the sample surface [66–69]. Logarithmic scale was commonly utilized to increase the image contrast in OCT images, thus the intrinsic optical attenuation coefficient could be derived through calculating the derivative of the logarithmic equation in OCT intensity signal as:

$$\mu =-\frac{1}{2}\cdot \frac{d\log I_{(z/0)}}{dz}$$

here, $I_{(z/0)}$ was the relative ratio of recorded OCT intensity to incident light intensity. The intrinsic optical attenuation coefficient at each voxel was calculated according to the slope of OCT intensity profile in a 10-pixel depth window (∼60 µm in-depth) [56].

2.9. Description of mathematical models

Four mathematical models (the exponential-linear model, Gompertz model, Logistic model, Boltzmann model) were employed to describe the growth kinetics of 3D tumor spheroids and necrotic tissues. For all the models, the volume of 3D tumor spheroids or necrotic tissues was expressed as the descriptive variable V, versus a function of time t.

The exponential-linear model is associated with many species that can potentially increase or decrease in a number of populations according to a geometric series [70]. This model of tumor growth presumes all tumor cells proliferate with a constant instantaneous rate of natural increase at specific time stages. The exponential growth of tumor cells is expressed by either a constant fraction with which the volume is proliferating, or an exponential change of the tumor volume, which is described as,

$$\{\begin{array}{c}\frac{dV}{dt}=(\alpha -\beta )V=a_{0}V,t\le \tau \\ \frac{dV}{dt}=a_1,t>\tau \end{array}$$

where, $a_0$ is the reproduce rate of tumor cells determined by the birth rate $\alpha$ and the death rate $\beta$ of tumor cells. The value of $\tau$ is determined by the reproduce rate $a_0$ and the linear phase $a_1$ as follows:

$$\tau =\frac{1}{a_0}\log \left(\frac{a_1}{a_0{V}_0}\right)$$

here, the coefficient $V_0$ is the initial volume of tumor spheroids [70,71].

The logistic model defines that the rate of population increase is limited by the population density called carrying capacity [72]. Generally, a class of models for quantification of tumor growth kinetics has a sigmoid curve. The dynamics of the population increase can be described by the differential equation as,

$$\frac{dV}{dt}=a_{0}V\left(1-\frac{V}{K}\right)$$

where, $a_0$ is the coefficient of proliferation kinetics, K is the carrying capacity that is an inflection point which asymptotically converges to the maximum volume in a growth curve [72–74].

The Gompertz model is used to describe the growth of the population as being slowest at the start and end-stage of a given time period in a sigmoid function, which is frequently employed to describe the number and volume of bacteria and cancer cells [75,76]. In the Gompertz model, the key characteristic is to exhibit the exponential decay of relative growth rate, and the defined formula can be derived as,

$$\frac{dV}{dt}=\alpha e^{-\beta t}V$$

where, $\alpha$ and $\beta$ are the birth rate and the death rate of tumor cells, respectively [75–77].

The Boltzmann model is proposed to exhibit the general growth from basic energetic principles [78]. This model emphasizes that the net growth rate is the result of the balance of synthesis and death within three distinct stages of the growth process, which assumes that the rate of growth of the tumor firstly increases, and subsequently declines with its size so that the rate of growth in tumor volume keeps dynamic changes. The differential formula of this model for the growth of biological process is defined as,

$$V=K+\frac{A_0-K}{1+e^{\frac{(t-t_0)}{\alpha }}}$$

where, $A_0$ is the initial tumor volume, $\text{K}$ is the maximum volume in a growth curve which presents the inflection point, $t_0$ is defined by $dA(t_0)/dt=0$ which is the time constant located in the inflection point [78].

2.10. Statistical analysis

To compare voxel-counting volumes with conventional diameter-based volumes, the paired student t-test was performed at each time point (day). A P-value of < 0.05 was employed to indicate the statistical significance between the paired measurements in voxel-counting and diameter-based volume calculations. Moreover, to validate the accuracy of automatic recognition of 3D tumor volume by our algorithm, a statistical analysis, based on the statistics of mean absolute error (MAE), Sørensen-Dice similarity coefficient, and Cohen’s Kappa coefficient in ROIs, was used to compare the difference between automatic and manual recognitions. MAE was used to measure the error between paired observations expressing the same objectives in statistics (the lower value presents the smaller error). The Sørensen-Dice similarity coefficient scores were calculated to demonstrate the degree of agreement. A Dice-score of 0 indicated there was no agreement and a Dice-score of 1 presented a perfect agreement. The Cohen’s Kappa coefficient was used to measure inter-rater reliability for qualitative items. A score is closer to 1 expresses a more robust agreement. In the fitting of growth kinetics of 3D tumor spheroids and necrotic tissues using the mathematical models, root mean square error (RMSE) and Akaike information criteria (AIC) were applied to estimate the out-of-sample prediction error and measure the difference between values predicted by models and the experimental results.

3. Results

3.1. Comparison of automatic and manual measurements

To verify the performance of the automatic and manual measurements, the intra-rater reproducibility was firstly calculated between each rater’s measurements. Each of the four raters was asked to label 3 OCT cross-sectional images twice. Our results in Table S1 showed these four raters achieved high degree of similarity among the two measurements.

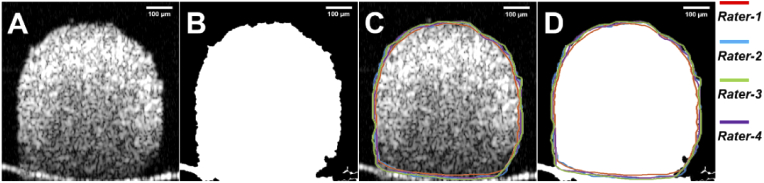
The performance of the automatic versus 4 manual measurements in OCT cross-sectional images were shown in Fig. 3. Compared to manual measurements, automatic measurement presented a MAE of 35593.4 ± 20766.6 µm² (Fig. 3(D)). A Dice-score of 0.94 ± 0.01 was achieved between automatically measured and manually measured tumor spheroid regions (Fig. 3(D)). The range of the Cohen’s Kappa coefficient was from 0.97 to 0.99 in scores. When only assessing images with at least moderate density of >0.5%, the Cohen’s Kappa coefficient improved further to a range between 0.98 and 0.99.

Fig. 3.

Automatic and manual measurements in cross-sectional OCT image. (A) Original cross-sectional OCT images. (B) Automatic processed OCT cross-sectional image. (C) Original OCT cross-sectional image following measurement by 4 manual raters. (D) Superimposition of the same OCT cross-sectional image from automatic measurement and 4 manual raters. The quantifiable tumor region boundary from the automatic algorithm was represented in white signal area and was indicated in red, blue, green, and purple profiles from 4 manual raters, respectively.

3.2. Volumetric changes of tumor spheroids

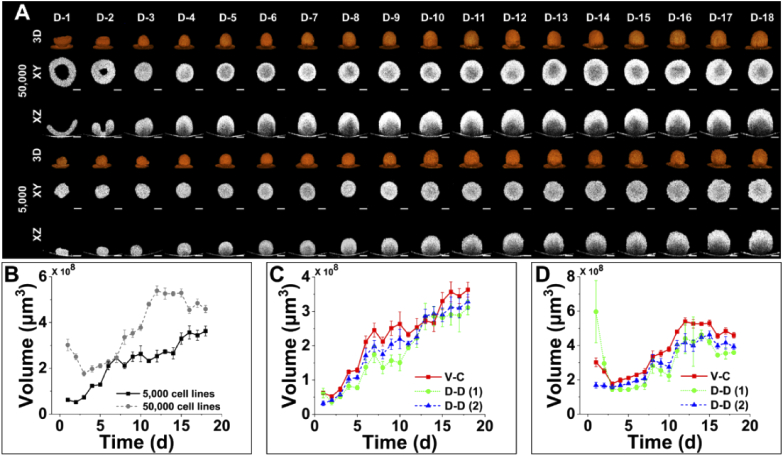
OCT was employed to image the tumor spheroids of OVCAR-8 cell lines with 5,000 and 50,000 initial cells over 18 days. Figure 4(A) showed the development of 5,000- and 50,000-cells OVCAR-8 tumor spheroids in en face (XY), cross-sectional (XZ), and 3D rendered images over 18 days, which was used to exhibit the growth dynamics of the samples. In the tumor spheroid, the length was defined as the diameter along horizontal direction in en face OCT images, the width was defined as the diameter along vertical direction in en face OCT images, and the height was defined as the diameter along vertical direction in cross-sectional (XZ) OCT images. Starting from day 3, the 5,000- and 50,000-cells OVCAR-8 spheroids kept a tightly stacked spherical shape throughout the 18 days of growth and development. The tilting substrates of OCT images of 5,000-cells spheroid on day 1 and day 2, and 50,000-cells spheroid on day 1 to day 3, were caused by rotating the petri dish for minimizing reflection.

Fig. 4.

Quantitative and morphological analyses of growth kinetics of 3D tumor spheroids (5,000- and 50,000-cells) size and volume measured with OCT over 18 days. (A) 3D and 2D OCT images of tumor spheroid growth over 18 days. Sequential 3D rendered, en face (XY), and cross-sectional (XZ) images to illustrate the structural changes of tumor spheroids over time. Scale bars: 100 µm. (B) Growth curve of tumor spheroid volume in 5,000- and 50,000-cells over 18 days (N=10). (C) Comparison of growth curves of 5,000-cells spheroid volumes between voxel-counting and two diameter-based methods. (D) Comparison of growth curves of 50,000-cells spheroid volumes between voxel-counting and two diameter-based methods. V-C, voxel-counting, D-D, (1) diameter-based ($\pi d^3$), D-D, (2) diameter-based ($\pi w^{2}l$).

From Fig. 4(A) and Table S2, 50,000 OVCAR-8 cells formed an irregular bowl-shape structure with the volume of 3.02×10⁸ µm³ (with length of 1005 µm, width of 978 µm, and height of 593 µm) on day 1. The shape of the tumor became a regular spheroid on day 3, with volume, length, and width decreased to 1.77×10⁸ µm³, 642 µm, and 678 µm, respectively. But the height increased to 725 µm. Then, the spheroid continued to grow and formed the largest spheroid structure with the volume of 5.39×10⁸ µm³ volume (with 975 µm in length, 975 µm in width, and 931 µm in height) on day 12. Afterward, the volume of tumor spheroid started to decline and eventually reached a volume of 4.59×10⁸ µm³ (with length of 861 µm, width of 897 µm, and height of 925 µm) on day 18. Similar results and changing tendency were observed in all 50,000-cell tumor spheroids investigated in this study. For the 5,000 OVCAR-8 cells tumor spheroid, it gathered to form an irregular volumetric shape with the volume of 6.24×10⁷ µm³ (with length of 487 µm, width of 485 µm, height of 337 µm) on the first day. The tumor shape became a regular spheroid on day 2, and the volume decreased to 5.21×10⁷µm³ (with length of 440 µm, width of 378 µm, and height of 464 µm). After that, the tumor spheroid kept fast-growing and reached 3.57×10⁸ µm³ in volume (with 837 µm in length, 828 µm in width, and 831 µm in height) on day 16. Afterward, the spheroid volume experienced no significant changes till day 18 with a volume of 3.63×10⁸ µm³ (with length of 882 µm, width of 858 µm, and height of 872 µm). All the 5,000-cells OVCAR-8 tumor spheroids kept the similar change tendency in volume, length, width, and height over 18 days.

As shown in Fig. 4(B), the growth kinetics of 5,000- and 50,000-cells OVCAR-8 spheroids were quantitatively measured using the voxel-counting method. The 5,000-cell line spheroids had a decrease of average volume at the first two days and started to quickly grow from day 3 to day 7, after which growth slowed down till day 14. Then, the average volume of tumor spheroids resumed a fast growth till day 16 but kept no significant change from day 15 to day 18. The average volume of 5,000-cells spheroids had an ∼7 times increase from day 2 to day 18. For the 50,000-cells spheroids, it kept decreasing in the average volume in the first three days, and experienced a fast growth in volume till day 12. After day 12, the average volume of 50,000-cells spheroids kept stable and gradually decreased. On day 6 and day 7, 5,000- and 50,000-cells spheroids reached a similar volume, which might be due to the higher growth rate in the 5,000-cells spheroids between day 5 and day 7 compared to the 50,000-cells. The comparison of the average volumes calculated using the voxel-counting method and the two traditional diameter-based measurements was showed in Fig. 4(C), (D), and Table S2. For the 5,000-cells spheroids, the volumes derived from the diameter-based ($d^3$) method were significantly smaller than the volumes obtained using voxel-counting measurement except for day 6 and day 18 (Table S2). The diameter-based ($w^{2}l$) volumes were significantly smaller compared to the voxel-counting volumes except for day 6. For 50,000-cells spheroids, the volumes calculated using the diameter-based ($d^3$) method were significantly larger compared to the volumes obtained from the voxel-counting method on day 1 and day 2. But the diameter-based ($d^3$) volumes were significantly smaller than the voxel-counting volumes from day 3 to day 18 except for day 6 and day 7. In contrast, the volumes obtained using the diameter-based ($w^{2}l$) were significantly smaller than the volumes measured by the voxel-counting method over 18 days except for day 11. Particularly, there was a decrease of volumes based on both the conventional diameter-based methods from day 8 to day 10, but the volumes measured from the voxel-counting calculation kept an increasing trend. Overall, the volumes obtained from the traditional diameter-based measurements were significantly smaller than the voxel-counting volumes, which could be attributed to the irregular shape of the spheroid of 5,000- and 50,000-cells. Our results suggested that the voxel-counting volume based on 3D OCT data could provide more robust and accurate quantification of 3D tumor spheroids compared to the conventional diameter-based methods especially when the spheroids were not in regular shape.

3.3. Morphological identification and quantification of necrotic tissues

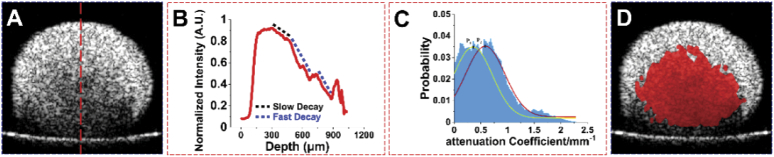
Figure 5 showed the detection of necrotic regions in 3D tumor spheroids based on intrinsic optical attenuation coefficient and the representative analysis of optical attenuation contrast of tumor spheroids. The intensity profile along the axial (depth) direction within tumor spheroids (red line in Fig. 5(A)) was plotted, as shown in Fig. 5(B) (example from the 50,000-cells OVCAR-8 spheroid on day 5). The intensity profile showed two distinct slopes (Fig. 5(B)), with a dashed black line marked the slow decay of intensity at the top portion of the tumor spheroid and dashed blue line marked the fast decay. The high attenuation regions (dashed blue line) and low attenuation regions (dashed black line) may indicate different tissue types, i.e. normal tumor spheroid and necrotic regions according to the previous studies [56].

Fig. 5.

Structural and quantitative analyses of the necrotic regions in tumor spheroids based on intrinsic optical attenuation coefficient contrast. (A) Cross-sectional OCT image from the 50,000-cells OVCAR-8 spheroid on day 5. (B) Normalized intensity profile along the corresponding A-scan labelled by the red dashed line in A. (C) Histogram of the relative frequency of intrinsic optical attenuation coefficient. (D) Regions with high attenuation coefficients above the threshold superimposed with the original cross-sectional OCT image.

To separate the high and low attenuation regions within the 3D tumor spheroids, we plotted the probability histogram of attenuation coefficients from the OCT intensity profile images as shown in Fig. 5(C). Two distinct high probability locations of attenuation coefficients existed in the entire tumor spheroid tissues. Then, the combination of two Gaussian curves were used to fit the histogram for the distribution of the probability of attenuation coefficients, where the peak points P1 and P2 were determined by the curve-fitting. We found that the best fitting result for the normal tissue was at peak-1 (P₁ = 0.34/mm) and the necrotic region was at peak-2 (P₂ = 0.56/mm) for all tumor spheroids detected in this study with R² > 0.95. Therefore, the threshold of high attenuation region was determined by the mean of the two peak values ($\overline{P}=(P_1+P_2)/2$, ∼ 0.45 mm^-1). The red binarized map in Fig. 5(D) represented the regions with attenuation coefficients above the threshold which was further superimposed with the original XZ cross-sectional OCT image.

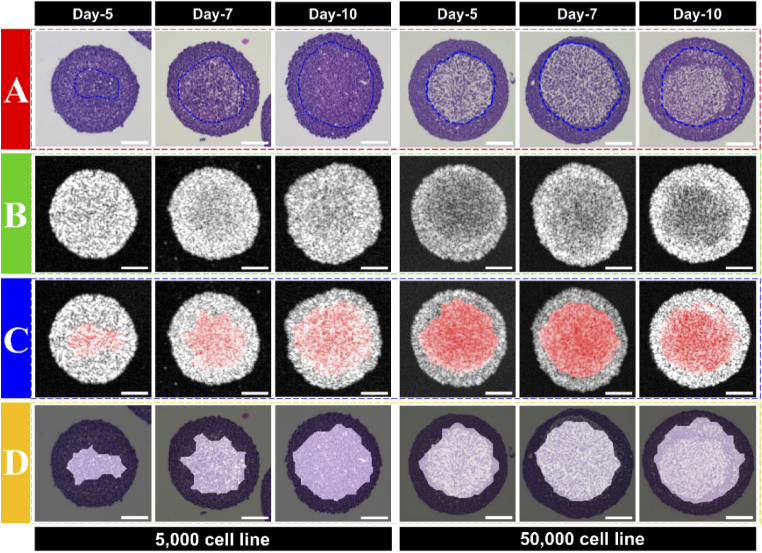
To confirm the accuracy of the necrotic region detected based on the noninvasive OCT intrinsic optical attenuation coefficient technique in OVCAR-8 tumor spheroids, the same histological tumor spheroid images were used as golden standard (Fig. 6). Figure 6(A) showed the histology images of 5,000- and 50,000-cells spheroids, and the necrotic regions within the tumor spheroids were indicated by the dashed blue line (edge of the necrotic region). The manual delineation in the histology images was marked by raters by cropping less dense and aggregated structure located within the tumor spheroids [56]. Figure 6(B) showed the original OCT intensity images, while the distinct high attenuation regions could not be seen clearly. Using the threshold (0.45 mm^-1) derived above, the necrotic regions were overlaid with the intensity images of the 5,000- and 50,000-cells spheroids (Fig. 6(C)). Figure 6(D) was the overlay of derived necrotic regions from OCT attenuation coefficient & histology images of the 5,000- and 50,000-cells spheroids. The necrotic regions indicated in the histology images (arears within dashed blue line) were generally consistent with the distribution of the high attenuation regions obtained from OCT attenuation coefficient images. A Dice-score of 0.92 ± 0.03 was obtained between detection based on intrinsic optical attenuation and necrotic regions in histology.

Fig. 6.

Comparison of necrotic regions based on optical attenuation contrast with histology images. (A) Histology of tumor spheroids on day-5, -7, and -10. (B) OCT intensity images. (C) Overlay the high attenuation coefficient region with OCT intensity images. (D) Overlay the high attenuation coefficient region with histology. Scale bars – 100 µm.

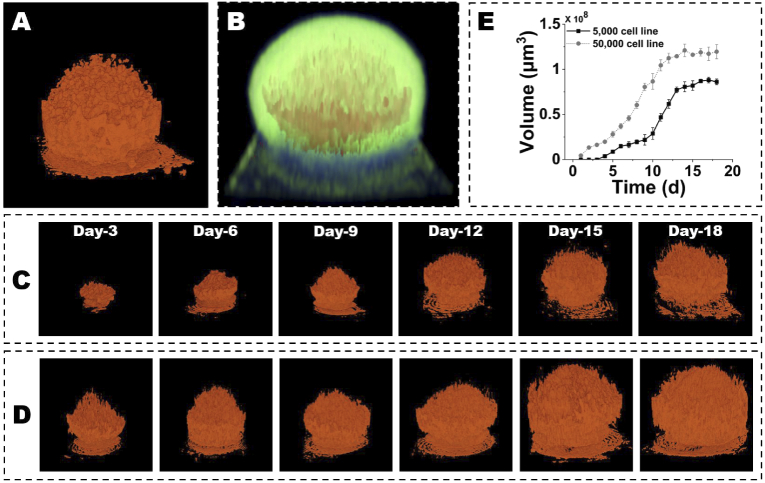
The 3D necrotic regions (Fig. 7(A)) were further reconstructed by stacking the binarized maps in all the cross-sectional images (Fig. S1). Afterward, the 3D necrotic region was superimposed with the 3D tumor spheroid (Fig. 7(B)). There was a clear increase in the volume of necrotic regions as the 5,000-cell line OVCAR-8 tumor spheroid grew (Fig. 7(C)). Similarly, in Fig. 7(D), the 50,000-cells spheroid also exhibited the growth of the volume in necrotic tissues. Additionally, we plotted the growth curve of necrotic cores from all the specimens of 5,000- and 50,000-cells over 18 days, as shown in Fig. 7(E). We found that the necrotic regions in 5,000-cells spheroids started on day 3, then a slow increase in the volume of necrotic regions existed till day 9 and a fast increase showed up from day 10 to day 13. In the end, the necrotic regions kept no significant change till day 18. In contrast, the 50,000-cells spheroids developed the necrotic core on day 1 and had a fast increase in the volume of necrotic regions from day 4 to day 13, then the volume kept stable till day 18.

Fig. 7.

3D growth kinetics of necrotic core volume within 5,000- and 50,000-cells spheroids on day-3, -6, -9, -12, -15, and -18. (A) 3D morphology of necrotic regions. (B) Superimposition of the 3D necrotic regions with tumor spheroid. (C) 3D growth kinetics of necrotic core volume within 5,000 cells spheroids on day-3, -6, -9, -12, -15, and -18. (D) 3D growth kinetics of necrotic core volume within 50,000-cells spheroids on day-3, -6, -9, -12, -15, and -18. (E) Growth curve of the necrotic region volume in 5,000- and 50,000-cells spheroids.

3.4. Description and prediction in growth kinetics of tumor spheroids

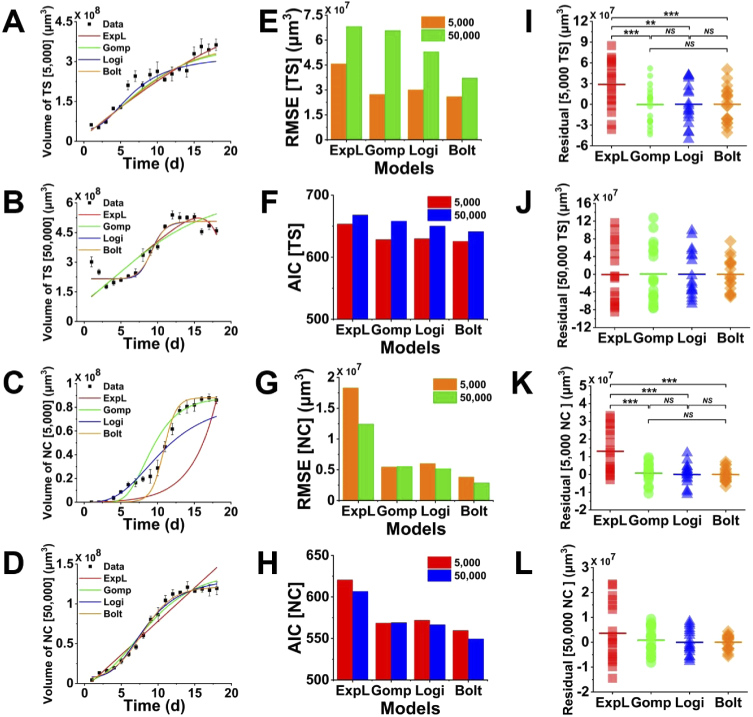
Four mathematical models (the exponential-linear model, Gompertz model, Logistic model, Boltzmann model) were evaluated for their descriptive power of spheroids growth and necrotic regions changes in volume. Figure 8(A)-(D) described the representative fitting using all the four mathematical models for tumor spheroids’ and corresponding necrotic regions’ growth curves over 18 days, respectively. The RMSE and AIC, as shown in Fig. 8(E)-(H), were used to estimate the relative quality of the four mathematical models for these given experimental data. Lower RMSE and AIC indicated the better fit to the experimental data. Additionally, Fig. 8(I)-(L) showed the comparison and corresponding statistical analysis of the residuals from the four fitting models.

Fig. 8.

Four mathematical models for fitting the tumor spheroid volume growth and necrotic region growth. (A-D) Representative growth curves of four models fitting the experimental data of tumor spheroid and necrotic region volumes with 5,000- and 50,000-cells. (E&G) Comparison of RMSE of the four models for fitting tumor spheroid and necrotic region volumes with 5,000- and 50,000-cells. (F&H) Comparison of AIC of four models fitting the tumor spheroid and necrotic region volumes with 5,000- and 50,000-cells. (I-L) Residuals in four models fitting tumor spheroid and necrotic region volumes with 5,000- and 50,000-cells. TS: tumor spheroid. NC: necrotic core.

We observed that the exponential-linear model fitted well at the start and end stages of overall 18 days in the 5,000-cells OVCAR-8 spheroids growth, but did not perform well from day 6 to day 10 (Fig. 8(A)). The other three models showed a relatively better fitting from the start and middle stages of tumor growth, while for the last four days the fitting results were not as good as the exponential-linear model. Figure 8(E), F showed that the Boltzmann model exhibited the lowest RMSE and AIC values in the 5,000-cells OVCAR-8 spheroids growth. From the comparison of the residuals for the four models (Fig. 8(I)), the value from the exponential-linear model was significantly higher than the other three models and there was no significant difference among the Gompertz, logistic, and Boltzmann models. Therefore, for 5,000-cells spheroids, the Boltzmann model was the best one to describe and predict the growth of the volume. For 50,000-cells OVCAR-8 spheroids (Fig. 8(B)), we found that logistic and Boltzmann models provided the relatively better fitting to the growth of tumor volume than the exponential-linear and Gompertz models, but the exponential-linear model fitted better to the decrease of tumor volume at the last four days. In Fig. 8(E), (F), the Boltzmann model showed the smallest RMSE and AIC values in the 50,000-cells OVCAR-8 spheroid growth. Since there was no significant difference existed in the residuals for the four models (Fig. 8(J)), we suggested that the Boltzmann model provided the best fit for the growth of 50,000-cells spheroids.

For modeling the necrotic regions, the exponential-linear model did not well depict the growth of OVCAR-8 tumor necrotic core in the volume data of either 5,000- or 50,000-cells spheroids. In 5,000-cells spheroids, the Gompertz model showed a good fit at the start and end stages in the growth of necrotic core but not well at the middle stage. Though, both the logistic and Boltzmann exhibited a good fit at the middle stage, the logistic did not fit well at the start stage and the Boltzmann did not provide a good fit at the end stage. Figure 8 K indicated that the residuals of the exponential-linear model were significantly higher than the other three models but there was no significant difference among the Gompertz, logistic, and Boltzmann models in the 5,000-cells spheroids. Nonetheless, from the RMSE and AIC plots, as shown in Fig. 8(G), (H), the Boltzmann model had the lowest RMSE and AIC values compared to the other three models in both the 5000- and 50,000-cells spheroids. Therefore, we suggested that the Boltzmann model was the best model to predict the growth of the necrotic regions in both the 5000- and 50,000-cells spheroids.

4. Discussion

In this study, we demonstrated that OCT was capable to acquire in situ 3D images of the morphological structures and necrotic regions of multicellular OVCAR-8 spheroids longitudinally in a label-free manner. The quantitative assessment of 3D tumor spheroids including the volume (both spheroids and necrotic regions within the spheroids) and growth kinetics was used to monitor the spheroids activity, which was unable to be resolved from conventional microscopy due to limited depth penetration, destructive fluorophore-labeling, and extensive steps for samples preparation [10,30–38]. The volumes of 5,000-cells spheroids had a fast increase at the initial stage (day 2 – day 7), a slow increase at the middle stage (day 7 – day 13), a fast increase before the end (day 14 – day 16), and a stable stage at the end (day 16 – day 18). Whereas 50,000-cells spheroids followed a fast decrease at the start (day 1 – day 3), a fast increase at the middle (day 3 – day 12), a stable stage before the end (day 12 – day 15), and a slow decrease at the end stage (day 15 – day 18). The growth patterns were generally consistent with the previously reported studies that the tumor spheroid volume exponentially increased in the early stage and the rate of volume growth started to decrease until the volume of the spheroid remained constant [2,10,79,80]. However, the volume growth of 5,000- and 50,000-cells spheroids showed some differences. First, the 50,000-cells spheroids had a volume decrease from day 1 to day 3, but the 5,000-cells only showed one-day (day 1 – day 2) for the volume decrease. This difference might be due to 50,000-cells spheroids need a longer time to aggregate as a spheroid to build close contact for reproducing physical communications and signaling pathways [81]. Second, the volume of 50,000-cells spheroids started to decrease at the last four days, but the volume of 5,000-cells spheroids remained constant. We suspected that OVCAR-8 spheroids with 50,000 initial cells could reach the largest volume faster and kept unchanged within four days. After the stable period, the spheroids started to decrease because the rate of dead cell composition within the spheroids exceeded the rate of live cell proliferation. In contrast, 5,000-cells spheroids had a slower rate of volume growth to reach the largest volume.

From en face OCT images, based on the conventional diameter-based ($\pi d^3$) method [56], 50,000-cells spheroids showed a massive diameter at the first two days, which yielded a false observation of spheroid volume. For the diameter-based ($\pi w^{2}l$) measurement [75], the volume of tumor spheroids in both 5,000- and 50,000- cells started to increase from day 1, leading to a false observation of tumor spheroid growth. The quantitative analyses of spheroids showed that the estimation of volume based on two diameter-based methods from en face and cross-sectional OCT images led to large quantification errors when tumor spheroids developed irregular shapes. On the other hand, the quantification of spheroids volume based on the voxel-counting measurement yielded a more accurate result. Furthermore, OCT provided a unique 3D view of multicellular tumor spheroids for monitoring the overall growth of volume, and offer complimentary depth information that was not available from traditional imaging modalities. Last, OCT resolution, the refractive index of cell spheroid, and individual cell size must be relevant parameters to consider in subsequent studies to introduce OCT as a new standard for spheroid model cancer evaluation.

Our observation demonstrated that the necrotic tissues were firstly formed in the center of the tumor spheroids which might be due to tumor cells could not get oxygen and nutrients in the core [82]. Similar to the necrotic regions forming in tumors in vivo, it has been reported that spheroids in vitro also form necrotic regions when cultured to 500 µm in diameter and above [83]. As the spheroid grows larger, transfer of oxygen and nutrient becomes limited, therefore creating pH gradients and resulting in the formation of the necrotic region [84]. After that, the necrotic region spread around because more tumor cells lost oxygen and nutrients supply with the increase of spheroid volume (Fig. 7(C), (D), (E)). In our results, regardless of en face, cross-sectional, or 3D reconstructions, necrotic regions showed a non-symmetric distribution within the spheroids, which was consistent with the previous study [56]. Since our method was noninvasive, progression of 3D tumor necrotic regions could be obtained over time. One interesting observation was that the necrotic regions within the tumor spheroid started on the first day in the 50,000-cells spheroids, while did not start until day 3 in the 5,000-cells spheroids. The possible cause was that more initial tumor cells resulted in less space in the spheroid and prevented tumor cells in the center from getting oxygen and nutrients at the early stage (day 1 to day 3), whereas fewer tumor cells had more vacancy in the spheroid. This could be confirmed by that the necrotic regions within 5,000-cells OVCAR-8 spheroids had a slow increase in volume of necrotic tissues from day 3 to day 9 and a fast increase did not start until from day 10. In contrast, the volume of necrotic tissues within 50,000-cells spheroids had a fast increase from the first day. Meanwhile, the superimposed attenuation coefficient map with histology images demonstrated that the necrotic regions occupied small areas in the 5,000-cells spheroids at day 5, but the necrotic regions in the 50,000-cells spheroids at day 5 already occupied large areas. Moreover, the volume of necrotic regions showed a similar trend as the volume of tumor spheroids. Still, the necrotic tissue volumes would not decrease when tumor spheroid volumes decreased in 50,000-cells spheroids. The probable cause was that the proliferating cells at the outer layer of the spheroids needed to remain a dynamic balance with the necrotic cells since the final size of the tumor spheroid were determined by the correlation of the thickness of a layer between the proliferating and necrotic tissues [85]. This phenomenon might indicate that the volume of necrotic regions within tumor spheroids related to the number of tumor cells and the speed of tumor growth. We need to notice that in the current manuscript, we verified the necrotic regions based on optical attenuation contrast from OCT only with limited histology images. In the future, we will section the whole tumor spheroid and reconstruct the 3D necrotic regions based on the HE staining and then compare with the volume of necrosis from OCT to better access OCT performance. All in all, in the recognition and location of necrosis areas, the most important point is how well the necrosis area by OCT matches the actual necrosis area. It may be too early to that conclude necrosis has been captured only by observing there is attenuation in the center and the approximate location is the same. In the subsequent study, we will also consider adding drugs that cause necrosis to the spheroid and see if the signal of the peripheral area becomes attenuated.

Finally, in 5,000- or 50,000-cells OVCAR-8 spheroids, we observed that the Boltzmann model was the best one to describe the growth kinetics of ovarian tumor spheroids. The previous studies demonstrated that the Gompertz model was the most effective model for the description and prediction of the growth of tumor volumes [75,86,87], and our results indeed showed that the Gompertz model had a good fit to the growth of the volume of tumor spheroids and necrotic regions compared to the exponential-linear and logistic models. However, the RMSE and AIC values indicated that the Boltzmann model had the smallest error to fit the growth of ovarian tumor spheroid and necrotic region volumes. Although the exponential-linear had a good fit at the middle stage in 50,000-cells spheroid volumes, the 5,000-cells spheroids did not perform a continuously exponential increase of volumes at the middle stage. At the start and end stages, the exponential-linear model was less agreeable to fit the change of the volume of tumor spheroid, which followed the description of the growth of tumors in the previous observations [75,86,88]. The logistic model showed a good fitting at the start and middle stages, whereas the linear decay in the volume of the relative growth rate of the logistic model was unable to describe the growth of tumor spheroids [86,89], especially at the end stage. In comparison, the Gompertz model gave a more accurate description of the tumor growth than the exponential-linear and logistic models, but the limitation of the Gompertz model was that the relative tumor growth rate became arbitrarily large for small tumor volumes [75]. Altogether, we suggested that the Boltzmann model was the best one to describe the growth of OVCAR-8 spheroids with different initial cell numbers.

5. Conclusion

In summary, we demonstrate that OCT is a promising imaging modality for visualizing and quantifying the 3D structure of multicellular ovarian tumor spheroids longitudinally. Compared to the conventional diameter-based measurements, voxel-counting method achieves a more accurate and robust quantification of the volumes of OVCAR-8 tumor spheroids. Furthermore, OCT is capable of identifying necrotic tissues within tumor spheroids based on the intrinsic optical attenuation coefficient, allowing to visualize the progression of necrotic tissues over time, which can serve as a promising alternative tool for cell function and metabolism test in tumor spheroids. Moreover, The Boltzmann model can be used to describe the growth of ovarian tumor spheroids and their necrotic tissues over time, which not only has important implications for biological and physiological mechanism of ovarian tumor and necrotic tissue growth, but also can assist in preclinical anticancer drug investigations.

Disclosures

The authors declare no conflicts of interest.

Data availability

Data underlying the results presented in this paper are not publicly available at this time but may be obtained from the authors upon reasonable request.

Supplemental document

See Supplement 1 ^{(1.1MB, pdf)} for supporting content.