Abstract
Purpose:
Rule-based approaches to determining glaucoma progression from visual fields alone are discordant and have tradeoffs. To better detect when glaucoma progression is occurring, we utilized a longitudinal data set of merged VF and clinical data to assess the performance of a Convolutional Long Short-Term Memory (LSTM) neural network.
Design:
Retrospective analysis of longitudinal clinical and visual field data.
Subjects:
From two initial datasets of 672,123 visual fields from 213,254 eyes and 350,437 samples of clinical data, persons at the intersection of both datasets with four or more visual fields and corresponding baseline clinical data (cup-to-disc ratio, central corneal thickness, and intraocular pressure) were included. After exclusion criteria, specifically the removal of VFs with high false positive / negative rates and entries with missing data, were applied to ensure reliable data, 11,242 eyes remained.
Methods:
Three commonly used glaucoma progression algorithms (Visual Field Index slope, Mean Deviation slope, and Pointwise Linear Regression) were used to define eyes as stable or progressing. Two machine learning models, one exclusively trained on visual field data and another trained on both visual field and clinical data, were tested.
Outcome Measures:
Area under the receiver operating characteristic (AUROC) curve and area under the precision-recall curve (AUPR) calculated on a held-out test set and mean accuracies from 3-fold cross validation were used to compare the performance of the machine learning models.
Results:
The convolutional LSTM network demonstrated 91–93% accuracy with respect to the different conventional glaucoma progression algorithms given 4 consecutive visual fields for each subject. The model that was trained on both visual field and clinical data (AUROC between 0.89 and 0.93) had better diagnostic ability than a model exclusively trained on visual fields (AUROC between 0.79 and 0.82, p<0.001).
Conclusions:
A convolutional LSTM architecture can capture local and global trends in visual fields over time. It is well suited to assessing glaucoma progression because of its ability to extract spatio-temporal features other algorithms cannot. Supplementing visual fields with clinical data improves the model’s ability to assess glaucoma progression and better reflects the way clinicians manage data when managing glaucoma.
Detecting visual field (VF) worsening is an important task in glaucoma management. Clinicians often make decisions for surgery or escalation of medical therapy based on changes in a patient’s visual field over time. Making these decisions, however, is challenging due to VF variability across tests which is often but not always due to poor reliability indices1. Manually reviewing VFs can be subjective and prone to error, especially given that patients usually have a small number of tests per year.2–4 Studies suggest that many tests over multiple years are required before progression can be accurately detected5. In response, multiple algorithms have been developed to aid in assessing glaucoma progression. Such algorithms can be split into two subsets: event-based and trend-based analysis.
Event-based analyses include algorithms which classify progression in a binary manner by comparing subsequent to initial visual fields. The most commonly used event-based algorithm is Guided Progression Analysis (GPA), which defines progression based on 3 consecutive visual fields following two baseline tests, where worsening is measured as deterioration at identical points in visual fields outside a 95% confidence interval.6 Though GPA had a relatively low false positive rate, it is variable and overly reliant on high quality baseline studies.7
Trend-based analyses commonly utilize linear regression to determine changes in global or local measures. Global measures include Visual Field Index (VFI) and Mean Deviation (MD). Local measures include pointwise threshold or age-corrected threshold values. Due to variability in visual fields, there can often be delays in detecting progression solely from trend-based analyses.8,9 In addition, Saeddi et al. found that significant discordance exists between six traditional glaucoma progression algorithms, including VFI Slope, MD Slope, and PLR.10 Only 2.5% of eyes analyzed were classified the same by all six algorithms. The lack of a standard for glaucoma progression has prompted research in developing an objective, interpretable approach.
Machine learning, the notion that systems can learn from prior experience or examples, is a tool for the future of assessing glaucoma progression. Studies have already found both unsupervised and supervised approaches to predicting disease progression effective for other conditions, such as Parkinson’s and Alzheimer’s.11,12 Machine learning has also been successfully utilized for the diagnosis of eye diseases. Ting, et al. evaluated a learning system for the diagnosis of diabetic retinopathy (DR) and other eye diseases, including glaucoma and macular degeneration (AMD), using 500,000 images across ethnicities and populations.13
Work has been done in applying machine learning for glaucoma progression. Caprioli, et al. compared the effectiveness of linear, quadratic, and exponential regression in assessing VF progression, concluding that exponential fit best modelled rate of decay when MD slope is used to define ground truth.14 Yousefi, et al. reported that assessing VF progression using machine learning is significantly more effective than traditional point-wise, region-wise, and global algorithms.15 Wang M., et al. classified different forms of visual field progression into 16 archetypes and defined progression as any significant straying from the normal archetype, or a stable rate of progression. They tested their model against multiple traditional algorithms as well as a subset of clinician graded sequences and found it outperformed AGIS, CIGTS, PoPLR, and MD.16 Numerous other unsupervised and supervised models including random forests, Bayesian techniques, and Recurrent Neural Networks have been tested in assessing glaucoma progression.17–19
A small number of studies have also attempted to supplement visual fields with other data. Hogarty et al. noted that the performance of machine learning classifiers in detecting glaucoma progression did not improve when VFs are complemented with Retinal Nerve Fiber Layer (RNFL) data.20 These findings are interesting as clinicians are putatively making determinations based on measures of optic nerve structure and function in addition to other clinical data but could be misleading due to a small train/test set. Kazemian, et al. developed a model for forecasting glaucoma progression at different intra-ocular pressure ranges for patients.21 Garway-Heath, et al. confirmed the effectiveness of combining VF and OCT data for assessing progression.22 These studies suggest that incorporating clinical or OCT data into models that assess VF progression may improve performance.
An important machine learning algorithm that is well suited to the determination of glaucoma worsening is the convolutional long short-term memory (LSTM) network. As a recurrent neural network (RNN), these are a special type of artificial neural network that can recognize temporal patterns in data by passing parameters between layers in a model.23 In this way, RNNs retain information about previous training examples, helping them learn relationships involving sequences of data like visual fields over time. LSTM networks are a special type of RNN that help resolve some issues with traditional RNNs by adding memory cells and forget gates that control when information enters memory and when it leaves or is forgotten.24 Also relevant to determining glaucoma worsening, LSTM networks have been successfully applied to problems where the input data represent an ordered sequence but where the time between individual samples is not necessarily relevant. Such problems include handwriting recognition, sentence parsing, and machine translation.
Convolutional neural networks (CNNs) are a type of deep learning algorithm traditionally used for image analysis. They are good at learning spatial relationships within images by extracting features from filters, or kernels, and assigning concurrent weights and biases to learn these features. The convolutional LSTM model was introduced by Shi et. al and is a good fit for the problem of assessing glaucoma progression because of its spatio-temporal nature. Convolutional LSTM layers are distinct from stacking convolutional layers on top of recurrent layers in that they compute convolutional operations in both input and recurrent transformations. This allows them to extract unique spatio-temporal features that other machine learning architectures cannot.25
The purpose of this study was twofold. First, to determine the effectiveness of a convolutional LSTM architecture in assessing glaucoma progression and second, to evaluate whether supplementing visual field data with clinical data would improve the model’s performance.
Methods
This study was reviewed and approved by the Johns Hopkins University School of Medicine Institutional Review Board and adhered to the tenets of the Declaration of Helsinki.
Data Sources
Clinical and in-office testing data were obtained from Johns Hopkins Wilmer Eye Institute clinical information systems and represent the routine clinical care of the patients involved. Data were transferred to an approved, secured server dedicated to machine learning analysis.
Inclusion/Exclusion Criteria
From two initial datasets of 672,123 visual fields from 213,254 eyes of 108,127 patients and 350,437 samples of clinical data from 55,460 patients, 12,366 patients at the intersection of both datasets with four or more visual fields and corresponding clinical data were included. 1,789 visual fields were excluded because they had false positive or negative rates greater than 20%1 or MD values worse than −15dB. This MD cutoff was chosen given the inherent difficulty of determining change in those with severe visual field loss. The clinical data were obtained from patients in the EHR who had a glaucoma diagnosis (ICD-10 codes starting with H40) and were seen by an eye care provider. Three clinical data elements were extracted: cup-to-disc ratio, central corneal thickness, and intraocular pressure. Patients with missing data in any of these columns were further excluded. After these criteria were applied, 11,242 eyes remained for analysis.
Reference Algorithms
Three commonly used automated progression algorithms were used to define the “truth” regarding visual field progression: Mean Deviation (MD) slope, Visual Field Index (VFI) slope, and Pointwise Linear Regression (PLR). For MD and VFI, the slope of the value over time was calculated using linear regression. If the slope was negative and it’s p-value less than 0.05, the patient was classified as progressing.26,27 For PLR, a visual field was determined to be progressing if the slope of regression for the threshold values of three individual points was negative and statistically significant (P<0.01).28 These three algorithms were used as the criteria for determining glaucoma progression. Table 1 displays the number of eyes marked as stable and progressing by each individual reference algorithm. Figure 1 displays the number of eyes marked as progressing by each reference algorithm as a Venn diagram.
Table 1.
Number of eyes marked as stable and progressing by each baseline algorithm.
| Baseline Algorithm / Ground Truth | Progressing | Stable |
|---|---|---|
| VFI Slope | 1997 | 9245 |
| MD Slope | 2410 | 8832 |
| PLR | 3144 | 8098 |
Figure 1.

Venn diagram displaying number of visual fields marked as progressing by each reference algorithm
Data Preparation
In order to test the effectiveness of supplementing visual fields with clinical data, two sets of input data were used: one with 54 features consisting of every 24–2 pattern visual field point and a second with 3 additional features from clinical data. Visual fields were represented as an 8×9 grid to preserve spatial relationships. The three additional features from clinical data were treated as auxiliary input included at later steps in the machine learning architecture. All input features were normalized to have a mean of 0 and standard deviation of 1. Because a majority of patients were deemed stable, we attempted weighting progressing eyes more heavily but this approach overcorrected and eventually decreased the network’s overall performance.
Machine Learning Architecture
The machine learning architecture consisted of a single convolutional LSTM layer with 32 filters and a 3×3 kernel size. Dilation and stride lengths were left at library defaults of 1. Batch normalization was used to increase the overall stability of the network by reducing covariate shift or the change in distribution of input data across layers. These layers were followed by two fully connected dense layers, with 4 and 1 nodes respectively, used to provide a final output corresponding to progressing or not. The design of the network was based on the results of Wen et al.29 To help prevent overfitting, a 25% dropout layer was included between the recurrent layers. Weights were initialized using a random normal distribution and L1 regularization was applied to the output of the convolutional layer. The input to the network was a multidimensional array consisting of 11,242 eyes with 4 visual fields each, all represented as 8×9 grids. The set of 4 visual fields per patient the model was trained on were a subset of the full time series, ensuring clinical usefulness. The final model architecture is displayed in Figure 2. In order to test the effectiveness of supplementing visual fields with clinical data, a second architecture with auxiliary input from an LSTM layer with 4 cells was trained and evaluated. The architecture for this model is displayed in Figure 3.
Figure 2.
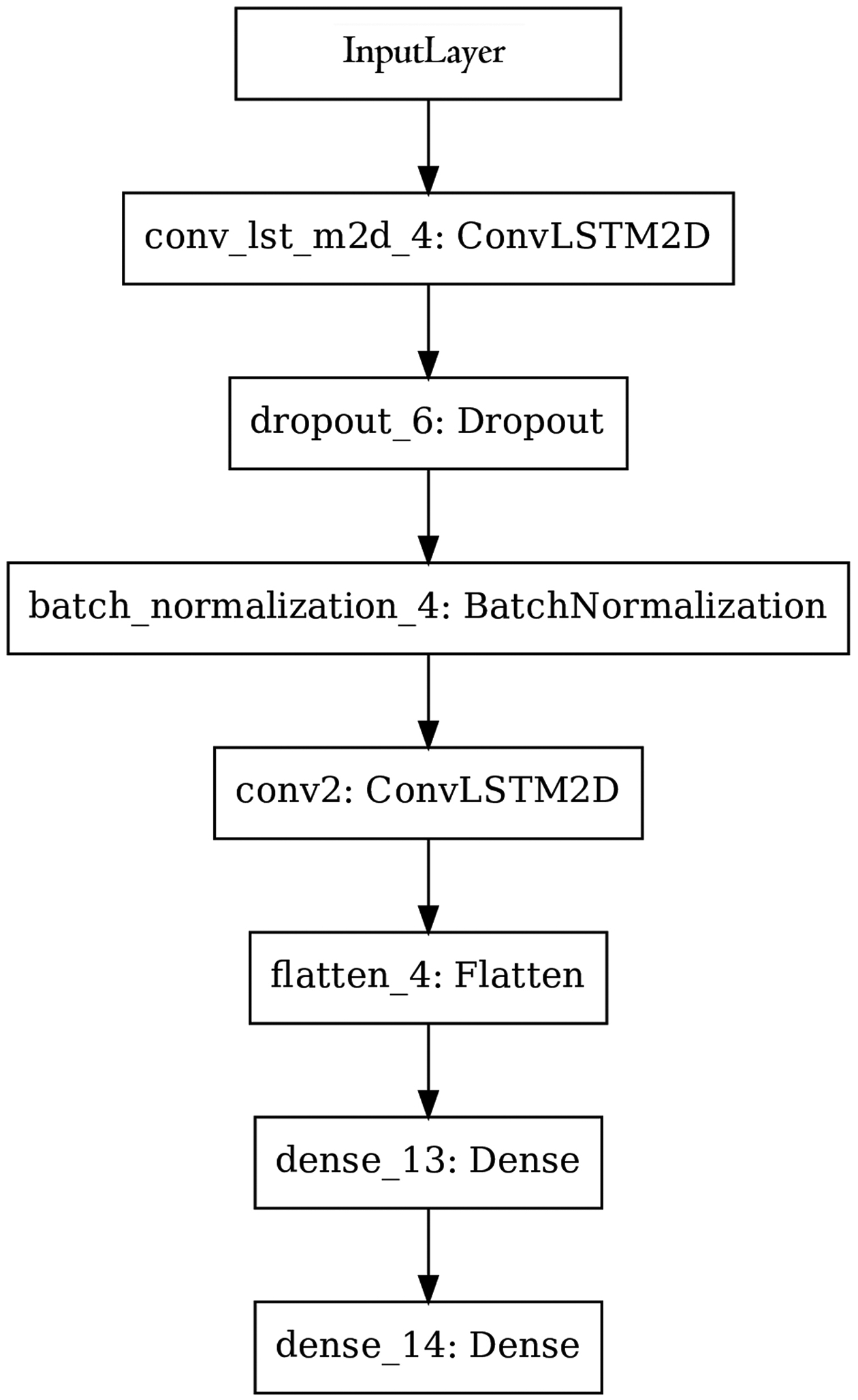
Machine learning architecture trained on visual field data. Input was a multi-dimensional array with timesteps, rows, columns, channels representing the longitudinal data.
Figure 3.

Machine learning architecture that incorporates data from visual fields and clinical data. Clinical data input was a multi-dimensional array with timesteps and features.
An Adam optimizer with learning rate of 0.001 and binary cross-entropy loss function was used. Additionally, gradient clipping was applied in order to prevent exploding gradients during training. All hyperparameters were optimized using a grid search that tested the performance of every combination of learning rates, initialization schemes, network architectures, and clipping norms. Binary cross entropy loss is used to assess the performance of models that have two classes. In the case of this study, this corresponded to stable and progressing. A model that perfectly classifies data has a loss of 0. For the general case, cross entropy loss is defined as the sum of ground truth values multiplied by the logarithm of the scoring from the model. The results of the VF only (Figure 2) and VF + clinical data (Figure 3) models were compared as described below.
Outcome Metrics
3-Fold Cross validation with disjoint, uniform, random splits was used in order to assess the accuracy of the model. These splits were iterated so that two groups of data were used as a training set and the third as a test set. Splits were partitioned by patient rather than eye in order to prevent an inter-eye correlation from biasing the results. Specificity and sensitivity values were calculated with a randomly selected held-out test set. A Receiver Operating Characteristic (ROC) curve generated on the same test set was used to compare the performances of individual models. Precision-recall (PR) curves generated from cross-validation were also included to account for class imbalance.
Additionally, in order to better understand the LTSM network after training, we determined the extent to which different points on the visual field contributed to the model’s decision making ability. Heatmaps for each model (MD slope, VFI slope, PLR) were created by subtracting the accuracy of the model after masking each individual point in the training dataset with the accuracy of the model trained on the original dataset.
Existing progression algorithms were implemented in Python 3.6.8 and the machine learning algorithms in Python using the Keras library (v2.2.4) on a Tensorflow backend (v1.14.0). Scikit-learn (v0.21.3), Scipy (v1.3.1), and StatsModels (v0.10.1) were used for statistical analysis.
Results
After inclusion criteria were applied, 11,242 eyes from 5,843 patients remained for analysis. The mean age of included patients was around 72 years old and the average date of their most recent visual fields was in 2018. For excluded patients, the mean age was 67 years and average date of most recent visual fields also in 2018. For included patients, the mean rate of change of MD for progressors was −0.97 dB / year and for non-progressors, +0.68 dB / year. For excluded patients, the mean rate of change of MD for progressors was −0.69 dB / year and for non-progressors, +0.60 dB / year. Further characteristics of the study population are displayed in Table 2.
Table 2.
Characteristics of included and excluded patients.
| Baseline Characteristics | Included Patients | Excluded Patients |
|---|---|---|
| Age (years) | 72 | 67 |
| MD (dB) | −3.7 | −3.8 |
| IOP (mmHg) | 15.2 | 16.0 |
| CCT (μm) | 538 | 568 |
| CDR | 0.644 | 0.539 |
| MD slope (dB/year, non-progressors) | +0.68 | +0.60 |
| MD slope (dB/year, progressors) | −0.97 | −0.69 |
IOP = Intraocular Pressure, CCT = Central Corneal Thickness, CDR= Cup-to-disc Ratio, MD = Mean Deviation.
Table 3 displays patient characteristics in the train and test sets. A Mann-Whitney U test revealed no statistically significant difference in IOP, CCT, CD Ratio, and rate of change of MD in the train and test set. There was a significant difference in the train and test set between mean patient age. We don’t believe the differences in age impacted model performance, as the mean of the distribution was similar and age was not relevant as input for training the model.
Table 3.
Characteristics of patients in the train and test sets and p-values from comparison of distributions. A p-value of <0.05 signifies a significant difference between both sets.
| Baseline Characteristics | Train Set | Test Set | p-value |
|---|---|---|---|
| Age (years) | 72 | 71 | <0.01 |
| MD (dB) | −3.77 | −3.64 | 0.09 |
| IOP (mmHg) | 15.2 | 15.4 | 0.25 |
| CCT (μm) | 537 | 539 | 0.46 |
| CDR | 0.64 | 0.65 | 0.57 |
| MD slope (dB/year, non-progressors) | +0.68 | +0.67 | 0.11 |
| MD slope (dB/year, progressors) | −0.97 | −0.96 | 0.42 |
IOP = Intraocular Pressure, CCT = Central Corneal Thickness, CDR = Cup-to-disc Ratio, MD = Mean Deviation (dB).
Area under the ROC (AUROC) curve and area under the precision-recall (AUPR) curve of the machine learning model trained exclusively on visual fields, with respect to different “gold standard” progression algorithms (MD slope, VFI slope, PLR), are shown in Table 4. Timesteps correspond to the number of sequential visual fields from each subject the model was trained on. For example, having two timesteps means the model made decisions based on two consecutive visual fields for a single eye. As expected, increasing the number of visual fields provided to the model increases both AUPR (improvement of between .044 and .434 per added timestep) and AUROC (improvement of between .011 and .074 per added timestep). This indicates that the inclusion of more VFs helped the LSTM network learn better.
Table 4.
Performance (area under the ROC curve, area under the PR curve) of a model trained on exclusively visual fields and a model trained on both visual fields and clinical data with respect to ground truth from traditional algorithms over different numbers of timesteps. The change in area under the ROC curve and area under the PR curve is displayed in parentheses after individual metrics in the model trained on clinical data and visual fields section.
| Reference | MD Slope | PLR | VFI Slope | |||
|---|---|---|---|---|---|---|
| Time steps | AUROC | AUPR | AUROC | AUPR | AUROC | AUPR |
| Model Trained on Only VFs | ||||||
| 2 | 0.703 | 0.398 | 0.651 | 0.373 | 0.695 | 0.401 |
| 3 | 0.741 | 0.442 | 0.759 | 0.465 | 0.783 | 0.471 |
| 4 | 0.815 | 0.519 | 0.794 | 0.490 | 0.794 | 0.526 |
| Model Trained on Clinical Data and VFs | ||||||
| 2 | 0.701 (−0.002) | 0.386 (−0.012) | 0.694 (+0.043) | 0.492 (+0.119) | 0.711 (+0.016) | 0.397 (−0.004) |
| 3 | 0.835 (+0.094) | 0.730 (+0.288) | 0.784 (+0.025) | 0.692 (+0.227) | 0.840 (+0.057) | 0.681 (+0.210) |
| 4 | 0.939 (+0.124) | 0.772 (+0.253) | 0.892 (+0.096) | 0.786 (+0.296) | 0.915 (+0.121) | 0.794 (+0.268) |
VF = Visual Field, MD = Mean Deviation, PLR = Pointwise Linear Regression, VFI = Visual Field Index.
Table 3 also shows that the inclusion of intraocular pressure, corneal thickness, and cup-disc ratio improved the performance of the algorithm. Intraocular pressure was the most important clinical feature, in that its exclusion had the greatest negative impact on model performance, as measured by AUROC. Central corneal thickness and cup-disc ratio were the second and third most important features, respectively. ROC curves for each model are shown in Figure 4 and corresponding AUROC values, AUPR values, and 95% confidence intervals in Table 5. Each set of curves in each figure had identical train-test datasets to ensure comparability of results. Table 6 shows model sensitivity at fixed specificity levels, as per the ROC curves in Figure 4.
Figure 4.

Receiver operating characteristic curves of the machine learning models trained against mean deviation slope (A), pointwise linear regression (B), and visual field index slope (C) with confidence bands. The model shaded blue was trained on clinical data and visual fields, the red model was trained exclusively on visual fields, and the green model trained exclusively on clinical data, each over 4 timesteps. Numeric values for this curve are listed in Table 5.
Table 5.
Performance (area under the ROC curve with 95% confidence interval, area under the PR curve with 95% confidence interval) of models trained on both clinical data and visual fields, exclusively visual fields, and exclusively clinical data given 4 timesteps of data with respect to ground truth from traditional algorithms corresponding to Figure 4.
| Reference | MD slope | VFI slope | PLR | |||
|---|---|---|---|---|---|---|
| Model | AUROC | AUPR | AUROC | AUPR | AUROC | AUPR |
| Clinical Data and Visual Fields | 0.939 (±0.008) | 0.772 (±0.121) | 0.892 (±0.012) | 0.786 (±0.045) | 0.915 (±0.009) | 0.794 (±0.060) |
| Visual Fields Only | 0.815 (±0.015) | 0.519 (±0.128) | 0.794 (±0.020) | 0.490 (±0.101) | 0.794 (±0.015) | 0.526 (±0.079) |
| Clinical Data Only | 0.743 (±0.018) | 0.507 (±0.058) | 0.756 (±0.019) | 0.467 (±0.151) | 0.792 (±0.014) | 0.625 (±0.121) |
MD = Mean Deviation, PLR = Pointwise Linear Regression, VFI = Visual Field Index.
Table 6.
Sensitivity (%) of models trained on both clinical data and visual fields, exclusively visual fields, and exclusively clinical data given 4 timesteps of data with respect to ground truth from traditional algorithms at different specificity levels.
| Reference | Model | Specificity Level | |||
|---|---|---|---|---|---|
| 80% | 85% | 90% | 95% | ||
| MD slope | VF+CD | 95% | 90% | 82% | 59% |
| CD Only | 55% | 45% | 36% | 24% | |
| VF Only | 64% | 58% | 47% | 32% | |
| VFI slope | VF+CD | 85% | 77% | 67% | 48% |
| CD Only | 53% | 45% | 36% | 20% | |
| VF Only | 64% | 60% | 53% | 38% | |
| PLR | VF+CD | 90% | 85% | 74% | 51% |
| CD Only | 58% | 47% | 35% | 20% | |
| VF Only | 62% | 54% | 42% | 26% | |
MD = Mean Deviation, PLR = Pointwise Linear Regression, VFI = Visual Field Index, VF = Visual Fields, CD = Clinical Data.
In order to test the null hypothesis that there was no change in AUROC between a model that uses exclusively visual fields and a model supplemented with clinical data, a Z-test was used. We accounted for clustering by using the fastAUC package in R. Results from the Z-test for individual plots are in Table 7 and indicate statistical significance (p<0.01) for every comparison, meaning that the diagnostic accuracy of a model supplemented by clinical data is better than a model that exclusively uses visual fields, when trained on 4 subsequent timesteps of data.
Table 7.
Statistical comparison of the area under receiver operating characteristic curves with respect to different definitions of glaucoma progression for model 1 (visual field only) and model 2 (visual field and clinical data).
| Reference Algorithm to Define Ground Truth for ROC Curves | |||
|---|---|---|---|
| MD Slope | PLR | VFI Slope | |
| Difference (Model 1AUROC – Model 2AUROC) | −0.124 | −0.098 | −0.121 |
| P-value | < 0.001 | < 0.001 | < 0.001 |
MD = Mean Deviation, PLR = Pointwise Linear Regression, VFI = Visual Field Index.
Additionally, Precision-Recall (PR) curves are shown in Figure 5 and corresponding area under the PR curve (AUPR) values in Table 5. While ROC curves can present overly optimistic views of algorithm performance in situations where there is large class imbalance, PR curves account for class imbalance.
Figure 5.

Precision recall curves of the machine learning models trained against mean deviation slope (A), pointwise linear regression (B), and visual field index slope (C) with confidence bands. The model labelled “CD+VF” was trained on both clinical data and visual fields, “VF Only” exclusively on visual fields, and “CD Only” exclusively on clinical data, each over 4 timesteps. Numeric values for this curve are listed in Table 5.
Mean accuracies were also calculated using cross-validation. The accuracy of the model trained on 4 timesteps of visual field and clinical data ranged from 91–93%.
In order to understand how often false positives indicated by one ground truth were true positives by others, we examined the number of eyes marked as progressing by the network, non-progressing by the reference algorithm the network was trained on, and progressing by another reference algorithm. Table 8 displays these results and reveals such situations were minimal.
Table 8.
Number of eyes marked as progressing by the network, non-progressing by the reference algorithm the network was trained on, and progressing by another reference algorithm. The first column indicates models trained on visual field and clinical data with respect to different reference algorithms and the first row indicates how different reference algorithms marked eyes.
| Reference | |||
|---|---|---|---|
| Model | MD Slope | VFI Slope | PLR |
| Trained using MD Slope | 0 | 7 | 10 |
| Trained using VFI Slope | 9 | 0 | 17 |
| Trained using PLR | 12 | 13 | 0 |
MD = Mean Deviation, PLR = Pointwise Linear Regression, VFI = Visual Field Index.
The heatmaps generated by iteratively excluding each visual field point from the training process did not reveal any clearly identifiable patterns of more and less “important” points (Figure 6).
Figure 6.
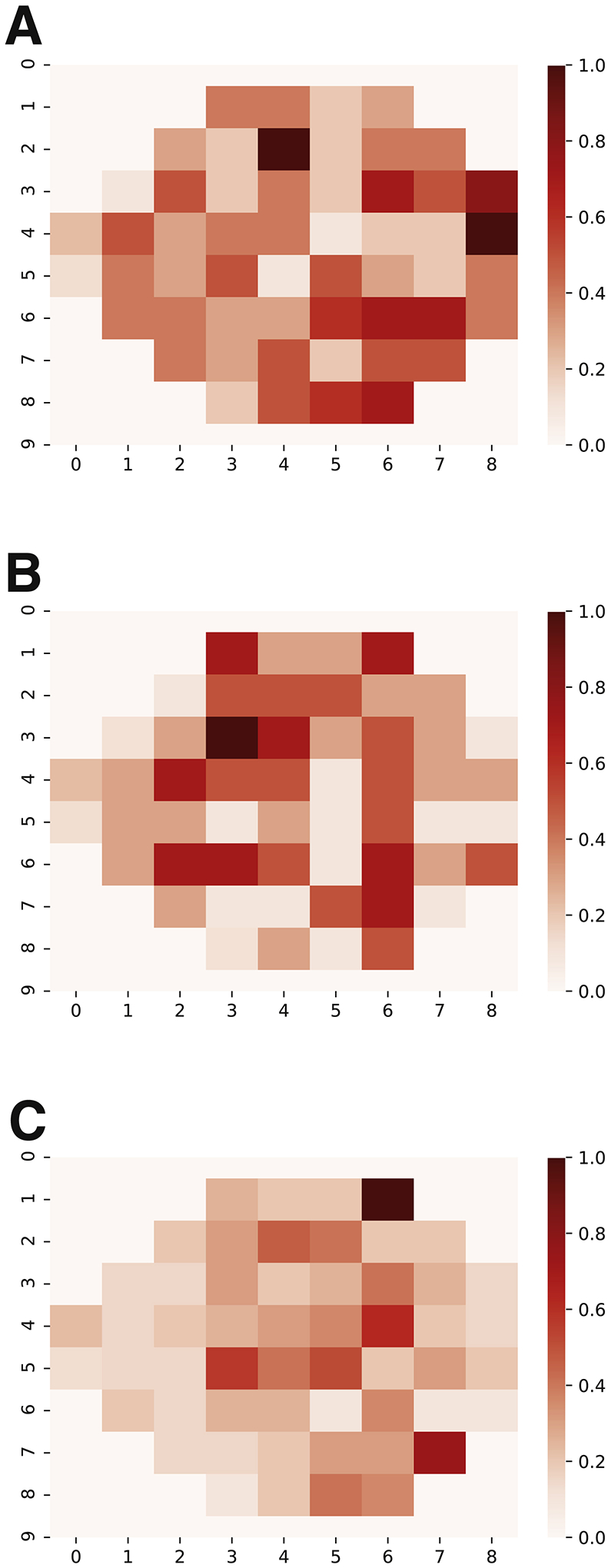
Heatmap of the machine learning models trained against mean deviation slope (A), pointwise linear regression (B), and visual field index slope (C). Each point was iteratively excluded from the training process. The scale from 0–1 represents the impact of each individual point on the model’s predictive ability, where 0 is the least impact and 1 is the greatest.
Discussion
The primary aims of this study were to test the ability of a convolutional LSTM model to identify glaucoma progression and to determine whether supplementing visual fields with clinical data can improve performance. Evaluation against previously described algorithms to define glaucoma worsening confirmed that the LSTM model was accurate in its predictions and could be trained to learn both global (based on MD, VFI) and local (based on PLR) changes in visual fields. Training distinct networks on two data sources, specifically visual fields alone and visual fields supplemented with basic clinical data (cup to disc ratio, corneal thickness, and intraocular pressure) showed that the network trained on the combined data performed better.
The convolutional LSTM architecture we developed performed well identifying glaucoma progression with AUROC values ranging from 0.89 to 0.93 when using multiple visual fields and baseline clinical data as inputs. Additionally, AUPR values which incorporate class imbalance indicate moderate performance ranging from 0.77 to 0.80 of the network trained on combined data. Differences in AUROC and AUPR values are primarily due to AUPR values incorporating class imbalance as a determinant of performance. Lower AUPR values were expected given the imbalance in the number of stable and progressing patients. Although there is no agreed-upon objective definition of glaucoma progression, the proposed machine learning model is spatio-temporal by nature and shows it can learn both pointwise (as determined by PLR) and global (as determined by MD and VFI) trends. The presence of convolutional layers may allow it to extract spatial features that are not reflected in prior work30,31. The usefulness of recurrent layers supports Park, et al.’s findings that an RNN architecture can more robustly predict future visual fields than traditional regression techniques18. The combination of these factors makes the proposed ML architecture interpretable and an important step forward in finding a system that can synthesize information relevant to glaucoma progression. Having an architecture that can incorporate multiple data sources is key to incorporating the same information used by clinicians which makes it more likely such a system will be used in clinical practice.
An important contribution of this work is the finding that supplementing visual fields with clinical data increased the performance of the model. The ROC curves of models with and without clinical data reveal that the sensitivity and specificity of the model using exclusively visual fields is significantly lower than those of a model supplemented by clinical data. This corroborates the findings of Garway-Heath, et al. and Kazemian, et al. by suggesting that including structural data alongside VFs improves model performance regardless of the machine learning architecture utilized21,22.
One limitation of this study is the class imbalance and relatively small train/test sets. Either or both of these might affect the ability of the LTSM network to learn but the former is a feature of “real world” data and so may help us reflect performance in that setting. Class imbalance may explain the high accuracy but low AUROC for the model trained exclusively on visual fields. The fact that the vast majority of eyes were determined to be stable (Table 1) makes it possible to achieve high accuracy simply by marking every eye as non-progressing. Though the ROC curves do imply that the proposed architecture had good specificity and sensitivity, there may have been other unknown, extraneous features the model learned that would hinder its ability to generalize given the small train/test sets. Another limitation is that only 4 visual fields were used to determine ground truth values from reference algorithms. This was done in order to ensure sufficiently large train and test sets. However, it could mean that some of the ground truth values are inaccurate and thus that the network didn’t effectively learn “progression.” This could be addressed in future studies by combining data from multiple institutions in order to have larger data sets from which to learn. The reference algorithms used in this study, MD, VFI, and PLR each have their own strengths and weaknesses. MD and VFI are correlated as they both represent global change in visual fields, however, glaucomatous progression typically tends to be local. PLR is a local measure but is sensitive to noise and can be highly variable, leading to greater number of false positives. Thus, it may be beneficial to include additional standards for identifying glaucoma progression such as physician assessment. A benefit of using rate-based reference algorithms in this study is that the LSTM network did not have time as one of its inputs. It is therefore more likely that the LSTM network is learning something more like an event-based model of glaucoma worsening (see Guided Progression Analysis in the Introduction). This fact and the inclusion of clinical data makes it less likely that the machine learning algorithm is simply learning the mathematics of the reference algorithms.
It is not clear that our results would generalize to other populations given that all data were collected from a single site, an academic medical center with highly specialized glaucoma care, which likely differs from other types of practice. Further research that examines the architecture presented in this paper at different institutions is necessary. A logical follow up to this study would be to compare the ConvLSTM against other ML models that have been described. Similarly, it will be interesting to determine whether inclusion of data regarding optic nerve structure such as photographs and computerized imaging will make the ML model better at predicting glaucoma progression. The clear challenge will be to define progression based not just on visual fields but also on structural changes in the optic nerve structural changes and determining whether worsening in both is required. Finally, it will be interesting to see whether and how ML algorithms can incorporate other data from the EHR (other diagnoses, medications, procedures, etc.) and whether such data will meaningfully augment the data used so far.
While there is much interest in the latest revitalization of machine learning, which promises great potential for the future of glaucoma management, we should remember that the field itself is not new and that it generated similar excitement more than 20 years ago but then failed to transform medicine in a meaningful way. There is also increased awareness of the fact that these powerful algorithms are only able to learn from the examples we provide so a system that learns glaucoma at one institution may not generalize to another. We should therefore be cautious this time that we carefully evaluate and confirm that the algorithms we develop can indeed be used in settings with different patient populations so that we are not disappointed by our artificial intelligence future.
A Convolutional Long Short-term Memory network was effective in predicting worsening of visual fields in glaucoma patients using prior tests. The model performed significantly better when supplemented with clinical data.
Financial Support:
Research at the Wilmer Eye Institute is supported by NEI Core grant EY001765 and Research to Prevent Blindness.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Conflict of Interest: Boland: Carl Zeiss Meditec – Consulting.
Presented at The Association for Research in Vision and Ophthalmology Annual Meeting, 2020
References
- 1.Yohannan J et al. , “Evidence-based Criteria for Assessment of Visual Field Reliability,” Ophthalmology, vol. 124, no. 11, pp. 1612–1620, 2017, doi: 10.1016/j.ophtha.2017.04.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Crabb DP, Garway-Heath DF. Intervals between visual field tests when monitoring the glaucomatous patient: wait-and-see approach. Invest Ophthalmol Vis Sci. 2012;53(6):2770. doi: 10.1167/iovs.12-9476 [DOI] [PubMed] [Google Scholar]
- 3.Heijl A, Bengtsson B, Chauhan BC, et al. A comparison of visual field progression criteria of 3 major glaucoma trials in early manifest glaucoma trial patients. Ophthalmology. 2008;115(9):1557–1565. doi: 10.1016/j.ophtha.2008.02.005 [DOI] [PubMed] [Google Scholar]
- 4.Giraud J-M, May F, Manet G, et al. Analysis of progression with gpa (Guided progression analysis) and mean deviation (Md) indexes of automated perimetry in ocular hypertension and glaucoma. Invest Ophthalmol Vis Sci. 2010;51(13):3997–3997. [Google Scholar]
- 5.Chauhan BC, Malik R, Shuba LM, Rafuse PE, Nicolela MT, and Artes PH, “Rates of Glaucomatous Visual Field Change in a Large Clinical Population,” Invest. Ophthalmol. Vis. Sci, vol. 55, no. 7, pp. 4135–4143, July. 2014, doi: 10.1167/iovs.14-14643. [DOI] [PubMed] [Google Scholar]
- 6.Katz J, Congdon N, Friedman DS. Methodological variations in estimating apparent progressive visual field loss in clinical trials of glaucoma treatment. Arch Ophthalmol. 1999;117(9):1137–1142. doi: 10.1001/archopht.117.9.1137 [DOI] [PubMed] [Google Scholar]
- 7.Aref AA, Budenz DL. Detecting visual field progression. Ophthalmology. 2017;124(12S):S51–S56. doi: 10.1016/j.ophtha.2017.05.010 [DOI] [PubMed] [Google Scholar]
- 8.Manassakorn A, Nouri-Mahdavi K, Koucheki B, Law SK, Caprioli J. Pointwise linear regression analysis for detection of visual field progression with absolute versus corrected threshold sensitivities. Invest Ophthalmol Vis Sci. 2006;47(7):2896–2903. doi: 10.1167/iovs.05-1079 [DOI] [PubMed] [Google Scholar]
- 9.Viswanathan A, Fitzke F, Hitchings R. Pointwise linear regression of glaucomatous visual fields. In: XIIIth International Perimetric Society Meeting. Gardone Riviera (BS), Italy: Kugler Publications; 1999:139–145. http://webeye.ophth.uiowa.edu/ips/cd/update98-99/139-146.pdf. [Google Scholar]
- 10.Saeedi OJ, Elze T, D’Acunto L, et al. Agreement and predictors of discordance of 6 visual field progression algorithms. Ophthalmology. 2019;126(6):822–828. doi: 10.1016/j.ophtha.2019.01.029 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Wang X, Wang F, Sontag D. Unsupervised learning of disease progression models. In: New York, USA: MIT; 2014. https://people.csail.mit.edu/dsontag/papers/WanSonWan_kdd14.pdf. [Google Scholar]
- 12.Fisher CK, Smith AM, Walsh JR. Machine learning for comprehensive forecasting of Alzheimer’s Disease progression. Scientific Reports. 2019;9(1):1–14. doi: 10.1038/s41598-019-49656-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Ting DSW, Cheung CY-L, Lim G, et al. Development and validation of a deep learning system for diabetic retinopathy and related eye diseases using retinal images from multiethnic populations with diabetes. JAMA. 2017;318(22):2211–2223. doi: 10.1001/jama.2017.18152 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Caprioli J, Mock D, Bitrian E, et al. A method to measure and predict rates of regional visual field decay in glaucoma. Invest Ophthalmol Vis Sci. 2011;52(7):4765–4773. doi: 10.1167/iovs.10-6414 [DOI] [PubMed] [Google Scholar]
- 15.Yousefi S, Goldbaum MH, Balasubramanian M, et al. Glaucoma progression detection using structural retinal nerve fiber layer measurements and functional visual field points. IEEE Trans Biomed Eng. 2014;61(4):1143–1154. doi: 10.1109/TBME.2013.2295605 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Wang M, Shen LQ, Pasquale LR, et al. An artificial intelligence approach to detect visual field progression in glaucoma based on spatial pattern analysis. Invest Ophthalmol Vis Sci. 2019;60(1):365–375. doi: 10.1167/iovs.18-25568 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Lee J, Kim YK, Jeoung JW, Ha A, Kim YW, Park KH. Machine learning classifiers-based prediction of normal-tension glaucoma progression in young myopic patients. Jpn J Ophthalmol. 2020;64(1):68–76. doi: 10.1007/s10384-019-00706-2 [DOI] [PubMed] [Google Scholar]
- 18.Park K, Kim J, Lee J. Visual field prediction using recurrent neural network. Sci Rep. 2019;9. doi: 10.1038/s41598-019-44852-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Murata H, Araie M, Asaoka R. A new approach to measure visual field progression in glaucoma patients using variational bayes linear regression. Invest Ophthalmol Vis Sci. 2014;55(12):8386–8392. doi: 10.1167/iovs.14-14625 [DOI] [PubMed] [Google Scholar]
- 20.Hogarty DT, Mackey DA, Hewitt AW. Current state and future prospects of artificial intelligence in ophthalmology: a review. Clin Experiment Ophthalmol. 2019;47(1):128–139. doi: 10.1111/ceo.13381 [DOI] [PubMed] [Google Scholar]
- 21.Kazemian P, Lavieri MS, Van Oyen MP, Andrews C, Stein JD. Personalized prediction of glaucoma progression under different target intraocular pressure levels using filtered forecasting methods. Ophthalmology. 2018;125(4):569–577. doi: 10.1016/j.ophtha.2017.10.033 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Garway-Heath DF, Zhu H, Cheng Q, et al. Combining optical coherence tomography with visual field data to rapidly detect disease progression in glaucoma: a diagnostic accuracy study. Health Technol Assess. 2018;22(4):1–106. doi: 10.3310/hta22040 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Cleeremans A, Servan-Schreiber D, McClelland JL. Finite state automata and simple recurrent networks. Neural Computation. 1989;1(3):372–381. doi: 10.1162/neco.1989.1.3.372 [DOI] [Google Scholar]
- 24.Hochreiter S, Schmidhuber J. Long short-term memory. Neural Computation. 1997;9(8):1735–1780. doi: 10.1162/neco.1997.9.8.1735 [DOI] [PubMed] [Google Scholar]
- 25.Shi X, Chen Z, Wang H, Yeung D-Y, Wong W, Woo W. Convolutional LSTM network: a machine learning approach for precipitation nowcasting. arXiv:150604214 [cs]. September 2015. http://arxiv.org/abs/1506.04214. Accessed February 3, 2020.
- 26.Cohen SL, Rosen AI, Tan X, Kingdom FAA. Improvement of the visual field index in clinical glaucoma care. Can J Ophthalmol. 2016;51(6):445–451. doi: 10.1016/j.jcjo.2016.10.001 [DOI] [PubMed] [Google Scholar]
- 27.Vesti E, Johnson CA, Chauhan BC. Comparison of different methods for detecting glaucomatous visual field progression. Invest Ophthalmol Vis Sci. 2003;44(9):3873–3879. doi: 10.1167/iovs.02-1171 [DOI] [PubMed] [Google Scholar]
- 28.Marín-Franch I, Swanson WH. The visualFields package: a tool for analysis and visualization of visual fields. J Vis. 2013;13(4). doi: 10.1167/13.4.10 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Wen JC, Lee CS, Keane PA, et al. Forecasting future Humphrey Visual Fields using deep learning. PLoS One. 2019;14(4). doi: 10.1371/journal.pone.0214875 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.LeCun Y, Haffner P, Bottou L, and Bengio Y, “Object Recognition with Gradient-Based Learning,” in Shape, Contour and Grouping in Computer Vision, Berlin, Heidelberg, 1999, p. 319. [Google Scholar]
- 31.Schmidhuber J, “Deep Learning in Neural Networks: An Overview,” Neural Networks, vol. 61, pp. 85–117, January. 2015, doi: 10.1016/j.neunet.2014.09.003. [DOI] [PubMed] [Google Scholar]


