Myofiber strain in healthy humans using DENSE and cDTI

Abstract

Purpose:

Myofiber strain, E_ff, is a mechanistically relevant metric of cardiac cell shortening and is expected to be spatially uniform in healthy populations, making it a prime candidate for the evaluation of local cardiomyocyte contractility. In this study, a new, efficient pipeline was proposed to combine microstructural cDTI and functional DENSE data in order to estimate E_ff in vivo.

Methods:

Thirty healthy volunteers were scanned with 3 long-axis (LA) and 3 short-axis (SA) DENSE slices using 2D displacement encoding and one SA slice of cDTI. The total acquisition time was 11 min ± 3 min across volunteers. The pipeline first generates 3D SA displacements from all DENSE slices which are then combined with cDTI data to generate a cine of myofiber orientations and compute E_ff. The precision of the post-processing pipeline was assessed using a computational phantom study. Transmural myofiber strain was compared to circumferential strain, E_cc, in healthy volunteers using a Wilcoxon sign rank test.

Results:

In vivo, computed E_ff was found uniform transmurally compared to E_cc (−0.14[−0.15,−0.12] vs −0.18 [−0.20,−0.16], p<0.001, −0.14 [−0.16, −0.12] vs −0.16 [−0.17,−0.13], p<0.001 and −0.14 [−0.16,−0.12] vs E_{cc_C}=−0.14 [−0.15,−0.11], p=0.002, E_{ff_C} vs E_{cc_C} in the endo, mid, and epi layers respectively).

Conclusion:

We demonstrate that it is possible to measure in vivo myofiber strain in a healthy human population in 10 min per subject. Myofiber strain was observed to be spatially uniform in healthy volunteers making it a potential biomarker for the evaluation of local cardiomyocyte contractility in assessing cardiovascular dysfunction.

Introduction

Cardiac function arises from the complex deformation of billions of cardiac muscle cells (cardiomyocytes) during the cardiac cycle (1). Aggregated cardiomyocytes form so-called “myofibers” that change orientation from epicardium to endocardium in a helical fashion (2). This unique microstructural architecture transforms uniaxial myofiber shortening into the circumferential, longitudinal, and radial deformation of the left ventricle (LV). Despite the mechanistic importance of myofiber strain (E_ff) to heart function, it has remained very difficult to measure in vivo owing to the challenges of acquiring and integrating both functional motion and microstructural cardiac data.

Cardiac deformation can be characterized using motion tracking methods that enable the measurement of the tissue displacement field. In particular, the Displacement ENcoding with Stimulated Echoes (DENSE) (3,4) approach provides spatiotemporally resolved maps of myocardial tissue displacement. DENSE encodes each component of tissue displacement from a reference state to a deformed state into the phase of the complex-valued MRI signal. The tissue displacement data is then used to estimate cardiac strain. However, since myofiber orientation data is typically not available, cardiac strains are usually computed assuming a geometry dependent cylindrical coordinate system along the longitudinal (E_ll), circumferential (E_cc), and radial (E_rr) directions of the LV. These descriptive strains are useful, but they are not mechanistically linked to cardiac contraction – except in the LV midwall where it is assumed that E_cc accord with myofiber strain (E_ff) owing to the presumed circumferential orientation of midwall myofibers. A direct measure of myofiber orientations across the myocardium is needed to eliminate this widely used assumption and enable E_ff calculation throughout the LV.

Currently, cardiac Diffusion Tensor imaging (cDTI) is the only approach that is able to interrogate cardiac microstructure in vivo. cDTI probes the mobility of water molecules within the myocardium, where they are hindered by the surrounding microstructure and undergo higher diffusivity in the direction of the cardiomyocyte long-axis. Therefore, cDTI provides a direct measure of the myofiber orientation (5). Recently, the development of first and second-order motion-compensated gradient waveform designs have enabled microstructural imaging in vivo despite the inherent respiratory and cardiac bulk motion (6–8). This approach has been used to characterize the in vivo microstructural remodeling in hypertrophic cardiomyopathy (9,10), dilated cardiomyopathy (9), and amyloidosis (11).

Measuring E_ff in vivo requires both microstructural and functional information, which is technically challenging and has only been reported in a few studies. Tseng et al. (12) produced the first measures of in vivo E_ff in healthy humans using a STEAM-based sequence for measuring cardiac microstructure and to measure cardiac velocity information. Wang et al. (13) used a finite element model to estimate E_ff by fusing in vivo 2D tagging and an ex vivo atlas of myofiber orientation. More recently, Perotti et al. (14) and Verzhbinsky et al. (15) proposed a post-processing approach to measure E_ff that combines in vivo cDTI and 3D displacement encoded DENSE data. However, the clinical translation of the approaches described above remains limited as they rely either on velocity rather than displacement data, integration of ex vivo cDTI data, or long 3D displacement encoded DENSE acquisitions.

In this work, we propose a new method that combines cDTI and a volume of short- and long-axis DENSE slices with 2D displacement encoding to enable the rapid measurement of in vivo myofiber strain (E_ff) in humans. The accuracy of the approach for measuring E_ff was evaluated using a computational phantom for a range of myofiber orientations. Finally, in vivo E_ff values were measured and reported for thirty (N=30) healthy volunteers.

Theory

Cardiac deformation can be assessed from displacement encoding methods such as DENSE. Like most motion encoding approaches, the displacement encoding in DENSE relies on a pair of gradients to encode and decode the cardiac motion into the phase of the complex-valued MR signal. However, the DENSE approach stores the magnetization along the longitudinal axis (M_z) after motion encoding and then restores it at each cardiac phase using a stimulated echo before motion decoding. Consequently, only the relative displacement between encoding and decoding is reflected in the MR phase. In practice, this encoded displacement corresponds to an Eulerian description of the displacement field. In order to measure tissue strains, the Eulerian description of the displacement field is first converted to a Lagrangian description using spatial and temporal fitting approaches (16). These tissue displacements in the Lagrangian description are spatially discretized to a set of nodes (one per pixel), and can be expressed as follows:

$${\overrightarrow{x}}_i({\overrightarrow{X}}_i,t)={\overrightarrow{X}}_i+\overrightarrow{u}({\overrightarrow{X}}_i,t)$$ [1]

where ${\overrightarrow{X}}_i$ is the position vector for the $i$-th node in the reference configuration corresponding to the first cardiac phase measured using DENSE, ${\overrightarrow{x}}_i$ represents the deformed position vector at time $t$, and $\overrightarrow{u}$ is the Lagrangian displacement field at time $t$.

To obtain a continuously defined $\overrightarrow{\mathrm{x}},{\overrightarrow{x}}_i$ is subsequently interpolated spatially using the scattered interpolant function (17) (Matlab, The MathWorks, Natick, MA, USA) with a ‘natural’ interpolation approach. Once $\overrightarrow{\mathrm{x}}$ is continuously defined, the deformation gradient tensor $\mathit{F}$ at each location $\overrightarrow{X}$ and time t can be expressed as

$$\mathit{F}\left(\overrightarrow{X},t\right)={\nabla }_{\overrightarrow{X}}\overrightarrow{x}.$$ [2]

In practice, $\mathbf{F}$ is computed numerically using a central finite difference scheme. The cardiac strain components ${\mathrm{E}}_{\mathrm{v}\mathrm{v}}$ along a chosen direction $\overrightarrow{\mathrm{v}}$ are then evaluated as

$$E_{vv}=\overrightarrow{v}\cdot \mathit{E}\overrightarrow{v}$$ [3]

where $\mathbf{E}$ is the Green-Lagrange strain tensor $\mathbf{E}=\frac{1}{2}(\mathbf{C}-\mathbf{I})$, $\mathbf{C}={\mathbf{F}}^{\mathbf{T}}\mathbf{F}$ is the right Cauchy-Green deformation tensor and I is the identity matrix. As shown in Figure 1, cardiac strains are traditionally measured along the longitudinal ($\overrightarrow{l}$), circumferential ($\overrightarrow{\mathrm{c}}$), and radial ($\overrightarrow{\mathrm{r}}$) directions of the LV, thereby producing the longitudinal (E_ll), circumferential (E_cc), and radial (E_rr) strain components. In this work, the myofiber orientation measured using cDTI, represented by the vector $\overrightarrow{f}$, is used to compute the myofiber strain (E_ff). To do so, we have developed an acquisition and analysis pipeline to compute E_ff across the LV in humans combining cDTI and DENSE methods.

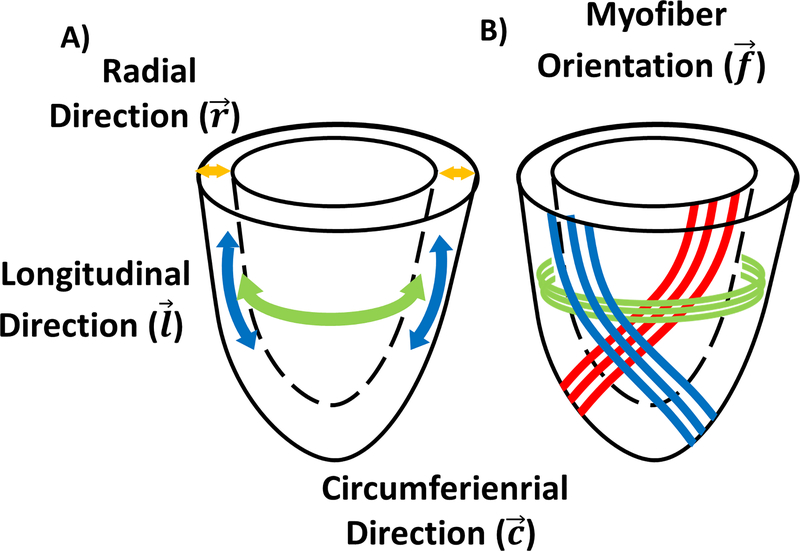
Figure 1:

(A) Arbitrary cylindrical coordinate system along the longitudinal (l), circumferential (c), and radial (r) directions of the left ventricle used to project the strain. (B) Representation of the helical orientation of the myofiber (f) from endocardium to epicardium. Please note that myofibers are not continuous throughout the heart.

Methods

Imaging Protocol Overview

Thirty healthy volunteers (N=30) were recruited for an MRI exam after obtaining signed statements of informed consent under an IRB approved protocol. Images were acquired on a single 3T MRI scanner (Prisma, Siemens Healthineers, Erlangen), using an 18-channel body phased-array coil and a 32-channel spine array coil.

DENSE acquisition

Six 2D spiral cine DENSE slices were acquired in three short-axis (SA) views and three long-axis (LA) views. SA slices corresponded to the base, mid, and apex locations of the LV. LA slices were acquired in 2, 4, and 3 chambers views. The sequence parameters were TE=1.08ms, TR=15ms, Flip Angle 15°, 2.2×2.2×8mm, Matrix 90×90, FOV 200×200mm with a reduced zonal excitation of 120×120mm. The multi-shot spiral readout was composed of four interleaves; two spiral interleaves were acquired per cardiac phase; 2784 samples per leave. 2D displacements were acquired using balanced 3-point displacement encoding with k_e=0.1 cycle/mm. The acquisition was ECG triggered and acquired during a breath-hold that required 14 RR-intervals per slice. At least 30 cardiac phases were acquired per volunteer using the beginning of systole as the reference configuration and with a temporal resolution of 15ms. The total acquisition time for the six slices was ~3 minutes.

The DENSE displacements were reconstructed off-line using the DENSE analysis tool (version 0.5.1, repository: https://github.com/denseanalysis/denseanalysis) in Matlab (MathWorks, Natick, MA, USA). Within the tool, DENSE images were segmented using motion guided segmentation with manual seeding (18). The voxel-wise Lagrangian displacement field was calculated using a 10th order polynomial temporal model and a linear spatial model with smoothness equal to 0.9. Using the DENSE analysis tool, the measured circumferential (E_{cc_M}) and radial (E_{rr_M}) strains were reported for the SA slices as well as the longitudinal (E_{ll_M}) strain for the LA slices.

cDTI acquisition

A single mid-ventricular short-axis slice was imaged during free-breathing with a mid-systolic trigger delay (TD~250 ms) using a custom motion-compensated single-shot spin-echo EPI cDTI sequence. The sequence parameters were TE=61 ms, inner-volume excitation, FOV 200×160 mm, acquisition matrix 128×104 leading to a resolution 1.6×1.6×8 mm, which was interpolated in-plane to 0.8×0.8×8 mm. Parallel imaging with 2x-GRAPPA, partial Fourier 6/8, and a readout bandwidth of 1860 Hz/px were used to reduce the EPI echo-train length in order to limit the image distortion. Two b-values (0 and 350 s/mm²) were acquired using six diffusion-encoding directions and ten repetitions each. The diffusion encoding gradient waveform was composed of four gradient lobes designed symmetrically around the 180° refocusing pulse to null both the first and second-order gradient moments (6). Gradient durations were 6.33/10.47/10.47/6.33 ms with a ramp time of 1.52 ms and a maximum amplitude of 74.37 mT/m. The single-shot acquisition was ECG and end-respiratory triggered using a navigator located on the right liver dome resulting in a TR of one breathing cycle (~4000 ms). A total of 70 cDTI images were obtained at mid-systole corresponding to an acquisition time of ~6 minutes.

cDTI reconstruction was performed off-line using a custom Matlab framework (https://github.com/KMoulin/DiffusionRecon) that included a rigid registration, an average of the ten repetitions, and a Fourier transform zero-filling interpolation. The non-diffusion weighted image and the six diffusion weighted directions were then fit to the second-order tensor using a non-linear least-squares approach (19). cDTI metrics including mean diffusivity (MD), fractional anisotropy (FA), and eigenvectors ($\overrightarrow{E_1},\overrightarrow{E_2},\overrightarrow{E_3}$), were directly extracted from the tensor model. After manual segmentation of the LV, the first eigenvector ($\overrightarrow{E_1}$) representing the myofiber orientation $\overrightarrow{f}$ was projected to the epicardial LV surface (10,20) and used to measure the helix angle (HA).

The uncertainty of the in vivo cDTI experiment was estimated using a bootstrapping approach (21). Among the ten repetitions acquired, a subset of five repetitions was randomly selected and averaged to reconstruct the diffusion tensor. This bootstrapping operation was repeated 1000 times to produce a distribution of reconstructed diffusion metrics. Finally, the uncertainty of the cDTI metrics (dMD, dFA, dHA) were estimated pixel-wise taking the 95% confidence (95CI) interval of each distribution.

Combination of cDTI and DENSE

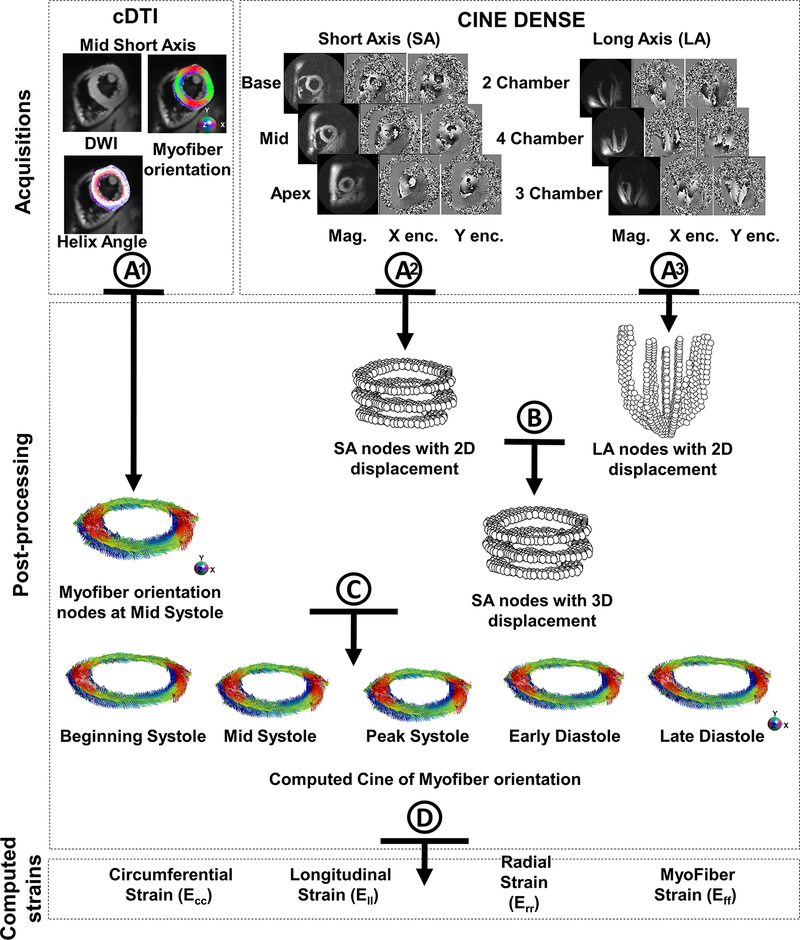
The analysis pipeline used to compute E_ff in humans with combined in vivo cDTI and DENSE is shown in Figure 2 and illustrated in Supporting Video S1. It is composed of four steps:

• A)cDTI voxels within the segmented LV were discretized as a set of nodes (one per voxel). About 2200 voxels per slice were identified. The Lagrangian DENSE displacements were also defined using a set of nodes. About 300 voxels per DENSE slice were identified. All nodes were expressed in a global coordinate system using their respective image quaternions. At the matching cardiac phase, the cDTI nodes were registered in-plane to the SA mid-ventricular DENSE nodes using a center of mass approach to account for the potential misalignment between the two acquisitions.
• B)The LA displacements are generally smooth. Therefore, the 2D displacement fields from LA and SA DENSE slices can be combined to obtain a SA 3D displacement field. 2D displacements from the LA were projected along the direction orthogonal to the SA slice and applied to the SA nodes using linear interpolation.
• C)The 3D SA displacement field was interpolated and differentiated to calculate the deformation gradient tensor F at each cDTI node (Equation 2). F was then used to reorient the myofiber orientation field $\overrightarrow{\mathrm{f}}$ from its initial configuration (mid-systole) to the DENSE reference configuration (beginning of systole). The same operation was repeated to define $\overrightarrow{\mathrm{f}}$ for each cardiac phase.
• D)Cardiac strains were then computed along the circumferential (E_{cc_C}), radial (E_{rr_C}), longitudinal (E_{ll_C}), and myofiber (E_{ff_C}) directions (Equation 3). Computed strain rates (strain temporal derivatives) were also reported in the circumferential (SR_{cc_C}) and myofiber (SR_{ff_C}) directions.

Figure 2:

Post-processing steps used to combine DENSE and cDTI data and calculate myofiber strain E_ff. After cDTI reconstruction (A₁), myofiber orientations were represented as nodes using one node per voxel. Cardiac displacement fields were also represented using nodes after the DENSE reconstruction (A₂ & A₃). (B) 2D Displacement fields from long-axis (LA) and short-axis (SA) are combined to obtain a SA 3D displacement field. (C) The SA 3D displacement field is interpolated and differentiated to generate a deformed cine of myofiber orientation during the cardiac cycle. (D) Finally, cardiac strains are calculated from the SA 3D displacement field and the myofiber orientations and using the beginning of systole as the reference configuration.

All analyses were performed in Matlab and the code for the post-processing pipeline to combine cDTI and DENSE is available at https://github.com/KMoulin/Eff.

Computational Phantom Validation

An in silico experiment was designed to validate the accuracy of the proposed cDTI and DENSE pipeline to estimate E_ff. A computational LV phantom was used to produce a cardiac-like displacement field. Given an initial LV geometry and a rule-based myofiber orientation field ($\overrightarrow{\mathrm{f}}$), the phantom numerically solves an optimization problem to define a displacement field of a chosen form that approximates as best as possible target E_ll, E_cc, E_rr, and E_ff strains. All simulations were performed in Matlab and the code to generate and analyze the computational phantom is available at: https://github.com/luigiemp/CardiacKinematicsPhantom.

The original mid-ventricular phantom was modified to include an apex-to-base LV geometry. The reference phantom configuration was a 3D LV shape, 85mm high from apex to base, with epicardial (epi) and endocardial (endo) radii of 35 mm and 25 mm at the base that are then linearly reduced toward the apex. The target endocardial and epicardial strains were [−0.15, −0.15] for E_ll; [−0.20, −0.16] for E_cc; [0.45, 0.30] for E_rr; and [−0.15, −0.15] for E_ff. A quadratic transmural distribution of myofiber orientation is adopted with corresponding HA ranging from 37° at endocardium, −9° in the mid-wall, and −45° at epicardium (22). Once the displacement field was simulated, the numerical “ground-truth” circumferential (E_{cc_GT}), radial (E_{rr_GT}), and longitudinal (E_{ll_GT}) strains were computed.

From the simulated displacement field, six cine DENSE simulated images were then generated,as described in (15), in the short-axis (SA) and long-axis (LA) views with sequence parameters matched to the in vivo balanced 3-point encoding cine DENSE protocol. These synthetic DENSE images underwent the same reconstruction steps as described for the in vivo processing. Similarly, the measured circumferential (E_{cc_M}) and radial (E_{rr_M}) strains were reported for the SA slices as well as the longitudinal (E_{ll_M}) strain for the LA slices. From the defined myofiber orientation field, synthetic cDTI orientation maps were generated with identical resolution as the in vivo cDTI protocol. Both simulated cDTI and cine DENSE images were then processed using the proposed pipeline from which the computed circumferential (E_{cc_C}), radial (E_{rr_C}), longitudinal (E_{ll_C}), and myofiber (E_{ff_C}) strains were extracted.

Finally, the robustness of the proposed pipeline to estimate in vivo E_ff was assessed with regard to the uncertainty of the myofiber orientation field. Variability was added to the myofiber orientation maps before combining them with DENSE to include variance of the transmural HA distribution.

Quantitative Analysis

All quantitative values (MD, FA, HA, dMD, dFA, dHA, E_cc, E_ll, E_rr, E_ff, SR_cc, and SR_ff) were reported as median [Quartile 1, Quartile 3] across all volunteers. HA as well as mid systolic SR_{cc_C}, SR_{ff_C}, and peak systolic E_{cc_C} and E_{ff_C} were also reported as a function of the transmural wall depth by dividing the wall into nine equally spaced bins. Peak-systole was determined as the cardiac phase corresponding to the lowest median E_cc value across all volunteers. Similarly, strain rates were reported at mid-systole, determined using the lowest median SR_cc across volunteers. Finally, the time-resolved median of E_{cc_C}, E_{ff_C}, SR_{cc_C,} and SR_{ff_C}, were reported throughout the cardiac cycle at three equally spaced transmural depths (endo, mid, epi).

All statistical analyses were carried out in SPSS (Version 26, IBM Corp.) using a non-parametric pair-wise Wilcoxon sign rank test. p<0.05 was considered statistically significant.

Results

Computational Phantom Validations

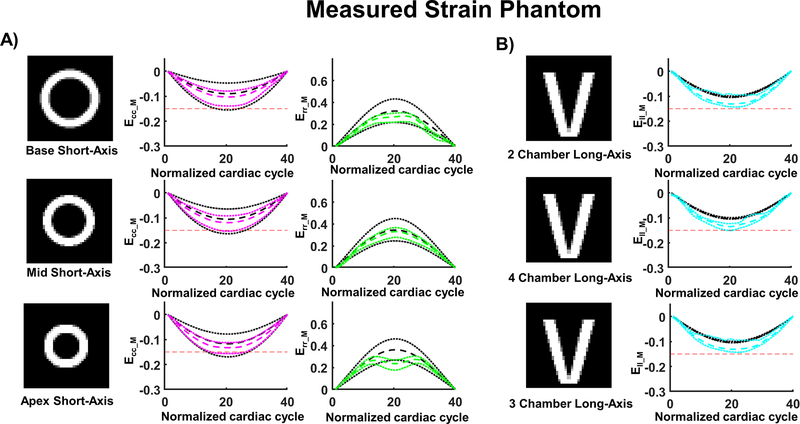
A comparison between ground truth strains and the strains extracted from the synthetic DENSE acquisitions for all slices are shown in Figure 3. For the SA slices at peak systole, the magnitude of measured circumferential strain was slightly higher than the ground truth strain (E_{cc_GT}= −0.09 [−0.16, −0.05], −0.13 [−0.18, −0.10], −0.12 [−0.17, −0.08] vs. E_{cc_M}= −0.10 [−0.14, −0.08], −0.12 [−0.15, −0.09], −0.13 [−0.16, −0.11] at the base, mid and apex, respectively). In contrast, the magnitude of measured radial strain was lower than the ground truth strain (E_{rr_GT}= 0.32 [0.22, 0.43], 0.38 [0.30, 0.47], 0.36 [0.27, 0.46] vs E_{rr_M}= 0.27 [0.22, 0.30], 0.33 [0.28, 0.37], 0.24 [0.18, 0.27] at the base, mid and apex, respectively). For all the LA slices at peak systole, the magnitude of measured longitudinal strain was higher than ground truth strain (E_{ll_GT}= −0.10 [−0.11, −0.10] vs E_{ll_M}= −0.13 [−0.14, −0.09]).

Figure 3:

Cardiac strains measured in the computational phantom using synthetic DENSE images. (A) Measured circumferential (E_{cc_M}) and radial strain (E_{rr_M}) are calculated from DENSE using 2D displacement encoding in a short-axis view at base, mid, and apical levels. (B) Measured longitudinal strain (E_{ll_M}) was calculated from DENSE using 2D displacement encoding in long axis 2-, 4-, and 3- chamber views. The red dashed line provides a −0.15 strain reference; the colored dashed and dotted lines represent the median strain and the first and third quartiles across the slice. The black dashed and dotted lines represent the median ground truth strain and the first and third quartile across the slice.

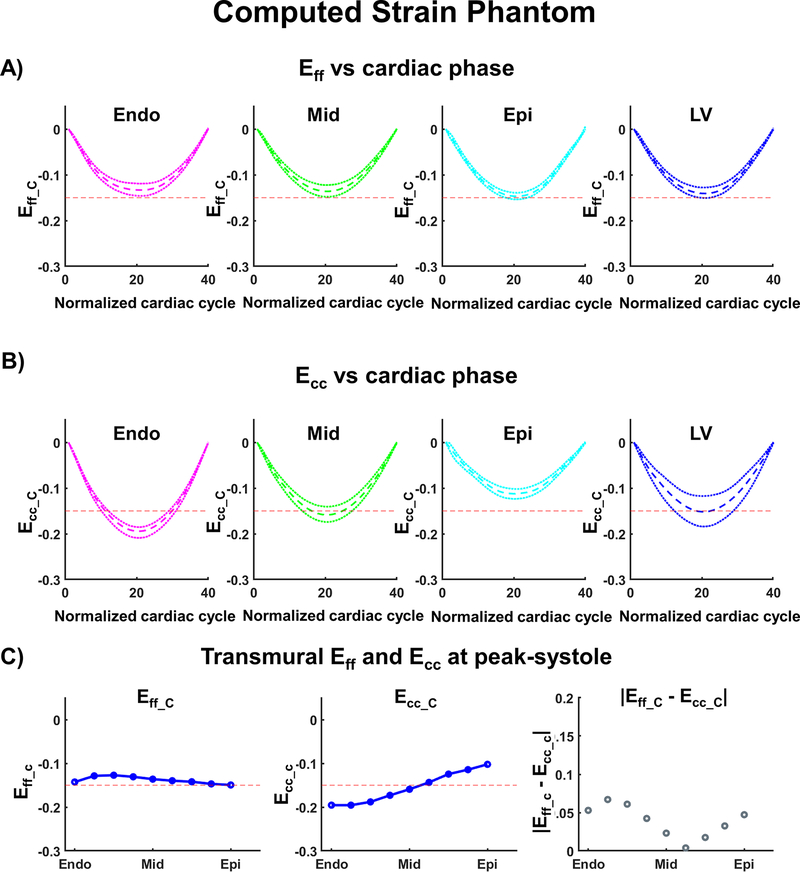
To evaluate the accuracy of computed E_ff, synthetic cDTI orientation maps were generated from a quadratic transmural distribution of myofiber orientations and combined with synthetic DENSE data using the proposed pipeline. The resulting E_{ff_C} are shown in Figure 4 and compared to E_{cc_C}. (E_{ff_C}= −0.13 [−0.15, −0.12], −0.14 [−0.15, −0.12], −0.15 [−0.15, −0.14] vs E_{cc_C}= −0.19 [−0.21, −0.19], −0.16 [−0.17, −0.14], −0.11 [−0.12, −0.10] in the endo, mid, and epi layers, respectively). At peak systole for the whole LV, the computed E_ff was slightly higher than E_cc (E_{ff_C}= −0.14 [−0.15, −0.13] vs E_{cc_C}= −0.15 [−0.18, −0.12]). At peak systole, the computed longitudinal strain was E_{ll_C}= −0.16 [−0.16, −0.16] and the computed radial strain E_{rr_C}= 0.27 [0.22, 0.29].

Figure 4:

Cardiac strain values for the computational phantom calculated after combining cDTI and DENSE. (A) Computed Myofiber strain (E_{ff_C}) and (B) circumferential strain (E_{cc_C}) at endo, mid, epi layers, and across the left ventricular (LV) wall. The red dashed line provides a −0.15 strain reference; the colored dashed and dotted lines represent the median strain and the first and third quartiles across the corresponding layer. (C) Transmural distribution of E_{ff_C}, E_{cc_C}, and the absolute difference between E_{ff_C} and E_{cc_C} at peak systole. Blue solid lines represent the transmural median.

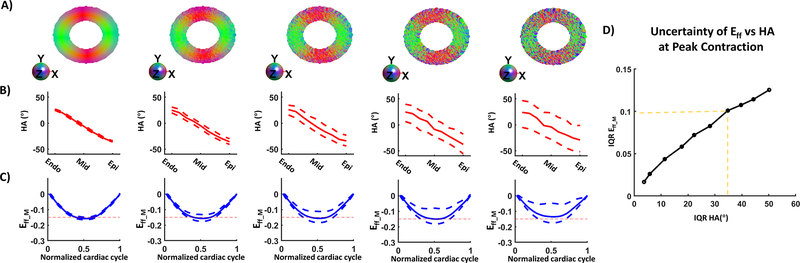
The robustness of the proposed pipeline to estimate E_ff was assessed with regard to the uncertainty in the myofiber orientation field. Variability was added to the myofiber orientation maps which resulted in an increase of IQR for the transmural HA distribution (Figure 5). Small variations in the HA (HA= 25.7 [24.1, 19.6] and −35.6 [−36.3, −34.2] ° at endo and epi) corresponded to tight range of E_{ff_C} at peak systole (E_{ff_C}= −0.16 [−0.17, −0.15]). As the spread of HA increased (HA= 19.6 [−3.4, 38.2], −29.2 [−48.6 −8.15] ° at endo and epi), so did the spread of E_ff (E_{ff_C}= −0.14 [−0.18, −0.06]).

Figure 5:

A) Myofiber orientation colored maps with no variance at the extreme left and with an added variance to the right. (B) Corresponding transmural HA distribution. C) Computed E_ff after combining DENSE with the myofiber orientation maps shown in A). D) Inter-quartile range (Quartile 1 – Quartile 3) of E_ff vs the Inter-quartile range of HA.

In vivo acquisition

A total of thirty healthy volunteers were scanned (8 males and 22 females, 54 ± 18 years old, 72 ± 13 beats per minute). The average acquisition time for one DENSE slice was 12 ± 2 s and 7 ± 3.5 min for the free-breathing cDTI SA slice. The total acquisition time was 11 min ± 3 min across volunteers. After manual segmentation of the LV, 311 [278, 355], 295 [274, 340] and 254 [210 291] voxels were identified for the DENSE acquisition in the Basal, Mid, and Apical slices, respectively. 2171 [1881 2520] voxels were identified for the Mid LV cDTI acquisition.

DENSE Strains

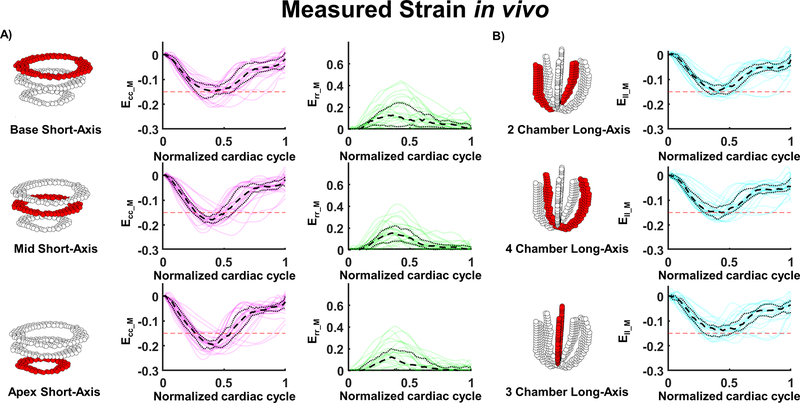
Before combining with cDTI data, cardiac strains were measured by using solely the DENSE acquisitions. Measured strains for each volunteer are displayed throughout the cardiac cycle in Figure 6. For the SA slices and at peak systole, the magnitude of measured circumferential strain (E_{cc_M}) was found to increase from base to apex (E_{cc_M}= −0.15 [−0.17, −0.12], −0.18 [−0.19, −0.16], −0.19 [−0.21, −0.18]) in the base, mid, and apex, respectively. Radial strain was similar for the three slices (E_{rr_M}= 0.11 [0.02, 0.24], 0.14 [0.08, 0.22], 0.10 [0.01, 0.19]) at base, mid, and apex, respectively). Longitudinal strain was also similar across slices (E_{ll_M}= −0.15 [−0.16, −0.12], −0.15 [−0.18, −0.13], −0.14 [−0.16, −0.12] in the 2-, 4-, and 3-chamber view respectively).

Figure 6:

Measured cardiac strains in healthy adults (N=30). (A) Circumferential (E_cc) and radial strain (E_rr) are calculated from DENSE using 2D displacement encoding in a short-axis view at base, mid, and apex levels. (B) Longitudinal strain (E_ll) was calculated from DENSE using 2D displacement encoding in long axis 2-, 4-, and 3-chambers views. The red dashed line provides a −0.15 strain reference.

cDTI Metrics

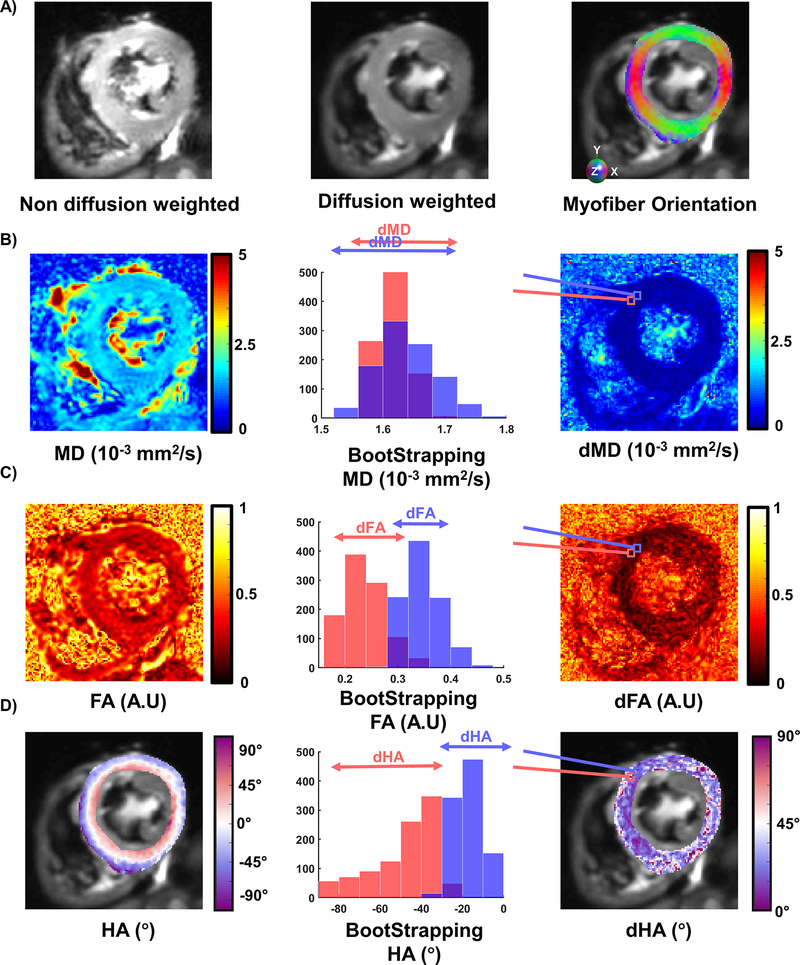
An example of cDTI acquisition and uncertainty maps are shown in Figure 7. cDTI metrics and corresponding uncertainty estimations per volunteer are given in Supporting Information Figure S1. In the SA mid-wall, MD was 1.52 [1.45, 1.59] x 10⁻³ mm²/s across volunteers (N=30) with corresponding dMD 0.22 [0.20, 0.31] x 10⁻³ mm²/s which was estimated using a bootstrapping approach. For all volunteers, FA was 0.36 [0.34, 0.38] A.U. and the uncertainty dFA was 0.23 [0.20 0.26] A.U.

Figure 7:

Example of DTI metrics and uncertainty estimation. A) Non-diffusion weighted, diffusion weighted and myofiber orientation colored maps. B) Mean diffusivity (MD) maps, two bootstrapped distributions displayed for two adjacent pixels exhibiting extreme differences. The 95% confidence interval of these distributions correspond to the uncertainty MD (dMD) maps displayed on the right. C) Fraction of anisotropy maps, bootstrapped distribution for two voxels, and corresponding dFA maps. D) Helix Angle (HA) maps, bootstrapped example and dHA maps.

The transmural HA distributions as a function of LV are shown in Figure 7–C. Transmural HA distribution was 40.4 [21.7, 49.8] °, 2.0 [−0.1, 5.8] °, and −26.5 [−33.3, 4.6] ° at endo, mid, and epi respectively. Across volunteers, the estimated uncertainty dHA was 34.5 [29.7, 48.3] ° overall and 36.6 [28.8, 45.7] °, 33.8 [24.6, 42.1] °, and 50.6 [46.3, 62.1] ° at endo, mid, and epi respectively.

In vivo Myofiber Strain and Strain Rate

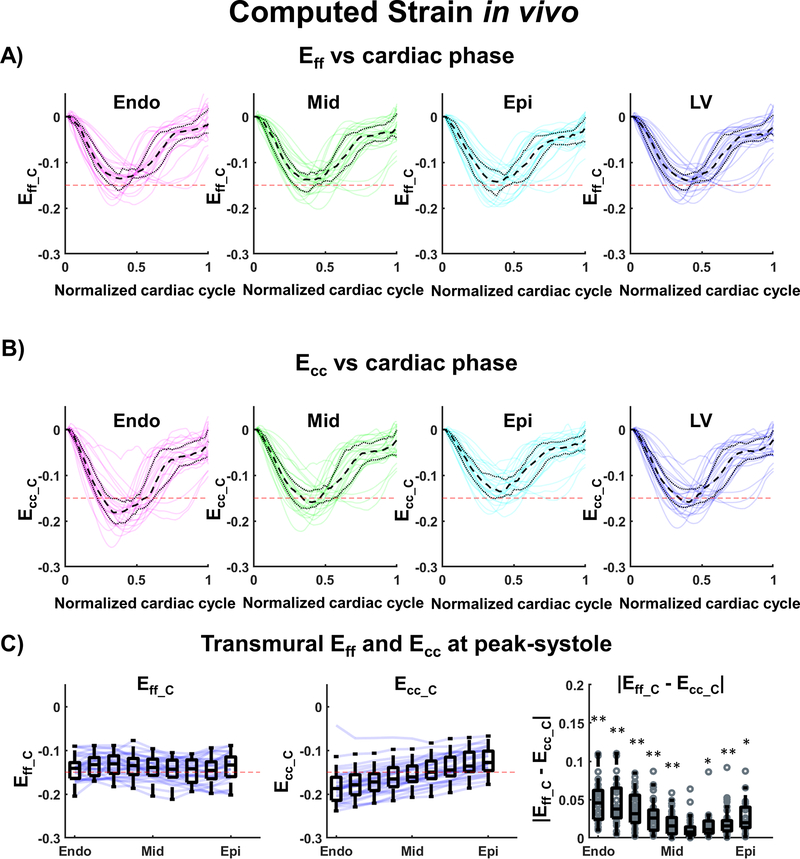
After combining cDTI and DENSE, strains were computed at the mid-ventricular SA slice level as shown in Supporting Information Figure S2. Figure 8A and 8B show a comparison of computed myofiber and circumferential strains during the cardiac cycle within endo, mid, and epi layers and over the entire LV. At peak systole, E_{ff_C} was smaller in magnitude than E_{cc_C} in the endo layer (E_{ff_C}= −0.14 [−0.15, −0.12] vs E_{cc_C}= −0.18 [−0.20, −0.16], p<0.001) and in the mid layer (E_{ff_C}= −0.14 [−0.16, −0.12] vs E_{cc_C}= −0.16 [−0.17, −0.13], p<0.001) and slightly larger in the epi layer (E_{ff_C}= −0.14 [−0.16, −0.12] vs E_{cc_C}= −0.14 [−0.15, −0.11], p=0.002). Across the whole SA LV at peak systole, statistical differences were observed between E_{ff_C} and E_{cc_C} (E_{ff_C}= −0.14 [−0.16, −0.13] vs E_{cc_C}= −0.16 [−0.17, −0.13], p<0.001). The distributions of E_{ff_C} and E_{cc_C} are shown in Figure 8C. E_{ff_C} is shown to be transmurally uniform, which indicates uniform myofiber shortening across the heart, while a transmural gradient is evident for E_{cc_C}. The transmural values for E_{ff_C} and E_{cc_C} as well as the statistical differences are reported in Table 1.

Figure 8:

Cardiac strain values across volunteers (N=30) calculated after combining cDTI and DENSE. (A) Computed Myofiber strain (E_{ff_C}) and (B) circumferential strain (E_{cc_C}) at endo, mid, epi layers, and across the left ventricular (LV) wall. The black dashed and dotted lines represent the median and the first and third quartiles across volunteers; the red dashed line provides a −0.15 strain reference; the colored solid lines are individual medians per volunteers. (C) Transmural distribution of E_{ff_C}, E_{cc_C}, and of the absolute difference of E_{ff_C} and E_{cc_C} at peak-systole. Blue solid lines represent the transmural median per volunteer and the box plots represent the median and IQR across volunteers. Statistical differences between E_{ff_C} and E_{cc_C} have been assessed using a pair-wise Wilcoxon sign rank test: p-values<0.01 are represented by (**) and p-values<0.05 by (*).

Table 1:

Transmural values and mid left ventricle (LV) values for computed myofiber strain (E_{ff_C}), circumferential strain (E_{cc_C}), myofiber strain rate (SR_{ff_C}), and circumferential strain rate (SR_{cc_C}).

Wall Segment	1 Endo	2	3	4	5 Mid	6	7	8	9 Epi	LV
Eff_C	−0.14 [−0.16, −0.13]	−0.13 [−0.15, −0.12]	−0.13 [−0.15, −0.11]	−0.14 [−0.15, −0.12]	−0.14 [−0.16, −0.12]	−0.15 [−0.16, −0.12]	−0.14 [−0.17, −0.13]	−0.15 [−0.17, −0.13]	−0.14 [−0.16, −0.12]	−0.14 [−0.17, −0.13]
Ecc_C	−0.18 [−0.21, −0.17]	−0.18 [−0.20, −0.16]	−0.17 [−0.19, −0.15]	−0.17 [−0.18, −0.14]	−0.16 [−0.17, −0.14]	−0.15 [−0.16, −0.12]	−0.14 [−0.16, −0.12]	−0.14 [−0.15, −0.11]	−0.13 [−0.15, −0.10]	−0.16 [−0.17, −0.13]
p-value	<0.001 (**)	<0.001 (**)	<0.001 (**)	<0.001 (**)	<0.001 (**)	0.797	0.019 (*)	0.004 (**)	0.010 (*)	<0.001 (**)
SRff_C (s−1)	−0.69 [−0.88, −0.57]	−0.67 [−0.88, −0.56]	−0.72 [−0.87, −0.55]	−0.72 [−0.89, −0.58]	−0.75 [−0.84, −0.65]	−0.76 [−0.83, −0.58]	−0.73 [−0.80, −0.64]	−0.71 [−0.79, −0.65]	−0.64 [−0.81, −0.60]	−0.70 [−0.81, −0.62]
SRcc_C (s−1)	−0.95 [−1.08, −0.83]	−0.89 [−1.03, −0.83]	−0.89 [−1.00, −0.76]	−0.83 [−0.97, −0.72]	−0.81 [−0.89, −0.68]	−0.77 [−0.86, −0.61]	−0.70 [−0.78, −0.55]	−0.68 [−0.76, −0.52]	−0.60 [−0.67, −0.47]	−0.80 [−0.87, −0.63]
p-value	<0.001 (**)	<0.001 (**)	<0.001 (**)	<0.001 (**)	0.01 (*)	0.171	0.530	0.185	0.185	0.012 (*)

Strains are reported at peak systole, and strain rate at mid systole. p-values are reported after pair-wise Wilcoxon sign rank test.

^(*)shows statistical differences for p<0.05 and

^(**)for p<0.01.

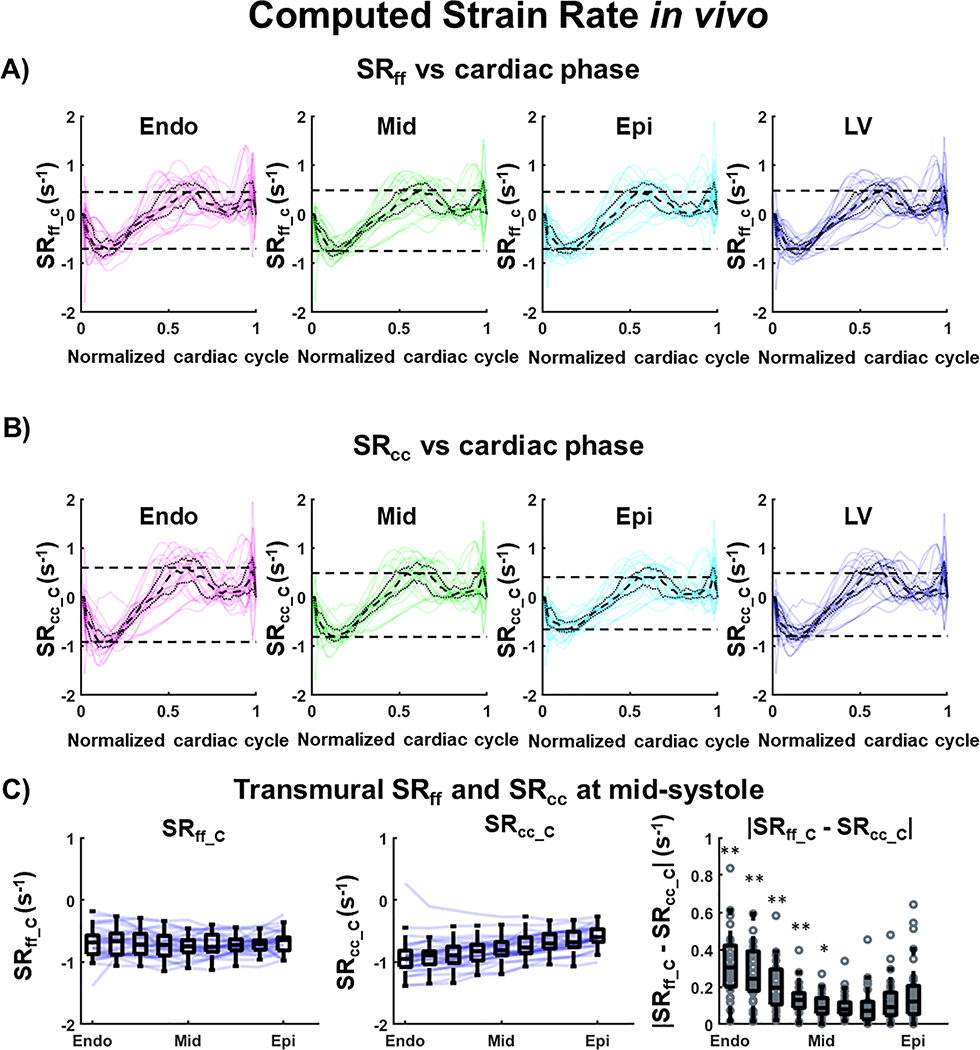
Strain rate comparisons between SR_{ff_C} and SR_{cc_C} during the cardiac cycle are shown in Figure 9A and 9B. Across volunteers at mid-systole, SR_{ff_C} was lower in magnitude than SR_{cc_C} in the endo layer (SR_{ff_C}= −0.68 [−0.88, −0.56] s⁻¹ vs SR_{cc_C}= −0.90 [−1.04, −0.80] s⁻¹, p<0.001) and in the mid layer (SR_{ff_C}= −0.75 [−0.84, −0.63] s⁻¹ vs SR_{cc_C}= −0.80 [−0.90, −0.67], p=0.008) and larger in the epi layer (SR_{ff_C}= −0.70 [−0.79, −0.64] s⁻¹ vs SR_{cc_C}= −0.64 [−0.72, −0.52], p=0.116). In mid-systole across the whole SA LV, statistical differences were observed between SR_{ff_C} and SR_{cc_C} (SR_{ff_C}= −0.70 [−0.81, −0.62] s⁻¹ vs SR_{cc_C}= −0.80 [−0.87, −0.63], p=0.012). As shown in Figure 9C, SR_{ff_C} was transmurally uniform compared to SR_{cc_C,} which exhibited a transmural gradient. Transmural distribution and statistical differences between SR_{ff_C} and SR_{cc_C} are reported in Table 1.

Figure 9:

Cardiac strain values across volunteers (N=30) calculated after combining cDTI and DENSE. (A) Computed Myofiber strain rate (SR_{ff_C}) and (B) circumferential strain rate (SR_{cc_C}) at endo, mid, epi layers, and across the left ventricular (LV) wall. The black dashed and dotted lines represent the median and the first and third quartile across volunteers; the red dashed line provides a −0.15 strain reference; the colored solid lines are individual medians per volunteers. (C) Transmural distribution of SR_{ff_C}, SR_{cc_C}, and of the absolute difference of SR_{ff_C} and SR_{cc_C} at mid-systole. Blue solid lines represent the transmural median per volunteer and the box plots represent the median and IQR across volunteers. Statistical differences between SR_{ff_C} and SR_{cc_C} have been assessed using a pair-wise Wilcoxon sign rank test: p-values<0.01 are represented by (**) and p-values<0.05 by (*).

Discussion

This work builds on previous efforts to combine cDTI and DENSE data and represents one of the first approaches to measure E_ff in vivo in humans. In this study, a new, efficient pipeline was proposed to combine microstructural and functional data in order to estimate myofiber strains. The result is the largest report (N=30) to date on in vivo E_ff in humans. At peak systole in the LV, E_ff was found to be transmurally uniform, while E_cc displayed a transmural gradient. The precision of the proposed post-processing pipeline was also assessed using a computational phantom, which demonstrated that the uncertainty in myofiber strain may be impacted by an uncertainty in myofiber orientation.

DENSE acquisition

Cardiac strains measured using only DENSE imaging were comparable to those in previous reports. In our work, the magnitude of measured circumferential strain was shown to increase from the base through the mid LV and to the apex (E_{cc_M}= −0.15 [−0.17, −0.12], −0.18 [−0.19, −0.16], −0.19 [−0.21, −0.18] respectively), which was also observed by Del-Cantos et al. (23) using MR Tagging (E_cc= −17.2±3.1, −20.1±3.1, −20.3±3.0 in base, mid, and apex, respectively). The magnitude of longitudinal strain across slices (E_{ll_M}= −0.15 [−0.16, −0.12], −0.15 [−0.18, −0.13], −0.14 [−0.16, −0.12]) corresponded to previous report of E_ll using DENSE (4) (E_ll= −0.16±0.02), but were slightly lower than global longitudinal strain (GLS) measured with feature tracking (24) (GLS= −0.20, CI: −0.21, −0.19) or Ultrasound imaging (GLS=−0.17±0.05/−0.16±0.05 in women/men) (25). Radial strain, E_rr (E_{rr_M} = 0.11 [0.02, 0.24], 0.14 [0.08, 0.22], 0.10 [0.01, 0.19] in apex, mid, and base, respectively) was found significantly lower than other reports using DENSE (E_rr=0.42±0.11) in Moore et al. (26) and (E_rr=0.33±0.10) in Zhong et al. (4). Cao et al. (27) showed a poor agreement in E_rr between DENSE (E_rr=0.4 ± 0.28), tagging (E_rr=0.32 ± 0.24) and three feature tracking methods (E_rr=0.47 0.26, E_rr=0.64 ± 0.33, E_rr=0.23 ± 0.9). The DENSE processing pipeline has been shown in previous in silico work (15,28) to induce significant error in computing E_rr, which may account for the poor reproducibility of E_rr (29–32), and the wide range of radial strain values reported in the literature.

cDTI acquisition

The cDTI acquisitions were acquired with a high-resolution protocol (1.6×1.6×8mm) compared to previous studies. Tensor invariants, such as MD and FA, and myofiber HA were reported. Across the thirty volunteers MD (1.59 [1.47, 1.67] x 10⁻³ mm²/s) and FA (0.38 [0.34 0.41] A.U.) were both in the range of previous reports using a similar motion compensated spin-echo approach (7,8,21,33,34).

The HA transmural distribution measured here (HA= 40.4 [21.7, 49.8] °, 2.0 [−0.1, 5.8] ° and −26.5 [−33.3, 4.6] ° at endo, mid, and epi, respectively) was also comparable to ex vivo (5) (HA= 66 ± 15, - 41 ± 26 ° at endo and epi, respectively) and in vivo reports (35) (HA= 37.2 [IQR: 3.9] −47.5 [IQR: 15.1] ° at endo, and epi, respectively).

Combination of cDTI and DENSE acquisitions

The proposed post-processing approach to combine cDTI and DENSE is in continuity of the study done by Verzhbinsky et al. (15). In this previous study, two SA slices of 3D displacement encoding DENSE were acquired immediately above and below one SA cDTI to estimate E_ff. In this work instead, a stack of 2D SA and LA DENSE slices were combined with the cDTI data. Unlike previous work, this pipeline employs a DENSE protocol that can be acquired in a single breath-hold per slice, which results in shorter total acquisition times. Additionally, because this approach relies on 2D displacements in the SA and LA planes, it is compatible with other 2D displacement encoding methods, such as tagging and feature tracking. However, an additional post-processing step is required to transform the 2D displacement fields into a registered 3D displacement field. For each of the post-processing steps described in Figure 2, noise may be introduced in the measures and may affect the accuracy of the proposed pipeline to estimate E_ff.

Uncertainty in cDTI

Measuring microstructural organization in the beating heart remains a major challenge. Both respiratory and cardiac bulk motion are sources of error that can lead to uncertainty in the cDTI metrics, which may be reflected in the computed E_ff. By adding variance to the myofiber orientation field, myofibers no longer lie exactly in the circumferential-longitudinal plane. As a result, strains along the perturbed myofibers include a component of radial thickening, leading to a positive shift in the E_ff estimation. This can be seen in the in silico experiment where the overall IQR of an idealistic transmural HA distribution increases (Figure 5). In vivo, the uncertainty in myofiber orientation cannot be directly measured through the HA IQR and instead has to be estimated using a bootstrapping approach. Here, MD and FA uncertainty (dMD= 0.31 [0.21, 0.41] x 10⁻³ mm²/s, dFA= 0.23 [0.20, 0.26] A.U.) were found comparable to the work of Aliotta et al. (21) (dMD= 0.38 ± 0.02 × 10⁻³mm²/s, dFA=0.20 ± 0.01 A.U.). However, Aliotta et al. also reported a lower uncertainty of the first eigenvector (dE₁= 15.5 ± 1.2 °) compared to the one measured on HA here (dHA= 34.5 [29.7, 48.3] °). This difference may be due to the fact that only 6 diffusion encoding directions were acquired in this work, which has been shown to increase uncertainty in myofiber orientation (36). According to our in silico experiment, this uncertainty in the myofiber orientation may result in a more positive shift of E_ff and thus the E_ff magnitude computed in this work may be slightly underestimated.

Myofiber Strain in vivo

Using the proposed pipeline to combine cDTI and DENSE, myofiber strain E_ff was computed in thirty volunteers in vivo. At peak systole and across volunteers E_ff was estimated to E_{ff_C}= −0.14 [−0.16, −0.13]. Early work by Tseng et al. (12) found a slightly lower magnitude of myofiber strain (E_ff= −0.12 ± 0.01) using cDTI and velocity encoding. McGowan et al. (37) found a similar strain (E_ff= −0.14±0.01) while Wang et al. (13) found a higher magnitude (E_ff= −0.18 ± 0.03), using both MRI tagging imaging and ex vivo myofiber orientations. Very similar results were found in our previous work (15) in healthy swine (E_ff= −0.14 [−0.16, −0,14]) using in vivo cDTI and 3D displacement encoded DENSE. Slightly lower E_ff magnitudes were obtained in healthy human in vivo (E_ff= −0.13 ± 0.02) using a single DENSE slice with an imposed incompressibility constraint (14).

Previous computational modeling work (38) has used an “adaptation hypothesis” to demonstrate that the observed transmural myofiber orientation gradient is optimal for minimizing the spatial variance of myofiber shortening. This work confirms that myofiber shortening has, in fact, a low spatial variance while in contrast, circumferential strain displays a transmural gradient. This work has also demonstrated that the circumferential strain can only be assumed equivalent to the myofiber strain in a fine layer between the mid-wall and epicardium, where the HA is approximately 0° and the myofiber and circumferential directions are aligned.

Limitations

One limitation of this study was the limited heart coverage of the cDTI acquisition, which only permitted analysis of myofiber strains at a single mid-ventricular LV position. Thus, it was not possible to estimate the myofiber strain distribution in the full LV from base to apex. However, several approaches have been proposed to increase the spatial coverage of cDTI (20,39,40) and should be considered in future work to develop E_ff maps that span the entire LV.

Another limitation is that myofiber strains were estimated through a post-processing pipeline that combines information acquired with two different sequences. These two datasets were measured with different readouts (Spiral vs EPI), spatial resolutions (2.5×2.5×8mm vs 1.6×1.6×8mm), and contrasts (TE/TR=1.08/15ms vs TE/TR=55/4000ms). Even though care was taken to co-register the two datasets retrospectively, the acquisitions may present some geometrical and spatial differences and may not overlap perfectly. This problem would be substantially alleviated by sequences that encode inherently registered displacement and diffusion information into the same sequence (12).

In this work, we use the commonly referenced term “myofiber”, which may incorrectly imply continuous fiber bundles that run throughout the heart. The heart is composed of a continuously branching syncytium of cardiomyocytes. The cDTI method doesn’t measure directly individual cardiomyocyte cell orientations, but rather the orientation of an aggregate of cardiomyocytes within a voxel. In general, in vivo and ex vivo cDTI studies have reported lower HA range compared to histology reports. Streeter et al. (2) showed that transmural HA distributions are mostly linear in most of the mid-wall and become steeper at the extreme endocardium and epicardium regions. Even though high-resolution cDTI was acquired here, HA distributions obtained were mostly linear. Additional work is needed to better understand the differences between some previous histologic reports and the data from in vivo cDTI.

Conclusion

We proposed an efficient acquisition and analysis method to combine microstructural cDTI and functional cine DENSE to estimate in vivo myofiber strain (E_ff). We demonstrated that it is possible to measure in vivo myofiber strain in a healthy human population in 10 minutes per subject. Myofiber strain is a mechanistically relevant metric that is spatially uniform in healthy populations, making it an intriguing candidate for the evaluation of local cardiomyocyte contractility in assessing cardiovascular dysfunction.

Supplementary Material

VIDEO S1

Supporting Information Video S1: Post-processing steps used to combine DENSE and cDTI data and calculate myofiber strain Eff. After cDTI reconstruction (A1), myofiber orientations were represented at nodes using one node per voxel. Cardiac displacement fields were also represented using nodes after the DENSE reconstruction (A2 & A3). (B) 2D Displacement fields from long axis (LA) and short axis (SA) are combined to obtain a SA 3D displacement field. (C) The SA 3D displacement field is interpolated and differentiated to generate a deformed cine of myofiber orientations during the cardiac cycle. (D) Finally, cardiac strains are calculated from the SA 3D displacement field and the myofiber orientations and using the beginning of systole as the reference configuration.