Simultaneous deep generative modeling and clustering of single cell genomic data

Abstract

Recent advances in single-cell technologies, including single-cell ATAC-seq (scATAC-seq), have enabled large-scale profiling of the chromatin accessibility landscape at the single cell level. However, the characteristics of scATAC-seq data, including high sparsity and high dimensionality, have greatly complicated the computational analysis. Here, we proposed scDEC, a computational tool for single cell ATAC-seq analysis with deep generative neural networks. scDEC is built on a pair of generative adversarial networks (GANs), and is capable of learning the latent representation and inferring the cell labels, simultaneously. In a series of experiments, scDEC demonstrates superior performance over other tools in scATAC-seq analysis across multiple datasets and experimental settings. In downstream applications, we demonstrated that the generative power of scDEC helps to infer the trajectory and intermediate state of cells during differentiation and the latent features learned by scDEC can potentially reveal both biological cell types and within-cell-type variations. We also showed that it is possible to extend scDEC for the integrative analysis of multi-modal single cell data.

The organization of chromatin accessibility across the whole genome reflects an epigenetic landscape of gene regulation^1,2. With the recent development in single-cell technology, it becomes feasible to characterize the epigenetic landscape of individual cells³. In particular, single-cell ATAC-seq (scATAC-seq) is an efficient method for the study of variation in chromatin accessibility both between and within populations at single cell level^4,5. However, the analysis of scATAC-seq presents unique methodological challenges due to the high dimensionality (hundreds of thousands possible peaks) and high data sparsity (only 1–10% peaks are detected per cell) ⁶.

Several computational approaches have been proposed to tackle the challenges in scATAC-seq analysis. scABC estimated weights of cells based on the number of distinct reads and applied a weighted K-medoids clustering to infer cell types⁷. cisTopic applied latent Dirichlet allocation (LDA) as a probabilistic model to identify the cis-regulatory topics enriched in different cells by optimizing topic-cell probability and region-topic probability simultaneously⁸. Cusanovich et al. proposed a pipeline which performs the term frequency-inverse document frequency transformation (TF-IDF) and singular value decomposition (SVD) iteratively to get a low dimensional representation of scATAC-seq data^4,9. Scasat introduced another pipeline which involved Jaccard similarity measure and multidimensional scaling (MDS) to reduce the high dimensionality in scATAC data¹⁰. SnapATAC divided genome into bins with equal size and builds a bins-by-cells binary count matrix and then applied principle component analysis (PCA) for a dimension reduction¹¹. Recently, deep generative models have emerged as a powerful framework for both representation learning and data generation^12–14. A newly developed method SCALE utilized a variational autoencoder (VAE) to learn the latent features of scATAC-seq data and then used a K-means by default for clustering the latent features¹⁵.

Here, we proposed a new approach for analyzing scATAC-seq data by simultaneously learning the Deep Embedding and Clustering of the cells in an unsupervised manner. Our method, named scDEC, was based on learning a pair of generative adversarial networks (GANs) (Fig. 1). Such a symmetrical and paired GAN architecture has been recently successfully applied to image style transfer¹⁶ and density estimation¹⁷. Here, we adopted this architecture to the new task of unsupervised clustering and applied it to the analysis of single cell genomic data. Unlike all current methods discussed above, where an external method (e.g., K-means) is typically required for clustering the latent features, the cell clustering process is directly modeled by neural networks in our method. Thus, cell clustering and latent feature representation learning will be jointly optimized during the training process. In other words, scDEC enables simultaneous learning of latent features and cell clustering. We demonstrated the advantage of this approach in a series of experiments, where scDEC showed superiority over competing methods. We also illustrated several downstream applications of scDEC in scATAC-seq analysis, including trajectory inference, donor effect removal and latent feature interpretation. Finally, we extend scDEC to multi-modal single cell analysis and demonstrate its effectiveness in a real data example.

Fig. 1.

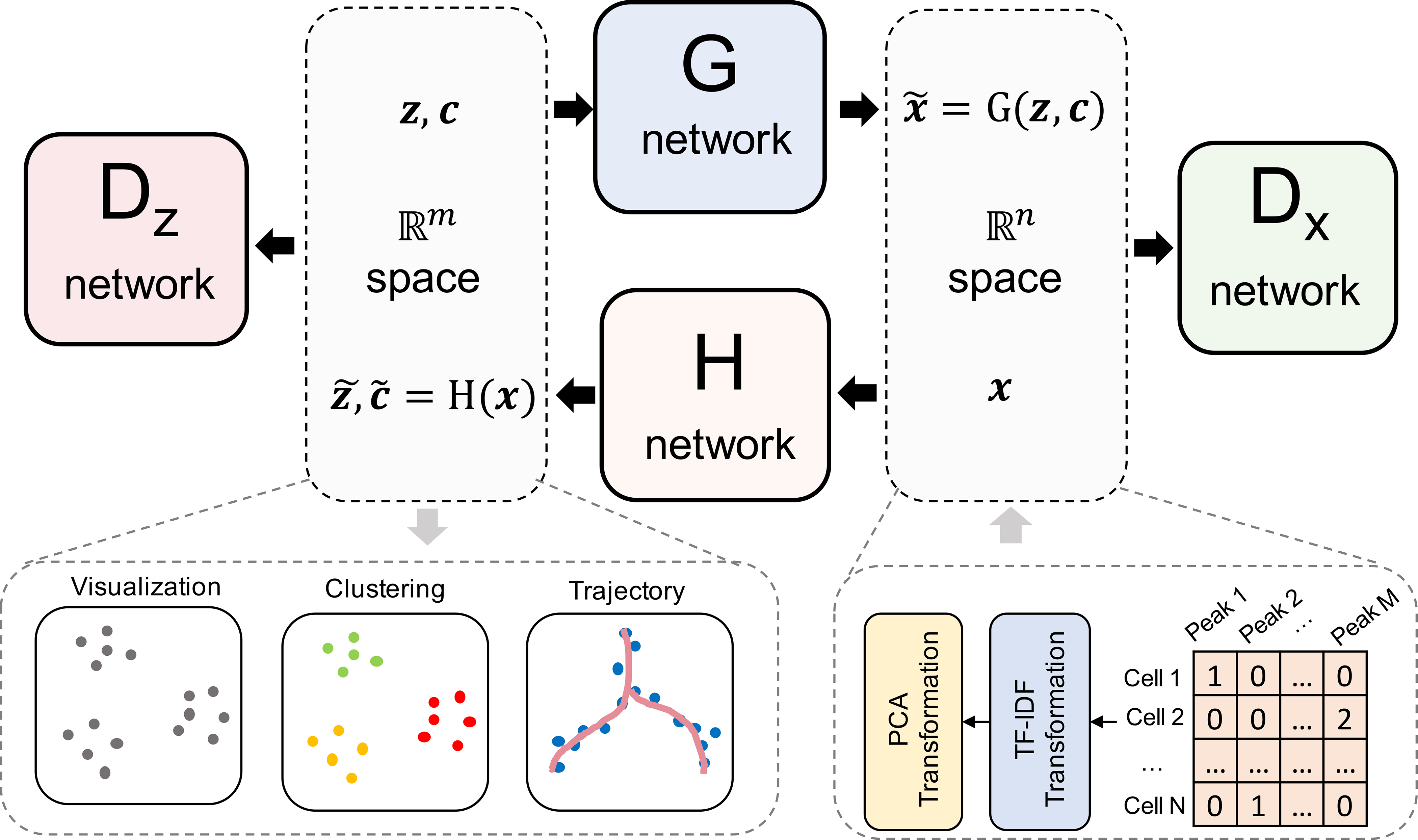
The illustration of scDEC model. The read count matrix of scATAC-seq will first be preprocessed by a TF-IDF transformation and a PCA dimension reduction (e.g., n = 20) before it is fed to the scDEC model. In the latent space, latent variables z and c sampled from a Gaussian distribution and a Category distribution respectively, will be concatenated together before they are fed to the G network. The H network has two outputs of which one corresponds to the latent embedding $(\tilde{\mathit{z}})$ and one corresponds to the estimated cluster label $(\tilde{\mathit{c}})$ through a softmax function. The D_x network works as a discriminator for discerning the true scATAC-seq data (x) from the generated data $(\tilde{\mathit{x}})$. The D_z network is another discriminator for distinguishing the learned continuous latent variable $(\tilde{\mathit{z}})$ from the real continuous latent variable (z).

Results

Overview of scDEC model

scDEC consists of two GAN models, which are utilized for transformations between latent space and data space (Fig. 1). The scATAC-seq data is first preprocessed through a TF-IDF transformation and a PCA dimension reduction before fed to the scDEC model. Assuming the input scATAC-seq data contains K cell types, a continuous latent variable z and a discrete latent variable c are introduced, where $\mathit{z}\sim \mathcal{N}(\mathbf{0},\mathbf{I})$ and c ~ Cat(K, w), respectively. We also provide an approach for estimating the number of cell subpopulations if K is unknown (Methods). The forward transformation through the G network can be considered as a process of conditional generation given an encoded style (z) and an indicated cluster label (c). The backward transformation through the H network aims at encoding a data point x to the latent space and inferring the cluster label, simultaneously. If we assume the last layer of H network contains m nodes (m> K), then $\tilde{\mathit{z}}$ denotes the output of the first m- K nodes and $\tilde{\mathit{c}}$ denotes the output of the remaining K nodes with an additional softmax function. D_x and D_z are two discriminator networks which are used for matching the distributions of data $\tilde{\mathit{x}}$ and $\tilde{\mathit{z}}$ to the empirical distribution of the data and latent variable distribution, respectively. (G, D_x) and (H, D_z) can be considered as two GAN models that are jointly trained. The G and H network each contains 10 fully-connected layers while D_x and D_z each has two fully-connected layers (see detailed hyperparameters in Supplementary Table 1). Note that the weights w in the Category distribution is also learned automatically via an updating scheme according to the feedback of inferred cluster labels by $\tilde{\mathit{c}}$ (Methods). After model training, the cluster labels are inferred based on $\tilde{\mathit{c}}$ (Methods). The output of the last layer of H network combined with $\tilde{\mathit{z}}$ and $\tilde{\mathit{c}}$ (before softmax) are useful for downstream analysis such as data visualization and trajectory analysis.

scDEC automatically identifies cell types in scATAC-seq data

To demonstrate the ability of scDEC for revealing differences between different cell subpopulations and identifying cell types in an unsupervised manner, we tested scDEC on four benchmark scATAC-seq datasets across different number of cells and cell types (see statistics and abbreviations in Supplementary Figure 1). Specifically, scDEC was benchmarked against six baseline comparison methods, including scABC⁷, SCALE¹⁵, cisTopic⁸, Cusanovich2018^4,9, Scasat¹⁰ and SnapATAC¹¹ (Methods). The performance of a method was evaluated on 1) whether different cell subpopulations can be clearly separated in a low-dimensional space, and 2) whether true cell type labels can be accurately inferred by clustering. To address the first question, we first applied each method to conduct a dimension reduction or to extract the latent features. The latent dimension was set to 15 for the two datasets with relatively smaller number of cells and cell types, and 20 for the two larger datasets. For each method, we constructed a t-SNE¹⁸ or UMAP¹⁹ plot based on the latent features and then visualized with the FACS sorting cell labels on the plot to see whether the subpopulations were well separated. To address the second question, for each method we evaluated its clustering results based on the FACS sorting cell labels using three commonly used metrics, namely Normalized Mutual Information (NMI), Adjusted Rand Index (ARI) and Homogeneity score (Homogeneity) (Methods). Since five of the comparing methods (except scABC) focused on learning a low-dimensional representation and require an additional clustering step, we used Louvain clustering²⁰, which was recommended by a benchmark study⁶, for clustering the latent features learned by these methods. The results are summarized for each dataset as below.

InSilico dataset⁵.

This dataset is an in silico mixture constructed by artificially combining six individual scATAC-seq experiments which were separately conducted on a different cell line. It is observed that cells from a minor cell type TF-1 (6.83%, in purple) are dispersed into several clusters by SCALE, Cusanovich2018, Scasat and SnapATAC while cisTopic and scDEC can well maintain the close distance in the low-dimensional representation (Fig. 2a). scDEC achieves an NMI of 0.871, an ARI of 0.896, and a Homogeneity of 0.866, which outperforms the best baseline method scABC (NMI=0.822, AIR=0.855, and Homogeneity=0.840) by a noticeable margin (Fig. 2e and Supplementary Figure 2).

Fig. 2.

Evaluation of scDEC compared with other baseline methods. a. Visualization of InSilico dataset by different methods. b. Visualization of Forebrain dataset by different methods. c. Visualization of Splenocyte dataset by different methods. d. Visualization of All_blood dataset by different methods. e. Clustering results of different methods across four datasets. f. Performance of different methods under different dropout rate on the Forebrain dataset.

Forebrain dataset²¹.

This dataset was derived from P56 mouse forebrain cells which contained eight different cell groups in adult mouse forebrain. Interestingly, all the baseline methods fail to distinguish three subtypes of excitatory neuron cells (EX1, EX2 and EX3) while scDEC shows a relatively clear separation among these three subpopulations of cells (Fig. 2b). Again, scDEC demonstrates a superior clustering performance by achieving the highest NMI of 0.750, ARI of 0.663 and Homogeneity of 0.759 (Fig. 2e and Supplementary Figure 3).

Splenocyte dataset²².

This dataset was collected from a mixture of mouse splenocytes after removing red blood cells, which finally resulted in 12 cell subpopulations. A major cell type follicular B cells (FO B, 42.89%), together with marginal zone B cells (MZ B) and transitional B cells (Trans B) are more or less mixed together by all baseline methods while scDEC illustrates a clearer separation (Fig. 2c). As the largest dataset (around 3k cells) among the four datasets, scDEC still achieves the highest NMI of 0.839, ARI of 0.884 and Homogeneity of 0.829 (Fig. 2e and Supplementary Figure 4).

All blood dataset²³.

This dataset involves cellular differentiation of multipotent cells during human hematopoiesis, containing 13 subpopulations of cells in total. Three types of cells, including monocyte cells (Mono), plasmacytoid dendritic cells (pDC) and CLP cells, can only be separated from other cells by cisTopic, Scasat and scDEC (Fig. 2d). scDEC still achieves the highest ARI (0.309) among all comparing methods. The overall clustering performance is comparable with Cusanovich2018 and slightly lower than cisTopic (Fig. 2e and Supplementary Figure 5).

scDEC achieves the best or second best (in one case) clustering results across multiple scATAC-seq datasets. scDEC shows consistently superior performance if we replace the Louvain clustering with the commonly used K-means clustering for the comparison methods (Supplementary Figure 6). Besides, the t-SNE visualizations of scDEC colored by the cluster label identified by scDEC across the above four benchmark datasets are also provided (Supplementary Figure 7). We also note that the performance of scDEC is not sensitive to the dimension of latent features (Supplementary Figure 8).

Next, we further investigate the performance of different methods at different dropout rate, in order to assess the ability of handing scATAC-seq data with different degree of sparsity. We downsampled the original reads in the Forebrain dataset by randomly dropped out the non-zero entities in the read count matrix with probability equal to the dropout rate. scDEC consistently demonstrates the best performance w.r.t the ARI metric for clustering at different dropout rate ranging from 0 to 50%. At the dropout rate of 50%, scDEC achieves an ARI of 0.279, compared to 0.202 of the best comparison method cisTopic (Fig. 2f).

scDEC facilitates cell type-specific motif discovery and trajectory inference

We next explore whether scDEC can help identity cell-type specific motifs, which is essential for understanding the context-specific gene regulation. To achieve this, we first applied scDEC model to the mouse forebrain dataset²¹ to infer the cluster label for each individual cell, and used chromVAR²⁴ to identify cluster-specific enriched motifs from the JASPAR database²⁵. We ranked cluster-specific enriched motifs (Methods) and discovered several significant motif enrichment patterns (Fig. 3a, Supplementary Table 2). Both single cluster-specific motifs and the co-occurrence of motifs in two (cluster 1 and 6) or three clusters (cluster 2,3 and 4) are observed, which might reveal the co-regulation mechanism underlying the corresponding multiple TFs. For example, En1, which is enriched in cluster 1 (one-sided Mann–Whitney U test, p-value=6.14×10⁻⁵¹), is a well-known marker for the brain fate in astrocytes (AC)²⁶. It is reported that Neurod2 (p-value=4.50×10⁻²³⁹) regulates the cortical projection neuron which constitutes the major excitatory neuron (EX) population²⁷. Meis1 (p-value=6.68×10⁻⁵⁹) was known to have crucial functions in neural differentiation from neural progenitors²⁸. Vax1 (p-value=2.84×10⁻¹²⁶) is a novel homeobox-containing gene that regulates the development of the basal forebrain²⁹. The impact of Elk1 (p-value=1.87 × 10⁻⁷¹) deficiency was proved to indicate the microglial (MG) activation³⁰. The compound loss of Sox9 (p-value=3.81×10⁻¹³⁷) may lead to a further decrease in oligodendrocyte (OC) progenitors³¹. Interestingly, among the three similar cell types (EX1-EX3), we also discovered several motifs that were only enriched in one or two specific clusters that correspond to EX cells identified by scDEC (Supplementary Figure 9). Several example literature-validated motifs are demonstrated in the t-SNE visualization according to the enrichment score calculated by chromVAR (Fig. 3b).

Fig. 3.

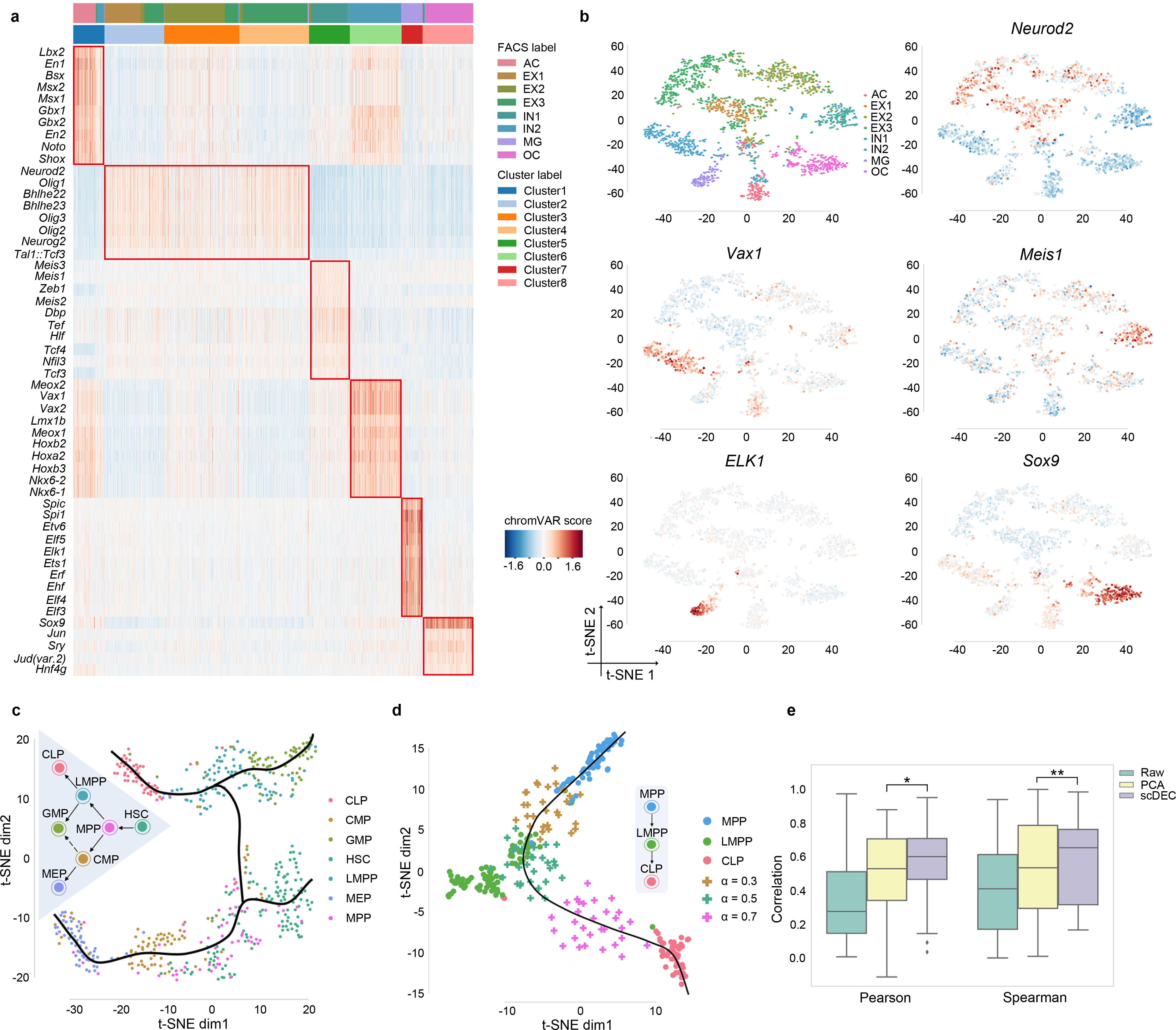
Cluster-specific motif recovery and trajectory inference. a. Heatmap of enriched motifs, each row denotes a motif and each column denotes a cell. Both cluster label and FACS label were provided and aligned. b. The t-SNE visualization of several literature-validated motifs. c. The hematopoiesis differentiation trajectory inferred by scDEC. d. The generated intermediate state between MPP and CLP. 30 data points were generated at different generation coefficient α. e. The generated intermediate scATAC data by interpolation on the latent label indicator has a higher correlation with the meta cell (the average profile of ground truth cells) than the scATAC-seq that were directly interpolated on the raw data and PCA reduced data. * p-value<1.28×10⁻¹⁶, ** p-value< 4.40×10⁻⁸

Next, we applied scDEC to trajectory inference during the hematopoiesis differentiation. We collected the cells from the donor BM0828 of the All blood dataset, which contains 533 cells across 7 subpopulations at different stage of differentiation. After obtaining the low-dimensional representation and the inferred cluster labels of scATAC-seq data, the smooth curves are annotated, which represent different cell lineages with the help of Slingshot software³² (Fig. 3c). The smooth curves with a tree-based structure are largely consistent with the true hematopoietic differentiation tree. Although it has been proved that CMP can differentiate into both GMP and MEP³³, only differentiation path from CMP to MEP is observed in this dataset. We then took the cells from MPP, LMPP and CLP for a further study, where there exists a differentiation path (MPP→LMPP→CLP). To fully exploit the generation power of scDEC, we first left LMPP out as the target cells for imputation and trained scDEC based on the remaining cells composing of only MPP and CLP cells. Then we imputed data by interpolating the latent label indicator (Methods) and visualized the imputed data together with the true data. Interestingly, when the interpolation coefficient α changes from 0 to 1, the imputed data seem to capture the dynamics differentiation path from MPP to CLP. Specifically, the generated scATAC-seq data are similar to the real LMPP data according to t-SNE visualization when α = 0.5 (Fig. 3d). Next, we asked whether the interpolation on the latent indicator is a more effective way of data generation than directly interpolating on the raw scATAC-seq. We averaged all the scATAC-seq data of LMPP cells as a meta-cell and calculated the Pearson correlation between generated data and meta-cell. The generated data by scDEC achieves a significantly higher correlation than generated data by direct interpolation and interpolation on PCA reduced data (Fig. 3e and Supplementary Table 3). To sum up, the generation power of scDEC shed light on recovering the missing cell types of scATAC data and exploring the intermediate state of two neighboring cell types of scATAC-seq data.

scDEC disentangles donor effect and promotes interpretation of latent features

Single-cell experiments are often conducted with notable differences in capturing time, equipment and even technology platforms, which may introduce batch effects in the data. To evaluate whether scDEC can automatically correct or alleviate batch effect in the training process. We collected three cell types (CLP, LMPP and MPP) of human hematopoietic cells from two donors with donor id BM0828 (donor1) and BM1077 (donor2), respectively²³. We mixed the cells from two donors together (200 cells from donor1 and 180 cells from donor2) and evaluated how well the variation due to cell types and donors are resolved in the embedding (i.e., latent representation) learned by scDEC and alternative methods. Note that the latent dimension of each method was fixed to 13 and no donor information was revealed to each method. Since the embedding by scDEC depends on the number of clusters K, we varied K from 2 to 6 and examine the gap statistic plot (Fig. 4d), which exhibited two peaks at K=3 and K=5, respectively. The embedding results for scDEC and alternative methods were shown in Fig. 4a and Supplementary Figure 10–13. It is seen that the three cell types as well as the donor effects in two of the cell types are well captured by scDEC (K=5), cisTopics and SnapATAC, but not by SCALE, whereas the donor effect in the third cell type (CLP) is too small to be discernible. It is interesting that at K=3 (the first peak of the gap statistic) the clustering results by scDEC matches the three cell types almost perfectly. Specifically, SCALE is basically unable to separate the three type of cells clearly. cisTopic and SnapATAC cannot alleviate the donor effect in LMPP or MPP cells as the same type of cells from two different donors were separated with a notable distance in the t-SNE plot (Fig. 4a). Considering the first mode where K=3, only 9 cells from donor1 and 17 cells from donor2 were wrongly clustered by scDEC, which illustrates a total error rate of 6.86%. Besides, scDEC also demonstrates an NMI of 0.754, ARI of 0.805 and Homogeneity of 0.757 which outperforms other comparison methods by a large margin (Fig. 4b and Supplementary Figure 13). In this sense our method can be used to adjust for donor- or batch- effects in clustering and visualization.

Fig. 4.

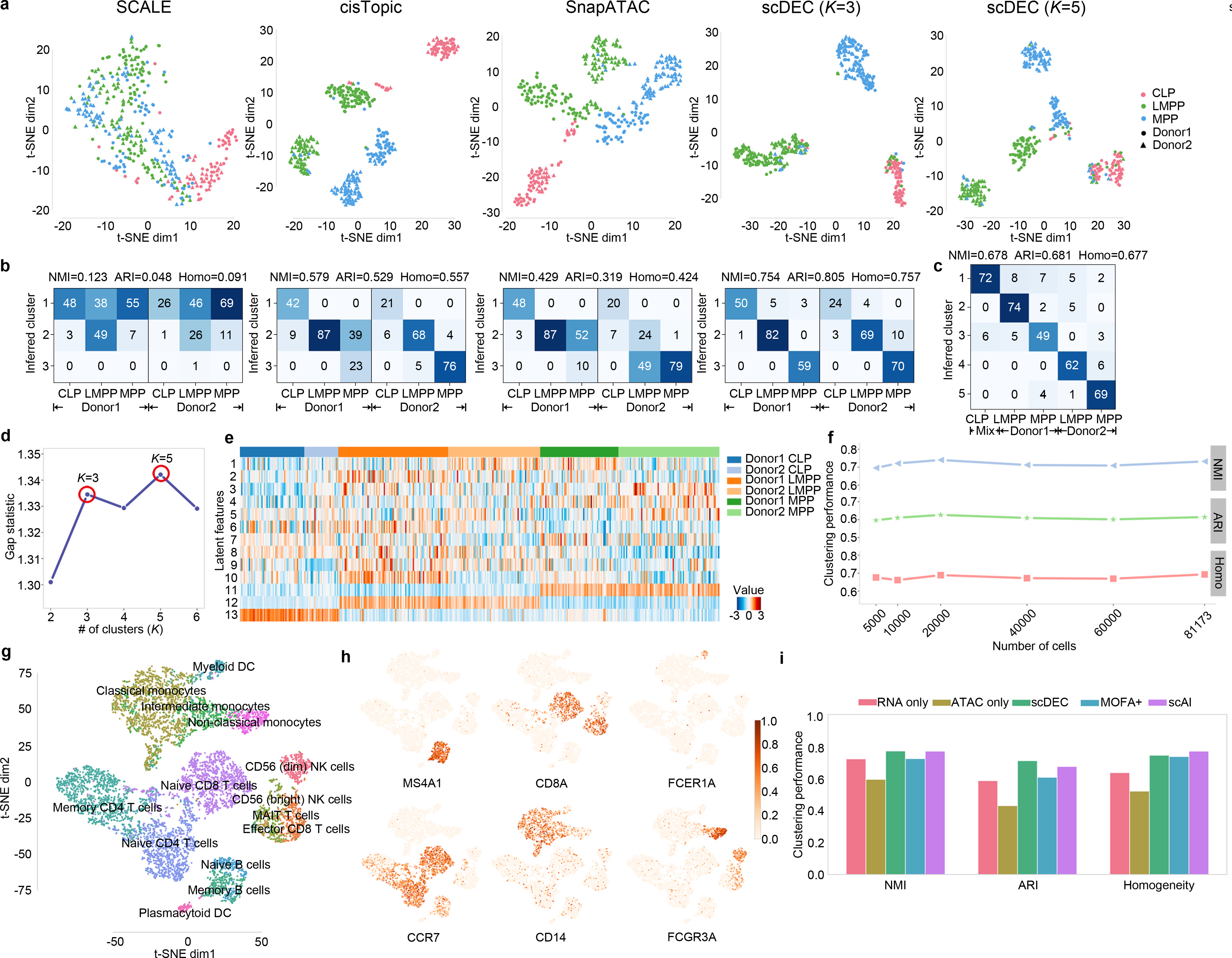
scDEC alleviates donor effect and is applicable to large dataset and multi-modal single cell dataset. a. The t-SNE visualization, for CLP, LMPP, MPP cells of the latent features learned by different methods. Different colors denote different cell types and different shape (circle or triangle) represents which donor it comes from. For scDEC, different K (3 and 5) results in different latent features visualization. b. The confusion matrix of the clustering by scDEC and comparing methods (K=3). The NMI, ARI and Homogeneity are also annotated on the top of the confusion matrix. c. The confusion matrix of the clustering by scDEC when K=5. The x-axis denotes the where the cell is coming from while the y-axis denotes the inferred cluster. Mix CLP denotes CLP cells from both donors. d. The gap statistic shows two modes at K=3 and K=5, respectively. e. The visualization of the latent features learned by scDEC. The first 10 dimensions correspond to the continuous latent variable $\tilde{\mathit{z}}$ and the last three features correspond to the discrete latent variable $\tilde{\mathit{c}}$. f. The clustering performance of scDEC when applying to a large mouse atlas dataset. g. The t-SNE visualization of around 10k PBMC cells colored by the annotated labels from the 10x Genomic R&D team. h. The same t-SNE plot colored by the normalized expression of the marker genes. i. The clustering performance of scDEC when applied to uni-modal single cell data and multi-modal single cell data (scRNA-seq and scATAC-seq measured in the same cell). The clustering performance of two comparison methods were also demonstrated.

Next, we carefully analyzed the latent feature learned by scDEC by visualization. We noticed that features corresponding to the latent discrete variable (feature 11–13) were highly correlated to biological cell types while other features more or less revealed within-cell-type variations (Fig. 4e). For example, feature 1 is highly expressed in the donor2 of LMPP and donor1 of MPP. Feature 10 can be a donor-specific indicator of LMPP. Besides, we proposed a strategy for mining motif information underlying the latent features (Supplementary Figure 14). Through the strategy, the top ranked motif (p-value=1×10⁻⁹⁰) for feature 2 is SP1, which was proved to affect multiple hematopoietic lineages³⁴. To sum up, the interpretable features in the latent space reveal both biological cell types and within-cell-type variations.

scDEC is capable of analyzing large scATAC-seq data

We further examine whether scDEC is applicable to extremely large scATAC-seq dataset. We collected a dataset from a mouse atlas study which contains 81,173 single cells from 13 adult mouse tissues using sci-ATAC-seq⁹. The original atlas study applies a computational pipeline to infer 40 cell types, which were regarded as “reference” cell label for the comparison of scDEC and other baselines methods. To investigate the scalability of scDEC, we randomly down-sampled the original dataset to different scale of dataset and scDEC shows a consistently good agreement with the reference cell label (Fig. 4f). For the full scale of the dataset, scDEC achieves an NMI of 0.732, ARI of 0.614 and Homogeneity of 0.693 while most comparison methods failed to handle the full dataset due to the memory limitation (500 GB for the computational environment). We compared scDEC to the deep learning method SCALE and noticed that scDEC achieves a higher consistency with “reference” label but a little slower running time (Supplementary Figure 15). We also noticed that the scDEC successfully identified most of the major reference cell type for each tissue (Supplementary Figure 16).

scDEC enables integrative analysis of multi-modal single cell data

It is natural to extend scDEC in multi-modal single cell data analysis where multiple types of molecules within the same cell are measured simultaneously. Here, we apply scDEC to a dataset from 10x Genomics which contains around 10k peripheral blood mononuclear cells (PBMC) with both measurements of scRNA-seq and scATAC-seq for each cell. Note that the granulocytes were removed by cell sorting of this dataset. After data preprocessing to scRNA-seq and scATAC-seq data, respectively, the two types of data are concatenated and fed to scDEC model (see Methods). As the PBMC dataset has no FACS sorting cell type labels, we used the cell type labels which were annotated by the 10x Genomics R&D team as surrogates. Most annotated cell types can be well distinguished by scDEC through the t-SNE visualization of the latent features (Fig. 4g). The visualization of different subpopulations of monocytes, T cells, and B cells also demonstrates a clearer separation than using scRNA-seq or scATAC-seq only (Supplementary Figure 17). The differentiable expression profiles of the several marker genes for PBMC cell types are illustrated in Fig. 4h. To name a few, MS4A1 is a well-known marker gene for B cells³⁵, which is highly expressed in a cluster identified by scDEC. FCER1A, a marker gene for dendritic cells (DC)³⁶, is observed to be highly expressed in a tiny cluster identified by scDEC. Given surrogate cell labels, we evaluate the clustering performance of scDEC when applied to one type of data (scRNA-seq or scATAC-seq) and both types of single cell data, respectively. scDEC achieves a significantly better clustering performance using both types of single cell data than using scRNA-seq or scATAC-seq alone (Fig. 4i). Finally, we also compare scDEC to two recent methods on multi-modal single cell data analysis. scDEC achieves a NMI of 0.779, ARI of 0.718, and Homogeneity score of 0.752, which outperforms MOFA+³⁷ and is comparable with scAI³⁸. To sum up, scDEC can be easily extended to integrative analysis of multi-modal single cell data analysis.

Discussion

In this study, we proposed scDEC for accurately characterizing cell subpopulations in scATAC-seq data using a deep generative model. Unlike previous studies that take dimension reduction and clustering as two independent tasks. scDEC intrinsically integrates the low-dimensional representation learning and unsupervised clustering together by carefully designing a GAN-based symmetrical architecture. scDEC can serve as a powerful tool for scATAC-seq data analysis, including visualization, clustering and trajectory analysis. In a series experiments, scDEC achieves competitive or superior performance compared to other baseline methods. In downstream applications, we focused on the generation power of scDEC, which can facilitate the intermediate cell state inference. The latent features learned by scDEC reveals both biological cell types and within-cell-type variations, which shed light on helping better understand the biological mechanism. Our examples also showed that scDEC can handle very large dataset and is applicable to multi-modal single cell data analysis.

We also provide several directions for improving scDEC. First, when applying scDEC to joint analysis of scRNA-seq and scATAC-seq data, it might be helpful for further enhance the clustering performance if scDEC model incorporates the relationship between genes and regulatory elements (REs). Second, the way of utilizing the generation power of scDEC can be further explored, especially in a complicated tree-based trajectory of cell differentiation or time-course single cell profiles of cell development. Third, we note that there are already several tools or pipeline for single cell batch-effect correction, such as Seurat-v3³⁹ and Harmony⁴⁰. It is interesting to explore how to integrate such procedure for data integrative analysis into scDEC model.

With scDEC, researchers could perform a scATAC-seq analysis or single cell joint ATAC/RNA-seq analysis of the cell types or tissues with interests. Then, one can simultaneously cluster single cells and uncover the biological findings underlying the learned latent features. We hope scDEC could help unveil the single-cell regulatory mechanism and contribute to understanding heterogeneous cell populations.

Methods

Data preprocessing

All the scATAC-seq datasets were uniformly preprocessed before fed to scDEC model. To reduce the level of noise, we only kept peaks that have at least one read count in more than 3% of the cells. Next, similar to Cusanovich et al⁹, we applied a term frequency-inverse document frequency (TF-IDF) transformation to the raw scATAC-seq count matrix, which is widely used technology in information retrieval and text mining^41,42. We calculated the “term frequency” by normalizing the raw reads count matrix for each cell through dividing the total reads count within that cell. The “inverse document frequency” will be calculated as the inverse frequency of each region to be accessible across all cells. The “inverse document frequency” will be log-transformed and multiplied by “term frequency”. The TF-IDF transformation helps increase proportionally to the number of times a peak appears in the cell, which gives a higher importance weight to the peaks with less frequency. Finally, a principle component analysis⁴³ (PCA) will be applied to reduce the dimension of the scATAC to 20, which is implemented with “Scikit-learn” package⁴⁴. scDEC shows robustness to the dimension of PCA (Supplementary Figure 8). The summary of all scATAC-seq datasets used in this study were provided in Supplementary Table 4.

Visualization

We use t-distributed stochastic neighbor embedding¹⁸ (t-SNE) as the default algorithm for visualization the latent features of scATAC-seq data learned by different methods by setting the visualization dimension to 2. The t-SNE was implemented with “Scikit-learn” package⁴⁴. The uniform manifold approximation and projection (UMAP)¹⁹ was also implemented as an additional visualization tool for latent features.

Adversarial training in scDEC model

The scDEC model consists a pair of two GAN models. For the forward GAN mapping, G network aims at conditionally generating samples ${\left\{{\tilde{\mathit{x}}}_i\right\}}_{i=1}^N$ that have a similar distribution to the observation data ${\left\{{\mathit{x}}_i\right\}}_{i=1}^N$ while the discriminator D_x tries to discern observation data (positive) from generated samples (negative). The backward mapping function H and the discriminator D_z aims to transform the data from data space to the latent space. Discriminators can be considered as binary classifiers where an input data point will be asserted to be positive (1) or negative (0). We use WGAN-GP⁴⁵ as the architecture for the GAN implementation where the gradient penalty of discriminators will be considered as an additional loss terms. We define the objective loss functions of the above four neural networks (G, H, D_x and D_z) in the training process as the following

$$\{\begin{array}{l}{\mathcal{L}}_{GAN}(\text{G})=-\underset{\mathit{z}\sim p(\mathit{z}),\mathbf{c}\sim \mathrm{Cat}(K,\mathit{w})}{\mathbb{E}}\left[{\text{D}}_x(\text{G}(\mathit{z},\mathit{c}))\right]\hfill \\ {\mathcal{L}}_{GAN}\left({\text{D}}_x\right)=-\underset{\mathit{x}\sim p(\mathit{x})}{\mathbb{E}}\left[{\text{D}}_x(\mathit{x})\right]+\underset{\mathit{z}\sim p(\mathit{z})\mathbf{c}\sim \mathrm{Cat}(K,\mathit{w})}{\mathbb{E}}\left[{\text{D}}_x(\text{G}(\mathit{z},\mathit{c}))\right]+\lambda \underset{\widehat{\mathit{x}}\sim \widehat{p}(\widehat{\mathit{x}})}{\mathbb{E}}\left[{\left({\Vert {\nabla }_{\widehat{\mathit{x}}}{\text{D}}_x(\widehat{\mathit{x}})\Vert }_2-1\right)}^2\right]\hfill \\ {\mathcal{L}}_{GAN}(\text{H})=-\underset{\mathit{x}\sim p(\mathit{x})}{\mathbb{E}}\left[{\text{D}}_z(\text{H}(\mathit{x}))\right]\hfill \\ {\mathcal{L}}_{GAN}\left({\text{D}}_z\right)=-\underset{\mathit{z}\sim p(\mathit{z})}{\mathbb{E}}\left[{\text{D}}_z(\mathit{z})\right]+\underset{\mathit{x}\sim p(\mathit{x})}{\mathbb{E}}\left[{\text{D}}_z(\text{H}(\mathit{x}))\right]+\lambda \underset{\overline{\mathit{z}}\sim \overline{p}(\overline{\mathit{z}})}{\mathbb{E}}\left[{\left({\Vert {\nabla }_{\overline{\mathit{z}}}{\text{D}}_z(\overline{\mathit{z}})\Vert }_2-1\right)}^2\right]\hfill \end{array}$$

where p(z) and Cat(K, w) denote the probability distribution of continuous variable and discrete variable in the latent space, respectively. In practice, sampling x from p(x) can be regarded as a procedure of randomly sampling from i.i.d observations data with replacement. $\widehat{p}(\widehat{\mathit{x}})$ and $\overline{p}(\overline{\mathit{z}})$ denote uniformly sampling from the straight line between the points sampled from true data and generated data. Minimizing the loss of a generator (e.g., ${\mathcal{L}}_{GAN}(\text{G})$) and the corresponding discriminator (e.g., ${\mathcal{L}}_{GAN}\left({\text{D}}_x\right)$) are somehow contradictory as the two networks (G and D_x) compete with each other during the training process. λ is a penalty coefficient which is set to 10 in all experiments.

Roundtrip loss

During the training, we also aim to minimize the roundtrip loss which is defined as ρ((z, c), H(G(z, c))) and ρ(x, G(H(x))) where z and c are sampled from the distribution of the continuous latent variable p(z) and the Category distribution Cat(K, w). The principle is to minimize the distance when a data point goes through a roundtrip transformation between two data domains. In practice, we used l₂ loss as the continuous part in roundtrip loss and used cross entropy loss as the discrete part in roundtrip loss. We further denoted the roundtrip loss as

$${\mathcal{L}}_{RT}(\text{G},\text{H})=\alpha \Vert \mathit{x}-\text{G}(\text{H}(\mathit{x})){\Vert }_2^2+\alpha {\Vert \mathit{z}-{\text{H}}_z(\text{G}(\mathit{z},\mathit{c}))\Vert }_2^2+\beta CE\left(\mathit{c},{\text{H}}_c(\text{G}(\mathit{z},\mathit{c}))\right)$$

where α and β are two constant coefficients which are both set to 10. H_z(∙) and H_c(∙) denote the continuous and discrete part of output from H(∙), respectively and CE(∙) represents the cross-entropy loss function. The idea of roundtrip loss which exploits transitivity for regularizing structured data has also been used in previous works^16,46.

Full training loss

Combining the adversarial training loss and roundtrip loss together, we can get the full training loss for generator networks and discriminator networks as $\mathcal{L}(\text{G},\text{H})={\mathcal{L}}_{GAN}(\text{G})+{\mathcal{L}}_{GAN}(\text{H})+{\mathcal{L}}_{RT}(\text{G},\text{H})$ and $\mathcal{L}\left({\text{D}}_x,{\text{D}}_z\right)={\mathcal{L}}_{GAN}\left({\text{D}}_x\right)+{\mathcal{L}}_{GAN}\left({\text{D}}_z\right)$, respectively. To achieve joint training of the two GAN models, we iteratively updated the parameters in the two generative models (G and H) and the two discriminative models (D_x and D_z), respectively. Thus, the overall iterative optimization problem can be represented as

$${\mathrm{G}}^{*},{\mathrm{D}}_x^{*},{\mathrm{H}}^{*},{\mathrm{D}}_z^{*}=\{\begin{array}{l}arg\underset{G,H}{\min }\mathcal{L}(\mathrm{G},\mathrm{H})\hfill \\ arg\underset{{\mathrm{D}}_x,{\mathrm{D}}_z}{\min }\mathcal{L}\left({\mathrm{D}}_x,{\mathrm{D}}_z\right)\hfill \end{array}$$

An Adam optimizer⁴⁷ with a learning rate of 2 × 10⁻⁴ was used for updating the weights in the neural networks. The training process is illustrated in Supplementary Table 5 in details.

Data generation in scDEC

We generate the state of intermediate cell by interpolating the latent indicator c of two “neighboring” cell types. Assume there are two cell types which correspond to the latent indicator c₁ and c₂, respectively. The generated data can be represented as $\text{G}(\mathit{z},\widehat{\mathit{c}})$ where $\widehat{\mathit{c}}=\alpha {\mathit{c}}_{\mathbf{1}}+(1-\alpha ){\mathit{c}}_{\mathbf{2}}$. Note that the α is the generation coefficient from 0 to 1 and z is still sampled from a standard Gaussian distribution. The interpolation of latent features have already been used for exploring and visualizing the transition from two type of images⁴⁸.

Network architecture in scDEC

All the networks in scDEC are made of fully-connected layers. The G network contains 10 fully-connected layers and each hidden layer has 512 nodes while the H network contains 10 fully-connected layers and each hidden layer has 256 nodes. D_x and D_z both contain 2 fully-connected layers and 256 nodes in the hidden layer. Batch normalization⁴⁹ was used in discriminator networks.

Updating the Category distribution

The probability w in the Category distribution Cat(K, w) is adaptively updated every 100 batches of data based on the inferred cluster label from $\tilde{\mathit{c}}$ of full training data (Supplementary Table 6).

Evaluation metrics for clustering

We compared different methods for clustering according to three metrics, normalized mutual information (NM)I⁵⁰, adjusted Rand index (ARI)⁵¹ and Homogeneity⁵². Assuming U and V are true label assignment and predicted label assignment given n data points, which have C_U and C_V clusters in total, respectively. NMI is then calculated by

$$\text{NMI}=\frac{{\sum }_{p=1}^{C_U}{\sum }_{p=1}^{C_V}\left|U_p\cap V_q\right|\log \frac{n\left|U_p\cap V_q\right|}{\left|U_p\right|\times \left|V_q\right|}}{\max (-{\sum }_{p=1}^{C_U}\left|U_p\right|\log \frac{\left|U_p\right|}{n},-{\sum }_{p=1}^{C_U}\left|V_q\right|\log \frac{\left|V_q\right|}{n})}$$

The Rand index⁵³ is a measure of agreement between two cluster assignments while ARI corrects lacking a constant value when the cluster assignments are selected randomly. We define the following four quantities 1) n₁ : number of pairs of two objects in the same groups in both U and V, 2) n₂: number of pairs of two objects in different groups in both U and V, 3) n₃: number of pairs of two objects in the same group of U but different group in V, 4) n₄: number of pairs of two objects in the same group of V but different group in U. Then ARI is calculated by

$$\text{ARI}=\frac{\left(\begin{array}{l}n\hfill \\ 2\hfill \end{array}\right)\left(n_1+n_4\right)-\left[\left(n_1+n_2\right)\left(n_1+n_3\right)+\left(n_3+n_4\right)\left(n_2+n_4\right)\right]}{\left(\begin{array}{c}n\\ 2\end{array}\right)-\left[\left(n_1+n_2\right)\left(n_1+n_3\right)+\left(n_3+n_4\right)\left(n_2+n_4\right)\right]}$$

Homogeneity is calculated by $\text{Homo}=1-\frac{H(U\mid V)}{H(U)}$, where

$$\{\begin{array}{l}H(U|V)=-{\sum }_{p=1}^{C_U}{\sum }_{q=1}^{C_V}\frac{\left|U_p\cap V_q\right|}{n}\log \frac{\left|U_p\cap V_q\right|}{{\sum }_{q=1}^{C_V}\left|U_p\cap V_q\right|}\hfill \\ H(U)=-{\sum }_{p=1}^{C_U}\frac{{\sum }_{q=1}^{C_V}\left|U_p\cap V_q\right|}{C_U}\log \frac{{\sum }_{q=1}^{C_V}\left|U_p\cap V_q\right|}{C_U}\hfill \end{array}$$

Estimating the number of clusters K

In order to apply scDEC to scATAC-seq where the number of cell types is unknown. We provide an algorithm for estimating the number of clusters K using gap statistic⁵⁴. We first compared the average within-cluster distance of the preprocessed scATAC-seq data and a reference dataset, which can be constructed with random matrix with the same size using K-means algorithm. The average within-cluster distance on the reference dataset was calculated for 1000 times by Monto Carlo simulation and the average result was used. The optimal choice of K is given for which the gap between the single cell data and the reference data is maximum. We note that this estimation of number of clusters K well matches the truth clusters numbers with the scATAC-seq used in this study (Supplementary Figure 18).

Identification of cluster-specific motifs and trajectory inference

The cluster-specific motifs are identified by Mann-Whitney U test⁵⁵ with the alternative hypothesis that the chromVAR scores²⁴ of cells in one cluster or multiple clusters have a positive shift compared with chromVAR scores of the rest of cells. Then the motifs will be ranked according to the p-values and the top-ranked motifs were illustrated.

We used Slingshot³² software with default parameters for trajectory inference in our study. Given the latent features and the cell cluster labels inferred by scDEC, Slingshot is able to annotate smooth curves, which represent the estimated cell lineages.

Baseline methods

We compared scDEC to multiple baseline methods in this study, including scABC⁷, SCALE¹⁵, cisTopic⁸, Scasat¹⁰, Cusanovich2018^4,9 and SnapATAC¹¹. SCALE was implemented from its original source code repository (https://github.com/jsxlei/SCALE). Other comparing methods were implemented directly from a benchmark study⁶. For the methods (cisTopic, Scasat, Cusanovich2018 and SnapATAC) that only learn a low-dimension embedding of the scATAC-seq data, we used Louvain clustering²⁰, which was recommended by the benchmark study⁶, as the default method for clustering the low-dimension embedding. Suggested by SCALE, we set the embedding dimension to a same number across different comparing methods within a comparing experiment.

MOFA+³⁷ and scAI³⁸ are two recent works on multi-modal single cell data analysis using matrix factorization frameworks. For MOFA+, we directly used the pretrained model on the same PBMC dataset, which can be downloaded from its website (https://biofam.github.io/MOFA2/). scAI was implemented from its source code (https://github.com/sqjin/scAI) and the number of factors is set to 20, which is the same as the dimension of latent features for scDEC. We applied K-means to the latent factors of MOFA+ and scAI in the clustering experiments. Note that the number of clusters K is set to 14 which is the number of cell types of the annotated label from the 10x Genomic R&D team.

Data preprocessing

Similar to SCALE, we filtered the scATAC-seq peaks by only keeping peaks that contain at least one read count in more than 3% of all cells. The uniform preprocessing could demonstrate the robustness of method across different scATAC-seq datasets. In the experiment of multi-modal single cell analysis, we applied a uniform preprocessing strategy to scRNA-seq and scATAC-seq. We first filtered the genes or peaks that have zero read count across all cells. Then the read count matrix of scRNA-seq or scATAC-seq will be normalized in which the read count of each gene (peak) was divided by the total count in each cell and multiplied by a scale factor (10,000 by default). Next, a log-transformation was applied with a pseudocount of 1. At last, a PCA transformation was applied to scRNA-seq and scATAC-seq, respectively. The top-25 components of each type of data were kept and then concatenated together (50 in total) before fed to scDEC.

Data availability

InSilico dataset was collected from GEO database with accession number GSE65360. The mouse forebrain dataset was downloaded from GEO database with accession number GSE100033. Splenocyte dataset can be accessed at ArrayExpress database with accession number E-MTAB-6714. All blood dataset can be accessed at GEO database with accession number GSE96772. The mouse atlas data is available at http://atlas.gs.washington.edu/mouse-atac. The human peripheral blood mononuclear cells (PBMCs) dataset used in multi-modal single cell analysis was downloaded from 10x Genomic website (https://support.10xgenomics.com/single-cell-multiome-atac-gex) with entry “pbmc_granulocyte_sorted_10k”. The preprocessed scATAC-seq data used as input for scDEC model in this study can be downloaded from https://doi.org/10.5281/zenodo.3977858⁵⁶.

Code availability

scDEC is an open-source software based on the TensorFlow library⁵⁷, which is available on Github (https://github.com/kimmo1019/scDEC) and Zenode (https://doi.org/10.5281/zenodo.4560834)⁵⁸. A CodeOcean capsule with several example datasets is available at https://codeocean.com/capsule/0746056/tree/v1⁵⁹. The pretrained models on both benchmark single cell datasets and 10x Genomic PBMCs multi-modal single cell dataset were provided.