On the application of additive manufacturing methods for auxetic structures: a review

Abstract

Auxetic structures are a special class of structural components that exhibit a negative Poisson’s ratio (NPR) because of their constituent materials, internal microstructure, or structural geometry. To realize such structures, specialized manufacturing processes are required to achieve a dimensional accuracy, reduction of material wastage, and a quicker fabrication. Hence, additive manufacturing (AM) techniques play a pivotal role in this context. AM is a layer-wise manufacturing process and builds the structure as per the designed geometry with appreciable precision and accuracy. Hence, it is extremely beneficial to fabricate auxetic structures using AM, which is otherwise a tedious and expensive task. In this study, a detailed discussion of the various AM techniques used in the fabrication of auxetic structures is presented. The advancements and advantages put forward by the AM domain have offered a plethora of opportunities for the fabrication and development of unconventional structures. Therefore, the authors have attempted to provide a meaningful encapsulation and a detailed discussion of the most recent of such advancements pertaining to auxetic structures. The article opens with a brief history of the growth of auxetic materials and later auxetic structures. Subsequently, discussions centering on the different AM techniques employed for the realization of auxetic structures are conducted. The basic principle, advantages, and disadvantages of these processes are discussed to provide an in-depth understanding of the current level of research. Furthermore, the performance of some of the prominent auxetic structures realized through these methods is discussed to compare their benefits and shortcomings. In addition, the influences of geometric and process parameters on such structures are evaluated through a comprehensive review to assess their feasibility for the later-mentioned applications. Finally, valuable insights into the applications, limitations, and prospects of AM for auxetic structures are provided to enable the readers to gauge the vitality of such manufacturing as a production method.

Introduction

Auxetic materials are a special class of materials that possess a negative Poisson’s ratio (NPR) as opposed to the positive values seen in conventional materials. Therefore, auxetic materials display an anomalous expansion and contraction in the dimensions along the transverse direction for tensile and compressive loads, respectively, as depicted in Fig. 1 [1]. Beginning with single crystals, auxetic behavior has been reported since the early 1920s [2]. However, a leap in the investigation was witnessed in 1987 when Lakes [3] reported the behavior of foam with a negative Poisson ratio. Whereas such behavior has been seen in a few natural materials, their minimal capabilities have pushed researchers to fabricate structures that are inspired by such materials. For instance, α-cristobalite, a silicon-dioxide polymorph, is one of the most profound examples of a naturally occurring auxetic material. Yeganeh-Haeri et al. [4] reported a maximum negative Poisson ratio of −0.5 for α-cristobalite in certain directions while having an average Poisson ratio of −0.16 for a single phase. Further, computational determinations by Keskar and Chelikowsky [5] predicted the occurrence of an NPR in low-density polymorphs of silica owing to the higher values of rigidity exhibited by silica tetrahedra. In addition, the presence of an auxetic behavior in yttrium-barium-copper oxide (YBa₂Cu₃O₇) has led researchers to investigate auxetic behavior in superconducting materials as well [6].

Fig. 1.

Behavior of auxetic structures under tensile and compressive loads

The initial success of auxetic materials has motivated researchers to design and fabricate stiffer structures for various engineering applications. However, the intrinsic responses of naturally occurring auxetic materials are insufficient to directly incorporate them into engineering structures. Hence, synthetic auxetic structures that facilitate improved responses are largely in demand. In this context, synthetic auxetic materials are classified into auxetic composites and auxetic cellular structures. Auxetic composites are primarily composite materials that exhibit an auxetic behavior as a result of the arrangement of their constituent materials [7]. In general, the constituent materials in auxetic composites also exhibit an individual auxeticity. Auxetic composites have better indentation resistance and energy absorption characteristics than the conventional composites. Apart from the auxetic composites prepared through the naturally occurring auxetic materials, auxetic composites can be synthesized from conventional materials as well by stacking them in a particular sequence to obtain an overall NPR. Such composites possess some common advantages such as a high specific stiffness, high specific strength, and light weight, which are also possessed by other conventional composites, making them suitable for highly demanding applications such as aerospace or automotive components.

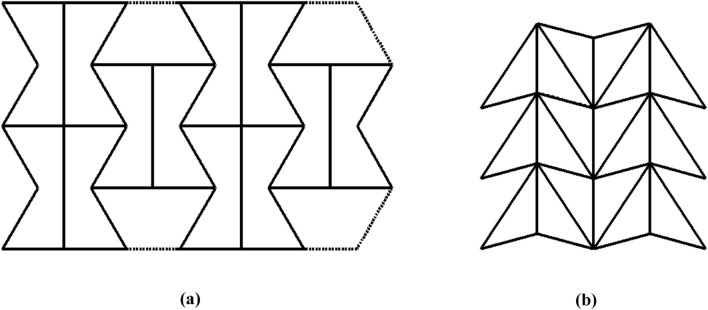
In parallel, auxetic materials with cellular structural arrangements exhibit auxetic behavior and superior mechanical properties owing to their internal auxetic unit cell structures as opposed to the intrinsic material properties as seen in auxetic composites [8]. These structural arrangements can exhibit a high NPR, which in turn alters the physical properties of the material, such as its density, stiffness, toughness, energy absorption capabilities, and damping ability. The mechanical properties of such a form of auxetics are higher compared with simple auxetic composite materials with layered configurations [9]. Some of the most common auxetic cellular structural configurations include honeycomb arrangements of re-entrant models, rotating unit models, missing-rib models, chiral structures, arrowhead models, Kirigami patterns, and star patterns, among others. Further, the performance of auxetic cellular structures can be enhanced by including auxetic microporous and molecular polymers [10]. A general geometrical classification of auxetic structures based on their deformation mechanisms is shown in Fig. 2, as inspired by previous studies [2, 11–17]. To this end, the extreme utilization of synthetic polymers and composites was made to obtain the desired functionality. In addition, these materials aided in the fabrication of auxetic structures that displayed an enhanced auxetic behavior and other required functionalities at lower production costs and increased flexibility [18, 19]. In a review on auxetic polymers presented by Liu and Hu [17], polymers were seen as a sustainable material source in the preparation of auxetic cellular structured materials. The ease in realizing the auxetic behavior using conventional polymeric materials through specialized processes broadened their application spectrum to areas such as biomedical and biomechanical devices [20]. This study proposed a molecular approach for the design of auxetic structures, significantly helping to overcome the low stiffness issue that was persistent with porous structures. Significant attention has been paid in recent years to developing and assessing fine 2D auxetic structures. For example, Hou et al. [21] proposed a novel methodology to develop isotropic auxetic composite structures through random inclusions. The NPR effect was governed by the structural design, the density of the inclusions, and the resultant hardening effect owing to the inclusions in the composite structure. Carneiro et al. [22] explained the usefulness of auxetic structures for a superior resistance against indentation, fracture, wear, and other different loading types. In addition, the variable permeability, acoustic absorption capabilities, and synclastic behavior of these structures promise great prospects for various technological advancements. To this extent, active auxetic materials that respond to stimuli such as heat, moisture, and pressure are made from responsive materials such as polymers and shape memory alloys [23]. Such materials offer a significant design flexibility and functional adaptability in areas including architecture, sporting equipment, and furniture. In addition, novel attempts such as exploring the molecular auxetic behavior in non-porous, synthetic liquid crystal elastomers put forward by Mistry et al. [24] are gaining prominence. For strains above −0.8, the Poisson’s ratio of the structures increased to −0.74, which was much larger than that of naturally occurring molecular auxetics.

Fig. 2.

General classification of auxetic structures based on their deformation mechanisms

Over the years, numerous manufacturing techniques have been experimented on to obtain substantial improvements in the fabrication of auxetic structures [25]. These methods have attempted to include numerous aspects such as versatility and flexibility in the design and manufacture of auxetic structures through the adoption of low-cost materials, efficient designs, additive manufacturing (AM) techniques and easier structural optimization methods. AM techniques have pioneered this drive with numerous advantages that make it the manufacturing method of choice. AM techniques are known to cater to a wide variety of specifics that subtractive manufacturing techniques fail to provide. These include lower wastages, faster fabrication, fabrication of complex and precise geometries, elimination of secondary hardware components, the minimal requirement for skilled labor, on-demand production, considerable energy savings, lesser inventory space, consolidated part fabrication, and easier design iterations, among many others. Similarly, through the adoption of AM techniques, auxetic metamaterials have a new-found interest in this context. Auxetic metamaterials are structures that derive their auxeticity as a result of their internal microstructure, as opposed to the unit cell structure and stacking sequence seen in auxetic composites and auxetic cellular structures. However, their auxeticity is hugely dependent on the base material used for the structure. Brass auxetic metamaterials suffer a loss in their auxetic behavior when subjected to buckling loads as the base material is changed from an elastomer to a ductile metal [26]. Through the control of the pattern scale factor and the volume fraction of the composite, a distinct difference in the NPR has been observed. Similarly, Valente et al. [27] presented fundamental studies on micro-and nano-scale metamaterials exhibiting an NPR based on the re-entrant honeycomb structure design. Grima [28] presented a global classification system for auxetic structures based on their geometry and deformation mechanisms. Their study also asserted that the scale-dependent behavior of auxetic materials allowed them to be extended to both the micro- and nano-dimensions.

Whereas modern research on auxetics has focused on the introduction of new materials and newer structures, there is an impending need to optimize the manufacturing routes adopted to realize auxetic structures. Such developments can result in lower energy requirements, reduced costs, and optimized performance of the resultant structures for their intended applications. Consequently, emerging manufacturing techniques such as AM need to be explored and developed to greater depths to realize new prospects for an optimized production and sustainability. Further, the adoption of AM techniques can immensely help in the production of small and intricate parts for sophisticated applications such as sensors, soft robotics, and other similar applications. In this regard, the integration of molecular auxetics and AM techniques has been leading the way. By scaling down such structures, a wide array of auxetic materials with higher moduli can be fabricated to cater to structural, nanotechnological, biomedical, and microelectronic needs [29–31]. Molecular dynamics (MD) simulations are utilized to uncover the strain-dependent Poisson ratio of entropic 2D surfaces [32]. This study suggests the adoption of a pre-straining of the materials up to the desired point to obtain a specific Poisson’s ratio.

From this foundational idea on auxetic structures and their immense potential, it can be asserted that this class of materials and structures can revolutionize many different engineering domains. However, they are limited by the lack of efficient processing techniques and newer engineering materials. Until now, most of such structures and materials discussed in the literature have not been applied to commercial products. The lack of efficient and sophisticated manufacturing tools has hindered their applications. At this juncture, composite materials and AM techniques have stepped up the platform to provide for more versatile structures that can produce the desired behavior. It is believed that the adoption of AM techniques can resolve the issues of incompatible manufacturing and can tremendously aid in the production of such structures for various applications. Hence, this paper focuses on assessing the progress, impact, and capabilities of AM technologies on the fabrication of auxetic structures for modern applications. A comprehensive overview of the different AM techniques along with the properties of the resultant structures, their applications, limitations, and prospects is provided in the upcoming sections.

Development of additive manufacturing for auxetic structures

Additive manufacturing holds the potential to help fabricate and develop auxetic structures with improved properties and multifunctional capabilities. As opposed to conventional processes such as braiding, molding, sintering, and spinning [33–40], AM offers substantial flexibility and versatility for the production of these composites. The adoption of AM has offered a sustainable trade-off between the cost and efficiency of the resultant structures. Hence, this section aims to provide a brief overview of the development on the AM front for the realization of auxetic materials and structures.

The growth of AM in fabricating auxetic structures has been incremental. AM techniques have been used to fabricate both 2D and 3D auxetic structures. In this front, octahedral cellular structures have been prepared using AM techniques through an experiment-assisted design route [41]. The electron beam machining (EBM) process has been used to fabricate Ti6Al4V structures with varying unit cell sizes. The same was extended for polymer composite materials through fused deposition modeling (FDM) [42]. This process was later simplified through the adoption of robotic systems for the direct ink writing of auxetic structures [43]. These developments have aided in much better automation prospects with higher efficiency and reduced stair-case effects. Moreover, the absence of an assembly system and relaxed movement allows for a simpler setup and faster production. These processes have also been used in the production of auxetic metamaterial systems. Wei et al. [44] successfully characterized bi-material metamaterials that could be used to program a wide range of coefficients of thermal expansion (CTEs). Their study effectively achieved programmable CTEs within the range of −369.01 10⁻⁶/°C to +694.00 10⁻⁶/°C. In a novel attempt, Peng et al. [45] devised a new class of light-weight, 3D metamaterials that could be used to simultaneously and continuously program the CTE and Poisson’s ratio. The structures follow a later bi-material configuration with re-entrant geometry features. The modifications in the geometrical parameters can aid in the mutual control of the CTE and Poisson’s ratio for both negative and positive values. Such an approach enables efficient shape morphing in structures and devices that are subjected to combined thermal and mechanical fields. Similar observations were made by Wei et al. [46] to obtain lightweight, cellular metastructures with tunable CTEs and NPRs. Furthermore, such planar metamaterials are curled to obtain cylindrical metastructures with multifunctional capabilities [47]. For such structures, the deformation characteristics are dependent on the number of circumferential cells in the cylinder. As indicated before, the CTE and Poisson’s ratio of these structures are controlled by modulating the geometrical parameters of the structure. However, past a specific number of circumferential cells, the CTE and Poisson’s ratio of these structures are almost equal to those of planar metastructures.

Laser-based AM techniques are known for their excellent resolution and good surface finish. These techniques can be used to fabricate both polymeric and metal structures with high precision. In addition, several materials can be manufactured using these methods. In later developments on this front, robotized laser-based AM for the 3D printing of metallic auxetic structures was introduced [48]. This in turn aids in the production of more durable and stronger auxetic structures through efficient control, minimal error, and excellent dimensional accuracies. Similarly, advanced auxetic structures were realized through selective laser sintering (SLS). The auxetic behavior of the structure is complemented by the 3D bandgap of a single-phase periodic structure [49]. Further enhancements in the production and analysis of such structures are possible by applying topology optimizations of compliant mechanisms and advanced finite element (FE) studies [50]. In addition, 3D printing techniques in conjunction with the knitting process help obtain auxetic structures with tailorable mechanical properties and high permeability [51]. The variation of the pore size and shape governs the properties of the resultant structures. Another major development on the AM front is the development of curved additive manufacturing [52]. This technique is extremely beneficial for the quick manufacture of lattice shell structures with minimal waste of the support materials [53].

Selective laser melting (SLM) is another type of AM method used to produce metallic auxetic structures realized from single-metal or alloyed powders. In this front, stainless-steel powders are used to produce auxetic structures with an S-shaped unit cell as seen in Refs. [54]. In addition to SLM, other laser-based processes including stereolithography (SLA) and direct metal laser sintering (DMLS) have also contributed to producing NPR structures of various kinds. With the introduction of 3D printing for biomaterials using dynamic optical projection SLA, biomedical scaffolds with regional auxetic behavior were successfully fabricated [55]. Similarly, auxetic bone screw structures with enhanced tensile properties were fabricated using 3D printing [56]. Furthermore, AM technologies are beneficial in producing auxetic scaffolds for tissue engineering requirements [57]. In addition to its use in biomaterials, AM is extremely advantageous in the production of advanced materials such as ionogels with a better conductivity response and larger extensibility [58]. Similarly, upon combining investment casting techniques with 3D printing, an auxetic lattice structure with good surface and bulk properties was obtained [59]. Novel 3D auxetic lattice structures were recently 3D printed based on the stretch-dominated concept with an optimized manufacturing route [60]. High-performance carbon fiber reinforced polymer composites are exploited to realize these structures. The experimental studies recommend the use of these structures in applications where high stiffness and auxeticity are desired.

In addition, 4D printing has been another pivotal AM technique that facilitates the production of active structures whose responses are triggered by external stimuli. This AM technique has proved to be a boon in the manufacturing of shape memory polymer (SMP) based auxetic structure [61]. Studies on the mechanical behavior of such materials showed an appreciable NPR of −0.18 with good retention of the initial shape in the absence of the actuating force. Materials like poly-lactic acid (PLA) and others have also been utilized to design reprogrammable mesh structures based on the same principle [62]. Direct printing approaches were followed for fabricating these structures with the flexibility of changing their shape through a reprogrammable mesh structure. Furthermore, in a study put forward by Wagner et al. [63], 4D printing of auxetic structures demonstrated greater active 3D printing with approximately 200% changes in the area. In a more specific study, Yousuf et al. [64] expounded on the adjustable stiffness and Poisson’s ratio of SMP honeycomb cellular structures. The mechanical and recovery characteristics of these structures analyzed through multiple programming and recovery cycles have shown promising results for their adaptation. Similarly, Wu et al. [65] developed active auxetic structures through direct light processing (DLP) 4D printing.

A detailed description of the various AM processes used in the fabrication of auxetic structures is provided in the upcoming section. Emphasis has been placed on envisaging the basic technique, advantages, and limitations of such processes along with their importance in the fabrication of auxetic structures.

Various additive manufacturing techniques for auxetic structures

As seen from the previous section, AM has undergone major developments to cater to the production of auxetic structures. Even though polymers and polymer-based materials exploit the additive manufacturing process at large, sufficient emphasis is placed on discussing metallic structures as well. Primarily, AM encapsulates the following processes: direct liquid-based melt deposition techniques such as FDM and inkjet printing, liquid-based polymerization techniques such as SLA and direct laser writing (DLW), and powder-based melting techniques such as SLM, SLS, EBM, and selective electron beam melting (SEBM) [66]. The sub-sections below discuss the implication of these techniques for the fabrication of auxetic structures. In the context of such structures, rather than offering significant property advancements, AM techniques offer a platform to realize these structures with ease. This allows for easier topological optimization and process parameter variation without huge investments into machinery and labor. In addition, the layer-wise manufacturing route adopted by a majority of AM techniques provides for easier overall compositional adjustments of the resultant structures.

FDM

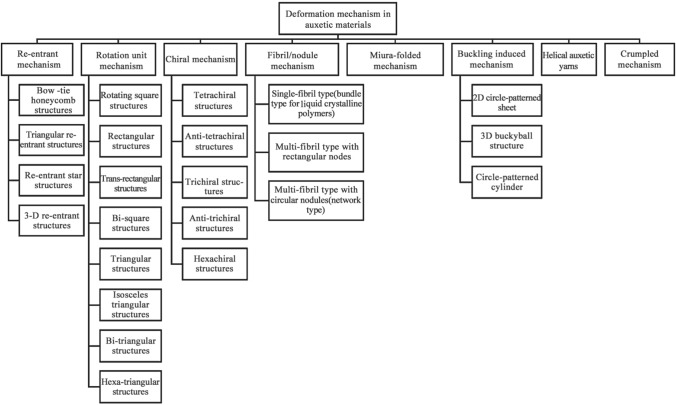
FDM is one of the most common methods of 3D printing. This approach features a direct deposition of the said material on the bed through a nozzle. Typically, FDM printers offer resolutions of up to 100 µm. This AM technique has been used extensively in realizing polymer and polymer composite parts. However, modern printers have advanced to include the printing of metallic structures as well. A representative illustration of this process is depicted in Fig. 3. The mechanical properties of auxetic structures made of standard 3D printing polymers such as PLA and acrylonitrile butadiene styrene have also been established [67]. This study demonstrates the feasibility of attaining auxetic behavior using basic 3D printed polymer structures. Similarly, graded auxetic structures were fabricated using FDM through parametric modeling [68]. The layer-wise deposition scheme offered by AM facilitates easier manufacturing with accurate layer distinction. The structures exhibited a variable NPR, which made them extremely applicable for fasteners, strain gauges, and piezoelectric devices. The incorporation of AM techniques in the manufacture of auxetic strut/honeycomb hybrid cell structures has facilitated an easier manufacture and comparison of these structures to other structures such as honeycombs, auxetic struts, and re-entrant structures. The novel hybrid structures displayed a 65% higher compressive strength and 30% higher energy absorption than re-entrant structures. In the meanwhile, increases of approximately 300% and 70% in the compressive strength and impact energy absorption were achieved when compared to honeycomb structures, respectively [69]. In addition to these factors, the deformation studies of these structures enable the tailoring of the NPR and the tensile strength of such structures. Such iterations in the design can be easily fabricated using FDM. The process can further be optimized easily in comparison to other manufacturing routes such that an extensive experimental report can be obtained. In a novel attempt, auxetic structures were 3D printed directly from pellets [70]. This hose-based extrusion system caters to the 3D printing of auxetic structures made from a soft elastomer, which are otherwise difficult to 3D print using regular filament.

Fig. 3.

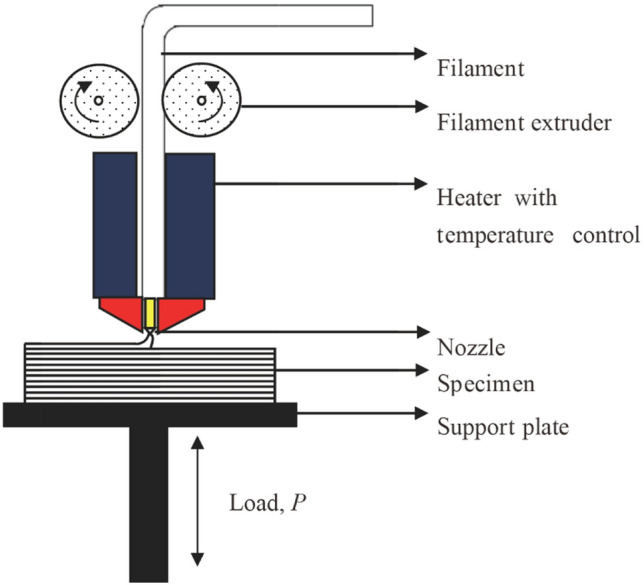
Schematic of FDM process

3D printing is used to fabricate auxetic lattice reinforced composites that achieve an enhanced and tunable mechanical performance. The structures are realized using FDM technology to validate the theoretical estimations of the response of these structures. It is possible to further tune these structures through process parameter optimizations and minimize defects and geometrical inconsistencies [71]. Furthermore, FDM technology has been used in the fabrication of aero-engine fan blades with gradient auxetic cellular configurations [72]. FDM has been useful in experimenting with AM for novel compositions such as lay wood. These composites contain approximately 40% wood-dust introduced into a PLA matrix. Auxetic lattice truss cores made from this material are 3D printed to obtain structures of different rib angles and cell sizes. The thickness and number of cells in the structure affect the Poisson’s ratio and the modulus of such structures [73]. The structures show significant weight reductions with an increased specific bending stiffness. Carbon fiber-reinforced polymer composites having a 3D auxetic cellular structure were manufactured using FDM [74]. The feasibility of FDM producing vertical structural components with the help of support structures has made it the method of choice for experimentation of such structures at minimal costs. Such structures have demonstrated a parabolic relationship between the Poisson’s ratio and its re-entrant angle when analyzed experimentally [75, 76]. Because the material is highly anisotropic, the properties of the parent materials seem to have a dominant effect on the auxetic behavior of the composites. Common 3D printing polymers such as PLA and tetra-polyurethane (TPU) were used to realize auxetic structures. These structures have demonstrated excellent shock absorption characteristics [77] as opposed to regular cellular structures [78]. In addition, among the various auxetic structures printed, re-entrant structures have displayed the highest Poisson’s ratio. A significant contribution was made by Ling et al. [79], who realized an auxetic re-entrant triangle and honeycomb structures through FDM. The fabricated structures exhibited the highest programmable NPR within the ranges of [−0.87, −7.01] and [−2.13, −10.24] for a re-entrant triangle and honeycomb structures. This range is by far the highest recorded experimental values for programmable auxetics. In a similar study, the authors successfully designed cylindrical metastructures having a programmable Poisson’s ratio [80]. These structures are proposed to be used in shape morphing structures such as foldable devices. These devices can be easily manufactured using FDM owing to the earlier mentioned advantages over other methods. FDM also supports the 4D printing of certain SMPs. As a result of the multilayer manufacturing advantage discussed earlier, FDM is suitable to preparing dual-material auxetic structures [81]. Soft hyper-elastic polymers were arranged with elasto-plastic SMPs for this purpose. The work affirms the feasibility of FDM to 4D print tunable meta-sandwiches with reversible energy absorption abilities. Thermo-mechanical estimations of FDM-based 4D printed auxetic structures helped in including self-bending features used for actuation of complex structures with 2D to 3D shape-shifting [82]. It can be seen that the printing speed has a predominant influence on the observed properties.

SLM and DMLS

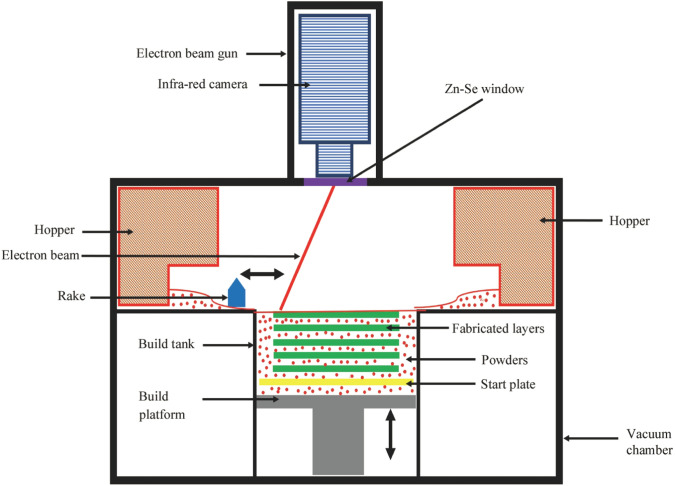
SLM is a laser-based additive manufacturing process that attends to the fabrication of metallic auxetic structures. The terms SLM and DMLS are often interchangeably used. However, there is a subtle difference with respect to the materials they are capable of handling. SLM melts pure metals whereas DMLS deals with metal alloys. The instrument consists of a chamber filled with metal powder deposited in thin layers on the build platform using a coater blade. A high-power CO₂ laser is applied to selectively melt the powdered metal to fuse 2D slices of the part. Once a layer is complete, the bed drops down by a height equivalent to the layer thickness, and the process is repeated until the part is fully formed. The process is carried out in a controlled atmosphere to prevent oxidation. A schematic representation of this process is shown in Fig. 4. SLM parts are characterized by a rough surface and require support structures when printing vertical components. The process is fast and can be used to produce complex shapes with a variety of metals. In addition, SLM offers a consolidated manufacturing approach that enables the printing of multiple parts at the same time. However, like most laser-based techniques, this technology is currently limited to small parts only and requires a lengthy post-processing to smoothen the surface.

Fig. 4.

Schematic representation of the SLM process

Auxetic structures prepared through SLM withstand greater cyclic compressive loads than their non-auxetic counterparts [83]. The structures prepared in this manner have variable mechanical properties in association with the direction in which they were loaded [84]. The brittleness of the cell wall material partially induced by excessive heating causes a premature failure of these structures. In addition, the results vary in terms of precision based on the number of cells in the structure [85]. Laser-assisted direct metal deposition offers great prospects in the fabrication of auxetic structures. Structures made of H13 tool steel [86] were realized through this method. Similarly, SLM can also be used to manufacture commercial steel variants such as SS316L stainless steel with great accuracy to fabricate auxetic structures [87]. SLM has also been used to manufacture stable thin and thick-walled AlSi10Mg lattice structures [88]. SLM aids in the production of these structures with the absence of traditional cross-linking, thereby allowing for the formation of a continuous lateral layer that provides the structure with stability under quasi-static loading. Lattice sandwiched panels with a different number of layers were prepared using SLM with AlSi10Mg alloy [89]. Upon comparing the body-centered cubic (BCC) and BCCz-type lattices prepared through this method, it was found that the densification and energy absorption characteristics were higher for the BCCz lattice. However, the crash load efficiency was better for the BCC-type lattice. In a similar study, the effect of the scanning rate on the quality of the produced parts was discussed [90]. It was found that lower scanning speeds, e.g., less than 1 000 mm/s, resulted in irregular molten pools and large pores in the structure. The fabrication of Ti-Ni alloys through SLM demonstrated two potential defects: porosity and cracking from the residual stresses [91]. These effects were seen to decrease with the use of linear energy density. However, upon heat-treatment at temperatures closer to the melting point of the formed intermetallic, these structures displayed high NPRs of −2.

SLM-manufactured titanium alloys were used to manufacture meta-implants for biomedical applications [92]. The structures exhibited improved implant-bone contact, which in turn improved the longevity of the implant. Studies by Maconachie et al. [93] showed that lattice structures prepared through SLM displayed a positive power relationship between the relative density and the observed mechanical properties. A feasible appropriation between bending-dominated and stretch-dominated structures, as demonstrated through SLM-manufactured stretch-dominated topologies, showed the same bending characteristics as regular bending-dominated structures. Furthermore, functionally graded F2BCC lattices fabricated using SLM showed enhanced compressive and energy absorption properties as compared to uniform structures [94]. The process aids in an excellent bonding between the particles, resulting in enhanced properties. The discrepancies concerning the properties obtained through theoretical and experimental approximations for SLM-manufactured structures can be minimized by adopting an FE based optimization route [95]. However, gradient auxetic structures made from SS316L powders using SLM have shown some inconsistencies concerning the porosity and the presence of unmelted grains [96]. However, these insufficiencies can be overcome by adopting a process optimization along with a composite-formulation optimization.

Selective laser sintering (SLS)

SLS has proven to be another effective laser-based method for fabricating lattice structures with intricate geometries. In a number of ways, SLS is similar to SLM except that SLS utilizes thermoplastic powders over metal or metal alloy powders. The operation of an SLS printer follows the same principle as that of an SLM printer. The need for high-end technology and a large amount of power hinders the application of SLS for the production of parts for commercial needs. However, unlike SLM, these parts do not require the aid of support structures because the non-sintered powder acts as a support material. Estimations of the energy absorption and impact properties of SLS-manufactured auxetic structures with polymer fillings showed that gelatinous fillings had negligible effects on the observed plateau stress and energy absorption properties [97]. However, when filled with polyurethane, there was an increase of approximately 40% of the energy that was absorbed by the structure. The use of SLS has been particularly inventive in the production of metal rubber. The method was used in the production of metal-rubber particle-based auxetic structures with an anti-tetrachiral honeycomb panel [98]. The structures exhibited relatively good damping capabilities along with a considerable weight reduction and high loading capabilities. Similarly, SLS was also used to fabricate spring systems with hyper-elastic properties and large NPRs [99].

Theodoras and Angelos [100] presented an innovative method for creating and optimizing auxetic cellular structures prepared through SLS. The method adopts a combination of physical and digital entities to create a hypothetical system through iterative experimentation. However, the fabrication of complex auxetic geometries using SLS can be made easily by the application of short command line controls for easier geometrical modifications [101]. 3D auxetic metamaterial lattices made from carbon nanotube reinforced composites have been prepared using SLS [102]. The adopted manufacturing strategy aided in an adequate enhancement for the manufacture of auxetic structures with programmable energy absorption. SLS-manufactured soft auxetic lattice structures made from TPU sustained a wide-range of compressive strains during experimental testing. The results suggest the usage of these structures in applications demanding high energy absorption and vibration damping characteristics [103].

SLS was used to manufacture tetrachiral honeycomb auxetic sandwiched composites [104]. The reduced number of ligaments in comparison to hexachiral structures with reduced density and easier manufacturing led to better absorption of the acoustic signals. Similarly, SLS has been assistive in realizing novel structures such as towel gourd tendrils-inspired cylindrical tetrachiral tubes [105]. These structures can be considered potential candidates for various applications in aerospace engineering and biomechanical devices. Yuan et al. [102, 106] put forward several processes and composite formulation optimization techniques to print high-quality polymeric materials and structures through the use of SLS. The aims for the prospective materials were a superior mechanical strength and good energy absorption characteristics.

EBM and SEBM

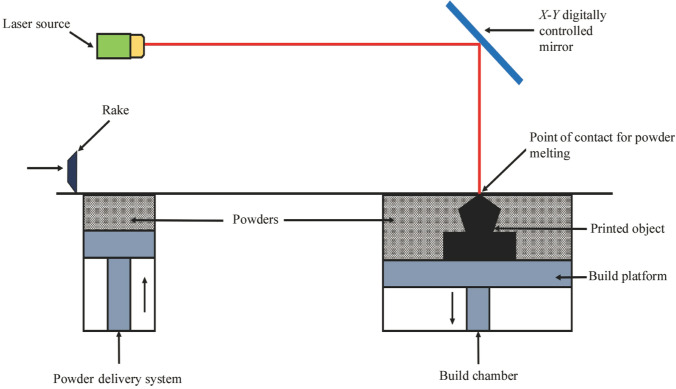
The EBM and SEBM techniques have seen widespread applications in producing conductive metallic auxetic structures with high precision and accuracy [10]. At first glance, EBM and SEBM may look like SLS 3D printing process. However, on closer examination, they vary from SLS in numerous ways. Primarily, the energy source and the choice of material are the two major differences with respect to SLS. EBM utilizes an electron beam instead of a CO₂ laser as seen in SLS and is capable of synthesizing structures made of conductive metals (typically Ti alloys). Because the technology is based on the interaction of electrical charges between the powdered metal and the electron beam, this method is incapable of producing plastic or ceramic parts. Initially, pre-heated metal powders are laid on the print bed placed in a vacuum chamber. Then, an electron beam controlled using suitable electromagnetic coils is pointed to the desired parts of the build platform. There is a selective beam movement that melts the powder resulting in a fusion of the particles. Upon completion of the first layer, the bed is moved downward, and a fresh layer of powder is introduced onto the platform. The earlier process is repeated, and this cycle is continued until the whole part is fabricated. This method offers a high print quality at fast speeds. The parts are dense owing to the complete melting of the powders. However, they are limited by the number of available materials and the smaller print volume. Such EBM 3D printers are expensive, which limits application in mass production along with the earlier mentioned factors. A schematic representation of the EBM process is illustrated in Fig. 5.

Fig. 5.

Schematic representation of the EBM process

In this regard, gas-atomized Ti6Al4V auxetic scaffolds were manufactured using EBM [107]. The results presented in this study suggest the application of EBM for a strut thicknesses of greater than 0.5 mm. Although structures with smaller dimensions can be manufactured, there is a significant variation with respect to the theoretical estimations of the properties of such structures. This ultimately compromises the reliability of such models. Although Ti6Al4V is the most suitable material for EBM, Gong et al. [108] suggested the application of this technique to other special metallic materials including intermetallics, tool steels, and Co-Cr alloys. It was observed that the specimens produced possess comparable, or in some cases, superior mechanical properties in comparison to their cast-wrought counterparts. Horn et al. [109] used EBM to manufacture low-stiffness structures such as tissue scaffolds and other implants that closely lied with the properties of bone. The structure was made using Ti6Al4V and other biocompatible metals. The high beam scanning speeds and vacuum environment reduce the induced thermal stresses and oxidative contamination. This helps in producing structures with a superior mechanical strength and higher densities owing to minimal voids within the structure. Yang et al. [110] fabricated auxetic structures of Ti6Al4V along with a pure ductile copper using EBM. These structures were experimentally analyzed to confirm their feasibility for high energy absorption applications. The 3D printed structures exhibited a prominent auxeticity and the observed experimental results showed a good correlation with the theoretical estimations.

EBM-manufactured non-stochastic Ti6Al4V auxetic structures have also shown improved bending parameters without the presence of a solid skin owing to the effective melting of the powders [111]. This significantly contributes to the higher bending properties of these structures, which are on par with those of regular sandwiched structures. However, the compressive and impact absorption characteristics do not improve the bending ability. A similar study by Suard et al. [112] focused on the stiffness prediction of auxetic cellular structures produced by EBM. The variation in the dimensional parameters of the theoretical model and the fabricated parts was compensated by adopting an “efficient volume ratio” through optimized EBM parameters for a lower stiffness boundary. However, additional physical and micro-structural characterization tests are needed for a more significant optimization of the process parameters. The inefficacies in determining the structural properties of Ti6Al4V in the physical model as compared to the theoretical model are partially resolved through FE modeling [113]. The experimental results are in close accord with the analytical values, indicating that the present approach can be used for the initial phase tuning of mechanical properties through process parameter optimization.

Mitschke et al. [114] adopted a novel approach to check for deformations in symmetric planar tessellations using SEBM. Their study focused on obtaining skeletal structures of stiff rods over linear and elastic cellular solids manufactured through SEBM. Similarly, graded chiral auxetics originating from a copper alloy powder fabricated using SEBM exhibited better control and reliability through experiment-assisted process optimizations [115]. SEBM-manufactured auxetic structures also showed high repeatability for compression tests on graded and uniform chiral auxetic structures [116], which was indicative of the high precision offered by the SEBM technique. The energy absorption of these structures also exhibited promising improvements with approximately a 48% increase in hybrid uniform structures and a 30% increase in hybrid graded structures [117]. SEBM was also used in the fabrication of auxetic Ti6Al4V cellular structures, achieving NPRs of approximately −0.4 along the loading direction [118]. Schwerdtfeger et al. [119, 120] showed that the mechanical properties of periodic auxetic structures prepared using SEBM showed a triadic dependence on the Poisson’s ratio, stiffness, and relative density.

SLA

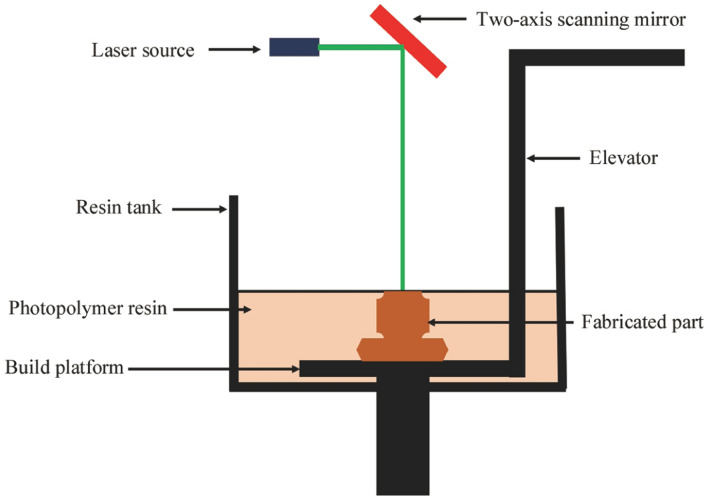
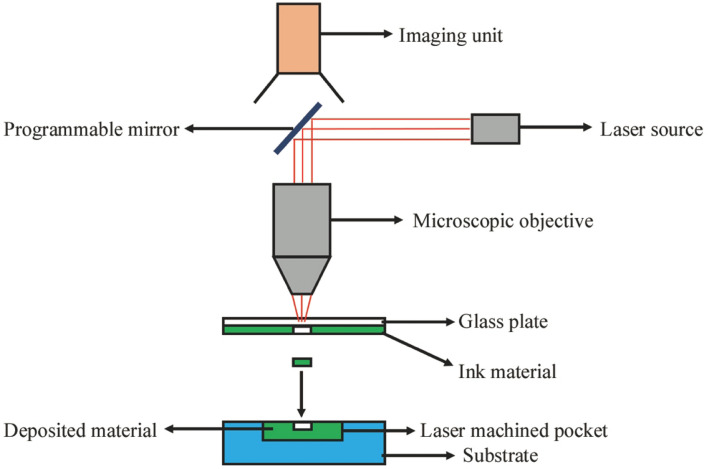
SLA is a resin 3D printing technique that converts a photosensitive liquid into a solid 3D part. SLA methods have found applications in developing 3D auxetic structures made from a liquid photopolymer [121]. SLA is one of the first AM techniques to be conceptualized and is one of the major manufacturing techniques used today, along with FDM and SLS. SLA 3D printers consist of a tank with a liquid photopolymer resin. The laser pointed toward the photopolymer and the first layer of the print was drawn in the resin. Solidification of the liquid resin is observed wherever the laser hits. The laser is directed to the appropriate coordinates using a computer-controlled X-Y mirror. Unlike other AM techniques that start from the bottom-most layer, most SLA printers begin upside down, i.e., the laser is pointed toward the build platform. Therefore, once the layer is fabricated, the platform is moved up by a distance equal to the layer thickness of the structure and the subsequent layers are printed. The process is repeated until the entire part is fabricated. Figure 6 shows this process. The DLP technique is an extension of SLA, where a digital projector screen is used to flash a single image of each layer across the entire platform. Therefore, the resolution of a DLP printer corresponds to the pixel size of the image as opposed to the laser’s spot size for SLA printers. SLA 3D printing offers the fabrication of the most precise and intricate 3D parts with an extremely good surface finish. This technique provides the tightest geometric tolerances amongst all other manufacturing techniques. And unlike other AM techniques, SLA can produce sufficiently large parts without compromising on the precision of the parts. However, the process appears to be extremely time-consuming and requires support structures to avoid breakage during printing or curing. Further, SLA 3D printing is limited in terms of commercial use by the unavailability of a variety of materials and the high printing costs.

Fig. 6.

Representation of SLA process

The advantages offered by SLA aid in the production of novel and high-quality auxetic structures with a significant weight reduction as compared to regular re-entrant auxetic structures [122]. Rubber-based materials with a cubic symmetry are example structures fabricated using SLA [123]. Nanolithography was used to realize mechanical metamaterial unit cells with strain-dependent solid-solid phase changes [124]. SLA was shown to be beneficial in producing cylindrical NPR structures with close dimensional tolerances and intricate geometries [125]. Similarly, mechanical metamaterial-based cylindrical shells prepared using SLA exhibited larger NPRs and lower stress concentration factors as compared to conventional re-entrant materials prepared through material deposition techniques [126]. SLA is extremely beneficial in the manufacture of ceramic auxetic structures with complex geometries. The structures can be built with great precision without the need for support structures [127]. SLA has also been used in poly-dimethyl siloxane-based auxetic re-entrant structures [128].

In addition, SLA techniques have been employed in the fabrication of intermedullary bone stents [129], involving less trauma and minimal tissue damage. The superior accuracy and resolution offered by SLA are adequate advantages in this fabrication process. The method has also been highly successful in the manufacture of intravascular stents through anti-chiral and re-entrant structures [130]. A novel unit cell structure comprising cylindrical beams fabricated using SLA has demonstrated superior mechanical properties and auxeticity as compared to several other structures [131]. The structures also require fewer parameters to completely define their auxetic nature. Consequently, quasi-static tests on these structures produce satisfactory results that enunciate their auxetic behavior and mechanical performance. Meanwhile, hinged 3D metamaterials were also 3D printed using SLA [132]. A high NPR of −16 was obtained through a combination of dissimilar materials and stiffnesses. This gives rise to a new class of metamaterials that can be used to optimize the performance of devices such as strain amplifiers and strain gauges. The technique was also applied in fabricating novel dome-shaped auxetic structures with various cellular configurations [133]. These metamaterial structures can be used to study band-gap formations, which can aid in the construction of civil structures through the attenuation of low-frequency seismic waves. One of the most profound applications of SLA was in the production of graded auxetic lattices. Such structures exhibited deformation modes that were differed from uniform auxetic structures [134]. They also show better energy absorption characteristics and critical deformation parameters as compared to their homogenous auxetic structures. The accuracy of these parts resulting from a well-calibrated manufacturing run adds to the strength parameters of the structure. Similarly, porous architectures of closed-form cellular structures prepared using SLA have high energy absorption characteristics and an improved indentation resistance owing to their enhanced auxeticity [135]. For smaller systems, these SLA-based structures can provide a cushioning effect upon impact.

DLW

The DLW method has introduced a new perspective on the AM of very small auxetic structures, usually at the micron and sub-micron levels, using photoactive resins [136]. Popularly called a “3D printing technology for the microscopic world” , this method can produce the smallest shapes and sizes, which cannot be achieved by other AM techniques. This method uses a nonlinear two-photon absorption (TPA) technique with a high spatial resolution. The laser beams used in this technique are of high intensity such that TPA occurs within the confined region of the laser. The highly focused beam has a prolate spheroidal shape obtained by rotating an ellipse about its major axis and inducing a spatially confined polymerization. In most cases, this shape is replicated inside the photoactive medium through photochemical reactions. This fundamental element is called a volume pixel or voxel and forms the building block of the 3D structures printed using DLW. 3D microstructures can be constructed by manipulating the position of the focus inside the photoactive medium and placing multiple voxels in close proximity to induce their overlap [137]. The free volume left between two voxels after their overlap is filled owing to the polymerization induced through the diffusion of the active species from the center of the laser focus. Figure 7 shows a typical DLW setup.

Fig. 7.

Schematic of DLW process

DLW structures have numerous applications owing to the possibility of part fabrications at the micron and sub-micron levels. The complexity of the shapes depends on the photochemistry of the materials used and the optical capabilities of the setup. 3D-DLW was seen to produce excellent microstructures at higher resolution values. However, as the size approaches the nanoscale dimensions, the fabrication demands secondary assistance from more complex devices. Because the part fabrication occurs at extremely low dimensions, process optimization is a challenging task when achieved through repeated experiments and imaging. To reduce, if not abate, such difficulties, a detailed modeling scheme was put forward by Guney and Fedder [138]. Another predominant issue in terms of obtaining high-quality prints is the shrinkage observed in the structures. This is a result of the accumulated stress DLW process and the subsequent processing of the prints. Hence, an estimation of the shrinkage while processing the materials through this method can enable a useful prediction of the shape distortions. Such inaccuracies can be overcome through a design alteration and changes in the process parameters.

Tunable auxetic structures with regular bow-tie designs are fabricated using DLW [139]. Although some inconsistencies at the microscopic level have decreased the auxetic behavior, it is still seen as a potential technique in the fabrication of auxetic structures for micron-level sensors and actuators. DLW has proven to be efficient in the production of gold nanoparticle-reinforced hybrid SZ2080 and hydrogelic PEG-DA-700 laser processable polymers. The method is seen to produce freely movable microstructures made of mechanical metamaterials and exhibited NPRs of as low as −0.44 [140]. Three-dimensional origami structures with appreciable foldability were fabricated using DLW [141]. The easier foldability is attributed to the reduced bending stiffness at the micro- and nano-dimensions. These structures possess a dynamic deformation-dependent auxeticity at the macroscale level. Hence, these structures can be applied to interact with mechanical waves for vibrational damping and energy absorption applications.

Common auxetic structures and their prominent characteristics

A comparative study of the different auxetic structures was carried out by Hou et al. [142], wherein sandwiched carbon fiber-polymer structures were utilized. An S-hinged unit cell design, as shown in Fig. 8 was proposed by Khare et al. [143]. The design derives its inspiration from the common re-entrant cell design, which permits an easier tuneability and stability of the unit cells along with lower fatigue damage. The 3D double-V structure is generated from an arrangement of multiple 2D double-V structures, as shown in Fig. 9 [144]. These structures exhibit a common three-stage compressive mechanical behavior similar to that of other cellular structures. However, they display a larger plateau stage with an increasing trend as a result of the lower Poisson’s ratio. A novel auxetic structure was realized from double-V structures, called a double-U structure [145]. The external and internal apexes of a double-V structure were introduced with a curvature to form the new structure. The results showed promising NPRs and moduli that lied closely with those of double-V structures for different directions of applied compressive loads

Fig. 8.

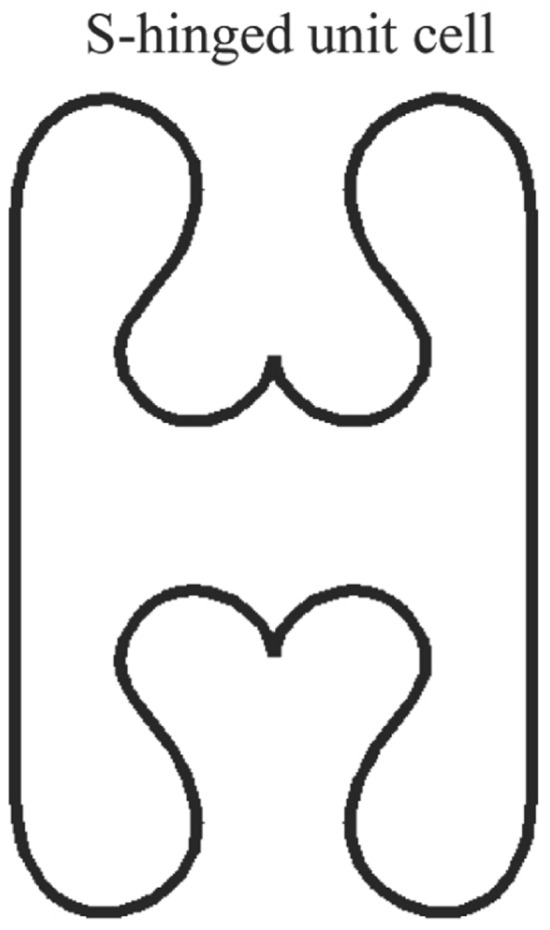
Unit cell structure of an S-hinged unit cell [143]

Fig. 9.

Double-V unit cell structure [144]

A layered topological framework integrated using tetrachiral honeycomb microstructures shows an exceptional coupling between the normal and angular strains, as described in preliminary laboratory studies [146]. An extension of this finding to bi-tetrachiral materials exhibited strong auxeticity with NPRs of approximately −0.7. Axisymmetric auxetic structures, as shown in Fig. 10, resulted in elevated Poisson’s ratios in the structures [147]. However, the specific Young’s modulus of the structure was enhanced as compared to honeycomb theories. In addition, the circumferential deformation effect of the structure that resulted from the unit cells enhanced its mechanical properties. On a similar front, Chen et al. [148] modified a classic re-entrant cell by embedding some additional ribs to enhance the energy absorption, stiffness, and strength parameters of the structure. Chiral 3D isotropic structures, as shown in Fig. 11, showed NPRs of close to −1 [149]. The structure maintained the isotropy and NPR when the compressive forces were increased during the initial linear elastic stage of deformation. The tuneability of this structure lies in the length of the ligaments, which can result in anisotropic structures with variable NPRs when changed. Composite structures with isotropic NPR effects were realized by adding random re-entrant structures into the matrix [21]. The isotropic NPR of the structure is dependent on the number of inclusions. That is, even if the inclusions have an NPR, the lower values of their addition in the structure may deem the structure to have a positive Poisson’s ratio.

Fig.10.

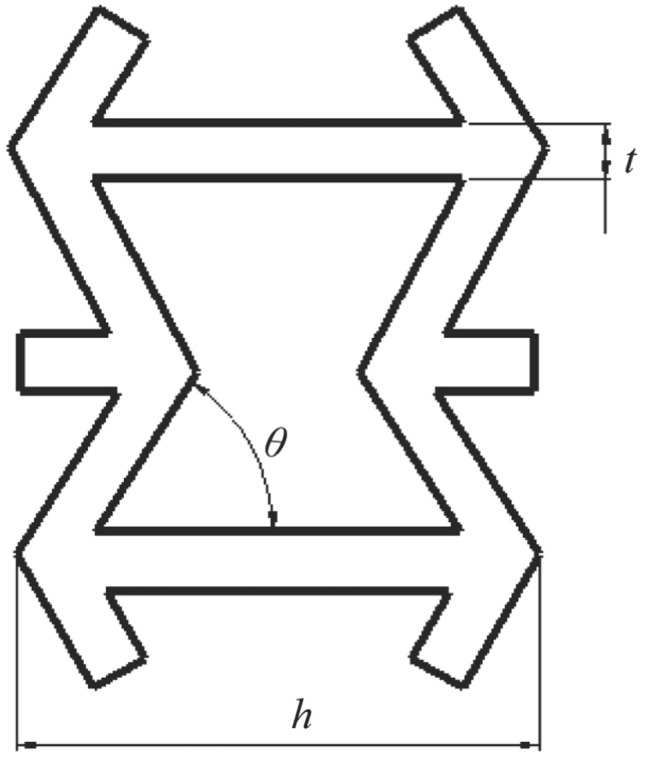
Axisymmetric auxetic unit cell based on the re-entrant model [147]

Fig. 11.

3D chiral structure unit cell[149]

The application of Kirigami techniques to cellular composite structures can produce honeycomb structures of diverse and arbitrary geometries [150]. A graded core configuration can result in excellent compressive properties with an appreciable NPR under both flatwise and edgewise loading conditions, with variable behavior. Three-dimensional chiral unit cells were also seen to be useful in producing cellular solids with amplified auxetic effects as a result of their enhanced internal rotation effects [151]. The effect was quantitatively proved through mechanical experiments, and the NPR was seen to have a linear relationship with the internal rotation parameter. As opposed to the regular sacrifice of an NPR for better mechanical properties, the auxetic cell design proposed by Li et al. [152] achieved optimum mechanical properties without having to decrease the auxeticity. The structures resembled a re-entrant and V-shaped lattice with vertical support walls throughout the length, as shown in Fig. 12. A similar optimization route was adopted by Lu et al. [153] for hexagonal unit cell structures.

Fig. 12.

Modified a re-entrant and b double-V structures with vertical support as mentioned in Ref. [152]

The 3D auxetic structures formed by rotating regular 2D cross-chiral elements in combination with other unit cells enhances the overall NPR [154]. The structures exhibit a uniform elastic behavior in all principal directions while maintaining an NPRs of close to −1. The structures are proposed for application to body armor, shock absorbers, and tunable filtrations. Similar observations were made for square grid structures, wherein alterations in the arrangement and modification of the geometric parameters of the square grid structures gave rise to an enhanced auxeticity [155]. For the fatigue life studies of the structures, the re-entrant honeycomb unit cells exhibited a better fatigue life over hexagonal honeycomb unit cells. This observation might serve as an indication of better fatigue properties in auxetic structures over normal materials in general [156]. Through a computationally assisted design and analysis, adaptive curvature auxetic structures were realized [157]. Their performance was estimated using particle spring systems (PSS) and finite element methods (FEMs), which aid in critical design optimizations and faster iterations. A peanut-shaped lattice structure developed by Wang et al. [158] produced large NPRs with lower stress levels than elliptical holes. The controlled porosity and smaller sizes of the unit cell increased the numerical value of the observed NPR, whereas the elastic properties had the minimal intervention.

Effects of process and geometric constraints on the mechanical properties of AM auxetic structures

A comparative understanding of how different processing and geometric parameters alter the observed properties in auxetic structures realized through AM is necessary to tune the auxetic structures for the maximum performance. This discusses some of the most critical mechanical properties such as the tensile strength, compressive strength, impact resistance, ballistic performance, and fatigue life.

Compressive properties

Compressive tests on the most common auxetic structures such as a missing rib model and a re-entrant model obtained through direct 3D printing showed different stress-strain responses, as indicated in Fig. 13 [159]. Although both structures show good in-plane NPRs, FE simulations can be used to tune the geometric parameters of the structure and achieve better results. The crash performances of the cylindrical tubes composed of conventional, honeycomb, and auxetic structures showed enhanced energy absorption capabilities at lower velocities [160]. It was seen that, among these three types, the specific energy absorption of auxetic structures was superior to that of honeycomb structures. The deceleration was almost uniform in the case of auxetic structures as opposed to the oscillating nature seen in honeycomb structures, thereby affirming the damping capabilities. On a similar front, auxetic cellular structures fabricated from inverted tetrapods with variable porosity showed a varying plateau region as a result of the graded porosity [161]. The plateau stress showed a progressive increase when the high porosity regions were placed in front. A converse behavior was observed when low porosity regions were put in front. SEBM-fabricated auxetic chiral structures showed behavioral anomalies when subjected to different strain rates [162]. The specific strength and the specific energy absorption showed dramatic improvements for larger loading velocities. Re-entrant auxetic structures showed a better specific strength at lower re-entrant angles [163]. The dominant effect of NPR is particularly useful to achieve structures of higher specific strength with lower mass values. Upon analyzing the fracture behavior of SLS structures, it was seen that SLS-prepared 3D cross-chiral structures exhibited a combined failure mode [164]. Plastic yielding was initially seen at the top and bottom struts, whereas for the other struts, plastic yielding was caused by an additional bending moment toward the end of the test. An elastic buckling failure was witnessed in general for the entire structure during the middle stages.

Fig. 13.

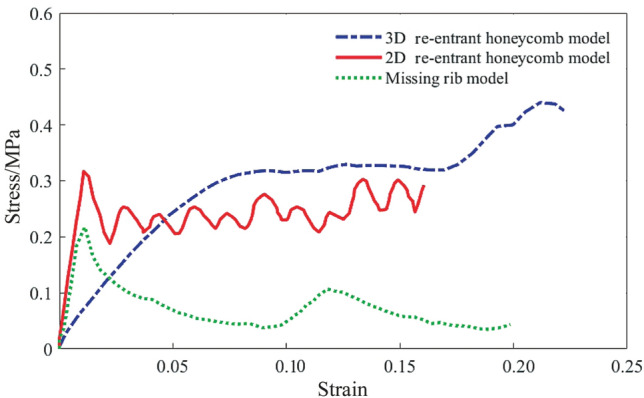
Comparison of the compressive behavior of re-entrant honeycomb and missing rib auxetic structures

A high strain-rate testing of auxetic cellular structures made from inverted tetrapods through additive manufacturing showed an ample dependence on the porosity of the structure [165]. As opposed to quasi-static loading, the dynamic loading of these structures alters the deformation mode from homogenous to shock mode as the velocities increase beyond a certain threshold. FE models were exploited to optimize the auxetic performance and mechanical properties of brass-auxetic metamaterials [26]. This has led to a significant reduction in buckling induced failures in such structures. In addition, the authors of this previous study proposed the introduction of pattern scale factors to retain the auxetic behavior of ductile materials, which was otherwise lost when an elastomeric base was replaced by a ductile one. The earlier effect was a result of the localization of the plastic deformation, which was seen to have a negligible influence on the current auxetic design. Studies on a thermally tunable Poisson’s ratio were carried out by Zhao et al. [166]. Experimental and theoretical investigations of these metamaterials showed that treatments involving higher temperatures reduced the strength of the composites. However, by contrast, the NPRs showed a dramatic decrease at a higher temperature. Figure 14 shows a comparison of the highest effective Poisson’s ratio and force observed for the structures through experimental and theoretical routes at different temperatures. The defects that arise from the manufacturing processes can be reduced through effective modeling to include strut defects within the lattice structure [167].

Fig. 14.

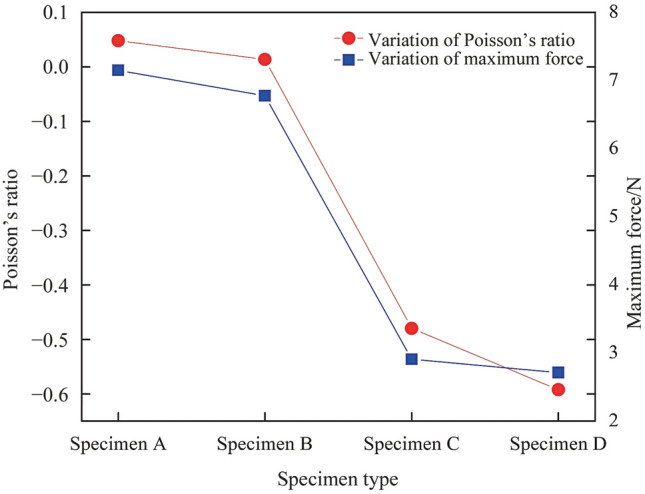
Variation of the Poisson’s ratio and the maximum force for structures compressed at 25 °C, experimentally– specimen A, 25 °C theoretically– specimen B, 70 °C experimentally– specimen C and 70 °C theoretically– specimen D

Impact and ballistic properties

Ballistic studies on auxetic re-entrant structures based on Ni-Ti showed that higher NPRs were observed for structures with lower re-entrant angles [168]. Densification of Ni-Ti toward the end of a projectile’s motion through the structure aided in better energy absorption characteristics. Blast resistance characteristics of re-entrant models with varying re-entrant parameters such as the angle and central distance to the horizontal length ratio were also quantified based on their crushing strength [169]. It was observed that the crushing strength increased for different values of the horizontal ratio at a given re-entrant angle. A similar inference can be made for different re-entrant angles at a constant horizontal ratio. Numerical estimations of auxetic composites made using a modified re-entrant design subjected to blast loadings showed reduced back-facet displacements as a result of plastic deformation and densification of the structure [170]. Studies by Liu et al. [171] on the crushing behavior of hexagonal honeycomb structures revealed an innate dependence on the Poisson’s ratio of the structures. It was seen that NPR structures yielded lower critical speeds and absorbed the most energy in certain deformation modes. In addition, the existence of NPR in these structures affects the crushing parameters such as the plateau stress and densified strain at higher crushing speeds. However, at lower crushing speeds, the topological diversity induced by the Poisson’s ratio is the dominant mechanism. Protective structures realized through auxetic metamaterials showed a buckling induced failure for quasi-static strain rates [172]. The material used was a silicone-based rubber fabricated using 3D printing along with support structures. Epoxy-based adhesives were used for mending ribs that broke while removing the support structure. For higher dynamic strain rates, the auxetic effect was lower, as seen in Fig. 15. Blast loading of an auxetic composite structure, which possessed a modified re-entrant structure provided the maximum efficiency for a smaller beam radii [173]. However, it was seen that the material properties had very minimal effects on the observed energy absorption characteristics.

Fig. 15.

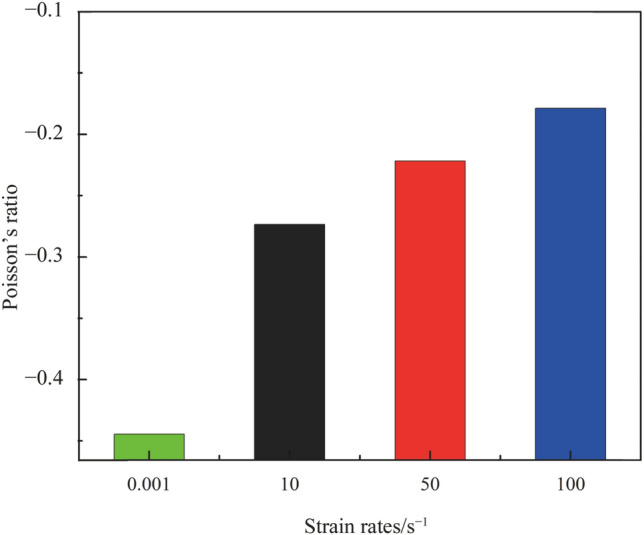
Variation of the Poisson’s ratio for different strain rates at a maximum strain of 0.30 [172]

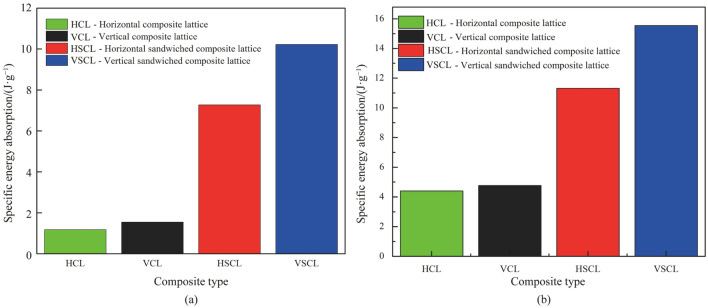
The energy absorption behavior of cylindrical auxetic structures composed of re-entrant unit cells was also studied. Cases with horizontal and vertical unit cell arrangements were considered. The former exhibit better specific energy absorption for lower and higher velocities as the relative density varies [174]. However, when the same arrangements are made using sandwiched composite panels, the specific energy absorption increases dramatically for both, with lower and higher velocities for varying relative densities. This is also illustrated in Fig. 16 for an 8% relative density at lower and higher velocities. In a study conducted by Najafi et al. [175], it was seen that auxetic structures with an arrowhead unit cell configuration achieved better specific energy absorption characteristics, followed by the anti-tetrachiral, re-entrant, and honeycomb variants in order. A similar FE-based study by Shepherd et al. [176] compared the energy absorption properties of similar structures with varying indenter configurations to record their strain variations. Further experimental estimations on polyurethane auxetic foam showed that, for a fixed mass of the impacting body, these structures exhibited a better impact absorption than conventional foam [177].

Fig.16.

Specific energy absorption of different auxetic lattices at a low velocities and b high velocities [174]

Impact studies on structures made of honeycomb re-entrant unit cells, prepared through 3D printing, showed an enhanced energy absorption as a result of plastic straining and not the energy dissipation [178]. An in-depth compression study on different structures composed of re-entrant cells was conducted by Shokri et al. [179]. The re-entrant cells were arranged in different manners to accommodate the structural space, and for a few variants, minor changes in the unit cell design were implemented as well. It was seen that a cross arrangement of re-entrant cells provided greater energy absorption. Drop weight impact tests on multiple auxetic cores were carried out by Beharic et al. [180]. The study established that the quasi-static properties and the drop impact characteristics were related. In addition, the buckling of the vertical struts seen in the auxetic cellular design aided in better energy absorption characteristics.

Fatigue properties

Fatigue life estimates for SLM printed auxetic re-entrant structures and non-auxetic structures showed that the former achieved better fatigue characteristics [83]. The non-auxetic variants were seen to fail as soon as the load was increased to 10 kN after subjecting them to 500 cycles of 6 kN. However, the auxetic variants sustained much larger cycles at higher loads. The auxetic structures fold and become denser upon failure, which leads to an induced hardening effect as opposed to the regular failure of non-auxetic structures. Fatigue life estimations of additively manufactured AlSi10Mg alloys were carried out by Ulbin et al. [181] through computational routes. The study illustrated the role of various topological geometries and their dimensional variations to maximize the fatigue life. The effects of geometric parameters on the auxetic behavior of a rubber-based re-entrant structure were studied by Filho et al. [182]. The thickness and width of the struts were one of the prime factors affecting the Poisson’s ratio and strength of the composites. A similar study by the authors showed the adaption of a swarm intelligence technique, which was useful in optimizing the re-entrant angle, width, and thickness of the structure for sustainable properties including the NPR, strength, and elastic modulus [183]. Low-cycle compression tests on 3D printed re-entrant auxetic structures again showed better results at approximately 500 cycles [184]. The non-auxetic structures encountered in this study succumbed to larger deformations earlier than their auxetic counterparts. The smaller mechanical hysteresis seen in auxetic counterparts during the loading of these materials indicates that they are suitable for structures that are repeatedly loaded.

Tensile properties

As for the variation in the mechanical properties such as tension and other related parameters, Zhang et al. [185] adopted a combined experimental and FE approach to determine large deformations of re-entrant auxetic structures. For this, stainless steel and epoxy resin with reactive diluents were used to 3D print re-entrant structures using SLM and SLA. In a comparison of the tensile behavior of stainless steel and polymeric (epoxy liquid resin) structures, these structures showed good mechanical responses while exhibiting a high auxeticity. This is also illustrated in Table 1, where a comparison of the different tensile parameters in both directions is presented. The mechanical behavior of SLS-manufactured cylindrical stents composed of tetrachiral and anti-tetrachiral ligaments was analyzed by Geng et al. [186]. The stents were subjected to tensile tests to determine the best configuration of the stent. Geometric parameters such as the circumferential struct number, radius of the struct, ligament angle, and the consequent variation in the stent length affected the Poisson’s ratio of the structure. Figure 17 shows a comparative analysis of the effect of these parameters on the Poisson’s ratio. It was seen that the stent possessing a circumferential struct number of 16 with the ligament oriented at 10° from the normal showed the highest NPR. Similar variations were observed for hyperelastic auxetic cellular materials with re-entrant structures [187]. In addition, a more prominent, and promising, auxetic behavior is witnessed when the material is stretched in the vertical direction rather than in the transverse direction. This is because stretching the structure in the vertical direction causes the inclined ribs of the re-entrant structure to require a smaller force at smaller angles. In the latter case, the auxetic behavior vanishes much earlier as opposed to the complete auxetic behavior of the former.

Table 1.

Experimental and analytical estimations of the tensile strength and the range of the Poisson’s ratio for large tensile deformations of the SLA-manufactured epoxy resin and SLM-manufactured stainless steel for two different loading directions [185]

Material	Loading direction	Experimental results		FEM results
		Fracture stress/MPa	Range of Poisson’s ratio	Fracture stress/MPa	Range of Poisson’s ratio
Stainless steel	X2	2.73	−4.0 to +0.5 (0 at 0.16 strain)	3.05	−4.0 to +2.5 (0 at 0.9 strain)
	X1	2.27	−0.2 to −0.8	4.98	−0.2 to −1.3
Epoxy liquid resin	X2	0.06	−3.5 to +3.0 (0 at 0.6 strain)	0.12	−3.5 to +6.0 (0 at 0.6 strain)
	X1	0.12	−0.75 to −2.0	0.12	−0.5 to −2.8

Fig. 17.

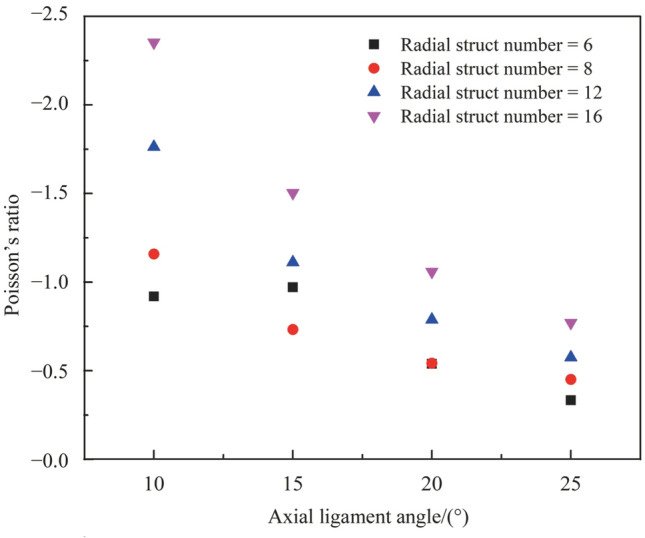
Variation of the NPR for the axial ligament angle for various radial/circumferential struct numbers [186]

Applications

The extensive studies conducted on novel manufacturing techniques showed that the auxetic structures could be the potential candidates for application in various engineering fields ranging from aerospace components to marine structures, defense, sports, actuators, and tissue engineering, among others. In addition, the developments in the AM of auxetic structures have further expanded their spectrum of application owing to the improved accuracy and ease in the fabrication of intricate structures. The application of AM auxetic structures for biomedical and tissue engineering devices is extremely helpful in producing customized and cost-effective devices [188]. Investigations by Mardling et al. [189] suggested the use of auxetic structures in various tissue engineering and biomedical applications. Auxetic structures manufactured through AM have been used to design and fabricate the femoral component for total hip replacements [190]. The production of oesophageal stents using auxetic structures reduces weaknesses usually presented by the use of welded joints [191]. The rotating square unit cell structure has been used extensively for this purpose [192]. The same can be extended for the fabrication of orthopedic implants with improved surface finish and strength using EBM [193]. Porous auxetic materials are used in the fabrication of smart bandages and smart filters where the pore size varies in accordance with the applied stress [194, 195]. In addition, they are one among the prime candidates for applications such as drug delivery and the removal of metabolic wastes. Using laser techniques, these materials can be used to fabricate adaptable scaffolds. Furthermore, auxetic scaffolds with nanometric precision were additively manufactured for tissue engineering applications [196]. Additively manufactured light-weight auxetic composites are used in the fabrication of surgical hernia meshes and compression garments [197]. Although detailed research has not been carried out at this stage, auxetic structures have prospective applications in prosthetic devices [198]. In addition, perforated auxetic structures with an auxetic foam lining can be used in full-body support structures [199]. One of the most recent applications of auxetic structures was the production of AM nasopharyngeal swabs for COVID-19 sample collection [200]. The quick and versatile manufacturing offered by AM was particularly useful in this scenario for a fast and distributed production.

In addition to biomedical applications, auxetic materials have been used for sports applications for better comfort and reliability. In this regard, auxetic foam shows great promise on this front owing to its superior energy absorption capabilities [201]. In a recent study, Duncan [202] suggested the use of auxetic foam structures in the production of personal protection equipment (PPE) for sports personnel with higher mechanical and impact properties. Some of the potential equipment includes cricket pads, shin pads, crash helmets, and car bumpers. Experimental studies on novel cylinder-ligament honeycomb auxetic structures affirm the applicability of these structures for sports helmet applications [203]. The structures showed significant indentation resistance and excellent resilience under compression. A combined AM and FE approach has also been adopted to produce sports PPEs of the highest quality [176]. The adoption of FE techniques has resulted in finer optimizations without the need to continuously fabricate these structures and subject them to physical tests. Auxetic structures have realized their potential in smart structures by functioning as actuators for smart beams and structures [204]. Nature-mimicking auxetic materials have high energy absorption capabilities that are useful in military protective sandwich plates and civil engineering structures [205]. Multifunctional architected materials made of Kevlar, realized through direct ink writing and freeze casting, possess ultra-low densities and superior mechanical properties [206]. Such structures can be used for aerospace and military applications for better impact protection devices and secondary structures [207].

In addition to protective equipment, auxetic materials make excellent pressure-fir fasteners and rivets that are easy to install and provide effective sealing [208]. Auxetic structures are also used to design blast pressure deflectors in armored ground carriers [209]. However, further enhancements in the properties of these structures are achieved through the addition of polyurea coatings. Such structures can be extensively used for tank linings, secondary coatings on bridges, marine structures, and many other applications [210–212]. Macroscopic and microscopic auxetic structures are used in aerospace components such as curved body parts, aircraft nose-cones, and aircraft wing panels [213]. Multifunctional auxetic honeycomb structures are used in actively cooled supersonic aircraft skins and lightweight structures with internal damping [214]. With a reduction of thermal stresses in auxetic structures, they have been proposed for use in aircraft structural components, pressure vessels, and other similar structures [215]. The superior heat dissipation capabilities of hexagonal auxetic honeycomb structures over other honeycomb structures promote a multifunctional applicability in terms of heat transfer, thermal protection, and catalysis [216]. The compressive and impact absorption of auxetic structures have made them suitable for applications that require strength and durability [217]. Auxetic structures are used in the production of auxetic textiles that have better compatibility, a lower density, improved air permeability, and other enhanced functionalities [218]. Such textile components are used to fabricate blast curtains, PPEs, maternity dresses, and dresses that grow as children grow.

Certain auxetic patterns suggested by Naboni and Mirante [219] can be exploited to have suitable properties for architectural applications. Hexatruss re-entrant structures were utilized to fabricate and analyze high elastic structures that can take extreme loads as demanded in architectural applications [220]. Kasal et al. [221] promoted the use of auxetic structures in furniture joints by comparing their withdrawal strength properties. The study suggested the use of metals or other tough materials as alternatives to polymeric materials, which did not provide satisfactory results. Stretchable sensors were manufactured from ionogel-based auxetic frameworks through 3D printing [58]. The electromechanical behavior of auxetic piezoelectric cellular solids aid in the design of special sensing and actuating devices [222]. Consequently, they have found immense potential in devices such as ultrasound and energy harvesters. 3D printed chiral auxetic metamaterials display sufficient stability under different external stimuli making them apt for applications such as drug delivery and camouflage [223]. Multifunctional metamaterials combined with Kirigami auxetics are used to obtain programmable electromagnetic responses for similar applications [224]. These structures show a detectable change in the conductivity on the application of bending or twisting loads. Further applications of auxetic structures are seen in the fabrication of electro-active bushings used as a dielectric elastomeric membrane within a circular auxetic structure [225].

Challenges, limitations, and future prospects of AM of auxetic structures

As with any conventional manufacturing method, AM is also characterized by several limitations. One of the primary limitations of the current AM techniques is the non-availability of sufficient materials that can be readily 3D printed. Although newer polymer and metal-based composite materials have produced recently, the primary constituents or the matrix material of such composites remain the same. Moreover, the addition of large quantities of inclusions is also not serviceable by most AM techniques. It leads to several issues such as nozzle clogging in FDM, improper melting in SLM and other laser-based techniques, a complicated extrusion of the polymer filaments, and an improper distribution of the fibers and particles, among many factors. These shortcomings may prove to be expensive in terms of the overall costs of manufacturing and the recurrent downtimes followed by subsequent maintenance [226]. This in turn imposes strict limitations on the extent of the fiber and particle concentration in achieving the optimal performance. In addition, thermosetting polymers have found minimal applicability for AM-based techniques. Hence, the non-availability of a large library of materials is a major drawback to the expansion of such approaches.

There needs to be more sophistication with respect to auxetic materials themselves. Currently, a vast majority of auxetic materials and cellular structured composites have limited flexibility in terms of favorable mechanical properties and the NPR. Hence, there is an impending need to develop multifunctional structures that can provide the necessary strength and the required auxetic functionality. Only then can such structures be used for demanding application with improved responses. Moreover, with the development of AM techniques for greater precision and accuracy, auxetic structures can be further explored without many complexities in their physical fabrication. However, AM techniques are time-consuming because of their layer-by-layer manufacturing approach. When considering the structural integrity and performance of AM-based auxetic structures, a major drawback here is the formation of voids [227–229]. This is a result of reduced and improper bonding between successive layers. This in turn leads to a high anisotropy and delamination that subsequently translates to poor mechanical properties. Another hindrance for AM auxetic structures is the appearance of staircase effects. Although it is considered to be a minor issue for internal structures, the quality of the external surfaces is substantially affected. Such shortcomings can render the process expensive while also diminishing its applicability. This downside is more pronounced in the fabrication of auxetic structures where there is a high involvement of complex geometries. In addition, whereas AM techniques aid in the fabrication of complex geometries, the extent of sophistication is often limited by the capabilities of the machine. Processes such as FDM offer great versatility and adaptability with lesser operational costs when compared with other manufacturing techniques. However, their resolution usually lies in the sub-millimeter range. Therefore, intricate geometries for the micron and sub-micron levels cannot be processed using this technique. Although other AM techniques are capable of catering to smaller resolutions, they are not widely preferred owing to the lack of suitable materials and the consequent loss in multifunctionality. Inherent material and manufacturing faults such as internal voids, unfilled sections, incorrect printing speeds, incorrect temperature profiles, faulty extrusion, and warping can severely affect the properties and performance of AM auxetic structures. Furthermore, most AM techniques are limited to the fabrication of small parts. Therefore, larger auxetic structures demand more sophistication and improvements in the AM techniques for a larger volume and quicker production of auxetic structures without affecting the auxetic behavior. AM is said to offer considerable cost savings because of the reduced recurring costs and abatement in manufacturing expenses for low volume production. However, the present costs for AM parts are quite high owing to the lower demand for such parts in the commercial space coupled with higher energy consumption. The energy consumption primarily depends on the duration of each job, which is in turn characterized by the complexity of the structure and other printing parameters. Although it is difficult to determine the specific energy consumption for a specific process, Sreenivasan and Bourell [230] suggested an average value of 52.2 MJ/kg. Because auxetic structures are usually characterized by such complex geometries, it is proper to expect a high cost per part in the current scenario. Furthermore, the cost of 3D printers itself is high. Additional functionalities such as a 3D scanner or a dual-nozzle extrusion setup for 3D printers increases the cost significantly. Therefore, for the production of cost-efficient parts, there is an immediate need to efficiently optimize the process and energy consumption of the processes.

These shortcomings in the AM used in auxetic structures can be mitigated to a certain extent by the adoption of computational tools for the regulation and optimization of structural and process parameters. An efficient feedback loop for continuous iterations is essential for maximizing the productivity of AM techniques for the fabrication of auxetic structures. A shift from traditional point-to-point printing to areal printing can have a significant benefit for the utilization of AM in auxetic structures. The use of areal printing techniques can reduce the time and energy requirements to produce auxetic parts, which in turn can reduce the overall expenses associated with the production. The thoughtful and efficient adoption of a combination of subtractive and transformative manufacturing technologies can further reduce, if not abate, the present shortcomings associated with the present AM techniques. This has given rise to a domain in manufacturing called hybrid manufacturing for quicker and more efficient production. Furthermore, with efficient cost models, the cost of parts produced by AM can be significantly optimized to encourage different industries and individuals to utilize AM for several applications [231]. Areas such as organ printing, biomedical scaffolding, and auxetic prosthetics, among many others can pave the way for quicker treatment protocols and easier access to assistive devices [232]. To conclude, AM for auxetic structures can rightly be called the “manufacturing technology of tomorrow” .

Several legal complications arise with the free use of AM machines. A patent and copyright infringement on the unlicensed use and manufacture of 3D printers makes manufacturing a laborious and expensive venture [233]. In addition, there will be severe problems in identifying a proper chain of manufacturing because AM has potential application in distributed manufacturing. Whereas distributed manufacturing can enable a faster production, it can be tougher to trace the line of events of an undesired activity. Another contributing factor that limits the use of AM processes is the non-availability of feasible standards [234]. Because the AM process is quite new to numerous industries, there is an absence of a distinct set of rules and regulations that can regulate the quality of AM parts. Hence, most industries are hesitant to adopt AM for such applications owing to a lack of quality assurance norms.