Evolutionary homology on coupled dynamical systems with applications to protein flexibility analysis

Abstract

While the spatial topological persistence is naturally constructed from a radius-based filtration, it has hardly been derived from a temporal filtration. Most topological models are designed for the global topology of a given object as a whole. There is no method reported in the literature for the topology of an individual component in an object to the best of our knowledge. For many problems in science and engineering, the topology of an individual component is important for describing its properties. We propose evolutionary homology (EH) constructed via a time evolution-based filtration and topological persistence. Our approach couples a set of dynamical systems or chaotic oscillators by the interactions of a physical system, such as a macromolecule. The interactions are approximated by weighted graph Laplacians. Simplices, simplicial complexes, algebraic groups and topological persistence are defined on the coupled trajectories of the chaotic oscillators. The resulting EH gives rise to time-dependent topological invariants or evolutionary barcodes for an individual component of the physical system, revealing its topology-function relationship. In conjunction with Wasserstein metrics, the proposed EH is applied to protein flexibility analysis, an important problem in computational biophysics. Numerical results for the B-factor prediction of a benchmark set of 364 proteins indicate that the proposed EH outperforms all the other state-of-the-art methods in the field.

1. Introduction

Homology, a tool from traditional algebraic topology, provides an algebraic structure which encodes topological structures of different dimensions in a given space, such as connected components, closed loops, and other higher dimensional analogues [48]. To study topological invariants in a discrete data set, one uses the structure of the data set, such as pairwise distance information, to build a simplicial complex, which can be loosely thought of as a generalization of a graph, and then compute the homology of the complex. However, conventional homology is blind to scale, and thus retains too little geometric or physical information to be practically useful. Persistent homology, a new branch of algebraic topology, embeds multiscale information into topological invariants to achieve an interplay between geometry and topology [18,37,45,50,46,60].

Given a continuum of topological spaces, called a filtration, persistence encodes the changing homology as a proxy for the shape and size of the data set by keeping track of when homological features appear and disappear over the course of the filtration. This flexibility means that the choice of filtration allows the use of persistent homology to be tailored to the data set given and the question asked. As a result, it has been utilized for analysis of data sets arising from many different domains. For biology related areas [63], persistence has been used in bioinformatics [52,72,15,13], neuroscience [82,32,33,31], and protein folding [92,90,93,43].

The 0-dimensional version of persistent homology was originally introduced under the name “size function” [40,41,77–79]. The generalized persistent homology theory and a practical algorithm was formulated by Edelsbrunner et al. [38]; the algebraic foundation was subsequently established by Zomorodian and Carlsson [96]. Recently, there have been significant developments and generalizations of persistent homology methodology [8,28,30,25,22,20,81,19,94, 11,69,36], further understanding of metrics and stability [27,24,29,12,34], and computational algorithms [67,35,59,84,62,7,6]. Persistent homology is often visualized by barcodes [23,45] where horizontal line segments called bars represent homology generators that survive over different filtration scales. The persistence diagram [37] is an equivalent representation that plots the births and deaths of the generators in a 2D plane.

Persistent homology is a versatile tool for data analysis. However, the difficulties inherent in the interpretation of the topological space of persistence barcodes [57,86,61] means that the most success in combining these topological signatures with machine learning methods has been found by turning persistence barcodes into features in a well-behaved space suitable for machine learning. Options for this procedure are quickly growing, and include persistence landscapes [10], algebraic constructions [2,21,51], persistence images [1, 93,13], kernel methods [76,92], and tent functions [74]. In 2015, Cang et al. constructed one of the first topology based machine learning algorithms and applied it for protein classification involving tens of thousands of proteins and hundreds of tasks [14]. This approach has been generalized for the predictions of protein-ligand binding affinity [16] and mutation-induced protein stability change [15], and further combined with convolutional neural networks and multi-task learning algorithms [17].

Although most persistent homology formulations are based on spatial data, such as point clouds, the use of homology for the analysis of dynamical systems and time series analysis predates and intertwines with the beginnings of persistent homology [50,58,44,4,78,77,79]. More recently, there has been increased interest in the combination of persistent homology with time series analysis [80]. Some common methods include computing the persistent homology of the Takens embedding [73,72,71,54,53,55], studying the sublevelset homology of movies [56,85], and working with the additional structure afforded by persistent cohomology [81,9,87]. Wang and Wei have defined temporal topological persistence via the solution of a time-dependent partial differential equation derived from differential geometry [88]. This method encodes spatial connectivity into temporal persistence in the Laplace-Beltrami flow, and offers accurate quantitative prediction of fullerene isomer stability in terms of total curvature energy for over 500 fullerene molecules. Stolz et al. have recently constructed persistent homology from time-dependent functional networks associated with coupled time series [83]. This work uses weight rank clique filtration over a defined parameter reflecting similarities between trajectories to characterize coupled dynamical systems.

All the aforementioned methods concern the global topology of a given data, such as the topology of the point cloud of a protein. Topology is inherently a global concept and describes a data as a whole. Such a global topology is useful for the global property of the object under description, e.g. band gap of a solid material, the binding affinity of an entire protein-ligand complex, and solubility of a molecule. It is noticed that relative homology was applied to extract the global topology of a localized region [39] and has been used to compare maps [3]. However, in science, engineering, and other fields, it is often desirable to understand the local property of an individual component of object, such as the topological property of a given atom in a molecule, the impurity in a solid, and a node in a network.

The objective of the present work is to introduce a new type of topological methods, called evolutionary homology (EH). The proposed EH describes the topological properties of an individual component that is determined by the given individual and its adjacency in a data. To this end, we embed the data into a dynamical system and systematically perturb each individual element (oscillator) of the dynamical system to generate topological response, which is recorded as temporal persistence. Specifically, simplicial complex filtration based on the trajectories of a set of chaotic oscillators coupled via the interactions of a physical system to obtain temporal topological persistence. We are particularly interested in the encoding of the topological connectivity of a real physical system into the chaotic dynamical system and the decoding of physical properties from the EH. To this end, we regulate the dynamical system by a generalized graph Laplacian matrix defined on the physical system with a distinct geometric structure. As such, the regulation encodes the structural information into the time evolution of the dynamical system. We use two well-studied dynamical systems, the Lorenz system and the Rössler system, to facilitate the control and synchronization of chaotic oscillators by weighted graph Laplacian matrices. These dynamical systems are chosen for their simplicity, rich dynamics and well-known chaotic behaviors. We create machine learning features from the EH barcodes by using the Wasserstein and bottleneck metrics. The resulting outputs in various topological dimensions are directly correlated with the physical properties of the dataset.

To demonstrate the quantitative analysis power of EH, we apply the present method to the prediction of protein thermal fluctuations characterized by experimental B-factors of C_α atoms. In this application, protein residues are represented by individual dynamical systems connected by a coupling matrix derived from given pairwise interactions of the residues. The protein flexibility is characterized by analyzing how the perturbations introduced to the systems are propagated and relaxed among oscillators, which create EH. We show that these coupled nonlinear dynamical systems provide more information compared to other methods. It is found that the present EH provides some of the most accurate B-factor predictions for a benchmark set of 364 proteins.

2. Methods

This section is devoted to the methods and algorithms. In Sec. 2.2, we give a brief discussion of coupled dynamical systems and their stability control via a correlation (coupling) matrix which embeds topological connectivity of a physical system into the dynamical system. We review persistent homology and persistence barcodes in Sec. 2.3. We formulate local topology or evolutionary homology on coupled dynamical systems in Sec. 2.4. Finally, we discuss the treatment of barcodes, the associated metrics, and the methods for learning in Sec. 2.5.

2.1. Overview

We aim to extract topological information from a coupled dynamical system for the prediction of its physical properties. In the coupled dynamical system, all objects are represented by the same set of mathematical rules. We assume that a measurement of pairwise interactions is given a priori. This pairwise interaction induces couplings among the individual objects such as atoms on a protein which leads to the synchronization of the system if the coupling is sufficiently strong. Then a perturbation is applied to an individual object which will be propagated through the coupled system and finally relax to the synchronous state. We define simplicial complexes and algebraic groups on the dynamical motion or trajectories of the coupled system. The time evolution plays the role of filtration and allows us to further define evolutionary homology. The resulting topological persistence over time enables us to predict the physical properties of the embedded system, such as protein flexibility, protein-protein binding interactions, and the affinity of protein-drug binding.

Protein flexibility analysis is considered a specific application to illustrate and validate our approach. Protein flexibility is an important property that strongly correlates to many protein functions, such as reactivity, allosteric signaling, DNA binding specificity, Alzheimer’s disease, etc. In our formulation, every protein residue is represented by a nonlinear oscillator. The pairwise interaction among protein residues is characterized by a spatial distance valued graph Laplacian function. The method introduced in this work describes the formation and change of high order topological invariants and how they quantify protein residue flexibility. This approach has shown to provide more accurate flexibility prediction than current state-of-the-art methods.

2.2. Coupled dynamical systems

The time evolution of complex phenomena is often described by dynamical systems, i.e., mathematical models built on differential equations for continuous dynamical systems or on difference equations for discrete dynamical systems. Most dynamical systems have their origins in Newtonian mechanics. However, these mathematical models typically only admit highly reduced descriptions of the original complex physical systems, and thus their continuous forms do not have to satisfy the Euler-Lagrange equation of the least action principle. Although a low-dimensional dynamical system is not expected to describe the full dynamics of a complex physical system, its long-term behavior, such as the existence of steady states (i.e., fixed points) and/or chaotic states, offers a qualitative understanding of the underlying system. Focused on ergodic systems, dynamic mappings, bifurcation theory, and chaos theory, the study of dynamical systems is a mathematical subject in its own right, drawing on analysis, geometry, and topology. Dynamical systems are motivated by real-world applications, having a wide range of applications to physics, chemistry, biology, medicine, engineering, economics, and finance.

The dynamical systems employed in this work are well-known chaotic oscillators, namely the Lorenz system and the Rössler system. These systems are selected for the following reasons. 1) They have well-known chaotic behavior. For certain parameter regions and initial conditions, these systems admit chaotic behavior resembling real world phenomena. This information is used to encode the interactions of the physical system. 2) The chaoticity of the Lorenz system and the Rössler system can be easily controlled via a coupling strategy [66,49,89,91] which enables us to appropriately design the proposed EH method. 3) Although the dynamics of the Lorenz system and the Rössler system are quite rich, they are easy to compute. Therefore, interactions of physical systems, such as protein residue-residue interactions and protein-ligand interactions, can be easily encoded to regulate their chaotic dynamics. The resulting dynamics are used in the computation of persistence.

2.2.1. Systems configuration

A brief review is given to establish notation and facilitate our topological formulation, largely following the work of Hu et al. [49] and Xia and Wei [91]. We consider a system with N objects, such as N atoms in a molecule or N neurons in a brain. We regard each object as an n-dimensional dynamical system, i.e., an n-dimensional oscillator. As such, the internal dynamics of N objects is governed by

$$\frac{d{\mathbf{u}}_i}{dt}=g\left({\mathbf{u}}_i\right),i=1,2,\cdots ,N,$$

where ui = {u_i,1,u_i,2, ⋯ ,u_i,n}^T is a column vector of size n.

In reality, objects are interacting with each other. As a result, there are external couplings among objects. The coupling of the objects can be very general. We consider an N ×N graph Laplacian matrix A defined for pairwise interactions

$$A_{ij}=\{\begin{array}{l}I(i,j),i\ne j\hfill \\ -\sum _{l\ne i}{A}_{il},i=j,\hfill \end{array}$$

where I(i, j) is a value describing the strength of influence on the ith object induced by the jth object. We assume undirected graph edges, so I(i, j) = I(j, i).

For specific application to protein flexibility, we consider a set of N atoms at positions ${\left\{{\mathbf{r}}_i\in {ℝ}^3\right\}}_{i=1}^N$. Then, I(i, j) represents non-covalent interactions between the ith atom and the jth atom and can be well-approximated by a radial basis function defined via the Euclidean distance between them [91].

Let u = {u₁, u₂, ⋯, u_N}^T be a column vector (of size N ∗ n) with ui = {u_i,1, u_i,2,·⋯ ,u_i,n}^T. The coupled system is an N ×n-dimensional dynamical system

$$\frac{d\mathbf{u}}{dt}=\mathbf{G}(\mathbf{u})+ϵ(A\otimes \Gamma )\mathbf{u},$$ (1)

where $\mathbf{G}(\mathbf{u})={\left\{g\left({\mathbf{u}}_1\right),g\left({\mathbf{u}}_2\right),\cdots ,g\left({\mathbf{u}}_N\right)\right\}}^T$, ϵ is a parameter, and Γ is an n×n predefined linking matrix. Weights are used so that the interaction strength between the objects represented by the oscillators can be quantitatively described. The term (A_i ⨂ Γ)u describes the difference between oscillator i and the other oscillators. Since the rows of A add up to 0, the oscillators will reach synchronized state given enough coupling strength.

The Lorenz attractor is described by

$$g_l\left({\mathbf{u}}_i\right)=\left[\begin{array}{c}\delta \left(u_{i,2}-u_{i,1}\right)\\ u_{i,1}\left(\gamma -u_{i,3}\right)-u_{i,2}\\ u_{i,1}{u}_{i,2}-\beta u_{i,3}\end{array}\right]$$ (2)

where δ, γ, and β are parameters determining the state of the Lorenz oscillator. The Rössler attractor is governed by

$$g_r\left({\mathbf{u}}_i\right)=\left[\begin{array}{c}-u_{i,2}-u_{i,3}\\ u_{i,1}+a{u}_{i,2}\\ b+u_{i,3}\left(u_{i,1}-c\right)\end{array}\right]$$ (3)

where a, b, c are model parameters. Both the Lorenz attractor and the Rössler attractor have three components and three parameters, but they have different phase space structures and chaotic behaviors.

2.2.2. Stability and controllability

Let s(t) satisfy ds/dt = g(s). We say the coupled systems are in a synchronous state if

$${\mathbf{u}}_1(t)={\mathbf{u}}_2(t)=\cdots ={\mathbf{u}}_N(t)=\mathbf{s}(t).$$

The stability can be analyzed using v = {u₁ − s, u₂ − s, ⋯, u_N − s}^T with the following equation obtained by linearizing Eq. (1)

$$\frac{d\mathbf{v}}{dt}=\left[I_N\otimes Dg(\mathbf{s})+ϵ(A\otimes \Gamma )\right]\mathbf{v},$$ (4)

where I_N is the N × N unit matrix and Dg(s) is the Jacobian of g on s.

The stability of the synchronous state in Eq. (4) can be studied by eigenvalue analysis of graph Laplacian A. Since the graph Laplacian A for undirected graph is symmetric, it only admits real eigenvalues. After diagonalizing A as

$$A{\varphi }_j={\lambda }_j{\varphi }_j,j=1,2,\cdots ,N,$$

where λ_j is the jth eigenvalue and ϕ_j is the jth eigenvector, v can be represented by

$$\mathbf{v}=\sum _{j=1}^N{\varphi }_j\otimes {\mathbf{w}}_j(t).$$

Then, the original problem on the coupled systems of dimension N ×n can be studied independently on the _n-dimensional systems

$$\frac{d{\mathbf{w}}_j}{dt}=\left(Dg(\mathbf{s})+ϵ{\lambda }_j\Gamma \right){\mathbf{w}}_j,j=1,2,\cdots ,N.$$ (5)

Let L_max be the largest Lyapunov characteristic exponent of the jth system governed by Eq. (5). It can be decomposed as L_max = L_g + L_c, where L_g is the largest Lyapunov exponent of the system ds/dt = g(s) and L_c depends on λ_j and Γ. In many numerical experiments carried out in this work, we set Γ = I_n, an n × n identity matrix. Then the stability of the coupled systems is determined by the second largest eigenvalue λ₂. The critical coupling strength ₀ can, therefore, be derived as ϵ₀ = L_g/(−λ2).. A requirement for the coupled systems to synchronize is that ϵ > ϵ₀, while ϵ ≤ ϵ₀ causes instability.

An example of chaos controlled by coupling is shown in Fig. 1. In this example, each alpha carbon atom (C_α) of protein PDB:1E68 is associated with a Lorenz oscillator and the underlying locations of the oscillators are used to construct the coupling matrix. The specific coupling matrix A = A^geo + A^seq used in this example is a sum of a graph Laplacian matrix defined using the geometric coupling,

$$A_{ij}^{\text{geo}}=\{\begin{array}{l}-1,\text{if}i\ne j\text{and}{d}_{ij}^{\text{org}}<{ϵ}_d,\hfill \\ -\sum _{l\ne i}{A}_{il}^{\text{geo}},i=j,\hfill \end{array}$$

and another which takes the amino acid sequence into account,

$$A_{ij}^{\text{seq}}=\{\begin{array}{l}{ϵ}_{\text{seq}},\text{if}(i+1+N)\mathrm{mod}N=j,\hfill \\ -{ϵ}_{\text{seq}},\text{if}(i-1+N)\mathrm{mod}N=j,\hfill \\ 0,\text{otherwise}.\hfill \end{array}$$

Here, d^org is the distance function in the original space; that is, the Euclidean distance between atoms in this example. The mod operator is used because the protein in this example is circular. The parameters used for the example of Fig. 1 are ϵ_seq = 0.7 for sequence coupling, ϵ_d = 4Å for spatial cutoff, and δ = 10, γ = 60, and β = 8/3 for the Lorenz system. The parameters in Eq. (1) are ϵ = 10 and

$$\Gamma =\left[\begin{array}{lll}0\hfill & 0\hfill & 0\hfill \\ 1\hfill & 0\hfill & 0\hfill \\ 0\hfill & 0\hfill & 0\hfill \end{array}\right].$$

Initial values for all oscillators are randomly chosen.

Fig. 1.

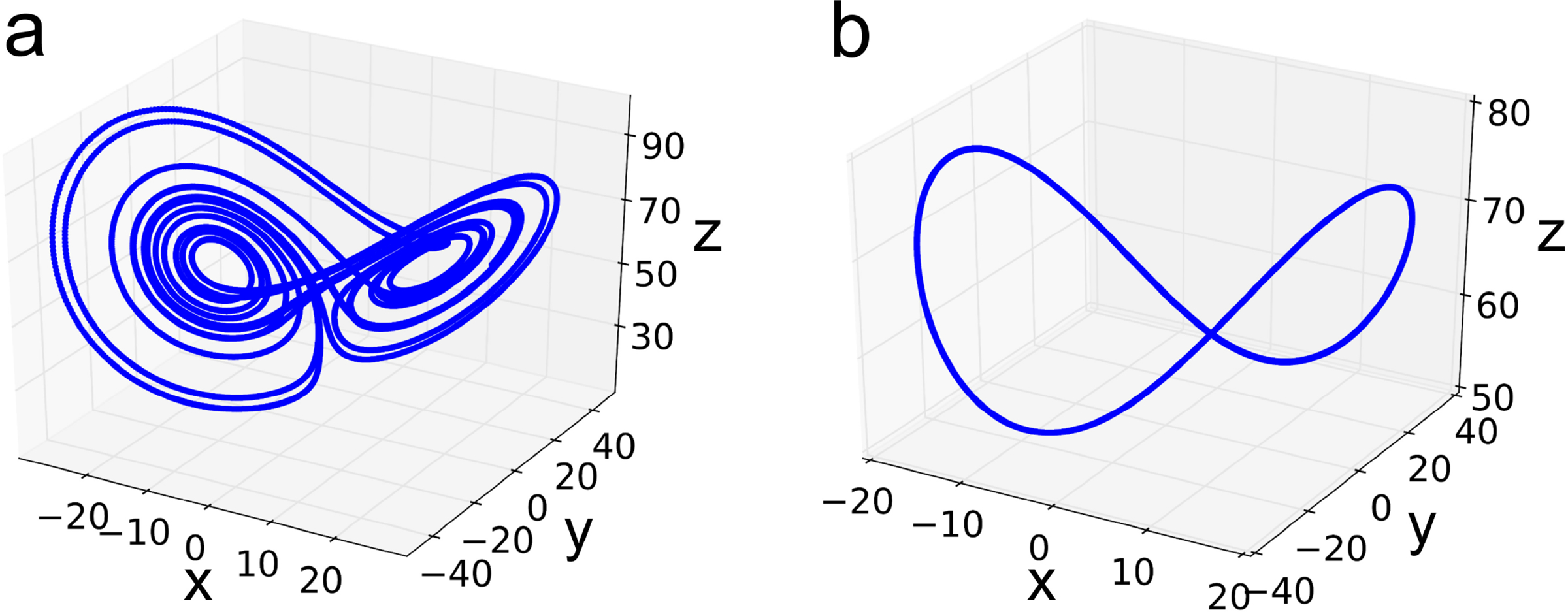
(a) Chaotic trajectory of one oscillator without coupling. (b) The 70 synchronized oscillators associated with the carbon C_α atoms of protein PDB:1E68 are plotted together.

2.3. Homology analysis preliminary

In this section, we review the TDA background that is essential for us to establish notations and facilitate our formulations. The interested reader can find further specifics in, e.g., Carlsson [18], or Edelsbrunner and Harer [37].

2.3.1. Simplicial complex and homology

Topological spaces can be approximated, represented, and discretized by simplicial complexes. An (abstract) simplicial complex is a (finite) collection of sets K = {σi}_i where each σ_i is a subset of a (finite) set K⁰ called the vertex set. We require that this collection satisfies the following condition: if σi ∈ K and τ is a face of σi (that is, if τ ⊆ σ_j commonly denoted _τ ≤ σ_i), then τ ∈ K_{. If σi has} k + 1 vertices, {v₀, v₁, ⋯, v_k} where every pair of vertices is nonequivalent, σ_{i is called a} k-simplex. The k_{-skeleton of a simplicial complex} K is the subcomplex of K consisting of simplices of dimension k and below. See Fig. 2 for an example.

Fig. 2.

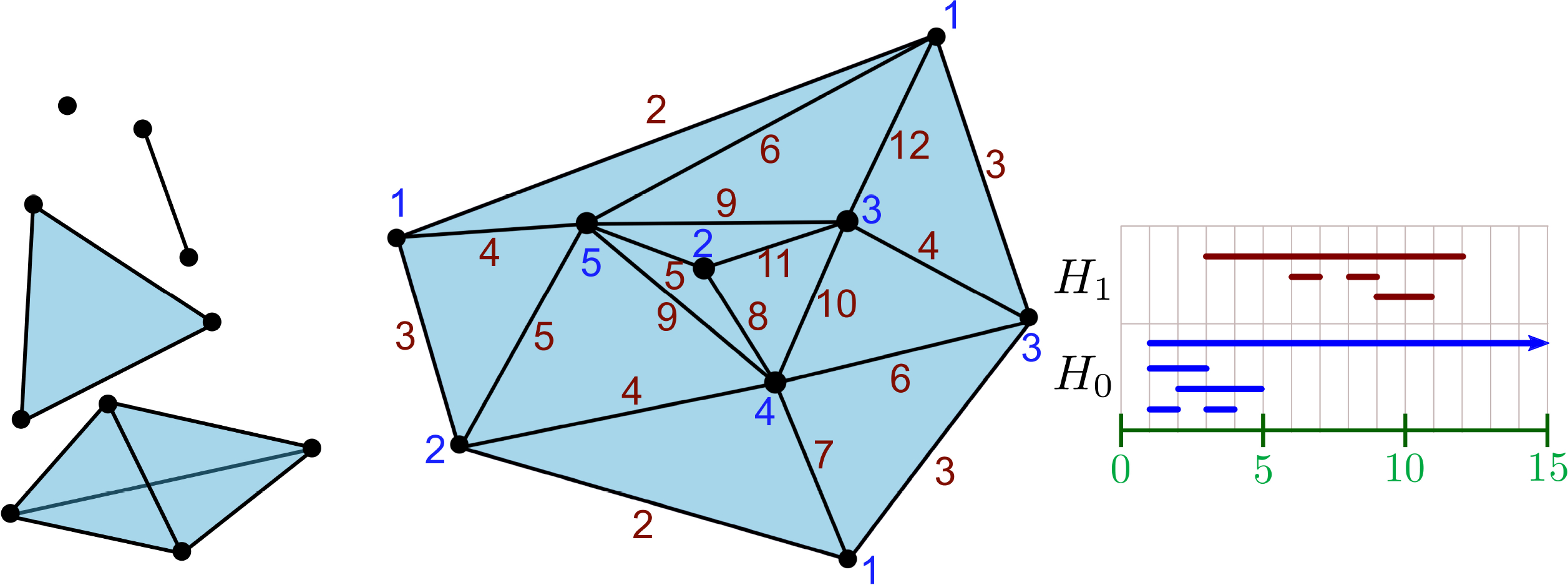
Examples of simplices of different dimensions (left), and a simplicial complex with a function given on the vertices and edges (middle). The barcode for the given function is drawn at right.

The homology group for a fixed simplicial complex gives a topological characterization which encodes holes of different dimensions. Homology groups are built using linear transformations called boundary operators. A k-chain of the simplicial complex K is a finite formal sum of the k-simplices in K, $\alpha =\sum a_i{\sigma }_i$ with coefficients $a_i\in {\mathbb{Z}}_2$. The group of all k-chains with addition given by the addition of the coefficients is called the k-th chain group and is denoted by C_k(K) or simply C_k when the choice of complex is obvious. Note that because ${\mathbb{Z}}_2$ is a field, C_k(K) is, in fact, a vector space.

The boundary operator ∂_k : C_k → C_k−1 is the linear transformation generated by mapping any k-simplex to the sum of its codim-1 faces; namely,

$${\partial }_k\left(\left\{v_0,v_1,\cdots ,v_k\right\}\right)=\sum _{i=0}^k\left\{v_0,\cdots ,{\widehat{v}}_i,\cdots ,v_k\right\},$$

where ${\widehat{v}}_i$ means that v_i is absent. The kth cycle group, Z_k(K), is the kernel of the boundary operator ∂_k with elements called k-cycles. The kth boundary group, B_k(K), is the image of the boundary operator ∂_k+1 and its elements are called k-boundaries. Since ∂_k ∘ ∂_k+1 = 0, B_k(K) is a subgroup of Z_k(K). Thus we can define the kth homology group, H_k(K), to be the quotient group Z_k(K)/B_k(K). Each equivalence class in H_k(K) can be thought of as corresponding to a k-dimensional “loop” in K going around a k + 1-dimensional “hole”: 1-dimensional classes give information about loops going around 2D voids, 2-dimensional classes give information about enclosures of 3D voids, etc. While the analogy is not as nice, 0-dimensional classes give information about connected components of the space.

2.3.2. Filtration of a simplicial complex and persistent homology

We now turn to the case where we have a changing simplicial complex and want to understand something about its structure. Consider a finite simplicial complex K and let f be a real-valued function on the simplices of K which satisfies the following: f(τ) ≤ f(σ) for all τ ≤ σ simplices in K. We will refer to this function as the filtration function. For any $x\in ℝ$, the sublevelset of K associated to _x is defined as

$$K(x)=\{\sigma \in K\mid f(\sigma )\le x\}.$$

Note first that because of our assumptions on f, K(x) is always a simplicial complex, and second that K(x) ⊆ K(y) for any x ≤ y. Further, as x varies, K(x) _{only changes at the function values defined on the simplices. Since} K is assumed to be finite, let {x₁ < x₂ < ⋯ < x_ℓ} be the sorted range of f. The filtration of K with respect to f is the ordered sequence of its subcomplexes,

$$\varnothing \subset K\left(x_1\right)\subset K\left(x_2\right)\subset \cdots \subset K\left(x_{\mathcal{l}}\right)=K.$$ (6)

The filtration of a simplicial complex sets the stage for a thorough topological examination of the space under multiple scales of the filtration parameter which is the output value of the filtration function f. Our choice of the filtration function f for coupled dynamical systems will be given in Sec. 2.4.2.

We are interested in studying the structure of a filtration like that of Eq. (6). Functoriality of homology means that such a sequence of inclusions induces linear transformations on the sequence of vector spaces

$$H_k\left(K\left(x_1\right)\right)\to H_k\left(K\left(x_2\right)\right)\to \cdots \to H_k\left(K\left(x_n\right)\right).$$ (7)

Persistent homology not only characterizes each frame in the filtration {K(xi)}i, but also tracks the appearance and disappearance (commonly referred to as births and deaths) of nontrivial homology classes as the filtration progresses. A collection of vector spaces {V_i} and linear transformations f_i : V_i → V_i+1 is called a persistence module, of which Eq. (7) is an example. It is a special case of a much more general theorem of Gabriel [42] that sufficiently nice persistence modules can be decomposed uniquely into a finite collection of interval modules [26,68]. An interval module ${\mathbb{I}}_{[b,d)}$ is a persistence module for which $V_i={\mathbb{Z}}_2$ if i ∈ [b, d) and 0 otherwise; and f_i is the identity when possible, and 0 otherwise.

Therefore, given the persistence module of Eq. (7), we can decompose it as ${\oplus }_{[b,d)\in B^k}{\mathbb{I}}_{[b,d)}$, and thus fully represent the algebraic information by the discrete collection B^k. These intervals exactly encode when homology classes appear and disappear in the persistence module. The collection of such intervals can be visualized by plotting points in the 2D half plane {(x, y) | y ≥ x} which is known as a persistence diagram; or by stacking the horizontal intervals, which is known as a barcode. In this paper, for no reason other than convenience, we represent our information using barcodes. We call the barcode resulting from a sequence of trivial homology groups the empty barcode and denote it by ∅. Thus, for every interval [b, d) ∈ B^k, we call b the birth time and _d the death time.

2.4. Evolutionary homology and its barcode representation

2.4.1. Kinematics

Consider a system of N not yet synchronized oscillators {u₁, ⋯, u_N} associated to a collection of N embedded points, $\left\{{\mathbf{r}}_1,\cdots ,{\mathbf{r}}_N\right\}\subset {ℝ}^d$. We assume the global synchronized state is a periodic orbit denoted s(t) for t ∈ [t0, t1] where s(t₀) = s(t₁). For flexibility and generality, we work on post-processed trajectories obtained by applying a transformation function on the original trajectories, ${\widehat{\mathbf{u}}}_i(t):=T\left({\mathbf{u}}_i(t)\right)$. The choice of function T is flexible and should fit the applications; in this work, we choose

$$T\left({\mathbf{u}}_i(t)\right)=\underset{t^{\prime }\in \left[t_0,t_1\right]}{\min }{\Vert {\mathbf{u}}_i(t)-\mathbf{s}\left(t^{\prime }\right)\Vert }_2,$$ (8)

which gives 1-dimensional trajectories for simplicity. Further, in our specific example, $\widehat{\mathbf{s}}(t):=T(\text{s}(t))=0$, but, again, this is not necessary in general.

We wish to study the effects on the synchronized system of N oscillators (an (N ×3)-dimensional system) after perturbing one oscillator of interest. To this end, we set the initial values of all the oscillators except that of the ith oscillator to $\mathbf{s}(\overline{t})$ for a fixed $\overline{t}\in \left[t_0,t_1\right]$. The initial value of the ith oscillator is set to $\rho (\mathbf{s}(\overline{t}))$ where ρ is a predefined function playing the role of introducing disturbance to the system. After the system starts running, some oscillators will be dragged away from and then go back to the periodic orbit as the disturbance is propagated and relaxed through the system. Let ${\widehat{\mathbf{u}}}_j^i(t)$ denote the modified trajectory of the jth oscillator after perturbing the ith oscillator at t = 0. We focus on the subset of nodes that are affected by the perturbation,

$$V^i=\left\{n_j\mid \underset{t>0}{\max }\left\{\underset{t^{\prime }\in \left[t_0,t_1\right]}{\min }{\Vert {\widehat{\mathbf{u}}}_j^i(t)-\widehat{\mathbf{s}}\left(t^{\prime }\right)\Vert }_2\right\}\ge {ϵ}_p\right\}$$

for some fixed ϵ_p determining how much deviation from synchronization constitutes “being affected”.

2.4.2. Filtration function defined for coupled dynamical systems

Assuming we have perturbed the oscillator for node n_i, let M = |V_i|. We will now construct a function f_i on the complete simplicial complex, denoted by K or K_M with M vertices. Here, we abuse notation and write V_i = {n₁, ⋯, n_M}. _{The filtration function $f:K_M\to ℝ$} is built to take into account the temporal pattern of the propagation of the perturbance through the coupled systems and the relaxation (going back to synchronization) of the coupled systems. It requires the advance choice of three parameters:

• ϵ_p ≥ 0, mentioned above, which determines when a trajectory is far enough from the global synchronized state, s(t) to be considered unsynchronized,

• ϵ_sync ≥ 0 which controls when two trajectories are close enough to be considered synchronized with each other, and

• ϵ_d ≥ 0 which is a distance parameter in the space where the points r_i are embedded, giving control on when the objects represented by the oscillators are far enough apart to be considered insignificant to each other.

We will define the function f_i by giving its value on simplices in the order of increasing dimension. Define

$$t_{\text{sync}}^i=\min \left\{t\mid {\int }_t^{\infty }{\Vert {\widehat{u}}_j^i\left(t^{\prime }\right)-{\widehat{u}}_k^i\left(t^{\prime }\right)\Vert }_{2}d{t}^{\prime }\le \frac{{ϵ}_{\text{sync}}}{2},\forall j,k\right\}.$$

That is, $t_{\text{sync}}^i$ is the first time at which all oscillators have returned to the global synchronized state after perturbing the ith oscillator. The value of the filtration function for the vertex n_j is defined as

$$f_i\left(n_j\right)=\min \left\{\{t\mid \underset{t^{\prime }\in \left[t_0,t_1\right]}{\min }{\Vert {\widehat{\mathbf{u}}}_j^i(t)-\widehat{\mathbf{s}}\left(t^{\prime }\right)\Vert }_2\ge {ϵ}_p\}\cup \{t_{\text{sync}}^i\}\right\}.$$ (9)

Next, we give the function value f_i for the edges of K. To avoid the involvement of any insignificant interaction between oscillators, an edge between n_j and n_k denoted by e_jk is allowed in the earlier stage of the filtration only if $d_{jk}^{\text{org}}\le {ϵ}_d$ where $d_{jk}^{\text{org}}$ is the distance between r_i and r_j in ${ℝ}^d$. Specifically, the value of the filtration function for the edge e_jk is defined as

$$f_i\left(e_{jk}\right)=\{\begin{array}{ll}\max \{\min \{t\mid {\int }_t^{\infty }{\Vert {\widehat{\mathbf{u}}}_j^i\left(t^{\prime }\right)-{\widehat{\mathbf{u}}}_k^i\left(t^{\prime }\right)\Vert }_{2}d{t}^{\prime }\le {ϵ}_{\text{sync}}\},f_i\left(n_j\right),f_i\left(n_k\right)\},\hfill & \text{if}{d}_{jk}^{\text{org}}\le {ϵ}_d\hfill \\ t_{\text{sync}}^i,\hfill & \text{if}{d}_{jk}^{\text{org}}>{ϵ}_d.\hfill \end{array}$$ (10)

It should be noted that to this point, f defines a filtration function because when $d_{jk}^{\text{org}}\le {ϵ}_d,f_i\left(n_j\right)\le f_i\left(e_{jk}\right)$ according to the definition given in Eq. (10). The property also holds when $d_{jk}^{\text{org}}>{ϵ}_d$ because $f_i\left(n_j\right)\le t_{\text{sync}}$ according to the definition in Eq. (9) and f_i(e_jk) equals t_sync in this case.

We extend the function to the higher dimensional simplices using the definition on the 1-skeleton. A simplex σ of dimension higher than one is included in K(x) if all of its 1-dimensional faces are already included; that is, its filtration value is defined iteratively by dimension as

$$f_i(\sigma )={\max }_{\tau \le \sigma }{f}_i(\tau ),$$

where the max is taken over all codim-1 faces of σ. Taking the filtration of K using this function (c.f. Eq. (6)) means that topological changes only occur at the collection of function values ${\left\{f_i\left(n_j\right)\right\}}_j\cup {\left\{f_i\left(e_{jk}\right)\right\}}_{j\ne k}$. Fig. 3 shows the filtration constructed for an example consisting of three trajectories.

Fig. 3.

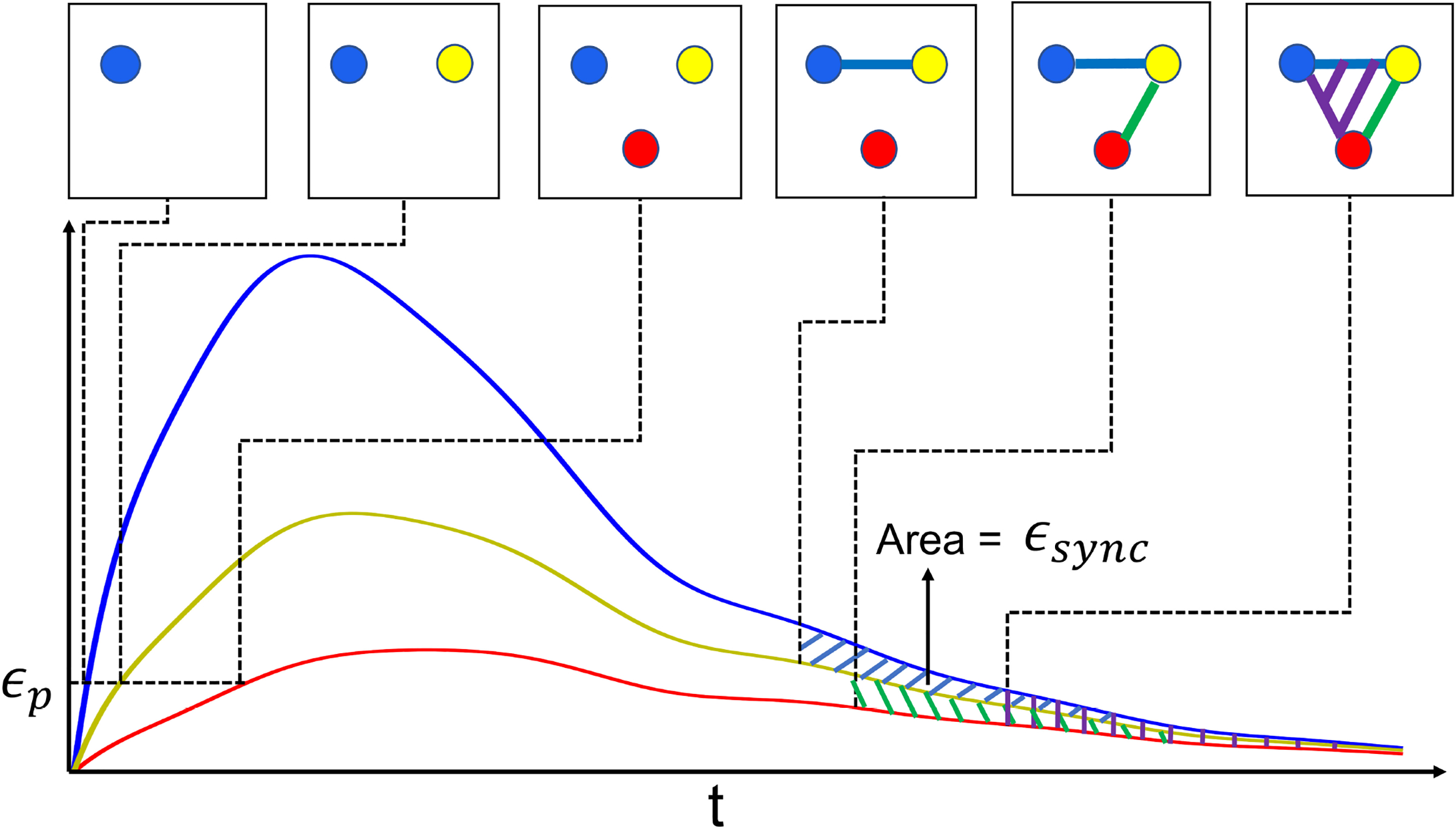
The filtration of the simplicial complex associated to three 1-dimensional trajectories (T(u)) as defined in Sec. 2.4.2. Here, each vertex corresponds to the trajectory with the same color. A vertex is added when its trajectory value exceeds the parameter ϵ_p; an edge is added when its two associated trajectories become close enough together that the area between the curves after that time is below the parameter ϵ_sync. Triangles and higher dimensional simplices are added when all necessary edges have been included in the filtration.

2.4.3. Computation of evolutionary homology

The previous section gives a function $f_i:K_{\left|V^i\right|}\to ℝ$ defined on the complete simplicial complex with |Vⁱ| vertices for each i = 1, ⋯, N. From the filtration defined by f_i, we then compute the persistence barcode for homology dimension k, which we call the kth EH barcode, denoted $B_i^k$. The persistent homology computation for dimension ≥ 1 on the filtered simplicial complex is done using the software package Ripser [6] using the fact that k-dimensional homology only requires knowledge of k and k + 1-dimensional simplices. The 0-dimensional homology is computed with a modification of the union-find algorithm.

Fig. 4 gives an example of the geometric configurations of two sets of points associated to Lorenz oscillators and their resulting EH barcodes. The EH barcodes effectively examine the local properties of significant cycles in the original space which is important when the data is intrinsically discrete instead of a discrete sampling of a continuous space. As a result, the point clouds with different geometry but similar barcodes using traditional persistence methods¹ may be distinguished by EH barcodes.

Fig. 4.

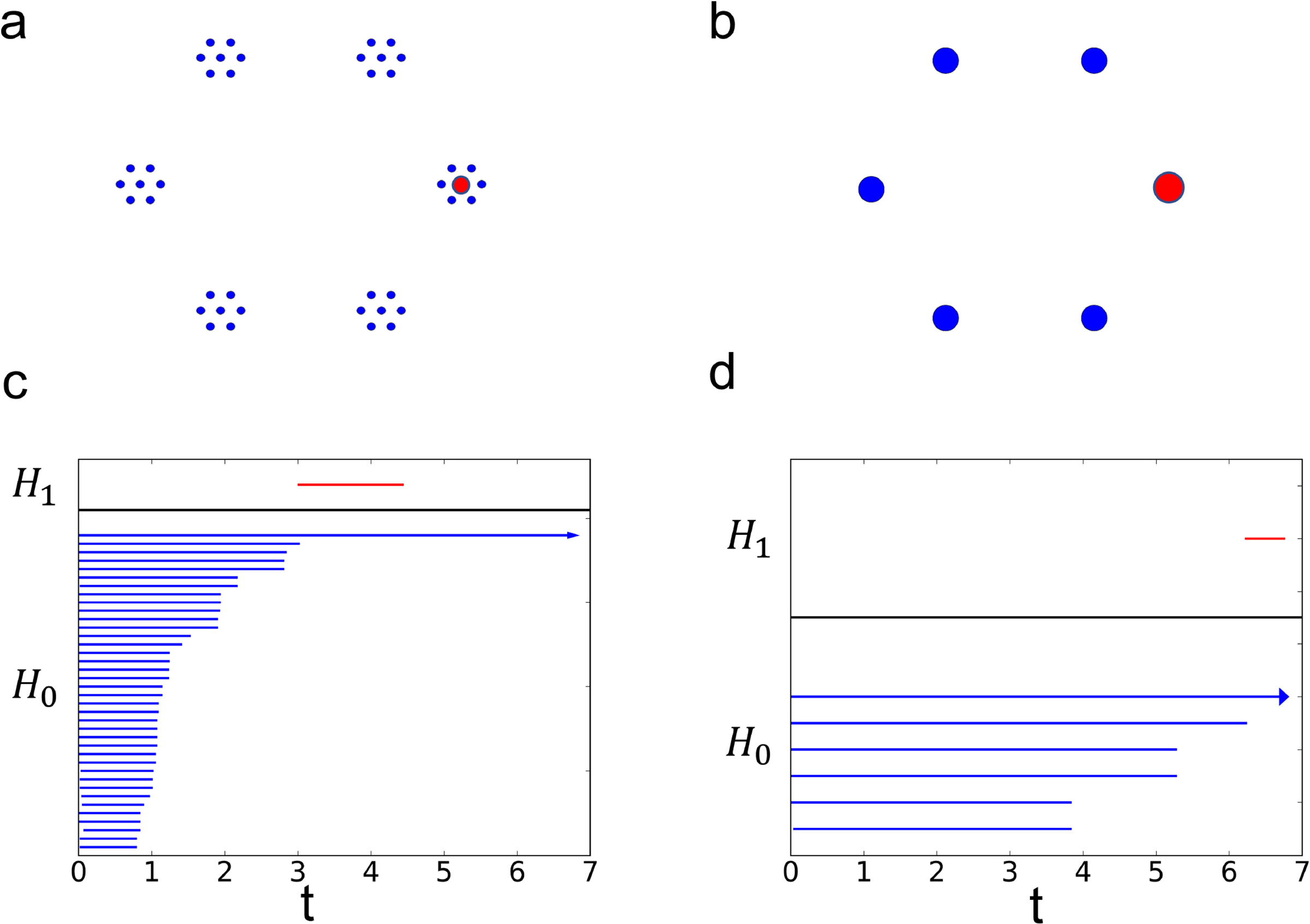
An example of the construction of the EH barcode. The geometry of two embedded systems is shown in Fig (a) and (b). Specifically, (b) consists of six vertices of a regular hexagon with side length of e₁; and (a) consists of the vertices in (b) with the addition of the vertices of hexagons with a side length of e₂ ≪ e₁ centered at each of the previous vertices; here, e₁ = 8 and e₂ = 1. Figs. (c) and (d) are the EH barcodes corresponding to Figs. (a) and (b) respectively. A collection of coupled Lorenz systems is used with parameters δ = 1, γ = 12, β = 8/3, μ = 8, k = 2, Γ = I₃, and ϵ = 12; see Eqs. (2), (11) and (1). In the model for the ith residue, marked in red, the system is perturbed from the synchronized state by setting u_i,3 = 2s₃ with s₃ being the value of the third variable of the dynamical system at the synchronized state and is simulated with step size h = 0.01 from t = 0 using the fourth-order Runge-Kutta method. The calculation of persistent homology using the Vietoris-Rips filtration with Euclidean distance on the point clouds delivers similar bars [corresponding to the 1-dimensional holes in (a) and (b) which are [e₁ − e₂, 2(e₁ − e₂)) and [e₁, 2e₁).

2.5. Topological learning

2.5.1. Metrics on the space of barcodes

The similarity between persistence barcodes can be quantified by barcode space distances. The most commonly used metrics are the bottleneck distance [27] and the p-Wasserstein distances [29]. The definitions of the two distances are summarized as follows.

The l^∞ distance between two persistence bars I₁ = [b₁, d₁) and I₂ = [b₂, d₂) is defined to be

$$\Delta \left(I_1,I_2\right)=\max \left\{\left|b_2-b_1\right|,\left|d_2-d_1\right|\right\}.$$

The distance between a bar I = [b, d) and null is analogously measured as

$$\lambda (I):=(d-b)/2=\underset{x\in ℝ}{\min }\Delta (I,[x,x)).$$

For two finite barcodes of dimension k, $B_1^k={\left\{I_{\alpha }^1\right\}}_{\alpha \in A^k}$ and $B_2^k={\left\{I_{\beta }^2\right\}}_{\beta \in B^k}$, a partial bijection is defined to be a bijection $\theta :A^{k^{\prime }}\to B^{k^{\prime }}$ where $A^{k^{\prime }}\subseteq A^k$ to $B^{k^{\prime }}\subseteq B^k$. In order to define the p-Wasserstein distance, we have the following penalty for θ

$$P(\theta )={\left(\sum _{\alpha \in A^{\prime }}\Delta {(I_{\alpha }^1,I_{\theta (\alpha )}^2)}^p+\sum _{\alpha \in A^k\backslash A^k}\lambda {(I_{\alpha }^1)}^p+\sum _{\beta \in B^k\backslash B^{k^{\prime }}}\lambda {(I_{\beta }^2)}^p\right)}^{1/p}$$

Then the p-Wasserstein distance is defined as

$$d_{W,p}\left(B_1^k,B_2^k\right)=\underset{\theta \in \Theta }{\min }P(\theta ),$$

where Θ is the set of all possible partial bijections from A^k to B^k. Intuitively, a partial bijection θ is mostly penalized for connecting two bars with large difference measured by Δ(·), and for connecting long bars to degenerate bars (the diagonals of persistence diagram), measured by λ(·).

The bottleneck distance is an _L∞ analogue to the _p-Wasserstein distance. The bottleneck penalty of a partial matching θ is defined as

$$P(\theta )=\max \left\{\underset{\alpha \in A^{\prime }}{\max }\left\{\Delta \left(I_{\alpha }^1,I_{\theta (\alpha )}^2\right)\right\},\underset{\alpha \in A^k\backslash A^k}{\max }\left\{\lambda \left(I_{\alpha }^1\right)\right\},\underset{\beta \in B^k\backslash B^{k^{\prime }}}{\max }\left\{\lambda \left(I_{\beta }^2\right)\right\}\right\}.$$

The bottleneck distance is defined as

$$d_{W,\infty }\left(B_1^k,B_2^k\right)=\underset{\theta \in \Theta }{\min }P(\theta ).$$

2.5.2. Learning with barcodes

Evolutionary homology provides a relatively abstract characterization of the objects of interest. It is potentially powerful in many applications, but may be difficult to use out of the box for machine learning or quantitative data analysis techniques. In regression analysis or the training part of supervised learning, with B_i being the collection of sets of barcodes corresponding to the ith entry in the training data, the problem can be cast into the following minimization problem,

$$\underset{{\theta }_b\in {\Theta }_b,{\theta }_m\in {\Theta }_m}{\min }\sum _{i\in I}L\left({\mathbf{y}}_i,\mathbf{F}\left({\mathbf{B}}_i;{\theta }_b\right);{\theta }_m\right),$$

where L is a scalar loss function, y_i is the collection of target values in the training set, F is a function that maps barcodes to suitable input for the learning models, and θ_b and θ_m are the parameters to be optimized within the search domains Θ_b and Θ_m respectively. The form of the loss function also depends on the choice of metric and machine learning/regression model.

A function F which translates barcodes to structured representation (tensors with fixed dimension) can be used with popular machine learning models including random forest, gradient boosting trees and deep neural networks. Another popular class of models are the kernel based models that depend on an abstract measurement of the similarity or distance between the entries.

Our choices for F, defined in Eq. (12) of Sec. 3.1, will arise from looking at the distance from the specified barcode to the empty barcode and there is no tuning of θ_b. In Sec. 3.3 where we quantitatively analyze protein residue flexibility, we evaluate our method by checking the correlation between each topological feature defined in Eq. (12) and the experimental value (blind prediction) as well as the correlation between the output of a linear regression with multiple topological features and the experimental value (regression). In the former case, there is no parameter to be optimized, while in the latter case, the specific minimization problem can be written as

$$\underset{{\theta }_m\in {ℝ}^{n+1}}{\min }\sum _{i\in I}{\left(y_i-\left[{\text{EH}}_i^{p_1,1},\cdots ,{\text{EH}}_i^{p_n,n},1\right]\cdot {\theta }_m\right)}^2,$$

where ${\text{EH}}_i^{p_k,k}$ is the topological parameter by computing the p_k-Wasserstein distance of the empty set to the kth barcode associated with the EH computation of the ith protein residue (node), I is the set of indexes of all residues in the protein and y_i is the experimental B-factor for the ith protein residue which quantitatively reflects flexibility.

3. Results

This section starts with protein flexibility analysis in Sec. 3.1. The analysis of ordered and disordered proteins is given in Sec. 3.2. Finally, the quantitative prediction of protein B-factors is described in Sec. 3.3.

3.1. Protein residue flexibility analysis

Proteins have many functions in life forms. They are consisted of one or multiple chains of amino acid residues and often fold into specific 3D structures. The amino acid residues have the same basic structure and different types of residues possess different side chains (often referred to as functional groups). The carbon atom connected to the side chain is called the alpha carbon and forms the backbone of a protein and depict the protein structure at residue level. For many functioning proteins, such as enzymes, certain levels of flexibility at designated locations are required to function correctly. The ability to predict protein flexibility is important in tasks including drug design, protein design, and protein stability analysis. In this section, we combine all the methods to formulate protein residue flexibility analysis using the EH barcodes. Consider a protein with N residues and let r_i denote the position of the alpha carbon (C_α) atom of the ith residue. The coupled systems defined in Eq. (1) are used to study protein flexibility with each protein residue represented by an oscillator (the Lorenz system or the Rössler system in this application). Define the distance for the atoms in the original space as the Euclidean distance between the Cα atoms, $d^{\text{org}}\left({\mathbf{r}}_i,{\mathbf{r}}_j\right)={\Vert {\mathbf{r}}_i-{\mathbf{r}}_j\Vert }_2$. A weighted graph Laplacian matrix is constructed based on the distance function d^org to prescribe the coupling strength between the oscillators and is defined as

$$A_{ij}=\{\begin{array}{l}{e}^{-{\left(d^{\text{org}}\left({\mathbf{r}}_i,{\mathbf{r}}_j\right)/\mu \right)}^{\kappa }},i\ne j,\hfill \\ -\sum _{l\ne i}{A}_{il},i=j,\hfill \end{array}$$ (11)

where μ and κ are tunable parameters. The matrix Γ is set to the identity matrix I.

To quantitatively study the flexibility of a protein, one needs to extract topological information for each residue. To this end, we go through the process given in the previous sections once for each residue. When addressing the ith residue, we perturb the ith oscillator at a time point in a synchronized system and take this state as the initial condition for the coupled systems. See Fig. 5 for an example of this procedure when perturbing the oscillator attached to a residue for a given embedding of one particular protein.

Fig. 5.

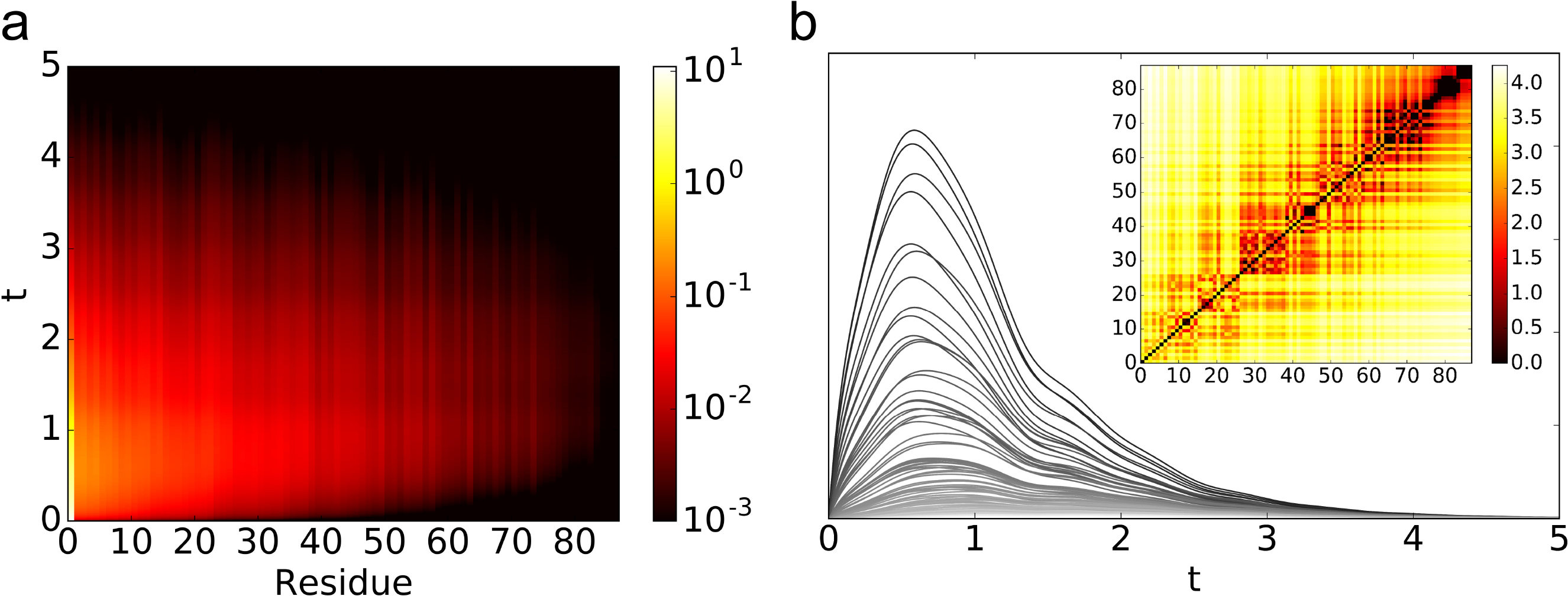
The result of perturbing residue 31 in protein (PDB:1ABA). (a) The modified trajectories as defined in Eq. (8) is plotted for each residue after the perturbation at t = 0 as a heatmap. The residues are ordered by the (geometric) distance to the perturbed site from the closest to the farthest. (b) The modified trajectories as defined in Eq. (8) is plotted for each residue after the perturbation at t = 0 as line plots. The darker lines are closer to the perturbed site. The heatmap shows filtration value for the edges as defined in Eq. (10) and the order of residues is the same as in (a). The parameters for the coupled Lorenz system and the perturbation method are the same as that of Fig. 4.

A collection of modified trajectories ${\left\{{\widehat{\mathbf{u}}}_i(t)\right\}}_{i=1}^N$ is obtained with the transformation function defined in Eq. (8). The persistence over time for ${\left\{{\widehat{\mathbf{u}}}_i(t)\right\}}_{i=1}^N$ is computed following the filtration procedure defined in Sec. 2.4.2. Let $B_i^k$ be the kth EH barcode obtained from the experiment of perturbing the oscillator corresponding to residue i. We introduce the following topological features to relate to protein flexibility:

$${\text{EH}}_i^{p,k}=d_{W,p}\left(B_i^k,\varnothing \right),$$ (12)

where $d_{W,p}$ for 1 ≤ p < ∞ is the p-Wasserstein distance and p = ∞ is the bottleneck distance. We will show that these features characterize the behavior of this particular collection of barcodes, which in turn, captures the topological pattern of the coupled dynamical systems arising from the underlying protein structure.

The interactions among residues are a major contribution to protein stability and flexibility. Here each protein residue is represented by a dynamical system. Their interactions are modeled by coupling of these dynamical systems. When this coupled system reaches synchronization state, a perturbation of one of the dynamical systems is introduced which serves as a probe to study the flexibility of the corresponding protein residue. Specifically, the flexibility of any given residue is reflected by how the perturbation induced stress is propagated and relaxed through the interactions in the system. Such a relaxation process will induce the change in the states of the nearby oscillators. Therefore, the records of the time evolution of this subset of coupled oscillators in terms of topological invariants can be used to analyze and predict protein flexibility.

The difference in results of the procedure can be seen in the example of Fig. 6 where the control of chaotic oscillators attached to a partially disordered protein (PDB:2RVQ) and a well-folded protein (PDB:1UBQ) is demonstrated. Clearly, the folded part of protein 2RVQ has strong correlations or interactions among residues from residue 25 to residue 110, which leads to the synchronization of the associated chaotic oscillators. In contrast, the random coil part of protein 2RVQ does not have much coupling or interaction among residues. Consequently, the associated chaotic oscillators remain in chaotic dynamics during the time evolution. For folded protein 1UBQ, the associated chaotic oscillators become synchronized within a few steps of simulation, except for a small flexible tail. This behavior underpins the use of coupled dynamical systems for protein flexibility analysis.

Fig. 6.

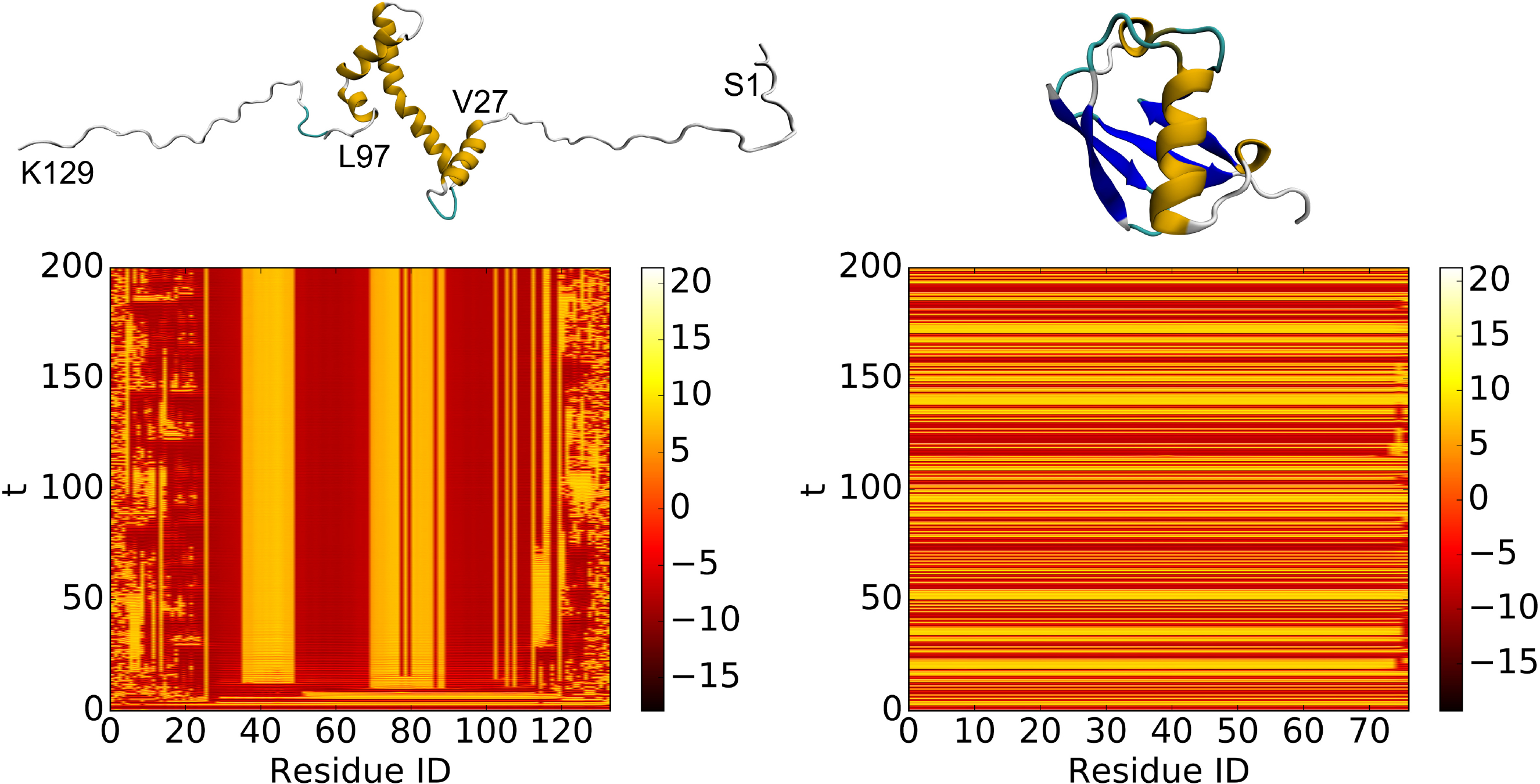
Left: partially disordered protein, model 1 of PDB:2RVQ. Right: well folded protien, PDB:1UBQ. The u_i,1 value of each dynamical system is plotted as heatmap. The Lorenz system defined in Eq. (2) is used with the parameters δ = 10, γ = 28, β = 8/3. The coupling matrix A defined in Eq. (11) has parameters μ = 14, κ = 2. The coupled system defined in Eq. (1) has parameters Γ = I₃ and ϵ = 12. The system is initialized with a random value between 0 and 1 and is simulated from t = 0 to t = 200 with step size h = 0.01. The system is numerically solved using the 4-th order Runge-Kutta method. It can be seen from the heatmaps that the oscillators corresponding to the disordered regions behave asynchronously.

3.2. Discovery of disordered and flexible protein regions

To illustrate the correlation between protein residue flexibility and the topological features defined in Eq. (12), we study several proteins with intrinsically disordered regions. Intrinsically disordered proteins lack stable 3-dimensional molecular structures. One such an example is the Tau protein that stabilizes microtubules and its malfunction is related to Alzheimer’s disease. Partially disordered proteins refer to the intrinsically disordered proteins that contain both stable structure and flexible regions. In nature, the disordered regions may play important roles in biological processes which requires flexibility.

In this section, we use the coupled Lorenz system parameters, perturbation method for the ith residue, and simulation described in Fig. 4 (δ = 1, γ = 12, β = 8/3, μ = 0, κ = 2, Γ = I₃, ϵ = 0.12). The simulation is stopped when all oscillators go back to synchronized state. This process is repeated for each residue. Two NMR structures of partially disordered proteins PDB:2ME9 and PDB:2MT6 are studied. The reconstructing 3D structures from NMR data often leads to multiple structure models that are all compatible to the NMR data. We compute the topological features for each model of the structures and take an average over the models. The results are plotted in Fig. 7. The disordered regions clearly correlate to the peaks of EH^∞,0 and the valleys of EH^∞,1, EH^1,0, and EH^1,1. The topological features are also able to distinguish between relatively stable coils (the coils that are consistent among the NMR models) and the disordered parts (the parts that differ among the NMR models).

Fig. 7.

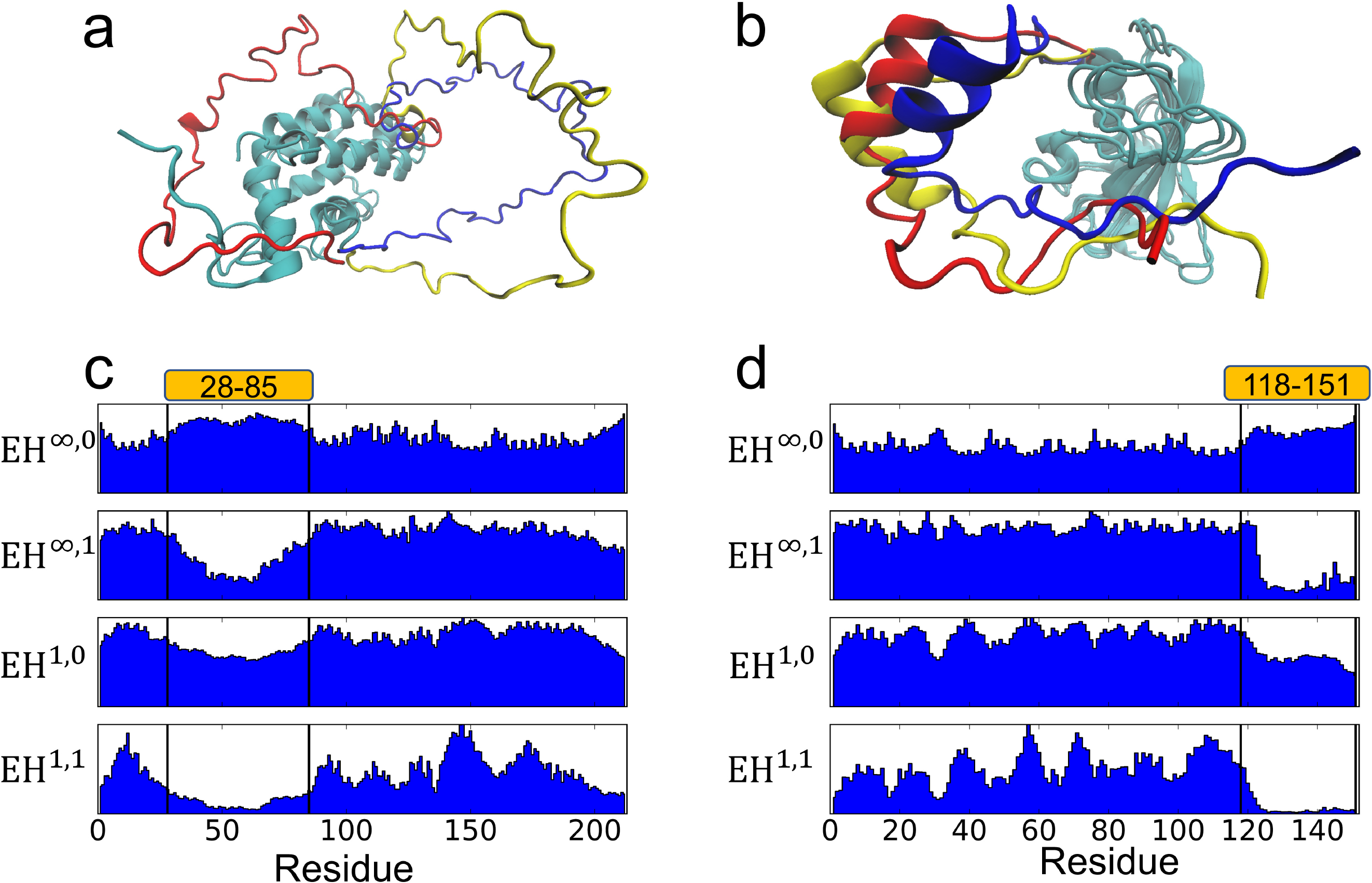
(a) Models 1–3 of PDB:2ME9 with the disordered region colored in blue, red, and yellow for the three models. (b) Similar plot as (a) for PDB:2MT6. (c) Topological features for PDB:2ME9 whose large disordered region is from residue 28 to residue 85. (d) Topological features for PDB:2MT6 whose large disordered region is from residue 118 to residue 151.

3.3. Protein B-factor prediction

B-factor describes how much an atom fluctuate around its mean position in crystal structures. Protein B-factors quantitatively measure the relative thermal motion of each atom and reflects atomic flexibility and dynamics. Though B-factor is also affected by factors such as the refinement methods, it is still a relatively robust measurement of atomic flexibility in proteins. In fact, high correlation (a correlation coefficient of about 0.8) of B-factors among homologous proteins has been reported [75]. The x-ray crystal structures deposited to the Protein Data Bank contain experimentally derived B-factors which can be used to validate the proposed method [70,64]. To analyze protein flexible regions, B-factor prediction is needed for protein structures built from computational models and some experimentally solved structures using NMR or cryo-EM techniques. Normal mode analysis (NMA) is one of the first methods proposed for B-factor predictions [47]. The Gaussian network model (GNM) [5] was known for its better accuracy and efficiency compared to a variety of earlier methods [95]. The multiscale flexibility-rigidity index (FRI), which is about 20% more accurate than GNM, has been established as the state-of-the-art in the B-factor predictions [65].

In this section, we compute the correlation between the topological features and the experimentally derived protein B-factors. Two oscillators are considered, the Lorenz system and the Rössler system. When Lorenz system is used, the same parameters are used as in Section 3.2 (δ = 1, γ = 12, β = 8/3, μ = 0, κ = 2, Γ = I₃, ϵ = 0.12). When Rössler system is used, the same coupling parameters are used (a = 0.1, b = 0.1, c = 4, μ = 0, κ = 2, Γ = I₃, ϵ = 0.12). We further test the proposed topological features by building a simple linear regression model with a least square penalty against the experimental B-factors. A collection of 364 diverse proteins reported in the literature is chosen as the validation data (The set of 365 proteins [64] excepts PDB:1AGN due to issue in reported B-factors [65]). The size of the proteins ranges from tens to thousands of amino acid residues. The topological features in the model are the same as the setup given in Sec. 3.2. An example of the resulting persistence barcodes for relatively rigid and relatively flexible residues are shown in Fig. 8.

Fig. 8.

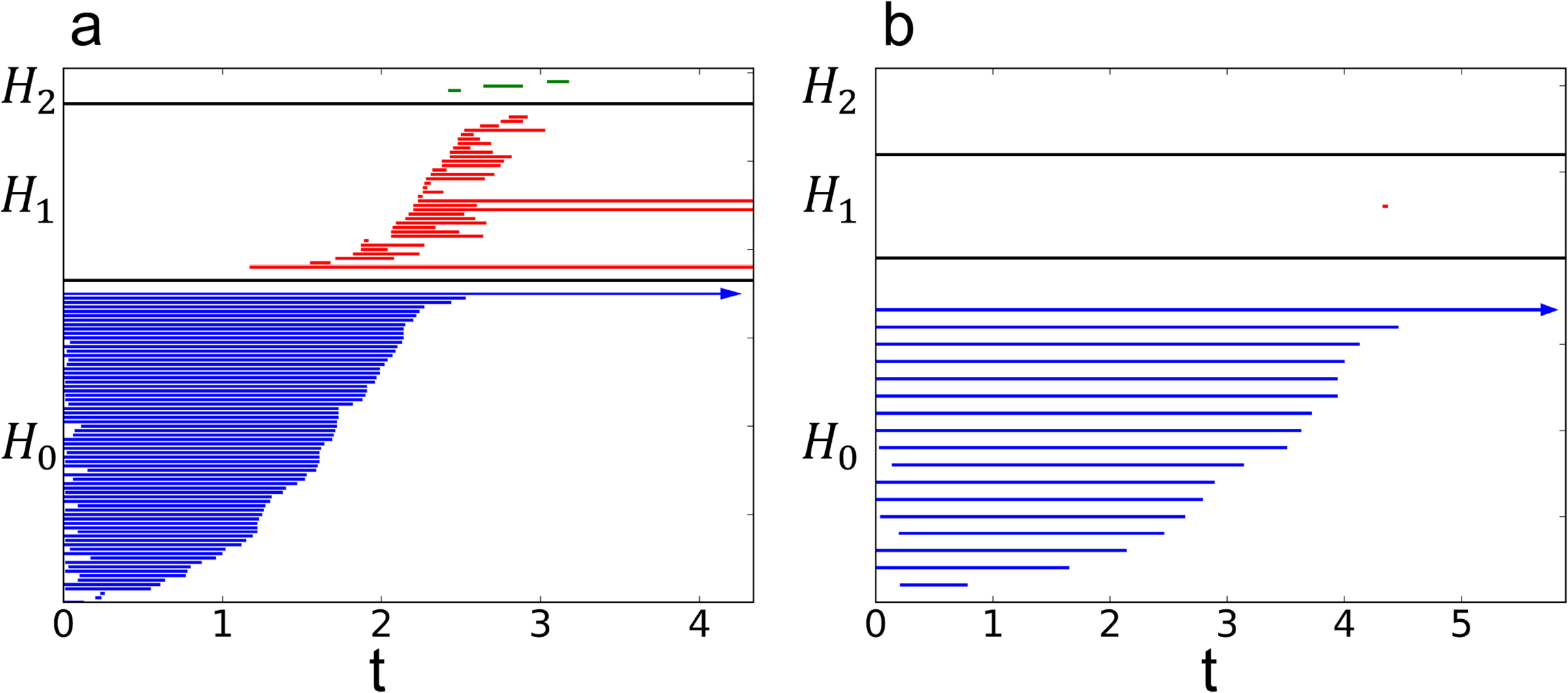
Barcode plots for two residues. (a) Residue 6 of PDB:2NUH with a B-factor of 12.13 Ų. (b) Residue 49 of PDB:2NUH with a B-factor of 33.4 Ų.

The computed topological features are plotted against a relatively small protein and a relatively large protein in Fig. 9. Clearly, 0-dimensional topological features, specifically EH^∞,0, provide a reasonable approximation to experimental B-factors. The regression using all topological information, EH, offers very good approximation to experimental B-factors. A summary of the results and a comparison to other methods is shown in Table 1 for the set of 364 proteins. It is seen that the present evolutionary topology based prediction outperforms other methods in computational biophysics. A possible reason for this excellent performance is that the proposed method gives a more detailed description of residue interactions in terms of three different topological dimensions and two distance metrics. This example indicates that the proposed EH has a great potential for other important biophysical applications, including the predictions of protein-ligand binding affinities, mutation induced protein stability changes and protein-protein interactions.

Fig. 9.

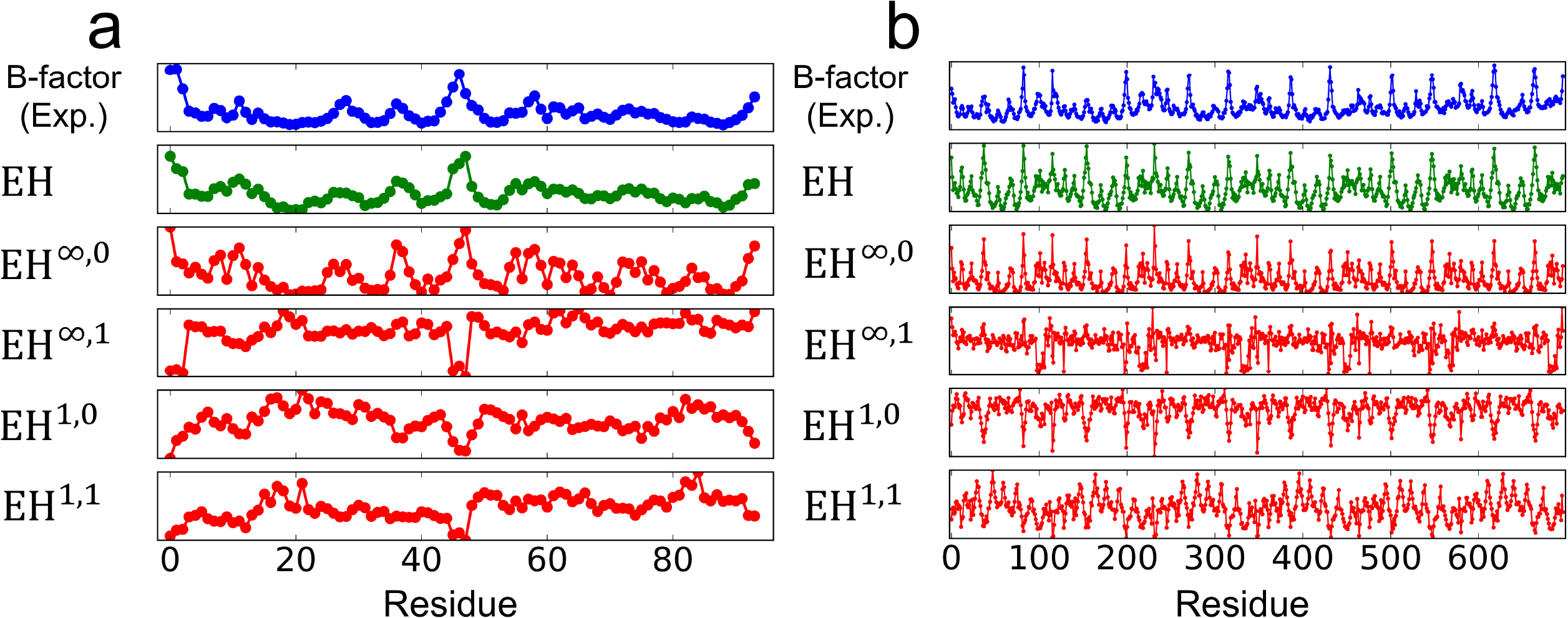
B-factors and the computed topological features. EH shows the linear regression with EH1,0, EH1,1, EH^∞,1, EH^∞,0, EH^1,0_, EH^1,1_, EH^2,0and EH^2,1 within each protein. The y-axes of the panels have different scales to show the correlation between the variances. (a) PDB:3PSM with 94 residues. (b) PDB:3SZH with 697 residues.

Table 1.

The averaged Pearson correlation coefficients (R_P) between the computed values (blind prediction for the topological features and regression for the rest of the models) and the experimental B-factors for a set of 364 proteins [65] and three sets of proteins of different sizes [70]. Top: Prediction R_Ps based on EH barcodes. Bottom: A comparison of the R_Ps of predictions from different methods based on the big protein set. Here, EH is the linear regression using EH^∞,0, EH^∞,1, EH^1,0, EH^1,1, EH^2,0, and EH^2,1 within each protein. For a few large and multi-chain proteins, to reduce the computation time and as a good approximation, we compute their EH barcodes on separated (protein) chains. The proteins that were analyzed on each separate chains include: 1F8R, 1H6V, 1KMM, 2D5W, 3HHP, 1QKI, and 2Q52 for both attractors; and additionally, 1GCO, 3LG3, 3W4Q, 2AH1, 3SZH, 4G6C for Rössler attractor. Note that there is an estimated upper limit (correlation coefficient of about 0.8) for B-factor prediction [75].

	All (364)		Small (33)		Medium (36)		Large (35)
Method	Lorenz	Rössler	Lorenz	Rössler	Lorenz	Rössler	Lorenz	Rössler
EH∞,0	0.586	0.469	0.476	0.504	0.569	0.531	0.565	0.500
EH∞,1	−0.039	0.119	−0.001	−0.010	−0.059	0.158	−0.062	0.105
EH∞,2	−0.097	0.003	−0.010	0.0	−0.099	0.0	−0.065	0.0
EH1,0	−0.477	0.486	−0.092	0.486	−0.521	0.542	−0.516	0.487
EH1,1	−0.381	0.204	−0.077	0.032	−0.384	0.276	−0.401	0.210
EH1,2	−0.104	0.002	−0.013	0.0	−0.105	0.0	−0.071	0.0
EH2,0	0.188	0.486	0.171	0.502	0.154	0.552	0.185	0.507
EH2,1	−0.258	0.015	−0.033	−0.022	−0.233	0.074	−0.276	−0.035
EH2,2	−0.100	0.002	−0.010	0.0	−0.102	0.0	−0.067	0.0
EH	0.691	0.698	0.746	0.773	0.701	0.729	0.663	0.665

Method	RP	Description
EH (Rössler)	0.698	Topological metrics
EH (Lorenz)	0.691	Topological metrics
mFRI	0.670	Multiscale FRI [65]
pfFRI	0.626	Parameter free FRI [64]
GNM	0.565	Gaussian network model [64]

For both dynamical systems, it was observed that the lowest topological dimension (EH^∗,0) generally has the strongest correlation to B-factors. The higher dimensional parameters (EH^∗,1 and EH^∗,2) still carry unique and valuable information which, in a fitting model, boosts the overall performance when paired with EH^∗,0 information. Moreover, the higher dimensional parameters are especially useful in the prediction of larger proteins (medium and large proteins in Table 1) indicating that high dimensions can potentially play important roles in the analysis of very complex systems. Despite the unstable performance in small proteins, all parameters show robust and superior performance in medium and large proteins. This observation further demonstrates the usefulness of the present method in handling datasets with very complex structures.

4. Conclusion

Most topological tools are constructed for the global topology of an object under study. The direct use of dynamical systems for the construction of topological persistence is scarce in general. In this work, we utilize dynamical system as a means to study the topology of an individual component of an object. We embed internal interactions of a complex physical object into a set of chaotic dynamical systems to couple chaotic oscillators together, which leads to the eventual synchronization of the dynamics. Simplices, simplicial complexes, and homology groups are subsequently defined based on trajectories of individual chaotic dynamical systems. The resulting topological tool, called evolutionary homology (EH), is able to analyze the topological invariants and its persistence over time of each individual component of a physical object. The resulting barcode representation of the topological persistence is able to unveil the quantitative local topology-local function relationship of individual subsystems of a physical object.

We choose the well-known Lorenz system and Rössler system as examples to illustrate our EH formulation. An important biophysical problem, protein flexibility analysis, is employed to demonstrate the proposed methods. Specifically, we construct weighted graph Laplacian matrices from protein residue networks to regulate the Lorenz or Rössler system, which leads to the synchronization of the chaotic oscillators associated with protein residue network nodes. The synchronization process for each individual oscillator reflects the corresponding C_α’s interaction pattern and is translated into topological invariants of various dimensions and their persistence over time. The Wasserstein and bottleneck metrics are used to quantitatively discriminate EH barcodes of various dimensions from different protein residues, unveiling their thermal fluctuations. The EH model is found to outperform other state-of-the-art methods, namely both geometric graph and spectral graph theory based approaches, in the protein B-factor predictions of a commonly used benchmark set of 364 proteins.

Finally, the proposed EH will be a powerful tool for studying the local properties of other physical systems, such as the impurities of solid materials and partially disordered proteins. By appropriately reorganization and combination of EH barcodes, the proposed EH method can also be applied to the study of the global properties of a physical object, such as the binding affinities of protein-drug, protein-protein, protein-metal and protein-nucleic acid interactions and the protein stability change upon mutation.