Censoring trace-level environmental data: statistical analysis considerations to limit bias

Abstract

Trace-level environmental data typically include values near or below detection and quantitation thresholds where health effects may result from low-concentration exposures to one chemical over time or to multiple chemicals. In a cook stove case study, bias in dibenzo[a,h]anthracene concentration means and standard deviations (SDs) was assessed following censoring at thresholds for selected analysis approaches: substituting threshold/2, maximum likelihood estimation, robust regression on order statistics, Kaplan-Meier, and omitting censored observations. Means and SDs for gas chromatography-mass spectrometry-determined concentrations were calculated after censoring at detection and calibration thresholds, 17% and 55% of the data, respectively. Threshold/2 substitution was least biased. Measurement values were subsequently simulated from two lognormal distributions at two sample sizes. Means and SDs were calculated for 30%, 50%, and 80% censoring levels and compared to known distribution counterparts. Simulation results illustrated (1) threshold/2 substitution to be inferior to modern after-censoring statistical approaches and (2) all after-censoring approaches to be inferior to including all measurement data in analysis. Additionally, differences in stove-specific group means were tested for uncensored samples and after censoring. Group differences of means tests varied depending on censoring and distributional decisions. Investigators should guard against censoring-related bias from (explicit or implicit) distributional and analysis approach decisions.

Introduction

Trace-level environmental measurement data below minimum reporting levels or limits (RLs) are left-censored when replaced by qualitative partial information (e.g., <RL) before statistical analysis.^1,2 RLs are used in this manner as censoring thresholds, or levels, and are often based (at least partially) on confidence in measurement identification, precision, and accuracy. They are typically derived from analytical chemistry techniques for classifying low-concentration data with consideration of the likelihood of producing false positive, false negative, or excessively uncertain measurement results. Historical perspectives, concepts, and methods for chemical detection, as well as recommendations for harmonizing nomenclature have been well-described in the literature.^3–6 A diverse array of terminology and methods exist for describing and estimating ”detection limits” and ”quantification limits” including, for example, instrumental detection limits (IDLs) based on signal-to-noise ratios, method detection limits (MDLs) based on statistical precision for analysis of blank matrices or low concentration standards, and quantitation limits (QLs) based on calibration models or determination of acceptable precision and accuracy. There are many approaches for establishing censoring thresholds, depending on analytes of interest, analytical instrumentation, the medium being analyzed, regulatory requirements, intended data uses, and analyst preference.^7–11 Where regulatory or standard method requirements are absent, these approaches are often laboratory-specific, sometimes making it difficult to compare or combine data across studies. Where regulatory or standard methods are present, reporting limits may be established to meet specified requirements or regulatory action limits (e.g. occupational exposure limits).

Censoring and analysis practices often protect against false positives (Type I error) through reliable detection and quantitation at the risk of inflated false negatives and biased results, the latter related to lost information.^12–15 The practices persist in part because of investigator concern about data uncertainty near or less than RL censoring thresholds and unfamiliarity with modern statistical treatments and software. Multivariate environmental and toxicological data exacerbate the old paradigm. These multivariate data are characterized by many values near or below censoring thresholds where health effects may not be expected from exposure to any individual chemical, however, may be observed due to the effect of exposure to multiple chemicals present at low environmental concentrations.^16,17 Many studies, for example, treat a censored less-than-RL measurement, often referred to as nondetect, as zero in summing environmental pollutants, e.g. polycylic aromatic hydrocarbons (PAHs), to calculate total concentration.^18–20 Arguably, the contribution of several such zeros could have a non-negligible effect on the resulting sum.

There is evidence of a growing effort to balance firmly held chemometric traditions for censoring against robust interpretation of environmental and toxicological data.^21–24 Historically, there have been many arguments for complete reporting rather than left-censoring data or omitting observations altogether.^2,7,25,26 There may, however, have been no option but to rely on data where the measurement values less than RL have been censored. For example, CDC has a long-standing practice of censoring National Health and Nutrition Examination Survey (NHANES) chemical measurement data values below the limit of detection (CDC publishes the limit of detection for each chemical and survey period) and substituting the detection limit divided by the square root of two in their place.²⁷ U.S. Environmental Protection Agency (EPA) ToxCast and ExpoCast programs have used CDC’s NHANES biomonitoring data in prioritization of 1936 chemicals in exposure assessment and in heuristics for prioritizing human exposure to 7968 chemicals with little or no exposure data.^28,29 More recently, citing an update in CDC procedure, all phthalate data values were used in analysis even when below the limit of detection.³⁰ This change in CDC procedure has potential for more-robust interpretation of the data and, perhaps, indicates that the perceived benefits from reporting rather than censoring these phthalates data out-weighed the challenges involved in their identification, quantification, and appropriate treatment in statistical analyses.

A further complication for robust interpretation of environmental and toxicological data is that the peer-reviewed literature varies widely in practices for publishing RL censoring thresholds, methods used to establish them, and treatment of measurements below them. Some papers describe, at least partially, the approaches used in establishing detection, corresponding statistical analysis, and the censoring threshold values.^18,31–33 Some papers give the percent detected or detection limit values but essentially no information on the approaches used in establishing them or on statistical treatment in analysis.^34,35 Other papers simply report “not detected” rather than giving the censoring threshold values or information on establishing detection.³⁶ In a time when reproducible science and making data public are enduring initiatives in both the public and private sectors, these gaps seem surprising. Indeed, calls for reproducible science through reporting methods and approaches and making data public are clear and long-standing.^{7,25,26,37–42}

Here, our goal is to examine potential for censoring- and analysis-related bias using both a case study of measurement data and a simulation study. Dibenzo[a,h]anthracene (DBA) concentration measurements were excerpted from an EPA cookstove study³⁴ of polycyclic aromatic hydrocarbons (PAHs). Health effects of PAHs and their mixtures released into the environment, e.g., by cookstoves, wildfires, gasoline-vehicle exhaust, and other sources, are of growing concern.^31,43–46 Epidemiology studies over the past five decades provide evidence that long-term exposure to ambient particular matter (PM) containing PAHs is associated with increased cardiovascular and lung-cancer mortality and that exposure to air pollution, including PM_2.5, from household use of solid fuels for cooking is a risk factor for mortality and cardiorespiratory disease.^47,48 Mutagenicity and lung toxicity associated with DBA and other PAHs have been studied experimentally in solid-fuel cookstove emissions and in flaming versus smoldering phases of biomass fuels; however, epidemiologic and experimental studies of the specific effects of DBA on disease incidence or severity following exposure are needed.^31,49,50 DBA, notably, is classified by EPA as a Group B2 PAH, one probably carcinogenic to humans, and is one of EPA’s 16 “priority” PAHs.^51,52 It is also anticipated to be a human carcinogen by PubChem and, in a proposed list of 40 PAHs in the environment, has one of the highest of the estimated Toxicity Equivalence Factors.^53,54 Assessing health risk becomes more complex when trace-level DBA data are censored and reported as “not detected” because the subsequent statistical analysis is affected and may produce biased results.

Specifically, in our novel analysis we assess whether bias results from Type I (i.e., threshold-based)¹⁵ left-censoring followed by estimation of means and standard deviations (SDs), on the original scale of the data, using substitution, parametric maximum likelihood estimation, semiparametric robust regression on order statistics, nonparametric Kaplan-Meier estimation (i.e., product-limit estimator), and complete case (i.e., omit nondetect observations) analysis approaches. We compare these censored-data approaches to use of all measurements without censoring in view of Cressie’s²⁵, Childress et al.’s⁷ and others’ suggestions to report measurement data, the detection limits, and the methods used in calculating the detection limits. We also perform group comparisons to assess whether censoring and statistical analysis decisions can substantively affect statistical significance tests of differences of means. Our assessment of bias illustrates that careful considerations of censoring and statistical analysis are pivotal for interpretation of environmental and toxicological data. The results presented here (1) bring new awareness to censoring considerations and of modern statistical treatment and software choices for informing research protocols, analyses, and interpretation of results, (2) encourage consideration of statistical analysis without censoring below a reporting level, and (3) encourage reporting of all (i.e., full, uncensored) measurement data whether or not censoring was used in the statistical analysis being reported, along with detection and quantitation level qualifiers, including censoring thresholds if applicable, and the methods used in calculating these.

Materials and Methods

We assessed bias related to left-censoring and subsequent statistical analysis of concentration measurements through case and simulation studies. The case study used DBA concentration measurements and the simulation study used a highly skewed lognormal distribution similar to the observed DBA distribution and also a moderately skewed lognormal distribution. In a related assessment, we tested differences of group means to determine whether censoring and statistical analysis decisions affected the hypothesis test results that compare DBA means for two stoves.

Case study

The data in our case study were generated in EPA cookstove combustion experiments to measure polycyclic aromatic hydrocarbon (PAH) concentrations in particulate matter (PM) and were determined using gas chromatography-mass spectrometry (GC-MS).³⁴ Our case study assessed bias by comparing means and SDs for the full, uncensored case study data set of GC-MS-determined measurements to means and SDs after left-censoring at the method detection limit (MDL) and, a second time, after left-censoring at the calibration curve lowest value (CCLV). The EPA cookstove experiment MDL was based on the 1-sided 99^th percentile t-statistic using the mean of seven samples in the region of the standard curve where there was a significant change in the sensitivity and was calculated using the 1992 version of EPA Method SW-846 (given in Supporting Information). Shen et al.³⁴ used quantified measurement values ≥CCLV in their paper; the CCLV (0.1 ng/μL) was approximately 4 times the MDL (0.023 ng/μL).

Chromatograms from the EPA cookstove experiments that had particle emission measurements less than CCLV were reanalyzed and quantified for our case study (Figure S1). All measurements with signal-to-noise ratio >1 were reported; this signal-to-noise ratio is where the instrument response to the analyte of interest in a sample exceeds the signal reported in the absence of the analyte. The resulting quantified measurements less than CCLV were appended to Shen et al.’s measurements ≥CCLV to create the full case study data set of GC-MS-determined measurements. DBA blanks were omitted from the case study data set as were five samples for which measurement values could not be quantified.

We selected DBA for our case study after examining the distributions of concentration measurements, without background correction or other adjustments, for nine PAHs reported by Shen et al.³⁴ DBA was the only analyte with a substantial percentage of measurement values in all three categories needed for our assessment of bias: 45% (n=21) ≥CCLV, 17% (n=8) less than MDL, and 38% (n=18) ≥MDL and less than CCLV, yielding a total of 55% (n=26) less than CCLV (Figure S2 and Tables S1 and S2). Normal, gamma, and lognormal distributions were considered as candidates for best-fitting parametric distributions for the case study’s full data set of GC-MS-determined measurements (Figure S3); Akaike Information Criterion (AIC) was used for selection.

Censoring- and analysis-induced bias in the mean and SD was assessed for two left-censored thresholds, MDL and CCLV, described above. DBA means and SDs were calculated after censoring (e.g., after not reporting quantitative values less than MDL) by using conventional censored-data approaches: substitution of half the censoring level (e.g., substitution of MDL/2), maximum likelihood estimation, robust regression on order statistics, Kaplan-Meier estimation, and complete case estimation, this latter where observations are omitted, i.e., data are truncated, at the censoring threshold⁵⁵ (Table S3). For parametric maximum likelihood estimation and semiparametric robust regression on order statistics, the best-fitting of normal, lognormal, and gamma probability distributions was selected using AIC. These computations were performed using statistical functions available in R and R EnvStats package version 2.3.1.^56–58 The best-fitting distribution was used in analysis except for robust regression on order statistics for censoring at the CCLV, where the lognormal distribution was assumed because the gamma distribution was not available for it in EnvStats at the time of this writing.⁵⁷

Bias in the mean was estimated by taking the differences of the mean calculated after censoring using each of the censored-data statistical approaches (i.e., substitution, maximum likelihood estimation, robust regression on order statistics, Kaplan-Meier estimation, and complete case estimation) and the mean for the full (i.e., uncensored) sample, all on the original scale. Bias in the SD was estimated similarly. Shumway et al.⁵⁹ commented: “It is unfortunate that, for most environmental data, the assumption that the underlying distribution is normal will not be appropriate, so the usual sample mean will not be a good estimator for the population mean.” At issue is precision estimation since the sample mean itself is always, without regard to the underlying distribution, an unbiased estimator of the true mean, assuming one exists. We calculated the maximum likelihood estimates of the mean and SD under the assumption of an underlying lognormal distribution and used these in calculating alternative bias estimates.

Simulation study

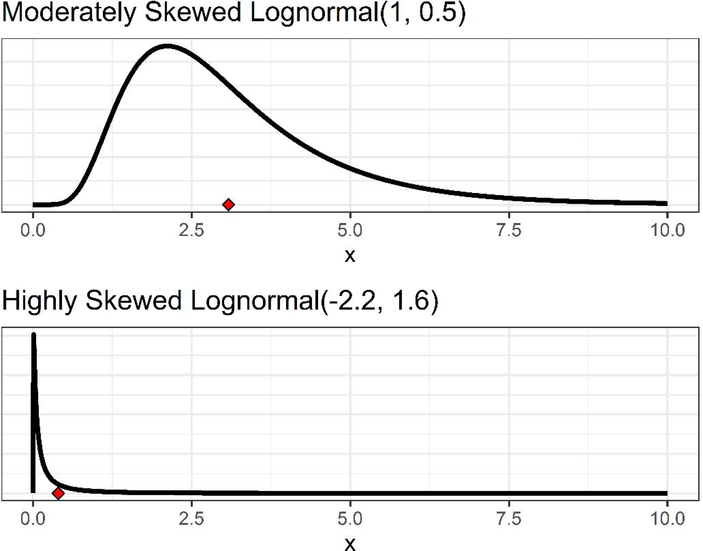
Data values were simulated for 1,000 data sets at sample size n=20 and 1,000 data sets at n=50 for each censoring level from two particular lognormal distributions. These distributions were a highly skewed lognormal and a moderately skewed lognormal (Figures 1 and S4). The highly skewed lognormal distribution is similar to the DBA case study data distribution, and, for comparison, the moderately skewed lognormal is closer to symmetric.

Figure 1.

The two lognormal distributions, one moderately skewed and the other highly skewed, used for generating samples in the simulation study. When X is a random variable from moderately skewed lognormal(μlog=1, σlog=0.5) distribution, the mean (indicated by the red diamond) and SD are 3.08 and 1.64, respectively, geometric mean and geometric SD are 2.72 and 1.65, respectively, and the logarithm of X is normally distributed with mean 1.00 and SD 0.50. Similarly when X is a random variable from highly skewed lognormal(μlog=-2.2, σlog=1.6) distribution, the mean (indicated by red diamond) and SD are 0.40 and 1.38, respectively, geometric mean and geometric SD are 0.11 and 4.95, respectively, and the logarithm of X is normally distributed with mean −2.20 and SD 1.60.

The distribution parameters, mean, and variance for the full, uncensored samples are known values. Censoring- and analysis-induced bias in the mean and SD was assessed for three singly left-censored thresholds (Type I censoring): smallest 30% of the data, smallest 50%, and smallest 80%. After censoring, the best-fitting of normal, lognormal, and gamma probability distributions was selected using AIC. Sample means, SDs, distribution parameters, and 95% approximate confidence intervals of the form (sample mean) ± t_n-1(SD)/√n were estimated after censoring, as in the case study, using the substitution, maximum likelihood estimation, robust regression on order statistics, Kaplan-Meier estimation, and complete case estimation approaches (Table S3, Example S1, and Supporting Information simulation code). The mean, SD, distribution parameters, and 95% confidence interval were also estimated for each full sample using conventional sample statistics and maximum likelihood estimation, the latter assuming an underlying lognormal distribution. Three full sample estimates were generated for each sample size, one corresponding to the 1,000 randomly generated samples for each censoring level. These computations were performed in R. Fewer than 1,000 data sets were assessed using robust regression on order statistics because samples where the gamma distribution was best-fitting were excluded.

Bias was estimated for the simulation study by comparing mean and SD for each of the statistical approaches to the known probability-distribution values. Differences between sample statistics and corresponding known values were calculated for each of the 1,000 samples generated at each sample size and averaged, except for robust regression on order statistics where the number of samples was smaller because of the EnvStats limitation described above. Actual coverage of the 95% approximate confidence intervals was estimated for each of the statistical approaches as the percentage of simulated samples where the confidence interval covered the true mean of the lognormal distribution.

Group comparisons and statistical significance

We compared groups in tests of differences to illustrate censoring-induced bias that can adversely affect use and interpretation of results. The small samples for EcoChula-XXL (n=15) and Butterfly Model 2668 (n=9), two stoves from the DBA case study, were augmented with resampled observations to yield n=45 and n=40 for stove type 1 and 2, respectively (Figure S5 and Table S4). These two stoves were selected because their sample means were similar enough for the comparison at 0.11 and 0.08, respectively, whereas Jiko Poa Rocket and Solgas/Repsol, the other two stoves in our case study, had sample means of 0.74 and 0.04, respectively. The normal, lognormal, and gamma probability distributions were examined for their fit to the full and censored data using AIC. Tests of group differences were performed for the full sample and for the data censored at the CCLV. t-tests assuming normality were used for the full sample and after substituting CCLV/2 for the censored data; maximum likelihood estimation assuming lognormally distributed data was performed for the full sample and for the censored data (Table S5).

Resampling to generate bootstrap samples was executed in the SAS SURVEYSELECT procedure.^60–62 Group comparisons were performed using functions from R packages EnvStats and NADA (Table S5 and Supporting Information group differences code).

Results and Discussion

Case Study

Estimates of the mean, SD, and relative standard deviation (RSD, i.e., the coefficient of variation, CV) for the DBA case study data (n=47) were calculated without censoring using conventional sample statistics and maximum likelihood estimation, the latter assumed data were lognormally distributed. The means were estimated to be 0.355 and 0.385, SD to be 0.572 and 1.293, and RSD to be 1.611 and 3.362, respectively. A histogram of the full sample (n=47) with fitted normal, lognormal, and gamma distributions indicates lognormal to be the best fitting of these three, a conclusion supported by their relative AIC statistics where smaller is better (83.9 for normal, −27.1 for lognormal, and −15.3 for gamma) (Table S6; Figure S3).

After censoring the eight observations with DBA measurement values less than MDL, estimates were calculated using several approaches, i.e., substitution, maximum likelihood estimation, robust regression on order statistics, Kaplan-Meier, and complete case analysis: the estimates of the mean ranged from 0.355 to 0.437, SD from 0.565 to 1.774, and RSD from 1.583 to 4.059 (Tables 1 and S3). After censoring at the CCLV, estimates were calculated using maximum likelihood estimation assuming the gamma distribution, as indicated by AIC, in addition to the five approaches used above (Table S6). The estimates of the mean ranged from 0.343 to 0.742, SD ranged from 0.549 to 3.504, and RSD from 0.922 to 6.523.

Table 1.

DBA case study descriptive statistics for censoring at the MDL and CCLV

Approach	Distribution	n Detected	Mean ± SD (ng/μL)	RSD
Uncensored
Full sample	Normal	47	0.355 ± 0.572	1.611
Full sample Maximum Likelihood Estimation	Lognormal	47	0.385 ± 1.293	3.362
After censoring 8 observations at MDL
Substitute MDL/2	Normal	39	0.355 ± 0.573	1.612
Maximum Likelihood Estimation	Lognormal	39	0.426 ± 1.677	3.936
Robust Regression on Order Statistics	Lognormal	39	0.437 ± 1.774	4.059
Kaplan-Meier	n/a	39	0.357 ± 0.565	1.583
After omitting 8 observations at MDL
Complete case	Normal	39	0.426 ± 0.606	1.611
After censoring 26 observations at CCLV
Substitute CCLV/2	Normal	21	0.359 ± 0.570	1.586
Maximum Likelihood Estimation	Lognormal	21	0.537 ± 3.504	6.523
Maximum Likelihood Estimation	Gamma	21	0.343 ± 0.665	1.940
Robust Regression on Order Statistics	Lognormal	21	0.401 ± 1.043	2.600
Kaplan-Meier	n/a	21	0.387 ± 0.549	1.418
After omitting 26 observations at CCLV
Complete case	Normal	21	0.742 ± 0.684	0.922

Bias in the mean and SD after censoring at the MDL was first estimated relative to the full sample estimates and ranged from approximately zero to 0.082 and approximately zero to 1.202, respectively (Table S7). It was of minimal magnitude (i.e., minimum absolute value) and approximately zero for both the mean and SD for substitution of the MDL/2. Bias relative to the full sample after censoring at the CCLV ranged from −0.012 to 0.387 for the mean and −0.023 to 2.932 for SD; it was of minimal magnitude using substitution of CCLV/2 at 0.004 for the mean and −0.003 for SD (Table S8). While these results essentially indicate unbiasedness, substitution is generally considered less defensible and more bias prone than theoretically sound approaches.^{13,14,15,21,63–68}

Bias after censoring at the MDL was also estimated relative to the full sample maximum likelihood estimates assuming an underlying lognormal distribution because these data do not appear to be from a normal distribution; these alternative estimates of bias ranged from −0.028 to 0.052 for the mean and -0.728 to 0.481 for SD. Bias magnitude was minimal for the Kaplan Meier approach for the mean (-0.028) and maximum likelihood estimation for the SD (0.384). Bias after censoring at the CCLV was also estimated relative to the full sample maximum likelihood estimates. These bias estimates, after censoring at the CCLV, ranged from −0.042 to 0.152 for the mean and −0.745 to 2.211 for SD; they were of minimal magnitude for the Kaplan Meier approach for the mean (0.002) and robust regression on order statistics for the SD (−0.251). We note that log-scale mean and variance estimates do not transform in an unbiased manner to their original scale, for which well-known adjustments are available.^15,59,69 Our work, however, directly estimated means and variances in their original scale using maximum likelihood and robust regression on order statistics (Table S3).⁷⁰

Our case study analysis employed straightforward comparison of means and SDs for censored GC-MS DBA measurement data relative to means and SDs using the full, uncensored data. These GC-MS DBA measurements are assumed to be correctly identified and are not differentially affected by corrections typically applied to calculate, for example, emission factors. That said, our estimates of bias are not ideal because they are based on a single sample and are themselves biased because we treat the full sample measurements as the truth (i.e., unbiased). The full sample measurements are subject to measurement error uncertainty, as are all analytical chemistry data. Additionally, it is expected that the smaller measurements have larger RSDs, which leads to greater uncertainty in measured values below a censoring threshold. While measurement precision may not be well-characterized for small measurements, there are sound statistical approaches that may be useful for filtering out measurement error noise for many analyses.^37,71–74 Finally, the lognormality assumption appears pivotal in comparisons of the analysis approaches in this case study and indicates that future work focused on assessment of distributional assumptions would be beneficial.

Simulation study

The simulation study, by design, complemented the case study and generated 1,000 samples for two sample sizes (n=20 and n=50) from two lognormal distributions: one moderately skewed and the other highly skewed to mimic the observed distribution from the case study. Important distinctions are (1) the true mean and variance of the underlying population distributions are known, (2) bias estimation based on many samples is, in expectation, more accurate, and (3) the bias estimates are tied only to the distributional characteristics, enhancing generalizability beyond DBA. We note that the average SD for the 1,000 samples is expected to be more accurate for a sample SD but is not unbiased for population SD.⁷⁵ Inherent bias relative to the population SD is because the sample SD is calculated as the square root, a concave nonlinear function, of the sample variance and underestimates the population SD as established by Jensen’s inequality.⁷⁶ As in the case study, however, our examination of bias in the mean and SD is focused on that induced by censoring and subsequent analysis decisions.

The lowest 30%, 50%, and 80% of the simulated sample values were singly censored followed by selecting the best-fitting of normal, lognormal, and gamma probability distributions using AIC. Even though the two probability distributions used to simulate data values were lognormal, distribution-fitting, as often occurs, did not always favor lognormal. For the moderately skewed lognormal data, across the censoring levels and censored-data analysis approaches, lognormal was found to be the best-fitting distribution ranging from 29% to 100% of the 1,000 samples of size n=20 and from 39% to 100% of the n=50 samples (Table S9). For the highly skewed lognormal data, lognormal was found to be best-fitting distribution ranging from 30% to 100% of the 1,000 samples of size n=20 and from 50% to 100% of the n=50 samples (Table S10). Difficulties in choosing a probability distribution for environmental data are well-known, whether the data are from a single or mixture distribution.^15,59 Distribution fitting is additionally challenged when quantitative data values less than RL are censored.

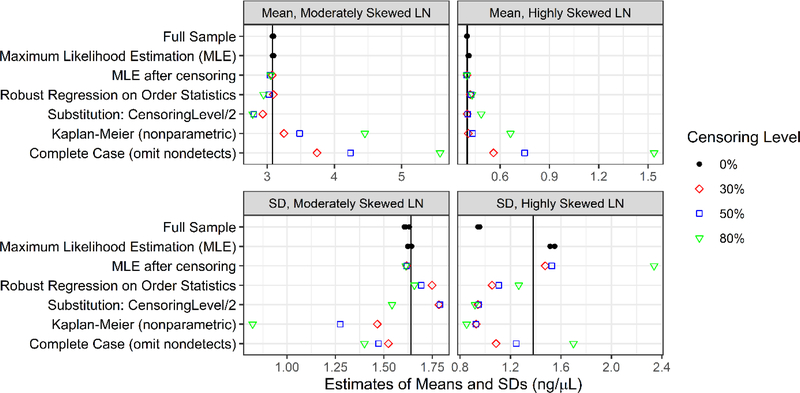
Bias relative to the mean and SD of the probability distributions (i.e., the true mean and SD) was estimated for each of the simulated samples and averaged. Bias for the moderately skewed and highly skewed lognormal distributions varied across the analysis approaches (Figure 2, Figures S6–S9, Tables S11–S14).

Figure 2.

Bias in estimates of the mean and SD from the simulation study for the moderately and highly skewed lognormal (LN) distributions is the difference of their estimated values (shown here for n=50) and true values, which are indicated by the reference lines. For the moderately skewed lognormal, the true mean is 3.08, and the true SD is 1.64. For the highly skewed lognormal, the true mean is 0.40, and the true SD is 1.38.

For the mean, taking together the results for the three censoring levels and both lognormal probability distributions, the full sample and full sample maximum likelihood estimation resulted in essentially no bias on average (Figure 2, Figures S6–S7, Tables S11–S12). Of the approaches after censoring, maximum likelihood estimation and robust regression on order statistics generally resulted in the least bias, in magnitude, with similar overall results to those for the full sample. Following these modern approaches in performance, substituting half the censoring level was somewhat negatively biased for the moderately skewed distribution and largely unbiased for the highly skewed distribution. The complete case (omitting observations) was clearly the most biased, and Kaplan Meier also performed poorly overall. In general, bias magnitude for the mean increased with increased censoring levels but sample size made little difference.

For the SD, taking together the results for the three censoring levels and both lognormal probability distributions, the full sample, full sample maximum likelihood estimation, maximum likelihood estimation after censoring, and robust regression on order statistics after censoring performed relatively well on average; however, results differed for the moderately and highly skewed distributions (Figure 2, Figures S8–S9, Tables S13–S14). Full sample maximum likelihood estimation was generally less biased in magnitude than full sample analysis and the best performing approach overall. Substituting half the censoring level, complete case, and Kaplan-Meier all performed relatively poorly. Kaplan-Meier was generally negatively biased and the worst-performing approach. Unlike for the mean, for the SD there does not appear to be a general pattern for bias magnitude with increased censoring levels.

Confidence intervals, with their dependence on both the mean and SD, are particularly useful in characterizing measurement uncertainty. Their estimation, however, is more difficult in the presence of censoring and the resulting small, or smaller, sample sizes.^57,77 We estimated 95% approximate confidence intervals of the form (sample mean) ± t_n-1(SD)/√n and compared actual coverage with the nominal 95% coverage. Taking together the results for the three censoring levels and both lognormal probability distributions, full sample maximum likelihood estimation achieved actual confidence interval coverages impressively close to 95%, ranging from 89.5% to 96.0% coverage, and was generally superior to all other approaches (Figures S10–S11, Tables S15–S16). The full sample maximum likelihood estimation confidence intervals, as a consequence, were more appropriate in characterizing measurement uncertainty than confidence intervals based on the mean and SD from any of the other approaches considered in our simulation study. Notably, actual confidence interval coverages worsened with increased censoring levels.

These results add to other studies that assessed a variety of software and analysis choices for estimating means and variances from observed and simulated measurement data with nondetects.⁶⁷ Maximum likelihood estimation has been found to perform well for estimating the mean in some simulated scenarios^15,63,65 but poorly in others, including for small data sets generally, for data sets where the distributional assumption was badly misspecified, or for data sets where measurements from a more sensitive analysis replaced censored data.^78,79 Regression on order statistics has been referred to by a variety of names over its history, including log-probit regression and log probability regression, and has its foundation in probability plotting and using the relative quartile range of the uncensored portion of the sample.^{2,63,65,80,81} It has also been found to perform well for estimating the mean in some simulated scenarios, although its robustness against departures from distributional assumptions may depend on software and algorithm assumptions.^15,65,67,79

It is noteworthy that while the average means and SDs reflect values that would be reasonably expected (Figure 2, Figures S6–S9), the means and SDs observed across the 1,000 samples varied considerably (Figures S12 and S13). Despite this variability, an unanswered question is how closely the randomly generated samples mimic measurement data that could be observed. Observed data are inherently uncertain, may be subject to instrument-specific identification difficulties, and carry potential that measurement error differentially biases both accuracy and precision of smaller reported values. Long-standing conventions to censor data below detection thresholds reflect scientists’ concerns over identification and uncertainty. Additionally, there is uncertainty around measurements below the lower end of a calibration range where instrument response can reflect differential nonlinearity. This potential additional bias in small measurements adds to scientists’ concerns as they grapple with determining whether a true, greater-than-noise signal is present. Limitations notwithstanding, our case and simulation studies suggest that censoring and subsequent analysis approaches can do more harm than good, particularly when analysis of data sets is of interest rather than solely characterizing individual measurements.

Our results illustrate that censoring and key analysis decisions, including distributional assumptions, affect results and their interpretation. These simulations suggest, in general, censored-data analysis approaches may be inferior to analysis using all measurement data. The overall least-biased (i.e., smallest bias magnitude) means and SDs for the lognormally distributed simulated samples were the full sample approaches, with full sample maximum likelihood estimation the better performer for n=50 (Figure 2, Figures S6–S9).

Group comparisons and statistical significance

This analysis compared two groups in tests of differences of means and illustrates that decisions on censoring and analysis approaches can substantively affect group means, SDs, and tests of differences of means that investigators report and interpret. In this analysis, censoring at the CCLV affected 53 of the 85 observations in the bootstrapped sample. Estimates of the mean and SDs for stove type 1 and stove type 2 varied across the analysis and distribution assumption choices (Tables 2 and S5). The full sample t-test for difference of stove type means found statistical significance at α=0.05 (p-value=0.023), and substituting CCLV/2 after censoring also produced a significant t-test (p-value=0.017) (Figures S14–S15). These t-tests, by default, naively assume that the underlying distribution is normal, which does not appear to be appropriate, particularly for stove type 1 (Figure S5), and is not supported by AIC statistics (Table S17). Additionally, substitution is known to yield biased estimates of means and SDs, and the direction and magnitude of bias depend on the expected proportion of censored values and the underlying data distribution.^63,65 In contrast, the full sample maximum likelihood estimation assuming lognormality yielded a non-significant z-test for difference of geometric means (p-value=0.103), while maximum likelihood estimation after censoring produced a marginally significant z-test for difference of geometric means (p-value=0.050). Results of t-tests repeated on log-transformed DBA data were similar to these maximum likelihood results.

Table 2.

Tests of group differences for resampled case study data for censoring at the CCLV

Approach	Distribution	Stove Type 1 (resampled from Eco Chula XXL)		Stove Type 2 (resampled from Butterfly Model)		p-value
		n	Mean ± SD (ng/μL)	n	Mean ± SD (ng/μL)
Uncensored
Full sample	Normal	45	0.139 ± 0.156	40	0.079 ± 0.056	0.023a
Full sample Maximum Likelihood Estimation	Lognormal	45	0.145 ± 0.225	40	0.089 ± 0.115	0.103b
After censoring 53 observationsc
Substitute CCLV/2	Normal	45	0.143 ± 0.153	40	0.081 ± 0.049	0.017a
Maximum Likelihood Estimation	Lognormal	45	0.146 ± 0.200	40	0.092 ± 0.045	0.050b

^aTest for difference of means (i.e., that difference of means is zero). Repeating the t-tests on log-transformed DBA data yielded p-value=0.111 for the full sample and p-value=0.051 after censoring.

^bTest for the difference between the two groups expressed as the ratio of their geometric means

^cStove 1: 25 observations were censored; Stove 2: 28 observations were censored

This analysis illustrates that statistical significance in a test of group differences can depend heavily on the distributional assumption. The distributional assumption can be a limitation of parametric and semiparametric approaches such as maximum likelihood estimation and robust regression on order statistics, respectively.¹⁵ The parametric test for difference of geometric means assumes a common distribution for the data from the two stoves, a distributional assumption which would not have been required for a nonparametric test for differences of empirical cumulative distribution functions. Another well-known caveat for maximum likelihood estimation is that its performance can suffer for small sample sizes, yielding biased estimates.⁸² In this analysis, group-specific maximum likelihood-estimated means and SDs were differentially affected by censoring. For example, for stove type 1, the mean ± SD was estimated as 0.145 ± 0.225 without censoring and 0.146 ± 0.200 after censoring, and, for stove type 2, 0.089 ± 0.115 without censoring and 0.092 ± 0.045 after censoring. Also, substitution gives biased results independent of sample size⁶³, so the outcomes of statistical group tests even for large data sets may be substantively affected and irreproducible.

This analysis was repeated for censoring at the MDL. While 53 (62.4%) of the 85 observations in the resampled data were censored at the CCLV, only 16 (18.8%) were censored at the MDL. The t-test results again were substantively different from those for maximum likelihood estimation, reinforcing distributional assumption importance (Table S18).

Our results for group means, SDs, and differences of means using resampled data illustrated that censoring and distributional decisions affected results. Estimates for the mean and SD and significance test results varied whether censoring at the CCLV or MDL (Table 2, Table S18). Decisions reached may vary widely from one study to another simply because of censoring and analysis choices, undermining reproducibility.

Recommendations

Whether or not censoring- and analysis-induced bias adversely affects use and interpretation of results is dependent on the data and on the research question. It is not always appropriate or necessary to use measurements less than RL; decisions may depend on the intended use of the data as well as chemical identification confidence and measurement uncertainty. Data uses such as comparisons to action levels or regulatory standards and assessments of differences in groups are strengthened by reduced bias and improved confidence intervals. The appropriateness of using data less than RL should be considered by each investigator and data user. However, each investigator and data user should remain aware of the potential for censoring-related bias corresponding to analysis and the (explicit or implicit) distributional decisions. We offer suggestions for several modern statistical treatment and software choices for consideration for research protocol specifications, analysis, and interpretation of results. We encourage investigators and data users to consider the pros and cons of analyzing full, uncensored measurement data or to try analysis both with and without censoring to gauge the effect of censoring and subsequent analysis decisions. We recommend investigators, journal editors, and data users to adopt Cressie’s²⁵, Childress et al.’s⁷, and others’ suggestions to report and publish: all measurement data without censoring along with data quality indicators, detection limits, reporting levels and other censoring thresholds, and the methods used in calculating these, without regard to the use of censoring in both primary and secondary analyses.