Resonant Soft X-Ray Scattering Provides Protein Structure with Chemical Specificity

SUMMARY

We introduce resonant soft X-ray scattering (RSoXS) as an approach to study the structure of proteins and other biological molecules in solution. Scattering contrast calculations suggest that RSoXS has comparable or even higher sensitivity than hard X-ray scattering because of contrast generated at the absorption edges of constituent elements, such as carbon and oxygen. Here, we demonstrate that working near the carbon edge reveals the envelope function of bovine serum albumin, using scattering volumes of 10⁻⁵ μL that are multiple orders of magnitude lower than traditional scattering experiments. Furthermore, tuning the X-ray energy within the carbon absorption edge provides different signatures of the size and shape of the protein by revealing the density of different types of bonding motifs within the protein. The combination of chemical specificity, smaller sample size, and enhanced X-ray contrast will propel RSoXS as a complementary tool to existing techniques for the study of biomolecular structure.

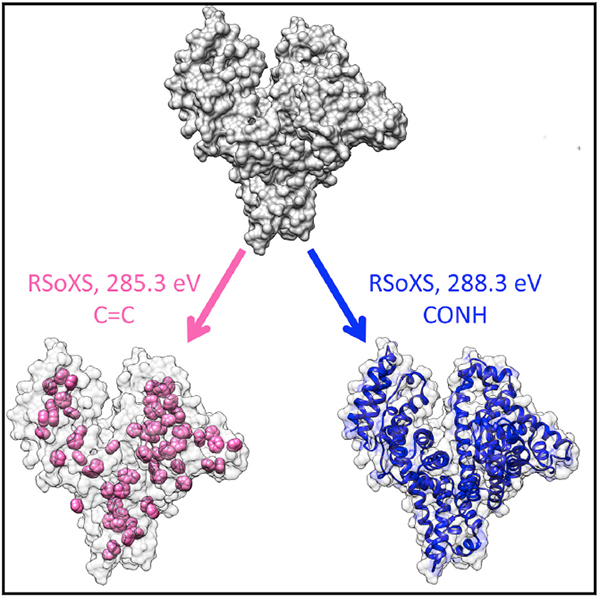
Graphical Abstract

In Brief

Ye et al. demonstrate resonant soft X-ray scattering as a tool to examine the shape and size of proteins in solution. Working at X-ray absorption edges provides an opportunity to selectively highlight structure associated with specific chemistries, thereby establishing a promising technique for the study of complex biological assemblies.

INTRODUCTION

The development of X-ray and electron microscopy tools to examine the structure of proteins has enabled mechanistic descriptions of protein function for a variety of biomolecules, including myoglobin (Perutz et al., 1965), insulin (Adams et al., 1969), the photosynthetic reaction center (Deisenhofer et al., 1985), adenosine triphosphate synthase (Abrahams et al., 1994), and ribosomes (Schluenzen et al., 2000). Often, a combination of techniques is crucial to minimize inherent limitations of any specific instrument. For example, X-ray or electron diffraction data are composed of reflections from the crystalline structure, and small-angle X-ray scattering (SAXS) yields complementary information as scattering profiles associated with shape and size. In addition, SAXS has been used to reveal complexation and aggregation of various proteins (Bale et al., 2016; Dueber et al., 2011; Stradner et al., 2004; Zhang et al., 2012) and has proven instrumental for the study of proteins with polydisperse or intrinsically disordered structures (Jehle et al., 2010) that are challenging to examine using electron microscopy or X-ray diffraction. A distinct advantage of SAXS-based techniques is the ability to examine structural evolution as a function of time in situ (Nishimura et al., 2009; Phillips et al., 2014; Wakabayashi et al., 1992), because unlike diffraction-based techniques, SAXS does not require vitrification, staining, or ex situ crystallization of proteins of interest. While SAXS has proven to be an important tool for structural biology, SAXS experiments are limited by the weak contrast between sample constituents within biological systems. At hard X-ray energies used for SAXS experiments, typically near 10 keV, contrast is mostly a function of the difference in electron density of components.

Resonant soft X-ray scattering (RSoXS), a technique recently developed to examine polymeric thin films, enhances contrast by tuning the X-ray energy with approximately 0.1 eV energy resolution (Collins et al., 2012; Guo et al., 2013; Virgili et al., 2007; Wang et al., 2011). The broad energy range accessible for RSoXS experiments in the soft X-ray regime (<2 keV) allows for K and L absorption edges of a variety of elements to be probed, some of which are ubiquitous (C, N, O) or at least common (e.g., Ca) in biological systems. Working at these absorption energies leads to enhanced contrast, by multiple orders of magnitude, between different moieties due to differences in bonding or elemental composition without the need for labeling, and with approximately nanometer resolution (Collins et al., 2012; Swaraj et al., 2010). Thus, RSoXS has the potential to become a next-generation small-angle scattering instrument that elucidates the structure of proteins and other biological systems.

As proof of principle of the utility of RSoXS for structural biology, we studied bovine serum albumin (BSA), which is a globular protein that functions as a carrier protein and is important for regulating fluid distribution between blood vessels and surrounding tissues (Putnam, 1975). BSA is a small (ca. 66 kDa) and relatively stable protein that has been characterized by crystallography (Majorek et al., 2012). In addition, it is sometimes used as a molecular weight standard for SAXS experiments (Akiyama, 2010). Thus, BSA is an appropriate model system for demonstrating the various capabilities of RSoXS for characterizing the structure of biological molecules. We demonstrate that RSoXS takes advantage of chemical specificity and can resolve differences in bonding environments within proteins. This reveals differences in the envelope function of BSA for distinctive types of bonds. Furthermore, because of the monochromated X-ray source in the soft X-ray regime (<2 keV), damage is localized to specific bonds. As a consequence, the overall effects of radiation damage on the structure are mitigated, thereby enabling experiments at higher doses than those for hard X-rays by multiple orders of magnitude.

RESULTS

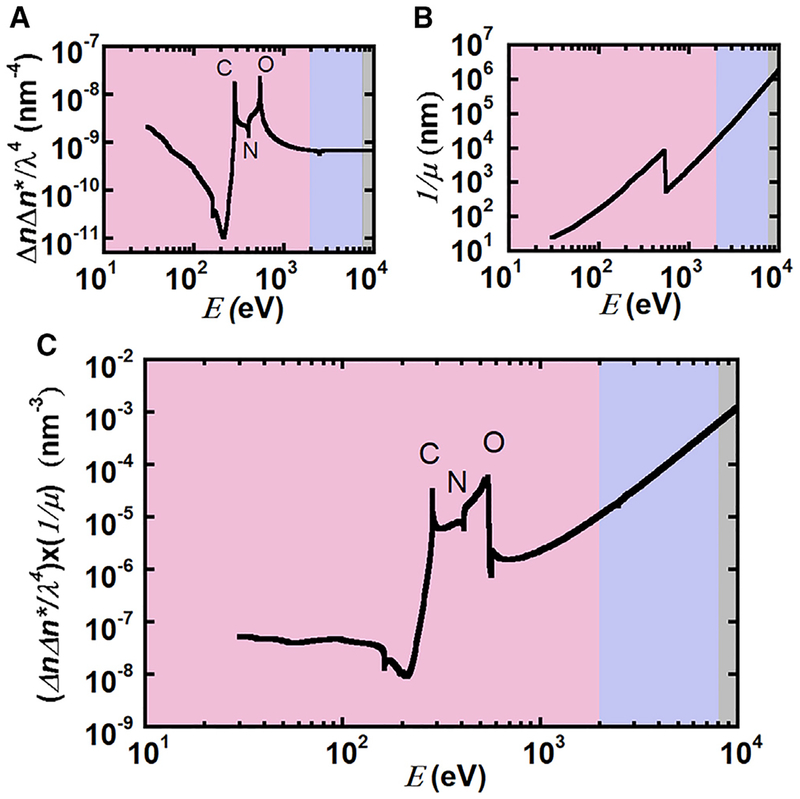
We demonstrate the expected enhancement of scattering intensity in the soft X-ray regime with respect to traditional hard X-rays (at 10 keV) by calculating the scattering contrast and attenuation length for BSA in phosphate buffered saline (PBS). Scattering intensities are proportional to the contrast, which contains contri butions from both dispersive (mass contrast) and absorption components of the refractive index. Figure 1A shows the predicted scattering contrast between BSA and PBS as a function of X-ray energy calculated from the real and imaginary parts of the constituent atomic scattering factors obtained from the Henke database (Henke et al., 1993). Although we use PBS in our calculations, water is the dominant species in the solvent, such that similar results are obtained for the contrast between BSA and various other buffers (e.g., 10 mM Tris and 10 mM HEPES). Contrast is enhanced in the soft X-ray regime, in particular at the carbon (~285 eV) and oxygen (~535 eV) absorption edges, suggesting that working at energies that are at resonance with these edges could lead to enhancements in scattering intensities by orders of magnitude. Scattering intensities are also proportional to the scattering volume, but are limited either by multiple scattering or by the absorption of the sample. For hard X-rays, multiple scattering is typically only a fraction of a percent for proteins in dilute solution (Fanchon and Geissler, 2000). Although Figure 1A shows a 30-fold enhancement in contrast for soft X-rays, Figure 1B shows the attenuation length for BSA in PBS decreases by a factor of 10³ at the carbon edge (ca. 285 eV). Thus, where near 10 keV sample thicknesses should be approximately 1 mm, in the soft X-ray regime (<2 keV) the path length should be between 10² and 10⁴ nm. The large reduction in sample thickness ensures multiple scattering is negligible for soft X-ray scattering from proteins in solution, but the significant absorption limits thicknesses of samples and therefore limits scattering intensities. Because the overall scattering intensity is proportional to the product of the sample volume (or thickness) and scattering contrast (ΔnΔn*/λ⁴), the maximum scattering intensity is the product of the attenuation length (1/μ) and scattering contrast as given by (Ade and Hitchcock, 2008; Als-Nielsen and McMorrow, 2011; Swaraj et al., 2010; Virgili et al., 2007):

$$l\alpha \frac{1}{\mu }\frac{\mathrm{\Delta }n\mathrm{\Delta }{n}^{*}}{{\lambda }^4}=\frac{1}{\mu }\frac{{\left({\delta }_a-{\delta }_b\right)}^2+{\left({\beta }_a-{\beta }_b\right)}^2}{{\lambda }^4}\alpha \frac{1}{\mu }\left[{\left(f_{a,1}-f_{b,1}\right)}^2+{\left(f_{a,2}-f_{b,2}\right)}^2\right],$$

where Δn and Δn* are the differences between the complex refractive indices of the two components and λ is the wavelength of the incident X-rays. The indices a and b represent each component in a binary mixture; here buffer and BSA. β_i and δ_i are imaginary and real parts of the refractive indices, respectively. f_i,1 and f_i,2 are the sum of the real (1) and imaginary (2) parts of the constituent atomic scattering factors for each component and can be determined from the Henke database in the forward scattering limit (Henke et al., 1993). As shown in Figure 1C, the product of the attenuation length and contrast indicates that scattering intensities at X-ray energies near the carbon or oxygen edge are approximately within a factor of 30 to that of hard X-rays (10 keV).

Figure 1. Attenuation Length and Scattering Contrast between BSA and 1×PBS in the Soft (Pink), Tender (Purple), and Hard (Gray) X-Ray Regime.

(A) Theoretical scattering contrast between BSA and PBS based on predicted absorption spectra as a function of X-ray energy, E, reveals enhanced contrast at the carbon and oxygen absorption edges within the soft X-ray regime.

(B) Attenuation length of 10 mg/mL BSA in PBS. The step change near 500 eV is due to the absorption edge of oxygen.

(C) The product of attenuation length and scattering contrast is proportional to the scattering intensity.

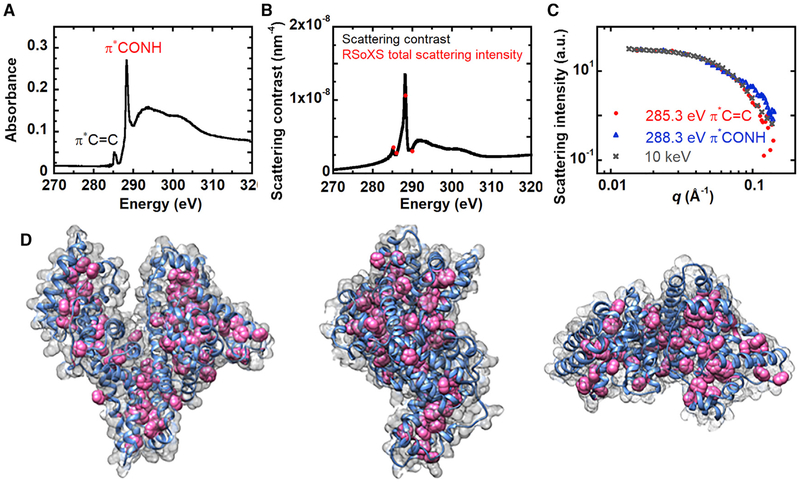
The f₁ and f₂ values from the Henke database cannot account for bonding environments and thus are not accurate at absorption edges. Nevertheless, because the X-ray energy resolution is 0.1 eV, small differences in the X-ray absorption due to different valence electronic structures could lead to significant contrast (Ade and Hitchcock, 2008; Ade et al., 2010; Swaraj et al., 2010; Virgili et al., 2007; Wang et al., 2011). We calculate the scattering contrast between BSA and PBS from experimentally measured near-edge X-ray absorption fine structure (NEXAFS) spectra of BSA near the carbon edge. Figure 2A shows the NEXAFS spectra for BSA films that were spin coated onto Si₃N₄ windows (solid-state samples). At the carbon K edge, there are two distinct resonance peaks. We attribute the dominant peak near 288 eV to the $\text{C}1\text{s}(\text{CONH})\to {\pi }_{\text{CONH}}^{*}$ transition in the peptide bond connecting amino acids (Gordon et al., 2003; Zubavichus et al., 2005, 2007). The peak near 285 eV represents $\text{C}1\text{s}(\text{C}=\text{C})\to {\pi }_{C=C}^{*}$ which is from aromatic rings in four types of amino acids, including phenylalanine, tyrosine, tryptophan, and histidine (Zubavichus et al., 2005). The scattering contrast as a function of energy near the carbon edge for BSA in PBS (Figure 2B; black curve) was then calculated using KKcalc (Watts, 2014) to improve the accuracy with respect to Figure 1A. KKcalc converts the measured NEXAFS spectra to imaginary atomic scattering factors (f₂) and merges the measured f₂ at the carbon K edge to the theoretical f₂ spectra away from the edge (e.g., 10 eV up to 500 keV except for 270 to 320 eV). f₁ is calculated from the Kramers-Kronig relationship using the entire energy range of the f₂ spectra. Scattering factors for BSA are shown in Figure S1.

Figure 2. Scattering Contrast between BSA and PBS Solutions Near the Carbon K Edge.

(A) BSA NEXAFS spectra.

(B) Total scattering intensity at different energies calculated from RSoXS (red dots) near the carbon edge for 10 mg/mL BSA in 1× PBS. Black curve is the scattering contrast.

(C) RSoXS scattering intensity profiles of 10 mg/mL BSA in 1× PBS at 285.3 eV and 288.3 eV (at resonance of the carbon K edge) and SAXS scattering intensity profile at 10 keV.

(D) Visualization of all carbon atoms (gray mesh), backbone CONH (blue), and aromatic rings containing C=C double bonds (pink) in the protein molecule (generated from crystallographic data PDB: 3V03).

The RSoXS sample chamber is under high vacuum, typically at 10⁻⁷ Torr, because absorption and scattering from air is significant in the soft X-ray regime. To examine aqueous solutions, we designed and fabricated sample cells composed of 100-nm-thick Si₃N₄ windows with a scattering path length of approximately 1 μm (see Figure S2). The actual path length varied in the sample cell due to flexing of the windows under high vacuum. Despite our best efforts to screen window quality and cell integrity, approximately 80% of cells failed under vacuum. Nevertheless, the presence of liquid within the sample cells was confirmed by measuring the absorption in the carbon pre-edge region (270–280 eV) and calculating the thickness of the liquid film by comparing with predictions based on the Henke database. Although windows can flex such that thicknesses are greater than 1 μm, liquid film thicknesses were 100–1,000 nm for all the studies presented here.

Prior to RSoXS experiments, monomodal distributions of BSA in PBS were confirmed using variable-angle dynamic light scattering (DLS; Figure S3). We performed RSoXS measurements on 10 mg/mL BSA in PBS at four different energies that are at and away from resonance of the carbon absorption edge: 285.3, 286, 288.3, and 290 eV. Scattering from buffer or aqueous solutions near the C edge is minimal, such that background scattering is mostly dominated by scattering from the Si₃N₄ windows (see Figure S4A). Thus, we normalize all data by the incident flux, and use scattering data from samples composed of PBS solutions only as the background to be subtracted. Due to variability in the windows, background scattering can vary, and therefore background scattering contributions are sometimes scaled to prevent unphysical results, such as negative intensities (Figure S4B).

The background-subtracted, azimuthally averaged scattering intensity for data collected at four energies is shown in Figure S5A; Figure 2C shows profiles at 285.3 eV and 288.3 eV, and Figure S5B shows the same data with error bars that represent the standard error of the mean obtained from integrating over all polar angles. We demonstrate reproducibility in Figure S5C, where data represent mean ± standard error of mean obtained by averaging scattering from three different samples. Scattering data as a function of concentration is explored in Figures S5D and S5E, where we show results from 5 mg/mL and 10 mg/mL solutions of BSA near the carbon edge and from 0.625 mg/mL to 10 mg/mL solutions of BSA for hard X-rays. Although we have not thoroughly explored concentration limits, soft X-ray data can be acquired at concentrations that are at least within an order of magnitude of concentrations used at 10 keV. Optimization of the acquisition time, sample thickness, and X-ray energy as well as further improvements of soft X-ray detectors may decrease the required concentration for proteins in solution.

A challenge in interpretation of scattering experiments is the lack of uniqueness, where multiple structures can lead to the same scattering profile. But, tuning the X-ray energy and therefore X-ray contrast alleviates this problem. We compare the total scattering intensity (Collins et al., 2013; Rambo and Tainer, 2013)(TSI = ʃ I(q)q²dq) with the contrast predicted from NEXAFS spectra. A single scaling parameter is needed because of the lack of absolute intensities in soft X-ray scattering data. Figure 2B shows the strong agreement between the measured total scattering intensity (red dots) and the predicted scattering intensities (black curve). Thus, contrast is dominated by the differences in the absorption spectra, and we can attribute the origin of scattering profiles to the components of the predicted contrast, BSA and PBS.

The scattering curves obtained for 285.3 and 288.3 eV (on-resonance, with different bonding motifs at the carbon absorption edge) show different scattering signatures in Figure 2C. The scattering curve at 285.3 eV, which emphasizes C=C bonds, agrees well with scattering obtained from SAXS at 10 keV (Figure 2C). Experimental scattering data collected at 285.3 eV and 10 keV shows better fitting to the theoretical SAXS curve obtained from the crystal structure of BSA using CRYSOL (Svergun et al., 1995) (see Figures S6A–S6C) than the scattering data collected at 288.3 eV. The pair distribution function, p(r), was calculated from scattering curves at 285.3 eV, 288.3 eV, and 10 keV (see Figure S6D). The maximum particle size (D_max) was estimated from the pairwise distributions and was found to be 101 Å for 285.3 eV, 105 Å for 288.3 eV, and 97 Å for 10 keV. Systematically varying D_max by 10% only increased the mean squared error in p(r) by about 5%, suggesting the differences in D_max values are not statistically significant. The p(r) at 10 keV is most consistent with the expected p(r) from a monomer, but a slight tail at large r suggests a small population of dimers could be present. Although we can similarly explain the origin in the tail in the soft X-ray data at 285.3 eV and 288.3 eV, a formulism to calculate the expected p(r) from soft X-ray scattering is not available. Nevertheless, differences in the shape of the pair distribution functions suggest that different aspects of the structure of BSA are highlighted at these different energies (Figure S6D).

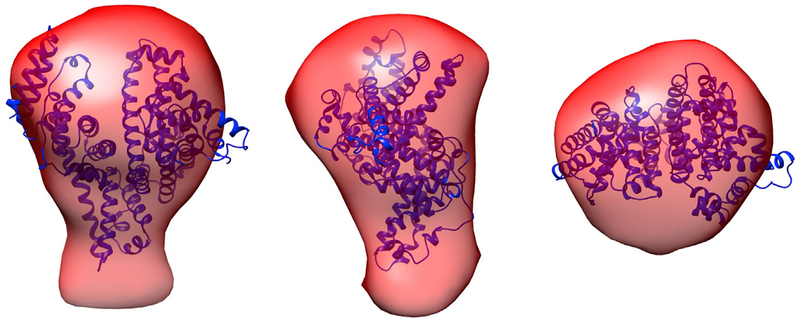
To examine the three-dimensional structure of BSA from RSoXS data, we generated envelopes from RSoXS and SAXS data using GASBOR (Svergun et al., 2001) and compared the envelopes with the crystal structure of BSA (PDB: 3V03) (Majorek et al., 2012). Figure 3 shows that at 285.3 eV, the envelope matches the crystal structure well. At 288.3 eV, the envelope emphasizes the peptide bonds and is slightly different than the envelope generated from RSoXS data collected at 285.3 eV and SAXS data collected at 10 keV (Figures S6E and S6F). Using Chimera (Pettersen et al., 2004), envelope volumes were calculated, giving mean values of 243 ± 6 nm³ for 285.3 eV, 270 ± 9 nm³ for 288.3 eV, and 254 ± 6 nm³ for 10 keV (error is the standard deviation calculated from analyzing ten reconstructions). As might be expected from the bond density maps shown in Figure 2D, the envelope is slightly larger when generated from RSoXS data at 288.3 eV instead of at 285.3 eV.

Figure 3. Overlay of the Envelope Generated at 285.3 eV and the Crystal Structure of BSA.

The red envelope is generated from RSoXS data and the blue ribbons represent the BSA backbone determined from the crystal structure (PDB: 3V03).

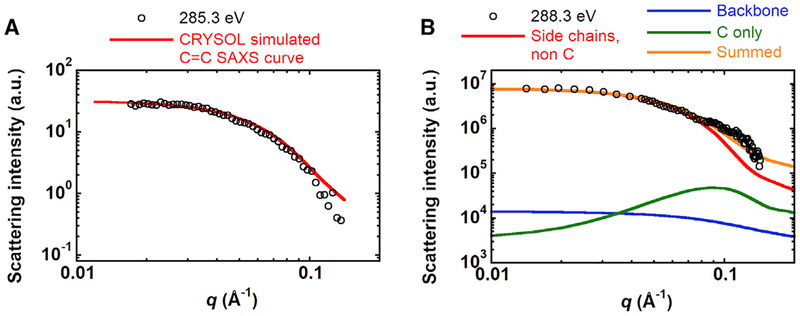
Tuning the X-ray contrast provides an opportunity to compare the predicted scattering that will depend on the internal distribution of bonds and elements with scattering curves obtained at various X-ray energies. Although a rigorous approach to predict RSoXS scattering for a given structure as a function of X-ray energy is not currently available, we propose a simple methodology. Starting with the crystal structure of BSA, we generated atomic coordinate files with only the aromatic rings of BSA to produce expected scattering curves using CRYSOL. Figure 4A shows that this predicted scattering compares well with RSoXS data at 285.3 eV (χ² of 13.4), which corresponds to the energy for the $1\text{s}(\text{C}=\text{C})\to {\pi }_{C=C}^{*}$ transition dipole moment. At higher energies, more resonances overlap, including the carbon step edge. Using the X-ray absorbance spectra as a guide, we generate three atomic coordinate files. One contains the protein backbone and corresponds to the $1\text{s}(\text{CONH})\to {\pi }_{\text{CONH}}^{*}$ resonance at 288.3 eV, a second is composed of the carbon atoms only, corresponding to the C step edge, and finally a third atomic coordinate file composed of the non-carbon atoms on the side chains that corresponds to the absorbance equal to that of the pre-edge region near 280 eV. Scattering profiles for each atomic coordinate file are generated and summed with weighing factors that are proportional to the X-ray absorbance at 288.3 eV, which are 1 for the non-carbon side-chain elements, 8.7 for the peptide backbone, and 4.5 for the profile generated from all C atoms. Figure 4B shows that this model well represents RSoXS data at 288.3 eV.

Figure 4. Predicted RSoXS Scattering Profiles.

(A) RSoXS data for BSA in PBS at 285.3 eV and CRYSOL-predicted scattering profile from aromatic carbons of BSA.

(B) RSoXS data for BSA in PBS at 288.3 eV and predicted scattering (summed) from a combination of the peptide backbone (backbone), all carbon atoms (C only), and non-carbon atoms on the side chains (side chains, non C) of BSA. The individual contributions to the total predicted scattering are determined from the relative X-ray absorbance of BSA.

We also compared the size of BSA in PBS obtained from RSoXS, SAXS, and DLS in terms of the radius of gyration (R_g) as shown in Table 1. Multi-angle DLS provides the hydrodynamic radius (R_h) of BSA in solution (Figure S3) while X-ray scattering yields particle size in terms of R_g as determined using DATGNOM from the ATSAS suite (Petoukhov and Svergun, 2007) using the low q data and Guinier analysis. The hydrodynamic radius of particles in solution includes the size of the actual particle plus the solvent molecules moving with it. On the other hand, the radius of gyration represents particle size as the average distance from the center of mass. Assuming the shape of a BSA molecule is close to an ellipsoid in PBS, R_g and R_h are related by R_g = 0.79R_h (He and Niemeyer, 2003). This relationship provides a way to compare the particle size obtained from X-ray scattering and DLS. The corresponding R_g determined from DLS is 30 Å. This is in good agreement with R_g obtained from SAXS (28 Å). and RSoXS at 285.3 eV (29 Å). and 288.3 eV (31 Å).

Table 1.

BSA Size Characterization

	Rh from DLSa (Å)	Rg from DLSa,b (Å)	Rg from SAXSc (Å)	Rg from RSoXS at 285.3 eVc (Å)	Rg from RSoXS at 288.3 eVc (Å)
10 mg/mL BSA in PBS	35 ± 1	30 ± 1	28 ± 1	29 ± 7	31 ± 4

Values are means ± SD.

^aMultiple measurements on same sample (n = 3).

^bAssuming R_g = 0.79R_h.

^cObtained from error of fit in ATSAS software (Petoukhov et al., 2012).

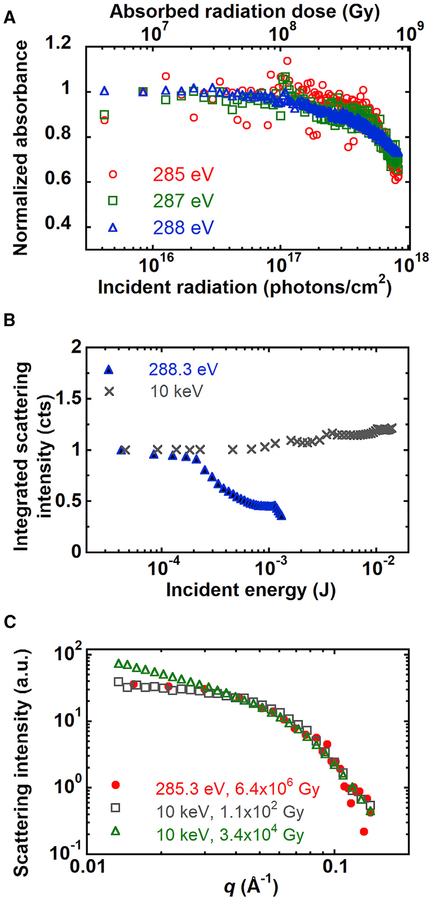
Radiation damage induced by X-rays and electron beams on soft materials is due to ionization, mass loss, and local heating (Williams and Carter, 2009). For SAXS experiments on protein solutions, radiation damage severely changes the scattering profile primarily due to induced protein aggregation (Kuwamoto et al., 2004). Thus, the X-ray exposure must be minimized for SAXS; with typical fluxes at synchrotrons (10¹³ photons/cm²/s), the exposure time is limited to a few seconds. Limited work on RSoXS of biological materials has been reported (Ingham et al., 2015; Ingham et al., 2016), and none on proteins in solution; as such, the effects of soft X-ray radiation damage on protein solutions or solid protein films has not been examined. Due to the monochromated X-ray source that is absorbed by specific types of bonds, the effect of the accumulated X-ray energy on biological samples could differ between the soft and hard X-ray regimes.

We performed radiation damage experiments on BSA films and on BSA solutions using soft X-rays. For BSA films, as the radiation dose increases, the absorption of the BSA film decreases (Figure 5A). This suggests ionization-induced radiation damage, such as chain scission or crosslinking (Coffey et al., 2002). We observed similar behavior for BSA in PBS solution by RSoXS, with the integrated scattering intensity decreasing as the radiation dose increases (Figure 5B). The critical dose is calculated by fitting the total scattering intensity versus radiation dose using I = I_d exp(−D/D_c) + I_b, where D_c is the critical dose and I_d and I_b are constants (Martin and Thomas, 1995). In units of incident energy, the characteristic value for damage of BSA in solution is 3.2 × 10⁻⁴ J at 288.3 eV. We calculate the critical dose in terms of the absorbed radiation (Hopkins and Thorne, 2016; Jeffries et al., 2015), as this reflects the maximum interaction between the sample and X-rays and the maximum attainable scattering intensities shown in Figure 1C (assuming equivalent detector efficiency, coherence, etc.). The critical dose for BSA in solution is 1.7 × 10⁷ Gy at 288.3 eV corresponding to 150 s of exposure time with an X-ray flux of 10¹⁵ photons/cm²/s (Figure S7A).

Figure 5. Effect of Radiation Damage on Absorbance and Scattering from a Film of BSA and a BSA Solution.

(A) Absorbance of BSA film as a function of soft X-ray radiation dose.

(B) Integrated scattering intensity of BSA in 1× PBS as a function of X-ray radiation dose at 288.3 eV and 10 keV.

(C) Comparison of scattering profiles at 285.3 eV and 10 keV with different X-ray doses.

We also examined radiation damage of BSA in PBS by hard X-rays. As the sample receives more energy, the integrated scattering intensities go up (Figure 5B), which is opposite to the trend observed by RSoXS. We estimate the critical dose for SAXS as 1.4 × 10³ Gy (corresponding to 20 s of exposure time) because of the sudden increase of total scattering intensity at this radiation dose (Figure S7B). This dose lies in the range of critical doses found for other proteins, which is from 2 × 10² Gy to 6.6 × 10⁷ Gy, depending on the protein species and dose rate (Hopkins and Thorne, 2016; Kuwamoto et al., 2004). Above this critical dose, the hard X-ray SAXS profiles change significantly at low q (Figure 5C). RSoXS data, on the other hand, are equivalent to low-dose hard X-ray data at doses that are multiple orders of magnitude higher (6.4 × 10⁶ Gy). Thus, we hypothesize that hard X-rays and soft X-rays damage BSA differently.

DISCUSSION

Here, we demonstrate the utility of RSoXS for determining the structure of proteins in solution and show that the soft X-ray regime offers advantages over hard X-rays for structural characterization of biological molecules. Because RSoXS can distinguish between different chemical moieties without the need for labeling, scattering contrast and intensities are enhanced by multiple orders of magnitude. While the product of the attenuation length and contrast shown in Figure 1C indicates that scattering intensities at X-ray energies near the carbon or oxygen edge can be similar to that of hard X-rays (10 keV), the scattering volume is significantly smaller for soft X-ray experiments. The optimum thickness at the carbon edge in the soft X-ray regime is approximately 1 μm, or 1,000 times lower than that at 10 keV, for BSA in PBS. Assuming a spot size of 100 μm × 100 μm, the scattering volume is 10⁻⁸ cm³, or 10⁻⁵ μL. Thus, RSoXS is ideally suited for the study of miniscule amounts of samples, which may be critical to enable the study of proteins that are challenging to scale up for traditional structural characterization experiments.

Although the attenuation length sets a maximum thickness and therefore a maximum dimension for objects that can be studied with soft X-rays, currently the lowest q accessible at Beamline 11.0.1.2 of the Advanced Light Source is about 0.001Å⁻¹ (Gann et al., 2012). In principle, the largest accessible scattering vector q_max corresponds to half the X-ray wavelength, λ/2, although this would require a back-scattering geometry. Assuming a practical limit for the scattering angle of about 60°, then q_max is 2π/λ. Table 2 shows that wavelengths in the soft X-ray regime are in the nanometer range. Thus, near the carbon edge, limited information (such as R_g from Guinier analysis) can be obtained from proteins with diameters smaller than the wavelength, i.e., radii smaller than 2 nm, which approximately corresponds to 30 kDa proteins assuming compact conformations (Erickson, 2009). We propose that predicting the expected scattering (e.g., from spherical or ellipsoid form factors) is important to establish that the achievable q range at the desired X-ray energy is appropriate for the study of interest.

Table 2.

Maximum Scattering Vector q_max Achievable in the Soft X-Ray Regime

Edge	Energy (eV)	λ (Å)	qmax (1/Å)a
Carbon	285	43.5	0.14
Calcium	349	35.5	0.18
Nitrogen	397	31.2	0.20
Oxygen	533	23.3	0.27
–	1,500	8.27	0.76

^aAssuming 60° as the largest scattering angle.

Systematically varying the X-ray energy allows for comparison between predicted scattering contrast and total scattering intensities. In this way, we can address a fundamental limitation in scattering, that multiple structures can lead to the same scattering profile, in a manner not typically possible in the hard X-ray regime. By comparing scattering contrast at various energies, the number of possible structures is greatly reduced. Tuning the X-ray energy also reveals different aspects of the protein structure; in the case of BSA, this corresponds to either the entire protein or the peptide backbone. When comparing experimental scattering data and the theoretical SAXS curve generated from the crystal structure of BSA using CRYSOL, we find that scattering data collected at 285.3 eV and 10 keV better fit the theoretical curve than scattering data collected at 288.3 eV. CRYSOL computes theoretical SAXS curves using a uniform contrast (electron density); thus, the enhanced scattering contrast associated with resonance phenomena is perhaps not fully captured. Instead, we present a simple scattering model that relies on guiding the relative contributions to the scattering intensity from the X-ray absorbance spectra and specifying the atomic positions from the BSA crystal structure. As shown Figure 4B, this approach is consistent with RSoXS data 288.3 eV. Thus, we propose that an opportunity lies in simultaneously reconciling multiple datasets of small-angle scattering curves generated at various incident X-ray energies with proposed protein structures to create robust models for protein conformations.

Radiation damage, or the consequence of radiation damage, is only apparent in RSoXS data at X-ray doses that are multiple orders of magnitude higher compared with hard X-rays. One possible explanation is a difference in local heating; we calculated the temperature elevation for BSA in PBS under both soft and hard X-ray radiation. Using 0.6 W m⁻¹ K⁻¹ as the thermal conductivity of water, 100 μm × 100 μm as the spot size for RSoXS, and 300 μm × 700 μm as the spot size for SAXS, the solution temperature increases 0.3 and 1.2 K for soft and hard X-rays, respectively, as the critical radiation dose for damage is achieved. This suggests that local heating is not the primary cause of radiation damage to BSA in either energy range. Instead, we speculate that ionization is crucial for radiation damage of BSA in both RSoXS and SAXS; the detailed mechanism, however, remains unknown. One possible explanation is that hard X-rays destroy all types of bonds and thereby induce protein denaturation. The denaturation could then result in protein aggregation and a subsequent increase in the scattering intensity at low q, confounding interpretation of the data. On the other hand, RSoXS may selectively damage certain types of bonds and thus localize damage. Alternatively, hard X-rays may induce crosslinking due to their non-discriminate bond damage, while soft X-ray irradiation only leads to chain scission; because larger objects scatter more, aggregation can make data interpretation more difficult than fragmentation. Nonetheless, these findings indicate that there is a larger acceptable dose for RSoXS than SAXS when characterizing proteins in solution.

In summary, we have established by both calculations and experiments that RSoXS can reveal the shape and size BSA in aqueous buffer solutions despite a scattering volume that is smaller than in hard X-ray experiments by multiple orders of magnitude. Furthermore, the effects of radiation damage on biological molecules is less apparent with soft X-rays in comparison with hard X-rays. Altogether, our results indicate that RSoXS is a technique complementary to high-resolution studies that could be transformative for the study of proteins in solution, in particular for material-limited samples or other complex assemblies.

STAR★METHODS

CONTACT FOR REAGENT AND RESOURCE SHARING

Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Esther Gomez (ewg10@psu.edu).

METHOD DETAILS

Solution Preparation

Bovine serum albumin, fraction V (EMD Millipore) was dissolved in 1× phosphate buffered saline (PBS) to make 10 mg/ml solutions. Serial dilutions were made from the 10 mg/ml BSA in 1× PBS stock solution to make a series of concentrations from 0.625 mg/ml to 5 mg/ml. BSA solutions and buffers were filtered with a 0.2 μm cellulose acetate (VWR) or polyethersulfonate (EMD Millipore) filter to remove dust and impurities prior to scattering experiments.

Multi-Angle Dynamic Light Scattering (DLS)

DLS measurements were performed on a Brookhaven Instruments BI-200 SM static/dynamic light scattering system using a 30 mW diode laser (λ = 637 nm). The autocorrelation function was recorded at five different scattering angles (30°, 60°, 90°, 120°, 150°). The mean decay rate (Γ) was calculated using the CONTIN algorithm (Provencher, 1982). The diffusion coefficient for proteins was obtained from a linear fit of Γ versus q². The hydrodynamic radius was calculated using the Stokes-Einstein equation, a viscosity of 0.941 cP, and the diffusion coefficient determined from DLS experiments.

Near Edge X-ray Absorption Fine Structure (NEXAFS) Spectroscopy

BSA films were spin-coated on 50 nm Si₃N₄ windows (Norcada). The thicknesses of BSA films were determined using a Rudolph Research/AutoEL ellipsometer. NEXAFS spectra were collected in a transmission geometry at beamline 6.3.2 of the Advanced Light Source, Lawrence Berkeley National Laboratory (Underwood et al., 1996). NEXAFS spectra were normalized by the empty beam intensity and the transmission of a blank Si₃N₄ window.

Calculation of Atomic Scattering Factors

The imaginary atomic scattering factor f₂ and real atomic scattering factor f₁ (Figure S1) for bovine serum albumin (BSA) were calculated using KKcalc (Als-Nielsen and McMorrow, 2011; Virgili et al., 2007; Watts, 2014). The NEXAFS spectra of a BSA film was used as input data for KKcalc. The imaginary component of the refractive index β for BSA was obtained from the attenuation coefficient (μ) as a function of the X-ray wavelength λ using

$$\mu =\frac{4\pi \beta }{\lambda }$$ (Equation 1)

and μ is obtained from the measured transmission coefficient T

$$T=e^{-\mu t}$$ (Equation 2)

where t is the sample thickness and (1/μ) gives the attenuation length. The sum of the imaginary atomic scattering factors f₂ is given by

$$\beta =\frac{r_e{\lambda }^2}{2\pi }\sum _j{\rho }_j{f}_{2,j}=\frac{r_e{\lambda }^2}{2\pi }{f}_2$$ (Equation 3)

where r_e is the electron radius, ρ_j is the number density of element j in BSA, and f_2;j is the imaginary contribution of the individual elements that constitute BSA. The f₂ spectra near the absorption edge was then scaled and merged to the theoretical f₂ spectra (calculated from the Henke database) away from the absorption edge (10 eV up to 500 keV, except for 270 to 320 eV). f₁ was calculated using the Kramers-Kronig relationship with the entire energy range of the f₂ spectra as indicated by the following equation:

$$f_1=Z^{*}-\frac{2}{\pi }P{\int }_0^{\infty }\frac{x{f}_2(x)}{x^2-E^2}dx$$ (Equation 4)

where Z* is the relative atomic mass and P denotes the Cauchy principal value. Figure S1 shows f₁ and f₂ for BSA derived from Henke database and the NEXAFS spectra is shown in Figure 2A of the main text.

SAXS

Approximately 20 μl of buffer or protein solution was placed in 2.0 mm-thick capillary tubes (Charles Supper). SAXS measurements were performed at room temperature at beamline 7.3.3 of the Advanced Light Source (ALS), Lawrence Berkeley National Laboratory, with an X-ray energy of 10 keV (Hexemer et al., 2010). SAXS data were collected at a 4 m sample to detector distance with a Pilatus 2M detector resulting in a q range from 0.015 to 0.2Å⁻¹.

SAXS data collected at the ALS was azimuthally averaged using the Nika package for Igor Pro (Wavemetrics) (Ilavsky, 2012). Dark counts, beam intensity fluctuations and solid angle corrections were minimal, and thereby ignored. Background scattering was subtracted using the scattering from a buffer solution with a scaling constant between 1 to 1.1 to account for differences in thicknesses of the capillaries.

SAXS experiments on a series of solutions that varied in concentration from 0.625 mg/ml to 10 mg/ml of BSA in 13 PBS were performed on beamline 4–2 at the Stanford Synchrotron Light Source (SSRL) (Martel et al., 2012). The incident X-ray energy was 11 keV and the sample to detector distance was 1.7 m resulting in a q range from 0.01 to 0.4Å⁻¹. For each concentration and buffer, 10 images with 1 second exposure time were taken and images were averaged.

Scattering data collected at SSRL was reduced and analyzed using the beamline software SAStool. Samples were run in the same capillary tube; scattering from buffer was subtracted from BSA solution scattering.

RSoXS

Approximately 4 μL of protein solution was pipetted on a 100 nm thick Si₃N₄ window with a total substrate size of 7.5 mm × 7.5 mm (Norcada). The top Si₃N₄ window, which has a 1 μm spacer and a 5 mm × 5 mm outer frame (Silson), was placed on top of the liquid. The entire sample cell was then sealed with epoxy (Loctite) and stored at room temperature for 24 hours to complete curing. RSoXS measurements were carried out at beamline 11.0.1.2 of the Advanced Light Source, Lawrence Berkeley National Laboratory (Gann et al., 2012). The sample to detector distance was kept at 50 cm and five horizontal detector positions were used to collect data over a q range from 0.01Å⁻¹ to 0.15Å⁻¹ near the carbon K edge (280 eV to 290 eV). Sample transmission was measured using a photodiode detector. Dark images were collected at different exposure times to aid in background subtraction.

RSoXS data were corrected for exposure time, dark counts, incident flux, and solid angle using the Nika package for Igor Pro (Wavemetrics) (Ilavsky, 2012). 1D scattering curves of scattering intensity vs scattering vector were obtained by azimuthally integrating intensities. Background scattering was taken as the scattering from PBS and subtracted. As shown in Figure S4A, the background is dominated by scattering from the windows. As a consequence, variability in the window scattering necessitates the use of a scaling factor for the background scattering prior to subtraction to prevent unphysical results such as negative intensities; values for this scattering factor are shown in Figure S4B.

Predicted Scattering Profiles

CRYSOL was used to generate scattering curves from crystallographic data for BSA (Svergun et al., 1995) that was then compared to experimental RSoXS and SAXS scattering curves, as shown in Figures S6A–S6C. Experimental scattering curves at 285.3 eV and 10 keV showed better fitting to the crystallographic structure, with χ² values of 7.6 for 285.3 eV and 6.1 for 10 keV, in comparison to scattering data collected at 288.3 eV (highest contrast near carbon edge, χ² = 28.9).

Radius of Gyration, Pair Distribution Functions, and 3D Envelopes from Scattering Data

The radius of gyration was determined using AUTORG from the Primus suite (Konarev et al., 2003).

Pairwise distribution functions were obtained from scattering data using GNOM (Svergun, 1992) in the ATSAS suite (Petoukhov et al., 2012). The pair distribution function p(r) for BSA monomers and dimers (PDB: 3V03) was also computed from predicted SAXS profiles that were generated using CRYSOL (Svergun et al., 1995).

3D envelopes of BSA were generated from RSoXS and SAXS data using GASBOR (Svergun et al., 2001). Ten independent GASBOR runs were aligned using SUPCOMB (Kozin and Svergun, 2001) and then averaged using DAMAVER (Volkov and Svergun, 2003) to construct the probability density map. The final envelope was visualized using the molmap command in Chimera software with the molmap threshold set to 0.03 for consistency (Pettersen et al., 2004).

Calculation of Radiation Dose

Radiation damage of BSA in 1× PBS due to X-rays was monitored as a function of radiation dose (D). The radiation dose was calculated from (Hopkins and Thorne, 2016; Jeffries et al., 2015):

$$D=\frac{E\tau f}{\rho t}\left(1-e^{-\mu t}\right)$$ (Equation 5)

where E is the energy per photon (J photon⁻¹), τ is exposure time (s), f is the flux (photons m⁻² s⁻¹) delivered to the sample and corrected for window transmission, ρ is the mass density, t is the sample thickness, and μ is the attenuation coefficient.

QUANTIFICATION AND STATISTICAL ANALYSIS

Statistical details of experiments can be found in the figure and table legends, the results section, and the Method Details section. Data are reported as mean ± standard deviation unless otherwise noted in figure and table legends.

DATA AND SOFTWARE AVAILABILITY

RSoXS, NEXAFS, and dynamic light scattering data are included in the paper. Raw data that support conclusions of this study are available from the corresponding authors upon reasonable request.

KEY RESOURCES TABLE

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Chemicals, Peptides, and Recombinant Proteins
Bovine serum albumin	Millipore Sigma	Cat #126579; CAS 9048-46-8
Phosphate buffered saline	Corning	Product #46–013-CM
Deposited Data
Crystal structure of bovine serum albumin	Majorek et al., 2012	PDB:3V03
Software and klgorithms
Henke Database (atomic scattering factors)	Henke et al., 1993	http://henke.lbl.gov/optical_constants/asf.html
Nika	Ilavsky, 2012	https://usaxs.xray.aps.anl.gov/software/nika
Igor	Wavematrics	https://www.wavemetrics.com/products/igorpro/igorpro.htm
ATSAS	Petoukhov et al., 2012	https://www.embl-hamburg.de/biosaxs/software.html
PRIMUS	Konarev et al., 2003	https://www.embl-hamburg.de/biosaxs/software.html
CRYSOL	Svergun et al., 1995	https://www.embl-hamburg.de/biosaxs/software.html
GNOM	Svergun, 1992	https://www.embl-hamburg.de/biosaxs/software.html
GASBOR	Svergun et al., 2001	https://www.embl-hamburg.de/biosaxs/software.html
SUPCOMB	Kozin and Svergun, 2001	https://www.embl-hamburg.de/biosaxs/software.html
DAMAVER	Volkov and Svergun, 2003	https://www.embl-hamburg.de/biosaxs/software.html
Chimera	Pettersen et al., 2004	https://www.cgl.ucsf.edu/chimera/
KKcalc	Watts, 2014	https://bitbucket.org/benajamin/kkcalc
CONTIN	Provencher, 1982	https://www.brookhaveninstruments.com/analytical-instrument-software
KaleidaGraph 4.5	Synergy Software	http://www.synergy.com/wordpress_650164087/kaleidagraph/

Highlights.

• Soft X-ray scattering provides structural information with chemical specificity

• Scattering in the soft X-ray regime enhances contrast by orders of magnitude

• Reconciling scattering at various energies leads to refined structural models

• Radiation damage is mitigated in the soft X-ray regime