Abstract
At the end of 2019, the SARS-CoV-2 virus caused an outbreak of COVID-19 disease. The spread of this once-in-a-century pathogen increases demand for appropriate medical care, which strains the capacity and resources of hospitals in a critical way. Given the limited time available to prepare for the required demand, health care administrators fear they will not be ready to face patient’s influx. To aid health managers with the Prioritization and Scheduling COVID-19 Patients problem, a tool based on Artificial Intelligence (AI) through the Artificial Neural Networks (ANN) method, and Operations Research (OR) through a Fuzzy Interval Mathematical model was developed. The results indicated that combining both models provides an effective assessment under scarce initial information to select a suitable list of patients for a set of hospitals. The proposed approach allows to achieve a key goal: minimizing death rates under each hospital constraints of available resources. Furthermore, there is a serious concern regarding the resurgence of the COVID-19 virus which could cause a more severe pandemic. Thus, the main outcome of this study is the application of the above-mentioned approaches, especially when combining them, as efficient tools serving health establishments to manage critical resources.
Keywords: OR in medicine, Scheduling, Prioritization and scheduling COVID-19 patients (PSP), Artificial Neural Networks (ANN) method, Fuzzy Interval Mathematical (FIM) model
1. Introduction
In March 2020, COVID-19 was declared as a pandemic disease [1]. Although very limited clinical information is available about the causing virus SARS-CoV-2 [2], the mortality rate of the disease was estimated at 5.7% [3]. In fact, COVID-19 presents higher risks to elderly people and those with underlying diseases such as cardiac dysfunctions and obesity [1], [4]. As a result of the rapid increase of COVID-19 patients influx and hospitals limited capacity, the general principles became closer to those used in wars by venerating quick healings. Since World War I, when the medical services of the French army adopted a protocol to manage injured soldiers, that the triage procedure has been continuously improving its efficiency in sorting, classifying and distributing sick and injured patients to medical staff [5]. In 2020, Italian healthcare workers facing increased numbers of COVID-19 patients have discussed a potential age limit to access to medical care [6]. The medical personnel were actually unable to respond to all requests due to resources constraints, e.g. lack of ventilators needed for the most critical cases.
The typical symptoms of the disease include fever, cough and breathing difficulty. A considerable proportion of the infected patients, estimated to be between 6%–10%, develops pneumonia and requires hospitalization and mechanical ventilation [7]. Since the availability of healthcare resources is critical [8], they should be efficiently rearranged to manage the influx of patients requiring intensive monitoring. To address this problem, there is a growing need for more reliable health services with suitable patient screening techniques.
In fact, the Prioritization and Scheduling Patients (PSP) problem is usually considered as a complex and combinatorial problem [1]. The PSP is conducted to provide health care/services for each patient in due course. Improper patient prioritization can lead to incorrect strategic decisions that can endanger patients’ lives. Furthermore, due to the number of COVID-19 patients worldwide, the healthcare industry needs an urgent solution to avert the risk of deteriorating patients in terms of their prioritization according to their critical health conditions. Indeed, a prioritization process requires synchronized consideration of the inverse relationship amongst the mentioned criteria. Additionally, “regular hospital means” do not allow to integrate the continuous flow of information to enrich/update decision-making and to help sift through enormous amounts of digital data to suggest next steps for treatments, guide providers to available information, or catch potential issues. The PSP process is considered a complex problem of AI and OR, which must comply with national health requirements and known standard routine procedures, highlighting the integration of different processes into a fully automated intelligent computing framework [9], [10], [11].
Both the fields of the AI and the OR are interested in developing approaches to solve difficult combinatorial problems, particularly in health management. Since several factors are a cause of increased risk in patients, as verified from medical practice, it is important to quantify those interactions to allow its integration with other methods. The AI and OR approaches are poised to play an increasingly prominent role in medicine and healthcare because of advances in computing power, learning algorithms, and the availability of large datasets sourced from medical records and wearable health monitors. In [10], Muñoz Lezcano et al. reviewed the most recent research efforts and approaches related to these new data driven techniques and tools in combination with the exploitation of the already available COVID-19 datasets.
AI methodologies include a large amount of information to deal with diverse real problems. Generally, the disadvantage of such representations is the fact that they exhibit intractable problems. Therefore, we are often constrained in using such formalisms in handling realistic size problems. However, actual scheduling problems may be multi-objective by nature. Thus, numerous approaches were developed to manage the multi-objective PSP problems [12]. Generally, OR solutions may be limited to models with restricted expressive power. In contrast, AI implements an understanding of certain outcomes and system’s behavior capable of supporting the decision-making process throughout the assessment of the predefined options, but it does not elaborate the best solutions. Thus, the key challenges to be addressed are the development of comprehensive representations of real COVID-19 problems and to guarantee efficient and rapid solutions. Hospitals may face the prospect of prioritizing patients and allocating scarce resources. Modeling should then serve for deciding on the best strategies to fight such critical situations.
The main objectives of the present study are threefold, namely (i) to apply an AI approach using the Artificial Neural Networks (ANN) method to predict the death or the recovery of patients infected with COVID-19, (ii) to apply an OR approach using the Fuzzy Interval Mathematical (FIM) model to select a suitable list of patients with the highest priority for a set of hospitals, and (iii) to combine the ANN method and the FIM model in order to provide an improved prioritization scheduling approach solving a multi-objective selection problem.
After this introduction, the other parts of paper are planned on the following procedure. In the next section, the literature review is detailed. In Section 3, the Prioritization and Scheduling of COVID-19 Patients (PSCOVP) Problem is described. In Section 4, the AI approach (through the ANN method) and the OR approach (through the FIM model) are introduced. Section 5 highlights the empirical analysis and discusses the results achieved. In the conclusion, final remarks are drawn.
2. Related literature
Literature is paying increasing attention to PSP problems and numerous reviews about patient prioritization and scheduling systems are available [13]. In healthcare systems, the complexity, the size and the funding requirements of the PSP problems are continually increasing [14]. Generally, those problems are considered complex decision-making procedures [15], and have been widely researched via mathematical programming [16], [17], [18]. Most of these studies deal with operational objective functions such as maximizing the use of normal working time and/or minimizing overtime and costs [19], [20]. Regarding optimization models, such procedures use a first-in-first-out (FIFO) criterion. The above-mentioned studies assume that patients with similar priority levels have similar needs and health status evolution. The latter is the most used criterion of assessing performance from patient’s perspective and is often used in prioritizing patients [21], [22].
In this field, the most researched constraints relate with resource availability, such as the available beds and specialists [18]. Min and Yih [23] considered the resources capacity such as the number of beds or the available medical staff, using linear programming. In the study of Sadki et al. [24], the PSP problem was investigated to minimize the total weighted cost caused by patient wait-times according to resource capacities. The PSP problem was studied by Gocgun and Puterman [25] through the available treatment capacity against the received requests to assess future demand. Hahn-Goldberg et al. [26] established a constraint programming-based approach to generate a template for patient’s accommodation. More recently, Rahimi et al. [27] reported the invalidity of a FIFO model through the analysis of waiting-times empirical distribution of different patients. In such strategy, the incorporation of patient prioritization methods in the PSP problem uses mathematical programming. Dogru, and Melouk [28] proposed a simulation approach for appointments optimization according to patients preferences and medical practices planning. Van den Broek [29] applied an integrated approach using linear programming and simulation models to solve the PSP problem. In this latter study, multiple criteria are requested for determining the priorities of patients. Creemers et al. [30] developed an analytical modeling to assess the performance of appointments scheduling. Admission scheduling of patients with different priorities is applicable in many fields [31]. Additionally, it is important to study resource allocation in healthcare management. Limited resources, such as bed shortages, causes patients flow blockage [32]. Therefore, specific literature proposes simulation models for bed management strategies [33]. The traditional techniques to allocate patients beds are First-Come-First-Serve (FCFS) and FIFO. A simulation model for beds allocation was developed by Cardona et al. [34] using the FIFO rule. In fact, hospitals departments do not only assess the scheduling. For instance, emergency services manage patients queue according to resources priorities. The work of Luscombe and Kozan [35] made an exception to this rule as the authors assumed that each emergency patient incoming after triage receipts a specific treatment before taking an additional treatment decision.
Overall, many problems resulting from the COVID-19 pandemic require each one a different model to elaborate the best solution. Concerning resources, the availability of beds and ventilators are the most recognized constraints. According to literature, bed management strategies include several categories such as bed reservation and patient’s prioritization. Several lines of research proposed simulation models for bed management of COVID-19 patients, reduction of patients boarding time and improvement of inpatient flow [36]. Using the FIFO rule, Xuehai et al. [37] elaborated a simulation model for beds allocation to COVID-19 patients waiting in a queue. Along with FCFS and FIFO procedures, it has also been considered the needed medical specialties and availability of ventilator machines in classifying and prioritizing patients for bed assignment. The work of Budi et al. [38] attributed patient’s admission priority by the expected length of stay and the severity level of COVID-19. It reported that a prioritized queue can minimize COVID-19 patients fatality cases, but increases their waiting time. White et al. [39] and Joseph et al. [40] categorized COVID-19 patients based on the resource capacities of the different hospitals studied, such as bed and ventilator resources. Chayu & Jin [41] tested a preference-based decision rule for COVID-19 patients, using simulation modeling. Data scientists aim to provide techniques and tools able to support clinicians with COVID-19 patients decisions, from management to the practice itself. Gupta et al. [9] proposed a prediction model of confirmed and death cases of COVID-19 based on a deep learning algorithm. Saiz and Barandiaran [11] solved a COVID-19 detection problem in chest X-ray images using a deep learning approach.
In addition, recovery or death prediction has also been established in elders who become disabled during hospitalization using multinomial logistic regression [42]. Using logistic regression, Lucas et al. [43] established a prediction of patient’s recovery from severe haemorrhagic shock. Good predictive models were elaborated by Al-Turaiki [44] for MERS-CoV infections via data mining methods.
All the above-mentioned research used conventional modeling techniques to solve PSP problems. However, several unconventional modeling approaches could be applied to establish a prioritization process through reliable predictive modeling procedures such as the ANN and FIM modeling. The main difficulties in a PSCOVP problem are connected to limited resources (e.g. beds), the priority of patient arrivals, the lack of communication between hospital’s units, timely information sharing and diversity of objectives to be optimized. In this work, we present a new approach of combination of ANN and FIM methods that incorporates multiple constraints/factors and objectives.
3. PSCOVP problem and selected data
The PSCOVP problem consists of COVID-19 patients waiting to be scheduled in a single hospital. It studies bed capacity allocation in a multi-hospital setting. Hospital beds are a critical but limited resource shared between distinct classes of COVID-19 patients. Consequently, hospital bed managers are under great pressure to optimally allocate the available bed capacity and the situation of COVID-19 patients. The PSCOVP can be modeled using the following indices, parameters, and decision variables:
| Indices and sets | |
| : Index of each patient; | |
| : Index of each sex; | |
| : Index of each age; | |
| : index of each period of illness; | |
| : Index of each pre-existing condition; | |
| : index of each degree of symptoms; | |
| : index of each hospital | |
| : index of each time | |
| : Set of patients | |
| : Set of patients sex | |
| : Set of patients ages | |
| : Set of patients period of illness | |
| : Set of hospitals | |
| : Set of time | |
| : Set of objectives | |
| Parameters | |
| : Number of beds available in hospital f in instant t | |
| : Survival weight by Sex, Age and Illness of patient n in instant t | |
| : Survival weight by Pre-Existing Condition of patient n in instant t | |
| : Survival weight by Symptoms Degree of patient n in instant t | |
| : Weight of objective o in instant t | |
| Decision variables | |
| : Positive deviation of objective in instant t | |
| : Negative deviation of objective in instant t | |
| : Positive deviation of objective in instant t | |
| : Negative deviation of objective in instant t | |
| : Positive deviation of objective in instant t | |
| : Negative deviation of objective in instant t | |
| : A decision variable; if the patient n with age i, sex j and period k is selected in hospital f in instant t; otherwise and if there is a disturbance in the choice of patients n in instant t. | |
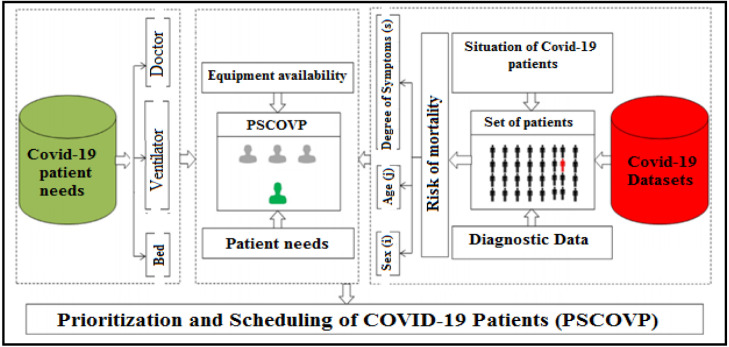
Let n be the number of covid-19 patients requesting an appointment with a hospital. From the medical record data, the patients’ sex i, age j, period of illness k, pre-existing condition p, and degree of symptoms s were verified at the time of admission. Let be the number of beds reserved for COVID-19 patients and equipped with requirements e in each hospital f in instant t. is a binary decision variable, if the patient n with age i, sex j and period of illness k is selected by a hospital f by reserving a bed equipped with requirements e in an instant t; otherwise and if there is a disturbance in the choice of patient n in instant t. The process includes a set of f hospitals receiving COVID-19 patients. Each hospital has a well-defined capacity in instant t. The PSCOVP problem facing hospitals is to define a subset of patients with a defined priority. The sum of the priority levels of selected patients is maximized while not exceeding the number the available beds. The World Health Organization (WHO) reports were an important input to solve the PSP. These data indicate the survival or death rates of several real COVID-19 patients in several countries. The gender , the age , the illness period , the underlying health conditions (pre-existing conditions) , the symptoms degree of each patient, and the outcome (death or survival). The problem can be defined as highlighted in Fig. 1.
Fig. 1.
Prioritization and Scheduling of COVID-19 Patients (PSCOVP) problem.
This paper solves the PSCOVP problem by using a three-step procedure. It first estimates patients’ health situations and their need for ventilators using the ANN method. After that, it proposes a FIM model to achieve the four main goals with respect to the available health resources:
- Objective , Maximize survival rates by Sex, Age and Illness period;
- Objective Maximize survival rates by Pre-Existing health Conditions;
- Objective Maximize survival rates by Symptoms Degree;
For each COVID-19 patient, a priority level (for each parameter , and ) is assigned by the hospital based on his/her level of situation.
In a third step, this paper discusses the use of a combined approach to solve a multi-objective PSCOVP problem based on results from the FIM and the ANN approaches. FIM-ANN approach was required to achieve two main goals, the precision of ventilator machine need via the ANN method and the optimization of their selections by the FIM model, simultaneously.
4. Methodology
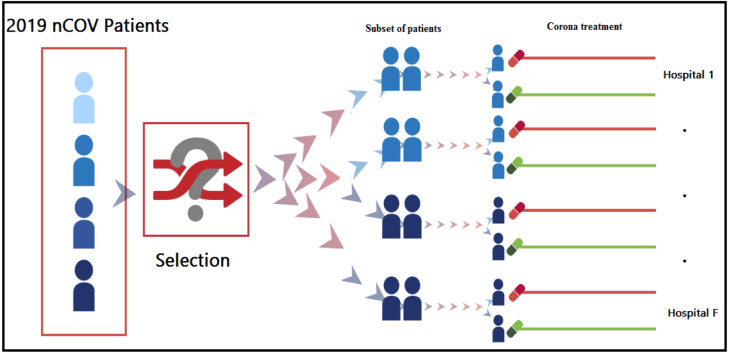
In this paper, the PSCOVP problem was studied to provide decision makers with a reliable tool to select patients (similarly to the principles of wartime triage), to achieve the main goals of lowest death rates and maximum survival rates, under the restrictions of hospitals’ available capacities (Fig. 2).
Fig. 2.
Principles applied to the selection of COVID-19 patients.
The definition of a COVID-19 patients list is a difficult and complex process that requires combining various factors needed to establish a prioritization, e.g. the identification of those needing to be placed on ventilators. The COVID-19 Mortality varies by region and over time depending on the testing volume, healthcare services quality and treatment options, time since the beginning of the outbreak and some parameters characterizing the population such as sex, age and health conditions [45].
Based on the actual conditions of a case study, multiple factors were considered, such as age, gender, medical pre-existing conditions, symptoms degree and the period of illness of the patients using the ANN method. Then, a FIM model was proposed to solve PSCOVP problem under specific constraints, e.g. available beds. To achieve an improved PSCOVP, the ANN process is used to estimate COVID-19 patient’s final health status and their need for ventilation. The FIM model is then used to solve the multi-objective problem under the allocation of the available bed capacity. Therefore, choosing an integrated ANN and FIM approach (ANN–FIM model) to solve a multi-objective PSCOVP problem with estimates of ventilator needs, is of paramount interest. The data used in the following sections was gathered from the Kaggle datasets [46] and Pivot tables (PT) are used to summarize, sort, reorganize, group, count, sum or average data stored in the Kaggle datasets [47].
4.1. Artificial neural network method
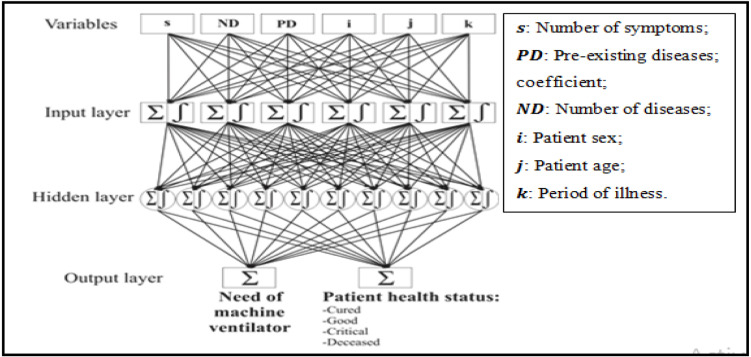
In this study, the back propagation (traingdx) learning rate, which is an efficient training method for the ANN approach [48], and the hyperbolic tangent sigmoid transfer function were used via MATLAB software. “tansig” was the applied activation function and the network training function was gradient descent w/momentum & adaptive lr back propagation. The back propagation algorithm involved three layers: an input layer formed by 6 neurons, a hidden layer covering 10 neurons and two output layers (Fig. 3). Each one of these layers contains one node or more [49]. The hyperbolic tangent function is defined as:
| (1) |
Fig. 3.
Structure of the ANN model.
In ANN modeling, the activation function is important to manipulate complicated situations. Its main role is to convert input signals to outputs. The output signal is used as an ‘input’ to the following layer. The activation function (y) is represented by the following equation where the entries (x ) are multiplied by the weights (w ) and the constant bias (Q ) is added. Thus, the output of the node i is calculated as follows:
| (2) |
A Multilayer perceptron MPL network is formed when connecting the nodes in series and in parallel [49].
Specific diseases present a higher risk condition for COVID-19 patients. Thus, we defined two variables characterizing pre-existing health conditions, the first represents the number of diseases from which the patient suffers (ND) and the second depends on the disease’s nature and fatality rate (PD). In fact, hypertension and cardiovascular diseases represent higher risk conditions for COVID-19 patients [4]. We also adopted the number of symptoms of COVID-19 patients (s) as a sign on the disease severity. Thus, a total of six input variables are considered to train the algorithm (age, gender, illness period, ND, s and PD). This prevents conflicting data from entering the ANN and weakens its understanding of the connection between performance measures [50], [51]. The two outputs incoming from the model are patient health status (survival/good/ critical/deceased) and the need for a ventilator machine.
4.2. Fuzzy interval mathematical model
Due to the fast dissemination of SARS-CoV-2 virus, hospitals may face increasing numbers of infected patients seeking for adequate care. Hospitals may become unable to tend to everybody due to the lack of medical resources. Since hospitals may not be able to provide intensive care to all patients, it may become necessary to establish criteria for the distribution of patients and the adequate allocation of limited resources. The selection of COVID-19 patients and their access to intensive care is a difficult and complex process since it involves several parameters that are hard to interpret. Thus, a model is elaborated to solve the multiplicity of possibly conflicting objectives.
The interval fuzzy model identification is an approach of functions approximation using a finite set of data parameters. Additionally, this method enables the compression of data when a large amount of information is considered. A multi-objective model based on fuzzy interval mathematical model is proposed to select COVID-19 patients for a set of hospitals. This proposed model is developed to accomplish four main goals under the limits of the available resources:
- Objective Maximize survival rates by Sex, Age and Illness period;
- Objective Maximize survival rates by Pre-Existing health Conditions;
- Objective Maximize survival rates by Symptoms Degree;
- Distance objective: Minimize distance between a patient’s home address and the hospital;
Several methods have been developed to solve multi-objective problems. One of the most frequently used Multi-objective techniques is Goal programming (GP), which was developed in the early 1960s and was used for problems with non-homogeneous parameters [52], [53].
In this section, four objective functions (Eqs. (3.1)–(3.4)) and seven constraints (Eqs. (4)–(10)) are used, and described below, to model and solve the considered problem.
Objective functions
| (3.1) |
| (3.2) |
| (3.3) |
| (3.4) |
The first objective is the minimization of unwanted deviations of survival rates by sex, age, and illness period. The second objective is the minimization of unwanted deviations of survival weight by patient’s pre-existing conditions. The third objective is the minimization of unwanted deviations of survival weight by symptoms degree. These deviations are deviation variables of targets under achievement and over achievement for each objective. The objective functions (3.1), (3.2), (3.3) seek to minimize the total weighted overachievement for goals and . The fourth objective is the minimization of the distance between a patient’s home address and the hospital.
Constraints
| (4) |
| (5) |
| (6) |
Constraints (4), (5) and (6) calculate, for a given solution , the respective positive and negative deviations from each goal.
| (7) |
Eq. (7) of the FIM model presents the bed capacity constraint. It ensures that the bed COVID-19 hospital capacity is respected.
| (8) |
Constraint (8) ensures that each COVID-19 patient is considered only once by hospital f in instant t.
| (9) |
Constraint (10) defines the domain of the decision variables.
| (10) |
Constraint (10) enforces non-negativity restrictions on the decision variables.
This model’s allocation objectives guarantee the admission of patients with the highest chance of recovery to intensive care. This section presents the procedure to generate a list of COVID-19 patients for each hospital based on their resource and the percent survival rates of each patient. This work draws from a sample of 1115 international cases from which 837 cases were used for evaluation and 278 cases were used for validation and verification of the fuzzy interval model.
Firstly, the percent death and survival rates were determined by evaluating the first 837 cases, as shown in Table 1, Table 2, Table 3. These tables were prepared using Pivot Tables (PT) functions, for data processing, and the Kaggle database of covid-19 reports. In Table 1, there were five indexes: Sex , Age , Period of illness , Pre-Existing health Condition and Degree of symptoms .
Table 1.
Percent survival rates according to sex, age and period of illness intervals.
|
|
Period of illness intervals (k) ±5% |
|||||
|---|---|---|---|---|---|---|
| Sex (i) | Age Intervals (j) Years | [0, 4] | [4, 8] | [8, 12] | [12, 16] | |
| Female | 0 | 10 | 100 | 97 | 92 | 85 |
| Female | 10 | 20 | 92 | 89 | 84 | 77 |
| Female | 20 | 30 | 87 | 84 | 79 | 72 |
| Female | 30 | 40 | 84 | 81 | 76 | 69 |
| Female | 40 | 50 | 73 | 70 | 65 | 58 |
| Female | 50 | 60 | 66 | 63 | 58 | 51 |
| Female | 60 | 70 | 54 | 51 | 46 | 39 |
| Female | 70 | 80 | 38 | 35 | 30 | 23 |
| Female | 80 | 90 | 29 | 26 | 21 | 14 |
| Male | 0 | 10 | 100 | 97 | 92 | 85 |
| Male | 10 | 20 | 89 | 86 | 81 | 74 |
| Male | 20 | 30 | 83 | 80 | 75 | 68 |
| Male | 30 | 40 | 72 | 69 | 64 | 57 |
| Male | 40 | 50 | 61 | 58 | 53 | 46 |
| Male | 50 | 60 | 50 | 47 | 42 | 35 |
| Male | 60 | 70 | 30 | 27 | 22 | 15 |
| Male | 70 | 80 | 18 | 15 | 10 | 6 |
| Male | 80 | 90 | 11 | 10 | 8 | 3 |
Table 2.
Percent death and survival weights according to the pre-existing conditions.
| Pre-existing condition | Death rate ±5% | Death weight ±5% | Survival weight ±5% |
|---|---|---|---|
| Cardiovascular disease | 10.50% | 28.689% | 14.262% |
| Diabetes | 7.30% | 19.945% | 16.011% |
| Chronic respiratory disease | 6.30% | 17.213% | 16.557% |
| Hypertension | 6.00% | 16.393% | 16.721% |
| Cancer | 5.60% | 15.301% | 16.940% |
| No pre-existing conditions | 0.90% | 2.459% | 19.508% |
| Sum | 36.60% | 100.000% | 100.000% |
Table 3.
Percent death and survival weights according to symptoms degree.
| Degree of symptoms | Death Rate ±5% | Death Weight ±5% | survival Weight ±5% |
|---|---|---|---|
| 5 | 34.00% | 44.024% | 11.195% |
| 4 | 25.00% | 32.371% | 13.526% |
| 3 | 12.00% | 15.538% | 16.892% |
| 2 | 6.00% | 7.769% | 18.446% |
| 1 | 0.17% | 0.220% | 19.956% |
| 0 | 0.06% | 0.078% | 19.984% |
| Sum | 77.23% | 100.000% | 100.000% |
The tables denote a set of interval parameters and variables; superscript means interval-valued feature; the () and () superscripts represent lower and upper bounds of an interval parameter and variables. The proposed model is elaborated to solve PSCOVP problem based on the survival weight, under the limits of available beds. To achieve an optimal PSCOVP, the ANN process was used to estimate COVID-19 patient situation and their need for ventilation, while the Fuzzy Interval mathematical (FIM) model solved multi-objective problems requiring available bed capacity allocation in a multi-hospital setting.
4.3. Combining approach
The ANN–FIM model is herein used to solve a multi-objective PSCOVP problem combining the artificial neural network and the fuzzy interval mathematical modeling. The ANN–FIM model is developed to achieve the two main goals, the survival weight, and the estimates of COVID-19 patient situations and their need for ventilation, under the limits of available beds. The established model enables to achieve the composition of hospital bed equipment necessary for each patient (with or without ventilator machine) via ANN and the optimization of their selections by the FIM model, simultaneously.
| Additional Indices | |
| : index of bed equipment; | |
| E | : Set of bed equipment (e=1,2), if the bed equipment includes a ventilator machine, otherwise; |
| Additional Parameters | |
| : Number of beds available in hospital f with equipment e in instant t | |
| : Estimates patients needing ventilation using ANN method | |
| : Estimates patients health status (recovery or death) using ANN method | |
| New decision variables | |
| : A decision variable; if the patient n with age i, sex j and illness period k is selected in hospital f by reserving a bed equipped with requirements e in instant t; otherwise and if there is a disturbance in the choice of patient n in instant t. | |
Additional Objective function
| (11) |
| (12) |
Using results given by the ANN approach, a relative weight was set for each patient concerning their needs for a ventilator machine and their estimated health status (recovery or death). According to the ANN estimations, is equal to 1 if the patient situation n is estimated as survival, 0 otherwise. is equal to 1 if the patient n is estimated to require the ventilator machine, 0 otherwise. Based on these results, we add two new objectives compared to the previous program:
The objective allows integrating the estimated need for ventilation using the ANN method.
The objective allows integrating the patients estimated health status using the ANN method.
The objective functions (11 and 12) seek to minimize the total weighted overachievement for goals and .
New Constraints
| (13) |
| (14) |
| (15) |
| (16) |
| (17) |
The total deviations were used in assessing the effectiveness of the optimization model solutions. Constraints (13), (14), (15), (16), (17) were formulated as goal constraints to achieve acceptable goal levels. Constraint (13) was considered in the model to evaluate the impact of age, sex, and illness period () on the severity of COVID-19. Constraint (14) guarantees high survival rates by pre-existing health conditions () due to the possible strategies. Constraint (15) was considered in the model to ensure high survival rates by symptoms degree (). Constraint (16) ensures the integration of covid-19 patients needing ventilation (), estimated using the ANN method. Constraint (17) controls the covid-19 patients’ health status (), estimated using the ANN method, to assist diagnosis in clinical decision making. Constraints (13), (14), (15), (16), (17) calculate, for a given solution , the respective positive and negative deviations from each goal.
| (18) |
Constraint (18) ensures that the COVID-19 equipment capacities are respected.
| (19) |
Constraint (19) ensures that each COVID-19 patient is considered only once in hospital f with equipment e in instant t.
| (20) |
Constraint (20) ensures that if the patient n with age i, sex j and illness period k is selected in hospital f by reserving a bed equipped with requirements e in instant t; otherwise, and if there is a disturbance in the choice of patient n in instant t.
| (21) |
Constraint (21) enforces non-negativity restrictions on the decision variables.
5. Results and discussion
Several researchers have used conventional modeling techniques for modeling and optimizing PSP problems. Unlike conventional approaches, the independence of unconventional modeling techniques on statistical assumptions guarantees the reliability of a model’s predictive capacity. However, to the knowledge of the authors, almost no research has paid attention to the combination of conventional/unconventional modeling approaches such as the ANN, the Multi-objective Goal programming (GP) and the Fuzzy Logic (FL) to study patient’s prioritization processes.
Accordingly, this work aimed to develop a combined PSP approach that goes beyond patient efficiency, to also consider a multidimensional priority performance. The performance of each COVID-19 patient was determined by the ANN method to prioritize patients in the Fuzzy Interval Mathematical (FIM) model. This multi-objective model was tested for its ability to improve results. In this context, there are two key goals: minimizing death rates and maximizing survival rates under the constraint of the available resources in each hospital.
5.1. Prediction of COVID-19 patients recovery or death using ANN modeling and the need of machine ventilator
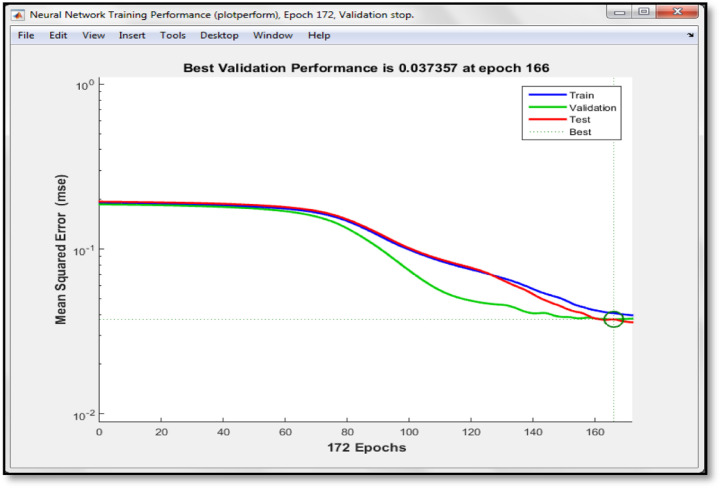
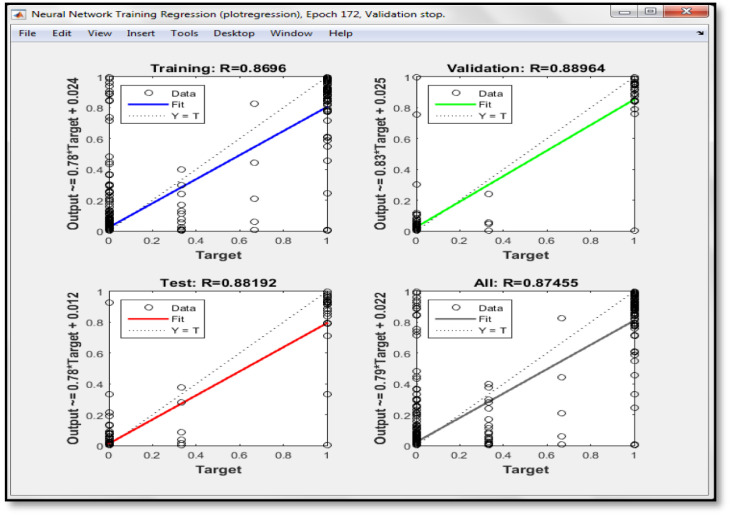
The ANN was used to predict the situation of patients suffering from COVID-19: survival, good situation, critical situation and death (deceased). The need for a ventilator was also predicted. First, the input dataset of the 1115 cases were collected and analyzed. 75% of the data (837 cases) were used for training the model and the remaining 25% (278 cases) were used for the validation and the verification of its prediction efficiency. Input parameters are: age, gender, PD, ND, s and illness period. Fig. 4 illustrates the validation curves. The figure shows the performances achieved throughout the training. It shows that, as the epochs increase, the root mean squared error of the training curve decreases. The best validation performance (0.037) was reached at epoch 172 (Fig. 4).
Fig. 4.
Validation plot of ANN analysis.
Fig. 5 shows the regression plot for the validation, the testing, and the training of the model.
Fig. 5.
Regression plot from ANN analysis.
The correlation coefficient characterizes the strength of the established relationship between the variables. The elaborated model exhibited good correlation coefficients (R2 higher than 0,8) which associates the real and the predicted situations. The latter results prove the efficiency of the model and its accuracy in the prediction of patient health status and its need for a ventilator. The data of the 25% (278 patients) of cases were used to test the ANN-model
Observed and predicted results about the need of a ventilator are shown in Table SD 1. This model allowed to predict the situation for 249 cases among 278 and exhibited a correlation coefficient equal to 0.9. For the second output, the predicted and the real health status are shown in Table SD 2. The elaborated model was able to correctly estimate the health status of 236 cases among 278, and this result exhibited a correlation coefficient equal to 0.85. The results of the validation process generated some disagreements between observed and estimated situations, even though, disagreements were of type ‘good versus survival’ and ‘critical versus death’.
5.2. Selection of COVID-19 patients using the FIM model
The selection of COVID-19 patients for a set of hospitals is a process for screening patient’s data and selecting those with the highest survival rates. Thus, PSCOVP is an evaluating procedure allowing to decide which patients have the priority for medical care and treatment. To achieve this objective, a FIM model was established. The model parameters are extracted from the collected data of the 1115 international COVID-19 patients. 1029 cases were used for evaluating the death and survival rates of each patient (Table 2, Table 3) and the remaining 278 cases were used for the validation and the verification of the proposed FIM model. The 278 patients are from three countries where a set of 150 hospital beds are available to receive COVID-19 patients, from which only 26 are equipped with ventilators. The suitable list of 2019-nCoV patient selections for each hospital was determined by the FIM model and solved with IBM ILOG CPLEX Optimization Software (Table SD 3).
Therefore, this model allows to select COVID-19 patients with priority to be received by hospitals by considering their age, gender, period if illness, pre-existing health conditions, and symptoms along with the fixed objectives. The FIM-model sensitivity analysis was conducted for the different levels of objective weights. The analysis evaluated the influence of objective weights on the proposed model. Results are shown in Table SD 2 and Table 4.
Table 4.
Comparison of FIM results with real observations.
| FIM results | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Mono-objective |
Multi-objective |
|||||||||
| Variable values | Objective only |
Objective only |
Objective only |
|||||||
| [1,1] | 150 | 43 | 88 | 150 | 150 | 150 | 150 | 150 | 150 | 149 |
| [0,1] | 0 | 214 | 124 | 0 | 0 | 0 | 0 | 0 | 0 | 2 |
| [0,0] | 128 | 21 | 66 | 128 | 128 | 128 | 128 | 128 | 128 | 127 |
| Comparison of FIM results with observed results | ||||||||||
| Comparison results | Objective only | Objective only | Objective only | |||||||
| Successful decision | 137 (93%) | 239 (92%) | 181 (85%) | 143 (96%) | 143 (96%) | 143 (96%) | 143 (96%) | 143 (96%) | 143 (96%) | 142 (94%) |
| Unsuccessful decision | 13 (07%) | 18 (08%) | 31 (15%) | 7 (04%) | 7 (04%) | 7 (04%) | 7 (04%) | 7 (04%) | 7 (04%) | 9 (06%) |
| Sum | 150 | 257 | 212 | 150 | 150 | 150 | 150 | 150 | 150 | 151 |
Overall, the proposed model is accurate and practical as it takes into consideration resource limitations in the PSP problem. Our comparisons were about the quality of the “correctness” of the FIM model decision to confirm or refute the observed results from the collected data. Comparing results obtained by the model and the real observed situations of the patients (death or survival), we noticed that:
-
•
In the first case (objective only), the selection decision for each variable is clearly precise so that each variable takes the values or . In addition, their overall success rate is 93%. This option, based only on the age and the sex factors, is not equitable when considered alone and not really taking much information into account.
-
•
In the second case (objective only), there are few disturbances in the choice of certain patients , and their overall success rate achieves 92% accuracy.
-
•
In the third case (objective only), there are major disturbances in the choice of some patients , which has influenced the new precision rate of the selection decision which decreased to 85%.
-
•
In the other case (multi-objectives , and ), the selection decision for each variable is clearly precise so that each variable takes the values or . In addition, their overall success decision rate has reached its peak.
By increasing and decreasing the other weights at the same time, the list of the selected patients tends to the first case (only objective ). Furthermore, when increasing and decreasing and simultaneously, the list of selected patients tends to the second case. Additionally, it can be noted that increasing and decreasing and simultaneously leads the list of selected patients to the third case by objective .
The FIM model alone does not consider the availability of ventilator machines as the available data do not specify the hospital bed equipment. To consider the availability of bed equipment such as ventilator machines, this study proposed to integrate the ANN results into the FIM model to improve the rate of precision of the selection decision.
5.3. Selection of COVID-19 patients using the ANN-FIM approach
In this section, the multi-objective PSCOVP problem was solved with a model combining the ANN and FIM modeling procedures to select COVID-19 patients for a set of hospitals. The new list of COVID-19 patient selections for each hospital was determined by the ANN–FIMmodel, as shown in Table SD 4 and Table 5. The new model elaborated prioritized patient according to their equipment needs. In fact, 25 patients were selected for beds equipped with ventilator machines and 125 patients were selected for beds without ventilators.
Table 5.
Comparison of FIM-ANN results with observed results.
| FIM-ANN Results | |||||||
|---|---|---|---|---|---|---|---|
| Variable values | |||||||
| [1,1] | 150 | 150 | 150 | 150 | 150 | 150 | 150 |
| [0,1] | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| [0,0] | 128 | 128 | 128 | 128 | 128 | 128 | 128 |
| Comparison of FIM results with observed results | |||||||
| Comparison results | |||||||
| Successful decision | 178 (100%) | 178 (100%) | 178 (100%) | 178 (100%) | 178 (100%) | 178 (100%) | 178 (100%) |
| Unsuccessful decision | 0 (00%) | 0 (00%) | 0 (00%) | 0 (00%) | 0 (00%) | 0 (00%) | 0 (00%) |
| Sum | 150 | 150 | 150 | 150 | 150 | 150 | 150 |
When combining FIM and ANN modeling (considering priorities of survival and death situations), the complex disturbance problem in the choice of certain patients is solved and the rate of selection decisions precision is equal to 100% for all cases. In addition, there is an exact correspondence (with a rate of evaluation of results equal to 100%) between the results established by the proposed model and the real data about patient’s situations. Selection decision for each variable is clearly precise so that each variable takes the values or . On the basis of these results and those given by the ANN modeling, we noticed that each critical variable changes its value from to when the ANN method estimates the survival of those cases, but it takes the value 0 otherwise. Therefore, it was shown that the hybridized ANN–FIM model performs better than the FIM model alone in terms of accuracy.
6. Conclusion
The present work presents a novel approach to select an appropriate list of COVID-19 patients to be accepted for medical care within hospitals. From previous studies, a research gap was found since most studies treated the problem of selecting patients from a minimal waiting time point of view, i.e. by using time objectives, without considering the patient’s final situation (death or survival). To overcome this problem, this work presents a model able to solve multi-objective problems with priority objectives. First, the ANN procedure was used to predict the death or recovery of the patients suffering from COVID-19 and their need for ventilators. Second, the FIM model was formulated to determine the list of patients selected for each hospital. The results from the FIM modeling revealed a disturbance in the choice of certain patients. To overcome this issue, this study proposed to integrate the ANN results into the FIM model to improve patient’s selection. Thus, an ANN–FIM multi-objective model was developed, in which the priority weights of the ANN and the FIM model constraints were considered. Finally, an improved solution to the PSCOVP was achieved by including survival/death rates and ventilator machine requirements. The results obtained indicate that combining the ANN method and the FIM model provide an effective analysis, able to cope with the scarce initial information in the selection of a list of COVID-19 patients with distinct priorities to a set of hospitals. The possibility to continuously improve and adapt the ANN–FIM framework is of paramount importance to the healthcare industry, especially in serious health crisis such as pandemics, from the response phase to the recovery phase. In the latter phase, as with the COVID-19 example, it is key to target the uncertainty linked to new variants and/or vaccination procedures.
CRediT authorship contribution statement
Mohamed Ali Elleuch: Methodology, Software, Validation, Writing - original draft, Writing - review & editing. Amal Ben Hassena: Resources, Data curation. Mohamed Abdelhedi: Software, Validation, Writing - review & editing. Francisco Silva Pinto: Conceptualization, Formal analysis, Writing - review & editing.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgements
The authors received no funding for this research and have no further conflicts of interest. Any errors and omissions are the responsibility of the authors. The usual disclaimer applies.
Footnotes
Supplementary material related to this article can be found online at https://doi.org/10.1016/j.asoc.2021.107643.
Appendix A. Supplementary data
The following is the Supplementary material related to this article.
.
References
- 1.WHO . Word-Health-Organization; 2020. Coronavirus Disease 2019 (COVID-19) Situation Report. [Google Scholar]
- 2.Chin A.W.H., Chu J.T.S., Perera M.R.A., Hui K.P.Y., Yen H.-L., Chan M.C.W., et al. Stability of SARS-CoV-2 in different environmental conditions. The Lancet Microbe. 2020 doi: 10.1016/s2666-5247(20)30003-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Baud D., Qi X., Nielsen-Saines K., Musso D., Pomar L., Favre G. Real estimates of mortality following COVID-19 infection. The Lancet Infect. Dis. 2020 doi: 10.1016/S1473-3099(20)30195-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Surveillances V. The epidemiological characteristics of an outbreak of 2019 novel coronavirus diseases (COVID-19)—China, 2020. China CDC Weekly. 2020;2(8):113–122. [PMC free article] [PubMed] [Google Scholar]
- 5.Pollock R.A. Triage and management of the injured in world war I: The diuturnity of Antoine De Page and a Belgian colleague. Craniomaxillofacial Trauma Reconstr. 2008;1(01):063–070. doi: 10.1055/s-0028-1098965. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Yascha M. 2020. The extraordinary decisions facing Italian doctors. https://www.theatlantic.com/ideas/archive/2020/03/who-gets-hospital-bed/607807/ [Google Scholar]
- 7.Luyt C.E., Sahnoun T., Gautier M., et al. Ventilator-associated pneumonia in patients with SARS-CoV-2-associated acute respiratory distress syndrome requiring ECMO: a retrospective cohort study. Ann. Intensive Care. 2020;10:158. doi: 10.1186/s13613-020-00775-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Ferguson Neil, Laydon Daniel, Nedjati-Gilan Gemma. Report 9: Impact of Non-Pharmaceutical Interventions (NPIs) To Reduce COVID-19 Mortality and Healthcare Demand. Imperial College COVID-19 Response Team; 2020. [Google Scholar]
- 9.Gupta Meenu, Jain Rachna, Taneja Soham, Chaudhary Gopal, Khari Manju, Verdú Elena. Real-time measurement of the uncertain epidemiological appearances of COVID-19 infections. Appl. Soft Comput. 2021;101 doi: 10.1016/j.asoc.2020.107039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Muñoz Lezcano S., López Hernández F.C., Corbi Bellot A. Data science techniques for COVID-19 in intensive care units. Int. J. Interact. Multimed. Artif. Intell. 2020;6(Regular Issue):8–17. doi: 10.9781/ijimai.2020.11.008. [DOI] [Google Scholar]
- 11.Saiz F., Barandiaran I. COVID-19 detection in chest X-ray images using a deep learning approach. Int. J. Interact. Multimed. Artif. Intell. 2020;6(Regular Issue):4. doi: 10.9781/ijimai.2020.04.003. [DOI] [Google Scholar]
- 12.Yenisey M.M., Yagmahan B. Multi-objective permutation flow shop scheduling problem: Literature review, classification and current trends. Omega. 2014;45:119–135. [Google Scholar]
- 13.Ben-Daya M. FMS Short term planning problems: a review. Manufact. Res. Technol. 1995;11:3–139. [Google Scholar]
- 14.World-Bank . 2014. Health expenditure. [Google Scholar]
- 15.Guerriero F., Guido R. Operational research in the management of the operating theatre: a survey. Health Care Manag. Sci. 2011;14(1):89–114. doi: 10.1007/s10729-010-9143-6. [DOI] [PubMed] [Google Scholar]
- 16.Geng Na, Xie Xiaolan. Optimizing contracted resource capacity with two advance cancelation modes. European J. Oper. Res. 2012;221(3):501–512. [Google Scholar]
- 17.Truong Van-Anh. Optimal advance scheduling. Manage. Sci. 2015 [Google Scholar]
- 18.Samudra M., Van Riet C., Demeulemeester E., Cardoen B., Vansteenkiste N., Rademakers F.E. Scheduling operating rooms: achievements, challenges and pitfalls. J. Sched. 2016;19(5):493–525. [Google Scholar]
- 19.Marques I., Captivo M.E., Pato M. An integer programming approach to elective surgery scheduling. OR Spectrum. 2012;34(2):407–427. [Google Scholar]
- 20.Cappanera P., Visintin F., Banditori C. Addressing conflicting stakeholders’ priorities in surgical scheduling by goal programming. Flex. Serv. Manuf. J. 2018;30:252–271. [Google Scholar]
- 21.Durán G., Rey P.A., Wolff P. Solving the operating room scheduling problem with prioritized lists of patients. Ann. Oper. Res. 2017;258(2):395–414. [Google Scholar]
- 22.Marques I., Captivo M.E. Different stakeholders’ perspectives for a surgical case assignment problem: Deterministic and robust approaches. European J. Oper. Res. 2017;261(1):260–278. [Google Scholar]
- 23.Min D., Yih Y. Scheduling elective surgery under uncertainty and downstream capacity constraints. European J. Oper. Res. 2010;206(3):642–652. [Google Scholar]
- 24.A. Sadki, X. Xie, F. Chauvin, Appointment scheduling of oncology outpatients, in: Automation Science and Engineering (CASE), 2011 IEEE Conference on, 2011, pp. 513–518.
- 25.Gocgun Y., Puterman M.L. Dynamic scheduling with due dates and time windows: an application to chemotherapy patient appointment booking. Health Care Manag. Sci. 2014;17:60–76. doi: 10.1007/s10729-013-9253-z. [DOI] [PubMed] [Google Scholar]
- 26.Hahn-Goldberg S., Carter M.W., Beck J.C., Trudeau M., Sousa P., Beattie K. Dynamic optimization of chemotherapy outpatient scheduling with uncertainty. Health Care Manag. Sci. 2014;17:379–392. doi: 10.1007/s10729-014-9268-0. [DOI] [PubMed] [Google Scholar]
- 27.Rahimi S.A., Dexter F., Gu X. Prioritizations of individual surgeons’ patients waiting for elective procedures: A systematic review and future directions. Perioper. Care Operat. Room Manag. 2018;10:14–17. [Google Scholar]
- 28.Dogru A.K., Melouk S.H. Adaptive appointment scheduling for patient-centered medical homes. Omega. 2018 [Google Scholar]
- 29.Van den Broek d’Obrenan A., Ridder A., Roubos D., Stougie L. Minimizing bed occupancy variance by scheduling patients under uncertainty. European J. Oper. Res. 2020;286(1):336–349. [Google Scholar]
- 30.Creemers S., Lambrecht M.R., Beliën J., den Broeke M.V. Evaluation of appointment scheduling rules: A multi-performance measurement approach. Omega. 2020 [Google Scholar]
- 31.Izady Navid. 2015. An integrated approach to demand and capacity planning in outpatient clinics. [Google Scholar]
- 32.Marynissen J., Demeulemeester E. Literature review on multi-appointment scheduling problems in hospitals. European J. Oper. Res. 2018;272(2):407–419. [Google Scholar]
- 33.Mathews K.S., Long E.F. A conceptual framework for improving critical care patient flow and bed use. Ann. Am. Thoracic Soc. 2015;12(6):886–894. doi: 10.1513/AnnalsATS.201409-419OC. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Cardona T.A., Guardiola I.G., Cudney E. IIE Annual Conference. Proceedings. Institute of Industrial and Systems Engineers (IISE; 2017. Simulation of va hospital length of stay for analyzing additional inpatient bed capacity; pp. 1320–1325. [Google Scholar]
- 35.Luscombe R., Kozan E. Dynamic resource allocation to improve emergency department efficiency in real time. European J. Oper. Res. 2016;255(2):593–603. [Google Scholar]
- 36.Currie C.S.M., Fowler J.W., Kotiadis K., Monks T., Onggo B.S., Robertson D.A., Tako A.A. How simulation modelling can help reduce the impact of COVID-19. J. Simul. 2020:1–15. doi: 10.1080/17477778.2020.1751570. [DOI] [Google Scholar]
- 37.Xuehai H., Xingyi Y., Shanghang Z., Jinyu Z., Yichen Z., Eric X. Sample-efficient deep learning for COVID-19 diagnosis based on CT scans. IEEE Trans. Med. Imaging. 2020 [Google Scholar]
- 38.Budi Setiawan S. Pengaruh perubahan waktu gilir kerja sebagai dampak covid-19 terhadap kinerja karyawan (studi kasus : pt. nusa halmahera mineral, maluku utara) J. Manajemen Pendidikan Dan Ilmu Sosial. 2020;1(1):234–243. [Google Scholar]
- 39.White D.B., Lo B. A framework for rationing ventilators and critical care beds during the COVID-19 pandemic. JAMA. 2020 doi: 10.1001/jama.2020.5046. [DOI] [PubMed] [Google Scholar]
- 40.Cavallo Joseph J., Donoho Daniel A., Forman Howard P. Hospital capacity and operations in the coronavirus disease 2019 (COVID-19) pandemic—Planning for the nth patient. JAMA Network. 2020 doi: 10.1001/jamahealthforum.2020.0345. [DOI] [PubMed] [Google Scholar]
- 41.Yang Chayu, Wang Jin. A mathematical model for the novel coronavirus epidemic in Wuhan, China. Math. Biosci. Eng. 2020;17(3):2708–2724. doi: 10.3934/mbe.2020148. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Hosoi A., Takizawa T., Konagaya R., Naitoh K. Prognostic medication: prediction by a macroscopic equation model for actual medical histories of illness with various recovery speeds. Artif. Life Robot. 2020:1–10. [Google Scholar]
- 43.Lucas A., Williams A.T., Cabrales P. Prediction of recovery from severe hemorrhagic shock using logistic regression. IEEE J. Transl. Eng. Health Med. 2019;7:1–9. doi: 10.1109/JTEHM.2019.2924011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Al-Turaiki I., Alshahrani M., Almutairi T. Building predictive models for MERS-CoV infections using data mining techniques. J. Infection Public Health. 2016;9(6):744–748. doi: 10.1016/j.jiph.2016.09.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Madjid M., Safavi-Naeini P., Solomon S.D., Vardeny O. Potential effects of coronaviruses on the cardiovascular system: A review. JAMA Cardiol. 2020 doi: 10.1001/jamacardio.2020.1286. [DOI] [PubMed] [Google Scholar]
- 46.Kaggle, 2020. https://www.kaggle.com. (Accessed 29 2020).
- 47.Jelen B., Alexander M. Indianapolis, Que.; 2006. Pivot Table Data Crunching; p. 274. ISBN 0-7897-3435-4. [Google Scholar]
- 48.Abdelhedi M., Jabbar R., Mnif T., Abbes C. Ultrasonic velocity as a tool for geotechnical parameters prediction within carbonate rocks aggregates. Arab. J. Geosci. 2020;13(4):180. [Google Scholar]
- 49.Yılmaz I., Yuksek A.G. An example of artificial neural network (ANN) application for indirect estimation of rock parameters. Rock Mech. Rock Eng. 2008;41(5):781–795. [Google Scholar]
- 50.Misiunas N., Oztekin A., Chen Y., Chandra K. DEANN: A healthcare analytic methodology of data envelopment analysis and artificial neural networks for the prediction of organ recipient functional status. Omega. 2016;58:46–54. [Google Scholar]
- 51.Safarzadeh A., Zaji A.H., Bonakdari H. Comparative assessment of the hybrid genetic algorithm–artificial neural network and genetic programming methods for the prediction of longitudinal velocity field around a single straight groyne. Appl. Soft Comput. 2017;60:213–228. doi: 10.1016/j.asoc.2017.06.048. [DOI] [Google Scholar]
- 52.Benítez-Fernández A., Ruiz F. A meta-goal programming approach to cardinal preferences aggregation in multicriteria problems. Omega. 2019;94 [Google Scholar]
- 53.Kilic H.S., Yalcin A.S. Modified two-phase fuzzy goal programming integrated with IF-TOPSIS for green supplier selection. Appl. Soft Comput. 2020 doi: 10.1016/j.asoc.2020.106371. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
.