Assisted dipeptide bond formation: glycine as a case study

Abstract

Peptide bond formation is a crucial chemical process that dominates most biological mechanisms and is claimed to be a governing factor in the origin of life. Dipeptides made from glycine are studied computationally via Density Functional Theory (DFT) using two different basis sets. This reaction was investigated from both a thermodynamic and kinetic point of view. The effect of explicit assistance via the introduction of discrete solvent molecules was investigated. Water, methanol, and cyclohexane were all employed as solvent media in addition to gas to investigate their effects on the mechanism of peptide bond formation. This computational investigation revealed that methanol is slightly better than water to leverage peptide bond formation both kinetically and thermodynamically, while cyclohexane, a non-polar and non-protic solvent, is the least effective after gas as a medium of solvation. Energetic results in the gas environment are very close to those obtained in polar and protic solvents, suggesting that peptide bonds can be formed under interstellar conditions.

Glycine; The origin of life; Peptide; DFT; Mechanism.

1. Introduction

Peptide bond formation is a vital process that has attracted the attention of the scientific community as it is a key concept in understanding the origin of life and elucidating the process of amino acids polymerization [1]. This exceptional type of chemical bond is required in any biological mechanism that involves amino acid interactions and the formation of biomolecules under prebiotic conditions [2, 3]. Since the beginning of the 20^th century, polypeptides of various types and structures have been synthesized. Although several attempts were carried out to form peptide bonds with high yield, these reactions usually require activated amino-acid precursors and heterogeneous supports [4]. The synthesis of peptides has also been performed in the gas phase such as in the case of ion-molecule reactions containing methionine and glutamic acid [5]. Several computational studies have described the hydrolysis or the condensation phenomena and explained the mechanistic insights behind the reaction [6, 7]. The peptide bond formation in this particular medium is extremely relevant in astrochemistry because it enables the study of prebiotic molecular synthesis in the interstellar medium [8]. Although simple entities such as H2, CO, and HCN were more abundant, biological building blocks such as the simplest amino acids were spotted in interstellar ice together with methanol, ammonia, and hydrogen cyanide [9].

Several studies have demonstrated that peptides can polymerize under certain conditions [10, 11, 12, 13, 14, 15, 16, 17, 18, 19]. The simplest example of peptide bond formation involves two glycine molecules via the condensation reaction as depicted in Eq. (1).

2Gly - > Gly-Gly + Η2Ο (1)

Glycine has the peculiarity of lacking a chiral center and is therefore optically inactive. Its neutral form is generally favored in the gas phase, while its zwitterionic form is favored in solution and the solid-state [20]. Li and coworkers studied the solvent effects on the cyclization of a dipeptide from neutral monomers [21]. Numerous computational studies have been conducted to investigate the formation mechanism of glycine through a radical-radical reaction involving t-HOCO and CH₂NH₂ [22]. Jensen et al. were interested in the uncatalyzed stepwise and concerted routes of peptide bond formation. The authors explained the effect of the entropy and the electronic structures of the transition state (TS) on the energetic barrier heights controlling this reaction [23].

Noncovalent interactions in diglycine and diglycine-water models were investigated computationally by Liu and coworkers. They indicated that the first water molecule binds simultaneously to both oxygen atoms of the carboxylate forming two loose H-bonds [24].

It was revealed by Bhunia et al., that the kinetic preference and the concerted/stepwise mechanism are very sensitive to the level of theory that has been used. For instance, B3LYP/6-31G (d,p) favored the concerted route to form the peptide bond. Whereas, it was the stepwise route that was dominant when the M062X/6-31G (d,p) level of theory was used [25].

Dornshuld et al. highlighted the stabilizing effect of a water molecule on the cis and trans products of the condensation via the H-bonds by 5–9 kcal mol⁻¹ [26]. Therefore, it is clear that solvent interactions have a drastic effect on the condensation process. This has been investigated computationally by implicitly surrounding the glycine within a cavity of continuum defined by macroscopic properties such as the dielectric constant. This approach represents properly nonspecific and long-range interactions. A second approach is available and consists of adding one or more discrete solvent molecules. This method targets generally to spot the catalytic actions and the specific effects of the solvent [27]. The number of explicit solvent molecules required to stabilize glycine is still not clear. For example, Jensen and Gordon used MP2 calculations on structures optimized at the HF level of theory and included diffuse and polarization functions for the basis set. They claimed that at least two water molecules are required to stabilize the glycine zwitterion [28]. Whereas, Ding and Krogh-Jespersen found that one molecule of water is sufficient to stabilize glycine at the same level of theory and by employing a 6-31G basis set with polarization and diffuse functions in some atoms [29]. Tortonda and coworkers studied the stabilization of neutral glycine with an explicit water molecule with MP2 calculation and found that the zwitterionic form cannot be stabilized by a single water entity. The same authors concluded that for this type of system, the discrete and continuum solvent models are complementary to explain water-glycine interactions and found that several explicit water molecules did not affect the mechanism of the concerted zwitterion formation [27]. Zou et al. investigated the microsolvation of the glycine in the presence of different numbers of explicit methanol molecules via DFT calculations. They found that the zwitterionic form can be stabilized by one methanol entity. If two or three methanol molecules are involved, they tend to be located near the carboxylic acid group of the neutral form of glycine. A bridge of methanol forms between the acid and the amino group in the zwitterionic case. Knowing that the amino group is connected to the carboxyl group through a water bridge, it was found that up to nine water molecules are required to explain the microsolvation of the zwitterionic glycine [30]. When five or six methanols are employed, the zwitterionic and the neutral form of glycine tend to be isoenergetic. The authors concluded that up to nine methanols are required to fully solvate a glycine molecule [31]. MP2 and B3LYP were all exploited with different basis sets to study the interaction between glycine and hydrogen peroxide. The authors stated that the stability of the solvent-glycine complex is sensitive to the selected glycine conformation [32].

In this paper, we investigate the thermodynamic and kinetic properties of peptide bond formation for glycine in polar and non-polar solvents that are defined both implicitly and explicitly. The molecules of water, methanol, and cyclohexane studied here, play the role of solvents and also the catalyst for the dipeptide formation when their concentration is low and the probability of collision with the amino acid is less frequent. The results of these mechanisms are compared with those obtained in vacuum.

1.1. Computational methodology

All DFT calculations were performed by Gaussian09, using the B3LYP functional together with the split-valence 6–311++G (2d, 2p) basis set. Additionally, we checked the influence of dispersion interactions by using the D3 version of Grimme's dispersion correction to included non-covalent bond interactions in the calculation of a single point energy at the end of the optimization. All structures were obtained in fully unrestrained geometry optimization and then optimized by considering the solvent effect of different solvents (ε = 78.39, water); (ε = 32.63, methanol) and (ε = 2.02, cyclohexane) using the polarizable continuum model (PCM). Vibrational frequency analysis was used to identify the optimized structure which was either minima or transition state, and intrinsic reaction coordinate (IRC) calculations were carried out to confirm each transition state connected the two minima along the reaction pathway.

Only the concerted pathway leading to the trans isomer was considered in this study because it was demonstrated that this configuration is favored thermodynamically (exothermic by ca. 5 kcal mol⁻¹) and kinetically (barrier height = 32 kcal mol⁻¹ and ca. 8 kcal mol⁻¹ lower than the concerted cis pathway) according to the CCSD(T)-F12/haTZ electronic energies [26]. The stepwise pathways have slightly larger barrier heights (by 4–8 kcal mol⁻¹) and were not considered in this study.

2. Results

2.1. Non-explicitly assisted dipeptide formation

The thermodynamic and kinetic descriptors in the gas and solvent phase were summarized in Tables 1 and 2. The comparison between the reaction enthalpy in gas and Polarized Continuum Model reveals that the formation of the peptide bond is exothermic in all the cases. The reaction was more exothermic in polar solvents such as in water and methanol. This can be quantitatively correlated to the dielectric constant, the dipole moment, and the van der Waals volume of the solvents of interest. For instance, water and methanol have a dipole moment equal to 1.85 kcal mol⁻¹ and 1.7 kcal mol⁻¹, respectively. Conversely, the dipole moment of cyclohexane is nil. The reaction in the implicit solvent and gas was spontaneous. Indeed, ΔG₀ equaled approximately -9 kcal mol⁻¹ in both cases. Kinetically, the energetic barrier was 46.11 kcal mol⁻¹ in the gas phase with the extended basis set and 44.38 kcal mol⁻¹ in water as described in Table 1, which is in agreement with the computational results obtained at CCSD(T)/6–311++G (d,p) level [3]. This leads to the conclusion that these types of media had no significant effect on the rate of the reaction. The utilization of the extended (6–311++G (2d, 2p)) basis set with B3LYP level of the theory gave similar results for all the thermodynamic descriptors. The energy correction brought by the dispersion effects added to the B3LYP method slightly reduced the kinetic and thermodynamic descriptors. Indeed, the energetic difference did not exceed 2 kcal mol⁻¹.

Table 1.

Thermodynamic and kinetic descriptors in the explicitly non-assisted diglycine formation in gas using B3LYP/6–311++G (2d,2p) in (kcal mol⁻¹): (A) without dispersion effects, (B) D3 version of Grimme dispersion with the original D3 damping function included.

method	ΔH₀	ΔG₀	Ea	ΔG#
A	-7.48	-7.86	27.70	46.11
B	-	-5.91	-	44.88

Table 2.

Thermodynamic and kinetic descriptors in the explicitly non-assisted diglycine formation with PCM in water, MeOH, and cyclohexane using B3LYP/6–311++G (2d,2p) in (kcal mol⁻¹): (A) without dispersion effects, (B) D3 version of Grimme dispersion with the original D3 damping function included.

Non assisted media	Method	ΔH₀	ΔG₀	Ea	ΔG#
in PCM (water)	A	-10.04	-7.6	29.4	44.38
	B		-10.2		34.58
in PCM (MeOH)	A	-10.02	-8.79	29	43.34
	B		-9.95		38.12
in PCM (C6H6)	A	-7.87	-7.46	26.55	46.4
	B		-7.63		42.88

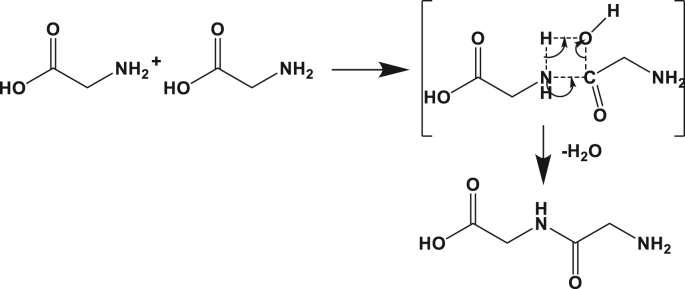
The IRC approach to determine the path of the chemical reaction between two glycines suggested the formation of a 4 membered atomic ring in the transition state. The suggested mechanism is illustrated in Figure 1 and Figure 2. It starts with the positioning of the carboxylic functional group in proximity to its amine homolog. In a concerted way, a bridge is formed between the two molecules through the carbon atoms of the carboxylic acid and the nitrogen of the amine group. Simultaneously, the hydroxyl group linked to the carbon is liberated in the form of water after withdrawing the mobile hydrogen atom that was connected to the nitrogen of the amine function.

Figure 1.

Schematic of the reaction mechanism for peptide bond formation between two amino acids in the gas phase.

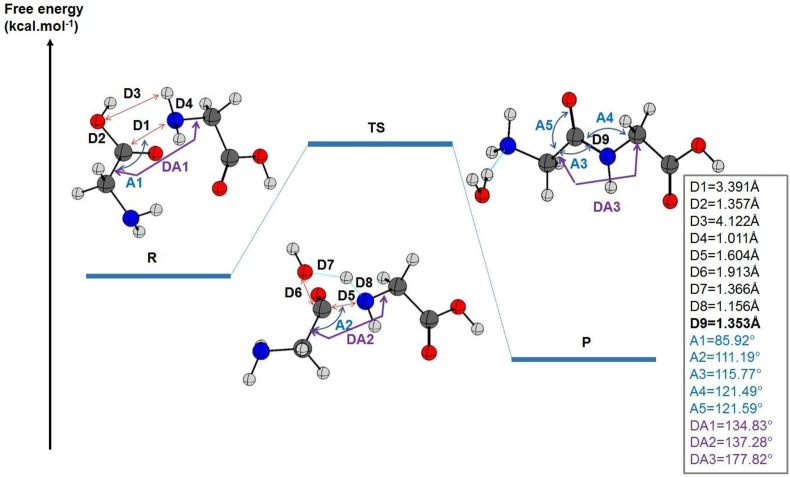
Figure 2.

The relative energies of the reactant R, product P, and the transition state TS for the peptide bond formation between two glycine molecules are given in kcal mol⁻¹ and calculated at the B3LYP/6–311++G (2d, 2p) level of theory including dispersion effects. The most relevant distances, angles, and dihedral angles in the gas state were listed on the right side. The length of the peptide bond is included (in bold).

The comparison of the structures of reactants, products, and transition states revealed that the distance between the closest nitrogen of the first glycine and the carbon of the neighboring molecule decreased from D1 = 3.391 Å to D5 = 1.604 Å during the TS. This distance was stabilized to D9 = 1.353 Å when the product was formed. By the same scenario, the dihedral angle between the C–N bond of the first glycine and the C–C bond of the second glycine increased progressively from DA1 = 114.83° at the starting point to DA2 = 137.28° in the TS structure and finally to DA3 = 177.82° in the product. It is noteworthy that during the transition state, the distance between the nitrogen approaching from the other glycine started to lose the link with its hydrogen. Therefore, the distance of the N–H was D4 = 1.011 Å in the reactant then increased to D8 = 1.156 Å.

Similarly, in the other glycine, the C–O moiety involved in peptide bond formation was dissociated progressively from its corresponding molecule and migrates to form a water molecule with the hydrogen dissociated from the nitrogen of the neighbouring molecule in the case of the gas phase. Thus, D2 increased from 1.357 Å in the reactant to D6 = 1.913 Å in the transition state.

2.2. Explicitly assisted dipeptide formation

2.2.1. Water assistance

When a water molecule was introduced explicitly to leverage the formation of the peptide bond, one could follow the migration of atoms between the two glycine molecules and the electronic exchange through the water molecule. The five distances that were used to monitor this mechanism are summarized in the table that joins Figure 3. D2 to D6 and D8 to D12 showed the distances between the six atoms that were involved in the reaction at the starting point and at the TS, respectively. The peptide bond was slightly longer at the TS with water assistance comparing to gas medium reaction.

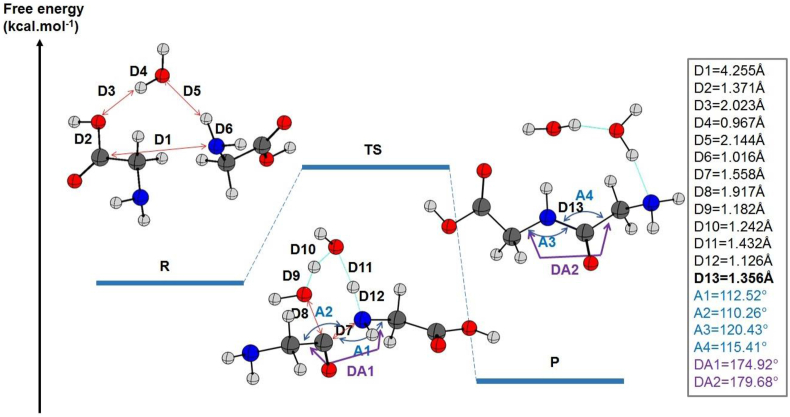
Figure 3.

The relative energies of the reactants, products, and their transition state (TS) state for the peptide bond formation between two glycine molecules are given in kcal mol⁻¹ and calculated at the B3LYP/6–31 (p,d), and B3LYP/6–311++G (2d, 2p) level of theory including dispersion effects. The most relevant distances, angles, and dihedral angles in the gas state were listed on the right side. The length of the peptide bond is included (in bold).

Peptide bond formation is exothermic in water (-12.83 kcal mol⁻¹) and the water molecule expressed explicitly with the glycines. This reaction is spontaneous for the peptide under the same conditions. Therefore, ΔG₀ is equal to -8.01 kcal mol⁻¹ and -7.6 kcal mol⁻¹ in explicit and implicit water at the extended basis set. When the water molecule was defined explicitly, the energetic barrier was 3.1 kcal mol⁻¹ lower than its homologue in PCM (ΔG^# equals 41.28 kcal mol⁻¹ in the explicitly assisted reaction as shown in Table 3 against 44.38 kcal mol⁻¹ using the PCM model described in Table 2).

Table 3.

Thermodynamic and kinetic descriptors in the explicitly assisted diglycine formation with water molecule using B3LYP/6–311++G (2d,2p) in (kcal mol⁻¹): (A) without dispersion effects, (B) D3 version of Grimme dispersion with the original D3 damping function included.

Method	ΔH₀	ΔG₀	Ea	ΔG#
A	-12.83	-8.01	15.68	41.28
B		-15.96		32.19

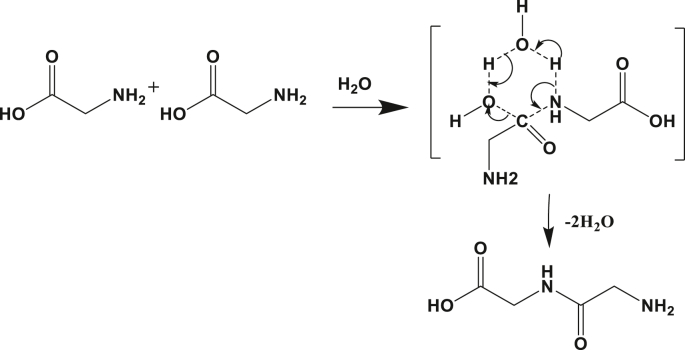
The mechanism of the reaction involves a transition state with the six-atom ring as described in Figure 4. The nitrogen atoms of the amine group approach from the carbon of the carboxylic acid and form a bond that links the two glycine molecules. The water molecule facilitates the exchange of the mobile proton of the nitrogen. Indeed, the assistant molecule pulls the hydrogen of the amine and releases its own hydrogen to the oxygen of the hydroxyl group of the carboxylic acid. It then becomes easy for the second water molecule to be released and the diglycine molecule is formed.

Figure 4.

Schematic of the reaction mechanism for explicitly assisted peptide bond formation by water molecules between two amino acids.

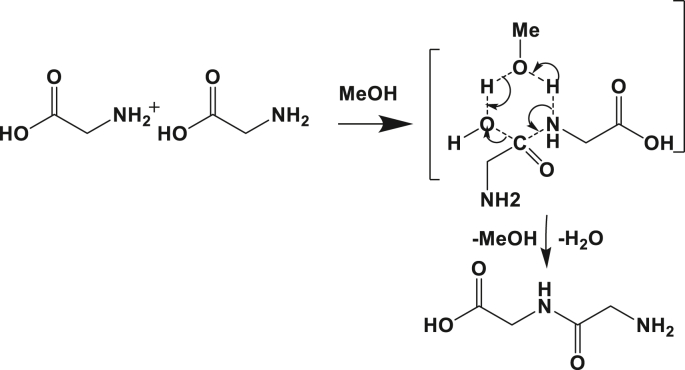
2.2.2. Methanol assistance

The explicit assistance of the diglycine formation with a methanol molecule decreased the heat of the reaction from ΔH₀ equal -12.63 kcal mol⁻¹ to -10.02 kcal mol⁻¹ in gas phase. The reaction in the presence of methanol became more spontaneous to produce the dipeptide (ΔG₀ = -9.02 kcal mol⁻¹). Kinetically, the energetic barrier of activation decreased by 2 kcal mol⁻¹ compared to its PCM homolog in the gas medium.

The mechanism of the peptide bond formation between the glycine molecules and assisted with a methanol molecule was very similar to the one proposed for the reaction in explicit water. Its corresponding transition state is also based on a 6-atom ring as depicted in Figure 5. The methanol molecule exchanges hydrogen between the amine and the carboxylic acid groups. It is clear that methanol plays the role of a catalyst because it participates in the mechanism, but it was not consumed at the end of the reaction. From the energetic barrier calculated at the same level of theory, the incorporation of a methanol molecule reduced this barrier by ca. 2 kcal mol⁻¹.

Figure 5.

Schematic of the reaction mechanism for explicitly assisted peptide bond formation by methanol molecule between two amino acids.

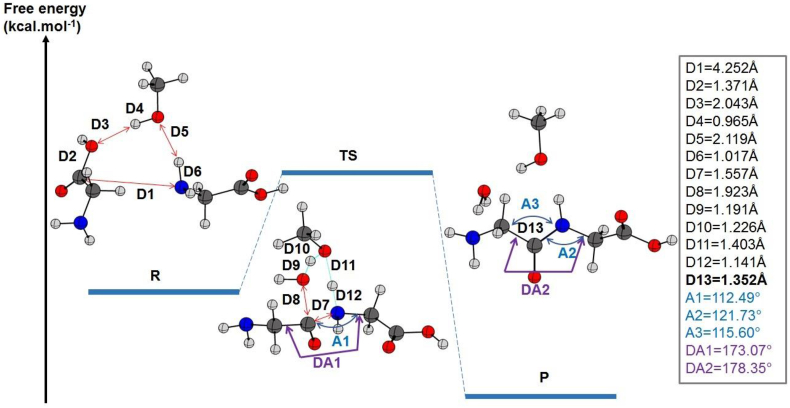
The inclusion of the dispersion effects, in this case, reduced the free energy of activation ΔG^# by 9.45 kcal mol⁻¹ as shown in Table 4. Similar to water, the explicit assistance with a methanol molecule led to a transition state with the same distance between the nitrogen and the carbon involved in the peptide bond formation. The variation of distances in the 6-membered ring is illustrated in Figure 6.

Table 4.

Thermodynamic and kinetic descriptors in the explicitly assisted diglycine formation with MeOH molecule using B3LYP/6–311++G (2d,2p) in (kcal mol-1): (A) without dispersion effects, (B) D3 version of Grimme dispersion with the original D3 damping function included.

Method	ΔH₀	ΔG₀	Ea	ΔG#
A	-12.63	-9.02	14.97	41.37
B		-14.92		31.92

Figure 6.

The relative energies of the reactants, products, and their transition state (TS) state for the peptide bond formation between two glycine molecules are given in kcal mol⁻¹ and calculated at the B3LYP/6–311++G (2d, 2p) level of theory including dispersion effects. The most relevant distances, angles, and dihedral angles in the gas state were listed on the right side. The length of the peptide bond is included (in bold).

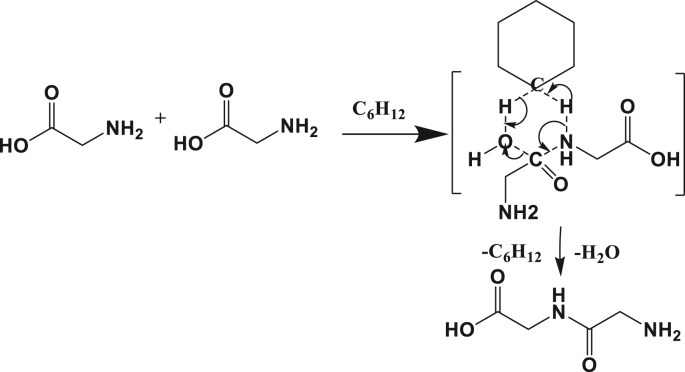
2.2.3. Cyclohexane assistance

Although cyclohexane is already known for not showing a proton exchange with glycine, the reaction model was described here to show the behavior of a non-polar, aprotic molecule as an assistant for dimerization. The diglycine formation in explicit cyclohexane is exothermic with ΔH₀ equal to -6.22 kcal mol⁻¹, which is just 1 kcal mol⁻¹ higher than the values calculated in PCM or the gas conditions. In terms of free enthalpy of the reaction, the assistance with cyclohexane still allowed spontaneous peptide formation but it is close to zero (ΔG₀ -2.97 kcal mol⁻¹). This thermodynamic descriptor is equal to -7.46 kcal mol⁻¹ and -7.86 kcal mol⁻¹ in PCM (cyclohexane) and gas, respectively. This reveals a more considerable difference when the cyclohexane was expressed explicitly.

Although the Gibbs free energy of the reaction stated that the dipeptide formation is spontaneous in the presence of the explicit cyclohexane molecule (ΔG₀ = -2.97 kcal mol⁻¹ as depicted in Table 5), this reaction seems to be kinetically not feasible as the free enthalpy of activation was 85 kcal mol⁻¹ with both basis sets. This can be explained by the inherent stability of the bond in the non-polar cyclohexane and the difficulty to exchange hydrogen atoms with other molecules. The transition state illustrated between brackets in Figure 7 shows the same 6-atom ring that involves the mobile protons of the amine and the carboxylic acid and the proton belonging to the cyclohexane.

Table 5.

Thermodynamic and kinetic descriptors in the explicitly assisted diglycine formation with cyclohexane molecule using B3LYP/6–311++G (2d,2p) in (kcal mol⁻¹): (A) without dispersion effects, (B) D3 version of Grimme dispersion with the original D3 damping function included.

Method	ΔH₀	ΔG₀	Ea	ΔG#
A	-6.22	-2.97	44.20	85.68
B	-	-4.91	-	71.86

Figure 7.

Schematic of the reaction mechanism for explicitly assisted peptide bond formation by cyclohexane molecule between two amino acids.

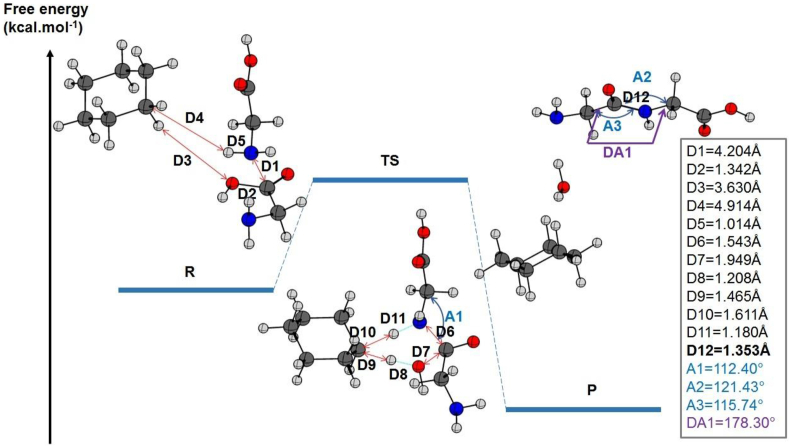
When dipeptide bond formation was assisted by an explicit cyclohexane molecule, the hydrogen covalently bonded to the cyclohexane was involved in the six-membered ring of the TS. Thus, the distances between the two closest hydrogens of cyclohexane to the glycine were D3 = 3.630 Å and D4 = 4.914 Å. During the transition state, these distances were reduced to D9 = 1.465 Å and D10 = 1.611 Å as illustrated in Figure 8. During the same transition phase, the C–O and N–H bond belonging to the transitioning ring was stretched.

Figure 8.

The relative energies of the reactants, products, and their transition state (TS) state for peptide bond formation between two glycine molecules are given in kcal mol⁻¹ and calculated at the B3LYP/6–311++G (2d, 2p) level of theory including dispersion effects. The most relevant distances, angles, and dihedral angles in the gas state were listed on the right side. The length of the peptide bond is included (in bold).

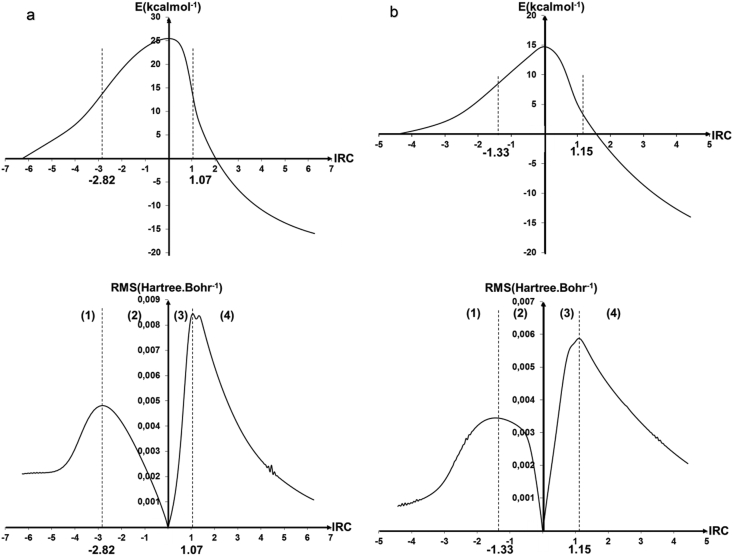
The reaction profiles shown in Figure 9 differentiate between the formation of the dipeptide by the explicit assistance of water or by the implicit solvation with the PCM model. The geometries of the solvated and the explicitly assisted transition states were examined in detail to explain the difference in their corresponding activation-free enthalpies. The energy profile as a function of the intrinsic coordinates of the reaction fits the Universal profile of a single step reaction.

Figure 9.

Energetic profiles and their corresponding first derivatives for the dipeptide bond formation: (a) implicitly assisted by water, (b) explicitly assisted by water. Dashed vertical lines represent the limiting IRC coordinates that describe the transition states. Regions 1 and 4 represent the reagent and the product states while regions 2 and 3 describe the activated molecule just before and after the transition states.

To discuss the reaction profiles, two conditions should be considered: first, it is necessary that the structures of the two IRC path boundaries correspond to the reagents and the products. Two, the energy gradient should exhibit four sequences described by extrema which are: (1) the reactants get closer from each other, (2) the formation of the transition state, (3) preparation of the product structures, and (4) the formation of the final compound. Figure 9 illustrates the IRC and its gradient showing the separation of the four sequences for each transition state which corresponds to the formation of the dipeptide by the explicit assistance of water or by the implicit solvation with the PCM model.

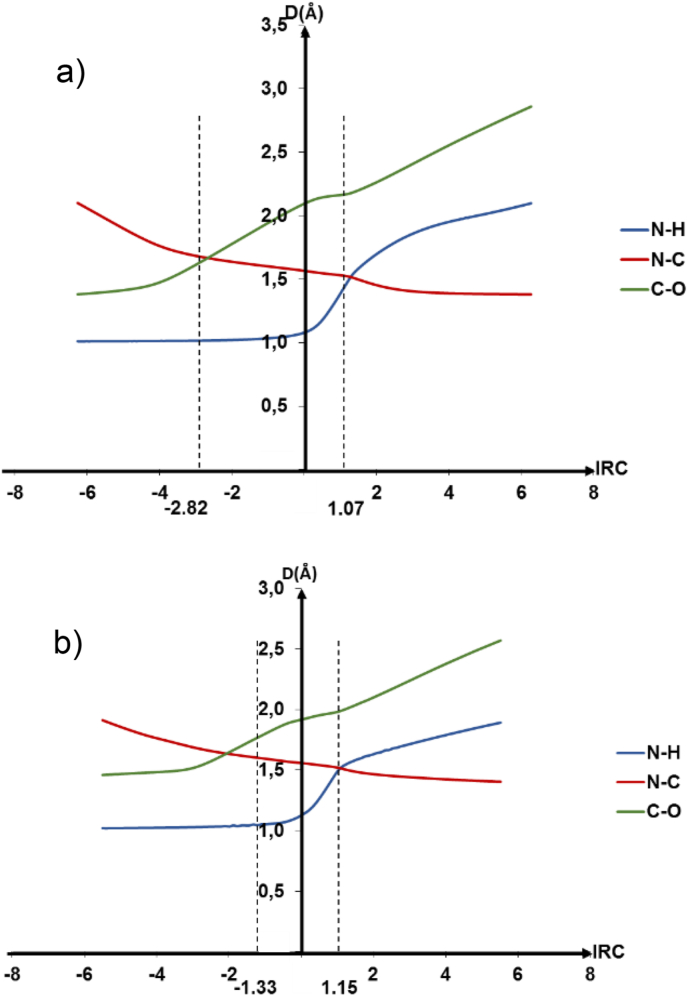
As illustrated in Figure 10, the C–O bond length increases from zone (2) to zone (4). While the N–H bond is stretched in zones (3) and (4). The variation of these two bonds occurs asynchronously. Besides, the bond N–C is formed in a monotonous way before and after the transition state. Nevertheless, some differences in the involved interatomic distances were observed. Therefore, the distance between the closest nitrogen to the first glycine and the carbon of the neighboring molecule as well as the C–O distance of the second glycine were larger in the transition state's geometry in the implicit solvation assistance. Contrarily, the N–H distance of the first glycine was shorter.

Figure 10.

Evaluation of the interatomic distances during the peptide bond formation: a) implicitly assisted by a water molecule, b) explicitly assisted by water molecule. Dashed vertical lines represent the limiting IRC coordinates that describe the transition states.

The imaginary frequency associated with TS_solvated (i.e. 475i cm⁻¹) is lower than that associated with TS_assisted (i.e. 966i cm⁻¹). This is an additional element consistent with a higher activation barrier in the solvated TS case since the transition state zones 2 and 3 of the influence of the formation of a solvated dipeptide bond and assisted by water were, respectively, equal to 3.89 and 2.48 au.

3. Discussion

Understanding the oligomerization mechanism of amino acids leading to the formation of peptides and proteins is a key step to uncover the origin of life. The instability of amino acids and the difficulty of their polymerization in an aqueous solution present a major problem. Kekegawa and coworkers found that high pressure and NH₃-rich environments stabilized glycine and alanine [33]. Besides, glycine was discovered in samples of comet Wild 2 returned by NASA's Stardust spacecraft, which strengthens the argument that life in the universe may be common rather than rare [34]. Electronic structure calculations based on the Density Functional Theory (DFT) were initially exploited to study the interaction between glycine and forsterite which is a well-known cometary dust component. The chemisorption energy ranged from 58 to 96 kcal/mol [35]. This range of energy is higher than what we found for the activation of the glycine condensation. On the one hand, this can be an indication that the chemical interaction with polar or non-polar surfaces especially in comets can be the limiting factor to trigger the condensation. On the other hand, the rigid surface of forsterite can play the role of the heterogeneous catalyst by promoting the interactions between the carboxylic acid and the amine groups.

Although it was stated that the standard Gibbs energies of the condensation reactions of the amino acid are uphill and the incorporation of geochemically produced condensing agents such as carbonyl sulfide, cyanamide, and polyphosphates was recommended to invert the unfavorable condensation Gibbs energies [36], we showed here that in the case of pure glycine the oligomerization is thermodynamically feasible and solvation reduces the activation energy required to ease the peptide bond formation. Kaiser et al. claimed that the radiation-induced, non-enzymatic formation of proteinogenic dipeptides in interstellar ice analogs is facile. This is a supplementary factor that is added to endorse the hypothesis of the diglycine formation in the catalyst-free environment [37].

A mineral catalyst such as hydroxyapatite also presented an alternative to harsh conditions of high temperature and pressure to promote peptide bond formation. Similar to protic solvents exploited in this work (i.e. water and methanol added explicitly in the neighborhood of glycine), the hydroxyapatite reduced the activation barrier for the formation of dipeptides by more than 50%. The presence of this mineral compound or similar catalyst decreased the distance between amino and carboxyl groups on neighboring molecules and extends the contact time of the reaction group [38].

Rimola et al. investigated computationally the pathways from the interstellar amino acids to prebiotic catalytic peptides [39]. For instance, the free enthalpy of condensation to form the dipeptide alanyl-glycine in H₂O was 4.13 kcal/mol at 37 ⁰C and pH 7. Comparing this Gibbs energy with the negative ones that we obtained for the glycine-glycine dipeptide condensation highlights the importance of the nature of amino acids that can undergo the exergonic condensation spontaneously. In our case, all the free energies obtained in the gas phase and the presence of explicit assisting molecules proved the exergonic character of the condensation and only the kinetic factor that is differentiating between the glycine environments. Therefore, the peptide bond formation in diglycine is mainly driven by the kinetic factors that can be overcome by the introduction of a homogeneous (i.e. by the utilization of autocatalysis) or a heterogeneous (i.e. In the case of physisorption and chemisorption with hydroxyapatite) catalyst. With the introduction of dispersion in the calculation of potential energy, the activation free enthalpy was reduced by at least 5 kcal mol⁻¹ which leads to closer values to the literature.

It is noteworthy that the activation energy of our water-assisted reaction is almost the same as in the case of the condensation of glycine and serine. Nevertheless, the mechanism is quite different as the proton of the hydroxyl group on the side chain of serine plays the role of the catalyst by protonating the amine of the glycine [40]. The catalysis of glycine condensation is not limited to protic solvents but it has been expanded by solid-phase catalysts such as sanidine feldspar surface [41] or with permanganate where the activation energy still 2 kcal/mol higher than our currently obtained result with water [42].

Oligopeptides are minimalistic forms of enzymes and present a huge unexplored pool of small molecules in organic synthesis and prebiotic chemistry scenarios. Therefore, diglycine is not limited to investigate the origins of biosynthesis in interstellar environments but also to study its potential as a therapeutic agent in drug development [43]. The formation of glycine dimers shows low activation energy compared to other amino acid dimers. This can be principally explained by its spherical structure that limits the access of water molecules to its hydration shell. For instance, histidine possesses an imidazole ring and nitrogen on its side chain that can form hydrogen bonds with water molecules and affect the activation energy of its condensation [44]. Quantum-based molecular dynamics simulations of the condensation of glycine rendered a similar activation barrier (i.e. 2 kcal/mol lower than our calculated result with water assistance). This confirms the robustness and the accuracy of our simplified model to study the kinetics of this peptide bond formation [45].

4. Conclusions

Peptide bond formation in a glycine-glycine system was investigated and the effects of explicit assistant molecules were studied. The solvents were introduced implicitly via the Polarized Continuum Model approach to include long-distance interactions. The introduction of discrete molecules near the glycine residues focuses more on steric and short–distance non-covalent interactions. Four types of media were studied in this paper: the vacuum that imitates interstellar conditions, water and methanol as polar and protic solvents to show hydrogen bonding effects on the stabilization of the dipeptide system, and finally cyclohexane as a non-polar and aprotic solvent. The comparison of the energetic barrier of activation showed that methanol and water had a stabilizing effect on the transition state of the reaction and the mobile proton of these protic molecules facilitates the synthesis of the peptide kinetically. The study of the free energy of the reaction also demonstrated that peptide bond formation was spontaneous in all of the studied cases. Cyclohexane was always the weakest assistant for promoting the reaction, demonstrating the importance of the mobile proton to leverage electronic exchange between the glycine molecules and the assisting molecule. The introduction of assisting effects have a crucial impact on the energetic descriptors of this reaction, thus this ought to be taken into consideration in order to account for both short-range interactions, such as hydrogen bonding and van der Waals interactions, and long-distance interactions, such as polarisability of the assisting molecule.

Declarations

Author contribution statement

Sofiene Achour: Conceived and designed the experiments, Performed the experiments.

Zied Hosni: Conceived and designed the experiments, Analyzed and interpreted the data, Wrote the paper.

Sarra Darghouthi: Analyzed and interpreted the data.

Christopher Syme: Contributed reagents, materials, analysis tools or data, Wrote the paper.

Funding statement

This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.

Data availability statement

Data will be made available on request.

Declaration of interests statement

The authors declare no conflict of interest.

Additional information

No additional information is available for this paper.