Design and simulation of mechanical ventilators

Abstract

During this period of COVID-19 pandemic, the lack of medical equipment (like ventilators) leads to complications arising in the medical field. A low-cost ventilator seems to be an alternative substitute to fill the lacking. This paper presents a numerical analysis for predicting the delivered parameters of a low-cost mechanical ventilator. Based on several manufactured mechanical ventilators, two proposed designs are investigated in this study. Fluid-structure interaction (FSI) analysis is used for solving any problems with the first design, and computational fluid dynamic (CFD) analysis with moving boundary is used for solving any issues with the second design. For this purpose, ANSYS Workbench platform is used to solve the set of equations. The results showed that the Ambu-bag-based mechanical ventilator exhibited difficulties in controlling ventilation variables, which certainly will cause serious health problems such as barotrauma. The mechanical ventilator based on piston-cylinder is more satisfactory with regards to delivered parameters to the patient. The ways to obtain pressure control mode (PCM) and volume control mode (VCM) are identified. Finally, the ventilator output is highly affected by inlet flow, length of the cylinder, and piston diameter.

Nomenclature

Δt

Time Step, s

Lc

Compressed length (m)

O2 Flow

Flow rate of Oxygen (L/min)

Volume

Delivered volume (L)

VT

Tidal Volume (L)

Upx

Piston displacement (m)

UAZ

Vertical displacement of Ambu-bag (m)

Prel

Relative pressure (Pa)

ρ

Density (kg/m³)

µ

Dynamic viscosity (kg/m.s)

P

Pressure (Pa)

PCM

Pressure control mode

VCM

Volume control mode

FSI

Fluid structure interaction

CFD

Computational fluid dynamic

PEEP

Positive end expiratory pressure

1. Introduction

COVID-19 outbreak has become a global issue as this new pandemic has strongly affected the world [1], [2]. This virus causes a substantial global health problem with very significant economic and social impacts [3], [4], [5], [6]. Studies have shown that most people affected by COVID-19 have mild symptoms, but other people, like adults over 65 and those with chronic illnesses, develop severe symptoms in the pulmonary system. This is reflected by the fact that the potentiality of these groups of people to exchange carbon dioxide and oxygen between blood and lungs begins to fall once they are attacked by the virus [7]. At this stage, patients are hospitalized to support their lung functions with mechanical ventilation, as it is the best medical treatment currently recommended by doctors. It has been reported that the early use of endotracheal intubation (invasive intubation) can cause secondary lung infection because of the risk of germs entering through the tube, which carries air and oxygen to the patient [7]. So, non-invasive ventilation could be an excellent choice to avoid the multiplication of lung damage induced by mechanical ventilation [8].

Faced with the large influx of patients, hospitals do not have enough respirators to meet their needs. The medical equipment industry offers various highly sophisticated devices in the market, but that available number still cannot meet the demand of hospitals. Thus, several enthusiastic research teams have used their competence to develop a simple design and low-cost respirators manufactured in a large number within a short period [8]. Among many low-cost ventilators, a published MIT student project using Ambu-bag, which is available freely online, is referred [9]. However, a respirator is not just a pump that forces air and oxygen into the patient's lung. One of the critical problems encountered by doctors during mechanical ventilation is Barotrauma [10], [11], [12]. Indeed, when there is difficulty adapting between the pressure delivered by the ventilator and that inside the lungs, an alveolar overdistention can occur, further causing barotrauma [13, 14].

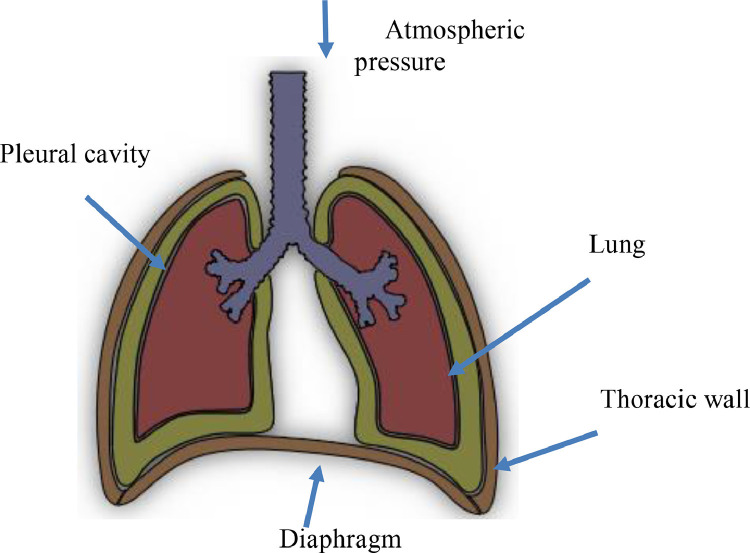
In the respiratory system (Fig. 1 ), breathing is controlled by the diaphragm, which is a muscle separating the abdomen from the chest, and the intercostal muscles, which are located between the bones of the rib cage. During inspiration, the diaphragm contracts and moves toward the abdomen cavity, and the intercostal muscles contract to lift the rib cage outward. As a result of these two muscle movements, the volume of the rib cage increases, and the pressure in the cavity where the lungs are housed, decreases. The increase in volume and the decrease in pressure urge outside air to fill the lungs, to balance the pressure in the lungs with external atmospheric pressure. During the expiration phase, the process is reversed, where the pressure inside the lungs increases above atmospheric pressure, thus resulted in a pressure difference which draws air out of the lungs [15], [16], [17].

Fig. 1.

The physiology of the breathing system [15].

Mechanical ventilation works entirely differently than the physiological breathing system. Instead of having depression during the inspiration, the mechanical ventilators push the gas by creating high position pressure. The ventilatory parameters are carefully adjusted by the doctor according to the ventilation mode that has been chosen. It is possible to change the inspired oxygen fraction between 21% and 100% while maintaining positive expiratory pressure (PEEP) in the circuit during expiration [8, 9].

A mechanical ventilator, inhalation circuit, exhalation circuit, and an artificial lung are required to simulate the complete breathing process. Several pieces of research were conducted to experimentally and theoretically study the ventilation parameters [18]. It is important to note that the inspiration stage is related to the ventilator.

Based on this review, there are no numerical simulations on flow produced by mechanical ventilators. This type of simulation is essential to evaluate the performance of the design before proceeding to the fabrication stage. The study of the mechanical ventilation process requires the use of fluid-structure interaction (FSI). The FSI problems play prominent roles in many scientific and engineering fields, yet a comprehensive study of such problems remains a challenge due to their strong nonlinearity and multidisciplinary nature [19], [20], [21], [22]. FSI method couples computational fluid dynamics used for fluid flow with finite element analysis used for the solid domain. It enables the investigation of the fluid behavior, structural behavior, and how they interact and affect each other. In a One-Way FSI study, the results obtained from the solution fluid or structural domain are used as a boundary condition when solving the different domain. In a Two-Way FSI study, at each sub-step, the fluid and structural domain solutions are solved in parallel. The solution must be converged before moving to the next step [23].

Thus, this present study is performed to contribute to improving these types of ventilators. ANSYS multiphysics software is used to simulate the gas flow and volume produced by a low-cost ventilator designed. Two ventilator designs are proposed and investigated. A two-way FSI analysis using a finite element method is used for the first design, while Computational fluid dynamics (CFD) analysis with a moving mesh is employed for the second design. In order to control the ventilation process, the effect of several parameters on the flow is analyzed.

The paper is organized as follows: after achieving the literature review and highlighting the purpose and originality of the work, the physical problem is described in Section 2. In this section, the mechanical ventilation process is well detailed. Then (in Section 3), the required details on design and modeling of the mechanical ventilators are given. The geometry, boundary conditions, material properties, and mesh adopted in this analysis are also provided in this section. In Section 4, the computed results are presented and discussed.

2. Mechanical ventilation process

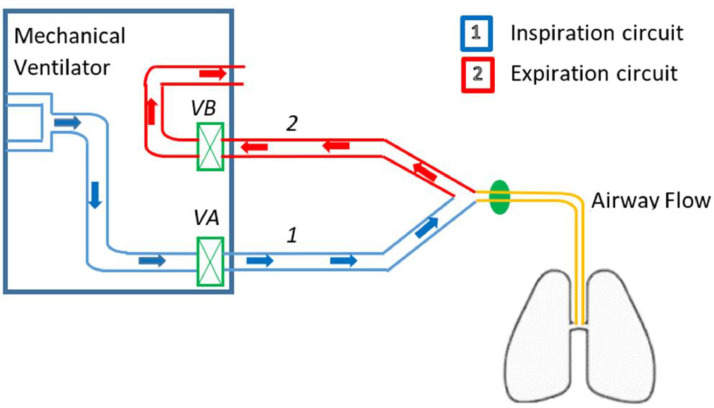
The operating principle scheme of mechanical ventilation is illustrated in Fig. 2 . Frequently, the respiratory cycle consists of the inspiratory time (TI) of 1 s and the expiratory time (TE) of 2 s [24]. In this case, the respiratory frequency is often 20 cycles per minute. Once inspiration gets triggered, the insulator opens the inspiratory valve VA (Fig. 2) and closes the expiration valve VB, causing the airway pressure to rise and then, compressed gas enters the lung. During expiration, the mechanism is reversed. The inspiratory valve is closed and the expiratory valve opens, causing the airway pressure to drop, and the gas leaves the lung (passive exhalation). These two valves always act in opposite ways. However, this mechanism cannot generate a PEEP. The regulation of the expiratory valve causes the desired PEEP by taking into account the resistance of the breathing circuit [25].

Fig. 2.

The operating principle scheme of mechanical ventilation [25].

There are two basic modes for mechanical ventilation according to variables that are controlled during inspiration. These include volume-controlled mode (VCM), which is commonly used, and pressure-controlled method (PCM) ventilations [26]. In PCM, the value of the maximum pressure is adjusted. However, the current volume and flow delivered to the patient depended on the importance of the inspiratory pressure and the set PEEP level [27]. In the VCM, the volume and the flow remain constant. Simultaneously, the pressures vary from one patient to another depending on the compliance and resistance of the respiratory system and the patient's inspiratory contribution [28].

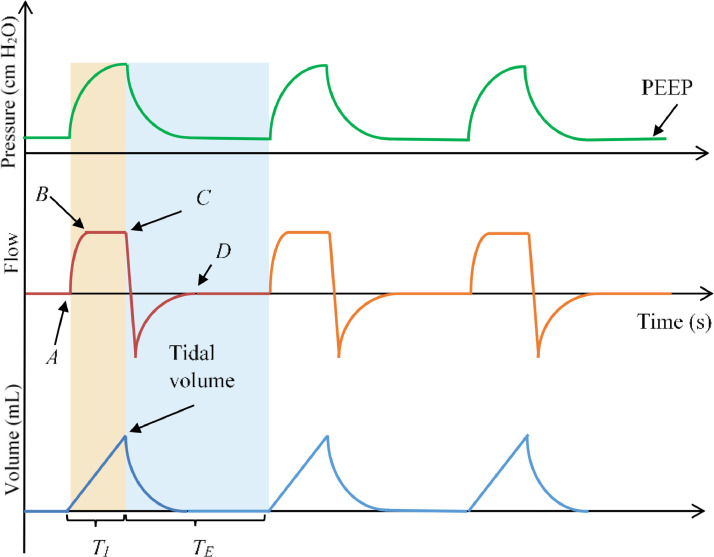
An example of a typical curve of pressure, flow, and volume over time during VCM are illustrated in Fig. 3 (time is along the x-axis) [29]. The case of VCM is chosen because it is most frequently used by doctors, as already mentioned. These curves are not deduced from a confirmed case of the ventilated patient but are purely theoretical. From Fig. 3, it can be seen clearly that when inspiration starts (point A), the flow increases considerably to reach a plateau (point B) and stays at that target level for the duration of inspiration before the expiration begins (point C). At this time, the pressure goes up gradually from PEEP and continues spreading until the preset tidal volume is delivered. The volume increases monotonically (linear rise) to reach the tidal volume (remember that volume = flow × time). During expiration, the flow curve goes below the time-axis and back to zero (point D). Simultaneously, the pressure drops to the set PEEP level, and the volume decreases and returns to zero.

Fig. 3.

Typical curves of flow, pressure, and volume in the case of VCM [29].

3. Design and modeling of mechanical ventilators

As previously mentioned, a mechanical ventilator, inhalation circuit, exhalation circuit, and an artificial lung are required to simulate the complete breathing process. Therefore, this study is focused on the simulation of the flow inside the mechanical ventilator. Two different ventilators, namely Ambu-bag and piston-cylinder-based ventilators, are considered in Sections 3.1 and 3.2. The flow rate and volume evolution as a function of time during the inspiration phase were calculated for each design (Circuit 1 in Fig. 2).

In this section, mathematical formulations and solution procedures for the two proposed designs are presented. For the Ambu-bag-based design (Section 3.1), the Fluid-structure interaction (FSI) analysis methodology is illustrated with boundary conditions, material properties, and mesh generated. However, for the piston-cylinder-based design (Section 3.2), the CFD analysis is more appropriate to evaluate the designed performance. The geometry, boundary conditions, material properties, and mesh adopted in this analysis are also presented. Therefore, flow rate and delivered volume by the ventilator are calculated. The pressure at the outlet is not calculated due to the calculation of pressure at the outlet of the mechanical ventilator requires the entire system to be simulated. In this case, the gas delivered flows to the atmospheric environment.

3.1. Ambu-bag-based design

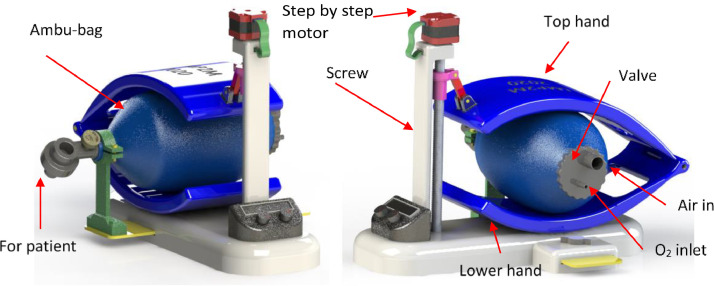
A modified version of the low-cost mechanical ventilator (Fig. 4 ) proposed in this study was designed using the Solid works software [30]. A one-step motor is used to deform the Ambu-bag by the displacement of the top hand. FSI analysis was conducted for this design. FSI occurs when Ambu-bag is bent, causing perturbation of gas flow, and then the gas generates a force on the solid.

Fig. 4.

Design of the Ambu-bag based on a low-cost mechanical ventilator [30]. .

3.1.1. Fluid flow formulation

The governing equations for unsteady laminar flow of a Newtonian fluid are given by [31]:

$$\frac{\partial \rho }{\partial t}+\frac{\partial }{\partial x_i}\left(\rho u_i\right)=0.$$ (1)

$$\frac{\partial }{\partial t}\left(\rho u_i\right)+\frac{\partial }{\partial x_j}\left(\rho u_i{u}_j\right)=-\frac{\partial P}{\partial x_i}+\frac{\partial {\tau }_{ij}}{\partial x_j}$$ (2)

where, ${\tau }_{ij}=\mu \left(\frac{\partial u_i}{\partial x_j}+\frac{\partial u_j}{\partial x_i}+\frac{2}{3}{\delta }_{ij}\frac{\partial u_i}{\partial x_j}\right)$. with xi are the coordinates' components, ui is the velocity components, ρ is the density, P is the pressure, and µ is the dynamic viscosity. The density and dynamic viscosity are equal to 1.2999 kg/m3 and 1.919 919 × 10−5 kg/m∙s, respectively.

The finite volume method (FVM) in the situation of moving mesh is set as following [32]:

$$\frac{d}{dt}\underset{V}{\int }\rho \varphi dV+\underset{S}{\oint }\rho \overrightarrow{n}\left(\overrightarrow{u}-\overrightarrow{u_b}\right)\varphi ds-\underset{S}{\oint }\rho {\Gamma }_{\varphi }\overrightarrow{n}\overrightarrow{\nabla }\varphi ds=\underset{V}{\int }{S}_{\varphi }dV$$ (3)

where V is an arbitrary moving control volume, S is a closed surface bounded V, $\overrightarrow{n}$ is the outward unit normal vector on the boundary surface, $\overrightarrow{u}$ is the fluid velocity vector, $\overrightarrow{u_b}$ is the boundary mesh velocity, Γϕ is the diffusion coefficient, and Sϕ is the volume source/sink of ϕ.

To include the effect of the piston surface motion on the mesh evolution during time variation, the mesh diffusion equation must be solved to get the grid displacements as [33]:

$$\nabla ·\left({\Gamma }_{\text{disp}}·\nabla \delta \right)=0$$ (4)

where δ is the displacement relative to the previous mesh locations. The mesh stiffness (Γdisp) determines the degree to which regions of nodes move together. The option of increase stiffness near small volumes is used in this study to preserve the mesh quality and limit mesh distortion. In this case, Γdisp, is obtained by this equation [33]:

$${\Gamma }_{\text{disp}}={\left(\frac{{\mathrm{V}}_{\text{ref}}}{\mathrm{V}}\right)}^{{\mathrm{C}}_{\text{stiff}}}$$ (5)

where Vref is a mean control volume of the numerical domain. In this study, we use the recommended value of the stiffness model exponent Cstiff, which is equal to 2.

3.1.2. Formulation of structural dynamic

Transient structural analysis was used to calculate the response of deformable solids, where the response at each time is the solution of the general equation of motion [34]:

$$\left[\mathrm{M}\right]\left\{\ddot{\mathrm{d}}\right\}+\left[\mathrm{C}\right]\left\{\dot{\mathrm{d}}\right\}+\left[\mathrm{K}\right]\left\{\mathrm{d}\right\}=\left\{\mathrm{F}\left(\mathrm{t}\right)\right\}$$ (6)

where d is the nodal displacement, $\dot{d}$ is the nodal velocity, and $\ddot{d}$ is the nodal acceleration. [M], [C], [K] and F(t) are mass matrix, damping matrix, stiffness matrix, and force vector, respectively. The stiffness matrix is updated at each time to take into account the nonlinearities due to geometry, material, and contact.

The properties of materials used in this analysis are given in Table 1 . The hands are supposed in aluminum material. The Ambu-bag valve is made of Acrylonitrile butadiene styrene (ABS) plastic material. The Ambu-bag is made from Polyvinyl chloride (PVC) or Silicon-rubber material, and all other parts are proposed to be fabricated using steel material.

Table 1.

Solid material properties [34].

Material	Properties
Silicon-rubber	Density = 1120 (kg/m3) Mooney-Rivlin 2 parameters C10 = 2.59 × 105 (Pa) C01 = 65 × 103 (Pa)	Incompressibility parameter D1 = 1.1 × 10−9 (Pa−1) Tensile yield strength = 8.97 × 106 (Pa) Tensile ultimate strength = 8.97 × 106 (Pa)
PVC plastic	Density = 1330 (kg/m3) Young's modulus = 32.4 MPa Poisson's ratio = 0.475	Shear modulus = 10.983 MPa Tensile yield strength =1.95 MPa Tensile ultimate strength = 1.95 MPa
Aluminum	Density = 2770 (kg/m3) Young's modulus = 71 GPa Poisson's ratio = 0.33
Steel	Density = 7850 (kg/m3) Young's modulus = 200 GPa Poisson's ratio = 0.3
ABS plastic	Density = 1040 (kg/m3) Young's modulus = 2.39 GPa Poisson's ratio = 0.399	Shear modulus = 854 MPa Tensile yield strength = 41.4 MPa Tensile ultimate strength = 41.4 MPa

It is challenging to model the behavior of the Ambu-bag made of hyperplastic material (Silicon-rubber) due to its nonlinearity, large deformation, and material instability [35]. In this study, the Mooney-Rivlin model was used for the Ambu-bag. The most commonly used model is the 2-term Mooney-Rivlin model. The two parameters for the Mooney-Rivlin form of the strain energy potential is written as [34]:

$$W={\mathrm{C}}_{10}\left({\mathrm{I}}_1-3\right)+{\mathrm{C}}_{01}\left({\mathrm{I}}_2-3\right)+\frac{1}{\mathrm{D}}{\left(J-1\right)}^2$$ (7)

where the principal defines the strain invariants (I1, I2, J) stretches at any deformation state (λ1, λ2, λ3) as:

$${\mathrm{I}}_2=\begin{array}{c}{\mathrm{I}}_1={\lambda }_1^2+{\lambda }_2^2+{\lambda }_3^2\\ {\lambda }_1^2{\lambda }_2^2+{\lambda }_2^2{\lambda }_3^2+{\lambda }_3^2{\lambda }_1^2\\ J={\lambda }_1{\lambda }_2{\lambda }_3\end{array}$$ (8)

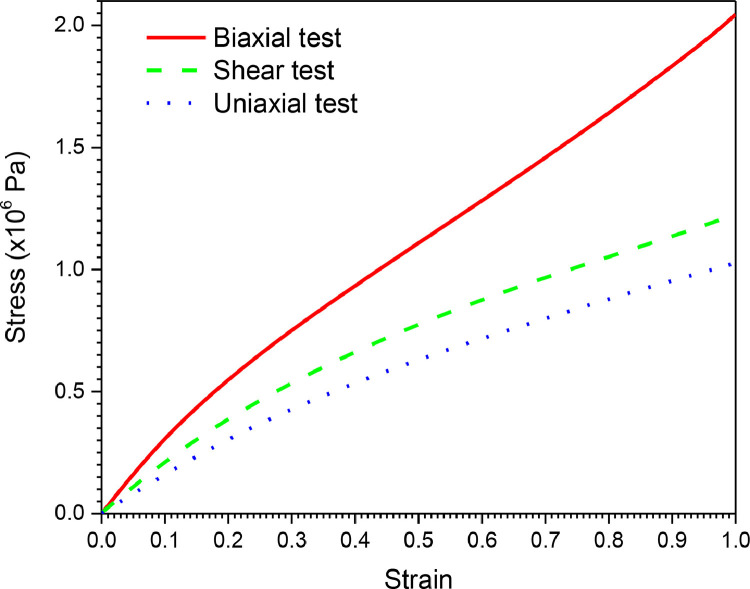
The stretch ratio$\lambda$ (or simply ‘stretch’) is defined as $\frac{\mathrm{L}}{{\mathrm{L}}_0}=\frac{{\mathrm{L}}_0+\Delta \mathrm{u}}{{\mathrm{L}}_0}=1+{\epsilon }_{\mathrm{E}}$, where ${\epsilon }_E$ is engineering strain. The parameters of this model are calculated using the data presented in Fig. 5 . Through the strain energy function, the stresses can be calculated as ${\mathrm{S}}_{\text{ij}}=\frac{\text{dW}}{\mathrm{d}{\mathrm{E}}_{\text{ij}}}$, where Eij are components of the strain tensor. For all of the preceding Mooney-Rivlin forms, the initial shear and initial bulk moduli are defined as ${\mu }_0=2\left({\mathrm{c}}_{10}+{\mathrm{c}}_{01}\right)$ and ${\kappa }_0=\frac{2}{\mathrm{d}}$.

Fig. 5.

Stress-strain curves for the silicon rubber material.

3.1.3. Formulation of fluid-structure analysis

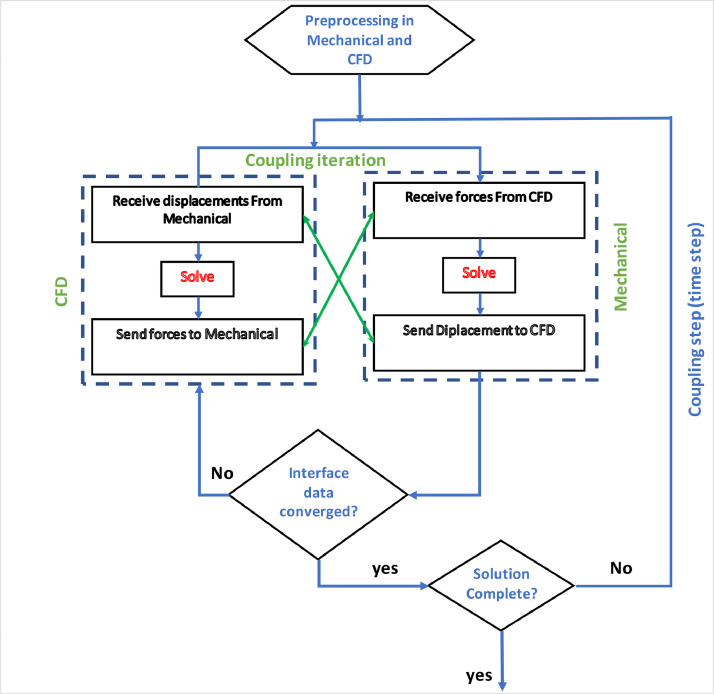
In FSI, the fields are solved separately, which are coupled by an iterative procedure in the ANSYS workbench (Fig. 6 ) [36], [37], [38]. For the two-way coupling procedure, the fluid pressure is transferred to the structural solver. Using this pressure as an external load, the displacement obtained from the structure solver is transferred to the CFD solver. This procedure is repeated until convergence is obtained [39], [40], [41].

Fig. 6.

Flowchart of the FSI solution procedure [36].

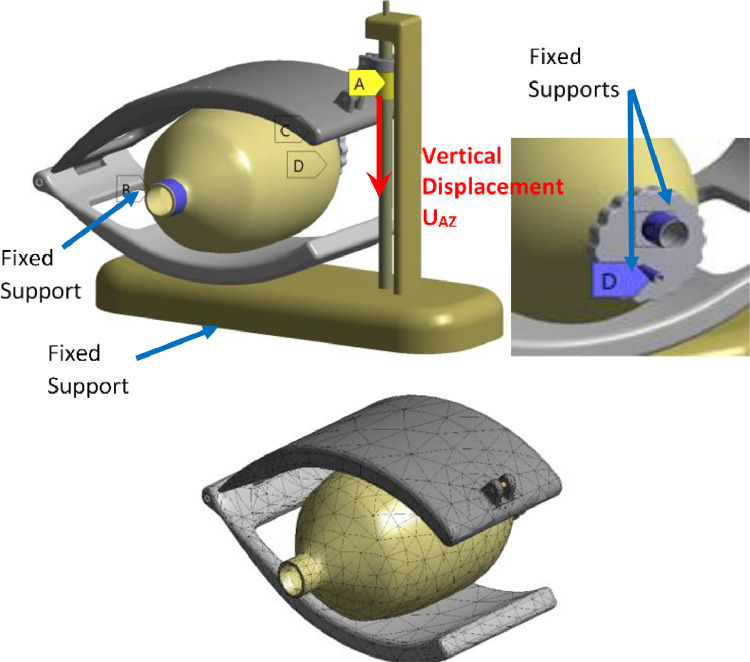
Fig. 7 illustrates the boundary conditions and the mesh of the solid domain. In this case, the top hand is supposed to move according to the vertical axis (UAZ) with a uniform velocity. During ventilation process, the top hand is moved by the screw in two steps. During the first step (1 s), it moves to compress the Ambu-bag for 9 cm. After that, the top hand returns to its initial position during the second step (2 s), as given by:

$${\mathrm{U}}_{\text{AZ}}=\left\{\begin{array}{c}-0.09·\text{Time},\text{for}0\mathrm{s}\le \text{Time}\le 1\mathrm{s}\\ 0.09·\left(\text{Time}-1\right)-0.09,\text{for}1.<\text{Time}\le 3\mathrm{s}\end{array}\right\}\left(m\right)$$ (9)

Fig. 7.

Boundary conditions and generated mesh for the structural domain.

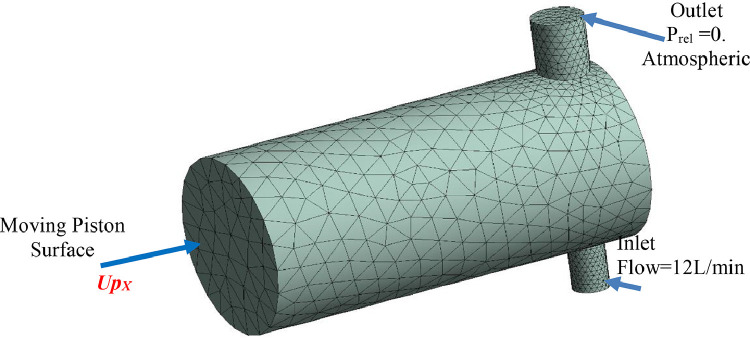
The design contains two fixed supports, as shown in Fig. 7. The boundary conditions for the fluid domain and the mesh generated are illustrated in Fig. 8 . It is important to note that the ventilator flows to the atmospheric environment, and the flow of the oxygen (O2) is set as:

$${\mathrm{O}}_2\text{Flow}=\left\{\begin{array}{c}12\frac{\mathrm{L}}{\min }0\mathrm{s}\le \text{Time}\le 1\mathrm{s}\\ 0.\frac{\mathrm{L}}{\min }1\mathrm{s}<\text{Time}\le 3\mathrm{s}\end{array}\right\}$$ (10)

Fig. 8.

Boundary conditions and generated mesh for fluid domain.

In the FSI problem, the challenge is to couple the Lagrangian structural mesh with the Eulerian fluid mesh. Once the new solid position is computed from the structural solver at every timestep, the fluid mesh has to be deformed to conform with the latest solid place. ANSYS CFX utilizes the Displacement Diffusion as mesh deformation method. The critical parameter in FSI analysis is the time step. The time step is taken as a fixed value of Dt = 0.01 s.

For the mesh of the two domains, tetrahedral elements which can fit better complex geometry are used. This type of mesh is suitable for problems involving mesh motion. In this case study, the solid domain contains 10,756 tetrahedral elements (Fig. 7), while the fluid domain contains 35,376 tetrahedral elements (Fig. 8).

To ensure the stability of the two-way transient FSI analysis, the optimum range of 1 to 10 was set for external coupling iterations and mesh displacement control. For CFD problem, a high-resolution advection scheme was used with a second-order backward Euler discretization algorithm. The convergence criterion was set to 10−4 for the maximum residuals, which could be obtained in all simulation runs. For the structural problem, the Newton-Raphson method is used for solving nonlinear equations.

3.2. Piston-cylinder based design

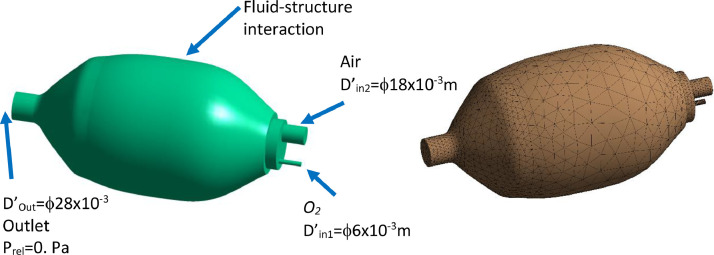
The second design proposed in this study is shown in Fig. 9 . In this design, a piston is moving in a cylinder actuated by a motor. The gas enters the cylinder from the inlet, compressed, and evacuates through the outlet.

Fig. 9.

The second mechanical ventilator design. .

The piston is displaced according to the two cases as follows:

Case A: Uniform rectilinear motion

$$\text{Upx}=\left\{\begin{array}{c}-0.1·\text{Time},\text{for}0<\text{time}\le 1\\ 0.05·\left(\text{Time}-1\right)-0.1,\text{for}1<\text{time}\le 3\end{array}\right\}\left(m\right)$$ (11)

Case B: Uniform decelerated rectilinear motion

$$\text{Upx}=\left\{\begin{array}{c}\frac{1}{2}\left(0.2\right)·\text{Tim}{\mathrm{e}}^2-0.2·\text{Time},\text{for}0\mathrm{s}<\text{time}\le 1\mathrm{s}\\ \frac{1}{2}\left(-0.05\right)·{\left(\text{Time}-1\right)}^2+0.1·\left(\text{Time}-1\right)-0.1,\text{for}1\mathrm{s}<\text{time}\le 3\mathrm{s}\end{array}\right\}\left(m\right)$$ (12)

In the first case, the piston is moved according to a uniform rectilinear motion. On the other hand, the second case follows a uniform decelerated rectilinear movement. Here, the piston velocity varies linearly from the initial velocity to the stagnation point (zero rates).

The gas flow, in this case, is transient laminar. The same equations for the first design are used here. Thus, the equations of continuity, mesh displacement, and momentum are solved. The time step in CFD analysis is estimated by the Courant Number (CN) as $\frac{{\mathrm{U}}_{\text{ref}}·\Delta \mathrm{t}}{\text{Element}\text{Size}}$, where Uref is the reference velocity. This parameter ensures that the fluid passes through a number of elements in one timestep. Generally, CN is taken to be a value between 2 and 10 [26]. The time step (Dt) is set to a fixed value equal to 0.01 s.

Fig. 10 displays the mesh and boundary conditions of the fluid domain, which contain 14,917 tetrahedral elements. The mesh is changed at each time step using the mesh deformation technique. For the moving mesh motion, the stiffness model exponent Cstiff is equal to 2.

Fig. 10.

The mesh and boundary conditions of the fluid domain of the piston-cylinder-based design.

4. Results and discussion

As mentioned before, this study focuses on the inspiration period. The two proposed mechanical ventilators are studied for one cycle of breathing. Therefore, two stages are considered: compression (1 s) and decompression (2 s). The analysis results of the first design using the FSI analysis are presented in Section 4.1. In Section 4.2, the results of the fluid flow with a moving piston are exposed. Finally, the effects of some essential parameters are investigated.

4.1. Results of AMBU-BAG based design

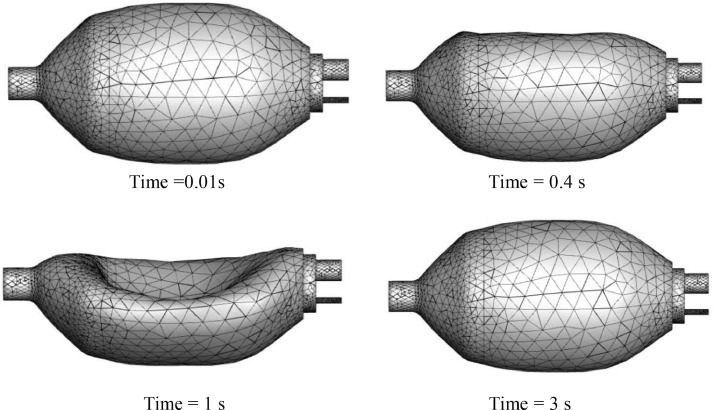
Fig. 11 shows the results of the total displacement of the solid domains for different instances. The maximum removal is obtained for a time equal to 1 s at the end of the top hand. The fluid domain's mesh history is presented in Fig. 12 , where each time step corresponds to a new mesh. The value of the orthogonality angle controls the quality of the mesh. During calculation over time, the solver stops when the minimum value of the orthogonality angle is below 0.2618 rad (15°) (written in Python language as minVal(Orthogonality Angle Minimum)@Default Domain < 15 [deg]). Then, the re-meshing starts, and a new mesh is transferred to CFX. The run continues until the end of the cycle.

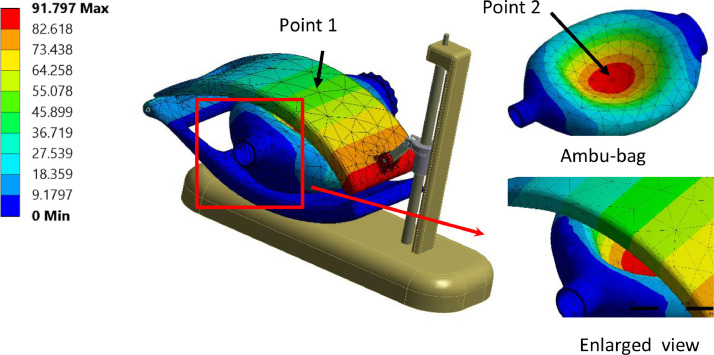
Fig. 11.

Total displacement of the ventilator with silicon-rubber Ambu-bag, at 1 s. (PVC material, 100% O2, inlet flow = 12 l/min, UAZ = 0.09 m).

Fig. 12.

Mesh history of fluid domain during one cycle of breathing. (PVC material, 100% O2, inlet flow = 12 l/min, UAZ = 0.09 m).

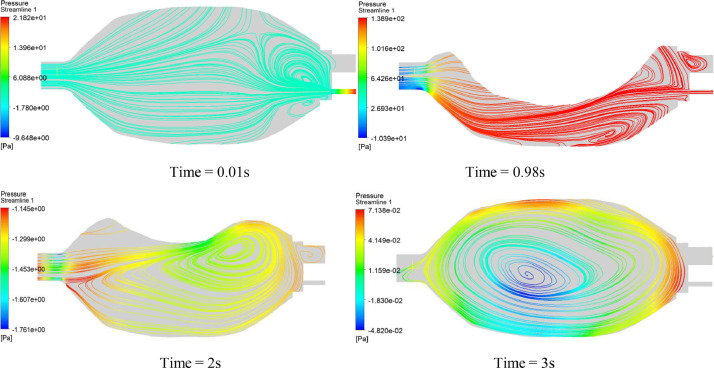
Fig. 13 presents the streamlines on the vertical plane for different instances. It can be seen that some vortices are present in the fluid domain either for the compression stage (1 s) or for the decompression stage (2 s). The minimum pressure current in the inside vortices cores will certainly cause perturbation in the flow, mainly in the inspiration period. The fluid flows from high-pressure zones to low-pressure zones. This is confirmed by the zoom view of Fig. 11, in which it can be observed that the Ambu-bag does not follow the motion of the top hand, and their displacements are different from each other.

Fig. 13.

Surface streamlines history on the vertical plane for the first design. (PVC material, 100% O2, inlet flow = 12 l/min, UAZ = 0.09 m).

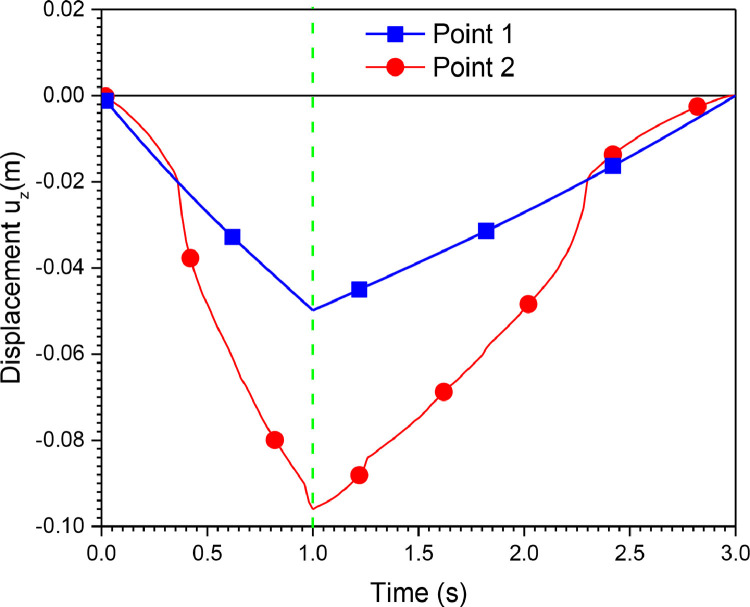
Also, Fig. 14 shows the vertical displacement of points 1 and 2. Point 1 belongs to the Ambu-bag, and point 2 belongs to the top hand, as indicated by Fig. 11. It can be confirmed that the response of Ambu-bag is more significant than the load applied.

Fig. 14.

Displacement uz of point1 and point 2 (PVC material, 100% O2, inlet flow = 12 l/min, UAZ = 0.09 cm).

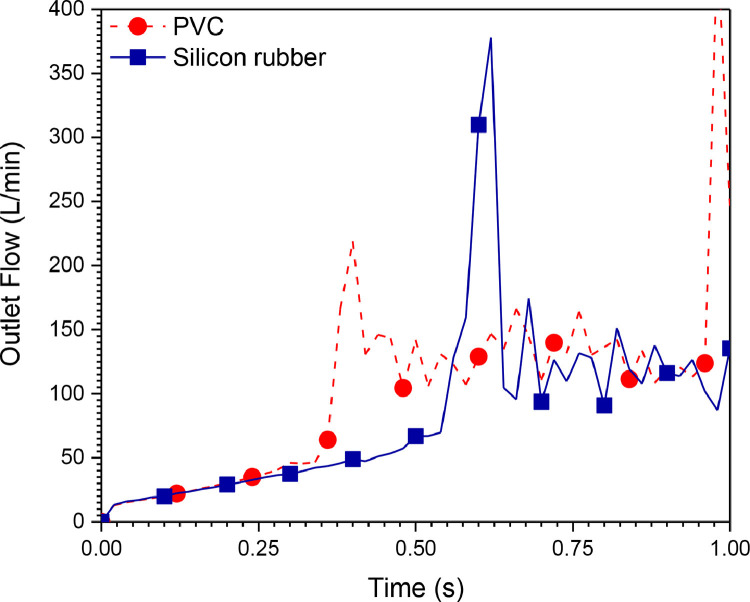
The flow delivered by this mechanical ventilator is presented in Fig. 15, Fig. 16 for different materials and compression distances, respectively. It can be seen from these figures that the system is not stable. The outlet pressure cannot be controlled because the flow contours are highly perturbed. The results obtained from the first system (Ambu-bag-based design) are not satisfactory. Consequently, another design is proposed. The following section represents the results obtained from the second mechanical ventilator (piston-cylinder-based design).

Fig. 15.

Outlet flow rate history (100% O2, inlet flow = 12 l/min, UAZ = 0.09 cm).

Fig. 16.

Outlet flow rate history for different compression displacements (UAZ) (Silicon rubber material, 100% O2, inlet flow = 12 l/min).

4.2. Results of piston-cylinder-based design

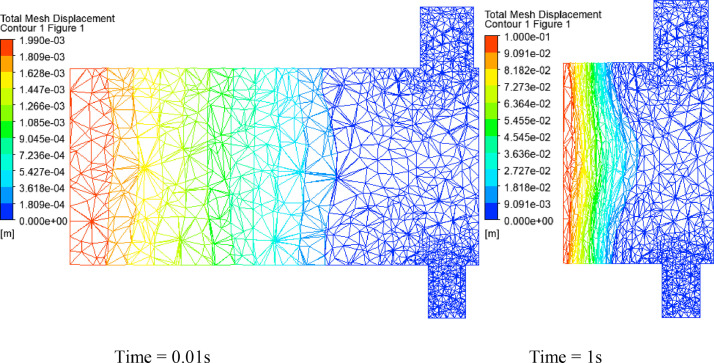
The displacement of the piston wall is modeled using dynamic and deformable meshes, in which the mesh nodes are adjusted to new locations. Fig. 17 illustrates the mesh displacement as the piston compressing the gas for two instances (one at the beginning and the other at the end of the piston motion). The higher values of deformation are felt near the piston wall.

Fig. 17.

Mesh displacement at different moments of the piston-cylinder system. (100% O2, inlet flow = 12 l/min, uniformly rectilinear, Lc = 150 × 10−3 m, Dp = 37 × 10−3 m).

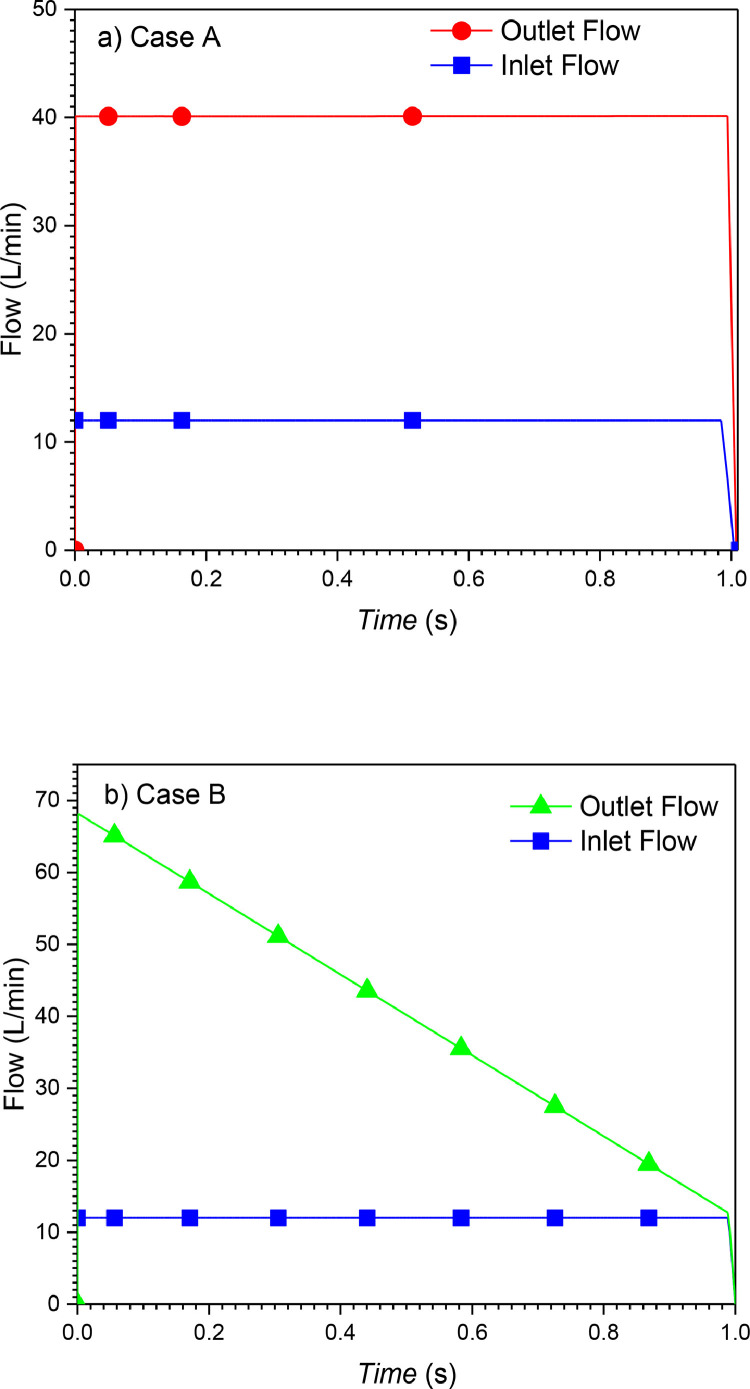
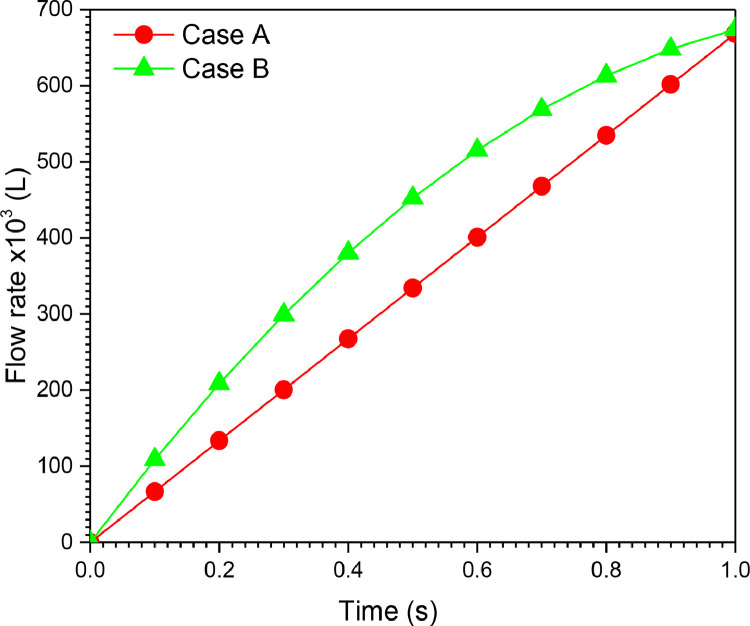
The history of flow during 1 s of the inspiration period at the inlet and the outlet of the piston-cylinder system are shown in Fig. 18 . It is important to note that the difference between the inlet and outlet flow of the ventilator is due to the flow added by gas compression.

Fig. 18.

Flow rate at the outlet and the inlet of Piston-cylinder ventilator for cases A and B. (100% O2, inlet flow = 12 l/min, Lc = 150 × 10−3 m, Dp = 37 × 10−3 m).

The volume at any instant is estimated from the flow curve as integral of flow over time as $\underset{0}{\overset{t}{\int }}Flow\left(t\right)·dt$. Fig. 19 illustrates the volume history during inspiration for the two cases of VCM and PCM modes. The tidal volume (VT) delivered by the ventilator during the inspiration period is 668.31 × 10−3 (L) for cases A (VCM mode) and B (PCM mode).

Fig. 19.

Volume history of Piston-cylinder ventilator for cases A and B. (100% O2, inlet flow = 12 l/min, Lc = 150 × 10−3 m, Dp = 37 × 10−3 m).

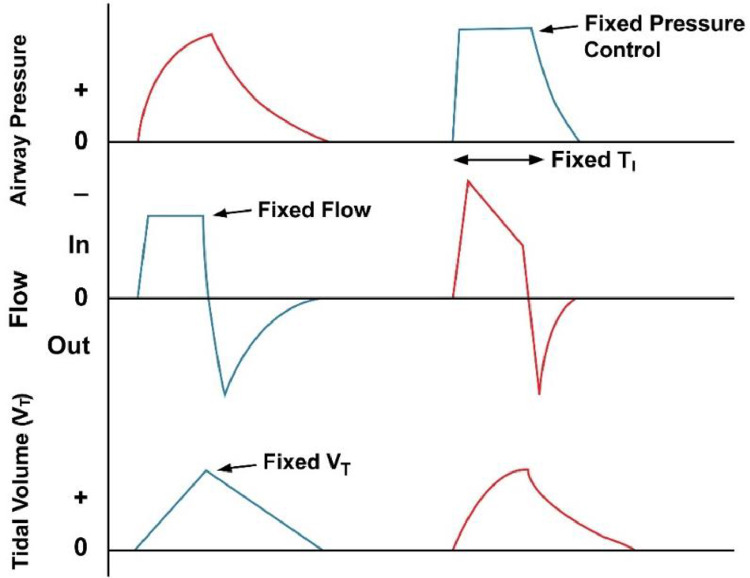
It can be seen clearly that the curve patterns in Fig. 19 are similar to the inspiration stage presented in Fig. 20 , where the two modes (PCM and VCM) are identified.

Fig. 20.

PCM and VCM modes of mechanical ventilation [42].

Consequently, the parameters of case A can be used to produce VCM mode, in which the flow is fixed. However, PCM can be produced by using the parameters of case B, in which the pressure is fixed.

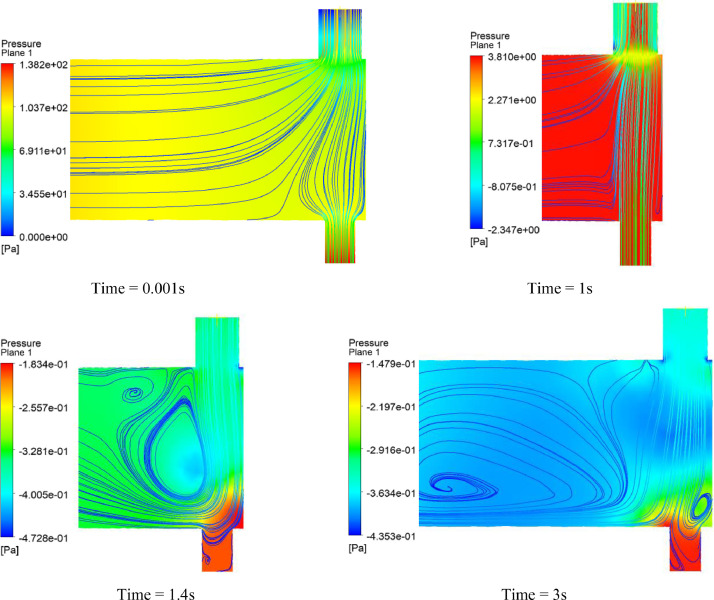
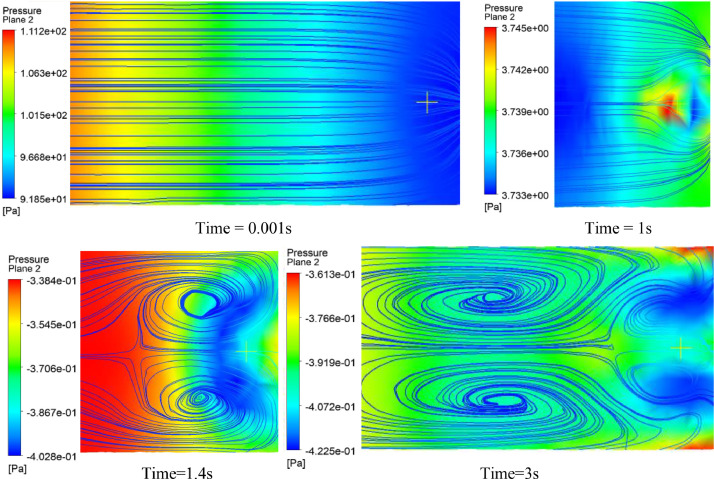
Fig. 21, Fig. 22 display the surface streamlines with isopressure contours in vertical and horizontal planes. It can be seen from the figures that the flow is regular, and no vortices are present during the inspiration stage, unlike the Ambu-bag-based design. However, at the second stage (during the return of the piston to its initial position), two large vortices were observed at time > 1 s, as shown in Fig. 22. The depression created by vortices allows the reverse flow from outside to inside the ventilator.

Fig. 21.

Surface streamlines on the vertical plane of the piston-cylinder ventilator. (100% O2, inlet flow = 12 l/min, uniformly rectilinear, Lc = 150 × 10−3 m, Dp = 37 × 10−3 m).

Fig. 22.

Surface streamlines on the horizontal plane of the piston-cylinder ventilator. (100% O2, inlet flow = 12 l/min, uniformly rectilinear, Lc = 150 × 10−3 m, Dp = 37 × 10−3 m).

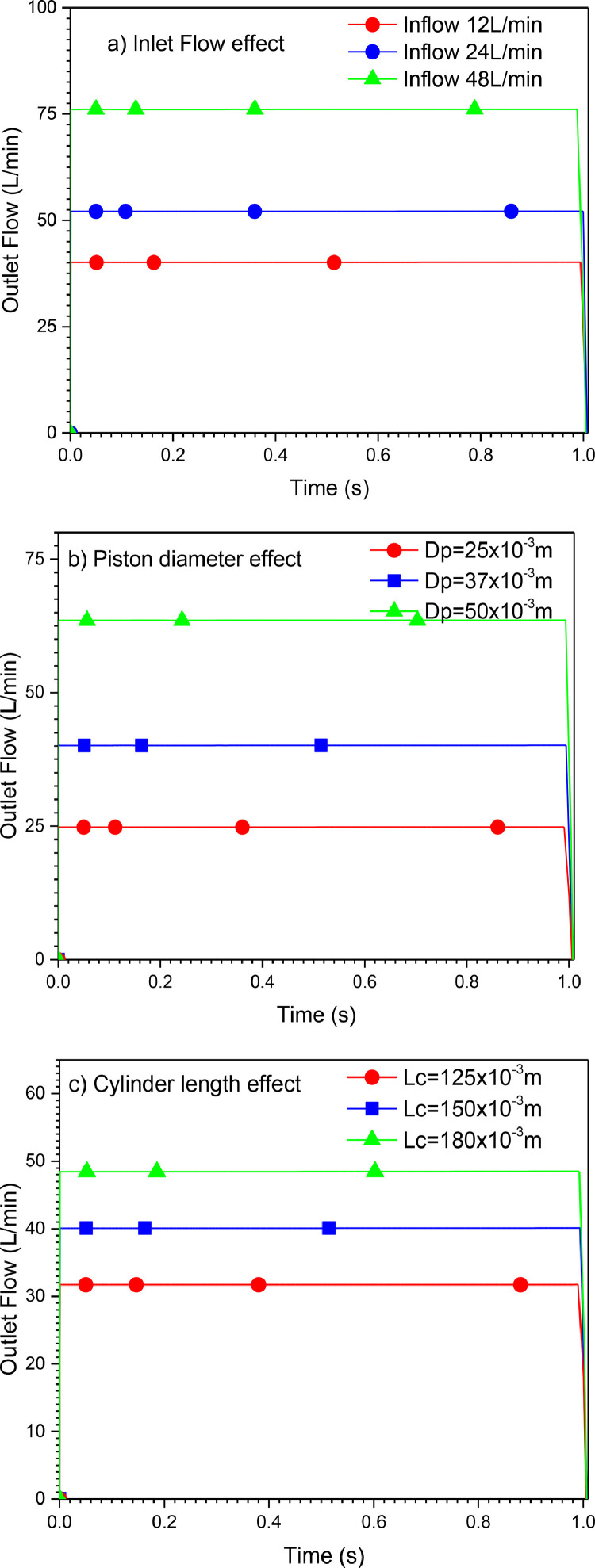
Finally, a parametric study is conducted to investigate the effect of different parameters on the outlet flow of the mechanical ventilator for VCM mode (Case A). Fig. 23 a shows the evolution of the outlet flows with varying inlet flows. The outlet flow increases as the inlet flow increases. Besides, the diameter of the piston (Dp) and length of the cylinder (LC) have an essential effect on the output data, as shown in Figs. 23b and c.

Fig. 23.

Effects of different parameters on the outlet flow. (100% O2, uniformly rectilinear Upx).

5. Conclusions

In this study, flow simulation produced by two proposed designs of low-cost mechanical ventilators was investigated. A finite element method was used to solve the set of coupled equations using ANSYS software. A transient solution during one cycle of inspiration was considered. A fluid-structure analysis was used to obtain the fluid response resulting from the Ambu-bag deformation. It was shown that the gas flow obtained is unstable. This first design (Ambu-bag-based design) is uncontrollable due to the susceptible hyper-elastic material of the Ambu-bag when force is applied. Utilization of this type of mechanical ventilators with this kind of material could lead to health problems like barotrauma.

On the other hand, a CFD study with a moving boundary was performed for the piston-cylinder-based ventilator, and the results obtained were more satisfactory than the first design (Ambu-bag-based design). In this situation, two different ways of displacement of the piston were used. Two modes of ventilation (VCM and PCM modes) were evaluated. VCM was realized by a uniform rectilinear motion and PCM is realized by a uniform decelerated rectilinear motion. In addition, the effects of inflow, cylinder length, and cylinder diameter on outflow were investigated. It was found that the pattern of the outflow and the volume inspired could be controlled by manipulating these parameters. Finally, these results could be further investigated in the future by including other parameters. This requires the addition of all respiratory circuits and an artificial lung to simulate the complete breathing process.

CRediT authorship contribution statement

Abdellah El-Hadj: Conceptualization. Mohamed Kezrane: Data curation. Hijaz Ahmad: Writing – review & editing. Houari Ameur: Formal analysis. S. Zamree Bin Abd Rahim: Validation. Abdelhakime Younsi: Writing – original draft. Hanaa Abu-Zinadah: Resources.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.