Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2021 Jun 4;21(12):5028–5035. doi: 10.1021/acs.nanolett.1c00801

Survival of Floquet–Bloch States in the Presence of Scattering

Sven Aeschlimann †,‡, Shunsuke A Sato ‡,, Razvan Krause †,‡, Mariana Chávez-Cervantes ‡, Umberto De Giovannini ‡,§, Hannes Hübener ‡, Stiven Forti ∥, Camilla Coletti ∥,⊥, Kerstin Hanff ‡,#, Kai Rossnagel #,@, Angel Rubio ‡,§,△, Isabella Gierz †,*
PMCID: PMC8227476  PMID: 34082532

Abstract

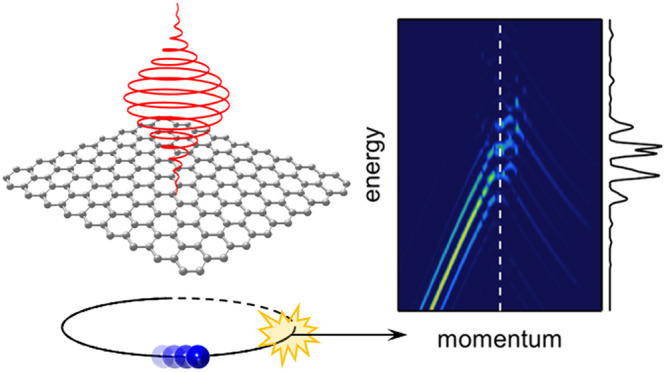
graphic file with name nl1c00801_0006.jpg

Floquet theory has spawned many exciting possibilities for electronic structure control with light, with enormous potential for future applications. The experimental demonstration in solids, however, remains largely unrealized. In particular, the influence of scattering on the formation of Floquet–Bloch states remains poorly understood. Here we combine time- and angle-resolved photoemission spectroscopy with time-dependent density functional theory and a two-level model with relaxation to investigate the survival of Floquet–Bloch states in the presence of scattering. We find that Floquet–Bloch states will be destroyed if scattering—activated by electronic excitations—prevents the Bloch electrons from following the driving field coherently. The two-level model also shows that Floquet–Bloch states reappear at high field intensities where energy exchange with the driving field dominates over energy dissipation to the bath. Our results clearly indicate the importance of long scattering times combined with strong driving fields for the successful realization of various Floquet phenomena.

Keywords: Floquet−Bloch states, dissipation, time- and angle-resolved photoemission spectroscopy, time-dependent density functional theory, driven two-level system with dissipation

With the recent development of strong-field terahertz and mid-infrared laser sources, Floquet engineering, where the coherent interaction of strong light fields with Bloch electrons inside a solid is used to manipulate the band structure of the material, becomes a viable approach for nonequilibrium materials design. Floquet theory predicts a number of fascinating phenomena, including dynamical localization of charge carriers1 and light-induced topological phase transitions.2,3 Many of these phenomena have been observed in optical lattices.4−6 In real solids, however, the ability of the Bloch electrons to coherently follow the driving field is limited by scattering. This has restricted the experimental observation of Floquet phenomena to materials with extremely long scattering times such as the topological insulator Bi2Se37,8 and exfoliated graphene at low temperatures.9 The possible survival of Floquet phenomena in the presence of dissipation is a hotly debated topic10 because of its relevance for future applications and the possibility to use dissipation to stabilize novel Floquet phases such as the time crystal11−14 or topological phases.15

Here, we use time- and angle-resolved photoemission spectroscopy (tr-ARPES) combined with time-dependent density functional theory (TDDFT) and a two-level model with relaxation to investigate the survival of Floquet–Bloch states in the presence of scattering. We find good agreement between TDDFT simulations and tr-ARPES measurements for subgap excitation of the bulk semiconductor WSe2. In the case of graphene, however, TDDFT simulations predict the opening of various band gaps in the electronic dispersion that are not observed in the tr-ARPES measurements. We resolve this discrepancy with the help of a simple model where a resonantly driven two-level system is coupled to a bath.16−19 This model shows that Floquet–Bloch states will be destroyed if scattering—activated by electronic excitations—prevents the Bloch electrons from following the driving field coherently. The model also shows that Floquet–Bloch states reappear at high field intensities where energy exchange with the driving field dominates over energy dissipation to the bath. Details about the experimental and theoretical methods and the data analysis are provided in the Supporting Information.

The experimental observation of Floquet–Bloch states with tr-ARPES is impeded by the fact that in the presence of a strong driving laser field photoemission occurs from Floquet–Bloch states (photon-dressed initial states) to Volkov states (photon-dressed free-electron final states).8,20,21 Photon-dressing of both the initial and the final state results in the formation of replica bands in the photoelectron spectrum that are separated from the original band structure by integer multiples of the drive photon energy. For the experimental geometry employed in the present study, the Volkov contribution to the first-order replica bands is zero for s-polarized (sp) driving pulses where the electric field vector lies in the plane of the sample surface and is perpendicular to the direction along which the transient band structure is measured. In this case, the experimental observation of first-order replica bands with tr-ARPES provides direct evidence for the formation of Floquet–Bloch states21 (Supporting Information).

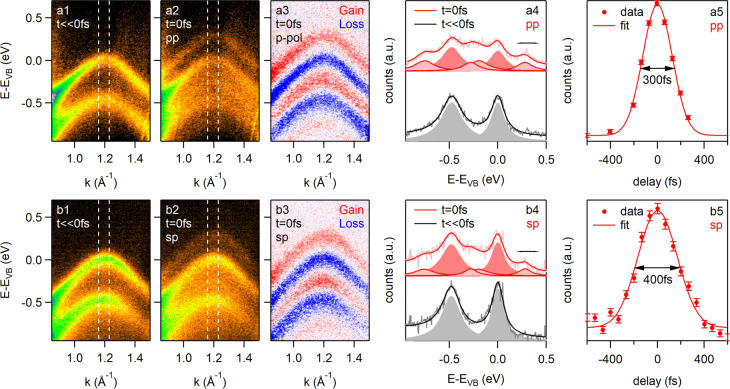
In Figure 1 we present tr-ARPES snapshots of the valence band of bulk WSe2 measured along the ΓK-direction in the vicinity of the K-point of the Brillouin zone. Panels a1 and a2 of Figure 1 show the measured band structure without and with p-polarized (pp) mid-infrared (MIR) driving field, respectively. The corresponding drive-induced changes of the photocurrent obtained by subtracting Figure 1(a1) from Figure 1(a2) are shown in Figure 1(a3). Dashed white lines in Figure 1(a1 and a2) indicate the area of integration for the energy distribution curves (EDCs) presented in Figure 1(a4). The corresponding data for sp driving pulses are presented in Figure 1(b1–b4).

Figure 1.

Figure 1

Open in a new tab

Rows a and b show the tr-ARPES data for WSe2 for pp and sp driving pulses, respectively, at ℏωdrive = 280 meV with a peak driving field of Evac = 2.1 MV/cm. Columns 1 and 2 show the photocurrent at negative pump–probe delay and at t = 0 fs, respectively. The dashed white lines mark the momentum range for the energy distribution curves (EDCs) in column 4. Column 3 shows the drive-induced changes of the photocurrent at t = 0 fs. These data were obtained by subtracting the data in column 1 from the data in column 2. Column 4 shows energy distribution curves (EDCs) extracted at the momentum range indicated by the dashed white lines in columns 1 and 2 together with Lorentzian fits. Continuous light (dark) lines are the data (fit). Filled gray areas show the individual Lorentzians at negative delay. Filled light (dark) red areas show the individual Lorentzians of the sidebands (main bands). Column 5 shows the intensity of the uppermost replica band obtained by integrating the transient EDCs in column 4 over the energy range indicated by the black arrow as a function of pump–probe delay together with a Gaussian fit.

We observe clear indications for the formation of replica bands for both pp and sp driving pulses. As discussed above (Supporting Information) the observation of replica bands for sp driving pulses indicates the formation of Floquet–Bloch states, while the replica bands appearing for pp driving pulses contain contributions from both Floquet–Bloch and Volkov states. From Lorentzian fits to the EDCs (Supporting Information) in Figure 1(b1–b4) we obtain replica band intensities of (23.3 ± 0.3)% and (15.0 ± 0.5)% for pp and sp driving pulses, respectively. The line width of the bands is found to be unaffected by the presence of the driving field within the error bars.

To determine the lifetime of the drive-induced replica bands we integrate the time-dependent EDCs presented in Figure 1(a4 and b4) over the energy range indicated by the black arrow. The time dependence of the resulting data can be well fitted with a Gaussian [see Figure 1(a5 and b5)], indicating that the lifetime of the drive-induced replica bands is determined by the pump–probe cross correlation. The duration of the MIR drive was 280 fs in panel a5 and 390 fs in panel b5 determined by the dispersion of the waveplates used to control the polarization.

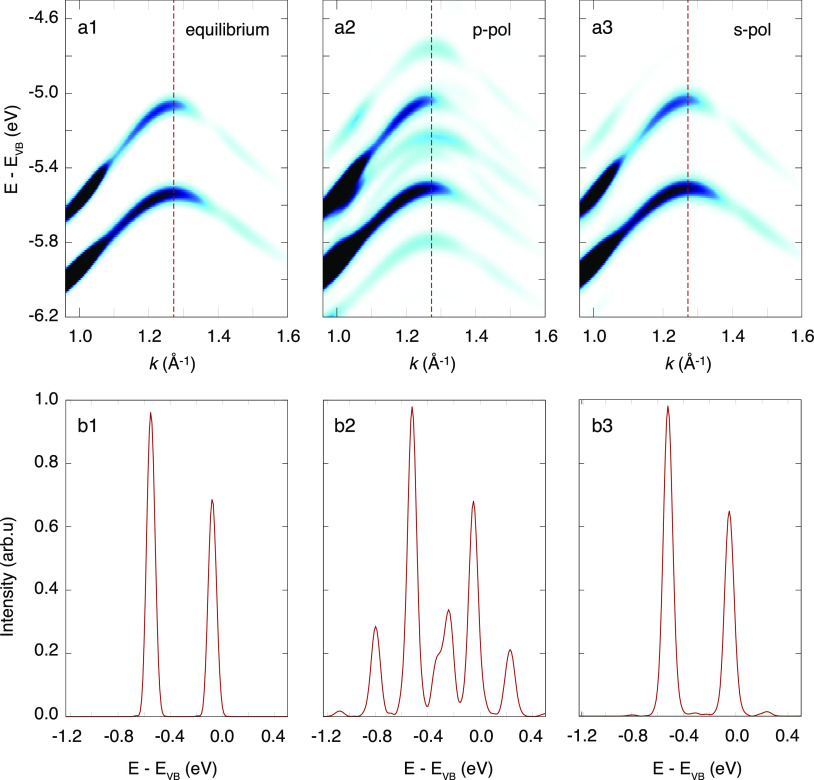
In Figure 2 we present TDDFT simulations for direct comparison with the tr-ARPES data in Figure 1. Figure 2(a1) shows the simulated spectrum without mid-infrared drive. Panels a2 and a3 of Figure 2 show the corresponding spectra in the presence of pp and sp driving pulses, respectively, with field strength and driving frequency matching the experimental values at the sample surface. In Figure 2(b1–b3) we show EDCs extracted along the dashed red lines in Figure 2(a1–a3). In good agreement with the tr-ARPES experiments in Figure 1 we find that, in the presence of both pp and sp driving pulses, replica bands appear in the simulated ARPES spectra. A comparison of the theoretical and experimental EDCs reveals that the theoretical replica band intensity is similar to the experimental value for pp driving pulses and significantly smaller than the experimental value for sp driving pulses.

Figure 2.

Figure 2

Open in a new tab

Simulated ARPES spectra for WSe2 at equilibrium (a1), in the presence of a pp driving pulse (a2), and in the presence of an sp driving pulse (a3). Dashed red lines in a1–a3 indicate the positions for the energy distribution curves (EDCs) in panels b1–b3. EDC through the K-point at equilibrium (b1), in the presence of a pp driving pulse (b2), and in the presence of an sp driving pulse (b3).

Having demonstrated the capability of our tr-ARPES setup to generate and resolve Floquet–Bloch states we now turn to the fascinating scenario of a light-induced topological phase transition in graphene. According to ref (2), strong driving with circularly polarized (cp) light fields is predicted to open a gap at the Dirac point and turn graphene into a topological insulator. Additional band gaps (Rabi gaps in the following) are predicted to open away from the Dirac point where the unperturbed band structure crosses the nth-order Floquet replica band.2,22 Because the matrix element for interband transitions in graphene is highly anisotropic23−25 with nodes (maxima) in the direction parallel (perpendicular) to the polarization of the driving field, these Rabi gaps are biggest along the direction in momentum space that is perpendicular to the polarization of the driving field. This is the case for sp driving pulses in the present study.

In Figure 3 we present TDDFT simulations that illustrate how mid-infrared driving pulses with different polarizations are expected to affect the ARPES spectrum of graphene. Again, driving frequency as well as field strength were chosen to match the experimental conditions. Figure 3(a1) shows the equilibrium spectrum of graphene. Note that the right branch of the Dirac cone is invisible because of photoemission matrix element effects.26,27 In the presence of a pp driving field the spectrum in Figure 3(a2) shows strong replica bands that, according to the model from ref (20), contain contributions from both Floquet–Bloch and Volkov states. For sp driving fields [Figure 3(a3)] the replica bands are found to be much weaker because of their pure Floquet–Bloch character (Supporting Information). Also, the simulations clearly show the predicted Rabi gaps. The spectrum for the topologically nontrivial state in the presence of a circularly polarized (cp) driving pulse is shown in Figure 3(a4). Aside from replica bands and Rabi gaps the spectrum shows a pronounced band gap at the Dirac point. In order to get a better impression of the intensity of the replica bands as well as the size of the dynamical band gaps, Figure 3(b1–b4) presents EDCs extracted along the dashed vertical lines in Figure 3(a1–a4). From Lorentzian fits to the EDC in Figure 3(b3) we extract a Rabi gap of 200 meV for the sp drive. For the cp drive, Lorentzian fits of the EDCs in Figure 3(b4) yield 100 meV for the Rabi gap and 60 meV for the gap at the Dirac point.

Figure 3.

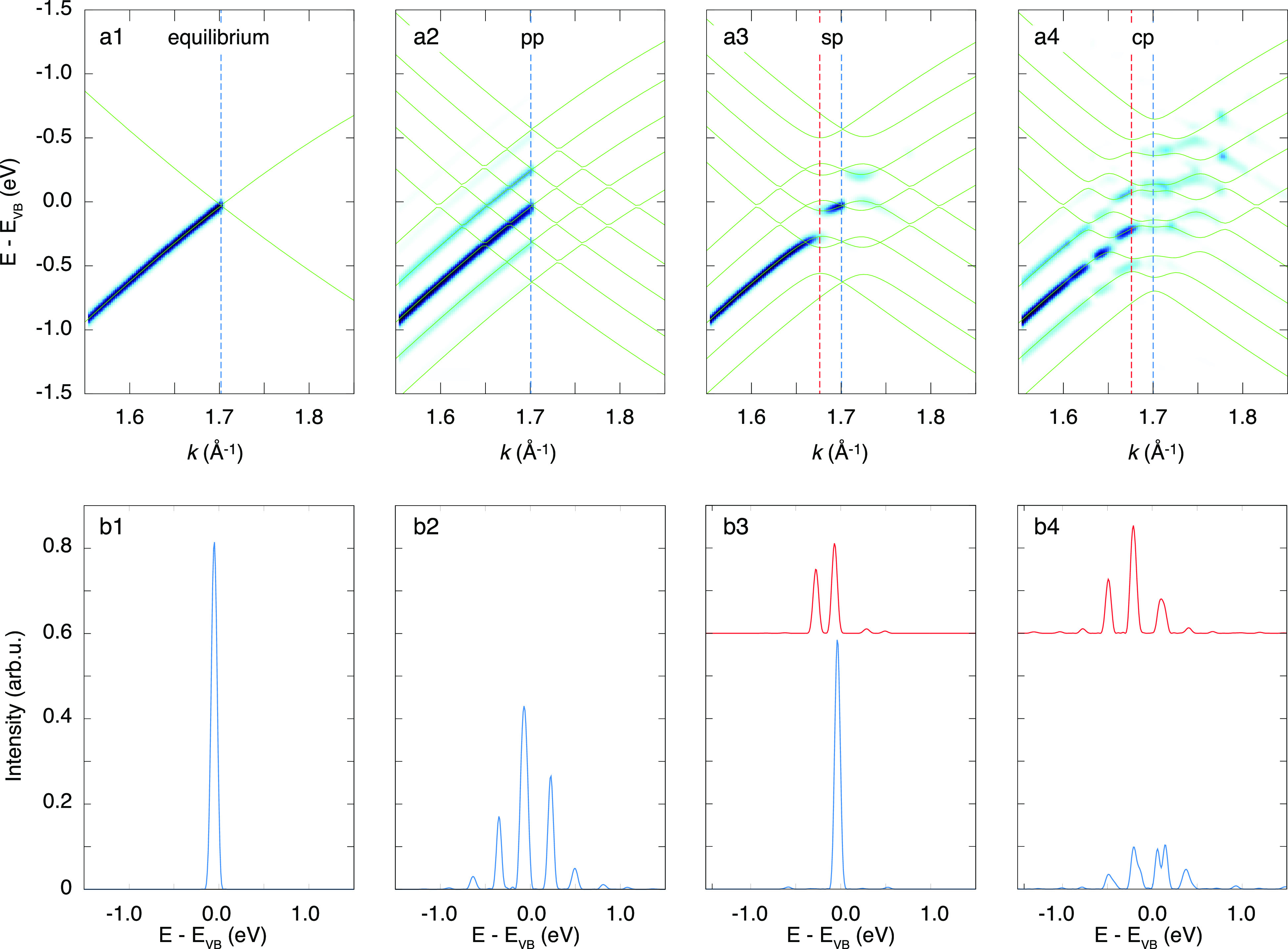
Figure 3

Open in a new tab

Simulated ARPES spectra for graphene together with initial state spectra (green lines) at equilibrium (a1), in the presence of a pp driving pulse (a2), in the presence of an sp driving pulse (a3), and in the presence of a cp driving pulse (a4). Blue and red dashed lines indicate the positions for the energy distribution curves (EDCs) in panels b1-b4. EDC through the Dirac point at equilibrium (b1), and in the presence of a pp driving pulse (b2). EDC through the Dirac point (blue) and at the position where the Rabi splitting is most pronounced (red) in the presence of an sp driving pulse (b3) and in the presence of a cp driving pulse (b4).

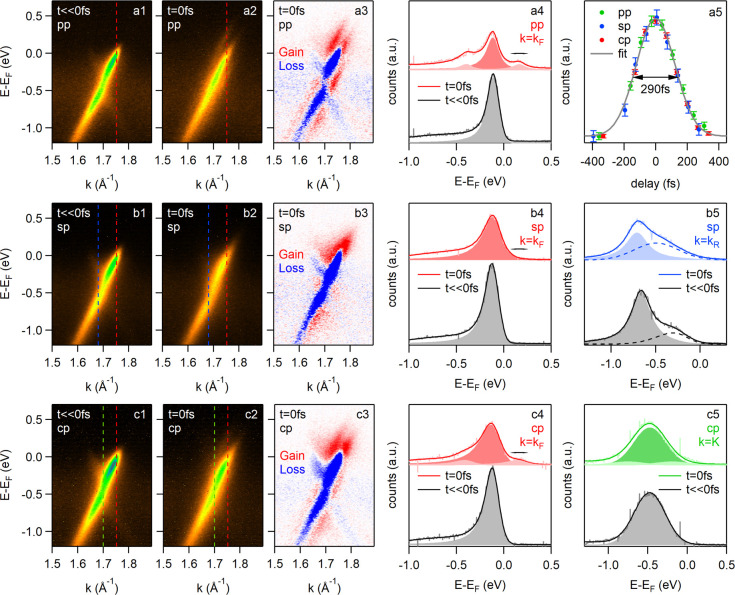
In Figure 4 we show the experimental data for direct comparison. The photocurrent at negative pump–probe delay is shown in column 1. In agreement with theory, only one of the two branches of the Dirac cone is visible in the spectrum. In contrast to the simulations that were performed for a neutral graphene layer, the epitaxial graphene samples used for the tr-ARPES experiment are n-doped with the Dirac point 0.4 eV below the Fermi level (Supporting Information). The second column of Figure 4 shows the photocurrent at zero pump–probe delay. The data for pp, sp, and cp driving pulses are shown in rows a, b, and c, respectively. Column 3 shows the drive-induced changes of the photocurrent for the three light polarizations.

Figure 4.

Figure 4

Open in a new tab

Rows a, b, and c show the tr-ARPES data for graphene for pp, sp, and cp driving pulses, respectively, at ℏωdrive = 280 meV with a peak driving field of Evac = 2.2 MV/cm. Columns 1 and 2 show the photocurrent at negative pump–probe delay and at t = 0 fs, respectively. Dashed lines mark the positions for the energy distribution curves (EDCs) in columns 4 and 5. Column 3 shows the drive-induced changes of the photocurrent at t = 0 fs. These data were obtained by subtracting the data in column 1 from the data in column 2. Column 4 shows EDCs at the Fermi momenta from column 1 and 2 together with Lorentzian fits. The data points in panel a5 were obtained by integrating the transient EDCs in column 4 over the energy range indicated by the black arrows. The gray line in a5 is a Gaussian fit. b5 shows EDCs through the Dirac point in b1 and b2 together with Gaussian fits. The dashed lines correspond to the second branch of the Dirac cone the intensity of which is suppressed because of photoemission matrix element effects. c5 shows EDCs at the momenta where the Rabi splitting is expected to occur in c1 and c2 together with Lorentzian fits. Filled gray areas show the individual peaks at negative delay. Filled light (dark) colored areas show the individual peaks of the sidebands (main bands).

To assess the formation of replica bands we extract EDCs close to the Fermi wave vector k = kF where the measured band structure is sharpest (column 4 of Figure 4). Replica bands are clearly resolved in Figure 4(a4) for pp driving pulses. The EDC for the sp drive, however, shows a single broad peak [Figure 4(b4)]. The EDC in Figure 4(c4) for cp driving pulses shows both broadening and replica bands, albeit not as well-resolved as in Figure 4(a4). The EDC in Figure 4(b5) for sp driving was extracted at the position of the putative Rabi gap k = kR. However, no gap is resolved in the data. The same holds for the topologically nontrivial gap for cp light: No gap is resolved in the EDC through the Dirac point at k = K shown in Figure 4(c5).

In order to extract the intensity of the replica bands as well as the peak widths, the EDCs in Figure 4 were fitted with an appropriate number of Lorentzian or Gaussian peaks (see figure caption and Supporting Information) (see figure caption) that are highlighted as shaded areas in the corresponding panels. The fit results are summarized in Table 1.

Table 1. Fit Results for the EDCs from Figure 4.

  fwhm intensity of replica bands
pp t < 0 fs k = kF 153 ± 2 meV 0%
pp t = 0 fs k = kF 153 ± 0 meV 12.5 ± 0.5%
sp t < 0 fs k = kF 189 ± 2 meV 0%
sp t = 0 fs k = kF 247 ± 4 meV 0%
sp t < 0 fs k = kR 269 ± 6 meV 0%
sp t = 0 fs k = kR 295 ± 15 meV 0%
cp t < 0 fs k = kF 198 ± 3 meV 0%
cp t = 0 fs k = kF 296 ± 5 meV 9.3 ± 0.3%
cp t < 0 fs k = K 466 ± 12 meV 0%
cp t = 0 fs k = K 480 ± 11 meV 7 ± 2%
Open in a new tab

The temporal evolution of the replica band intensity and/or broadening of the main band is shown in Figure 4(a5) together with a Gaussian fit. Similar to the case of WSe2 discussed earlier, we find that the lifetime of the drive-induced band structure changes is determined by the pump–probe cross-correlation.

Our findings can be summarized as follows: (1) We are able to resolve replica bands close to the Fermi edge whenever the driving field contains a pp component (i.e., pp and cp light). The intensity of the replica bands is found to be higher for pp than for cp light. (2) We observe a strong broadening of the spectra whenever the driving field contains an sp component (i.e., sp and cp light). This broadening is more pronounced for sp than for cp driving pulses. (3) We cannot resolve any band gap opening at k = kR or k = K. From the absence of Rabi gaps and replica bands for sp driving fields we conclude that no Floquet–Bloch states are formed in graphene under the present experimental conditions. Further, the absence of replica bands for sp driving fields suggests that the observed replica bands for pp driving fields likely originate from Volkov states alone.

Compared to the good agreement between theory and experiment in the case of WSe2, the agreement is rather poor in the case of graphene. We attribute this to the fact that the present TDDFT simulations neglect scattering events (Supporting Information) which turn out to be crucial to understand the observed broadening of the Dirac cone in the presence of sp and cp driving pulses as discussed in detail below. For Floquet–Bloch states to form, the interaction between the Bloch electrons and the light field needs to be coherent. It has been suggested that coherence will be destroyed if the scattering time of the Bloch electrons τ is shorter than or comparable to the period of the driving field Tdrive.1 Considering this, our results suggest that coherent driving of the Bloch electrons is possible in WSe2 but not in graphene.

One obvious difference between the two materials is that WSe2 has a band gap of ∼1 eV, whereas graphene is a semimetal. At room temperature the WSe2 valence band is completely filled and the conduction band is completely empty. Hence, the scattering phase space for Bloch electrons is zero and the scattering time is infinite. In neutral graphene the density of states at the Fermi level is zero. However, because of the absence of a band gap, any driving pulse with arbitrary frequency will generate electron–hole pairs. This increases the scattering phase space, and the scattering time becomes finite. The situation is even worse in the case of epitaxial graphene that exhibits a strong n-doping with the Dirac point ∼0.4 eV below the Fermi level resulting in a free carrier density of ne ≈ 1013 cm–2. Typical scattering times for photoexcited Dirac carriers in graphene are on the order of 10 fs,28 comparable to the period of the drive, which is 15 fs in the present study. Therefore, we conclude that scattering is detrimental for the formation of Floquet–Bloch states.

In the following we will present a simple model that allows us to investigate the influence of decoherence on Floquet–Bloch states and the corresponding quasienergy spectrum. We consider a resonantly driven two-level system with dissipation,19 the time propagation of which is described by the following quantum master equation

graphic file with name nl1c00801_m001.jpg 1

where ρ(t) is the density matrix of the system, H(t) the Hamiltonian, and D[ρ(t)] the relaxation operator. The Hamiltonian of the two-level system is given by

graphic file with name nl1c00801_m002.jpg 2

where Δ is the energy gap of the two-level system; σi are the Pauli matrices, and F0 and ωdrive are the amplitude and the frequency of the driving field, respectively. We use a simple relaxation time approximation for the dissipation operator

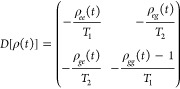graphic file with name nl1c00801_m003.jpg 3

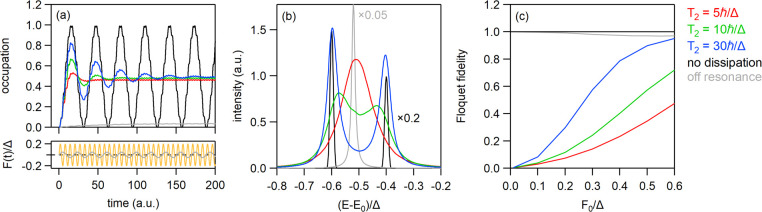
where ρij is a matrix element of the density matrix, where i, j = g denotes the ground state and i, j = e denotes the excited state. The longitudinal relaxation time T1 accounts for the finite lifetime of the excited state, while the transverse relaxation time T2 accounts for decoherence. Solving eq 1 yields ρee(t) that is plotted in Figure 5a for different values of T2 for T1 = 60ℏ/Δ. Without dissipation (T1 = T2 = ∞) ρee(t) is found to oscillate between zero and one with the Rabi frequency ωR = F0/ℏ. In addition, we observe fast oscillations with the frequency of the driving field ωdrive. For finite T1 the Rabi oscillations are observed to be strongly damped with a lifetime that decreases with decreasing T2. We also evaluate the quasienergy spectrum of the two-level system in the presence of dissipation as described in ref (19). In Figure 5b we plot the quasienergie spectrum for different values of T2 for T1 = 60ℏ/Δ. Without dissipation (T1 = T2 = ∞) we observe two sharp peaks that correspond to the Rabi splitting of the ground state. At finite T1, the peaks are found to broaden and the Rabi splitting is found to decrease with decreasing T2 until the two components merge into a single broad peak when T2 < 1/6 TR where TR = 2π/ωR.

Figure 5.

Figure 5

Open in a new tab

Theoretical results for a resonantly driven two-level system coupled to a bath. T1 was set to 60 ℏ/Δ. The case without dissipation corresponds to T1 = T2 = ∞. (a) Population dynamics of the upper electronic level for different decoherence times T2 (upper panel) in the presence of an external driving field (lower panel). (b) Quasienergy spectrum of the driven electronic system once a steady state is reached for different decoherence times T2. (c) Floquet fidelity of the nonequilibrium steady states as a function of field strength for different decoherence times T2. Gray lines correspond to off-resonant driving with T2 = 5 ℏ/Δ.

In order to quantify to what degree the eigenstates of the driven dissipative system can be described by Floquet states we define the Floquet fidelity18 as SF = |det F| with the Floquet fidelity matrix F. The matrix elements of F

graphic file with name nl1c00801_m004.jpg 4

are given by the absolute square of the overlap between natural orbitals |NOi(t)⟩ (eigenvectors of the single-particle density matrix) and the Floquet states |ΨF,j(t)⟩ averaged over one period T of the driving field. SF = 1 if all the natural orbitals are identical to Floquet states. If the natural orbitals are fully delocalized in the Floquet basis, they are poorly represented by Floquet states and SF = 0. In Figure 5c we plot the Floquet fidelity as a function of T2 for different strengths of the driving field for T1 = 60 ℏ/Δ. The Floquet fidelity is found to increase with increasing T2 and with increasing field strength F0. We find that, even in the presence of considerable decoherence, Floquet states can be recovered for sufficiently high driving fields. We also computed the situation where the driving frequency is much smaller than the gap (see gray lines in Figure 5). In this case, the occupancy of the excited state remains small (Figure 5a), the quasienergy spectrum shows a single sharp peak for the ground state (Figure 5b), and the Floquet fidelity is always close to one (Figure 5c).

We interpret our results as follows. As the valence band in semiconducting WSe2 is completely filled, the only possibility for the Bloch electrons to follow the driving field is a coherent motion through the Brillouin zone. In this case, Floquet–Bloch states are generated quite easily, in agreement with the observation of sharp replica bands for sp light in Figure 1. In metallic graphene, however, a coherent motion of the driven Dirac carriers is possible only between two scattering events. If the scattering time τ becomes comparable to or shorter than the period of the drive Tdrive, Floquet effects are expected to be smeared out by collisions.1 Nevertheless, our model indicates that Floquet–Bloch states will survive in the presence of scattering, provided that the field strength is high enough. In this case, energy exchange with the drive will dominate over energy dissipation to the bath, the influence of scattering will become negligible, and Floquet states will be restored.

In the present study, the driving field strength was limited by the appearance of space charge effects in the tr-ARPES experiments. The maximum possible field strength turned out to be too low to generate Floquet–Bloch states. 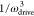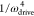Alternatively, one might consider increasing the driving frequency such that, for a given scattering time, τ > Tdrive.1 However, the size of the Rabi gaps decreases as 1/ωdrive,22 the size of the dynamical band gap at the Dirac point as Inline graphic,2 and the intensity of the replica bands even as Inline graphic.8,20,21 Therefore, it is unlikely that measurable Floquet effects survive at high driving frequencies.

Our findings seem to contradict the recent observation of a light-induced anomalous Hall effect in graphene using ultrafast transport experiments.9 In contrast to our work on epitaxial graphene, the transport experiments were performed on exfoliated flakes where the Fermi level could be controlled via an applied gate voltage. The resulting carrier mobility was 10 000 cm2 V–1 s–1 in the vicinity of the Dirac point, 1 order of magnitude higher than typical carrier mobilities for graphene/SiC(0001).29 Furthermore, the transport experiments were performed at 80 K, whereas the tr-ARPES experiments were performed at room temperature. Because of these differences, it its quite likely that in the ultrafast transport experiments τ > Tdrive, while in the present tr-ARPES experiments τ < Tdrive.

In summary, we have used tr-ARPES to investigate the band structure changes induced by strong mid-infrared driving of WSe2 and graphene. Good agreement between tr-ARPES and TDDFT simulations for WSe2 indicates the formation of Floquet–Bloch states. In the case of graphene, however, TDDFT simulations predict the formation of replica bands, Rabi gaps, and a gap at the Dirac point, none of which are observed experimentally. Instead, tr-ARPES reveals a pronounced broadening of the spectral features that we attribute to decoherence via scattering supported by simulations based on a resonantly driven two-level system with dissipation.

Our results clearly reveal the practical limitations of Floquet engineering. Floquet–Bloch states are readily generated in semiconductors using subgap excitation. There, however, the induced band structure changes are trivial and leave the transport properties unaffected. More intriguing phenomena such as light-induced topological phase transitions often rely on resonant driving of the material. These proposals can be implemented successfully only if the scattering time of the respective excited states is long enough, limiting the approach to materials with extremely long scattering times. Topological insulators such as Bi2Te3 where scattering times in excess of 1 ps have been reported30 and exfoliated graphene at low temperature9 might be among the few materials that fulfill the severe requirements of Floquet engineering.

Acknowledgments

This work was supported by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) through CRC 925 (Project 170620586), CRC 1277 (Project 314695032), and the Cluster of Excellence “CUI: Advanced Imaging of Matter”. Further, the work received funding from the European Research Council (Starting Grant 851280 and Advanced Grant 694097), the European Union Graphene Flagship under Grant Agreement Nos. 785219 and 881603, Grupos Consolidados (IT1249-19), and JSPS KAKENHI (Grant Number JP20K14382). The Flatiron Institute is a division of the Simons Foundation.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.nanolett.1c00801.

  • Details about sample growth, tr-ARPES setup, Floquet and Volkov states, data analysis, and simulations (PDF)

The authors declare no competing financial interest.

Supplementary Material

nl1c00801_si_001.pdf (161.1KB, pdf)

References

  1. Dunlap D. H.; Kenkre V. M. Dynamic localization of a charged particle moving under the influence of an electric field. Phys. Rev. B: Condens. Matter Mater. Phys. 1986, 34, 3625–3633. 10.1103/PhysRevB.34.3625. [DOI] [PubMed] [Google Scholar]
  2. Oka T.; Aoki H. Photovoltaic Hall effect in graphene. Phys. Rev. B: Condens. Matter Mater. Phys. 2009, 79, 081406. 10.1103/PhysRevB.79.081406. [DOI] [Google Scholar]
  3. Lindner N. H.; Refael G.; Galitski V. Floquet topological insulator in semiconductor quantum wells. Nat. Phys. 2011, 7, 490. 10.1038/nphys1926. [DOI] [Google Scholar]
  4. Lignier H.; Sias C.; Ciampini D.; Singh Y.; Zenesini A.; Morsch O.; Arimondo E. Dynamical Control of Matter-Wave Tunneling in Periodic Potentials. Phys. Rev. Lett. 2007, 99, 220403. 10.1103/PhysRevLett.99.220403. [DOI] [PubMed] [Google Scholar]
  5. Jotzu G.; Messer M.; Desbuquois R.; Lebrat M.; Uehlinger T.; Greif D.; Esslinger T. Experimental realization of the topological Haldane model with ultracold fermions. Nature 2014, 515, 237. 10.1038/nature13915. [DOI] [PubMed] [Google Scholar]
  6. Eckardt A. Colloquium: Atomic quantum gases in periodically driven optical lattices. Rev. Mod. Phys. 2017, 89, 011004. 10.1103/RevModPhys.89.011004. [DOI] [Google Scholar]
  7. Wang Y. H.; Steinberg H.; Jarillo-Herrero P.; Gedik N. Observation of Floquet-Bloch States on the Surface of a Topological Insulator. Science 2013, 342, 453–457. 10.1126/science.1239834. [DOI] [PubMed] [Google Scholar]
  8. Mahmood F.; Chan C.-K.; Alpichshev Z.; Gardner D.; Lee Y.; Lee P. A.; Gedik N. Selective scattering between Floquet-Bloch and Volkov states in a topological insulator. Nat. Phys. 2016, 12, 306. 10.1038/nphys3609. [DOI] [Google Scholar]
  9. McIver J. W.; Schulte B.; Stein F.-U.; Matsuyama T.; Jotzu G.; Meier G.; Cavalleri A. Light-induced anomalous Hall effect in graphene. Nat. Phys. 2020, 16, 38. 10.1038/s41567-019-0698-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Dehghani H.; Oka T.; Mitra A. Dissipative Floquet topological systems. Phys. Rev. B: Condens. Matter Mater. Phys. 2014, 90, 195429. 10.1103/PhysRevB.90.195429. [DOI] [Google Scholar]
  11. Wilczek F. Quantum Time Crystals. Phys. Rev. Lett. 2012, 109, 160401. 10.1103/PhysRevLett.109.160401. [DOI] [PubMed] [Google Scholar]
  12. Else D. V.; Bauer B.; Nayak C. Floquet Time Crystals. Phys. Rev. Lett. 2016, 117, 090402. 10.1103/PhysRevLett.117.090402. [DOI] [PubMed] [Google Scholar]
  13. Zhang J.; Hess P. W.; Kyprianidis A.; Becker P.; Lee A.; Smith J.; Pagano G.; Potirniche I.-D.; Potter A. C.; Vishwanath A.; Yao N. Y.; Monroe C. Observation of a discrete time crystal. Nature 2017, 543, 217. 10.1038/nature21413. [DOI] [PubMed] [Google Scholar]
  14. Choi S.; Choi J.; Landig R.; Kucsko G.; Zhou H.; Isoya J.; Jelezko F.; Onoda S.; Sumiya H.; Khemani V.; von Keyserlingk C.; Yao N. Y.; Demler E.; Lukin M. D. Observation of discrete time-crystalline order in a disordered dipolar many-body system. Nature 2017, 543, 221. 10.1038/nature21426. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Dehghani H.; Oka T.; Mitra A. Out-of-equilibrium electrons and the Hall conductance of a Floquet topological insulator. Phys. Rev. B: Condens. Matter Mater. Phys. 2015, 91, 155422. 10.1103/PhysRevB.91.155422. [DOI] [Google Scholar]
  16. Arecchi F.; Bonifacio R. Theory of optical maser amplifiers. IEEE J. Quantum Electron. 1965, 1, 169–178. 10.1109/JQE.1965.1072212. [DOI] [Google Scholar]
  17. Meier T.; Thomas P.; Koch S. W.. Coherent Semiconductor Optics; Springer: Berlin, 2007. [Google Scholar]
  18. Sato S. A.; McIver J. W.; Nuske M.; Tang P.; Jotzu G.; Schulte B.; Hübener H.; De Giovannini U.; Mathey L.; Sentef M. A.; Cavalleri A.; Rubio A. Microscopic theory for the light-induced anomalous Hall effect in graphene. Phys. Rev. B: Condens. Matter Mater. Phys. 2019, 99, 214302. 10.1103/PhysRevB.99.214302. [DOI] [Google Scholar]
  19. Sato S. A.; De Giovannini U.; Aeschlimann S.; Gierz I.; Hübener H.; Rubio A. Floquet states in dissipative open quantum systems. J. Phys. B: At., Mol. Opt. Phys. 2020, 53, 225601. 10.1088/1361-6455/abb127. [DOI] [Google Scholar]
  20. Park S. T. Interference in Floquet-Volkov transitions. Phys. Rev. A: At., Mol., Opt. Phys. 2014, 90, 013420. 10.1103/PhysRevA.90.013420. [DOI] [Google Scholar]
  21. Madsen L. B. Strong-field approximation in laser-assisted dynamics. Am. J. Phys. 2005, 73, 57–62. 10.1119/1.1796791. [DOI] [Google Scholar]
  22. Syzranov S. V.; Fistul M. V.; Efetov K. B. Effect of radiation on transport in graphene. Phys. Rev. B: Condens. Matter Mater. Phys. 2008, 78, 045407. 10.1103/PhysRevB.78.045407. [DOI] [Google Scholar]
  23. Trushin M.; Schliemann J. Anisotropic photoconductivity in graphene. EPL (Europhysics Letters) 2011, 96, 37006. 10.1209/0295-5075/96/37006. [DOI] [Google Scholar]
  24. Malic E.; Winzer T.; Bobkin E.; Knorr A. Microscopic theory of absorption and ultrafast many-particle kinetics in graphene. Phys. Rev. B: Condens. Matter Mater. Phys. 2011, 84, 205406. 10.1103/PhysRevB.84.205406. [DOI] [Google Scholar]
  25. Aeschlimann S.; Krause R.; Chávez-Cervantes M.; Bromberger H.; Jago R.; Malić E.; Al-Temimy A.; Coletti C.; Cavalleri A.; Gierz I. Ultrafast momentum imaging of pseudospin-flip excitations in graphene. Phys. Rev. B: Condens. Matter Mater. Phys. 2017, 96, 020301. 10.1103/PhysRevB.96.020301. [DOI] [Google Scholar]
  26. Shirley E. L.; Terminello L. J.; Santoni A.; Himpsel F. J. Brillouin-zone-selection effects in graphite photoelectron angular distributions. Phys. Rev. B: Condens. Matter Mater. Phys. 1995, 51, 13614–13622. 10.1103/PhysRevB.51.13614. [DOI] [PubMed] [Google Scholar]
  27. Daimon H.; Nakatani T.; Imada S.; Suga S. Circular dichroism from non-chiral and non-magnetic materials observed with display-type spherical mirror analyzer. J. Electron Spectrosc. Relat. Phenom. 1995, 76, 55–62. 10.1016/0368-2048(95)02476-X. [DOI] [Google Scholar]
  28. Gierz I.; Calegari F.; Aeschlimann S.; Chávez Cervantes M.; Cacho C.; Chapman R. T.; Springate E.; Link S.; Starke U.; Ast C. R.; Cavalleri A. Tracking Primary Thermalization Events in Graphene with Photoemission at Extreme Time Scales. Phys. Rev. Lett. 2015, 115, 086803. 10.1103/PhysRevLett.115.086803. [DOI] [PubMed] [Google Scholar]
  29. Emtsev K. V.; Bostwick A.; Horn K.; Jobst J.; Kellogg G. L.; Ley L.; McChesney J. L.; Ohta T.; Reshanov S. A.; Röhrl J.; Rotenberg E.; Schmid A. K.; Waldmann D.; Weber H. B.; Seyller T. Towards wafer-size graphene layers by atmospheric pressure graphitization of silicon carbide. Nat. Mater. 2009, 8, 203. 10.1038/nmat2382. [DOI] [PubMed] [Google Scholar]
  30. Reimann J.; Schlauderer S.; Schmid C. P.; Langer F.; Baierl S.; Kokh K. A.; Tereshchenko O. E.; Kimura A.; Lange C.; Güdde J.; Höfer U.; Huber R. Subcycle observation of lightwave-driven Dirac currents in a topological surface band. Nature 2018, 562, 396. 10.1038/s41586-018-0544-x. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

nl1c00801_si_001.pdf (161.1KB, pdf)

Articles from Nano Letters are provided here courtesy of American Chemical Society

RESOURCES