Mechanical Anisotropy Assessment in Kidney Cortex Using ARFI Peak Displacement: Preclinical Validation and Pilot In Vivo Clinical Results in Kidney Allografts

Abstract

The kidney is an anisotropic organ, with higher elasticity along versus across nephrons. The degree of mechanical anisotropy in the kidney may be diagnostically relevant if properly exploited; however, if improperly controlled, anisotropy may confound stiffness measurements. The purpose of this study is to demonstrate the clinical feasibility of acoustic radiation force (ARF)-induced peak displacement (PD) measures for both exploiting and obviating mechanical anisotropy in the cortex of human kidney allografts, in vivo. Validation of the imaging methods is provided by preclinical studies in pig kidneys, in which ARF-induced PD values were significantly higher (p < 0.01, Wilcoxon) when the transducer executing asymmetric ARF was oriented across versus along the nephrons. The ratio of these PD values obtained with the transducer oriented across versus along the nephrons strongly linearly correlated (R² = 0.95) to the ratio of shear moduli measured by shear wave elasticity imaging. On the contrary, when a symmetric ARF was implemented, no significant difference in PD was observed (p > 0.01). Similar results were demonstrated in vivo in the kidney allografts of 14 patients. The symmetric ARF produced PD measures with no significant difference (p > 0.01) between along versus across alignments, but the asymmetric ARF yielded PD ratios that remained constant over a six-month observation period post-transplantation, consistent with stable serum creatinine level and urine protein-to-creatinine ratio in the same patient population (p > 0.01). The results of this pilot in vivo clinical study suggest the feasibility of 1) implementing symmetrical ARF to obviate mechanical anisotropy in the kidney cortex when anisotropy is a confounding factor and 2) implementing asymmetric ARF to exploit mechanical anisotropy when mechanical anisotropy is a potentially relevant biomarker.

I. Introduction

CHRONIC kidney disease (CKD), a progressive and irreversible pathologic syndrome, is a major public health problem worldwide. Patients with CKD have increased risk for end-stage renal disease (ESRD), acute kidney injury, cardiovascular disease, and premature death [1]. When CKD progresses to ESRD, treatment often involves dialysis or kidney transplantation. Of these options, kidney transplantation is the most cost-effective with the best survival outcomes [2]. However, the majority of allografts do not function for the remainder of a recipient’s lifetime [3], and 20%–30% of grafts fail in living recipients by 10 years [4]. Efforts to preserve kidney function are critical to extending the lifetime of a kidney allograft. Kidney biopsy is the gold standard to identify grafts in need of intervention to prevent failure. However, it is susceptible to sampling errors, and its invasive nature is associated with hematuria, hematomas, arterio-venous fistula and, in rare cases, transplant loss [3]. An alternative, noninvasive method for detecting early kidney allograft pathology is vitally needed.

A sensitive and specific indication of early allograft dysfunction is parenchymal fibrosis [3], [5]-[7]. The noninvasive detection and quantification of such fibrotic changes are clinically relevant to diagnosing and monitoring graft health. Ultrasound-based methods such as compression elastography [8]-[12], transient elastography [13], [14], and acoustic radiation force (ARF)-induced shear wave velocity (SWV) [15]-[20] have been applied to identify correlations between parenchymal stiffness and fibrosis extent, but results have been inconsistent. The variability in the findings may be due to the anisotropic nature of the kidney parenchyma, in which the elasticity is higher along versus across the nephrons [21]. Thus, if imprecisely controlled, measurement orientation could confound stiffness measurements. One approach to standardizing elasticity assessments in the mechanically anisotropic kidney is to use rotationally invariant techniques [22].

Alternatively, the degree of mechanical anisotropy in the kidney parenchyma could be exploited to detect changes in the structure and composition of parenchymal tissue.

Hossain and Gallippi [23] and Hossain et al. [24] recently developed a novel ARF-based method for selectively obviating or exploiting mechanical anisotropy in transversely isotropic (TI) materials. To obviate anisotropy and achieve rotationally invariant stiffness estimates in simulated TI materials, a spatially symmetric ARF impulse (ARFI) excitation point spread function (PSF) was used. By so doing, ARFI-induced peak displacements (PD) did not vary with material orientation. To exploit anisotropy, a spatially asymmetric ARFI excitation PSF was used. Then, the degree of anisotropy (DoA) was assessed as the ratio of PDs achieved when the long axis of the asymmetric ARF was aligned along versus across the materials’ axis of symmetry (AoS). One of the main advantages of this method is that the DoA is estimated from displacements observed in the ARFI region of excitation (ROE), so it is not necessary to observe shear wave propagation. Another advantage is that by adjusting the shape of the ARF PSF, anisotropy may be selectively obviated or exploited.

By extension, if we consider the kidney cortex as a TI material with the AoS oriented along the nephrons, the methods developed by Hossain and Gallippi [23] and Hossain et al. [24] may be applicable to selectively exploiting or obviating mechanical anisotropy to assess renal allograft health. The overall goal of this study is to demonstrate, in a pilot clinical study, the feasibility of in vivo mechanical anisotropy assessment by ARFI PD ratio in human kidney allografts. First, for validation purposes, mechanical anisotropy measures by ARFI PD ratio were compared to those achieved by shear wave elasticity imaging (SWEI)-derived [25] shear moduli ratio in pig kidney, ex vivo and in vivo, with varying degrees of mechanical anisotropy.

II. Materials and Methods

A. Acoustic Radiation Force Impulse and Shear Wave Elasticity Imaging Data Acquisition and Processing

ARFI and sWEI imaging in pigs were performed using a Siemens S3000 Helix and 9L4 transducer, while human imaging was performed with the siemens Acuson Antares and VF7-3 linear array transducer (Siemens Healthcare, Ultrasound Division Unit, WA, USA). Both systems were equipped for research purposes, and the Axius direct ultrasound research interface was used to customize beam sequencing and to collect raw radio frequency (RF) data. Table I summarizes the parameters of the ARFI imaging for each transducer. For both human and animal experiments, ARFI data were acquired using F/1.5 (asymmetric) and F/5.0 (symmetric) focal configurations. The (lateral, elevational) extents of the ARFI excitations, measured at the focal depth using the methods described in [24], were: (0.71 and 1.85 mm) for asymmetric and (2.33 and 1.86 mm) for symmetric ARF when the 9L4 transducer was used; (0.71 ± 0.01 and 2.24 ± 0.075 mm) for asymmetric and (2.31 ± 0.03 and 2.21 ± 0.08 mm) for symmetric ARF when the VF7-3 transducer was used. Asymmetry ratios (ARs) for each ARFI excitation, calculated as the ratio of elevational over lateral PSF extent, are presented in Table I. Note that system power levels were held constant for both focal configurations, so the more tightly focused asymmetric ARFI excitations yielded, on average, 2.69 ± 0.50 (9L4) and 1.46 ± 0.52 (VF7-3) times larger displacements than symmetric ARF.

TABLE I.

ARFI and SWEI Excitation and Tracking Parameters. VF7-3 and 9L4 Were Used to Image Transplants and Pigs’ Kidney, Respectively. Asymmetry Ratio (AR) = Elevation/Lateral = Degree of Asymmetry in the ARFI Excitation PSF

Parameter		Value
Transducer		VF7-3	9L4
Bandwidth		53%	55%
Elevational Lens focus (mm)		37.5	40
Sampling frequency (MHz)		40	40
ARF duration		70 μs	70 μs
ARF excitation center freq. (MHz)		4.21	4.0
ARF F/#		1.5 and 5.0	1.5 and 5.0
ARF focus (mm)		37 ± 1*	36
ARF excitation PSF AR	F/1.5	3.15 ± 0.11*	2.60
	F/5.0	0.96 ± 0.03*	0.80
Tracking center freq. (MHz)		6.15	6.0
Tracking Tx F/#		1.5	1.5
Tracking Rx F/#**		0.75	0.75
Tracking Tx focus (mm)		37 ± 1*	36

^*mean ± standard

^**Aperture growth and dynamic Rx focusing enabled

For ARFI imaging, the lateral field of view (FOV) was 2 cm, with 40 evenly spaced lateral lines. Each interrogated lateral position received an ARFI excitation with normal incidence by laterally translating ARFI subapertures. Note that the tradeoff between lateral FOV, which decreases with increasing ARFI subaperture size, and ARFI PSF AR, which increases with increasing ARFI subaperture size. In this work, a F/1.5 ARFI focal configuration was deemed sufficiently asymmetric while enabling a 2 cm lateral FOV.

Lateral positions were acquired in a nonserial order across the lateral FOV to minimize heating and reduce interference between consecutive ARF excitations. First, a single ensemble was captured from the far left of the FOV, then in the middle of the FOV, then one position to the right of the far left, then one position to the right of the middle, and so on, such that no two consecutive ensembles were captured in two adjacent lateral locations. One spatially matched B-mode image was acquired preceding each ARFI acquisition for anatomical reference. The lateral FOV of the B-mode image was 4 cm, with evenly spaced 220 lateral lines.

The acquired raw RF data were transferred from the scanner to a computational workstation for custom analysis. ARFI-induced motion was measured using 1-D axial normalized cross correlation (NCC) [26] with parameters: 4× spline-based upsampling of RF data (natively sampled at 40 MHz), 376-μm kernel length (i.e., 1.5λ, where λ is the wavelength of the tracking pulse assuming a speed of sound of 1540 m/s), and an 80-μm search region. A quadratic filter [27] was applied to the NCC-derived displacement versus time profiles to reduce motion artifacts. Then, the maximum displacement was displayed to render 2-D ARFI PD images. Raw RF data were used to generate B-mode images, which were calculated as the log compressed the absolute value of the Hilbert-transformed RF data.

SWEI ensembles consisted of two reference pulses, 1 ARF impulse, and 60 tracking lines. The ARF excitation duration was 70 μs with F/1.5 focal configuration. The ARF location was kept constant, and the tracking beam location shifted within the SWV measurement region of interest (ROI). The ARF excitation was repeated 29×, and tissue motion was tracked in 29 evenly spaced lateral locations ranging from 1.0 to 8.25 mm from the push location. The ensemble length in each lateral tracking location was 6 ms. As described earlier for ARFI, displacements were measured using 1-D axial normalized cross correlation [26]. To increase the SNR of the displacement data, a moving-average filter [movmean function in MATLAB (Mathworks Inc., Natick, MA, USA)] was implemented in the axial direction with a window size of 0.5 mm. Then, directional filtering [28] was applied to remove shear wave reflections. Next, for each axial location, time to peak (TTP) displacement was calculated, and SWV was estimated by fitting a straight line to lateral location versus TTP in lateral sliding windows of 2.0-mm length. Fits with R² < 0.9 were considered poor and were not used in SWV estimations. Finally, the shear modulus was estimated from the SWV (V) as, μ = ρ V², where ρ is the density, assumed to be 1000 kgm⁻³.

The [mechanical index, spatial-peak temporal average intensity (I_spta)] values associated with the employed ARFI excitations were (1.79 and 11.0 W/cm²) for VF7-3 and (1.6 and 2.3 W/cm²) for 9L4. These values were measured using asymmetric focal configuration with 70% system power. Acoustic intensity measurements were made using an HGL-0200 hydrophone (Onda, Sunnyvale, CA, USA) in a water tank (21 °C) and then adjusted to account for attenuation in soft tissue (attenuation α = 0.3) using the methods described in [29] and [30].

B. Preclinical Experimental Protocol

All animal experiments were reviewed and approved by the University of North Carolina at Chapel Hill Institutional Animal Care and Use Committee. Experiments involved 2 male and 1 female pigs with a mean body weight of 74.4 ± 9.3 kg at the time of imaging. All pigs were anesthetized. Typically, pigs were sedated with telazol (2–3 mg/kg IM). Atropine sulfate (0.03 mg/kg SQ) was given as an antisialagogue prior to endotracheal intubation to reduce excess pharyngeal secretion. Following sedation, pigs were fitted with a nose cone for the administration of inhaled isoflurane (4%–5%) to induce anesthesia. Once palpebral reflexes were absent and the jaw musculature relaxed, pigs were intubated and maintained on isoflurane for the duration of the experiment. Respiration was spontaneous throughout the procedures. Intravenous fluid (0.9% NaCl) was infused at approximately 5 mL/kg/hr. An ear vein catheter was introduced for saline infusions (5 mL/min). A pressure catheter (SPR-350S, Millar Inc., Houston, TX, USA) was placed in one femoral artery, and blood pressure was monitored continuously using LabChart software (ADinstruments, Colorado Springs, CO, USA). Pigs were placed in the supine position, and the areas of skin over the abdomen and flank were shaved and prepped with an aseptic technique in accordance with guidelines established by the Division of Laboratory Animal Medicine. The right kidney of each pig was exposed via midline and lateral flank laparotomy incisions and the combination of sharp and blunt dissection.

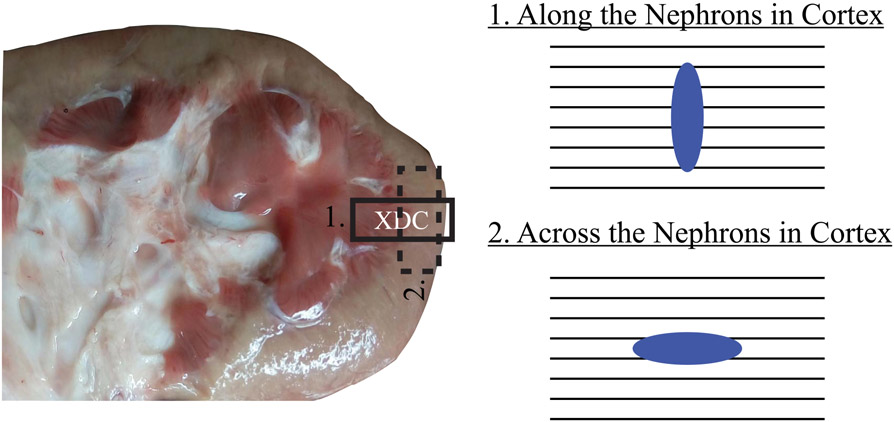
Each exposed kidney was imaged in the baseline condition by ARFI and SWEI [29] using the imaging parameters described earlier. A stereotactic clamp was used to hold the transducer and maintain its position during data acquisition. The transducer was placed on the superior pole of the kidney with the lateral FOV aligned along the direction of the nephrons. Both the medulla and cortex were visible in this view. ARFI and SWEI data sets were acquired in immediate succession. Then, the transducer was rotated 90° such that the lateral FOV was aligned across the nephrons in the cortex, and ARFI and SWEI data sets were acquired in this position. Transducer positioning during data acquisitions is represented in Fig. 1.

Fig. 1.

Approximate position of the transducer (XDC) in along and across the nephrons with corresponding nephrons-PSF orientations at both alignments. Black lines: orientations of the nephron. Blue ellipse: PSF at the focal depth for an asymmetric ARF.

After imaging the exposed kidney in the baseline condition, the renal vein was ligated, and ARFI and SWEI imaging were performed as done for the baseline condition in approximately the same location (identified grossly by skin markings and finely by anatomical features apparent on B-mode). Finally, the renal vein was released and the renal artery was ligated, and ARFI and SWEI imaging were again performed in approximately the same location. It has previously been demonstrated that renal vein ligation induces distention with increased cortical stiffness, while renal artery ligation induces ischemia with decreased cortical stiffness [21], [31], [32]. Note that in the context of this work, the purpose of ligating the renal vein and artery was not to directly study the impacts of distention and ischemia on cortical mechanical anisotropy. Rather, the intention was to compare ARFI-derived PD ratios to SWEI-derived shear moduli ratios in kidney cortex exhibiting a range of mechanical anisotropy. However, for greater readability, venous and arterial ligation conditions will from here forward be referred to as “distention” and “ischemia,” respectively.

The imaging focal depth was maintained at 3.6 cm for all pigs, focal configurations, orientations, and ligation conditions using acoustic standoff pads (AquaFlex, Civco, IA, USA). Two repeated acquisitions were collected for each case in the event of scanner error. Measurements over two repeated acquisitions were averaged.

After in vivo imaging was completed, the contralateral (left) kidneys were harvested for ex vivo ARFI and SWEI imaging in a water bath. It was expected that excision would alter kidney mechanical anisotropy, therefore, ex vivo imaging was performed to increase the range of examined mechanical anisotropy. The transducer was clamped in a rotation stage (Newport Corporation, Irvine, CA, USA) for a 90° rotation from along to across the nephrons alignments. The experiment was performed in a vibration isolation table. The ex vivo ARFI and SWEI imaging parameters and methods, including transducer positioning at the superior pole with orientations along and across the nephrons alignments, were as described earlier for in vivo data acquisitions.

C. Clinical Experimental Protocol

All procedures were approved by the University of North Carolina Chapel Hill Institutional Review Board, and informed consent was obtained for all subjects. Data sets were collected under an ongoing clinical study (ClinicalTrials.gov No. NCT03079882) at the University of North Carolina (UNC) at Chapel Hill, Chapel Hill, NC, USA. ARFI imaging of kidney allografts was performed at two, four, and six months after transplantation in 14 (N = 14) transplant patients. All patients had stable serum creatinine levels and urine protein-to-creatinine ratios, so all allografts were considered healthy without clinical indication for biopsy. Note that protocol biopsies are not part of the routine standard of care for kidney transplant patients at UNC Hospitals. Table II summarizes patient characteristics and serum creatinine levels and urine protein-to-creatinine ratios at the three imaging time points.

TABLE II.

Kidney Transplant Patients’ Characteristics

Parameter	Values
Male, N		8
Female, N		6
Age, (mean ± standard deviation), years		54.15 ± 15.44
Body mass index, kg/m2		26.62 ± 4.18
African American, N		6
Caucasian, N		8
Living donor, N		4
Deceased donor, N		10
	2 months	4 months	6 months
Serum Creatinine (mean ± standard), mg/dL	1.40 ± 0.34	1.44 ± 0.37	1.31 ± 0.23
Urine Protein to creatinine ratio gm/gm	0.12 ± 0.37	0.06 ± 0.17	0.05 ± 0.05

In patients, in vivo ARFI imaging was performed as described earlier by an experienced sonographer. Patients were imaged on an inclined (15° from horizontal) bed in the supine position. The patients were asked to remain motionless during imaging. Imaging was performed in the superior pole of the kidney. In the longitudinal view, the lateral FOV was aligned along nephrons, and both kidney parenchyma and a portion of the kidney sinus were visible. The imaging focal depth was selected based on the position of the sinus, generally between 3.5 and 4.0 cm. Then, the sonographer rotated the transducer 90° such that it was aligned across the nephrons in the cortex, and ARFI data were acquired. For each transducer orientation (along and across the nephrons) and for each ARFI focal configuration (asymmetric and symmetric), three repeated acquisitions were collected to mitigate potential error from unexpected patient motion during data collection. Measurements over the three repeated acquisitions were averaged. If any repeated measures changed due to patients movements or contained noise, those measures were removed before taking the average. The acquired raw RF data were processed as described earlier.

D. ARFI Anisotropy Estimation and Validation

To evaluate the degree of mechanical anisotropy from each ARFI and SWEI data set, ROIs with dimensions 2.5 mm × 3 mm (axial × lateral) were selected. The axial and lateral ROI sizes were determined by the axial range over which the asymmetric ARFI PSF AR was expected to be consistent and the expected spatial extent of the continuous cortex, respectively.

ROI positioning was performed using only B-Mode guidance as follows. For both pig and human data sets, ROIs were positioned axially between 0.5 mm below and 2.0 mm above the imaging focal depth. Laterally, for data acquired with the transducer aligned along nephrons (comprising sinus, medulla, and cortex), ROIs were centered in the cortex approximately 2.25 mm left of the rightmost edge of the kidney. Note that in some cases the rightmost edge of the kidney was slightly outside the lateral ARFI FOV. In these cases, the lateral center of the ROI was positioned approximately 1.5 mm left of the rightmost part of the ARFI FOV contained cortex.

For data acquired with the transducer aligned across the nephrons, lateral ROI placement varied between pigs and human data sets. In pig kidneys, which were exteriorized for imaging, the orientation of the transducer could be highly controlled such that the entire across-nephron FOV contained only cortex. In this case, ROIs were laterally centered in the ARFI FOV. In human kidney allografts, which were imaged transcutaneously, the orientation of the transducer with respect to kidney anatomy was less controllable due to differences in how the allografts sat in the abdomen. Therefore, the across-nephron FOV could contain the medulla. To evaluate only the cortex, the lateral centers of ROIs were positioned as described for the along-nephron data. The median PD or shear modulus value in each ROI was found, and DoA was calculated as

$${\text{DoA}}_{\text{PD}}=\frac{{\text{PD}}_{\text{across}}}{{\text{PD}}_{\text{along}}}$$ (1)

$${\text{DoA}}_{\mu }=\frac{{\text{SWV}}_{\text{along}}^2}{{\text{SWV}}_{\text{across}}^2}=\frac{{\mu }_L}{{\mu }_T}$$ (2)

where DoA_PD and DoA_μ are DoA in terms of PD and in terms of the shear elastic modulus (μ), respectively. PD_along and PD_across represent PD when the transducer is aligned along and across the nephrons, respectively. Similarly, SWV_along and SWV_across represent SWV when the transducer is aligned along and across nephrons, respectively. When considering (1) and (2), it is important to understand that PD_along is inversely proportional to the longitudinal shear elastic modulus (μ_L). Similarly, PD_across is inversely proportional to the transverse shear elastic modulus (μ_T) [23], [24]. Thus, DoA_PD in (1) reflects the ratio of μ_L over μ_T, which is consistent with DoA_μ (2). To validate PD-derived mechanical anisotropy estimates, DoA_PD were statistically correlated with DoA_μ. The difference in PD was also evaluated as PD_across–PD_along.

E. Statistical Methods

PD using asymmetric and symmetric focal configurations was compared between “along” and “across” the nephrons using paired Wilcoxon signed rank test [33]. PD ratios in human subjects were grouped by imaging time points. Two paired Wilcoxon sign rank tests were carried out to compare the PD ratio at two versus four months and at two versus six months post-transplantation [33]. Similarly, paired Wilcoxon sign rank tests were carried out to compare serum creatinine level and urine protein-to-creatinine ratios at two versus four months and at two versus six months after post-transplantation [33]. Statistical significance was based on p ≤ 0.01. All statistical analyses were carried out using MATLAB. Note that the Wilcoxon sign rank test compares the medians of two groups.

III. Results

A. Preclinical Validation

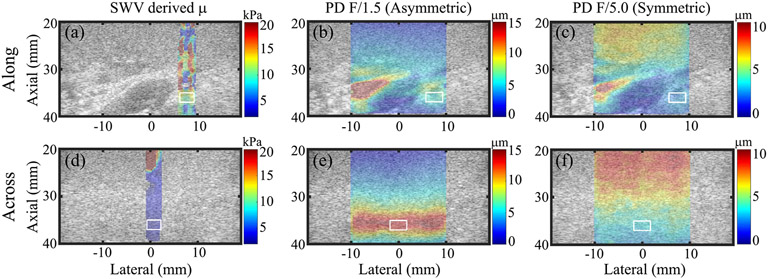
For an example pig kidney imaged in vivo at baseline, Fig. 2 shows SWEI-derived shear modulus (μ, left column) and ARFI PD achieved using asymmetric (middle column) and symmetric (right column) ARF focal configurations. Note that sWV-derived shear modulus was higher along [Fig. 2(a)] versus across [Fig. 2(d)] nephrons, as expected. Conversely, PD achieved using the asymmetric ARF was lower along [Fig. 2(b)] versus across [Fig. 2(e)] nephrons because PD and shear elastic modulus are inversely related. However, PD achieved using the symmetric ARF was similar in both transducer orientations [Fig. 2(c) and (f)].

Fig. 2.

SWV-derived μ images (left column) and ARFI PD images of in vivo pig kidney using asymmetric (middle column) and symmetric (right column) ARF focal configurations. Images are overlaid with transparency on the matched B-modes. Top and bottom rows: images when the transducer was oriented along and across nephrons, respectively. White contours: measurement regions of interest in the cortex. Note that the color bar units and ranges differ between columns.

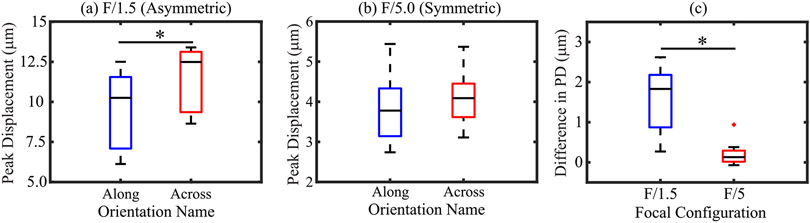
Fig. 3 shows box plots of PD using asymmetric [Fig. 3(a)] and symmetric [Fig. 3(b)] ARF focal configurations in along and across the nephron alignments. The data include in vivo acquisitions at baseline (N = 3), with distention (N = 3), and with ischemia (N = 2) as well as ex vivo (N = 3) acquisitions. PD in along versus across alignments was significantly different from each other for the asymmetric ARF focal configuration [Fig. 3(a)] but this was not so for the symmetric ARF focal configuration [Fig. 3(b)]. Fig. 3(c) shows box plots of the difference in PD across versus along nephrons for asymmetric and symmetric ARFs. The difference in PD was significantly higher (p < 0.01) for asymmetric than symmetric ARF. The median difference was 1.72 and 0.11 μm for asymmetric and symmetric ARFs.

Fig. 3.

In in vivo pig kidney, PD using (a) asymmetric and (b) symmetric ARF focal configurations oriented along and across nephrons. (c) Difference in PD_along and PD_across derived using asymmetric (blue) and symmetric (red) ARF focal configurations. An asterisk (*) indicates the statistically significant difference. Black lines inside boxes, top box edges, and bottom box edges represent the median, 25th, and 75th percentile values, respectively.

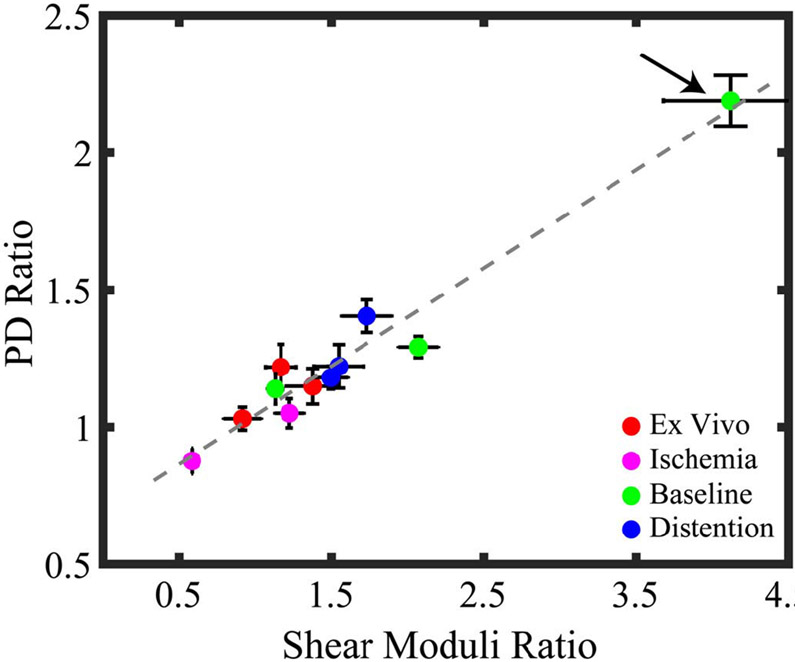
Fig. 4 shows the linear regression between ARFI PD ratios for the asymmetric ARF and SWEI-derived shear moduli ratios. The data include in vivo acquisitions at baseline, with distention, and with ischemia as well as ex vivo acquisitions. Note that one in vivo data set with ischemia was discarded due to an imaging system error during the acquisition. The PD ratio acquired using the asymmetric ARF increased linearly with the ratio of shear moduli, with an R² value of 0.95. Note that one pig had outlier PD and shear moduli ratios at baseline (arrow). When this outlier data point was rejected, the R² value for the linear regression was 0.75.

Fig. 4.

PD ratio versus shear moduli ratio in pig renal cortex using an asymmetric ARF focal configuration. Color indicates kidney condition, and marker and error bar indicate the median and interquartile range of ratio values in the ROIs. Arrow indicates a pig with higher anisotropy at baseline than the other pigs. The R² value of the linear regression was 0.95 when the outlier is included and 0.75 when the outlier is rejected.

B. Demonstration of Clinical Feasibility

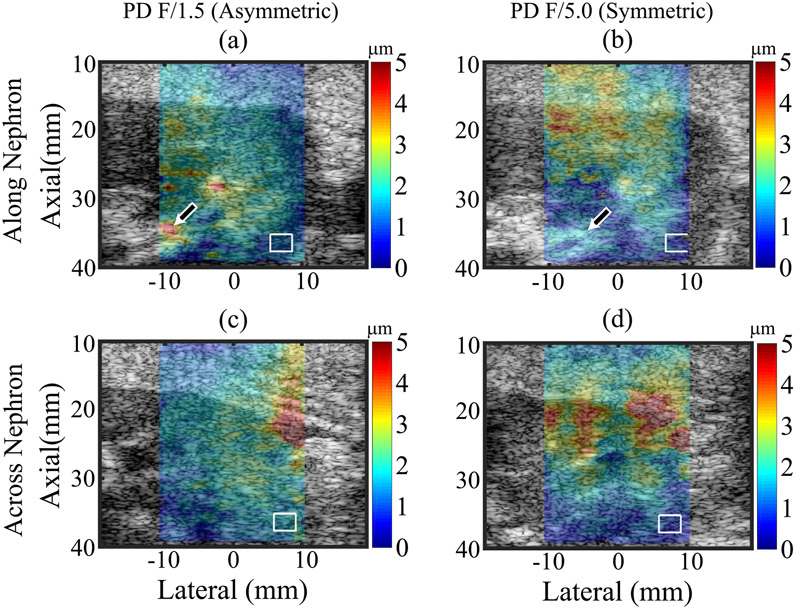
Fig. 5 shows PD superimposed with transparency on matched B-mode images of a kidney transplant patient (31-year-old male, BMI = 20.7 kg/m², serum creatinine level = 1.32 mg/dL, urine protein-to-creatinine ratio = 0.07 gm/gm, and focal depth = 37 mm). Similar to pigs, PD was lower along versus across nephrons for asymmetric ARF, whereas for symmetric ARF, PDs were similar in both orientations. Note that ROIs were offset in Fig. 5(b) compared to Fig. 5(a), (c) and (d). The rightmost edge of ARFI FOV was in the cortex in Fig. 5(b), but the rightmost edge of ARFI FOV was outside of the kidney in Fig. 5(a), (c) and (d).

Fig. 5.

ARFI PD images using asymmetric (left column) and symmetric (right column) ARF focal configurations superimposed with transparency on the B-Mode images of a kidney transplant patient. Top and bottom rows: images when the transducer was oriented along and across nephrons, respectively. White contours: measurement regions of interest in the cortex. Arrows: renal sinus.

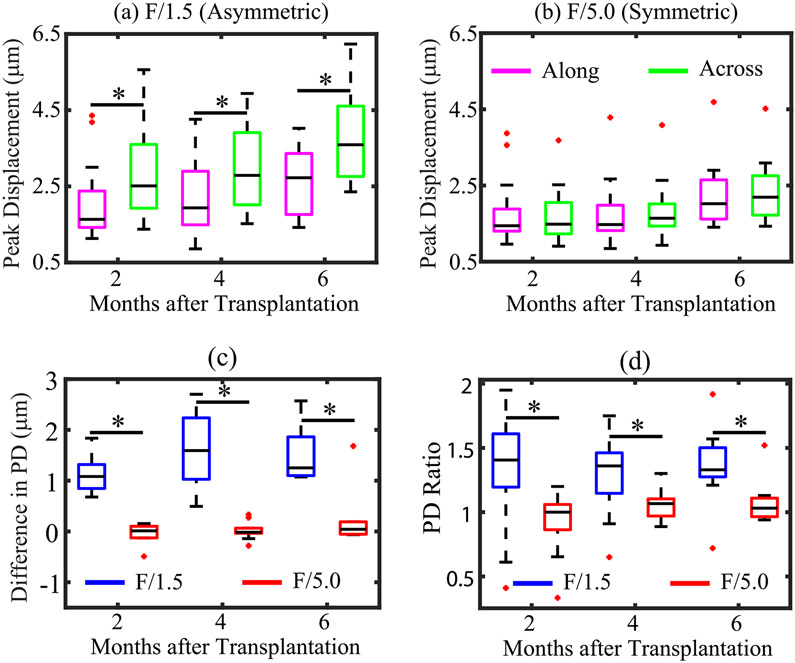
For all 14 patients, Fig. 6 shows box plots of PD values obtained using asymmetric [Fig. 6(a)] and symmetric [Fig. 6(b)] ARF-aligned along and across the nephrons. PDs were statistically different in along versus across alignments for the asymmetric, but not the symmetric, ARF. Fig. 6(c) shows box plots of the difference in PD across versus along nephrons (PD_across–PD_along) for asymmetric and symmetric ARF as a function of imaging time point. At all three time points, the difference in PD was significantly higher (p < 0.01) for asymmetric than symmetric ARF. For asymmetric ARF, median difference in PD was 1.1, 1.6, and 1.3 μm, while for symmetric ARF, median difference in PD was 0.01, 0.01, and 0.04 μm, at two, four, and six months post-transplantation. Notably, the difference in PD remained relatively stable across all imaging time points for asymmetric and symmetric ARF. Fig. 5(d) shows that PD ratio using asymmetric and symmetric ARF was not significantly different between two versus four months (F/1.5: p = 0.58; F/5: p = 0.11) and two versus six (F/1.5: p = 0.24; F/5.0: p = 0.25) months after transplantation. These stable PD ratio values are consistent with serum creatinine level and urine protein-to-creatinine ratios, which did not significantly differ between two versus four months (serum creatinine: p = 0.87 and urine protein-to-creatinine ratio: p = 0.54) and two versus six (serum creatinine: p = 0.95 and urine protein to creatinine ratio: p = 0.81) months after transplantation (Table II). At all three time points, the PD ratio was significantly higher (p < 0.01) for asymmetric than symmetric ARF.

Fig. 6.

For human renal allografts, in vivo, PD in the renal cortex as a function of imaging time point using (a) asymmetric and (b) symmetric ARF aligned along (magenta) and across (green) nephrons. Black asterisk (*) indicates statistically significant PD in along versus across alignments. (c) Difference in PD, and (d) PD ratio as a function of imaging time point using asymmetric (blue) and symmetric (red) ARF PSFs. Black asterisk (*) indicates statistical difference between asymmetric and symmetric ARF focal configurations. For all panels, black lines inside boxes, top box edge, and bottom box edge represent median, 25th, and 75th percentile values, respectively, and red dots indicate outliers.

IV. Discussion

A novel ARF-based method for clinically evaluating mechanical anisotropy in the kidney cortex has been demonstrated in vivo in transplant patients. In this new approach, the kidney is interrogated with a geometrically asymmetric ARF excitation, and the ratio of ARFI PDs achieved with the transducer aligned along versus across the nephrons reflects the degree of mechanical anisotropy. Alternatively, when mechanical anisotropy is a confounding factor to be obviated, employing a geometrically symmetric ARF excitation achieves directionally independent PD measures.

Figs. 3 and 4 show that while PD varied with transducer orientation in pig kidney cortex for the asymmetric ARF (F/1.5), and while the asymmetric ARF yielded PD ratios that linearly correlated with the ratio of SWEI-derived longitudinal and transverse elastic shear moduli, PD was rotationally invariant for the symmetric ARF (F/5.0). These results support that while mechanical anisotropy may be exploited by using an asymmetric ARF, the symmetric ARF supports the evaluation of renal mechanical property without the confounding effects of directional differences. Notably, the symmetric ARF exhibits consistent AR over a larger axial range (14 mm) than the asymmetric ARF (3 mm). This implies that the symmetric ARF can be used to achieve rotationally invariant mechanical property assessment over a larger axial range than demonstrated herein. In this work, the evaluated axial ranges of the symmetric and asymmetric ARF cases were kept consistent to ensure that the same tissue regions were interrogated.

Pigs were selected for validation testing because the animal model enabled in vivo evaluation of mechanical properties during induced ischemia (renal artery ligation) and distention (renal vein ligation). For both PD- and SWEI-derived shear moduli ratios, ischemic cortex (pink markers in Fig. 4) generally had lower anisotropy ratio than distended cortex (blue markers). A possible explanation for this outcome is an error in transducer alignment. When the transducer is exactly aligned along versus across the nephrons, the highest PD- and SWEI-derived ratios will result. When the transducer is misaligned, the resulting PD and SWEI outcomes reflect a mixture of both moduli, and thus the associated ratio of outcome measures is artifactually reduced. Therefore, it may be that more perfect transducer alignment in the cases of distention caused the ratios to be higher than the ischemia ratios. Alternatively, another possible explanation for higher PD- and SWEI-derived shear modulus ratios in distention versus ischemia is that in ischemia, the reduction in perfusion decreases the longitudinal modulus more than the transverse, resulting in a net decrease in the ratio. Similarly, it is possible that in distention, the increase in perfusion increases the longitudinal modulus relative to the ischemic condition, resulting in a higher anisotropy ratio. Previous studies [21], [31], [32] demonstrating that ischemia decreases and distention increases cortical stiffness support such an explanation.

It is relevant to consider that in the baseline condition, one pig kidney exhibited PD- and SWEI-derived shear moduli ratios that were higher than those in the other kidneys (arrow in Fig. 4). This outlier measurement could reflect true differences in the fundamental mechanical properties of that specific kidney. Alternatively, as described earlier, it may be that more perfect transducer alignment caused the outlier PD- and SWEI-derived shear moduli ratio measurements. Future work will evaluate approaches to optimizing transducer alignment. Apart from alignment error, another possible explanation for the outlier value could be heterogeneity in the elevational dimension of the measurement region (that is not evident in the associated B-Mode image). If the measurement ROIs unknowingly contains medulla and/or sinus, PD- and SWEI-derived modulus measurements would be confounded. Furthermore, in heterogeneous regions, shear wave reflections from structures in elevation could introduce error in SWV measurements. Transducers capable of elevational focusing could be implemented to mitigate this potential error. Another possible explanation for the outlier PD- and SWEI-derived shear moduli ratio is variability in measurement location between baseline, ischemia, and distention conditions.

Fig. 4 generally suggests that SWEI-derived shear moduli ratio has better contrast than the PD ratio for detecting mechanical anisotropy, although a systematic evaluation of such has not yet been conducted. Despite a potential loss of contrast, there are three primary benefits to evaluating anisotropy by PD ratio as opposed to SWEI-derived shear moduli ratio. First, depending on the depth of the kidney and the strength of the ARF, there may not be sufficient displacement magnitude outside the ROE to reliably measure SWV over the required measurement kernel in the kidney. Note that in the presented work, ARFI PD was 1–6 μm at the focal depth of the ROE [Fig. 6(a)]. Second, heterogeneity in the kidney could complicate SWV measurement by introducing complex wave reflections and limiting the possible lateral extent of the measurement kernel. Finally, SWV measurement requires observation of displacement profiles at multiple lateral locations, which reduces frame rate and increases ARF dose unless a plane wave imaging method [34] is implemented. A potential drawback to plane wave imaging is the lack of transmit focusing, which leads to loss of SNR and resolution and challenges applications in deep tissues and obese patients. To increase SNR, coherent spatial compounding may be employed. However, coherent compounding reduces the frame rate relative to conventional plane wave imaging.

The clinical application of ARFI PD ratio estimation to evaluating mechanical anisotropy in renal allografts is presented in Figs. 5 and 6. Fig. 6 shows that as in the preclinical case, the asymmetric ARF exploits mechanical anisotropy in the human kidney cortex, while the symmetric ARF obviates it, in vivo. Furthermore, for asymmetric ARF, the PD ratio does not statistically change over a six-month period after transplantation. This result is consistent with serum creatinine level and urine protein-to-creatinine ratio stability (Table II), which suggests no clinically meaningful graft pathology. Note that as described earlier, protocol biopsies are not standard care for kidney transplant patients at UNC Hospitals, so no histologic correlate was available for comparison. However, the data were collected as part of an ongoing clinical longitudinal study, so future time points are expected to be validated by histology.

A limitation to the clinical study is that in some data sets, the medulla and cortex were not readily discernable by B-mode imaging. To avoid evaluating PD in regions of the medulla, the measurement ROIs were positioned close to the outer edge of the kidney. However, it is possible that some ROIs contained portions of the medulla. It is expected that the medulla and cortex exhibit a different mechanical anisotropy [21], so including medulla in the ROI would be a source of error. Another limitation to the clinical study is small sample size and few time samples. Ongoing work will include more patients and longer observation periods. Finally, it is important to consider that phase aberration may have altered ARFI PSF AR from expectation. If phase aberration rendered the PSF less asymmetric than expected, then PD ratio would have been underestimated. Future work will evaluate the impact of phase aberration on PD ratio assessment and develop aberration correction strategies as needed.

This pilot feasibility study represents a first step toward evaluating if PD ratio is a relevant clinical biomarker for renal transplant health. Ongoing investigations aim to determine if PD ratio noninvasively indicates the need for biopsy with higher sensitivity and specificity than serum creatinine level or protein-to-creatinine ratio, which are nonspecific for renal dysfunction and lacks clear diagnostic thresholds [35].

Beyond biopsy indication, more work is needed to determine if the PD ratio could eventually be relevant as a noninvasive alternative to biopsy. A substantial challenge to achieving this goal will be demonstrating successful differentiation of underlying pathology, including inflammation, vascular disease, and scarring. Consistent with prior work [21], the preclinical results are shown in Fig. 4 suggest that the degree of perfusion impacts PD ratio, which may be relevant for detecting vascular disease. However, scarring is also expected to impact mechanical anisotropy. Differentiating vascular disease from scarring or other pathologies will likely require an evaluation of both elastic and viscous properties, as recently described by Hossain et al. [36], [37]. The authors implemented a new ARF-based mechanical property assessment method, viscoelastic response (VisR) ultrasound [38]-[41], to evaluate elastic and viscous properties independently of each other in the transplanted kidneys of patients undergoing clinically indicated biopsy. The results showed that the VisR elasticity parameter, “relative elasticity,” distinguished allografts with vascular disease and tubular/interstitial scarring from control allografts with no suspected renal pathology. Furthermore, the VisR viscosity parameter, “relative viscosity,” distinguished allografts with only vascular disease from control allografts. Thus, evaluating both elastic and viscous anisotropy could help to not only detect renal transplant disease but also differentiate its underlying pathology.

V. Conclusion

This study demonstrates the clinical feasibility of ARFI-PD ratio as a measure of mechanical anisotropy in the allografts of renal transplant patients. In healthy allografts, PD ratios were stable over two, four, and six months post-transplantation. Preclinical validation studies in pig kidneys showed that PD ratios linearly correlated with SWEI-derived shear moduli ratios ex vivo as well as in vivo at baseline, with arterial ligation, and with venous ligation. Further, mechanical anisotropy was exploited by using an asymmetrical ARF, but a symmetric ARF generally obviated anisotropy and enabled angle-independent mechanical property assessment in the anisotropic cortex. Thus, when mechanical anisotropy is of interest as a renal biomarker, an asymmetric ARF should be implemented. However, when anisotropy is considered a confounding factor due to unknown or uncontrollable transducer orientation with respect to nephron alignment, a symmetric ARF should be used. This work represents a critical first step toward clinically translating ARFI PD ratio as a relevant, new, noninvasive biomarker for monitoring kidney transplant health.

Biography

Md Murad Hossain (GS’16) received the B.Sc. degree in electrical engineering from the Islamic University of Technology, Gazipur, Bangladesh, in 2009, and the M.Sc. degree in electrical engineering from George Mason University, Fairfax, VA, USA. He is currently pursuing the Ph.D. degree with the joint Department of Biomedical Engineering, The University of North Carolina at Chapel Hill, Chapel Hill, NC, USA, and the North Carolina State University, Raleigh, NC, USA.

His research interests include acoustic radiation force imaging and medical signal processing.

Randal K. Detwiler received the B.S. degree from Capital University, Bexley, OH, USA, in 1982, and the M.D. degree from The Ohio State University, Columbus, OH, USA, in 1986.

He is an Allan Brewster Distinguished Professor of Medicine with The University of North Carolina at Chapel Hill, Chapel Hill, NC, USA, where he is also the Medical Director of the Kidney and Pancreas Transplantation Center. His research interests include all clinical aspects of kidney transplantation with particular emphasis on BK virus nephropathy, transplant focal segmental glomerulosclerosis, and promotion of kidney donation.

Emily H. Chang received the B.S. degree from Stanford University, Stanford, CA, USA, in 1995, and the M.D. degree from The University of North Carolina at Chapel Hill, Chapel Hill, NC, USA, in 2007.

She is currently an Assistant Professor of medicine with The University of North Carolina at Chapel Hill. Her research interests include ultrasound, chronic kidney disease and dialysis, mechanisms of kidney fibrosis and injury, and electrolyte disorders.

Melissa C. Caughey received the B.S. degree in biological sciences from North Carolina State University, Raleigh, NC, USA, in 1998, the M.P.H. degree from Emory University, Atlanta, GA, USA, in 2010, and the Ph.D. degree from The University of North Carolina at Chapel Hill, Chapel Hill, NC, USA, in 2014, with a focus on epidemiology.

She is currently an Instructor with the University of North Carolina School of Medicine. Her research interests include medical imaging biomarkers, biostatistical analysis, and the development of medical imaging technologies.

Melrose W. Fisher received the B.S. degree in registered nurse from The University of North Carolina at Chapel Hill, Chapel Hill, NC, USA, in 1983.

She is currently a Clinical Nurse Coordinator. She has over 30 years’ experience working with physicians and patients at the University of North Carolina Chapel Hill Medical Center. Her research interests include acoustic radiation force impulse ultrasound technology study.

Timothy C. Nichols received the B.S. degree (Hons.) from Stanford University, Stanford, CA, USA, and the M.D. degree from the Medical College of Virginia, Richmond, VA, USA, and trained as an internist, cardiologist, and researcher in atherosclerosis, thrombosis, and hemostasis.

He is currently a Professor of medicine and pathology and laboratory medicine with The University of North Carolina at Chapel Hill, Chapel Hill, NC, USA, and also the Director of the Francis Owen Blood Research Laboratory (FOBRL), Chapel Hill, NC, USA. His research focuses on atherosclerosis in familial hypercholeterolemia pigs and inherited bleeding disorders in hemophilic and von Willebrand disease dogs all of which are produced and maintained at the FOBRL.

Elizabeth P. Merricks was born in Ahoskie, NC, USA. She received the B.Sc. degree in medical technology and the Ph.D. degree in pathology from The University of North Carolina at Chapel Hill, Chapel Hill, NC, USA, in 1991 and 2010, respectively.

She is currently a Research Specialist with the Department of Pathology and Laboratory Medicine, The University of North Carolina at Chapel Hill. Her research interests include large animal models of disease (bleeding diatheses, atherosclerosis, hyper-cholesterolemia, and resultant renal complications) and new methods for long-term storage of blood products.

Robin A. Raymer received the B.S. degree in animal science from North Carolina State University, Raleigh, NC, USA, in 1979.

She is retired from the Francis Owen Blood Research Laboratory, The University of North Carolina at Chapel Hill, Chapel Hill, NC, USA. Her research interests are in hemophilia and thrombosis.

Margaret Whitford, photograph and biography not available at the time of publication.

Dwight A. Bellinger received the B.A. degree from George Washington University, Washington, DC, USA, in 1969, the D.V.M. degree from the University of Georgia, Athens, GA, USA, in 1976, and the Ph.D. degree in comparative medicine from Wake Forest University, Winston-Salem, CA, USA.

He is currently Professor Emeritus and a Visiting Scientist with the Department of Pathology and Laboratory Medicine, The University of North Carolina at Chapel Hill, Chapel Hill, NC, USA. His research interests include cardiovascular disease, hemophilia, and animal models.

Lauren E. Wimsey received the B.S. degree in animal science and the Doctor of Veterinary Medicine degree from North Carolina State University, Raleigh, NC, USA, in 2005 and 2009, respectively.

She is currently an Assistant Professor with a joint appointment at the Francis Owen Blood Research Laboratory and the Department of Comparative Medicine, The University of North Carolina at Chapel Hill, Chapel Hill, NC, USA. Her research interests include hemostasis and clotting disorders, hypertension, atherosclerosis, and related diseases.

Caterina M. Gallippi (A’07–M’17) received the B.S.E. degree in electrical engineering and a certificate in engineering biology from Princeton University, Princeton, NJ, USA, in 1998, and the Ph.D. degree in biomedical engineering from Duke University, Durham, NC, USA, in 2003, with a focus on ultrasonic imaging.

She is currently an Associate Professor with the joint Department of Biomedical Engineering, The University of North Carolina at Chapel Hill, Chapel Hill, NC, USA, and the North Carolina State University, Raleigh, NC, USA. Her research interests include radiation force imaging, adaptive signal filtering, multidimensional motion tracking, and magnetomotive ultrasound.