Different Kinetic Reactivity of Electrons in Distinct TiO₂ Nanoparticle Trap States

Abstract

Electrons added to TiO₂ and other semiconductors often occupy trap states, whose reactivity can determine the catalytic and stoichiometric chemistry of the material. We previously showed that reduced aqueous colloidal TiO₂ nanoparticles have two distinct classes of thermally-equilibrated trapped electrons, termed Red/e⁻ and Blue/e⁻. Presented here are parallel optical and electron paramagnetic resonance (EPR) kinetic studies of the reactivity of these electrons with solution-based oxidants. Optical stopped-flow measurements monitoring reactions of TiO₂/e⁻ with sub-stoichiometric oxidants showed a surprising pattern: an initial fast (seconds) decrease in TiO₂/e⁻ absorbance followed by a secondary, slow (minutes) increase in the broad TiO₂/e⁻ optical feature. Analysis revealed that the fast decrease is due to the preferential oxidation of the Red/e⁻ trap states, and the slow increase results from re-equilibration of electrons from Blue to Red states. This kinetic model was confirmed by freeze-quench EPR measurements. Quantitative analysis of the kinetic data demonstrated that Red/e⁻ react ~5 times faster than Blue/e⁻ with the nitroxyl radical oxidant, 4-MeO-TEMPO. Similar reactivity patterns were also observed in oxidations of TiO₂/e⁻ by O₂, which like 4-MeO-TEMPO is a proton-coupled electron transfer (PCET) oxidant, and by the pure electron transfer (ET) oxidant KI₃. This suggests that the faster intrinsic reactivity of one trap state over another on the seconds–minutes timescale is likely a general feature of reduced TiO₂ reactivity. This differential trap state reactivity is likely to influence the performance of TiO₂ in photochemical/electrochemical devices, and it suggests an opportunity for tuning catalysis.

Graphical Abstract

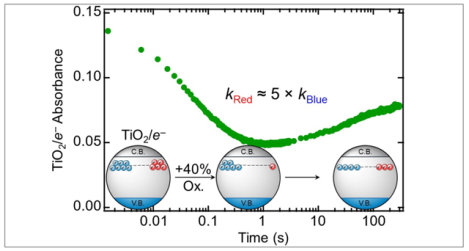
Introduction

Metal oxide semiconductors have long garnered interest across the physical sciences due to their attractive chemical, photochemical, electrochemical, optical, and electronic properties. One important feature is their ability to store and transport multiple charge carriers (redox equivalents). Understanding the chemical reactivity of such charge carriers in nanoscale metal oxides is crucial in their applications in renewable energy technologies and catalysis.¹ In-depth spectroscopic studies of reduced titanium dioxide (TiO₂) have identified various shallow and deep electron traps at diverse defect sites, including surface and interstitial Ti(III) centers and oxygen atom vacancies.^2–8 The relaxation of photo-generated delocalized conduction band electrons to trap states occurs very quickly, typically on the fs–ns timescale.^8–11 Much slower relaxations can occur up to tens of ms, attributed to proton involvement.¹² As such, trapped electrons play an important role in the function of almost all TiO₂-containing devices.^{8, 13–15}

Presented here are kinetic studies of thermally equilibrated electron trap states in colloidal aqueous TiO₂ nanoparticles (NPs). We examine the chemical reactivity of the reduced NPs on the seconds-to-minutes timescale more typical of catalysis. Our results are consistent with previous kinetic studies of colloidal TiO₂ by many groups, by many different techniques.^16–30 Such studies are complementary to the much more common work using transient, ultrafast kinetics by transient spectroscopies or under continuous UV illumination.³¹

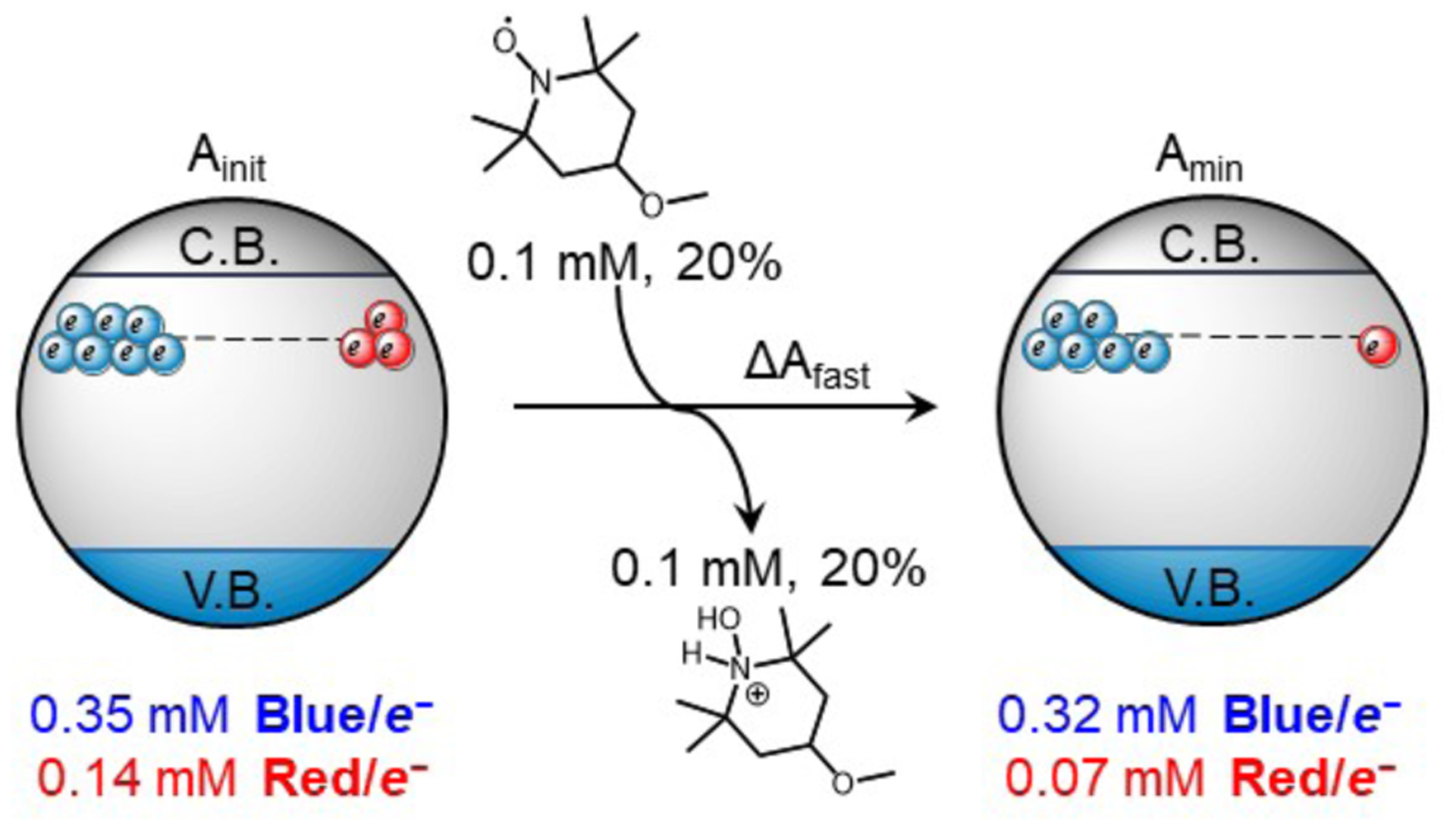
The current studies build on our prior discovery that the occupied trap states in these particular reduced colloidal TiO₂ NPs fall into two distinct types. On the basis of their optical spectra (Figure 1), we termed these trap states Red/e⁻ and Blue/e⁻.⁷ The Red/e⁻ and Blue/e⁻ trap states are generated via UV-photochemical reduction and are stable under an inert atmosphere. The EPR spectra of the Red/e⁻ and Blue/e⁻ indicated that these trap states are structurally distinct and have different symmetries (Figure 1).⁷ These states are in thermal equilibrium, with the Red/e⁻ higher in enthalpy (ΔH°) by 3.0 ± 0.6 kcal/mol (130 ± 30 meV), based on their relative ratio as a function of temperature.⁷ Surprisingly, re-equilibrations of the electrons between the Red/e⁻ and Blue/e⁻ traps upon changes in temperature were slow, occurring over at least several minutes. While the Red/e⁻ states have a higher ΔH°, at equilibrium the Red/e⁻ and Blue/e⁻ states have the same free energies (ΔG).

Figure 1:

(A) A TiO₂/e⁻ EPR spectrum (dashed trace) with simulated rhombic (Blue/e⁻) and axial (Red/e⁻) EPR components. (B) The molar absorptivity (ε) of the TiO₂/e⁻ optical spectrum (dashed trace) with simulated Red/e⁻ and Blue/e⁻ component peaks. Thermally equilibrated TiO₂/e⁻ colloids under our general conditions (Table-SI 8.1) typically contain Red/e⁻ and Blue/e⁻ electrons in a roughly 40:60 ratio. The simulated spectra were derived by fitting TiO₂/e⁻ EPR and optical spectra with both Red/e⁻ and Blue/e⁻ components as described in Peper et. al.⁷

We show here that Red/e⁻ and Blue/e⁻ react at different rates with solution-based oxidants. The reaction of Red/e⁻ with the nitroxyl radical 4-methoxy-2,2,6,6-tetramethyl-1-piperidinyloxyl (4-MeO-TEMPO) occurs ~5 times more quickly than the reaction of Blue/e⁻. Such differential trap-state reactivity can be observed because of the unusually simple Red/e⁻ and Blue/e⁻ system. While the electronic landscapes of TiO₂ and other semiconductor materials are typically more complex, containing a variety of reduced trap states,^{4–10, 32–33} the faster reactivity of one trap state over another is likely a common feature of NP reaction chemistry. For example, these results help to explain the typical ill-defined, multi-exponential behavior observed in kinetic studies of TiO₂^{4, 16, 34} and other nanomaterials.^{30, 35–38} These results show the importance of trap state populations in the performance of TiO₂ materials.³¹ They also raise questions about the connections and contrasts between fast-timescale photoinduced processes and slower-timescale, equilibrated and thermochemically-driven chemical reactions of trap states.

Methods

Anatase titanium dioxide nanoparticles (diameter = 4±1 nm) were synthesized via hydrolysis of titanium tetrachloride (TiCl₄) as previously described, see Supporting Information (SI)-Sections 1.3–1.5.^{7, 16} The resulting white solid TiO₂ product was re-suspended in neutral 18 MΩ cm water (without ligands) to give a transparent colloid (3g solid product L⁻¹) with pH 2.2–2.4, due to residual HCl from the synthesis. The colloid concentrations were roughly 30 μM in nanoparticles, with each NP containing ~1,000 Ti atoms.

Photochemical reduction of the colloidal NP suspension in the presence of 0.1–0.15 M methanol resulted in a blue coloration of the colloid and the appearance of EPR signals (SI-Sections 2.1 and 4.1).¹⁶ As previously reported, the optical and EPR signals of the reduced nanoparticles (TiO₂/e⁻) result from two structurally distinct trap states. The Red/e⁻ states have a longer-wavelength, a higher intensity optical absorbance (λ_max = 740 nm) and a broad axial EPR signal, while the Blue/e⁻ states have a low-intensity, blue-shifted absorbance (λ_max = 470 nm) and a rhombic EPR signal (Figure 1).⁷ Room temperature TiO₂/e⁻ samples were handled inside a N₂ glovebox or with gas tight syringes, and colloids exposed to air were kept at temperatures < −78 °C. The reduced colloids were stable under both conditions. The extent of colloid reductions, evaluated in terms of the concentration of electrons, [e⁻] (mol e⁻ L⁻¹), were determined via standard optical titrations with 4-MeO-TEMPO as previously described (SI-Section 2.2).^{7, 17} Photolysis of TiO₂ colloids (30 μM NPs) for 5 hours typically gave 1.0–1.5 mM e⁻.

The time course of TiO₂/e⁻ oxidations by various quantities of 4-MeO-TEMPO, potassium triiodide (KI₃) or O₂ were followed by optical spectroscopy via stopped-flow techniques (SI-Section 3.1–3.3). Additionally, the reaction of TiO₂/e⁻ and 4-MeO-TEMPO was followed by freeze-quench EPR spectroscopy (SI-Section 4.2). In both the stopped-flow and freeze-quench experiments, gas-tight syringes were used to mix equal volumes of TiO₂/e⁻ colloid and a pH-matched solution of the oxidant. The typical experimental conditions were pH 2.2–2.4, 15 μM TiO₂ nanoparticles, and 0.05–0.075 M methanol, where concentrations given refer to the solutions after mixing. For each specific experiment presented, these and other details are given in Table-SI 8.1.

Results

I. 100% Oxidation of TiO₂/e^–

The addition of excess 4-MeO-TEMPO to photochemically reduced TiO₂ results in the disappearance of the blue TiO₂/e⁻ color and the appearance of new diamagnetic ¹H NMR signals, consistent with the formation of protonated hydroxylamine 4-MeO-TEMPO-H(H⁺) (Figure-SI 2.2–2.3). The full oxidation of TiO₂/e⁻ (0.55 mM e⁻) by just over one equivalent of 4-MeO-TEMPO (0.57 mM) occurs in less than 2 seconds as indicated by the disappearance of the broad TiO₂/e⁻ optical signal in Figure 2. The change in TiO₂/e⁻ absorbance with oxidation is not uniform across the spectrum, resulting in a subtle blueshift in the TiO₂/e⁻ optical density, from λ_max = ~600 to ~460 nm (black markers, Figure 2). We will return to this blueshift in Section I of the Discussion below.

Figure 2:

Optical spectra monitoring the disappearance of TiO₂/e⁻ (0.55 mM e⁻) absorbance upon mixing with 4-MeO-TEMPO (0.57 mM). Black markers highlight the blueshift in the λ_max of the broad TiO₂/e⁻ absorbance band.

II. Sub-stoichiometric Oxidation of TiO₂/e⁻

Reactions of photochemically reduced NPs with sub-stoichiometric oxidants were monitored from 1.5 ms to 300 s using an optical stopped-flow instrument (SI-Section 3). These measurements revealed two distinct and surprising optical trends upon addition of 0.4 oxidizing equivalents of 4-MeO-TEMPO to TiO₂/e⁻ (0.49 mM e⁻), Figure 3A. The initial TiO₂/e⁻ absorbance (A_init) decreased quickly, within ~2 seconds, to a minimum value (A_min) before increasing slowly over several minutes to a final value (A_fin). The fast and slow changes in absorbance intensity are respectively coupled to blue- and red-shifts in the broad TiO₂/e⁻ absorbance peak. The same qualitative optical trends were observed in reactions with other sub-stoichiometric oxidants, including KI₃ and O₂ (Figure 3B and SI-Sections 3.5, 3.6). Based on the optical spectra in Figure 1, these changes suggest initial depletion of the more absorbing Red/e⁻ followed by slow re-establishment of the Red/e⁻ – Blue/e⁻ equilibrium, as discussed in more detail below.

Figure 3:

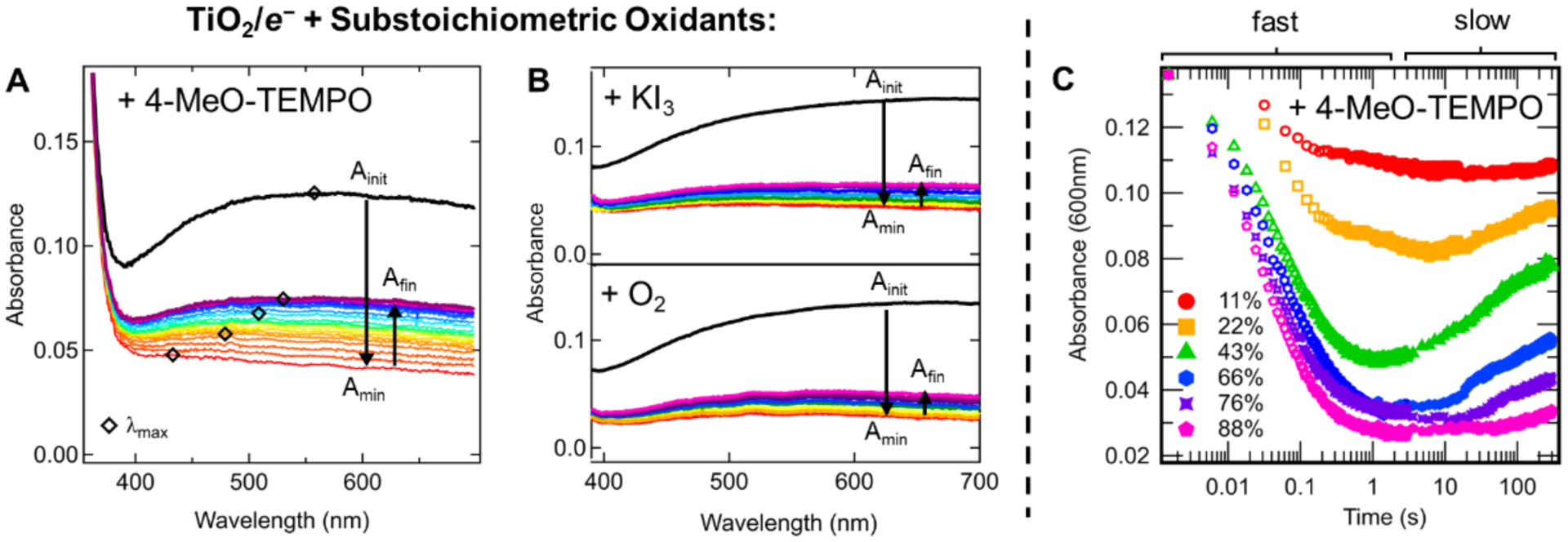
(A) Optical spectra monitoring the oxidation of TiO₂/e⁻ (0.49 mM e⁻) by 0.4 oxidizing equivalents of 4-MeO-TEMPO (0.19 mM). Black markers highlight the redshift in λ_max in the secondary, slow absorbance increase from A_min to A_fin. (B) Optical spectra following reactions of TiO₂/e⁻ (0.50 mM e⁻) with (top) 0.50 oxidizing equivalents KI₃ (0.125 mM I₂) and (bottom) ~0.50 oxidizing equivalents of O₂ (0.065 mM O₂). (C) Kinetic traces: Absorbance at 600 nm of a TiO₂/e⁻ colloid (0.50 mM e⁻) as a function of time after mixing with various oxidizing equivalents of 4-MeO-TEMPO. Absorbance is plotted versus a log time scale to show details of both the fast and slow absorbance changes.

The sub-stoichiometric reactivity of TiO₂/e⁻ with 4-MeO-TEMPO was broadly evaluated. The fast and slow reaction phases, and their distinct timescales, are seen clearly in the full kinetic traces following TiO₂/e⁻ (0.50 mM e⁻) absorbance upon reaction with various quantities of sub-stoichiometric 4-MeO-TEMPO, (Figure 3C and SI-Section 3.4). The magnitudes of the fast, slow, and total absorbance changes (ΔA_fast, ΔA_slow, and ΔA_tot = A_fin - A_init) as a function of %TiO₂/e⁻ oxidation are discussed below.

In order to further probe the sub-stoichiometric oxidation of TiO₂/e⁻, the time course of the reaction with 4-MeO-TEMPO was followed by EPR spectroscopy using freeze-quench techniques. A colloid of photochemically reduced TiO₂ NPs (0.69 mM e⁻) was mixed with 0.46 oxidizing equivalents 4-MeO-TEMPO (0.32 mM) and allowed to rest (i.e., react) for 0.1 – 600 s before being shot into liquid nitrogen. The frozen samples were maintained at T ≤ −78 °C and prepared for EPR measurements at 10 K (SI-Section 4.2). The EPR spectra collected after different resting times are shown in Figure 4. The actual reaction quench times are somewhat longer than the resting times indicated in the Figure 4 legend, because water droplets freeze relatively slowly in liquid nitrogen (the Leidenfrost phenomenon).³⁹ We crudely estimate the average sample freezing time of 1–2 seconds (SI-Section 4.4).

Figure 4:

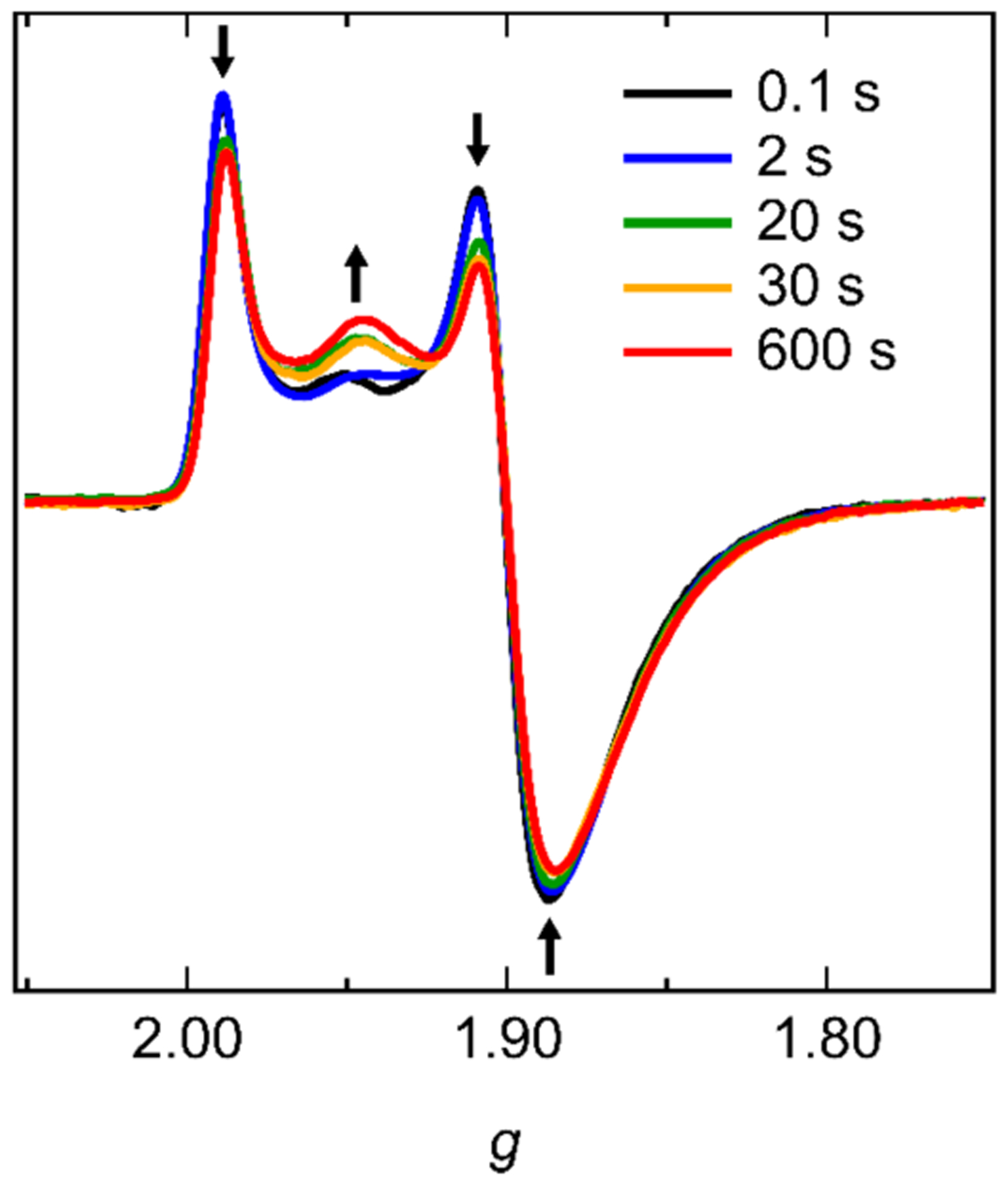
EPR spectra collected after mixing TiO₂/e⁻ (0.69 mM e⁻) and 0.46 oxidizing equivalents 4-MeO-TEMPO (0.32 mM) via freeze-quench techniques. The arrows denote spectral trends as a function of resting time. The resting times indicated in the legend underestimate of the actual reaction quench times due to slow freezing (see text and SI-Section 4.4). All spectra are baseline corrected and normalized to total spin density, SI-Section 4.3.

The EPR signals are consistent with Ti(III)-based electrons previously observed in this (and other) reduced TiO₂ systems.^5–7 The change in the freeze-quench spectra as a function of resting time qualitatively shows a shift in spin density from the rhombic signal, characteristic of Blue/e⁻, to the axial signal of Red/e⁻. The EPR signal of unreduced 4-MeO-TEMPO radical is completely absent from the 2 s spectrum, and only a very small 4-MeO-TEMPO signal (<1% of the total spin density) is observed in the baseline of the 0.1 s spectrum (Figure-SI 4.3). The absence of 4-MeO-TEMPO in these early EPR spectra is consistent with the optical experiment, which shows the complete oxidation of TiO₂/e⁻ by 1 equivalent 4-MeO-TEMPO in less than 2 seconds (Figure 2). These data confirm that the oxidation of TiO₂/e⁻ by 4-MeO-TEMPO is fast, occurring in a couple seconds (SI-Section 4.4).

Because the reaction of 4-MeO-TEMPO and TiO₂/e⁻ is already complete by the first timepoint of the freeze-quench experiment, the EPR spectra in Figure 4 (nominally 0.1 – 600 s) represent colloids containing the same concentration of electrons, the initial [TiO₂/e⁻] minus 0.46 oxidizing equivalents 4-MeO-TEMPO. The spectral differences between the freeze-quench samples therefore correspond to changes in the electronic environments of the remaining trapped electrons.

The freeze-quench EPR spectra were well-simulated with a rigid two-state parameter set consisting of an axial and a rhombic signal, Figure 5A.⁴⁰ The ratio of the axial to rhombic signals for each freeze-quench spectrum was optimized via least squares fitting, with the g and gStrain values held constant (SI-Section 4.5). The axial and rhombic percentages of total spin density in the simulation of each freeze-quench spectrum are plotted as a function of resting time in Figure 5B. The spectrum collected 0.1 s after the sub-stoichiometric oxidation of TiO₂/e⁻ by 4-MeO-TEMPO is only 20% axial. This %axial is the lowest we have ever observed compared to equilibrated TiO₂/e⁻ samples under these conditions (SI-Section 4.1). The spectra obtained over the ten minutes following the reaction showed an increase in the axial component from 20 to 33% of total spin density (Figure 5B).

Figure 5:

(A) The experimental (black) and simulated (green) EPR spectra collected 20 s after mixing TiO₂/e⁻ (0.69 mM e⁻) and 0.46 oxidizing equivalents 4-MeO-TEMPO (0.32 mM). The weighted axial and rhombic simulation components are included (dashed traces). Axial signal: g = 1.9376, 1.8289 and gStrain = 0.0474, 0.0462, and rhombic signal: g =1.987, 1.8966, 1.8667 and gStrain = 0.0152, 0.0185, 0.0384. (B) The optimized %axial (Red/e⁻) and %rhombic (Blue/e⁻) of total spin density as a function of the nominal resting time (see text).

The TiO₂/e⁻ EPR spectra are much broader than those of molecules, requiring large gStrain parameters in the simulation. This broadening is likely due to both the collection of random orientations present in our frozen solutions, and to a distribution of spin signals arising from a range of similar, but not identical, electronic trap states.⁷ Because of this inhomogeneity, the analysis of the freeze-quench EPR data with a rigid two-state model can only be semi-quantitative and the simulation parameters presented in Figure 5A are not unique (i.e. multiple combinations of parameters appear to fit the spectra well). We present three additional simulations of the freeze-quench EPR spectra, performed by two independent researchers, in SI-Section 4.5. Importantly, the four independent simulations (SI-Figures 4.4–4.5) give the same 12±2% increase in %Red/e⁻ over the time-course of the freeze-quench experiment (SI-Figure 4.6). This consistency across simulations provides strong support that the shift in electron density depicted in Figure 5B is an accurate representation of the post-oxidation re-equilibration of the remaining electrons from Blue/e⁻ (rhombic) to Red/e⁻ (axial) trap states.

Discussion

TiO₂ NPs are good reducing agents and react within seconds with both proton-coupled electron transfer oxidants (the TEMPO nitroxyl radical and O₂) and the I₃^– oxidant that just accepts electrons. Our observations of rapid reactions of colloidal TiO₂ with excess oxidant are consistent with previous kinetic studies.^16–30 However, we are not aware of prior studies reporting relative rates of different trap states in solution reactions of this kind.

The treatment of reduced TiO₂ NPs with sub-stoichiometric oxidant gives rise to unusual observations: the TiO₂/e⁻ absorbance rapidly decays and then rises partially back to its original value (Figure 3). The freeze-quench EPR experiments (Figure 4) connect this unusual observation to the distinct Red/e⁻ and Blue/e⁻ trap states previously identified in this colloidal TiO₂/e⁻ system.⁷ In this Discussion, we show that both the EPR and optical kinetic experiments demonstrate the preferential oxidation of Red/e⁻ over Blue/e⁻ in the fast sub-stoichiometric oxidation of TiO₂/e⁻ (Scheme 1, ΔA_fast). This kinetic disparity disrupts the Red/e⁻ and Blue/e⁻ trap state equilibrium, leading to the slower second reaction phase—the re-equilibration of electrons from Blue/e⁻ to Red/e⁻ states (Scheme 1, ΔA_slow).

Scheme 1:

Proposed reaction scheme for the oxidation of TiO₂/e⁻ by 50% 4-MeO-TEMPO. The initial fast reaction primarily of the Red/e⁻ with 4-MeO-TEMPO (ΔA_fast) is followed by the slow re-equilibration of Red/e⁻ and Blue/e⁻ (ΔA_slow).

In an effort to further understand the different kinetic reactivity of the Red/e⁻ and Blue/e⁻ trapped states, we have applied a traditionally molecular, physical-organic relative rates approach. Applying this type of methodology to NP reactions is typically challenging due to the existence of multiple, inhomogeneous distributions of trap states and complex kinetic behavior (typically multi-exponential under pseudo-first-order conditions). Therefore, this Discussion is divided into three sections, with increasing complexity and quantitation. Section I brings together the direct spectroscopic evidence supporting the two-phase reaction depicted in Scheme 1. Next, Section II builds a simplistic, qualitative kinetic model that reproduces the unusual optical trends of sub-stoichiometric TiO₂/e⁻ oxidation. Finally, Section III presents a quantitative estimate of the relative and absolute rate constants for the Red/e⁻ and Blue/e⁻ oxidation. Together, these different levels of analysis strongly support the two-phase reaction depicted in Scheme 1.

I. Spectroscopic Evidence for Scheme 1

Addition of ≥1 equivalent of 4-MeO-TEMPO to TiO₂/e⁻ resulted in the complete loss of the TiO₂/e⁻ optical absorption within 2 seconds. However, the absorbance decay was not uniform across the TiO₂/e⁻ spectrum (Figure 2). This was an initial indication that the two classes of trapped electrons (Red/e⁻ and Blue/e⁻) differ in kinetic reactivity. If the Red/e⁻:Blue/e⁻ ratio of trapped electrons were maintained throughout the oxidation reaction, the TiO₂/e⁻ absorption feature would have decreased uniformly across the optical spectrum. Instead, longer wavelengths decayed at an increased rate, resulting in a blueshift in λ_max. This indicates that Red/e⁻ (λ_max = 740 nm) react more quickly than Blue/e⁻ (λ_max = 470 nm) with 4-MeO-TEMPO.

Addition of sub-stoichiometric amounts of oxidant resulted in a rapid initial ~2 second drop in absorbance (ΔA_fast) that mirrored the results of the 100% oxidation reaction (Figure 3). However, in the sub-stoichiometric oxidations, ΔA_fast showed a larger than anticipated absorbance decay based on the amount of oxidant added. For instance, in the 40% oxidation by 4-MeO-TEMPO, ΔA_fast corresponded to a loss of nearly 70% of A_init (Figure 3A). The large absorbance change per %oxidation (ΔA_fast/Δ[e⁻] ≡ ε_fast) indicated the preferential oxidation of Red/e⁻ over Blue/e⁻. This is because Red/e⁻ have a higher molar absorptivity than the Blue/e⁻ (ε_Red = 630 M⁻¹cm⁻¹ > ε_Blue = 85 M⁻¹cm⁻¹ at 600 nm, Figure 1B). Following this initial phase, the slower (minutes) absorbance recovery occurred with a redshift in the optical spectrum of the TiO₂/e⁻ (Figure 3A). This indicates an increase in the Red/e⁻ population during the second kinetic phase.

Together these results are consistent with the reactivity depicted in Scheme 1. The thermodynamic equilibrium of Red/e⁻ and Blue/e⁻ trap states is disturbed upon fast oxidation of TiO₂/e⁻, due to the higher kinetic reactivity of Red/e⁻ with 4-MeO-TEMPO (Scheme 1, ΔA_fast). The fast oxidation is followed by the slow re-equilibration of electrons from Blue to Red trap states (Scheme 1, ΔA_slow).

The parallel freeze-quench EPR spectra that followed the time course of the sub-stoichiometric oxidation of TiO₂/e⁻ (Figure 4) provide strong and independent support for this description of the reaction. First, the freeze-quench data confirm that the oxidation of TiO₂/e⁻ by 4-MeO-TEMPO is fast under these reaction conditions. Since 4-MeO-TEMPO radical is readily observed by EPR spectroscopy, the almost complete depletion of the radical in the earliest freeze-quench spectrum confirms the reduction of 4-MeO-TEMPO is finished in less than a few seconds (Scheme 1, ΔA_fast, SI-Section 4.4).

Second, the freeze quench data confirm the faster oxidation of Red/e⁻ over Blue/e⁻ by 4-MeO-TEMPO. In our previous study, Red/e⁻ and Blue/e⁻ were correlated with the respective axial and rhombic EPR signals (Figure 1A).7 The spectra of early-time free-quench samples show low axial:rhombic ratios (low Red/e⁻ populations), relative to the longer equilibrated TiO₂/e⁻ colloids, particularly the 600 s spectrum. This validates the higher kinetic reactivity of Red/e⁻ relative to Blue/e⁻ (Scheme 1, ΔA_fast).

Finally, the freeze-quench EPR spectra collected over the slow, second kinetic phase of the reaction shows a shift in the EPR spin density from the rhombic to the axial signal as a function of resting time (Figure 5B). These spectra confirm that the secondary optical changes result from the slow equilibration of electrons from Blue/e⁻ to Red/e⁻ states (Scheme 1, ΔA_slow).

II. Qualitative kinetic model of Red/e⁻ and Blue/e⁻ oxidation

A deeper analysis of the optical and EPR studies offers two important conclusions about the kinetics of Red/e⁻ and Blue/e⁻ reactivity with 4-MeO-TEMPO. First, these data sets inform the distinct timescales of the two reactions shown in Scheme 1. As per the discussion above, the transition from the fast to the slow phase of the reaction (from TiO₂/e⁻ oxidation to trap state equilibration) occurs at roughly the time of the minimum optical absorbance in the stopped-flow experiments ($t_{A_{\mathit{\text{min}}}}$). For the reaction with 4-MeO-TEMPO, $t_{A_{\mathit{\text{min}}}}$ occurs ~2 s after mixing, while the secondary slow absorbance increase, resolving at $t_{A_{fin}}$, lasts for several minutes (Figure 3C). Thus, as indicated in the qualitative model in Scheme 2, the oxidation of TiO₂/e⁻ within a few seconds (eqs 1 and 2), and the trap state re-equilibration over minutes (eq 3), occur on substantially different timescales (eq 4).

Scheme 2:

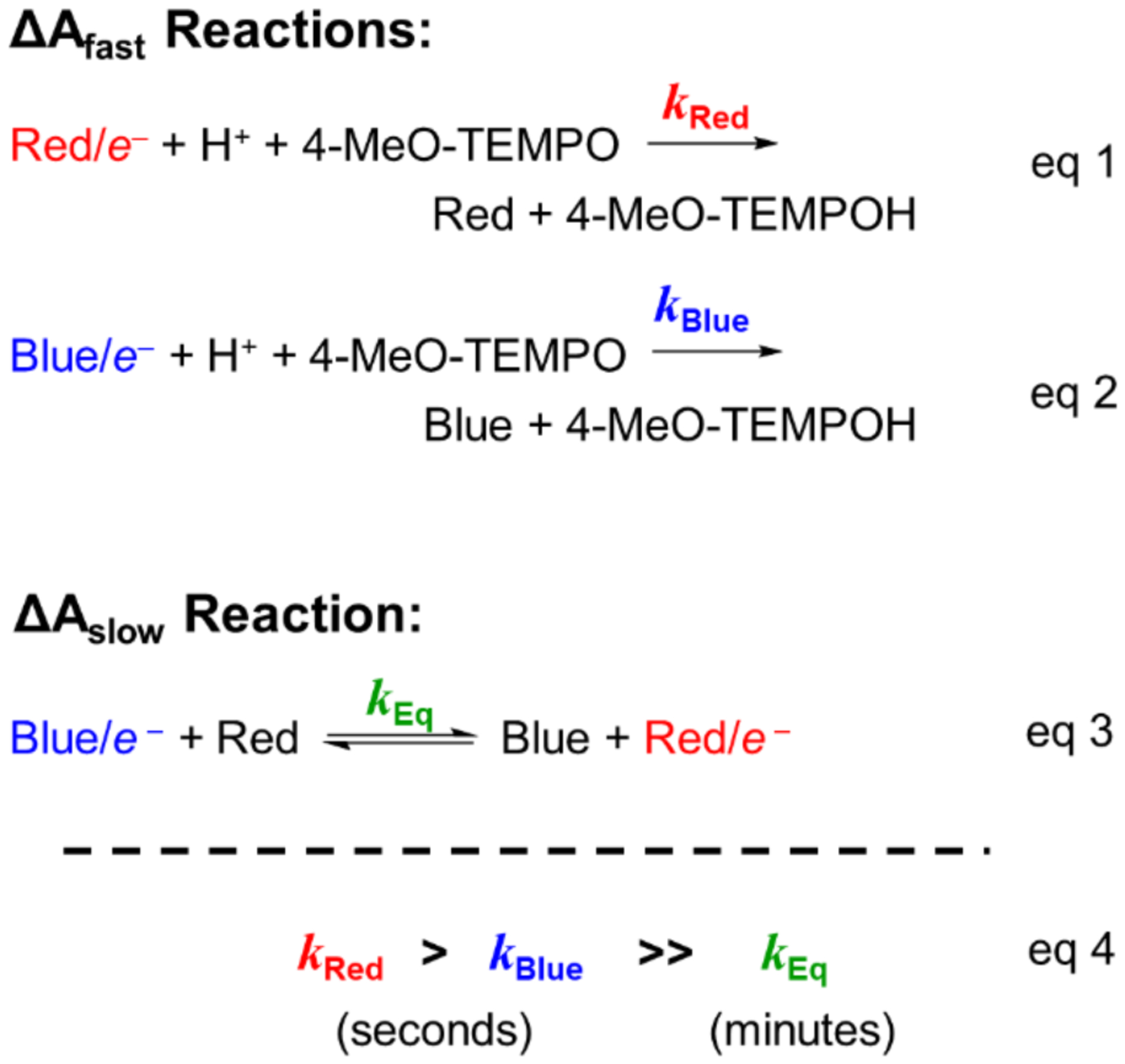
Simplified kinetic model of Red/e⁻ and Blue/e⁻ reactivity with 4-MeO-TEMPO.

Second, we can conclude that the initial, fast absorbance decay (ΔA_fast, Figure 3C) is due to the reaction of both Red/e⁻ and Blue/e⁻ with 4-MeO-TEMPO (eqs 1 and 2). This is clear from the optical data following the reaction of TiO₂/e⁻ with ≥1 equivalent oxidant, which shows complete reaction of all the electrons within 2 s of mixing (Figure 2). Photochemically reduced TiO₂/e⁻ colloids under these conditions typically have ~40% Red/e⁻ and ~60% Blue/e⁻. If only the Red/e⁻ were reactive, the oxidation of TiO₂/e⁻ by excess 4-MeO-TEMPO would proceed rapidly only to ~40% completion, and then continue at the much slower, minute timescale of the trap state equilibration reaction (eq 3). Instead, we observe oxidation of both Red/e⁻ and Blue/e⁻, within a couple of seconds, before significant trap state equilibration occurs (eq 4). While the Red/e⁻ react faster than the Blue/e⁻, these results indicate that both trap states are oxidized within seconds by 4-MeO-TEMPO. Both the Red/e⁻ and the Blue/e⁻ react with 4-MeO-TEMPO much faster than they equilibrate with each other.

These conclusions have implications for the nature of the Red/e⁻ and Blue/e⁻ trap states and their reactions. One could imagine, for instance, that the slower reactions of Blue/e⁻ could be the result of their being more buried in the nanoparticles, while the Red/e⁻ are more at the NP surface. Then the reaction of Blue/e⁻ with 4-MeO-TEMPO could be slower because they require diffusion through the NP or perhaps detrapping of the electron into conduction band states. However, we feel that a diffusive or detrapping process would likely also lead to equilibration of the two trap states (since electron trapping in such materials is usually rapid on these timescales^8–12). Yet the reactions of both states are roughly two orders of magnitude faster than their equilibration. This suggests that both the Red/e⁻ and the Blue/e⁻ are close enough to the NP surface to react with 4-MeO-TEMPO directly. Perhaps this is because these NPs appear to be irregular in shape, with both crystalline (anatase) and amorphous regions, such that all of the trap states are close to the surface.

The generality of this model is demonstrated in the reactions of TiO₂/e⁻ with two additional oxidants, KI₃ and O₂ (SI-Sections 3.5–3.7). TiO₂/e⁻ suspensions are quickly and completely oxidized by stoichiometric amounts of these oxidants, as seen with 4-MeO-TEMPO (Scheme-SI 3.1). Stopped-flow studies show that these reactions with the three oxidants occur at different rates. Time traces for fully stoichiometric oxidations are shown in SI-Figure 3.7. Figures 3B and 6 above compare sub-stochiometric reactions of the oxidants under similar conditions: TiO₂/e⁻ suspensions with 0.50 mM e⁻ plus ~0.5 oxidizing equivalents of each oxidant. The differences in reaction rates are indicated by the differences in the initial, ΔA_fast phase of these reactions in Figure 6. The two-electron reduction of KI₃ occurs in ~0.2 s; the proton-coupled reduction of 4-MeO-TEMPO is about an order of magnitude slower (~2 s) and the multi-proton, multi-electron reduction of O₂ still slower (~10 s) (SI-Sections 3.5 and 3.6).

Figure 6:

Kinetic traces monitoring the sub-stoichiometric oxidation of TiO₂/e⁻ (0.50 mM e⁻) by (A) 0.50 oxidizing equivalents KI₃ (0.125 mM), (B) 0.48 oxidizing equivalents of 4-MeO-TEMPO (0.24 mM), and (C) ~0.50 oxidizing equivalents of O₂ (0.065 mM). The fuchsia arrows highlight the timescales of the ΔA_fast phase of the sub-stoichiometric reactions.

Despite the differences between KI₃, 4-MeO-TEMPO and O₂ – in their oxidation rates and their electron transfer (ET) vs. proton-coupled electron transfer (PCET) oxidation nature – the same reactivity pattern outlined in Schemes 1 and 2 is observed for all three reagents. The optical absorbance initially drops rapidly and then partially recovers to a higher level, just as seen in oxidation by 4-MeO-TEMPO (Figure 3). The data imply that the KI₃ and O₂ oxidations of TiO₂/e⁻, including both the Red/e⁻ and the Blue/e⁻, are much faster than trap state equilibration. These results indicate that the faster reactivity of one trap state over another is likely a general feature of TiO₂/e⁻ reactivity.

The relative rates of k_Red, k_Blue, and k_Eq outlined in Scheme 2 were used to evaluate the changes in the fast and slow phases of the sub-stoichiometric reactions as a function of %TiO₂/e⁻ oxidation. In the six reactions of Figure 3C ranging from 11–88% TiO₂/e⁻ oxidation, the magnitude of the slow absorbance increase, ΔA_slow, becomes larger from 11–43% oxidation and then diminishes from 43–88% oxidation. The initial increase and then decrease in the magnitude of ΔA_slow as a function of %oxidation is easier to see in Figure 7B where the ΔA for each reaction phase is plotted as a function of %TiO₂/e⁻ oxidation. For reference, the magnitudes of the three arrows overlaying the 43% oxidation trace in Figure 7A (reprinted from Figure 3C) correspond to the 3 points plotted at 43% TiO₂/e⁻ oxidation in Figure 7B. Figure 7B also shows that the dependence of ΔA_fast on %oxidation gets more shallow as %oxidation increases, as seen by the change in slope. Interestingly, the shifts (or inflections) of the ΔA_fast and ΔA_slow trends in Figure 7B are centered around ~40% oxidation. This is the %Red/e⁻ in the initial TiO₂/e⁻ colloid prior to reaction (%Red/e⁻_init).

Figure 7:

(A) TiO₂/e⁻ absorbance as a function of time after addition of 0.43 oxidizing equivalents of 4-MeO-TEMPO (from Figure 3C). The magnitudes of the three overlaying arrows (ΔA_fast, ΔA_slow, and ΔA_tot) correspond to the 3 points (respectively, fuchsia, yellow, and black) plotted at 43% TiO₂/e⁻ oxidation in panel B. (B) The ΔA_fast, ΔA_slow, and ΔA_tot of the six kinetic traces reported in Figure 3C plotted versus %TiO₂/e⁻ oxidation and [4-MeO-TEMPO]. Error bars signify ±1σ between multiple kinetic experiments. (C) ΔA_fast, ΔA_slow, and ΔA_tot for simulated reactions starting from a theoretical colloid with a 40:60 Red/e⁻:Blue/e⁻ ratio and adding 0–100% oxidant. In the simulations the relative rates of the kinetic model (eq 4) were approximated as k_Red ≫ k_Blue ≫ k_Eq. The full details of the kinetic simulations are reported in SI-Section 5.

In order to elucidate the origins of these striking experimental trends, the reactions presented in Figure 3C and Figure 7B were simulated starting from a colloid with a 40:60 Red/e⁻ :Blue/e⁻ ratio and adding 0–100% oxidant. For simplicity, the relative rates in this simulation were approximated as k_Red ≫ k_Blue ≫ k_Eq, such that all of the Red/e⁻ were oxidized before any of the Blue/e⁻, and equilibration occurred only after all of the oxidant was consumed (SI-Section 5). The ΔA_fast, ΔA_slow, and ΔA_tot of the simulated sub-stoichiometric oxidations plotted in Figure 7C very nicely capture the experimental trends. This strong agreement supports the approach of the qualitative kinetic model and confirms that the relative rates of eq 4 are the origin of the optical trends overserved in the sub-stoichiometric oxidations of TiO₂/e⁻.

The qualitative kinetic model provides insights into both reaction phases. The initial, fast decrease in TiO₂/e⁻ absorbance (ΔA_fast in Figure 7) tracks the oxidation of TiO₂-based electrons by 4-MeO-TEMPO. During this oxidation, the Red/e⁻:Blue/e⁻ ratio decreases because the electrons in the Red/e⁻ trap states are oxidized faster (k_Red ≫ k_Blue). When less than ~40% 4-MeO-TEMPO was added, the oxidized electrons come predominantly from the Red/e⁻. In this region, ΔA_fast is large and has a steep negative dependence on %TiO₂/e⁻ oxidation because of the higher absorbance of the Red/e⁻ (Figure 7B,C; ε_Red = 7.4 × ε_Blue at 600 nm). Once %TiO₂/e⁻ oxidation exceeds the initial ~40% of Red/e⁻, then the Blue/e⁻ states are also oxidized. Because of the lower absorbance of Blue/e⁻, the slope of ΔA_fast vs. %TiO₂/e⁻ oxidation plot becomes shallower.

The simulation thus predicts a sharp change in the slope of ΔA_fast when %oxidation = %Red/e⁻_init (Figure 7C, fuchsia) because this is the point where the transition occurs between oxidation of only Red/e⁻ (steep slope ≅ −ε_Red) to include Blue/e⁻ (shallow slope ≅ −ε_Blue). The experimental data in Figure 7B show a more gradual transition from steep to shallow slopes. This shows that the oxidation of Blue/e⁻ is partially competitive with Red/e⁻, as discussed in the next section.

The secondary, slow absorbance increase (ΔA_slow in Figure 7A and B) results from the re-equilibration of electrons from Blue to Red trap states following the fast oxidation reaction. The magnitude of ΔA_slow is largest (i) when the Red/e⁻:Blue/e⁻ equilibrium position (40:60) is most perturbed during the oxidation reaction, and (ii) when the largest amount of Blue/e⁻ remain after oxidation to re-equilibrate. As %TiO₂/e⁻ oxidation increases, the perturbation of the Red/e⁻:Blue/e⁻ equilibrium increases, but less of the initial [TiO₂/e⁻] remain for reequilibration. These opposing contributions give rise to the initial increase and then decrease in the magnitude of ΔA_slow as a function of %oxidation in Figure 7B and C (yellow triangles). In the simulations, the maximum in the ΔA_slow trend in Figure 7C occurs exactly at the equivalence of %oxidation and %Red/e⁻_init (40%, Figure 7C), where all the Red/e⁻ are oxidized and the maximum amount Blue/e⁻ remains to reequilibrate. In the experimental data (Figure 7B), the maximum in ΔA_slow occurs when %oxidation is slightly greater than %Red/e⁻_init, because of the competitive oxidation of Blue/e⁻.

In summary, a qualitative simulation assuming that the TiO₂/e⁻ oxidations occur in three distinct phases, k_Red ≫ k_Blue ≫ k_Eq, captures the striking trends in the experimental absorbance changes (Figure 7B and C). Both the inflection in the ΔA_fast as a function of %TiO₂/e⁻ oxidation by 4-MeO-TEMPO and the peak in the ΔA_slow are reproduced. The same pattern of reactivity was observed using KI₃ or O₂ as the oxidant (Figure 6). The success of qualitative model confirms the two phases of the reaction (Scheme 2) and sets the foundation for the more rigorous quantitative analysis in the following section.

III. Quantitative Analysis of Red/e⁻ and Blue/e⁻ Reactivity During ΔA_fast

The prior section showed both (i) that that the reaction of 4-MeO-TEMPO with Red/e⁻ is faster than with Blue/e⁻, and (ii) that these rates must be somewhat competitive. The relative rates, k_Red:k_Blue, were estimated by evaluating the 20% TiO₂/e⁻ oxidation reaction as a pseudo-competition experiment. This reaction decreased the TiO₂/e⁻ concentration from its initial 0.5 mM e⁻ to 0.4 mM (Scheme 3 and SI Section 6). Measured absorbances at 600 nm gave the individual Red/e⁻ and Blue/e⁻ concentrations before and after the reaction (using A_init at $t_{A_{\mathit{\text{init}}}}$, A_min at $t_{A_{\mathit{\text{min}}}}$ and ε_Red and ε_Blue;⁷ eqs 5 and 6). Note that in this system, the observed composite epsilon of TiO₂/e⁻ (ε_obs(t)) is not constant but changes based on the Red/e⁻:Blue/e⁻ ratio (SI-Figure 2.4). This analysis showed that 70% of the 0.2 equivalents of 4-MeO-TEMPO were reduced by Red/e⁻ and 30% were reduced by Blue/e⁻. Assuming two independent simple second-order reactions (eqs 1, 2), the [Red/e⁻] and [Blue/e⁻] concentrations at $t_{A_{\mathit{\text{min}}}}$ were calculated for various rate constant ratios k_Red:k_Blue. Comparisons of the predicted and experimental concentrations indicated that k_Red is 8 ± 3 times faster than k_Blue (SI-Section 6).

Scheme 3: [Red/e⁻] and [Blue/e⁻] before and after the ΔA_fast phase of TiO₂/e⁻ oxidation by 0.2 equivalents of 4-MeO-TEMPO.^a.

^a Kinetic trace in SI-Figure 6.1. [Red/e⁻] and [Blue/e⁻] determined from A_init and A_min at 600 nm, [TiO₂/e⁻]_init, and ε_Red and ε_Blue.⁷

$${\text{A}}_{\text{t}}={\left[\text{Ti}{\text{O}}_2/e^{-}\right]}_{\text{t}}\times {\text{ε}}_{\text{obs}}(\text{t})$$ eq 5

$${\text{ε}}_{\text{obs}}(\text{t})=\%\text{Red}/e^{-}\times {\text{ε}}_{\text{Red}}+\%\text{Blue}/e^{-}\times {\text{ε}}_{\text{Blue}}$$ eq 6

In order to estimate the absolute values of k_Red and k_Blue, a more quantitative kinetic model was developed. The same assumption of independent, second order processes gave the rate law in eq 7 for the consumption of 4-MeO-TEMPO (Scheme 4). Based on the respective assignments of $t_{A_{\mathit{\text{init}}}}$ and $t_{A_{\mathit{\text{min}}}}$ as the beginning and end of the 4-MeO-TEMPO reduction reaction, [4-MeO-TEMPO]_t = [4-MeO-TEMPO]_init at $t_{A_{\mathit{\text{init}}}}$ and 0 mM at $t_{A_{\mathit{\text{min}}}}$. However, because the concentration of 4-MeO-TEMPO and ε_obs(t) change throughout the TiO₂/e⁻ oxidation reaction, the [4-MeO-TEMPO]_t at timepoints (t) between $t_{A_{\mathit{\text{init}}}}$ and $t_{A_{\mathit{\text{min}}}}$ cannot be uniquely determined. Thus, traditional kinetic modeling of the optical spectra over time is not straightforward with this system. Therefore, three different methods were used to estimate the time course of [4-MeO-TEMPO]_t throughout the sub-stoichiometric TiO₂/e⁻ oxidation reactions: The percent conversion was estimated (1) using A₆₀₀ as a simplistic metric for reaction progress, (2) assuming a second order disappearance of 4-MeO-TEMPO, and (3) assuming two competitive second order processes consuming 4-MeO-TEMPO. With the three different methods, [TiO₂/e⁻]_t was calculated by assuming mass balance and was used (in combination with eq 5 and 6) to extract [Red/e⁻]_t and [Blue/e⁻]_t. For further details of these three fitting methods see SI-Section 7.1.

Scheme 4: Quantitative kinetic model of Red/e⁻ and Blue/e⁻ reactivity with 4-MeO-TEMPO^b.

^bEqs 1 and 2 are also in Scheme 2 above. Because we believe that the protons required for the reactions are associated with the TiO₂-based trapped electrons,¹⁷ they are not included in our rate law.

The concentration profiles of [4-MeO-TEMPO]_t, [Red/e⁻]_t, and [Blue/e⁻]_t from each method were globally fit to the rate law in eq 7 to give optimized rate constants k_Red and k_Blue (Figure-SI 7.3–7.5). The A_600nm resulting from the modeled [Red/e⁻]_t, and [Blue/e⁻]_t versus time fits well to the experimental data highlighting the accuracy of this model (Figure 8). The resulting rate constants were consistent across all three methods and gave k_Red ≈ 1 × 10⁵ M⁻¹s⁻¹ and k_Blue ≈ 2 × 10⁴ M⁻¹s⁻¹ (Table-SI 7.1). These are only estimated rate constants because the Red/e⁻ and Blue/e⁻ likely contain distributions of similar but non-identical trapped electrons, so the assumption of simple second order kinetics in eq 7 for each is an approximation. The extracted k_Red/k_Blue suggest that Red/e⁻ react ~5 times faster than Blue/e⁻ with 4-MeO-TEMPO, in good agreement with the results of the pseudo-competition experiment described above.

Figure 8:

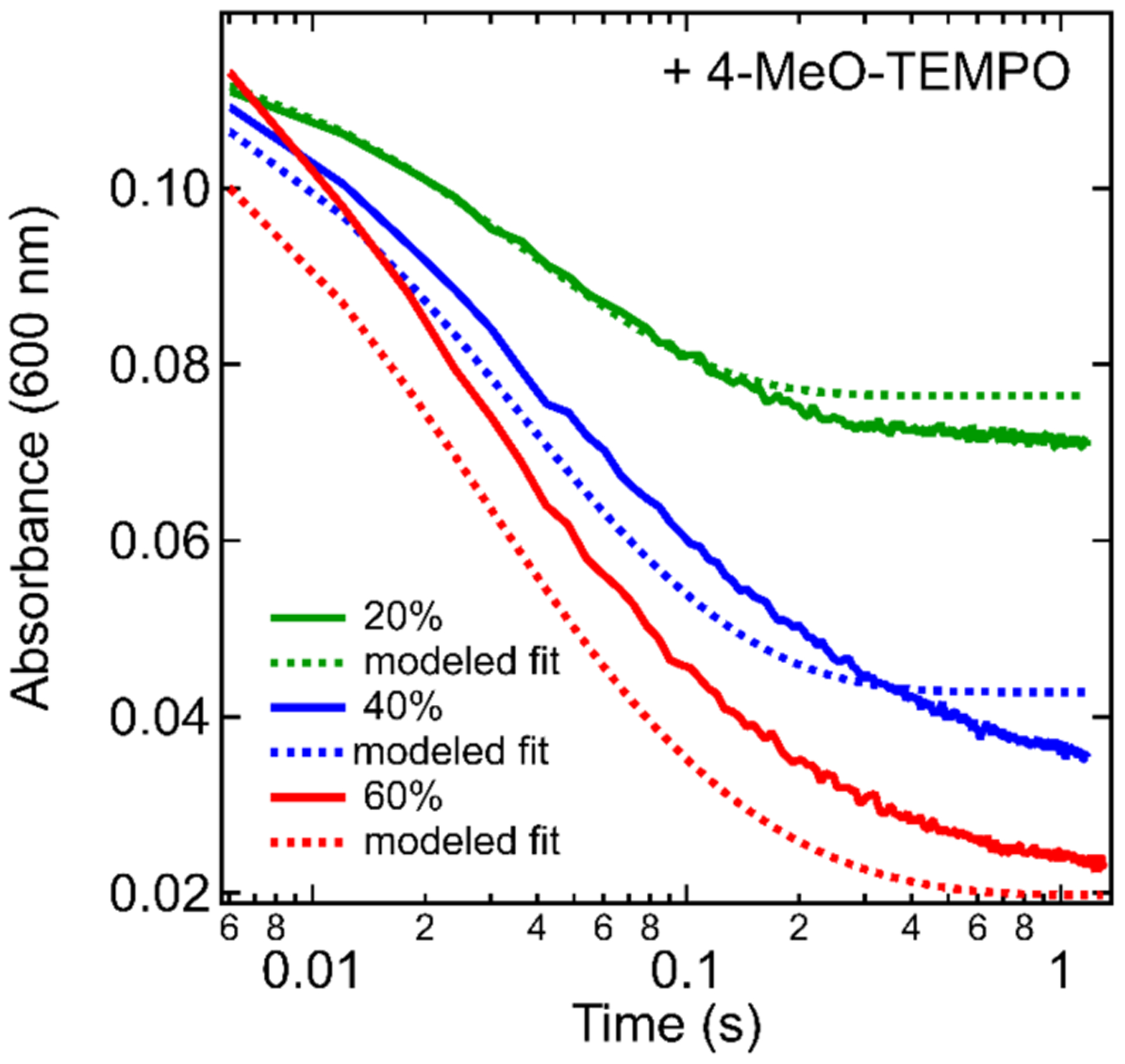
Experimental (solid lines) and modeled (dashed lines, method 3) A_600nm vs. time plots for the ΔA_fast portion of reactions of TiO₂/e⁻ (0.49 mM e⁻) with 0.2 (green), 0.4 (blue), and 0.6 (red) oxidizing equivalents of 4-MeO-TEMPO. (SI-Section 7.1).

Conclusions:

The oxidation kinetics of two distinct classes of trapped electrons, termed Red/e⁻ and Blue/e⁻, in aqueous, colloidal TiO₂/e⁻ nanoparticles are presented here. Stopped-flow optical and freeze-quench EPR experiments demonstrate that the Red/e⁻ react faster than Blue/e⁻ with solution-based oxidant 4-MeO-TEMPO. Qualitative and semi-quantitative models confirm this kinetic behavior, with k_Red ≅ 5 × k_Blue ≫ k_Eq, with k_Red ≈ 1 × 10⁵ M⁻¹s⁻¹ and k_Blue ≈ 2 × 10⁴ M⁻¹s⁻¹. The disparity in reactivity between the trap states is the origin of the very peculiar “decrease then increase” trend in the optical absorbance of TiO₂/e⁻ during sub-stoichiometric reactions. This is due to fast oxidation of primarily Red/e⁻ being followed by slow re-equilibration of electrons to the thermodynamic Red/e⁻:Blue/e⁻ equilibrium. The same optical trends were observed in sub-stoichiometric reactions with two additional oxidants, KI₃ and O₂. This commonality is surprising because these oxidants are very different—KI₃ is a simple electron only oxidant, 4-MeO-TEMPO is a proton-coupled electron transfer (PCET) oxidant⁴¹, and O₂ reduction involves a many reaction steps.^{16, 42} The more rapid reactivity of the Red/e⁻ with all three oxidants suggests that there are intrinsic differences in the reactivity of the Red/e⁻ and Blue/e⁻ trap states.

Implications and Outlook:

The preferential kinetic reactivity of one trap state over another observed here is likely a common feature in most TiO₂ systems,^{4–10, 32–33, 43} and perhaps for many other semiconductor materials. Differences in trap state occupancy and reactivity seem likely to contribute to the complex kinetics commonly observed for reactions of colloidal NPs.^{16, 34–35}

The reactivity difference between Red/e⁻ and Blue/e⁻ is common to a pure ET oxidant (KI₃) and single- or multi-PCET reagents (4-MeO-TEMPO or O₂). This could perhaps be due to different physical locations of the two states, perhaps with the Blue/e⁻ requiring a diffusive or detrapping step to react. However, this explanation seems inconsistent with the reactions with oxidants being much faster than trap-state equilibration. Previous temperature-equilibration studies showed the Red/e⁻ to be higher in enthalpy than the Blue/e⁻, by 3.0 ± 0.6 kcal mol⁻¹ (130 ± 30 meV).⁷ While this is could provide an explanation of the higher reactivity of Blue/e⁻, ET and PCET reactivity should follow free energy differences, which could not be estimated due to the unknown concentrations of unoccupied traps. In general, the thermochemistry of nanoscale reactions is challenging to precisely define, especially when electron transfer is coupled to proton transfer as is the case here.^44–45 Efforts to understand this chemical reactivity are underway, by more precisely defining the structures and stoichiometries of the trap states, and the nature and energetics of the rate limiting steps.

The millisecond timescale of the reactivity reported is of the order of typical turnover frequencies for electrocatalysis and photo(electro)chemical catalysis. Therefore, this study raises the tantalizing possibility that a future ability to intentionally tune trap states could be useful in catalytic applications.