Matching in cluster randomized trials using the Goldilocks Approach

Abstract

In group or cluster-randomized trials (GRTs), matching is a technique that can be used to improve covariate balance. When baseline data are available, we suggest a strategy that can be used to achieve the desired balance between treatment and control groups across numerous potential confounding variables. This strategy minimizes the overall within-pair Mahalanobis distance; and involves iteratively: 1) making pairs that minimize the distance between pairs of clusters with respect to potentially confounding variables; 2) visually assessing the potential effects of these pairs and resulting possible randomizations; and 3) reweighting variables of selecting weights to make pairs of clusters. In step 2, we plot the between-arm differences with a parallel-coordinates plot. Investigators can compare plots of different weighting schemes to determine the one that best suits their needs prior to the actual, final, randomization. We demonstrate application of the approach with the Mupirocin-Iodophor Swap Out trial. A webapp is provided.

1. Introduction

Individually randomized trials with blinding are the most rigorous way of determining whether a causal relation exists between an intervention and an outcome (e.g. Ref. [1]). However, for scientific and practical design reasons some interventions must be delivered to groups of subjects. Trials where groups are randomized are called group-randomized or cluster-randomized trials (GRTs). Three reasons for conducting a GRT are: (i) because implementation occurs at the cluster level, (ii) to avoid treatment contamination between subjects who are in contact with one another, and (iii) to measure intervention effects among cluster members who do not themselves receive treatment [2,3]. GRTs are “the gold standard when allocation of identifiable groups is necessary” [4].

One challenge in GRTs is that there is typically a small number of clusters. Many GRTs have fewer than 30 independent clusters to randomize, and most have fewer than 200. Thus, even though each cluster may have thousands of individuals [2], there may well be concern about confounding. In contrast, in large individually randomized trials investigators expect randomization to balance potential confounders across each arm of the trial. The smaller number of randomizable cluster in GRTs makes imbalance a threat to the causal interpretation of any observed treatment effect.

Several approaches to this problem have been proposed, including minimization [5], constrained randomization [6,7], and matching or stratification (see, e.g. Ref. [8]). Briefly, minimization can be seen as a sequential assignment of each randomized cluster to each arm such that the imbalance after the addition of that cluster is minimized. It is better suited to studies in which clusters are accrued as they are randomized. In cases where many clusters are assembled before randomization begins, it is dependent on the initial cluster and can be nearly deterministic.

Covariate constrained randomization effectively enumerates all possible treatment assignments and eliminates those that do not meet with desired features of balance. Usually schemes that have less than some maximum value of covariate difference are selected, and then one is chosen at random. For each group to have equal probability of assignment to each arm of the trial, half of the selected schemes should have it in one arm, the other half in the other. Although this is not impossible, it is unlikely. To some trialists, any deviation from an equal probability of assignment to each arm will be unacceptable; in any case it is unclear how to make principled decisions about how much inequity in arm assignment probability is allowable.

Extensive simulations compared analyses of constrained randomization, simple randomization, and the truth for both binary and continuous, normally distributed outcomes [9,10]. For continuous outcomes, they demonstrate that adjustments for covariates at the analysis stage are important even after design based adjustments. An adjusted F-test must be used, and permutation tests must account for the balanced scheme, otherwise constrained randomization improves power while maintaining type I error rates. For binary outcomes, prior knowledge should drive careful selection of covariates used in constrained randomization to maximize power and maintain type I error rates.

Other research shows that constrained randomization has smaller total sum of squares distance than simple randomization, minimization, matching, and stratification when all clusters are known in advance [11].

In stratified randomization similar clusters are grouped together prior to randomization, and randomization takes place within these smaller groups. There is debate about the optimal sizes of these groups. In particular, there is disagreement about the merits of matching, which involves grouping 2 clusters together, vs. stratification, where more than 2 clusters are grouped [12].

If there are a small number of groups in a trial, stratification is most useful when there are only a few covariates to balance. Otherwise, strata of size 4 are said to have all the advantages of matching with none of the drawbacks [13].

Many authors address the value of matching in GRTs in both the design stage and in the analysis [2,3,8,12,[14], [15], [16], [17], [18], [19], [20]]. Murray argues that “the choice of matching or stratification [of] factors is critical to the success of the procedure” [8]. Others suggest that caution must be used when matching a small number of clusters due to the decrease in power [2,[18], [19], [20]]. Breaking the matches, i.e., ignoring the matching during data analysis, addresses this [15], but perhaps only when there is a small number of large clusters [17]. Breaking the matches may also increase the type I error rate for analyses that are not the intervention effect [17]. Further drawbacks include difficulties in estimating the intracluster correlation coefficient, an inability to test for homogenity of odds ratio, and predictions that are restricted to cluster-level baseline risk factors [17]. Another complication involves removal of a cluster due to protocol violations [21].

Imai et al. develop an estimator that gives accurate standard errors when matched pairs are used; ignoring the matching gives slightly conservative standard errors [16]. However, in one trial “matching actually led to a loss in statistical efficiency” [19,22]. Despite this ongoing debate, few authors discuss how to match the clusters [7].

This article describes an extension of methods discussed previously [14]. We suggest a method suitable for a priori matching using baseline data. In section 2, we outline our method. In section 3, we show how it was applied in a large cluster-randomized trial, the Mupirocin-Iodophor Swap Out trial [23]. In section 4 we discuss the implications of our approach.

2. Methods

We suggest an approach to the complex topic of balancing randomization in GRTs. We match the clusters on many variables, using a “weighting” scheme to suggest which variables are most important. Then we perform many practice or “false” randomizations to obtain a distribution of the possible average arm differences that might be obtained when actual randomization occurs. Investigators assess these distributions to determine if potential randomizations would result in sufficiently balanced treatment assignments. If not, the weighting scheme is adjusted and the process begins again. The details follow. Our approach is the same of that proposed by Greevy and colleagues [24], of which we were unaware until writing this manuscript. In our approach, we facilitate weight selection through a novel visual approach for assessing the potential randomization quality for a given set of weights.

The initial step involves prioritizing variables (1, 2, …, n) from clusters (1, 2, …, m) to be randomized. We have

$$\begin{array}{l}{V}_1=({\upsilon }_{11}\text{,}{\upsilon }_{12}\text{,}\dots \text{,}{\upsilon }_{1n})\\ V_2=({\upsilon }_{21}\text{,}{\upsilon }_{22}\text{,}\dots \text{,}{\upsilon }_{2n})\\ ⋮=⋮\\ V_m=({\upsilon }_{m1}\text{,}{\upsilon }_{m2}\text{,}\dots \text{,}{\upsilon }_{mn})\end{array}$$

where v_ij is the j^th variable from cluster i: each V_i contains pertinent variables from cluster i. From here, we compute the Mahalanobis distance between two clusters. This is the generalized n-dimensional distance across the variables; for two clusters a and b it is calculated as $d(V_a,V_b)=\sum _{k=1}^n\frac{{(v_{ak}-v_{bk})}^2}{s_k^2}$ where $s_k^2=\frac{1}{m}\sum _{l=1}^m{(v_{lk}-v_{\cdot k})}^2$ and $v_{\cdot k}=\frac{1}{n}\sum _{i=1}^m{v}_{ik}$.

Then we find the way of pairing the clusters that minimizes the global Mahalanobis distance across all of the possible pairs of clusters. This is a short way of describing a lengthy process: we pair cluster 1 with cluster 2 and cluster 3 with cluster 4, and so forth. Then we calculate the Mahalanobis distance between each of these pairs, and sum it. Then we pair cluster 1 with cluster 3 and cluster 2 with cluster 4, and we continue until we have the summed Mahalanobis distance for all of the possible ways to pair the clusters. The set with the minimum sum is the best way to match the clusters. This process can be done in the R statistical programming environment [25] using the nmatch function in the designmatch package [26].

Once the matching is completed, we have pairs $(C_{11},C_{12}),(C_{21},C_{22}),\mathrm{...},(C_{\frac{m}{2}1},C_{\frac{m}{2}2}),$ where $C_{ij}$ is the $j$th cluster in the $i$th pair. The first match in each pair will be randomized to either treatment or control, the second to the other arm. If cluster $C_{11}$ is randomized to treatment, we denote this as $C_{11}^T$, and this implies $C_{12}^C$, where the superscript indicates either treatment ($T$) or control ($C$). Next, we find the per variable difference between the two groups, averaged across the clusters in the trial:

$$d_j=\frac{\left|{\sum }_{i=1}^{\frac{m}{2}}{C}_{ij}^T-{\sum }_{i=1}^{\frac{m}{2}}{C}_{ij}^C\right|}{\frac{m}{2}}$$

for $j=\mathrm{1,2},\mathrm{...},n.$ This generates the vector $D=(d_1,\dots ,d_n)$ of the average pairwise difference between the arms for each variable. When the trial is complete, these differences are likely to be reported as evidence of the balance achieved in the randomization.

We repeat this process of randomization R times and find D_r, the vector of average differences between the two arms for the rth practice randomization. For study designs with more than 2 arms, D_r can be redefined as, for example, the standard deviation between the arms. To visualize we draw a parallel coordinates plot where the j^th axis plots the difference between study arms for variable j. On the plot we include D_r for all practice randomizations r = 1, 2, …, R, as shown in the Figures below.

Upon review of the plot, we may find that the balance between the arms is unacceptable for some variables. For example, the mean or maximum distance between the arms may be too large. To accommodate this possibility, we introduce “weights” S = (s₁, s₂, …, s_n), which control the strength of matching on each variable. We have

$$v_{ij}^{\ast }=\prod _{i=1}^m{v}_{ij}{s}_j$$

which we combine to form

$$\begin{array}{l}{V}_1^{\ast }=\left(v_{11}^{\ast },v_{12}^{\ast },\dots ,v_{1n}^{\ast }\right)\\ V_2^{\ast }=(v_{21}^{\ast },v_{22}^{\ast },\dots ,v_{2n}^{\ast })\\ ⋮=⋮\\ V_m^{\ast }=(v_{m1}^{\ast },v_{m2}^{\ast },\dots ,v_{mn}^{\ast }).\end{array}$$

If s_j > s_j∗, we are multiplying variable j by a larger value than variable j∗, and this has the effect of increasing the distance between clusters for variable j, relative to variable j∗. Then, counter-intuitively, when we re-run the matching algorithm, we will get closer matches for variable j than variable j∗, because the Mahalanobis distance minimization will minimize this larger distance on variable j. Similarly, as the weight s_v for some variable v approaches 0, the distance between any two clusters with respect to variable v becomes very small, relative to the other variables. If s_v = 0, v is effectively not included in the matching at all – all clusters are perfectly matched on that variable during the matching process, and any two clusters make an equally good match on that variable. After selecting the weights S and matching on V ∗, we again repeatedly find the vector of between-arm differences for each variable D_r and plot it.

The cost of a high weight for variable j in this process is that closer matches for variable j may result in reduced closeness in another variable. If so, compromises must be made. Investigators can perform iterative selections of the weights S and arrive at a set of weights S that generates a distribution of randomizations that best reflect the most desired and tolerable differences in specific characteristics between arms.

3. Results

To demonstrate the usefulness of this technique we present a brief summary of our randomization process using baseline data from the Mupirocin-Iodophor Swap Out trial (www.clinicaltrials.gov, NCT03140423) [23]. This trial follows the REDUCE MRSA trial [27] in which universal use of mupirocin nasal swabs and daily bathing with chlorhexidine was shown to markedly reduce methicillin resistant Staphylococcus aureus (MRSA) clinical cultures and all-cause bloodstream infection in adult intensive care units (ICU) of hospitals belonging to HCA Healthcare (HCA). One concern about the mupirocin regimen is that S. aureus resistance to mupirocin is relatively common in some communities and so the agent would be ineffective for many patients. Another is that routine use of mupirocin, an antibiotic, may provide selective pressure for resistant strains, thus rendering mupirocin less effective for all uses. It would thus be desirable to be able to use a substitute nasal component of the decolonizing regimen for which resistance is less likely to be present or to develop as a result of treatment. The Swap Out trial is a cluster-randomized non-inferiority trial, comparing the antibiotic mupirocin (the current standard of care) to the antiseptic iodophor for nasal decolonization of ICU patients to assess impact on Staphylococcus aureus clinical cultures and all-cause bloodstream infection during routine chlorhexidine bathing.

Baseline data collected from HCA's centralized data warehouse were available for matching prior to randomization. We used data from 20 months from 137 participating hospitals. Investigators prioritized 16 baseline variables into several categories. For this trial, the investigators put the highest priority on baseline values of the primary outcome measures, Staphylococcus aureus ICU-attributable clinical cultures per 1000 days, MRSA ICU-attributable cultures per 1000 days, and all pathogen ICU-attributable bloodstream infections per 1000 days, as well as average monthly attributable days, regional mupirocin resistance estimates, percent of ICU admissions with a prior history of MRSA, current usage of mupirocin (percent of mupirocin use in the first 5 days of ICU admission), and current usage of chlorhexidine (percent adherence to daily chlorhexidine gluconate for bathing). Of secondary importance were median ICU length of stay, and mean Elixhauser total score [28]. Of tertiary importance were the percentage of ICU Medicaid patients, and whether or not a facility uses polymerase chain reactions to identify MRSA in blood. The next group included percent of admissions involving a skilled nursing facility, and the percent of surgical admissions. The final group included whether the ICU had specialty units for oncology, bone marrow transplant, or transplant units, and if the ICU has bone marrow transplant or transplant units.

Prior to randomization, investigators used an interactive web-based application, built using the Shiny package in R, which implements the strategy described in section 2. The application accepted an Excel spreadsheet as input. This enabled the investigators to quickly and easily change the weights applied to each potential matching variable. The application allowed the investigators to set the desirable maximum between-arm differences for each variable as well as the relative weights. We input tolerable maximum differences between study arms as well as desirable ranges of differences for each variable and compared many sets of variable weights until we found one that was suitable.

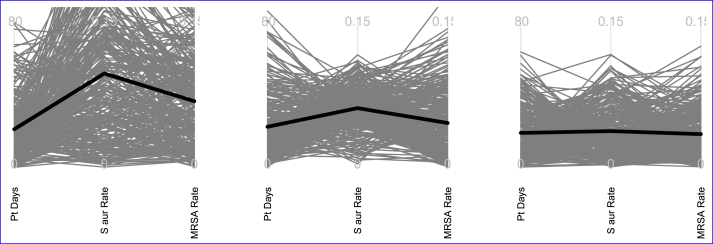
To begin, we show a version of this process using just three of the 16 variables; the actual randomization preparation is described below. Fig. 1 demonstrates how preparation for randomization would proceed using 1) attributable patient days per month, 2) Staphylococcus aureus rate, and 3) MRSA rate. To read a parallel coordinates plot, trace a single gray line from “Pt Days” to “S aur rate” to “MRSA rate”; this shows the between-arm differences obtained from a single randomization. The investigators agreed that the tolerable maximum absolute mean difference between treatment and control arms for these variables were: 80 attributable patient days per month, 0.15 difference in Staphylococcus aureus infection rates, and 0.15 difference in MRSA rates. These define the top of our axis lines in each graph. The black line indicates the mean value of all points on each axis. We can also use this value to help decide whether the matching was acceptable. To be completely clear, this process begins in the knowledge that none of the particular practice arm assignments that resulted in these D values will be used in the actual trial: these are hypothetical randomizations that might be applied to the hospitals. In contrast, the pairs established with these weights are set by the minimizing process and are fixed.

Fig. 1.

Possible randomizations for 3 different sets of weights for three attributes: average monthly attributable days (Pt days), Staphylococcus aureus ICU-attributable cultures per 1000 days (S aur rate), MRSA ICU-attributable cultures per 1000 days (MRSA rate). Each light gray line represents a single randomization and the black line is the mean difference between arms. The left image has no weighting and two axes exceed maximum values. The center image is matched well on the middle axis, but the first and third have some randomization draws that would exceed the desired maximum values for the mean difference between the groups. The right image reaches a happy medium.

The graph on the left is a parallel coordinates plot displaying the results of 300 randomizations when all the weights are equal, equivalent to using the raw values of each variable. The number of possible randomizations for a given matching is $2^{\frac{m}{2}}$ so more than 300 may need to be assessed for an accurate representation. The values in the plot show that several randomizations exceeded the desired maximum between-arm difference in the second and third axis: there is a reasonable chance that if randomization occurred with this weighting, the Staphylococcus aureus and MRSA rates would be imbalanced between the treatment and control arms. To rectify this, we should increase the weights s_r for those variables. In the center graph a weight of 8 has been applied to the Staphylococcus aureus rate. In this graph, the matching of hospitals is strongly adjusted so that hospitals with similar Staphylococcus aureus rates are paired. This results in smaller mean difference between the treatment and control arms for that variable. The values on the middle axis are all well below the desired maximum value: if randomization occurred using these strengths we are likely to get suitable balance in this variable. Unfortunately, there is a penalty. Hospitals with similar Staphylococcus aureus rates do not have similar attributable patient days per month and MRSA rates, which results in a few of these values exceeding the maximum tolerable difference between arms. In particular, the chance of a trial randomization with a difference in MRSA rates greater than 0.15 is too high with these weights. The right plot shows the randomizations when the matching weights for each variable were 1, 4, and 2, respectively. This plot shows all 300 randomizations comfortably below the predetermined maximum mean arm differences.

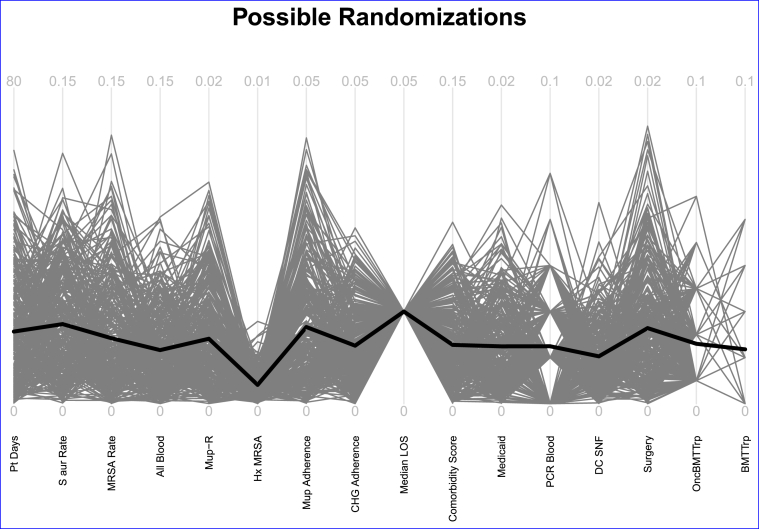
In the actual study, we used this approach with all 16 variables listed above. After trying many weights we chose a set of weights that balanced the covariates between the two arms, as seen in Fig. 2. Weights are recorded in the figure legend. For all the variables, none of these randomizations resulted in intolerable between-arm differences, and for most, the mean difference was much closer to 0 than the maximum tolerable. When it was time to assign the hospitals to their interventions, we used these weights to match hospitals in the study into pairs, then formally randomized one member of each match to treatment and the other to control. Note that some weights were 0; these variables were not used in the matching, but the figure still helps to visualize the between-arm differences obtained in the planning randomizations.

Fig. 2.

Weighting scheme used in the Mupirocin-Iodophor Swap Out Trial. The variables are: patient days (Pt days, weight = 1), Staphylococcus aureus ICU-attributable cultures per 1000 days (S aur rate, weight = 4), MRSA ICU-attributable cultures per 1000 days (MRSA rate, weight = 2), all pathogen ICU-attributable bloodstream infections per 1000 days (All Blood, weight = 4), regional mupirocin resistance estimates (Mup R, weight = 2), percent of ICU admissions with a prior history of MRSA (Hx MRSA, weight = 1), baseline usage of mupirocin (percent of mupirocin use in the first 5 days of ICU admission (Mup Adherence, weight = 1), current usage of chlorhexidine (percent adherence to daily chlorhexidine gluconate for bathing (CHG Adherence, weight = 1), median ICU length of stay (Median LOS, weight = 3), mean Elixhauser total score (Comorbidity Score, weight = 1), percent ICU patients insured by Medicaid (Medicaid, weight = 0), whether or not a facility uses polymerase chain reactions to identify MRSA in blood (PCR Blood, weight = 0), percent admissions involving a skilled nursing facility (DC SNF), percent surgical admissions (Surgery, weight = 1), whether the ICU had specialty units for oncology, bone marrow transplant, or transplant units (OncBMTTrp, weight = 2), if the ICU has bone marrow transplant or transplant units (BMTTrp, weight = 0). Note that Median LOS has the same value for all the re-randomizations. That is, for this variable, every assignment of treatment and control within the pairs results in the same mean difference in median length of stay between the control and treatment arms. This is likely due to the very small variability of this variable. The vast majority of the hospitals had the same median length of stay.

4. Discussion

In this article, we discuss using an iterative process to 1) make pairs that minimize the Mahalanobis distance between pairs of clusters with respect to potentially confounding variables; 2) visually assessing the potential effects these pairs and the resulting randomization; and 3) reweighting variables by selecting weights to make pairs of clusters. This process is similar to that proposed by Greevy and colleagues [24]. The main differences are i) that we use a visualization method, the parallel coordinates plot, to help investigators assess the effects of different weighting schemes and that ii) we emphasize and clarify that weighting must be an iterative and collaborative process. We also show a study where the method was applied, as opposed to a hypothetical example. In addition to the ongoing Swap Out trial shown in the Results section [23], we also used the method in a recently completed and published trial [27,29].

For general use, we recommend deciding on tolerable maximum differences between study arms a priori and testing many combinations of variable weights (S) until one is found which ensures that the eventual randomization is likely to satisfy. We call this the Goldilocks Approach, after the well-known fable, The Three Bears, in which Goldilocks tries three bowls of porridge – one is too hot, another too cold, and the third is just right [30]. More than three attempts to find a suitable combination of variable weights may be needed.

Another advantage of the Goldilocks Approach is that many covariates can be accounted for in this method, and many more explored. We also note that each cluster has equal probability of being assigned to treatment or control, something that constrained randomization forgoes.

It may bear reinforcement at this point that the many randomizations performed in the Goldilocks Approach do not constitute a search for the study randomization and treatment assignment with acceptable covariate balance. That description better suits the constrained randomization approach described previously. In contrast, the treatment assignments used in Goldilocks Approach are purely hypothetical. We should think of them as addressing the question: “If we were to match with these weights, what sort of covariate balance would we be likely to obtain in our actual randomization?” After we have found the set of weights that are just right, we formally randomize to assign the members of each matched set to a study arm. We expect a covariate balance that is similar to the ones seen in the parallel coordinates plot, but it is unlikely to be identical to any of the ones seen.

While it is often possible to obtain satisfactory balance on many covariates at the same time using the Goldilocks approach, there are limits, of course. For example, we can effectively require perfect matches on categorical variables by using large weights for them. If some categories have few members, the matches on the remaining variables are unlikely to be very close. For example if we place a large weight on suburban vs. urban hospital location, and have only 8 urban hospitals, we will be unlikely to find good matches on the other characteristics among those 8 hospitals.

The web-based application described above can be found at bit.ly/GoldilocksApp, and an instructional video explaining the use is here bit.ly/GoldilocksVid. We invite the community to use these resources, which are still under development.

While the Goldilocks approach to trial randomization cannot ensure balance between the treatment and control arms, it allows us as investigators to explore different weighting schemes. Choosing weights and assessing their likely impact means that the effects of matching and balance for relevant potential confounders can be observed and compared. Investigators who conduct GRTs and plan to match can use this method prior to randomizing to help ensure balance between treatment and control arms.

As our reviewers noted, we must also recommend caution when matching in both the design phase and analysis phase of research. Matching has consequences. It can result in reduced power and difficulties in calculating the intracluster correlation coefficient along with the multitude of faults mentioned in the introduction. Take care.

While the Goldilocks approach to trial randomization cannot ensure balance between the treatment and control arms, it allows us as investigators to explore different weighting schemes. Choosing weights and assessing their likely impact means that the effects of matching and balance for relevant potential confounders can be observed and compared. Investigators who conduct GRTs and plan to match can use this method prior to randomizing to help ensure balance between treatment and control arms.

Declaration of competing interest

All authors have no conflicts of interest to declare.