Phylogenetic Permulations: A Statistically Rigorous Approach to Measure Confidence in Associations in a Phylogenetic Context

Abstract

Many evolutionary comparative methods seek to identify associations between phenotypic traits or between traits and genotypes, often with the goal of inferring potential functional relationships between them. Comparative genomics methods aimed at this goal measure the association between evolutionary changes at the genetic level with traits evolving convergently across phylogenetic lineages. However, these methods have complex statistical behaviors that are influenced by nontrivial and oftentimes unknown confounding factors. Consequently, using standard statistical analyses in interpreting the outputs of these methods leads to potentially inaccurate conclusions. Here, we introduce phylogenetic permulations, a novel statistical strategy that combines phylogenetic simulations and permutations to calculate accurate, unbiased P values from phylogenetic methods. Permulations construct the null expectation for P values from a given phylogenetic method by empirically generating null phenotypes. Subsequently, empirical P values that capture the true statistical confidence given the correlation structure in the data are directly calculated based on the empirical null expectation. We examine the performance of permulation methods by analyzing both binary and continuous phenotypes, including marine, subterranean, and long-lived large-bodied mammal phenotypes. Our results reveal that permulations improve the statistical power of phylogenetic analyses and correctly calibrate statements of confidence in rejecting complex null distributions while maintaining or improving the enrichment of known functions related to the phenotype. We also find that permulations refine pathway enrichment analyses by correcting for nonindependence in gene ranks. Our results demonstrate that permulations are a powerful tool for improving statistical confidence in the conclusions of phylogenetic analysis when the parametric null is unknown.

Introduction

Despite the availability of complete genomes for many species, identifying the genetic elements responsible for a phenotype of interest is difficult because there are millions of genetic differences between almost every pair of species. One strategy to link genotypes and phenotypes is to take advantage of convergent evolutionary events in which multiple unrelated species have evolved similar characteristics. Such events represent natural biological replicates of evolution during which species may have experienced similar genetic changes driving similar phenotypic changes. When lineages independently evolve or lose a shared phenotype, convergent molecular signals can be used to identify specific genetic elements associated with the phenotypic shift.

Diverse analytic approaches have been developed to use convergent phenotypes to identify specific genetic elements underlying a trait. The methods include analyzing convergent amino acid substitutions (Foote et al. 2015) and convergent shifts in evolutionary rates (Hiller et al. 2012; Wertheim et al. 2015; Prudent et al. 2016; Hu et al. 2019; Kowalczyk et al. 2019) as well as investigating convergent gene loss (Hiller et al. 2012; Meyer et al. 2018). Methods that analyze convergent shifts in evolutionary rates (rather than convergence to any specific sequence) have been particularly successful. We have previously developed one such method called RERconverge (Kowalczyk et al. 2019; Partha et al. 2019) to link genetic elements to convergently evolving phenotypes based on evolution across a sequence of interest. Our method has been successfully used to identify the genetic basis of adaptation to a marine habitat (Chikina et al. 2016), regression of ocular structures in a subterranean habitat (Partha et al. 2017), and evolution of extreme life span and body size phenotypes (Kowalczyk et al. 2020) in mammals. Other groups have developed similar methods for identifying convergent shifts in evolutionary pressure. The Forward Genomics algorithm, which correlates percent sequence change along a phylogeny with phenotypic changes (Hiller et al. 2012; Prudent et al. 2016), has been used to identify genetic elements underlying low levels of biliary phospholipid levels in horses and guinea pigs, the loss of ability to synthesize vitamin C in some primates, bats, and guinea pigs, as well as the loss of ocular structures in two independent subterranean mammals. Both RERconverge and Forward Genomics involve a phylogenetic inference step and a subsequent test for phenotype association. More sophisticated but computationally intensive methods that consider the phenotype at the phylogenetic inference step have also been developed, notably PhyloAcc (Hu et al. 2019), although these methods are difficult to scale to genome-wide analyses. A related but distinct approach is to assess the association between gene loss (the limiting case of relaxed evolutionary pressure) and convergent phenotypes. A recent study used phylogenetic generalized least squares (PGLS) (Grafen 1989) to compute associations between gene losses and diverse traits and found a large number of significant associations (Prudent et al. 2016).

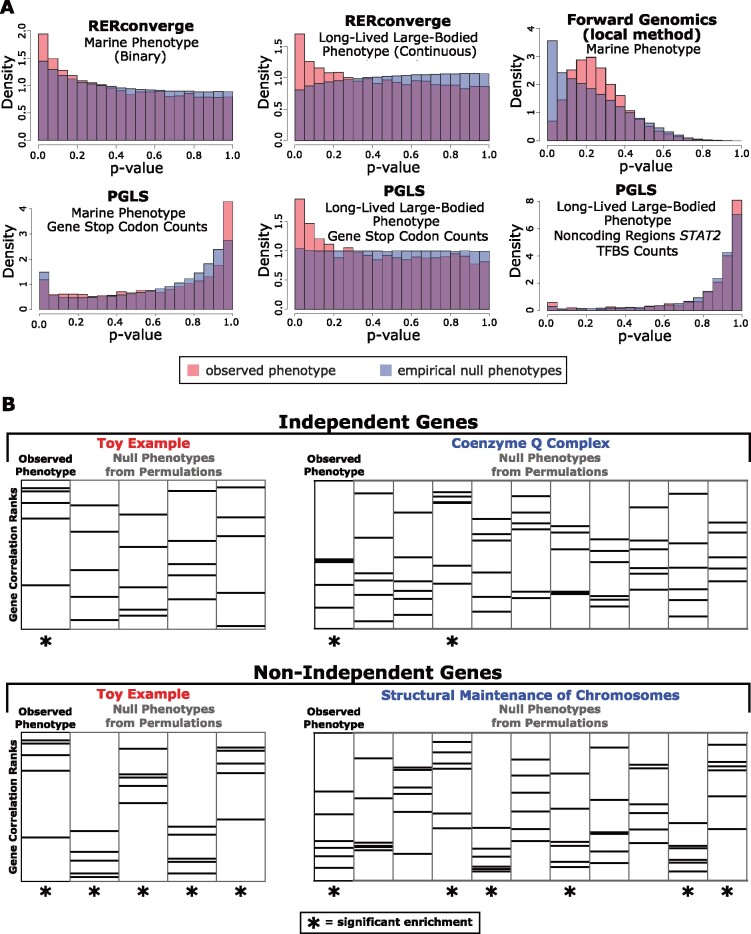
Importantly, these methods are often applied in a genome-wide discovery context. As such, the general approach can be summarized as using a statistical test to calculate the association between convergent phenotypes and some measure of molecular evolution (evolutionary rate or gene loss) across a large number of genomic regions, followed by multiple hypothesis testing corrections. If an enrichment of small P values is observed, then it is presumed that some genes (or other genetic elements) are truly associated with the phenotype. This conclusion rests on the assumption that under the null hypothesis of no association, each data point is sampled independently from a common null distribution, in which case uniform P values would be observed. However, when applied to genome-scale data sets, phylogenetic methods often show atypical statistical behavior in which the expected uniform distribution of P values is not observed when using null phenotypes (fig. 1A). For example, the standard RERconverge analysis is anti-conservative when applied to the marine phenotype but conservative when applied to the long-lived large-bodied phenotype. Forward Genomics likewise produces large deviations from the expected null. This issue exists for even the widely used PGLS method, which produces a near-uniform null when applied to gene loss in long-lived large-bodied mammals, but an extremely skewed distribution when applied to loss of transcription factor binding sites in the same phenotype.

Fig. 1.

Permulations reveal statistical anomalies in genetic element- and pathway-level analyses because parametric P values deviate from the expected uniform distribution when assessed on null phenotypes. (A) P value histograms comparing P values obtained using an observed phenotype (red) compared with P values obtained from 500 (or more, see Results) null phenotypes from permulations. We evaluate a binary phenotype (marine) and a continuous phenotype (long-lived and large-bodied) through RERconverge, a binary phenotype (marine) through Forward Genomics, and a binary phenotype (marine) and a continuous phenotype (long-lived and large-bodied) through PGLS with gene stop codon counts and noncoding element STAT2 TFBS counts. In all cases, the empirical null from permulations (shown in blue) is nonuniform. Since null P value distributions are often nonuniform (shown in blue), observed parametric P values from standard statistical tests (shown in red) cannot be interpreted using traditional strategies. (B) Pathway enrichment statistics from RERconverge long-lived large-bodied analyses demonstrate artificially inflated significance because genes in many pathways are nonindependent. Accordingly, null phenotypes from permulations often show false signals of enrichment. Permulations correct for nonindependence by quantifying the frequency at which significant pathway enrichment occurs due to chance.

PGLS is specifically designed to account for autocorrelations arising from phylogenetic dependence. Therefore, the fact that a nonuniform null is observed for even the PGLS method demonstrates that deviations from the expected null cannot be explained by the phylogenetic structure of the data alone, but can also result from other sources of dependence that arise in the context of large multiple alignment data sets. Differences in genome quality (Hosner et al. 2016), nucleotide frequencies (Romiguier and Roux 2017), a misspecified phylogeny, or other unknown systematic effects all create systematic biases that accumulate when the method is applied to thousands of genomic regions. As such, even if the tests can be proven to be theoretically valid under some assumptions (such as the well-understood PGLS model), they are not guaranteed to produce the expected uniform distribution when applied repeatedly to data from the same multiple sequence alignment. This deviation from the null expectation can result in overestimated statistical confidence and produce spurious genotype–phenotype associations.

The problem is further compounded when results from genetic elements are aggregated at the pathway level. Beyond the existing biases that arise from the nature of multiple sequence alignments, gene set analyses suffer additional nonindependence induced by the evolutionary process itself. It is well established that genes that are functionally related experience correlated evolutionary pressure and thus evolve in a dependent fashion (Juan et al. 2008; Clark et al. 2012, 2013). One extreme example of such coevolution is “reductive evolution,” where losing a member of interacting proteins decreases the selection pressure for preserving its interacting partners (Ochoa and Pazos 2014). As a result of coevolution, many functionally related genes “travel in packs” in association with a phenotype, meaning that if one gene in a group appears to be associated with a phenotype, the other genes in the group will as well because they do not evolve independently. The result is that a function could appear as associated with the phenotype due to random chance instead of actual involvement, causing an erroneous inference of enrichment.

The implication of coevolution is apparent when we apply standard pathway enrichment analysis to gain insight into which groups of functionally related genes are overrepresented among convergently evolving genes, as implemented in standard tools such as GOrilla, GO::TermFinder, and RERconverge enrichment functions (Boyle et al. 2004; Eden et al. 2007, 2009; Kowalczyk et al. 2019). Figure 1B demonstrates how correlated evolutionary rates can cause problems in pathway enrichment analyses. When genes are ranked based on gene–phenotype associations, coevolving genes tend to have clustered ranks. Such clusters make it easier to observe enrichment of extreme ranks, or coevolving genes that all have either high or low ranks, due to chance alone, and therefore the typical null expectation does not hold. Even when using a null phenotype, genes appear to cluster at the extremes of the ranked list. The clustering, and resulting enrichment, is caused by the genes traveling in packs, in which case simple enrichment tests assign undue confidence to an essentially spurious enrichment.

Rigorous statistical handling needs to be employed to address these sources of bias. Systematic solutions have been devised to correct issues with nonindependence, both in the contexts of quantitative genetics (Allison et al. 2002) and phylogenetics (Stone et al. 2011). However, these systematic approaches often make assumptions on the evolutionary process or other distributional assumptions, which may not accurately represent the data. We argue that an empirical approach that is grounded in the observed data can provide better calibration against sources of bias. In the context of gene expression, this problem is typically handled by performing label permutations (Subramanian et al. 2005; Majewski et al. 2010; Ritchie et al. 2015) and, in certain cases, parametric adjustments (Wu and Smyth 2012). However, simple label permutations are not applicable to associations involving a phylogeny as they would not preserve the underlying phylogenetic relationships, thereby producing false positives.

Here, we develop a novel strategy that combines permutations and phylogenetic simulations to generate null phenotypes, termed “permulations.” The strategy addresses statistical nonindependence empirically by generating phenotype permutations from phylogenetic simulations. In this way, the strategy preserves the underlying phylogenetic dependence by sampling permutations from the correct covariance structure. It also more accurately mimics the null expectation for a given phenotype by exactly matching the distribution of observed phenotype values for continuous phenotypes and exactly matching the number and structure of foreground branches (branches on which the phenotype changes) for binary phenotypes. We use these “permulated” phenotypes to calculate empirical P values for gene–phenotype associations and pathway enrichment related to a phenotype. In doing so, we have created a statistical pipeline that accurately reports confidence in relationships between genetic elements and phenotypes at the level of both individual elements and pathways.

New Approaches

Permulations: A Hybrid Approach of Using Permutations and Phylogenetic Simulations to Generate Null Statistics

The goal of permulations is to empirically calibrate P values from phylogenetic methods by producing permutations of the phenotype tree that account for the structure in the data. The permulation method requires a master species tree and a species phenotype (either continuous or binary). The method then returns a set of phenotypes that are random but preserve the phylogenetic dependence of the input phenotype. We typically generate 1,000 such permulated phenotypes, which are then used in the framework of a certain phylogenetic method (e.g., RERconverge) to compute gene–trait associations, resulting in 1,000 empirical null statistics for each gene. Similarly, we can also run enrichment analyses using the permulated phenotypes to produce 1,000 empirical null statistics for each pathway. Finally, for each gene or pathway, we calculate the empirical P value as the proportion of empirical null statistics that are as extreme or more extreme than the observed parametric statistic for that gene or pathway. Since empirical null statistics capture the true null distributions for genes and pathways, the empirical P values represent the confidence that we have to reject the null hypotheses of no association, correlation, or enrichment given the underlying structure of our data. Note that permulations do not eliminate the need for multiple hypothesis correction; even with a corrected null model, the likelihood that false discoveries are made from performing multiple statistical inferences simultaneously still exists. Our permulation methods for binary and continuous phenotypes have been included in the publicly available RERconverge package for R (Kowalczyk et al. 2019) (published on github at https://github.com/nclark-lab/RERconverge, last accessed March 20, 2021), with a supplementary walkthrough (see supplementary walkthrough, Supplementary Material online) also available as a vignette included in the RERconverge package.

Phylogenetic Permulation for Continuous Phenotypes

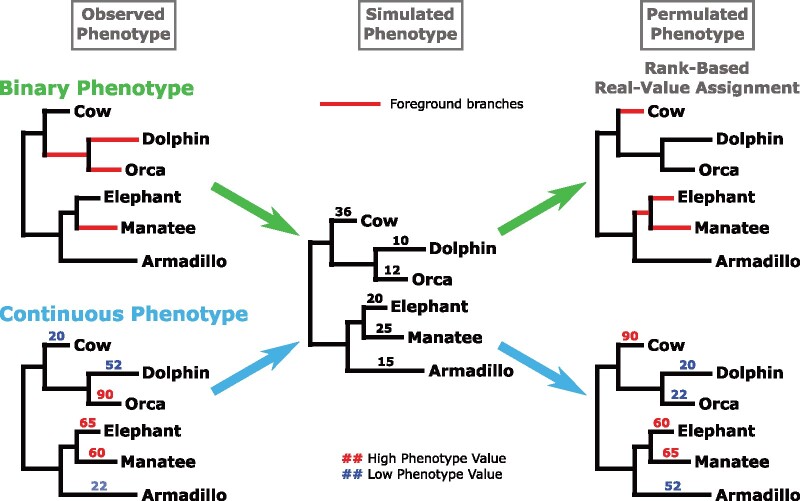
For continuous traits, generating permulated phenotypes is a two-step process. First, null phenotype values are simulated. Second, real phenotype values are assigned based on the simulated values. In step one, given the master tree with branch lengths representing average evolutionary rates and phenotype values for each species, we simulate a random phenotype using the Brownian motion model of evolution. The Brownian motion model takes a “random walk” down the master tree phylogeny to assign phenotype values. Since more closely related species are a shorter “walk” from each other, they are more likely to have more similar phenotype values than more distantly related species. In step two, real phenotype values are assigned to species based on ranks of the simulated values. The species with the highest simulated value is assigned the highest observed value, the species with the second-highest simulated value is assigned the second highest observed value, and so on. By doing so, observed phenotypes are shuffled among species with respect to the underlying phylogenetic relationships among the species. Since simulated values are more similar among more closely related species compared with distantly related species, the newly reassigned real values follow the same pattern (fig. 2).

Fig. 2.

Permulated phenotypes were generated by simulating phenotypes and then assigning observed phenotype values based on the rank of simulated values. Simulations were performed using Brownian motion phylogenetic simulations and a phylogeny containing all mammals with branch lengths representing the average evolutionary rate along that branch genome-wide. For binary phenotypes, foreground branches for permulated phenotypes are assigned based on the highest-ranked simulated values while preserving the phylogenetic relationships between foregrounds. For continuous phenotypes, observed numeric values were assigned directly to species based on ranks of simulated values.

Phylogenetic Permulation for Binary Phenotypes

For binary traits, the critical feature is the number of foreground species and their exact phylogenetic relationship, and hence the inferred number of phenotype-positive internal nodes or equivalently phenotypic transitions. The two-step process proposed above does not guarantee to perfectly preserve this structure. Instead, we employ a rejection sampling strategy where the simulation is used to propose phenotypes that are accepted only if they match the stricter requirements. Specifically, species are ranked based on simulated values, and a set of top-ranked species chosen to match the number of foreground species in the observed phenotype are proposed as a null phenotype. The proposed phenotype is only accepted if it preserves the phylogenetic relationships among chosen foregrounds, as observed in the actual foregrounds (fig. 2, Binary Phenotype). Using the simulation as the proposed distribution ensures that phylogenetically dependent phenotypes are generated and thus speeds up the construction of null phenotypes over what can be achieved from random selection.

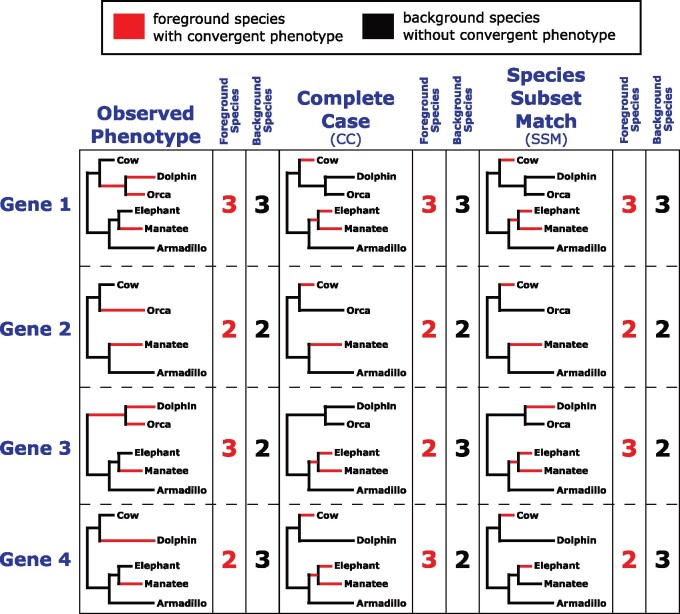
We present two binary permulation strategies: the complete case (CC) method and the species subset match (SSM) method. The SSM method accounts for the fact that not all genes have orthologs in all species, whereas the CC method ignores species presence/absence for simplicity. The strategies encompass the trade-off between computational feasibility and statistical exactitude—in some cases, it may not be possible to perform the SSM method, in which case the CC method is a viable alternative. The CC method is the first and simpler strategy. The CC method performs permulations using the master tree in which all species are present and therefore generates permulated trees that contain the complete set of species. Since not all species will have sequences available for all genes and the CC method produces one set of permulated phenotypes for all the genes, the exact number of foreground and background species per genetic element may not be preserved because of species presence/absence in those alignments (fig. 3). Thus, the CC method is an imperfect but fast method to generate null phenotypes, but we recommend use of the SSM method whenever feasible.

Fig. 3.

Examples of toy binary phenotypes permulated using the CC method or the SSM method. For the CC method, top-ranked simulated values are assigned as foreground branches regardless of gene-specific species absence. For the SSM method, top-ranked simulated values are assigned as foreground branches after considering gene-specific species absence so the number of foreground and background species for each gene is consistent across every permulated phenotype. Note that in the case of genes with all species present (e.g., gene 1), CC and SSM methods are identical.

In contrast, the SSM method accounts for the presence/absence of species in different gene trees. For each permulation, the SSM method generates separate null phenotypes for each tree in the set of genetic elements. Since genetic element-specific trees contain exactly the species that have that genetic element, the null phenotypes exactly match the observed phenotypes for that genetic element in terms of number of foreground and background species (fig. 3). Additionally, unlike the CC method, null phenotypes for a single permulation iteration are distinct, and potentially unique, from each other because they are generated on a genetic element-by-genetic element basis. Although the SSM method is statistically more ideal than the CC method, it is much more computationally intensive and may not be feasible for very large data sets. For example, the CC method took 7 s to produce 50 permulated traits for 200 genes, whereas the SSM method took ∼15.5 min.

Data Sets for Method Evaluation

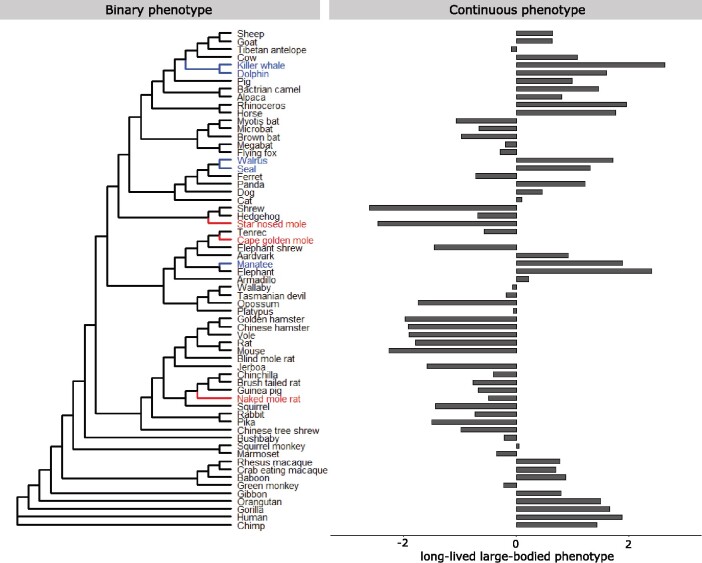
We evaluated the performance of our permulation methods by using RERconverge to find genetic elements that demonstrated convergent acceleration of evolutionary rates in association with convergent phenotypic adaptations that are well characterized, namely the evolution of the marine mammal phenotype (Chikina et al. 2016; Meyer et al. 2018), the subterranean mammal phenotype (Partha et al. 2017), and the long-lived large-bodied mammal phenotype (Kowalczyk et al. 2020). For the remaining part of this article, we will refer to these phenotypes as the marine phenotype, the subterranean phenotype, and the long-lived large-bodied phenotype, respectively. We used the set of protein-coding gene trees across 63 mammalian species previously computed by Partha et al. (2019). These trees have the “Meredith+” tree topology (Kowalczyk et al. 2020) (fig. 4), a modification of the tree topologies published by Meredith et al. (2011) and Bininda-Emonds et al. (2007), resolved for their differences across various studies as originally reported by Meyer et al. (2018).

Fig. 4.

Meredith+ tree topology and the binary and continuous phenotypes evaluated. Binary phenotypes include the marine mammal phenotype and the subterranean mammal phenotype (foreground branches are indicated in blue and red, respectively). The continuous phenotype evaluated is the long-lived large-bodied phenotype as constructed based on the first principal component between species body size and maximum longevity (Kowalczyk et al. 2020).

For the binary marine phenotype, we set three independent lineages as foreground species that possessed the marine trait (blue branches in fig. 4, Binary Phenotype): pinnipeds (Weddell seal, walrus), cetaceans (bottlenose dolphin, killer whale, the cetacean ancestor), and sirenians (West Indian manatee) (Chikina et al. 2016). For the subterranean phenotype, we set as foregrounds three independent subterranean species for which high-quality genomes were available in our data set: naked mole-rat, star-nosed mole, and cape golden mole (red branches in fig. 4, Binary Phenotype).

Finally, for the continuous long-lived large-bodied phenotype, we used the “3L” trait as defined in previous work (Kowalczyk et al. 2020). The numerical phenotype was constructed by calculating the first principal component (PC1) between body size and maximum life span across 61 mammal species (fig. 4, Continuous Phenotype). PC1 therefore represents the agreement between body size and life span—species like whales with long life spans and large sizes have large phenotype values and species like rodents with short life spans and small sizes have small phenotype values. For example, killer whale, elephant, and rhino have the highest values (2.63, 2.40, and 1.95) because they are both large and long-lived, whereas shrew, star-nosed mole, and mouse have the smallest values (−2.62, −2.46, and −2.27) because they are small and short-lived. Human, while longest-lived among the mammals included, has the fifth largest value (1.87) because humans are relatively small compared with the other mammals. Likewise, large grazing animals like cow also have smaller PC1 values (1.08, the 15th largest value) because although cows are large, they are not very long-lived given their body size.

Results

Permulation of Binary Phenotypes Improved Power and Type I Error Control

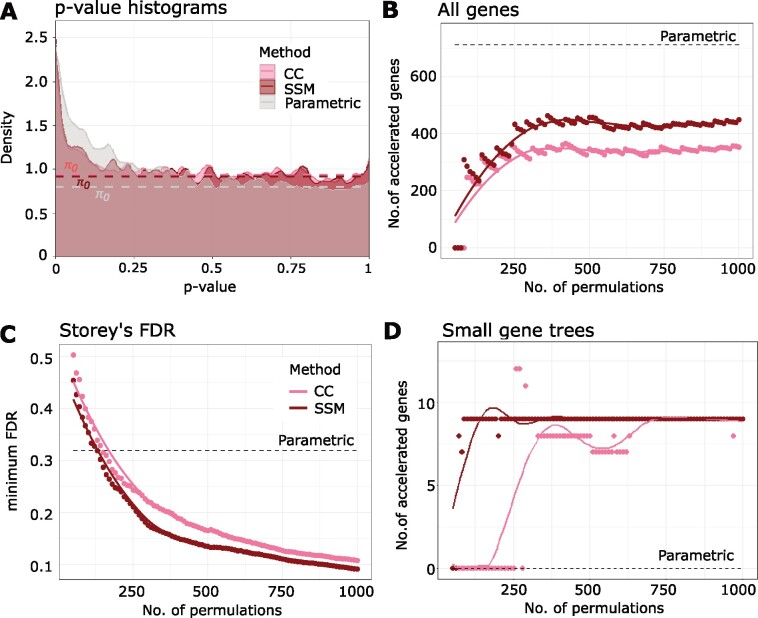
To evaluate the performance of the permulation methods compared with the parametric method for binary phenotypes, we first used RERconverge to find genetic elements with convergently accelerated evolutionary rates in species with the marine phenotype. We considered three P-value calculation methods: parametric, CC permulations, and SSM permulations. The resulting P values were corrected for multiple hypothesis testing using Storey’s correction (Storey and Tibshirani 2003; Storey et al. 2020). We see in figure 1A that the parametric P values for the association of genes with the observed marine phenotype (red histogram) were enriched for small P values. According to the standard parametric approach, which assumes a simple null hypothesis with uniformly distributed P values, the enrichment of low P values indicated the possible presence of genes with evolutionary rate shifts that were significantly correlated with marine adaptation. However, when we constructed the empirical null P value distribution using 1,000 permulations of the marine phenotype, the null distribution of parametric P values was not uniform. In fact, the enrichment of low P values was also present in the null distribution (blue histogram), although a lesser enrichment than the observed, meaning that observing low P values by chance was more likely than expected. Thus, if we used standard multiple testing procedures directly on the parametric P values, we would identify more positive genes than the true number of positives, in other words causing an undercorrection of P values.

To demonstrate that our permulation strategy effectively corrected for the background P value distribution, we plotted similar histograms of the empirical P values for the marine phenotype versus 1,000 permulated phenotypes, generated from both CC and SSM permulations. With permulations, we can see that although some enrichment of small empirical P values was observed for the marine phenotype, the empirical P values for the null phenotypes were almost perfectly uniform, meaning that our permulation methods were able to construct the correct null distribution (supplementary fig. 1, Supplementary Material online). When we overlaid the P value histograms of the parametric and empirical P values for the marine phenotype, we can see that compared with the parametric method, the histograms for the CC and SSM permulations had steeper slopes at low P values, indicating that the permulation methods had better Type I error control (fig. 5A). Furthermore, the histograms for the permulation methods plateaued at higher π₀ than the parametric method, consistent with the postulation that the parametric method would identify more (possibly false) positives. These findings were also observed when we defined genes with significant evolutionary acceleration in marine mammals (i.e., “marine-accelerated” genes) by setting a rejection threshold of Storey’s false discovery rate (FDR) ≤ 0.4 (the high threshold was set considering the high minimum FDR from the parametric method), as shown in figure 5B. For the permulation methods, as the number of permulations increased, the number of identified marine-accelerated genes increased and eventually stabilized after ∼400 permulations. The asymptotic numbers of marine-accelerated genes identified by permulations (∼350 genes for CC permulation and ∼450 genes for SSM permulation) were much smaller than the ∼700 genes identified through parametric statistics, demonstrating improved Type I error control.

Fig. 5.

Permulation of binary phenotypes corrects for inflation of statistical significance in finding evolutionarily accelerated genes in marine mammals. (A) Histogram of parametric and permulation P values for the marine phenotype from the parametric, the CC permulation, and the SSM permulation methods. (B) Permulation methods identify fewer accelerated genes in marine mammals compared with the parametric method, correcting for the inflation of significance. The rejection region of the multiple hypothesis testing is set to be Storey’s FDR ≤ 0.4, considering the weak power of the parametric method. (C) Binary permulation methods have greater statistical power compared with the parametric method, as shown by the minimum FDR calculated using Storey’s method. (D) Permulation methods can identify accelerated genes that are missing in many species (gene tree size ≤30), whereas the parametric method fails to do so.

Surprisingly, although the permulation methods identified fewer significantly accelerated regions, we could have greater confidence in their significance. Figure 5C shows the minimum FDRs achieved by the permulation methods with increasing number of permulations. The figure shows that the permulation methods provided better control of FDRs compared with the parametric method with only a few permulations (above ∼125 permulations). With increasing permulations, the minimum FDR continued to drop to reach levels below 0.1 at 1,000 permulations, whereas the minimum FDR from parametric statistics was higher at above 0.3. Use of the permulation null substantially improved the statistical power of the method and provided much higher confidence in detecting true correlations between evolutionary rate shifts and the convergent phenotype of interest.

Last, we found that permulation methods could identify marine-accelerated genes that were missing in many species, that is, genes with phylogenetic trees containing few species. In contrast, the parametric method failed to identify any such gene (fig. 5D).

Binary Permulation Methods Improved Gene-Level Detection of Functional Enrichment

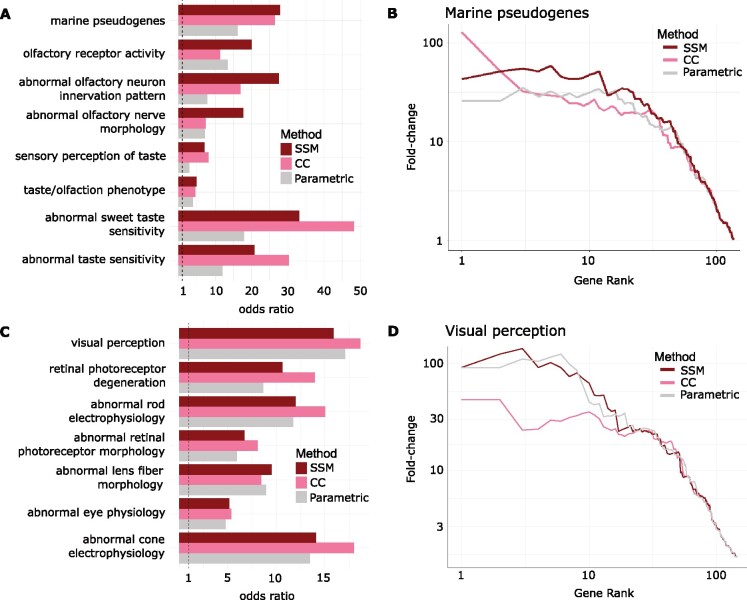
We have demonstrated that the permulation methods showed favorable statistical properties based on the distribution of P values. We expected that this approach also improved the biological signal of rate convergence analysis. To address this question, we asked if the marine-accelerated genes identified by binary permulations were enriched for functions that were consistent with the marine phenotype. Our group previously identified marine-specific pseudogenes that should be undergoing accelerated evolution in marine mammals due to relaxation of evolutionary constraint (Meyer et al. 2018). Putative pseudogenes associated with marine mammals were identified using Bayes Traits software (Pagel and Meade 2006) to find signals of coevolution between marine status and pseudogenization. In addition, our group also previously found that marine-accelerated genes that evolved under relaxed constraint were enriched for genes responsible for the loss of olfactory and gustatory functions (Chikina et al. 2016). Thus, to represent the “ground truth,” we selected a collection of gene sets relevant to olfactory and gustatory functions from the Mouse Genome Informatics database and top-ranking marine-specific pseudogenes with Bayes Traits FDR values <0.25.

We then performed the one-tailed Fisher’s exact test to measure the enrichment of the functions in the marine-accelerated genes from the parametric and permulation methods. The Fisher’s exact test odds ratios indeed showed that the CC and SSM permulation methods generally magnified or maintained the effect sizes of enrichment across the gene sets compared with the parametric method (fig. 6A). At worst, the permulation methods matched the performance of the parametric method (e.g., “taste/olfaction phenotype” gene set). The improved performance of the permulation methods was also demonstrated in the example precision-recall curves for the marine-associated pseudogenes in figure 6B.

Fig. 6.

Binary permulation methods have matching or improved power compared with the parametric method in detecting enrichments of functions consistent with known phenotypes. (A) Fisher’s exact test odds ratios showing that marine-accelerated genes identified by the permulation methods have greater enrichment of gustatory genes, olfactory genes, and marine pseudogenes, compared with the parametric method. (B) Precision-recall curves for the enrichment of the marine pseudogenes in the identified marine-accelerated genes. Greater area under the curve (curves that have higher values on the left side of the plot) have greater enrichment. (C) Fisher’s exact test odds ratios showing that subterranean-accelerated genes identified by the permulation methods have greater or comparable enrichment of ocular genes, compared with the parametric method. (D) Precision-recall curves for the enrichment of the visual perception genes in the identified subterranean-accelerated genes.

To see whether this observation generalized to other phenotypes, we repeated the whole analysis to find genes that were accelerated in species with the subterranean phenotype. As subterranean-accelerated genes have been found to be enriched in ocular functions (Prudent et al. 2016; Partha et al. 2017, 2019), we picked gene sets relevant to vision-related functions as the ground truth. In general, the signals we obtained from RERconverge for the subterranean phenotype were much weaker than in the marine phenotype case, but the enrichment was still captured in the rankings of the genes. Similar to the marine phenotype, permulation methods generally improved or matched the performance of the parametric method (fig. 6C and D).

Binary Permulation Method Corrects for False Positives in Related Approaches

In addition to performing permulations using RERconverge, we tested our methods using Forward Genomics and PGLS. Other methods, such as PhyloAcc, would require tens of millions of computational hours to generate 500 permulations, and thus permulations were not scalable to those analyses (from the analysis with RERconverge, the number of identified accelerated genes plateaued after 400–500 permulations were used (fig. 5B)).

Forward Genomics (Hiller et al. 2012; Prudent et al. 2016), like RERconverge, tests for an accelerated evolutionary rate in a set of foreground species by correlating a normalized substitution rate with phenotypes using Pearson correlation. It works only for binary phenotypes and has demonstrated success in coding and noncoding elements. Forward Genomics’ “global method” uses substitution rate with respect to each tree’s root to correlate with trait loss and identify convergent relaxed selection; therefore, it does not correct for evolutionary relatedness. The “local branch method,” an improvement on the original approach, uses substitution rate with respect to the most recent ancestor to identify relaxed selection, which substantially improves its power (Prudent et al. 2016). We used the most recent version of both the global and the local methods to test for associations between gene evolutionary rates and the binary marine phenotype.

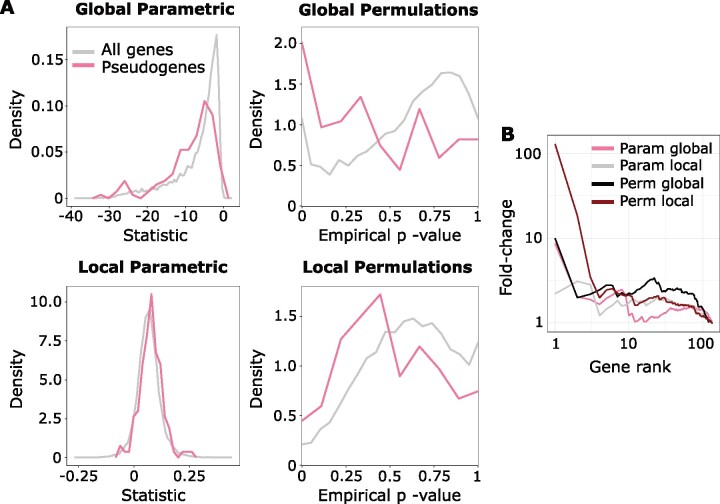
Both global and local Forward Genomics methods had unusual P value distributions. The local method identified high proportion of positives with significant P values (fig. 1A), whereas P values from the global method were highly concentrated around 0.5 (global P values not shown). Adjusting for multiple testing further exaggerated this issue. For the global method, due to the number of genes with very low P values, the lowest possible Benjamini-Hochberg (BH) corrected parametric P value was 0.531, and for the local method, the lowest possible corrected P value was 0.465. For the local method, out of 18,797 genes, more than half of the genes (12,438) had the lowest possible corrected parametric P value. As such, it was impossible to designate a significance cutoff because it would either include no genes or include most of the genes. Applying the permulation strategy to Forward Genomics output, we found that of the same set, 889 had corrected empirical P values that were ≤0.465 (the minimum observed corrected parametric P value), allowing for a more reasonable selection of a rejection threshold. Thus, permulation can improve statistical performance even for a statistic with known flaws.

We further investigated our results from Forward Genomics at the pathway level in addition to analyzing results at the individual gene level. We used the marine pseudogenes as a ground truth set of genes that should be undergoing accelerated evolution in marine species, to test our ability to detect pathway enrichment of these genes. As shown in figure 7A, the global and local parametric test statistics showed slight enrichment for elements that were pseudogenized in marine mammals, and the difference was improved when empirical P values were computed. Figure 7B shows the same data as precision-recall plots, clearly demonstrating that the permulation correction improved the predictive power of both methods.

Fig. 7.

Binary permulation methods improve Forward Genomics’ positive predictive value and power. (A) Distributions of Forward Genomics statistics and corresponding permulation P values for local and global methods. Both global and local statistics show slight shifts (to the left for global statistics and to the right for local statistics) indicating enrichment of marine mammal pseudogenes under accelerated evolution (global AUC = 0.6235; local AUC = 0.6196). Permulation P values show a more dramatic shift toward significant values for marine pseudogenes under accelerated evolution for the global method (AUC = 0.6653) and about the same shift for the local method (AUC = 0.6086) compared with parametric statistics. (B) Precision-recall curves for the enrichment of pseudogenes in marine-accelerated genes using parametric statistics and permulation P values for both local and global methods. Permulated values represent a unique ranking in which ties in permulation P values for genes are broken based on parametric statistics. Permulation methods perform at least as well as both global and local methods, indicated by curves that are higher at the left side of the plot.

Next, we tested the effect of permulations on PGLS results. PGLS tests for association between two traits across species while adjusting for the phylogenetic relationships among those species. In doing so, it numerically corrects for nonindependence due to phylogenetic relatedness. Note that unlike RERconverge and Forward Genomics, PGLS does not require evolutionary rate information and is therefore a more generalized phylogenetic analysis. We tested PGLS using both the binary marine and the continuous long-lived large-bodied phenotype for coevolution with stop codon counts across genes. We additionally tested the continuous phenotype for coevolution with STAT2 transcription factor binding site counts across noncoding regions.

Like other methods, PGLS demonstrated unexpected null behavior that varied across genomic data sets and phenotypes (fig. 1A). Although the null distribution of P values for associations between the long-lived large-bodied phenotype and the stop codon counts showed only a slight inflation of low P values (5.2% of null P values below 0.05) and otherwise nearly uniform distribution, tests using the marine phenotype and the transcription factor binding site counts showed much different behavior. Permulations for associations between the marine phenotype and stop codon counts revealed that, although there might appear to be a meaningful enrichment of low observed P values, such enrichment was observed even when analyzing permulated phenotypes. Conversely, although the enrichment of low observed P values appeared relatively less for associations between the long-lived large-bodied phenotype and transcription factor binding site counts in noncoding regions, such enrichment was indeed meaningful because it was greater than observed when analyzing permulated phenotypes. Together, these observations indicate that PGLS may exhibit aberrant statistical behaviors that the exact nature of the behaviors may vary greatly across data sets, and that permulations are a valid strategy to identify and correct those behaviors.

Permulations Improve Power to Detect Genes Correlated with a Continuous Phenotype

When we used RERconverge to evaluate the long-lived large-bodied mammal phenotype, a continuous phenotype, we observed that the Type I error rate was in fact too low. We demonstrated this by performing 1,000 permulations to generate 1,000 null statistics and P values for each gene, calculating empirical P values as the proportion of null statistics that were as extreme or more extreme than the observed statistic per gene. As shown in figure 1A, the parametric null P value distribution for genes associated with the long-lived large-bodied phenotype was nonuniform and in fact sloped down at low P values. This indicates that observing small P values due to chance alone happened less often in our data set than we would typically expect compared with the standard uniform expectation. In practice, the result of the nonuniform null was an overcorrection of parametric P values using a standard multiple hypothesis testing correction. In other words, for this data set, corrected parametric P values were larger than they should be when using multiple hypothesis testing correction (such as a BH correction) that assumed a uniform null. The null distribution of “empirical” P values, however, did follow a standard uniform null by construction, so BH corrected empirical P values represented our true, higher confidence in a correlation between gene evolutionary rate and phenotypic evolution. We observed that this increased confidence in our data—after multiple hypothesis testing correction, only 24 parametric P values remained significant at an α threshold of 0.15, whereas 305 empirical P values remained significant. Regardless of the increase in power, empirical P values provide a more accurate representation of confidence in rejecting the null hypothesis and thus are a more valid metric than parametric P values.

Permulations Correct Pathway Enrichments for Genes with Correlated Evolutionary Rates

After generating null P values and statistics from permulations for either binary or continuous traits, those values can be used to calculate null pathway enrichment statistics. Empirical P values for pathways are then calculated as the proportion of null pathway enrichment statistics as extreme or more extreme than the observed statistic. This procedure corrects for gene sets with correlated evolutionary rates, that is, genes whose rates will travel in packs regardless of any relation to the phenotype (fig. 1B). Such groups of genes will tend to show enrichment more often than would be observed if the genes’ rates were independent after conditioning on phenotype, resulting in false signals of pathway enrichment.

Permulations account for the nonindependence problem by explicitly incorporating it into the null distribution used to calculate empirical P values. In the demonstrated case of the coenzyme Q complex, only one permulation out of the ten depicted shows enrichment due to random chance (indicated by an asterisk [*] below the vertical bar in fig. 1B), which would correspond to an empirical P value of 0.1 in this toy example. This interpretation is identical to the standard P value interpretation—the proportion of times we expect to see a statistic as extreme or more extreme than observed “assuming that the null expectation is true.” In the case of permulations, we simply explicitly calculate the null expectation rather than using a predefined distribution (t-distribution, F-distribution, etc.). In the case of enrichment for a pathway with independent genes, the significance of the empirical P value will agree with the significance of the parametric P value because the null expectation from permulations agrees with the typical null expectation.

In the case of a pathway with genes with nonindependent evolutionary rates, the empirical P value will be larger than the parametric P value because the empirical P value will penalize for nonindependence. An example with “Structural Maintenance of Chromosomes” genes shows that although there is an apparent enrichment based on the observed phenotype, half (five out of ten) of permulated phenotypes show at least as strong enrichment for an empirical P value of 0.5. Therefore, although the pathway does appear to be enriched from parametric statistics, its enrichment is actually not exceptional given the null expectation for that set of genes.

Empirical P values are calculated for every pathway individually. Table 1 shows top enriched pathways under accelerated evolution and decelerated evolution in association with the long-lived large-bodied phenotype. Although most significantly enriched pathways under decelerated evolution based on parametric P values also demonstrate significant empirical P values, many pathways under significant acceleration show nonsignificant empirical P values. Thus, this phenotype shows little evidence for accelerated pathway evolution associated with phenotypic evolution.

Table 1.

Top-Enriched Pathways with Quickly Evolving Genes and Slowly Evolving Genes in Association with the Long-Lived Large-Bodied Phenotype According to Parametric P Values.

Pathway Enrichment
Positive				Negative
Pathway	Statistic	P Adjusted	Perm P Adjusted	Pathway	Statistic	P Adjusted	Perm P adjusted
Olfactory Signaling	0.217	9.25e−43	0.199	Cytokine–cytokine receptor interaction	−0.181	3.40e−20	0.0913
Gprotein-coupled receptors signaling	0.0606	8.34e−7	0.596	Mitotic cell cycle	−0.132	6.03e−12	0.213
Biological oxidations	0.150	1.10e−6	0.276	Immune system	−0.0600	1.54e−6	0.0913
Valine and isoleucine degradation	0.219	3.32e−5	0.354	DNA replication	−0.122	2.81e−6	0.352
Fatty acid metabolism	0.215	8.26e−5	0.352	Fanconi anemia	−0.212	4.45e−5	0.221

Note.—Due to the number of pathways, the lowest possible BH corrected permulation P value is 0.0913. Values in italics show significance at α = 0.25. Note that many accelerated pathways that appear to be enriched based on parametric P values are not enriched based on permulation P values.

Comparison of Phylogenetic Simulations, Permutations, and Permulations

Alternatives to permulations include either permutations or simulations alone. Permutations involve randomly assigning phenotype values to species regardless of the underlying phylogenetic relationships among those species. Meanwhile, simulations refer to the first step of permulations—phenotype values are generated based on predicted phenotype evolution along the phylogenetic tree. However, unlike permulations, simulations do not include reassigning the observed values based on simulated values and thus do not preserve the distribution of the original phenotype values.

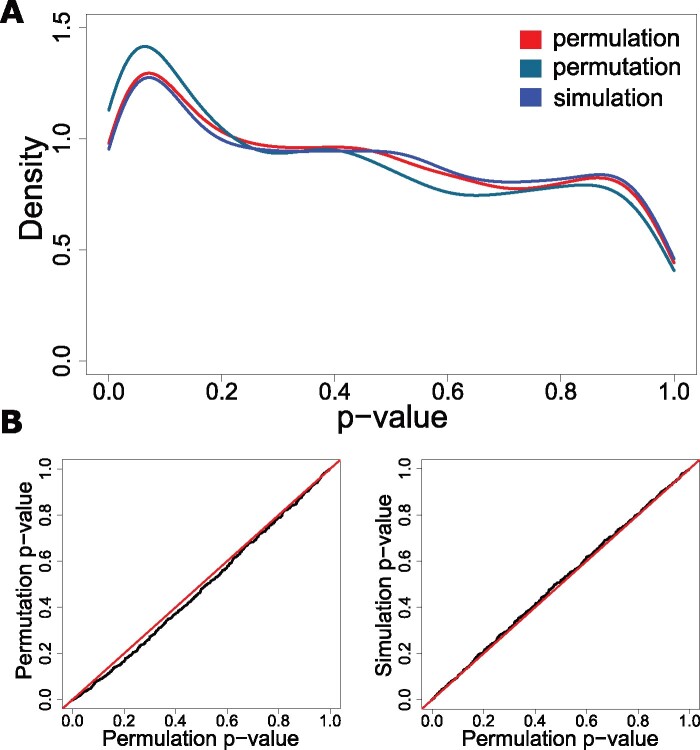
At the pathway level, permulations result in P values that are about equally as conservative as phylogenetic simulations alone and more conservative than permutations alone (fig. 8). Both permulations and simulations are preferred to permutations because null phenotypes generated from permulations or simulations reflect the underlying phylogenetic relationships among species, whereas null phenotypes from permutations do not. Therefore, the empirical null generated from permulations or simulations more closely represents the true null expectation for phenotype evolution. Although permulations and simulations show similar performance, we prefer permulations because permulated phenotypes exactly match the distribution of observed phenotypes and thus create null phenotypes uniquely tailored to a particular continuous phenotype of interest. Such matching eliminates statistical anomalies that can arise due to discrepancies in range and distribution of permulated phenotypes compared with observed phenotypes.

Fig. 8.

Permulations P values are more conservative than permutation P values and about equally as conservative as simulation P values. All plots demonstrate enrichment for canonical pathways associated with the long-lived large-bodied phenotype. (A) Density plots representing the empirical P value distributions for the three methods to generate null P values. Permulation and simulation curves are very similar, whereas the permutation curve demonstrates a stronger enrichment of low P values and therefore less conservative P values. (B) Q–Q plots comparing empirical P values from permulations to empirical P values from simulations and permutations also demonstrate that permulation P values are more conservative than permutation P values and about equally as conservative as simulation P values.

Discussion

We present permulations, a set of novel empirical methods to address problems of nonindependence and bias in phylogenetic analysis. The methods use phylogenetic relationships among species alongside known values of an observed phenotype to inform Brownian motion simulations from which permuted phenotypes are then generated. By doing so, the methods empirically construct the possibly composite null distribution and account for this complexity in multiple hypothesis testing. For permulation of binary phenotypes, the phylogenetic characteristics preserved are the number of foreground branches and the underlying relationships among foreground branches. For continuous phenotypes, the exact distribution of phenotype values is preserved in addition to the underlying phylogenetic relationships among species.

From testing the strategy on binary and continuous phenotypes, we find that our permulation strategy is an effective approach for overcoming challenges in multiple testing with composite nulls in comparative phylogenetic studies. We discuss with examples how our binary and continuous permulation methods fix issues of both undercorrection and overcorrection of P values for specified phenotypes and subsequently improve the quality and confidence of prediction. Note that although our examples demonstrate the usefulness of permulations, they are not necessarily representative of how empirical null distributions will deviate from the typical null for all phenotypes over all phylogenies for all sets of genetic elements. In fact, we expect permulations to behave differently as those variables change, and thus the best way to determine how permulations will affect a particular data set is to run the permulation analyses.

Devising a systematic solution for such problems is difficult because the causes of complex null distributions in phylogenetic studies can be confounding. The necessity for incorporating phylogenetic information to correct for phylogenetic effects is well understood (Felsenstein 1985; Stone et al. 2011; Sakamoto and Venditti 2018), and some systematic solutions have been designed to tackle the problem, including phylogenetic independent contrast (PIC) (Felsenstein 1985), PGLS (Grafen 1989), phylogenetic autoregression (Cheverud and Dow 1985; Gittleman and Kot 1990), and phylogenetic mixed models (Lynch 1991; Housworth et al. 2004; Hadfield and Nakagawa 2010). However, systematic solutions usually make phylogenetic or distributional assumptions that can lead to inaccuracies if the assumptions do not accurately represent the data. For example, PIC makes an assumption that the observed phenotype evolved by Brownian motion, and it can lead to overcorrection when the selection giving rise to the observed data did not actually cause strong phylogenetic effects (Martins 2000). In addition, phylogenetic mixed models usually assume that evolution along the phylogeny follows a Brownian motion process and that the resulting phenotype values are normally distributed. Without fully understanding the underlying evolutionary mechanism, incorrect assumptions can lead to overcorrection or undercorrection of statistical confidence. Empirically correcting P values using permulation methods allows us to circumvent the need to artificially deconstruct this unknown correlation structure in the data. Importantly, although our permulation methods are based on Brownian motion simulations, the simulated trait values themselves are not incorporated in the null phenotypes, and instead are only used as a way to incorporate phylogenetic dependencies in informing how trait values should be permuted across the phylogeny. In this sense, the choice of simulation model is not important.

For binary phenotypes, our permulation methods choose permuted foreground sets by matching the number of foregrounds and their underlying relationships to those observed in the actual phenotype. This approach of defining null phenotypes can be justified by phylogenetic nonindependence, a notion that arises from the implications of shared ancestry (Felsenstein 1985). At the time of divergence, closely related species diverging from a common ancestor are likely to experience similar selective pressures as the ancestor as well as similar genetic predispositions to respond to the selection pressures. With progressing evolutionary time, the daughter species will evolve independently in response to their respective environments. Such similarities in environmental pressures and genetic predispositions diminish with increasing evolutionary distance between species, meaning that the variance in phenotype values will increase with increasing divergence in evolutionary time. Considering this phylogenetic nonindependence and that adaptations to selection pressures are often assumed to be reflected in evolutionary rates, it is reasonable to preserve the pattern of divergence between foreground species to construct hypothetical null phenotypes, in finding correlations between evolutionary rates and phenotypes. It is impossible to pick a new set of foreground branches with perfectly matching divergence times, but matching divergence patterns can serve as a justifiable workaround because the general implications of shared ancestry on phylogenetic nonindependence among the new set of foregrounds would apply in a similar way.

We developed two versions of permulation methods for binary phenotypes. The CC algorithm produces one permuted phenotype from the master tree to apply for all genes simultaneously, whereas the SSM algorithm produces distinct permuted trees for each gene, accounting for the differences in species membership in different gene trees. This makes the CC method statistically imperfect. For example, a gene that is missing in some species will have a phylogenetic tree that is missing some branches. Because the CC method produces permuted trees from the master tree that contains all species, it may not conserve the number and relationships of foregrounds across the permulations of the example gene (e.g., genes 3 and 4 in fig. 3). In contrast, the SSM method accounts for differences in numbers and patterns of foregrounds among different genes and addresses each gene independently. This means that the SSM method is the ideal implementation of our concept of binary permulations. However, the CC method is both computationally much faster and accounts for the fact that existing comparative genomics methods take in phenotype inputs in different forms. For example, Forward Genomics requires one phenotype tree to apply for all genes, whereas HyPhy RELAX requires multiple phenotype trees with matching topology to each gene. Regardless of the statistical flaw, our results demonstrate that applying the CC method on Forward Genomics is beneficial for improving prediction (fig. 7). The CC method is significantly faster than the SSM method because it only produces one permuted tree for each permulation, instead of a heterogeneous set of permuted trees applying to different genes. Therefore, in the case of limited computational resources or very large data sets in which using the SSM method is infeasible, the CC method can serve as a good alternative.

Our results also demonstrate that binary permulations improve the sensitivity of RERconverge to identify significantly accelerated genes that are missing in many species (fig. 5D), that is, genes with small trees. Because of lower species numbers, genes with small trees suffer from lower statistical power compared with genes with large trees (e.g., the number of ways to permute a small tree is much fewer compared with a large tree). As such, pooling all the P values together to perform multiple testing correction unfairly penalizes genes with small trees. Calculating empirical P values from multiple empirical permulations is a way to correct for this imbalance in power by indirectly incorporating important covariates, which accounts for the number of foregrounds, backgrounds, and the ratio and phylogenetic relationship between them. Indeed, the pooled null empirical P values have a uniform distribution (supplementary fig. 1, Supplementary Material online), establishing the validity of applying standard multiple testing methods to identify significant divergence in evolutionary rates. Future work can evaluate if such benefits are similarly observed when applied to other comparative genomics methods.

Permulations grant increased power to detect genes associated with a continuous phenotype as suggested by the shape of the empirical null distribution (fig. 1). When P values from permulations are compared with permutations or simulations of trait values, we find that permulation P values are more conservative than P values from permutations alone and equally as conservative as P values from simulations alone. This suggests that permulations offer a valid alternative to phylogenetic simulations. Importantly, permulations preserve the exact distribution and range of phenotype values, a critical characteristic related to the power of the correlation calculated between gene evolution and phenotype evolution. Thus, permulations more accurately match the power between observed and permulated statistics compared with observed and simulated statistics.

Although many of our tests of the permulation strategy were performed using RERconverge, permulations are applicable to any similar methods. When using permulations to calculate empirical P values using Forward Genomics, an alternative evolutionary rates-based method, we show that we can quantify a realistic confidence level at which we believe a gene is under accelerated evolution in a subset of species. Even when using the Forward Genomics global method, a deprecated method that does not account for phylogenetic relationships among species, permulations improved the ability to detect accelerated evolution in marine pseudogenes (fig. 7). The improvement is likely due to permulations indirectly capturing phylogenetic information through their construction. For the Forward Genomics local method, permulations captured realistic confidence levels without losing the ability to detect accelerated evolution in marine pseudogenes. Theoretical P values directly from the Forward Genomics method (fig. 1A) show over half of the genome under significantly accelerated evolution related to the marine phenotype (12,438 out of 18,797 genes with the lowest possible BH corrected P value), which is biologically highly unlikely (Eyre-Walker and Keightley 1999; Eyre-Walker et al. 2002; Eyre-Walker et al. 2006; Kryukov et al. 2007). Permulations reduce the number of genes under significantly accelerated evolutionary rates to a more modest number (889 genes if using the same confidence level cut-off) to more accurately reflect both the biology of the system and our confidence in identifying genes with significant evolutionary rate shifts.

Our permulations also reveal aberrant statistical behavior in PGLS. Designed to correct for phylogenetic relatedness when testing for coevolution of traits, PGLS indeed demonstrates a near-uniform empirical P value distribution for one set of tests for coevolution of the long-lived large-bodied phenotype and gene stop codon counts. However, the method’s behavior is dramatically different when testing for coevolution of gene stop codon counts with the binary marine phenotype. It likewise shows undesirable behavior when testing for coevolution of STAT2 transcription factor binding site counts across noncoding regions. In addition to revealing a nonuniform null, the exact identity of noncoding regions with significant observed and permulation P values is different, completely altering analysis results. These findings suggest that phylogenetic methods may behave in unexpected ways, and permulations are a valid strategy to investigate those behaviors and perform appropriate statistical corrections.

Finally, permulations demonstrate a crucial correction to pathway enrichment statistics that corrects for coevolution among genes in a pathway of interest. Since pathways often contain functionally related genes that evolve at similar rates, performing pathway enrichment treating each gene as an independent observation is statistically incorrect and will result in erroneous conclusions. Performing permulations at the pathway level identifies pathways that are falsely shown to be enriched and correctly quantifies the confidence at which we may state that a pathway is enriched. We argue that a strategy like permulations is essential in virtually all cases of pathway enrichment calculations to account for gene nonindependence driven by correlated evolutionary trends.

Overall, permulations are an important statistical consideration that should be undertaken to accurately report results from evolutionary rates-based analyses as presented here. Regardless of whether permulation allows for greater or fewer null hypothesis rejections at a given threshold, they are an accurate depiction of statistical power given a data structure. In the absence of a known parametric null that accurately represents a data set, a permulation-style approach is an important tool to calculate statistical confidence.

Materials and Methods

RERconverge

RERconverge finds associations between genetic elements and phenotypes by detecting convergent evolutionary rate shifts in species with convergent phenotypes. The method operates on any type of genetic element and has been used successfully for both protein-coding and noncoding regions. Prior to running RERconverge, phylogenetic trees for each genetic element are generated using the PAML program (Yang 2007) or related method, with branch lengths that represent the number of substitutions that occurred between a species and its ancestor. Raw evolutionary rates are converted to relative evolutionary rates (RERs) using RERconverge functions, readTrees and getAllResiduals, which normalize branches for average evolutionary rate along that branch genome-wide and correct for the mean–variance relationship among branch lengths (Partha et al. 2019). RERs and phenotype information are then supplied to correlateWithBinaryPhenotype or correlateWithContinuous Phenotype functions to calculate element–phenotype associations. Kendall’s τ associations are calculated for binary phenotypes, and Pearson correlation values are calculated for continuous phenotypes, both by default.

After calculating association statistics, signed log P values for associations are used to calculate pathway enrichment using the rank-based Wilcoxon Rank Sum test. The fastWilcoxGMTAll function in RERconverge calculates pathway enrichment statistics over a list of pathway annotations using all genes in a particular annotation set as the background.

Phylogenetic Simulations

As shown in figure 2, each permulated phenotype is generated by first performing a phylogenetic simulation using an established phylogenetic topology. To generate the master tree, whose branch lengths represent the average evolutionary rates of all genetic elements in the data set for each species, the function readTrees in RERconverge can be used. Next, the master tree and the trait values (binary or continuous) are used to compute the expected variance of the phenotype per unit time, and subsequently perform a Brownian motion simulation to simulate branch lengths; the R package GEIGER (Harmon et al. 2008) is used to perform both operations. Simulated values are then used in different ways for binary and continuous phenotypes to generate permulated phenotypes.

Implementation of Permulation Methods

In RERconverge, CC and SSM permulations are performed using the getPermsBinary function, by setting the argument “permmode” to “cc” or “ssm,” respectively. The function requires the user to supply information on the original foreground species and their relationships by specifying 1) the names of the extant (tip) foreground species and 2) an R list object containing pair(s) of sister species whose common ancestor(s) is to be included in the foreground set as well (see examples in supplementary walkthrough, Supplementary Material online). Using these inputs, the function infers the original phenotype tree and assigns the phenotype values to the correct branches (1 for foreground and 0 for background), which is subsequently used as constraints for the permulation. Phylogenetic simulations are then run using the master tree to assign simulated branch lengths to the tree branches.

For the CC permulation, the n tip branches with the highest trait values from the simulation, where n is the number of observed tip foregrounds, are selected as the new foregrounds. The function then calls the foreground2Tree function in RERconverge with “clade” set to “all” to construct a binary tree with a foreground set that includes all branches (tip and internal) in the foreground clades. A valid permulation has the same number of internal and tip foreground branches as the original phenotype. Thus, permulated phenotypes with an incorrect foreground configuration are rejected and phenotype generation is repeated until the correct number of permulations is achieved. Note that the CC method uses the same permulated phenotype for every genomic element, so statistics for some genes will not be calculated for some permulations because of species presence/absence across genes. In other words, some genes will have fewer total permulations because of the way permulated phenotypes are constructed. The exact number of foreground and background species may also differ across each permulated phenotype for the same gene.

The SSM permulation matches the tree topology of the permulated phenotypes to the tree of individual genes. To do this, the SSM permulation follows the same steps as described above, with an additional step of trimming off branches that are missing in the gene tree. In this case, the m longest tip branches (where m is the number of observed tip foregrounds in the gene tree) are chosen as new tip foregrounds to run foreground2Tree. Thus, in the SSM method, genes with different tree topologies will have different sets of permulations. However, for each unique topology, the number and phylogenetic relationships of the foregrounds are preserved. Figure 3 shows examples of CC- and SSM-permulated trees for four genes with distinct topologies.

For the continuous phenotype, the function simpermvec generates a permulated phenotype given the original phenotype vector and the underlying phylogeny with appropriate branch lengths. The master tree from the RERconverge readTrees function is appropriate to use for simulations. In most cases, the user will not have to use the simpermvec function directly—instead, the getPermsContinuous function that calculates null empirical P values for gene correlations and pathway enrichments will call simpermvec internally.

After calculating empirical null statistics and P values, empirical P values per gene are calculated by finding the proportion of null statistics from permulated phenotypes that are as extreme or more extreme than the statistic calculated using the real phenotype. This proportion represents the proportion of times that random chance produces a concordance between gene and phenotype evolution that is as strong as the observed statistic, given the underlying structure of the data. In RERconverge, the permpvalcor function calculates the empirical P values for a given set of permulation association statistics. Note that since empirical P values are a proportion of total permulations, the precision of empirical P values is based on the total number of permulations performed. For example, with 1,000 permulations, the lowest reportable P value is 0.001 and empirical P values calculated as 0 must be reported as <0.001 because we only have precision to report P values to the thousandths place.

Finally, to determine the number of permulations that can provide sufficient correction for systematic bias, the function plotPositivesFromPermulations can be used to plot how the number of significantly accelerated or conserved genetic elements changes with increasing number of permulations (fig. 5B). From the generated plot, users can determine the minimum number of permulations by evaluating when the number of positives start to stabilize.

Empirical P Values for Pathway Enrichment

Empirical null statistics and P values for pathways are calculated using the empirical null statistics and P values for individual genes. For each set of empirical null statistics generated from a particular permulated phenotype, genes are assigned the log of the empirical null P value times the sign of the empirical null statistic for that permulation. Empirical null pathway statistics are calculated for each permulation using those values with the RERconverge function fastWilcoxGMTall that performs a Wilcoxon Rank Sum test comparing values from genes in a pathway to values in background genes. The function getEnrichPerms calculates null enrichment statistics given a set of null correlation statistics, or, alternatively, getPermsBinary and getPermsContinuous calculate both null correlation and null pathway enrichment statistics simultaneously by default for the binary and continuous phenotypes, respectively. Empirical P values for pathway enrichment are then calculated as the proportion of empirical null statistics that are as extreme or more extreme than the observed enrichment statistic using the permpvalenrich function. Pathways that show significant parametric P values and nonsignificant empirical P values are likely cases of genes “moving in packs” and are not truly significantly enriched.

Phylogenetic Generalized Least Squares

PGLS analyses were conducted through R as implemented in the “nlme” package using the gls function. Within-group correlation structure was defined using the corBrownian function from the “ape” package and a master tree with branch lengths representing genome-wide evolutionary rates per species.

Noncoding regions were identified based on evolutionary convergence from phastCons scores across the 63 mammal species as described here: https://github.com/nclark-lab/RERconverge/blob/master/NoncodingRegionWorkflow (last accessed March 20, 2021). Stop codon calls per gene were obtained from Meyer et al. (2018) and were based on genome-wide calls across species.

TFBS calls were obtained using the HOCOMOCO STAT2 binding site motif based on position weight matrix scores. Calls for 29,880 noncoding regions corresponding to human chromosome 1 were used for analyses. Of those regions, 560 had a sufficient number of calls and variation in calls across species to calculate PGLS statistics.

Supplementary Material

Supplementary data are available at Molecular Biology and Evolution online.