Salt bridge dynamics in protein/DNA recognition: a comparative analysis of Elk1 and ETV6

Abstract

Electrostatic protein/DNA interactions arise from the neutralization of the DNA phosphodiester backbone as well as coupled exchanges by charged protein residues as salt bridges or with mobile ions. Much focus has been and continues to be paid to interfacial ion pairs with DNA. The role of extra-interfacial ionic interactions, particularly as dynamic drivers of DNA sequence selectivity, remain poorly known. The ETS family of transcription factors represents an attractive model for addressing this knowledge gap given their diverse ionic composition in primary structures that fold to a tightly conserved DNA-binding motif. To probe the importance of extra-interfacial salt bridges in DNA recognition, we compared the salt-dependent binding by Elk1 with ETV6, two ETS homologs differing markedly in ionic composition. While both proteins exhibit salt-dependent binding with cognate DNA that corresponds to interfacial phosphate contacts, their nonspecific binding diverges from cognate binding as well as each other. Molecular dynamics simulations in explicit solvent, which generated ionic interactions in agreement with the experimental binding data, revealed distinct salt-bridge dynamics in the nonspecific complexes formed by the two proteins. Impaired DNA contact by ETV6 resulted in fewer backbone contacts in the nonspecific complex, while Elk1 exhibited a redistribution of extra-interfacial salt bridges via residues that are non-conserved between the two ETS relatives. Thus, primary structure variation in ionic residues can encode highly differentiated specificity mechanisms in a highly conserved DNA-binding motif.

Introduction

The biological functions of many DNA-binding proteins are related to their sequence selectivity. Functionally specific proteins are typically associated with high selectivity for cognate DNA sites over nonspecific sequences. Type II restriction endonucleases are classic examples for which stringent selectivity is essential for maintaining the integrity of the host genome against invasive DNA.¹ Under optimal conditions, the selectivity (ratio of cognate-to-specific affinity) of EcoRI binding to cognate sites over even one-base-different sequences is >10⁴, and greater still when both binding and catalysis are considered.^2,3 In contrast, proteins with housekeeping or architectural roles show more relaxed sequence preferences. While specificity can be treated relatively as a competition equilibrium involving both cognate and nonspecific DNA,⁴ determination of absolute affinities affords unique insight into their biophysical basis, especially upon perturbation by salt or other solution parameters.

Transcription factors comprise a large class of eukaryotic DNA-binding proteins that regulate gene expression, a major functional component of cellular responsiveness to the environment. In humans, ~10% of all genes encode for transcription factors, which are classified according to their DNA-binding domains into a remarkably restricted number of structural motifs.⁵ The ETS-family transcription factors represent attractive models for understanding how a diverse range of molecular properties arise in the context of a highly conserved winged helix-loop-helix motif. Their molecular diversity parallels their history as one of the most ancient transcription factor families in metazoan (animal) evolution,⁶ as well as myriad physiologic and disease processes in which ETS factors are involved.^7,8 The hallmark of ETS proteins is their eponymous DNA-binding domain that recognizes 10-bp sequences harboring a central core consensus, 5′-GGA(A/T)-3′, with flanking bases that vary according to subtle preferences among ETS homologs.⁹

While cognate binding by ETS factors has received extensive attention, including a substantial collection of high-resolution complex structures, data on nonspecific binding remain scarce. Work by others^10–12 and us^13,14 has begun to fill this gap using the ETS domains of Ets-1 and ETV6 as models. We have used the characteristic quenching of the intrinsic tryptophan fluorescence to measure binding to polymeric nonspecific DNA, and carried out full-spectral analyses of the emission by singular value decomposition to estimate binding affinities and cooperativity parameters. In combination with cognate binding affinities as measured by biosensor-SPR, resolution of both specific and nonspecific affinities affords an unambiguous determination of the specificity ratio.

In the case of ETV6, cognate binding exhibited strong salt dependence that corresponded to the observed number of DNA phosphate contacts in the co-crystal structure.¹² However, nonspecific binding was less salt-dependent,¹⁴ even though the same DNA-contact interface was determined by NMR to be involved in both cognate and nonspecific binding.¹¹ Proteins with multiple DNA-binding domains (in the same polypeptide chain or via quaternary structure) can engage DNA nonspecifically in a variety of low-affinity configurations. Other factors, including ETS proteins, harbor a single DNA-binding surface which mediates both cognate and nonspecific binding in a more conformationally constrained manner.^10–12 The biophysical chemistry that drives their specificity, especially insofar as how conserved homologs are differentiated among each other, remains poorly understood. Since ionic interactions constitute a major contributor to DNA binding, one approach to this problem is to compare the cognate and nonspecific binding of structural homologs that differ in ionic composition. Following this strategy, we carried out a comparative study in the salt-dependent DNA-binding properties of Elk1, a structural homolog of ETV6. Their primary structures are well conserved in the DNA-contact surface, which is centered on a recognition helix H3, but diverge sharply elsewhere, particularly in the composition of charged residues [Fig. 1A]. Nevertheless, the co-crystal structures of both proteins in their cognate complexes are nearly superimposable [Fig. 1B], while exhibiting distinct spatial distributions of electrostatic and solvation properties [Fig. 1C]. In this work, we made direct measurements of Elk1 binding to cognate and nonspecific DNA over a wide range of ionic conditions to dissect the electrostatic contributions to target specificity. The experiments revealed that major differences in target selectivity between the Elk1 and ETV6 were due to ionic differences in their nonspecific complexes. Molecular dynamics (MD) simulations of the complexes revealed how dynamic surface salt bridges participate differentially in DNA target selection within a highly conserved structural framework.

Fig. 1.

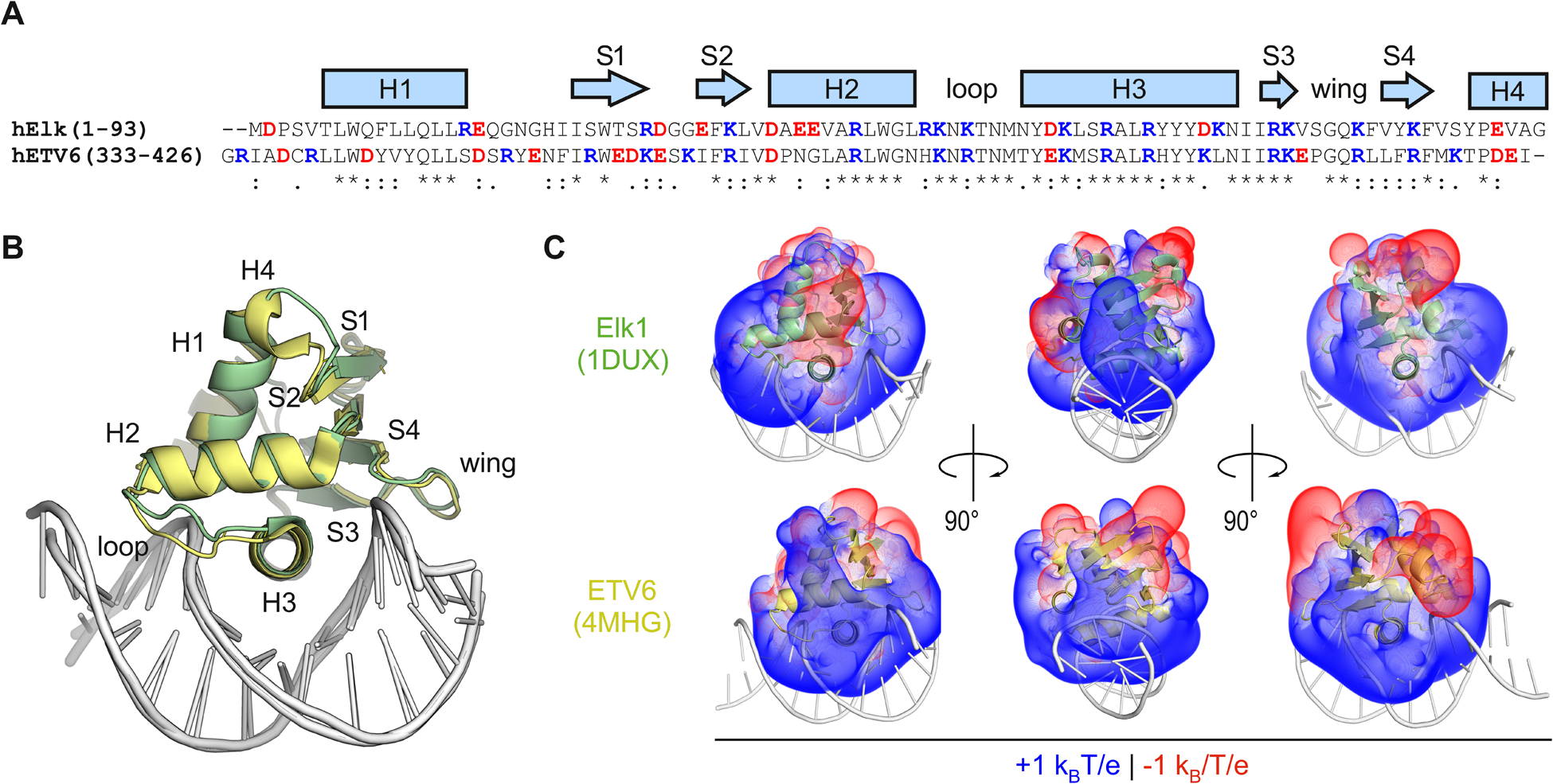
The divergent primary structures of the ETS relatives Elk1 and ETV6 encode distinct electrostatic properties in a high conserved DNA-binding motif. (A) Sequence alignment of the ETS domains of human Elk1 and ETV6. Acidic and basic residues are colored red and blue, respectively. Identity (*) as well as conservative (:) and semi-conservative (.) substitutions are indicated. (B) Structural alignment of the co-crystal structures of ETS domains of Elk1 (PDF: 1DUX) and ETV6 (4MHG) in complex with cognate DNA. The RMSD for the proteins was 0.7 Å. (C) Solvation of the proteins in the crystal structures was modeled by the Poisson–Boltzmann equation. Volumes corresponding to ±1k_BT/e (k_B, Boltzmann constant; e, electronic charge) at 25 °C in implicit water containing 0.15 M NaCl were computed using APBS software.¹⁵ The bound DNA is rendered post-calculation to orient the reader.

Material and methods

Nucleic acids

Salmon sperm DNA was purchased from Sigma-Aldrich (D1626) and used without further purification. The concentration was determined by UV absorption at 260 nm at 6600 (M bp)⁻¹ cm⁻¹. A full-length clone of human Elk1 (cDNA clone MGC:64973) in pCMV-SPORT6 was purchased from the Harvard Plasmid Repository. 5′-Biotinylated DNA oligos as follows were purchased from Integrated DNA Technologies (Coralville, IA) and annealed to form duplex hairpins as previously described.¹⁶

Molecular cloning

A construct encoding the minimal DNA-binding (ETS) domain of human Elk1 (residues 1 to 93, without the auto-inhibitory domain) was amplified from the full-length clone by PCR and ligated into the NcoI/XhoI sites of pET28b. The cloned construct consists of the open reading frame for the Elk1 ETS domain plus a C-terminal thrombin cleavage site followed by a 6 × His tag. The recombinant plasmid was transformed into DH5α E. coli and sequence-verified by Sanger sequencing.

Protein expression and purification

Heterologous expression of Elk1 in BL21*(DE3) E. coli was performed as previously described for other ETS domains.¹⁷ In brief, cells at log-growth phase were induced for 4 hours with 0.5 mM IPTG, harvested by centrifugation, lysed by sonication, and extracted by immobilized metal affinity chromatography on Co-NTA resin (Gold Biotechnology). After cleaving the C-terminal 6 × His tag with thrombin overnight at room temperature, the target protein was purified by cation exchange chromatography on Sepharose SP (GE). Protein concentrations were determined by UV absorption at 280 nm using an extinction coefficient of 25 440 M⁻¹ cm⁻¹.

Biosensor-surface plasmon resonance (SPR)

SPR measurements were performed with a Biacore T200 biosensor (GE) in a 4-channel system as previously described.^18,19 In brief, 5′ biotinylated DNA sequences of interest were immobilized on streptavidin-functionalized CM5 chips on flow cells 2 to 4 at low density to ~150 RU (response unit). Flow cell 1 was used as a reference cell and contained no immobilized DNA. The experimental buffer contains 25 mM Na₂HPO₄/NaH₂PO₄, pH 7.4, 1 mM EDTA, 0.05% v/v P20 surfactant and sufficient NaCl to achieve the desired total Na⁺ concentration. Mass transfer was minimized by running the fluidics at a high flow rate, 50 μL min⁻¹. Reference-subtracted sensorgrams from flow cell 1 were analyzed to estimate equilibrium constants K_D from steady-state data as previously described.^18,19 Briefly, steady-state signal was fitted with a one-site model:

$${\text{RU}}_{\text{obs}}={\text{RU}}_{\text{max}}\frac{C_{\text{f}}}{K_{\text{D}}+C_{\text{f}}}$$ (1)

where RU_obs is the change in response unit when a protein binds to DNA at equilibrium state, RU_max is the response at saturation, C_f is the free protein concentration, and K_D is the equilibrium dissociation constant.

Fluorescence quench binding experiments

Nonspecific binding of mixed-sequence salmon sperm DNA was measured through the quenching of intrinsic tryptophan fluorescence as previously reported.^13,14 Fluorescence was measured in a starting volume of 500 μL at an initial Elk1 concentration of 200 nM using a Cary Eclipse instrument (Agilent). The sample was excited at 280 nm, and emission spectra were recorded from 320 nm to 450 nm. Both emission and excitation slits were set to 10 nm. The concentration of salmon sperm DNA needed for titration at each step was corrected for dilution in the sample, which totaled less than 10% in volume. Each spectrum was recorded in triplicate, averaged, and subtracted from a reference scan of buffer alone. The concentration-dependent spectra at each NaCl concentration were encoded as column vectors in a matrix A and analyzed by singular value decomposition (SVD). In brief, A was decomposed to a product of three matrices U, S, and V:

$$A=US{V}^T$$ (2)

U consists of n basis vectors that correspond to orthogonal spectral features, S is a diagonal matrix with ordered singular values, and V^T consists of n row vectors that describe the titration of the basis vectors. The magnitudes of the singular values quantify the contribution of each u vector (spectral feature) to the total spectral variation i.e., trace of the matrix S, Tr(S). Typically, the first singular value accounted for >95% of Tr(S). Binding isotherms were represented by the vectors v^T which described the fractional DNA-bound ETS domain (F_b) as follows:

$$F_{b,i}\equiv \frac{{[\text{ETS}]}_b}{{[\text{ETS}]}_t}=\frac{x_i-x_{\text{min}}}{x_{\text{max}}-x_{\text{min}}}$$ (3)

where x_i represents the i-th element of v^T and the min and max subscripts denote to the estimated values corresponding the bound and unbound states. Nonspecific binding was fitted to the McGhee–von Hippel equation,^20,21 using a previously reported site size of 5.2 bp.¹¹ Parametric estimates are given ± S.E. following non-linear least-square analysis.

Molecular dynamics simulations

Explicit-solvent simulations of Elk1 and Elk1/DNA complexes were performed in version 2020.2 of the GROMACS environment. Elk1 and ETV6 constructs mimicking the experimental systems were generated by homology-modeling to the co-crystal cognate Elk1²² and ETV6¹¹ complexes using I-TASSER.²³ The protonation states of ionizable residues in the protein were computed using PROPKA3.²⁴ At pH 7.4, in addition to the charged N- and C-termini, the Elk1 protein harbored 10/16 positively/negative charged residues, while ETV6 contained 12/20 such residues. All computed pK_a values were at least one unit away from 7.4. The charged sidechains belonged exclusively to Asp, Glu, Arg, Lys, and Arg residues; His residues were judged as non-protonated at pH 7.4 by PROPKA3. The DNA duplexes were 13 bp length (24 negative charges total) and centered at the recognition helix of the proteins. DNA bases were changed to the experimental sequences using 3DNA.²⁵

Systems were individually set up in dodecahedral boxes 1.0 nm wider than the longest dimension of the solute, solvated with TIP3P water, and neutralized with Na⁺ and Cl⁻ to a nominal salt concentration of 0.15 M. The Amber14sb/parmbsc1 forcefield was used.²⁶ All simulations were carried out at an in silico temperature of 298 K (modified Berendsen thermostat²⁷) and a pressure of 1 bar (Parrinello–Rahman ensemble). Electrostatic interactions were handled by particle-mesh Ewald summation with a 1 nm distance cutoff. A timestep of 2 fs was used and H-bonds were constrained using LINCS. After the structures were energy-minimized by steepest descent. The system was then equilibrated as an NVT ensemble for 1.0 ns to thermalize the system, followed by another 1.0 ns of equilibration as an NPT ensemble at 1 bar. The final NPT ensemble was simulated without restraints for at least 600 μs, recording coordinates, energies and velocities every 1.0 ps. Post-processing, including corrections for periodic boundary effects, was performed with the following tools provided by GROMACS: TRJCONV, CLUSTER, MINDIST, RDF, RMS, and RMSF.

Quantum chemical calculations

Geometry optimization and point-energy calculations were performed by hybrid density functional theory (DFT) methods using Spartan 18 (Wavefunction, CA). Calculations were carried out using the ωB97x-D hybrid density functionals²⁸ and a continuum solvation model (CPCM) at a dielectric of 78.3 for water. As simplified models of residues in a polypeptide context, l-amino acids were constructed with unionized amine and carboxylic acid attached to the Cα carbon, while the sidechains were charged as expected at pH 7.4. To handle anionic species in the model systems, diffuse basis sets were used for geometry optimization and energy calculations. Nonbonded systems were first optimized without constraints with the 6–31+G* basis set using default tolerances. Single-point energies were then calculated with the 6–311++(2d,p) for residue pairs positioned at separation distances r along a linear geometric dimension as defined in the text and figure legends. Interaction energies were zeroed to the energy at r = 10 nm.

Bioinformatic analysis

Primary structures of ETS domains were extracted as defined in the UniProt database. Pairwise evolutionary distance calculations based on the Poisson correction model were performed with MEGA X.²⁹ Isoelectric points were computed using ExPASy ProtParam. Statistical inferences were performed using OriginPro (Northampton, MA).

Results and discussion

Quantitative definition of cognate and nonspecific DNA binding by Elk1

Typical of ETS proteins, Elk1 binds a variety of cognate DNA sequences, over a helical turn, harboring a central 5′-GGA(A/T)-3′ core. The core, which is contacted by the protein’s winged helix-loop-helix motif in the major groove, is flanked by variable sequences that are primarily contacted at the phosphate backbone in the minor groove (Fig. 1). To characterize specific binding by Elk1, we examined the E74 sequence (5′-CTGAATAACCGGAAGTAACTCATC-3′), a natural DNA target site.³⁰ A scrambled sequence (5′-CGCAAAAGCTGAGATGGCGTGCC-3′) served as a nonspecific control. The DNA oligos were 5′-biotinylated and immobilized at low densities on streptavidin-coated sensor chips. High flow rates (>50 μL min⁻¹) were used to minimize mass transfer and rebinding effects at lower salt concentrations.¹⁹ The immobilized DNAs were exposed to a range of concentrations of Elk1 to determine their dissociation constants under steady-state conditions.

At 0.15 M Na⁺, Elk1 bound the E74 site tightly. In stark contrast, the nonspecific SD1 sequence bound Elk1 negligibly across the same range of protein concentrations. Cognate binding at this Na⁺ concentration was characterized by rapid association and slow dissociation [Fig. S1, ESI†]. Mass transfer and rebinding effects were dominant even at the instrument-maximum flow rate of 100 μL min⁻¹. To overcome mass transfer and rebinding, we acquired sensorgrams starting at 0.2 M Na⁺ [Fig. 2A]. The steady-state data was well described by formation of a 1 : 1 complex [Fig. 2B]. This behavior was consistent with the literature on native Elk1 binding single copies of the cognate sequence as obligate monomers.³¹ The binding constant to both cognate DNA sequences became sharply weaker with increasing salt concentration, by ~10³ fold from 0.2 to 0.6 M Na⁺ [Fig. 2C and Table S1, ESI†]. Over this range of NaCl concentrations, Hofmeister effects on hydro-phobic hydration are insignificant. The salt-dependent profile exhibited a linear log–log salt dependence in accord with the disposition of ions upon binding:

$$-\frac{\partial \text{log}{K}_{\text{D}}}{\partial \text{log}\left[{\text{Na}}^{+}\right]}\equiv \Delta m_{\text{obs}}$$ (4)

Fig. 2.

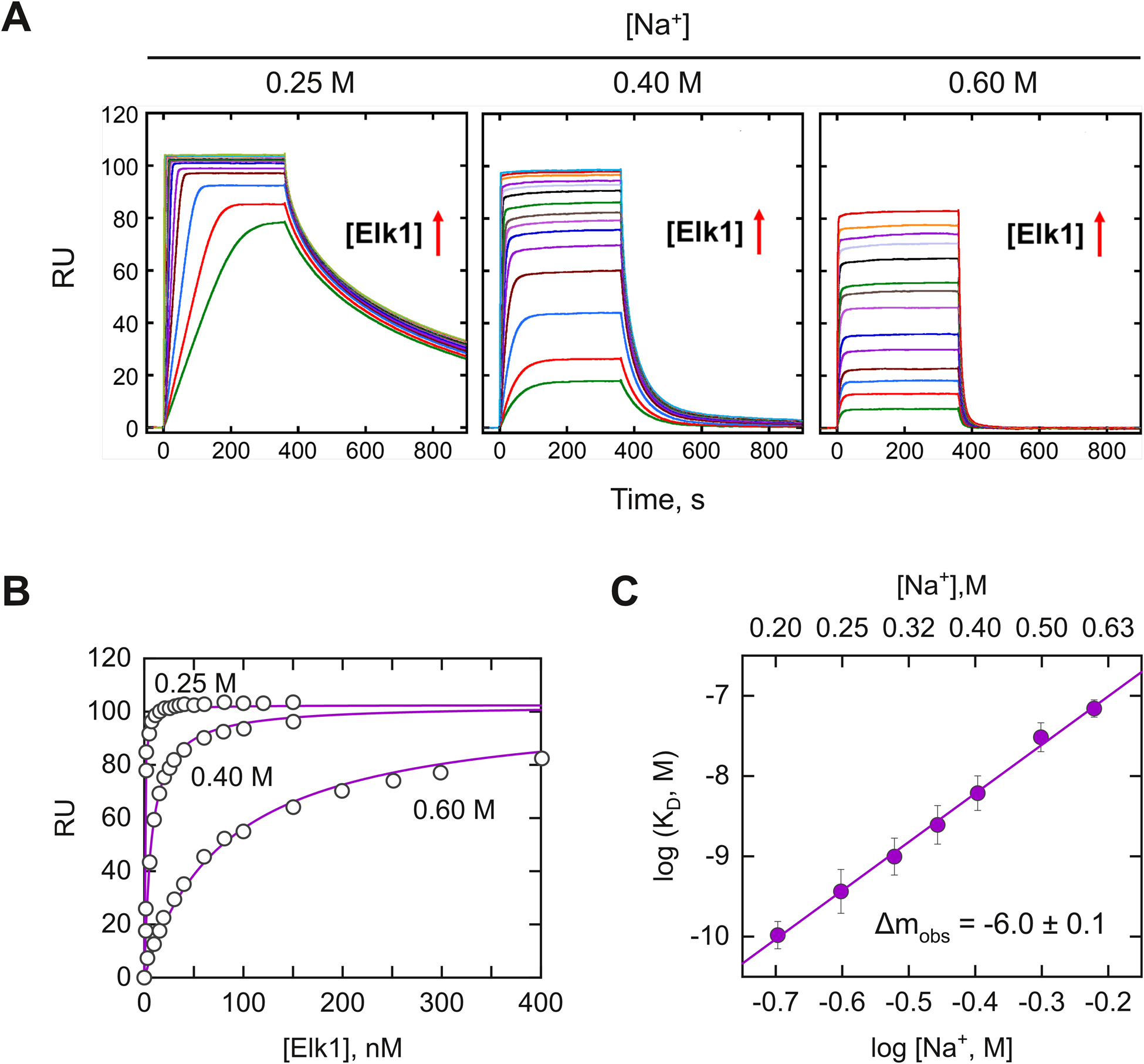
Measurement of site-specific binding by the DNA-binding domain of Elk1 by bio-sensor SPR. (A) Representative sensograms of DNA binding to the E74 site by graded concentrations of Elk1 at the indicated bulk salt concentrations. Elk1 concentrations were varied from 1 to 150 nM at 0.2 M Na⁺, from 1 to 250 nM at 0.4 M Na⁺, and from 5 to 400 nM at 0.6 M Na⁺. Exposure of the DNA-immobilized biosensor to Elk1 in the flow solution commenced at t = 0 s. Upon achieving steady state, (~400 s), the biosensor was washed with buffer alone. (B) Representative fits of the binding signal in the plateau region of the sensorgram with a 1 : 1 binding model at different salt concentrations. (C) Salt dependence of the equilibrium dissociation constants of Elk1 with E74. Error bars represent S.E. of the fits. Parametric values were given in Table S1 (ESI†).

Negative values of the ion number Δm_obs signify ion release. Their slopes indicated that 6.0 ± 0.1 ions were released by the cognate Elk1–DNA complex upon binding.

To quantify the nonspecific binding affinity of Elk1, we deployed an intrinsic fluorescence method by following the quench for three tryptophan residues upon DNA binding. We used polymeric salmon sperm DNA as a mixed-sequence nonspecific (NS) substrate in which the occurrence of cognate sites is statistically negligible. Fig. 3A–C showed the emission spectra of 200 nM Elk1 upon titration with NS DNA at representative Na⁺ concentrations. The tryptophan fluorescence was more than 80% quenched at 200 μM bp NS DNA. Full-spectral analyses by single value decomposition (see Methods) showed that the concentration-dependent spectral variation was essentially described (96%) by the most significant component. Titration profiles represented by the transition vector for this component, shown in Fig. 3D–F, were fitted with the McGhee-von Hippel model^20,21 to yield average estimates of the intrinsic dissociation constant and cooperativity parameter. With Na⁺ concentrations, in addition to an attenuation in affinity, nonspecific binding became more cooperative [Table S2, ESI†]. The emergent cooperativity with increasing salt suggested charge-charge repulsion in filling the nonspecific DNA lattice with Elk1. The salt dependence of the nonspecific binding affinity yielded Δm_obs = −3.1 ± 0.5 [Fig. 3G], about half of that for cognate binding. If the canonical DNA binding surface is involved in nonspecific binding, the salt-dependent data implicate additional interactions that have not yet been identified.

Fig. 3.

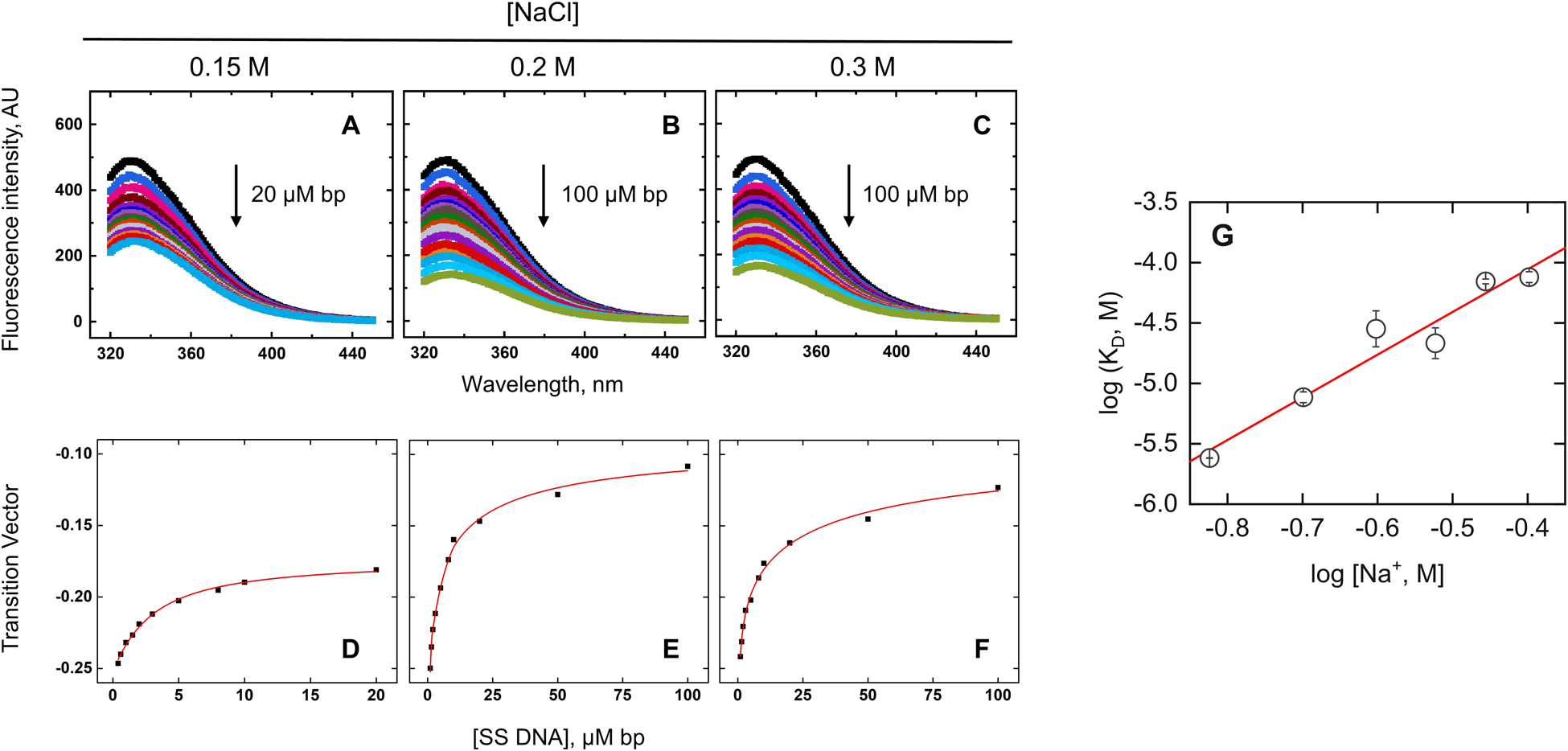
Nonspecific binding of the ETS domain of Elk1. (A–C) Representative fluorescence spectra of Elk1 in the absence (black) or in the presence (colored) up to the indicated concentration of salmon sperm DNA in bp and bulk NaCl concentrations. (D–F) SVD analysis of fluorescence spectra. Symbols represent progress of the titration as indicated by the most significant component from singular value decomposition of the emission spectra. Curves represent fits to the data by the McGhee von Hippel isotherm. (G) Salt dependence of equilibrium dissociation constants. Error bars represent S.E. in K_D from the fits. Parametric values were given in Table S2 (ESI†).

The electrostatic basis of target selectivity

Armed with salt-dependent binding for Elk1 to cognate and nonspecific DNA, we proceeded to compare the data with reported data on ETV6.¹⁴ The availability of data for the two homologs under identical solution conditions enabled a definitive comparison as summarized in Fig. 4A. For ETV6, the cognate target was 5′-CGGCCAAGCCGGAAGTGAGTGCC-3′, termed SC1. To control for the different cognate sequences, we tested Elk1 binding to SC1. Across the same salt range, Elk1 bound SC1 more weakly by ~3-fold (Table S1, ESI†), but exhibited identical salt dependence as E74. The electrostatic properties of Elk1 cognate complexes are therefore conserved.

Fig. 4.

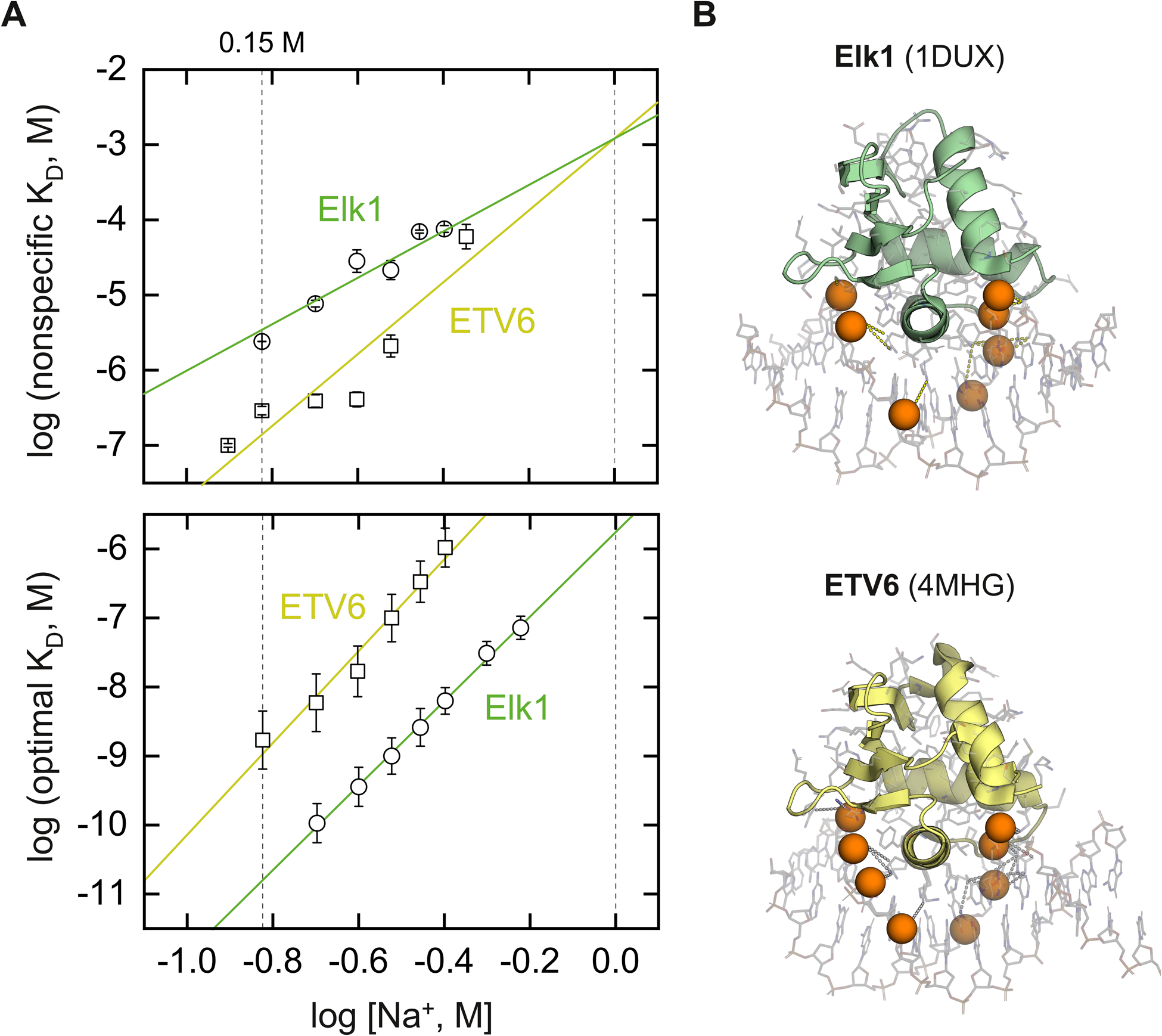
Salt-dependent DNA binding of two ETS homologs, Elk1 and ETV6. The experimental constructs consist of minimal DNA-binding domains, without auto-inhibitory or other modules that modify binding. (A) Nonspecific (top) and cognate (bottom) DNA binding by the ETS domains of Elk1 and ETV6 under identical salt régimes. Lines represent linear fits to the data. In the case of nonspecific binding, the data was globally fitted with a common intercept on the abscissa. Floating the intercepts did not statistically improve the fit as judged by the Fisher F-test for sums of squares (p = 0.38). The specific DNA target was E74 for Elk1 and SC1 for ETV6.¹⁴ (B) Identification of DNA backbone phosphates within 5 Å of a basic protein in the co-crystal cognate complexes of 1DUX and 4MHG. For clarity, the P atoms of the contacted phosphates are rendered as spheres.

To interpret salt-dependent binding structurally, we dissected the observed ion numbers Δm_obs in terms of the release of condensed counter-ions from phosphate contacts by the protein and other contributions. The counter-ion release from DNA is described by polyelectrolyte theory (PE):

$$\Delta m_{\text{obs}}=\Delta m_{\text{PE}}+\Delta m_{\text{other}}=\phi z+\Delta m_{\text{other}}=\left(\psi -\frac{2.53}{Np}\right)z+\Delta m_{\text{other}}$$ (5)

Δm_PE is proportional to the number of DNA phosphate contacts z by a coefficient φ consisting of Ψ = Ψ_S + Ψ_C = 0.88 for B-form DNA, which combines the effects of counterion condensation (Ψ_C = 0.76) and ion screening (Ψs = 0.12).³² A correction for end-effects is applied for oligomeric dsDNA harboring N_p phosphates.³³ For the 24-bp synthetic hairpins used in the SPR experiments, the corrected coefficient is φ = 0.77. Having accounted for counter-ion release from DNA, Δm_other captures all other contributions not accounted for by phosphate neutralization.

The measured ion numbers for cognate binding by Elk1 and ETV6 correspond closely to the number of phosphates within 5 Å (measured from either of the O atoms) of cationic heteroatoms in the co-crystal structures of Elk1 (1DUX) and ETV6 (4MHG): 7 and 8 respectively [Fig. 4B]. Correlation with co-crystallographic evidence therefore supported the neutralization of DNA backbone phosphates as the electrostatic component of cognate binding by Elk1 and ETV6. However, without experimental structures of the nonspecific complexes, the structural basis of nonspecific binding remained unclear.

NMR analysis by the McIntosh group has established that the cognate binding surface on ETV6 was also involved in nonspecific binding.¹¹ Similar observations were made also for Ets-1,¹⁰ an archetypal ETS domain. Previous studies of Ets-1 by molecular dynamics (MD) simulations showed that signature base-specific contacts were rapidly replaced, on the ns timescale, by indirect backbone readout when the core DNA consensus (5′-GGAA-3′) was mutated.³⁴ These results are expected for ETS domains which harbor a single copy of the helix-turn-helix DNA-binding motif. Together with the strong structural conservation of the ETS domains for Elk1 and ETV6 (Fig. 1B), the distinct surface distributions of DNA-binding cationic charges (Fig. 1C), and a good fit of their nonspecific binding as monomers (Fig. 3), available evidence supported the specific complexes as reasonable representatives of the nonspecific ensembles.

On this basis, to gain insight into the nonspecific structures, we performed all-atom molecular dynamics (MD) simulations of the Elk1 and ETV6 complexes with the same cognate and nonspecific sites as in the experiments. For the simulations, we replaced the DNA hairpins from the experiments with truncated duplexes matching the corresponding cognate sequences. Nonspecific DNA was composed by mutating the 5′-GGAA-3′ core consensus to 5′-GAGA-3′, an established approach to abolishing cognate ETS binding experimentally.¹⁶ We used the cognate co-crystal structures for Elk1 (1DUX) and ETV6 (4MHG) to template the nonspecific complexes. The Amber14SB forcefield was used for the protein and parmbsc1 parameters²⁶ were used for the DNA. After setup and equilibration steps (see Materials and methods), we carried out triplicate simulations without constraints in explicit TIP3P water containing 0.15 M NaCl. Each replicate was seeded with different initial velocities. Runs of 600 ns were judged to be sufficient for equilibration of the macromolecular conformation on the basis of RMS deviations [Fig. S2, ESI†], and literature data that 100 ns was sufficient to achieve convergence of local water and ion densities to 0.5 Å resolution.³⁵

We first analyzed the electrostatic contributions from DNA backbone neutralization by enumerating the contacts with basic protein residues. Classically, the experimental ion number represents the electrostatic contribution from counter-ion release as the protein perturbs the ionic atmosphere of the DNA.³⁶ Recent studies suggest that ionic protein/DNA contacts dynamically interconvert between contact (i.e., solvent-excluded) and solvent-separated ion pairs.^37,38 The detailed relationship between these dynamics and counter-ion release is not currently defined. However, condensed monovalent counter-ions on DNA are significantly dehydrated relative to in bulk solution,³⁹ emphasizing the importance of solvent exclusion in the contact ion pair. We therefore considered the direct contact minimum as a sensible metric for counter-ion release. We measured the distance spanned by phosphate O atoms with the nearest cationic N atoms in the N-terminus and the sidechains of Arg and Lys. For statistics, we scaled the cutoff distance based on matching the median number of contacts (±median absolute deviation, or MAD ≡ median(|x_i – median(x)|), on account of the non-Gaussian distributions) in the cognate complexes with the corresponding experimental ion numbers. A cutoff of 3.5 Å yielded 7 ± 1 for Elk1 and 8 ± 1 contacts for ETV6 in matching agreement with the experimental ion numbers for the cognate complexes [Fig. 5A]. These contacts remained stable in number in the trajectories.

Fig. 5.

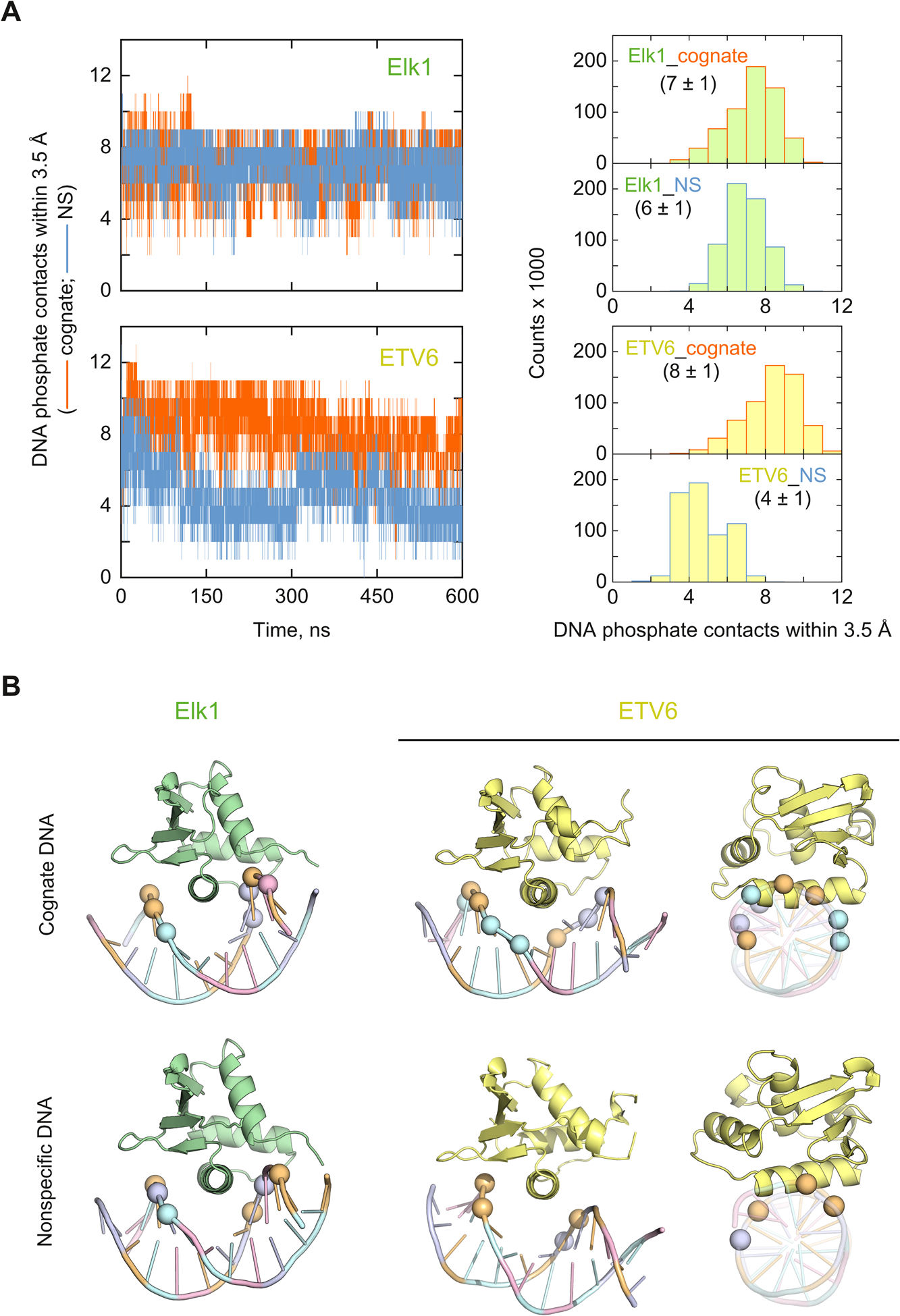
Molecular dynamics simulations of DNA backbone contacts in the cognate and nonspecific complexes of Elk1 and ETV6. (A) Representative trajectories of the number of phosphate contacts by cationic protein N atoms (N-terminus and sidechains of Arg and Lys residues). The histograms of phosphate contacts were accumulated from the final 200 ns of triplicate trajectories. (B) Average cartoon structures of each complex, rendered with the median number of closest phosphates according to the histograms in Panel A. For clarity, only the P atoms are marked as spheres, colored according to base identity.

Turning to the nonspecific complexes, Elk1 retained a marginally lower but stable number of contacts (6 ± 1) relative to its cognate complex. In contrast, the nonspecific ETV6 complex lost about half its DNA contacts by 200 ns. At this cutoff, the median DNA contacts in the ETV6 nonspecific complex (4 ± 1) also agreed with the experimental ion number.To further test the convergence of these changes, we simulated the ETV6 and Elk1 nonspecific complexes out to 2 μs. Neither complex showed systematic changes beyond those already observed by 600 ns [Fig. S3, ESI†]. We also established that complexes formed with other nonspecific sequences exhibited the same behavior [Fig. S4, ESI†]. The average MD models [Fig. 5B] showed that nonspecifically bound ETV6 was partially expelled from the major groove, losing phosphate contacts on both sides of the contact surface flanking the recognition helix H3. In contrast, the Elk1 nonspecific complex maintained significantly more contacts (6 ± 1) than its ETV6 counterpart and only slightly lower from the Elk1 cognate complex. Correspondingly, and unlike ETV6, there was no significant difference in the orientation of the protein between the cognate and nonspecific Elk1 complexes.

The absence of major changes in backbone contacts in the nonspecific Elk1 complex prompted us to examine the disposition of ions elsewhere on the complex, to account for the significant difference from ETV6. We began with a parsimonious approach, by analyzing the radial distribution functions (RDFs) g of Na⁺ and Cl⁻ around charged atoms on the protein as a whole: the sidechain heteroatoms of Asp, Glu, Arg, and Lys residues, as well as the N- and C-termini. None of the His residues was protonated according to PROPKA3.²⁴ When scaled by the bulk volume densities ρ₀, the RDFs yield local densities ρ(r) = g(r)·ρ₀ for each ion as a function of radial distance r, and enable direct comparisons of the disposition of ions around the DNA-bound proteins.

Fig. 6A shows the local densities of Na⁺ and Cl⁻ around the charge-bearing N and O atoms on both cognate- and nonspecifically-bound Elk1 and ETV6 from the pooled final 200 ns trajectories of triplicate simulations. The results showed pronounced differences among DNA-bound Elk1 and ETV6. Nonspecifically bound Elk1 was associated with greater than twice the Na⁺ density than its cognate counterpart at the primary maximum, while the ETV6 complexes were similar to each other. Thus, nonspecifically bound Elk1 was associated with a higher density of Na⁺ around its charged atoms than in the cognate complex. In all cases, Na⁺ constituted the dominant contribution while Cl⁻ was preferentially excluded. A significant influence from the DNA, a polyanion, was expected but could not be isolated in the computation of ρ(r) for the complexes. By performing the same analysis on unbound Elk1, we confirmed an asymmetric disposition of Na⁺ and Cl⁻ even in the absence of DNA [Fig. S5, ESI†]. In any event, since both Elk1 complexes made essentially the same number of DNA backbone contacts (Fig. 4), the lower local Na⁺ density around cognate-bound Elk1 suggested the release of additional ions into the bulk solution.

Fig. 6.

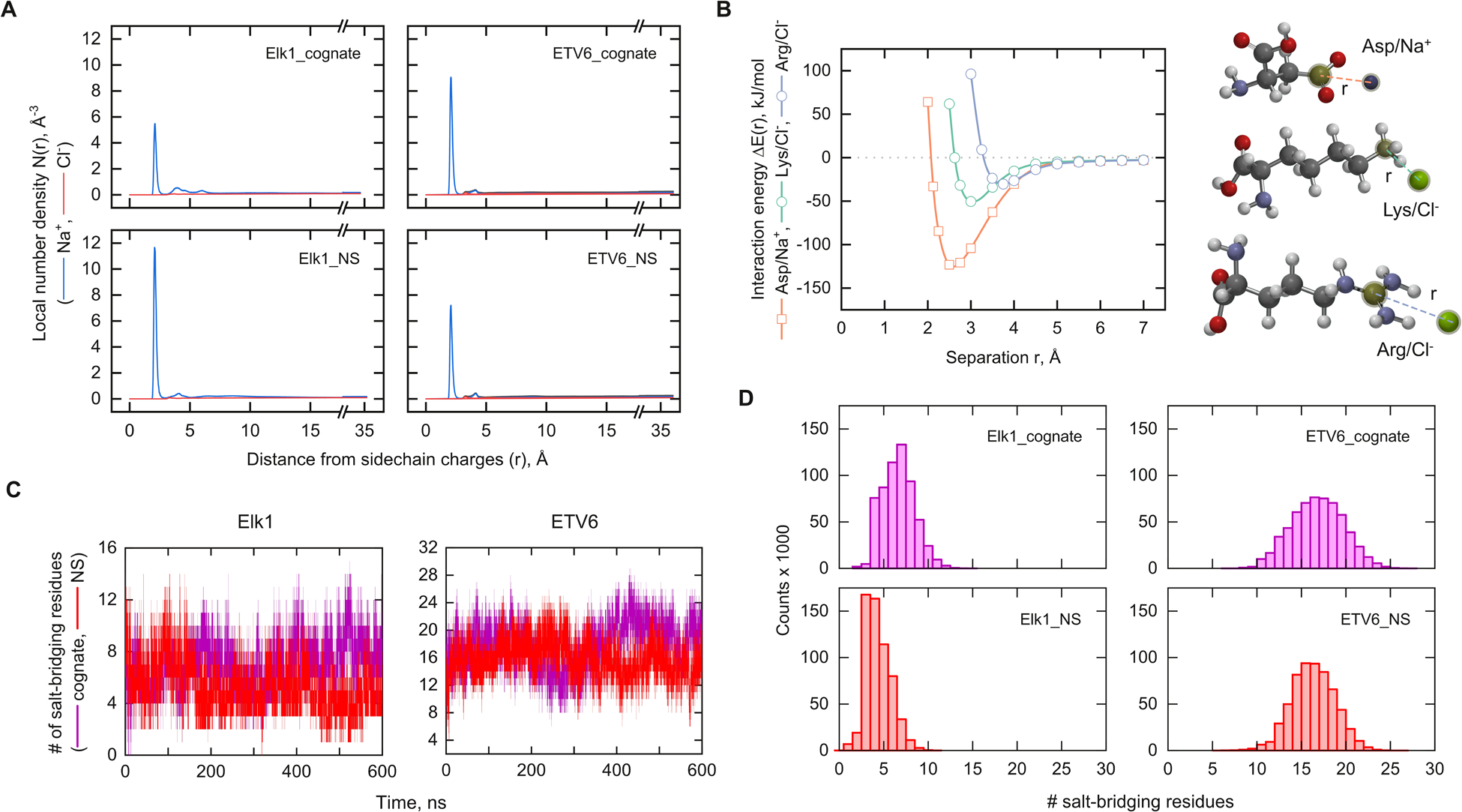
MD analysis of ionic contacts on the cognate and nonspecific complexes of Elk1 and ETV6. (A) Local number density of mobile ions as a function of distance from charged atoms on the backbone as well as acidic and basic sidechains. Each simulation contained sufficient Na⁺ (blue) and Cl⁻ ions (red) to neutralize the charge of the complex and yield a nominal salt concentration of 0.15 M. (B) Hybrid DFT interaction energy of model pairs of sidechains and counterions as a function of separation distance as indicated. See Materials and methods for details. The single minima correspond to the contact minimum. Solvent-separated ion pairs are quantitatively negligible in these systems (cf. Panel A) and are not considered here. (C) Representative trajectories of the number of salt-bridging residues based on a cutoff distance of 4.5 Å. (D) Histograms of contacts from the final 200 ns of triplicate simulations.

MD simulations in classical non-polarizable forcefields are known to over-estimate the strengths of salt bridges.⁴⁰ To establish whether the ionic dispositions reported by the local ionic densities ρ(r) reflected fundamental energetics of counter-ion interactions, we carried out quantum chemical calculations using hybrid density functional theory (DFT) methods. Using the ωB97x-D functional²⁸ and diffuse basis sets to handle electron-rich systems, we computed the interaction energies of Asp/Na⁺ (Glu was assumed to be analogous), Lys/Cl⁻ and Arg/Cl⁻ models. To render the quantum calculations tractable, a continuum water model (CPCM) was used. We note that implicit solvent models are sensitive only to contact ion pairs,⁴¹ which are the dominant species for both complexes (Fig. 6A) and unbound protein (Fig. S5, ESI†). Their ρ(r) functions in explicit solvent show dominant maxima at <3 Å, corresponding to direct contact ion pairs. Secondary maxima that correspond to solvent-separated ion pairs are quantitatively minor. Moreover, the differences between the minimum energies among attractive ion pairs occur at the contact minima in dilute solution.^41,42 For the present purpose, the complete potential of mean force is therefore not required. With these features in mind, the hybrid DFT calculations showed that the electrostatic attraction for Na⁺ was more than twice stronger than Cl⁻ at their corresponding contact minima [Fig. 6B], at distances in accord with the ρ(r) results in explicit solvent. Thus, the ionic concentration in favor of Na⁺ could be rationalized, in addition to the presence of nearby DNA, by its substantially stronger attraction with acidic residues. These results also identified acidic residues as the material targets for analyzing the ionic disposition in nonspecific Elk1 binding.

To efficiently survey the electrostatic interactions by acidic residues in the MD trajectories, we analyzed the trajectories of the entire ensembles of salt bridge contacts for each DNA complex of Elk1 and ETV6 [Fig. 6C]. At a 4.5 Å cutoff around charge-bearing protein atoms, triplicate trajectories of Elk1 showed fewer intramolecular salt bridges (median ± MAD) in the nonspecific complex (4 ± 1) than the cognate complex (7 ± 1). Most of the 26 charged residues were not interacting with each other [Fig. 6D]. At the same cutoff, many more of the 32 charged residues in ETV6 were bridged and at statistically the same density in both complexes (16 ± 2). In conjunction with the RDF analysis in Fig. 6A, these results showed that reduced salt-bridging in Elk1 was replaced by increased interactions with mobile Na⁺.

To identify the salt-bridging acidic residues, we compared the minimum distances they made with cationic atoms in the basic residues of each complex. The distances reflect the engagement of acidic residues in salt bridges with nearby basic residues by capturing the salt-bridging preferences (median distance) and dynamics (MAD) of the acidic residues. The impact of DNA target identity on ionic dispositions beyond the release of DNA counterions is therefore communicated in the differences in these statistics between the cognate and nonspecific complex [Fig. 7A].

Fig. 7.

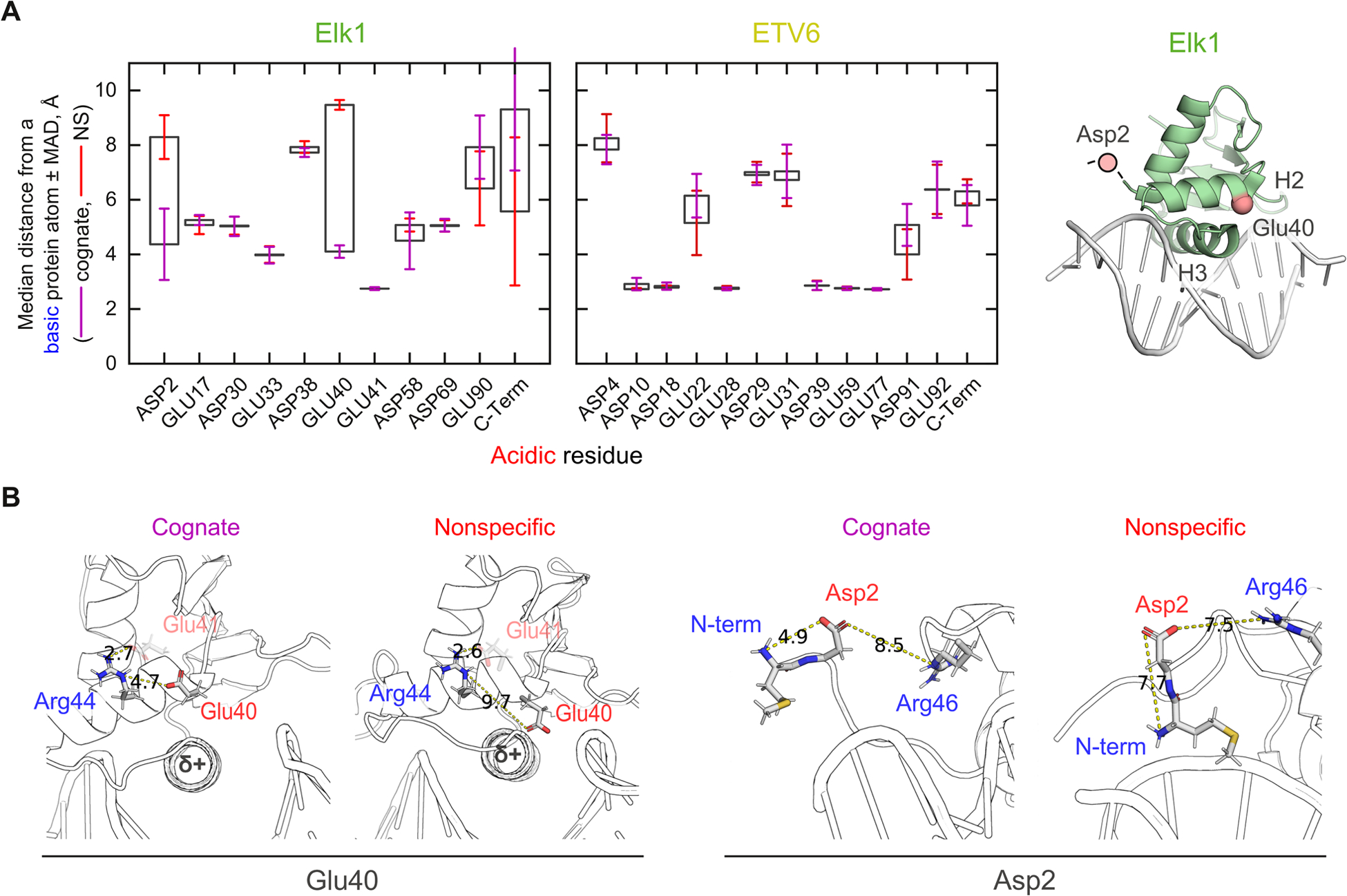
Structural basis of electrostatic heterogeneity between the ETS homologs Elk1 and ETV6. (A) Median distance of closest approach between cationic atoms from any basic residue to an anionic atom of acidic residues. “Error bars” represent the median absolute deviations in the cognate (purple) and nonspecific (red) complex. The two residues showing persistent differences between the two complexes, Asp2 and Glu40, are mapped to the Elk1 co-crystal structure (1DUX). Asp2 is part of the crystallographically unresolved N-terminus. (B) Representative structures of cognate- and nonspecifically bound Elk1 showing the interactions of Glu40/Arg44 and Asp2/N-terminus. Shown are middle structures of the dominant cluster fitted to each pair of residues. Numbers denote shortest distance in Å.

Consistent with the ensemble results in Fig. 6D, the cognate and nonspecific ETV6 complexes showed no acidic residue differing in net exposure to nearby basic residues. In contrast, two non-conserved residues (Asp2 and Glu40) in Elk1 exhibited persistent differences between the cognate and nonspecific Elk1 complexes i.e., median separations >3 Å with non-overlapping MAD bars. These criteria ensured that dynamic interconversion of contact and solvent-separated ion pairs (which are spatially distinguished by ~3 Å) were not mistakenly included as truly abrogated salt bridges. To establish the generality of these features in nonspecifically bound Elk1, we examined Elk1 in complex with another nonspecific sequence. The alternate DNA complex, which exhibited the same median number of DNA contacts as well, recapitulated as the distinct behavior of Asp2 and Glu40 as well [Fig. S6, ESI†]. The results thus supported an important role for these two residues in the electrostatic properties of the nonspecific Elk1 complex.

Scrutinizing the Elk1 residues more closely, Glu40 (as well as its neighbor Glu41) is not conserved in the corresponding helix H2 of ETV6. In the cognate Elk1 complex, Arg44 situated one helical turn downstream via sidechain-sidechain interactions with Glu40, but even more strongly with neighboring Glu41 based on distance considerations. [Fig. 7B]. In the nonspecific complex, the Glu41/Arg44 linkage was tightly maintained (Fig. 7A), but the interactions with Glu40 were lost. This transition was accompanied by a shift in the helical axis of H2, bringing the Glu40 carboxylate to ~4 Å from the N-terminus of the recognition helix H3. When complexed with DNA, H3 is significantly occluded from solvent. The resultant reduced-dielectric environment is known to enhance helix-charge interactions.⁴³ Since the N-terminal terminus is the partially positive end of the helical dipole, the distortion in helix-loop-helix structure from H2 to H3 of the nonspecific Elk1 complex could cause Glu40 to trade the Glu40/Arg44 salt bridge for favorable helix-charge interactions with H3.

A second major difference between cognate- and nonspecifically bound Elk1 is found in the residue Asp2 which, situated in the short and disordered N-terminal segment to helix H1, exhibited broader dynamics (MAD bars). In the MD cognate complex, the sidechain of Asp2 was dynamically interacting with the N-terminus of Met1 (Fig. 7B). This localized interaction, which cannot be discerned in crystal structures due to the disordered nature of positions up to residue 5, is biologically relevant as Met1 is the first residue in the mature Elk1 protein in vivo (GenBank AAA52384.1).⁴⁴ In the nonspecific complex, the basic N-terminus abandoned Asp2 in favor of dynamic contacts with the DNA backbone instead. Compared with the cognate complex, the RMS fluctuations of the phosphate oxygen atoms in the nonspecifically bound DNA were locally attenuated in the vicinity of the N-terminus [Fig. S7, ESI†]. The increased persistent DNA phosphate near the N-terminal ammonium of Elk1 could therefore compete effectively against Asp2 in the nonspecific complex. In both cognate and nonspecific complexes, the nearest cationic sidechain, belonging to Arg46, remained too distant to influence the situation. In summary, Glu40 and Asp2 were the most prominent among the acidic residues in Elk1 to become disengaged from intramolecular salt bridges and therefore more available to mobile Na⁺ upon nonspecific binding. As neither residue was conserved in ETV6 (Fig. 1), we concluded that the dynamics of salt bridges did not contribute significantly to the overall ionic disposition of DNA binding by ETV6.

Energetic contributions of salt-bridge perturbations to DNA affinity

Experimental evidence indicates ionic differences are responsible for the energetic differences in nonspecific binding by Elk1 and ETV6 (Fig. 4A). At 0.15 M Na⁺, the nonspecific Elk1 complex is ~10-fold lower in affinity than the ETV6 counterpart (ΔΔG° ~ 6 kJ mol⁻¹), contributing to the very high specificity ratio for Elk1 over ETV6. Focusing first on the protein/DNA interface, the nonspecific Elk1 complex makes two more DNA backbone contacts than ETV6. We can estimate the free energy contribution from the condensed counter-ion release from DNA:³⁶

$$\Delta \Delta {\text{G}}^{°}=-\Delta n\cdot \phi \text{RTln}\left[{\text{Na}}^{+}\right]$$ (6)

or −3.6 kJ mol⁻¹ at 0.15 M NaCl for Δn = 2. Other unfavorable contributions thus offset this surplus and dominate nonspecific binding by Elk1.

Outside the DNA contact interface, disrupted salt bridges in the Elk1 nonspecific complex alter the disposition of associated mobile ions. Does the replacement of bridged residues with mobile counter-ions make a significant contribution to the binding energetics? To probe the potential energy differences between these interactions, we used hybrid DFT calculations to estimate the potential energy of salt bridges formed by the sidechains of acidic and basic residues. Using model pairs of Asp with Arg or Lys, which have been geometry-optimized at the ωB97x-D/6–31+G* level, the interaction potentials of the salt bridges were less than half the summed energies for the corresponding pair with Na⁺ and Cl⁻ [Fig. S8, ESI†]. These differences could be partly understood in terms of the longer separation at the energy minima for the salt bridges relative to that for the Na⁺ interactions. Solvent-separated pairs, which are not considered in these calculations, may be comparable in magnitude but no more favorable than contact ion pairs.^37,38 The single-point energy calculations do not consider conformational adjustments to steric clashes and other repulsive forces that would modify the results based on static structures. Nevertheless, a potential energy advantage in favor of Na⁺-condensed states must therefore also be overcome in nonspecific Elk1 binding.

A major energetic contribution still to be considered concerns entropic differences between a salt bridge and the condensation of mobile ions. One is any difference in the extent of hydration of the charged groups. Differential release of hydration water directly contributes to the overall free energy.⁴⁵ Also of importance is the loss of translational entropy imposed on the condensed counter-ions. Since associated ions are not restrained in the sense of a bound ligand, a useful concept is the adsorption entropy ΔS_ad, which describes a dynamic confinement with fewer restricted degrees of freedom. At $T\Delta S_{\text{ad}}^{\circ }~-5\text{\hspace{0.17em}kJ\hspace{0.17em}}{\text{mol}}^{-1}$ per ion,⁴⁶ a fraction of the value for static docking, this free energy penalty is still significant for replacing of 3 ± 1 salt-bridging residues with mobile ions in the nonspecific Elk1 complex (Fig. 6D). Finally, conformational stability, particularly entropic components, could impact DNA site preference. Unbound ETS domains and duplex DNA are well-folded structures in the unbound state. In general, macromolecules and their complexes retain significant conformational entropies owing to manifold rotational and vibrational degrees of freedom in the folded state.⁴⁷ For mixed-sequence DNA duplexes of lengths used in our experiments, we expect comparable conformational entropies. Even though ETS domains form cognate and nonspecific complexes via the same interface, conformational entropies are expected to diverge due to local differences in salt bridge configurations and DNA backbone fluctuations. In summary, ionic interactions within and outside the protein/DNA interface are sufficient in magnitude and variety to bias the energetics of DNA site selection.

Implications of divergent nonspecific binding modes in the evolution of ETS transcription factors

ETS domains are eukaryotic descendants of the ancient helix-turn-helix motif.⁴⁸ Their primary structure has diversified extensively with the evolution of novel physiology in animals.^49,50 The current classification of ETS proteins⁹ reflects this diversification in Class II to IV members from ancestral Class I relatives while retaining a highly conserved structural scaffold. A review of the literature suggests broader phylogenetic variations in nonspecific DNA binding in the ETS family. On the one hand, the altered orientation of the nonspecific ETV6 complex, with the concomitant loss of about half its phosphate contacts, is reminiscent of a H3-mutant of PU.1,⁵¹ a Class III ETS-family member closer phylogenetically to ETV6 than Elk1.⁵² As this PU.1 mutant binds cognate sites with as low affinity as nonspecific DNA,⁵³ a dislocated complex structure may be a shared feature in nonspecific binding by closely related (Classes II and III) ETS proteins. On the other hand, the more conserved binding pose observed in the nonspecific Elk1 complex was also found in MD simulations of nonspecifically bound Ets-1,³⁴ another Class I relative. An overarching phylogenetic trend in the primary structure of ETS domains is an increasing bias for basic over acidic residues. The human ETS paralogs show a statistically significant correlation between the isoelectric point of their ETS domains and evolutionary distance [Fig. 8]. The results from the literature and this study therefore suggest that the increasing density of basic residues in more recent ETS relatives renders the canonical binding mode less tolerant to nonspecific DNA. Electrostatics also play a role in direct ETS/protein partnerships, such as the recruitment of Jun-Fos heterodimers to composite DNA binding sites.⁵⁴ Computationally, while electrostatic interactions are clearly discerned in the long ns-timescales sampled by simulations under constant conditions, conformational dynamics at longer timescales may be made probed by enhanced sampling techniques such as replica exchange MD. The role of electrostatics in site selectivity therefore integrates an interplay of charge and conformational dynamics that are complex, multi-factorial, and a ripe problem for future studies.

Fig. 8.

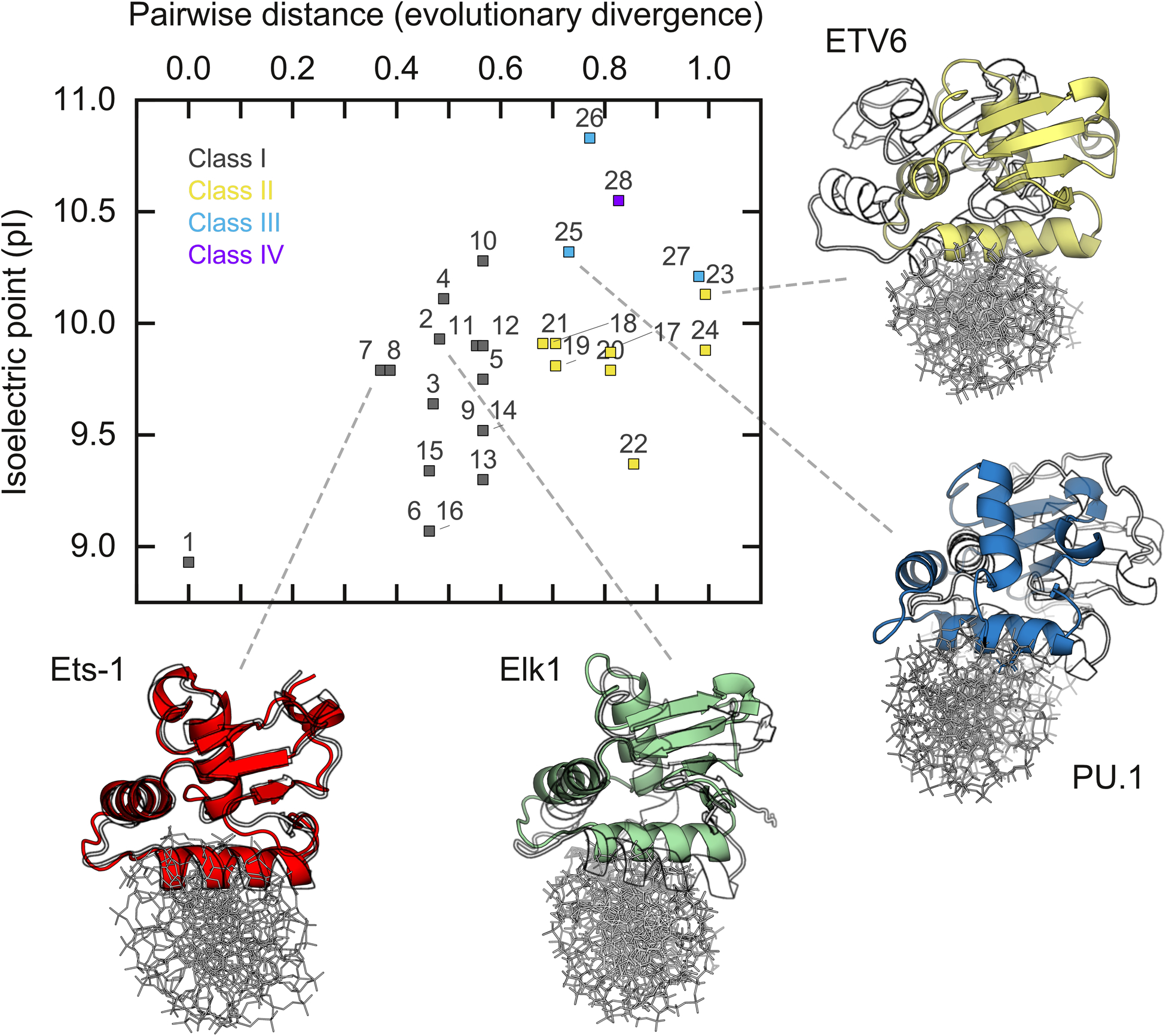
Phylogenetic correlation in electrostatic composition of human ETS domains with nonspecific DNA binding. Evolutionary distance, defined as the pairwise rate of amino acid substitution per residue, was computed from the primary structures of each ETS domain. A listing of the ETS proteins indexed in the plot is given in Table S3 (ESI†). The ETS paralog with the lowest pI (GABPα, index 1) was chosen as the reference. The correlation is statistically significant at p = 0.0023 by the Pearson correlation test. Average structures of cognate and nonspecific complexes were aligned by the DNA and rendered with the nonspecifically bound protein in black and white. Elk1 and ETV6 structures are from this study (cf. Fig. 4C). Ets-1 structures are taken from.³⁴ For PU.1, the nonspecific complex is taken as a point-mutant (N236Y) that renders cognate binding nonspecific in affinity.⁵¹

Conclusion

Nonspecific binding is a major reservoir of DNA-binding proteins in the eukaryotic nucleus, yet detailed understanding of their structure and dynamics remains scarce. Labile protein salt-bridges have been previously proposed as a mechanism for competing with DNA backbone contacts by low-specificity proteins such as integrated host factor.⁵⁵ In stark contrast, ETS proteins such as Elk1 are highly specific sequence discriminators bearing salt bridges outside the DNA contact interface. The present work shows that the divergent ionic composition in Elk1 and ETV6 endow different modes of nonspecific binding, wherein extra-interfacial salt bridges on Elk1 but not ETV6 are dynamically sensitive to DNA identity. The present results highlight electrostatic contacts outside the canonical DNA-binding surface as an area of interest in furthering our understanding of target selectivity by DNA-binding proteins.