Modeling the Effect of Oxygen on the Chemical Stage of Water Radiolysis using GPU-based Microscopic Monte Carlo Simulations, with an Application in FLASH Radiotherapy

Abstract

Oxygen plays a critical role in determining the initial DNA damages induced by ionizing radiation. It is important to mechanistically model the oxygen effect in the water radiolysis process. However, due to the computational costs from the many body interaction problem, oxygen is often ignored or treated as a constant continuum radiolysis-scavenger background in the simulations using common microscopic Monte Carlo tools. In this work, we reported our recent progress on the modeling of the chemical stage of the water radiolysis with an explicit consideration of the oxygen effect, based upon our initial development of an open-source graphical processing unit (GPU)-based MC simulation tool, gMicroMC. The inclusion of oxygen mainly reduces the yields of e_h and H· chemical radicals, turning them into highly toxic $O_{\dot{2}}^{-}$ and $H{O}_{\dot{2}}$ species. To demonstrate the practical value of gMicroMC in large scale simulation problems, we applied the oxygen-simulation-enabled gMicroMC to compute the yields of chemical radicals under a high instantaneous dose rate ${\dot{D}}_i$ to study the oxygen depletion hypothesis in FLASH radiotherapy. A decreased oxygen consumption rate (OCR) was found associated with a reduced initial oxygen concentration level due to reduced probabilities of reactions. With respect to dose rate, for the oxygen concentration of 21% and electron energy of 4.5 keV, OCR remained approximately constant (~0.22 μM/Gy) for ${\dot{D}}_i$ ’s of 10⁶, 10⁷ Gy/s and reduced to 0.19 μM/Gy at 10⁸ Gy/s, because the increased dose rate improved the mutual reaction frequencies among radicals, hence reducing their reactions with oxygen. We computed the time evolution of oxygen concentration under the FLASH irradiation setups. At the dose rate of 10⁷ Gy/s and initial oxygen concentrations from 0.01%~21%, the oxygen is unlikely to be fully depleted with an accumulative dose of 30 Gy, which is a typical dose used in FLASH experiments. The computational efficiency of gMicroMC when considering oxygen molecules in the chemical stage was evaluated through benchmark work to Geant4-DNA with simulating an equivalent number of radicals. With an initial oxygen concentration of 3% (~10⁵ molecules), a speedup factor of 1228 was achieved for gMicroMC on a single GPU card when comparing with Geant4-DNA on a single CPU.

1. INTRODUCTION

It is well known that oxygen plays a critical role in DNA damages produced by ionizing radiation. First, dissolved oxygen promotes the production of deleterious reactive oxygen species (ROS), such as superoxide and hydroperoxyl radicals, which are very toxic to cells. Second, oxygen can fix the DNA damages rapidly after their occurrence, forming stable organic peroxides and making it difficult to repair them (Alper and Howard-Flanders, 1956). It is an important research topic to accurately model the presence of oxygen in the water radiolysis process and the impact on radiobiological endpoints, such as DNA damages.

Monte Carlo (MC) simulation is commonly accepted as one of the most accurate methods to model radiation transport and interactions with matters because of the faithful modeling based on physics principles. Yet, in the context of studying the oxygen effects, simplifications in modeling have to be made in most of the MC packages due to the heavy computational burden, primarily in the modeling of the chemical stage of the water radiolysis process. In fact, MC simulations of the chemical stages is challenging due to the spatial-temporal simulation that spans over multiple order of magnitudes in time and the transport of a large number of radicals, which is an interacting many-body problem caused by the mutual competitive chemical reactions between the radiolytic molecules. Hence, to reduce the computational burden, the oxygen is sometimes ignored (Meylan et al., 2017; Ramos-Mendez et al., 2018) or treated as a temporally constant and spatially uniform background (Boscolo et al., 2020; Colliaux et al., 2015) that serves as a scavenger for the radiolytic radicals. The method assuming a constant uniform background ignores the spatial and temporal variations of chemical reactions, an important factor in certain scenarios. For instance, when rapid consumptions of oxygen due to reactions with radicals occur, temporal variation of oxygen concentration may not be omitted. Meanwhile, as the oxygen distribution is sparse compared to the very short reaction radii, reactions with oxygen happens non-uniformly, making spatial variation a factor to consider.

Modeling the effect of oxygen is of particular importance in the context of ultrahigh dose rate radiotherapy termed as FLASH radiotherapy (Bourhis et al., 2019) that has lately attracted a lot of attentions. FLASH radiotherapy holds the potential of better sparing normal tissue, while maintaining the tumor control probability, than radiotherapy delivered at a conventional dose rate, as having been demonstrated using electron (Favaudon et al., 2014), photon (Montay-gruel et al., 2018; Montay-gruel et al., 2017), and proton beams (Buonanno et al., 2019). However, the mechanism of FLASH radiotherapy remains unclear and oxygen depletion has been pointed out as one of the factors contributing to the advantage of FLASH radiotherapy (Vozenin et al., 2019a; Spitz et al., 2019). In this hypothesis, a hypoxia or anoxic environment created by radiolytic oxygen depletion (Wilson et al., 2012; Weiss et al., 1974) under the FLASH condition in normal tissue raises its radiation tolerance, hence enlarging the window between normal tissue complication probability and tumor control probability. To understand the effect of oxygen, several studies have been performed (Pratx and Kapp, 2019; Spitz et al., 2019). Spitz et al (Spitz et al., 2019) estimated the constant of oxygen consumption rate (OCR) due to different factors. Pratx et al (Pratx and Kapp, 2019) further investigated whether oxygen depletion could occur during the chemistry stage of radiolysis under different dose rates with a constant OCR independent of the initial oxygen concentration. Yet, as oxygen concentration decreases, the probability for oxygen molecules reacting with other molecules is expected to decrease, leading to a gradually reduced OCR. Hence, it is desired to perform a detailed mechanistic modeling study to investigate the time evolution of chemical yields under the FLASH condition.

The purpose of this paper is twofold. First, we will report our recent progress on the modeling of oxygen effects in the water radiolysis process using GPU-based MC simulations. In our previous work (Tsai et al., 2020), we presented our developments on an open-source (https://github.com/utaresearch/gMicroMC) GPU-based MC simulation package, gMicroMC, for the simulations of water radiolysis and computations of DNA damages. We demonstrated that GPU acceleration technology can improve computational efficiency by hundreds of times compared to conventional CPU-based computations in the context of microscopic MC simulation. The current study further improved gMicroMC’s function by including the oxygen-related reactions in the modeling of the chemical stage of the water radiolysis. We will present the implementation in gMicroMC to process the chemical stage with the presence of oxygen. This development is expected to greatly facilitate the research using MC simulations to investigate the impacts of oxygen effects. The second purpose of this paper is to use the improved gMicroMC package to study the hypothesis of oxygen depletion in the FLASH condition, which could demonstrate the advantages of gMicroMC in terms of supporting large scale microscopic MC simulations. Specifically, we will apply gMicroMC under the FLASH condition to investigate the OCR under different dose rates and initial oxygen concentrations. To our knowledge, this is the first time that the time evolutions of radical yields under the FLASH condition are computed in a step-by-step MC simulation program with oxygen species explicitly included in the modeling.

2. MATERIALS AND METHOD

2.1. Implementation of oxygen in gMicroMC

gMicroMC is a GPU-based MC simulation package for the simulations of the water radiolysis process and the computations of DNA damages (Tsai et al., 2020). It divides the simulation into four stages: physical stage (< 10⁻¹⁵ s), physicochemical stage (10⁻¹⁵~10⁻¹² s), chemical stage (10⁻¹²~10⁻⁶ s) and searching for DNA damage. In the physical stage, it transports primary and secondary electrons and generates positions and types of ionized and excited water molecules, which can be completed at femtosecond scale. In the physicochemical stage, it computes the de-excitation process of these water molecules through predefined channels and probabilities, generating the initial distribution of radicals. The radicals then evolve through the thermalization process and reach thermal equilibrium at around 1 picosecond post irradiation. After that, the simulation in the chemical stage diffuses these radicals and checks mutual reactions among them in a step-by-step simulation scheme. This stage is typically assumed to last for 1 microsecond. Beyond that, the local concentrations of the radicals will be attenuated significantly and the cellular repair process enters into play (Bernal et al., 2015). Finally, searching for DNA damages is performed based on the positions of energy-deposit events and radicals and the DNA geometry.

The advantage of gMicroMC is the high computational efficiency realized via GPU parallelization and GPU-friendly parallel simulation algorithms in all four stages, which substantially improves the efficiency of this computationally challenging problem. The specific GPU parallelization is as follows. In the physical stage, each GPU thread is responsible for simulating the transport and interaction of one incident or secondary electron until reaching the cut-off energy. In the physicochemical stage, each GPU thread handles the decay of one excited or ionized water molecule following the predefined pathways, or deals with the thermalization of a sub-excitation electron. As for the chemical stage, each GPU thread is responsible for the diffusion of one radical and its mutual reaction with other radicals until the radical is tagged as ‘dead’ after one reaction, and the kernel will restart to deal with the daughter radical. To reduce the searching burden of the mutual reaction, a grid data approach is employed, in which, the entire space is divided into small grids with the grid size twice the largest reaction distance such that each radical only reacts with those radicals in the same grid or adjacent grids. Finally, in the DNA-damage computation stage, each GPU thread is responsible for one recorded energy deposition event or one radical, checking its spatial overlap with the DNA geometry. Interested readers could find more details in literatures of Tsai et al. (2020) and Lai et al. (2020).

The initial development of gMicroMC did not include oxygen in the simulation process. To enable this feature, we considered oxygen-related reactions with parameters listed in previously published studies (Plante, 2011). Because of the absence of $O^{.}{}^{-}$, O₃, $O_{\dot{3}}^{-}$, O(3P) in the physicochemical stage, we only considered three radicals in addition to those already included in the original gMicroMC, namely hydroperoxyl radical $H{O}_{\dot{2}}$, superoxide radical $O_{\dot{2}}^{-}$ and hydroperoxide anion $H{O}_2^{-}$. All the chemical species in this study are listed in Table 1, after including the oxygen to form a self-contained reaction list.

Table 1.

Radical species and diffusion coefficients D. The root-mean-square distance λ traveled for t = 1 μs was calculated as $\lambda =\sqrt{6Dt}$.

Species		D (x109 nm2s−1)	λ (nm)	Reference
Existing in original gMicroMC	eh	4.9	171.5	(Kreipl et al., 2008)
	OH·	2.8	129.6	(Kreipl et al., 2008)
	H·	7.0	204.9	(Kreipl et al., 2008)
	H+	9.0	232.4	(Kreipl et al., 2008)
	H2	4.8	169.7	(Kreipl et al., 2008)
	OH−	5.0	173.2	(Kreipl et al., 2008)
	H2O2	2.3	117.5	(Kreipl et al., 2008)
Added in this work	O2	2.4	120.0	(Plante, 2011)
	$H{O}_{\dot{2}}$	2.3	117.5	(Plante, 2011)
	$O_{\dot{2}}^{-}$	1.75	102.5	(Plante, 2011)
	$H{O}_2^{-}$	1.4	91.7	(Plante, 2011)

As for the simulation, we first sampled the initial position of oxygen molecules. Let us denote the oxygen concentration in percentage by $P_{o_2}(\%)$, which means the ratio of partial oxygen pressure in water to the atmosphere pressure P_atm with P_atm = 760 mmHg. Equivalently, $P_{O_2}$ can be expressed in mmHg, i.e. the partial oxygen pressure in water. $P_{O_2}(\mathit{\text{mmHg}})=P_{o_2}(\%)*P_{atm}$. Additionally, we will also use $P_{O_2}$ in μM $\left(P_{O_2}\left(\mu M\right)\right)$ to denote the concentration of dissolved oxygen molecules in the unit of μM. $P_{O_2}(\mu M)=P_{O_2}(\mathit{\text{mmHg}})*H_c\text{with}{H}_c=1.26\mu M/\mathit{\text{mmHg}}$ being the coefficient of Henry’s Law for oxygen dissolving in water (Wenger et al., 2015). In the rest of this paper, $P_{O_2}(\%)$ will be always used to specify the oxygen concentration, while $P_{O_2}(\%)\left(P_{O_2}(\mathit{\text{mmHg}}),P_{O_2}(\mu M)\right)$ will be explicitly stated in some places. For a region of interest (ROI) studied, we first extended the volume along both directions of the x, y and z axes by Δr, which is estimated as the root-mean-square diffusion length of the oxygen under a given temporal duration t of the chemical stage. For example, we took Δr = 120 nm when t = 1 μs since the diffusion length was about 120 nm (Table 1). Once other t values were used, we would change Δr accordingly. The purpose of this extension is to ensure an equilibrium oxygen diffusion background within the ROI during the simulation, especially at the area close to the ROI boundaries. We denoted the volume of the extended region as V. The number of initial oxygen molecules was decided as $N_{O_2}=P_{O_2}(\%)*P_{atm}*H_c*N_A*V$, which were then uniformly sampled inside the region.

The existence of oxygen was assumed to not affect the physical stage and the physicochemical stage. In fact, the concentration of water molecule is ~55.6 MM but the concentration of dissolved oxygen is ~0.2 mM for $P_{o_2}=21\%$. Hence, the probability for the incident initial particles to collide with dissolved oxygen in the physical stage is low and can be safely ignored. However, the dissolved oxygen molecules could play a crucial role in determining the temporal production and spatial distribution of radicals, as the chemical stage can last for microseconds and radicals can spread out through diffusion. The oxygen is then expected to have a high probability to participate in the reactions with radicals. The chemical reactions included in this study are summarized in Table 2. During the transport simulation of the chemical stage, we followed the same algorithm as described in our previous publication (Tian et al., 2017) with the extended list of chemical reaction channels in Table 2 included.

Table 2.

Chemical reactions and reaction rate constants k_obs. H₂O molecules were ignored in the chemical equations assuming they were everywhere.

	Index	Reaction channels	kobs (1010 L ∙ mol−1 ∙ s−1)	Reference
Existing in original gMicroMC	1	eh + eh → 2OH− + H2	0.5	(Kreipl et al., 2008)
	2	eh + OH· → OH−	2.95	(Kreipl et al., 2008)
	3	eh+H· → OH− + H2	2.65	(Kreipl et al., 2008)
	4	eh + H+ → H·	2.11	(Kreipl et al., 2008)
	5	eh+H2O2 → OH· + OH−	1.41	(Kreipl et al., 2008)
	6	OH· + OH· → H2O2	0.44	(Kreipl et al., 2008)
	7	OH·+H· → H2O	1.44	(Kreipl et al., 2008)
	8	H· + H· → H2	1.20	(Kreipl et al., 2008)
	9	H+ + OH− → H2O	14.3	(Kreipl et al., 2008)
	10	H2 + OH· → H·	0.00417	(Kreipl et al., 2008)
Added in this work	11	$e_h+O_2\to {O_{\dot{2}}}^{-}$	1.74	(Plante, 2011)
	12	$e_h+H{O}_{\dot{2}}\to H{O}_2^{-}$	1.29	(Plante, 2011)
	13	$e_h+O_{\dot{2}}^{-}\to 2O{H}^{-}+H_2{O}_2$	1.29	(Plante, 2011)
	14	$OH·+H{O}_{\dot{2}}\to O_2$	0.79	(Plante, 2011)
	15	$OH·+O_{\dot{2}}^{-}\to O_2+O{H}^{-}$	1.07	(Plante, 2011)
	16	$OH·+H{O}_2^{-}\to H{O}_{\dot{2}}+O{H}^{-}$	0.832	(Plante, 2011)
	17	$H·+O_2\to H{O}_{\dot{2}}$	2.1	(Plante, 2011)
	18	$H·+H{O}_{\dot{2}}\to H_2{O}_2$	1.0	(Plante, 2011)
	19	$H·+O_{\dot{2}}^{-}\to H{O}_2^{-}$	1.0	(Plante, 2011)
	20	$H^{+}+O_{\dot{2}}^{-}\to H{O}_{\dot{2}}$	4.78	(Plante, 2011)
	21	$H^{+}+H{O}_2^{-}\to H_2{O}_2$	5.0	(Plante, 2011)

2.2. Studies to validate simulations of the chemical stage with oxygen included

During the development of gMicroMC, we noticed that another MC simulation package TRAX-Chem (Boscolo et al., 2020) had updated its functions to support the oxygen in chemical stage simulation by treating oxygen as a uniform constant background. The results have been compared with other studies for 5 MeV proton under oxygen partial pressure of $P_{O_2}=21\%$ (160 mmHg, 201.1 μM). This study provided a CPU-based simulation code to benchmark our development.

As the support to proton transport in gMicroMC is under development, in this study, we used GEANT4-DNA (Incerti et al., 2010) to produce secondary electrons generated by an incident 5 MeV bombarding into a 10 μm thick water slab. The reason to choose a thin slab as the simulation volume of interest was to ensure that the proton does not lose energy significantly within the volume of interest, and hence the results were relevant to the proton with 5 MeV energy. As such, we simulated the proton transport using GEANT4-DNA (GEANT4 version 10.5.1) and recorded the initial positions, energy values, and directions of secondary electrons, as well as locations and types of ionized and excited water molecules caused by the proton inside the water slab. After that, electron transport simulation in the physical stage was performed using gMicroMC, generating ionized and excited water molecules. These water molecules, together with those directly generated from protons, were fed into the physicochemical stage simulation of gMicroMC, generating the initial distribution of chemical radicals. These radicals were subsequently simulated to go through the chemical stage. During the simulation, we recorded the yield, or G value, of different radicals and compared the time evolution of yield of hydrated electron with published data from previous works (Boscolo et al., 2020; Colliaux et al., 2015). The G value calculates the ratio between the number of molecules of the chemical species and the deposited energy to generate such a number of molecules in the unit of # of molecules/100 eV. In addition, we also performed simulations for 10 MeV proton beams. The simulation setup was the same as we did for the 5 MeV one. Radicals in the first 10 μm water slab were tracked and the yields of e_h, H·, $O_{\dot{2}}$ and $H{O}_{\dot{2}}$ at 1 μs under oxygen concentration levels of $P_{O_2}=0$, 0.01%, 0.5%, 1%, 3%, 5%, and 7% were recorded and compared with available data reported by Boscolo et al. (2020).

2.3. Simulation setup under a conventional dose rate

Conventional dose rate usually refers to an average dose rate less than 0.03 Gy/s (Favaudon et al., 2014; Vozenin et al., 2019b). For a primary electron with a kinetic energy E_k of 4.5 keV, its typical traveling length l is 1 μm, and hence we could assume its energy all deposits in a sphere with a radius of l. To estimate the potential intertrack interactions, we estimated the electron visiting rate $\dot{e}$ to a water sphere with a radius of 2l as $\dot{e}=\dot{D}/\left(E_K/m_S\right)\approx 1.4s^{-1}$. This corresponds to a time interval Δt = 0.7 s between two adjacent primary electrons. Noticing that the typical consideration of the physical and chemical duration triggered by an incident particle in the DNA damage computation is 1 μs, it is then unlikely that secondary products from different primary particles would overlap spatially or temporally. Hence, to study the impacts of oxygen on radical yields, it is sufficient to consider the single electron irradiation. We initialized an electron (E_k = 4.5 keV) at the origin of the global coordinate with its momentum direction randomly sampled in the 4π angular range. We then performed the first two stage simulation in gMicroMC and recorded the initial radical distribution. Considering the stochastic nature of MC simulations, we repeated the simulation for N times and determined the ROI as the smallest circle containing all radicals from all runs. Assuming the chemical stage lasts for 1 μs, we sampled the initial oxygen distribution in an extended region following the method introduced in section 2.1. We then performed the chemical stage simulation for each radical list with the presence of oxygen, in which, the radicals and molecules were tracked until they reacted or the chemical stage ended. Oxygen concentrations of $P_{O_2}=0$ were considered to cover different scenarios of biological interest. $P_{O_2}=21\%$ (160 mmHg, 201.1 μM) corresponds to the normoxia situation under the standard atmosphere. $P_{O_2}=3\%$ (23 mmHg, 28.7 μM) and $P_{O_2}=9\%$ (69 mmHg, 86.1 μM) cover the physoxia condition (McKeown, 2014; Zhang et al., 2016). We empirically chose N = 1000 times for each configuration as a tradeoff between the simulation accuracy and the simulation time cost, and reported the average G values of different chemical species as a function of time after irradiation. With 1000 simulations, the maximum uncertainty of G values was reduced to 0.5%, while the total simulation time was tolerable, ranging from less than one hour to a few days.

2.4. Simulation setup under the FLASH condition

Under FLASH condition, there is a high chance that chemical species from different initial particle tracks can react with each other due to a much shorter time interval between two adjacent source particles. Still take the 4.5 keV primary electron as an example. An instantaneous dose rate of 10⁶ Gy/s will be equivalent to Δt=20 ns for a water sphere with a radius of 2 μm, which is much shorter than the chemical duration of 1 μs. Hence, the beam time structure is one of the most important issues to be considered in the simulation. As shown in Figure 1, there can be multiple temporal-scales to be considered. The total irradiation time is labeled as T, which was used to calculate the nominal average dose rate ${\dot{D}}_a=D_{\mathit{\text{total}}}/T$, where D_total is the total delivered dose. The criteria of ~40 Gy/s for ${\dot{D}}_a$ was reported to define the FLASH condition in early studies (Favaudon et al., 2014), which was in contrast with the dose rate for conventional photon beam of only ~0.03 Gy/s. The radiation is usually delivered in a pulse mode, for instance, using a medical linear accelerator. Let t_i represent the time interval between two adjacent pulses and t_p the duration of a pulse. The instantaneous dose rate can be computed as ${\dot{D}}_i=\frac{D_{\mathit{\text{total}}}}{T}*\frac{t_i}{t_p}$. For a typical linear accelerator, t_i is of the order of milliseconds with t_p of microseconds, which makes ${\dot{D}}_i$ about three orders of magnitudes larger than ${\dot{D}}_a$. Specific values of ${\dot{D}}_i$ for observing a reproducible FLASH effect ranges from 10⁴ Gy/s to 10⁹ Gy/s (Bourhis et al., 2019). In this study, we will focus on ${\dot{D}}_i$ rather than ${\dot{D}}_a$ to test the oxygen depletion hypothesis, because ${\dot{D}}_i$ characterizes the reaction intensity between radicals and oxygen molecules. From the time structure shown above, oxygen regeneration can be ignored within a pulse, because the pulse only lasts for microseconds and one microsecond corresponds a diffusion distance of the oxygen molecule of only ~120 nm (Table 1), ~1 percent of the cell nucleus dimension (11 μm).

Figure 1.

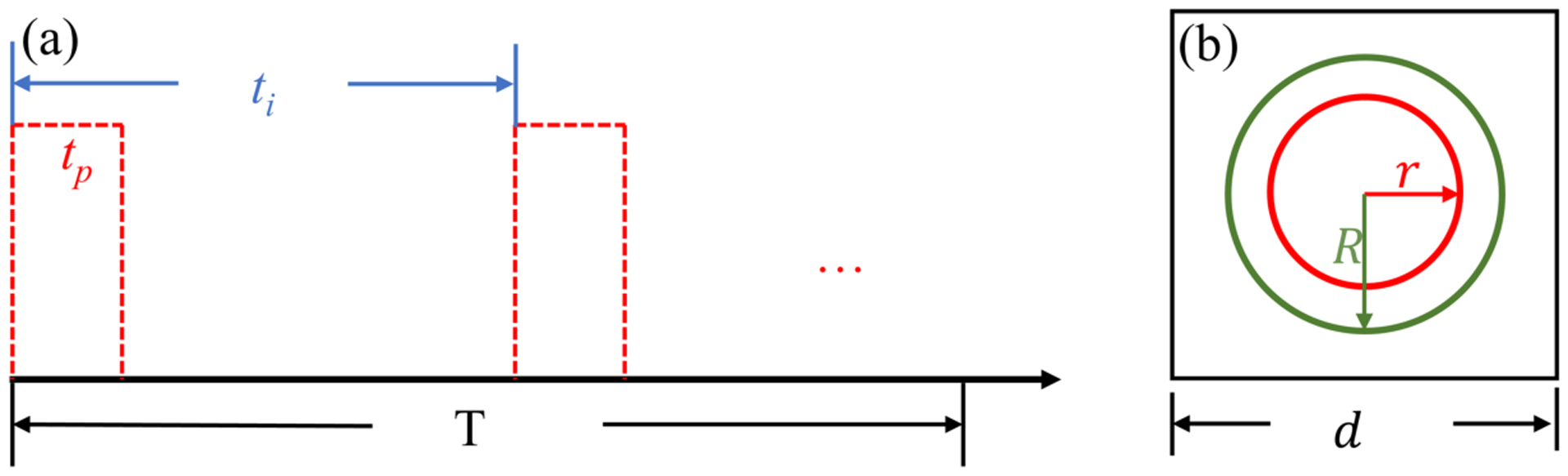
(a) Time structure of radiation in FLASH condition. T: total irradiation time. t_i: time interval between the beginning of two successive pulses. t_p: temporal width of a single pulse. (b) Cross section of the simulation geometry. Inner circle with a radius of r is the ROI. The circle with a radius of R is the sampling region for source particles. The square with side d is the sampling region for oxygen molecules.

In this study, we focused on the simulation of electron particles with kinetic energy E_k = 4.5 keV from a pulse width t_p = 1 μs. The chemical stage is determined as t_c = 1 μs post irradiation, to ensure enough time for radicals produced at the end of the pulse to propagate. The simulation geometry is shown in Figure 1(b). We set the ROI as a sphere with radius r = 1.5 μm. The initial electrons were sampled inside a sphere V_e with radius R = r + l(E_k) with l(E_k) being the maximum length that an electron with kinetic energy E_k can travel. Here, l(E_k) is taken as 1 μm. The oxygen molecules were initialized in a cubic volume with each side d = 2(r + Δr). Here, Δr = 300 nm is computed following the method given in section 2.1, with the reference time duration t=t_p + t_c = 2 μs. As mentioned in section 2.1, the purpose of this extension is to ensure an equilibrium oxygen diffusion background within the ROI during the simulation, especially at the ROI boundaries.

With the beam temporal structure considered, we initialized an electron with its spatial position randomly sampled within V_e, initial time randomly within [0, t_p], and traveling direction uniformly in the 4π spherical anglar range. We then simulated its physical and physicochemical stages, and recorded all the produced chemical species. We repeated this process until the deposited energy E_d inside the ROI reached the predefined value of ${\dot{D}}_i*t_p*\frac{4\pi }{3}{r}^3\rho$, where ρ = 1 g/cm³ is the density of the medium. In this way, we obtained the initial temporal and spatial distributions of all radicals from these primary electrons.

Next, we performed the chemical stage simulation in a step-by-step fashion (Tian et al., 2017). Every time when the simulation process was advanced by a time interval, we checked the pre-generated group of radicals, and included those initiated inside the time step into the simulation. This approach allowed us to model the time evolution of the chemical stage with radicals trigged by source electrons gradually included into the simulation. Through the entire simulation, all radicals and molecules were tracked until they reacted or the chemical stage ended.

We considered cases with different dose rates ${\dot{D}}_i={10}^6$, 10⁷, 10⁸ Gy/s and oxygen concentrations $P_{O_2}=0.01\%$ 0.1%, 0.5%, 1%, 3%, 9%, 21%. The dose rates were chosen to be consistent with the one pulse mode implemented in the current FLASH radiotherapy experiments, which started above 10⁶ Gy/s. In addition to the oxygen concentration levels used in section 2.3, we included 0.01% ~ 1% in this section to cover the hypoxia condition (McKeown, 2014; Zhang et al., 2016). For each case, we tracked the G-value evolution for all radical types and calculated the OCR defined as the ratio between the reduction of oxygen concentration and the dose of the pulse for the specific oxygen concentration $P_{O_2}$, $OCR\left(P_{O_2}\right)=\frac{\Delta N\left(O_2\right)}{N_A}*\frac{\rho }{E_d}$. Here, ΔN(O₂) is the difference in the number of oxygen molecules between the beginning of the pulse and 1 μs post irradiation. N_A is the Avogadro constant. The unit for OCR is μM/Gy.

In the FLASH mode, the simulated number of electrons is much larger than that considered for the conventional mode described in section 2.3. Hence, to achieve similar uncertainty level, we could repeat the simulation for fewer times. In our study, we have empirically selected the repetition time of 20 for all dose rates under each oxygen configuration. We then reported the average G-values and OCRs in section 3.3.

2.5. Evaluation of oxygen concentration evolution and oxygen enhancement ratio

The OCR computed above depends on the initial oxygen concentration level. Under the irradiation, as the oxygen concentration is continuously consumed, the variation of the oxygen concentration is governed as

$$\frac{d{P}_{O_2}}{dt}=-OCR\left(P_{O_2}\right)*{\dot{D}}_i.$$ (1)

To quantitatively describe this process, we first fit the OCR computed above under different oxygen concentrations as a continuous function of oxygen concentration in the hyperbolic form (Grimes et al., 2014; Longmuir et al., 1971)

$$OCR\left(P_{O_2}\right)=OC{R}_{max}*\frac{P_{O_2}}{P_{O_2}+\alpha },$$ (2)

where OCR_max and α are fitting parameters.

During an experiment, a number of pulses of radiation are delivered. The oxygen concentrations and cumulative delivered dose between two successive pulses can be expressed as

$$P_{O_2}(j+1)=P_{O_2}(j)-OCR\left(P_{O_2}(j)\right)*{\dot{D}}_i*t_p,$$ (3)

$$D(j+1)=D(j)+{\dot{D}}_i*t_p,$$ (4)

where j is the index of pulses. This expression allowed us to iteratively evaluate time evolution of oxygen concentration. Note that this expression only considered oxygen consumption by radiation and ignored oxygen regeneration caused by diffusion. In contrast, if the OCR is assumed to be a constant, OCR_C, the residual oxygen concentration would be $P_{O_2}(0)-OC{R}_C*D(j)$.

We further estimated changes in biological effects due to changes in oxygen concentration using oxygen enhancement ratio (OER), which is the ratio of radiation dose without oxygen to that with oxygen to achieve the same biological effect. An empirical formula was used (Grimes and Partridge, 2015),

$$OER\left(P_{O_2}\right)=1+\frac{{\Phi }_O}{{\Phi }_D}\left(1-e^{-\phi P_{O_2}}\right),$$ (5)

where $\frac{{\Phi }_O}{{\Phi }_D}=1.63$ and φ = 0.26 mmHg⁻¹.

3. RESULTS AND DISCUSSIONS

3.1. Validation of simulations of the chemical stage with oxygen included

Figure 2 shows the comparison of the calculated chemical yield of hydrated electron e_h for a 5 MeV proton as a function of time after irradiation computed by our study and two other previous studies (Boscolo et al., 2020; Colliaux et al., 2015). The oxygen concentration was 21% (160 mmHg, 201.1 μM). t = 0 was the moment for the proton entering into the water. The simulation results of gMicroMC generally agreed well with results in the other two works. The differences, mainly the quicker consumption of hydrated electrons by gMicroMC before 10 ns, may be attributed to different values of diffusion rates and reaction rates from different studies and different simulation methods. For example, Brownian bridge method (Karamitros et al., 2014) was employed in gMicroMC (Tian et al., 2017) to take the ‘crossing’ event into consideration, whereas the other two studies did not considered this effect. Figure 3 showed the comparison of the yields of different radicals and the oxygen consumption rates at 1 μs for a 10 MeV proton beam between our package and the work of Boscolo et al. (2020). In general, the yields of $O_2^{-}$ and $H{O}_{\dot{2}}$, the major products of reactions with oxygen, were consistent between the two packages. The oxygen consumption rates matched with each other as well. Yet, there are also some notable differences. For example, as shown in Figure 3 (a), difference exists for the absolute residual amounts of e_h and H·, the main radicals reacting with oxygen, and the absolute yields of $O_2^{-}$ and $H{O}_{\dot{2}}$ at different oxygen levels. Since we are using different packages to generate the initial distribution of the radicals from water radiolysis, the observed difference may come from different parameters used in different packages. When comparing the OCRs at the low oxygen concentration level from the two simulations, our simulated OCR goes down closer to 0 when the oxygen level drops to 0%, which is thought to be more consistent with the real situation.

Figure 2.

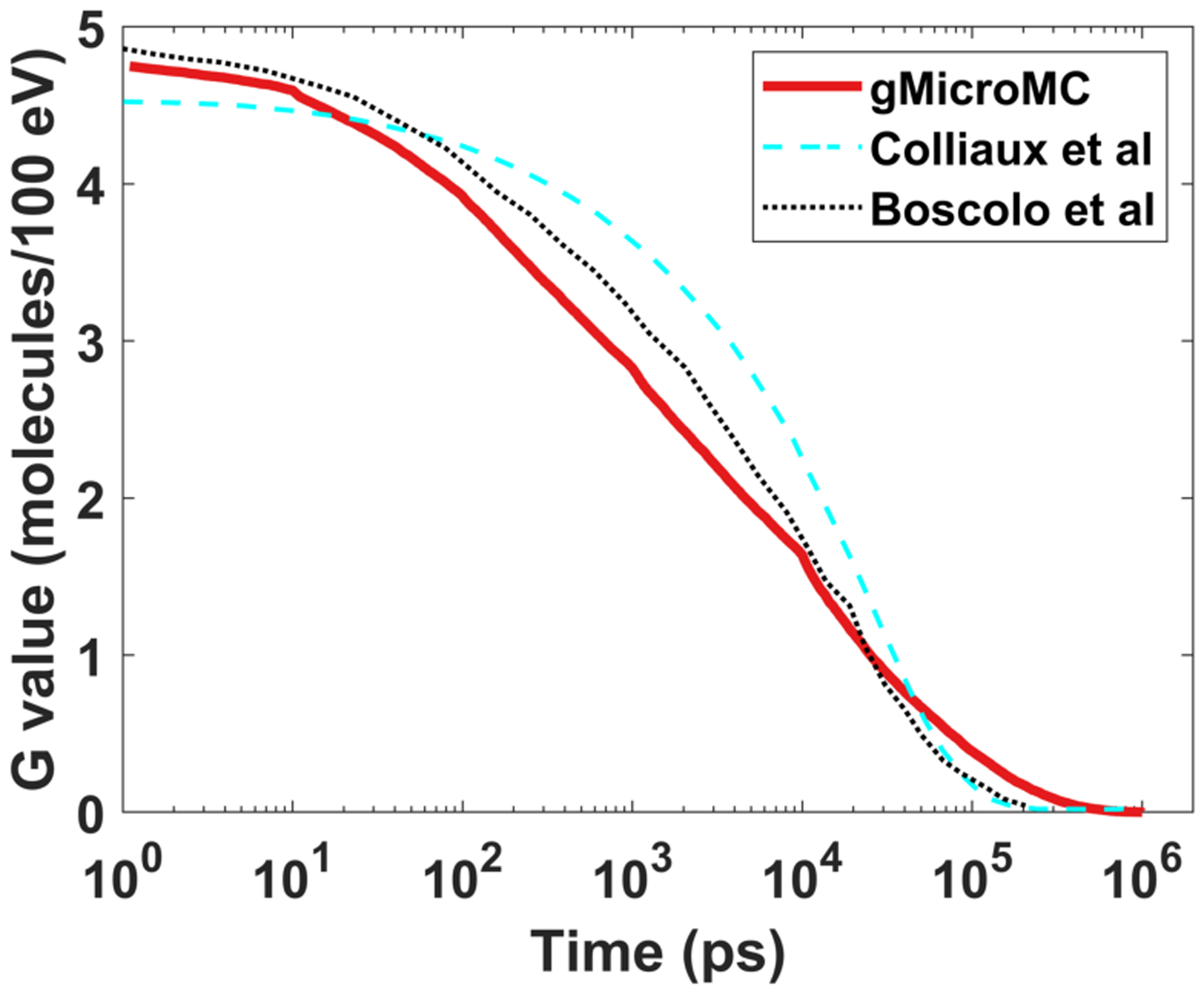
Time-dependent yield of e_h radical produced by a 5 MeV proton for $P_{O_2}=21\%$ (160 mmHg, 201.1 μM).

Figure 3.

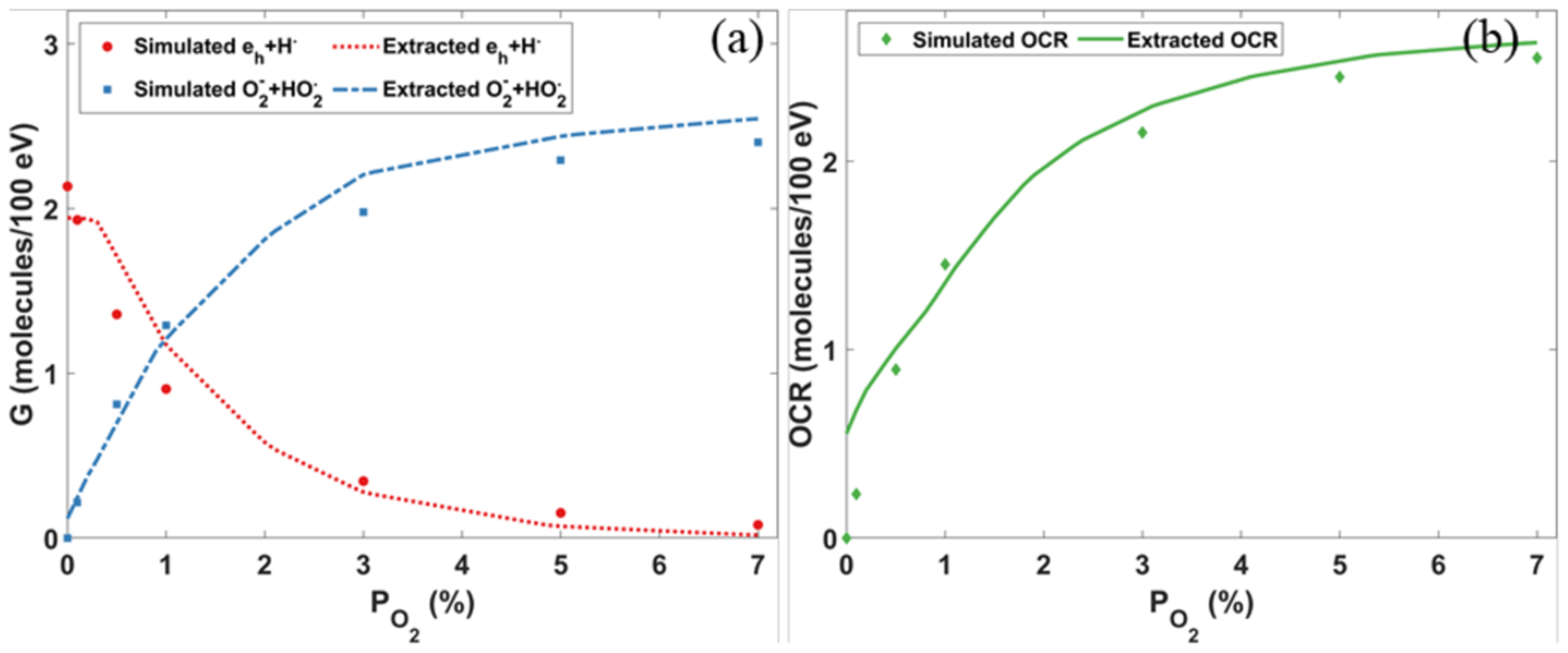
(a) Yields of different radicals and (b) oxygen consumption rates (OCR) at 1 μs as a function of oxygen concentration levels for the 10 MeV proton beam. Extracted data were from Boscolo et al. (2020).

3.2. Effect of oxygen under a conventional dose rate

We studied the cases with single 4.5 keV electron propagating in a water medium, corresponding to the situation of a conventional dose rate. Figure 4 shows the time evolution of the yields of major chemical species under different oxygen concentrations.

Figure 4.

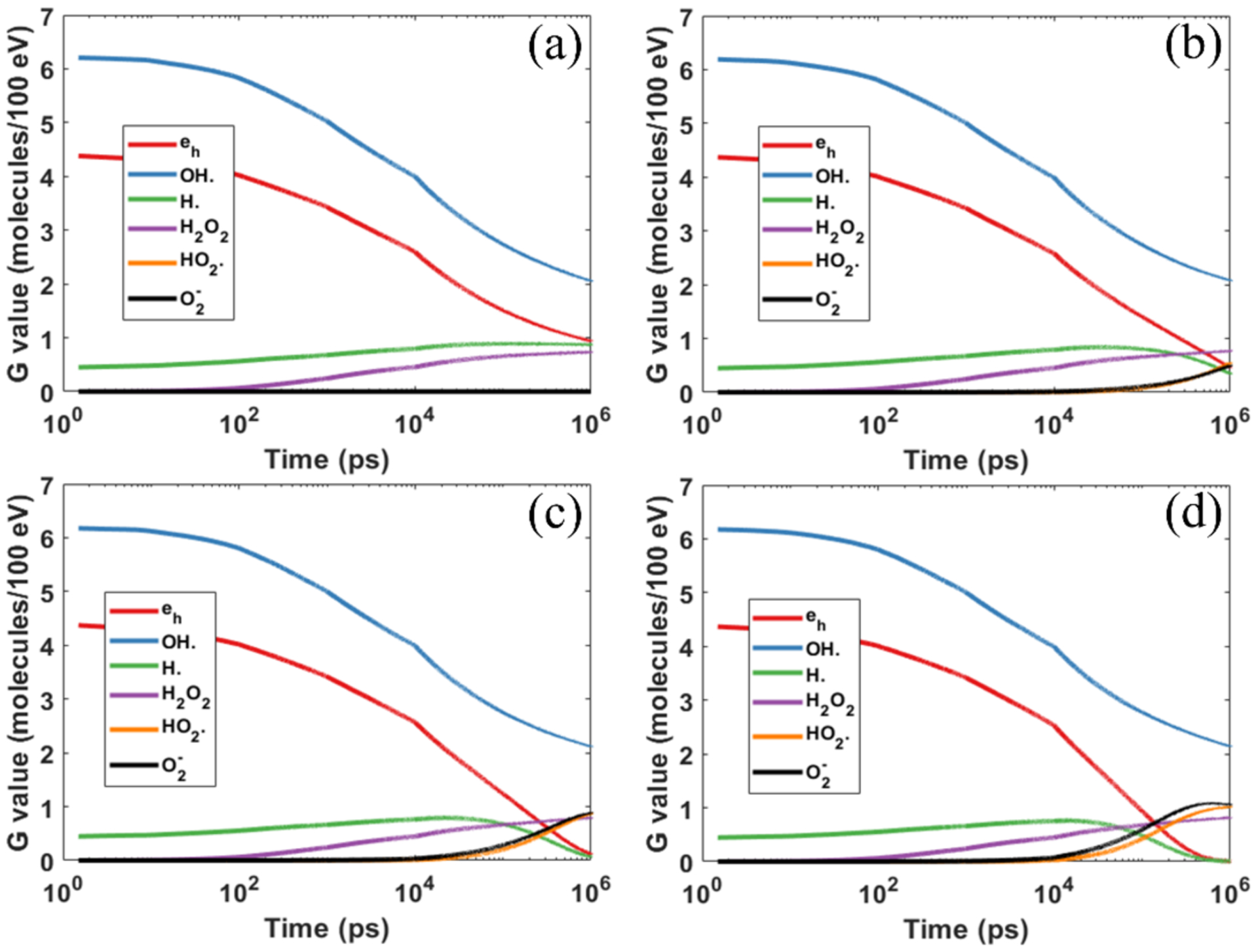
Yields of different chemical species as a function of diffusion time under different oxygen concentrations of (a) 0% (b) 3% (c) 9% and (d) 21%.

There are a few important observations. First, the impacts of oxygen on various chemical species were found to be different. The reductions of hydrated electron e_h and hydrogen radical H· became more significant with an increasing oxygen concentration level. Yet, yields of hydroxyl OH· and hydroperoxide H₂O₂ only increased slightly. This can be understood as following. As indicated in Table 2, oxygen predominantly reacts with e_h and H· (lines 11 and 17), which accounts for the rapid reduction of e_h and H· with the increase of oxygen concentration. Meanwhile, the active reactions of oxygen with e_h and H· radicals in turn reduce the reaction probabilities of OH· with e_h and H· radicals. This leads to a reduced consumption of OH·, and hence an increased production of H₂O₂. Numerical results are shown in Table 3. The production of OH· and H₂O₂ increased by 6% and 12%, respectively, when $P_{O_2}$ increased from 0 to 21%.

Table 3.

G values (molecules/100 eV) of different molecules at 1 μs under different oxygen concentrations.

$P_{O_2}$	eh	OH·	H·	H2O2	$H{O}_{\dot{2}}$	${O_{\dot{2}}}^{-}$
0%	0.94	2.02	0.87	0.73	0	0
3%	0.46	2.08	0.34	0.77	0.55	0.50
9%	0.12	2.12	0.07	0.79	0.87	0.89
21%	0.00	2.14	0.00	0.82	1.02	1.06

Second, massive amounts of $H{O}_{\dot{2}}$ and $O_{\dot{2}}^{-}$ were produced, but the productions saturated after a certain time, which was found to be dependent on the initial oxygen concentration. The saturation time for $P_{O_2}=9\text{\%}$ occurred at about 1 μs, while it was around 0.4 μs for $P_{O_2}=21\text{\%}$. This trend was also observed by Boscolo et al. (2020), while a slight difference existed regarding the specific values for the saturation time between the two works.

Third, it required ~10 ns to observe a noticeable oxygen effect. From a probabilistic perspective, the species e_h and H· must diffuse a long enough distance to meet oxygen molecules and react with them. Take the case with $P_{O_2}=21\text{\%}$ (160 mmHg, 201.1 μM) as an example, where the rise of the yield of $O_{\dot{2}}$ and $H{O}_{\dot{2}}$ can be clearly seen at 10 ns. The average distance $d_{O_2}$ between oxygen molecules can be estimated as $d_{O_2}~\sqrt[3]{1/\left(P_{O_2}*N_A\right)}=20.2nm$. The time it takes for e_h to meet with an oxygen molecule can be estimated by $\sqrt{6*\left(D_{O_2}+D_{e_h}\right)*\Delta t}=d_{O_2}$, which gave Δt = 9.3 ns. This fact also highlighted the need to perform simulations for a relatively long time to investigate effects of oxygen via MC simulations. Previous simulations sometimes stop the chemical stage at 1 ns or 2.5 ns to reduce the computational burden, which is likely not sufficient to fully capture the effect of oxygen.

It can be observed that the time evolution of the yield curves contained some discontinuities, for instance, at 10 ns. This was caused by the change of time step size in gMicroMC (Tian et al., 2017). A larger time step size generally leads to a higher reaction probability and hence a steeper change of G value shown in the logarithmic plot. It is the same reason for the discontinuities observed in Figure 5.

Figure 5.

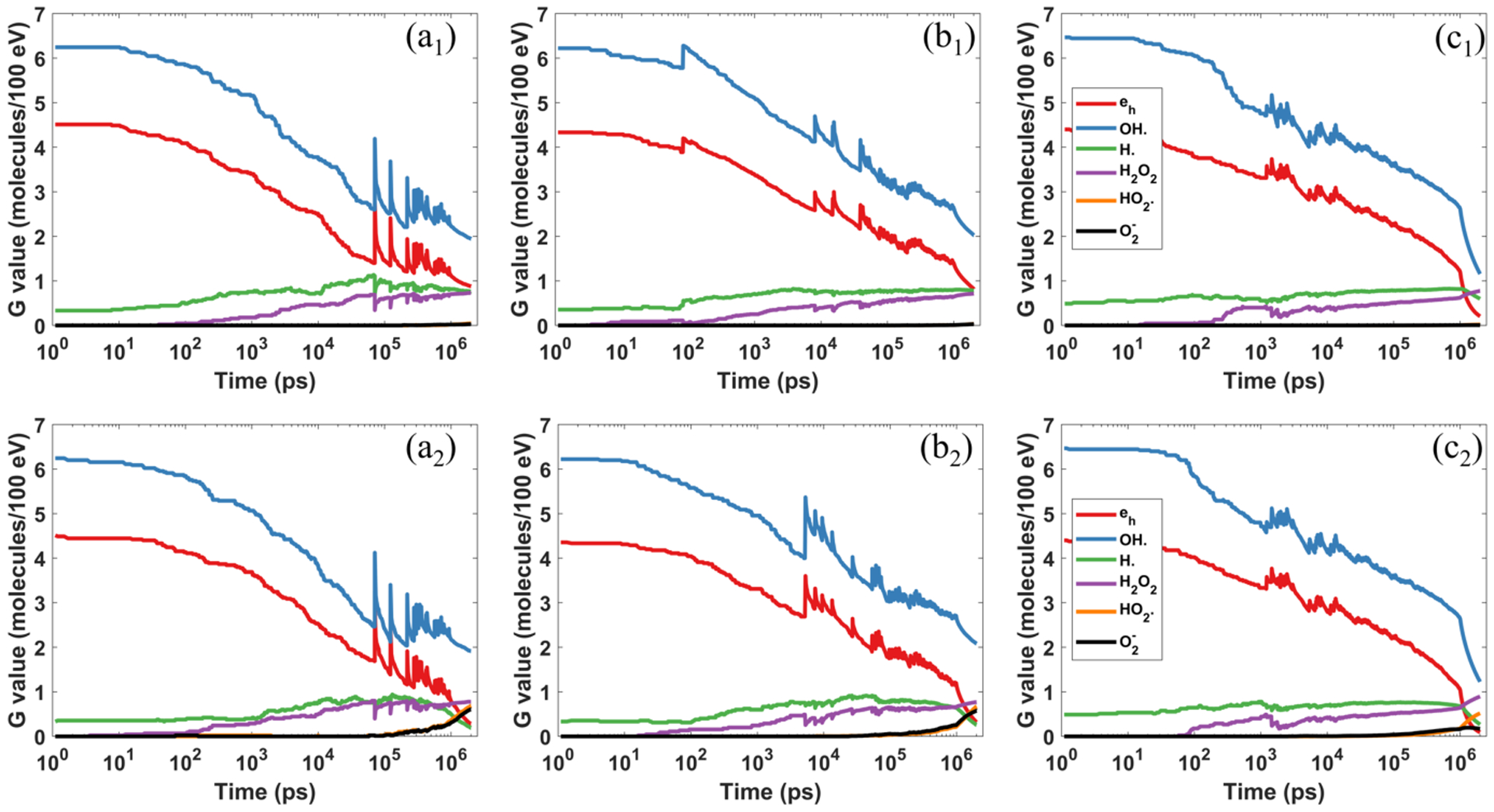
Comparison of the chemical yields under different dose rates of FLASH radiation with ${\dot{D}}_i=(\text{a}){10}^{6}Gy/s$ (b) 10⁷ Gy/s and (c) 10⁸ Gy/s. Top and bottom rows represent $P_{O_2}=0.1\%$ (hypoxia) and 3% (physoxia). Note, the results were from a representative simulation to show the specific radical evolutions and the spike positions and amplitudes may vary for different simulation runs.

3.3. Effect of oxygen under the FLASH condition

Figure 5 shows the evolution of the chemical yields for different instantaneous dose rates ${\dot{D}}_i$ under different $P_{O_2}$ with the initial electron energy of E_k = 4.5 keV. One notable feature in these curves is the existence of spikes. These spikes were caused by the inclusion of new OH· and e_h radicals generated by new primary electrons at the corresponding moments. Specifically, the large number of additional OH· and e_h radicals increased G values, causing spikes in these two species. In contrast, since the numbers of other radicals were unchanged, and the deposit energy was increased, the G values of radicals other than OH· and e_h were reduced at those moments.

Comparing the three columns of Figure 5, it was found that the dose rate has impacts on radical yields due to spatial density of radicals. We then summarized the mean G values from the 20 runs for critical radicals in Table 4. From both Figure 5 and Table 4, the results indicated that the probability of mutual reactions among radicals generated by initial electrons increased along with the increased dose rate, as the spatial density of radicals increased, and hence they were more likely to react. This can be seen from two aspects. First, both yields of e_h and $O_{\dot{2}}^{-}$ decreased for ${\dot{D}}_i={10}^{8}Gy/s$ compared to that for ${\dot{D}}_i={10}^{7}Gy/s$. As $O_{\dot{2}}^{-}$ can only be generated by the reactions between oxygen and e_h, simultaneous reduction of e_h and $O_{\dot{2}}^{-}$ implied that e_h was largely consumed even without the participation of oxygen. Second, the yield of OH· reduced for ${\dot{D}}_i={10}^{8}Gy/s$, compared to that for ${\dot{D}}_i={10}^{7}Gy/s$. But as discussed in Sec 3.2, the inclusion of oxygen dose not lead to the reduction of OH·. Hence, the reduction of OH· suggested increased reactions between OH· and other radicals.

Table 4.

G values (molecules/100 eV) of different molecules at 1 μs post irradiation under different oxygen concentrations.

Dose rate (Gy/s)	$P_{O_2}$	eh	OH·	H·	H2O2	$H{O}_{\dot{2}}$	$O_{\dot{2}}^{-}$
106	0.1%	0.83	1.92	0.79	0.75	0.04	0.03
	3%	0.28	1.94	0.21	0.81	0.70	0.62
	21%	0	2.04	0	0.82	1.05	1.03
107	0.1%	0.82	2.03	0.78	0.72	0.03	0.03
	3%	0.32	2.08	0.26	0.77	0.67	0.58
	21%	0	2.13	0.01	0.82	1.11	1.01
108	0.1%	0.20	1.16	0.60	0.78	0.02	0.01
	3%	0.09	1.23	0.27	0.90	0.52	0.17
	21%	0	1.31	0.02	1.00	1.24	0.40

The dependence of OCR on initial $P_{O_2}$ levels for different ${\dot{D}}_i$ are plotted in Figure 6(a) with E_k = 4.5 keV. The OCR quickly dropped as the initial oxygen concentration decreased because of the reduction in reaction probability between oxygen and radicals. Numerically, for ${\dot{D}}_i={10}^{7}Gy/s$, the OCR dropped from ~0.23 μM/Gy for an oxygen concentration level of 21% to ~0.0007 μM/Gy, when the concentration was decreased to 0.01%. In terms of the dependence on dose rate, for $P_{O_2}=21\%$, it remained unchanged at ~0.22–0.23 μM/Gy for ${\dot{D}}_i={10}^6~{10}^{7}Gy/s$. When the dose rate was increased to 10⁸ Gy/s, OCR dropped rapidly to 0.19 μM/Gy. We knew from Figure 4 that radicals must travel a long enough distance to react with oxygen molecules from a probabilistic view. Mutual reactions between radicals may happen before they collide with oxygen molecules, but the overlap between different tracks was very unlikely for small ${\dot{D}}_i$. Only when ${\dot{D}}_i$ exceeds a certain threshold, it will show the consequence of reduced OCR. To investigate this threshold, we have performed two new simulations with ${\dot{D}}_i=2\times {10}^{7}Gy/s$ and ${\dot{D}}_i=5\times {10}^{7}Gy/s$. We plotted the variation of OCR versus dose rate with $P_{O_2}=21\%$ in Figure 6(b). We found that for all simulated dose rates larger than 10⁷ Gy/s, the OCR drops quickly. We hence estimate that the threshold dose rate is around ${\dot{D}}_i={10}^{7}Gy/s$, under the current setup with a pulse width of 1 μs.

Figure 6.

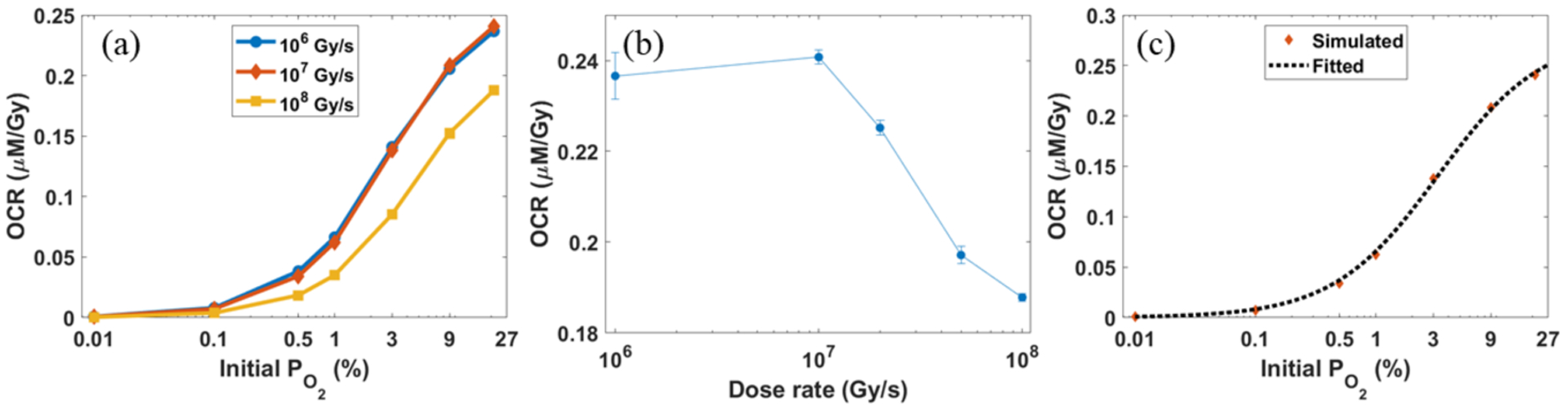
(a) Average OCRs for different instantaneous dose rates ${\dot{D}}_i$ from our simulation study. (b) The average OCRs for different dose rates with ${\text{P}}_{{\text{O}}_2}=21\%$. Error bars represent the standard deviations from 20 simulation runs. (c) The simulated OCRs and the fitted OCR curve under different initial oxygen concentration levels with ${\dot{D}}_i={10}^{7}Gy/s$.

From Figure 6(a), we used Equation (2) to fit $OCR\left(P_{O_2}\right)$. As an illustration, we showed the results for ${\dot{D}}_i={10}^{7}Gy/s$ in Figure 6(c). The fitting parameters OCR_max and α were 0.270 μM/Gy and 0.030, respectively.

With the fitted OCR curve, we computed the time evolutions of oxygen concentration using Equation (3) for the irradiations under a dose rate of ${\dot{D}}_i={10}^{7}Gy/s$ and an initial oxygen concentration of $P_{O_2}=21\%$ and 0.1%, respectively. The results are plotted in Figure 7(a). If 0.001% was taken as the criteria of oxygen depletion, it would require 1770 Gy and 500 Gy to reduce oxygen to this level for initial $P_{O_2}=21\%$ and 0.1%, respectively. On the other hand, after D_total = 30 Gy, a typical dose used in FLASH experiments, the residual oxygen concentrations for different initial $P_{O_2}$ were computed and plotted in Figure 7(b). Notably, the final oxygen concentration was always above zero. As a comparison, we plotted the residual $P_{O_2}$ under the assumption of a constant OCR_C = 0.42 mmHg/Gy)(0.53 μM/Gy) (Pratx and Kapp, 2019). In this case, the oxygen would be depleted, if the initial $P_{O_2}$ was lower than 1.6%.

Figure 7.

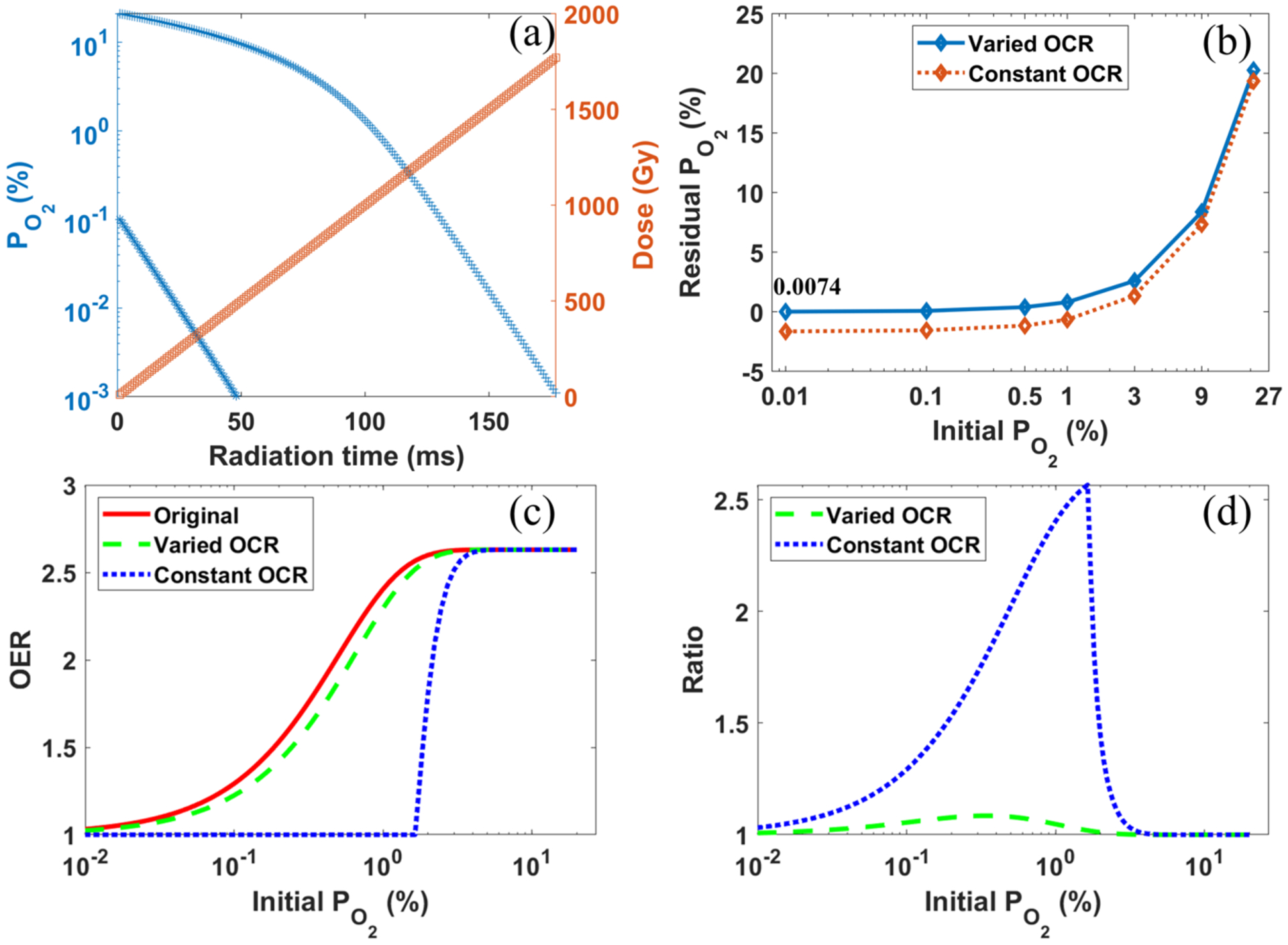
(a) The time evolution of oxygen concentration $P_{O_2}$ and total dose for ${\dot{D}}_i={10}^7\text{Gy}/\text{s}$ with two different initial oxygen levels. (b) The residual oxygen concentration for ${\dot{D}}_i={10}^7\text{Gy}/\text{s}$ after receiving a dose of 30 Gy. (c) The OERs as a function of the initial oxygen concentration levels under conventional radiotherapy (“Original”), and under FLASH radiotherapy of ${\dot{D}}_i={10}^{7}Gy/s$ with a constant OCR (“Constant OCR”) and from our calculation (“Varied OCR”). (d) The ratio of OER between conventional radiotherapy and FLASH radiotherapy as a function of different initial oxygen levels, with constant and varied OCRs, respectively.

In the low dose rate conventional radiotherapy, oxygen regeneration should be considered, and the cells can be viewed as exposing to a constant oxygen concentration surrounding. Consequently, we used the initial $P_{O_2}$ value to compute the OER for conventional radiotherapy. Its behavior with different initial $P_{O_2}$ was plotted in Figure 7(c) by the red solid line. As for the FLASH radiation, assuming the oxygen regeneration is ignored, we then computed its OER with the oxygen level at the end of the radiation. Its behavior with different initial $P_{O_2}$ and a total dose of 30 Gy is plotted in Figure 7(c) by the dash lines. OER dropped from 1.3 to 1.2 for the initial hypoxia oxygen concentration of $P_{O_2}=0.1\%$, from 2.63 to 2.62 for physoxia condition of $P_{O_2}=3\%$, and stayed almost unchanged for normoxia condition of $P_{O_2}=21\%$. In contrast, with a constant consumption rate of OCR_C = 0.42 mmHg/Gy (Pratx and Kapp, 2019), the changes in OER were from 1.3 to 1 for $P_{O_2}=0.1\text{\%}$, and from 2.63 to 2.50 for $P_{O_2}=3\%$.

The reduction in OER for FLASH radiotherapy compared to conventional radiotherapy provides the possibility of dose escalation, with potentially improved dose tolerance of normal tissues (Vozenin et al., 2019a). The ratio between OERs of the conventional radiotherapy and that of FLASH radiotherapy is plotted in Figure 7(d). With a constant OCR, an OER ratio as large as 2.61 at the initial oxygen level of 1.6% can be obtained, which corresponds to the sharp fall-off of OER for FLAH-RT with constant OCR in Figure 7(c). In contrast, the maximum ratio was only about 1.08, once the varied OCR obtained from our simulation was used for the computation of the OER. We comment that the calculation overestimated the oxygen concentration for conventional radiotherapy and hence its OER, because oxygen consumption occurs, as long as there exists radiation radicals. Meanwhile, it underestimated the oxygen concentration for FLASH radiotherapy and its OER, because we used the minimum value of oxygen concentration after the radiation and ignored oxygen regeneration. Therefore, we overestimated the ratio between OER of conventional radiotherapy and that of FLASH radiotherapy.

3.4. Computational efficiency

Since one of the motivations of this study was to demonstrate the practical value of gMicroMC to handle computationally challenging MC simulation problems in the presence of oxygen, we report the computational time required to perform the study. Due to the lack of the step-by-step simulation support of oxygen effect in the chemical stage in other CPU-based MC packages, we effectively evaluated the efficiency of our package by comparing to GEANT4-DNA under simulations of approximately the same number of molecules in the region of interest for the chemical stage. Although Geant4-DNA is distinct from gMicroMC that it cannot simulate radical interactions from different tracks simultaneously, this comparison is still valid, because the simulation time is mainly determined by the number of molecules. For the simulation of 10³ molecules ($P_{O_2}=0\text{\%}$) with the chemical stage ending at 1 μs, the speedup factor was ~30 for gMicroMC running on one Nvidia Titan Xp GPU (1.58 GHz) card as compared to GEANT4-DNA running on a single core of Intel i7-6850K CPU (3.6 GHz). When the molecule number increased to 10⁵ ($P_{O_2}=3\%$), the speedup factor increased to 1228 (Table 5). We did not perform the simulations for the case of $P_{O_2}=21\%$ with Geant4-DNA, because the computation time can be 4~5 orders higher than that for the zero-oxygen case. In contract, gMicroMC can handle the simulation in an affordable time. It took twenty hours to simulate seven million molecules for the FLASH cases with the chemical stage ends at 2 μs. It needs to be pointed out that both techniques can be further accelerated using, e.g. multi GPUs for gMicroMC or a CPU cluster for GEANT4-DNA.

Table 5.

Time performance for gMicroMC and GEANT4-DNA running same number of molecules to 1 μs

$P_{O_2}$	Number of molecules	GEANT4-DNA	gMicroMC
0%	~ 103	61 s	2 s
3%	~ 105	70000 s	57 s
21%	~ 106	-*	227 s

^*simulation not performed due to long computation time.

4. DISCUSSIONS

The current study only investigated the impact of oxygen on the chemical yields of radicals. It is probable of more relevance to study the impact on DNA damages. Actually, gMicroMC is able to achieve this goal with its DNA geometry model (Tsai et al., 2020). However, as the DNA damages are generated only by the hydroxyl radicals in gMicoMC, and the existence of oxygen was not found to significantly change the hydroxyl radical yield (Table 3 and Figure 4), oxygen in the simulation would then unlikely change the DNA damages. We have performed a simulation to compute DNA damages under the conventional dose rate and compared the results with those at $P_{O_2}=0\text{\%}$. The damages were found to be slightly increased by ~8% at $P_{O_2}=3\%$ and ~10% at $P_{O_2}=21\%$. Moreover, the DNA damage calculation in current gMicroMC did not consider other aspects of oxygen, such as the oxygen fixation hypothesis on the DNA repair process triggered by the initial damages. To consider the biological consequence of DNA damages, it would be necessary to include these into the simulation, for instance, by considering the variation of DNA damage probability with regards to oxygen concentration (Forster et al., 2018).

In section 2.2, when we computed the G-values for different chemical species, we considered only those secondary electrons initially produced inside the 10 um water slab. This may cause a concern that the boundary-crossing electrons could alter the computational results. Yet, when we simulated the secondary electron distributions for the first few tens of micrometers along its depth direction with Geant4, we found that the kinetic energies of most secondary electrons were of a few hundred eVs, or equivalently, their travel lengths were of a few hundred nanometers. Hence, only those secondary electrons produced within a few hundred nanometers from the slab boundary could have a non-zero boundary-crossing probability. Additionally, the produced radicals all had diffusion lengths of a few hundred nanometers with a chemical stage duration of 1 μs (Table 1), which further implied that the boundary effect was quite limited. To verify our estimation, we performed a new simulation by considering all secondary electrons in a slab 2 um thicker than the slab-of-interest and computed the G values for radicals inside the slab-of-interest. Comparing the newly computed G values to that obtained in section 2.2, the mean and maximum absolute differences between the two simulations were 2% and 3.8%, respectively, for all radicals with G values higher than 0.1 molecules per 100 eV, indicating that the boundary-crossing electrons did have limited impact on the results.

Pratx and Kapp (2019) analyzed the oxygen depletion at different dose rates. They solved differential equations for the diffusion of dissolved oxygen molecules from a blood microvascular structure to the cells under different dose rates and estimated the OER according to different remaining oxygen concentration after radiation. It was concluded that the oxygen depletion can be achieved at a low oxygen concentration level with a high dose rate. However, under a typical dose level of 30 Gy used in FLASH experiments, we found the oxygen is unlikely to be depleted, although it may occur at a very high dose level, e.g. 1000 Gy. In addition, due to the decreased OCR with reduced oxygen concentration, our simulation results showed a relatively small OER change. The different conclusions from Pratx et al. and ours were caused by the different treatments of OCRs. A constant OCR (the ‘L_ROD’ term in their paper) was assumed in Pratx and Kapp (2019), whereas the OCR may not be a constant, as shown in our simulation via mechanistic modeling of the chemical stage, because the probability for radicals to meet and react with oxygen molecules decreases, as the oxygen distribution gradually becomes sparser in the space. On the other hand, Labarbe et al. (2020) considered the oxygen effect in FLASH by solving a system of ordinary differential equations (ODEs) representing the biological reactions at more than 1 μs post irradiation with presence of oxygen. They reported that the oxygen reactions were suppressed under FLASH dose rates. However, the reason differs. In their study, the decreased oxygen reaction, and hence a reduced production of the radiobiological damaging radicals, was attributed to an increase of self-recombination of alkyl radical R· after typical chemical stage of 1 μs. In our simulation, the reduced OCR is due to an increased mutual reaction between radicals in chemical stage. It may require more efforts to specify the overall oxygen effects in the FLASH radiotherapy.

The computations were performed using electrons with E_k = 4.5 keV. We have also performed the simulation using electrons with E_k = 0.3 keV, as the two energies play important roles in water radiolysis, creating spurs, blobs, and short tracks for DNA damages (Ward, 1988). Quantitative results were slightly different. For instance, for E_k = 0.3 keV, the calculated OCR were 0.31, 0.32 and 0.23 μM/Gy for dose rates of 10⁶, 10⁷ and 10⁸ Gy/s, respectively, at the oxygen concentration level of 21%. However, the same behavior in terms of OCR reduction with reduced oxygen concentration was observed. The oxygen may not be depleted under FLASH condition and the consequent change of OER due to oxygen consumption was also small. With a further analysis, the findings from our current simulation studies could be extendable to the preclinical photon or electron FLASH radiotherapy. The reason is of two-fold. First, in our simulation study, we initialized our primary electrons with a uniform spatial distribution and an isotropic momentum direction, which is found consistent with secondary electron distributions from MeV photon or electron beams in a water phantom (Figure 8). We obtained Figure 8 via shooting three irradiation beams (1 MeV photon, 1MeV electron and 4.5 MeV proton) along the z axis into a water phantom and recording the secondary electron distributions in the spherical coordinate system. From Figure 8, the maximum difference for the polar (cos(θ)) distribution of secondary electrons from the photon and electron beams are 3.1% and 4.5%, and that for the azimuthal (ϕ) distribution are 0.4% and 0.6%, respectively. In contrast, there is a significant forward distribution for those electrons generated from the proton beam, which alters the uniform distribution assumption in our simulation. Second, the electron energies of 4.5 keV and 0.3 keV used in our study are also found representative for the second electron spectrum from the MeV photon and electron beams. Specifically, we found that the portions of secondary electrons with kinetic energies ⩽ 4.5 keV are 64.9% and 99.9% for the 1 MeV photon and electron beams, respectively. In the former case, if we take those secondary electrons produced from the photon interactions as primary, their further induced secondary electrons have kinetic energies well below 4.5 keV, just as that for the 1 MeV electron case. In the overall water radiolysis process triggered by the 1 MeV photon or electron beams, these low energy secondary electrons (below 4.5 keV) contribute more than 99% to the total radical productions. Combining all these factors, we reasonably referred that the simulated energies of the electrons well represent the situation for x-ray or electron FLASH radiotherapy.

Figure 8.

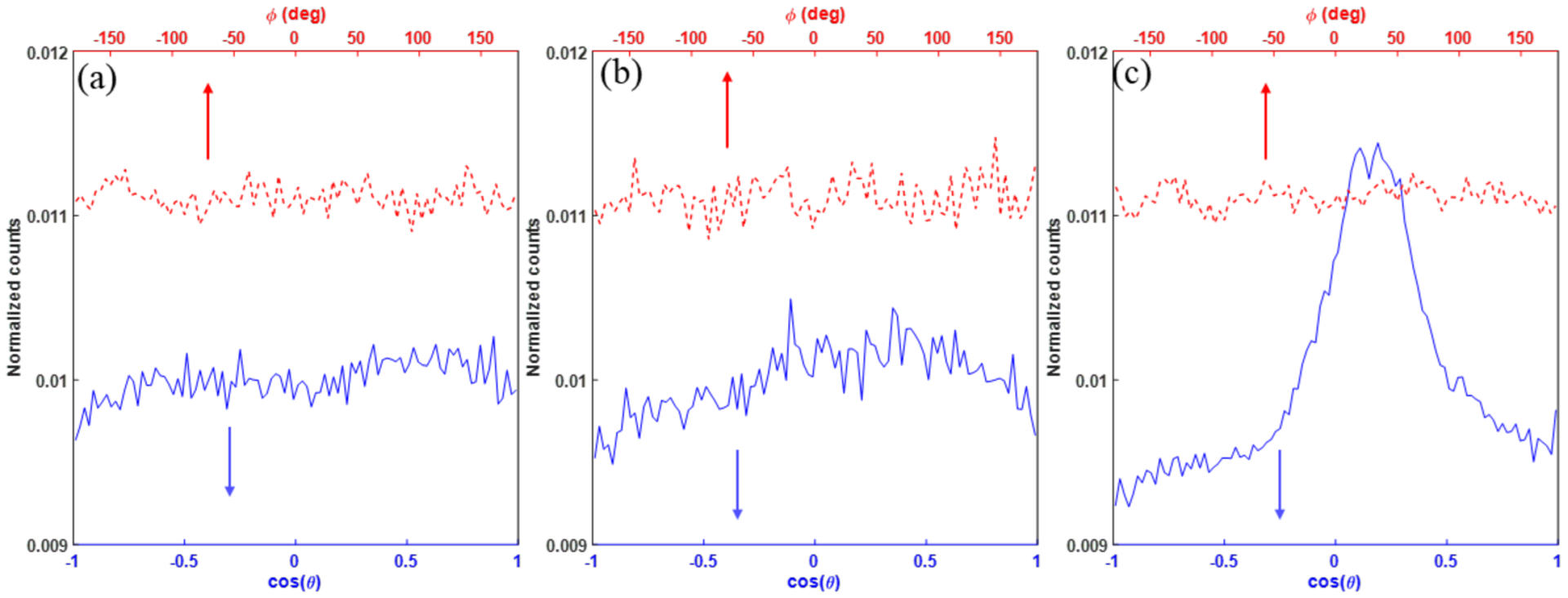
Angular distributions of secondary electrons from (a) 1 MeV photon (b) 1 MeV electron and (c) 4.5 MeV proton beams. θ and ϕ are polar and azimuth angles in the spherical coordinate system. The incident beam direction is along z axis.

As shown in our previous study (Lai et al., 2020) and other similar studies (Zhu et al., 2020; Shin et al., 2019; Lampe et al., 2018), one important aspect affecting result validity in MC simulations is the uncertainty introduced by unrefined parameter values. As specific to this study, uncertainties in the diffusion and reaction rates can be of concern. Take reaction 11 in Table 2 as an example, total diffusion rates of 7.3 and 6.6 nm²/ns, and reaction rates of 1.74 × 10¹⁰ and 1.9 × 10¹⁰ dm³mol⁻¹s⁻¹ were used in gMicroMC and TRAX-CHEM (Boscolo et al., 2020), respectively. There was a ~10% difference between the two packages, which will lead to about 10% differences of the reaction radii. To study its impact on our simulation results, we reperformed the computations at $P_{O_2}=21\%$ for electrons with E_k = 4.5 keV and the reaction radii changed by 10%. The yields of different chemical species were found only minimally changed with a maximum of the change being 0.3%. The robustness can be understood as following. Oxygen distribution is very sparse compared to the reaction radii. Mean distance between oxygen molecules is ~20 nm for $P_{O_2}=21\%$ (160 mmHg, 201.1 μM) while the radii are usually less than 1 nm. Hence, the uncertainties in the reaction radii caused by different reaction rates and diffusion rates is very small compared to the large distance between reactants. Asides from the uncertainty triggered by ill-defined parameters, the stochastic nature of MC simulation would introduce uncertainty as well. Unlike the case for conventional dose rate mode, where 1000 runs were needed to reduce the uncertainty to 0.5% level, the simulation results for FLASH mode were relative more robust because there are already many electrons within one pulse. For all oxygen concentrations, 20 runs were adequate to reduce the uncertainty to a level of 3% for 10⁶ Gy/s and well below 2% for cases with higher dose rates.

As discussed in (Colliaux et al., 2015), it is expected that the results, e.g. in terms of yields, computed by explicitly treating oxygen as molecules and as a continuum background in MC simulations should be similar. However, this is only valid in certain scenarios. For instance, when the oxygen consumption occurs in a spatially small and temporally large scale, oxygen diffusion can compensate the consumption, making the oxygen distribution spatially and temporally approximately unchanged. Another scenario is when irradiation tracks are dense enough and most reactions happen among radicals. In this case, the effect of oxygen inhomogeneity may be ignored. However, the FLASH condition does not fall in these categories, which hence likely requires the method explicitly treating oxygen as molecules. Oxygen diffusion length for 2 μs is only 170 nm and it would be difficult for oxygen to diffuse from the outside of the ROI to the middle of the ROI to compensate the oxygen consumption.

5. CONCLUSION

In this paper, we reported our recent progress on the modeling of the chemical stage of the water radiolysis with an explicit consideration of the oxygen reaction effect, and its implementation in the open-source GPU-based MC simulation tool, gMicroMC. To demonstrate the practical value of gMicroMC in large scale simulation problems, we applied the oxygen-simulation-enabled gMicroMC to compute the yields of chemical radicals under a high instantaneous dose rate ${\dot{D}}_i$ to study the oxygen depletion hypothesis in FLASH experiments. We computed the time evolution of oxygen concentration under FLASH irradiation setups. At the dose rate level of 10⁷ Gy/s and initial oxygen concentrations from 0.01%~21%, the oxygen is unlikely to be fully depleted with an accumulative dose of 30 Gy, which is a typical dose used in most FLASH experiments. gMicroMC is found efficient in simulating the chemical stage with oxygen effect explicitly considered. With an initial oxygen concentration of 3% (~10⁵ molecules), a speedup factor of 1228 was achieved for gMicroMC on a single GPU card when comparing with Geant4-DNA on a single CPU.