Skip to main content
NCBI home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2021 Jun 11;125(24):5326–5334. doi: 10.1021/acs.jpca.1c03631

Size-Resolved Electron Solvation in Neutral Water Clusters

Loren Ban 1, Bruce L Yoder 1, Ruth Signorell 1,*
PMCID: PMC8237264  PMID: 34114470

Abstract

graphic file with name jp1c03631_0006.jpg

Cluster-size-resolved ultrafast dynamics of the solvated electron in neutral water clusters with n = 3 to ∼200 molecules are studied with pump–probe time-of-flight mass spectrometry after below band gap excitation. For the smallest clusters, no longer-lived (>100–200 fs) hydrated electrons were detected, indicating a minimum size of n ∼ 14 for being able to sustain hydrated electrons. Larger clusters show a systematic increase of the number of hydrated electrons per molecule on the femtosecond to picosecond time scale. We propose that with increasing cluster size the underlying dynamics is governed by more effective electron formation processes combined with less effective electron loss processes, such as ultrafast hydrogen ejection and recombination. It appears unlikely that any size dependence of the solvent relaxation dynamics would be reflected in the observed time-resolved ion yields.

1. Introduction

The everlasting interest in the hydrated electron has resulted in a wide range of experimental and theoretical studies on the formation mechanisms, the relaxation dynamics, and its electronic properties in liquid water, amorphous ice, and anionic, neutral, and sodium-doped water clusters.1−49 Recent experiments using time-resolved photoelectron spectroscopy (TRPES) of neutral water clusters50−52 and bulk liquid53 enabled the first detailed comparison of the relaxation dynamics following direct excitation of water above and below band gap. It was suggested that the relaxation dynamics observed in the first few picoseconds is dominated by slow and fast solvent responses with characteristic solvation times of ∼200 fs and ∼1–2 ps, respectively. An intriguing result is the apparent independence of the hydrated electron signatures on the system size. Similar solvation dynamics, vertical binding energies (VBE), and survival probabilities are reported for both neutral clusters (average sizes ranging from 300 to 500 water molecules50−52) and bulk liquid (liquid microjet53) (see Table 1 in ref (51)). Likewise, the solvation dynamics and VBEs in neutral clusters and bulk liquid are also found to be largely independent of the excitation energy from below to above band gap in the region from 7.7 to 15.5 eV.

In contrast to water cluster anion studies,4,22 TRPES studies of larger, neutral clusters cannot exploit the full potential of cluster studies because cluster size selection is generally not possible for the latter. Size selection of neutral clusters is still limited to small clusters (e.g., by using inhomogeneous electric54,55 and magnetic56 fields), and the same holds for photoelectron–photoion coincidence studies.57,58 Thus, PES of larger, neutral clusters represents the average behavior of a broad cluster size distribution. However, progress in the measurement of size distributions of neutral clusters makes it now possible to determine the accurate average cluster size and width of the distribution.59−61

To shine more light on the 100 fs to ps dynamics of the hydrated electron after direct laser excitation of neutral water clusters, we report here a complementary approach that exploits time-resolved time-of-flight mass spectrometry (TOF-MS) instead of TRPES. In contrast to TRPES, TOF-MS allows us to retrieve cluster-size-resolved dynamics, albeit at the price of losing electronic information. Furthermore, these studies provide time-resolved information about clusters with fewer than 200 molecules, for which no TRPES studies have been reported yet. To this end, we record time-dependent water cluster ion yields following below band gap excitation with femtosecond laser pulses of 7.8 eV energy and subsequent ionization with femtosecond laser pulses of 4.7 eV energy. The results are compared with our previous TRPES study performed with the same pump–probe excitation scheme.51 The time-resolved TOF-MS provides complementary cluster-size-resolved information about hydrated electron formation and loss processes.

2. Experimental Section

The experimental setup was previously used and described in refs (50), (51), and (62), with the major difference here being the use of time-of-flight mass spectrometric (TOF-MS) detection instead of photoelectron detection. Neutral water clusters were generated in a pulsed supersonic expansion through an Even-Lavie valve63 with Ne as carrier gas. TOF spectra of the ions were recorded after femtosecond pump–probe excitation. Pump pulses with 7.8 eV photon energy from high harmonic generation (HHG) were isolated in a time-preserving monochromator. At this pump energy, solvated electrons can be generated in water clusters below band gap. Probe pulses with 4.7 eV photon energy were generated by nonlinear frequency conversion in a pair of BBO crystals. The instrument response function (IRF) was determined from 1 + 1′ nonresonant ionization of both Xe and O2 and has a width of ∼194 fs (Figure S1).

TOF spectra of the ionized clusters were detected on a shot-to-shot basis, which proved to be crucial for a pump–probe signal with a count rate of about 0.1 ions/shot. At such low count rates, the usual procedure of averaging TOF-MS traces would require accumulating many more laser shots to obtain usable signal, which would make it virtually impossible to maintain the stability required for recording pump–probe scans. We amplify the electron current generated by the ions at the detector62 and record the TOF trace with an oscilloscope (Teledyne LeCroy WaveRunner 625Zi, 2.5 GHz). The oscilloscope was operated in an event counting mode where only the TOF at the maxima of the electron current are stored on a shot-to-shot basis. Because only TOFs for current maxima above a certain threshold are stored, the signal is free of electronic noise. The sampling resolution (number of bins per TOF interval) is, however, limited because of the repetition rate of the experiment which sets an upper limit for the number of bins in a given TOF interval. We selected a TOF window of 20 μs at an ion extraction voltage of 25 kV, which limits the detectable ion mass to m/z ∼ 104 (∼600 water molecules). This range was sufficient to record signal from the whole cluster size distribution generated by the valve. Detecting at a rate of ∼200 Hz, the TOFs were binned with maximal resolution of our oscilloscope (5000 bins/interval, bin width of 4 ns), resulting in sampling of about 5 data points across a typical ion signal peak. Our detection scheme enables single-molecule resolution for clusters up to ∼200 water molecules. We note that this method only works in the limit where not more than one ion with the same TOF is detected within a single laser shot.

3. Results

3.1. Time-Resolved Mass Spectra

Figures 1 and 2 show TOF spectra as a function of the pump–probe delay Δt, with the assignment of the cluster size in terms of the number of water molecules n – 1 (upper abscissa). These spectra were obtained by subtracting the background spectrum S(n)bg recorded at Δt = −10 ps time delay from the TOF spectra S(n,Δt) recorded at time delay Δt (Figure S2). The cluster ion signals at Δt = 0 fs (zero time delay) arise largely from (1 + 1′) two-photon ionization of neutral water clusters (H2O)n by the pump and probe lasers with a total photon energy of ∼12.5 eV. Small (H2O)n cluster signals are also observed in the background spectrum S(n)bg (Figure S2), which arise from multiphoton ionization by the probe laser (4.7 eV). Following photoionization, water clusters undergo fast proton transfer and dissociate into H+(H2O)n−1.64−68 For water clusters probed at these photon energies, further dissociation and water evaporation do not play a significant role.64,67,68 Therefore, the time-dependent ion yields of the H+(H2O)n−1 clusters represent the time-dependent ion yields of the corresponding neutral (H2O)n clusters (vide infra). Furthermore, the spectrum recorded at Δt = 0 fs, S(n,0 fs) (second trace in Figure 1), represents the size distribution of the neutral clusters, with an average cluster size of ⟨n⟩ ∼ 100 and maximum cluster sizes of n ∼ 300.

Figure 1.

Figure 1

Open in a new tab

Background subtracted TOF spectra S(n,Δt) – S(n)bg of neutral (H2O)n clusters as a function of the pump–probe time delay Δt. The (H2O)n clusters were excited by a pump pulse of 7.8 eV photon energy and ionized by a probe pulse of 4.7 eV photon energy. The number n – 1 of molecules in a cluster H+(H2O)n−1 is indicated in the upper abscissa.

Figure 2.

Figure 2

Open in a new tab

Background-subtracted TOF spectra from Figure 1 in the region of H+(H2O)n−1<5 (panel a, blue), H+(H2O)12<n−1<24 (panel b, red), and H+ (H2O)33<n−1<44 (panel c, green). The time delay Δt is indicated on the right.

The cluster-size-resolved ion yield shows clear trends as a function of the time delay Δt (Figures 1 and 2). No signal of probe-induced dynamics is observed at negative Δt, in line with previous studies employing the same probe energy.50−53 The ion yields are highest at time delays within the IRF (0 and 100 fs) and decrease with increasing Δt. The high yield within the IRF time mainly results from direct (1 + 1′) two-photon ionization. The systematic decrease of the ion yield at longer Δt represents the decrease in the solvated electron signal with Δt, as previously observed by photoelectron spectroscopy (Figure 3 and ref (51)). In addition to the general loss of ion signal, the shape of the size distribution also changes with increasing Δt: the ion yield of smaller clusters decreases more rapidly than that of larger clusters with increasing Δt.

Figure 3.

Figure 3

Open in a new tab

(a) Time-dependent cluster ion yield Itot(Δt) (circles) with fit results (black line) for a sequential kinetic model with two decaying (blue and green dashed lines) and an impulsive (yellow dashed-dotted line) signal component. (b) Time-dependent total ion yield (thick black line) and total electron signal51 (blue dashed line) after subtraction of the impulsive signal component and scaling to the same maxima. In both panels, the abscissa is linear up to 0.9 ps (vertical line) and logarithmic for longer times.

Figure 2 focuses on three specific size regions. For the smallest clusters (n – 1 < 5, Figure 2a), most of the cluster signal is detected for delays comparable to the width of the IRF. These signals mainly arise from impulsive 1 + 1′ ionization51,53 (see above). The signature of the IRF is also visible in the O2+ peak (at ∼1.1 μs), which mainly originates from 1 + 1′ ionization of residual O2 in the vacuum chamber (Figure S2). Signals arising from actual pump-induced dynamics (i.e., from solvated electrons) are very low for these smallest clusters and only visible at Δt longer than the IRF. Strong contributions from cold water monomers and residual background in the vacuum chamber (high noise) prevent the retrieval of reliable time-dependent information for H2O and (H2O)2. In the size region n – 1 = 13–23 (Figure 2b) there is an increase in the intensity of the signals from pump-induced dynamics compared to Figure 2a, which becomes more pronounced for even larger clusters with n – 1 = 34–43 (Figure 2c). The observed pump–probe dynamics is clearly cluster-size-dependent.

3.2. Comparison with Dynamics from Photoelectron Imaging

Our previous photoelectron imaging study of water clusters using the same pump–probe scheme as in the present work (7.8 eV pump and 4.7 eV probe) has revealed that the observed dynamics result from the formation and relaxation of solvated electrons in the clusters.51 The comparison of the present ion experiments with the previous photoelectron experiments provides further indications that the dynamics depends on the cluster size. To shed more light on this, let us compare the ion experiments for an average cluster size of ⟨n⟩ ∼ 100 with the previous photoelectron experiment for ⟨n⟩ ∼ 500—a difference that should be large enough to detect a dependence of the dynamics on the average cluster size. Note that photoelectron studies for average cluster sizes above ⟨n⟩ ∼ 250 find no pronounced effect of the system size on the dynamics,50−53 while photoelectron studies for ⟨n⟩ < 250—for which size-dependent effects are more likely to manifest—are still missing. Because photoelectron studies of neutral clusters cannot provide any cluster-size-resolved information, we can only compare the time-dependent total electron yield Iel(Δt) from ref (51) with the total ion yield Itot(Δt), that is, with the sum of the ion signal over all different cluster sizes:

3.2. 1

To be able to compare decay times and to account for differences in the IRF, we need to analyze Iel(Δt) and Itot(Δt), with the same kinetic model. The three-step sequential model (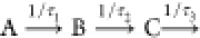Inline graphic) used in ref (51) cannot be employed here because it has too many free parameters that would be underdetermined by single electron/ion yield curves. We thus use a reduced kinetic model involving two steps with characteristic exponential decay times (see the Supporting Information for details):

3.2. 2

The fit results for Itot(Δt) are shown in Figure 3. The probe signal arising from states A (dashed blue line) and C (dashed green line) together with the impulsive signal component (dash-dotted yellow line), which follows the IRF, make up the total signal (thick black line). Variable parameters in the fit are the amplitude of the three signal components (PIRF, Pa, and Pc) and the decay time of the first step (τa), while the decay time of the second step is fixed at the previously determined value τc = 17.0 ps51 because our ion yield curves (Figure 3a) do not contain any information about very slow decay processes, such as diffusion-controlled geminate recombination.3,37,39,53,69,70 The impulsive signal component (dashed-dotted yellow line) is modeled by a Gaussian distribution with a fixed width FWHMIRF = 194 fs (Figure S1).

Figure 3 illustrates that the experimental ion yields (black circles) are well reproduced by the model (black line) with a decay time τa = 491 ± 110 fs for the first step. The equivalent fit for the electron yields (not shown) results in a substantially longer decay time τa = 1055 ± 342 fs. Because the average cluster size is ⟨n⟩ ∼ 100 for the ions and ⟨n⟩ ∼ 500 for the electrons, this indicates slower dynamics in larger clusters. This can also be seen when comparing the time-dependent ion and electron yields after subtraction of the respective impulsive (IRF) contribution and scaling to the same maximum value (Figure 3b). The faster decay of the ion yield (thick black line) compared with the electron yield (dashed blue line51) is clearly visible. Figure 3b also includes ion yields for subsets of clusters sizes: one for large clusters (151 ≤ n ≤ 195, thin red line) and the other for small ones (17 ≤ n ≤ 24, thin green line). These examples of size-resolved ion yield curves confirm the trend of faster dynamics in smaller clusters (see also Figure 4).

Figure 4.

Figure 4

Open in a new tab

(a) Symbols: time-dependent normalized ion yield, I(n,Δt), for specific cluster size intervals (indicated in the legend). The error bar represents a typical uncertainty. Lines: corresponding fit results from the two-step kinetic model (eq 2). The gray shaded area is the normalized IRF recorded for residual O2 gas. The abscissa is on a linear scale up to 0.6 ps (vertical line) and logarithmic at longer times. (b) Amplitude Pa, Pc, and PIRF from the kinetic model. (c) Decay constant τa from the kinetic model. n̅ indicates the cluster size at the center of each size interval. The shaded areas in panels b and c represent typical uncertainties estimated from the fit confidence intervals.

3.3. Cluster-Size Resolved Dynamics

For a quantitative comparison of size-dependent ion yield curves, we introduce the normalized ion yield for cluster size n:

3.3. 3

To a first approximation, the background-corrected ion signal for cluster size n at zero pump–probe delay (S(n, 0 fs) – S(n)bg, see section 3.1) is proportional to the product of cluster abundance, cluster size, molecular photoexcitation cross sections, and light intensities; that is, I(n,Δt) is proportional to the abundance of monomers in the form of clusters of a particular size n. The normalized ion yield I(n,Δt) is thus proportional to the ion yield per molecule for clusters with size n (termed normalized ion yield). Figure 4a shows the normalized ion yields (symbols) as a function of pump–probe delay. For clarity, we show averages over size intervals instead of displaying data for all ∼200 individual cluster sizes. n̅ indicates the size at the center of each interval. The gray shaded area indicates the case of a purely impulsive signal which follows the IRF, here recorded for residual O2 gas.

At zero time delay, I(n,0 fs) is 1 by definition for all cluster sizes (Figure 4a and eq 3). For clusters with n < 14 (represented by (H2O)3–4 in Figure 4a, blue circles), I(n,Δt) decreases with increasing Δt, approaching zero (within the uncertainty; see typical error bar) for Δt longer than the width of the IRF, FWHMIRF. In the smallest clusters, longer-lived electrons that could be ionized by the probe pulse (4.7 eV)—here presolvated and solvated electrons—either never form or decay on time scales faster than the IRF. The term presolvated electron is used here for electrons that have been ejected from the molecule but not yet substantially localized, while the term solvated electron comprises electrons at all stages of different degrees of solvation (see the Discussion for details). Clear signals of such longer-lived electrons are only found for clusters with n ≳ 14, for which I(n,Δt) first increases on the time scale of the IRF and then continuously decreases with Δt on a 100 fs to ps time scale. In particular, I(n,Δt) increases systematically with increasing cluster size at all Δt > FWHMIRF; that is, the yield of longer-lived electrons per molecule is systematically higher in larger than in smaller clusters.

The results from the fits (colored lines in Figure 4) with the two-step sequential model (eq 2) reproduce the experimental data well. These fit results (full lines) are also shown in Figure 5 for two examples ((H2O)17–24 and (H2O)151–195) together with the impulsive component (dashed-dotted yellow line) and the two decay components (blue and green dashed lines). The refined fitted amplitudes, PIRF, Pa, and Pc and decay time τa, which now depend explicitly on the cluster size, are shown in Figures 4b and 4c, respectively, as a function of n̅. The behavior of Pa essentially reflects the above-mentioned increase of I(n,Δt) with increasing cluster size; that is, the observation that the yield of longer-lived electrons per molecule is higher in larger than in smaller clusters. The evolution of Pa reveals that this increase is pronounced for clusters with ∼14 < n < ∼50, while it levels off within the uncertainty for clusters above this size. For n ≲ 14, Pa is zero within the uncertainty; that is, no longer-lived electrons are detected for these smallest clusters (see also Figure 4a). τa systematically increases with cluster size, although this increase barely exceeds the typical uncertainty. An increase of τa indicates that the dominant processes that cause depletion of the normalized signal on the 100 fs to ps time scale slow down with increasing cluster size.

Figure 5.

Figure 5

Open in a new tab

Time-dependent normalized ion yield I(n,Δt) (circles) with fit results (black line) from the sequential kinetic model with two decay components (blue and red dashed lines) and an impulsive component (yellow dashed-dotted line) for the cluster size interval (a) 17 ≤ n ≤ 24 and (b) 151 ≤ n ≤ 195. In both panels, the abscissa is linear up to 0.6 ps (vertical line) and logarithmic for longer times.

4. Discussion

How can this cluster-size dependence be interpreted? At an excitation energy of 7.8 eV, it has been suggested that solvated electrons are generated by water dissociation and proton and electron transfer processes after one-photon absorption into the 1B1 (Ã) excited state.37−39,62,73,74 These processes and electron localization likely occur on the time scale of the IRF.15,25,30,31,34,42,51,72−74 The presolvated electrons further relax by fast and slow solvent rearrangement on time scales around 200–300 fs and 1–2 ps, respectively (see Table 1 in ref (51)), resulting in ground-state solvated electrons. The 1B1 state and all the different types of presolvated and solvated electrons can be ionized by the probe laser and thus contribute to the ion signal. The contribution of each species depends on its abundance and its ionization cross section. Other processes such as rapid H ejection from the clusters and fast recombination of electron and hole cannot contribute to the ion signal because the probe laser has not enough energy to ionize the resulting species. These loss processes can only decrease the ion signal. All these processes are expected to depend on cluster size (vide infra).

The orbital size of the 1B1 state and the electron ejection/delocalization length at a photon energy of 7.7 eV lie around ⟨r0⟩ ∼ 0.5 nm.8,39,53,75 ⟨r0⟩ exceeds the radii of the smallest clusters with n ≲ 14 (r = 0.24–0.46 nm) and becomes smaller than the radii of clusters with 25 < n < 195 (r = 0.56–1.11 nm). In the smallest clusters (n ≲ 14), electron localization (at the surface or in the interior of the cluster) is likely negligible because electron scattering is ineffective due to the large extent of the electron cloud compared with the cluster size and the relatively small number of degrees of freedom in these clusters. Furthermore, such small clusters offer only a few suitable localization sites—if any at all. The loss processes, by contrast, are expected to be very effective in the smallest clusters. In fact, for excitation of small neutral water clusters (n ≤ 10) at 7.8 eV, Liu et al.66 reported that H ejection is the dominant pathway with proton transfer and other mechanisms contributing only 10% in the smallest clusters and up to 15% for n = 10. Fast electron–hole recombination might also contribute substantially to the loss in clusters where electron delocalization lengths exceed the cluster size. Such fast recombination processes differ from the (much slower) diffusive recombination primarily by the incomplete separation between hole (ion core in the cluster) and electron. This is the result of confinement in clusters that are small compared with the ejection/delocalization length so that incomplete shielding of opposite charges and finite overlap between electron and hole wave functions facilitate recombination. The resulting very low probability of electron solvation together with the occurrence of highly efficient loss processes is in agreement with our experimental observations in Figure 4a, that is, with the fact that essentially no longer-lived solvated electrons are formed in clusters with n ≲ 14. Interestingly, near-zero kinetic energy electron attachment to neutral water clusters leads to a similar critical size of n ≥ 11 to observe the solvated electron in anions (H2O)n–.76,77

Following the same line of argument, it also appears reasonable that per molecule more longer-lived solvated electrons are observed with increasing cluster size (Figure 4a; note that the normalized ion yield is proportional to the ion yield per molecule as explained in section 3.3, eq 3). Together with the number of degrees of freedom, both the effectiveness of electron scattering and the number of suitable localization sites should rapidly increase with cluster size. Then it is not surprising either that this increase is most pronounced when the cluster size becomes comparable to the delocalization length. This is the case for clusters containing a few ten molecules and might explain the particularly pronounced increase of Pa for clusters with 14 ≲ n ≲ 50 seen in Figure 4b. In addition, the loss channels become less important (H ejection) or slow down (recombination) with increasing cluster size. While the dissociation of a water OH bond is hardly affected by the cluster size, H ejection from the cluster is increasingly less likely the larger the clusters become. If the H atom is retained in the cluster, OH bond dissociation is not any more necessarily a loss process, since intracluster H atom chemistry can lead to the formation of solvated electrons by reaction of the H atom with H2O molecules (producing solvated electrons and hydronium ions).39 At the same time, recombination should also slow down as the spatial confinement relaxes and the (dielectric) shielding of opposite charges improves with increasing cluster size (larger electron–hole separation). A slowing down of the loss processes is consistent with the increase in the decay constant τa (Figure 4c). The increase in the probability of solvated electron formation together with the slowing down of the loss processes also explains why per molecule more longer-lived solvated electrons are observed with increasing cluster size for clusters with n ≳ 14 (Figure 4a; note that the normalized ion yield is proportional to the ion yield per molecule as explained in section 3.3, eq 3).

As mentioned above, different types of solvated electrons could have different ionization cross sections (probe laser 4.7 eV). Cluster-size-dependent abundances of those species could then leave their trace in the size-resolved ion yield curves. The relevance of this phenomenon is, however, difficult to assess conclusively—in particular without further knowledge on species-dependent ionization cross sections. For water anion clusters with n ≲ 200, surface-solvated and partially embedded electrons were observed, with partially embedded clusters prevailing for sizes with n ≳ 40.78,79 Surface-solvated electrons have not been identified for neutral water clusters with n ≳ 200,50,51 and it is yet unknown whether such surface species occur at all in smaller neutral clusters. If surface species existed and if surface and embedded electrons had substantially different ionization cross sections, they could in principle contribute to the normalized ion yield in Figure 4a. However, it appears unlikely that such surface effects would dominate over the above-mentioned electron formation and loss processes in determining the observed trends in the normalized ion yield. Furthermore, even if the solvent relaxation dynamics itself depended on the cluster size (which we cannot exclude a priori), this dependence would have to be very pronounced, and the ionization cross sections of different species formed during the relaxation process would have to differ substantially to influence the normalized ion yield significantly. This does not appear very plausible. On the contrary, the only minor changes in the vertical binding energy observed beyond about 250–500 fs suggest that the species occurring along the relaxation path are rather similar, presumably with similar ionization cross sections as well.50,51 Thus, even if the relaxation dynamics depended pronouncedly on cluster size, this would not reflect in a pronounced change of the ion yield. From these considerations, we expect only a subtle influence of solvent relaxation processes on the normalized ions yields and thus on the observed dynamics.

5. Conclusions

We have employed pump–probe time-of-flight mass spectrometry to study cluster-size resolved dynamics of solvated electrons in water clusters with n < 200 molecules, after below band gap excitation at 7.8 eV photon energy into the 1B1 excited state. The observed ultrafast dynamics is likely dominated by cluster-size-dependent formation and loss processes of the solvated electron. Though it is plausible that the fraction of surface-solvated and embedded solvated electrons and solvent relaxation dynamics also depend on the cluster size, it appears unlikely that the ionization cross sections of those species differ sufficiently to observe such effects in the present ion yield experiments.

In clusters below a minimum size of n ∼ 14, solvated electrons cannot be sustained in any detectable amount. This can be explained by the large spatial extent of the excited-state electron cloud of the 1B1 state compared with the cluster size together with the relatively small number of degrees of freedom in these clusters. As a result, inelastic electron scattering, which is required for the electron to localize, is ineffective and the number of available localization sites is low, while loss processes, such as ultrafast H ejection from the clusters after OH bond dissociations and electron–hole recombination with the counterion, are highly efficient and thus dominate.

In larger water clusters, by contrast, the comparison of time-dependent ion yields with previously recorded electron yields reveals that solvated electrons are generated and sustained over many picoseconds. The yield of longer-lived (>100–200 fs) solvated electrons per molecule increases systematically with increasing cluster size. This can be explained as the result of a combination of size-dependent processes: The rapidly increasing number of degrees of freedom in clusters with n ≳ 14 increases the number of available localization sites and the effectiveness of inelastic electron scattering, resulting in a higher probability of solvated electron formation. At the same time, the effectiveness of the loss processes decreases with increasing cluster size: H ejection from the cluster becomes less likely and electron–hole recombination slows down as the confinement relaxes.

Acknowledgments

We thank Christopher W. West for help with the sequential dynamics model. We thank David Stapfer and Markus Steger for technical support. This project has received funding from the European Union’s Horizon 2020 research and innovation program from the European Research Council under the Grant Agreement No. 786636, and the research was supported by the NCCR MUST, funded by the Swiss National Science Foundation (SNSF), through ETH-FAST, and through SNSF project no. 200020_200306. R.S. is a grateful recipient of a Humboldt Research Prize from the Alexander von Humboldt Foundation and a Mildred Dresselhaus Guestprofessorship from the Centre for Ultrafast Imaging in Hamburg.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpca.1c03631.

  • Additional details on the experiment and data analysis (PDF)

The authors declare no competing financial interest.

Notes

Data required to reproduce the results presented in the paper can be found in the open access data collection of ETHZ at 10.3929/ethz-b-000485019.

Special Issue

Published as part of The Journal of Physical Chemistry virtual special issue “Daniel Neumark Festschrift”.

Supplementary Material

jp1c03631_si_001.pdf (721.2KB, pdf)

References

  1. Yamamoto Y.; Suzuki Y.-I.; Tomasello G.; Horio T.; Karashima S.; Mitrić R.; Suzuki T. Time- and Angle-Resolved Photoemission Spectroscopy of Hydrated Electrons Near a Liquid Water Surface. Phys. Rev. Lett. 2014, 112 (18), 187603. 10.1103/PhysRevLett.112.187603. [DOI] [PubMed] [Google Scholar]
  2. Yamamoto Y.-I. I.; Karashima S.; Adachi S.; Suzuki T. Wavelength Dependence of UV Photoemission from Solvated Electrons in Bulk Water, Methanol, and Ethanol. J. Phys. Chem. A 2016, 120 (8), 1153–1159. 10.1021/acs.jpca.5b09601. [DOI] [PubMed] [Google Scholar]
  3. Elles C. G.; Jailaubekov A. E.; Crowell R. A.; Bradforth S. E. Excitation-Energy Dependence of the Mechanism for Two-Photon Ionization of Liquid H2O and D2O from 8.3 to 12.4eV. J. Chem. Phys. 2006, 125 (4), 044515. 10.1063/1.2217738. [DOI] [PubMed] [Google Scholar]
  4. Young R. M.; Neumark D. M. Dynamics of Solvated Electrons in Clusters. Chem. Rev. 2012, 112 (11), 5553–5577. 10.1021/cr300042h. [DOI] [PubMed] [Google Scholar]
  5. Chen X.; Bradforth S. E. The Ultrafast Dynamics of Photodetachment. Annu. Rev. Phys. Chem. 2008, 59 (1), 203–231. 10.1146/annurev.physchem.58.032806.104702. [DOI] [PubMed] [Google Scholar]
  6. Bragg A. E.; Verlet J. R. R. R.; Kammrath A.; Cheshnovsky O.; Neumark D. M. Electronic Relaxation Dynamics of Water Cluster Anions. J. Am. Chem. Soc. 2005, 127 (43), 15283–15295. 10.1021/ja052811e. [DOI] [PubMed] [Google Scholar]
  7. Griffin G. B.; Young R. M.; Ehrler O. T.; Neumark D. M. Electronic Relaxation Dynamics in Large Anionic Water Clusters: (H2O) n– and (D2O) n– (N = 25–200). J. Chem. Phys. 2009, 131 (19), 194302. 10.1063/1.3263419. [DOI] [PubMed] [Google Scholar]
  8. Savolainen J.; Uhlig F.; Ahmed S.; Hamm P.; Jungwirth P. Direct Observation of the Collapse of the Delocalized Excess Electron in Water. Nat. Chem. 2014, 6 (8), 697–701. 10.1038/nchem.1995. [DOI] [PubMed] [Google Scholar]
  9. Herbert J. M.; Coons M. P. The Hydrated Electron. Annu. Rev. Phys. Chem. 2017, 68 (1), 447. 10.1146/annurev-physchem-052516-050816. [DOI] [PubMed] [Google Scholar]
  10. Uhlig F.; Marsalek O.; Jungwirth P. Electron at the Surface of Water: Dehydrated or Not?. J. Phys. Chem. Lett. 2013, 4 (2), 338–343. 10.1021/jz3020953. [DOI] [PubMed] [Google Scholar]
  11. Casey J. R.; Schwartz B. J.; Glover W. J. Free Energies of Cavity and Noncavity Hydrated Electrons Near the Instantaneous Air/Water Interface. J. Phys. Chem. Lett. 2016, 7 (16), 3192–3198. 10.1021/acs.jpclett.6b01150. [DOI] [PubMed] [Google Scholar]
  12. Borgis D.; Rossky P. J.; Turi L. Electronic Excited State Lifetimes of Anionic Water Clusters: Dependence on Charge Solvation Motif. J. Phys. Chem. Lett. 2017, 8 (10), 2304–2309. 10.1021/acs.jpclett.7b00555. [DOI] [PubMed] [Google Scholar]
  13. Horio T.; Shen H.; Adachi S.; Suzuki T. Photoelectron Spectra of Solvated Electrons in Bulk Water, Methanol, and Ethanol. Chem. Phys. Lett. 2012, 535, 12–16. 10.1016/j.cplett.2012.03.051. [DOI] [Google Scholar]
  14. Coons M. P.; You Z. Q.; Herbert J. M. The Hydrated Electron at the Surface of Neat Liquid Water Appears to Be Indistinguishable from the Bulk Species. J. Am. Chem. Soc. 2016, 138 (34), 10879–10886. 10.1021/jacs.6b06715. [DOI] [PubMed] [Google Scholar]
  15. Stähler J.; Deinert J.-C. C.; Wegkamp D.; Hagen S.; Wolf M. Real-Time Measurement of the Vertical Binding Energy during the Birth of a Solvated Electron. J. Am. Chem. Soc. 2015, 137 (10), 3520–3524. 10.1021/ja511571y. [DOI] [PubMed] [Google Scholar]
  16. Sagar D. M.; Bain C. D.; Verlet J. R. R. Hydrated Electrons at the Water/Air Interface. J. Am. Chem. Soc. 2010, 132 (20), 6917–6919. 10.1021/ja101176r. [DOI] [PubMed] [Google Scholar]
  17. Nowakowski P. J.; Woods D. A.; Verlet J. R. R. Charge Transfer to Solvent Dynamics at the Ambient Water/Air Interface. J. Phys. Chem. Lett. 2016, 7 (20), 4079–4085. 10.1021/acs.jpclett.6b01985. [DOI] [PubMed] [Google Scholar]
  18. Elkins M. H.; Williams H. L.; Neumark D. M. Isotope Effect on Hydrated Electron Relaxation Dynamics Studied with Time-Resolved Liquid Jet Photoelectron Spectroscopy. J. Chem. Phys. 2016, 144 (18), 184503. 10.1063/1.4948546. [DOI] [PubMed] [Google Scholar]
  19. Riley J. W.; Wang B.; Woodhouse J. L.; Assmann M.; Worth G. A.; Fielding H. H. Unravelling the Role of an Aqueous Environment on the Electronic Structure and Ionization of Phenol Using Photoelectron Spectroscopy. J. Phys. Chem. Lett. 2018, 9 (4), 678–682. 10.1021/acs.jpclett.7b03310. [DOI] [PubMed] [Google Scholar]
  20. Coe J. V.; Arnold S. T.; Eaton J. G.; Lee G. H.; Bowen K. H. Photoelectron Spectra of Hydrated Electron Clusters: Fitting Line Shapes and Grouping Isomers. J. Chem. Phys. 2006, 125 (1), 014315. 10.1063/1.2212415. [DOI] [PubMed] [Google Scholar]
  21. Ma L.; Majer K.; Chirot F.; Von Issendorff B. Low Temperature Photoelectron Spectra of Water Cluster Anions. J. Chem. Phys. 2009, 131 (14), 144303. 10.1063/1.3245859. [DOI] [PubMed] [Google Scholar]
  22. Ehrler O. T.; Neumark D. M. Dynamics of Electron Solvation in Molecular Clusters. Acc. Chem. Res. 2009, 42 (6), 769–777. 10.1021/ar800263z. [DOI] [PubMed] [Google Scholar]
  23. Lietard A.; Verlet J. R. R. R. Selectivity in Electron Attachment to Water Clusters. J. Phys. Chem. Lett. 2019, 10 (6), 1180–1184. 10.1021/acs.jpclett.9b00275. [DOI] [PubMed] [Google Scholar]
  24. Faubel M.; Siefermann K. R.; Liu Y.; Abel B. Ultrafast Soft X-Ray Photoelectron Spectroscopy at Liquid Water Microjets. Acc. Chem. Res. 2012, 45 (1), 120–130. 10.1021/ar200154w. [DOI] [PubMed] [Google Scholar]
  25. Turi L.; Rossky P. J. Theoretical Studies of Spectroscopy and Dynamics of Hydrated Electrons. Chem. Rev. 2012, 112 (11), 5641–5674. 10.1021/cr300144z. [DOI] [PubMed] [Google Scholar]
  26. Kambhampati P.; Son D. H.; Kee T. W.; Barbara P. F. Solvation Dynamics of the Hydrated Electron Depends on Its Initial Degree of Electron Delocalization. J. Phys. Chem. A 2002, 106 (10), 2374–2378. 10.1021/jp014291p. [DOI] [Google Scholar]
  27. Lian R.; Oulianov D. A.; Shkrob I. A.; Crowell R. A. Geminate Recombination of Electrons Generated by Above-the-Gap (12.4eV) Photoionization of Liquid Water. Chem. Phys. Lett. 2004, 398 (1–3), 102–106. 10.1016/j.cplett.2004.09.081. [DOI] [Google Scholar]
  28. Kratz S.; Torres-Alacan J.; Urbanek J.; Lindner J.; Vöhringer P. Geminate Recombination of Hydrated Electrons in Liquid-to-Supercritical Water Studied by Ultrafast Time-Resolved Spectroscopy. Phys. Chem. Chem. Phys. 2010, 12 (38), 12169. 10.1039/c0cp00762e. [DOI] [PubMed] [Google Scholar]
  29. Paik D. H.; Lee I. R.; Yang D. S.; Baskin J. S.; Zewail A. H. Electrons in Finite-Sized Water Cavities: Hydration Dynamics Observed in Real Time. Science 2004, 306 (5696), 672–675. 10.1126/science.1102827. [DOI] [PubMed] [Google Scholar]
  30. Wilhelm J.; VandeVondele J.; Rybkin V. V. Dynamics of the Bulk Hydrated Electron from Many-Body Wave-Function Theory. Angew. Chem., Int. Ed. 2019, 58 (12), 3890–3893. 10.1002/anie.201814053. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Luckhaus D.; Yamamoto Y.; Suzuki T.; Signorell R. Genuine Binding Energy of the Hydrated Electron. Sci. Adv. 2017, 3 (4), e1603224 10.1126/sciadv.1603224. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Zeuch T.; Buck U. Sodium Doped Hydrogen Bonded Clusters: Solvated Electrons and Size Selection. Chem. Phys. Lett. 2013, 579, 1–10. 10.1016/j.cplett.2013.06.011. [DOI] [Google Scholar]
  33. West A. H. C.; Yoder B. L.; Luckhaus D.; Saak C. M.; Doppelbauer M.; Signorell R. Angle-Resolved Photoemission of Solvated Electrons in Sodium-Doped Clusters. J. Phys. Chem. Lett. 2015, 6 (8), 1487–1492. 10.1021/acs.jpclett.5b00477. [DOI] [PubMed] [Google Scholar]
  34. Pizzochero M.; Ambrosio F.; Pasquarello A. Picture of the Wet Electron: A Localized Transient State in Liquid Water. Chem. Sci. 2019, 10 (31), 7442–7448. 10.1039/C8SC05101A. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Siefermann K. R.; Liu Y.; Lugovoy E.; Link O.; Faubel M.; Buck U.; Winter B.; Abel B. Binding Energies, Lifetimes and Implications of Bulk and Interface Solvated Electrons in Water. Nat. Chem. 2010, 2 (4), 274–279. 10.1038/nchem.580. [DOI] [PubMed] [Google Scholar]
  36. Signorell R.; Yoder B. L.; West A. H. C. C.; Ferreiro J. J.; Saak C.-M. M. Angle-Resolved Valence Shell Photoelectron Spectroscopy of Neutral Nanosized Molecular Aggregates. Chem. Sci. 2014, 5 (4), 1283–1295. 10.1039/C3SC53423E. [DOI] [Google Scholar]
  37. Madsen D.; Thomsen C. L.; Thøgersen J.; Keiding S. R. Temperature Dependent Relaxation and Recombination Dynamics of the Hydrated Electron. J. Chem. Phys. 2000, 113 (3), 1126–1134. 10.1063/1.481891. [DOI] [Google Scholar]
  38. Bartels D. M.; Crowell R. A. Photoionization Yield vs Energy in H2O and D2O. J. Phys. Chem. A 2000, 104 (15), 3349–3355. 10.1021/jp9941460. [DOI] [Google Scholar]
  39. Crowell R. A.; Bartels D. M. Multiphoton Ionization of Liquid Water with 3.0–5.0eV Photons. J. Phys. Chem. 1996, 100 (45), 17940–17949. 10.1021/jp9610978. [DOI] [Google Scholar]
  40. Pépin C.; Goulet T.; Houde D.; Jay-Gerin J. P. Observation of a Continuous Spectral Shift in the Solvation Kinetics of Electrons in Neat Liquid Deuterated Water. J. Phys. Chem. A 1997, 101 (24), 4351–4360. 10.1021/jp970354l. [DOI] [Google Scholar]
  41. Loh Z.-H.; Doumy G.; Arnold C.; Kjellsson L.; Southworth S. H.; Al Haddad A.; Kumagai Y.; Tu M.-F.; Ho P. J.; March A. M.; et al. Observation of the Fastest Chemical Processes in the Radiolysis of Water. Science 2020, 367 (6474), 179–182. 10.1126/science.aaz4740. [DOI] [PubMed] [Google Scholar]
  42. Lan J.; Kapil V.; Gasparotto P.; Ceriotti M.; Iannuzzi M.; Rybkin V. V. Simulating the Ghost: Quantum Dynamics of the Solvated Electron. Nat. Commun. 2021, 12 (1), 766. 10.1038/s41467-021-20914-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Trabattoni A.; Colaizzi L.; Ban L.; Wanie V.; Saraswathula K.; Månsson E. P.; Rupp P.; Liu Q.; Seiffert L.; Herzig E. A.; et al. Photoelectron Spectroscopy of Large Water Clusters Ionized by an XUV Comb. J. Phys. Photonics 2020, 2 (3), 035007. 10.1088/2515-7647/ab92b1. [DOI] [Google Scholar]
  44. Forysinski P. W.; Zielke P.; Luckhaus D.; Corbett J.; Signorell R. Photoionization of Small Sodium-Doped Acetic Acid Clusters. J. Chem. Phys. 2011, 134 (9), 094314. 10.1063/1.3559464. [DOI] [PubMed] [Google Scholar]
  45. Lübcke A.; Buchner F.; Heine N.; Hertel I. V.; Schultz T. Time-Resolved Photoelectron Spectroscopy of Solvated Electrons in Aqueous NaI Solution. Phys. Chem. Chem. Phys. 2010, 12 (43), 14629–14634. 10.1039/c0cp00847h. [DOI] [PubMed] [Google Scholar]
  46. Buchner F.; Schultz T.; Lübcke A. Solvated Electrons at the Water-Air Interface: Surface versus Bulk Signal in Low Kinetic Energy Photoelectron Spectroscopy. Phys. Chem. Chem. Phys. 2012, 14 (16), 5837. 10.1039/c2cp23305c. [DOI] [PubMed] [Google Scholar]
  47. Shreve A. T.; Elkins M. H.; Neumark D. M. Photoelectron Spectroscopy of Solvated Electrons in Alcohol and Acetonitrile Microjets. Chem. Sci. 2013, 4 (4), 1633–1639. 10.1039/c3sc22063j. [DOI] [Google Scholar]
  48. Elkins M. H.; Williams H. L.; Shreve A. T.; Neumark D. M. Relaxation Mechanism of the Hydrated Electron. Science 2013, 342 (6165), 1496–1499. 10.1126/science.1246291. [DOI] [PubMed] [Google Scholar]
  49. Karashima S.; Yamamoto Y. I.; Suzuki T. Resolving Nonadiabatic Dynamics of Hydrated Electrons Using Ultrafast Photoemission Anisotropy. Phys. Rev. Lett. 2016, 116 (13), 137601. 10.1103/PhysRevLett.116.137601. [DOI] [PubMed] [Google Scholar]
  50. Gartmann T. E.; Ban L.; Yoder B. L.; Hartweg S.; Chasovskikh E.; Signorell R. Relaxation Dynamics and Genuine Properties of the Solvated Electron in Neutral Water Clusters. J. Phys. Chem. Lett. 2019, 10 (17), 4777–4782. 10.1021/acs.jpclett.9b01802. [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. Ban L.; West C. W.; Chasovskikh E.; Gartmann T. E.; Yoder B. L.; Signorell R. Below Band Gap Formation of Solvated Electrons in Neutral Water Clusters?. J. Phys. Chem. A 2020, 124 (39), 7959–7965. 10.1021/acs.jpca.0c06935. [DOI] [PMC free article] [PubMed] [Google Scholar]
  52. Svoboda V.; Michiels R.; LaForge A. C.; Med J.; Stienkemeier F.; Slavíček P.; Wörner H. J. Real-Time Observation of Water Radiolysis and Hydrated Electron Formation Induced by Extreme-Ultraviolet Pulses. Sci. Adv. 2020, 6 (3), eaaz0385 10.1126/sciadv.aaz0385. [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. Yamamoto Y.; Suzuki T. Ultrafast Dynamics of Water Radiolysis: Hydrated Electron Formation, Solvation, Recombination, and Scavenging. J. Phys. Chem. Lett. 2020, 11 (14), 5510–5516. 10.1021/acs.jpclett.0c01468. [DOI] [PubMed] [Google Scholar]
  54. Chang Y.-P.; Horke D. A.; Trippel S.; Küpper J. Spatially-Controlled Complex Molecules and Their Applications. Int. Rev. Phys. Chem. 2015, 34 (4), 557–590. 10.1080/0144235X.2015.1077838. [DOI] [Google Scholar]
  55. Bieker H.; Onvlee J.; Johny M.; He L.; Kierspel T.; Trippel S.; Horke D. A.; Küpper J. Pure Molecular Beam of Water Dimer. J. Phys. Chem. A 2019, 123 (34), 7486–7490. 10.1021/acs.jpca.9b06460. [DOI] [PubMed] [Google Scholar]
  56. Barnes J. V.; Beck M.; Hartweg S.; Luski A.; Yoder B. L.; Narevicius J.; Narevicius E.; Signorell R. Magnetic Deflection of Neutral Sodium-Doped Ammonia Clusters. Phys. Chem. Chem. Phys. 2021, 23 (2), 846–858. 10.1039/D0CP04647G. [DOI] [PubMed] [Google Scholar]
  57. Hartweg S.; Yoder B. L.; Garcia G. A.; Nahon L.; Signorell R. Size-Resolved Photoelectron Anisotropy of Gas Phase Water Clusters and Predictions for Liquid Water. Phys. Rev. Lett. 2017, 118 (10), 103402. 10.1103/PhysRevLett.118.103402. [DOI] [PubMed] [Google Scholar]
  58. Müller J. P.; Zhavoronkov N.; Hertel I. V.; Schulz C. P. Time-Resolved Excited State Energetics of the Solvated Electron in Sodium-Doped Water Clusters. J. Phys. Chem. A 2014, 118 (37), 8517–8524. 10.1021/jp502238c. [DOI] [PubMed] [Google Scholar]
  59. Schläppi B.; Ferreiro J. J.; Litman J. H.; Signorell R. Sodium-Sizer for Neutral Nanosized Molecular Aggregates: Quantitative Correction of Size-Dependence. Int. J. Mass Spectrom. 2014, 372, 13–21. 10.1016/j.ijms.2014.08.021. [DOI] [Google Scholar]
  60. Bobbert C.; Schütte S.; Steinbach C.; Buck U. Fragmentation and Reliable Size Distributions of Large Ammonia and Water Clusters. Eur. Phys. J. D 2002, 19 (2), 183–192. 10.1007/s10053-002-8868-2. [DOI] [Google Scholar]
  61. Yoder B. L.; Litman J. H.; Forysinski P. W.; Corbett J. L.; Signorell R. Sizer for Neutral Weakly Bound Ultrafine Aerosol Particles Based on Sodium Doping and Mass Spectrometric Detection. J. Phys. Chem. Lett. 2011, 2 (20), 2623–2628. 10.1021/jz201086v. [DOI] [Google Scholar]
  62. Gartmann T. E.; Hartweg S.; Ban L.; Chasovskikh E.; Yoder B. L.; Signorell R. Electron Scattering in Large Water Clusters from Photoelectron Imaging with High Harmonic Radiation. Phys. Chem. Chem. Phys. 2018, 20 (24), 16364–16371. 10.1039/C8CP02148A. [DOI] [PubMed] [Google Scholar]
  63. Even U. The Even-Lavie Valve as a Source for High Intensity Supersonic Beam. EPJ. Technol. Instrum. 2015, 2 (1), 17. 10.1140/epjti/s40485-015-0027-5. [DOI] [Google Scholar]
  64. Belau L.; Wilson K. R.; Leone S. R.; Ahmed M. Vacuum Ultraviolet (VUV) Photoionization of Small Water Clusters. J. Phys. Chem. A 2007, 111 (40), 10075–10083. 10.1021/jp075263v. [DOI] [PubMed] [Google Scholar]
  65. Bodi A.; Csontos J.; Kállay M.; Borkar S.; Sztáray B. On the Protonation of Water. Chem. Sci. 2014, 5 (8), 3057–3063. 10.1039/C4SC00791C. [DOI] [Google Scholar]
  66. Liu H. T.; Müller J. P.; Beutler M.; Ghotbi M.; Noack F.; Radloff W.; Zhavoronkov N.; Schulz C. P.; Hertel I. V. Ultrafast Photo-Excitation Dynamics in Isolated, Neutral Water Clusters. J. Chem. Phys. 2011, 134 (9), 094305. 10.1063/1.3556820. [DOI] [PubMed] [Google Scholar]
  67. Dong F.; Heinbuch S.; Rocca J. J.; Bernstein E. R. Dynamics and Fragmentation of van Der Waals Clusters: (H2O)n, (CH3OH)n, and (NH3)n upon Ionization by a 26.5eV Soft x-Ray Laser. J. Chem. Phys. 2006, 124 (22), 224319. 10.1063/1.2202314. [DOI] [PubMed] [Google Scholar]
  68. Litman J. H.; Yoder B. L.; Schläppi B.; Signorell R. Sodium-Doping as a Reference to Study the Influence of Intracluster Chemistry on the Fragmentation of Weakly-Bound Clusters upon Vacuum Ultraviolet Photoionization. Phys. Chem. Chem. Phys. 2013, 15 (3), 940–949. 10.1039/C2CP43098C. [DOI] [PubMed] [Google Scholar]
  69. Pimblott S. M. Independent Pairs Modeling of the Kinetics Following the Photoionization of Liquid Water. J. Phys. Chem. 1991, 95 (18), 6946–6951. 10.1021/j100171a040. [DOI] [Google Scholar]
  70. Goulet T.; Jay-Gerin J.-P. On the Reactions of Hydrated Electrons with OH· and H3O+. Analysis of Photoionization Experiments. J. Chem. Phys. 1992, 96 (7), 5076–5087. 10.1063/1.462751. [DOI] [Google Scholar]
  71. Thomsen C. L.; Madsen D.; Keiding S. R.; Thøgersen J.; Christiansen O. Two-Photon Dissociation and Ionization of Liquid Water Studied by Femtosecond Transient Absorption Spectroscopy. J. Chem. Phys. 1999, 110 (7), 3453–3462. 10.1063/1.478212. [DOI] [Google Scholar]
  72. Mozumder A. Conjecture on Electron Trapping in Liquid Water. Int. J. Radiat. Appl. Instrumentation. Part C. Radiat. Phys. Chem. 1988, 32 (2), 287–291. 10.1016/1359-0197(88)90200-7. [DOI] [Google Scholar]
  73. Signorell R. Electron Scattering in Liquid Water and Amorphous Ice: A Striking Resemblance. Phys. Rev. Lett. 2020, 124 (20), 205501. 10.1103/PhysRevLett.124.205501. [DOI] [PubMed] [Google Scholar]
  74. Michaud M.; Wen A.; Sanche L. Cross Sections for Low-Energy (1–100eV) Electron Elastic and Inelastic Scattering in Amorphous Ice. Radiat. Res. 2003, 159 (1), 3–22. 10.1667/0033-7587(2003)159[0003:CSFLEE]2.0.CO;2. [DOI] [PubMed] [Google Scholar]
  75. Christiansen O.; Nymand T. M.; Mikkelsen K. V. A Theoretical Study of the Electronic Spectrum of Water. J. Chem. Phys. 2000, 113 (18), 8101–8112. 10.1063/1.1316035. [DOI] [Google Scholar]
  76. Knapp M.; Echt O.; Kreisle D.; Recknagel E. Electron Attachment to Water Clusters under Collision-Free Conditions. J. Phys. Chem. 1987, 91 (10), 2601–2607. 10.1021/j100294a031. [DOI] [Google Scholar]
  77. Barnett R. N.; Landman U.; Cleveland C. L.; Jortner J. Surface States of Excess Electrons on Water Clusters. Phys. Rev. Lett. 1987, 59 (7), 811–814. 10.1103/PhysRevLett.59.811. [DOI] [PubMed] [Google Scholar]
  78. Barnett R. N.; Landman U.; Cleveland C. L.; Jortner J. Electron Localization in Water Clusters. II. Surface and Internal States. J. Chem. Phys. 1988, 88 (7), 4429. 10.1063/1.453801. [DOI] [Google Scholar]
  79. Herburger A.; Barwa E.; Ončák M.; Heller J.; Van Der Linde C.; Neumark D. M.; Beyer M. K. Probing the Structural Evolution of the Hydrated Electron in Water Cluster Anions (H2O)n-, n ≤ 200, by Electronic Absorption Spectroscopy. J. Am. Chem. Soc. 2019, 141 (45), 18000–18003. 10.1021/jacs.9b10347. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

jp1c03631_si_001.pdf (721.2KB, pdf)

Articles from The Journal of Physical Chemistry. a are provided here courtesy of American Chemical Society

RESOURCES