Validating model-based Bayesian integration using prior–cost metamers

Significance

Over the last decade, Bayesian modeling has emerged as a unified approach for capturing a wide range of behaviors such as perceptual illusions, cognitive decision making, and motor control. Despite its remarkable success, the Bayesian approach has been challenged by the issue of model identifiability; that is, the components of a Bayesian model (e.g., prior and cost function) are not uniquely determined by the behavior. Here, we create an experimental paradigm that provides a way to adjudicate whether and when humans build and use the internal models of priors and cost functions. Our work provides a path toward resolving the controversies surrounding the notion of the Bayesian brain.

Abstract

There are two competing views on how humans make decisions under uncertainty. Bayesian decision theory posits that humans optimize their behavior by establishing and integrating internal models of past sensory experiences (priors) and decision outcomes (cost functions). An alternative hypothesis posits that decisions are optimized through trial and error without explicit internal models for priors and cost functions. To distinguish between these possibilities, we introduce a paradigm that probes the sensitivity of humans to transitions between prior–cost pairs that demand the same optimal policy (metamers) but distinct internal models. We demonstrate the utility of our approach in two experiments that were classically explained by Bayesian theory. Our approach validates the Bayesian learning strategy in an interval timing task but not in a visuomotor rotation task. More generally, our work provides a domain-general approach for testing the circumstances under which humans explicitly implement model-based Bayesian computations.

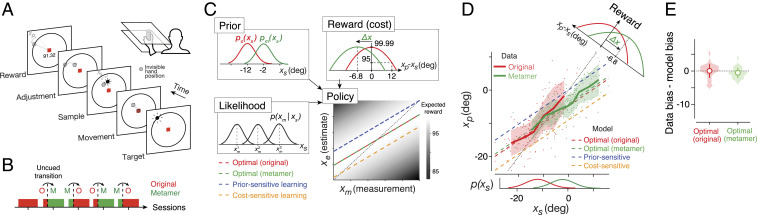
Bayesian decision theory (BDT) provides a normative framework for how to make optimal decisions under uncertainty (1–4). Imagine an agent whose decision has to be adjusted based on the state of the environment. According to BDT, the optimal decision policy can be computed from three sources of information (Fig. 1A): the prior probability distribution of the underlying state, the likelihood function of the state derived from noisy sensory evidence, and a cost (or reward) function that specifies possible decision outcomes. Optimal integration of these ingredients would enable the agent to maximize its expected reward (or minimize expected cost).

Fig. 1.

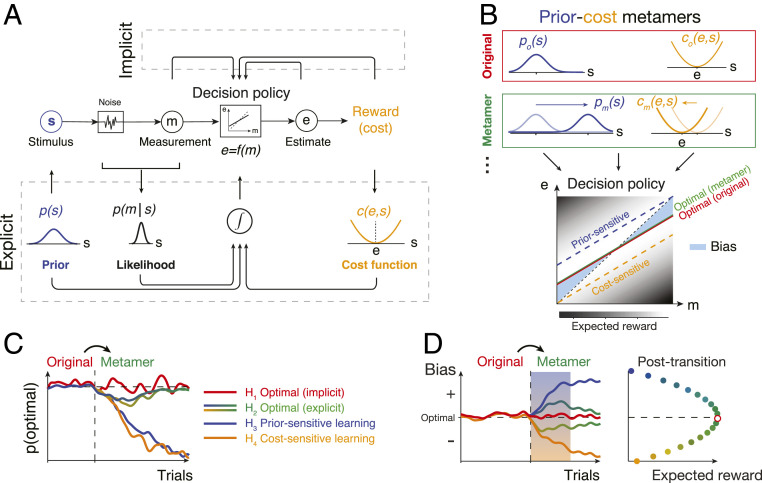
Testing Bayesian models of behavior using prior–cost metamers. (A) Ideal-observer model. An agent generates an optimal estimate (e) of stimulus (s) based on a noisy measurement (m). To do so, the agent must compute the optimal decision policy (rectangular box; e = f(m)) that maximizes expected reward. The decision policy can be computed using either an implicit (Top) or explicit (Bottom) learning strategy. In implicit learning, the policy is optimized through trial and error (e.g., model-free reinforcement learning) based on measurements and decision outcomes (arrows on top). In explicit learning, the agent derives the optimal policy by forming internal models for the stimulus prior probability, p(s), the likelihood of the stimulus after measurement, p(m|s), and the underlying cost function, c(e,s). (B) Prior–cost metamers are different p(s) and c(e,s) pairs that lead to the same decision policy. Red box: an original pair (subscript o) showing a Gaussian prior, p_o(s), and a quadratic cost function, c_o(e,s). Green box: a metameric pair (subscript m) whose Gaussian prior, p_m(s), and quadratic cost function, c_m(e,s), are suitably shifted to the right and left, respectively. (Bottom) The optimal decision policy (e = f(m)) associated with both the original (red) and metamer (green) conditions is shown as a line whose slope is less than the unity line (black dashed line; unbiased). The colored dashed lines show suboptimal policies associated with an agent that is only sensitive to the change in prior (blue) or only sensitive to the change in the cost function (orange). The policy is overlaid on a gray scale map that shows expected reward for various mappings of m to e. (C) Simulation of different learning models that undergo an uncued transition (vertical dashed line) from the original pair to its metamer. H₁ (implicit): after the transition, the agent continues to use the optimal policy associated with the original condition. Since this is also the optimal policy for the metamer, probability of behavior being optimal (SI Appendix, Eq. S16), p(optimal), does not change. H₂ (explicit): immediately after the transition, the agent has to update its internal model for the new prior and cost function. This relearning phase causes a transient deviation from the optimality (blue-to-green and yellow-to-green lines after the switch). After learning, the behavior becomes optimal since the optimal policy for the metamer is the same as the original. H₃ (prior sensitive): the agent only learns the new prior, which leads to a suboptimal behavior. H₄ (cost sensitive): same as H₃ for an agent that only learns the new cost function. (D) Same as C for the response biases as a behavioral metric. Similar to p(optimal) in C, bias of the implicit model (H₁) remains at the optimal level and expected reward remains at the maximum level (Right). The explicit model (H₂) shows transient deviation from the optimal bias (blue-to-green and yellow-to-green lines) and expected reward decreases (Right). Prior-sensitive and cost-sensitive models have opposite signs of biases and larger decrease in expected reward (Right).

BDT can capture human behavior in a variety of domains including perception (5–10), sensorimotor function (11–14), multimodal integration (15–18), and high-level cognitive function (19–21). Based on the remarkable success of BDT, it has been proposed that the brain performs Bayesian computations by explicitly representing the sensory likelihood, prior knowledge, and cost function (22–26).

However, the notion of the Bayesian brain is fiercely debated (27–29). Some proponents have taken the strong view that the brain has distinct representations of the likelihood, prior, and cost function (22, 24, 30), while many others remain agnostic about the underlying mechanism (31–33). Critics argue that the success of Bayesian models is unsurprising given the degrees of freedom researchers have in choosing the prior distribution, likelihood function, and cost function. The crux of the disagreement is about the value of formulating the optimization process in terms of a specific prior distribution and a specific cost function given that learning these components is not essential for learning the optimal policy (22, 34, 35). A perfectly reasonable alternative (Fig. 1A) is that humans use trial-by-trial observations to incrementally arrive at the optimal solution without explicit reliance on the prior distribution and/or cost function (36–40). Moreover, from a theoretical perspective, the choice of the prior and cost function is not unique. For example, an optimal agent may choose an option more frequently either because it is more probable or because it is more rewarding. More generally, in decision-making tasks, there are usually numerous pairs of priors and cost functions that, when combined, could lead to indistinguishable decision policies (Fig. 1B). Analogous to the notion of metamers in perception (41–43), we will refer to such pairs of priors and cost functions as prior–cost metamers. Because of the existence of such metamers, it remains an important and unresolved question whether decisions are made based on independently learned priors and cost functions.

Here, we turn the problem of prior–cost metamers on its head to develop a general experimental strategy to test whether human decisions rely on independently learned priors and cost functions. The key idea behind our approach is to ask whether human behavior in a decision-making task exhibits signs of relearning when we covertly switch from one prior–cost pair to another pair that is associated with exactly the same optimal decision policy (Fig. 1 C and D for model simulation). According to BDT, optimal behavior depends on having learned the prior and cost function independently. Under this model-based hypothesis, changing to a new pair would lead to a transient change in decision policy until the observer relearns the new pair (“explicit” in Fig. 1 C and D). Alternatively, if the optimal behavior were to emerge through trial and error without learning the prior and cost, then the observer should show no sensitivity to the switch and the behavior should remain optimal (“implicit” in Fig. 1 C and D). We applied this approach to two tasks—a time-interval reproduction task (44, 45) and a visuomotor rotation (VMR) task (11)—both of which were classically explained in terms of BDT. Our results substantiated the role of independently learned priors and cost functions in the timing task but not in the VMR task. Accordingly, future behavioral studies can take advantage of our approach based on metamers to rule out the possibility of non-Bayesian strategies in Bayesian-looking behaviors (37, 46).

Results

Although we can use Newton’s Laws to explain how an apple falls from a tree, we would not conclude that the apple “implements” Newton’s Laws. In the same vein, the fact that we can explain a person’s behavior in terms of the BDT does not necessarily mean that their brain relies on explicit representations of priors and cost functions. Here, we develop an experimental approach to investigate whether Bayesian computations rely on explicit knowledge about priors and cost functions. We explore this question in the context of two behavioral tasks, a time-interval reproduction task and a VMR task. Previous work has shown that human behavior in both tasks is nearly optimal and can be explained in terms of integrating priors and cost functions (11, 44). Here, we test whether optimal performance in these tasks can indeed be attributed to explicit reliance on priors and cost functions.

Our experimental approach for both tasks is the same. We start the experiment with a specific choice of prior and cost function; after performance saturates, we covertly switch to a prior–cost metamer associated with the same optimal policy. The key question we ask is whether the behavior immediately after the switch reflects any sign of transient relearning of the new prior–cost pair. Under one hypothesis (H₁, Fig. 1 C and D), the optimal behavior emerges through trial and error without explicit learning of the prior and cost (e.g., model-free reinforcement learning [RL]). We will refer to this strategy as implicit learning since the optimality does not rely on an explicit model of the prior and/or cost. This hypothesis predicts that behavior shows no sensitivity to the switch and remains optimal because the optimal policy is the same as the one associated with the originally learned prior–cost pair. Under another hypothesis (H₂), optimal behavior depends on learning the prior and cost as prescribed by the BDT. We will refer to this strategy as explicit learning since the agent has to build an internal model for the prior and cost. This hypothesis predicts that the behavior transiently deviates from optimality while the new prior and cost are being learned, but the asymptotic behavior would be optimal, as H₁. For comparison, we will also test two additional hypotheses, one in which the behavior is assumed to be solely sensitive to the prior (H₃) and one in which the behavior is assumed to be solely sensitive to the cost function (H₄). These hypotheses provide an informative benchmark to examine whether participants exhibit differential sensitivity to the prior or cost function.

Time-Interval Reproduction Task: Ready-Set-Go.

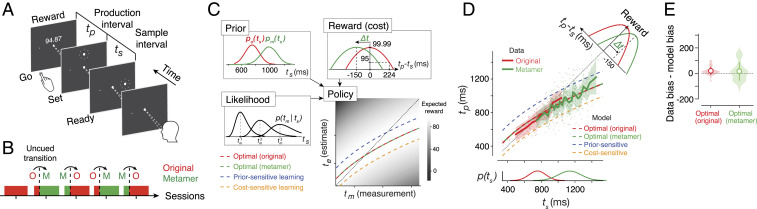
In the Ready-Set-Go (RSG) task (Fig. 2A), participants measure a time interval between the first two beats of an isochronous rhythm (“Ready” and “Set” flashes) and are asked to press a button at the expected time of the third omitted beat (“Go”). We refer to the sample interval between Ready and Set as t_s and the production interval between Set and Go as t_p. We evaluated performance in RSG by what we refer to as a “metronomic function,” which quantifies t_p as a function of t_s. On each trial, t_s is sampled from a prior probability distribution, and participants receive graded numeric feedback as reward (R) depending on the absolute error between t_p and t_s. We set the value of R according to a truncated quadratic function with a maximum of 100 and a minimum of 0 (Fig. 2C). We will use the terms reward and cost function interchangeably to refer to the functional relationship between R and error (t_p – t_s).

Fig. 2.

Prior–cost metamers in the RSG task. (A) Time-interval reproduction task (“Ready-Set-Go”). While looking at a central spot, participants measure a sample interval (t_s) demarcated by two flashes (Ready and Set) and initiate a delayed button press (Go) to produce a matching interval (t_p) immediately after Set. At the end of each trial, participants received a numerical score whose value was determined by a cost/reward function (see panel C). (B) Experimental sessions. In the first session that served as a baseline, participants performed the task with the original prior–cost set (“O”). In the subsequent four sessions, we introduced an uncued transition between the original and metamer (“M”) in an alternating fashion. In these sessions, the pre- and posttransition included ∼170 and ∼500 trials, respectively. In all panels, we use red for the original condition and green for the metamer. (C) Prior–cost metamers. (Top Left) The original prior, p_o(t_s), is a Gaussian distribution (mean: 750 ms, SD: 144 ms) and its metamer, p_m(t_s), is a mixture of Gaussian distribution (see Materials and Methods). (Top Right) Reward (or cost) function is an inverted quadratic function of the error, t_p − t_s, that is truncated to have only positive values. The original cost function is centered at zero error, and the metamer is the same function shifted by ∆t. (Bottom Left) The likelihood function for t_s based on noisy measurement, t_m, denoted p(t_m|t_s). The likelihood function is asymmetric and broader for longer t_s because measurement noise is assumed to scale with t_s. (Bottom Right) The optimal policy function that prescribes how an ideal observer should derive an estimate, t_e, from t_m. By design, the optimal policy for the original (H₁) and metamer (H₂) are identical. The plot also shows suboptimal policies for a prior sensitive (blue; H₃) and cost sensitive (orange; H₄) overlaid on a gray scale map showing average expected reward for different mapping of t_m to t_e. When the original pair switches to its metamer, H₃ and H₄ predict positive and negative offsets, respectively, relative to the optimal policy. (D) Data from a representative session showing t_p as a function of t_s (dots: individual trials; solid lines: running average across trials; shaded area: SEM). Prediction from H₁ to H₄ are shown in the same format as C. (Bottom) The original and metamer priors. (Top Right) The original and metamer cost functions. (E) Bias in the original and metamer contexts. Violin plot showing the difference between the observed and optimal bias across all participants and all sessions with transitions (n = 40; shaded region: distribution; open circles: grand averages; error bars: SD). Bias was computed as the root-mean-squared difference between running average of t_p and t_s.

Before analyzing the participants’ behavior, we characterized the predictions of various hypotheses regarding behavior in the context of two metameric pairs. Under both H₁ (implicit) and H₂ (explicit), the behavior is expected to be asymptotically optimal (i.e., after learning). We determined the form of the optimal policy by characterizing the behavior of an ideal observer performing the RSG task. An ideal observer integrates the likelihood function associated with the measured interval (t_m) with the prior and the cost function to derive an optimal estimate (t_e) that maximizes expected reward. This Bayes-optimal integration manifests as a nonlinear relationship between t_e and t_m (Fig. 2 C, Bottom Right). Accordingly, the t_p values for a participant that employs an optimal strategy should exhibit characteristic biases toward the mean of the prior. At first glance, the bias in the optimal policy may seem counter intuitive. However, biasing responses in this way reduces the variance of responses such that the performance improvement due to reduced variance is larger than the performance drop due to the addition of biases. We also predicted the behavior for the prior-sensitive (H₃) and cost-sensitive (H₄) hypotheses after the switch to its metamer. According to H₃, t_p values should exhibit an overall positive bias toward longer intervals. In contrast, under H₄, t_p values should exhibit an overall negative bias. Moreover, since both hypotheses are suboptimal, they predict an overall drop in expected reward.

Next, we collected data from 11 participants performing the RSG task in the context of two distinct metameric prior–cost pairs across five daily sessions (Fig. 2B). In the first session, participants performed the task under the “original” pair, which consisted of a Gaussian prior distribution and a cost function that was centered at zero error, when t_p = t_s (Fig. 2C, red). For the original pair, participants’ t_p increased with t_s and exhibited systematic biases toward the mean of the prior (Fig. 2D, red). Similar to numerous previous studies (44, 45, 47–50), this behavior was consistent with predictions of the ideal-observer model (SI Appendix, Fig. S1).

Our goal for the subsequent four sessions was to test participants’ behavior after a covert switch between the original pair and its metamer. To design the metamer (green in Fig. 2C), we used the same truncated quadratic form for the cost function but shifted it by −150 ms (Δt) such that the maximum value of R was now associated with responding 150 ms earlier than the third beat (t_p = t_s − 150 ms). Next, we designed the metameric prior. Intuitively, the new prior has to be shifted in the positive direction to counter the negative shift in the cost function and lead to the same decision policy. However, to achieve a perfect metamer, the new prior cannot be Gaussian (see Materials and Methods). We modeled the new prior as a Gaussian mixture model (GMM) whose parameters were adjusted such that the integration of the GMM and shifted cost function produced the same optimal policy. Note that the exact form of the GMM depends on measurement noise level and was therefore customized for each participant independently (see Materials and Methods). For each subject, we verified that the optimal policy for the original and metamer were indeed the same (SI Appendix, Fig. S2).

Participants’ behavior in the context of the metamer showed similar biases toward the mean (Fig. 2D, green; reference SI Appendix, Fig. S2 for all subjects) and was asymptotically matched to that of the ideal observer (Fig. 2E, green; P = 0.137, t test for equal bias between data and optimal model). In other words, participants’ behavior during both the original and its metamer was captured by the same optimal policy. This finding is consistent with both the implicit (H₁) and explicit (H₂) learning strategy.

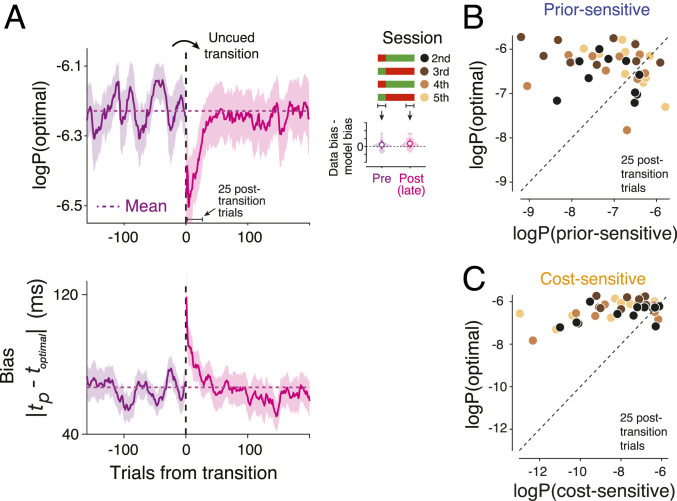
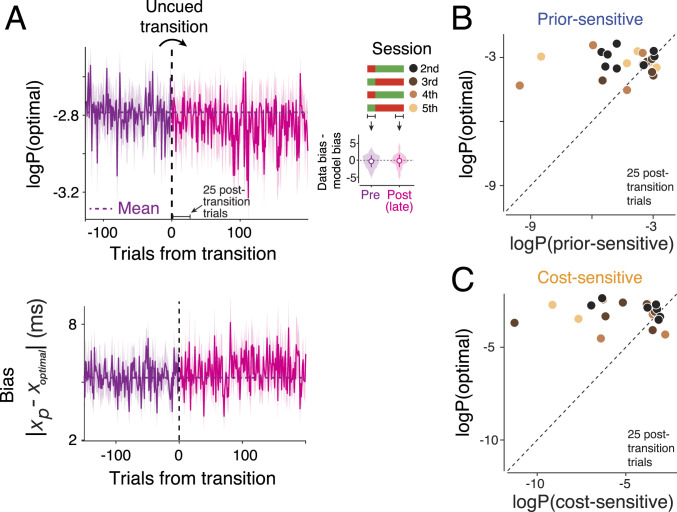
Our main interest, however, is to distinguish between the implicit (H₁) and explicit (H₂) learning strategies. Recall that any transient deviation from the behavior of an ideal observer after the switch would provide evidence against the implicit learning strategy of using the original policy (no relearning). Therefore, we estimated the log probability of behavioral data under the ideal-observer model before, immediately after, and long after the covert switch. As expected, the magnitude of bias across the participants was nearly matched to that of an ideal observer before the switch (Fig. 3 A, Right Inset). After the transition, the probability of data under the ideal-observer model dropped sharply and transiently (Fig. 3 A, Left) and within ∼50 trials, moved back to the pretransition level (nonparametric Friedman test for effect of transition on mean P (optimal policy) across [−25 to 0], [1 to 25], [26 to 50] trials with respect to the transition, P = 0.020; post hoc signed rank test for 25 trials before versus after the transition, P = 0.081; post hoc signed rank test for 1 to 25 trials versus 26 to 50 trials after the transition, P = 0.003). Note that the transient deviation from the ideal-observer behavior was small in comparison with what is expected from a purely prior-sensitive (H₃; Fig. 3B) or cost-sensitive (H₄; Fig. 3C) strategy.

Fig. 3.

Behavior immediately after the switch to a new prior–cost condition in the RSG task. (A) (Top) Log probability of the optimal policy, denoted “logP(optimal)” under the data across a few hundred trials before and after the transitions (vertical dashed line) averaged across subjects and sessions (n = 40; shaded area: SEM; purple: pretransition; magenta: posttransition; horizontal dotted line: log probability of the optimal policy averaged across 100 pretransition trials). Data from individual trials are smoothed using a causal Gaussian kernel (SD: 10 trials), separately for the pre- and posttransition. Twenty-five posttransition trials are also highlighted as a window of interest for later analyses. Legend on the right illustrates the alternating transitions between the original (red) and metamer (green) across four sessions. (Right Inset) The average difference between observed and optimal bias in the pre- and posttransition epochs plotted in the same format as Fig. 2E. Pretransition includes all trials before transition. Posttransition includes the last 200 trials (to avoid misestimation due to the transient). (Bottom) Response bias in the same format as logP(optimal). The bias was computed as the absolute difference between t_p and the optimal estimate (t_optimal = f^ideal(t_s); SI Appendix, Eq. S3) to better illustrate the time course of the transient suboptimality. (B) Comparison of the optimal policy, logP(optimal), with the suboptimal prior-sensitive policy, denoted logP(prior-sensitive), based on the data in the 25 posttransition trials across participants and sessions (n = 40; see legend in A). (C) Same as B for the cost-sensitive model.

We performed several control analyses to rule out alternative explanations for the transient deviation from optimal policy. First, it is possible that the transient deviation from optimality was due to the fact that participants experienced new t_s values after the prior was switched. We ruled out this possibility by analyzing only the trials whose t_s values overlapped with the distribution of t_s before the transition (SI Appendix, Fig. S3). Second, the suboptimal behavior after transition could be a manifestation of the nonlinear optimal policy. Specifically, if subjects were to linearly extrapolate from the learned optimal policy for the new t_s values after transition, we would expect their behavior to transiently deviate from the optimal nonlinear policy. Given the concave shape of the optimal policy in RSG (Fig. 2C), the linear extrapolation scheme predicts that subjects should consistently overestimate t_s; that is, behavior appears prior sensitive for the original-to-metamer transitions and cost sensitive for the metamer-to-original transitions (SI Appendix, Fig. S4). This was not consistent with data from individual subjects (see Fig. 5 C–E for examples), and further analyses of learning dynamics augur poorly for the plausibility of the extrapolation model (SI Appendix, Fig. S4).

Fig. 5.

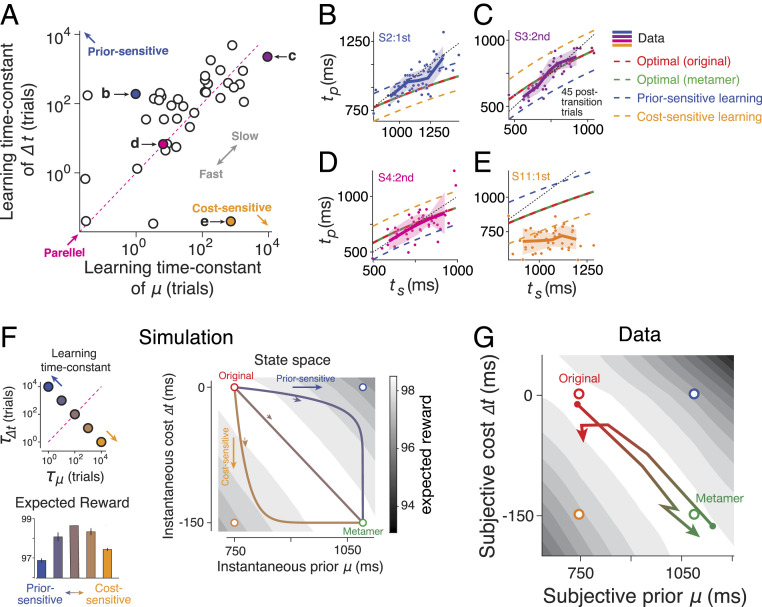
Parallel learning of prior and cost function and its computational consequences. (A) Learning time constant for adjusting the mean of the prior (μ) and the shift in the cost function (∆t) after prior–cost transitions. We inferred the learning time constants by fitting exponential curves to learning dynamics (Fig. 4). For many participants, the learning time constants were comparable as evident by the points near the unity line (“parallel,” magenta dotted line). Points above the unity line indicate faster adjustment for μ relative to ∆t, which is expected from a participant that is more prior sensitive (blue circle). Points below the unity line indicate faster adjustment for ∆t relative to μ, which is expected from a participant that is more cost sensitive (orange circle). Two outlier data points on the Top Right were not included in the plot (n = 40 across subjects and sessions). (B–E) Behavior of four example participants in the first 45 posttransition trials (dots: individual trials; solid line: average across bins; shaded region: SEM). The title of each plot indicates the participant (e.g., S2) as well as the session with transitions (e.g., “second”), and the colors correspond to the specific points in A. For each example, the predictions from various optimal and suboptimal models are also shown (legend). (F) Simulation with varying learning time constants. (Top Left) We selected five pairs of the learning time constants for μ and ∆t, indexed by the corresponding time constants, τ, and τ_Δt, respectively. The pairs ranged from faster prior learning (blue), to parallel learning (brown), to faster cost learning (orange). (Right) Learning trajectory of μ and ∆t for three example points in the Top Left (with the corresponding colors) during the transition from the original prior–cost set (red circle) to its metamer (green circle). Faster prior learning first moves the state toward the prior-sensitive model (open blue circle) and then toward the end point. Faster cost learning first moves the state toward the cost-sensitive model (open orange circle). When the learning time constants are identical (brown), the state moves directly from the original to the metamer. The gray scale color map shows expected reward as a function of μ and ∆t (SI Appendix, Eq. S19). (Bottom Left) Average reward along the learning trajectory for the points in the Top Left. Results correspond to the averages of 500 simulated trials (error bar: SEM). (G) Learning trajectories across participants based on average learning time constants in A shown separately while transitioning from original to metamer (red to green) and from metamer to original (green to red). Note that, on average, the expected reward (gray scale color map, same as F) remains high.

The transient deviation from optimality may also be a manifestation of subjects’ exploring new solutions after detecting changes in the stimuli and/or reward, much like bouts of exploration during an ε-greedy learning strategy (39). A key prediction from such “exploration” periods is an increase of variance. We tested this prediction by quantifying t_p variance after transitions and found no evidence of such increase (SI Appendix, Fig. S3). The idiosyncratic biases of subjects during learning were also inconsistent with random explorations. Specifically, some subjects were more sensitive to the change in prior, whereas others responded more rapidly to the change in the cost function (prior sensitive versus cost sensitive; see Fig. 5). These sensitivities are inconsistent with random explorations (SI Appendix, Fig. S3) and suggest instead that explorations about the prior and cost function were distinct and advanced independently. We also note that any explanation of the transient behavior in terms of increased explorations would need a mechanism for detecting covert changes in the prior and cost function. In theory, subjects could detect the change either by detecting the presence of new stimuli or by detecting a change in reward frequency. Detecting a change in the stimulus would only be possible if subjects already had a memory of past stimuli, which is equivalent to having a prior representation in the first place. Detecting a change in reward can be accomplished if subjects have a prior estimate of expected reward that they can use to compute reward prediction error (RPE) and initiate explorations. However, we already anticipated this possibility in our experimental design (see Materials and Methods) and adjusted the cost function to ensure that subjects did not experience any change in average expected reward during the transition. Finally, one could still argue that subjects use a representation of prior and cost to detect the change but then engage in a process of implicit learning. To test this “hybrid” model, we considered three RL models, a Q agent (51) with an action-value table, a Deep Q network (52), and a Deep Deterministic Policy Gradient algorithm (53). We trained these RL models on the original prior–cost pair and then examined their behavior after metameric transitions. To make these models as strong of a contender as possible, we assumed that they could detect transitions immediately.

After excessive training (see Materials and Methods), all three models were able to find the optimal policy for the original prior–cost through implicit learning (i.e., trial-and-error exploration; SI Appendix, Fig. S5). We then exposed the models for the transition assuming that they immediately detect the transition and start exploration. However, none of the models were able to capture the observed learning dynamics in data regardless of the choice of hyperparameters such as learning rate and exploration rate (SI Appendix, Fig. S5). Notably, the models were simply inadequate in terms of how fast they could reach back to the optimal policy (i.e., sample inefficient). Together, these results reject H₁ (implicit), H₃ (prior sensitive), and H₄ (cost sensitive) but not H₂ (explicit), suggesting that participants were sensitive to both the prior and cost function despite the metameric relationship between the prior–cost pairs before and after the switch.

Learning Dynamics of the Prior–Cost Metamer.

So far, we have established that participants were sensitive to transitions between prior–cost metamers, which suggests an underlying dynamic process for learning the new prior and cost function. To characterize this dynamic process, we sought to track the participants’ internal estimate of the prior and cost function during the learning process. To do so, we built an observer model in which the prior and cost function could change dynamically during learning. From a statistical (fitting) perspective, parameterizing the full prior distribution and cost function throughout learning is not feasible. We therefore built a simplified model in which the profile of the prior and cost function was the same as those associated with the original pair (i.e., Gaussian and quadratic, respectively). However, we allowed the mean (μ) and SD of the prior and the shift in the cost function (∆t) in the model to be determined dynamically based on the observed behavior. We will use “subjective prior” and “subjective cost function” to refer to μ and ∆t, respectively.

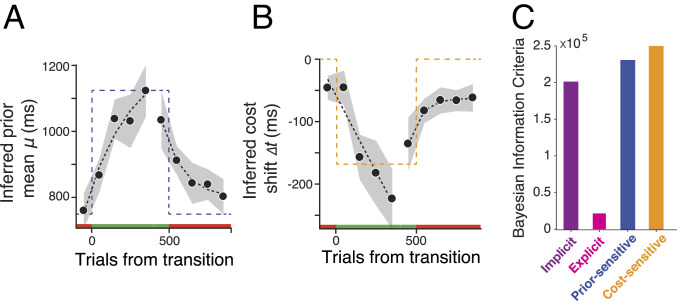
We fitted this observer model to each participant’s behavior using a running window of 100 trials and tracked the fits to subjective prior and cost function from before to after the transition. Across participants, μ and ∆t changed systematically and in accordance with the changes in the experimentally imposed prior and cost function (Fig. 4 A and B; reference SI Appendix, Fig. S6 for the SD of the prior). We also use Bayesian Information Criterion to evaluate the data with respect to the implicit (H₁), explicit (H₂), prior-sensitive (H₃), and cost-sensitive (H₄) hypotheses (Fig. 4C). Results provided clear evidence in support of the explicit hypothesis. Together, these analyses substantiate the presence of a dynamic learning process for the prior and cost function after the transition and provides an estimate of the underlying time course of learning in this task.

Fig. 4.

Time course of learning the new prior and cost function across subjects. (A and B) The inferred mean of the prior (μ) during two types of transitions between the original and metamer conditions (red and green above the abscissa). The mean was inferred from fits of an observer model to behavior in running windows of 100 trials at different time points before and after the transition (black circles: average across participants and sessions, n = 40; shades: SEM; black dotted line: exponential fit; dashed line: the experimentally imposed prior mean). (B) The inferred shift in the subjective cost function (Δt) during transitions between the original and metamer conditions shown with the same format as A. (C) Model comparison using Bayesian information criteria (BIC). The smaller BIC values indicate the better models.

One important observation from the learning dynamics was that the prior and cost function changed in parallel and at comparable speeds (Fig. 4 A and B). Indeed, fitting the learning curve for the prior and cost function with an exponential function led to comparable learning time constants (Fig. 5A; P = 0.42, signed rank test). To gain a deeper understanding of the computational consequences of this parallel learning, we performed a series of simulations in which we varied the learning time constant for the prior and cost function (Fig. 5F). The simulations indicated that when the prior learning was faster than the cost function, the behavior after the transition became more like the prior-sensitive model (H₃) and led to a reduction of expected reward. A higher learning rate for the cost function also reduced performance by causing the behavior to become more like the suboptimal cost-sensitive model (H₄). The best performance during transition was associated with cases when two learning time constants were comparable. This result provides a normative argument that it may be beneficial to have comparable learning time constants for the prior and cost.

To further explore the desiderata for optimal relearning, we estimated the expected reward in a state space (Fig. 5 F and G) comprised of the mean of the subjective prior (μ) and the shift in the cost function (∆t). As expected, when the subjective prior mean and cost shift match the objective values (original and metamer in Fig. 5 F and G), the expected reward is maximum. Any other point in the space would give rise to suboptimal reward amounts. However, we unexpectedly found a continuum of the prior–cost pairs that can achieve almost the maximum reward, in between the original and metamer sets we devised. Therefore, if the subjects learned the new prior and cost in parallel—that is, navigating the state space diagonally—the expected reward would not decrease as subjects remain in the continuous regime of the optimal reward. In contrast, the reward would decline rapidly as subjects sequentially update their internal prior or cost function.

One intriguing conclusion from these simulations is that when prior and cost learning are suitably coordinated, the behavior may remain optimal throughout the relearning process. In other words, a participant’s behavior may show no sign of learning (i.e., no deviation from ideal-observer model) even while they are in the process of learning the new prior and cost function. With this consideration in mind, we analyzed the behavior of individual participants asking whether such coordinated learning for the prior and cost function was evident in their behavior (Fig. 5 B–E). Results revealed a diversity of learning time constants for the prior and cost function ranging from relatively faster prior learning (Fig. 5B), to comparable learning time constants for the prior and cost function (Fig. 5 C and D), to faster cost learning (Fig. 5E). However, there was no systematic difference between the two time constants across participants (Fig. 5A).

The diversity of learning time constants for the prior and cost function across participants provides a coherent explanation for various findings that we originally found puzzling. First, it explains why we were able to infer the prior mean and the shift in the cost function across participants (Fig. 4 A and B). If the learning dynamics were identical across participants, we would have not been able to infer those dynamics because of the metameric relationship between the two conditions. Second, since the prior and cost learning time constants were comparable across participants, the deviation from the ideal-observer policy after prior–cost switches was small (Fig. 3A) compared with the prior-sensitive and cost-sensitive strategies (Fig. 3 B and C). Third, the parallel learning enables participants to maintain a steady performance after prior–cost switches (SI Appendix, Fig. S7).

VMR Task.

In the VMR task (Fig. 6A), participants use a manipulandum to move a cursor from the center of a visible ring to the remembered position of a target flashed briefly on the circumference of that ring. As soon as the cursor begins to move, we make the cursor invisible and change its angular position relative to the angular position of the hand by a rotation angle, x_s. While moving, the cursor reappears briefly (100 ms) when it is midway, which provides limited sensory information about x_s to the participants. On each trial, x_s was sampled from a Gaussian prior distribution (Fig. 6C), and a numerical feedback, R, was provided depending on the error between x_s and the corresponding correction, x_p, which we defined as the angle between the hand position and the target on the ring. We set the value of R according to a truncated quadratic function with a maximum of 100 and a minimum of 0 (Fig. 6C).

Fig. 6.

Prior–cost metamers in the VMR task. (A) VMR task. Participants move a manipulandum (vertical cylinder) to maneuver a cursor on a horizontal display (Top Right) from the center of the screen (red square) to a target flashed briefly on the circumference of a visible ring (“Target”: black circle on the ring). The moving cursor is occluded while moving except from a brief reappearance halfway along the path (“Sample”: black circle). The cursor position is covertly rotated by an angle (x_s) relative to the position of the hand (gray circle). Participants have to use x_s and apply a matching counterrotation (x_p) to bring the cursor to the target position (“Adjustment”). At the end of each trial, participants received a numerical score whose value was determined by a cost/reward function (see panel C). (B) Experimental sessions shown in the same format as Fig. 2B. (C) Prior–cost metamers shown in the same format as in Fig. 2C. (Top Left) The original prior, p_o(x_s), is a Gaussian distribution (mean: −12 deg, SD: 7.5 deg) and its metamer, p_m(x_s), is also a Gaussian distribution shifted by 10 deg (see Materials and Methods). (Top Right) Reward (or cost) function is an inverted quadratic function of the error, x_p − x_s, that is truncated to have only positive values. The original cost function is centered at zero error, and the metamer is the same function shifted by ∆x. (Bottom Left) The likelihood function for x_s based on noisy measurement, x_m, denoted p(x_m|x_s). (Bottom Right) The optimal policy function that prescribes how an ideal observer should derive an estimate, x_e, from x_m. By design, the optimal policy for the original (H₁) and metamer (H₂) are identical. The plot also shows suboptimal policies for a prior sensitive (blue; H₃) and cost sensitive (orange; H₄) overlaid on a gray scale map showing average expected reward for different mapping of x_m to x_e. H₃ and H₄ predict positive and negative offsets, respectively, relative to the optimal policy. (D) Data from a representative session showing x_p as a function of x_s shown in the same format as in Fig. 2D. (E) Bias in the original and metamer contexts (n = 36) in the same format as in Fig. 2E.

Similar to the RSG task, we characterized the predictions of various hypotheses regarding behavior in the context of two metameric pairs. Under the implicit (H₁) and explicit (H₂) learning strategies, the behavior is expected to be asymptotically optimal (i.e., after learning). We determined the form of the optimal policy by characterizing the behavior of an ideal observer that integrates the likelihood function based on a noisy measurement, x_m, with the prior and the cost function to derive an optimal estimate, x_e, that maximizes expected reward (Fig. 6C). With a Gaussian likelihood function, a Gaussian prior, and a quadratic cost function, the optimal policy is to map x_m to x_e linearly with a bias toward the mean (i.e., slope of less than 1; see Materials and Methods). Under the prior-sensitive (H₃) and cost-sensitive (H₄) hypotheses, x_p values would exhibit an overall positive and negative bias, respectively (Fig. 6C), and would lead to lower reward than expected under the optimal policy. Note that linearity of the optimal policy in the VMR task is due to the relatively simple form of the likelihood function (Gaussian with a fixed SD) compared with the RSG task in which variability scales with the base interval.

We collected data from 10 of the participants who also performed the RSG task (with task sequence counterbalanced across subjects). Our experimental procedure was the same as in RSG: an original prior–cost pair in the first session and alternations between the original and its metamer in the subsequent four sessions (Fig. 6B). The original prior was centered at −12 degrees, and the original cost function was centered at 0. Participants’ behavior exhibited biases toward the mean as expected by the optimal policy, indicating that subjects did not fully compensate for the rotation based on the midmovement measurement (Fig. 6D for representative data; reference SI Appendix, Fig. S9 for all participants; Fig. 6E, red, P = 0.561, t test, null: equal bias between data and optimal model).

Next, we designed the prior–cost metamer (Fig. 6C). For the prior, we shifted the Gaussian distribution by 10 deg so that the new mean was at −2 deg. For the cost function, we derived the appropriate shift in the cost function (Δt) needed to create a metameric pair (i.e., matching optimal policy). Note that the shift in the cost function had to be customized separately for each participant depending on the measurement noise fits in the first session. Participants’ behavior in the context of the metamer showed similar biases toward the mean (Fig. 6D, green; SI Appendix, Fig. S9 for all participants) and was asymptotically matched to that of the ideal observer (Fig. 6E, green; P = 0.052, t test for equal bias for data and optimal model). In other words, participants used the same optimal policy for both the original and its metamer, consistent with both the implicit (H₁) and explicit (H₂) learning strategy.

To distinguish between the implicit (H₁) and explicit (H₂) learning strategy, we tested whether there was any transient change in decision policy immediately after the switch between the two prior–cost pairs. Unlike RSG, participants’ behavior did not exhibit any transient deviation from the optimal policy after the switch (Fig. 7A and SI Appendix, Figs. S10 and S13 for reward) and was better explained by the optimal policy than a purely prior-sensitive (H₃) or cost-sensitive (H₄) strategy, even with the first 25 trials after the switch (Fig. 7 B and C and SI Appendix, Fig. S10). Together, these results suggest that, in VMR, participants rely on an implicit learning strategy (H₁) without explicit learning of the prior and cost function.

Fig. 7.

Behavior immediately after the switch to a new prior–cost condition in the VMR task. (A–C) Results are shown in the same format as in Fig. 3. Unlike the RSG task, behavior does not exhibit any transient deviation from optimal policy after the switch. Note that, in A, no smoothing was used to not mask any transient.

Although direct comparison of the different results across RSG and VMR tasks is not feasible due to their distinct task domains and noise characteristics (see Discussion), we performed several control analyses to rule out alternative explanations for the difference between RSG and VMR. First, one possibility is that subjects might experience a smaller drop of reward during transitions in VMR than in RSG, being less likely to detect the transition in VMR. We however did not observe any noticeable difference in the amount of reward change across transitions between the two tasks (SI Appendix, Fig. S17). In fact, the actual reward subjects received remained steady for both tasks (SI Appendix, Fig. S17) as we matched the overall expected reward across transitions with careful design of the cost functions. Second, we tested whether subjects who participated first in the RSG task showed the transient suboptimality only in RSG but not in VMR that they completed afterward (and vice versa). We did not find any effect of the task sequence and observed the transient deviation from optimality in RSG, but not in VMR, consistently across both groups of subjects (SI Appendix, Fig. S16). Finally, participants might exhibit the transient suboptimality only in earlier sessions and adapt more rapidly in later sessions. However, this pattern of “saving” or metalearning (54, 55) was not observed when we analyzed the time course of optimality and bias separately for individual sessions (SI Appendix, Fig. S14; see also SI Appendix, Fig. S8 for RSG).

One experimental advantage of the VMR task was that it provided a continuous readout of subjective estimate of the rotation angle. For instance, the angle of initial hand movement (x⁰_p) can serve as a proxy for the internal prior that subjects had before the midmovement measurement was made. If the subjects learned the prior distribution of x_s, they would aim at the target with an angle that roughly corresponds to the mean of the prior at the beginning of the trials. As the prior changed across the transition, x⁰_p may track changes of the internal prior if subjects updated the prior. To test whether the x⁰_p reflects the prior, we analyzed its time course around the transition (SI Appendix, Fig. S15). We made two observations: First, x⁰_p was indeed overall negative and close to the mean of the original prior (−12 deg), suggesting that subjects internalized the prior and prepared their movement accordingly to minimize later adjustments with midmovement feedback. Second, we did not find any systematic changes in x⁰_p across the transition. These results provide additional evidence supporting the conclusion that subjects used a fixed learned decision policy (i.e., implicit learning strategy).

Discussion

The success of the BDT in capturing human decision making under uncertainty (2–4, 22, 25) has been taken as evidence that the human brain relies on internal models for prior probability, sensory likelihoods, and reward contingencies. However, the success of BDT does not necessarily mean that the human brain establishes such internal models. Indeed, numerous researchers have argued instead that the brain relies on heuristics (27, 56) and gradual learning of optimal policies (29, 39, 40).

There have been numerous attempts to experimentally test the key prediction of BDT. For example, some studies have changed one element of the BDT during experiments and studied how human observers adapt to the change (45, 57–59). However, this approach inevitably changes the corresponding optimal decision policy and therefore could not be used to distinguish between explicit and implicit learning hypotheses. One potential approach for tackling this problem is to ask whether knowledge about the prior and cost would transfer to a new behavioral setting (36, 37). For example, one can expose participants to two prior–cost conditions, P₁,C₁, and P₂,C₂, and ask whether behavior remains optimal when participants are tested in cross conditions, that is, P₁,C₂ and P₂,C₁. If task performance stays at the optimal level under the new pair, it indicates that participants can flexibly integrate learned priors and cost functions in accordance with BDT. However, implementation of this approach can be challenging since it requires participants to fully learn and flexibly access distinct priors and cost functions. As such, deviations from optimality using this approach may be due to bounded computational capacity that humans have in switching between internal models.

To fill this gap, we developed an experimental paradigm that capitalizes on the issue of model identifiability in BDT (60). Since there is no one-to-one correspondence between an optimal decision policy and its underlying BDT elements (likelihood, prior, and cost function), it is possible to design Bayesian metamers that involve different prior–cost pairs but are associated with the same optimal policy. This approach parallels fruitful uses of metamers in perception (41–43) and machine learning (61). The key idea is that an observer whose decisions rely on implicit learning should “see” the pairs as metamers because they correspond to the same policy. In contrast, an observer that makes direct use of priors and cost functions will see the two pairs as distinct and will therefore be sensitive to transitions between them.

We demonstrated the utility of our approach in the RSG and VMR tasks that humans perform nearly optimally. Switching between metamers led to transient deviations from the optimal policy in the RSG but not VMR task. These findings are consistent with the interpretation that the optimal policy in the RSG—not VMR—task relies on internal models for the prior and cost function. What factors might underlie the difference between the two tasks? Although we ruled out potential differences across the tasks in the detectability and awareness of the transition (see Results), one remaining important factor that differs between the two tasks is the complexity of the decision policies. Recall that the optimal policy in the VMR task was a linear mapping between measurements and estimates. It is conceivable that the sensorimotor system has powerful machinery to rapidly adapt to new linear sensorimotor mappings without the need to relearn internal models of the prior and cost function. In contrast, the nonlinear optimal policy in the RSG task may necessitate the relearning of the prior and cost function for making adjustments to the policy although we tested and ruled out an alternative model with linear extrapolation for RSG (SI Appendix, Fig. S4). It may also be that the difference is due to inherent differences between sensorimotor timing (RSG) and sensorimotor reaching (VMR). Future studies can apply our methodology to experiments involving different forms of priors, cost functions, and optimal policies to understand the conditions under which the brain adopts explicit versus implicit learning strategies (62, 63).

An additional insight from our study was the importance of learning dynamics. Our simulations indicated that when learning time constants for the prior and cost function are comparable, learning new internal models would not incur any transient performance loss. One would therefore not be able to reject implicit learning if learning time constants for prior and cost were matched. This may however not be a problem in practice when individual learning time constants vary considerably, as was the case across subjects in our study (Fig. 5). Our framework may also fail to discriminate between explicit and implicit learning when learning takes only a few trials (40, 64). This is likely not a problem in our experiment since it takes more than a few trials to adjust to new statistics in the presence of intrinsic sources of variability (e.g., internal timing variability). More generally however, our framework is not suitable for experimental settings in which learning does not impact behavioral responses or when learning dynamics are too fast to measure. Currently, it is not clear what methodology one could use to dissociate between implicit and explicit learning for such challenging scenarios.

Our framework can be flexibly extended in different ways. For example, one can further validate BDT using likelihood-cost and likelihood-prior metamers. The use of likelihood-cost metamers may be particularly valuable when the likelihood and cost can be manipulated (6, 11, 15) but the prior is thought to be hardwired, perhaps as a result of development and/or evolution (10). For the prior–cost metamers that we focused on, there is a great deal of flexibility in choosing the parametric form of the prior and cost function. This flexibility can be used to validate conclusions that previous studies made about the role of a specific form of prior distribution (65) and/or cost function (44, 66) in human sensorimotor behavior. Finally, the specific design considerations for the metamer are not limited to linear shifts of the prior and/or cost function, which contributes to generation of the continuum of prior–cost metamerism (Fig. 5) but can be adjusted based on experimental needs.

It is important to carefully titrate the prior and cost function in our framework. If the stimuli associated with the new prior are widely different from the original prior, participants may have to engage in a learning process to establish the optimal decision policy for the new stimuli. This learning may present itself as a transient deviation from optimality and can thus be misinterpreted for explicit learning. One strategy that can reduce the chance of such misinterpretation is to design metamers that involve fully overlapping ranges of stimuli (i.e., have the same domain) but with different probability profiles (e.g., different variance or skewness). This strategy would ensure that participants have observed all possible stimuli in the metamer before the transition. Furthermore, if the transition to the metamer leads to an overall increase or decrease in reward, participants might notice the change and initiate exploratory behavior to update the decision policy. This concern is unlikely to have impacted our results since we adjusted the metamer cost function to ensure the overall expected reward was unchanged after the transition. Nevertheless, it is important to design the cost function metamers carefully so as to avoid misattributing implicit learning of a new policy to explicit Bayesian learning.

Care must be taken in interpreting the results of metameric experiments such as ours. For example, one implicit assumption of our methodology is that the implicit learning strategies do not involve updating the decision policy. This is a reasonable assumption for certain kinds of implicit learning such as model-free RL with direct policy optimization (39, 67, 68) because the metamer by design generates no incentive (or “gradient”) for updating policy. We further showed that the transient behavior in RSG cannot be explained by alternative models based on random exploration, linear extrapolation, and sophisticated deep RL (52, 53). However, the model space for implicit learning is enormous, and the dichotomy between the implicit and explicit learning can become blurred when it comes to latent representations of reward expectation and decision policy. For example, the explicit model-based learning can take a form of directed exploration guided by sensory prediction error (SPE) between the prior expectation and current measurement as well as RPE between the expected and actual rewards. It is noteworthy that the internal model of prior (i.e., memory of previous stimuli) and cost function (i.e., reward expectation) in the explicit learning can provide a natural means for detecting need for changing decision policy and for rapidly generalizing over new priors and cost functions in a sample-efficient way (40, 64). However, given that the implicit learning model does not have the latent representation of the prior and cost function, one still has to invoke a separate change-detection mechanism to adjust the learning rate after change detection.

Our analysis of learning dynamics in RSG suggests that updating priors and cost functions likely involves different neural systems. This conclusion is consistent with the underlying neurobiology (69). Humans and animals update their prior beliefs when observed stimuli deviate from predictions, which can be quantified in terms of the SPE (22, 30, 70, 71). The cerebellum is thought to play a particularly important role in supervised SPE-dependent learning of stimulus statistics in sensorimotor behaviors (72–75). In contrast, learning cost functions is thought to depend on computing RPEs between actual and expected reward (76–78). This type of learning is thought to involve the midbrain dopaminergic system (79) in conjunction with the cortico-basal ganglia circuits (69, 80–82). Finally, the information about the prior and cost function has to be integrated to drive optimal behavior. Currently, the neural circuits and mechanisms that are responsible for this integration are not well understood (83–85). Future work could take advantage of our methodology to systematically probe behavioral settings that rely on model-based BDT as a rational starting point for making inquiries about the underlying neural mechanisms.

Materials and Methods

Eleven participants (age: 18 to 65 y, six male and five female) participated in the experiments after giving informed consent. All participants were naive to the purpose of the study, had normal or corrected-to-normal vision, and were paid for their participation. All experiments were approved by the Committee on the Use of Humans as Experimental Subjects at the Massachusetts Institute of Technology.

Procedures.

All 11 participants completed five experimental sessions of the RSG time-interval reproduction task, and 10 of them completed five sessions of the VMR task. The testing sequence for the two tasks was counterbalanced across participants. In each session, a participant was seated in a dark quiet room and asked to perform the task of interest for ∼60 min. For both tasks, stimuli and behavioral contingencies were controlled by an open-source software (MWorks; mworks-project.org/) running on an Apple Macintosh platform.

Before the first session, participants received detailed instruction about task contingencies and completed dozens of practice trials. We used the data from the first session to make baseline measurements of various participant-specific parameters needed for adjusting experimental parameters in the remaining sessions (see SI Appendix for details). The data from the remaining sessions were used to ask whether humans use implicit versus explicit Bayesian integration strategy (Fig. 1).

RSG Time-Interval Reproduction Task.

In RSG, subjects have to measure an interval between two cues (Ready followed by Set) and reproduce that interval as accurately as possible immediately afterward. Details of the RSG task are provided in SI Appendix.

VMR Reaching Task.

In VMR, subjects have to use a manipulandum to move a cursor from a center position to a target position. Experimentally, the movement vector of the cursor is rotated relative to that of the hand. Subjects are provided sensory feedback about the cursor position midway along the path to make corrections. Details of the VMR task are provided in SI Appendix.

Prior–Cost Metamers.

Each experiment was associated with a prior distribution (interval distribution in the RSG task and rotation angle distribution in the VMR task) and a cost function (how subjects received feedback based on their performance). We tested subjects in each task using two prior–cost metamers. Details about designing prior–cost metamers for are provided in SI Appendix.

Models and Analysis.

All analyses were performed using custom code in MATLAB (MathWorks, Inc.). We first removed outlier trials for each data set across all participants and sessions. We applied different algorithms to the two tasks as their response profile was inherently different (i.e., nonlinear metronomic function for the RSG task and linear policy for the VMR). For the RSG task, we excluded trials in which the relative error, defined as (t_p – t_s)/t_s, deviated more than 3 SDs from its mean (mean: 0.50%; SD: 0.28% across subjects). For the VMR task, we first fitted a linear regression model relating x_p and x_s and excluded trials for which the error from the linear fit was more than 3.5 times larger than the median absolute deviation (mean: 3.4%; SD: 2% across data sets). We verified that outlier trials were not concentrated immediately after the switch between the prior–cost pairs.

Details regarding Models and Analysis are provided in SI Appendix.

Data Availability

Anonymized MATLAB data have been deposited in Jazlab Resources (https://jazlab.org/resources/) and can be found at https://github.com/jazlab/HS_MJ_metamer_2021.