Spontaneous activity competes with externally evoked responses in sensory cortex

Significance

Humans and animals recognize light tactile stimulations on some occasions while at others miss even stronger stimuli. The explanation of this apparent paradox lies in the competition between spontaneously and externally evoked responses in the brain. Brief bursts of beta-oscillations have been implicated in reduced detection rates, yet the underlying mechanism remained unknown. Here, we report that neural networks exhibit synchronization during beta-bursts, followed by reduced firing rates, thus explaining the diminished detection rate on the single trial level. Through monitoring the brain’s electrical activity before and during tactile stimulation, we found that the masking influence of burst occupancy on perception can be counterbalanced in real time by adjusting the stimulus intensity, thereby overcoming this active inhibition of sensory cortex.

Abstract

The interaction between spontaneous and externally evoked neuronal activity is fundamental for a functional brain. Increasing evidence suggests that bursts of high-power oscillations in the 15- to 30-Hz beta-band represent activation of internally generated events and mask perception of external cues. Yet demonstration of the effect of beta-power modulation on perception in real time is missing, and little is known about the underlying mechanism. Here, we used a closed-loop stimulus-intensity adjustment system based on online burst-occupancy analyses in rats involved in a forepaw vibrotactile detection task. We found that the masking influence of burst occupancy on perception can be counterbalanced in real time by adjusting the vibration amplitude. Offline analysis of firing rates (FRs) and local field potentials across cortical layers and frequency bands confirmed that beta-power in the somatosensory cortex anticorrelated with sensory evoked responses. Mechanistically, bursts in all bands were accompanied by transient synchronization of cell assemblies, but only beta-bursts were followed by a reduction of FR. Our closed loop approach reveals that spontaneous beta-bursts reflect a dynamic state that competes with external stimuli.

The brain is constantly active, even at resting states in the absence of external stimuli (1). Spontaneously active resting-state networks (RSNs) were found in memory, visual, auditory, tactile, and sensorimotor regions, with activity patterns similar to task-evoked responses (2, 3). Functional connectivity studies in humans suggest that a default network, spontaneously activated at resting states and deactivated upon increased cognitive demands, antagonizes a network involved in active attention to external sensory input (4–8). However, whether the activity in different networks is anticorrelated is under debate, and their antagonizing mechanisms and influence on local circuits remain unknown (9).

Here, we utilized the occupancy of high-power bursts in the beta-band (15 to 30 Hz) of local field potentials (LFPs) as an indicator of spontaneous activity to investigate its influence on detection in real time. Several lines of evidence relate the RSN to beta-bursts. First, spontaneous correlated oscillatory activity in beta (termed “beta-connectome”) (10) was reported in anatomical regions corresponding to the RSN (11, 12). A recent study derived this beta-connectome from burst occupancy (10). Second, beta-oscillations are dominant during the resting state (13) and bursts are responsible for virtually all beta-band power modulation (14). Third, task-dependent desynchronization of beta was observed in the somatosensory (15, 16), visual (17), auditory (18), and motor (19) cortices, resembling RSN deactivation (4, 7). The task-dependent averaged power modulation was attributed to changes in burst rates in rodents, nonhuman primates, and humans (14, 20, 21). Fourth, the burst duration (50 to a few hundred milliseconds) (22) is similar to “packets” of neural activity, which are conceived as messages initiated in a particular cortical region and spread as a wave over the cortex. Most of these packets are generated spontaneously, and spontaneous and sensory-evoked packets are remarkably similar (23).

We found that bursts in all bands indicate transient synchronization of flexible neuronal networks, but only beta-bursts were followed by a reduction in population firing rate (FR). High occupancies of beta-bursts predicted reduced detection, and this effect can be counterbalanced bidirectionally in real time by adjusting the stimulus intensity according to burst occupancy.

Results

Rats Detect Forepaw Vibration.

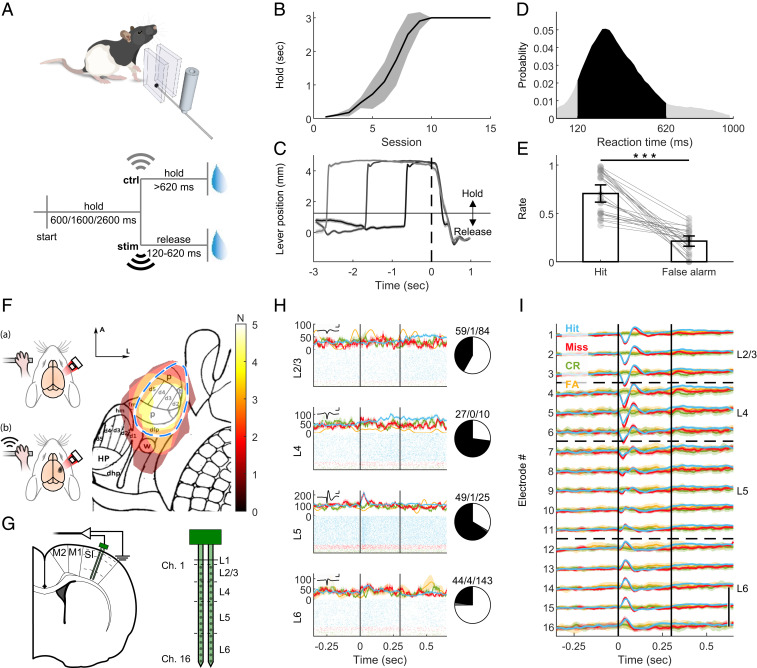
To investigate the relationship between externally and internally generated activities in detection, we developed a detection task in rats (Fig. 1A, SI Appendix, Fig. S1, and Materials and Methods). To allow future translation of our findings to writing in sensations into the brain needed for neuroprosthetics, we targeted the forepaws of the rats with a vibrotactile stimulus. The freely moving rats pulled and held a lever and released it upon detection of vibration generated by a piezo actuator. As unimanual and bimanual actions are represented differently in the cortex (24), we ensured unimanual manipulation of the lever by enclosing it between two walls. The rats could choose which paw to use, and 40% (two out of five rats) preferred the left paw. Beta-activity shows different dynamics during periods of waiting for stimuli compared to poststimulus movement (19). Therefore, it is important to ensure a well-controlled waiting period with minimal movement. To this end, we introduced a holding duration prior to the stimulus, in which the rats had to hold and pull the lever beyond a 1-mm threshold. To prevent the rats from using a timing strategy, this holding period was pseudorandomly defined. Trained rats were able to hold the lever steadily for 600, 1,600, or 2,600 ms (Fig. 1 B and C and SI Appendix, Fig. S1) and to respond to the 300-ms, 300-Hz, 28-μm sinusoidal lever vibration within 369.7 ± 6.3 ms (hit, mean reaction time [RT] ± 95% CI, n = 25 sessions, five rats, Fig. 1D and SI Appendix, Fig. S1). To prevent the use of the piezo sound as a cue, in 20% of trials we vibrated a control lever located in the cage but out of the rats’ reach. In these control trials, the rats had to keep holding the lever >620 ms (correct rejection [CR]) to obtain a reward. Failure to release the lever within 620 ms (the RT window) in vibration trials (miss) or releasing the lever in the RT window in catch trials (false alarm [FA]) resulted in no reward and a 1-s timeout. The hit rate of trained rats was significantly higher than the FA rate (Fig. 1E, Wilcoxon z = 5.98, P = 2.28 × 10⁻⁹), yielding a d′ value of 1.56 ± 0.25 (mean over sessions ± 95% CI).

Fig. 1.

Rats detect forepaw vibration. (A, Upper) Simplified illustration of the behavioral setup. A lever was enclosed between two walls and could be moved on the horizontal dimension. Piezo actuator clamped to the lever conveyed the vibrotactile stimulus. For more details, see SI Appendix, Fig. S1. (A, Lower) Task design. To start a trial, the freely moving rats had to pull the lever in their preferred direction and hold it for one of three pseudorandom durations. Upon vibration (stim), the rats had to release the lever within 120 to 620 ms to gain a sucrose water reward. In 20% of the trials, an actuator located in the chamber but clamped to a lever out of the rat’s reach was activated (ctrl). The rat had to keep holding for longer than 620 ms in order to gain a reward. (B) Holding training progress. Mean ± 95% CI of the holding duration of five rats. Rats had to hold the lever passed the threshold position for at least the holding time to obtain a reward. (C) Rats learned to hold the lever steadily and respond to the cue. Mean ± 95% CI of the lever position (measured by the angle encoder) at “hit” trials. Time t = 0 indicates the stimulus onset. Horizontal line at ∼1 mm indicates the hold/release threshold. Trials with holding time = 600 ms are indicated in black, 1,600 ms in gray, and 2,600 ms in light gray. (D) Histogram of reaction (release) times in stim trials. Vibration was presented from t = 0 to t = 300 ms. Black area: RTs within the allowed response window. Gray: RTs of early or late release trials. n = 25 sessions from five rats. (E) Hit rate: Ratio of trials with lever release within <620 ms after real stimulus onset, from all vibration trials. False alarm rate: Ratio of responded trials within <620 ms after control actuator onset from all control trials. Bars indicate the mean and error bars the 95% CI. Gray circles and lines show individual sessions. ***z = 5.977, P = 2.28 × 10⁻⁹, Wilcoxon rank sum test. (F) Intrinsic signal imaging. (Left) Schematic illustration of procedure. (A) The brains of lightly anesthetized rats were imaged through the thinned skull under 855 nm illumination. Upon vibrotactile stimulation of the forepaw (B), responsive cortex absorbed more light compared to blank trials. See Materials and Methods for details. (Right) Responsive areas of five rats overlaid on projected published somatotopic map (26). N (color bar) indicates number of rats. Blue dashed line: assumed SI forepaw location based on map. p, palm; t, thumb (pollux); d1 to 5, digits; dfp, dorsal forepaw; fm, forelimb muscle; hm, hindlimb muscle; w, wrist whiskers; dhp, dorsal hindpaw; HP, hindpaw; (Scale bar: 1 mm.) A, anterior; L, lateral. (G, Left) Schematic illustration of implantation locations of the 2-shank, 32-channel probe. SI: primary forelimb somatosensory cortex. M1: primary motor. M2: secondary motor. Dashed lines: estimated borders between cortical layers. (G, Right) Magnified illustration of the probe, indicating the location of channel relative to surface and tip and estimated borders between cortical layers as shown in H and I. (H, Left) Peristimulus time histogram (PSTH, Top) and raster plots (Bottom) of representative single units in layers 2/3, 4, 5, and 6. Blue: hit. Red: miss. Green: CR. Yellow: FA. Inset: averaged waveform of the unit. (Scale bar: 1 ms/250 μV.) (H, Right) Number of positively modulated (black), negatively modulated (gray) and nonmodulated (white) single units. (I) Mean ± 95% CI of the LFP color coded as in H. Vertical black lines indicate stimulus onset and offset (t = 0 to 0.3 s). (Scale bar: 200 μV.) CR; correct rejection. FA; false alarm. See also SI Appendix, Figs. S1, S2, S8, and S9.

Evoked Activity Encodes the Presence, Not the Detection, of a Sensory Cue.

We investigated the cortical response to vibration via chronically implanted multielectrode laminar probes. To ensure accurate positioning while avoiding extensive bleeding from surface vasculature, we developed a survival intrinsic signal imaging (based on cerebral blood flow) (25) and an implantation surgical procedure for rats (Fig. 1 F and G, SI Appendix, Fig. S2, and Materials and Methods). With this approach, we were able to take differences in vasculature and somatotopy between individuals into account, which allowed a more precise positioning of the probes compared to estimations based on classic somatotopic maps (26) of primary somatosensory cortex (SI) location.

We further validated the insertion location by detecting stimulus-evoked modulation of single-unit firing rate (Fig. 1H) and LFP (Fig. 1I). The LFP showed depolarization followed by hyperpolarization in dorsal electrodes and hyperpolarization in ventral electrodes. Analysis of the event-related potentials (ERPs) (Fig. 2A and SI Appendix, Fig. S2B) and current source density (CSD) (SI Appendix, Fig. S2C) immediately following the stimulus revealed the strongest response at electrodes located 600 to 800 μm below the surface. This response peaked 25 ms after stimulus onset, as expected from layer 4 (L4) of SI receiving a direct thalamocortical input (27, 28). Furthermore, histology (SI Appendix, Fig. S2D) confirmed the position of these specific electrodes at the granular layer.

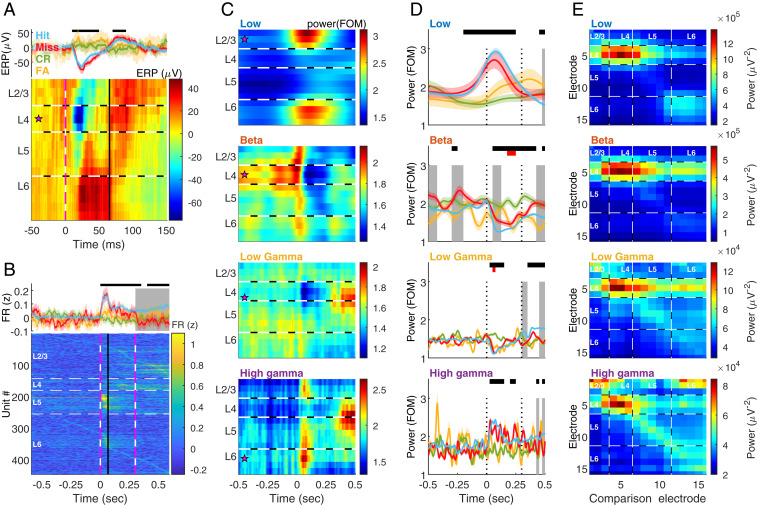
Fig. 2.

Band and layer differences in detection. (A) ERP, calculated as the mean of raw LFP aligned to stimulus onset (time t = 0). (A, Upper) Mean ± 95% CI on electrode 5 (located in L4) averaged over hit (blue), miss (red), correct-rejection (CR, green), and false-alarm (FA, yellow) trials. Top black bar indicates significant (P < 0.01) difference between hit and control trials, in ANOVA for repeated measures with Tukey’s critical value for multiple comparisons. Main effect of time: F_{9, 11637} = 8.5, P = 3.6 × 10⁻³, time × behavior: F_{27, 11637} = 8.18, P = 2.14 × 10⁻⁵. (A, Lower) The ERP on each electrode at hit trials. Magenta star: the electrode used in the Upper panel. Horizontal black and white dashed lines indicate the estimated borders between layers. Vertical pink and white dashed line designates stimulus onset (t = 0). Vertical black line denotes phase transition from de- to hyperpolarization in L4 at hit trials (blue trace in Upper passes 0 after the trough, t = 0.065). n = 10 sessions from five rats. (B, Upper) mean ± 95% CI of the z-normalized FR of all units (n = 447 units from five rats), color coded as in A. Piezo activation started at t = 0 and lasted 0.3. Top black bar indicates significant (P < 0.01) difference between hit and control trials, in ANOVA for repeated measures with Tukey’s critical value for multiple comparisons. Gray background indicates a significant (P < 0.01) difference between hit and miss. Main effect of time: F_{40, 53520} = 25.6, P = 1.14 × 10⁻¹⁸⁶, time × behavior: F_{80, 53520} = 9.47 P = 2.03 × 10^−82. (B, Lower) FR during hit trials. Units are sorted according to layer and timing of maximal FR. Horizontal white dashed lines indicate the estimated borders between layers. Vertical pink and white dashed lines designate stimulus onset (t = 0) and offset (t = 0.3). Vertical black line denotes t = 0.065, is as in A. At time t = 0 to t = 0.065 s (depolarization phase of the ERP at L4) the FR in L5 was significantly higher at hit and miss trials compared to CR and FA (P < 10⁻⁶, two-way ANOVA with Tukey’s post hoc). There were no differences between hit and miss trials (P = 1.0 in all layers). The FR in L5 was significantly (P < 3.77 × 10⁻⁹) higher than in all other layers. (C) Induced power spectrograms of hit trials, computed by transforming the LFP to the frequency domain using Morlet wavelets, normalizing to the median per frequency and averaging over hit trials. Low: 3 to 10 Hz. Beta: 15 to 30 Hz. Low gamma: 40 to 90 Hz. High gamma: 95 to 120 Hz. Magenta star: most modulated channel used in D. FOM, fraction of the median. (D) Comparison of the power dynamics of each band in the different behavioral categories. Behavioral color coding (hit, miss, CR, and FA), black bars and gray background are the same as in B. Red bars indicate difference between CR and FA. Main effect for intersection time × behavior: low: F_{117, 43797} = 9.38, P = 1.93 × 10⁻¹¹; beta: F_{117, 43797} = 2.03, P = 9.3 × 10⁻⁴; low gamma: F_{117, 43797} = 2.57, P = 7.56 × 10⁻¹²; high gamma: F_{117, 43797} = 1.57, P = 4.2 × 10⁻⁴. Differences between hit and miss trials prior to and during stimulus (0 to 0.3 s, dotted black lines) were observed only in beta. (E) Localization of ongoing bursts in all bands and using each electrode for comparison. Mean of the maximal power detected on each electrode (ordinate) during bursts in each band, as a function of the electrode used for burst detection (comparison electrode, abscissa). Note that in all bands the strongest localization was at L4 (electrodes 4 to 6). Low frequencies were localized also in deep layers (Bottom Right corner, electrodes 11 to 15). Low and high gamma exhibited local synchronization (increased power on the diagonal). In addition, high gamma showed strong synchronization in superficial layers (electrodes 1 to 3). Dashed white lines: estimated borders between cortical layers. See also SI Appendix, Figs. S2–S5 and S9.

The ERP was stimulus dependent, as it was absent in control trials. However, it was detection independent, as no differences were observed between hit and miss trials (Fig. 2 A, Upper). The population FR exhibited similar stimulus-evoked dynamics. Upon stimulus presentation, but not activation of the control piezo, the population FR exhibited a robust increase (Fig. 2B and SI Appendix, Fig. S3 A and B). This response was observed in units across all layers and was strongest in layer 5 (L5). The population FR in SI was shown to drive higher cortical areas to detect a stimulus (29). Nonetheless, during the depolarization phase of the ERP (0 to 65 ms, Fig. 2A) the stimulus-induced response in FR was similar in hit and miss trials (SI Appendix, Fig. S3C). The FR differed between hit and miss after 65 ms in L2/3 and after stimulus offset (300 ms) in L4, plausibly due to the movement toward the reward spout, since forepaw motor and sensory cortices overlap in rodents (30). Hence, the existence of a stimulus, but not its detection, is encoded by FR and ERP in SI. This raises the question of whether other neuronal signals are associated with detection in SI.

Band and Layer Differences in Detection.

LFP oscillations are a putative neuronal signal to be associated with detection in SI. Neuronal networks oscillate in a broad range of frequencies, and these oscillations are an effective mechanism to generate temporal synchrony (31). Neural oscillations are divided into frequency bands [here and by others (21, 32, 33) termed low (3 to 10 Hz), beta (15 to 30 Hz), low gamma (45 to 90 Hz), and high gamma (95 to 120 Hz)] and categories, according to the response to an external stimulus (34): evoked responses are time and phase locked to the stimulus, and computed as the power of the ERP in the frequency domain (SI Appendix, Fig. S4A). Induced responses are time locked, but not phase locked, to the stimulus and extracted as the power averaged over trials (Fig. 2C and SI Appendix, Fig. S4B).

We found a relationship between bands, cortical depth, and the stimulus-related categories. Similar to recent findings in monkeys (33), induced power in low frequencies was highest in superficial and deep layers (Fig. 2C), and strongly correlated with the amplitude of the evoked response (power in 3 to 10 Hz vs. power of the ERP, Pearson’s ρ = 0.97, P = 0, SI Appendix, Fig. S5D). The activity in high gamma was strongest in superficial and deep layers at stimulus onset and L4/5 during movement (Fig. 2C). The high-gamma power strongly correlated with the population firing rate (ρ = 0.86, P = 1.07 × 10⁻²⁸⁷ in superficial layers, SI Appendix, Fig. S5D, and ρ = 0.82, P = 1.33 × 10⁻²³⁸ in deep layers), indicating a close relationship between FR and the induced oscillatory response in the high-gamma range as reported in refs. 33, 35. Both the low-frequency–evoked response and the high-frequency–induced response did not differ between hit and miss trials prior to and during the stimulus (Fig. 2D).

A third and less understood LFP oscillation category refers to internally driven oscillations (34, 36). These ongoing oscillations are thought to represent spontaneous neuronal activity (11). In the gamma band, spontaneous activity in L4 decreased upon stimulus presentation (Fig. 2C) and negatively correlated with the FR (ρ = −0.27, P = 2.7 × 10⁻¹⁸, SI Appendix, Fig. S5D), yet with no difference between detection outcomes (Fig. 2D). Like high gamma (95 to 120 Hz), low-gamma activity in the range of 45 to 90 Hz differed between hit and miss trials during movement. In the beta-band, the intrinsically generated activity was strongest in L4. Upon stimulus presentation beta-power decreased. The beta-power was significantly higher in miss trials before and during stimulation (Fig. 2D, gray shading), and, in agreement with primate data (33, 35), negatively correlated to the FR (ρ = −0.66, P = 8.57 × 10⁻¹², SI Appendix, Fig. S5D). In agreement with a recent detection study in monkeys (37), we found no significant difference in the primary sensory cortex between CR and FA in ERP, FR, and in all bands during the prestimulus period. FA and CR differed transiently in beta toward the end of the stimulus, and in low gamma at stimulus onset (Fig. 2D, red horizontal bars).

Real-Time Impact of Beta on Detection.

Collectively, the data presented in Fig. 2 indicate that while the presence of the sensory input is associated with modulations of FR, ERP, and power in low and high frequencies, detection is associated with the state of intrinsically generated oscillations in the beta-band. However, the power analysis so far was based on averaging over trials. In order to better understand the relationship between brain signals and behavior, it is important to reveal their trial-by-trial association (38). Since the occurrence of transient high-power synchronization (bursts) correlate strongly with power modulation (14) (SI Appendix, Fig. S5), and bursts are dominant at L4 (Fig. 2E), we used burst occupancy (defined as the number of timepoints during waiting time exceeding the 90th power percentile, Materials and Methods and SI Appendix, Fig. S4D) as a proxy for the power of ongoing beta-activity in individual trials (39). We categorized trials according to their prestimulus burst occupancy and found that in trials with high burst occupancy, the success rate was significantly lower (SI Appendix, Fig. S6A) and the RT (SI Appendix, Fig. S6B) significantly higher.

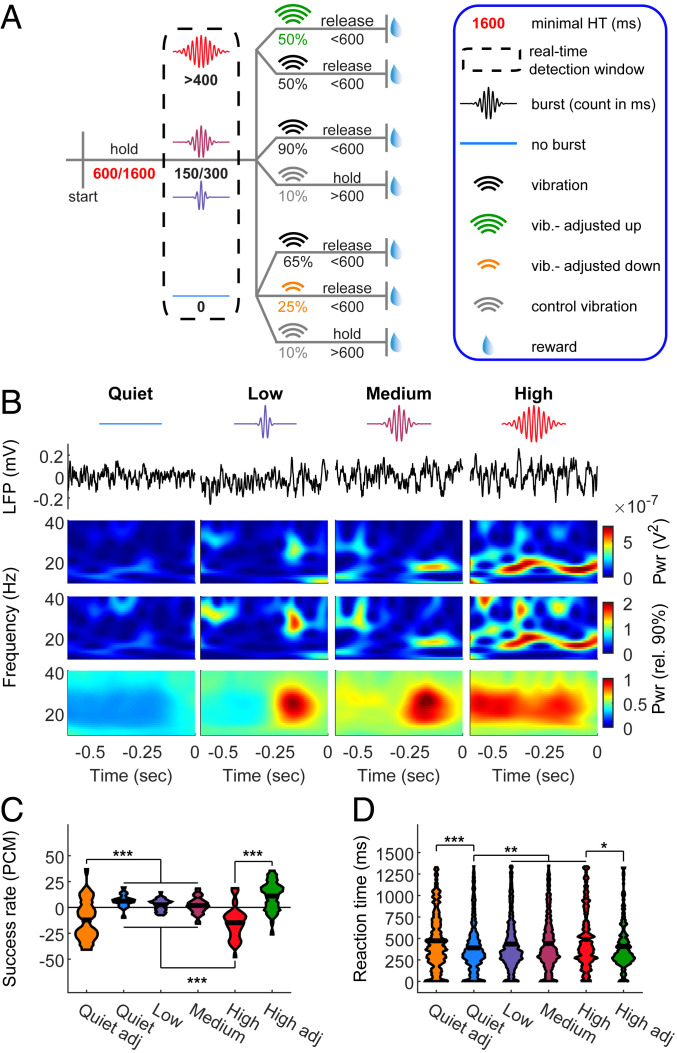
To further establish the impact of beta-bursts on perception, we sought to use their occurrence as the independent variable and assess the dependent behavioral outcome. Since the bursts are highly heterogeneous (22), direct brain stimulation is not expected to mimic the naturally occurring signal. To overcome this obstacle, we developed a system for real-time burst detection (22). It enabled us to estimate the occupancy of spontaneously occurring beta-bursts in each trial and to control the timing and amplitude of the vibrotactile stimulus (Fig. 3 A and B). To facilitate amplitude modulation with the best resolution possible in our system (2 μm), we set the standard value per rat as the amplitude resulting in d′ ∼ 1 at trials devoid of bursts during the holding time (8.8 ± 1.36 μm, d′ = 0.99 ± 0.18, mean ± 95% CI, n = 5 rats). Confirming our offline findings (SI Appendix, Fig. S6), in trials with high burst occupancy, rats had a lower success rate and longer RT (Fig. 3 C and D). Importantly, in line with our hypothesis of the impact of beta-bursts on detection, increasing the vibration amplitude by 2 μm rescued performance in high-burst-occupancy trials. This adjustment effect was bidirectional, as in trials with no bursts in the holding time decreasing the vibration amplitude by 2 μm resulted in detection performance similar to high-burst-occupancy trials. Taken together, these results demonstrate a direct impact of prestimulus beta-burst occupancy on detection.

Fig. 3.

Real-time impact of beta on detection. (A) Task design. Beta-bursts were detected in real time. A near-threshold stimulus was given upon detection of exactly 0 (quiet), 150 (low), 300 (medium), or more than 400 (high) burst samples during the detection window and the 600 ms preceding it. For adjustments, in a subset of “high” trials the stimulus amplitude was increased by 2 μm, and in a subset of “quiet” trials it was reduced by 2 μm. (B) Intrinsic brain signal triggered stimulation. First line: reference to trial types as appeared in A. Second line: raw LFP examples of one trial per condition. Third line: the power spectra of the trials in the second line. Fourth line: power spectra normalized to the 90th percentile. Note that while qualitatively similar, the normalized spectra represent higher frequencies stronger than the nonnormalized spectra. Lower line: average of all trials. Stimulus onset was at time t = 0. (C and D) Effect of stimulus locking to intrinsic brain signal and amplitude adjustment on success rate (presented as PCM, (C) and RT (D). The widths of the shapes in C indicate the distribution of sessions (n = 35 from five rats), and in D the distribution of trials (N = 458, 1,264, 1,192, 945, 281, and 262 for quiet adjusted, quiet, low, medium, high, and high adjusted, respectively). Black horizontal lines indicate the mean. Main effects: (C) F_{5, 204} = 23.06, P = 2.49 × 10⁻⁴⁸; (D) F_{5, 4396} = 9.29, P = 8.18 × 10⁻⁹. *P < 0.05, **P < 0.01, ***P < 0.001, ANOVA with Tukey’s critical value for multiple comparisons. See also SI Appendix, Fig. S6.

Bursts Indicate Transient Synchrony of Flexible Cell Assemblies.

Our data thus far suggest that spontaneous activity, reflected in beta-power, has an opposite role on detection to that of stimulus-evoked activity (manifested in FR and ERP, mirrored in low- and high-frequency power). But is there a direct relationship between beta-oscillations and FR? Previous attempts to experimentally assess the effect of beta on stimulus-evoked FR remained controversial (40). A possible explanation for this controversy is that modulation of ongoing oscillations is not necessarily time locked to the stimulus.

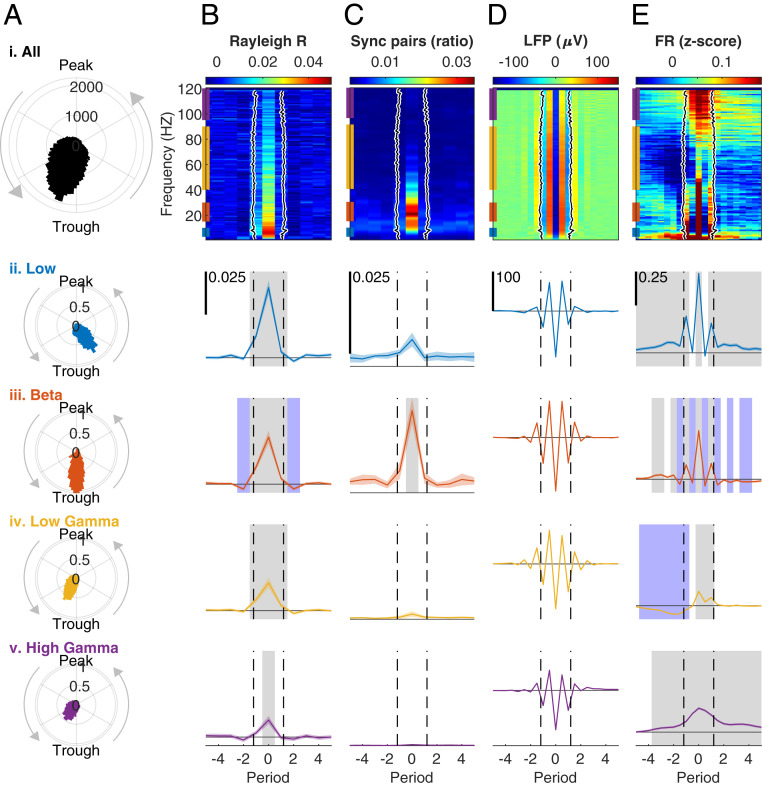
We found a strong positive correlation between power and burst occupancy in all frequencies between 15 and 120 Hz in our task (SI Appendix, Fig. S5). This motivated us to use the timing of the burst power peak as the time reference point to relate oscillations to spiking activity of single units, pairs of units, and the population (Fig. 4). All units exhibited a preference to phases of depolarization (150 to 210°) in all bands, with phases in beta closest to the trough (Fig. 4A). Based on this phase preference, we defined the participating units in each burst as units firing within 30° from the trough (41) and discovered that the coalition of synchronized units was dynamic. On average, each unit participated in 26.5 ± 1.2% of the beta-bursts, and each burst involved 28.0 ± 0.1% of the units recorded concurrently (mean ± 95% CI). When comparing the participating units in two consecutive bursts, 32.6 ± 0.3% of the units were shared and the rest were interchanged between bursts.

Fig. 4.

Bursts indicate transient synchrony of flexible cell assemblies. (A) Phase locking of single units to the LFP. (i) Histogram of the mean LFP phase at spike times of each unit during bursts in each frequency from 1 to 120 Hz. Mean angle (M) = 150.4 (trough at 180). Resultant vector length (Rayleigh’s R) = 0.497. Rayleigh test for nonuniformity of circular data z = 15,767, P = 0. (ii to v) Probability density function (PDF) histograms of the mean phase at spike times of each unit during bursts at each frequency band. (ii) Low frequencies (3 to 10 Hz), M = 213.02, R = 0.715, z = 2,180.7, P = 0. (iii) Beta (15 to 30 Hz), M = 187.65, R = 0.795, z = 3,922.5, P = 0. (iv) Low gamma (45 to 90 Hz), M = 138.75, R = 0.556, z = 8,409.6, P = 0. (v) High gamma (95 to 120 Hz), M = 129.41, R = 0.445, z = 2,745.1, P = 0. Band color code corresponds to the bars on the Left edge of the colormaps in B–E, i. (B) Mean resultant vector length (Rayleigh’s R). To facilitate the comparison between different frequencies, the time axis was converted into periods in each frequency. Period 0 indicates the nearest trough to the timepoint with burst power maximum. (i) Colormap computed for each unit in each period of all bursts in each of the frequencies 1 to 120 Hz, normalized to baseline (mean of periods −10 to −7) and averaged over units. Black line: the mean burst duration in each frequency, defined as the time interval around a peak in which the power exceeded the 90th percentile. Black shading indicates the 95% CI (calculated over bursts, total n = 332,401, 2,817 ± 81.43 [mean ± 95% CI] per frequency) and is too small to be seen. (ii to v). Mean ± 95% CI of the mean R averaged over frequencies in each band. Gray and blue shading in ii to v indicate period bins with a significant (P < 0.05) increase or decrease, respectively, in a repeated-measures ANOVA with Tukey’s adjustment for multiple post hoc comparisons compared to baseline. Dashed black lines indicate mean burst duration in the band. The horizontal line indicates zero. Scale bar appears in the Top Left corner of ii and is identical in iii to v. Main effects: (ii) F_{20, 9060} = 27.48, P = 2.45 × 10⁻⁷. (iii) F_{20, 9060} = 25.32, P = 7.0 × 10⁻⁷. (iv) F_{20, 9060} = 22.33, P = 3.06 × 10⁻⁶. (v) F_{20, 9060} = 7.66, P = 0.0059. (C) The ratio of synchronized unit pairs from all possible pairs in each session (n = 861.7 ± 378.25, mean ± 95% CI pairs per session), calculated separately for each period in each frequency. A pair was defined synchronized if the spike trains were significantly (P < 0.05) interdependent after correction for nonstationarity, using the algorithm proposed in ref. 46. The black line in i and dashed black lines in ii to v indicate burst duration as in B. In all bands (ii to v) the highest value was at period 0, but only in beta it was higher than baseline in the post hoc test and there was a significant main effect in the repeated-measures ANOVA. (ii) F_{20, 160} = 1.39, P = 0.27. (iii) F_{20, 160} = 12.32, P = 0.008. (iv) F_{20, 160} = 1.14, P = 0.32. (v) F_{20, 160} = 2.20, P = 0.18. (D) Mean LFP around bursts. (i) Colormap of all frequencies. To allow differentiation between peaks and troughs the time resolution was increased to half periods. The black line indicates mean burst duration as in B. (ii to v) Mean ± 95% CI of the LFP averaged over the frequencies of each frequency band. Dashed black lines indicate mean burst duration in the band as in B. (ii) n = 16,124 bursts. (iii) n = 47,512. (iv) n = 123,164. (v) n = 77,215. (E) Normalized population FR computed by summing the spikes from all units recorded in a session (n = 44.7 ± 8.36) at each timepoint, converting into FR by convolution with a 25-ms long, 0.34-ms standard deviation Gaussian, normalizing (z score), subtracting the baseline defined as the mean in periods −10 to −7 and averaging over bursts. (i) Black line as in B. (ii to v) Mean ± 95% CI of the population FR averaged over the frequencies of each frequency band. Gray and blue significance shading and dashed black line as in B. Main effects: (ii) F_{40, 644160} = 54.22, P = 1.88 × 10⁻¹³. (iii) F_{40, 1900240} = 40.67, P = 1.82 × 10⁻¹⁰. (iv) F_{40, 5534960} = 38.11, P = 6.72 × 10⁻¹⁰. (v) F_{40, 3087800} = 49.64, P = 1.86 × 10⁻¹². See also SI Appendix, Fig. S7.

Previous studies compared the spike–LFP relation within and outside epochs of high beta-power (40–44). We wanted to gain further insight about the temporal dynamics within bursts. Thus, and in order to facilitate comparison between different frequencies, we converted the timescale to periods per frequency with the time of period zero (P0) defined as the nearest trough to the power peak (45). Single units demonstrated stronger LFP–spike coherence one period before to one period after P0 (low, beta, and low gamma) or at P0 (high gamma, Fig. 4B). Only in beta the coherence before and after the burst (periods −2 and 2) fell below the baseline (BL). To investigate the effect of bursts on pairwise synchrony, we identified significantly dependent unit pairs based on their spike trains while taking changes in FR into account (46). We found that in all bands, the ratio of pairs with significantly dependent spike trains from total possible pairs was highest at P0, but only in beta this measure was significant (Fig. 4C).

By aligning the raw LFP traces of single bursts and averaging over all bursts (Fig. 4D), we found that in all bands the averaged burst consisted of one strong trough and two secondary troughs, which is in line with previous reports about beta-bursts (22, 45) and expands this finding to the broad LFP spectrum. Next, we tested the effect of bursts on FR at the population level (Fig. 4E). We found that at P0 FR was significantly higher than baseline in all bands. During bursts in the low-frequency band, the FR followed the LFP peaks and troughs (ρ = 0.732 ± 0.12), with relatively long transitions before and after the burst. During beta-oscillations, the FR also closely followed the LFP (ρ = 0.802 ± 0.03). Unlike low frequencies, during peaks in the LFP (hyperpolarization), the FR dropped below baseline. The FR at peaks stayed below baseline for four periods after the burst power peak, supporting an inhibitory effect of beta (10, 47). In low gamma and high gamma, the FR no longer followed the LFP peaks and troughs (ρ = 0.343 ± 0.04 for low gamma and ρ = 0.236 ± 0.02 for high gamma). The overall effect of high-gamma bursts on FR was positive, suggesting that population spiking activity mirrored the power of high frequencies. In low gamma, the FR was subbaseline before the burst and returned to average levels after the burst. The increase in spike-field coherence, unit synchronization, and FR observed at P0 was also evident when comparing burst times to epochs immediately preceding and following them (SI Appendix, Fig. S7).

Taken together, our results provide empirical evidence for transient synchrony of flexible networks during bursts, as was hypothesized in previous theoretical work (31, 48). Only in the beta-band, the transient increase in FR was followed by reduced FR, in line with the “hold” (inhibitory) function of self-generated beta (10, 47).

Discussion

It is plausible that beta-bursts represent an internally generated coactivation of wide cortical areas. As long as this baseline activity is low, an incoming stimulus would deactivate the spontaneously active network and shift the focus from the internal state to the external environment (1). A recent study (49) demonstrated that sensory-motor beta-bursts correlated with an increase in the task-suppressed hemodynamic signal in the sensory-motor network. Importantly, beta-bursts were also associated with phasic inhibition of tonically active networks, the dorsal-attention and salience networks during the task, and the default mode network during rest.

Inhibition of behavior, increase in spike–field coherence, and synchronization between units during epochs of high beta-power are consensus (41, 42, 47, 50). However, the relationship between FR and beta, which is important for understanding the underlying mechanism of the behavioral inhibition, remained an open question. On the one hand, there is ample evidence for negative correlation between averaged beta-power and population FR (33, 35). On the other hand, during beta-bursts single units tend to fire bursts of action potentials around the LFP trough (41, 43). Over epochs of high beta-power, single units were found to increase but also decrease FR (44) or have no systematic relationship with the LFP (41, 42). Due to this ambiguity and the strong effect of tasks on FR, it was recently suggested that there is no relationship between beta and FR beyond task-driven comodulations (40).

In this study, we analyzed the temporal dynamics of FR within bursts, in a period-to-period resolution. The result of this analysis suggests another explanation to the FR-LFP ambiguity. During and around beta-bursts, the FR exhibited complex dynamics: increase before the burst, locking to the LFP during the burst (increase during troughs, decrease during peaks) and decrease after the burst (Fig. 4E). Depending on the population size and analysis method, these complex dynamics may result in inconsistent effects when averaging over the entire burst duration. Nonetheless, we found a systematic increase in FR during the burst and decrease after the burst (compared to before), both in single unit (SI Appendix, Fig. S7C) and population (SI Appendix, Fig. S7D) levels. Therefore, we suggest the postburst decrease in FR as an intrinsic mechanism for the behavioral inhibition.

The period-by-period analysis also revealed that in low gamma, bursts are preceded by reduced FR and followed by return to baseline. In a recent study (51) the spike-triggered LFP average of stimulated cortical neurons exhibited a hyperpolarization–excitation cycle with period fitting to low gamma. This may suggest that a pyramidal/interneuron network gamma (PING) (52) is activated by first allocating inhibitory neurons.

Another important issue in analytical approaches is the temporal reference point (task locked and burst locked). Aligning the FR to both reference points can explain why the stimulus-evoked FR does not change with performance (53) (Fig. 2B), while beta-bursts are followed by decreased FR and reduced detection. In SI, the evoked FR is time locked to the stimulus and decodes it robustly. Beta-bursts mark a wide synchronization (11, 12) with an inhibitory aftereffect, time locked to an internally generated event. Since they are decoupled from the external stimulus (54), the FR changes are not consistently measured when looking at the stimulus time. Assuming the bursts indicate packets generated in different cortical regions and travel as a wave through the cortex (3, 23), it is conceivable that in higher areas, the event generated in SI is represented as a burst and computed alongside packets generated in other sources. This idea is supported by the finding that poststimulus multiunit activity and a linear combination of prestimulus brain signals, including beta, can differentiate hit from miss as well as FA from CR trials, dominantly in the dorsolateral prefrontal cortex (dlPFC) (37). Future multisite-recording and burst-detection experiments could test this hypothesis further.

The basal forebrain (BF) is another potential source of cortical LFP bursts. GABAergic BF neurons discharge clusters of rhythmic action potentials in frequencies matching beta and low gamma (13 to 57 Hz), thus able to play a role as pacemakers (55). During the ∼150-ms epochs of spike clusters, these cortical-projecting neurons are highly correlated, leading to spontaneous transient (∼200 ms) increases in cortical oscillation power (56). Since GABAergic BF projections target GABAergic cortical interneurons, this fast and transient effect is believed to result from disinhibition (56, 57). The coordinated spike clusters are more prevalent in wakefulness compared to sleep (56), suggesting that also cholinergic BF-cortical projecting neurons are involved. BF-cortical cholinergic innervation has an important role in wakefulness and arousal (58). Acetylcholine can modulate oscillations in the beta- and low-gamma bands (58, 59), presumably by a modulatory effect on pyramidal cells (PCs). Activation of muscarinic receptors on PCs increases their excitability and reduces their afterhyperpolarization (60), making them more likely to respond more strongly to the disinhibition of the coordinated rhythmic GABAergic input.

Another neuromodulator related to the oscillatory activity is dopamine; systemic administration of L-DOPA (a dopamine precursor) upmodulates spontaneous (stimulus unrelated) beta-power and stimulus-related low- and high-gamma power in primary visual (V1) cortex (54). The lack of dopaminergic receptors in V1 (54) suggests that this effect involves additional regions, such as the basal ganglia (BG). The involvement of BG in beta-bursts was demonstrated in patients and animal models of Parkinson’s disease (PD), in which the BG dopaminergic system is disrupted. In PD, the beta-power in several structures of the BG (subthalamic nucleus, globus pallidus, and striatum) comodulates with cortical beta-bursts (61). Furthermore, multi- and single-unit activities in BG phase lock to cortical beta-oscillations specifically during bursts. The duration of beta-bursts is prolonged in PD, associated with the symptoms and shortens upon treatment (62, 63), implying that disturbed BG circuits fail to terminate beta-synchronization (64).

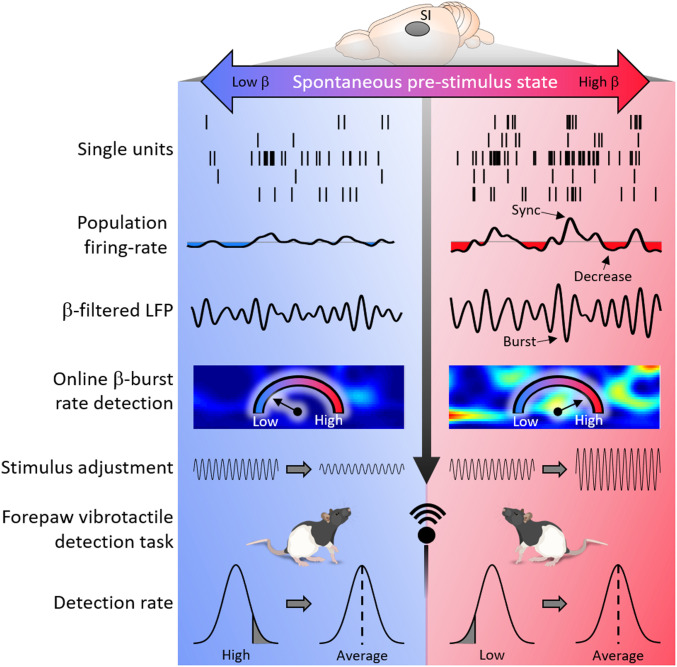
In conclusion, our results reveal that beta-bursts reflect increased spontaneous activity and predict reduced detection. This suggests that beta indicates a dynamic internal state that competes with the detection of external stimuli (Fig. 5). Understanding this internal state is key for the development of effective approaches of writing natural or artificial information into the brain for optimized perception and learning as well as for neuroprosthetic approaches.

Fig. 5.

Beta indicates a dynamic state that competes with detection of external stimuli. Spontaneously accruing LFP bursts indicate transient synchrony of flexible cell assemblies. In beta, bursts are followed by a reduction of firing rate and their occupancy is anticorrelated with cue detection. Real-time burst-occupancy detection and adjustment of the stimulus intensity brings the performance back to the average level and thus allows a trial-by-trial counterbalance of the dynamic brain-state effect.

Materials and Methods

Animals.

In this study we used five adult (8 wk at beginning of training) female Sprague–Dawley rats (Charles River). All procedures were in accordance with the guideline RL 2010 63 EU and were approved by the Regierungspräsidium Freiburg. We kept the rats in a reversed 12-h light cycle, and during behavioral training gave water only during training sessions for 5 d per week and ad libitum over the weekend. All rats maintained >85% ad libitum body weight and appropriately increased weight with age.

Behavioral Setup.

We developed a delayed go/no-go task and setup for freely moving rats (Fig. 1 and SI Appendix, Fig. S1). To allow noise-free electrophysiological recordings, we placed the rats in an open-top 30 × 26 × 40 cm glass cage, positioned on a wood plate to ensure the rats are not grounded. A 2 × 12 mm infusion cannula (1464LL, Acufirm), to which we glued a 7-mm diameter three-dimensional (3D)-printed ball, served as a lever. The lever was clamped to a holder via a strain gauge (SEN-14728, Sparkfun) 1 cm above the cage floor and between two 65 × 35 mm retractable Plexiglas walls. The change in resistance on the strain gauge was read by the electrophysiological recording system and software (RZ2 bioamp, Tucker-Davis Technologies [TDT]) and served as a touch sensor. The holder was centered by two pairs of magnets (adhesive force 2.5 kg, model S-08-08-N, Supermagnete). We controlled the distance between magnets, and thus their force, by attaching them to M12 screws. The axis of the holder was connected to a 10-bit magnetic angle encoder (AEAT-6010, Avago Technologies), reporting the left–right position.

To deliver tactile stimulation, we clamped to the lever a piezo actuator with a 30-μm travel range (P-841.20, Physik Instrumente) powered by an E-625.S0 amplifier (Physik Instrumente). We controlled the input function to the amplifier by the RZ2 bioamp. We controlled the behavioral procedure, including activation of the red cage light, reward delivery infusion syringe pump (PHM-107, Med Associates), and cage speaker (ENV-224 AM, Med Associates) with Med Associates behavioral-control cabinet and software (Med-PC).

To calibrate the output voltage to lever movement, we used an optical precision micrometer (optoCONTROL 2520-46, Micro-Epsilon). Then, we translated the lever movement to potential on the gauge sensor and used the gauge sensor to calibrate the lever movement before each session. Since the piezo actuation requires high voltage (±30 V), we shielded the actuator with a light-weight 3D printed shield covered with a silver/copper shielding aerosol (#247-4251, RS Components). The shield surrounded the actuator without touching it and connected to the ground. An additional shielded piezo actuator connected to a lever served as a no-touch control. The noise and artifacts generated by the behavioral setup were <3 μV rms.

Behavioral Training.

We initially trained the rats to hold the lever steadily. First, we acclimated the rats to the behavioral setup for one 30-min session. Then, with the restricting walls open, we rewarded the rats with 3% sucrose water accompanied by a 12-kHz pure tone clicker upon touching and/or moving the lever. After associating touching the lever with the reward, we narrowed the gap between the walls to 2 cm, and automatically increased the holding duration in steps of 10 ms after each successful hold. If a rat used its mouth or both forepaws, we manually decreased the reward size and increased the reward size upon unimanual manipulation. We inspected the preferred holding direction and paw of each rat, and hold was defined as moving and keeping the lever beyond a-1 mm threshold. Typically, the rats pulled the lever ∼5 mm, until reaching a mechanical limit (SI Appendix, Fig. S1). The rats reached a 3-s holding duration within 10 to 15 sessions (SI Appendix, Fig. S1, n = 5 rats).

Next, we introduced the vibrotactile stimulus. To discourage timing, we randomized the holding duration until stimulus presentation between 600, 1,600, and 2,600 ms (with 4:4:1 ratio, Fig. 1 and SI Appendix, Fig. S1). The shortest waiting duration was chosen to be sufficiently long to ensure proactive responses to the external stimulus (65) and allow for a 500-ms prestimulus window for baseline analysis with controlled movements of the rat. Since there were no significant differences between the different waiting times in both behavioral performance (SI Appendix, Fig. S8) and electrophysiological signals (SI Appendix, Fig. S9), they were grouped together in analysis. The prestimulus window was matched with a similar length poststimulus window that covered the RT in most trials. The allowed RT window was automatically decreased from 2,000 to 620 ms. A RT shorter than 120 ms was not rewarded, due to a physiological minimal detection duration (65, 66). To rule out a response to the vibrator sound, in 20% of the trials, we used a control vibration, outside the reach of the rats. In these trials, the rat had to continue holding for longer than the allowed RT window. The stimulus was a 300-ms sinusoid wave with frequency of 300 Hz. Throughout the behavioral task, we used the 12-kHz pure tone clicker to indicate correct trials (hit in vibration trials, CR in catch trials) to the rats, and white noise to indicate errors (late releases [miss] in vibration trials, early releases [FA] in catch trials). After an error, at least 1 s with the lever at center (time out) had to pass until a new trial could be started.

Surgery and Intrinsic Signal Imaging.

The rat forepaw somatosensory cortex spans ∼1.5 × 2 mm (26), with some changes between individuals in the exact location of the responsive area and the blood vessels above it. To minimize damage from the probe insertion while accurately localizing the forelimb SI, we inserted the probe to a cortical area clear from big blood vessels that responded to a vibrotactile stimulus. For that, we utilized intrinsic signal imaging (Fig. 1F and SI Appendix, Fig. S2A). This method is based on small (∼0.1%) changes in absorption of red light by active cortical areas (25). To detect these small changes, it is important to maintain low anesthesia (0.8 to 1.2% isoflurane) with minimal pain.

For preparation, we used 3% isoflurane (CP Pharma) in oxygen-enriched air to anesthetize the rats and administered 10 mg kg⁻¹ carpofen (Rimadyl, Zoetis) as an analgesic. We positioned the rats in a custom-built stereotactic frame equipped with a mouth holder with a palate bar (model 929-B, David Kopf Instruments), head-restraining mask, and blunt ear bars. Before cutting the skin, we injected locally 200 μL lidocaine (0.5% wt/vol, bela-pharm) over the scalp, and applied 2% lidocaine gel (Aspen Pharma) on the affected skin after cutting. We thinned the skull above the somatosensory cortex, until brain vasculature was visible upon application of saline (0.9%). We paid special attention not to heat the brain tissue or cause bleeding. Then, we covered the thinned bone with 1% agar at 37 °C and covered it with a coverslip (12-mm diameter, thickness no. 1, Carl Roth). We captured a reference picture of the brain with a complementary metal oxide semiconductor (CMOS) camera (HD1-D1312-160-CL, Photonfocus) with tandem lenses (2× optical magnification) under power LED green illumination (530 nm, Lumileds) and controlled by an Imager 3001 system (Optical Imaging). Then, we reduced the isoflurane concentration to 0.8 to 1.2%, until high-frequency, low-amplitude whisking was visible. Afterward, we commenced the intrinsic signal acquisition under infrared LED illumination (855 nm, Würth Elektronik). We positioned a metal cannula glued to a vibrator (3V ERM motor, Digikey no. 1597-1244-ND, Seeed Technology Co.) under the forepaw of the rat, recorded the baseline signal for 4 s at 15 frames s⁻¹, and stimulated for 4 s. The interstimulus interval was 17 s. To determine the responding area, we compared the change in absorption at frames 90 to 140 (stimulus) to frames 10 to 59 (baseline) between stimulation and control (no vibration) trials.

Next, we increased anesthesia to 3% isoflurane and finalized a small (<1 mm) craniotomy over a responsive cortical area free of big blood vessels. Without removing the dura, we inserted the 2-shank, 32-channel laminar probes (E32+R-150-S2-L6-200-NT, ATLAS Neuroengineering) at a speed of 5 μm/s using a custom-made motorized inserter to a final depth of 2,300 μm. While holding the probe with a vacuum holder (ATLAS), we applied a sealant (Kwik-Cast, World Precision Instruments) over the craniotomy and thinned skull and ultraviolet (UV)-cured cemented the probe to the skull (RelyX, 3M). As ground and reference, we wrapped a silver wire (130-μm diameter, Science Products) around two self-tapping skull screws (J.I. Morris Company) positioned above the cerebellum. For increased stability and reduced noise, we also cemented the custom-made electrode interface board and protected it with a custom-made implantable metal M18 screw and cup (Froelich AG). Rats were given >7 d of recovery before continuation of behavioral and electrophysiological recordings.

Data Acquisition.

We sampled the broadband signal at 24,414 Hz using a digital head stage (ZD32, TDT). Spiking activity was bandpass filtered between 300 and 5,000 Hz, and LFP was low-pass filtered at 500 Hz and down-sampled to 976.5625 Hz. The Med Associates system registered behavior at 100 Hz and synchronized with the electrophysiological signal via transistor-to-transistor logic (TTL) communication.

Real-Time Burst Detection.

For real-time LFP burst detection (Fig. 3) we used our recently reported method (22). We filtered the raw signal in real time by narrowband bandpass filters centered on frequencies 1 to 32 Hz in steps of 1 Hz. To allow timepoint-by-timepoint power comparison between frequencies, it is important to use filters with constant time delays. Therefore, we used Bartlett finite-impulse-response (FIR) filters with an order of 256 yielding a full power width at half magnitude (FWHM) of 5 Hz and total delay of 130 ms. The circuit within RZ2 bio-amp estimated power as the square of the amplitude upon detection of turning points (peaks and troughs) of the filtered LFP of each frequency. The power value was latched until the next extrema detection, yielding time resolution of half a period. In the beginning of each session, the rats were given free rewards for 30 s, in which initial power values were buffered and sent to a Matlab routine to calculate the current power percentiles in each frequency and feed them back to the RZ2 bio-amp. This routine continued to estimate the power percentiles over the passing 2 min throughout the session. Timepoints were defined as “burst-on” if the power in the frequencies 15 to 30 Hz exceeded the 90th percentile and was higher than the frequency above and frequency below. As long as a burst was “on” in one of the beta-frequencies, a TTL signal was sent to the Med Associates behavioral controller, which summed them during trials into burst occupancy. After the minimal holding duration (600 or 1,600 ms), we allowed an additional 1-s window of beta-burst detection. Burst-on timepoints were summed over the 600 ms before and during the detection window. If the burst occupancy was exactly 0 (quiet), 150 (low), 300 (medium), or more than 400 (high) burst-on samples, the detection window was terminated and a vibrotactile stimulus was sent. Half of the high-burst-occupancy trials and a quarter of quiet trials were pseudorandomly chosen for adjusted cue amplitude. To investigate the effect of the minimal detectable changes in amplitude in our system (2 μm), we reduced the vibration amplitude to the minimal level resulting in d′ of 1 at quiet trials for each rat (8.8 ± 1.36 μm, d′ = 0.99 ± 0.18, mean ± 95% CI, n = 5 rats).

Data Analysis.

To calculate the ERPs (Fig. 2A and SI Appendix, Fig. S2B), we aligned the raw LFP to the stimulus onset time and averaged over trials (n = 10 sessions, 5 rats). To measure the CSD (SI Appendix, Fig. S2C), we first calculated the second spatial derivatives of the LFP and then averaged them over trials.

For FR, we sorted the broadband signal into units using KiloSort (67), inspected each cluster, and defined units based on wave shape and existence of refractory periods. The binary spike-time array (1 for spike, 0 otherwise) of each unit was transformed into FR by convolution with a 25-ms Gaussian (0.37-ms SD) and normalized (z score). We defined units as modulated if the absolute z value of the FR in hit trials crossed a threshold of 0.37 (e⁻¹), was significantly different at t = 0 to 0.5 s compared to baseline of t = −0.5 to 0 s (t test), and differed control trials at t = 0 to 0.5 s. If all three conditions were met and the modulation direction (increase or decrease in FR) compared to BL was identical to the direction compared to control trials, the unit was considered modulated. Population FR was calculated similarly to ref. 42, by summing the number of spikes from all units per timepoint, convolving with a 25-ms Gaussian and normalizing (z score).

For time-frequency representation, we transformed the LFP data from the time domain to the frequency domain by convolving it with complex Morlet wavelets seven cycles wide in each frequency using the Fieldtrip toolbox (68) for Matlab (Mathworks, version R2018a). The power at each timepoint (at ∼1 kHz) was obtained as the squared magnitude of the complex wavelet-convolved data. The number of cycles was chosen as a tradeoff between temporal and frequency precisions, which was shown to capture LFP bursts in all frequency bands (21, 22, 45, 69). To assess the evoked response (SI Appendix, Fig. S4A) we used the ERP as input signal. For induced response calculations (Fig. 2 C and D and SI Appendix, Figs. S4B and S5) we transformed the raw LFP (of the whole session) to the frequency domain, then removed artifactual segments defined as timestamps in which the LFP exceeded 1 mV and 500 ms before and after them (22), and normalized each frequency to the 90th percentile of its artifact-free power. For comparison between behavioral outcomes (Fig. 2D) and correlation with FR or ERP (SI Appendix, Fig. S5D), we chose the most modulated channel for each band, defined as the channel with the biggest power range during the period of 300 ms before to 300 ms after the stimulus.

For offline burst detection for comparison with averaged power dynamics (SI Appendix, Figs. S5 and S6), we computed burst occupancy in a similar manner to the online algorithm, from one electrode located in L4. We defined a timepoint (∼1 ms) as having a burst (burst-on) in a specific frequency if the power in that frequency was higher than the power in the frequency above and the frequency below (in steps of 1 Hz). In addition, the power had to exceed the 90th power percentile of that frequency (calculated over the whole session). Trials were divided into occupancy bins (quiet, low, medium, and high, SI Appendix, Fig. S6), by summing the number of burst-on timepoints in the 600-ms waiting time prior to the stimulus. Quiet trials had 0 burst-on timepoints, low: 1 to 150, medium: 151 to 300, and high: >301 burst-on timepoints. To calculate burst-occupancy dynamics (SI Appendix, Fig. S5), we averaged the burst-on timepoints over hit trials and normalized to the median occupancy of each frequency in the time window [−0.5 0.5] s (stimulus present at [0 0.3] s).

To calculate the laminar localization of ongoing oscillations (Fig. 2E and SI Appendix, Fig. S4C) and to investigate the burst–spike relationship (Fig. 4 and SI Appendix, Fig. S7), we also defined a single timepoint for bursts. As reported before, bursts were defined as peaks in the time-frequency plane (21, 69), exceeding the 90th power percentile (SI Appendix, Fig. S4D). For laminar localization, we detected bursts based on the LFP power in one electrode (the comparison electrode) and averaged the power over bursts at the interval −200 to 200 ms, relative to the power peak on all electrodes. We repeated the analysis taking each electrode as comparison electrode and for each band (low: 3 to 10 Hz, beta: 15 to 30 Hz, low gamma: 45 to 90 Hz, and high gamma: 95 to 120 Hz).

For spike–field analysis, phase histograms (Fig. 4 A, i) were calculated as the circular-mean of the phases of all spikes from each unit in each frequency using the CircStat toolbox (70). Then, the mean phases of each unit were averaged over frequencies per band (Fig. 4 A, ii–v). Units were considered as participating in a burst if they fired within 30° from the trough in the LFP filtered to the burst frequency closest to the peak-power timepoint (41). This timepoint was defined as period 0 (P0). The ratio of shared units between successive bursts was defined as the number of units participating in both bursts divided by the number of units participating in any of the bursts. For investigation of the period-by-period effect of bursts on spiking activity (Fig. 4 B–E), we aligned the time series to P0. Then, we converted the time to period units by allocating spikes ± 0.5 period durations from timepoints 10 times the period of each frequency before P0 to 10 periods after, in steps of one period (Fig. 4 B and C). Half a period resolution in Fig. 4 D and E was obtained by averaging the LFP or FR around the peaks and troughs ± 0.25 periods. Burst duration (black traces in Fig. 4 B–E) was defined as the number of consecutive timepoints before and after the power-peak timepoint in which the power in the peak frequency exceeded the 90th percentile (SI Appendix, Fig. S4D).

To measure spike–field coherence (Fig. 4B), we calculated the resultant vector length (Rayleigh’s R) of the spikes occurring in each period of each frequency. Since the R value is sensitive to the number of spikes with higher values at higher frequencies, we normalized it for every burst by subtracting the mean R at periods −10 to −7. To investigate pairwise synchrony (Fig. 4C), we adopted a parametric statistic approach to test for pairwise dependencies of spike trains with correction for nonstationarity (46). We input the spike trains masked for each period for all the bursts in each frequency into the algorithm provided by Russo and Durstewitz (46). The ratio of pairs per session was defined as the number of significantly (P < 0.05) synchronized pairs divided by the number of all possible pairs in the sessions. The input for the FR analysis (Fig. 4E) was the z-normalized population FR averaged for each half period around peaks and troughs and baseline (periods −10 to −7) subtracted.

We analyzed the effect of bursts on spike–field coherence, unit synchronization, and FR analysis also with the timescale of before, during, and after the burst (SI Appendix, Fig. S7). For that, we defined the burst duration as a time interval t_[0,T]. Then, for each burst, we defined the time interval t_{[−T−1,−1]} as a “before burst” interval, and the time interval t_[T+1,2T+1] as an “after burst” interval.

We presented success rates of different burst-occupancy bins (Fig. 3C and SI Appendix, Fig. S6A) as percent change from the mean (PCM). As reaction times (Fig. 3D and SI Appendix, Fig. S6B) we took the duration between vibration initiation and the lever passing the hold threshold.

Histology.

To validate the depth of the electrode used for real-time burst detection, we created an electrical lesion. On the day before perfusing the rats, we applied a 10-μA current for 14 s (71) through this electrode using a constant current stimulator (STMISOLA, Biopac). We killed the animals by administration of 800 mg/kg sodium pentobarbital (Narcoren, WDT) and perfused transcardially with phosphate-buffered saline (PBS) and ice-cold 4% paraformaldehyde. Two days after extracting the brains, we transferred them into a solution of 30% wt/vol sucrose in PBS at 4 °C for equilibration. Then, we sectioned the brains into 50-μm thin slices on a freezing cryostate (SM 2010R, Leica). In order to delineate laminar boundaries, we blocked the slices with 5% bovine serum albumin (BSA) in PBS for 1 h and incubated in anti-NeuN primary antibody (rabbit polyclonal, Millipore catalog #ABN78, Merck-Millipore, diluted 1:500 in PBS). Afterward, we incubated the slices for 3 h with the secondary antibody (CY3 rabbit anti-mouse, AP160C, diluted 1:250 in PBS) washed in PBS for 3 × 10 min. We obtained images using an Axioplan 2 microscope (Zeiss), using Epiplan Neofluar 10× HD DIC (NA 0.30, air) and Plan Apochromat 20× M27 (NA 0.80, air) objectives.

Statistics.

Data are presented as mean ± 95% CI unless otherwise stated. We tested the difference between hit rate (hit/[hit + miss]) and false alarm rate (FA/[FA + CR]) (Fig. 1E) with a two-sided Wilcoxon rank sum test. To measure the difference between behavioral outcome types (hit, miss, CR, and FA) in FR and LFP over time (Fig. 2 A, B, and D and SI Appendix, Fig. S9), we divided the analyzed period into 25-ms time bins, and performed a two-way repeated-measures analysis of variation (ANOVA, time × behavioral outcome) with Tukey’s critical value for multiple comparisons. We used one-way ANOVA for repeated measures to test the effect of bursts on spiking activity per period (Fig. 4) or before/during/after burst (SI Appendix, Fig. S7). To calculate the descriptive FR difference maps (SI Appendix, Fig. S3C), we calculated the P value at each timepoint using a two-sided t test comparing the average FR of the units located at each cortical depth at different behavioral outcomes. To assess the effect of burst occupancy on success rate (Fig. 3C and SI Appendix, Fig. S6A) and reaction time (Fig. 3D and SI Appendix, Fig. S6B) we used a one-way ANOVA with Tukey’s adjustment for multiple post hoc comparisons. Post hoc analyses were performed only when the relevant main effects were found significant (P < 0.05). All statistical tests were performed in Matlab, with significant level of α = 0.05. Statistical values can be found in Results and figure legends.

Data Availability

Electrophysiological signals, behavioral events data, and analysis code have been deposited in GitHub and are publicly accessible at https://github.com/Optophys/Spontaneous (DOI: 10.5281/zenodo.4903463) (72).