Paradoxical stabilization of relative position in moving frames

Significance

Every eye movement drags the visual scene over our retinas and yet nothing appears to move. We now report a small-scale version of this visual stability with a square frame moving on a monitor in a well-lit room. Probes flashed before and after the frame’s motion are also stabilized in the frame’s coordinates—as if the frame were stationary—shifting perceived locations by up to half the screen’s width from their physical locations. Paradoxically, with these small frames, this ∼100% stabilization occurs despite visible frame motion. Unlike motion-induced position shifts, frame-induced shifts are independent of speed and depend instead on the distance the frame travels. This powerful discounting of motion may reveal a critical component of visual stability.

Abstract

To capture where things are and what they are doing, the visual system may extract the position and motion of each object relative to its surrounding frame of reference [K. Duncker, Routledge and Kegan Paul, London 161–172 (1929) and G. Johansson, Acta Psychol (Amst.) 7, 25–79 (1950)]. Here we report a particularly powerful example where a paradoxical stabilization is produced by a moving frame. We first take a frame that moves left and right and we flash its right edge before, and its left edge after, the frame’s motion. For all frame displacements tested, the two edges are perceived as stabilized, with the left edge on the left and right edge on the right, separated by the frame’s width as if the frame were not moving. This stabilization is paradoxical because the motion of the frame itself remains visible, albeit much reduced. A second experiment demonstrated that unlike other motion-induced position shifts (e.g., flash lag, flash grab, flash drag, or Fröhlich), the illusory shift here is independent of speed and is set instead by the distance of the frame’s travel. In this experiment, two probes are flashed inside the frame at the same physical location before and after the frame moves. Despite being physically superimposed, the probes are perceived widely separated, again as if they were seen in the frame’s coordinates and the frame were stationary. This paradoxical stabilization suggests a link to visual stability across eye movements where the displacement of the entire visual scene may act as a frame to stabilize the perception of relative locations.

Vision simplifies the dynamic world around us by coding motions and positions of objects relative to the frame that surrounds them (1, 2), up to and including the frame of the whole visual field. Studies have shown that frames and backgrounds have very powerful influences on vision, changing what we judge to be “up” (3, 4) and what direction we think is straight ahead (5, 6). When a frame is in motion, it can alter the impression of our own motion (7) or that of an object within the frame (1, 2, 8, 9).

Here we report that a moving frame also triggers a paradoxical stabilization. When a frame is in motion for a second or less, and probes are flashed just before and after the motion, the separation between the probes is seen as if the frame were stationary. This stabilization is found for probes flashed on the edges of the frame (experiment 1) or within the frame (experiment 2) and it holds even though the edges of the frame are clearly seen to move (Movie S1 and Fig. 1). These effects are the strongest illusions of position yet reported for steady gaze and we suggest that there are links between this paradoxical frame stabilization and visual stability—our ability to see the world as stable despite the large shifts of the visual scene on our retinas every time we move our eyes.

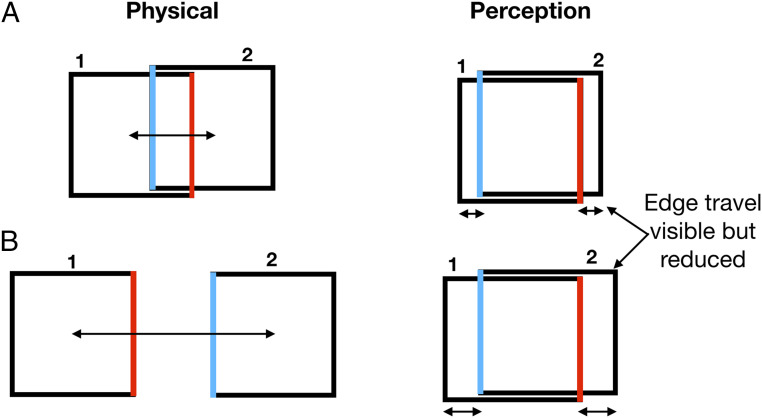
Fig. 1.

Paradoxical frame stabilization. (A) The frame moves left and right by 2/3 of its width but instead of seeing the interedge spacing of 1/3 the frame’s width, as marked by the blue and red edges, the separation of the edges appears almost as large as the entire frame’s width—as if the frame were not moving. Paradoxically, the edges of the frame are still seen to move, although less so than their real travel. (The slight vertical offset of the frame is a graphical convenience; the frames had no vertical displacement in the experiments.) (B) If the frame moves more than its width, the red edge is physically to the left of the blue and yet the blue still appears to the left of red, separated again by almost the width of the frame (Movie S1).

Our first experiment examines this paradoxical stabilization of relative position and the following experiments reveal equivalent effects of this stabilization on probes flashed within the frame.

Results

Experiment 1: Flashes at the Edges of a Moving Frame Are Localized as if the Frame Were Not Moving.

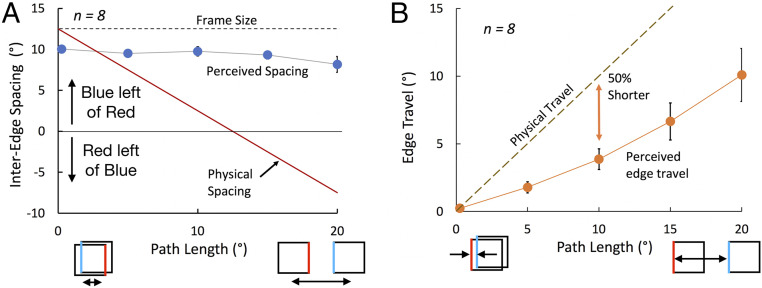
Participants report the perceived separation between parts of the frame flashed just before and just after the frame moves. In the first condition, the right edge of the frame flashed when it was the left end of its path, and then the left edge when the frame was at the right end of its path (Fig. 2, Left). In the second condition, the left edge flashed at both the left and right ends of the frame’s path so that the physical separation between the flashes was equal to the frame’s travel (Fig. 2, Right). Participants adjusted a pair of markers at the upper right of the display to indicate how far apart the flashed edges appeared. The results are clear and dramatic. As the physical separation between the flashed edges changed from 12.5° to −7.5°, the perceived separation remained relatively constant (Fig. 3A) at a value only slightly less than the 12.5° physical width of the square. Importantly, the same separation was reported even when the frame was virtually static (the baseline judgment—the leftmost data point). The measurement technique appears to underestimate the width of the frame so that the relatively constant setting at all path lengths indicates that the perceived separation was actually quite close to the perceived full width of the frame (average of 91.5% of baseline separation across the four nonbaseline settings). Remarkably, this was true even when edges had reversed their relative positions (at the two longer path lengths). A one-way ANOVA showed no significant effect of path length on the perceived spacing [Greenhouse–Geisser corrected F(1.45, 11.31) = 2.65, P = 0.127]. Despite this effective stabilization of relative positions, the movement of a single edge was clearly seen in condition 2 and did vary with the physical travel, being on average about 50% of the physical distance (Fig. 3B). The large but constant perceived interedge spacing in condition 1 is paradoxical: it would be expected only if the frame itself were perceived as stationary. But it is not—the perceived travel of the single edge showed that the motion of the frame was clearly visible, even if reduced.

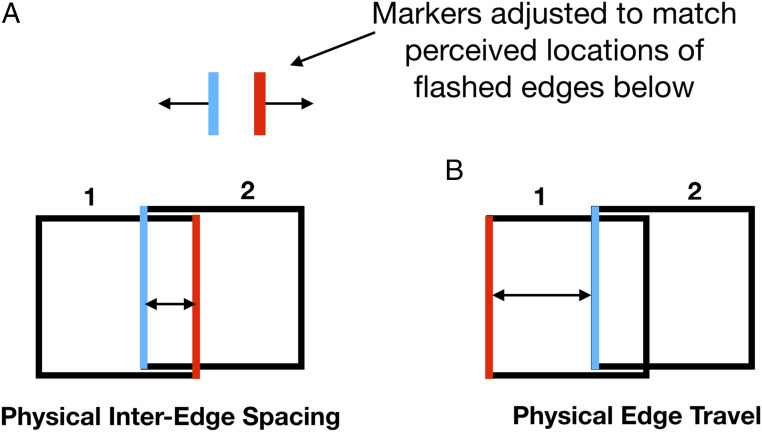
Fig. 2.

Measuring perceived frame travel. (A) In the first condition, opposite edges of the frame flash at the two ends of the travel as in Fig. 1A. Participants adjusted a pair of markers at the upper right of the display to indicate how far apart the flashed edges appeared. (B) In the second condition, the left edge is flashed at the two ends of travel and the space between them is the distance the frame travels. Participants again adjusted markers to indicate the perceived spacing.

Fig. 3.

(A) Interedge spacing (as shown in Fig. 2A). The perceived distance between the blue and red flashed edges remains positive (blue left of red) and constant even when it is physically negative (where red is actually left of blue). The leftmost data point is the baseline judgment of the frame’s width when the frame is virtually stationary. Frame size was 12.5° and motion duration was 166 ms. (B) Single edge travel (as shown in Fig. 2B). The frame’s perceived motion (orange symbols) is about 50% of its physical motion. Error bars show ±1 SE where larger than the data symbols.

In summary, the locations of the flashed edges appear to be reported in the coordinate system of the frame as if it were stationary, even though the frame’s movement is quite apparent (but underestimated).

Experiment 2: Stabilization-Induced Position Shifts.

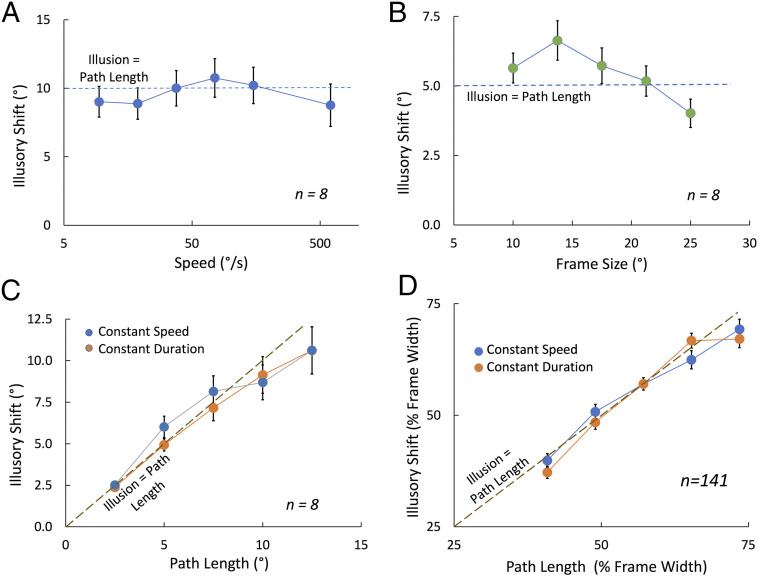
Here we examine whether probes flashed inside the frame are also perceived in the coordinate system of the paradoxically stabilized frame, shifted far from their physical locations. In this experiment (Fig. 4 and Movie S2) a frame moved left and right while two targets were flashed at the same physical location on the screen every time the motion reversed direction. The first flashed when the frame was at the left end of its travel, so that the flash was close to the right side of the frame. The second flashed when the frame was at the right end of its travel placing the same flash location close to the left side of the frame (Fig. 4). As before, participants adjusted a pair of markers at the upper right of the display to indicate how far apart the flashes appeared. The first condition tested the perceived separation of the flashes over a 64-fold variation of the frame’s speed with the frame size set at 15° and the path length at 10°. Despite being physically superimposed, the two flashes appeared to be shifted away from each other by about the distance the frame had traveled (Fig. 5A). There was no significant effect of speed on the perceived shift [Greenhouse–Geisser corrected F(1.47, 18.71) = 2.013, P = 0.19], and the average illusory shift was 96% of the path length across the six speeds. The flashes were therefore seen in their location in the frame as if the frame were almost stationary! Surprisingly, this stabilization held up even at the slowest speed we tested (a bit more than 1 s for each traverse) but clearly the effect must drop off quickly at even slower speeds like that seen at the beginning of Movie S1 where each traverse lasted 1.5 s and there appears to be no stabilization.

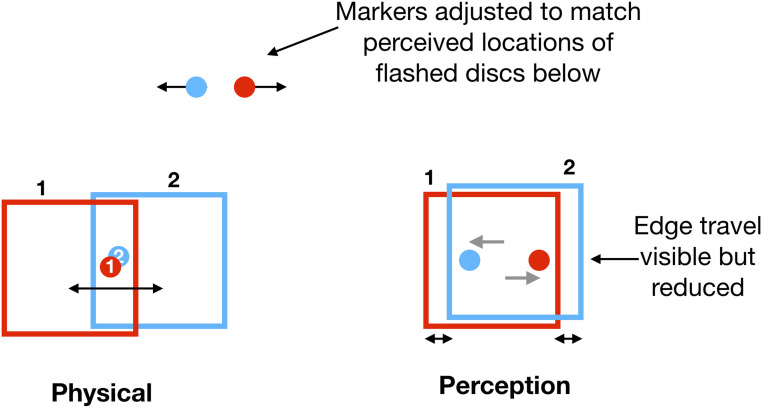
Fig. 4.

Probes flashed within the frame. Flashed probes are seen at their locations relative to the frame, as if it was almost stationary, shifted far from their physical locations. The frames are shown in red and blue for convenience. The frames were actually white on a gray background (Movie S2).

Fig. 5.

(A) Illusory shift of flashed probes as a function of the frame’s speed (on a log scale). Path length was 10° and frame size 15°. (B) Illusory shift as a function of frame size. Path length was 5° and speed 30°/s. (C) Illusory shift as a function of path length for constant speed (30°/s) or constant motion duration (500 ms). Frame size is 15°. (D) Same as in C but for 141 participants run online. In all cases, error bars show ±1 SE when larger than the data symbols.

In the second condition, the speed and the frame’s path length were fixed at 30°/s and 5°, respectively, while the size of the frame varied from 10° to 25°. There was significant variation with size with the perceived shift dropping at larger frame sizes [Fig. 5B, F(4, 28) = 11.17, P = 0.000015] perhaps because the frame was getting close to the borders of the monitor. Nevertheless, overall, the apparent offset between the flashes was close to the path length—the average across the five frame sizes was 109% of the path length.

In the third condition, the frame size was fixed at 15° while the path varied from 2.5° to 12.5°. On half the trials, the speed was held constant at 30°/s while on the other half, the duration of movement was held constant at 500 ms. The settings (Fig. 5C) show that the perceived offset of the flashes increased relatively linearly with the path length of the frame and did so similarly whether the speed was constant or the duration of travel was constant. The mean setting was slightly but significantly higher for constant speed than constant duration [F(1, 7) = 14.39, P = 0.007] and there was a significant interaction [F(4, 28) = 6.81, P = 0.001]. However, these two effects accounted for only 0.4% and 1.0% of the total variance (eta-squared), whereas the variation in path length accounted for 92.1%. Averaged across the five path lengths, the illusory shift was 97% of path length.

We were able to repeat this last condition as an online experiment with York University undergraduates (see demonstration here https://run.pavlovia.org/mthart/pubdemo/html/), as part of a battery of cognitive tests. The monitor size and viewing distance varied from participant to participant and these values were available for about 50% of them. The results for these participants showed that the size of the frame in degrees of visual angle did not affect the outcome significantly, so we averaged the results across all participants. The frame’s travel and the perceived separation are reported as percent of the frame size (Fig. 5D). The effects for the 141 participants who remained after screening (SI Appendix, Supplemental Information) were quite similar to those for the 8 in-person participants. Perceived offset was again determined by the frame’s path length and did not differ between the constant speed and constant duration conditions. The illusory shift was 97% of the path length (averaged across path lengths).

In summary, experiment 2 showed that the illusory shift of the flashed probes was always approximately equal to the path length of the frame, whatever the frame’s speed, size, or path length.

Discussion

Surprisingly, our data show that when a frame moves by less than about twice its width at a moderate to rapid speed, the relative distances between probes flashed before and after the motion are seen in frame coordinates as if the frame were not moving. How can this transformation into stationary frame coordinates occur? The frame appears to be moving quite well—nobody reports that the frames are motionless. It is only our data that reveal that the frame’s displacement is discounted in the judgments of the separation between the flashes. At the same time, the measurements of a single edge of the frame do show that the frame is seen to move, even though less than its physical travel. This produces the impression of robust motion, hiding the paradoxical stability of relative positions.

There have been many demonstrations of the effects of frames on position, orientation, and motion decomposition (1–10), but none with effects of this magnitude. What is different here is that the probes are flashed, removing the constraints on perceived location imposed by the continuously present probes used by Duncker (2) and Wallach (8) and others since them (10). The frame-induced shift with flashed probes approaches a 100% effect in several conditions—the shift had virtually the same amplitude as the frame motion that produced it. This is important because this magnitude is now in the range of the motion discounting seen with saccades where the image shifts on the retina but perceived locations are stable—a 100% discounting of motion. As a result, the frame-induced shift with flashed probes offers a possible window into visual stability, something that no other position effects have yet offered. Moreover, the use of flashed probes allows us to characterize the properties of the frame effect (e.g., dependence on frame displacement, independently of speed) without the confound of the continuing presence of location information from the target.

Why Are Relative Positions Stabilized?

The effect we report here is not simply a reorganization of the visual elements in frame-specific coordinates as proposed by Johansson in 1950 (1) and others (2, 8). The critical difference is that, in Johansson’s displays, the elements within a moving frame are seen to move relative to the frame, but they also are seen to share the common motion of the frame. In contrast, in our examples, the flashes escape the common motion—the displacement of the frame has been discounted and they have been effectively stabilized in world coordinates. We could say that the flashes are stabilized in frame coordinates, but this would only be accurate if the frame were stationary, which is paradoxically not the case. As a result, it may be more appropriate to characterize the stabilization as being in world coordinates. We have no mechanistic explanation for this effect, although it could be a consequence of the extraction of the frame-relative positions as suggested by Johansson (1). Perhaps the flashed probes do not seem to move along with the frame because they occur only before and after the motion. In contrast, probes in Johansson’s displays were always presented during the frame’s motion. Our frame stabilization may also be a small-scale application of a more general process that stabilizes the visual field when the eyes move; more on this below.

What Can Act as a Frame?

Here we use an outline square, but we have also found similar results with a moving cloud of random dots where even a few dots are enough to trigger the position shift of the probes (11). This suggests that anything that moves as a group probably engages motion discounting and the paradoxical stabilization it produces. Further studies could clarify what qualifies as a group and also what transformations (e.g., translation, expansion/contraction, warping) produce stabilization.

Eye Movement Confounds.

One alternative explanation of the frame stabilization is tracking eye movements. If the eyes were to smoothly pursue the frame, it would be more or less stable on the retina and flashes at the same location on the screen will fall on very different locations on the retina. This might lead to a stabilization of the frame and a perceived shift of the flashes. However, the everyday effects of pursuit are quite different—a tracked object does not appear to be stabilized, and the positions of flashes during pursuit are also compensated for the pursuit motion—although not completely (12). Whatever the case, it is easy to verify that the effects reported here persist with fixation (see Movies S1 and S2 and fixate a corner of the movie or another landmark on or near the display) and that they are no different with free viewing or with actual pursuit of the frame, as long as the flashes themselves are not directly fixated. As an additional control for eye movements, Movie S3 presents two frames moving side by side with a fixation between them, a procedure used in two previous experiments on motion-induced position shifts to control for eye movements (13, 14). The motions of the two frames are out of phase so no eye movements can account for the large and similar separations seen between the physically superimposed dots within both frames.

Is the Frame Effect Limited to the Periphery?

Steady fixation on the flashed probe does suppress the effect for many viewers and the participants were instructed to avoid looking directly at the flashes. A stationary point near the flashes (whether fixated or not) will also eliminate the frame’s effect. Both situations offer high certainty information about the flash location. The perception of position is based on many sources—for example, target position, target motion, and surround motion, and the contributions of target motion or surround motion will be evident only when the direct position input from the target has high uncertainty—as it will if it is flashed briefly and is alone with few or no nearby reference points. This does not mean that the frame effect is only seen when the flashes are in the periphery though. A strong effect is seen for a stationary fixation point just outside the frame (Movie S3) and this holds even for viewing quite small frames as was the case for many who ran online on laptops (experiment 2d) or when viewing the demonstration movies from far away or on cell phones. In these cases, the flashes may be less than a degree from the fovea. So the frame effect is not limited to the periphery but is suppressed with extended fixation or a static reference within the frame. Note that neither the static monitor frame nor the adjustment dots appear to limit the effect in the experiments here—the effect still reached up to a 100% of the frame displacement in some conditions, surely the maximum the effect can reach.

Relation to Motion-Induced Position Shifts.

How are these frame effects related to the many varieties of motion-induced position shifts such as the flash lag (15), flash grab (14), or the shortening of motion paths (16)? In all these cases, motion also causes a shift in perceived position (reviews in refs. 17–20). However, there are several differences. First, the frame effects reported here are fairly constant across speeds up to quite high values (experiment 2), whereas motion-induced position shifts for the flash lag (21) and for the flash grab (14) are speed dependent. Second, the perceived length of an oscillating motion path is shortened to about 70% of its true length (16), perhaps due to position averaging (22). We also find the frame’s path shortened here (experiment 1)—but significantly more, to 50% of its actual value. More importantly, even this shortening could not explain the perceived stability of relative positions, which was equivalent in some conditions to a 100% path shortening—a full discounting of the frame’s motion. Third, the frame stabilization had relatively global effects on position (Fig. 5B)—it was not greatly affected by the distance between the contours and the flash—in contrast, motion-induced position shifts like the flash grab decrease rapidly as the test moves away from the moving contour (14). Finally, the differences between many motion-induced effects and this frame effect for flashed probes is not just quantitative. The effect is notably larger than others, by about a factor of 10, and critically, this brings it into the range of the effects seen during saccades. This opens directions for possibly understanding visual stability that other motion-induced shifts cannot provide. So, despite the resemblance of the motion and frame-induced effects, there are quantitative and qualitative differences that distinguish the two. It is likely that some stimuli (23) may trigger both frame stabilization and motion effects, and further studies will be required to clearly understand whether the two are related and how they are different.

Relevance of Our Test Conditions to Saccade Conditions.

Experiment 2a did bracket typical saccade speeds. The frame displacement of 10° in this experiment would be matched by a 10° saccade and a 10° saccade has an average duration of around 50 ms, a mean speed of 200°/s, and peak speed about 400°/s (24). The two fastest speeds we tested were 150°/s and 600°/s with durations of 66 ms and 16 ms, respectively. The frame effects at these speeds did not differ from those at lower speeds (Fig. 5A). Note the difference compared to induced motion with a steady probe where the effect becomes noticeable only when the frame’s motion is very slow, for example, less than three times motion threshold (25, 26). These speeds are much too slow to have any relevance to the abrupt displacement of the visual field that occurs with saccades. In contrast, the frame effect that we see here was reliably large even for most abrupt displacement—a single jump in 16 ms. Informal experiments with the same amplitudes but with speed variations that imitate saccade trajectories (and a display running at 1,440 Hz) showed that the frame effect is, if anything, stronger in these conditions.

Visual Stability.

Are the effects of a moving frame linked in any way to visual stability, where the eyes move but the scene appears stable? Our results offer a plausible, partial link. Specifically, the positions of objects would appear to be the same after a saccade, despite a large shift on the retina because, as we suggest here, the perception of position is dominated by position relative to the background—which remains unchanged after an eye movement. There have been many proposals to explain visual stability, some that rely on extraretinal information, such as the assumption of a stable world (27, 28), the subtraction of efference copy (29, 30), or the remapping or updating of attended or landmark targets (31–35). Others suggest that purely retinal information is sufficient based on the discounting of common motion or displacement (36). The stabilization of moving frames reported here falls in this second group of mechanisms, as the subtraction of the frame’s displacement is based solely on retinal signals. However, this falls short of an explanation of visual stability for two obvious reasons. The first is that we found the motion of the frame itself was not discounted—it was clearly seen to move even though its amplitude was reduced (Fig. 3B). Possibly, the residual motion of the frame may have been due to its relative motion with respect to the real stationary background, such as the monitor edges and the experimental room. Additional experiments will evaluate whether the perceived amplitude of the frame’s motion decreases further as stationary visual landmarks are removed. The second reason is that retinal motion on its own was never an adequate explanation for visual stability. Specifically, stabilization is not seen for retinal motion in the absence of eye movement commands. When pushing your eyeball or viewing a scene in a moving mirror or an unsteady video (review in ref. 37), the visual scene clearly moves. Moreover, if an eye movement is attempted but produces no retinal motion due to afterimages (38), paralyzing the extraocular muscles (39, 40), or optical stabilization (41), the world nevertheless seems to move. Clearly, extraretinal signals are important for visual stability; nevertheless, the robust frame stabilization reported here suggests that the frame effect would be an effective contributor, along with extraretinal signals, to stabilizing the visual world when the eyes move.

Simulated Saccades.

The discounting of frame motion has been reported previously in simulated saccade studies (42–47). In these experiments, the display area, usually a reference ruler, is quickly shifted on a monitor or with a mirror. Probes presented at least 50 to 100 ms before the displacement are reported to be at their original location in the frame (e.g., retaining their ruler coordinates). However, because of the measurement technique, there is some doubt about whether the frame motion is discounted: the participants may have reported where they remembered the flash on the ruler at the time it flashed, well before the ruler moved. In contrast, our report technique avoids the ambiguity of the moving reference ruler and our results show that the separation between probes flashed before and after the motion is stabilized in world coordinates. One earlier saccade study did test the effect of a 1.5° frame displacement on flashed probes (48). They separate the two frame positions by 500 ms and reported a large perceptual effect but no effect of the frame position on a saccade to the flash.

To conclude, we have demonstrated that when frames move, their displacements may be strongly suppressed, but more strikingly, probes in or on the frame that are flashed just before and after the frame’s movement are seen in the frame coordinates as if the frame were stationary: the frame’s motion between the first and second flash is largely discounted in perceiving the separation between the flashes. We suggest that this identifies a mechanism that contributes in part to the compensation for eye movements where the frame is the entire visual field.

Materials and Methods

In-Person Experiments.

Participants.

Eight individuals, including two of the authors, participated in the in-person experiments of this study (one female; age range: 22 to 75, mean age = 46 ± 7.4). All participants other than the two authors were naive to the purpose of this study and had normal or corrected-to-normal vision. This study was approved by the York University Human Participants Review Committee and the Committee for the Protection of Human Subjects at Dartmouth College. Written, informed consent was obtained from each participant prior to their experimental sessions.

Apparatus.

All stimuli were generated on an Apple Macintosh G4 computer with custom software written in C using the Vision Shell Graphics Libraries (49). The display was presented on an LCD monitor with 60-Hz refresh rate and resolution of 800 × 600 pixels. The size of the display area was 40° × 30° (degrees of visual angle). Response adjustments were made with a track pad or mouse. Head movements were restrained with a chin rest and the viewing distance was 57 cm.

Stimuli.

The screen was filled with a uniform midgray background while the lighter square frame had 50% contrast (Michelson) with the background. The square’s size varied depending on the experiment, but its contour always subtended 0.6°. The frame’s motion path was centered horizontally on the display and the vertical center of the frame was 3.75° below the display’s vertical midpoint to provide space for the measurement markers at the top right. Probes were alternately red and blue. In the first experiment, the probes were superimposed on the left or right contour of the frame and had the same width and height as the contour. In the second and third experiments, the two flashed probes were discs of 1.5° in diameter. In the continuous motion condition of experiment 3, the single probe was red and also 1.5 ° in diameter. In all conditions, two adjustment markers were present in the upper right of the display, 10° horizontally from the screen center and 16.5° above the midpoint. In experiment 1, the markers were red and blue vertical bars 0.6° wide and 1.5° tall; in experiment 2, they were discs with the same size and color as the probes.

Procedure.

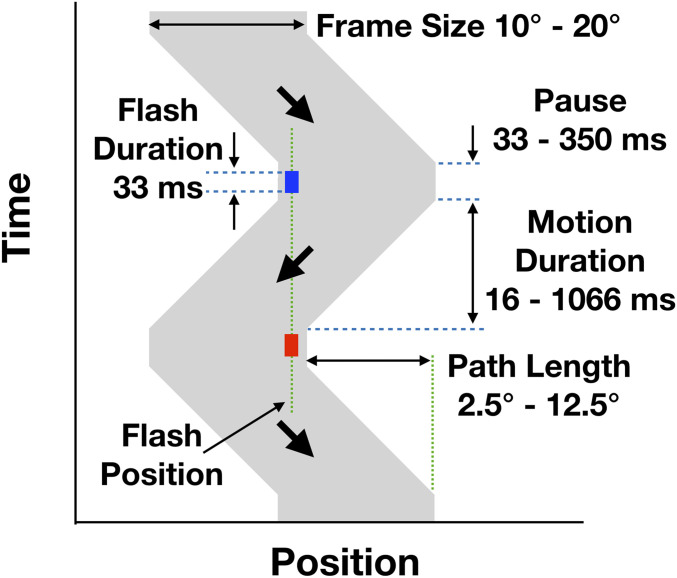
Common to both experiments, each trial began with a beep, following which the frame was present continuously and moved repeatedly back and forth horizontally. With one exception, the red and blue probes flashed alternately each time the motion reversed direction. They were presented for 33 ms, centered in the pause of the frame’s motion at the end of each transit. The pause at the end of the motion was adjusted to avoid the deterioration of the frame’s effect seen for short intervals between the repeating flashes (11). In any condition where the motion duration was less than 333 ms, the pause was increased from 33 ms (default value) to keep the interflash interval at 366 ms. Participants were instructed to look around the display wherever they wanted as they made their setting but to avoid fixating directly on a probe. Using a mouse or a trackpad, they adjusted the two markers at the top right until their separation matched that of the flashed discs (or the angle of the continuous path). When they were satisfied with their match, they pressed the space bar, and the next trial began. There were four repetitions of each trial. The responses were self-paced; participants could take a break at any time. The two experiments were run separately, and the sessions lasted about 10 and 20 min, respectively.

Experiment 1: Frame edges, left vs. right edge condition.

The frame was 12.5° across, the motion duration was 166 ms, and the pause was 200 ms. The path length took one of five values: 0.25°, 5°, 10°, 15°, and 20°. The shortest value was given a small offset so that it had some reversal transient. When the frame was at the left end of the trajectory, its right side briefly flashed red; when the frame reached the right end of the trajectory, its left side briefly flashed blue. Participants adjusted the two markers to indicate the separation they saw between the red and blue edges. Note that there was no overlap between frames at its leftmost and rightmost positions for the path lengths of 15° and 20° so the red right edge and blue left edges of the frame reversed locations in screen coordinates. The left edge condition was the same as the first condition except that it was the left edge that flashed at both ends of the frame’s travel. It flashed red at the leftmost end and blue at the rightmost end. All the trials for the two conditions were randomly intermixed for a total of (10 × 4) 40 trials.

Experiment 2: Flashed discs (Fig. 6), speed condition.

Fig. 6.

Timing for experiment 2. The frame moved left and right. The motion paused at each reversal of direction; during the pause, the flashed probe was presented for 33 ms. The two flashes always had the same physical location. The pause had a minimum duration that was the same as the flash, 33 ms, but was longer whenever necessary to maintain a minimum of 366 ms between the onset of the two flashes.

The frame was 15° across and the path length was 10°. The motion took one of six durations: 16 ms, 66 ms, 133 ms, 266 ms, 533 ms, and 1,066 ms. The motion paused at each end of the travel for at least 33 ms and the flash of 33 ms was centered in that pause. The pause durations for the six motion durations were 350 ms, 300 ms, 233 ms, 100 ms, 33 ms, and 33 ms, respectively. For size condition, the path length was 5° and the motion duration was 166 ms with a pause of 200 ms at each reversal. The frame size took one of five values: 10°, 13.75°, 17.5°, 21.25°, and 25°. For path length condition, the frame was 15° in size. Path length took one of five values: 2.5°, 5°, 7.5°, 10°, and 12.5°. On half the trials, the motion duration was fixed at 500 ms with a 33-ms pause so that the speed increased as the path length increased. On the other half of the trials, the motion duration was adjusted to keep the speed of the moving frame constant at 30°/s, so 83 ms, 166 ms, 250 ms, 333 ms, 416 ms, with pauses of 283 ms, 200 ms, 33 ms, 33 ms, and 33 ms, respectively. All the trials for the three conditions were randomly intermixed for a total of (21 × 4) 84 trials.

Analysis.

The four settings for each condition were averaged and then the mean and SEM across participants were calculated and plotted in Figs. 3 and 5. When SE for a participant was high, a second session was run. The participant means for each condition were entered in the one-way and two-way ANOVAs reported in the text and available at https://osf.io/y5xrn/wiki/home/.

Online Experiment.

Participants.

Participants were recruited from the York University population and provided prior, written, informed consent. We selected only participants with self-reported normal or corrected-to-normal vision. All procedures were approved by the York University Human Participant Review Committee. We applied several inclusion criteria (see below). There were 274 participants with a complete dataset and 141 remained following screening. The mean age was 22.1 ± 6.2 y (range: 17 to 50) including 106 females; 121 were right-handed, 15 left-handed, and 5 other.

Apparatus.

The task was created in PsychoPy Builder (50) and ran on the Pavlovia platform (https://pavlovia.org/). It was accessed from a Qualtrics questionnaire, embedded with other tasks as well as questions about the participant, the device used, and the presence of any surrounding distractions. We selected only those who indicated using a laptop or a PC (i.e., no phone or tablet), and who reported using a mouse or trackpad for the task (no touch screen), and who did not report any major disruptions during the task. Since each person used a different device, the screen size and viewing distance was variable. We asked people to measure the distance from the bridge of their nose to the center of the screen and to adjust an on-screen rectangle to a credit card pressed to the screen. Not all of the participants were able to do this, but for those who did (n = 59), we calculated the size of the stimuli in degrees of visual angle (dva). An analysis of the perceived shift as a function of stimulus size (dva) across these participants showed that the effects were not influenced by the retinal size of the stimulus, allowing us to average results across all participants.

Stimuli.

On the bottom of the participant’s browser window were instructions that remained throughout the session and the number of completed trials over the total number of trials was shown at the top left of the screen. On the left were a pair of discs, one red, one blue, for adjustment that were also presented continuously. On the right side, the frame moved left and right and red and blue probes were flashed at each reversal of direction. See a demonstration version here https://run.pavlovia.org/mthart/pubdemo/html/. The frame was a square whose height and width were 24.5% of the smaller of the height or width of the browser window, running in full screen mode. All further spatial values are given in percent of the frame width. The width of the frame’s contour was 8% of the frame size. The diameter of the adjustment and the flashed discs was 10.2% of the frame’s width. The separation of the two discs on the left could be controlled by moving the mouse or track pad left and right to indicate the perceived distance between the two flashed discs on the right. All 214 participants’ operating systems reported a refresh rate of 60 Hz and the dots were flashed for a duration that should ensure two frames (67 ms) with a 30-Hz refresh rate, so four frames (67 ms) for the 60-Hz refresh. Four catch trials were included with probes alone and no frame.

Procedure.

There were exactly 22 trials in the experiment. In 12 of the trials, the probes were flashed at the same location. There were again five different path lengths: 41%, 49%, 57%, 65%, and 73% of the frame’s width combined with the two conditions: constant speed and constant duration. In the constant speed case, the motion duration increased in step with the path length (500 ms, 600 ms, 700 ms, 800 ms, and 900 ms, respectively) making the frame’s speed a constant 82% of the frame’s width per second. In the constant duration case, the duration was 700 ms throughout, resulting in five different speeds. There was one trial for each combination, except for 57% and 700 ms, present in both conditions, which had two trials in each set. There were an additional six stimuli with a vertical offset of 61% of the frame’s width between the two flashed probes. Three path lengths for the frame’s movement—41%, 57%, and 73% of the frame’s width—were combined in both constant speed and constant duration trials, one of each. For constant speed, the motion duration increasing with the horizontal offset to give a constant horizontal velocity of 82% of the frame’s width per second. For the three constant duration trials, there was a fixed 700-ms motion duration. These data are not reported but are available with the rest of the data on the Open Science Framework (OSF) site (see below). Finally, there were four catch trials where the probes were flashed with no frame present. Two of these had no vertical offset but a horizontal offset of 61% of the absent frame’s width, one with the red probe on the left, one with the red probe on the right. Two had only a vertical offset of 61% of the absent frame’s width and no horizontal offset one with red on top and one with blue on top. These data were intended to screen participants for accuracy but all responses were reasonable.

The 22 stimuli were ordered randomly for each participant, with a 1-s intertrial interval. Participants were asked to change the horizontal position of the two continuously present dots on the left of the screen so that their horizontal offset (as well as angle in some stimuli) matched that of the two flashed dots on the right. When they were satisfied with their setting, they pressed the space bar, ending the trial and starting the next. It took participants on average about 6.5 min to complete the task.

Given the nature of online experiments, participants may not have been fully focused on the task, or may have misunderstood the short, written instructions. Based on the self-report criteria described above, 33 participants were removed for reports such as “just clicked as quickly as possible,” “didn’t understand the instructions,” “interrupted during test.” Of the remaining 241, 100 participants were removed for not meeting performance criteria. To eliminate outliers who may have been pressing the space bar without making adjustments, we required that settings on the 12 main trials had to all be less than three times the maximum frame movement and that a maximum of two settings could be 0. Of the original 274 participants, 141 remained.

Analysis.

We used descriptive statistics (means and SEs) to plot the effects of the frame’s five different movement amplitudes and the two main conditions (constant velocity and constant speed) on perceived distance between the red and blue dots. As with the main data, we also fit a linear mixed effects model to the responses, using a restricted maximum likelihood (REML) criterion with a Nelder–Mead optimizer, participant as a random effect, condition as a categorical fixed effect, and frame movement amplitude as a numeric fixed effect with a standard linear link function. These analyses do not add anything substantive to the results as plotted and so are not included in the main text. They are available with the raw data on the OSF site.

Data Availability

The raw data, summary statistics, ANOVAs, and linear mixed effects analyses, as well as the code and the three movies are available at OSF, https://osf.io/y5xrn/wiki/home/ (52).