A Mutual Multi-Scale Triplet Graph Convolutional Network for Classification of Brain Disorders Using Functional or Structural Connectivity

Abstract

Brain connectivity alterations associated with mental disorders have been widely reported in both functional MRI (fMRI) and diffusion MRI (dMRI). However, extracting useful information from the vast amount of information afforded by brain networks remains a great challenge. Capturing network topology, graph convolutional networks (GCNs) have demonstrated to be superior in learning network representations tailored for identifying specific brain disorders. Existing graph construction techniques generally rely on a specific brain parcellation to define regions-of-interest (ROIs) to construct networks, often limiting the analysis into a single spatial scale. In addition, most methods focus on the pairwise relationships between the ROIs and ignore high-order associations between subjects. In this letter, we propose a mutual multi-scale triplet graph convolutional network (MMTGCN) to analyze functional and structural connectivity for brain disorder diagnosis. We first employ several templates with different scales of ROI parcellation to construct coarse-to-fine brain connectivity networks for each subject. Then, a triplet GCN (TGCN) module is developed to learn functional/structural representations of brain connectivity networks at each scale, with the triplet relationship among subjects explicitly incorporated into the learning process. Finally, we propose a template mutual learning strategy to train different scale TGCNs collaboratively for disease classification. Experimental results on 1, 160 subjects from three datasets with fMRI or dMRI data demonstrate that our MMTGCN outperforms several state-of-the-art methods in identifying three types of brain disorders.

I. Introduction

BRAIN disorders have been treated as a public health challenge with an alarming proportion [1]. People affected by brain disorders range from children to the elderly and show completely different symptoms. Attention-deficit/hyperactivity disorder (ADHD), a neurodevelopmental disorder in childhood that usually lasts into adulthood, exhibits a combination of age-inappropriate levels of inattention, hyperactivity, and impulsive behavior [2], [3]. Mild cognitive impairment (MCI) and cerebral small vessel disease (cSVD) are associated with aging, and both cause cognitive decline and dementia [4], [5]. Although the definitions of these disorders have been made over the past few decades, the etiological bases and neural substrates are still not fully understood.

As an exciting non-invasive tool to study the brain, magnetic resonance imaging (MRI) helps to model the functional and structural mechanisms of the brain [6]-[9]. In particular, functional MRI (fMRI) and diffusion MRI (dMRI) can not only reflect the local spatial information about brain structure and function, but also maintain detailed functional and structural connectivity maps of the brain [10]-[12]. These imaging modalities have been used to help identify brain disorders from different views [13]. For example, fMRI has been employed to analyze ADHD that has shown large-scale brain functional network impairment [14], [15]. Compared with healthy controls, subjects with Alzheimer’s disease (AD) and MCI have shown changes in brain functional and structural connectivity based on fMRI and dMRI data [16]-[19]. White matter hyperintensity (WMH), as a sign of cSVD with dMRI, seems to be more intuitive in terms of impairment of brain structural connectivity [4], [5], [20]. The human connectome [21]-[23], representing a set of brain regions and their structural and/or functional interactions as a network, helps reveal potential patterns differentiating between patients and healthy controls (HCs) [24].

With the development of deep learning algorithms [25]-[28], especially convolutional neural networks (CNNs), more researchers employ these data-driven techniques to identify potential neuroimaging biomarkers for automated brain disease identification. By explicitly capturing topological information of networks, graph convolutional neural networks (GCNs) help to mine useful patterns of brain connectivity networks for disease classification [29], [30]. Nevertheless, there are at least two disadvantages in existing GCN-based methods for brain functional/structural connectivity network analysis. 1) Previous studies usually use a single template for ROI partition, which would restrict the following analysis to a single spatial scale. 2) Existing studies generally focus on modeling the pairwise relationship between brain networks (with each network corresponding to a specific subject), without considering potential high-order association (such as triplet relationship [31], [32]) among subjects.

In this letter, we propose a mutual multi-scale triplet graph convolutional network (MMTGCN) for brain disorder identification based on functional/structural connectivity networks. As illustrated in Fig. 1, we first employ T different templates (with coarse-to-fine ROI definitions) to partition each brain into multiple ROIs for generating multi-scale brain functional/structural connectivity networks, with each template corresponding to a specific spatial scale and ROI definition. We then develop a triplet GCN (TGCN) model to learn functional/structural representations of brain connectivity networks at each scale, with the triplet relationship among subjects explicitly incorporated into the learning process. We further propose a template mutual learning strategy to train these multi-scale TGCNs collaboratively for disease classification, where each TGCN can borrow knowledge from other TGCNs via a Kullback Leibler (KL) divergence loss function.

Fig. 1.

Illustration of the proposed Mutual Multi-scale Triplet Graph Convolutional Network (MMTGCN) for brain disorder identification based on fMRI/dMRI data. We first use multi-scale templates for coarse-to-fine parcellation of brain regions and construction of functional/structural connectivity networks. Multiple triplet GCN (TGCN) are designed to learn network representations, with each TGCN corresponding to a template. Each TGCN inputs a triplet of three networks/subjects (e.g., ${\mathbf{X}}_a^t$, ${\mathbf{X}}_p^t$, and ${\mathbf{X}}_n^t$) with the same graph architecture but different signals, and outputs the similarity among the triplet. Note that each subject (e.g., ${\mathbf{X}}_a^t$) is represented by a brain graph which contains a set of features F and an adjacency matrix A. Each row of F is a feature vector assigned to each node (i.e., brain region). A template mutual learning scheme is designed to fuse results of multi-scale TGCNs for classification.

The preliminary work of this method was reported in MICCAI [30]. In this journal version, we have made several novel contributions. 1) We design a template mutual learning strategy to fuse multi-scale TGCNs for brain disorder classification. This is different from the work in [30] that used a weighted voting strategy to fuse outputs of multi-scale TGCNs. 2) We evaluate the proposed method on three datasets with fMRI and dMRI data, with results demonstrating its efficacy in representing both functional and structural connectivity networks for classification of three types of brain disorders. 3) We describe the optimization algorithm in detail and release the code to the public.¹ 4) We study the influence of several major components on the performance of the proposed method.

The remainder of this letter is organized as follows. Section II introduces the most relevant studies. In Section III, we introduce materials used in this work and the details of the proposed method. In Section IV, we first introduce experimental settings and competing methods, and then present results on three datasets. Section V investigates the influence of several key components of the proposed method and discusses limitations of the current study and future research directions. We conclude this letter in Section VI.

II. Related Work

A. Machine Learning for Brain Disorder Identification

With the development of neuroimaging and artificial intelligence techniques, many MRI-based machine learning algorithms have been proposed to model the abnormality of human brain connectome and to distinguish patients from HCs. For example, researchers have developed a series of traditional machine learning methods to find alterations on functional/structural connectivity between brain ROIs. Tang et al. [33] used PCA and Student’s t-test to reduce the dimension of features extracted from T1-weighted and diffusion tensor images (DTI) for AD classification. Ahmed et al. [34] proposed an imaged-derived biomarker and multi-kernel learning method to identify AD/MCI subjects. In this method, several ROIs (e.g., bilateral, hippocampus, and amygdala area) were manually selected to analyze brain abnormalities caused by AD/MCI. Nir and Villalon-Reina [16] used a whole brain tract clustering and compact fiber representation method to investigate elderly healthy control, AD, and its prodromal stage (i.e., MCI) based on the brain’s white matter circuitry. Dodero et al. [35] proposed a manifold framework based on Riemannian geometry and kernel methods to analyze brain functional/structural connectivity. The regularized graph Laplacian helps to describe the similarity between graphs.

Deep learning methods have been recently used to analyze the whole brain connectome. Mao et al. [36] employed a spatial-temporal CNN framework that factorized convolution kernel and learned features (via residual units) of fMRI data for ADHD identification. Kam et al. [37] proposed a whole brain functional networks (BFNs), by jointly considering static and dynamic functional connectivity (FC) for MCI diagnosis. Zheng et al. [38] presented a novel ensemble approach on regionalized neural networks to exploit regional patterns and structural information. Wang et al. [39] proposed a spatial-temporal convolutional recurrent neural network for automated prediction of AD progression and network hub detection from rs-fMRI data. However, existing machine/deep learning methods generally ignore the important topology information of brain connectivity networks and thus may lead to a sub-optimal performance in brain disorder identification.

B. Graph Convolution for Brain Connectivity Analysis

Existing studies have revealed that functional/structural connectivity in human brain networks could depict activity patterns in the human brain, and these connectivity patterns have the unique graph/network architectures at the whole-brain scale [40]. That is, nodes in a graph can represent subjects/ROIs accompanied by a set of features, and the graph edges incorporate associations between subjects/ROIs in an intuitive manner. Therefore, graph learning that considers the important topology attributes of brain connectivity networks has unique advantages in describing the functional/structural characteristics of the brain. In particular, graph convolutional networks (GCNs) generalize convolution operations from Euclidean data (such as 2D or 3D images) into non-Euclidean graph data [41]-[43]. Recent studies have shown that GCNs are effective in learning brain network representations when compared to other methods [29], [44], [45]. Parisot et al. [44] and Kaiz et al. [46] treated every subject as a node (associated with neuroimaging-based feature vectors) in a graph and integrated phenotype information as edge weights. However, these methods rely on non-imaging data for connectivity construction and also cannot model high-order associations among subjects.

Several studies [29], [47] abstract each subject as a graph based on imaging data. These methods were developed to learn network representations via Siamese graph convolution, and the final label of a test subject was determined by its similarity with a known subject. For instance, Ktena et al. [29] proposed to employ Siamese GCN (SGCN) to analyze brain functional connectivity networks for autism classification, with two weight-shared GCNs measuring the difference between paired graphs/networks. These methods usually construct brain connectivity matrices/networks with one selected template, which may limit the related analysis to only a single spatial scale. Also, they seldom consider high-order (e.g., triplet) relationships between subjects, while previous studies have shown that modeling triplet relationship is very helpful to boost learning performance [31], [32]. Even though a multi-scale triplet GCN (MTGCN) was developed to capture such triplet relationship [30], a simple ensemble (e.g., weighted fusion) strategy is used to fuse results of multi-scale GCN modules, which ignore the complementary topology information provided by multi-scale templates. To this end, we propose a mutual multi-scale triplet GCN (MMTGCN) for brain disorder identification based on functional/structural connectivity networks. In MMTGCN, a unique template mutual learning strategy is designed to fuse multi-scale triplet GCNs, through which each GCN (w.r.t. a particular template) can borrow knowledge from the other ones.

III. Materials and Method

A. Subjects and Image Pre-Processing

Three datasets containing 1, 160 subjects with fMRI or dMRI data are used to validate our proposed framework. Specifically, there are 627 subjects in the ADHD-200 dataset with resting-state fMRI data acquired from ADHD patients and health controls (HCs)², 367 subjects in the ADNI dataset with resting-state fMRI data acquired from MCI patients and HCs³, and 163 subjects in a white matter hyperintensity (WMH) dataset with dMRI data acquired from cSVD patients and HCs from a local hospital. The detailed information of these datasets can be found in Table I. Parameters for fMRI in ADHD-200 and ADNI can be found online. The parameters of dMRI in WMH are listed here: TR/TE = 8, 000/80.8 ms, slice thickness = 2mm without slice gap, flip angle = 90°, matrix size = 128×128, and FOV = 256×256.

TABLE I.

Demographic Information of Studied Subjects in Three Datasets. The Values Are Denoted as “Mean ± Standard Deviation”. FC: Functional Connectivity; SC: Structural Connectivity; F/M: Female/Male

Dataset	Category	Data	Subject	Gender (F/M)	Age
ADHD-200	ADHD	FC (fMRI)	276	68/208	11.2±2.9
	HC		351	178/173	11.6±3.4
ADNI	MCI	FC (fMRI)	191	60/131	72.6±7.6
	HC		179	96/83	76.4±6.5
WMH	cSVD	SC (dMRI)	55	26/29	66.3±11.9
	HC		108	51/57	64.83±10.8

The fMRI data were pre-processed with the pipeline of Data Processing Assistant for Resting-State fMRI (DPARSF). Specifically, the first ten volumes were discarded to allow for magnetization equilibrium. The remaining volumes were processed by the following operations: 1) slice timing correction; 2) head motion correction; 3) spatial normalization to the Montreal Neurological Institute (MNI) template with 3 × 3 × 3 mm³ resolution; 4) spatial smoothing using a full width at half maximum Gaussian smoothing kernel with a size of 4mm, and 5) linear detrend and fast Fourier transform based temporal high-pass filtering (from 0.01 Hz to 0.10 Hz). Besides, five different nuisance signals of head motion parameters, white matter, cerebrospinal fluid (CSF), global signals, and the mean frame-wise displacement (i.e., micro-head motion) were all regressed out. The registered fMRI volumes were parcelled into M ROIs according to one specific template. For a subject with fMRI data, we represent each node as an M-dimensional feature vector, with each element representing the Pearson’s correlation coefficient between this ROI and another ROI.

The dMRI data were pre-processed with FMRIB’s diffusion toolbox (FSL).⁴ The processing operations include: 1) skull stripping using the Brain Extraction Tool (BET), 2) filed bias correction using the nonuniform intensity normalization (N3) algorithm [48], 3) eddy current induced distortion, and 4) adjusting diffusion gradient tables. Then, fractional anisotropy (FA) images were extracted from the DWI data after diffusion tensor fitting [49]. The thresholds of FA use default value (0.2 ~ 1) to stop tracking when FA is outside of the threshold range. The individual diffusion metric images were transformed from native space into the standard MNI space via spatial normalization. For a subject with dMRI, each node/ROI is represented by an M-dimensional feature vector, where each element denotes the averaged FA value along the structural pathway between this ROI and one of the other ROIs. More details can be found in the Supplementary Materials.

B. Proposed Method

We attempt to deal with three challenging issues in brain connectivity network analysis, i.e., 1) how to make use of complementary spatial and topology information provided by different templates; 2) how to model the triplet associations among subjects; and 3) how to fuse multi-scale network representations for brain disorder identification. We develop a mutual multi-scale triplet graph convolutional network (MMTGCN) for automated brain disorder identification, including three major components: 1) construction of multi-scale connectivity networks, 2) representation learning via triplet GCNs, and 3) template mutual learning for classification.

1). Multi-Scale Connectivity Network Construction:

To cap-ture multi-scale spatial and topology information of brain connectivity networks, we employ T different templates (containing coarse-to-fine ROI definitions) to generate coarse-to-fine functional or structural connectivity (FC or SC) matrices. Each subject (processed with one specific template) can be represented as a graph (i.e., FC or SC matrix), where each node corresponds to an ROI defined in a template space. To be specific, for each FC matrix, the connectivity denotes the Pearson correlation of their mean time-series signals between a pair of ROIs. For each SC matrix, the connectivity denotes the value of fractional anisotropy between a pair of ROIs. According to the calculation process, each matrix is actually a complete graph, where each node is connected with all the other nodes and these edges are defined by its corresponding functional or structural connectivity.

Since spectral GCNs are used to analyze brain connectivity networks in this work, as a special form of Laplacian smoothing, convolution operations on each node with spectral GCN models not only use features of itself but also consider neighbors that are connected with [50]. If we simply treat subjects as complete graphs, spectral GCN models will drop the node-centralized local topology information due to a strong but unnecessary hypothesis that each node is fully connected with all the other nodes. In this work, we employ Spectral GCN to learn new graph representations. Under Laplacian smoothing in Spectral GCN [42], features of nodes within each connected component of the graph would converge to be similar. If we employ a fully-connected graph structure, the new features of each node will tend to be similar, and thus, have less discriminative ability for classification. Hence, instead of treating each subject’s connectivity matrix as a fully-connected (i.e., complete) graph, we propose to use k-nearest neighbor (k-nn) to keep each node connected only to its k-nearest nodes. Such refined connectivity patterns help to model the node-centralized local topology information, because each node is connected to its k-nearest nodes. In this way, one can focus on the local topology centered on each node. This is different from conventional methods that use the complete graph and ignore the local node-specific topology.

Besides, we aim to model shared group-level graph topology between all subjects for brain disorder classification. For each subject, we can generate an adjacent matrix based on its original functional/structural connectivity network, where each ROI only connects to its top k similar neighbors (measured by Euclidean distance between features of paired ROIs). Then, the group-level topology structure based on all training subjects can be defined as: $\overline{\mathbf{A}}=\frac{1}{N_h}{\sum }_{i=1}^{N_h}{\mathbf{A}}_i+\frac{1}{N_p}{\sum }_{j=1}^{N_p}{\mathbf{A}}_j$, where A_i denotes the k-nn graph for the i-th training subject, and N_h and N_p represent the number of health control subjects and the number of patients in the training set, respectively. More details can be found in the Supplementary Materials.

To this end, we first employ T different templates to calculate related FC/SC matrices of training subjects and then construct a group-level k-nn graph by connecting each node with its k-nearest neighbors. We keep all subjects shared the same topology (reflected by nodes and their connectivities). Using T templates, we can generate T k-nn graphs for each subject correspondingly. These multi-scale graphs reflect the group-level topology of FC/SC networks in multiple template spaces. Furthermore, the signal/representation of each node is an M-dimensional feature vector, where M denotes the number of nodes/ROIs defined by one specific template. For a subject with fMRI data, the M-dimensional feature vector for each node is defined as the temporal correlation of the high amplitude, low-frequency spontaneously generated BOLD signal between an ROI and the other ROIs [51].

For a subject with DTI data, each node is represented by an M-dimensional feature vector, where each element denotes the averaged FA value along the structural pathway between this ROI and one of the other ROIs. In this way, each subject can be represented by the group-level graph topology and node signals/representations in multi-scale template spaces.

2). Representation Learning via Triplet GCN:

Compared with traditional convolution with Euclidean data (e.g., 2D or 3D images), graph convolutional network (GCN) tries to generalize operations to the non-Euclidean data (e.g., graphs). Recently, Siamese GCN (SGCN) [29] was proposed for autism classification based on fMRI data. As shown in Fig. S5 of the Supplementary Materials, this SGCN framework only models the pairwise relationship of subjects/samples, ignoring their underlying high-order (e.g., triplet) associations. Several studies propose to model high-order (e.g., triplet) relationship between subjects [31], [32], [52]-[54]. In this work, we employ a triplet learning framework to measure inter-subject similarity based on new graph embeddings learned by GCN. To mine the triplet similarity between subjects, we develop a triplet GCN (TGCN) module (corresponding to a specific template) in the proposed MMTGCN, which contains three parallel graph convolutional networks (with shared parameters). Since T templates with coarse-to-fine ROI parcellation are used to provide more spatial information, MMTGCN consists of T TGCNs for multi-scale network representation learning.

As can be seen from Fig. 1, the t-th TGCN inputs a triplet {${\mathbf{X}}_a^t$, ${\mathbf{X}}_p^t$, ${\mathbf{X}}_n^t$}, containing an anchor subject ${\mathbf{X}}_a^t$, a positive sample X_p, and a negative sample ${\mathbf{X}}_n^t$, where X denotes subject’s brain graph which contains a set of features F and an adjacency matrix A. Each row of F is a feature vector assigned to each node. That is, ${\mathbf{X}}_p^t$ and ${\mathbf{X}}_a^t$ are from the same category, while ${\mathbf{X}}_n^t$ and ${\mathbf{X}}_a^t$ are from different categories. In this work, each TGCN encourages that the anchor and positive samples (belonging to the same category) are similar based on their learned graph representations. Similarly, the representations of different categories (i.e., the anchor and negative samples) are encouraged to be dissimilar. Specifically, the l₂-norm based triplet loss function of the t-th TGCN is defined as:

$$\begin{gathered} L_{td(t)}={\sum }_{k=1}^O[\Vert f_t({\mathbf{X}}_{a,o}^t)-f_t({\mathbf{X}}_{p,o}^t){\Vert }_2^2 \\ -\Vert f_t({\mathbf{X}}_{a,o}^t)-f_t({\mathbf{X}}_{n,o}^t){\Vert }_2^2+{\lambda }_t{]}_{+}, \end{gathered}$$ (1)

where O is the number of input triplet collections in a minibatch, [h]₊ = max {h, 0}, and f_t (·) is an embedding function in the t-th TGCN. Also, λ_t is a margin parameter used to enlarge the inter-category distance. Finally, TGCN outputs the similarity of the anchor subject X_a belonging to a particular class (i.e., positive or negative).

3). Template Mutual Learning for Classification:

Based on T TGNCs (with each one corresponding to a particular template), we need to fuse their results for classification. Previous studies usually employ ensemble learning strategies (e.g., voting or weighted voting) to perform template fusion [30], [49], [55], where each learning task based on a specific template can not explicitly borrow knowledge from other tasks/templates. In this work, we assume that different templates have complementary spatial and topology information that can be transferred to other templates for performance boosting. Inspired by [56], we propose a mutual learning strategy to collaboratively learn those T TGCNs, where they can teach each other throughout the training process. The Kullback-Leibler (KL) divergence is used to measure the difference between different TGCNs. To the best of our knowledge, this is among the first attempts to collaborative learn multi-scale GCNs for neuroimaging-based brain disorder classification. In contrast, Zhang et al. [56] focused on employing CNN architectures for classification of natural images or face images. This work is also different from previous neuroimaging-based brain disorder studies that simply fuse multi-scale features (e.g., via fully-connected layers in GCN) or average outputs of multi-scale GCNs (e.g., via weighted voting or majority voting) [49], [55].

Specifically, a mimicry loss is designed to align each template’s class posterior with the class probabilities of other templates. In this way, these T TGCNs can be trained collaboratively. We denote N samples from C classes as $\mathcal{X}=\{x_a{\}}_{a=1}^N$ and their corresponding label set as $\mathcal{Y}=\{y_a{\}}_{a=1}^N$ with y_a ∈ {1, 2, ⋯ , C}. Then, the probability of the sample x_a belonging to the class c measured by the t-th TGCN (parameterized by θ_t) is computed as:

$$p_t^c({\mathbf{x}}_a)=\frac{exp(L_{td(t)}^c)}{{\sum }_{c=1}^{C}exp(L_{td(t)}^c)},$$ (2)

where the logit $L_{td(t)}^c$ denotes the output of the “softmax” layer in θ_t based on Eq. (1).

To measure the difference between the real and predicted labels based on θ_t, a cross entropy error is employed in the objective function, defined as follows:

$$L_{TRI(t)}={\sum }_{i=1}^N{\sum }_{c=1}^{C}I(y_i,c)log(p_t^c(x_i)),$$ (3)

where the indicator function is defined as:

$$I(y_i,c)=\{\begin{array}{cc}1,\hfill & if{y}_i=c\hfill \\ 0,\hfill & if{y}_i\ne c,\hfill \end{array}\phantom{\}}$$ (4)

Since multi-scale templates are employed to depict brain connectivity networks, each TGCN calculates the inter-subject triplet distance based on multi-scale graph embeddings. We assume that even though features of each subject are derived from different templates, the inter-subject distance should still keep similar. To this end, we use the Kullback Leibler (KL) divergence from P_r and P_t with N samples on C classes to measure the similarity between $p_r^c(x_i)$ and $p_t^c(x_i)$. Here, P_r and P_t denote predictions of the r-th and the t-th TGCN, respectively. Specifically, the KL mimicry loss is defined as:

$$D_{KL}(P_r\mid \mid P_t)={\sum }_{r=1,r\ne t}^T{\sum }_{i=1}^N{\sum }_{c=1}^C{p}_r^c(x_i)log\frac{p_r^c(x_i)}{p_t^c(x_i)},$$ (5)

The objective function for optimizing the t-th TGCN (aided by other T – 1 TGCNs via collaborative learning) will be defined as:

$$L_{{\theta }_t}=L_{TRI(t)}+\frac{1}{T-1}{\sum }_{r=1,r\ne t}^T{D}_{KL}(P_r\mid \mid P_t),$$ (6)

where the first term encourages that all T TGCNs learn collaboratively to predict labels of training samples (via the triplet loss L_{T RI(t)}), and the second term encourages each TGCN to match the probability estimate of their T – 1 peers (via the KL mimicry loss).

Based on the results of T TGCNs, a weighted fusion strategy is used for the final classification, defined as:

$$L_{Fusion}={\sum }_{t=1}^T{\gamma }_t{L}_{{\theta }_t},$$ (7)

where ${\gamma }_t={\omega }_t∕{\sum }_{t=1}^T{\omega }_t$ represents the weight of the t-th TGCN module, and ω_t is the classification accuracy achieved by the t-th TGCN on the training data. Since template mutual learning algorithm can boost the performance of each triplet GCN (TGCN) by borrowing complementary spatial and topology information from other TGCNs, the optimization of this mutual learning is conducted iteratively until convergence. The optimization details are summarized in Algorithm 1 of the Supplementary Materials.

4). Implementation:

To construct multi-scale FC/SC networks based on fMRI/dMRI data, we employed T = 4 templates with coarse-to-fine ROI definitions. As shown in Fig. S2 of the Supplementary Materials, these templates include: Automated Anatomical Labelling with 116 ROIs (AAL116) [57], Craddock with 200 ROIs (CC200) [58], Brainnetome with 273 ROIs (BN273) [22], and Bootstrap Analysis of Stable Clusters with 325 ROIs (BASC325) [59]. In this way, each subject can be represented by 4 brain connectivity matrices.

At the training stage, for each training subject X_a, we randomly select a pair of positive and negative subjects from the training set to generate a triplet set $\{{\mathbf{X}}_{a,q},{\mathbf{X}}_{p,q},{\mathbf{X}}_{n,q}{\}}_{q=1}^Q$. To handle the limited number of training subjects, we repeat such random selection process Q times to augment the triplet samples for network training. Based on validation data (i.e., 10% subjects randomly selected from the training set), we empirically set Q = 25 for both the ADNI and ADHD-200 datasets, and Q = 15 for the WMH dataset. At the testing stage, following [60], we treat each unseen test subject as the anchor subject, and randomly select 5 pairs of subjects from the training set (with these paired subjects from two different categories). We then construct five triplets, by combining the testing subject (i.e., anchor) with each of these 5 pairs. The prediction results for these 5 triplets are treated equally to get a final decision for the test subject. This strategy tries to overcome the bias caused by random sampling for positive and negative subjects. Also, k is chosen from [5, 40] (step size: 2) via cross-validation for k-nn graph construction.

We implement the proposed MMTGCN based on Pytorch [61], and the model was trained by a single GPU (NVIDIA GeForce GTX TITAN with 12GB memory). In M2TGCN, each of T TGCNs contains three parallel weight-shared GCNs, with each GCN consisting of 3 layers of graph convolutional layers and 1 fully connected layer. Each graph convolutional layer is followed by batch normalization, ReLU activation, and 0.5 dropout. The objective function in Eq. (6) is optimized by the Adaptive Moment Estimation (Adam) optimizer [62]. The value of learning rate is set as 0.001, while the number of epochs and batch size are empirically set as 200 and 16, respectively.

IV. Experiments

A. Experimental Settings

A five-fold cross-validation strategy is used to evaluate the performance of different methods. Specifically, we first divide all subjects into 5 subsets (with roughly equal size). Then, we treat one subsets as test set, while all other four subsets are used as training data. Such process is repeated five times to avoid bias by the random partition during the cross-validation process. Finally, results of classification are averaged over all iterations. Four metrics are used to evaluate the classification performance, i.e., classification accuracy (ACC), sensitivity (SEN), specificity (SPE) and the area under curve (AUC).

B. Methods for Comparison

The proposed MMTGCN is first compared with three conventional machine/deep learning methods, as well as their multi-template variants, including 1) principal component analysis with random forest as the classifier, with and without multiple templates (denote as MPR and PR), 2) clustering coefficient with RF, with and without multiple templates (denote as MCR and CR), 3) CNN with the triplet sampling strategy, with and without multiple templates (denote as MTCNN and TCNN). The details of these methods are given as follows.

1. PR & MPR: In the PR method, we use PCA [63], [64] to perform feature dimension reduction based on the principal components of the original FC/SC matrices of each subject. In our experiments, we select the number of components via cross-validation from the range of [5, 50] (step size: 1). Then, RF [65] classifier is employed for classification. As the multi-scale variant of PR, multi-scale RP (MRP) shares the same templates as MMTGCN and employs a weighted fusion strategy [30].

2. CR & MCR: In the CR method, the clustering coefficient (CC) [66] measures the clustering degree of each node in a graph as network representation, and RF is used as the classifier. The sparsity parameter in CC is chosen from {0.10, 0.15, ⋯ , 0.40} according to cross-validation performance. We select the number of trees in RF from the range of [50, 200] with the step size of 10. In addition, the depth of each tree is selected from [1, 6] with the step size of 1. Similar to MPR, multi-scale CR (MCR) use the same T template for coarse-to-fine ROI parcellation and the weighted fusion strategy for multi-template-based classification.

3. TCNN & MTCNN: TCNN employs a triplet representation learning strategy [67]. Its input is the original FC/SC matrices of each subject to learn graph embeddings by capturing the triplet similarity among subjects. Three convolutional layers and a fully connected layer are included in TCNN. Specifically, the first convolution layer has 4 channels, and the size of corresponding kernel is 5 × 5. Both the second and third layers have 8 channels, and the corresponding kernels have the size of 4×4, and 3×3, respectively. Similar to MMTGCN, multi-scale TCNN (MTCNN) use the same templates and the weighted fusion strategy for classification.

We further compare MMTGCN with two GCN-based methods, including Siamese GCN (SGCN) [29] and triplet GCN (TGCN) [30], as well as their multi-scale variants denoted as MSGCN and MTGCN, respectively.

1. SGCN & MSGCN: SGCN aims to model the pairwise relationship among subjects, containing 3 graph convolutional layers and 1 fully connected layer. Each graph convolutional layer is followed by batch normalization, ReLU activation, and 0.5 dropout. The contrastive loss is used in SGCN, optimized by the Adam optimizer with the learning rate of 0.001, 200 epochs and the batch size of 16. The sampling number is the same as that used in MMTGCN. As the multi-scale variant of SGCN, MSGCN shares the same template pool as MMTGCN and uses a weighted fusion strategy for classification.

2. TGCN & MTGCN: Different from SGCN that models the pairwise relationship, TGCN captures the triplet relationship among subjects. Similar to SGCN, TGCN consists of 3 graph convolutional layers and 1 fully connected layer. The triplet loss is used in TGCN, optimized by the Adam optimizer with the learning rate of 0.001, 200 epochs and the batch size of 16. The sampling number is the same as that used in MMTGCN. As a multi-template method, MTGCN uses the same T templates for ROI parcellation as in MMTGCN and the weighted fusion scheme for classification.

C. Results on Functional Connectivity Networks

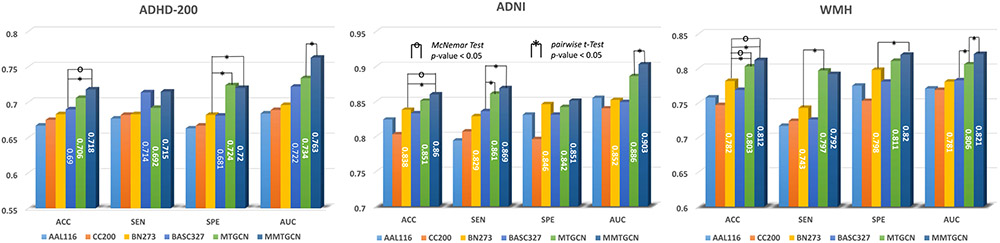
We compare our MMTGCN with eleven competing methods on both ADHD-200 and ADNI datasets with FC networks derived from rs-fMRI. The experimental results are reported in Table II, where ‘*’ denotes that the result of MMTGCN/MTGCN is statistically significantly better than other methods (with p < 0.05) based on pairwise t-test. If MMTGCN is significantly better than MTGCN, no matter MTGCN are significantly better than other methods or not, we only put ‘*’ at the upper right corner of MMTGCN; If MMTGCN is not significantly better than MTGCN meanwhile MTGCN is significantly better than the best result of other methods, we only put ‘*’ on MTGCN. The ROC curves of different methods are plotted in Fig. 2.

TABLE II.

Classification Results in Terms of “mean(Standard Deviation)” Achieved by Eleven Methods on Three Datasets, While ADHD and ADNI Have Rs-fMRI Data and WMH has With dMRI Data. Terms Denoted by ‘*’ or ‘o’ Represents That the Result of MTGCN or MMTGCN is Statistically Significantly Better Than Other Comparison Methods (With p < 0.05) Based on Pairwise t-Test or McNemar’s [68] Test

Metric	ADHD-200
	PR	MPR	CR	MCR	TCNN	MTCNN	SGCN	MSGCN	TGCN	MTGCN	MMTGCN (Ours)o
ACC	0.594(0.028)	0.614(0.031)	0.616(0.029)	0.625(0.037)	0.642(0.037)	0.653(0.047)	0.658(0.033)	0.666(0.026)	0.690(0.026)	0.706(0.023)	0.718(0.015)*
SEN	0.596(0.043)	0.619(0.058)	0.594(0.064)	0.613(0.027)	0.668(0.038)	0.659(0.034)	0.639(0.029)	0.659(0.028)	0.687(0.021)	0.691(0.016)	0.715(0.024)*
SPE	0.595(0.035)	0.611(0.024)	0.627(0.042)	0.631(0.044)	0.636(0.042)	0.657(0.034)	0.661(0.029)	0.686(0.035)	0.691(0.024)	0.714(0.021)*	0.720(0.014)
AUC	0.551(0.032)	0.582(0.056)	0.573(0.046)	0.624(0.042)	0.642(0.043)	0.652(0.040)	0.659(0.032)	0.694(0.037)	0.722(0.023)	0.734(0.016)	0.763(0.017)*
Metric	ADNI
	PR	MPR	CR	MCR	TCNN	MTCNN	SGCN	MSGCN	TGCN	MTGCN	MMTGCN (Ours)o
ACC	0.716(0.042)	0.732(0.037)	0.713(0.036)	0.730(0.022)	0.765(0.036)	0.781(0.029)	0.770(0.032)	0.797(0.026)	0.838(0.021)	0.851(0.018)	0.860(0.013)*
SEN	0.723(0.042)	0.752(0.041)	0.716(0.053)	0.743(0.054)	0.749(0.053)	0.763(0.024)	0.788(0.029)	0.839(0.027)	0.829(0.016)	0.861(0.022)*	0.869(0.017)
SPE	0.715(0.062)	0.729(0.052)	0.720(0.049)	0.718(0.037)	0.784(0.046)	0.812(0.037)	0.767(0.018)	0.767(0.026)	0.846(0.024)	0.842(0.019)	0.851(0.013)
AUC	0.761(0.053)	0.797(0.028)	0.747(0.032)	0.759(0.028)	0.798(0.041)	0.818(0.043)	0.838(0.023)	0.848(0.029)	0.852(0.021)	0.886(0.017)	0.903(0.013)*
Metric	WMH
	PR	MPR	CR	MCR	TCNN	MTCNN	SGCN	MSGCN	TGCN	MTGCN	MMTGCN (Ours)
ACC	0.631(0.035)	0.653(0.032)	0.614(0.041)	0.636(0.039)	0.703(0.043)	0.721(0.037)	0.733(0.043)	0.758(0.027)	0.782(0.020)	0.803(0.011)*	0.812(0.012)
SEN	0.515(0.043)	0.548(0.051)	0.45(0.063)	0.535(0.047)	0.514(0.059)	0.612(0.052)	0.653(0.041)	0.648(0.019)	0.743(0.018)	0.797(0.023)*	0.792(0.014)
SPE	0.678(0.058)	0.668(0.043)	0.646(0.052)	0.651(0.057)	0.735(0.046)	0.758(0.052)	0.744(0.025)	0.779(0.025)	0.798(0.023)	0.811(0.017)*	0.820(0.015)
AUC	0.587(0.036)	0.605(0.041)	0.564(0.035)	0.596(0.028)	0.663(0.067)	0.707(0.053)	0.734(0.047)	0.755(0.024)	0.781(0.026)	0.806(0.019)	0.821(0.017)*

Fig. 2.

Results of ROC curves and AUC values achieved by eleven different methods on three datasets (i.e., ADHD-200, ADNI, and WMH).

From Table II and Fig. 2 (a)-(b), one can have the following interesting observations. First, compared with four traditional machine learning models (i.e., PR, MPR, CR, and MCR), deep learning methods generally achieve better performance on both datasets. For example, in terms of ACC values, TCNN obtains the improvement of 1.7% and 3.3% compared with the best baseline methods (i.e., MCR on ADHD-200 and MPR on ADNI), respectively. Especially, MMTGCN and MTGCN achieve at least 9% improvement than these four traditional methods. These findings imply that, when dealing with high dimensional functional/structural connectivity networks, deep learning methods that automatically learn network representations could be more effective in brain disorder identification, compared with conventional methods that employ handcrafted features. Second, five GCN-based methods that capture new graph topology via k-nn usually outperform TCNN and MTCNN based on fully-connected graphs. For instance, TGCN achieves more than 4% improvement in terms of most metrics, compared with TCNN. This may due to that using k-nn to mine graph topology of functional/structural connectivity networks can help remove those redundant or even noisy information, thus boost the classification performance. Besides, compared with methods that model the pairwise relationship among subjects (i.e., SGCN and MSGCN), three triplet sampling based methods (i.e., TGCN, MTGCN, and MMTGCN) achieve better performance in most cases. It implies that capturing the triplet association among subjects help boost the learning performance. Furthermore, multi-template methods (i.e., MPR, MCR, MTCNN, MSGCN, and MTGCN) generally outperform their single-template counterparts (i.e., PR, CR, TCNN, SGCN, and TGCN), with at least 1% improvement in terms of four evaluation metrics. Especially, our MMTGCN achieves the overall best performance among six multi-template methods. The possible reason is that functional connectivity networks derived from multi-scale templates contain complementary information, which helps boost the classification performance.

D. Results on Structural Connectivity Networks

We also evaluate our MMTGCN on the WMH dataset with structural connectivity networks derived from dMRI, with results shown in Table II and Fig. 2 (c). Note that the patients and healthy controls in WMH are not balanced (see Table I). Similar to the results on functional connectivity data, Table II and Fig. 2 (c) suggest that deep learning methods still perform better than traditional machine learning methods on the structural connectivity data. In addition, on the small-sized and unbalanced WMH dataset, TGCN-based methods (i.e., TGCN, MTGCN and MMTGCN) improve the SEN values by at least 9%, compared with the other methods. And such improvement does not come at the cost of drastically reducing the SPE values. Besides, our MMTGCN yields significantly better ACC and SEN values (with p < 0.05), compared the other ten competing methods. These results validate the effectiveness of MMTGCN in identifying patients with brain disorders based on structural connectivity networks.

E. Comparison With State-of-the-Art

We further compare our method with several state-of-the-art studies on brain connectivity analysis in three classification tasks (i.e., MCI vs. HC, ADHD vs. HC, and WMH vs. HC), with results shown in Table III. In this table, we also report the number of subjects and data modality used in different studies. It’s worth noting that the results in Table III are not fully comparable, because different studies may use different numbers of subjects and different data modalities. From Table III, we can see that our method achieves competitive results compared with existing studies in both tasks of WMH vs. HC and ADHD vs. HC classification. In MCI vs. HC classification, the ACC value of our method is slightly worse than three competing methods. The possible reason is that we employ the largest dataset (with 191 MCI and 179 HC subjects) that brings much difficulty to the classification task, and the brain pathological changes of many MCI subjects may be very subtle [69]-[71].

TABLE III.

Comparison With State-of-the-Art Methods in Three Different Classification Tasks (i.e.MCI Vs. HC, ADHD Vs. HC, and WMH Vs. HC). P: Patients; H: Healthy Controls

Task	Method	Subject (P/H)	Modality	Performance
MCI vs. HC	FW-Lasso+SVM [72]	28/33	fMRI	ACC:0.869; AUC:0.900
	SSGSR [73]	52/52	fMRI	ACC:0.885; AUC:0.965
	CWSGR [74]	50/49	fMRI	ACC:0.889; AUC:0.923
	MMTGCN (Ours)	191/179	fMRI	ACC:0.860; AUC:0.903
ADHD vs. HC	TMMC [75]	285/483	fMRI	ACC:0.797
	DeepFMRI [76]	118/98	fMRI	ACC:0.731
	4-D CNN [36]	359/429	fMRI	ACC:0.713; AUC: 0.800
	MMTGCN (Ours)	276/351	fMRI	ACC:0.728; AUC:0.763
WMH vs.HC	DNN [77]	104/96	MRI	ACC:0.725
	MMTGCN (Ours)	55/108	DTI	ACC:0.812; AUC:0.821

V. Discussion

A. Effectiveness of Multi-Scale Templates

In the proposed MMTGCN, four different templates are employed to construct coarse-to-fine functional/structural connectivity networks. To evaluate the effectiveness of multi-scale template learning, we perform experiments on three datasets, by comparing MMTGCN with its four single-template variants, denoted as “AAL116”, “CC200”, “BN273”, and “BASC327”, respectively. Since MTGCN also uses multiple templates, we compare MMTGCN with MTGCN in the experiments. Note that MTGCN employs a weighted fusion strategy for template fusion, while MMTGCN uses a mutual learning strategy. The results are reported in Fig. 3.

Fig. 3.

Performance of six different methods on three datasets. The proposed MMTGCN and MTGCN employ four templates, with the weighted fusion or template mutual learning for template fusion, respectively. Four single-template variants of MMTGCN are denoted as “AAL116”, “CC200”, “BN273”, and “BASC327”, respectively. We highlight the results that are statistically significantly different (with p < 0.05) using pairwise or McNemar t-test.

As we can see from Fig. 3, two multi-template methods (i.e., MMTGCN and MTGCN) generally outperform four single-template methods. These results imply that multi-scale templates can provide richer topology information for boosting the learning performance. Besides, Fig. 3 suggests that using a single template with more ROIs can not guarantee better performance, compared with that using templates with less ROIs. This is consistent with previous studies that generate brain connectivity networks based on multi-scale templates [55]. The possible reason is that more ROIs lead to high-dimensional node features that may contain redundant or noisy information, thereby reducing classification performance.

B. Effectiveness of Template Mutual Learning

To fuse results of multiple TGCNs, we develop a template mutual learning scheme for classification. Now we investigate its effectiveness, by comparing T TGCNs (T = 4 in MMTGCN and each TGCN corresponding to a specific template) with their variants based on independent learning. The experimental results are reported in Fig. 4, where the terms denoted as “*_s” and “*_m” represent TGCN without and with mutual learning for a specific template, respectively.

Fig. 4.

Performance of MMTGCN with and without template mutual learning. The terms denoted as “*_s” and “*_m” represent MMTGCN without and with template mutual learning, respectively. We highlight the results that are statistically significantly different (with p < 0.05) using pairwise t-test.

As we can see from Fig. 4, TGCNs with mutual learning are superior to their counterparts in most cases. For instance, when collaborative training is conducted through mutual learning, each of four TGCNs achieves at least 2% improvement in terms of ACC values on each dataset, compared with their independent learning peers. The underlying reason could be that the proposed template mutual learning strategy helps to maintain the internal consistency between multi-scale TGCNs by learning each TGCN to match the probability estimate of its T – 1 peers. As far as we know, MMTGCN is among the first attempt to employ the mutual learning strategy to fuse multi-scale FC/SC networks (defined by multiple templates) into a unified framework for brain disease classification.

C. Effectiveness of Triplet Sampling

We employ a triplet sampling strategy in MMTGCN to model the triplet relationship among subjects, and now we perform experiments to study its effectiveness. In this group of experiments, we compare two triplet sampling based methods (i.e., MMTGCN and MTGCN) with MSGCN that uses the pairwise sampling scheme, with results reported in Fig. 5.

Fig. 5.

Performance of methods using triplet sampling (i.e., MTGCN and MMTGCN) or pairwise sampling strategies (i.e., MSGCN).

As can be seen from Fig. 5, both MMTGCN and MTGCN perform better than MSGCN (with pairwise sampling) on three datasets in terms of both ACC and AUC values. This may be due to the higher-order relationship between subjects captured by triple sampling, which helps to discover the true data structure, thereby improving the classification results. Besides, considering that we usually have limited (e.g., tens or hundreds) subjects in neuroimaging datasets, triple sampling can be used as a flexible data augment strategy. More discussions on random pairing of training samples and network initialization can be found in the Supplementary Materials.

D. Limitations and Future Work

Several limitations need to be considered to further improve the current MMTGCN framework. 1) The proposed method is based on fixed group-level topology (determined by k-nn) of FC/SC matrices, which may introduce bias when modeling the true network topology. It’s interesting to design an end-to-end adaptive GCN model to capture topology of FC/SC matrices in a data driven manner, which will be one of our future work. 2) The current analysis is only based on a single modality, without considering the underlying association between structural and functional connectivity networks. It is desired to jointly analyze functional and structural connectivity patterns to help us better understand the pathophysiological characteristics of brain diseases. 3) We equally treat subjects from different imaging sites in this work, without considering the distribution difference of different sites. As another future work, we plan to perform data harmonization to analyze brain functional/structural connectivity networks.

VI. Conclusion

This letter proposed a mutual multi-scale triplet graph convolutional network (MMTGCN) for classification of brain disorders based on fMRI or dMRI data. Specifically, we first employ four different templates to construct brain functional/structural connectivity network for each subject. Then a triplet GCN (TGCN) is designed to learn network representations at each scale, with the triplet relationship among subjects explicitly incorporated into the learning process. A template mutual learning strategy is developed to train multi-scale TGCNs collaboratively for disease classification. Experimental results on three datasets with fMRI or dMRI suggest that MMTGCN outperforms several state-of-the-art methods.