Relations between Executive Functions and Academic Outcomes in Elementary School Children: A Meta-Analysis

Abstract

The primary goal of this study was to examine developmental patterns among the relations between components of EF (working memory [WM], inhibitory control, shifting), and academic outcomes (reading, mathematics, language) in elementary-school-age children. These relations were examined within the context of the development of EF and of academic skills utilizing an extension of the unity and diversity, intrinsic cognitive load, and dual process theories. Using meta-analytic methods, we summarized results from 305 studies with 292 independent samples, representing 64,167 elementary-school-age children (42–191 months old [M=101 months, SD=24.49 months]). Results indicated that accounting for general EF (by including the correlations among EF tasks in meta-analytic path models and accounting for effects between all three EF components and academic outcomes simultaneously) produced weaker relations between EF and academic skills than the bivariate relations which have been reported in prior meta-analytic reviews. However, although reduced, all relations between EF and academic outcomes remained significant throughout elementary school. Whereas WM was consistently moderately associated with reading, math, and oral language across development, the developmental trends for the relations between inhibitory control and shifting with academic outcomes varied based upon the academic skill examined. On the academic side, whereas the relations between reading and language skills with EF components varied throughout elementary school, few developmental changes were found in the relations between EF components and math skills across elementary school. Future directions and implications of findings for the conceptualization of the impact of EF on academics are discussed within the context of relevant theoretical models.

In recent years, executive function (EF) has garnered considerable attention across various areas of research. EF is a domain general cognitive construct consisting of separable components that enable individuals to achieve goal-directed outcomes (Miyake et al., 2000), such as focusing on and completing learning tasks in a school setting. Across studies, concurrent and longitudinal associations between EF and academic outcomes have been demonstrated (e.g., Allan et al., 2014; Isquith et al., 2004; McClelland et al., 2007). Poor EF is concurrently associated with difficulties in reading (e.g., Christopher et al., 2012; de Jong et al., 2009), mathematics (e.g., Andersson, 2008; Bull & Scerif, 2001), and language (e.g., Lonigan et al., 2016; McClelland et al., 2007), and it is longitudinally predictive of academic difficulties and school dropout (Duncan et al., 2007; Eisenberg et al., 2000; Vitaro et al., 2005). Furthermore, children diagnosed with specific learning disorders in reading, mathematics, or both, demonstrate poorer performance on EF tasks than do their typically developing peers (Swanson & Jerman, 2006; Swanson et al., 2009). Although the exact mechanisms through which EF affects academics are yet unknown, the substantial associations consistently reported between these constructs have resulted in growing interest in EF as a potential target for school-based interventions aimed at improving academic outcomes (Blair & Raver, 2014; Jacob & Parkinson, 2015; Schmitt et al., 2015). Consequently, a better understanding of the dynamic relations between EF and academic achievement across development may provide important opportunities for effective identification of children at risk for later academic difficulties as well as for the development of best-practice interventions and instructional strategies to best support children’s learning.

Several cognitive theories have been proposed that each may partially explain the relations between EF components and academic outcomes across childhood. The intrinsic cognitive load (Chandler & Sweller, 1991; Sweller, 1994) theory suggests that the relation between EF and academics is affected primarily by the complexity of academic tasks, regardless of age. Dual process theories (e.g., Evans & Stanovich, 2013) suggest that the relation between EF and academics is affected primarily by the difficulty of academic tasks and the ease with which academic tasks are completed. In this paper, we argue that although these theories offer an important theoretical foundation for understanding the relations between EF and academics, each is likely insufficient to explain the complex relations between EF and academics. We propose an application of both of these cognitive theories, which have been primarily utilized to explain phenomena in adults, to explain the relations between EF and academics in childhood--a time period during which both constructs are undergoing rapid development. As such, we propose an integrated theoretical model that accounts for the specific type of academic task being completed by the child, with consideration of both child- (e.g., developmental stage, degree to which specific skills are automatized) and task-level factors (e.g., inherent task complexity) that influence performance on such tasks. Although recent meta-analyses have examined the relations between EF and academics (e.g., Allan et al., 2014; Friso-van den Bos et al., 2013; Jacob & Parkinson, 2015; Swanson et al., 2009), including how such relations change across development (e.g., Peng et al., 2016; Peng et al., 2018; Yeniad et al., 2013), no meta-analysis has comprehensively examined the unique relations between each component of EF and children’s performance in reading, mathematics, and oral language, all of which are critical for academic success.

Theoretical Models Explaining the Relation between EF and Academics

In the intrinsic cognitive load theory, it is assumed that some academic tasks are inherently more complex than others, regardless of amount of instruction in or personal experience with these tasks. The theory proposes that more complex academic tasks utilize more cognitive/executive resources because these tasks require both the completion of problem solving directly related to the goal of the task as well as completion of other activities that require the use of cognitive resources (Chandler & Sweller, 1991; Sweller, 1994). For example, completing a math word problem requires greater cognitive resources than completing a simple addition problem. Specifically, whereas an addition problem allows for direct problem solving (e.g., accessing long-term memory), a word problem requires the completion of multiple steps and both sequential processing of information and storage demands (i.e., decoding the sentences, accessing background information from long-term memory, finding the mathematic terms, and determining the necessary mathematic operation, in addition to completing the direct problem solving of the math equation). In other words, academic tasks with more steps require greater cognitive resources than do academic tasks with fewer steps.

Dual process theories assume that two cognitive processing systems are involved in the performance of cognitively demanding tasks: autonomous processing and controlled processing (e.g., Evans & Stanovich, 2013). Autonomous processing includes cognitive processing that does not require controlled attention or input from higher order cognitive processes. It tends to be automatic, associative, and fast. Controlled processing requires engagement of higher-level cognitive processes. It is slow, deliberate, and sequential. Controlled processing places demands on a limited-resource cognitive system. Based upon dual process theories, the relation between EF and academics is based upon the difficulty of the academic task and the efficiency with which the academic task is completed (Evans & Stanovich, 2013). From a developmental perspective, throughout elementary school, academic skills continue to be learned and automatized; thus, the difficulty of academic tasks and the ease with which they are completed is strongly associated with exposure to and instruction within a given academic domain. Peng et al. (2018) hypothesized that as skills become more familiar--either through experience or learning, they become increasingly automatic and require fewer cognitive resources. Therefore, grade and age, presumably correlated with exposure and instruction, would be expected to play important moderating roles in the relation between EF and academics.

A distinction between intrinsic cognitive load and dual process theories is the emphasis they place on the complexity versus the difficulty of the academic tasks to be completed. Complexity, in this case, refers to the number of cognitive operations needed to successfully complete the task. In contrast, difficulty refers to the cognitive demands of a single task. Intrinsic cognitive load theory proposes that complexity is central to demand for cognitive resources whereas dual process theories propose that difficulty, among other factors, is central to demand for cognitive resources. In the case of complexity, the number of operations required is a part of the task and does not change with development or mastery. For example, reading comprehension is complex because regardless of age and experience it always requires multiple cognitive operations, including accurate and fluent decoding of words and identification of lexical entries of words. Alternatively, reading comprehension is difficult because it places many cognitive demands, including demands associated with maintenance of information in short-term memory, recall of information from long-term memory, integration of information from long- and short-term memory, integration of information across the text, making inferences, and monitoring comprehension (e.g., Cain et al., 2004; Oakhill & Cain, 2012; Perfetti, 2007). As discussed below, some component processes of reading become more automatized with increased instruction and exposure. Therefore, from an intrinsic cognitive load perspective, the contribution of EF to academic skills would be expected to remain stable over development because the number of cognitive operations remains constant. In contrast, from a dual process perspective, the contribution of EF to some academic skills should decrease over development because some aspects of the task become automatized and, therefore, less difficult. We hypothesize that the framework provided by dual process theories better accounts for the unique relations between EF and most academic skills (i.e., EF is more strongly associated with more difficult academic skills and the difficulty of academic skills varies across development); however, we remain open to the possibility that there are some academic skills for which no such developmental trends are observable in elementary school-age children. In such a case, intrinsic cognitive load theory would better account for the unique relations between EF and specific academic skills (i.e., EF is more strongly associated with more complex academic skills across development).

Both the concept of inherent cognitive demands that are consistent across development and the concept of task difficulty varying throughout development are likely insufficient to explain the complex relations between EF and academics. First, inherent demand and automaticity likely interact with one another. Specifically, higher-order academic skills (e.g., reading comprehension) are likely to require greater cognitive resources than are lower-order academic skills (e.g., decoding). These higher-order academic skills tend to be unconstrained in the sense that there is not a relatively small and finite set of information to be learned (i.e., there is no true mastery; Paris, 2005), and they require contributions of lower-order academic skills (e.g., reading comprehension requires decoding, fluency, and vocabulary; e.g., Hoover & Gough, 1990; Kim, 2015). As children get older and their experiences with these higher-order academic skills increase, so too does the degree to which performance on parts of tasks become automatized. Although children might not fully master such tasks, the cognitive demands required by these tasks are likely to decrease over time. In other words, although higher-order academic tasks are likely to always demand more cognitive resources than are lower-order academic tasks, the cognitive demands imposed decrease with age and experience.

Automaticity is complicated by several factors. Different academic tasks, even within the same academic domain, follow different developmental trajectories, and although some skills may be learned quickly and become automatized, other academic skills have the potential to continue developing throughout the lifespan (Paris, 2005). Thus, examining specific academic skills (e.g., decoding, reading comprehension, calculation), rather than broad classes of academic skills (i.e., reading, math), is vital to understanding the impact of EF on academic achievement. Additionally, assessments of academic tasks are often designed to increase in complexity as children achieve mastery of a specific skillset (e.g., a shift in content of math assessments from addition of single-digit numbers to addition of double-digit numbers), and, although such subskills may become automatized, children may not completely master the broader skill being assessed (e.g., addition skills). Similarly, as the relative cognitive demands imposed by a higher-order academic task decreases due to familiarity or automaticity, the specific demands of that task are likely to change (e.g., word problems requiring computation with whole numbers vs. word problems requiring computation with fractions), decreasing the level of automaticity and increasing the cognitive demands.

The relation between EF and academics also is likely to be impacted by the developmental trajectory of EF, which varies depending on the specific EF skills examined. The ages at which each component of EF is most impactful for each academic domain are unknown. To articulate the relation between EF and academics in childhood fully, a more complex model is needed than what is offered by either the intrinsic cognitive load or duel process theories. We propose an extension of these theories within the context of a developmental lens that emphasizes the importance of the specific components of EF (e.g., working memory, inhibitory control, shifting) and the specific academic task being examined--rather than the broad category in which these tasks fall--as well as the fact that these skills are being examined during a time at which they are continuing to develop. According to this framework, the importance of specific components of EF for a specific academic task will change across development, as (a) children’s experience, familiarity, and exposure to academic tasks increases and the cognitive demands of such tasks decrease, and (b) specific components of EF emerge as distinct constructs.

Defining Executive Function

The most common theoretical model of EF is the unity and diversity model, in which EF is characterized as three separable components: inhibitory control, working memory (WM), and shifting that represent distinct cognitive abilities (Teuber, 1972; Miyake, 2000; Miyake & Friedman, 2012). Inhibitory control is defined as the ability to inhibit a dominant response in favor of a subdominant response. WM is defined as the ability to maintain, update, and manipulate information within memory. Shifting is defined as the ability to switch attention between mental sets or tasks, or the ability to engage and disengage with specific aspects within tasks (Miyake et al., 2000; Miyake & Friedman, 2012). The unity and diversity model also assumes that these three components, in part, draw from a general underlying cognitive ability, representing unity among these components (Snyder et al., 2015).

EF is first evident in infancy (e.g., Pelphrey et al., 2004; Reznick et al., 2004), and exhibits substantial development between the ages of three and nine (e.g., Anderson, 2002; Diamond & Taylor, 1996; Espy et al., 1999). However, the three EF components appear to have different developmental trajectories that affect the age at which a component is measurable as a distinct construct. Whereas inhibitory control and WM are measurable as distinct constructs in early childhood and throughout elementary school, shifting develops in late childhood and early adolescence (e.g., Best & Miller, 2010). Prior to school entry and into early elementary school, the results of some factor analytic studies indicate that EF is best characterized by a single factor (e.g., Willoughby et al., 2010; Wiebe et al., 2011); however, results of other studies indicate that in preschool EF is best characterized as distinct but related WM and inhibitory control factors (e.g., Lerner & Lonigan, 2016). At some point in adolescence, all three components of EF emerge as separate factors (e.g., Lehto et al., 2003; Shing et al., 2010), and, by early adulthood, factor analytic studies indicate that EF may be best characterized by separate WM and Shifting factors and a common overarching EF factor that subsumes inhibitory control (Friedman et al., 2008, 2011; Miyake & Friedman, 2012).

A significant problem in the examination of EF is task impurity. That is, isolated measurement of a single EF component is not possible because all EF tasks assess the construct of interest as well as common EF, non-EF processes related to task performance, and error (Shipstead et al., 2010; Snyder et al., 2015). For example, measures labeled as assessments of inhibitory control often require following a “do the opposite” rule (i.e., inhibit a dominant response in favor of a subdominant response). Although a measure of inhibitory control, such tasks also require maintenance of a set of rules within memory and manipulation of these rules based on the demands of each specific task item, requiring input from the WM system. Successful performance also likely requires shifting attention from distractors in the environment toward goal-directed activity. As a result, disentangling EF components, both theoretically and operationally, is difficult, and synthesizing results requires applying labels based on what is most prominently assessed while interpreting results within the context of task impurity. Thus, a full account of the relations between EF and academic skills cannot focus on a single EF dimension because any single EF dimension includes aspects of the other dimensions as well as common EF.

Most prior meta-analyses of the relation between EF and academic skills have focused on either EF in general (e.g., Booth et al., 2010; Jacob & Parkinson, 2015) or a single component of EF (e.g., WM, inhibitory control, shifting; Allan et al., 2014; Daneman & Merikle, 1996; Peng et al., 2016, 2018; Yeniad et al., 2013). As detailed above, EF appears to follow a developmental trajectory in terms of how distinct the components of EF are from each other. This developmental trajectory should affect the degree to which a component of EF could be specifically related to academic outcomes; that is, a component of EF that is not distinct from other EF components at a particular age cannot be uniquely related to an academic outcome. Moreover, because it is likely that different components of EF are related to academic skills via different mechanisms (see subsection below), different components of EF are likely to have stronger associations with some academic outcomes than with others, depending on the specific task requirements of the academic outcome. Additionally, as the nature or demand in academic outcomes changes across development, it is possible that mechanisms through which EF are related to some academic outcomes also change. Consequently, advancing the understanding of the relations between EF and academic outcomes, including the potential mechanisms responsible for these relations, requires (a) consideration of all EF components, (b) consideration of whether a relation is specific to a particular component of EF or is the result of EF generally, (c) consideration of the specific academic outcome, and (d) consideration of both the development of EF and the development of specific academic skills.

Defining Academic Outcomes

Academic achievement encompasses a wide array of content areas. The most common content areas taught and assessed throughout elementary school are English language arts, math, social studies (or history), and science (Common Core State Standards Initiative, 2010), with English language arts and math acting as foundational skills for all other academic domains. Within the context of elementary school, instruction in social studies and science are largely integrated within reading instruction (i.e., taught by readings from textbooks and picture books) and science instruction is often combined within a broader math/STEM (science, technology, engineering, and mathematics) program. To examine the relation between EF and these foundational academic skills, our focus in this study is on the skills of reading, oral language, and math. What follows is a discussion of each of these content areas and the different component skills within each content area.

Reading skills.

There are multiple taxonomies of reading (e.g., Carver, 1997; Ehri, 2005; National Early Literacy Panel [NELP], 2008; National Institute of Child Health and Human Development [NICHD], 2000) that cover different aspects of reading and reading-related skills. For instance, the National Reading Panel Report (NICHD, 2000) was organized around findings in five areas: phonological awareness, phonics, fluency, reading comprehension, and vocabulary. The NELP (2008) examined three reading outcomes: decoding, fluency, and reading comprehension. Most reading assessments utilize some variant of the three domains used by the NELP. Decoding is the ability to translate printed words into speech and is most commonly measured as the accuracy with which single words can be read aloud. In decoding, words can be processed phonologically (i.e., translating graphemes into phonemes and then mapping the combination of phonemes onto a specific lexical representation), orthographically (i.e., visual recognition of letter patterns as a specific lexical representation), or both (Coltheart, 2005; Seidenberg & McClelland, 1989). Early in the process of learning to read, children tend to rely on phonological processing. Through repeated exposure, however, words are mapped onto their phonological, orthographic, and lexical representations, allowing children to read words as sight words using the more efficient orthographic route. In a language like English, which has a more opaque orthography (i.e., inclusion of exception words that cannot be read using the letter-sound phonological route), children must directly map the orthographic pattern of some words onto their lexical representations. Reading fluency is the speed and efficiency with which words are read accurately and is most commonly measured as the number of words read from a list or in connected text in a fixed period of time. Reading comprehension is the understanding of the meaning of connected text and is typically measured as the accuracy or recall of, summaries of, or inferences made from written sentences, paragraphs, or longer passages.

Reading comprehension is a higher-level reading process that relies on accurate and fluent decoding and on linguistic comprehension (i.e., the understanding of language; Gough & Tunmer, 1986; Lonigan et al., 2018). Linguistic comprehension is typically measured as children’s oral language skills, as outlined below. Whereas reading comprehension, decoding, and fluency are reading skills (i.e., they all involve extraction of meaning from text), we argue that oral language represents a construct that, although necessary for successful reading comprehension, is not a reading skill. In other words, oral language is an academic content area that is necessary for but distinct from reading. Previous meta-analyses examining the relations between EF and academic outcomes have yielded varied results regarding the relations between EF and reading (Jacob & Parkinson, 2015; Peng et al., 2018). One possible explanation for these varied results is that some studies have included oral language measures (e.g., vocabulary) as estimates of reading ability (e.g., Peng et al., 2018) and others have excluded such measures (e.g., Jacob & Parkinson, 2015), making it difficult to determine the relative contribution of EF to these distinct academic constructs.

Oral language skills.

Bloom and Lahey (1978) offer a commonly accepted taxonomy of language organized around five language outcomes: vocabulary, phonology, syntax, pragmatics, and morphology. Most language assessments utilize a subset of the domains outlined by the Bloom and Lahey taxonomy. Results of recent studies examining parts of this taxonomy indicate that language domains are highly related, and that oral language can be explained by a subset of these domains (e.g., Foorman et al., 2015; Lonigan & Milburn, 2017). For example, Longian and Milburn (2017) found that oral language was best characterized by two highly related vocabulary and syntax constructs in preschool- and elementary-school-age children. Vocabulary is the lexicon of words that an individual can express, comprehend, or both in verbal interactions. Vocabulary is most commonly measured as the number of objects, actions, or attributes correctly named or defined (expressive vocabulary) or as the number of words correctly understood, as determined by the ability to choose a correct pictorial representation of a spoken word (receptive vocabulary). Syntax is the ability to accurately structure and construct sentences in accordance with the rules of language. Although not an original domain of Bloom and Lahey’s taxonomy, we argue that listening comprehension is an important additional domain of oral language. Listening comprehension is the ability to understand the meaning of verbally presented information and is typically measured as the accuracy in recall of, summaries of, or inferences made from verbally presented sentences, paragraphs, or passages. Listening comprehension is a higher-level process that relies on a foundational understanding of syntax and vocabulary.

Math skills.

As with reading, there are multiple taxonomies of math (e.g., Common Core State Standards Initiative, 2010; National Council of Teachers of Mathematics [NCTM], 1989) that are comprised of different aspects of math skills. The taxonomy proposed by NCTM (the Curriculum and Evaluation Standards for School Mathematics) was organized around five content areas (numbers and operations, algebra, geometry, measurement, and data analysis and probability) and five process standards (problem solving, reasoning and proofs, communication, connections, and representation). The majority of math education in the United States was organized based upon the five content areas outlined in by NCTM, until the release of the Common Core State Standards Initiative (2010), which expanded the list to eight content areas for elementary-school-age children (counting and cardinality, operations and algebraic thinking, number and operations [in base 10 and in fractions], measurement and data, geometry, ratios and proportional relationships, understanding the number system, expressions and equations, and statistics and probability). Both taxonomies were organized by grade bands, with the Common Core State Standards Initiative indicating that certain content areas were not applicable to specific grade levels. For instance, within the context of elementary school, counting and cardinality was only applicable to kindergarten instruction. Based upon these taxonomies, the content areas for which elementary-school-age children most consistently receive instruction include numbers and operations, algebra, geometry, and measurement. Most math assessments are designed to measure a combination of these content areas, rather than assessing content areas independently by domain--making evaluation of a single domain difficult. However, these assessments are well-designed to examine NCTM process standards. In elementary school, the most common formally assessed process standards are reasoning of proofs and problem solving. Reasoning of proofs is often referred to as either math calculation (i.e., the ability to accurately complete math equations without a timed component) or math fluency (i.e., the ability to accurately complete math equations with a timed component). Problem solving is the ability to generate and solve an equation based upon information presented within the context of a passage.

The constrained and unconstrained model.

The constrained and unconstrained model of reading development (Paris, 2005) offers a framework within which the development of individual reading, oral language, and math skills can be considered. The constrained and unconstrained model proposes that academic skills can be categorized as constrained or unconstrained based upon the ability to master or automatize these skills. Constrained skills involve those skills for which the pool of knowledge to be learned is relatively small and finite (e.g., 26 letters of the alphabet, 44 phonemes in the English language, 10 digits). Constrained skills can, therefore, be completely mastered and automatized. Unconstrained skills involve skills for which the pool of knowledge to be learned is a relatively limitless set (e.g., vocabulary) and for which mastery continues developing throughout the lifespan. These skills are less likely to be automatized.

Based upon the constrained and unconstrained model, we hypothesize that letter knowledge, phonological awareness, decoding, and syntax are constrained skills, that reading fluency is less constrained, and that vocabulary, and listening and reading comprehension are the least constrained. Although Paris specifically highlighted reading skills in this framework, we further hypothesize that there are also constrained and unconstrained mathematics skills. For example, number recognition and counting are relatively constrained skills. Although numbers continue to infinity, numbers are based on the base-10 system, meaning that children need only learn the digits 0–9 and how to apply the base-10 system to these numbers. Math fluency and problem solving are less constrained skills because they involve the combined application of two finite skills: math operations (e.g., addition, subtraction, multiplication, division) and number recognition. Word problem solving is the least constrained because it involves a relatively infinite combination of reading or listening comprehension (themselves unconstrained skills), math operations, and problem solving.

Consideration of constrained versus unconstrained skills is important to the framework we propose for examining the relation between EF and academics. Constrained skills are those skills that are most likely to become automatized early in development and only place a demand on EF until they are mastered. For example, typically developing adolescents do not need to sound out graphemes and blend phonemes to read words; they are able to sight read by drawing on information in long-term memory without substantial executive demands. In contrast, unconstrained skills can place a substantial demand on EF, as they are likely to both have greater intrinsic cognitive loads and become automatized more slowly or not at all due to task difficulty.

Understanding Relations between EF Components and Academics

Multiple hypotheses have been proposed for the underlying mechanisms through which the components of EF impact academic achievement. Based upon findings derived from the multicomponent model of WM (Baddeley, 1986), WM is hypothesized to play a particularly important role in reading by allowing the establishment of connections between graphemes and phonemes when decoding (Baddeley, 1979; McDougall et al., 1994), and allowing the coordination of processing information in text (e.g., decoding words), maintaining information (e.g., maintaining initial phonemes in memory while sounding out the rest of a word, maintaining previously read words in memory while retrieving new word meanings), and integrating information from long-term memory (e.g., Cain et al., 2004) to allow for effective reading comprehension. Similarly, WM plays an important role in math (e.g., DeStefano & Lefevre, 2004) by allowing for the maintenance and processing of information across the completion of multi-step arithmetic and word problems (e.g., Fürst & Hitch, 2000; Imbo & Vandierendonck, 2007; Imbo et al., 2007), allowing for counting and keeping track of operations while calculating (e.g., Noël et al., 2004), and allowing for completing math problems that require mental representation of the calculation, spatial awareness, or both (e.g., geometry, number line, carrying numbers; De Smedt et al., 2009; Lee & Kang, 2002; Trbovich & Lefevre, 2003). Overall, WM is necessary for all academic tasks inasmuch as they require both processing and storage or maintenance of information.

The relation between inhibitory control and academics is often explained within the context of the executive attention systems model (Posner & Rothbart, 2007), which hypothesizes that the attention system is composed of the abilities to alert, orient, and exert executive attention to stimuli in the environment. Based on this model, executive attention (which includes aspects of inhibitory control and shifting) is behaviorally important to academic achievement because it allows children to orient attention toward classroom activities and goal-directed behaviors while inhibiting desires and impulses that are counter to academic success (e.g., walking around the classroom instead of reading or attending to a toy instead of to the teacher). Cognitively, executive attention is important when reading, listening, or completing math problems because, among other things, incorrect answers or actions need to be inhibited (e.g., during reading and listening, incorrect word meanings need to be inhibited [e.g., homonyms, homophones, heteronyms], incorrect use of appropriate operations need to be inhibited when completing math problems [e.g., number carrying in addition, number borrowing in subtraction, use of common denominators in addition or subtraction of fractions]). Inhibitory control also allows for suppression of inappropriate problem solving strategies (Lubin et al., 2013), recall of related but incorrect number facts (e.g., retrieval of “5” rather than “6” for the equation “2 × 3 =”), and recall of prepotent number representations (e.g., prepotent response that larger numbers equate to larger magnitude whereas in fractions larger denominators equate to smaller magnitude; Bull & Lee, 2014).

Shifting affects reading and oral language via its impact on the ability to integrate new linguistic information with background knowledge (i.e., shifting attention between long-term storage and information from text or oral language), to monitor real-time comprehension (i.e., shifting attention between current information and previously learned information or read text), or to use metacognitive comprehension strategies such as stopping reading to seek out additional information to improve comprehension (e.g., Kieffer et al., 2013). The prevailing hypothesis about the mechanism through which shifting impacts math performance concerns the role of shifting on the ability to switch between operations/procedures, between problem solving strategies, and between steps within multistep problems (Andersson, 2008; Bull & Scerif, 2001).

Current Study

The purpose of this meta-analysis was to examine developmental changes in the relations of EF and academic outcomes across the elementary school years. To do so, we used meta-analytic path analyses to examine the relations between the three primary components of EF on specific academic skills, while controlling for the correlations between the components of EF (i.e., accounting for general EF). Our analyses are framed within the context of three cognitive theories, which we apply to elementary-school-age children (a time period in development when both EF and academics are undergoing rapid development) and consider from a developmental perspective. This led to the following hypotheses regarding the relations between EF and academic skills:

1. We hypothesized that controlling for general EF (by including the correlations among EF tasks in meta-analytic path models and accounting for effects between all three EF components and academics simultaneously) when evaluating relations between components of EF and specific academic skills would result in weaker relations between EF and academic skills than the bivariate relations which have been reported in prior meta-analytic reviews (e.g., accounting for the correlations between WM, inhibitory control, and shifting would decrease the relation between WM and reading as compared to examining the bivariate relation between WM and reading).

2. We predicted that WM and inhibitory control would each be more strongly predictive of academic outcomes in late-elementary school than in early-elementary school, as these components of EF become increasingly distinct across the elementary years (e.g., Lehto et al., 2003, Shing et al., 2010). In contrast, we predicted that shifting would not be uniquely predictive of academic outcomes, particularly in early-elementary school, as evidence suggests it is not measurably distinct from WM and inhibitory control until early adolescence (e.g., Best & Miller, 2010; Lee, Bull, & Ho, 2013; Lehto et al., 2003).

3. Given the different theoretical models explaining why EF is important for academics, both based upon the type of EF skill examined and the academic outcome examined, we considered these relations at as fine-grained a level as possible, given available data. Therefore, we examined these relations both at the level of broad academic skills (i.e., reading, oral language, and math) and at the level of specific academic skills. (e.g., word problem solving, math fluency, calculation). We hypothesized that the relative importance of EF skills for lower-order academic tasks, particularly those that are constrained and can be mastered and automatized (e.g., word reading), would be greater in the early-elementary school than in the late-elementary school. In contrast, we hypothesized that the relative importance of EF skills for higher-order academic tasks (e.g., reading comprehension) would either be consistent across the early- and late-elementary grades or would be more important in later grades than in earlier grades (as task difficulty increases to match advancement in skill development). Thus, we hypothesized that the difference in relations of EF with higher- and lower-order academic skills would widen across development.

Method

Literature Search and Coding

All analyses were based on research articles generated from a systematic database search from January 1960 through June 2017. Articles were sought as part of a larger study and included a term related to EF (e.g., “executive function,” “self-regulation”) and a term related to either academic skills (e.g., “reading ability,” “mathematics,”) or externalizing behaviors (e.g., “behavior disorder,” “Attention Deficit Hyperactivity Disorder,” “Oppositional Defiant Disorder”). For a full list of search terms see Supplemental Online Materials (SOM) Appendix A. This search was restricted to school-age children in kindergarten through sixth grade (i.e., children 5 – 12 years old). Studies in which 50% or more of the sample age- or grade-range fell within the inclusion criteria were retained, regardless of the number of children examined in each grade. Exclusion criteria included studies that did not report on novel quantitative data (e.g., meta-analyses, literature reviews, qualitative analyses), case studies, studies of children classified as English language learners or who were tested in their non-native/non-dominant language, or studies of children with gross neurological, sensory, or motor impairment, history of seizures, traumatic brain injury, tic disorders, intellectual disability, diagnosis of Autism Spectrum Disorder, extremely low birth weight, born addicted to or exposed to drugs or alcohol, currently addicted or dependent on drugs or alcohol, and incarcerated or hospitalized children. Studies including only externalizing behaviors as an outcome were not included in the current analyses. Only studies that included a report of bivariate correlations between a performance-based measure of EF¹ and either a measure of academic ability or measure of externalizing behavior problems were included.

Articles for this meta-analysis were identified primarily through a computer search of the PsychINFO, ERIC, and Medline databases. A hand search of citations in prior relevant reviews was also conducted. Unpublished literature was searched through Dissertation and Masters abstract indices in ProQuest via each of the three databases and by e-mailing researchers likely to have conducted work in this area. This process resulted in 10,859 articles retrieved (after duplicates were removed).

A team of six coders reviewed and coded the entirety of the 10,859 articles referenced above. Articles were reviewed for eligibility in two tiers. First titles and abstracts were reviewed for mention of exclusionary criteria. Then the methods and results sections of remaining articles were reviewed both for exclusionary criteria and inclusion of bivariate correlations. Twenty percent of these articles were double coded for eligibility (97% reliability was obtained). If bivariate correlations were missing but a study met all inclusion criteria, authors were contacted, and correlations were requested. Figure 1 depicts how many studies were excluded at each stage of data collection and screening. Of the 10,859 articles retrieved, 531 articles contained bivariate correlations between a performance-based measure of EF and either an academic measure or a measure of externalizing behavior (or authors provided bivariate correlations following email request) and met all inclusion criteria. These articles were then coded following the coding scheme detailed below. A random sample of 20% of the 531 articles was selected to be double coded by trained undergraduate research assistants. Inter-rater reliability was 97%. Discussion among raters, with the ultimate decision being made by the first author, resolved any coding conflicts. For the analyses in this study, only the subset of articles pertaining to the relation between EF and academic achievement in reading, math, or oral language were utilized. This resulted in the inclusion of 299 studies from 293 articles/dissertations (citations available in SOM Appendix B), representing 65,605 elementary school-age children.

Figure 1.

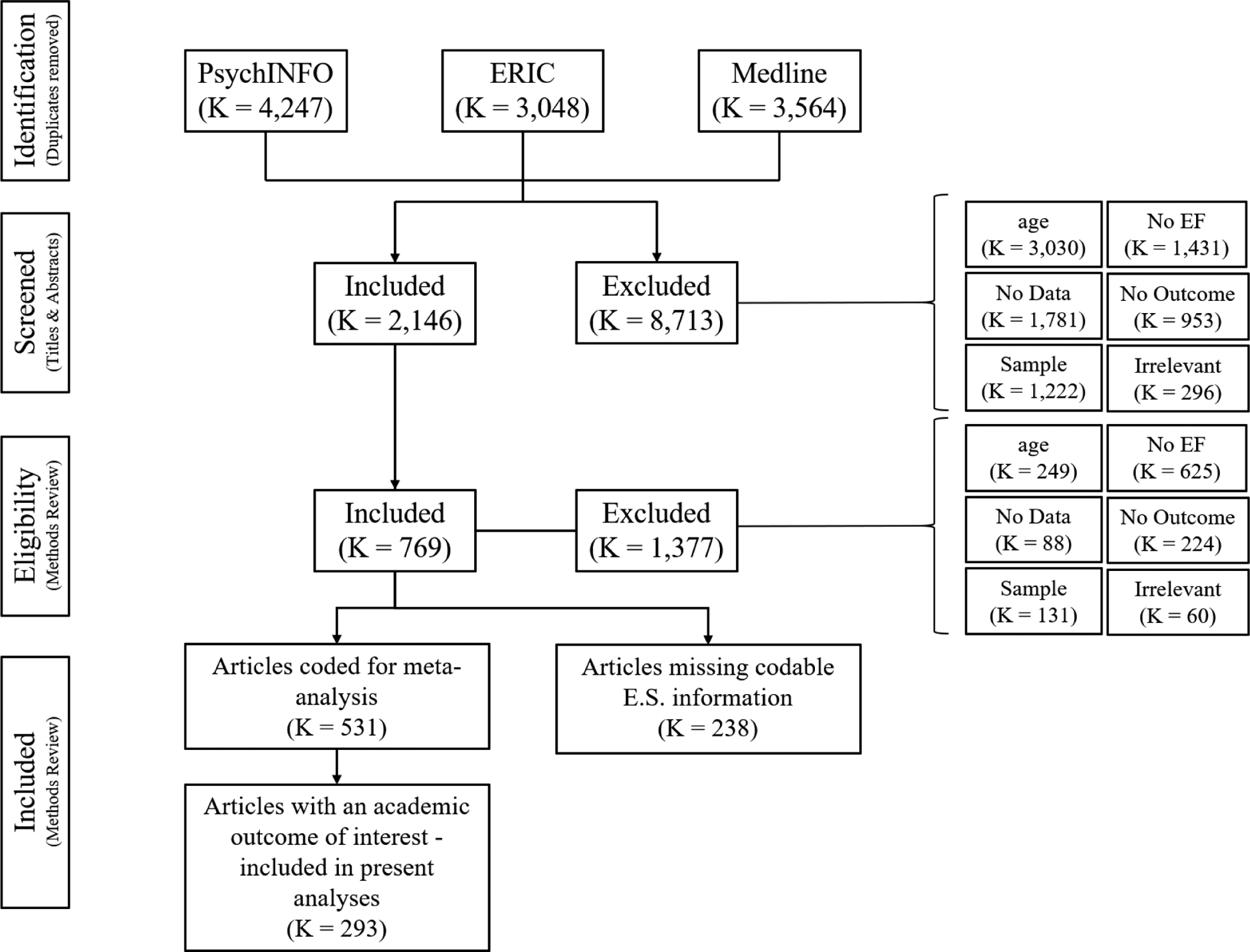
Flowchart of general meta-analysis procedures.

Note. K = number of articles.

Race and ethnicity information was not reported in 179 articles. Of the studies that reported race and ethnicity, 46.5% of the children were reported to be White, 17.2% African American/Black, 12.9% Hispanic, 1.1% Asian, 4.5% other or mixed race. Race/ethnicity was unknown or not reported for 17.9% of participants. Children’s mean age reported within study ranged from 42 to 191 months. Across studies, the average age of children was 100.81 months (SD = 24.49), with 31 studies failing to report age information. Of the 305 studies, 65 included mainly participants in kindergarten through first grade (5 – 7 years old), 44 included mainly participants in grades two through three (7 – 9 years old), and 64 included mainly participants in grades four through six (9–12 years old). Across studies, 54% of the participants were male; however, information on child sex was not reported in 36 studies (10,442 participants).

EF Measures

For the purposes of this study, EF components were operationalized based on the definitions of inhibitory control, WM, and shifting provided in Miyake et al. (2000). Tasks were coded based on the description of the task regardless of how the task was labeled in the source study. Specifically, a task was coded as a measure of inhibitory control if the outcome was primarily a measure of the ability to inhibit a predominant response in favor of a subdominant response, WM if the outcome was primarily a measure of the ability to maintain and manipulate information in short-term memory, and shifting if the outcome was primarily a measure of the ability to switch between mental sets or tasks. For a list of performance-based EF tasks that were included and how they were coded, see SOM Appendix C.

Tasks measuring skills tangentially related to EF (e.g., short-term and long-term memory) were not included in this meta-analysis, regardless of how they were labeled in their original study. Notably, forward-span tasks were not coded as measures of EF despite occasionally being labeled as WM in studies because such tasks primarily assess short-term rather than WM. Exceptions were made for forward-span tasks with substantial manipulation requirements (e.g., counting span tasks that require the child to maintain numbers in forward order while counting). Similarly, delay aversion and delay of gratification tasks were not included despite frequently being labeled as inhibitory control in studies.

Studies that reported on composites or factor scores made up of tasks that examined more than one EF skill (e.g., a composite of WM and shifting tasks) were coded as measures of general EF. These composites and factors were included in the examination of the relation between academic outcomes and general EF, but they were not included in analyses examining the relation between academic outcomes and WM, inhibitory control, or shifting. Composites and factors that included both performance-based tasks and either report-based measures of EF or performance-based tasks of skills tangential to EF (e.g., short-term memory, long-term memory, acting out behaviors) were coded as EF only if 50% or more of the included measures were performance-based tasks of inhibitory control, WM, or shifting.

Academic Measures

Academic outcomes were based upon scores on either standardized (1,830 effects) or unstandardized (783 effects) measures of academic achievement, administered either in the child’s classroom or in a laboratory setting. Standardized measures consisted of commonly used academic assessment tools (e.g., subtests from the Woodcock-Johnson-III and Kaufman Test of Educational Achievement; McGrew & Woodcock, 2001; Kaufman, 2014). Unstandardized measures included experimental and curriculum-based measures of academic achievement.

Across studies, a range of academic skills were examined. To provide the most accurate estimate of the relation between EF and reading, math, and oral language, academic outcomes were grouped based upon the skills they assessed. Measures were categorized as examining reading if the primary construct assessed was reading comprehension, word or non-word decoding, or reading fluency. Measures were categorized as examining math if the primary construct assessed was word problems, calculation, or math fluency. Measures were categorized as examining oral language if the primary construct assessed was listening comprehension, vocabulary (expressive or receptive), or grammar/syntax. These constructs were defined as:

Reading comprehension.

Reading comprehension is the ability to read and process text for meaning. Measures of reading comprehension required children to read passages and either answer questions about the literal or inferential meaning of the passage or provide missing information to complete the passage and demonstrate understanding.

Decoding.

Decoding is the ability to recognize letters/combinations of letters and match them with sounds (phonemes) to facilitate reading words, sentences, and passages. Measures of word and nonword decoding without a timed component were coded as decoding measures. Measures for which the outcome was reading speed were coded as reading fluency. Phonological Awareness tasks in which words are broken down into component sounds are often also labelled as decoding but were not included in this study because they assess skills related to but distinct from reading. Specifically, phonological awareness tasks which were spoken language tasks and did not require any direct reading of words or non-words were not included as decoding measures.

Reading fluency.

Reading fluency is the ability to quickly and efficiently read text. Measures of reading fluency required children to read words, nonwords, or passages with speed and accuracy.

Listening comprehension.

Listening comprehension is the ability to gather meaning from verbally presented information. Measures of listening comprehension required children to listen to sentences or passages and answer questions about the literal or inferential meaning of what they heard.

Vocabulary.

Vocabulary was split between expressive and receptive vocabulary measures. Receptive vocabulary is the ability to comprehend and respond to words. Most measures of receptive vocabulary either provided an array of pictures and asked children to point to the picture that best matched the word or orally provided the definition of a word and required them to choose a picture or word that best fit that definition. Expressive vocabulary was defined as the words that an individual can express or produce when speaking. Measures of expressive vocabulary either asked children to name a word depicted pictorially or provided a word and asked children the definition of that word.

Grammar/Syntax.

Syntax refers to the structure and construction of sentences. Measures of grammar/syntax visually or verbally present children with sentences or passages and require them to a) identify grammar or syntax errors and/or to correct these errors, b) provide a grammatically correct missing word(s), or c) identify a picture that depicted the sentence in order to demonstrate understanding of different aspects of grammar or sentence structure.

Word problems.

Math computations presented in context, requiring the child to generate and solve an equation based on the information provided.

Calculation.

Math calculation was operationalized as measures requiring basic math computations (addition, subtraction, multiplication, and division) without a timed component and presented outside the context of word problems. When measures contained an explicit timed component, they were coded as math fluency.

Math fluency.

Math fluency is the ability to recall and answer math computation questions quickly and efficiently. Although all measures of math fluency had a timed component, the amount of time allocated, and number of computations presented varied across measures.

Moderators

Age and Grade.

For the meta-analytic path-analyses, studies were split into early- and late-elementary school, due to constraints in the data that prohibited narrower age/grade bands to be examined. Early-elementary school was defined as kindergarten through second grade (5–8 years) and late-elementary school was defined as third through sixth grade (8–12 years).

Study quality.

Due to the risk of study quality biasing findings, study quality was assessed utilizing the NIH Quality Assessment Tool for Observational Cohort and Cross-sectional Studies (NIH National Heart, Lung and Blood Institute, 2013). The NIH Quality Assessment Tool results in a single rating for each study of either 0 (poor), 1 (fair), or 2 (good) quality, which is entered as a moderator to examine the impact of quality on main effects.

Statistical Analyses

Publication bias was assessed using Egger’s regression test (Egger et al. 1997; Sterne & Egger 2005) and contour corrected funnel plots. Egger’s test was conducted by modifying the three-level random effects models to include the standard error of the effect sizes as a moderator. Significant slope parameters for the standard error indicate a linear relation be effect size and standard error (i.e., presence of funnel plot asymmetry). Erring on the conservative side, analyses are considered biased if the intercept differs from zero at p ≤ .10 (Egger et al., 1997). Results of these assessments can be found in Supplemental Online Material (Appendix E).

Bivariate correlations between inhibitory control, WM, shifting and measures of academic outcomes served as effect sizes (r). Prior to combining effects, all correlations were converted to Fisher’s z-scores to reduce the impact of the correlations on the effect size variance calculation. After analyses were completed, effects were converted back to correlations.

Examining univariate relations.

Three-level meta-analyses (Maas et al., 2004) were conducted using the Metafor package for R (Viechtbauer, 2010) to estimate restricted maximum-likelihood random-effect models. Meta-analysis assumes statistical independence of effects. When multiple effect sizes are reported from the same study or from the same sample, dependency issues are introduced that reduce heterogeneity and may result in an increased chance of Type I error (e.g., Cheung, 2014). A common method to address this issue involves computing an average effect within study prior to conducting meta-analyses; however, averaging effects within studies has been criticized as artificially reducing the variance/heterogeneity between effects (Becker, 2000; Cheung & Chan, 2008; Van den Noortgate et al., 2013). Conducting a three-level meta-analysis allows for multiple effects from the same study to be retained within the meta-analyses and accounts for the non-independence of these effects by nesting them within study or sample (Cheung, 2015; Van den Noortgate et al., 2013). As per Cheung, a three-level meta-analysis is defined by the following equation:

$$y_{ij}={\beta }_0+u_{\left(2\right)ij}+u_{\left(3\right)j}+e_{ij}$$

Wherein y_ij represents the ith effect in the jth cluster. β₀ represents the average population, u represents study specific heterogeneity, and e represents sampling variance. For the purposes of our analyses the k value was based upon the number of effects rather than the number of studies. In these analyses, participants (Level 1) were nested within effect sizes (Level 2) which were nested within independent samples (Level 3). Independent samples were usually defined based upon publication. However, on several occasions, articles presented results from multiple studies with distinct samples. Additionally, there were several instances of partial or full overlap of samples across studies. To determine whether the same sample was used across multiple studies, a hand search of methods sections was conducted to determine whether a prior study was cited in the authors’ description of the sample. In addition, the list of authors for each study was examined to determine if the authors overlapped across studies. The method sections from any studies with at least one overlapping author (regardless of authorship position) were compared to determine the amount of overlap across samples². In cases in which 50% or more of the sample overlapped across studies, the nesting variable (Level 3) was coded as the sample rather than the study.

To examine the relation between EF components and broad academic domains, 16 three-level meta-analyses were conducting to examine the association between EF, WM, inhibitory control, and shifting with overall academic achievement, reading, math, and oral language. To examine the relation between EF components and specific academic subskills (reading comprehension, decoding, reading fluency, calculation, word problems, math fluency, listening comprehension, vocabulary, and grammar/syntax), 34 three-level meta-analyses were conducted. Notably, the relations between shifting and grammar/syntax and listening comprehension could not be examined due to too few studies reporting effects between these constructs.³

Heterogeneity in effect sizes is indicated based on the Q (Cochran, 1954) and I² statistics (Bryk & Raudenbush, 1992; Higgins & Thompson, 2002; Maas et al., 2004). Traditional Q statistics, calculated by summing the square deviations of study effect size estimates while weighting each effect estimate by its inverse variance, were utilized for the three-level meta-analyses (Cheung, 2014). Given that Q values are often overpowered to detect heterogeneity in meta-analyses with large numbers of studies and/or large sample sizes (Higgins et al., 2003), the I² statistic was also calculated. I² ranges from 0 to 100, where 100 indicates complete heterogeneity and 0 indicates complete homogeneity. Although I² can also be calculated separately for level 2 and 3 in three-level meta-analyses (Cheung, 2014), we chose to calculate a single I²; therefore, I² can be interpreted as the index or percentage of heterogeneity that is attributable to between study variability rather than sampling error (Cheung, 2015).

Examining unique relations.

Four meta-analytic path analyses were conducted using the metaSEM package in R (Cheung, 2015) to estimate restricted maximum-likelihood random-effect models. For each analysis, effects within study were averaged prior to analysis, such that each study was able to contribute a single effect per path. For example, if a study included one measure of WM, one measure of math achievement, and two measures of reading achievement, the study would contribute two effects to the analyses: the correlation between WM and math and the average of the correlations between WM and each measure of reading achievement. As such, k in these analyses represents the number of studies. All analyses were conducted in three steps. First, to optimize the number of studies that were included in analyses, effects were pooled across studies and the pooled effects were used to impute missing data (i.e., if a study was missing an effect for a specific path but included effects for other paths, the missing path was imputed to prevent listwise deletion of that study from analyses). Step one was then re-run with the imputed dataset, and, finally, these results were used to model the path analyses.

Four meta-analytic path analyses were conducted to examine (a) the unique influence of WM, inhibitory control, and shifting on reading, math, and oral language, (b) the unique influence of EF components on reading subskills, (c) the unique influence of EF components on math subskills, and (d) the unique influence of EF components on oral language subskills. In all models, WM, inhibitory control, and shifting were entered as correlated exogenous variables predicting academic subskills. Grammar/syntax and listening comprehension were dropped from the oral language model, because too few studies reported correlations between these academic skills and inhibitory control and shifting to accurately run the analysis.

To assess whether the relation between EF and academic outcomes varied as a product of age, all four models were examined again, in a series of eight meta-analytic subgroup path analyses, examining early-elementary school (kindergarten through second grade or five to eight years old) and late-elementary school (third through sixth grade or older than eight years old).

Results

Forest plots depicting the average correlation between EF components and reading, oral language, and math are available in SOM Appendix D. Most effect sizes and confidence intervals were to the right of the vertical line of no effect (r = .00), indicating a positive relation between EF component skills and academic domains. The possibility of publication bias across these overall effects was assessed using traditional and contour corrected funnel plots (SOM Figures S10–21a–b). Study effects appeared to be symmetrically spaced around the overall mean effect size, with the exception of the relation between inhibitory control and oral language. Only two of 12 Egger’s tests were statistically significant (the correlation between EF and oral language and the correlation between inhibitory control and oral language); making publication bias unlikely for most study effects. Additional tests of publication bias are reported in supplemental materials (SOM Appendix E Table S1).

The results of study quality moderation analyses (SOM Table S2) indicate that study quality did not affect the relations between EF and academic outcomes, except for the relation between inhibitory control and math for which studies with a fair rating were more likely to report stronger relations between inhibitory control and math than were studies with a good rating.

Univariate Relations

Average effect sizes for the association between EF components and overall academic ability, reading, math, and oral language domains are shown in Table 1. All effects were significantly greater than zero. All EF components were significantly related to all academic domains. Correlations ranged from .22 (shifting with oral language) to .39 (WM with math), and the largest correlations were consistently between WM and academic domains. For all combinations of EF and academic domains, both the Q and I² statistics indicated substantial heterogeneity of effect sizes between studies.

Table 1.

Average Effects of EF components with Academics

		95% CI		Variance (σ)
	Effect Size	LL	UL	Effect Level	Study Level	Q (df)	I2	K	m
EF with Academics	.33***	.31	.35	.02	.02	17,208.30*** (2,595)	84.92	2596	293
WM with Academics	.35***	.33	.37	.01	.02	8,381.18*** (1,661)	80.18	1662	250
IC with Academics	.26***	.23	.29	.02	.02	5,259.60*** (636)	87.91	637	108
Shifting with Academics	.26***	.22	.31	.01	.02	1,861.77*** (249)	86.63	250	56
EF with Reading	.32***	.30	.35	.02	.03	6,911.36*** (1,085)	84.30	1086	184
WM with Reading	.35***	.32	.38	.01	.03	3,723.37*** (730)	80.39	731	157
IC with Reading	.26***	.22	.29	.03	.01	2,081.52*** (240)	88.47	241	65
Shifting with Reading	.24***	.20	.27	.02	.002	448.20*** (89)	80.14	90	34
EF with Math	.36***	.33	.38	.01	.02	6,792.04*** (1033)	84.79	1034	144
WM with Math	.39***	.36	.41	.01	.01	2,832.00*** (625)	77.93	626	126
IC with Math	.29***	.24	.34	.01	.02	2,081.62*** (270)	87.03	271	59
Shifting with Math	.28***	.20	.35	.01	.04	1,166.01*** (123)	89.45	124	37
EF with Oral Language	.29***	.27	.32	.01	.02	3,007.48*** (449)	85.07	450	127
WM with Oral Language	.31***	.28	.35	.01	.02	1,563.27*** (280)	82.09	281	106
IC with Oral Language	.23***	.19	.27	.003	.01	850.40*** (123)	85.54	124	42
Shifting with Oral Language	.22**	.16	.29	.01	.01	137.74*** (34)	75.32	35	18

Note. Reading = effects for EF with comprehension, reading fluency, & decoding; Math = effects for EF with calculation, word problems, & math fluency; Oral Language = effects for grammar/syntax, listening comprehension, & vocabulary; Academics = Reading, Math, & Language skills combined. EF = combined WM, IC, & shifting; WM = working memory; IC = inhibitory control; K = number of effects; m = number of studies.

^*p < .05,

^**p < .01,

^***p < .001.

Analyses of academic subskills.

Analyses were conducted to examine whether the relations between EF components and reading, math, and oral language were driven by the relations between EF components and specific academic subskills. Because all EF components were determined to be equivalently related to word and non-word decoding (see SOM Table S4), these skills were examined together as overall decoding in subsequent analyses. Similarly, because all EF components were equivalently related to receptive and expressive vocabulary (see SOM Table S4), receptive and expressive vocabulary were combined as a single vocabulary outcome in subsequent analyses. WM, inhibitory control, and shifting were significantly related to all reading, math, and oral language (see Table 2) subskills. Across academic domains, subskills were most strongly associated with WM, except for math fluency, which was most strongly associated with inhibitory control. The relations between overall EF (the effects of WM, inhibitory control, and shifting combined) with reading, math, and oral language skills can be found in SOM Table S5.

Table 2.

Average Effects of EF components with Specific Reading, Math, and Language Subskills

		95% CI		Variance (σ)
	Effect Size	LL	UL	Effect Level	Study Level	Q	I2	K	m
Working Memory
Comprehension	.36***	.33	.39	.01	.02	1,028.91***	70.94	300	84
Reading Fluency	.25***	.21	.30	.01	.01	407.94***	71.56	117	38
Decoding	.37***	.32	.41	.01	.05	1,920.62***	85.47	280	90
Calculation	.37***	.34	.40	.004	.01	1,025.93***	70.66	302	79
Word Problems	.43***	.40	.47	.01	.01	854.82***	82.10	154	51
Math Fluency	.29***	.25	.33	.01	.01	359.53***	66.34	122	33
Grammar/Syntax	.37***	.28	.46	.003	.04	323.07***	83.59	54	24
Listening Comp	.37***	.31	.43	.01	.01	160.98***	80.12	33	18
Vocabulary	.29***	.26	.33	.01	.02	868.99***	80.55	170	84
Inhibitory Control
Comprehension	.28***	.21	.35	.001	.02	170.32***	74.75	44	21
Reading Fluency	.23***	.15	.31	.05	.01	858.83***	91.03	78	16
Decoding	.27***	.22	.33	.001	.02	615.22***	84.56	96	37
Calculation	.27***	.20	.33	.002	.03	581.58***	80.05	117	32
Word Problems	.33***	.25	.40	.01	.03	976.35***	90.17	97	22
Math Fluency	.36***	.27	.44	.02	.004	77.83***	71.73	23	12
Grammar/Syntax	.37***	.28	.46	.003	.04	323.07***	83.59	54	5
Listening Comp	.31***	.24	.38	.01	.00	23.45**	61.62	10	4
Vocabulary	.21***	.17	.26	.002	.01	764.54***	87.31	98	38
Shifting
Comprehension	.30***	.22	.34	.00	.02	85.02***	74.12	23	14
Reading Fluency	.23***	.14	.31	.04	.00	217.73***	88.52	26	10
Decoding	.20***	.13	.27	.003	.01	115.53***	74.03	31	13
Calculation	.29***	.19	.39	.01	.04	380.06***	88.16	46	19
Word Problems	.35***	.22	.47	.01	.06	400.64***	90.52	39	17
Math Fluency	.16***	.08	.23	.02	.00	98.34***	80.68	20	8
Grammar/Syntax	---	---	---	---	---	---	---	---	---
Listening Comp	---	---	---	---	---	---	---	---	---
Vocabulary	.20***	.14	.27	.01	.01	83.17***	65.13	30	16

Note. K = number of effects; m = number of studies; Comprehension = reading comprehension; Listening Comp = listening comprehension; df for Q can be calculated based upon K-1.

^*p < .05,

^**p < .01,

^***p < .001.

Unique Relations

Model 1: EF with academic domains.

Model 1 provided excellent fit to the data (see Appendix F for model fit statistics). When examined across elementary school, all three EF components were uniquely related to reading, math, and oral language (see Table 3). The strongest relations were with WM. The results of the chi-square difference tests (see Table 4) indicated that WM was significantly more strongly related to reading than were inhibitory control and shifting, and WM was more strongly related to oral language than was inhibitory control. WM was also significantly more strongly related to math than was inhibitory control. WM was more strongly related to math than to oral language and more strongly related to reading than to oral language, but it was equivalently related to reading and math.

Table 3.

Results of Meta-Analytic Path-Analyses

		Included Grades for Analytic Sample
		K – 6th		K – 2nd		3rd – 6th
	EF	β	CI	β	CI	β	CI
Broad Academics
Reading	IC	.15	.10 – .19	.19	.15 – .24	.08	.14 – .15
	WM	.27	.25 – .30	.26	.22 – .31	.29	.25 – .32
	SH	.12	.07 – .18	.15	.09 – .20	.10	.00 – .20
Math	IC	.18	.13 – .22	.20	.14 – .26	.15	.07 – .22
	WM	.29	.26 – .32	.29	.25 – .33	.28	.24 – .32
	SH	.17	.10 – .25	.23	.17 – .29	.14	.01 – .22
Oral Language	IC	.12	.07 – .18	.18	.12 – .25	.03	−.05 – .11
	WM	.23	.20 – .26	.24	.20 – .28	.24	.19 – .28
	SH	.15	.09 – .21	.18	.12 – .25	.13	.04 – .21
Reading Subskills
Comprehension	IC	.16	.08 – .23	.24	.20 – .28	.10	−.02 – .21
	WM	.26	.21 – .30	.24	.18 – .30	.29	.23 – .35
	SH	.14	.03 – .25	.19	.07 – .31	.08	−.09 – .25
Decoding	IC	.13	.08 – .18	.18	.13 – .23	.07	−.01 – .15
	WM	.27	.23 – .31	.24	.19 – .28	.30	.25 – .35
	SH	.11	.06 – .16	.12	.08 – .16	.05	−.09 – .18
Fluency	IC	.16	.07 – .25	.10	−.13 – .32	.21	.13 – .28
	WM	.17	.13 – .22	.24	.15 – .32	.15	.09 – .20
	SH	.11	.05 – .25	.14	−.02 – .30	.15	.00 – .30
Math Subskills
Word Problems	IC	.19	.12 – .26	.17	.09 – .24	.21	.03 – .39
	WM	.32	.27 – .36	.33	.27 – .39	.31	.25 – .37
	SH	.29	.23 – .34	.29	.22 – .37	.28	.10 – .45
Fluency	IC	.25	.13 – .37	---	---	.27	.12 – .42
	WM	.23	.18 – .27	---	---	.20	.15 – .24
	SH	.02	−.08 – .12	---	---	.02	−.10 – .12
Calculation	IC	.15	.08 – .21	.16	.07 – .25	.12	.02 – .22
	WM	.28	.25 – .31	.30	.26 – .34	.27	.22 – .31
	SH	.19	.11 – .26	.19	.13 – .25	.21	.05 – .36
Oral Language Subskills
Vocabulary	IC	.11	.04 – .17	.12	.04 – .21	.08	−.04 – .20
	WM	.25	.21 – .29	.22	.14 – .29	.27	.22 – .32
	SH	.16	.08 – .24	.25	.15 – .36	---	---
Syntax	IC	---	---	---	---	.26	.17 – .36
	WM	---	---	---	---	.29	.16 – .42
	SH	---	---	---	---	---	---
Comprehension	IC	---	---	---	---	.03	−.22 – .28
	WM	---	---	---	---	.29	.21 – .37
	SH	---	---	---	---	---	---

^*= p < .05;

^**= p < .01;

^***= p < .01

Table 4.

Chi-square difference tests examining the differences between paths in models pertaining to academic domains

		Chi Square constrained model
Constrained Paths		Full Sample (5–12 years)	Grades K-2 (5–8years)	Grades 3–6 (>8 years)
IC – Reading	IC – Math	0.85	0.07	1.68
IC – Reading	IC – Language	0.50	0.05	1.08
IC – Math	IC – Language	2.09	0.19	4.94*
WM – Reading	WM – Math	0.41	0.76	0.02
WM – Reading	WM – Language	4.28*	0.65	2.96
WM – Math	WM – Language	7.03**	2.75	2.34
SH – Reading	SH – Math	1.24	5.07*	0.23
SH – Reading	SH – Language	0.55	0.78	0.16
SH – Math	SH – Language	0.20	1.30	0.03
IC – Reading	WM – Reading	19.76***	4.10*	23.12***
IC – Reading	SH – Reading	0.39	1.30	0.05
WM – Reading	SH – Reading	17.29***	8.14**	9.00**
IC – Math	WM – Math	13.01***	4.69*	9.78**
IC – Math	SH – Math	0.002	.46	0.01
WM – Math	SH – Math	5.67*	1.74	3.34
IC – Language	WM – Language	8.05**	1.67	16.61***
IC – Language	SH – Language	0.44	0.00	1.98
WM – Language	SH – Language	3.74	1.46	3.83*

Note. Chi square for original model = 0; df for original model = 0. For all constrained models df = 1. Bolded paths indicate larger effects. WM = working memory; IC = inhibitory control; SH = shifting; Language = Oral Language. Critical value 2.84.

^*= p < .05;

^**= p < .01;

^***= p < .01

Model 1 was examined in two subgroup analyses to determine whether the effects differed between early- and late-elementary school (Table 3). As was the case with the overall sample, WM, inhibitory control, and shifting were each uniquely predictive of reading, math, and oral language when examined within the context of early-elementary school. In late-elementary school, WM and shifting continued to significantly predict all academic domains. However, inhibitory control no longer significantly predicted oral language in late-elementary school. Comparison of confidence intervals for effects in early- and late-elementary school indicate that the relations between inhibitory control and reading and oral language and the relation between shifting and math decreased significantly from early- to late-elementary school. In both early- and late-elementary school, WM was more strongly related to reading than were inhibitory control and shifting. Additionally, WM was more strongly related to math than was inhibitory control and shifting throughout elementary school, and WM was more strongly related to oral language than was inhibitory control and shifting in late-elementary school.

Model 2: EF with reading subskills.

Model 2 provided excellent fit to the data (see Appendix F for model fit statistics). All three EF components were uniquely related to reading comprehension, fluency, and decoding, with the strongest relations for WM (see Table 3). Substantial age-related effects were found for Model 2 (see Table 3). In both early- and late-elementary school, WM was moderately related to all reading subskills. In early-elementary school, both inhibitory control and shifting were significantly related to reading comprehension and decoding but not to reading fluency. In contrast, in late-elementary school, both inhibitory control and shifting were significantly related to reading fluency but not to comprehension or to decoding.

The results of the chi-square difference tests (see Table 5) indicated that when examined across elementary school, WM was more strongly related to decoding than were inhibitory control and shifting, and WM was more strongly related to comprehension than was inhibitory control. WM continued to be more strongly related to decoding than was shifting regardless of the age examined; however, WM was only more strongly related to decoding and comprehension than was inhibitory control when examined in late-elementary school. Additionally, in the overall model, WM was more strongly related to decoding and comprehension than it was to reading fluency. However, these differences were only found in later-elementary school; in early-elementary school WM was equally related to all reading skills.

Table 5.

Chi-square difference tests examining the differences between paths in models pertaining to reading skills

		Chi Square constrained model
Paths Constrained		Full Sample (5–12 years)	Grades K-2 (5–8years)	Grades 3–6 (>8 years)
IC – Comprehension	IC – Fluency	0.002	1.50	2.31
IC – Comprehension	IC – WNW	0.33	4.08*	0.16
IC – Fluency	IC – WNW	0.33	0.46	5.76*
WM – Comprehension	WM – Fluency	6.69**	0.01	10.98***
WM – Comprehension	WM – WNW	0.14	0.003	0.09
WM – Fluency	WM – WNW	10.26**	0.003	15.12***
SH – Comprehension	SH – Fluency	0.02	0.22	0.38
SH – Comprehension	SH – WNW	0.18	1.11	0.09
SH – Fluency	SH – WNW	0.44	0.05	1.08
IC – Comprehension	WM – Comprehension	3.99*	0.00	6.48**
IC – Comprehension	SH – Comprehension	0.07	0.49	0.02
WM – Comprehension	SH – Comprehension	2.76	0.40	3.74*
IC – Fluency	WM – Fluency	0.06	0.99	1.11
IC – Fluency	SH – Fluency	0.02	0.07	0.34
WM – Fluency	SH – Fluency	0.15	0.81	0.001
IC – WNW	WM – WNW	15.74***	2.50	18.71***
IC – WNW	SH – WNW	0.29	2.39	0.05
WM – WNW	SH – WNW	18.05***	10.63**	9.06**

Note. Chi square for original model = 0; df for original model = 0. For all constrained models df = 1. Bolded paths indicate larger effects. WM = working memory; IC = inhibitory control; SH = shifting WNW= word and nonword decoding.

^*= p < .05;

^**= p < .01;

^***= p < .01

Model 3: EF with math subskills.

Model 3 provided excellent fit to the data (see Appendix F for model fit statistics). All three EF components were uniquely related to word problems, math fluency, and calculation, with one exception--shifting was not uniquely related to math fluency (see Table 3). However, few studies reported correlations between shifting and math fluency; therefore, this non-significant relation should be interpreted with caution. The relations between EF components and math subskills were highly consistent across elementary school, with two notable exceptions (see Table 3). First, in early-elementary school, too few studies reported relations of inhibitory control and shifting with math fluency; therefore, math fluency was dropped from the model. Second, comparison of confidence intervals indicated that the relation between WM and word problems was significantly stronger in late-elementary school than it was in early-elementary school.

The results of the chi-square difference tests (see Table 6) indicated that in the overall sample WM was more strongly related to word problem solving and calculation than was inhibitory control, and WM was more strongly related to calculation and math fluency than was shifting. Shifting was more strongly related to word problem solving than was inhibitory control in early-elementary school and inhibitory control was more strongly related to math fluency than was shifting in late elementary school. Additionally, WM was more strongly related to word problems and calculations than it was to fluency in late-elementary school. Finally, shifting was more strongly related to word problem solving and calculations than to math fluency in late-elementary school.

Table 6.

Chi-square difference tests examining the differences between paths in models pertaining to math skills

		Chi Square constrained model
Paths Constrained		Full Sample (5–12 years)	Grades K-2 (5–8years)	Grades 3–6 (>8 years)
IC – Word Prob	IC – Fluency	0.70	---	0.21
IC – Word Prob	IC – Calculation	0.98	0.01	0.80
IC – Fluency	IC – Calculation	2.27	---	2.57
WM – Word Prob	WM – Fluency	10.07**	---	8.38**
WM – Word Prob	WM – Calculation	2.07	0.49	1.85
WM – Fluency	WM – Calculation	4.93*	---	4.29*
SH – Word Prob	SH – Fluency	24.05***	---	6.92**
SH – Word Prob	SH – Calculation	4.61*	4.73*	0.41
SH – Fluency	SH – Calculation	7.43**	---	4.08*
IC – Word Prob	WM – Word Prob	7.87**	8.58**	0.98
IC – Word Prob	SH – Word Prob	3.55*	3.89*	0.22
WM – Word Prob	SH – Word Prob	0.80	0.42	0.11
IC – Fluency	WM – Fluency	0.13	---	0.60
IC – Fluency	SH – Fluency	6.44**	---	5.17*
WM – Fluency	SH – Fluency	12.26***	---	8.01**
IC – Calculation	WM – Calculation	11.79***	6.29*	6.55**
IC – Calculation	SH – Calculation	0.49	0.17	0.60
WM – Calculation	SH – Calculation	4.13*	7.74**	0.43

Note. Chi square for original model = 0; df for original model = 0. For all constrained models df = 1. Bolded paths indicate larger effects. WM = working memory; IC = inhibitory control; SH = shifting; Word Prob = word problems.

^*= p < .05;

^**= p < .01;

^***= p < .01

Model 4: EF with oral language subskills.

Model 4 provided excellent fit to the data (see Appendix F for model fit statistics). All three EF components were uniquely related to vocabulary, with the strongest relation between WM and vocabulary (see Table 3). The results of the chi-square difference tests (see Table 7) indicated that WM was more strongly related to vocabulary than was inhibitory control in late-elementary school but not in early-elementary school. As noted earlier, grammar/syntax and listening comprehension were not included in the model in early-elementary (Table 3) school because too few studies reported correlations between these academic skills and inhibitory control and shifting. However, in late-elementary school, enough studies reported correlations of inhibitory control with grammar/syntax and listening comprehension to be included in the analyses. As in early-elementary school, in late-elementary school WM was significantly related to vocabulary as well as to grammar/syntax and listening comprehension (Table 3). In contrast, inhibitory control was significantly related to grammar/syntax, but not to vocabulary or listening comprehension in late-elementary school.

Table 7.

Chi-square difference tests examining the differences between paths in models pertaining to oral language skills

		Chi Square constrained model
	Constrained Paths	Full Sample (5–12 years)	Grades K-2 (5–8years)	Grades 3–6 (>8 years)
IC – Vocabulary	IC – Syntax	---	---	6.99**
IC – Vocabulary	IC – L. Comp	---	---	0.13
IC – Syntax	IC – L. Comp	---	---	3.21
WM – Vocabulary	WM – Syntax	---	---	0.09
WM – Vocabulary	WM – L. Comp	---	---	0.14
WM – Syntax	WM – L. Comp	---	---	0.001
IC – Vocabulary	WM – Vocabulary	10.22**	2.04	8.82**
IC – Vocabulary	SH – Vocabulary	0.78	2.85	---
WM – Vocabulary	SH – Vocabulary	3.72	0.19	---
IC – Syntax	WM – Syntax	---	---	0.10
IC – Syntax	SH – Syntax	---	---	---
WM – Syntax	SH – Syntax	---	---	---
IC – L. Comp	WM – L. Comp	---	---	3.62
IC – L. Comp	SH – L. Comp	---	---	---
WM – L. Comp	SH – L. Comp	---	---	---

Note. Chi square for original model = 0; df for original model = 0. For all constrained models df = 1. Bolded paths indicate larger effects. WM = working memory; IC = inhibitory control; SH = shifting; L. Comp = Listening Comprehension.

^**= p < .01

Discussion

The primary goal of this study was to examine developmental patterns among the relations between components of EF (i.e., working memory, inhibitory control, shifting) and academic skills (i.e., reading, mathematics, oral language). This study extends the results of previous meta-analyses via the inclusion of oral language skills and the inclusion of all three components of EF. Building off of several cognitive theories, including dual process (Evans & Stanovich, 2013) and intrinsic cognitive load (Chandler & Sweller, 1991) theories, we situated our investigation within a developmental framework that considered the key roles of child- (e.g., age, degree to which certain academic skills are automatized) and task-level factors (e.g., the inherent difficulty of academic tasks) in the relations between EF and academic skills. We made three specific predictions based on this framework. First, controlling for general EF by accounting for the correlations between specific components of EF and accounting for effects between all three EF components and academics simultaneously would reduce the overall magnitude of relations between components of EF and academic outcomes. Second, WM and inhibitory control would be more predictive of academic outcomes in late- versus early-elementary school as those components of EF become increasingly distinct, whereas shifting would not uniquely predict academic outcomes as it does not emerge as a distinct component of EF until adolescence (Lee et al., 2013). Third, we expected that EF would be most strongly related to constrained academic skills in early-elementary school (before such skills are automatized), whereas EF would be most strongly related to complex, unconstrained academic skills in late-elementary school. Overall, the results of our meta-analysis were consistent with our hypotheses, although some patterns of results for specific components of EF and academic skills varied. Specific results pertaining to each hypothesis are discussed below.

Relations Between Components of EF and General Academic Skills

Meta-analytic path analyses indicated that accounting for the effect of general EF (by accounting for the correlation between EF components and accounting for effects between all three EF components and academics simultaneously) resulted in weaker relations between EF and academic skills than the bivariate relations that have been reported in prior meta-analytic reviews (e.g., Peng et al., 2018). This is consistent with the “unity” component of the unity and diversity theory of EF and suggests that throughout elementary school general executive ability plays an important role in academic achievement. Although the size of the relations between specific EF components and academic skills were reduced when controlling for general EF (with the exception of the correlations of WM and shifting with vocabulary), all components of EF remained uniquely predictive of all academic outcomes in the broad sample of children in kindergarten through sixth grade. Thus, although general EF plays an important role in academic achievement, the specific components of EF also appear to be uniquely important for reading, math, and oral language. This pattern of findings is consistent with prior research indicating broad, consistent relations between EF and academic achievement (e.g., Allan et al., 2014; Jacob & Parkinson, 2015, Peng et al., 2018; Friso-van den Bos et al., 2013). However, the relatively small magnitude of relations between the components of EF and academic achievement suggest that improvement in any specific domain of EF is unlikely to improve academic achievement substantially. This is consistent with Jacob and Parkinson’s (2015) conclusion that EF interventions do not significantly improve academic achievement. Recent theory and evidence suggest the relations between EF and academic achievement are reciprocal (Peng & Kievit, 2020), which may explain the consistent relations across elementary school observed in this study. Future research could leverage comprehensive longitudinal data to evaluate potential bi-directionality in the relations between EF and academic achievement.

Developmental Changes in the Relations between EF and General Academic Skills

WM was moderately associated with reading, math, and oral language in both early- and late-elementary school when all academic subskills were considered simultaneously. In contrast, the relations between inhibitory control and shifting across early- and late-elementary school varied by skill. Inhibitory control was more strongly related to academic achievement in early-elementary school than in late-elementary school (although the relation between inhibitory control and math was not significantly different across early and late elementary school). Although the magnitude of the relations between shifting and academic achievement were generally larger in early- than in late-elementary school, this difference was only statistically significant for math achievement.

It is important to consider this pattern of results within a developmental framework, as EF and academic skills continue to develop throughout elementary school. Prior research indicates that WM and inhibitory control become increasingly separable throughout the elementary school years (e.g., Lehto et al., 2003; Shing et al., 2010), whereas shifting is not a distinct component of EF in the elementary years (Lee et al., 2013). Consistent with such evidence, we hypothesized that in early-elementary school relations between EF and academics would be accounted for mostly by general EF, whereas in late-elementary school the aspects of EF unique to WM and inhibitory control would be more strongly associated with academic outcomes. However, no relations were consistent with this hypothesis. In fact, in early-elementary school, the unique relations between components of EF and academic achievement were always significant, suggesting that all three EF components influence academic achievement beyond general cognitive ability as early as kindergarten. The unique effect of inhibitory control on reading and oral language decreased from early- to late-elementary school. These findings may suggest that by late-elementary school inhibitory control is no longer distinct from general EF. This would be consistent with the findings of Miyake and Friedman (2012) that indicated that by early adulthood, when what is common across EF is accounted for there is no unique variance left for inhibitory control. However, the unique effect of inhibitory control on math remained consistent across elementary school, casting some doubt on this interpretation. One alternative explanation is that inhibitory control remains a unique component of EF throughout elementary school and that the changes in magnitude of effects across elementary school for some academic skills reflect the development of those academic skills rather than the development of EF skills. Specifically, it is possible that by late-elementary school children have received instruction in, practice with, and generally developed reading and oral language skills to the point at which their difficulty level has diminished and therefore the cognitive demand to inhibit a predominant response in favor of a subdominant response placed by these academic tasks have diminished.

Overall, the results of the meta-analytic path analyses examining the relation of EF components with broad academic skills supported the unity and diversity model of EF. However, the results did not support the idea that inhibitory control is subsumed by the “unity” component of EF, at least in elementary school-age children. Thus, adolescence and young adulthood may prove more fruitful developmental stages at which to examine the transition of inhibitory control from a unique component of EF to a representation of general EF. Surprisingly, shifting which has not previously emerged as a unique component of EF in childhood (e.g., Best & Miller, 2010), did uniquely predict academic skills in this study. However, notably, effects for the relations between shifting and academic skills were derived from far fewer studies (approximately half) than the effect for the relations between WM and inhibitory control with academic skills. Further, of the studies reporting on the relations between shifting and academic outcomes, the majority reported on late-elementary school (third through sixth grade). As such, although the findings from this meta-analysis suggest that the diversity component of EF is best represented by three distinct skills, future research is needed to definitively determine whether shifting is truly a unique aspect of EF in school-age children, especially in early-elementary school-age children.

Developmental Changes in the Relations between EF and Academic Subskills

For the most highly constrained skills (i.e., decoding, calculations⁴), the pattern of results did not consistently support the hypothesis that the components of EF would be most strongly related to constrained skills in early-elementary school. For example, although inhibitory control and shifting were more strongly related to decoding in early-elementary school than in late-elementary school, working memory demonstrated the opposite pattern. It is possible that inhibitory control and shifting are more important in early-elementary school because they allow for better orientation of attention toward classroom activities and instruction at a time when foundational reading skills are being learned (Posner & Rothbart, 2007). As children progress through school, they become more accustomed to navigating the cognitive demands of the classroom. At the same time, children’s decoding skills are becoming refined, with simple words being recognized by sight and sounding out words only required for words which remain unfamiliar words (with unfamiliar words becoming increasingly likely to only be longer words that are more phonologically and orthographically complex as children learn to recognize more and more simple words). Decoding complex words may tax working memory to a greater extent than does decoding simpler words, potentially accounting for the increased relation between working memory and decoding across the elementary school years.

None of the specific components of EF were differentially related to calculation skills across early- and late-elementary school. As children’s calculation skills in the early-elementary years (i.e., addition, subtraction) become automatized, instruction shifts to focusing on other, more difficult calculations (i.e., multiplication, division). Similarly, measures of math calculation span broad content areas including addition, subtraction, multiplication, division, fractions, decimals, and percentages. Therefore, despite increased automaticity of early calculation skills, relations between EF and calculation may remain similar across the elementary-school period due to changing requirements within calculation tasks. Our data only allowed us to examine these shifts at the level of calculation tasks as a whole rather than at the level of specific process skills (e.g., addition vs. subtraction). Future longitudinal research could explore how the relations between the components of EF and specific aspects of calculation change as EF skills develop and calculation skills become automatized.

For reading fluency skills⁵ (which are less constrained than word reading but more constrained than reading comprehension), the pattern of results varied for each component of EF. Specifically, the relation between inhibitory control and reading fluency increased across the elementary years, the relation between WM and fluency decreased across the elementary years, and the relation between shifting and fluency did not change across the elementary years. One possible explanation for the increased importance of inhibitory control for reading fluency across the elementary years is that as children get older, they are more likely to rely on sight reading rather than sounding out or decoding words. Sight reading requires pulling information from long-term storage and inhibiting inaccurate previously learned information. For example, when asked to read the word three children must inhibit words such as the, there, and tree which are phonologically and orthographically similar to three. Prior research indicates words with many phonological neighbors (i.e., words that differ from a target word by only one phoneme) are read faster than words with fewer phonological neighbors (Yates et al., 2005). Given the potential reciprocal relations between cognition and academic skills (Peng & Kievit, 2020), it is possible that practicing inhibition of phonological neighbors increases children’s sight-word reading fluency. In turn, improvements in reading fluency may lead to additional opportunities for practice inhibiting phonological neighbors when reading, bolstering children’s inhibitory control (and the relation between inhibitory control and reading fluency). Additionally, older children have a larger lexicon, which means they must inhibit a greater amount of competing information in favor of the word they are asked to read. Although depth and knowledge of words also typically increases with age, the impact of inhibition of competing words may continue to be particularly important for measures of single word reading (which the majority of reading fluency tasks examined in this meta-analyses were) that do not provide the same context that sentences or paragraphs provide. Alternatively, it is possible that this increased association is partially attributable to the way in which inhibitory control is measured in early- and late-elementary school. Specifically, in late-elementary school inhibitory control tasks are more likely to utilize a reaction time outcome, whereas in early-elementary school inhibitory control tasks are more likely to utilize an accuracy outcome. It is possible that the timed component of the inhibitory control task in late-elementary school may inflate the relation between inhibitory control and reading fluency, which also has a timed component.

For the least constrained skills (i.e., reading comprehension, word problem solving, vocabulary knowledge), results supported the hypothesis that the components of EF would either be consistently related to unconstrained skills across elementary school or would be more strongly related to unconstrained skills in late-elementary school than in early-elementary school, lending some support for our developmental framework. The relation of reading comprehension with WM and shifting did not change across the elementary years, but the relation with inhibitory control decreased across the elementary years. As with the relation between inhibitory control and overall reading, which also decreased across elementary school (discussed above), it is possible that this decreased association is attributable to an increased proficiency in reading comprehension by late-elementary school, which results in decreased cognitive demand. It is also possible that reading comprehension remains equivalently cognitively demanding but relies on different cognitive skills across development. Specifically, in early-elementary school, the focus of instruction is learning to read for comprehension, whereas in late-elementary school there is a shift toward reading comprehension as a mechanism for learning other topics. Therefore, in early-elementary school, orienting attention toward classroom activities and goal-directed behaviors while inhibiting desires and impulses during reading instruction may be more important as reading comprehension is still developing. In late-elementary school, reading comprehension is expected to already be developed and to begin to be applied; therefore, inhibition may become less important than the recall and application of rules and previously learned information. For word problem solving, results provided some support for our developmental framework, as relations between EF and word problem solving either remained the same (for inhibitory control and shifting) or increased (for working memory) across elementary school. This suggests that a complex task like solving a word problem which involves decoding, oral language skills, and calculation skills, consistently taxes EF regardless of developmental period, and may tax working memory to a greater degree across development as problems become more complex. The relation of vocabulary knowledge with WM and inhibitory control did not differ across the early- and late-elementary years⁶; however, it should be noted that the magnitude of these relations were small across elementary school and was not statistically significant in late-elementary school. This calls into questions the actual importance of inhibitory control for vocabulary across elementary school.

General Discussion

Reading.

In early-elementary school, WM and inhibitory control were equivalently related to reading comprehension and decoding. However, by late-elementary school WM was significantly more strongly related to reading comprehension and decoding than was inhibitory control. One possible explanation for these findings is that as inhibitory control emerges as a construct unique from general EF, it becomes less predictive of and important for academic success. In other words, inhibitory control may be predictive of reading in early-elementary school inasmuch as it is a proxy for general EF (despite efforts to account for general EF statistically) and when it emerges as a distinct construct by late-elementary school its predictive ability decreases. This would be consistent with findings from recent factor-analytic studies that indicate that, in adults, when what is common across EF is accounted for there is no unique variance left for inhibitory control (Friedman et al., 2008, 2011; Miyake & Friedman, 2012). Contrary to our original hypotheses, significant unique relations were found between shifting and overall reading, reading comprehension, and decoding in early-elementary school. However, shifting consistently had the weakest relation with reading achievement compared to other components of EF and was not significantly related to comprehension or decoding in late-elementary school. Taken together these results suggest the need to interpret significant associations between shifting and reading skills with caution.

Oral language.

Our findings generally indicated that working memory played the strongest role in children’s oral language skills, with shifting also playing a larger role than inhibitory control. Taken together, results of this meta-analysis indicate that regardless of age, oral language places a substantial demand on the ability to maintain and manipulate information in memory. This is consistent with the definition of vocabulary as primarily the ability to recall lexical information from long-term memory. In addition, these results suggest that, at least in early-elementary school, oral language requires the ability to shift between sets of information or rules. One possible explanation for the association between shifting and oral language is that vocabulary is primarily learned through the integration of new linguistic information with background knowledge, which requires shifting attention between long-term storage and verbally presented information (e.g., Torgesen et al., 1994; Walczyk, 2000). Additionally, children must simultaneously attend to their own thoughts and plan what they will say next while listening and comprehending speech of others. Thus, children with better shifting abilities may benefit more from daily verbal interactions, and high-quality verbal interactions may in turn promote the development of shifting skills. However, the relation between shifting and oral language remains a relatively understudied area.

Math.

Contrary to our original hypotheses, few developmental changes were found in the relations between EF components and math skills across early- to late-elementary school. The general consistency of relations between EF components and math skills across elementary school may indicate that, consistent with the intrinsic cognitive load theory (Chandler & Sweller, 1991; Sweller, 1994), math skills have an inherent task complexity that remains consistent across development. However, this study only examined children through sixth grade. As such, it is possible that as children continue to gain experience with and exposure to math into adolescence the relations between EF components and math may vary. Future work is necessary to determine whether this pattern of consistency and thus the theory of inherent task complexity holds throughout late childhood and early adolescence.

Overall, working memory is more strongly related to math achievement than is inhibitory control or shifting. This is a relatively unsurprising finding, given the strong theoretical ties between WM and the ability to maintain and process information across the completion of multi-step math problems (e.g., Fürst & Hitch, 2000; Imbo & Vandierendonck, 2007; Imbo et al., 2007), keep track of operations while calculating (e.g., Noël et al., 2004), and complete math problems that require mental representations (De Smedt et al., 2009; Lee & Kang, 2002; Trbovich & Lefevre, 2003). The lack of developmental patterns found for the relations between inhibitory control and math skills was somewhat surprising given the pattern of results found for the relations between inhibitory control, reading skills, and vocabulary. One possible explanation for why inhibitory control was more consistently related to math than to reading and to oral language skills throughout elementary school, is that math skills may be more difficult and thus require greater cognitive resources than do reading and oral language skills. (e.g., Bull et al., 2008; Clark et al., 2010; Espy et al., 2004). It is also possible that reading, oral language, and math tasks decrease in difficulty throughout development to similar degrees but at different points in development due to differences in instructional time dedicated to each domain (e.g., Skibbe et al., 2013) and differential exposure to related activities (Cannon & Ginsburg, 2008; Skwarchuk et al., 2014). Future work is necessary, however, to determine which, if any, of these possibilities explain why inhibitory control is more consistently related to math skills than to reading skills and oral language across elementary school.

An alternative explanation for the developmental patterns found for math, compared to reading and oral language, is that whereas reading and oral language tasks assess specific discrete academic content areas, math tasks tend to assess broader content areas and are instead categorized based upon math processes. For example, word problem assessments include questions that span topic areas (e.g., number identification, addition, multiplication, fractions, decimals, basic algebra, geometry, and measurement). As such, it is possible that as children acquire greater mastery of reading and vocabulary these tasks become less cognitively demanding, and this effect can be detected because the assessments of these skills measure (to the degree possible) a single reading or language skill. In contrast, math skills may follow this same general pattern; however, the effect cannot be detected because as one math skill is mastered, assessments introduce additional content for which the child may not have a similar level of mastery, thus requiring greater cognitive resources.

Limitations

Despite the strengths of this study, including the large number of studies summarized and the examination of multiple EF components and multiple academic domains, there were several limitations. First, across univariate analyses, results remained heterogeneous, indicating that other factors may also moderate the relation between EF and academics. There were several important moderators that could not be examined. For example, sex differences have been reported for the relation of inhibitory control with academic outcomes (Matthews et al., 2009); however, too few studies have reported correlations separately by sex to synthesize the results in this manner. Similarly, we were interested in the relative association between EF components and academic outcomes across development. Although we examined differences in early- and late-elementary-school-age children, we were unable to examine these associations separately at a grade-by-grade level because too few studies reported correlations separately by grade. Second, this study focused on the academic skills most commonly taught and assessed throughout elementary school. Future studies may benefit from meta-analytic examination of the relation between EF and other academic skills taught and assessed primarily in early- (e.g., letter recognition or magnitude judgment) or late-elementary school (e.g., algebra). Third, there were several areas that we were unable to examine using a meta-analytic approach because they remain largely understudied--specifically, the association between EF and oral language. We were unable to examine the relations of shifting with grammar/syntax and listening comprehension. Although we did examine the relation of inhibitory control with grammar/syntax and listening comprehension, the results of these analyses should be interpreted with caution as a limited number of effects from a restricted number of unique studies were available for examination. These areas, therefore, remain key areas for future research.

Conclusions

This study is the first meta-analysis that systematically and comprehensively investigated the relations between all three components of EF with multiple academic outcomes, while controlling for the overlap between EF components. Overall, the results indicate that a developmental model in which EF components become increasingly predictive of academic outcomes as children get older and EF components become more differentiated is likely too simple. Similarly, the concept of inherent cognitive demands that are consistent across development and the concept of task difficulty varying throughout development were found to be insufficient to explain the complex relations between EF and academics when utilized as independent models. Rather, the results suggest that different EF components become more or less important for different academic subskills at different ages or developmental levels as the specific EF component and academic subskill develop. The fact that the overall and relative associations between different components of EF and different academic subskills change across development illustrates the importance of considering the influences of development on both EF and academic skills as well as the specific demands of different academic tasks.

Given the substantial relations found between each of the EF components and academic skills, early screening for deficits in any of the three components of EF seems prudent to provide children with opportunities for early academic support or intervention. Screening for EF deficits may allow earlier identification of children at risk for academic difficulties than would be identified by assessment of academic skills alone, and such screening would allow for these children to receive academic interventions before substantial academic deficiencies accrue. Specifically, identification of children with EF deficits would enable educators to provide targeted instruction to children who are currently succeeding on lower-level academic skills by allocating all their EF resources to these skills but who might later demonstrate academic difficulties when instruction shifts towards a greater focus on higher-level academic skills. It may be particularly useful to screen for deficits in WM, given the results indicating that WM is a key component driving the association between EF and academic achievement. Finally, it is difficult to synthesize results and draw definitive conclusions without clear operationalized definitions of the constructs of interest. In this study, we attempted to bridge the gaps between clinical, developmental, and educational psychology and to provide cohesive definitions of EF components to better understand their relations to academic achievement outcomes. The use of a similar framework is necessary for future research to improve our understanding of how EF components impact academic outcomes in children.

Public Significance Statement:

This study demonstrated that executive function skills have moderate relations with reading, oral language, and mathematics. These relations are strongest for working memory. Results suggest that to better understand the relations between EF and academics and how these relations vary across development, a more complex and nuanced model, which takes into account developmental trajectories of EF and academics and specific task demands, is needed.