Generalization in Clinical Prediction Models: The Blessing and Curse of Measurement Indicator Variables

Supplemental Digital Content is available in the text.

Abstract

OBJECTIVE:

Specific factors affecting generalizability of clinical prediction models are poorly understood. Our main objective was to investigate how measurement indicator variables affect external validity in clinical prediction models for predicting onset of vasopressor therapy.

DESIGN:

We fit logistic regressions on retrospective cohorts to predict vasopressor onset using two classes of variables: seemingly objective clinical variables (vital signs and laboratory measurements) and more subjective variables denoting recency of measurements.

SETTING:

Three cohorts from two tertiary-care academic hospitals in geographically distinct regions, spanning general inpatient and critical care settings.

PATIENTS:

Each cohort consisted of adult patients (age greater than or equal to 18 yr at time of hospitalization), with lengths of stay between 6 and 600 hours, and who did not receive vasopressors in the first 6 hours of hospitalization or ICU admission. Models were developed on each of the three derivation cohorts and validated internally on the derivation cohort and externally on the other two cohorts.

INTERVENTIONS:

None.

MEASUREMENTS AND MAIN RESULTS:

The prevalence of vasopressors was 0.9% in the general inpatient cohort and 12.4% and 11.5% in the two critical care cohorts. Models utilizing both classes of variables performed the best in-sample, with C-statistics for predicting vasopressor onset in 4 hours of 0.862 (95% CI, 0.844–0.879), 0.822 (95% CI, 0.793–0.852), and 0.889 (95% CI, 0.880–0.898). Models solely using the subjective variables denoting measurement recency had poor external validity. However, these practice-driven variables helped adjust for differences between the two hospitals and led to more generalizable models using clinical variables.

CONCLUSIONS:

We developed and externally validated models for predicting the onset of vasopressors. We found that practice-specific features denoting measurement recency improved local performance and also led to more generalizable models if they are adjusted for during model development but discarded at validation. The role of practice-specific features such as measurement indicators in clinical prediction modeling should be carefully considered if the goal is to develop generalizable models.

There has been a surge of interest to develop clinical prediction models using machine learning to address important problems in critical care, such as predicting early onset of sepsis (1–6), acute respiratory distress syndrome (7–9), and, more recently, deterioration due to coronavirus disease 2019 (COVID-19) (10). An important question when considering the practical impact of such models is the extent to which these models will generalize beyond their development environment. For instance, it may be useful to know whether a model trained on general inpatient data will perform well on patients in the ICU or even on patients from a different health system. This information might help hospital administrators assess whether a proprietary model released by a vendor (e.g., an electronic health record [EHR] company) should be trusted or whether the hospital should develop its own model. This is an especially timely issue as many hospitals attempt to deploy prediction models for COVID-19 (10).

Although it is becoming increasingly expected that researchers externally validate clinical prediction models (11, 12), there is scant work addressing what factors affect external generalization (13–16). In this work, we explore the generalization of clinical prediction models related to hemodynamic decompensation and shock, using onset of vasopressors as our primary outcome. Shock is a major cause of mortality in the ICU (17), and fluid administration is typically the first-line treatment for hypovolemic shock (18). However, for refractory cases of shock, vasopressor therapy may be initiated (19). Advance warning that a patient may require vasopressors could help the primary care team. Onset of vasopressors may also serve as a proxy for acute decompensation, potentially enabling other early-targeted therapy (2, 6, 17, 20, 21). However, existing studies predicting vasopressor onset have only used data from a single site (22–24). Given the ubiquity of vasopressor use in critical care, it serves as an appropriate test case to probe the generalization of clinical prediction models. In this work, we develop and externally validate models to predict the onset of vasopressor therapy, with a specific aim to understand how measurement indicator variables affect generalizability. Rather than use more sophisticated machine learning approaches (e.g., deep learning [25, 26]), we limit analysis to logistic regressions in order to easily understand the contributions of each predictor variable. We use data from two tertiary teaching hospitals from unique geographical regions (Northeast and Mid-South, United States) to investigate the impact that differing clinical practice patterns have on generalization.

MATERIALS AND METHODS

Datasets

This retrospective, multicenter study analyzed EHR data from two tertiary-care academic hospitals: Beth Israel Deaconess Medical Center (BIDMC) in Boston, MA (utilizing a subset of the MIMIC-III database containing all ICU admissions between 2008 and 2012 [27]), and Methodist LeBonheur Healthcare (MLH) in Memphis, TN (all admissions between July 2016 and April 2018). This study is reported using the Transparent Reporting of a Multivariable Prediction Model for Individual Prognosis or Diagnosis guidelines (28, 29) and was approved by the Institutional Review Board at University of Tennessee Health Sciences Center (16-04985-XP).

Preprocessing

We created three cohorts to develop and validate prediction models for vasopressor onset. We created a cohort of ICU admissions from BIDMC, a cohort of ICU admissions from MLH, and a cohort of general floor admissions from MLH. Although vasopressor use on the general floor is rare, we include this cohort as a contrast to the generalizability of our models (in addition to the fact that identifying rapid decompensation on the general floor may also be valuable). We restricted analysis to adult (age greater than or equal to 18 yr) admissions, with an ICU or overall length of stay between 6 and 600 hours as appropriate. Finally, we excluded cases where vasopressors were administered within the first 6 hours of admission. Refer to the online supplement for additional information: Figure E1 (http://links.lww.com/CCX/A679) shows flow diagrams detailing the filtering and Table E1 (http://links.lww.com/CCX/A679) shows the vasopressors included in our study.

For each admission, we define a terminal time and right-align on these end times. For cases where vasopressor therapy is initiated, this terminal time is the time of first vasopressor, whereas for controls, we randomly sampled a time between 6 hours and 90% of their length of stay. See Figure E2 (http://links.lww.com/CCX/A679) in the online supplement for the distribution of vasopressor onset times and control end times.

Model Development

We used two classes of predictor variables in our multivariable regression models: more objective continuous-valued physiologic data and more subjective binary indicator variables indicating which measurements were recently taken. We use the term “more objective” rather than “objective” for the continuous-valued physiologic data, because the presence of a value still depends on the fact that a clinician thought it was important to measure it. We then fit regressions using both variable sets together and separately. The physiologic variables comprised age and 30 distinct vital signs and laboratory results. We fit second-order polynomial regressions by using the most recent measurement value along with its square. Such a quadratic model can capture the fact that clinicians may view certain measurements with respect to a reference range, with both abnormally low or high values indicating increased risk. Missing values were filled in using manually selected values from the normal clinical reference range, rather than using the population mean or model-based imputation. For the binary indicators, we used manually selected indicators that denoted whether a variable was measured in the past hour, in the past 8 hours, or ever measured (we did not use all indicator types for all variables as they are often redundant, e.g., for labs often ordered together). In total, we constructed 97 features: 35 indicator features and 62 physiologic features (age and the 30 vitals and labs along with their squares). We fit models for predicting the onset of vasopressors for each hour between 1 and 12 hours in advance. For a given training cohort and feature set, there were thus 12 distinct regression models, one per hour. See Table E2 (http://links.lww.com/CCX/A679) in the online supplement for a complete list of features with summary statistics.

For each cohort and combination of features (physiologic-only, indicator-only, and both physiologic and indicator features), we first fit Least Absolute Shrinkage and Selection Operator-penalized logistic regressions (30) to perform variable selection, using 10-fold cross validation to select the penalty parameter. Then, we refit a final unpenalized logistic regression using the selected variables on each full dataset. To handle sparsity in the outcome, we weighted each observation by the inverse of its class frequency. To improve calibration, we used isotonic regression (31), a standard approach for recalibrating model predictions that preserves their ranking.

We evaluated each regression in a manner analogous to how it was fit by examining the quality of predictions as a function of hours prior to potential vasopressor onset. We validated each model on all three datasets, calculating in-sample performance on the development data and out-of-sample performance on the two external validation sets.

Statistical Analysis

We assessed discrimination using C-statistics (area under the receiver operating characteristic curve [AUROC]), area under precision-recall (AUPR) curves, and positive predictive values at different sensitivities. We assessed calibration using Brier scores, calibration curves, and the Hosmer-Lemeshow test. Wald tests with p < 0.05 were used to assess statistical significance of regression coefficients, and no corrections were made for multiple testing. All analysis was conducted in the Python programming language (Version 3.7.1; Python Software Foundation, Fredericksburg, VA). Regressions were fit using the glmnet_python (Version 3.7.1; Python Software Foundation) package, and all other statistical analyses were conducted using the statsmodels (Version 0.9.0; Python Software Foundation) package.

RESULTS

Table 1 summarizes the background characteristics of the three cohorts, separated by the primary outcome. The BIDMC ICU cohort contained 12,999 admissions with 1,499 (11.5%) receiving vasopressors. The MLH ICU cohort contained 2,137 admissions with 265 (12.4%) receiving vasopressors. The MLH general floor cohort contained 59,750 total admissions, with 539 (0.9%) ultimately receiving vasopressors. There were no notable differences in age or sex between the sites, but there was a significantly higher proportion of African Americans at MLH (53.7%) compared with BIDMC (9.5%). The ICU cohorts had higher overall acuity as measured by maximum Acute Physiology and Chronic Health Evaluation II scores (32) within 24 hours of admission (medians: 16 BIDMC, 12 MLH ICU, and 5 MLH floor) and had higher inhospital mortality (21.2% BIDMC, 16.8% MLH ICU, and 1.8% MLH floor).

TABLE 1.

Background Characteristics of Cohorts

Variable	Methodist Floor: 539 Inpatient Stays, Vasopressor Administered (0.9%)	Methodist Floor: 59,211 Inpatient Stays, No Vasopressor Administered (99.1%)	Methodist ICU Stays: 265 ICU Stays, Vasopressor Administered (12.4%)	Methodist ICU Stays: 1,872 ICU Stays, No Vasopressor Administered (87.6%)	Beth Israel: 1,499 ICU Stays, Vasopressor Administered (11.5%)	Beth Israel: 11,500 ICU Stays, No Vasopressor Administered (88.5%)
Age, median (5%, 25%, 75%, and 95% quantiles)	66.0 (36.6, 56.0, 75.0, 87.0)	59.0 (25.0, 43.0, 72.0, 88.0)	64.0 (35.0, 54.0, 71.0, 86.0)	62.0 (31.0, 53.0, 72.0, 85.0)	67.1 (37.8, 56.6, 77.9, 88.3)	64.1 (27.9, 51.1, 77.8, 90.0)
Male sex, n (%)	314 (58.3)	24,575 (41.5)	147 (55.5)	961 (51.3)	861 (57.4)	6,311 (54.9)
Inhospital mortality, n (%)	213 (39.5)	843 (1.4)	118 (44.5)	242 (12.9)	547 (36.5)	2,214 (19.3)
LOS (ICU, for ICU cohorts; admission for floor cohort), hr, median (5%, 25%, 75%, and 95% quantiles)	225.8 (50.2, 124.9, 345.2, 574.7)	69.4 (22.9, 44.3, 119.2, 268.8)	205.1 (17.0, 93.0, 324.5, 497.9)	72.2 (12.8, 32.8, 189.7, 421.3)	130.8 (28.9, 67.4, 255.3, 474.0)	42.9 (18.3, 26.2, 70.9, 185.3)
LOS ≥7 d, n (%)	363 (67.3)	8,349 (14.1)	152 (57.4)	511 (27.3)	600 (40.0)	696 (6.0)
Self-reported race, n (%)
Black/African-American	265 (49.2)	31,695 (53.5)	163 (61.5)	1,123 (60.0)	102 (6.8)	1,130 (9.8)
White/Caucasian	256 (47.5)	24,995 (42.2)	89 (33.6)	693 (37.0)	1,098 (73.2)	8,392 (73.0)
Other	6 (1.1)	625 (1.0)	3 (1.1)	21 (1.1)	44 (2.9)	348 (3.0)
Asian	4 (0.7)	444 (0.7)	1 (0.4)	6 (0.3)	56 (3.7)	301 (2.6)
Hispanic/Latino	5 (0.9)	1,128 (1.9)	8 (3.0)	26 (1.4)	42 (2.8)	488 (4.2)
Unknown/unable/declined	3 (0.6)	324 (0.5)	1 (0.4)	3 (0.2)	157 (10.5)	841 (7.3)
Acute Physiology and Chronic Health Evaluation II score in first 24 hr (no chronic health points), median (5%, 25%, 75%, and 95% quantiles)	9 (2, 6, 14, 23)	5 (0, 3, 8, 13)	13 (4, 8, 18, 26)	12 (4, 8, 17, 25)	20 (9, 15, 25, 31)	15 (7, 11, 20, 27)
Highest lactate in first 24 hr, median (5%, 25%, 75%, and 95% quantiles)	3.6 (1.2, 2.1, 9.5, 15.2)	2.0 (1.1, 1.4, 3.0, 7.2)	2.5 (1.2, 1.8, 3.9, 9.4)	2.2 (1.1, 1.5, 3.4, 8.0)	2.3 (1.0, 1.7, 3.5, 7.3)	1.8 (0.8, 1.3, 2.6, 4.8)
Presence of lactate measurement in first 24 hr, n (%)	48 (8.9)	527 (0.9)	52 (19.6)	186 (9.9)	1,268 (84.6)	7,282 (63.3)
Lowest mean arterial pressure in first 24 hr, median (5%, 25%, 75%, and 95% quantiles)	65 (45, 57, 77.3, 99)	84 (59, 73, 95, 114)	65 (49, 57.5, 75, 101.8)	71 (46.1, 62, 83, 100)	58 (40, 50.5, 67, 85)	61 (41, 54, 69, 83)
Lowest Glasgow Coma Scale in first 24 hr, median (5%, 25%, 75%, and 95% quantiles)	15 (3, 14, 15)	15 (13, 15)	15 (3, 11, 15)	15, (3.6, 10, 15, 15)	11 (3, 5, 15)	14 (3, 9, 15)

LOS = length of stay.

Background characteristics of the three cohorts: the Methodist LeBonheur Healthcare (MLH) floor cohort, the MLH ICU cohort, and the Beth Israel Deaconess Medical Center ICU cohort. Each cohort is further broken down by the primary outcome in this study, whether or not vasopressor therapy was ever initiated or not. Median values along with 5%, 25%, 75%, and 95% quantiles are presented for continuous variables. There is a higher proportion of African Americans at MLH, with no other major demographic differences. The ICU cohorts have higher overall acuity, as evidenced by their higher inpatient mortality and Acute Physiology and Chronic Health Evaluation (APACHE)-II scores. Note that the APACHE-II score was calculated without using chronic health points due to data availability.

Our quantitative results suggest the inclusion of both sets of features improves the quality of models in-sample. Figure 1 shows in-sample and out-of-sample discriminations (AUROC and AUPR) as a function of hours before potential onset of vasopressors. Results for models trained on that cohort indicate in-sample performance, whereas results for models trained on a different cohort measure generalization. Across all datasets, the best models were those derived from that dataset, as illustrated by the relative clustering of lines with the same color at the top of each pane. Optimal in-sample performance was always achieved by models that used both the physiologic and indicator features. When validated out-of-sample, there is more variability, although models using solely the indicator features generally perform the worst out-of-sample compared with other models developed on the same data.

Figure 1.

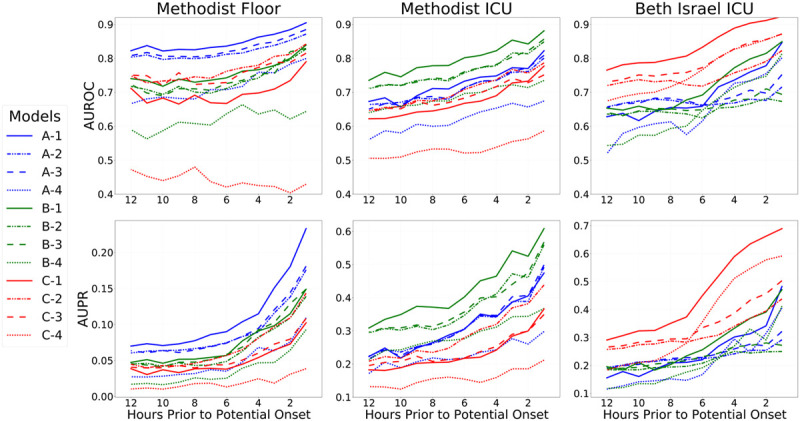
Results on all three cohorts, as a function of hours in advance of potential vasopressor onset. Models were trained to predict potential onset each hour from 1 hr in advance, up until 12 hr in advance, and models were evaluated in the same fashion (i.e., each 4-hr model was then evaluated internally and externally at 4 hr in advance across datasets). Top row shows areas under the receiver operating characteristic curve curves (AUROCs, also known as C-statistics), and the bottom row shows areas under the precision-recall (AUPR) curves as metrics assessing overall discrimination. Each column shows the performance of all fitted models on one cohort: Methodist floor (left), Methodist ICU (center), and Beth Israel ICU (right). Results within a column for models trained on that data source are in-sample results measuring internal validity, whereas results for models learned from other data sources are out-of-sample and measure external validity. For each evaluation data source, results on 12 different models are shown. Models with a name beginning with “A” were fit from the Methodist floor data and appear in blue throughout. Models with a name beginning with “B” were fit from the Methodist ICU data and appear in green throughout. Models with a name beginning with “C” were fit from the Beth Israel ICU data and appear in red throughout. Models with a name ending in “−1” are the combined models that use both physiologic and measurement indicator variables, both when fitting models and during evaluation; their lines are solid. Models with a name ending in “−2” are the combined models that use both physiologic and measurement indicator variables during model fitting but only use physiologic variables during evaluation; their lines are dashed-dotted. Models with a name ending in “−3” are the models solely using physiologic variables; their lines are dashed. Models with a name ending in “−4” are the models solely using the measurement indicator variables; their lines are dotted. An important finding in the figure is that models learned on a data source always perform better in-sample on that data source when compared with models learned from other data sources; this is seen by the clustering of blue, green, and red lines at the top of each relevant pane. Another key finding is that the combined models (solid lines) always perform best in-sample but not out-of-sample.

External validity of the physiologically-driven feature models was improved if the more practice-driven indicator features were included only during model training and not during evaluation. We performed a post hoc analysis by testing an additional fourth model, using the regression coefficients from models learned using both features, but only utilizing physiologic features during evaluation. Figure 2 confirms this hypothesis for models derived from BIDMC, although results are less clear for models derived from MLH data. The figure shows the relative performance change of the two physiologic models compared with the combined model that uses both physiologic and indicator features. The best BIDMC-derived models, in terms of external generalization, used the physiologic component of the combined model but ignored indicators (line C-2). It consistently outperformed the combined model and often outperformed the original physiology-only model.

Figure 2.

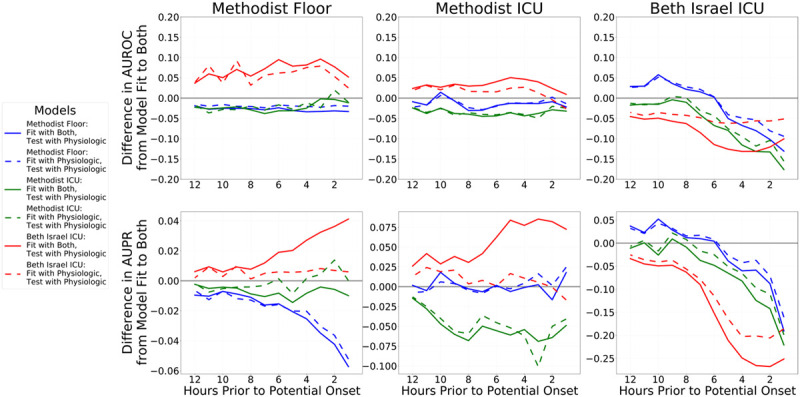
Differences in performance between the combined models (lines ending in “−1” in Figure 1) compared with the physiology-only models (lines ending in “−3” in Figure 1) and models using the physiologic component of the combined model but discarding the indicators component at evaluation (lines ending in “−2” in Figure 1). The difference in performance between the combined model and physiology-only models is shown in dashed lines, and the difference in performance between the full combined model and just using the combined model’s physiologic components are shown in solid lines. Blue lines denote models fit to Methodist floor data, green lines denote models fit to Methodist ICU data, and red lines denote models fit to Beth Israel ICU data. The top row shows differences in areas under the receiver operating characteristic curves (AUROCs, also known as C-statistics), and the bottom row shows differences areas under the precision-recall (AUPR) curves as metrics assessing overall discrimination. Values above 0 indicate that the model under evaluation performed better than the combined model’s performance; values less than 0 indicate that the combined model performed better. Each column shows the performance of all fitted models on one cohort: Methodist floor at left, Methodist ICU at center, and Beth Israel ICU at right. Results within a column for models trained on that data source are in-sample results measuring internal validity, whereas results for models learned from other data sources are out-of-sample and measure external validity. The right column shows that both the physiology-only models and using only the physiologic components of the combined models both perform worse than the combined model when validated internally on Beth Israel data, with the physiology-only models a bit better. However, out-of-sample, this is flipped: the combined model typically fares worst and using only the physiologic component of the combined model is best, with physiology-only models faring somewhere in the middle. For models fit to Methodist data, there are less obvious differences between the physiology-only models and using just the physiologic components of the combined models, and in fact, the full combined models typically fare best.

To determine which factors contributed most to observed differences in generalization, we examined the regression coefficients and specific trends from models predicting potential vasopressor onset in 4 hours. More detailed quantitative results on discrimination and calibration of these models can be found in Figures E3 and E4, and Table E3 (http://links.lww.com/CCX/A679). Figure 3 shows a subset of important regression coefficients along with 95% CIs for these models. Specifically, we visualized only those features with a statistically significant (p < 0.05, Wald test) sign change between coefficients derived from different datasets. Among the eight instances in the top row where two physiologic features differed in sign across datasets, all involved BIDMC models, and there were no significant sign changes among models derived from either MLH cohort. Likewise, BIDMC was involved in all 10 instances in the bottom row where significant sign changes between the datasets occurred; in only two of these 10 cases were there also sign changes between the two MLH-derived model coefficients. This suggests models learned from BIDMC are more different from MLH-derived models than the models from the two MLH cohorts that are from each other.

Figure 3.

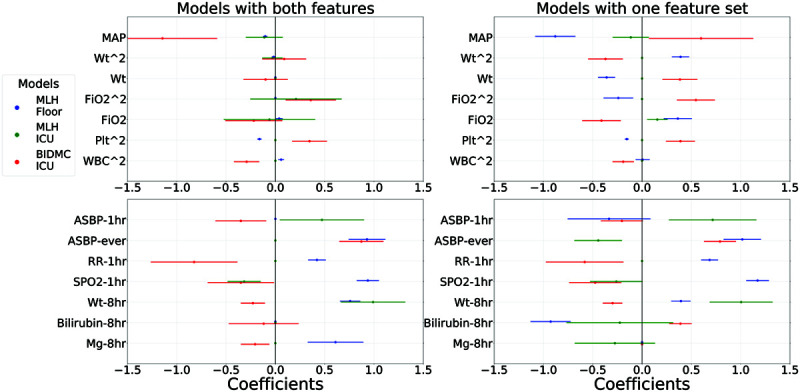
Learned coefficients from the 4 h models for each of the three cohorts, but only specific features where there is at least one statistically significant difference in sign between coefficients for two different cohorts (as indicated by Wald test p values of <0.05 for both coefficients and with both coefficients of opposite sign). Points are shown for the point estimate of each regression coefficient, along with 95% CIs. Top row shows physiologic features, and the bottom row shows the indicator features. Models trained on Methodist floor data are shown in blue, Methodist ICU data in green, and Beth Israel ICU data in red. Left column shows coefficients from the combined models that use both physiologic and indicators during model fitting, whereas the right column shows results from the models fit separately to only physiology variables (top) and only indicators (bottom). There are six statistically significant sign changes among the physiology-only model coefficients, and all six involved a Beth Israel-derived model. This number decreases to only 2 when examining the combined model and is evidenced that the use of indicators during model fitting helps learn more robust physiologic relationships that generalize better. There are five statistically significant sign changes in both the indicators-only models and the indicator components of the combined models. In both cases, all five again involved a Beth Israel model, along with one significant change between a Methodist floor and ICU model. ASBP = arterial systolic blood pressure, BIDMC = Beth Israel Deaconess Medical Center, MAP = mean arterial pressure, MLH = Methodist LeBonheur Healthcare, Plt = platelets, RR = respiration rate.

To better understand the specific physiologic relationships learned by models, Figure 4 visualizes fitted model trends from the same 4-hour models for six different physiologic variables. Each pane shows the quadratic or linear relationship between a clinical variable and risk of onset of vasopressors learned by the physiology-only model and the combined model across datasets. In the top row, there are no major changes in trends between the combined model and the physiology-only model for each dataset and all models learn intuitive relationships (e.g., that low systolic blood pressure and high heart rate imply increased risk of requiring vasopressors). In the bottom row, we visualize relationships that exhibit more change between the combined and physiology-only models. For instance, the bizarre relationship for mean arterial pressure (MAP) learned by the BIDMC physiology-only model (line “C-2”) corrects itself to a more intuitive relationship in the combined model, with lower blood pressures now associated with higher risk as expected.

Figure 4.

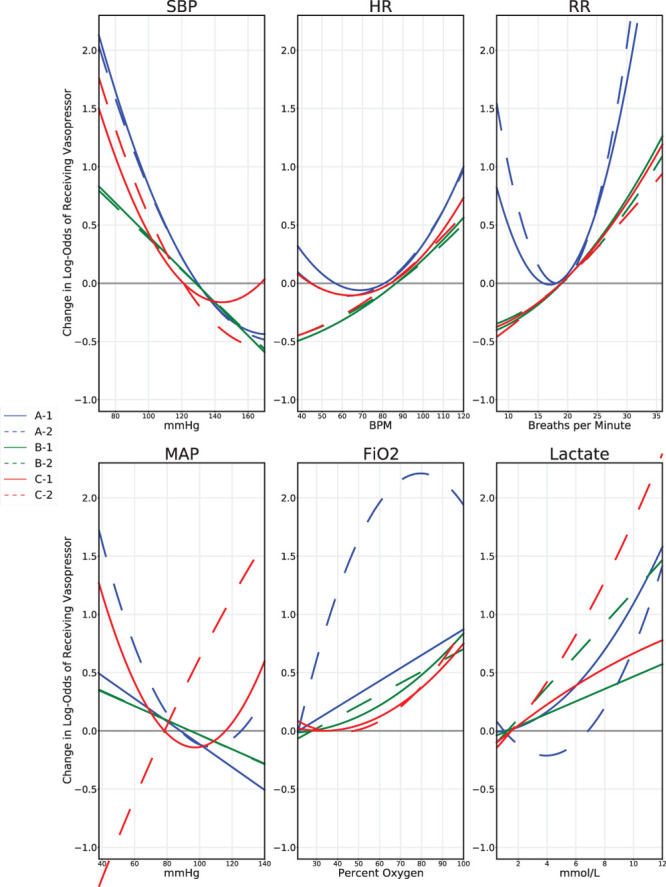
Visualizations of model predictions for different physiologic variables are shown, from the 4-hr onset models. Each pane shows a different predictor variable. From top left, clockwise, they are: systolic blood pressure (SBP), heart rate (HR), respiration rate (RR), mean arterial pressure (MAP), Fio₂, and lactate. Models with a name beginning with “A” were fit from the Methodist floor data and appear in blue throughout. Models with a name beginning with “B” were fit from the Methodist ICU data and appear in green throughout. Models with a name beginning with “C” were fit from the Beth Israel ICU data and appear in red throughout. Models with a name ending in “−1” are the combined models that use both physiologic and measurement indicator variables; their lines are solid. Models with a name ending in “−2” are the models that use only physiologic variables during model fitting; their lines are dashed. The curves indicate a model’s change in log-odds of risk of vasopressor as a function of that predictor variable on the x-axis. The y-axis is shifted such that 0 coincides with the mean of each feature value; the units on the y-axis are relative and not absolute, only denoting change in log-odds as a function of modifying this single predictor. Variables displayed in the top row are examples of predictors where there were no major changes between the combined model and physiology-only models. The difference in RR between the Methodist floor cohort and the two ICU cohorts likely reflects the fact that ICU patients are more likely to be on ventilators. The bottom row shows examples of predictors where there were large changes between the combined and physiologic-only models. The bizarre MAP relationship learned by the Beth Israel ICU physiology-only model is corrected in the combined model, with low MAP associated with higher risk of vasopressor need. Likewise, the strange fitted curves learned by the Methodist floor model for Fio₂ and for lactate appear more reasonable in the combined model.

DISCUSSION

Measurement Indicator Variables Alone Fail to Generalize

We found that models using physiologic features rather than practice-driven indicator features are more likely to generalize. Models utilizing only the indicators performed poorly in external validation compared with other models from the same datasets. Indicator-only models from BIDMC performed well in-sample but often predicted no better than chance when validated on external data. This suggests that these sorts of practice-driven features may contain unique personnel, workflow, and training biases that are nontransferable outside the development site. We urge caution when developing clinical prediction models using such features, as strong performance in-sample does not guarantee that the learned relationships will generalize.

Combined Models Do Not Generalize Well Across Sites

Combined models utilizing both the more subjective indicators along with the more objective physiologic data often generalized across locations at the same site. Figure 1 shows that, in terms of AUROC, the combined models outperformed the physiologic-only models in the 21 of 24 cases where MLH ICU models were validated on the MLH floor or vice versa. However, combined models learned from BIDMC perform better than the physiologic-only models on the MLH datasets in only two of 24 cases. This likely occurred, because the MLH cohorts are derived from the same hospital and likely share more similarities in practice patterns. On the other hand, BIDMC is in a geographically distinct location and part of a different hospital system; it likely has many differing practice patterns. This is reflected in the poor generalization of the BIDMC combined and indicator-only models to MLH data. We conclude that practice-driven features, such as the indicators that we used, seem to improve generalizability for similar contexts. Although they should still never be used in isolation, these sorts of features might help in situations where models are intended to be applied to multiple out-of-sample locations where practice context is related, for example, to different units in the same hospital. However, when relying upon these types of practice-driven features in real clinical environments, it is crucial that robust monitoring systems are used to detect shifts as practice patterns likely change over time, possibly requiring model retraining (33–35). Failure to do so may result in severe degradations in model performance (36).

Adjusting for Practice-Driven Features Only During Model Development May Improve Generalization Across Sites

Even trends learned from seemingly objective physiologic features may not be entirely immune to practice pattern influence. The top-right pane of Figure 3 highlights six instances of significant sign changes between the coefficients of physiology-only models across datasets. When integrated with indicators, these discordances largely disappear in the top-left pane of Figure 3. The inclusion of indicators in the combined model thus appears to improve actually the generalization of the learned physiologic trends. Figure 2 also verifies this theory, as results from BIDMC-derived models demonstrate that using solely the physiologic information from the combined models (i.e. ignoring indicators when making new predictions) typically improves performance, when compared with either the original physiologic-only model or the whole combined model. BIDMC may benefit most from this experiment, as its indicator features seem to have the strongest signal among the three cohorts considered: the BIDMC indicator-only model has similar AUROCs to the physiologic-only model within 6 hours of vasopressor onset and has even higher AUPRs. Our findings in this dataset are consistent with previous studies that found that healthcare process variables such as time of measurement can be strongly predictive of the outcome (37, 38). Thus, the physiologic features extracted from the BIDMC combined model seem to learn something more akin to true biology, and hence generalize better. The results in Figure 4 also qualitatively support this argument. For instance, the association between MAP and the risk of requiring vasopressors in the combined model makes more sense than that in the physiologic-only model. Instances of disagreement, for instance, between the respiration rate trend from the MLH floor model compared with the ICU models, may still be more representative of practice patterns, as patients in the ICU often require ventilation. Thus, even more objective clinical data, like the physiologic features used in our analysis, should not automatically be expected to generalize, as practice patterns may influence even these more objective information sources. We suggest practitioners try developing models using both more objective and subjective sources of information as available and seeing to what extent models generalize when only using the fitted model components from the more objective features. In some cases, such as the ones explored in this study, it appears this procedure may control for some of the influence of practice patterns in the more objective features.

Limitations

Our primary goal was to evaluate the role that more objective physiologic variables and more subjective measurement indicator variables have on the external validity of clinical prediction models. Thus, we only considered logistic regressions on a modest number of variables so that the results were easy to interpret. Although more complex machine learning methods (e.g., deep learning or random forests) might result in higher predictive performance, one prior study found random forests did not outperform logistic regressions for predicting vasopressor onset (24). In general, there is scant evidence that more complex machine learning consistently outperforms regressions in many clinical prediction modeling applications (39).

Furthermore, we developed our models on retrospective EHR data, which may limit the applicability of the model if used prospectively (40). Although we use unique geographic comparisons, both sites represent large urban tertiary teaching facilities, and therefore, the results of this study may be limited to practices and procedures restricted to larger hospitals. An interesting direction for future work would be to confirm the results of this study in a larger collection of datasets, such as the electronic ICU database (41). Additionally, we only used structured data available from the EHR, so it is possible the implications we found regarding practice-specific features do not apply to clinical prediction models developed using other data sources like unstructured clinical notes or radiographic images. Although, in this work, the only form of practice pattern–dependent features used were measurement indicators, many other potential predictors exist, such as variables accounting for interventions like fluids that were previously administered. Previous articles have also explored how such measurement indicators may reflect site-specific practice patterns, as well as information bias and systematic measurement errors (42).

CONCLUSIONS

We fit regression models to predict the onset of vasopressors using two classes of predictors: more objective clinical data and more subjective practice-specific indicator variables denoting recency of measurements. Models performed well and had good discrimination in-sample and modest discrimination when evaluated across data sources to different geographic sites or locations in the hospital, but use of practice-specific features in isolation always had poor external validity. However, they did provide value when used in models combining both feature sets. In some instances, the indicator features appeared to adjust for idiosyncratic site-specific variability, leading to improved generalization in the learned physiologic trends. These findings suggest clinical prediction models should be carefully evaluated on independent data sources when subjective institutional-specific features are being used.