Rectified Gaussian Scale Mixtures and the Sparse Non-Negative Least Squares Problem

Abstract

In this paper, we develop a Bayesian evidence maximization framework to solve the sparse non-negative least squares problem (S-NNLS). We introduce a family of probability densities referred to as the Rectified Gaussian Scale Mixture (R-GSM), to model the sparsity enforcing prior distribution for the signal of interest. The R-GSM prior encompasses a variety of heavy-tailed distributions such as the rectified Laplacian and rectified Student-t distributions with a proper choice of the mixing density. We utilize the hierarchical representation induced by the R-GSM prior and develop an evidence maximization framework based on the Expectation-Maximization (EM) algorithm. Using the EM-based method, we estimate the hyper-parameters and obtain a point estimate for the solution of interest. We refer to this proposed method as rectified Sparse Bayesian Learning (R-SBL). We provide four EM-based R-SBL variants that offer a range of options to trade-off computational complexity to the quality of the E-step computation. These methods include the Markov Chain Monte Carlo EM, linear minimum mean square estimation, approximate message passing and a diagonal approximation. Using numerical experiments, we show that the proposed R-SBL method outperforms existing S-NNLS solvers in terms of both signal and support recovery, and is very robust against the structure of the design matrix.

I. Introduction

This work considers the following signal model

$$\mathit{y}=\mathbf{\Phi }\mathit{x}+\mathit{\upsilon },$$ (1)

where the solution vector $\mathit{x}\in {ℝ}_{+}^M$ is assumed to be non-negative, the matrix Φ ∈ ℝ^N×M is fixed and obtained from the physics of the underlying problem, y ∈ ℝ^N is the measurement, and υ is the additive noise, modeled as a zero mean Gaussian with uncorrelated entries e.g. υ ~ 𝒩(0, σ²I).

Recovering x using the signal model in Eq. (1) is known as solving the non-negative least squares (NNLS) problem. NNLS has a rich history in the context of methods for solving systems of linear equations [1], density estimation [2] and non-negative matrix factorization (NMF) [3], [4], [5], [6]. NNLS is also widely used in applications such as text mining [7], image hashing [8], speech enhancement [9], spectral decomposition [10], magnetic resonance chemical shift imaging [11] and impulse response estimation [12]. The maximum-likelihood solution for the model in Eq. (1) is given by

$$\underset{\mathit{x}\ge \mathbf{0}}{\text{minimize}}{\Vert \mathit{y}-\mathbf{\Phi }\mathit{x}\Vert }_2.$$ (2)

In many applications, N < M and Eq. (1) is under-determined, meaning that there are more unknowns than equations and a unique solution to Eq. (2) may not exist. Recovering a unique solution is possible, if more information is known a-priori about the solution vector. For example, a useful assumption is that the solution vector is sparse and contains only a few non-zero elements [13], [14], [15]. In this case, the sparsest solution (e.g. assuming a noiseless scenario) can be recovered by modifying Eq. (2) to

$$\underset{\mathit{x}\ge \mathbf{0},\mathit{y}=\mathrm{\Phi }\mathit{x}}{\text{minimize}}{\Vert \mathit{x}\Vert }_0,$$ (3)

where ‖․‖₀ is the ℓ₀ pseudo-norm, which counts the non-zero elements in x. The number of non-zero elements in x is also referred to as the cardinality of the solution. Then, the design objective in Eq. (3) is to minimize the number of non-zero elements in x, while satisfying the optimization constraints. We refer to Eq. (3) as the sparse NNLS (S-NNLS) problem.

The S-NNLS problem is becoming increasingly popular in certain applications, where the non-negative solution has to be recovered from a limited number of measurements. For example, in [16] an S-NNLS recovery method was applied to magnetic resonance imaging (MRI) data to reconstruct narrow fiber-crossings from a limited number of acquisitions. In [17], another method was used to uncover regulatory networks from micro-array mRNA expression profiles from breast cancer data. In [18], [19], an S-NNLS method was applied to functional MRI data to estimate sparsely repeating spatio-temporal activation patterns in the human brain. S-NNLS solvers are also used in applied mathematics for creating dictionaries for sparse representations, such as sparse NMF and non-negative K-SVD [3], [20].

Directly solving Eq. (3) is not tractable, since the ℓ₀ penalty is not convex and the problem is NP-hard [21], [22]. Therefore, ‘greedy’ algorithms have been proposed to approximate the solution [23], [24], [25], [26], [27]. An example is the class of algorithms known as Orthogonal Matching Pursuit (OMP) [23], [28], which greedily select snon-zero elements of x. In order to adapt OMP to the S-NNLS problem, the criterion by which a new non-zero element of x is selected is modified to select the one having the largest positive value [27]. Another approach in this class of algorithms finds an x, such that ‖y − Φ x‖₂ ≤ ε and x ≥ 0 using the active-set Lawson-Hanson algorithm [1] and then prunes x until ‖x‖₀ ≤ K, where K is a pre-specified desired cardinality [3].

Greedy algorithms are computationally attractive, however they may lead to sub-optimal solutions. Therefore, convex relaxations of the ℓ₀ penalty have been proposed [22], [29], [30], [31], [32]. One simple alternative replaces the ℓ₀ with an ℓ₁ norm and reformulate the problem in Eq. (3) as

$$\underset{\mathit{x}\ge \mathbf{0}}{\text{minimize}}{\Vert \mathit{y}-\mathbf{\Phi }\mathit{x}\Vert }_2+\lambda {\Vert \mathit{x}\Vert }_1,$$ (4)

where λ > 0 is a suitably chosen regularization parameter to account for the measurement noise. The advantage of the formulation in Eq. (4) is that, it is a convex optimization problem and can be solved by a number of methods [32], [33], [34], [35]. One such approach is to estimate x through projected gradient descent [36].

In fact, the ℓ₁ norm penalty in Eq. (4) can be replaced by any arbitrary sparsity inducing surrogate function g(x), thus leading to alternative methods based on solving the following optimization problem

$$\underset{\mathit{x}\ge \mathbf{0}}{\text{minimize}}{\Vert \mathit{y}-\mathbf{\Phi }\mathit{x}\Vert }_2+\lambda g(\mathit{x}).$$ (5)

For example, a surrogate function $g(\mathit{x})={\sum }_{i=1}^M\text{ log }(x_i^2+\beta )$ has been considered [37], [38], which leads to an iterative reweighted optimization approach.

An alternative view on the S-NNLS problem is to cast the entire problem in a Bayesian framework and consider the maximum a-posteriori (MAP) estimate of x given y

$${\mathit{x}}_{\mathit{\text{MAP}}}=\underset{\mathit{x}}{\text{arg max}}p(\mathit{x}|\mathit{y}).$$ (6)

There is a strong connection between the MAP framework and deterministic formulations like the one in Eq. (5). Recently, it has been shown that formulations of the form in Eq. (5) can be represented by the formulation in Eq. (6) with a proper choice of p(x) [39]. For example, considering a separable p(x) of the form

$$p(\mathit{x})=\prod _{i=1}^{M}p(x_i),$$ (7)

the ℓ₁ regularization approach in Eq. (4) (e.g. choice of g(x) = ‖x‖₁ in Eq. (5)) is equivalent to the Bayesian formulation in Eq. (6) with an exponential prior for x_i. In this paper, our emphasis will be on Bayesian approaches for solving Eq. (1).

A. Contributions of the paper

• We introduce a family of non-negative probability densities, referred to as the rectified Gaussian scale mixture (R-GSM) to model non-negative and sparse solutions.

• We discuss how the R-GSM prior encompasses other sparsity promoting non-negative priors, such as the rectified Laplacian and rectified Student-t distributions, through a proper choice of mixing density.

• We detail how the R-GSM prior can be utilized to solve the sparse NNLS problem, using an evidence maximization based estimation procedure that utilizes the expectation-maximization (EM) framework. We refer to this technique as rectified Sparse Bayesian Learning (R-SBL).

• We provide four alternative EM-based approaches, that offer a range of options to trade-off computational complexity to the quality of the E-step computation, including the Markov Chain Monte Carlo EM, linear minimum mean square estimation, approximate message passing and a diagonal approximation.

• We use extensive empirical results to show the robustness and superiority of the R-GSM priors and R-SBL algorithm for the S-NNLS problem. Especially, under various i.i.d. and non-i.i.d. settings for the design matrix Φ.

B. Organization of the paper

In Section II, we discuss the advantages of scale mixture priors for p(x) and introduce the Rectified Gaussian Scale Mixture (R-GSM) prior. In Section III, we define the Type I and Type II Bayesian approaches to solve the S-NNLS problem and introduce the R-SBL framework with the R-GSM prior. We provide details of an evidence maximization based estimation procedure in Section III-B. We present empirical results comparing the proposed R-SBL algorithm to existing baseline methods in Section V.

II. Rectified Gaussian Scale Mixtures

We assume separable priors of the form in Eq. (7) and focus on the choice of p(x_i). The choice of prior plays a central role in the Bayesian inference [40], [41], [42]. For the S-NNLS problem, our prior must be sparsity inducing and satisfy the non-negativity constraints. Consequently, we consider the hierarchical scale mixture prior

$$p(x_i)={\int }_0^{\infty }p(x_i|{\gamma }_i)p({\gamma }_i)d{\gamma }_i.$$ (8)

Scale mixture priors were first considered in the form of Gaussian Scale Mixtures (GSM) where p(x_i|γ_i) = 𝒩(x_i; 0, γ_i) [43]. Super-gaussian densities are suitable priors for promoting sparsity [40], [44] and most of those priors can be represented in the form shown in Eq. (8) with a proper choice of p(γ_i) [45], [46], [47], [48], [49]. This has made scale mixture based priors valuable for the general sparse signal recovery problem. Another advantage of the scale mixture prior is that, it establishes a Markovian structure of the form

$$\mathit{\gamma }\to \mathit{x}\to \mathit{y},$$ (9)

where inference can be performed in the x domain (referred to as Type I) and in the γ domain (Type II). Experiment results in the standard sparse signal recovery problem show that performing inference in the γ domain consistently achieves superior performance [39], [40], [50], [51].

The Type II procedure involves finding a maximum-likelihood (ML) estimate of γ using evidence maximization and approximating the posterior p(x | y) by p(x | y, γ_ML). The performance gains can be understood by noting that γ is deeper in the Markovian chain than x, so the influence of errors in performing inference in the γ domain may be diminished [39], [50]. Also, γ is close enough to y in the Markovian chain such that meaningful inference about γ can still be performed, mitigating the problem of local minima that is more prevalent when seeking a Type I estimate of x [50].

Although priors of the form shown in Eq. (8) have been used in the compressed sensing literature (where the signal model is identical to Eq. (1) without the non-negativity constraint) [39], [52], [53], such priors have not been extended to solve the S-NNLS problem. Considering the findings that the scale mixture prior has been useful for the development of sparse signal recovery algorithms [39], [50], [54], we propose a R-GSM prior for the S-NNLS problem, where p(x_i|γ_i) in Eq. (8) is the rectified Gaussian (RG) distribution. We refer to the proposed Type II inference framework as R-SBL.

The RG distribution is defined as

$${𝒩}^R(x;\mu ,\gamma )=\sqrt{\frac{2}{\pi \gamma }}\frac{e^{-\frac{{(x-\mu )}^2}{2\gamma }}u(x)}{\text{erfc }(-\frac{\mu }{\sqrt{2\gamma }})},$$ (10)

where μ is the location parameter (e.g. is not the mean), γ is the scale parameter, u(x) is the unit step function, and erfc(x) is the complementary error function.¹

As noted in previous works [55], [56], closed form inference computations using a multivariate RG distribution are tractable only if the location parameter is zero (e.g. by effectively getting rid of the erfc(․) term). Although a non-zero μ could provide a richer class of priors, possibly to model approximately sparse or non-sparse solutions, considering the tractability issues and the potential overfitting problems (twice as many parameters), we focus on the R-GSM priors with μ = 0 to promote sparse non-negative solutions. It is a pragmatic choice and adequate for the problem at hand.

When μ = 0, the RG density simplifies to

$${𝒩}^R(x;0,\gamma )=\sqrt{\frac{2}{\pi \gamma }}{e}^{-\frac{x^2}{2\gamma }}u(x).$$ (11)

Thus, the R-GSM prior introduced in this work have the form

$$p(x)={\int }_0^{\infty }{𝒩}^R(x;0,\gamma )p(\gamma )d\gamma .$$ (12)

Different choices of p(γ) lead to different choices of priors and some examples are presented below.

A. R-GSM representation of sparse priors

We can utilize the proposed R-GSM framework to obtain other sparse non-negative priors. For instance, consider the rectified Laplace prior p(x) = λe^−λxu(x). By using an exponential prior for $p(\gamma )=\frac{{\lambda }^2}{2}{e}^{-\frac{{\lambda }^2\gamma }{2}}u(\gamma )$, we can express p(x) in the R-GSM framework [57] as

$$p(x)=2u(x){\int }_0^{\infty }𝒩(x|0,\gamma )\frac{{\lambda }^2}{2}{e}^{-\frac{{\lambda }^2\gamma }{2}}u(\gamma )d\gamma$$ (13)

$$=\lambda e^{-\lambda x}u(x).$$ (14)

Similarly, by considering the R-GSM with p(γ) given by the Gamma(a, b) distribution, we obtain a rectified Student-t distribution for p(x), and Eq. (8) simplifies as in [40] to

$$p(x)=2u(x){\int }_0^{\infty }𝒩(x|0,\gamma )\frac{{\gamma }^{a-1}{e}^{\frac{-\gamma }{b}}}{a^b\mathtt{\Gamma }(\mathtt{a})}d\gamma$$ (15)

$$=\frac{2b^a\mathtt{\Gamma }(a+\frac{1}{2})}{{(2\pi )}^{\frac{1}{2}}\mathtt{\Gamma }(a)}{(b+\frac{x^2}{2})}^{-(a+\frac{1}{2})}u(x),$$ (16)

where Γ is defined as $\mathtt{\Gamma }(a)={\int }_0^{\infty }{t}^{a-1}{e}^{-t}\mathit{\text{ dt}}$. More generally, all of the distributions represented by the GSM have a corresponding rectified version represented by a R-GSM, e.g. contaminated Normal and slash, symmetric stable and logistic, hyperbolic, etc. [43], [45], [46], [47], [48], [49].

B. Relation to other Bayesian works

In [55], a modified Gaussian prior was considered for the NNLS problem. The authors used a Gaussian prior of arbitrary mean and variance and performed a non-negative rectification using a ‘cut’ function. Their goal was to better represent non-sparse signals by avoiding the selection of μ = 0, as we consider in our work. Our R-GSM prior substantially differs from this work as we consider a mixture of zero-location RG distributions for the prior, as opposed to a single Gaussian density with the ‘cut’ rectification. Our design objective is to induce sparsity by using a hierarchical hyper-parameter γ.

In [58], a non-negative generalized approximate message passing (GAMP) approximation was proposed, using a Bernoulli non-negative Gaussian mixture prior of arbitrary location and scale parameters. This extended the prior given in [55] but used a fixed number of mixture components e.g. L = 3. The sparsity was enforced by using a Dirac delta function and an additional sparsity rate λ that would ‘favor’ the Dirac function and attenuate other mixture components, simultaneously. The authors had to infer a bulk of parameters including the scale, location, and mixture weights as well as the sparsity rate simultaneously. Our R-SBL approach differs from [58] as we only consider a sparsity inducing hyper-parameter γ, and our mixture components are strictly located at zero. Our approach simplifies the overall inference procedure and the problem formulation. We also consider an infinite number of mixture components, as opposed to considering a fixed number of components.

Finally, we consider a more general class of priors than the existing methods since the R-GSM prior is based on an arbitrary mixing density p(γ). As indicated in Section II-A, different selections of p(γ) lead to more flexible and a more generalized priors for the spase solution.

III. Bayesian Inference with Scale Mixture Prior

We detail the Type I and Type II methods for solving the S-NNLS problem with an R-GSM prior. Though this paper is dedicated to Type II estimation because of its superior performance in sparse signal recovery problems [39], [50], we briefly introduce Type I in the following section for the sake of completeness.

A. Type I estimation

Using Type I to solve the S-NNLS problem translates into calculating the MAP estimate of x given y

$$\underset{\mathit{x}}{\text{arg min}}{\Vert \mathit{y}-\mathbf{\Phi }\mathit{x}\Vert }_2^2-\lambda \sum _{i=1}^M\text{ln }p(x_i).$$ (17)

Some of the ℓ₀ relaxation methods described in Section I can be derived from a Type I perspective. For instance, by choosing an exponential prior for p(x_i), Eq. (17) reduces to the ℓ₁ regularization approach in Eq. (4) with the interpretation of λ as being determined by the parameters of the prior and the noise variance. Similarly, by choosing a Gamma prior for p(x_i), Eq. (17) reduces to

$$\underset{\mathit{x}}{\text{arg min}}{\Vert \mathit{y}-\mathbf{\Phi }\mathit{x}\Vert }_2^2+\lambda \sum _{i=1}^M\text{ln }(b+\frac{x_i^2}{2}),$$ (18)

which leads to the reweighted ℓ₂ approach to the S-NNLS problem described in [37], [38]. A unified Type I approach for the R-GSM prior can be readily derived using the approaches as discussed in [39], [45].

B. Type II estimation

The Type II framework involves finding a ML estimate of γ using evidence maximization and approximating the posterior p(x | y) by p(x | y, γ_ML). Then, appropriate point estimates and the solution x can be estimated. We refer to this approach as the Rectified Sparse Bayesian Learning (R-SBL).

Several strategies exist for estimating γ. The first strategy considers the problem of forming a ML estimate of γ given y [39], [40], [59], [60]. In our case, p(γ | y) does not admit a closed form expression, making this approach difficult. The second strategy, which is investigated in this paper, aims to estimate γ by utilizing an EM algrotihm [39], [52], [60]. In the EM approach, we treat (x, y, γ) as the complete data and x as the hidden variable. Utilizing the current estimate γ^t, where t refers to the iteration index, the expectation step (E-step) involves determining the expectation of the log-likelihood, Q(γ, γ^t) given by

$$Q(\mathit{\gamma },{\mathit{\gamma }}^t)=E_{\mathit{x}|\mathit{y};{\mathit{\gamma }}^t}[\text{ln }p(\mathit{y}|\mathit{x})+\text{ln }p(\mathit{x}|\mathit{\gamma })+\text{ln }p(\mathit{\gamma })]$$ (19)

$$\doteq \sum _{i=1}^M{E}_{\mathit{x}|\mathit{y};{\mathit{\gamma }}^t}[-\frac{1}{2}\text{ ln }{\gamma }_i-\frac{x_i^2}{2{\gamma }_i}+\text{ln }p({\gamma }_i)],$$ (20)

where ≐ indicates that constant terms, and terms that do not depend on γ have been dropped since they do not affect the M-step. For simplicity, we assume a non-informative prior on γ [40]. In the M-step, we maximize Q(γ, γ^t) with respect to γ by taking the derivative and setting it equal to zero, which yields the update rule

$${\gamma }_i^{t+1}=E_{\mathit{x}|\mathit{y},{\mathit{\gamma }}^t,{\sigma }^2}[x_i^2]≔\langle x_i^2\rangle .$$ (21)

To compute $\langle x_i^2\rangle$, we first consider the multivariate posterior density p(x|y, γ, σ²) which has the form (e.g. see Appendix VII-B for details)

$$p(\mathit{x}|\mathit{y},\mathit{\gamma })=c(\mathit{y})e^{-\frac{{(\mathit{x}-\mathit{\mu })}^T{\mathbf{\sum }}^{-1}(\mathit{x}-\mathit{\mu })}{2}}u(\mathit{x}),$$ (22)

where μ and Σ are given by [40], [52], [61]

$$\mathit{\mu }=\mathbf{\Gamma }{\mathbf{\Phi }}^T{({\sigma }^2\mathit{I}+\mathbf{\Phi }\mathbf{\Gamma }{\mathbf{\Phi }}^T)}^{-1}\mathit{y}$$ (23)

$$\mathbf{\sum }=\mathbf{\Gamma }-\mathbf{\Gamma }{\mathbf{\Phi }}^T{({\sigma }^2\mathit{I}+\mathbf{\Phi }\mathbf{\Gamma }{\mathbf{\Phi }}^T)}^{-1}\mathbf{\Phi }\mathbf{\Gamma },$$ (24)

and Γ = diag(γ). The posterior in Eq. (III-B) is known as a multivariate RG (or a multivariate truncated normal [62]). The normalizing constant c(y) in the multivariate RG does not have a closed form expression. Note that the M-step in Eq. (21) only requires the marginal density. However, the marginals of a multivariate RG are not univariate-RG’s, and also do not admit a closed form expression [62], which unfortunately means no immediate closed form expression for the marginal moments.

However, we can approximate the first and the second moments 〈x_i〉 and $\langle x_i^2\rangle$ of the multivariate RG posterior. In the following, we propose four different approaches for this purpose that offer a trade-off between computational complexity and theoretical accuracy.

1) Markov Chain Monte Carlo EM (MCMC-EM)

Advances in numerical methods made it possible to sample from complex multivariate distributions [63], [64], [65]. Numerical methods are particularly useful when the first and second order statistics of a posterior density do not have a closed form expression. In this case, the E-step can be performed by drawing samples using numerical Markov Chain Monte Carlo (MCMC) and then calculating the sample statistics. This is usually referred as MCMC-EM [66], [67]. First, we consider the Gibbs sampling approach in [68], [69]. We use hat notation to refer to the empirical estimates of various parameters (e.g. Σ̂).

We use the multivariate truncated normal (TN) definition in [69] and write

$$\mathtt{\text{TN}}(\mathit{x};\hat{\mathit{\mu }},\hat{\mathbf{\sum }},\mathit{R},{\mathit{\alpha }}_L,{\mathit{\alpha }}_U)=$$ (25)

$$\left(c_{\mathit{\text{tn}}}{e}^{-\frac{{(\mathit{x}-\hat{\mathit{\mu }})}^T{\hat{\mathbf{\sum }}}^{-1}(\mathit{x}-\hat{\mathit{\mu }})}{2}}\right){\mathbf{1}}_{{\mathit{\alpha }}_L\le \mathit{\text{Rw}}\le {\mathit{\alpha }}_U},$$ (26)

where 1_(·) is the indicator function and c_tn is the normalizing constant for the density. In the case of a multivariate rectified Gaussian, the truncation bounds are α_L = 0 and α_U = ∞, and R = I. By introducing the transformation, w = L̂⁻¹(x − μ̂) where L̂ is the lower triangular Cholesky decomposition of Σ̂, it can be shown that w is TN(w; 0, I, L̂, ${\mathit{\alpha }}_L^{\ast },{\mathit{\alpha }}_U^{\ast }$), with new truncation bounds ${\mathit{\alpha }}_L^{\ast }={\mathit{\alpha }}_L-\hat{\mathit{\mu }}=-\hat{\mathit{\mu }}$ and ${\mathit{\alpha }}_U^{\ast }={\mathit{\alpha }}_U-\hat{\mathit{\mu }}=\mathbf{\infty }$.

The Gibbs sampler then proceeds by iteratively drawing samples from the conditional distribution p(w_i| y, γ̂, σ², w_−i), where w_−i refers to the vector containing all but the i’th element of w. Given a set of samples drawn from w, we can generate samples from the original distribution of interest by inverting the transformation: ${\{{\mathit{x}}^n\}}_{n=1}^N={\{\hat{\mathit{L}}{\mathit{w}}^n+\hat{\mathit{\mu }}\}}_{n=1}^N$. Then, the first and second empirical moments can be calculated from the drawn samples using

$$\langle x_i\rangle \approx \frac{1}{N}\sum _{n=1}^N(x_i^n),$$ (27)

$$\langle x_i^2\rangle \approx \frac{1}{N}\sum _{n=1}^N{(x_i^n)}^2,$$ (28)

and the EM step can be iterated by updating ${\hat{\gamma }}_i^{t+1}=\langle x_i^2\rangle$.

After convergence, a point estimate for x is needed. The optimal estimator of x in the minimum mean-square-error (MMSE) sense is simply x̂_mean = 〈x̂_i〉. An alternative point estimate is to use x̂_mode, given by

$${\hat{\mathit{x}}}_{\mathit{\text{mode}}}=\underset{\mathit{x}}{\text{arg max}}p(\mathit{x}|\mathit{y},\hat{\mathit{\gamma }},{\sigma }^2)$$ (29)

$$=\underset{\mathit{x}\ge 0}{\text{arg min}}{\Vert \mathit{y}-\mathbf{\Phi }\mathit{x}\Vert }_2^2+\lambda \sum _{i=1}^M\frac{x_i^2}{{\hat{\gamma }}_i},$$ (30)

where Eq. (30) can be solved by any NNLS solver. The estimate x̂_mode could be a favorable point estimate because it chooses the peak of p(x| y, γ̂, σ²), which could be multi-modal and not well-characterized by its mean.

For the sparse recovery problem, we experienced very slow convergence with Gibbs sampling. Convergence was particularly slow for higher problem dimensions and at larger cardinalities. The latter was expected as a sparse solution is harder to recover in those cases. Thus, we resorted to Hamiltonian Monte Carlo (HMC), which is designed specifically for target spaces constrained by linear or quadratic constraints [65]. HMC improves the MCMC mixing performance by using the gradient information of the target distribution [66].

Despite use of the state of the art MCMC techniques, MCMC-EM might still converge to poor local minima solutions and result in sub-optimal performance [70], [71], [72]. Particularly, performance may be even poorer for underdetermined problems. Though MCMC-EM is not thoroughly investigated for sparse recovery problems, here we list four major issues for consideration:

1. Convergence: MCMC-EM based algorithms can get stuck in a local minima depending on the problem dimensions and complexity of the search space. This is true even for well-posed problems [67], [73]. In under-determined problems, the solution set for Eq. (2) may contain many local minima and thus, a good MCMC-EM implementation should try to avoid local minima.

2. Computational Limits: Current MCMC sampling techniques are not optimal for drawing large sample sizes N from high dimensional multivariate posterior densities. Therefore, the number of available samples is often limited by computational constraints [63], [64], [65].

3. Quality of Parameter Estimates: Since the MCMC samples are determined by random sampling at each iteration, the estimates of γ̂, μ̂, and Σ̂ depend highly on the quality of the MCMC estimates x̂, which in turn affects the quality of next cycle of MCMC samples. This may lead EM algorithm to converge to a sub-optimal solution.

4. Structure of Empirical Σ̂: When M is large and the dimensions of the empirical scale matrix are also large, Σ̂ may be no longer a good numerical estimate [71], [74], [75]. This could happen when the problem is inherently under-determined with N < M, and reveals itself as Σ̂ being close to singular. Therefore, regularization methods for Σ̂ are often used to alleviate this problem [71], [72].

The scale matrix Σ̂ has direct control over the search space for MCMC and spurious off-diagonal values tend to increase the number of local-minima. Therefore, to address the issues listed above, we incorporated ideas from prior work to regularize the estimates of Σ̂:

• As in [71], [72], we assume that Σ̂ is sparse and we prune its off-diagonal elements, when they drop below a certain threshold T_p. This prevents the spurious off-diagonal values in Σ̂ from affecting the next cycle of MCMC samples and improves future estimates of γ̂.

• We incorporate the shrinkage estimation idea presented in [72], [74] and regularize Σ̂ as a convex sum of the empirical Σ̂ and a target matrix T such that, Σ̂ = λ Σ̂ + (1 − λ)T. A simple selection is the matrix Σ̂_β which is Σ̂ with diagonal elements scaled by a factor β. Though this approach does not guarantee convergence to a global minimum and the solution could still be a local minima or a saddle point solution, we empirically observed better recovery performance.

2) Linear minimum mean square estimation (LMMSE)

The LMMSE approach is motivated by the complexity of the MCMC-EM approach. Examining the parameters being computed, one can interpret them as finding the MMSE estimate of x and the associated MSE. This motivates replacing the MMSE estimate by the simple LMMSE estimate of x. The affine LMMSE estimate for x is

$$\hat{\mathit{x}}={\mathit{\mu }}_{\mathit{x}}+{\mathit{R}}_{\mathit{x}}{\mathbf{\Phi }}^T{(\mathbf{\Phi }{\mathit{R}}_{\mathit{x}}{\mathbf{\Phi }}^T+{\sigma }^2\mathit{I})}^{-1}(\mathit{y}-\mathbf{\Phi }{\mathit{\mu }}_{\mathit{x}}),$$ (31)

where R_x is the covariance matrix of x and is diagonal. The estimation error covariance matrix is given by [76]

$${\mathit{R}}_{\mathit{e}}={\mathit{R}}_{\mathit{x}}-{\mathit{R}}_{\mathit{x}}{\mathbf{\Phi }}^T{(\mathbf{\Phi }{\mathit{R}}_{\mathit{x}}{\mathbf{\Phi }}^T+{\sigma }^2\mathit{I})}^{-1}\mathbf{\Phi }{\mathit{R}}_{\mathit{x}}.$$ (32)

To elaborate, in the E-step where γ is fixed at γ^t, the entries of x are independent, and the prior mean and the prior covariance will be equal to the mean and variance of the independent univariate RG distributions with p(x_i|γ_i) = 𝒩^R (0, γ_i). The mean of a univariate rectified Gaussian density with zero location parameter is given by [77]

$${\mu }_{x,i}=\sqrt{\frac{2{\gamma }_i}{\pi }},$$ (33)

and the variances, which are the diagonal entries of the diagonal matrix R_x, are given by

$$R_{x,\mathit{\text{ii}}}={\gamma }_i(1-2/\pi ).$$ (34)

Using the values of μ_x and R_x from Eq. (33) and Eq. (34) in Eq. (31) we obtain the LMMSE point estimate for the solution vector. Similarly, the update for γ (M-step) is given by

$${\gamma }_i={\hat{x}}_i^2+R_{e,\mathit{\text{ii}}}.$$ (35)

This is sufficient to implement the EM algorithm. Upon convergence, the mean point estimate is simply x̂_mean = x̂, and the mode point estimate can be obtained by utilizing the converged values γ_i in Eq. (30).

3) Generalized approximate message passing (GAMP)

In this section, we present an EM implementation using the generalized approximate message passing algorithm (GAMP) [78]. A different GAMP based non-negative Gaussian mixture approach was used in [58], which uses an i.i.d. Bernoulli non-negative Gaussian mixture prior with a fixed and known mixture order that is independent of M. To overcome the known convergence issues with the type of GAMP algorithm in [58] when a non-i.i.d. design matrix Φ is used [79], [80], [81], we incorporate the damping technique used in [81] into the proposed R-SBL GAMP algorithm.

GAMP is a low complexity iterative inference algorithm. The low complexity is achieved by applying quadratic and Taylor series approximations to loopy belief propagation. Under the prior p(x) and the likelihood p(y|x), GAMP can approximate the MMSE estimate when used in the sum-product mode, or it can approximate the MAP estimate when used in its max-sum mode.

The sum-product version of the algorithm computes the mean and variance of approximate marginal posteriors on x_i, where the approximate posteriors are given by

$$p(x_i|r_i;{\tau }_{r_i})\propto p(x_i)𝒩(x_i;r_i,{\tau }_{r_i}),$$ (36)

where r_i approximates a corrupted version (AWGN) of the true x_i as

$$r_i\approx x_i+{\overline{r}}_i$$ (37)

$${\overline{r}}_i~𝒩(0,{\tau }_{r_i}).$$ (38)

In the large system limit and when the design matrix Φ is i.i.d sub-Gaussian, the approximation in Eq. (37) was shown to be exact [78], [82]. Therefore, in sum-product mode, the MMSE estimate x̂_i produced by GAMP corresponds to the MMSE estimate of x_i given r_i, and is given by the conditional mean in Eq. (39) below. Where τ_xi in sum-product GAMP, corresponds to the MMSE associated with the estimate x̂_i and is given in Eq. (40) as the conditional variance of x_i given r_i

$${\hat{x}}_i=𝔼\{x_i|r_i;{\tau }_{r_i}\}$$ (39)

$${\tau }_{x_i}=\text{Var}\{x_i|r_i;{\tau }_{r_i}\}.$$ (40)

Similarly, in the max-sum version of GAMP, the MAP estimate x̂_i is given using the proximal operator in Eq. (41) as the MAP estimate of x_i given r_i, while τ_xi in the max-sum GAMP corresponds to the sensitivity of the proximal thresholding and is given by Eq. (42)

$${\hat{x}}_i={\text{prox}}_{-\text{ln }p(x_i)}(r_i;{\tau }_{r_i})$$ (41)

$${\tau }_{x_i}={\tau }_r{\text{prox}\prime }_{-\text{ln }p(x_i)}(r_i;{\tau }_{r_i})$$ (42)

$${\text{prox}}_f(\hat{a},{\tau }^a)\triangleq \underset{x\in \mathit{R}}{\text{arg min}}f(x)+\frac{1}{2{\tau }^a}{|x-\hat{a}|}^2.$$ (43)

When implementing the EM algorithm, the approximate posterior computed by the sum-product GAMP can be used to efficiently approximate the E-step [83]. Moreover, in the case of max-sum GAMP, even though the algorithm does not provide marginal distributions, in the large system limit and under i.i.d sub-Gaussian Φ the assumption of r_i being an AWGN corrupted version of the true x_i still holds [82]. Thus, similar to the approach in [58], an extra step can be added to compute marginal distributions using Eq. (36). The computed marginals can be used to approximate the E-step. For the assumed rectified Gaussian scale mixture prior p(x|γ) the details of finding x̂_i and τ_xi estimates in both the sum-product and max-sum cases are shown in Appendix VII-A.

Upon the convergence of the GAMP algorithm, the approximate E-step of the EM algorithm is complete, and we can proceed to evaluate the M-step in Eq. (21) as

$$\langle x_i^2\rangle ={\int }_{x_i}{x}_i^{2}p(x|r_i;{\tau }_{r_i})={\tau }_{x_i}+{\hat{x}}_i^2.$$ (44)

The R-SBL GAMP algorithm based on the E and M-steps described above is summarized Table I. We note that for the AWGN case, the output function of the GAMP algorithm used to evaluate s and τ_s in Table I, is the same for both sum-product and max-sum GAMP [78].

TABLE I.

R-SBL GAMP Algorithm

Initialization

S ← |Φ|2 (component wise magnitude squared)

Initialize ${\dot{\mathit{\tau }}}_x^0>0$

s0, ẋ0 ← 0

for n = 1, 2, …․, Nmax

Initialize ${\mathit{\tau }}_x^1\leftarrow {\dot{\mathit{\tau }}}_x^{n-1},{\mathit{x}}^1\leftarrow {\dot{\mathit{x}}}^{n-1}$

E-Step approximation

for k = 1, 2, …․, Kmax

$1/{\mathit{\tau }}_p^k\leftarrow \mathit{S}{\mathit{\tau }}_x^k$

${\mathit{p}}^k\leftarrow {\mathit{s}}^{k-1}+{\mathit{\tau }}_p^k\mathbf{\Phi }{\mathit{x}}^k$

${\mathit{\tau }}_s^k\leftarrow \frac{{\sigma }^{-2}{\mathit{\tau }}_p^k}{{\sigma }^{-2}+{\mathit{\tau }}_p^k}$

${\mathit{s}}^k\leftarrow (1-{\theta }_s){\mathit{s}}^{k-1}+{\theta }_s({\mathit{p}}^k/{\mathit{\tau }}_p^k-\mathit{y})/({\sigma }^2+1/{\mathit{\tau }}_p^k)$

$1/{\mathit{\tau }}_r^k\leftarrow {\mathit{S}}^{\top }{\mathit{\tau }}_s^k$

${\mathit{r}}^k\leftarrow {\mathit{x}}^k-{\mathit{\tau }}_r^k{\mathbf{\Phi }}^{\top }{\mathit{s}}^k$

if MaxSum then

${\mathit{\tau }}_x^{k+1}\leftarrow {\mathit{\nu }}^k$

x̂k+1 ← ηku(rk)

else

${\mathit{\tau }}_x^{k+1}\leftarrow {\mathit{\nu }}^{k}g(\frac{{\mathit{\eta }}^k}{{\mathit{\nu }}^k})$

${\hat{\mathit{x}}}^{k+1}\leftarrow {\mathit{\eta }}^k+\sqrt{{\mathit{\nu }}^k}h(\frac{{\mathit{\eta }}^k}{{\mathit{\nu }}^k})$

end if

if ‖x̂k+1 − x̂k‖2/x̂k+1‖2 < εgamp, break

end for %end of k loop

if MaxSum

${\dot{\mathit{x}}}^i\leftarrow {\mathit{\eta }}^{k+1}+\sqrt{{\mathit{\nu }}^{k+1}}h(\frac{{\mathit{\eta }}^{k+1}}{{\mathit{\nu }}^{k+1}}),{\dot{\mathit{\tau }}}_x^i\leftarrow {\mathit{\nu }}^{k+1}g(\frac{{\mathit{\eta }}^{k+1}}{{\mathit{\nu }}^{k+1}})$

else

${\dot{\mathit{x}}}^n\leftarrow {\hat{\mathit{x}}}^{k+1},{\dot{\mathit{\tau }}}_x^n\leftarrow {\mathit{\tau }}_x^{k+1}$

end if

M-Step

${\mathit{\gamma }}^{n+1}\leftarrow {|{\dot{\mathit{x}}}^n|}^2+{\dot{\mathit{\tau }}}_x^n$

if ‖ẋn − ẋn−1‖2/‖ẋn‖2 < εem, break

end for %end of i loop

In Table I, all squares, divisions and multiplications are taken element wise. K_max is the maximum allowed number of GAMP iterations, ε_gamp is the GAMP normalized tolerance parameter, I_max is the maximum allowed number of EM iterations and ε_em is the EM normalized tolerance parameter.

4) Diagonal approximation (DA)

We know a-priori that the posterior in Eq. (III-B) does not admit a closed form expression. However, to implement the EM algorithm, we only need the marginals of the posterior. We first note that, if the scale matrix Σ is diagonal then we could evaluate the normalizing constant c(y) in closed form, since the multivariate RG posterior can be written as a product of univariate marginals (e.g. see Appendix VII-B for details).

In the diagonal approximation (DA) approach, we resort to approximating the posterior in Eq. (III-B) with a suitable posterior density e.g. p(x|y, γ) ≈ p̃(x|y, γ), which could be written as a product of independent marginal densities i.e. p̃(x_i|y, γ). This approximate posterior density is derived in Appendix VII-B as

$$\stackrel{\sim }{p}(\mathit{x}|\mathit{y},\mathit{\gamma })=\prod _{i=1}^M\stackrel{\sim }{p}(x_i|\mathit{y},\mathit{\gamma })$$ (45)

$$=\prod _{i=1}^M\sqrt{\frac{2}{\pi {\sum }_{\mathit{\text{ii}}}}}\frac{e^{-\frac{{(x_i-{\mu }_i)}^2}{2{\sum }_{\mathit{\text{ii}}}}}u(x_i)}{\text{erfc }(-\frac{{\mu }_i}{\sqrt{2{\sum }_{\mathit{\text{ii}}}}})},$$ (46)

where μ_i is the i’th element of μ and Σ_ii is the i’th diagonal element of Σ obtained using Eqs. (23) and (24). The marginal p̃(x_i|y, γ) in Eq. (46) is the univariate RG density defined in Eq. (10). In other words we have p̃(x_i|y, γ) = 𝒩^R(x_i; μ_i, Σ_ii). Then, the univariate RG marginals are well-characterized by their first and second moments given in [77], with the first moment given as

$$\langle x_i\rangle ={\mu }_i+\sqrt{\frac{2{\sum }_{\mathit{\text{ii}}}}{\pi }}\frac{e^{-\frac{{\mu }_i^2}{2{\sum }_{\mathit{\text{ii}}}}}}{\text{erfc }(-\frac{{\mu }_i}{\sqrt{2{\sum }_{\mathit{\text{ii}}}}})},$$ (47)

and the second moment is given as

$$\langle x_i^2\rangle ={\mu }_i^2+{\sum }_{\mathit{\text{ii}}}+{\mu }_i\sqrt{\frac{{\sum }_{\mathit{\text{ii}}}}{\pi }}\frac{e^{-\frac{{\mu }_i^2}{2{\sum }_{\mathit{\text{ii}}}}}}{\text{erfc }(-\frac{{\mu }_i}{\sqrt{2{\sum }_{\mathit{\text{ii}}}}})}.$$ (48)

Note that the moments of p̃(x_i|y, γ) are approximations to the moments of the exact marginals which do not admit closed form. However, we can perform EM using the approximate moments to approximate the true solution. EM can be carried out by setting ${\gamma }_i^{t+1}=\langle x_i^2\rangle$ and iterating over t. After convergence of γ_i’s, the mean point estimate is obtained as x̂_mean = 〈x_i〉. The mode point estimate x̂_mode can be calculated by using converged values of γ_i’s in Eq. (30).

If the diagonal elements of Σ are large valued or become large over EM iterations as compared to off-diagonals, then DA is expected to work well. Note that assuming a diagonal Σ was also motivated by previous work [71], [74], [75], [84], [85] for various applications. In this work, we empirically report that DA has very good sparse recovery performance and has low complexity.

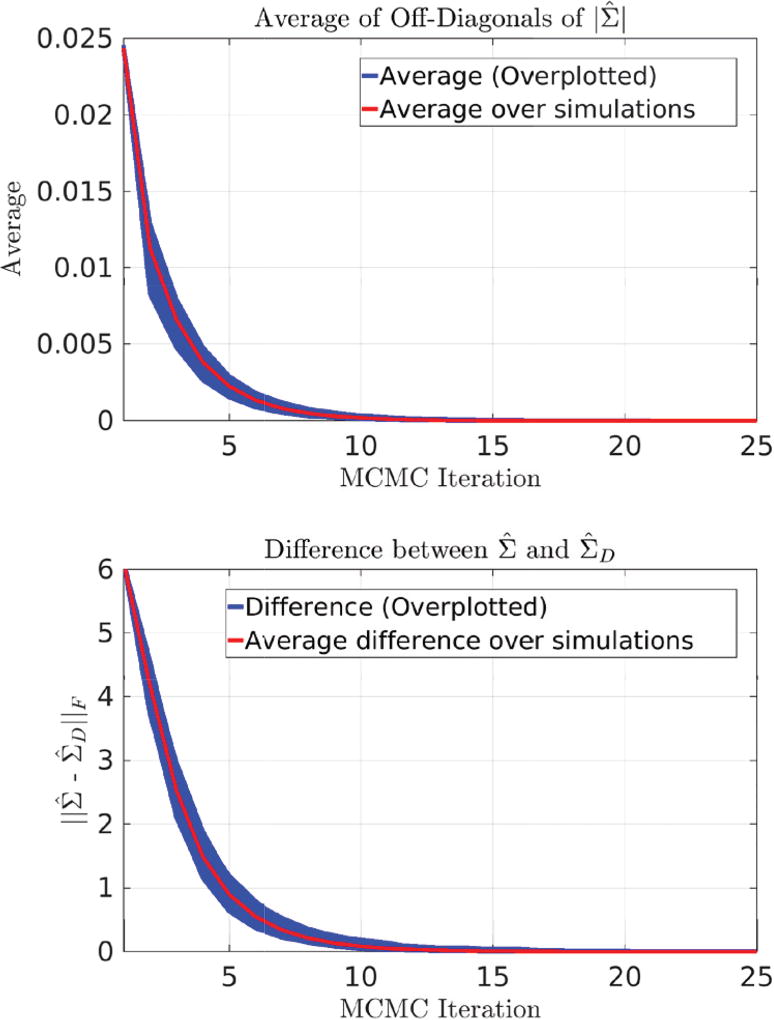
To further support the DA approximation, we present empirical findings regarding the structure of Σ. We performed sparse recovery simulations using Eq. (1) with the MCMC-EM approach as the ground truth (i.e. without regularizing the MCMC estimates of Σ̂). We assumed that x was of size 200 with 10 non-zero elements drawn from 𝒩^R(0, 1). The dictionary Φ ∈ ℝ^50×200 columns were normally distributed Φ ~ 𝒩 (0, I). We solved this problem for 1,000 simulations and overlay plots of the average absolute value of the off-diagonals of Σ̂ as a function of MCMC-EM iteration in the first row of Fig. 1.

Fig. 1.

Top: Empirical observations for the structure of Σ. We performed S-NNLS recovery using MCMC-EM (without regularizing the estimates of Σ) and monitored the average value of off-diagonals for |Σ|. We simulated for 1,000 runs and overplotted the results (blue lines). The average of average off-diagonals for |Σ| over 1,000 results is shown with the red line. The exponentially decreasing behavior suggests that the off-diagonal magnitudes of Σ decrease over MCMC iterations, suggesting that true Σ is close to a diagonal form. Bottom: Distance between true Σ and a diagonal matrix formed by it’s diagonal entries Σ_D for the same experiment. This suggests that true Σ approaches to a diagonal matrix over MCMC iterations.

We see that the average of off-diagonal elements decreased exponentially as a function of MCMC-EM iteration, and the average of this behavior over 1,000 simulations (e.g. red line) has a final value of 10⁻⁴ after 10 iterations. This indicates the off-diagonals of Σ̂ of the true posterior (with MCMC sampling) indeed become close to zero. Moreover, in the second row of Fig. 1, we overlay plots of the Frobenius norm of the difference between Σ̂ and Σ̂_D, where Σ̂_D is the diagonal matrix consisting of diagonal elements from Σ̂. This shows that as MCMC-EM converges, the true Σ becomes close to a diagonal matrix. These results suggest that, if there is flexibility in choosing the dictionary Φ as in compressed sensing, then proper choice of Φ can lead to the DA approach producing high quality approximate marginals p̃(x_i|y, γ) that are close to the true marginals.

C. Computational complexity of proposed methods

For computational comparisons, we assume that N ≤ M. Under this assumption, the time complexity of the DA algorithm is 𝒪(N² M) per EM iteration. This complexity is similar to the original SBL algorithm in [44], [52] and is largely due to the computationally intensive matrix inversion step e.g. (σ² I + ΦΓΦ^T)⁻¹ given in Eq. (23). Time complexity of the LMMSE algorithm is also 𝒪(N² M) per EM iteration. This complexity is determined from a similar matrix inversion step (ΦR_xΦ^T + σ² I)⁻¹ in Eq. (32) (e.g. note that R_x is diagonal). The GAMP algorithm bypasses the computationally intensive matrix inversion and the resulting complexity is 𝒪(N M) time [51]. This is linear in both problem dimensions and significantly faster than the both the DA and LMMSE methods. For the MCMC-EM algorithm, the actual computational cost is determined by the random Hamiltonian MCMC sampling, which is explained in more detail in [65].

IV. Experiment Design

In this section, we provide the layout of our numerical experiments. In the following, we provide extensive comparisons between the proposed R-SBL variants LMMSE, GAMP, MCMC and DA to the baseline S-NNLS solvers, including NNGM-AMP [58], SLEP-ℓ₁ [86], and NN-OMP [87]. In all of the experiments below, we generate sparse vectors ${\mathit{x}}^{\mathit{\text{gen}}}\in {ℝ}_{+}^{400}$, such that ‖x^gen‖₀ = K and random dictionaries Φ ∈ ℝ^100×400. We normalize the columns of Φ by $1/\sqrt{N}$ as in [88]. For a fixed Φ and x^gen, we compute the measurements y = Φ x^gen and use the baseline algorithms and the proposed R-SBL variants to approximate x^gen.

In the first set of experiments, we simulate a ‘noiseless’ recovery scenario, where the noise variance is set as σ² = 10⁻⁶, the non-zero entries of the solution vector are drawn from a rectified Gaussian density 𝒩^R (0, 1) and the dictionary columns are i.i.d. Normal distributed as Φ ~ 𝒩 (0, I). We experiment with cardinalities K = {10, 20, 30, 35, 40, 45, 50}.

In the second set of experiments, we construct various dictionary types to analyze the robustness of our R-SBL method and the baseline solvers for the general S-NNLS problem. The dictionary structures considered here are similar to the ones used in [51], [89] are not necessarily i.i.d. Gaussian, and can be low-rank, coherent, ill-posed, and non-negative as described below:

1. Coherent dictionaries: We introduce coherence among the columns of an original dictionary Φ = 𝒩 (0, I) and report recovery performances for a fixed K = 50. This is done by multiplying Φ with a coherence matrix C, to obtain a dictionary Φ_c with coherent columns. C is the Cholesky factor of the Toeplitz(ρ) matrix with a coherence parameter ρ. We experimented with different coherence values by selecting ρ = {0.1, 0.2, …, 0.80, 0.85, 0.90, 0.95}.

2. Low-rank dictionaries: We construct rank-deficient dictionaries such that, Φ = AB, where A ∈ ℝ^N×R, B ∈ ℝ^R×M and R < N. The elements of A and B are i.i.d. Normal. The rank ratio R/N is considered as a measure of rank deficiency, where smaller values indicate more deviation from an i.i.d. dictionary. We experiment with R/N = {1, 0.95, …, 0.4} and report recovery performances for a fixed K = 50.

3. Ill-conditioned dictionaries: We experiment with ill-conditioned dictionaries with a condition number κ > 1. For a fixed κ, the dictionary is constructed as Φ = USV^T. Here, U and V contain the left and right singular vectors of an i.i.d. Gaussian matrix, and S is a diagonal matrix containing the eigenvalues. We decay the elements of S with S_i+1,i+1 = κ^{−1/N− 1} S_i,i for i = 1, 2, …, N − 1. The value of κ measures the deviation from an i.i.d. Gaussian dictionary. We experimented for the condition numbers κ = {8, 10, …, 28}. Larger κ values indicate more deviation from an i.i.d. dictionary.

4. Non-negative dictionaries: Non-negative dictionaries are used in sparse recovery applications such as sparse NMF [3] and NN K-SVD [20] where a positive mapping is required on the solution vector. We construct non-negative dictionaries Φ, with columns that are drawn according to Φ ~ RG(0, I). We experiment with cardinalities K = {10, 20, 30, 35, 40, 45, 50}.

In the third set of experiments, we set the noise variance σ² for υ such that the signal to noise ratio (SNR) is 20 dB and repeat the first set of experiments. This experiment was meant to assess the robustness of R-SBL variants under noisy conditions.

In the fourth set of experiments, we investigate recovery performance for a variety of different distributions for non-zero elements of x and different Φ. We draw the nonzero elements of x^gen randomly, according to the following probability distributions:

1. NN-Cauchy (Location: 0, Scale: 1)

2. NN-Laplace (Location: 0, Scale: 1)

3. Gamma (Location: 1, Scale: 2)

4. Chi-square with ν = 2

5. Bernoulli with p(0.25) = 1/2 and p(1.25) = 1/2

where the prefix ‘NN’ stands for non-negative. These distributions are obtained by taking the absolute value of the respective probability densities. We generate random dictionaries according to the following densities:

1. Normal (Location: 0, Scale: 1)

2. ±1 with p(1) = 1/2 and p(−1) = 1/2

3. {0, 1} with p(0) = 1/2 and p(1) = 1/2

In all of the experiments detailed here, the results we present were averaged over 1,000 simulations. Moreover, the R-SBL MCMC approach was only used in the first set of experiments to demonstrate the high quality of the parameter estimates obtained with the low complexity approaches such as DA, LMMSE and GAMP. We omit the MCMC in other experiments due to computational constraints.

A. Performance metrics

To evaluate the performance of various S-NNLS algorithms, we used the normalized mean square recovery error (NMSE) and the probability of error in the recovered support set (PE) [22]. We computed the NMSE between the recovered signal x̂ and the ground truth x^gen using:

$$\text{NMSE}={\Vert \hat{\mathit{x}}-{\mathit{x}}^{\mathit{\text{gen}}}\Vert }^2/{\Vert {\mathit{x}}^{\mathit{\text{gen}}}\Vert }^2.$$ (49)

The PE metric was computed using:

$$\text{PE}=\frac{\mathit{\text{max}}\{|S|,|\hat{S}|\}-|S\cap \hat{S}|}{\mathit{\text{max}}\{|S|,|\hat{S}|\}},$$ (50)

where the support of the true solution was S and the support of x̂ was Ŝ. A value of PE = 0 indicates that the ground truth and recovered supports are the same, whereas PE = 1 indicates no overlap between supports. Averaging the PE over multiple trials gives the empirical probability of making errors in the recovered support. The averaged values of NMSE and PE over 1,000 simulations for each experiment are reported in the experiment results.

B. MCMC implementation

We used the MCMC implementation presented in [65]. The Matlab and R codes are available at https://github.com/aripakman/hmc-tmg. MCMC parameters explained in Section III-B1 were selected as follows. The off-diagonal pruning of the empirical scale parameter Σ̂ was performed with a threshold of T_p = 5 × 10⁻². Diagonal scaling was performed with a factor of β = 1.7, and a shrinkage parameter of λ = 0.5. These values were empirically determined to minimize the NMSE for the first set of experiments.

V. Experiment Results

Here, we show that in all of the sparse recovery experiments detailed above, the proposed R-SBL variants perform better than the baseline solvers in terms of NMSE and PE. The R-SBL variants outperform the baseline solvers when the dictionary is non i.i.d., coherent, low-rank, ill-posed or even non-negative, illustrating the robustness of R-SBL to different characteristics of the dictionary Φ.

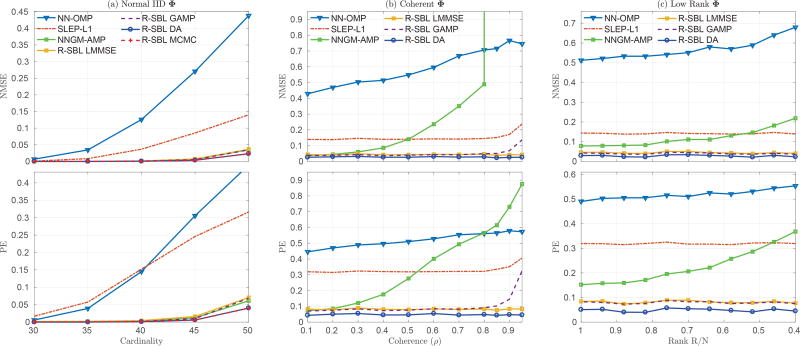
In Fig. 2 (a), we show the sparse recovery performance of the R-SBL variants and the baseline solvers as a function of the cardinality for the first set of experiments. As the cardinality of the ground truth solution increases (e.g. after K = 30) the performances of NN-OMP and SLEP-ℓ₁ deteriorate both in terms of MSE and PE. On the other hand, R-SBL variants and NNGM-AMP are quite robust with very small recovery error. At the largest cardinality of K = 50, we see that R-SBL DA and MCMC outperform other methods. The DA variant is nearly identical to MCMC in terms of MSE and PE. This is expected since MCMC prunes off-diagonal elements of the scale matrix Σ iteratively, when they drop below a certain threshold.

Fig. 2.

Sparse recovery performances (NMSE and PE) of the R-SBL variants and the baseline S-NNLS solvers for various Φ. In (a), the dictionary elements were drawn from i.i.d Normal Φ and sparse recovery results are shown for cardinalities K = 30 to K = 50. R-SBL DA achieves the best recovery performance. R-SBL LMMSE and GAMP are similar to NNGM-AMP and are much better than SLEP-ℓ₁ and NN-OMP. In (b), the dictionary columns are coherent with the coherence degree ρ indicated in the x-axis. R-SBL variants are extremely robust to increasing coherence and result in very small NMSE and PE across all ρ values. NNGM-AMP breaks down after ρ = 0.2 and its performance deteriorates with increasing ρ. SLEP-ℓ₁ is better than NNGM-AMP after ρ = 0.5. In (c), the dictionary is rank-deficient with rank-ratio R/N indicated in the x-axis. R-SBL variants are superior to baseline sparse recovery methods across all R/N values.

A. Coherent Dictionaries

In Figure 2 (b), we show the recovery performance of the proposed R-SBL variants and the baseline solvers when the dictionary is coherent. The degree of dictionary coherence is shown on the horizontal axis with ρ, which ranges from 0.1 to 0.95. The proposed R-SBL variants are extremely robust to increasing coherence and outperform the baseline solvers in terms of both NMSE and PE. SLEP-ℓ₁ is robust to increasing coherence, but performs worse as compared to R-SBL variants. NNGM-AMP breaks down after ρ = 0.3 and performs worse than SLEP-ℓ₁ after ρ = 0.5 and than NN-OMP after ρ = 0.8. The LMMSE and DA variants are not affected by the coherence level and achieve better recovery even for ρ = 0.95. The performance of R-SBL GAMP slightly deteriorates after an extreme coherence of ρ = 0.90, but is still better than the baseline solvers.

These results demonstrate that the proposed R-SBL variants are robust to dictionary coherence and are superior to the baseline solvers. The robustness our R-SBL framework seems to be inherited from the robustness of the original SBL algorithm to the structure of Φ [51], [90], which uses a GSM prior on x. Our R-GSM prior on x seems to provide a similar robustness to the R-SBL algorithm.

B. Low-rank Dictionaries

In Figure 2 (c), we show the recovery performance of the proposed R-SBL variants and the baseline solvers for rank-deficient dictionaries. The degree of rank deficiency is shown on the horizontal axis with the rank ratio R/N. The R-SBL variants outperform the baseline solvers both in terms of NMSE and PE for all values of R/N. The recovery performances of the R-SBL variants are extremely robust against the changes in R/N. Among the R-SBL variants, DA performs slightly better than LMMSE and GAMP. The GAMP performs similar to LMMSE. The recovery performance of NNGM-AMP is better than NN-OMP and SLEP-ℓ₁, however its performance degrades as R/N gets smaller.

C. Ill-conditioned Dictionaries

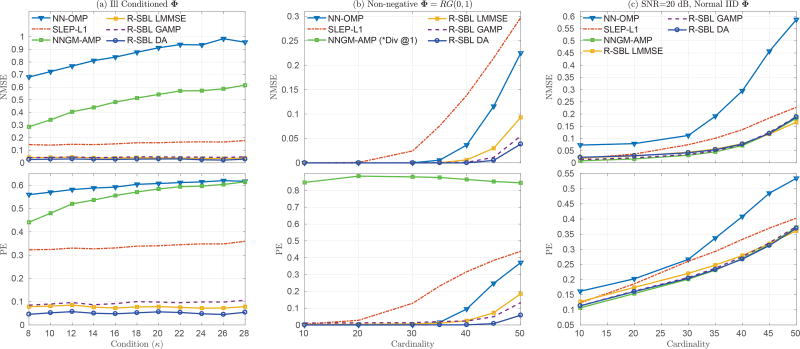
In Figure 3 (a), we demonstrate the recovery performance for ill-conditioned dictionaries. The condition number on the horizontal axis varies from κ = 8 to κ = 28. The proposed R-SBL variants perform significantly better than the baseline solvers across different κ values in terms of NMSE and PE. The recovery performance of the R-SBL variants is also extremely robust to different selections of κ. The SLEP-ℓ₁ is better than NN-OMP and NNGM-AMP in terms of recovery performance, and is also robust to the selection of κ. The NN-OMP and NNGM-AMP approaches rapidly deteriorate in recovery performance with increasing κ values.

Fig. 3.

Sparse recovery performances of the S-NNLS solvers for various Φ. In (a), the dictionary is ill-conditioned with condition number κ given in the x-axis. R-SBL variants outperform the baseline solvers for various κ and are very robust to the value of κ. R-SBL DA achieves the lowest NMSE and PE. SLEP-ℓ₁ is superior to NNGM-AMP. In (b), the dictionary is non-negative with elements drawn from i.i.d. RG(0, 1). The recovery performances are given for various cardinality K in the x-axis. R-SBL variants achieve superior recovery across all values of K. NNGM-AMP diverges regardless of the value of K and is unable to recover a feasible solution. In (c), the dictionary is i.i.d. Normal and SNR is 20 dB. In the noisy setting, when the dictionary is i.i.d. and signed, R-SBL variants perform similar to NNGM-AMP under noisy conditions, but are superior to SLEP-ℓ₁ and NN-OMP at larger cardinalities.

D. Non-negative Dictionaries

In certain sparse recovery applications, such as sparse NMF and non-negative K-SVD, a positive mapping is desired on the solution vector and the dictionary may contain non-negative elements. In Figure 3 (b), we demonstrate the recovery performance of the S-NNLS solvers when the dictionary is non-negative with elements drawn from i.i.d. RG(0, 1). The cardinality K on the horizontal axis of Figure 3 (b) varies from K = 10 to K = 50. The NNGM-AMP approach was not able to recover a solution for non-negative dictionaries and point estimates for x diverged for different K. Therefore, the NMSE values for NNGM-AMP were not shown in Figure 3 (b). Unlike in Figure 2 (a), where the dictionary can be both positive and negative, NN-OMP performs better than the SLEP-ℓ₁ solver. The proposed R-SBL variants outperform the baseline approaches. Among the R-SBL variants, DA performs slightly better than the GAMP, and GAMP is slightly better than LMMSE.

E. Noisy Conditions

We compared the recovery performance of the proposed R-SBL variants and the baseline solvers in a noisy setting, where the dictionary is i.i.d. Normal distributed. In this case, the observations were contaminated with additive white Gaussian noise to have a signal to noise ratio (SNR) of 20 dB. Figure 3 (c) shows the NMSE and PE versus the cardinality. Compared with the noiseless case in Figure 2 (a), the performances of all of the methods noticeably reduced. However, the proposed R-SBL variants performed better as compared to the NN-OMP and SLEP-ℓ₁ solvers, and performed similar to the NNGM-AMP approach.

F. Other types of x^gen and Φ

In this fourth set of experiments, the dictionary Φ was drawn according to i.i.d. Normal, ±1 Bernoulli, and {0, 1} Bernoulli distributions. We experimented with different distributions for the non-zero elements of x^gen, as shown in Tables II, III and IV.

TABLE II.

NMSE and PE results for various distributions for x^gen. The dictionary is i.i.d Normal distributed.

		Φ is i.i.d Normal
	xgen	NN-OMP	SLEP-ℓ1	NNGM AMP	R-SBL (LMMSE)	R-SBL (GAMP)	R-SBL (DA)
NMSE	RG	0.4460	0.1439	0.0389	0.0488	0.0428	0.0313
	NN-Cauchy	0.0097	0.0086	0.0020	0.0004	0.0003	0.0002
	NN-Laplace	0.1566	0.0693	0.0091	0.0066	0.0059	0.0034
	Gamma	0.1476	0.0661	0.0074	0.0065	0.0045	0.0024
	Chi-square	0.1583	0.0673	0.0091	0.0077	0.0066	0.0035
	Bernoulli	0.5845	0.1265	0.0052	0.0524	0.0416	0.0339
PE	RG	0.4601	0.3208	0.0711	0.0873	0.0823	0.0549
	NN-Cauchy	0.2307	0.3509	0.2142	0.0187	0.0200	0.0408
	NN-Laplace	0.3202	0.3137	0.0407	0.0292	0.0229	0.0118
	Gamma	0.3091	0.3093	0.0416	0.0260	0.0207	0.0080
	Chi-square	0.3200	0.3086	0.0473	0.0307	0.0280	0.0133
	Bernoulli	0.4852	0.3283	0.0101	0.1714	0.1514	0.1264

TABLE III.

NMSE and PE results for various distributions for x^gen. The dictionary is i.i.d ±1 Bernoulli distributed.

		Φ is ±1 Bernoulli
	xgen	NN-OMP	SLEP-ℓ1	NNGM AMP	R-SBL (LMMSE)	R-SBL (GAMP)	R-SBL (DA)
NMSE	RG	0.3996	0.1387	0.0409	0.0504	0.0415	0.0332
	NN-Cauchy	0.0083	0.0077	0.0023	0.0005	0.0004	0.0003
	NN-Laplace	0.1368	0.0712	0.0101	0.0096	0.0090	0.0050
	Gamma	0.1294	0.0665	0.0079	0.0061	0.0051	0.0023
	Chi-square	0.1267	0.0667	0.0109	0.0083	0.0094	0.0055
	Bernoulli	0.5610	0.1180	0.0113	0.0466	0.0412	0.0363
PE	RG	0.4272	0.3182	0.0794	0.0950	0.0824	0.0568
	NN-Cauchy	0.1810	0.3475	0.2307	0.0187	0.0175	0.0321
	NN-Laplace	0.2909	0.3131	0.0508	0.0369	0.0333	0.0163
	Gamma	0.2682	0.3072	0.0472	0.0274	0.0248	0.0093
	Chi-square	0.2769	0.3104	0.0532	0.0357	0.0369	0.0195
	Bernoulli	0.4734	0.3290	0.0154	0.1727	0.1571	0.1345

TABLE IV.

NMSE and PE results for various distributions for x^gen. The dictionary is i.i.d {0, 1} Bernoulli distributed.

		Φ is {0, 1} Bernoulli
	xgen	NN-OMP	SEEP-E	NNGM AMP	R-SBL (LMMSE)	R-SBL (GAMP)	R-SBL (DA)
NMSE	RG	0.2063	0.2497	Diverged	0.0873	0.0520	0.0386
	NN-Cauchy	0.0085	0.0188	Diverged	0.0031	0.0286	0.0002
	NN-Laplace	0.0960	0.1406	Diverged	0.0296	0.0070	0.0043
	Gamma	0.0901	0.1335	Diverged	0.0283	0.0047	0.0022
	Chi-square	0.0894	0.1360	Diverged	0.0327	0.0077	0.0054
	Bernoulli	0.2203	0.2586	Diverged	0.0747	0.0682	0.0558
PE	RG	0.3558	0.4070	0.8404	0.1782	0.0950	0.0581
	NN-Cauchy	0.2651	0.4434	0.8314	0.1131	0.4480	0.0354
	NN-Laplace	0.3140	0.4071	0.8398	0.1193	0.0371	0.0134
	Gamma	0.3102	0.4016	0.8354	0.1240	0.0275	0.0087
	Chi-square	0.3126	0.4072	0.8377	0.1341	0.0363	0.0171
	Bernoulli	0.3803	0.4120	0.8399	0.2689	0.1705	0.1455

For i.i.d. Normal Φ in Table II, the R-SBL DA generally outperforms the baseline solvers and other R-SBL variants when x^gen is RG, NN-Cauchy, NN-Laplace, Gamma and Chi-square distributed. The LMMSE variant achieves slightly better performance in terms of PE for the NN-Cauchy distribution. The NNGM-AMP is better than LMMSE and GAMP variants, when x^gen is RG, however it fails in terms of PE when x^gen is NN-Cauchy. The NNGM-AMP approach shows better performance when x^gen is Bernoulli. This is expected since the prior density for NNGM-AMP is a Bernoulli non-negative Gaussian mixture. The R-GSM prior, on the other hand, is not well matched to the Bernoulli distribution, as it is a mixture of continuous distributions. Overall, we see that R-SBL DA approach results in the best recovery performance. In Table III, we present the results for when Φ is ±1 Bernoulli. The recovery performances observed in Table III are very similar to Table II and overall, R-SBL DA approach enjoys better recovery performance.

In Table IV, we show recovery results for {0, 1} Bernoulli distributed Φ. The R-SBL DA and LMMSE variants achieve superior recovery when compared to the baseline solvers. The NNGM-AMP approach diverges for different x^gen, because the dictionary was non-negative, which is consistent with our previous observation when the dictionary elements were drawn from i.i.d. RG(0, 1) in Figure 3 (b).

G. Recovery time analysis

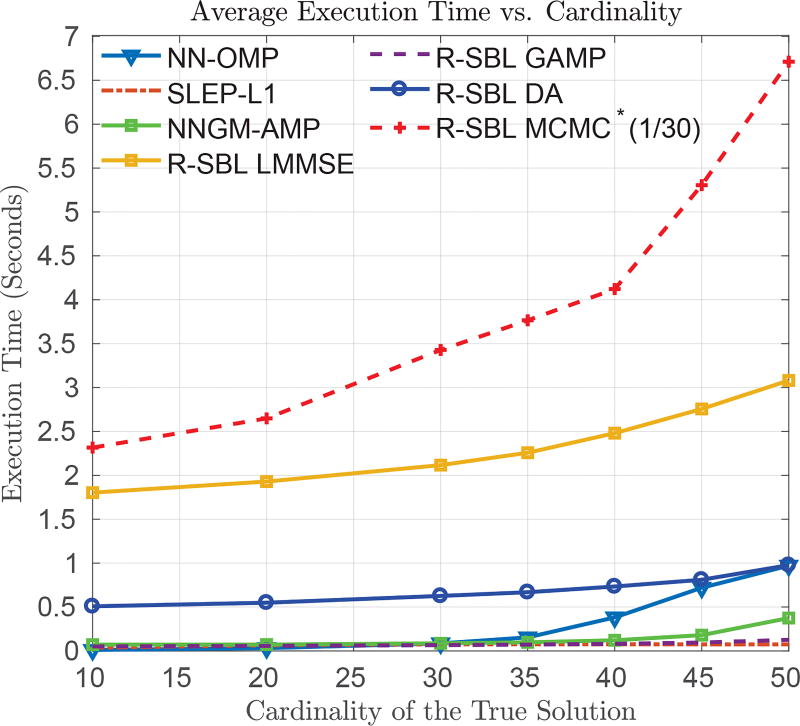
In Section III-C, we presented the worst case computational complexity of the DA, LMMSE and GAMP variants per EM iteration. As the execution time also depends on how fast an EM approach converges to the final solution, we provide an analysis of average execution times for different cardinality values. First, we provide a simple way to speed up the proposed R-SBL algorithms. We prune the problem size, when the elements of γ become smaller than a given threshold. For example, when an index of the vector γ becomes smaller than i.e. γ_i ≤ ε_γ, we ignore the computations regarding that index in the next iterations. This effectively reduces the problem dimensions and improves execution time.

In Fig. 4, we included the average execution times of the proposed algorithms, in units of seconds. The pruning threshold was selected as ε_γ = 10⁻⁵ for all methods. For the EM based methods, we monitored the convergence of the γ’s in EM iterations. We stopped the EM updates, when ‖γ^t − γ^t−1‖₂ ≤ 10⁻³, where t is the current EM iteration index. For other approaches, we monitored the linear equality constraints and stopped the algorithms when ‖y − Φx̂^t‖₂ ≤ 10⁻³, where x̂^t is the solution estimate at iteration t.

Fig. 4.

Execution times of the S-NNLS solvers as a function of cardinality for the noiseless scenario.

As expected due to computationally intensive random sampling, R-SBL MCMC is the slowest method. For display purposes, we scaled down the average MCMC execution time values by 30. The LMMSE approach takes about 3 seconds for K = 50 to recover the optimal solution and is the second slowest method. Even though the complexity of DA and LMMSE is similar, DA achieves much faster convergence and takes about 0.5 to 1 seconds as K increases.

For this particular experiment, GAMP is the fastest R-SBL variant regardless of the cardinality and is similar to SLEP-ℓ₁. However, since complexity of GAMP is 𝒪(NM), for very large problem sizes (e.g. large N and M) GAMP may become slower despite the superior recovery performance. In this case, a convex solver may be preferable depending on the desired recovery performance. R-SBL GAMP is faster than NNGM-AMP at larger cardinalities. Finally, NN-OMP is similar to SLEP-ℓ₁ but it’s execution time increases for larger cardinalities. Considering the fast recovery speed and good recovery performance of R-SBL GAMP under various Φ types, GAMP is a very good candidate for time sensitive sparse recovery applications.

H. Application on real data: Face Recognition

Here, we present a face recognition (FR) application, based on the non-negative sparse representations considered in [91], [92], [93]. Our goal is to show that the R-SBL approach works in real-world applications involving real-data. A sparse representation classifier (SRC) for FR was initially proposed in [94] using the ℓ₁ penalty without the non-negativity constraints. The SRC approach was found to be robust against occlusion, disguise, pixel corruptions, and achieved superior results as compared to well-known FR algorithms [94], [92], [95], [96].

In the SRC framework, the dictionary Φ represents the training samples, and each column of Φ contains training features from a single face image. A single person might have more than one training image, and hence multiple columns of Φ might correspond to the same person. For a given test face y in vectorized form, a vector x is obtained by solving Eq. (1), using ℓ₁ sparsity, with the assumption that only a few non-zero entries will exist in the solution x. Ideally, the index of maximal non-negative entry in x is used to select the corresponding column in Φ. This should correspond to one of the training samples for the correct person. In [92], the SRC performance was further improved, by adding the non-negativity constraint on x in addition to the ℓ₁ sparsity. The authors have showed their algorithm to be more robust against noise, and to be computationally more effective as compared to the original SRC approach.

In our experiment, we consider the R-SBL framework for the FR problem and compare it with the baseline solvers. Note that, SLEP-ℓ₁ was considered as the non-negative ℓ₁ minimization counterpart of R-SBL in place of [92]. We used the public AR dataset [97], and selected the first 30 males and 30 females for the FR problem. Each person in the dataset has 26 face images with different facial expression, illumination and disguise (e.g. sunglasses and scarves). The first 13 images of each person (M = 13 × 60 = 780) were selected as the training set, and the remaining 780 face images were used for testing. For feature selection, we used the down-sampling method used in [91], [92], [94], where the pixel dimensions of each face image were down-sampled to have a total of N pixels. In separate experiments, each 165×120 pixel image was down-sampled by a factor of {1/28, 1/26, …, 1/6}, yielding feature dimensions of minimum of N = 30 to a maximum of N = 650.

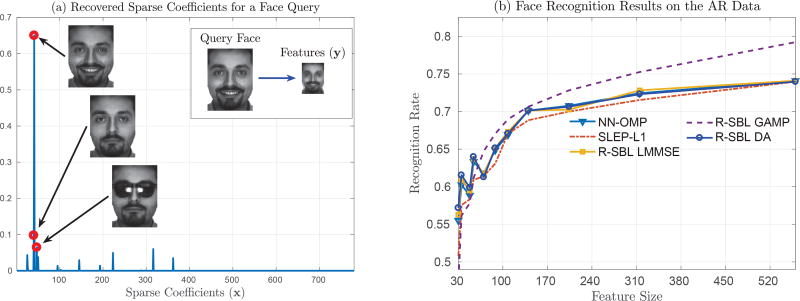
The overall process is shown in Figure 5 (a), where a query face is shown in the top right-hand side. This image was down-sampled and the original feature dimension was reduced from 19, 800 to 512. After sparse recovery with R-SBL, the original faces belonging to several largest non-zero elements of x are shown. As desired, the maximal positive index of x belongs to the same person in the query face.

Fig. 5.

(a) Illustration of the sparse FR process. A query face is down-sample to obtain an observation y. Using the training dictionary Φ, a sparse solution is obtained using R-SBL variants and baseline solvers to satisfy y = Φx. The index that corresponds to the maximum value in x is used to select a corresponding column from Φ. This corresponds to the correct individual. (b) FR accuracy for different feature sizes using all test samples. R-SBL GAMP enjoys better FR performance for different feature sizes.

In Figure 5 (b), we performed FR using all 780 samples in the test set and measured the recognition rate for different feature sizes. The recognition rate was computed by counting the number of test samples for which R-SBL recovered the correct individual from x. This count was normalized by 780. Overall, the R-SBL variants with the exception of R-SBL GAMP performed similar to the baseline solvers for large feature sizes. This is expected since the recovery problem was highly sparse, and the cardinality was very small K = 13 as compared to the length of x e.g. largest length of x is 780. R-SBL GAMP was superior to all algorithms for large feature sizes and performed significantly better in identifying the correct individual. NNGM-AMP diverged for this application and did not yield reportable results.

VI. Conclusion

In this work, we introduced a hierarchical Bayesian method to solve the S-NNLS problem. We proposed the rectified Gaussian scale mixture model as a general and versatile prior to promote sparsity in the solution of interest. Since the marginals of the posterior were not tractable, we constructed our R-SBL algorithm using the EM framework using four different approaches. We demonstrated that our R-SBL approaches outperformed the available S-NNLS solvers, in most cases by a large margin. The proposed R-SBL framework is very robust to the structure of Φ and performed well regardless of Φ being i.i.d. and non-i.i.d. The performance gains achieved by R-SBL variants are consistent across different non-negative data distributions for x, different structures for the design matrix Φ, in coherent, low-rank, ill-posed and non-negative settings. The DA variant was found to be a fairly easy to implement S-NNLS solver with simple closed-form moment expressions.

Biographies

Alican Nalci (S’15) received the B.Sc. degree in Electrical and Electronics Engineering from Bilkent University, Ankara, Turkey, in 2013. He received the M.Sc. degree in Electrical and Computer Engineering from the University of California San Diego, La Jolla, CA, USA, in 2015, where he is currently pursuing a Ph.D. degree. His research interests include sparse signal recovery, machine learning, signal processing and functional magnetic resonance imaging (fMRI).

Igor Fedorov (S’15) receieved the B.Sc. and M.Sc. degrees in Electrical Engineering from the University of Illinois at Urbana-Champaign in 2012 and 2014, respectively. He is currently pursuing a Ph.D. degree in Electrical Engineering at the University of California San Diego, La Jolla, CA, USA. His research interests include sparse signal recovery, machine learning, and signal processing.

Maher Al-Shoukairi (S’17) received his B.Sc. degree in Electrical Engineering from the University of Jordan in 2005. He received his M.Sc. degree in Electrical Engineering from Texas A&M University in 2008, after which he joined Qualcomm Inc. on the same year to date. He is currently pursuing his Ph.D. degree in Electrical Engineering at the University of California, San Diego.

Thomas T. Liu received the B.S degree in Electrical Engineering from the Massachusetts Institute of Technology, Cambridge, MA, USA, and the M.S. and Ph.D. degrees from Stanford University, Stanford CA, USA, in 1988, 1993, and 1999, respectively. Since 1999 he has been with the University of California San Diego, La Jolla, CA, USA, where he is currently a Professor in the Departments of Radiology, Psychiatry, and Bioengineering and Director of the UCSD Center for Functional MRI.

Bhaskar D. Rao (S’80-M’83-SM’91-F’00) received the B.Tech. degree in electronics and electrical communication engineering from the Indian Institute of Technology of Kharagpur, Kharagpur, India, in 1979, and the M.S. and Ph.D. degrees from the University of Southern California, Los Angeles, CA, USA, in 1981 and 1983, respectively. Since 1983, he has been at the University of California at San Diego, San Diego, CA, USA, where he is currently a Distinguished Professor in the Department of Electrical and Computer Engineering.

Appendix

A. Full derivation of GAMP

We use the R-GSM prior p(x|γ) and evaluate Eq. (39) and Eq. (40) to find the first two moments of the approximate marginal posterior under the sum-product GAMP mode

$${\hat{x}}_i=𝔼\{x_i|r_i;{\tau }_{r_i}\}={\int }_{x_i}{x}_{i}p(x_i|r_i;{\tau }_{r_i})$$ (51)

$$={\int }_{+}{x}_i{𝒩}^R(x_i|0,{\gamma }_i)𝒩(x_i,r_i,{\tau }_{r_i}),$$ (52)

then using Gaussian multiplication rule², we obtain

$${\hat{x}}_i={\int }_{+}{x}_i\Upsilon {𝒩}^R(x_i|{\eta }_i,{\nu }_i),$$ (53)

where η_i and ν_i are given in Eq. (55) and Eq. (56).

We find the mean of the resulting rectified Gaussian

$${\hat{x}}_i={\eta }_i+\sqrt{{\nu }_i}h(\frac{{\eta }_i}{{\nu }_i})$$ (54)

$${\eta }_i=\frac{r_i{\gamma }_i}{{\tau }_{r_i}+{\gamma }_i}$$ (55)

$${\nu }_i=\frac{{\tau }_{r_i}{\gamma }_i}{{\tau }_{r_i}+{\gamma }_i}$$ (56)

$$h(a)=\frac{\phi (a)}{{\mathrm{\Phi }}_c(a)},$$ (57)

where φ refers to the pdf and Φ_c refers to the complementary cdf of a zero-mean and unit-variance Gaussian distribution. The conditional variance of x_i given r_i is simply

$${\tau }_{x_i}=\mathit{\text{var}}\{x_i|r_i;{\tau }_{r_i}\}={\int }_{x_i}{x}_i^{2}p(x_i|r_i;{\tau }_{r_i})-{\hat{x}}_i^2$$ (58)

$$={\int }_{+}{x}_i^2{𝒩}^R(x_i|0,{\gamma }_i)𝒩(x_i,r_i,{\tau }_{r_i})-{\hat{x}}_i^2,$$ (59)

using Gaussian pdf multiplication rule

$${\tau }_{x_i}={\int }_{+}{x}_i^2\Upsilon {𝒩}^R(x_i|{\eta }_i,{\nu }_i),$$ (60)

we find the variance of the resulting rectified Gaussian

$${\tau }_{x_i}={\nu }_{i}g(\frac{{\eta }_i}{{\nu }_i})$$ (61)

$$g(a)=1-h(a)(h(a)-a).$$ (62)

In the case of max-sum GAMP implementation, we evaluate Eq. (41) and Eq. (42)

$${\hat{x}}_i=\underset{{\hat{x}}_i\ge 0}{\text{arg min}}\frac{x_i^2}{2{\gamma }_i}+\frac{1}{2{\tau }_{r_i}}{|{\hat{x}}_i-r_i|}^2$$ (63)

$${\hat{x}}_i=\{\begin{array}{cc}\frac{r_i{\gamma }_i}{{\tau }_{r_i}+{\gamma }_i}={\eta }_i\hfill & \text{if }{\hat{x}}_i\ge 0\hfill \\ 0\hfill & \text{if }{\hat{x}}_i<0\hfill \end{array}$$ (64)

Using Eq. (42)

$${\tau }_{x_i}=\{\begin{array}{cc}\frac{{\tau }_{r_i}{\gamma }_i}{{\tau }_{r_i}+{\gamma }_i}={\nu }_i\hfill & \text{if }{\hat{x}}_i\ge 0\hfill \\ 0\hfill & \text{if }{\hat{x}}_i<0^3\hfill \end{array}$$ (65)

Upon convergence of the max-sum, the approximate marginals are obtained using Eq. (54) and Eq. (61).

B. Approximate marginals and moments using DA

We derive the approximate moments used in the R-SBL DA approximation. We start with the posterior p(x | y, γ) and use chain rule to write

$$p(\mathit{x}|\mathit{y},\mathit{\gamma })=\frac{p(\mathit{y}|\mathit{x},\mathit{\gamma })p(\mathit{x}|\mathit{\gamma })}{{\int }_{\mathit{x}}p(\mathit{y}|\mathit{x},\mathit{\gamma })p(\mathit{x}|\mathit{\gamma })d\mathit{x}}.$$ (66)

Here p(y | x, γ) is a Gaussian density due to the Gaussian noise assumption. Since p(x | γ) is a rectified Gaussian density the numerator of Eq. (66) is a Gaussian multiplied by a rectified Gaussian, which results in a rectified Gaussian density. Then, we can simply write

$$p(\mathit{x}|\mathit{y},\mathit{\gamma })=c(\mathit{y})e^{-\frac{{(\mathit{x}-\mathit{\mu })}^T{\mathbf{\sum }}^{-1}(\mathit{x}-\mathit{\mu })}{2}}u(\mathit{x}),$$ (67)

where c(y) is the normalizing constant for the posterior density and μ and Σ are given by Eqs. (23) and (24), respectively. Let Σ = LL^T and r = x − μ, so that d x = dr and Σ⁻¹ = L^−T L⁻¹. Therefore, we have

$$1=c(\mathit{y}){\int }_{-\mathit{\mu }}^{\infty }{e}^{\frac{-{\mathit{r}}^T{\mathit{L}}^{-T}{\mathit{L}}^{-1}\mathit{r}}{2}}d\mathit{r}.$$ (68)

Now, let z = L⁻¹r, which implies that dr = |L|dz and

$$c(\mathit{y})=\frac{1}{|\mathit{L}|{\int }_{-\mathit{\beta }}^{\infty }{e}^{-{\mathit{z}}^T\mathit{z}/2}d\mathit{z}},$$ (69)

where β = L⁻¹μ is the lower limit of the new integral in vector form. The lower limit β depends on a linear combination of elements of μ since L is not diagonal. Thus, the integral in the denominator of Eq. (69) is not tractable as the integration limits are not separable and the multidimensional integral over z in Eq. (69) is not separable as a product of one dimensional integrals.

Assume that, we are interested in an approximate density p̃(x | y, γ), instead of the exact posterior. We calculate an approximate c̃(y) by approximating Σ with its diagonal i.e. Σ_d = diag(Σ) ≈ Σ. In this case, the new L is diagonal with entries $\sqrt{{\sum }_{\mathit{\text{ii}}}}$. Thus, the integral in Eq. (69) is separable and the approximate normalizing constant c̃(y) has closed form

$$\stackrel{\sim }{c}(\mathit{y})=\frac{1}{{|{\mathbf{\sum }}_d|}^{1/2}{\prod }_{i=1}^M\sqrt{\frac{\pi }{2}}\text{ erfc }(-\frac{{\mu }_i}{\sqrt{2{\sum }_{\mathit{\text{ii}}}}})}.$$ (70)

Approximating the actual normalizing constant with c̃(y), we write the approximate posterior as

$$\stackrel{\sim }{p}(\mathit{x}|\mathit{y},\mathit{\gamma })=\frac{e^{-\frac{{(\mathit{x}-\mathit{\mu })}^T{\mathbf{\sum }}_d^{-1}(\mathit{x}-\mathit{\mu })}{2}}u(\mathit{x})}{{\prod }_{i=1}^M\sqrt{\frac{\pi {\sum }_{\mathit{\text{ii}}}}{2}}\text{ erfc }(-\frac{{\mu }_i}{\sqrt{2{\sum }_{\mathit{\text{ii}}}}})}$$ (71)

$$=\prod _{i=1}^M\sqrt{\frac{2}{\pi {\sum }_{\mathit{\text{ii}}}}}\frac{e^{-\frac{{(x_i-{\mu }_i)}^2}{2{\sum }_{\mathit{\text{ii}}}}}u(x_i)}{\text{erfc }(-\frac{{\mu }_i}{\sqrt{2{\sum }_{\mathit{\text{ii}}}}})}$$ (72)

$$=\prod _{i=1}^M\stackrel{\sim }{p}(x_i|\mathit{y},\mathit{\gamma })$$ (73)

Eq. (73) shows that multivariate p̃(x | y, γ) is separable into product of univariate densities. The univariate density p̃(x_i|y, γ) is the univariate RG density defined in Eq. (10) e.g. p̃(x_i|y, γ) = 𝒩^R(x_i; μ_i, Σ_ii). The first and second moments of a univariate RG density are well-known in closed form (i.e. Eqs. (47) and (48)) and are used in the R-SBL DA algorithm.