Circuit Models of Low-Dimensional Shared Variability in Cortical Networks

SUMMARY

Trial-to-trial variability is a reflection of the circuitry and cellular physiology that make up a neuronal network. A pervasive yet puzzling feature of cortical circuits is that despite their complex wiring, population-wide shared spiking variability is low dimensional. Previous model cortical networks cannot explain this global variability, and rather assume it is from external sources. We show that if the spatial and temporal scales of inhibitory coupling match known physiology, networks of model spiking neurons internally generate low-dimensional shared variability that captures population activity recorded in vivo. Shifting spatial attention into the receptive field of visual neurons has been shown to differentially modulate shared variability within and between brain areas. A top-down modulation of inhibitory neurons in our network provides a parsimonious mechanism for this attentional modulation. Our work provides a critical link between observed cortical circuit structure and realistic shared neuronal variability and its modulation.

In Brief

Population-wide fluctuations of neural population activity are widely observed in cortical recordings. Huang et al. show that wave dynamics in spatially ordered recurrent networks give rise to low-dimensional shared variability, which can be suppressed by depolarizing inhibitory neurons.

INTRODUCTION

The trial-to-trial variability of neuronal responses gives a critical window into how the circuit structure connecting neurons determines brain activity (Kass et al., 2018; Shadlen and Newsome, 1998; Doiron et al., 2016). This idea, combined with the widespread use of population recordings, has prompted deep interest in how variability is distributed over a population (Cohen and Kohn, 2011; Kohn et al., 2016). There has been a proliferation of datasets in which the shared variability over a population is low dimensional (Lin et al., 2015; Rabinowitz et al., 2015; Ecker et al., 2014; Williamson et al., 2016; Schölvinck et al., 2015), meaning that neuronal activity waxes and wanes as a group. In accord, one-dimensional measures such as local field potentials (Kelly et al., 2010; Middleton et al., 2012) and summed population firing rates (Okun et al., 2015; Schölvinck et al., 2015) can predict a majority of pairwise correlations. Further, the synthesis of diverse population datasets paints a picture in which low-dimensional shared variability is a signature of cognitive state, such as overall arousal, task engagement, and attention (Doiron et al., 2016; Schmitz and Duncan, 2018), as well as predictive of behavioral performance (Ni et al., 2018). Such low-dimensional dynamics portend a theory for the genesis and modulation of shared population variability in recurrent cortical networks.

Theories of cortical variability can be broadly separated into two categories: ones in which variability is internally generated through recurrent network interactions and ones in which variability originates external to the network. Networks of spiking neuron models where strong excitation is balanced by opposing recurrent inhibition produce high single-neuron variability through internal mechanisms (Shadlen and Newsome, 1998; van Vreeswijk and Sompolinsky, 1996; Amit and Brunei, 1997). However, these networks famously enforce an asynchronous state and as such fail to explain population-wide shared variability (Renart et al., 2010). This lack of success is contrasted with the ease of producing arbitrary correlation structure from external sources. Indeed, many past cortical models assume a global fluctuation from an external source and accurately capture the structure of population data (Doiron et al., 2016; Ponce-Alvarez et al., 2013; Wimmer et al., 2015; Kanashiro et al., 2017; Hennequin et al., 2018). However, these phenomenological models begin with an assumption of low-dimensional variability from an unobserved source to explain the variability in a recorded population. In this way, these models are some-what circular, begging the question of what the mechanisms underlying the assumed external variability are. Thus, while neuronal variability has a rich history of study, there remains an impoverished mechanistic understanding of the low-dimensional structure of population-wide variability (Latham, 2016).

Determining whether output variability is internally generated through network interactions or externally imposed upon a network is a difficult problem, in which single-area population recordings may preclude any definitive solution. In this study we consider attention-mediated shifts in population variability obtained from simultaneous recordings of neuron pairs both within and between visual areas. In particular, attention reduces within area correlations (area V4; Cohen and Maunsell, 2009) while simultaneously increasing between area correlations (areas V1 and MT; Ruff and Cohen, 2016a). We show that such differential correlation modulation is a difficult constraint to satisfy with a model in which fluctuations are strictly external to the network. Nevertheless, as discussed above, contemporary recurrent network models are at a loss to explain population-wide variability. A central goal of this study is to put forth a new circuit-based theory of low-dimensional variability in recurrent networks and explore how plausible modulation schemes can differentially control within and between area correlations.

The asynchronous solution of classical balanced networks necessitates that inhibition dynamically tracks and cancels any correlations stemming from recurrent excitation (Renart et al., 2010). This requirement has forced theorists to assume that the time course of inhibitory synapses is faster than that of excitatory synapses (Renart et al., 2010; Rosenbaum and Doiron, 2014; Rosenbaum et al., 2017; Monteforte and Wolf, 2012; van Vreeswijk and Sompolinsky, 1996). However, this is at odds with recorded synaptic physiology, in which excitatory conductances rise and decay faster than inhibitory ones (Geiger et al., 1997; Salin and Prince, 1996; Xiang et al., 1998; Angulo et al., 1999). Recently, we have extended the theory of balanced networks to include a spatial component to network architecture (Rosenbaum et al., 2017; Pyle and Rosenbaum, 2017; Rosenbaum and Doiron, 2014) and found network solutions in which firing rate balance and asynchronous dynamics are decoupled from one another (Rosenbaum et al., 2017). In this study, we consider multi-area models of spatially distributed balanced networks and show that when inhibition has slower kinetics than excitation in these networks, matching physiology, they internally produce low-dimensional population-wide variability. Unlike networks that lack spatial structure, these networks produce spiking activity that robustly captures the rich diversity of firing rate and correlation structure of real population recordings. Further, attention-mediated top-down modulation of inhibitory neurons in our model provides a parsimonious mechanism that controls population-wide variability in agreement with the within and between area experimental results.

There is a long-standing research program aimed at providing a circuit-based understanding for cortical variability (Shadlen and Newsome, 1998; van Vreeswijk and Sompolinsky, 1996; Amit and Brunel, 1997; Rosenbaum et al., 2017; Kass et al., 2018). Our work is a critical advance through providing a mechanistic theory for the genesis, propagation, and modulation of realistic low-dimensional population-wide shared variability based on established circuit structure and synaptic physiology.

RESULTS

Attentional Modulation of Shared Variability within and between Cortical Areas

Multi-electrode recordings from visual area V4 during an orientation change detection task show that the mean spike count correlation coefficient between neuron pairs in V4 is largely reduced when the monkeys were cued to pay attention to the neurons’ spatial receptive field (Figure 1A; Cohen and Maunsell, 2009). Recently, simultaneous recordings from two visual areas, MT and V1, during a similar attention task (Ruff and Cohen, 2016a), show that in addition to a reduction of mean spike count correlations between neuron pairs within an area (mean pairwise attention-related MT correlation decrease was 0.019, Wilcoxon rank-sum test, p = 0.017; mean pairwise attention-related V1 correlation decrease was 0.008, Wilcoxon rank-sum test, p = 4.9 × 10⁻⁶; Ruff and Cohen, 2016a), there is an attention-mediated increase of spike count correlations across areas V1 and MT (Figure 1B). This differential modulation of within and between area correlations offers a strong constraint from which to build circuit models of population-wide variability.

Figure 1. Attentional Modulation of Population Variability within and between Cortical Areas.

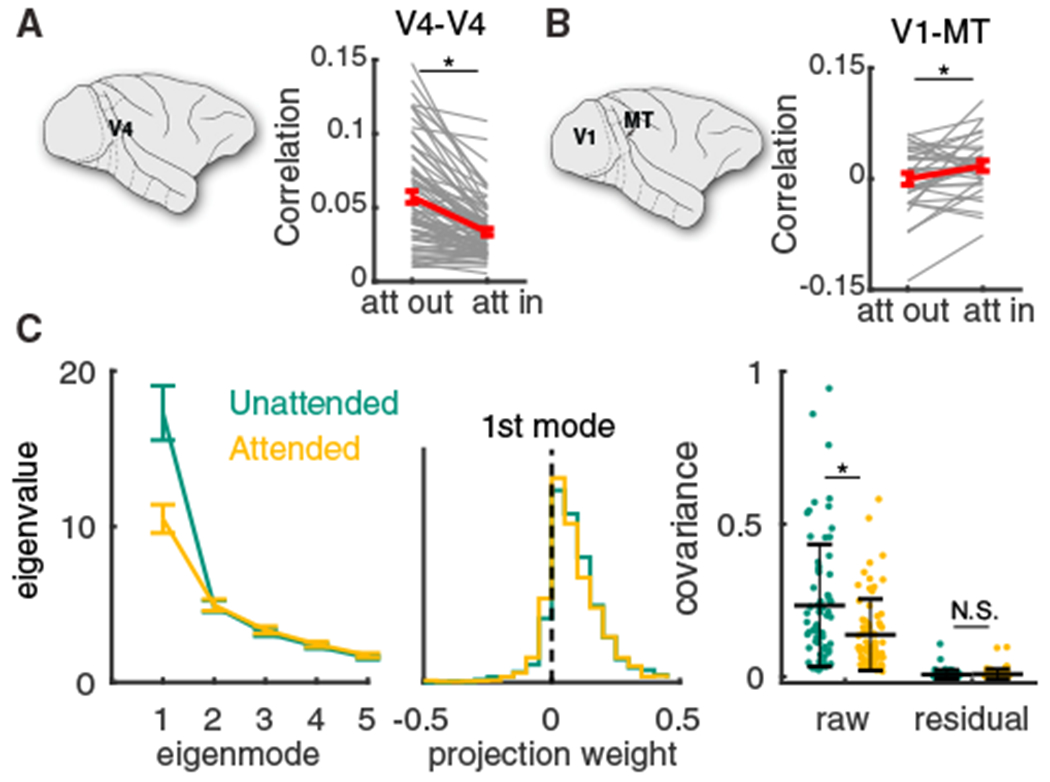
(A) Mean spike count correlation r_SC per session obtained from multi-electrode array recording from V4 was smaller when attention was directed into the receptive fields of recorded neurons (n = 74 sessions, two-sided Wilcoxon rank-sum test between attentional states, p = 3.3 × 10⁻⁶; reproduced from Cohen and Maunsell, 2009). Gray lines are individual session comparisons and the red line is the mean comparison across all sessions (error bars represent the SEM).

(B) Same as (A) for the mean spike count correlation r_SC between V1 units and MT units per session (n = 32 sessions, paired-sample t test, p = 0.0222; data reproduced from Ruff and Cohen, 2016a).

(C) Left: the first five largest eigenvalues of the shared component of the spike count covariance matrix from the V4 data (Cohen and Maunsell, 2009). Green, unattended; orange, attended; data from n = 72 sessions with 43 ± 15 neurons. Error bars are SEM. Middle: the vector elements for the first (dominant) eigenmode. Right: the mean covariance from each session in attended and unattended states before (raw) and after (residual) subtracting the first eigenmode (mean ± SD in black). Two-sided Wilcoxon rank-sum test (attended versus unattended), mean covariance, p = 1.3 × 10⁻³; residual, p = 0.75.

Before we explore population variability in circuit models of cortex, we first quantify how variability is structured across a recorded population. Using dimensionality reduction tools, we partition the V4 covariance matrix into the shared variability among the population and the private noise to each neuron (Cunningham and Yu, 2014; Williamson et al., 2016). The eigenvalues of the shared covariance matrix represent the variance along each dimension (or latent variable), while the corresponding eigenvectors represent the projection weights of the latent variables onto each neuron (STAR Methods). The V4 data show a single dominant eigenmode (Figure 1C, left; for single-session results, see Figure S1), indicating a primarily one-dimensional latent structure in the population variability. The projection weight of the dominant eigenmode onto the individual neurons is primarily of the same sign (Figure 1C, middle, weights are dominant positive), meaning that the latent variable causes positive correlations across the population. Indeed, after subtracting the first eigenmode the mean residual covariances are very small (Figure 1C, right). Moreover, attention affects population-wide variability primarily by quenching this dominant eigenmode (Figure 1C, left, orange versus green) and the attentional modulation in the dominant eigenmode is highly correlated with the modulation in mean covariance (Figure S1C). The low-dimensional structure of shared variability in our data is consistent with similar analysis in other cortices (Williamson et al., 2016; Lin et al., 2015; Ecker et al., 2014), as well as alternative analysis of the same V4 data using generalized point process models (Rabinowitz et al., 2015).

Constraints for Circuit-Based Models of Shared Variability

Armed with the V4 and V1-MT population analysis, we next explore the constraints that circuit models must satisfy to capture attentional modulation that differentially modulates the shared variability within and between cortical areas. Since the population-wide fluctuations are well described by a single latent variable that influences all neurons (Figure 1C), we represent the aggregate population responses with scalar random variables: MT and V1 (Figure 2A).

Figure 2. Model Constraints for Shared Variability within and between Areas.

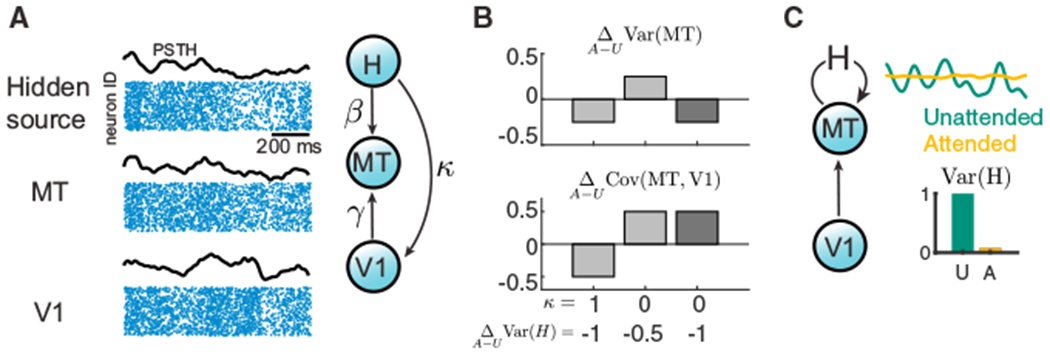
(A) Left: hidden variable model for connected cortical areas, V1 and MT, where the response variability of MT comes from both its upstream area V1 and a hidden source H. Due to the low-dimensional structure of shared variability in population activity (Figure 1C), we use the mean population rate (black curves) to represent the population spiking activity from each area (blue dot rasters). Right: the hidden source H projects to MT and V1 with strengths β and κ, respectively. The feedforward projection strength from V1 to MT is γ.

(B) Examples of attentional changes in the variance of MT, $\underset{A-U}{\Delta }\mathrm{Var}\left(\mathrm{MT}\right)$, and the covariance between MT and V1, $\underset{A-U}{\Delta }\mathrm{Cov}\left(\mathrm{MT},\text{V}1\right)$. We consider combinations of shared H (κ = 1) versus private H (κ = 0) and a moderate reduction in hidden variability $\left(\underset{A-U}{\Delta }\mathrm{Var}\left(H\right)=-0.5\right)$ versus a large reduction $\left(\underset{A-U}{\Delta }\mathrm{Var}\left(H\right)=-1\right)$. Attention-mediated simultaneous decreases in Var(MT) and increase in Cov(MT, V1) occur for private variability with a large reduction in hidden variability (dark gray). The other combinations cause a shift in the same direction for within and between area variability (light gray). Other model parameters are γ^U = 0.5, γ^A = 1, Var^U(H) = 1, β = 1, and Var(V1) = 1, independent of attentional state. U, unattended; A, attended. For general analysis, see Methods S1.

(C) The differential modulation of shared variability within and between areas (Figures 1A and 1B) suggests the hidden variable H is internally generated within area MT and that attention should quench the variance of H substantially.

To begin, we assume that population responses are linear in their inputs and that V1 projects to MT with strength γ. We suppose a hidden source of variability, H, which projects to MT and V1 with strength β and κ, respectively (Figure 2A); without loss of generality, we take β = 1. In total, we have MT = γV1 + H and V1 = X₀ + κH where X₀ is independent from H. We assume that attention acts to reduce the variability of the hidden variable, Var(H), and to increase the coupling strength γ.

We first consider how attention affects the covariance between MT and V1 in our model; our linear system gives the following:

$$\text{Cov}\left(\text{MT},\text{V}1\right)=\gamma \text{Var}\left(\text{V}1\right)+\kappa \text{Var}\left(\text{H}\right).$$ (Equation 1)

For κ > 0, an attention-mediated reduction of Var(H) acts to reduce the covariance between V1 and MT. This is at odds with our cortical recordings (Figure 1B). We explore the case in which κ = 0 to circumnavigate the tension between an increase in γ and a decrease in Var(H). This assumes that MT has a source of variability that is private from V1.

With κ = 0, the variance of the MT population obeys

$$\text{Var}\left(\text{MT}\right)={\gamma }^2\text{Var}\left(\text{V}1\right)+\text{Var}\left(\text{H}\right).$$ (Equation 2)

The contributions to MT variability from the upstream area V1 and the hidden source H are clear. Further, attention drives opposing influences on Var(MT) through an increase in γ being countered by a decrease in Var(H). However, unlike the case of Cov(MT,V1), we cannot simply choose γ to be zero to mitigate this competition (because V1 would then not drive MT). Indeed, if the decrease in Var(H) is only moderate, then attention will increase both Cov(MT, V1) and Var(MT) (Figure 2B, middle), again at odds with experiments (Figures 1A and 1B). In total, with an assumption of H being private to MT (κ = 0), then to have a reduction in Var(MT) combined with an increase in Cov(MT, V1 ), we require that the attention-mediated suppression in the variability of H be large (Figure 2B, right). These arguments can be generalized over a range of parameters (Methods S1; Figure S2).

In sum, we have exposed three constraints that, if satisfied, will cause cortical circuit models of population-wide variability to capture the differential modulation of within and between area variability.

1. The shared variability across a neuronal population is low dimensional.

2. There is a source of attention-mediated population-wide variability in downstream areas that is private from upstream areas.

3. The attention-mediated suppression of the private variability needs to be substantial.

The second constraint could be produced by each cortical population being paired with an external variability source that projects exclusively to that area. This solution requires strong assumptions about how the cortex devotes and organizes biological resources to drive neuronal variability. In contrast, we explore the more parsimonious hypothesis whereby recurrently coupled networks produce low-dimensional variability through internal interactions, and hence variability is private to the population by construction (Figure 2C). Further, if the variability is internally generated, then the third constraint requires a strong nonlinearity to fully suppress variability in the attended state. In the next sections, we investigate how a physiologically realistic network of spiking neuron models can satisfy these three constraints.

Population-wide Correlations with Slow Inhibition in Spatially Ordered Networks

Networks of spiking neuron models where strong excitation is balanced by opposing recurrent inhibition internally produce high single-neuron variability (Figure 3Ai) with a broad distribution of firing rates (Figure 3B, top purple curve; van Vreeswijk and Sompolinsky, 1996; Amit and Brunel, 1997; Renart et al., 2010). However, these networks enforce an asynchronous solution (Figure 3C, top purple), and as such fail to explain population-wide shared variability (Renart et al., 2010; Williamson et al., 2016). Typically, balanced networks have disordered connectivity, where connection probability is uniform between all neuron pairs. This approximation ignores the abundant evidence that cortical connectivity is spatially ordered with a connection probability falling off with the physical distance between neuron pairs (Levy and Reyes, 2012; Horvát et al., 2016; Mariño et al., 2005). Recently we and others have extended the theory of balanced networks to include such spatially dependent connectivity (Rosenbaum et al., 2017; Rosenbaum and Doiron, 2014; Darshan et al., 2018; Pyle and Rosenbaum, 2017). Briefly, we model a two-dimensional lattice of integrate-and-fire neurons, meaning neuron locations tile a space with x and y coordinates. Each neuron receives both feedforward projections from a layer of external Poisson processes and recurrent projections from within the network (STAR Methods); the connection probability of all projections decays like a Gaussian with distance. If the spatial scale of feedforward inputs is narrower than the scale of recurrent projections, the asynchronous state no longer exists (Rosenbaum et al., 2017), giving way to a solution with spatially structured correlations (Figures 3Aii and 3D, purple; Video S1). Nevertheless, the mean correlation across all neuron pairs vanishes for large network size (Figure 3C, bottom purple curve), in stark disagreement with a majority of experimental studies (Cohen and Kohn, 2011; Doiron et al., 2016) as well as with our motivating population data (Figures 1A and 1B).

Figure 3. The Spatial and Temporal Scales of Synaptic Coupling Determine Internally Generated Variability.

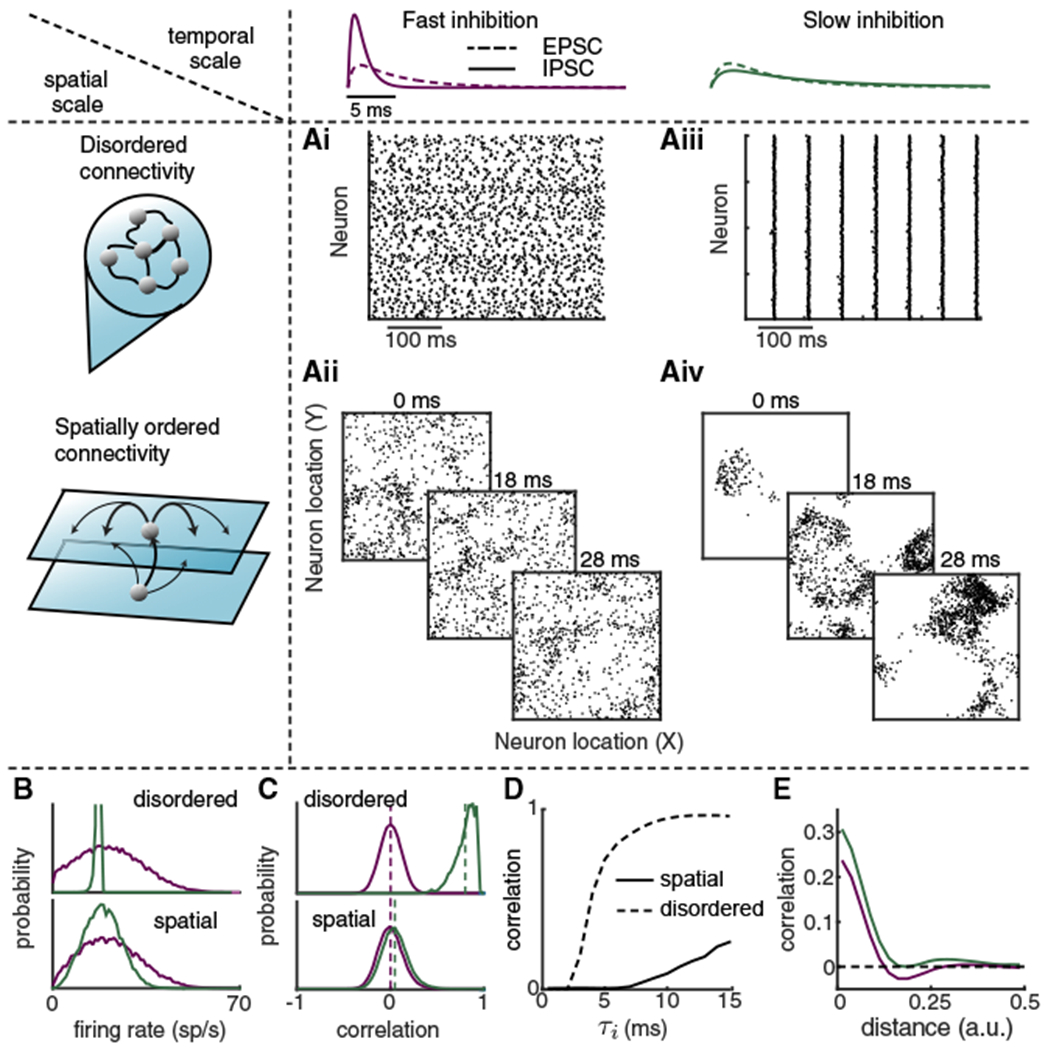
(A) Networks of excitatory and inhibitory neuron models were simulated with either disordered connectivity (Ai and Aiii) or spatially ordered connectivity (Aii and Aiv), and with either fast inhibition (τ_i = 1 ms; Ai and Aii) or slow inhibition (τ_i = 8 ms; Aiii and Aiv). The integral of inhibitory postsynaptic current overtime is conserved as we change τ_i. In all models the timescale of excitation was τ_e = 5 ms. In the disordered networks, spike train rasters assume no particular neuron ordering. In the spatially ordered networks, three consecutive spike raster snapshots are shown with a dot indicating that the neuron at spatial position (x, y) fired within 1 ms of the time stamp.

(B) Distributions of firing rates of excitatory neurons in the disordered (top) and spatially ordered (bottom) models, with faster inhibitory kinetics (purple) compared to slower inhibitory kinetics (green).

(C) Same as (B) for the distributions of pairwise correlations among the excitatory population.

(D) Mean correlation among the excitatory population as a function of the inhibitory decay time constant (τ_i).

(E) Pairwise correlation as a function of distance between neuron pairs for spatially ordered models with slower inhibitory kinetics (green) compared to faster inhibitory kinetics (purple).

Many previous balanced network models assume that the kinetics of inhibitory synaptic currents are faster than those of excitatory currents (Renart et al., 2010; van Vreeswijk and Sompolinsky, 1996; Lim and Goldman, 2014; Amit and Brunel, 1997), including our past work (Rosenbaum et al., 2017; Rosenbaum and Doiron, 2014; Pyle and Rosenbaum, 2017). However, this assumption is at odds with physiology in which excitatory α-amino-3-hydroxy-5-methyl-4-isoxazolepropionic acid (AMPA) receptors have faster kinetics than those of the inhibitory γ-aminobutyric acid (GABAa) receptors (Geiger et al., 1997; Xiang et al., 1998; Salin and Prince, 1996; Angulo et al., 1999). When the timescales of excitatory and inhibitory synaptic currents match experimental values in networks with disordered connectivity, the activity becomes pathologic, with homogeneous firing rates (Figure 3B, top green) and excessive synchrony (Figures 3Aiii and 3C, top green), as has been previously remarked (Börgers and Kopell, 2005). This consequence is likely the ad hoc justification for the faster inhibitory kinetics in disordered balanced model networks.

When the spatially ordered model has synaptic kinetics that match physiology, a population-wide turbulent dynamic emerges (Figure 3Aiv; Video S2). This dynamic produces a small, but non-zero, mean pairwise spike count correlation across the population (r_SC = 0.04), comparable to experiment (Figure 1A, right). Further, both firing rates and pairwise correlations are broadly distributed (Figures 3B and 3C, bottom green curves). Low (but significant) correlation is a robust feature of spatially ordered networks. This is clear from the gradual rise in mean correlation with inhibitory timescale for the two-dimensional spatially ordered network (Figure 3D, solid curve), in contrast to the rapid rise of correlation to pathologic values in the disordered network (Figure 3D, dashed curve). Further, this weak sensitivity of correlations on inhibitory timescale is restricted to networks with two spatial scales (i.e., x and y), since networks constrained to one spatial dimension (i.e., neurons are arranged on a ring) also show excessive synchrony when the inhibitory timescale is large (Figure S3).

Our previous work that studied a spatially ordered model with fast inhibition identified a signature spatial organization for correlation, namely positive for nearby neuron pairs and negative for farther away neuron pairs, so that the overall correlation was small (Rosenbaum et al., 2017). In contrast, the spatial model with slow inhibition has positive net correlation across all pair distances (Figure 3E, green)–this is critical for the mean r_SC to be positive. In sum, when realistic spatial synaptic connectivity is paired with realistic temporal synaptic kinetics in balanced networks, internally generated population dynamics produce spiking dynamics whose marginal and pairwise variability conform to experimental results. The spatially ordered model with slow inhibition is thus well positioned to satisfy the three constraints required to match how attention modulates within and between area correlations.

Attentional Modulation of Low-Dimensional Population-wide Variability

We model the V1 and MT network by extending our spatially ordered balanced networks with slow inhibition to include three layers: a bottom layer of independent Poisson processes modeling thalamus, and middle and top layers of integrate-and-fire neurons modeling V1 and MT, respectively (Figure 4A; STAR Methods). We follow our past work with simplified firing rate networks (Kanashiro et al., 2017) and model a top-down attentional signal as an overall static depolarization to inhibitory neurons in the MT layer (Figure 4A). This mimics cholinergic pathways that primarily affect interneurons (Kuchibhotla et al., 2017; Kim et al., 2016) and are thought to be engaged during attention (Schmitz and Duncan, 2018). The increased recruitment of inhibition during attention reduces the population-wide fluctuations in the MT layer (Figure 4B) and decreases pairwise spike count correlations of MT-MT neuron pairs (Figure 4C), while simultaneously increasing the correlation of V1-MT neuron pairs (Figure 4D). Further, neuron pairs with larger firing rate increases also show larger correlation reductions (Figure S4), in agreement with population recordings during both spatial and feature attention (Cohen and Maunsell, 2011). Finally, there is a slight attention-mediated decrease of both the average firing rates of MT neurons (~3%) and MT neuron spike count Fano factor (~20%) (Figure S5). In total, our model and its simple implementation of attentional modulation capture the main aspects of the pairwise co-variability in the V1-MT dataset (Figure 1B). However, it remains to show that our model does this by satisfying the three constraints identified with our heuristic model (Figure 2).

Figure 4. Top-Down Depolarization of MT Inhibitory Neurons Captures the Differential Attentional Modulation of Shared Variability within and across V1 and MT.

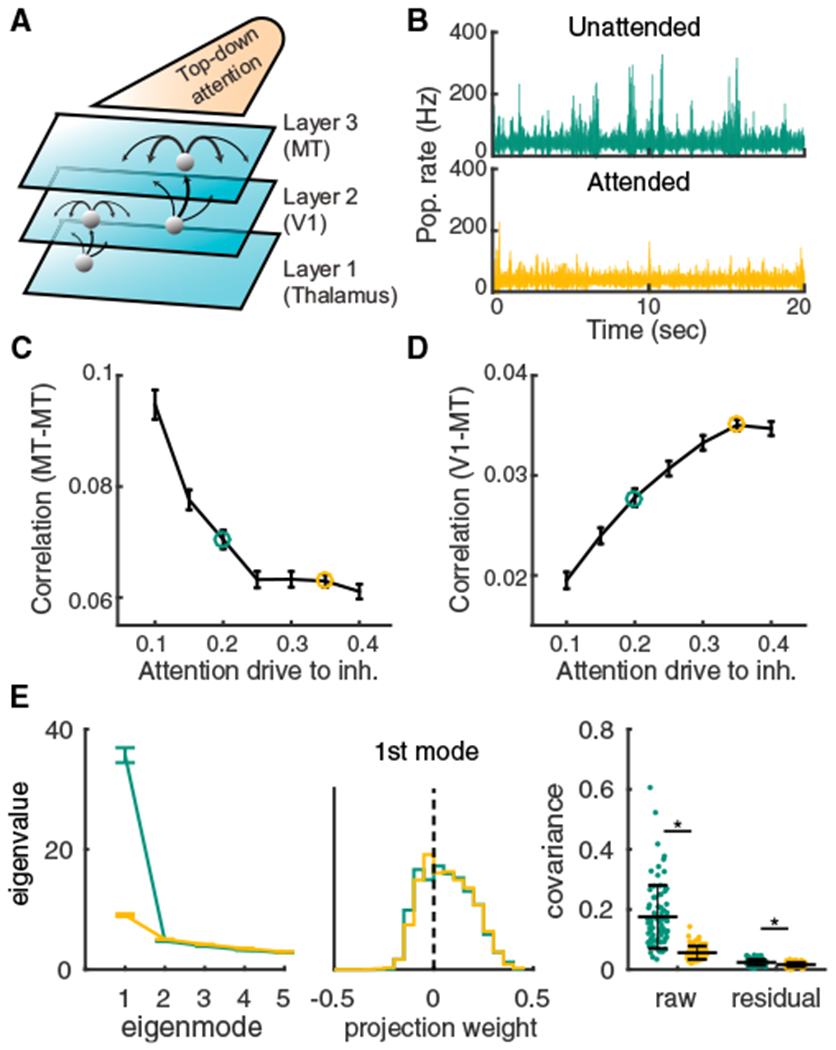
(A) Thalamus, V1, and MT are modeled in a three-layer hierarchy of spatially ordered balanced networks. Top-down attentional modulation is modeled as a depolarization of static current, μ_l, to MT inhibitory neurons. In both V1 and MT the recurrent projections are broader than feedforward projections (V1, ${\alpha }_{\text{ffwd}}^{\left(2\right)}=0.05,{\alpha }_{\mathrm{rec}}^{\left(2\right)}=0.1;\text{MT},{\alpha }_{\text{ffwd}}^{\left(3\right)}=0.1,{\alpha }_{\text{rec}}^{\left(3\right)}=0.2)$ and recurrent inhibition is slower than excitation (τ_i = 8 ms, τ_e = 5 ms).

(B) Population averaged firing rate fluctuations from MT in the unattended state μ_l = 0.2, green) and the attended state μ_l = 0.35, orange).

(C) Mean spike count correlation (r_SC) of excitatory neuron pairs in MT decreases with attentional modulation.

(D) Mean r_SC between the excitatory neurons in MT and the excitatory neurons in V1 increases with attention. Error bars are SEM.

(E) Left: the first five largest eigenvalues of the shared component of the spike count covariance matrix. Green, unattended; orange, attended; n = 80 sessions with 50 neurons each. Error bars are SEM. Middle: the vector elements for the first (dominant) eigenmode. Right: the mean covariance from each session in attended and unattended states before (raw) and after (residual) subtracting the first eigenmode (mean ± SD in black). Two-sided Wilcoxon rank-sum test (attended versus unattended), mean covariance, p = 1.3 × 10⁻²¹; residual, p = 3.5 × 10⁻⁸.

The first model constraint is that the population-wide variability must be low dimensional. We analyzed the spike count covariance matrix constructed from a subsampling of the spike trains in the third layer of our network model (n = 50 neurons). The network with slow inhibition produces shared variability with a clear dominant eigenmode that mimicked many of the core features observed in the V4 data (Figure 4E compared with Figure 1C). The projection weights of the dominant mode are mostly positive (Figure 4E, middle) and the distribution of mean covariance across sessions is skewed to the positive side (Figure 4E, right). Removing the first eigenmode also results in small residual covariance (Figure 4E, right). Further, the top-down attentional modulation of inhibition also suppresses this dominant eigenmode (Figure 4E, right, orange versus green).

The agreement between model and data breaks down when inhibitory temporal kinetics and the spatial wiring structure are changed. When the model has fast inhibition, the shared variability does not have a dominant eigenmode (Figure S6A), the raw mean correlation coefficient is near zero (Figure S6C), and attentional modulation has a negligible effect on population variability (Figures S6A–S6C, orange versus green). Experimental measurements of local cortical circuitry show that excitation and inhibition project on similar spatial scales (Levy and Reyes, 2012; Mariño et al., 2005). Inhibitory projections that are broader than excitatory produce strong positive and negative correlations within the network, owing to a competitive dynamic across the network. The resultant population-wide correlations are not low dimensional (Figure S6F), while still being high in magnitude, as has been noted in past work from spiking networks with lateral inhibition (Keane and Gong, 2015; Pyle and Rosenbaum, 2017; Williamson et al., 2016). Nonetheless, as in the case with fast inhibition, the mean correlation coefficient is near zero (Figure S6H), and attentional modulation has only a negligible effect (Figures S6F–S6H, orange versus green).

In sum, satisfying our first constraint of shared variability having low-dimensional structure over the population requires inhibition that is neither faster nor anatomically broader than excitation–both features of real cortical circuits (Levy and Reyes, 2012; Mariño et al., 2005; Salin and Prince, 1996; Geiger et al., 1997; Xiang et al., 1998; Angulo et al., 1999). Further, a simple recruitment of inhibition through top-down drive can restore stability and quench low-dimensional population variability.

Relating Low-Dimensional Variability to Spatiotemporal Pattern Formation

To provide intuition about how recurrent circuitry shapes low-dimensional shared variability, we considered a firing rate model that incorporates both the spatial architecture and synaptic dynamics that are central to our spiking model (STAR Methods). While firing rate models lack a principled connection to spiking network models, they do produce qualitatively similar dynamics in recurrent networks and their simplicity makes them amenable to analysis techniques from dynamical systems theory (Ermentrout, 1998).

Solutions in which firing rates are constant over time are interpreted as asynchrony within the network, since only dynamical co-fluctuations in firing rates would model correlated spiking. We focus on how the stability of the asynchronous firing rate solution depends upon the temporal (τ_i) and spatial (σ_i) scales of inhibition. A firing rate solution is stable if the linearized dynamics are such that every eigenmode has eigenvalues with strictly negative real part. Since our network is spatially ordered, the eigenmodes are also organized in space, each with their own distinct wave number (spatial frequency). If the solution loses stability at a particular eigenmode, then the spatiotemporal dynamics of the resulting network firing rates will inherit the spatial scale of that eigenmode–this process is termed spatiotemporal pattern formation (Cross and Hohenberg, 1993).

If τ_i and σ_i are near those of recurrent excitation, then a stable firing rate solution exists (Figure 5A, gray region; Figure 5B, top left, black curve with (τ_i = 5ms). Our past work explored activity within this regime (Rosenbaum et al., 2017). When τ_i increases and excitation and inhibition project with the same spatial scale (σ_i = σ_e), firing rate stability isfirst lost at an eigenmode with zero wave number (Figure 5B, left). This creates population dynamics with a broad spatial pattern, allowing variability to be shared over the entire network. Simulations of the three-layered spiking network model in this regime show turbulent dynamics that extend across the entire network (Figure 5B, right; Video S3). In contrast to this case, when σ_i increases yet inhibition projects lateral to excitation (σ_i > σ_e) stability is first lost at a non-zero wave number (Figure 5C, left). This creates population dynamics with coherence over a band of higher spatial frequencies, producing higher dimensional shared variability, as evident in the spatially patchy spiking dynamics of the three-layered spiking network in this regime (Figure 5C, right; Video S4). Thus, the spatial and temporal scales of inhibition determine in large part the spatiotemporal patterns of network activity.

Figure 5. Stability Analysis of a Two-Dimensional Firing Rate Model.

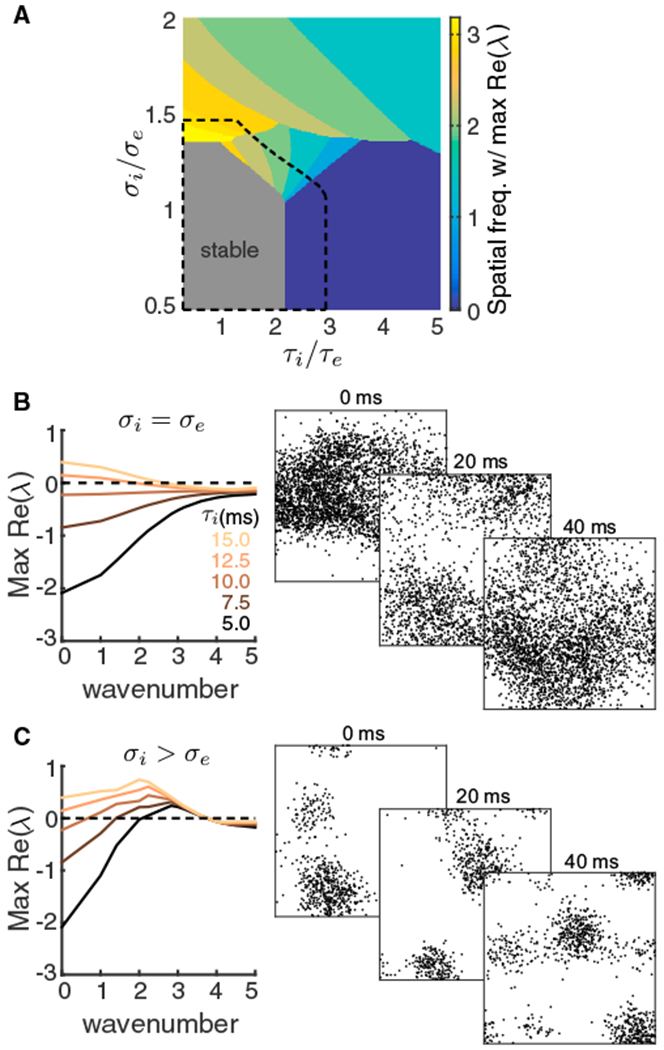
(A) Bifurcation diagram of a firing rate model as a function of the inhibitory decay timescale τ_i and inhibitory projection width σ_i. The excitatory projection width and time constant are fixed at σ_e = 0.1 and τ_e = 5 ms respectively. Color represents the wavenumber with the largest real part of eigenvalue and the gray region is stable. Top-down modulation of inhibitory neurons modeling attention expands the stable region (black dashed).

(B) Left: the real part of eigenvalues as a function of wavenumber for increasing τ_i, when σ_i = σ_e. Right: three consecutive spike raster snapshots of a spiking neuron network with σ_i = σ_e and slow inhibition (same network as in Figure 4 in the unattended state).

(C) Same as (B) for σ_i larger than σ_e. Right: spike raster snapshots of a spiking neuron network with broad inhibitory projections, where the excitatory and the inhibitory projection widths of layer 3 were ${\alpha }_{\text{e}}^{\left(3\right)}=0.1$ and ${\alpha }_{\text{i}}^{\left(3\right)}=0.2$, respectively. Other parameters were the same as in (B).

In the firing rate network, we can also model attention as a depolarization to the inhibitory neurons, as was done in the network of spiking neuron models. In the firing rate network, attentional modulation expanded the stable region in the bifurcation diagram (Figure 5A, dashed black line). In other words, attention increased the domain of firing rate stability. Thus, with τ_i > τ_e chosen so that in the unattended state the network was unstable at a low spatial frequency yet with attention the network was in the stable regime, our model captures the large attention-mediated quenching of population-wide shared variability reported in the population recordings (Figure 1C) and network of spiking neuron models (Figure 4E).

In general, dynamical systems can transition through an instability point by changing any one of many model parameters. This suggests that tonic drive to inhibitory neurons is not the only mechanism that can capture the neuronal correlates of attentional modulation. For example, by reducing the strength of recurrent excitation, providing direct hyperpolarization to excitatory neurons, among other cellular and circuit modulations, our model can mimic the shift in network stability achieved through top-down drive to inhibition (Figure S7). However, despite these differing biophysical models of attention, the mechanisms all share an attention-mediated shift toward inhibition stabilizing runaway excitation.

Finally, our model predicts that population-wide variability is due to a dynamical instability that propagates spiking activity broadly over space. The sparse sampling of spiking activity in our neuronal recordings (<100 neurons spanning a few square millimeters of cortical tissue) makes a direct test of this prediction difficult. The pairwise covariance from both our model simulations (Figure 6A) and V4 data (Figure 6B) decreases with the distance between neurons in both the attended and unattended states. The large covariance for nearby neurons in the model is for neuron pairs that are within one spatial footprint of the excitatory and inhibitory coupling (distances < 0.25 in Figure 6A); the 400 mm electrode spacing in the V4 data does not permit a sampling of small distances between neurons. For the larger distances the decrease in covariance is gradual, consistent with a previous V4 population dataset (Smith and Sommer, 2013). Further, there is a near spatially uniform reduction of covariance by attention in both the model and V4 data (Figures 6A and 6B, compare orange and green). While these agreements between model and data are promising, a simple decay of covariance with distance can be replicated with many different models, notably our model with fast (Figure S6D) or broad (Figure S6I) inhibition.

Figure 6. Distance Dependence of Pairwise and Population-wide Variability.

(A) Pairwise covariance of spike counts from our spiking model as a function of the distance between the neurons.

(B) Same as (A) but for the V4 data. Here the distance is between the electrodes that recorded the neuron pair.

(C) The distance dependence functions of the first five covariance components computed from factor analysis of the model spiking activity in the unattended state. For mode i the product of the eigenmode loading onto a pair of neurons is plotted as a function of the distance between the neurons. To properly compare the modes, we scaled each curve by the eigenvalue λ_i for that mode.

(D) Same as (C) but for the V4 data in the unattended state. Shaded regions are SEM. See Table S2 for the number of pairs at each distance value for the V4 data; for the model we used n = 80 sessions of 500 neurons each.

A more stringent test of our model is to compare how the spatial dependence of pairwise covariance decomposes over the low-dimensional latent variable space. The loss of stability at the zero spatial Fourier mode in our model produces global fluctuations over the network (Figure 5B). In the factor analysis of the shared covariance, this is reflected by the dominant eigenmode being uniform across neuronal space (Figure 6C, black curve). In other words, this dominant latent variable projects to all neurons irrespective of their location and drives global correlations across the network. By contrast, the higher eigenmodes contain covariance structure that is spatially localized (Figure 6C, colored curves). This feature is specific to our model, since there is no spatial invariance of the dominant mode in the spiking network when inhibition is either fast (Figure S6E) or spatially broad (Figure S6J). Analysis of the V4 data clearly identifies a spatial invariance of the dominant eigenmode (Figure 5D, black curve), validating our model prediction.

Chaotic Population-wide Dynamics Reflect Internally Generated Variability

The attention-mediated differential modulation of within and between area correlations (Figure 1) leads us to propose our second and third model constraints–that shared variability has a sizable internally generated component and that attention must quench this variability. The third constraint requires that the mechanisms that produce internally generated variability sensitively depend on top-down modulations. The firing rate model captured this sensitivity through a spatiotemporal pattern-forming transition in network activity. However, the firing rate model does not internally produce trial-to-trial variability that can be compared to experiment, and we thus return to analysis of the network of spiking neuron models to probe how trial-to-trial variability is internally generated through recurrent coupling.

To isolate the sources of externally and internally generated fluctuations in the third layer of our network, we fixed the spike train realizations from the first layer (thalamic) neurons as well as the membrane potential states of the second layer (V1) neurons, and only the initial membrane potentials of the third layer (MT) neurons were randomized across trials (Figure 7A). This produced deterministic network dynamics when conditioned on activity from the first two layers, and consequently any trial-to-trial variability is due to mechanics internal to the third layer.

Figure 7. Chaotic Population Firing Rate Dynamics Are Quenched by Attention.

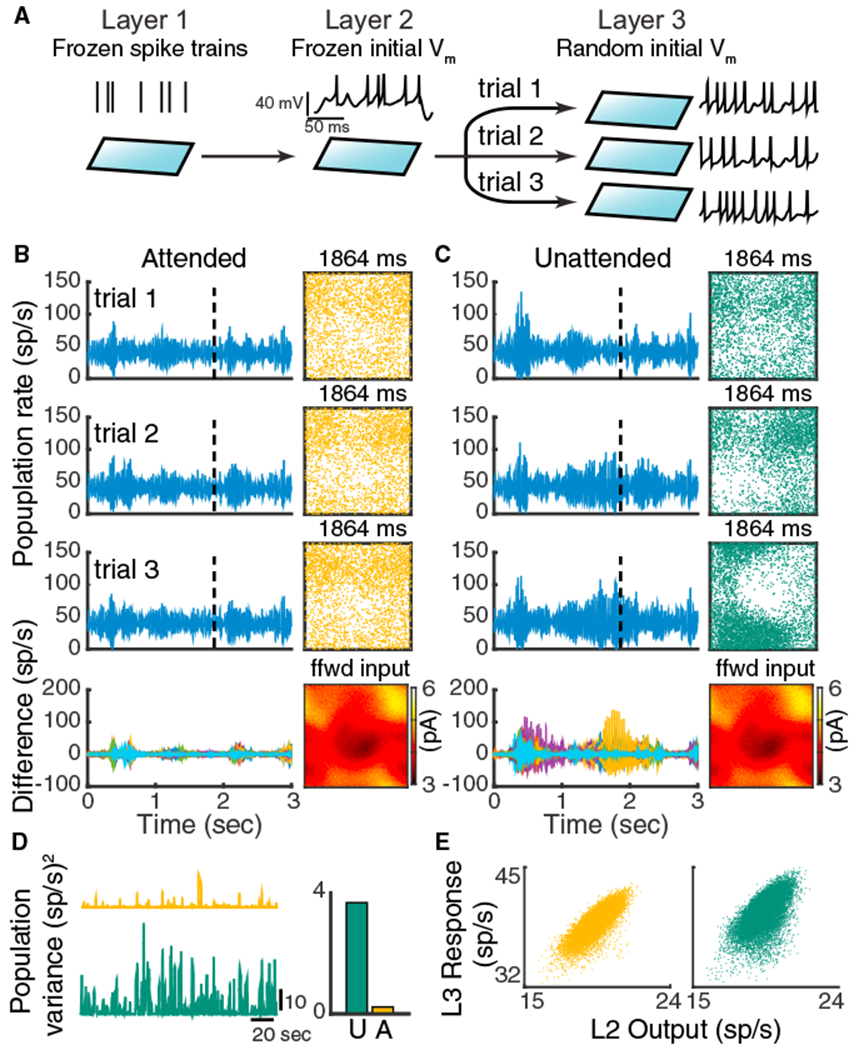
(A) Schematic of the numerical experiment. The spike train realizations in layer one and the initial states of the membrane potential of layer two neurons are identical across trials, while in each trial we randomized the initial states of the layer three neuron’s membrane potentials.

(B) Three representative trials of the layer three excitatory population rates in the attended state (left, rows 1–3). Bottom row: difference of the population rates across 20 trials. Right (rows 1–3): snapshots of the neuron activity at time point 1,864 ms. Each dot is a spike within 2 ms window from the neuron at that location. Right bottom: the synaptic current each layer three neuron receives from layer two at time 1,864 ms.

(C) Same as (B) for the network in the unattended state.

(D) Trial-to-trial variance of layer three population rates as a function of time. Right: mean variance across time.

(E) The layer three population rate tracks the layer two population rate better in the attended state. Both outputs and responses are smoothed with a 200 ms window.

The spike trains from third layer neurons in both the unattended and attended states have significant trial-to-trial variability despite the frozen layer one and two inputs. This is reflective of a well-studied chaotic network dynamic in balanced networks in which the spike times from individual neurons are very sensitive to perturbations that affect the spiking of other neurons (Monteforte and Wolf, 2012; London et al., 2010). To investigate how this microscopic (single neuron) variability possibly manifests as macroscopic population activity, we considered the trial-to-trial variability of the population-averaged instantaneous firing rate. While the population firing rate is dynamic in the attended state, there is very little variability from trial to trial (Figure 7B, left; Figure 7D, orange). A consequence of this low population-wide variability is the faithful tracking of the spatiotemporal structure of layer two outputs by layer three responses (Figure 7B, right; Figure 7E, orange). This tracking reflects the higher correlation between layer two and three spiking in the attended state (Figure 4D), and represents the attention-mediated increase in V1 to MT coupling (g) in our linear model (Figure 2).

In contrast, in the unattended state there is significant population-wide recruited activity. The periods of spiking coherence across the network are not trial locked and rather contribute to sizable trial-to-trial variability of population activity (Figure 7C, left; Figure 7D, green). This degrades the tracking of layer two outputs (Figure 7C, right; Figure 7E, green) and ultimately lowers the correlation between layer two and three spiking (Figure 4D). Taken together, while the network model is chaotic in both the attended and unattended states, the chaos is population-wide only in the inhibition-deprived unattended state. Furthermore, since the population-wide variability is internally generated in the MT layer, our framework satisfies our second model constraint of private variability.

The nonlinear pattern-forming dynamics of the spatially distributed recurrent network impart extreme sensitivity to the population-wide internally generated variability. Indeed, in our model the trial-to-trial population rate variability is almost extinguished with attention (Figure 7D, right). In our heuristic model with hidden variable H this amounts to Var(H) reducing drastically with attention, which is precisely what is needed to account for the differential modulation of within and between area correlations (compare Figure 2B with Figure 7D, right). Thus, our model satisfies the third constraint we derived from our hidden variable model, namely that the shared variability in MT should be substantially quenched by attention.

DISCUSSION

There is a long-standing research program aimed at understanding how variability is an emergent property of recurrent networks (van Vreeswijk and Sompolinsky, 1996; Amit and Brunel, 1997; Monteforte and Wolf, 2012; London et al., 2010; Rosenbaum et al., 2017; Rosenbaum and Doiron, 2014). However, models are often restricted to simple networks with disordered connectivity. Consequently, in these networks population-wide activity is asynchronous, at odds with many experimental findings (Cohen and Kohn, 2011; Doiron et al., 2016). A parallel stream of research focuses on spatiotemporal pattern formation in neuronal populations, with a rich history in both theoretical (Ermentrout, 1998) and experimental contexts (Sato et al., 2012). Yet a majority of these studies consider only trial-averaged activity, with tacit assumptions about how spiking variability emerges (but see Keane and Gong, 2015 and Rosenbaum et al., 2017). In this study we combined these modeling traditions with the goal of circuit-based understanding of the genesis and modulation of low-dimensional internally generated shared cortical variability.

Population-wide Variability in Balanced Networks

Our model extends classical work in balanced cortical networks (van Vreeswijk and Sompolinsky, 1996; Renart et al., 2010) to include two well-accepted experimental observations. First, cortical connectivity has a wiring rule that depends upon the distance between neuron pairs (Horvát et al., 2016; Levy and Reyes, 2012). Theoretical studies that model distance-dependent coupling commonly assume that inhibition projects more broadly than excitation (Ermentrout, 1998; Compte et al., 2003; Keane and Gong, 2015). However, measurements of local cortical circuitry show that excitation and inhibition project on similar spatial scales (Levy and Reyes, 2012; Mariño et al., 2005), and long-range excitation is known to project more broadly than inhibition (Bosking et al., 1997). Our work shows that local inhibitory projections are required for internally generated population variability to be low dimensional (Figure S6F).

The second observation is that inhibition has temporal kinetics that are slower than excitation (Salin and Prince, 1996; Geiger et al., 1997; Angulo et al., 1999; Xiang et al., 1998). Past theoretical models of recurrent cortical circuits have assumed that inhibition is not slower than excitation (Renart et al., 2010; van Vreeswijk and Sompolinsky, 1996; Stringer et al., 2016; Lim and Goldman, 2014), including past work from our group (Rosenbaum et al., 2017; Rosenbaum and Doiron, 2014; Pyle and Rosenbaum, 2017). Consequently, these studies could only capture the residual correlation structure of population recordings once the dominant eigenmode was subtracted (Rosenbaum et al., 2017; Williamson et al., 2016). When inhibition has kinetics that are slower than excitation, the asynchronous solution is unstable. In disordered networks with strong coupling, this causes pathologic levels of rhythmic synchrony (Figure 3Aiii), often requiring sources of external variability that are independent over neurons to tame network activity (Börgers and Kopell, 2005). In contrast, we have shown that networks with slow inhibition and neuronal coupling that depend upon two spatial dimensions produce spiking dynamics that are only weakly correlated, with firing rate and correlation values that match experiment (Figures 3Aiv and 4). In total, by including accepted features of cortical anatomy and physiology, long ignored by theorists, our model network recapitulates low-dimensional population-wide variability to a much larger extent than previous models.

The above narrative is somewhat revisionist; there are several well-known theoretical studies in disordered networks in which one-dimensional population-wide correlations do emerge, notably in networks where rhythmic (Amit and Brunel, 1997) or “up-down” (Compte et al., 2003; Stringer et al., 2016) dynamics are prominent. Networks with dense yet disordered connectivity ensure that all neuron pairs receive some shared inputs from overlapping presynaptic projections. In such a network, if the asynchronous state becomes unstable then this shared wiring will correlate spiking activity across the entire network. In other words, any shared variability will be one dimensional (scalar) by construction. In contrast, the ordered connectivity in our network is such that neuron pairs that are distant from one another have no directly shared presynaptic connections. Consequently, when asynchrony is unstable, one-dimensional population dynamics are not preordained; rather, the spatial network can support higher dimensional shared variability depending on the temporal and spatial scales of recurrent coupling (Figures S6 and 5). From the vantage of this model, we discovered the conditions for recurrent architecture and synaptic physiology for low-dimensional shared variability.

Recently, several studies have shown that networks of firing rate models with a low-rank perturbation of the recurrent connectivity structure can exhibit low-dimensional coherent chaotic dynamics (Mastrogiuseppe and Ostojic, 2018; Landau and Sompolinsky, 2018). Such a low-rank connectivity effectively embeds a feedforward loop in the network and thus drives the population activity in one direction. However, such a low-rank connectivity requires each neuron projects a component of its activity to the whole population, a circuit assumption that lacks biological evidence. In contrast, our network simply incorporates spatially ordered connectivity, which has been commonly observed in most cortical areas (Horvát et al., 2016). The recurrent wiring structure within our network is high-rank due to the distance-dependent connections; cell pairs that are distant from one another do not share presynaptic inputs. The low-dimensional variability in our model emerges from a network instability at zero spatial Fourier mode that produces activity that propagates broadly across the network through polysynaptic connections.

Internal versus External Population Variability

Our circuit model assumed that the component of population-wide variability that is subject to attentional modulation was internally generated within the network. While our model is a parsimonious explanation of the data, it does not definitively exclude mechanisms in which variability is inherited from outside sources. Fluctuations from external sources are an often assumed and straightforward mechanism for population-wide spiking variability (Doiron et al., 2016; Hennequin et al., 2018; Ponce-Alvarez et al., 2013; Wimmer et al., 2015; Kanashiro et al., 2017; Bondy et al., 2018). For instance, pupil diameter is an indicator of overall brain state and arousal level, and fluctuations in pupil diameter are correlated with the fluctuations in cholinergic and noradrenergic projections to sensory cortex (Reimer et al., 2016). The reduction of population-wide variability reported in aroused states and during locomotion is likely a reflection of the quenching of these external fluctuations (McGinley et al., 2015). While it is tempting to extend this idea to variability modulation in selective attention, there are some key differences that complicate this interpretation. Whole-brain state is not changing when attention is directed into or out of the receptive field of a neuron, and thus the neuronal correlates of arousal are possibly distinct from those of attention. Further, the differential modulation of r_SC between and within cortical areas (Figures 1A and 1B) is difficult to explain with just a single “brain state” latent variable (Figure 2A). Rather, we expect that arousal would reduce both within and between area population-wide variability.

Nevertheless, it is popular to associate the variability within a lower area as inherited from top-down projections (Bondy et al., 2018; Wimmer et al., 2015). However, cooling experiments that inactivate top-down projections from visual areas V2 and V3 to area V1 produce only a slight reduction in single V1 neuron variability (Gómez-Laberge et al., 2016). In contrast, the bottom-up transfer of variability from lower to higher visual areas can be significant (Gómez-Laberge et al., 2016; Ruff and Cohen, 2016b). Additional multi-area population recordings between connected brain regions will be needed to probe how correlated variability flows along bottom-up and top-down pathways.

A second way to change population output variability is to keep input fluctuations fixed and shift the operating point of the network through an additional static top-down modulation. Here “operating point” designates the mean firing rates and neuronal gains about which the network will filter and transfer inputs. This shift in operating point allows the nonlinearities inherent in spiking dynamics to change the gain of how input variability transfers to output variability (Doiron et al., 2016). This mechanism has been suggested for how top-down or bottom-up modulation affects population variability in recurrent excitatory-inhibitory cortical networks (Kanashiro et al., 2017; Hennequin et al., 2018). Our model of variability modulation is similar, since the top-down attentional signal does shift the operating point of our nonlinear network; however, there are some key distinctions.

In disordered networks (Kanashiro et al., 2017) or networks with only one-dimensional structure (Hennequin et al., 2018), an external source of fluctuations is required; otherwise, the network is either in the asynchronous or pathologically synchronous solution depending upon parameter choices (Figures 3Ai, 3Aiii, and 3D). Since these networks do not produce variability internally, the operating point shift merely changes how the network filters the external fluctuations. However, in our model the two-dimensional spatial structure supports rich internal chaotic network dynamics outside the asynchronous state, yet with population-wide correlations that are a reasonable mimic of experiment (Figures 3Aiv, 3C, and 3E). There is no need to assume a source of external fluctuations.

Spatiotemporal chaos is a hallmark feature of systems that are far from equilibrium in physics, chemistry, and biology (Cross and Hohenberg, 1993). In particular, low-viscosity fluids produce a special brand of spatiotemporal chaotic behavior labeled turbulence, characterized by the presence of vortices and eddies in the fluid flow (Davidson, 2015). Like our network, the character of turbulent flow is very dependent upon the dimension of the fluid, with one-dimensional fluids not showing turbulence, and two-dimensional turbulent flow having larger spatial scales than the flow in full three-dimensional fluids (Davidson, 2015). The dynamics within recurrent networks of neurons are certainly not equivalent to that of fluids; nevertheless, the fluid analogy to our work is tempting since the chaotic dynamics of our two-dimensional network have a macroscopic character that permits low, but non-vanishing, pairwise correlations that extend broadly over the network. The effect of top-down attention is to not only shift the operating point of the network but also dampen the macroscopic chaotic dynamics of the network. In other words, attention not only attenuates the transfer of population-wide variability, as in other models (Kanashiro et al., 2017; Hennequin et al., 2018), but also quenches the variability that is to be transferred. This permits a near-complete attention-mediated suppression of internally generated correlations (Figure 7D). This extreme sensitivity allows top-down inputs to easily control the processing state of a network.

State-dependent shifts in population-wide variability are widespread throughout cortex (Doiron et al., 2016) and are often a signature of cognitive control. The circuit structure of our network is not a special feature of the primate visual system, but rather a generic property of most cortices. We thus expect that the basic mechanisms for population-wide variability and its modulation exposed in our study will be operative in many regions of the cortex, and in many animal systems.

STAR★METHODS

CONTACT FOR REAGENT AND RESOURCE SHARING

Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Brent Doiron (bdoiron@pitt.edu).

METHOD DETAILS

Spiking neuron network

The network consists of three layers. Layer 1 is modeled by a population of N₁ = 2,500 excitatory neurons, the spikes of which are taken as independent Poisson processes with a uniform rate r₁ = 10 Hz. Layer 2 and Layer 3 are recurrently coupled networks with excitatory (α = e) and inhibitory (α = i) populations of N_e = 40,000 and N_i = 10,000 neurons, respectively. Each neuron is modeled as an exponential integrate-and-fire (EIF) neuron whose membrane potential is described by:

$$C_m\frac{\text{d}{V}_j^{\alpha }}{\text{d}t}=-g_L\left(V_j^{\alpha }-E_L\right)+g_L{\Delta }_T{e}^{\left(V_j^{\alpha }-V_T\right)/{\Delta }_T}+l_j^{\alpha }\left(t\right).$$ (Equation 3)

Each time $V_j^{\alpha }\left(t\right)$ exceeds a threshold V_th, the neuron spikes and the membrane potential is held for a refractory period τ_ref then reset to a fixed value V_re. Neuron parameters for excitatory neurons are τ_m = C_m/g_L = 15 ms, E_L = −60 mV, V_T = −50 mV, V_th = −10 mV, Δ_T = 2 mV, V_re = −65 mV and τ_ref = 1.5 ms. Inhibitory neurons are the same except τ_m = 10 ms, Δ_T = 0.5 mV and τ_ref = 0.5 ms. The total current to each neuron is:

$$\frac{l_j^{\alpha }\left(t\right)}{C_m}=\sum _{k=1}^{N_F}\frac{J_{jk}^{\alpha F}}{\sqrt{N}}\sum _n{\eta }_F\left(t-t_n^{F,k}\right)+\sum _{\beta =\text{e},\text{i}}\sum _{k=1}^{N_{\beta }}\frac{J_{jk}^{\alpha \beta }}{\sqrt{N}}\sum _n{\eta }_{\beta }\left(t-t_n^{\beta ,k}\right)+{\mu }_{\alpha },$$ (Equation 4)

where N = N_e + N_i is the total number of the network population. Postsynaptic current is

$${\eta }_{\beta }^{\left(t\right)}=\frac{1}{{\tau }_{\beta d}-{\tau }_{\beta r}}\{\begin{array}{ll}{e}^{-t/{\tau }_{\beta \text{d}}}-e^{-t/{\tau }_{\beta \text{r}}},& t\ge 0\\ 0,& t<0\end{array}$$ (Equation 5)

where τ_er = 1 ms, τ_ed = ms and τ_ir = 1 ms, τ_id = 8 ms. The feedforward synapses from Layer 1 to Layer 2 have the same kinetics as the recurrent excitatory synapse, i.e., ${\eta }_F^{\left(2\right)}\left(t\right)={\eta }_e\left(t\right)$. The feedforward synapses from Layer 2 to Layer 3 have a fast and a slow component.

$${\eta }_F^{\left(3\right)}\left(t\right)=p_{\text{f}}{\eta }_{\text{e}}\left(t\right)+p_{\text{s}}{\eta }_s\left(t\right)$$ (Equation 6)

with p_f = 0.2, p_s = 0.8. η_s(t) has the same form as Equation 5 with a rise time constant ${\tau }_r^S=2\text{ms}$ and a decay time constant ${\tau }_d^S=100\text{ms}$. The excitatory and inhibitory neurons in Layer 3 receive static current μ_e and μ_i, respectively.

Neurons on the three layers are arranged on a uniform grid covering a unit square Γ = [0, 1] × [0, 1]. The probability that two neurons, with coordinates x = (x₁, x₂) and y = (y₁, y₂) respectively, are connected depends on their distance measured periodically on Γ:

$$p_{\alpha \beta }\left(\mathbf{\text{x}},\mathbf{\text{y}}\right)={\overline{p}}_{\alpha ,\beta }g\left(x_1-y_1;{\alpha }_{\beta }\right)g\left(x_2-y_2;{\alpha }_{\beta }\right).$$ (Equation 7)

Here $p_{\alpha ,\beta }$ is the mean connection probability and

$$g\left(x;\sigma \right)=\frac{1}{\sqrt{2\pi }\sigma }\sum _{k=-\infty }^{\infty }{e}^{-{\left(x+k\right)}^2/\left(2{\sigma }^2\right)}$$ (Equation 8)

is a wrapped Gaussian distribution. Excitatory and inhibitory recurrent connection widths of Layer 2 are ${\alpha }_{\mathrm{rec}}^{\left(2\right)}:={\alpha }_{\text{e}}^{\left(2\right)}={\alpha }_{\text{i}}^{\left(2\right)}=0.1$ and feedforward connection width from Layer 1 to Layer 2 is ${\alpha }_{\text{ffwd}}^{\left(2\right)}=0.05$. The recurrent connection width of Layer 3 is ${\alpha }_{\mathrm{rec}}^{\left(3\right)}=0.2$ and the feedforward connection width from Layer 2 to Layer 3 is ${\alpha }_{\text{ffwd}}^{\left(3\right)}=0.1$. A presynaptic neuron is allowed to make more than one synaptic connection to a single postsynaptic neuron.

The recurrent connectivity of Layer 2 and Layer 3 have the same synaptic strengths and mean connection probabilities. The recurrent synaptic weights are J_ee = 80 mV, J_ei = −240 mV, J_ie = 40 mV and J_ii = −300 mV. Recall that individual synapses are scaled with $1/\sqrt{N}$ (Equation 4); so that, for instance, $J_{ee}/\sqrt{N}\approx 0.36\text{mV}$. The mean connection probabilities are ${\stackrel{\_}{p}}_{\mathrm{ee}}=0.01,{\stackrel{\_}{p}}_{\mathrm{ei}}=0.04,{\stackrel{\_}{p}}_{\mathrm{ie}}=0.03,{\stackrel{\_}{p}}_{\mathrm{ii}}=0.04$. The out-degrees are $K_{\mathrm{ee}}^{\mathrm{out}}=400,K_{\mathrm{ei}}^{\mathrm{out}}=1600,K_{\mathrm{ie}}^{\mathrm{out}}=300$ and $K_{\mathrm{ii}}^{\mathrm{out}}=400$. The feedforward connection strengths from Layer 1 to Layer 2 are $J_{\mathrm{eF}}^{\left(2\right)}=140\text{mV}$ and $J_{\mathrm{iF}}^{\left(2\right)}=100\text{mV}$ with probabilities ${\stackrel{\_}{p}}_{\mathrm{eF}}^{\left(2\right)}=0.1$ and ${\stackrel{\_}{p}}_{\mathrm{iF}}^{\left(2\right)}=0.05$ (out degrees $K_{\mathrm{eF}2}^{\mathrm{out}}=4000$ and ${\text{K}}_{\mathrm{eF}2}^{\mathrm{out}}=500$). The feedforward connection strengths from Layer 2 to Layer 3 are $J_{\mathrm{eF}}^3=25\text{mV}$ and $J_{\mathrm{iF}}^3=15\text{mV}$ with mean probabilities ${\stackrel{\_}{p}}_{\mathrm{eF}}^{\left(3\right)}=0.05$ and ${\stackrel{\_}{p}}_{\mathrm{iF}}^{\left(3\right)}=0.05$ (out-degrees are $K_{\mathrm{eF}3}^{\mathrm{out}}=2000$ and ${\text{K}}_{\mathrm{iF}3}^{\mathrm{out}}=500$). Only the excitatory neurons in Layer 2 project to Layer 3.

The spatial models in Figures 3Aii and 3Aiv contain only Layer 1 and Layer 2. In the model with disordered connectivity, the connection probability between a pair of neurons is ${\stackrel{\_}{p}}_{\alpha \beta }$, independent of distance. Other parameters are the same as the spatial model. The decay time constant of IPSC (τ_id) was varied from 1 to 15 ms (Figure 3E). The rise time constant of IPSC (τ_ir) is 1 ms when τ_id > 1 and 0.5 ms when τ_id = 1 ms.

The parameters used in Figures 4C and 4D are μ_i = [0.1, 0.15, 0.2, 0.025, 0.3, 0.35, 0.4] mV/ms and μ_E = 0 mV/ms. The mean firing rates in Layer 2 are $r_{\text{e}}^{\left(2\right)}=19\text{Hz}$ and $r_{\text{i}}^{\left(2\right)}=9\text{Hz}$. In the further analysis (Figures 4E, 5C, 5D, 6B, and 6C), we used μ_l = 0.2 mV/ms for the unattended state and μ_l = 0.35 mV/ms for the attended state. In simulations of the spatial model with broad inhibitory projection (Figure 6C), ${\alpha }_{\text{e}}^{\left(3\right)}=0.1,{\alpha }_{\text{i}}^{\left(3\right)}=0.2$ Other parameters were not changed.

The slow component of feedforward excitation (Equation 6) allows for large spike count Fano factors (Figure S5), but when replaced with the same fast kinetics of recurrent excitation the low dimensional population-wide variability and its attentional modulation are qualitatively unaffected (Figure S8).

All simulations were performed on the CNBC Cluster in the University of Pittsburgh. All simulations were written in a combination of C and MATLAB (MATLAB R 2015a, MathWorks). The differential equations of the neuron model were solved using forward Euler method with time step 0.01 ms.

Neural field model and stability analysis

We use a two dimensional neural field model to describe the dynamics of population rate (Figure 6). The neural field equations are

$${\tau }_{\alpha }\frac{\partial r_{\alpha }\left(x,t\right)}{\partial t}=-r_{\alpha }+{\varphi }_{\alpha }\left(w_{\alpha e}\ast r_e+w_{\alpha i}\ast r_i+{\mu }_{\alpha }\right),$$ (Equation 9)

where r_α(x, t) is the firing rate of neurons in population α = e, i near spatial coordinates x ∈ [0, 1] × [0, 1]. The symbol ∗ denotes convolution in space, μ_α is a constant external input and $w_{\alpha \beta }\left(x\right)={\stackrel{\_}{w}}_{\alpha \beta }g\left(x;{\sigma }_{\beta }\right)$ where $g\left(x;{\sigma }_{\beta }\right)$ is a two-dimensional wrapped Gaussian with width parameter σ_β, β = e, i. The transfer function is a threshold-quadratic function, ϕ_α(x) = k_α[x²]₊. The timescale of synaptic and firing rate responses are implicitly combined into τ_α. In networks with approximate excitatory-inhibitory balance, rates closely track synaptic currents (Renart et al., 2010), so τ_α represents the synaptic time constant of population α = e, i.

For constant inputs, μ_e and μ_i there exists a spatially uniform fixed point, which was computed numerically using an iterative scheme (Rosenbaum and Doiron, 2014). Linearizing around this fixed point in Fourier domain gives a Jacobian matrix at each spatial Fourier mode (Rosenbaum and Doiron, 2014)

$$J\left(\overrightarrow{n}\right)=\left[\begin{array}{cc}\left(-1+g_e{\tilde{w}}_{ee}\left(\overrightarrow{n}\right)\right)/{\tau }_e& g_e{\tilde{w}}_{ei}\left(\overrightarrow{n}\right)/{\tau }_e\\ g_i{\tilde{w}}_{ie}\left(\overrightarrow{n}\right)/{\tau }_i& \left(-1+g_i{\tilde{w}}_{ii}\left(\overrightarrow{n}\right)\right)/{\tau }_i\end{array}\right].$$

where $\overrightarrow{n}=\left(n_1,n_2\right)$ is the two-dimensional Fourier mode, ${\tilde{w}}_{\alpha \beta }\left(\overrightarrow{n}\right)=w_{\alpha \beta }\exp \left(-2{\Vert \overrightarrow{n}\Vert }^2{\pi }^2{\sigma }_{\beta }^2\right)$ is the Fourier coefficient of w_αβ(x) with ${\Vert \overrightarrow{n}\Vert }^2=n_1^2+n_2^2$ and g_a is the gain, which is equal to ${{\varphi }^{\prime }}_{\alpha }\left(r_{\alpha }\right)$ evaluated at the fixed point. The fixed point is stable at Fourier mode $\overrightarrow{n}$ if both eigenvalues of $J\left(\overrightarrow{n}\right)$ have negative real part. Note that stability only depends on the wave number, $k=\Vert \overrightarrow{n}\Vert$, so Turing-Hopf instabilities always occur simultaneously at all Fourier modes with the same wave number (spatial frequency).

For the stability analysis in Figure 6A, τ_i varies from 2.5 ms to 25 ms, σ_i varies from 0.05 to 0.2, and τ_e = 5 ms and σ_e = 0.1. The rest of the parameters were ${\stackrel{\_}{w}}_{ee}=80$, ${\stackrel{\_}{w}}_{ei}=-160$, ${\stackrel{\_}{w}}_{ie}=120$, ${\stackrel{\_}{w}}_{ii}=200$, k_e = 1, k_i = 1, μ_e = 0.48 and μ_i = 0.32. Depolarizing the inhibitory population (μ_l = 0.5) expands the stable region (Figure 6A, black dashed).

QUANTIFICATION AND STATISTICAL ANALYSIS

Datasets

Each of the two datasets (recordings from V4 and recordings from V1 and MT) was collected from two different rhesus monkeys as they performed an orientation-change detection task. All animal procedures were in accordance with the Institutional Animal Care and Use Committee of Harvard Medical School, University of Pittsburgh and Carnegie Mellon University.

For analysis in Figures 1A, 1C, 5A, and 5B, data was collected with two microelectrode arrays implanted bilaterally in area V4 (Cohen and Maunsell, 2009). In our analysis, we include stimulus presentations prior to the change stimulus from correct trials, excluding the first stimulus in a trial to avoid adaptation effects. Spike counts during the sustained response (120 - 260 ms after stimulus onset) are considered for the correlation and factor analysis. Neurons recorded from either the left or right hemisphere in one session are treated separately. There are a total of 42,496 trials for 72,765 pairs from 74 recording sessions. Two sessions from the original study were excluded for factor analysis due to inadequate trials. The trial number and unit number of each session is summarized in Table S1.

For analysis in Figure 1B, data was collected with one microelectrode array implanted in area V1 and a single electrode or a 24-channel linear probe inserted into MT (Ruff and Cohen, 2016a). Again, our analysis includes full contrast stimulus presentations prior to the change stimulus from correct trials and excludes the first stimulus in a trial to avoid adaptation effects. Spike counts are measured 30 - 230 ms after stimulus onset for V1 and 50 - 250 ms after stimulus onset for MT to account for the average visual latencies of neurons in both areas. There are a total of 1,631 V1-MT pairs from 32 recording sessions.

Noise correlation

To compute the noise correlation of each simulation, 500 neurons were randomly sampled without replacement from the excitatory population of Layer 3 and Layer 2 within a [0, 0.5]x[0, 0.5] square (considering periodic boundary condition). Spike counts were computed using a sliding window of 200 ms with 1 ms step size and the Pearson correlation coefficients were computed between all pairs. Neurons of firing rates less than 2 Hz were excluded from the computation of correlations. In Figures 4C and 4D, for each μ, there were 50 simulations and each simulation was 20 s long. Connectivity matrices and the initial states of each neuron’s membrane potential were randomized in each simulation. The first 1 s of each simulation was excluded from the correlation analysis. Standard error was computed based on the mean correlations of each simulation. For simulations of Figure 3E, there was one simulation of 20 s per τ_id and the connectivity matrices were randomized for each simulation. To compute the noise correlation, 1000 neurons were randomly sampled without replacement in the excitatory population of Layer 2 within a [0, 0.5]x[0, 0.5] square. Correlations are computed between firing rates that are smoothed with a Gaussian window of width 10 ms.

Factor analysis

Factor analysis assumes spike counts of n simultaneously recorded neurons $x\in {\mathcal{R}}^{n\times 1}$ is a multi-variable Gaussian process

$$x\sim \mathcal{N}\left(\mu ,L{L}^T+\Psi \right)$$

where $\mu \in {\mathcal{R}}^{n\times 1}$ is the mean spike counts, $L\in {\mathcal{R}}^{n\times m}$ is the loading matrix of the m latent variables and $\Psi \in {\mathcal{R}}^{n\times 1}$ is a diagonal matrix of independent variances for each neuron. We choose m = 5 and compute the eigenvalues of LL^T, λ_i (i = 1,2,…,m), ranked in descending order. The corresponding eigenvectors are denoted as v_i and the covariance components are ${\lambda }_i{v}_i{v}_i^T\left(i=1,2,\mathrm{\dots }m\right)$. The covariance matrix is approximated as

$$\mathrm{Cov}\left(x,x\right)=\sum _{i=1}^m{\lambda }_i{v}_i{v}_i^T+\Psi .$$ (Equation 10)

We compute the residual covariance after subtracting the first mode as

$$Q=\mathrm{Cov}\left(x,x\right)-L_1\times L_1^T,$$ (Equation 11)

where Cov(x, x) is the raw covariance matrix of x and L₁ is the loading matrix when fitting with m = 1. The mean raw covariance and residual (Figures 4E and 1C, right) are the mean of the off-diagonal elements of Cov(x, x) and Q, respectively.

When applying factor analysis on model simulations (Figure 4E), we randomly selected 50 excitatory neurons from Layer 3, whose firing rates were larger than 2 Hz in both the unattended and attended states. There were 15 simulations of 20 s each per connectivity matrices realization, and there were 8 realizations of connectivity matrices in total. Spike trains were truncated into 140 ms spike count window with a total of 2,025 counts per neuron. There were 80 non-overlapping sampling of neurons (10 sampling per realization of connectivity matrices) and we applied factor analysis on each sampling of neuron spike counts.

To compute the distance dependent functions of each covariance component ${\lambda }_i{v}_i{v}_i^T$ (Figures 5C and 5D), we randomly selected 500 excitatory neurons from Layer 3, whose firing rates were larger than 2 Hz in both the unattended and attended states. To compute the distance dependent functions of covariance as well as convariance components for the V4 data (Figures 5A and 5B), the pairs across sessions were pooled to compute the mean and SEM at each distance value. The distance values were discrete since neurons were recorded with an multi-electrode array with a distance between adjacent electrodes being 400 μm. The number of pairs at each distance value are shown in Table S2.

Measure internal variability

To study the chaotic population firing rate dynamics of Layer 3 (Figure 7), we fixed the spike trains realizations from Layer 1 neurons, the membrane potential states of the Layer 2 neurons and all connectivity matrices. Only the initial membrane potentials of Layer 3 neurons were randomized across trials. There were 10 realizations of Layer 1 and Layer 2, each of which was 20 s long. For each simulation of Layer 2, 20 repetitions with different initial conditions were simulated for Layer 3. The connectivity matrices in Layer 3 were the same across the 20 repetitions but different for each realization of Layer 1 and Layer 2. The realizations of Layer 1 and Layer 2 and the connectivity matrices were the same for the attended and unattended states. Trial-to-trial variance of Layer 3 population rates (Figure 7D) was the variance of the mean population rates of the Layer 3 excitatory population, smoothed by a 200 ms rectangular filter, across the 20 repetitions. The first second of each simulation was discarded.

DATA AND SOFTWARE AVAILABILITY

The data that support the findings of this study are available from the corresponding author upon request. Computer code for all simulations and data analysis can be found at https://github.com/hcc11/SpatialNeuronNet.

KEY RESOURCES TABLE

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Software and Algorithms
Algorithms for simulation of spiking neuron networks	This paper	https://github.com/hcc11/SpatialNeuronNet
MATLAB	MathWorks	https://www.mathworks.com

Highlights.

• Low-dimensional shared variability can be generated in spatial network models

• Synaptic spatial and temporal scales determine the dimensions of shared variability

• Depolarizing inhibitory neurons suppresses the population-wide fluctuations

• Modeling the attentional modulation of variability within and between brain areas