Dynamics of the SARS-CoV-2 nucleoprotein N-terminal domain triggers RNA duplex destabilization

Abstract

The nucleocapsid (N) protein of betacoronaviruses is responsible for nucleocapsid assembly and other essential regulatory functions. The N protein N-terminal domain (N-NTD) interacts and melts the double-stranded transcriptional regulatory sequences (dsTRSs), regulating the discontinuous subgenome transcription process. Here, we used molecular dynamics (MD) simulations to study the binding of the severe acute respiratory syndrome coronavirus 2 N-NTD to nonspecific (NS) and TRS dsRNAs. We probed dsRNAs’ Watson-Crick basepairing over 25 replicas of 100 ns MD simulations, showing that only one N-NTD of dimeric N is enough to destabilize dsRNAs, triggering melting initiation. dsRNA destabilization driven by N-NTD was more efficient for dsTRSs than dsNS. N-NTD dynamics, especially a tweezer-like motion of β2-β3 and Δ2-β5 loops, seems to play a key role in Watson-Crick basepairing destabilization. Based on experimental information available in the literature, we constructed kinetics models for N-NTD-mediated dsRNA melting. Our results support a 1:1 stoichiometry (N-NTD/dsRNA), matching MD simulations and raising different possibilities for N-NTD action: 1) two N-NTD arms of dimeric N would bind to two different RNA sites, either closely or spatially spaced in the viral genome, in a cooperative manner; and 2) monomeric N-NTD would be active, opening up the possibility of a regulatory dissociation event.

Significance

Coronaviruses display a unique discontinuous transcription mechanism, in which the N protein plays a major role. N-NTD promotes dsRNA melting, releasing the nascent negative strand via a poorly described mechanism. It specifically recognizes the body TRS, a conserved RNA motif located at the 5′-end of each open reading frame, catalyzing the melting of the RNA duplex and transferring of the nascent strand to the leader TRS. Here, we describe a counterintuitive mechanism of N-NTD-induced dsRNA destabilization based on MD simulation and kinetic modeling using the experimental data of its melting activity. These data impact directly in the understanding of the mechanism by which N protein acts in the cell, guiding future experiments.

Introduction

The recent pandemic of severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2), the causative agent of coronavirus disease 2019, has become a global health emergency (1,2). SARS-CoV-2, a member of the Coronaviridae family, is an enveloped virus containing a large nonsegmented positive-sense single-stranded RNA genome (3,4). The 5′ two-thirds of the coronaviruses’ genome, corresponding to open reading frame (ORF) 1a/b, is translated into two polyproteins (pp1a and pp1ab) that are proteolytically processed into 16 nonstructural proteins (5). These nonstructural proteins assemble in the viral replicase-transcriptase complex at the endoplasmic reticulum membrane, being responsible for genome replication and transcription (6). Conversely, the 3′ one-third of the genome is translated into accessory proteins as well as the four structural proteins—spike (S), membrane (M), envelope (E), and nucleocapsid (N)—through a unique process of subgenomic mRNA (sgmRNA) transcription (7,8).

N is one of the most abundant viral proteins in the infected cell. It is a 46 kDa multifunctional RNA-binding protein that packs the viral RNA in a helical nucleocapsid (9). In addition, N localizes at the replicase-transcriptase complex at early stages of infection and plays a central role in the regulation of RNA synthesis (10, 11, 12). It is composed of two functionally distinct folded domains, which are interspersed by an intrinsically disordered linker region enriched in arginine and serine residues. Both the two domains and the linker region contribute individually to RNA binding (13). The N protein N-terminal domain (N-NTD) has been shown to interact with regulatory RNA sequences during subgenome transcription, whereas its C-terminal domain is responsible for N protein dimerization, which is crucial for nucleocapsid assembly (14,15). The recently reported solution structure of SARS-CoV-2 N-NTD reveals a right hand-like fold, composed of a five-stranded central β-sheet flanked by two short α-helices, arranged in a β4-β2-β3-β1-β5 topology (16). The β-sheet core is referred to as the hand’s palm, and the long β2-β3 hairpin, mostly composed of basic amino acid residues, corresponds to the basic finger. The positively charged cleft between the basic finger and the palm has been suggested as a putative RNA-binding site (16).

Genome replication is a continuous process in coronaviruses. In contrast, transcription is discontinuous and involves the production of sgmRNAs (17). Regulation of sgmRNA synthesis is dependent on transcriptional regulatory sequences (TRSs) located either at the 5′-end of the positive-strand RNA genome, known as the leader TRS (TRS-L), or at the 5′-end of each viral gene coding for structural and accessory proteins, called the body TRS (TRS-B). The TRS-L and TRS-B share a similar core sequence, which allows for a template switch during sgmRNA synthesis. Once the TRS-B has been copied, the nascent negative-strand RNA is transferred to the TRS-L, and transcription is terminated (17,18). Multiple well-orchestrated factors, including TRS secondary structure and RNA-RNA and RNA-protein interactions, influence sgmRNA transcription (17). Coronaviruses’ N-NTD specifically interacts with the TRS and efficiently melts an RNA duplex formed between TRS and its complementary strand (cTRS), facilitating template switch and playing a pivotal role in the regulation of discontinuous transcription (10,16,17,19). Despite its relevance for the viral replication cycle, the molecular basis underlying the specificity of interaction of the SARS-CoV-2 N-NTD with the TRS remains elusive. Thus, understanding the mechanism by which SARS-CoV-2 N-NTD specifically recognizes TRS RNA at atomic detail is paramount for the rational development of new antiviral strategies.

Here, we present a hypothesis for the molecular mechanism by which SARS-CoV-2 N-NTD destabilizes double-stranded (ds) RNA, the initial step of the dsRNA melting process. We showed by molecular dynamics (MD) simulations (25 replicas of 100 ns) that N-NTD destabilizes dsRNA’s Watson-Crick (WC) basepairing by decreasing the number of the RNA-RNA hydrogen bonds and perturbing the local rigid-body geometric parameters of dsRNA. The destabilization is more significant for TRS than for a nonspecific (NS) dsRNA sequence. Moreover, a tweezer-like motion between β2-β3 and Δ2-β5 loops of N-NTD seems to be a key dynamic feature for selectivity and, consequently, dsRNA destabilization. We also constructed kinetic models for characterizing the melting activity of the dimeric N protein assuming 1:1 and 2:1 (N-NTD/dsRNA) stoichiometries, revealing that only one N-NTD is sufficient for dsRNA melting.

Materials and methods

Molecular docking

To perform the docking, we took advantage of experimental data previously published (16), in which SARS-CoV-2 N-NTD interaction with an NS dsRNA (5′-CACUGAC-3′ and 5′-GUCAGUG-3′) was monitored by chemical shift perturbation (CSP) titration experiments. Structural models for the N-NTD/dsNS complex were constructed using the HADDOCK server (version 2.2) (20). The coordinates used as input were obtained from the solution NMR structure of SARS-CoV-2 N-NTD (Protein Data Bank (PDB): 6YI3) (16), and the x-ray structure of a synthetic 7-mer dsRNA (PDB: 4U37) (21) mutated using the w3DNA server (version 2.0) (22) to generate the same NS dsRNA sequence as that used in the CSP titration experiments (5′-CACUGAC-3′ and 5′-GUCAGUG-3′). In addition, histidine protonation states at pH 7.0 were set according to the PROPKA server (23). In total, 2000 complex structures of rigid-body docking were calculated by using the standard HADDOCK protocol with an optimized potential for liquid simulation parameter (24). The final 200 lowest-energy structures were selected for subsequent explicit solvent (water) and semiflexible simulated annealing refinement (first step: 2000 K and 8 ps; second step: 1000 K and 16 ps; third step: 1000 K and 16 ps; and final solvated refinement step: 300 K and 2.5 ps), to optimize side chain constants. The final structures were clustered using the backbone root mean-square deviation (RMSD) with a cutoff of 7.5 Å (25).

Next, the structural model of the N-NTD/dsTRS (5′-UCUAAAC-3′ and 5′-AGAUUUG-3′; sense and antisense sequences) complex was generated from the lowest-energy structure of the N-NTD/dsNS complex, derived from the cluster with the lowest HADDOCK score, by mutating the dsRNA sequence using w3DNA (22). Therefore, both complexes have identical geometries, varying only the dsRNA sequence. Structural conformation of the constructed model for N-NTD/dsTRS complex was displayed using the web application http://skmatic.x3dna.org for easy creation of Dissecting the Spatial Structure of RNA-PyMOL schematics (26).

MD simulation

MD calculations for N-NTDs, dsRNAs, and N-NTD/dsRNA complexes were performed using GROMACS (version 5.0.7) (27). The molecular systems were modeled with the corrected AMBER14 package, including the ff14sb protein (28) and ff99bsc0χOL3 RNA (29) force fields, as well as the TIP3P water model (30). The ff99bsc0χOL3 force field parameterizes the glycosidic torsion angle χ of the AMBER package for RNA, removing the destabilization of the anti-configuration and preventing formation of the ladder-like structural distortions in RNA simulations (29). The structural models of N-NTD (PDB: 6YI3), dsRNAs (mutated PDB: 4U37), and N-NTD/dsRNA complexes (from molecular docking) were placed in the center of a cubic box solvated by a solution of 50 mM NaCl in water. The protonation state of ionizable residues at pH 7.0 was set according to the PROPKA server (23). Periodic boundary conditions were used, and all simulations were performed in an isothermal-isobaric (NPT) ensemble, keeping the system at 298 K and 1.0 bar using the Nosé-Hoover thermostat (τ_T = 2 ps) and Parrinello-Rahman barostat (τ_P = 2 ps and compressibility = 4.5 × 10⁻⁵ bar⁻¹). A cutoff of 12 Å for both Lennard-Jones and Coulomb potentials was used. The long-range electrostatic interactions were calculated using the particle mesh Ewald algorithm. In every MD simulation, a time step of 2.0 fs was used and all covalent bonds involving hydrogen atoms were constrained to their equilibrium distance. A conjugate gradient minimization algorithm was used to relax the superposition of atoms generated in the box construction process. Energy minimizations were carried out with the steepest descent integrator and conjugate gradient algorithm, using 1000 kJ mol⁻¹ ⋅ nm⁻¹ as the maximal force criterion. 100,000 steps of MD were performed for each canonical (NVT) and NPT ensemble equilibration, applying force constants of 1000 kJ mol⁻¹ nm⁻² to all heavy atoms of N-NTD, dsRNAs, and N-NTD:dsRNA complexes. At the end of preparation, 25 replicas of 100 ns MD simulation of each molecular system with different seeds of the random number generator were carried out for data acquisition, totalizing 2.5 μs. All the MD simulations started from the same set of coordinates. Following dynamics, the trajectories of each molecular system were firstly concatenated individually and analyzed according to the RMSD, number of contacts, number of hydrogen bonds, and local basepair parameters of the dsRNAs. RMSDs were calculated for the backbone atoms of protein and nucleic acid. The number of contacts for distances lower than 0.6 nm were quantified between pairs of atoms of the N-NTD and dsRNAs. The occurrence of RNA-RNA, protein-nitrogenous base, and protein-RNA hydrogen bonds were calculated between the heavy atoms using a cutoff distance of 3.5 Å and maximal angle of 30°. The local basepair parameters (angles (°): buckle, opening, and propeller; distances (nm): stretch, stagger, and shear) for free and N-NTD-bound dsNSs and dsTRSs were determined by using the do_x3dna tool (31) along with the 3DNA package (32). These local basepair parameters of each of the 25 runs and of selected replicas were analyzed together as histogram plots exhibiting population distributions. The percentage of persistency of protein-RNA hydrogen bonds was obtained from the plot_hbmap_generic.pl script (33). The number of protein-RNA hydrogen bonds with a persistence higher than 10% was counted with respect to amino acid and nucleotide residues for each 25 replicas. After individual analysis of each simulation, the last 50 ns of the 25 trajectories of free and dsRNA-bound N-NTD were concatenated in single files, and these new trajectories were used to evaluate the root mean-square fluctuation (RMSF) of the C_α atoms and principal component analysis (PCA). PCA scatter plots were generated for free and dsRNA-bound N-NTDs, as well as conformational motions being filtered (30 frames) from the eigenvectors of the first and second principal components (PC1 and PC2, respectively). We also concatenated (pooled) the trajectories of all 25 replicas of the MD simulations of free N-NTD with its bound states (N-NTD/dsNS and N-NTD/dsTRS) and generated PCA scatter plots. The conformational space was quantified by fitting an elliptical shell with 95% (confidence) of the density for each scatter plot and making its extent proportional to the area (S_el) of this shell. This strategy guarantees that the same eigenvectors are used for all systems. The structural representations of the motions from PC1 and PC2 were prepared using PyMol (34).

Kinetic simulations

The Kinetiscope program (version 1.1.956.x6; http://hinsberg.net/kinetiscope/) was used to simulate the kinetics of dsRNA melting by the SARS-CoV-2 N-NTD. This software is based on a stochastic algorithm developed by Bunker et al. (35) and Gillespie (36). Simulations were performed under constant volume, pressure, and temperature (298.15 K). An initial concentration of 50 nM dsTRS was used, and a total of 2439 initial numbers of particles were calculated. N-NTD concentration ranged from 0 to 2 μM for model 1 and from 0 to 4.5 μM for model 2. The maximal number of events was set to 10 million, and simulations lasted for at least 100 s.

Results

Structural models of the N-NTD/dsRNA complexes and their validation from MD simulations

In this work, we probed the dynamical behavior of SARS-CoV-2 N-NTD interaction with an NS and a biologically relevant RNA sequence (TRS). During discontinuous transcription, N-NTD acts on the TRS-B duplex, promoting its melting and delivering the nascent negative-strand RNA to the TRS-L (template switch). This template switch enables the transcription of subgenomic RNAs. To guide the selection of the TRS-specific sequence, we aligned the nucleotide sequences of TRS-Bs from each SARS-CoV-2 ORF (NCBI reference sequence: NC_045512.3) with the TRS-L sequence (Fig. S1). Remarkably, there is no consensus among the TRS-B sequences. Even the triple adenine motif, which was previously identified as essential for N-NTD binding, is not present in the TRS-Bs of ORF E and ORF6. The closest to a consensus sequence is the triple adenine flanked by pyrimidine residues. Thus, we chose the core sequence 5′-UCUAAAC-3′ (antisense 5′-AGAUUUG-3′) as representative of TRS, as it is identical among the TRS-Bs of ORFs N and M as well as TRS-L.

To choose the optimal size of the dsRNA and pursue the computational simulations, we considered the previous experimental data available for SARS-CoV-2 N-NTD and the mechanical properties of dsRNAs. The only experimentally validated structural information available for the N-NTD/dsRNA interaction was performed with the 7-mer NS oligonucleotide used in this work (16). Differently from DNA structure, which favors long stretches of the double helix, the most frequent RNA sequences occurring in nature exhibit short canonical helices, generally containing no more than 12 consecutive basepairs (37). A possible explanation for this structural feature may be related to the mechanical properties of dsRNA, which stretches ∼3 times more than dsDNA under an external force, unwinding upon elongation, whereas DNA overwinds when stretched. Interestingly, the formation of tertiary RNA structures frequently involves contacts between canonical dsRNA helices (38). It is worth mentioning that dsRNA-binding domains are small, around 100 amino acids long, and thus, they specifically recognize short dsRNA segments (39,40). For the reasons above, we decided to perform the computational simulations with the experimentally supported 7-mer dsRNA.

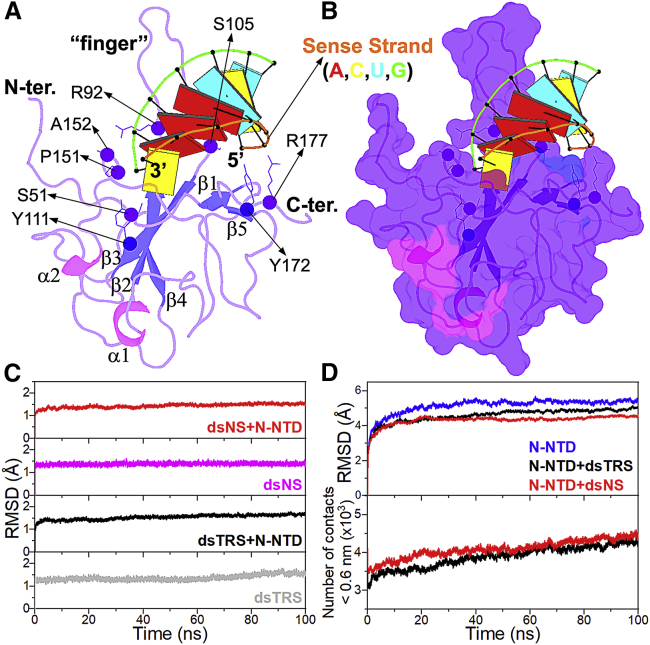
We calculated the structural model of the N-NTD/dsTRS complex based on the experimental data for the N-NTD interaction with an NS dsRNA (5′-CACUGAC-3′ and 5′-GUCAGUG-3′; sense and antisense, dsNS) (16) using the HADDOCK 2.2 server (20). The structural restraints of the N-NTD/dsNS complex were defined from CSPs titration by NMR spectroscopy (16). The lowest-energy structure of the N-NTD/dsNS complex from the cluster with the lowest HADDOCK score (fraction of common contacts = 0.8 ± 0.1 Å, interface-RMSD = 1.0 ± 0.6 Å, and ligand-RMSD = 2.2 ± 1.2 Å) was used to mutate the dsNS molecule to obtain the TRS sequence (sense 5′-UCUAAAC-3′ and antisense 5′-AGAUUUG-3′) and, therefore, to generate the N-NTD/dsTRS complex structure. Fig. 1, A and B show the structural model of the N-NTD/dsTRS complex, in which the TRS RNA is inserted in a cleft located between the large protruding β2-β3 loop, named the finger, and the central β-sheet of N-NTD, referred to as the palm. The structural model also revealed that residues S51, R92, S105, Y111, P151, A152, Y172, and R177 are involved in polar contacts with the dsTRS (Fig. 1 A). Analysis of the electrostatic surface potential of N-NTD revealed that the dsRNA-binding pocket is positively charged, with the finger being the highest charged region (Fig. S2). This result is consistent with the charge complementarity of the nucleic acid phosphate groups that exhibit negative charge.

Figure 1.

Structural model of the N-NTD/dsRNA complex and its validation from MD simulations. (A) Structural model of the N-NTD/dsTRS complex determined by molecular docking calculations and mutation of dsNS nucleotide sequence. N-NTD is presented as a cartoon, and dsTRS is denoted as a ribbon model with basepairing as colored rectangles. The color of the rectangles corresponds to the nitrogenous base of the dsRNA sense strand, namely A: red, C: yellow, U: cyan, and G: green. The large protruding β2-β3 loop is referred to as the finger. The residues involved in polar contacts with the dsTRS are presented as sphere (α-carbon) and lines (side chain). The α-helix and β-sheet secondary structures are colored in magenta and blue, respectively. (B) Surface representation of the structural model of the N-NTD/dsTRS complex. (C) Average RMSD values for dsNS and dsTRS in their free and N-NTD-bound states. (D) Average RMSD values for N-NTD in its free and dsRNA-bound state (top) and average number of contacts between N-NTD and dsRNA atoms (distance <0.6 nm) (bottom). The average values correspond to 25 MD simulations with the same starting point. To see this figure in color, go online.

We performed 25 calculations of 100 ns MD simulations to investigate the stability of the structural models of N-NTD in complex with either a dsNS or dsTRS, as well as each of the biomolecules separately (dsNS, dsTRS, and N-NTD). Fig. 1 C shows the average RMSD values of the backbone atoms (C5′, C4′, C3′, O3′, P, and O5′) from the starting structure (refined HADDOCK model) for the dsNS and dsTRS in their free and N-NTD-bound states, which were significantly stable along the 100 ns MD simulations. Similar results are observed for the average RMSD values of the backbone atoms for free and dsRNA-bound N-NTD over the simulations (Fig. 1 D, top). Evaluation of the average number of contacts between N-NTD and dsRNAs (distance < 0.6 nm) revealed that the dsNS and dsTRS are in close interaction with N-NTD throughout the 100 ns MD simulations (Fig. 1 D, bottom). These parameters (RMSD and contacts) validate the structural models generated for the N-NTD/dsRNA complexes as well as the molecular structures of the investigated biomolecules (dsNS, dsTRS, and N-NTD). The nonaveraged values of the analyzed parameters for each of the 25 MD simulations are provided in Figs. S3–S11.

Stability of dsNS and dsTRS basepairing upon N-NTD binding

To gain further insights into the molecular events that trigger dsRNA destabilization as part of the N-NTD melting activity, we used the MD simulations to probe the stability of the free and N-NTD-bound dsRNA. It is worth mentioning that these simulations do not probe the dsRNA melting activity per se but the initial steps of the melting reaction, as the whole process happens on a timescale of seconds.

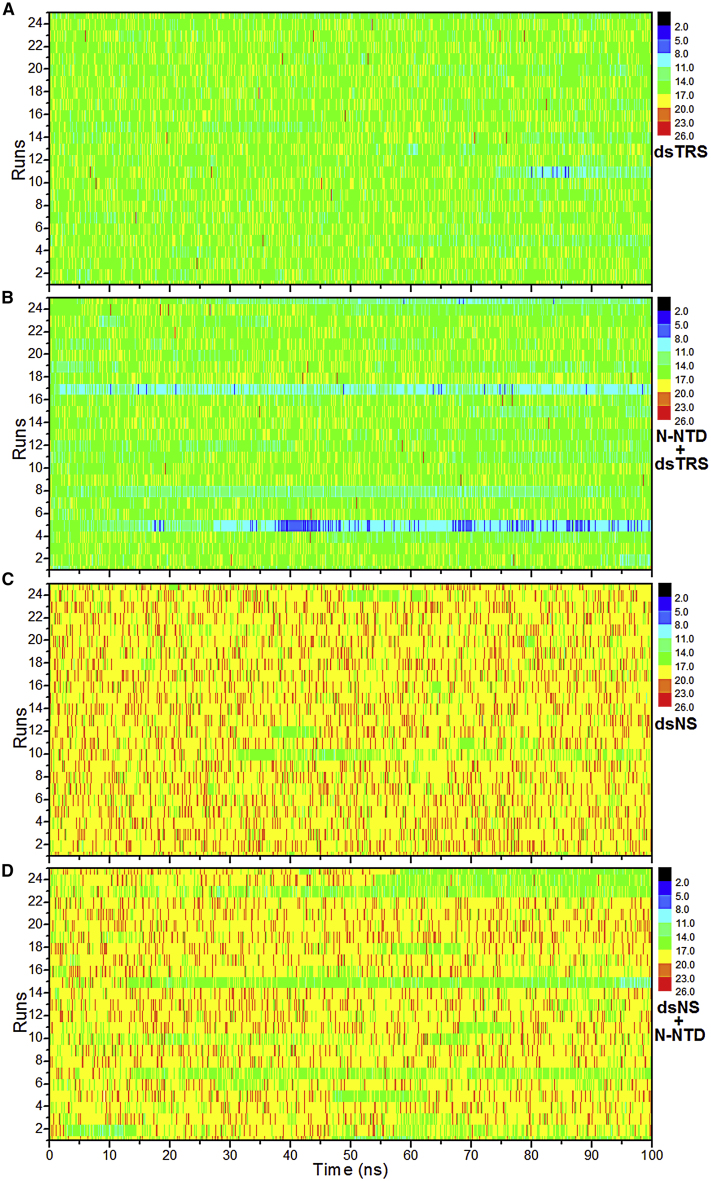
To estimate the stability of the WC basepairing of dsNS and dsTRS complexed with N-NTD, we evaluated the RNA-RNA hydrogen bonds formed between sense and antisense strands of the dsRNA bound to N-NTD. The RNA-RNA hydrogen bonds of the free RNA molecules were investigated as a control parameter. The MD simulations of the free dsRNAs reflect transient hydrogen bonds typical of A-type dsRNA, with the expected average number of hydrogen bonds (18 for dsNS and 16 for dsTRS), maintained throughout the 100 ns simulations for all 25 replicas. Fig. 2 shows the number of RNA-RNA hydrogen bonds for 25 replicas of MD simulations of the free and N-NTD-bound dsTRS. It is possible to note that the score profile of RNA-RNA hydrogen bonds for free dsTRS (Fig. 2 A) was different than that of N-NTD-bound dsTRS (Fig. 2 B). This difference is mainly due to a considerable reduction in the number of RNA-RNA hydrogen bonds in at least four replicas of the set of 25 MD simulations (runs 5, 8, 17, and 25), suggesting that dsTRS WC basepairing was destabilized by interaction with the N-NTD. The score profile of the RNA-RNA hydrogen bonds for the N-NTD-bound dsNS (Fig. 2 C) was also reduced, especially for runs 15 and 23 (Fig. 2 D). Note that the reduction of the number of hydrogen bonds is more pronounced for the N-NTD-bound dsTRS than for dsNS. For runs 5, 8, 17, and 25 of the bound dsTRS, the number of hydrogen bonds dropped to a range between 2 and 11 (from dark blue to cyan, Fig. 2 B), whereas for the bound dsNS, this number dropped to a range of 11–17 (from light green to dark green, Fig. 2 D). It is important to highlight that the color scale is the same for all MD simulations, being that the difference between the predominant color observed for dsTRS (mostly green) and dsNS (mostly yellow) is due to the maximal number of WC hydrogen bonds in each dsRNA.

Figure 2.

Stability of the WC basepairing via RNA-RNA hydrogen bonds of dsRNAs. The number of RNA-RNA hydrogen bonds formed between the sense and antisense strands of dsNS and dsTRS in their free states (A and C) and in complex with N-NTD (B and D) over the 100 ns simulations for the 25 MD replicas (runs) is shown. The plot takes into consideration the canonical WC basepairing, which represents the majority of hydrogen bonds (18 for dsNS and 16 for dsTRS), and noncanonical transient hydrogen bonds. The color bar denotes the correspondence between the color code and the number of RNA-RNA hydrogen bonds.

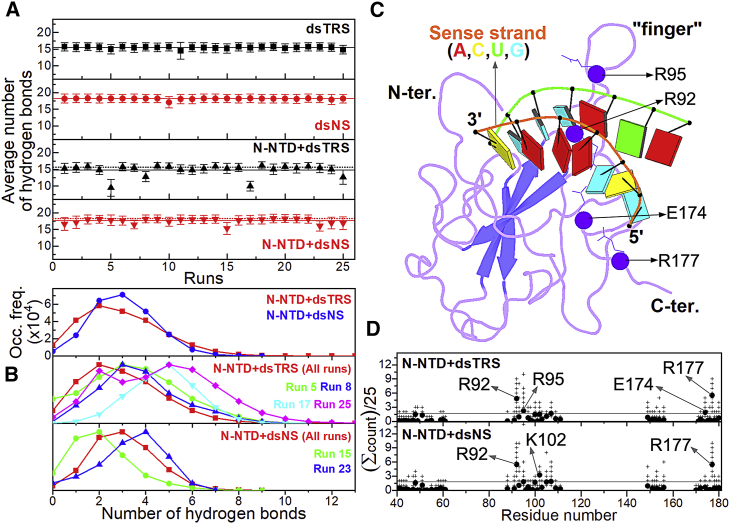
We also performed a quantitative analysis of WC basepairing by calculating the average number of RNA-RNA hydrogen bonds throughout the 100 ns MD simulations for each of the 25 replicas. For the free dsRNAs, the average numbers of RNA-RNA hydrogen bonds were constant for the 25 runs (Fig. 3 A) with an overall average value of 18.2 ± 0.2 and 15.5 ± 0.3 for dsNS and dsTRS, respectively. It is worth noting that the expected value of WC hydrogen bonds for dsNS and dsTRS are 18 and 16, respectively, and that the MD simulations reproduced the dynamic break-and-formation fluctuations of WC hydrogen bonds for free dsRNAs.

Figure 3.

Analysis of the RNA-RNA and protein-RNA hydrogen bonds. (A) The average number of RNA-RNA hydrogen bonds between the sense and antisense strands of dsNS (red) and dsTRS (black) in their free states (squares and circles) and in complex with N-NTD (up and down triangles, respectively) for each of the 25 replicas of 100 ns MD simulation. The black and red solid lines denote the overall average values for the 25 runs, which are also presented numerically with their respective SDs. The dotted line shows the overall average values for the 25 runs for the free dsRNA. The standard deviation along the MD simulation for each replica is denoted by the error bars. (B, top) Distribution of the occurrence frequency of the number of hydrogen bonds between the nitrogenous bases of dsRNA (dsTRS in red and dsNS in blue) and N-NTD for the 25 replicas along the 100 ns MD simulations. (Middle) Normalized distribution of occurrence frequency of the number of protein-nitrogenous base hydrogen bonds for all 25 replicas (red) and runs 5 (green), 8 (blue), 17 (cyan), and 25 (magenta) of the N-NTD/dsTRS complex. (Bottom) Normalized distribution of the number of protein-nitrogenous base hydrogen bonds for all 25 replicas (red) and runs 15 (green) and 23 (blue) of the N-NTD/dsNS complex. (C) Structural model of the N-NTD/dsTRS complex representative of the MD simulation for run 5. The protein is shown in a purple cartoon, and dsTRS is denoted as a ribbon model with nitrogenous bases and basepairing as colored squares and rectangles, respectively. The color of the squares corresponds to the type of nitrogenous base, namely A: red, C: yellow, U: cyan, and G: green, and the rectangles refer to the nitrogenous base color of the dsRNA sense strand. (D) Average counts per replica of protein-RNA hydrogen bonds with percentage of persistence higher than 10% as a function of the residue number (solid circle). The crosses show the counts for each replica. The horizontal line shows the threshold of the average counts averaged over all residues plus one SD. To see this figure in color, go online.

For most runs, the behavior of N-NTD-bound dsRNAs was similar to that of their free states, in which dynamic break-and-formation fluctuations of the RNA-RNA hydrogen bonds were observed. In the case of dsTRSs, there was a significant decrease in the average number of RNA-RNA hydrogen bonds for the runs 5, 8, 17, and 25 due to a long-lasting break of these bonds over 100 ns simulations, which resulted in partial (runs 8, 17, and 25) or total (run 5) RNA strand separation. For dsNS, runs 15 and 23 also showed a long-lasting break of RNA-RNA hydrogen bonds along the 100 ns MD simulations, leading to a partial RNA strand separation (Fig. 3 A). The N-NTD-bound dsTRS showed more events of partial and total strand separation than the protein-bound dsNS. Fig. 3 B shows a total separation event of the WC basepairing observed in run 5 for dsTRS, whereas a similar behavior with partial strand separation occurred in runs 8, 17, and 25 (Fig. S12). For the runs with only transient breaks of RNA-RNA hydrogen bonds (Fig. S13), the presence of N-NTD also promoted more pronounced dynamic break-and-formation fluctuations of these hydrogen bonds. Excluding the runs with long-lasting breaks of WC hydrogen bonds, we calculated the overall average number of RNA-RNA hydrogen bonds of 17.6 ± 0.8 and 15.5 ± 0.4 for the N-NTD-bound states of the dsNS and dsTRS, respectively. Note that increased dynamic break-and-formation fluctuations were more noticeable for dsNS.

We also analyzed the protein-RNA interaction along the MD simulations. The hydrogen bonds formed between the nitrogenous bases of dsRNA and N-NTD exhibited a transient nature. For most runs, these transient interactions displayed periods with a high number of protein-nitrogenous base hydrogen bonds (up to 13 for dsTRS and up to 9 for dsNS), followed by periods with no hydrogen bonds. These periods are typically of tens of nanoseconds (Fig. S14). To quantify the presence of protein-nitrogenous base hydrogen bonds along the 100 ns MD simulations, we analyzed the distribution of their frequency of occurrence. When all 25 replicas are considered, the distribution plot showed the highest occurrence of two hydrogen bonds for N-NTD/dsTRS and three for N-NTD/dsNS (Fig. 3 B, top). This can be explained by the fact that the dsNS has more hydrogen bond-forming sites (acceptor and donor) than the dsTRS. The distribution plot for the N-NTD/dsNS complex is more symmetric in reference to the maximal occurrence frequency, whereas the plot for the N-NTD/dsTRS complex is asymmetric, leaning toward the occurrence of a higher number of protein-nitrogenous base hydrogen bonds. This profile aspect indicates that the transient nature of these interactions is more pronounced for the simulations of the N-NTD-bound dsTRS than dsNS (Fig. 3 B, top).

Next, we analyzed the distribution plots of individual replicas for which we observed destabilization of RNA-RNA hydrogen bonds of the dsRNAs. For dsTRS, runs 5, 8, 17, and 25 displayed distribution curves with higher occurrence frequencies of frames containing a higher number of protein-nitrogenous base hydrogen bonds when compared to the curve with all replicas (shifted to the right, Fig. 3 B, middle). In contrast, replicas 15 and 23 for dsNS showed a conflicting behavior (Fig. 3 B, bottom). Run 15 exhibited a distribution plot with higher occurrence frequencies of frames with a lower number of protein-nitrogenous base hydrogen bonds (shifted to the left) when compared to the entire distribution, considering all 25 replicas, whereas run 23 displayed an opposite behavior (shifted to the right). These results suggest that the breaking down of RNA-RNA hydrogen bonds in runs 5, 8, 17, and 25 for dsTRS possibly leads to an increase in occurrence frequencies of a higher number of protein-nitrogenous base hydrogen bonds. In contrast, the same cannot be suggested for dsNS. However, we cannot claim that the formation of protein-RNA hydrogen bonds between N-NTD and the nitrogenous bases of TRSs (single strand and/or duplex) is replacing the RNA-RNA hydrogen bonds of the dsRNA because we observed transient increases in occurrence frequencies of a higher number of protein-nitrogenous base hydrogen bonds for runs without a significant break in the RNA-RNA hydrogen bonds (Figs. S15 and S16). Nevertheless, this last observation indicates that the transient protein-nitrogenous base hydrogen bonds can compete with WC basepairing and consequently increase the propensity of dsRNA destabilization.

To identify the main amino acid residues participating in the hydrogen bonds between N-NTD and all atoms of dsRNAs, we counted the number of protein-RNA hydrogen bonds with a percentage of persistence higher than 10% for the 25 runs (Tables S1–S50) and plotted the average count as a function of the residue number (Fig. 3 D). Most counts were observed for the N-terminal region (residues 40–61), the finger (β2-β3 loop, residues 88–111), α2-β5 loop (residues 149–156), and the β5 and C-terminal region (residues 170–180). The identified regions are the same observed in the CSP titration by NMR, the only N-NTD-dsRNA data available experimentally (16). For dsTRS, a significant count (higher than average plus standard deviation (SD)) of protein-RNA hydrogen bonds was observed for R92, R95, E174, and R177. Most of these hydrogen bonds involving arginine residues occur with dsRNA phosphate groups, making them also a salt bridge. We also observed a minor count of protein-RNA hydrogen bonds between the arginine residues and the ribose. The significant count for E174 is remarkable because it is unique for dsTRS, and it is characterized by the formation of protein-RNA hydrogen bonds with the nitrogenous bases. For dsNS, significant counts were identified for R92, K102, and R177. As for dsTRS, R92 and R177 are involved in hydrogen bonds with dsRNA phosphate groups. In contrast, K102 makes hydrogen bonds with the nitrogenous base. We also counted the protein-RNA hydrogen bonds from the perspective of the dsRNAs. Interestingly, the higher counts were observed for the 5′-end of the negative-sense strand (Fig. S17).

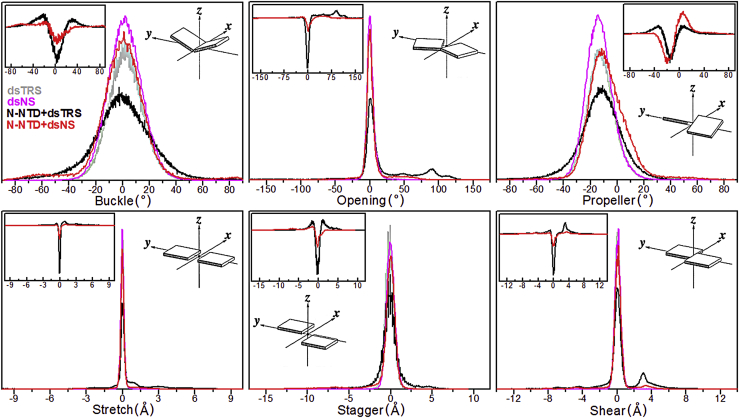
To further understand the stability of the WC basepairing for N-NTD-bound dsNS and dsTRS, we used the do_x3dna tool (31) along with the 3DNA package (32) to analyze the local basepair parameters (angles: buckle, opening, and propeller; distances: stretch, stagger, and shear) from the MD simulations. Fig. 4 shows the population distributions of these local basepair parameters for runs 5, 8, 17, and 25 (for dsTRS), and runs 15 and 23 (for dsNS), both free and complexed with N-NTD, as well as the difference between the distributions of the free and N-NTD-bound states. These replicas were selected based on the results presented in Fig. 3 A, as their average numbers of RNA-RNA hydrogen bonds were significantly lower than the overall average values. From Fig. 4, it is clear that N-NTD perturbs the population distributions of the local basepair parameters of dsRNAs, most notably for dsTRS.

Figure 4.

Normalized population distributions of the local basepair parameters. Normalized population distributions of local basepair parameters (angles: buckle, opening, and propeller; distances: stretch, stagger, and shear) for runs 5, 8, 17, and 25 of dsTRS and runs 15 and 23 of dsNS in their free form (dsTRS in light gray and dsNS in magenta, respectively) and complexed with N-NTD are shown (N-NTD + dsTRS in black and N-NTD + dsNS in red). The normalization was defined with respect to the highest distribution curse for each basepair parameter. The plot insets correspond to the difference between the population distributions of N-NTD-bound dsRNA minus its free state for dsNS (red) and dsTRS (black). The scheme insets illustrate the geometrical definition of each local basepair parameter (41). To see this figure in color, go online.

The distribution of dsTRS buckle angles revealed a reduction in the population at ∼0° (basepairing planarity) and increase in subpopulations at ∼±30° due to the interaction with the N-NTD. This can be clearly seen by the difference in distributions between the N-NTD-bound and free states (inset in buckle plot of Fig. 4). A similar but less intense effect was observed for the population distribution of dsNS buckle angles. For the opening angles, one can note a higher perturbation of population distribution for dsTRS than for dsNS upon binding to N-NTD. For dsTRS, the opening angle population at ∼0° (basepairing closure) decreased significantly, whereas subpopulations emerged for angles higher than 50°, remarkably at ∼90°. The distribution of the propeller angles showed a reduction in the equilibrium populations at −12.6 and −13.8° for dsTRS and dsNS, respectively, after interaction with N-NTD, with an increase in subpopulations around 0° (less twist), which was significantly larger for dsNS. However, we observed an extra subpopulation of propeller angles at approximately −30° for dsTRS after binding to N-NTD, which was not seen for dsNS (see the inset in propeller plot in Fig. 4).

Investigation of the stretch, stagger, and shear distances for dsNS and dsTRS showed that the equilibrium population at ∼0 Å decreased for both dsRNAs as a result of N-NTD binding. However, this reduction is more drastic for dsTRS than dsNS, as can be seen in the inset for the respective plots in Fig. 4. In addition to this reduction effect, we also verified that N-NTD-bound dsTRS exhibited clear subpopulations at ∼1, ∼±1.5, and ∼3 Å for the stretch, stagger, and shear distances, respectively.

N-NTD-induced perturbations in the population distributions of angle and distance basepair parameters (buckle, opening, propeller, stretch, stagger, and shear) of dsRNAs for the selected replicates (runs 5, 8, 17, and 25 for dsTRS and runs 15 and 23 for dsNS) indicate that both dsRNAs suffered WC basepairing destabilization upon N-NTD binding. However, this destabilization effect is more evident for the N-NTD/dsTRS complex, as the above analysis of angle and distance parameters suggests an impairment of basepairing planarity accompanied by an increase in the separation between the nitrogenous bases of the complementary dsRNA strands upon N-NTD binding. This result agrees well with the analysis of the RNA-RNA hydrogen bonds formed between the sense and antisense dsRNA strands (see Fig. 3 A). It is worth mentioning that, even though basepairing destabilization was more pronounced for dsTRS than dsNS, dsNS suffered a greater reduction in the RNA duplex twist, as suggested by the N-NTD-induced perturbation of the propeller angles.

Conformational flexibility of free and dsRNA-bound N-NTD

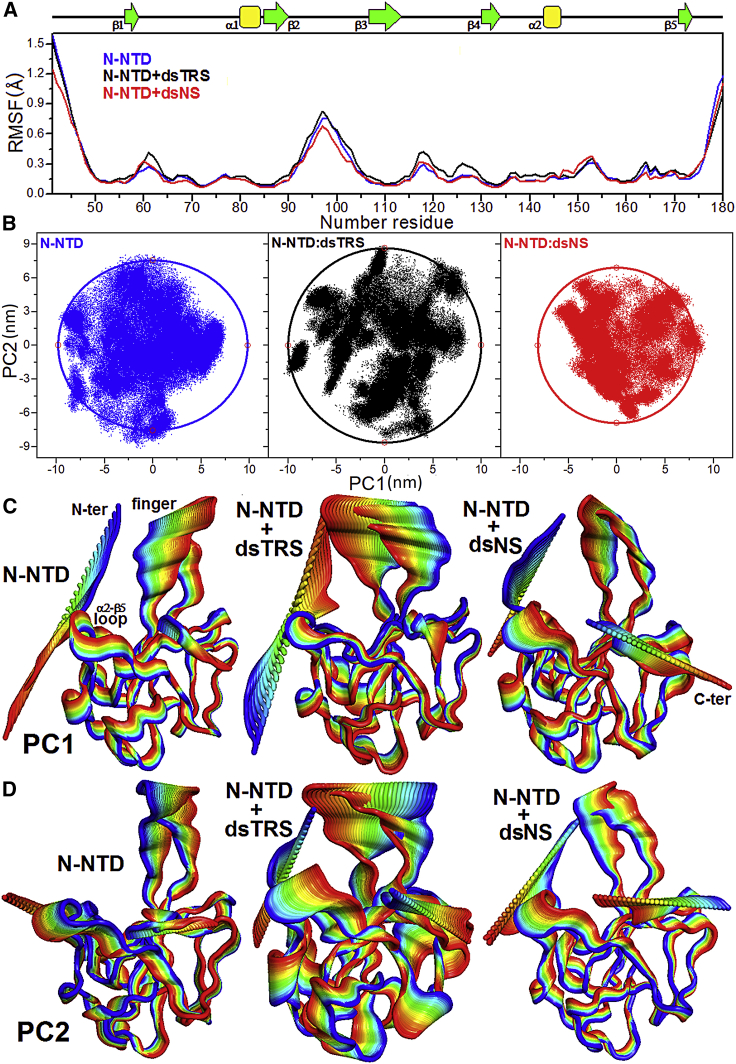
To further understand how dsRNA binding changes the conformational dynamics of N-NTD, we concatenated the last 50 ns (stable RMSD values) of the 25 replicas for both free and dsRNA-bound N-NTD and performed an analysis of RMSF and PCA of the MD trajectories (Fig. 5). Fig. 5 A shows that both free and dsRNA-bound N-NTD exhibited significantly increased values of RMSF for residues in the N- and C-terminal regions as well as the β2-β3 loop (finger), suggesting large conformational flexibility. In addition to these regions, the N-terminal portions of the β1-Δ1 loop (residues 58–65) and β3-β4 loop are especially noteworthy. The β1-Δ1 and β3-β4 loops displayed an increase in their dynamics in the N-NTD/dsTRS complex when compared to free N-NTD and N-NTD/dsNS complex, even though they are not directly involved in the interaction. The conformational flexibility of the basic finger is similar for free and dsTRS-bound N-NTD, with a tendency of a slight gain in flexibility for the dsTRS-bound N-NTD, whereas dsNS-bound N-NTD became more rigid. In general, we observed an increase in flexibility of N-NTD loop regions when bound to dsTRS. Remarkably, conformational dynamics of the N-NTD/dsNS complex was similar to that of the free state, with the exception of the N-terminal region and basic finger, in which conformational dynamics decreased upon dsNS binding.

Figure 5.

Analysis of N-NTD conformational flexibility in its free and dsRNA-bound states. (A) RMSF values as a function of residue number for N-NTD in its free state (blue line) and complexed with either dsTRS (black) or dsNS (red). The secondary structures along the sequence are indicated at the top. (B) PCA scatter plots PC1 and PC2 for free N-NTD (blue dots, left) and for N-NTD complexed with either TRS (black dots, middle) or NS (red dots, right) dsRNAs. The extent of the conformational space for each scatter plot was measured by fitting an elliptical shell (solid lines) that contains 95% of the density. (C and D) Motions filtered from the eigenvectors of PC1 (C) and PC2 (D) for the dynamics data of N-NTD in its free form and complexed with either dsTRS or dsNS. The motion direction is indicated by the color variation from blue to red. To perform the RMSF and PCA calculations, the last 50 ns of trajectories of the 25 replicates were concatenated for each of the molecular systems (free or dsRNA-bound N-NTD), resulting in MD simulations of 1.25 μs. To see this figure in color, go online.

The PCA scatter plot generated for free and dsRNA-bound N-NTD revealed a significant difference between the free domain and the complexes, as evident from the characteristic structures plotted along the direction of the first and second principal components (PC1 and PC2, respectively). 25 replicas of the MD simulations using different seeds of the random number generator provided a great exploration of the conformational space for free and dsRNA-bound N-NTD, resulting in trajectories of 1.25 μs. We analyzed the conformational space by fitting an elliptical shell that contains 95% (confidence) of the density for each scatter plot. The extent of the conformational space is proportional to area (S_el) of the elliptical shell. Despite the already wide conformational space of N-NTD (S_el = 929 nm²), the interaction with dsTRS made it even wider (S_el = 1083 nm²), whereas binding to dsNS made it more constrained (S_el = 708 nm²; Fig. 5 B). We also analyzed the conformational space for trajectories of all 25 replicas of free N-NTD concatenated with its bound states (N-NTD/dsNS and N-NTD/dsTRS). By doing so, we guaranteed that the eigenvectors are the same used for all systems. The PCA scatter plots from this last analysis (Fig. S18) showed a similar profile with a wide conformational space for free NTD (S_el = 833 nm²), even wider for dsTRS-bound N-NTD (S_el = 1002 nm²), and constrained for dsNS-bound N-NTD (S_el = 616 nm²).

An investigation of the motions filtered from the eigenvectors of PC1 and PC2 revealed that dsTRS-bound N-NTD exhibited the largest conformational dynamics when compared to free and dsNS-bound N-NTD, which were similar (Fig. 5, C and D). We highlight that the most evident motions took place in the N- and C-termini as well as the basic finger (β2-β3 loop) for both free and dsRNA-bound N-NTD. However, the eigenvectors of PC1 and PC2 for the N-NTD/dsTRS complex suggested a wide motion between the basic finger and the Δ2-β5 loop located at the palm, similar to a tweezer. Interestingly, this tweezer-like motion was intrinsic to the residues located at the dsRNA-binding cleft in N-NTD (Fig. 1 A).

Our results of conformational flexibility from RMSF and PCA for free and dsRNA-bound N-NTD corroborated each other and suggest a significant contribution of the N- and C-termini and the basic finger (β2-β3 loop) to N-NTD dynamics. They also revealed that N-NTD interaction with dsTRS led to a general gain in protein conformational flexibility when compared to its free state. We suggest that this flexibility gain of dsTRS-bound N-NTD over 25 replicas of concatenated simulations may be a key structural factor to promote dsTRS WC basepairing destabilization upon N-NTD binding, as determined by the break of RNA-RNA hydrogen bonds (Figure 2, Figure 3 A) and perturbation of the local basepair parameters (Fig. 4).

Modeling the dsRNA melting activity

Based on the MD simulations performed herein, we suggest that one molecule of N-NTD is enough to destabilize the WC basepairing of one RNA duplex, which is possibly the first step for dsRNA melting. To investigate the stoichiometry of the dsRNA melting, we simulated the experimental data obtained by Grossoehme et al. (10) using two contrasting kinetic models: 1) assuming that melting activity is the result of binding of one N-NTD to one dsRNA and 2) assuming that two N-NTD molecules bind to one dsRNA (sandwich model). The simulation strategy is detailed in the Supporting materials and methods.

In their work, Grossoehme et al. (10) measured dsRNA melting activity of N-NTD using fluorescent resonance energy transfer (FRET) from 5′ Cy3-labeled sense RNA strand (TRS) and 3′ Cy5-labeled antisense RNA strand (cTRS). In those experiments, the highest FRET efficiency (∼0.9) was obtained for dsRNA in the absence of N-NTD. Increasing the N-NTD concentration led to the dsRNA melting curve, which is characterized by an exponential decay of FRET efficiency as a function of N-NTD concentration. The melting curves reached either zero for an N-NTD construct that contains the C-terminal serine/arginine-rich motif or a plateau for N-NTD itself (10).

Because the FRET efficiency is a measure of the molar fraction of dsRNA, in the simulated kinetic models presented here, we report the molar fraction of dsRNA as a function of N-NTD concentration, simulating the dsRNA melting curve (Fig. 6). We used the elementary rate constants for individual chemical steps to produce an absolute time base (Fig. 6 A). The starting condition mimics exactly the experimental condition, varying the concentration of N-NTD over 50 nM dsRNA (dsTRS). The predictions were validated by direct comparison to the experimental data (10).

Figure 6.

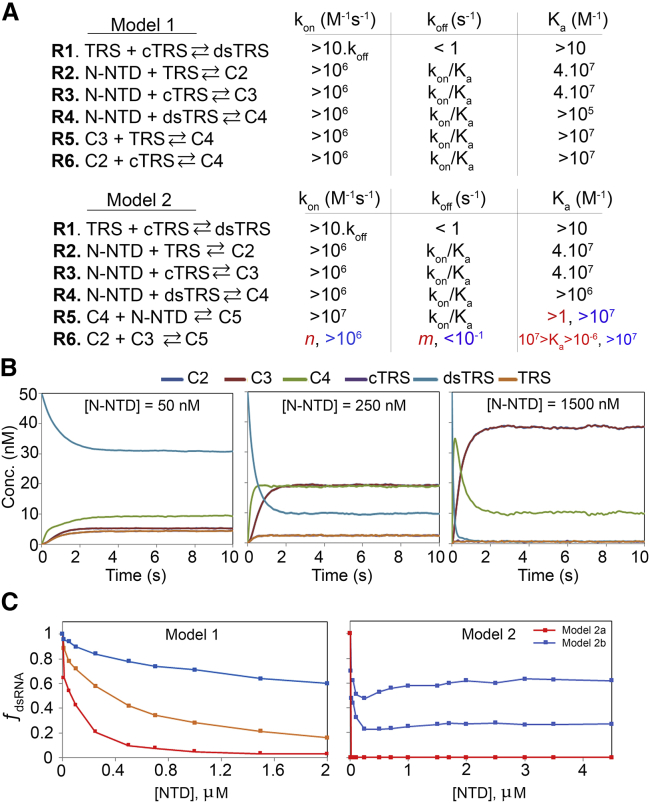
Simulation of the kinetics of dsRNA-melting activity. (A) Reactions R1–R6 for models 1 and 2. Model 1 implies the melting activity with stoichiometry of 1 N-NTD for 1 dsRNA (C4), and model 2 implies the formation of a sandwich with a stoichiometry two N-NTDs and one dsRNA (C5). At the right of each reaction are the ranges of k_on, k_off, and K_a in which the simulation produces a dsRNA-melting curve, respecting the boundaries described in the text. For reaction R6 of model 2, the color code refers to the color of the simulated melting curves for model 2. (B) Illustration of the kinetics of dsRNA-melting for model 1 in three different concentrations of N-NTD (50, 250, and 1500 nM). (C) Simulated dsRNA-melting curve for model 1 and 2. We used the starting concentration of 50 nM of dsRNA for all simulations. For model 1 simulations, we used the following reaction rates: k_on (R1) = 4 × 10⁻¹ M⁻¹ s⁻¹ and k_off = 8 × 10⁻⁴ s⁻¹; k_on (R2, R3) = 4 × 10⁷ M⁻¹ s⁻¹ and k_off = 1 s⁻¹; k_on (R4) = 1 × 10⁷ M⁻¹ s⁻¹ and k_off = 1 s⁻¹; k_on (R5, R6) = 4 × 10⁷ M⁻¹ s⁻¹ and k_off = 1 s⁻¹ (red); k_on (R5, R6) = 4 × 10⁸ M⁻¹ s⁻¹ and k_off = 1 s⁻¹ (orange); and k_on (R5, R6) = 6 × 10⁸ M⁻¹ s⁻¹ and k_off = 1 × 10⁻¹ s⁻¹ (blue). For model 2 simulations, we used the following reaction rates: k_on (R1) = 4 × 10⁻¹ M⁻¹ s⁻¹ and k_off = 8 × 10⁻⁴ s⁻¹; k_on (R2, R3) = 4 × 10⁷ M⁻¹ s⁻¹ and k_off = 1 s⁻¹; k_on (R4) = 1 × 10⁷ M⁻¹ s⁻¹ and k_off = 1 s⁻¹; k_on (R5) = 1 × 10⁸ M⁻¹ s⁻¹ and k_off = 1 s⁻¹ (red); k_on (R6) = 1 × 10⁻¹ M⁻¹ s⁻¹ and k_off = 1 × 10⁸ s⁻¹ (red); k_on (R6) = 1 × 10⁶ M⁻¹ s⁻¹ and k_off = 1 × 10⁻¹ s⁻¹ (blue, bottom); and k_on (R6) = 1 × 10⁷ M⁻¹ s⁻¹ and k_off = 1 × 10⁻¹ s⁻¹ (blue, top). To see this figure in color, go online.

To simulate the melting curve, we had to constrain the kinetic space, which is large because each model is composed of six reactions and 12 individual rate constants, assuming the following boundaries: (B1) the kinetic model must be complete, complying with all possible reactions for a given mechanism; (B2) the presence of N-NTD must lead to catalysis, with the melting of dsRNA being faster than the annealing reaction; (B3) the equilibrium of the annealing is shifted toward the dsRNA; and (B4) the equilibrium for the melting activity must be reached in less than 133 s (10).

The criterion for choosing the rate constants for the annealing reaction (R1; Fig. 6) was that it must be significantly slower than the melting activity (catalysis). To yield an equilibrium shifted toward the dsRNA, we used k_on = 4 × 10⁻¹ M⁻¹ ⋅ s⁻¹, which is true below the melting temperature of the dsRNA, values measured for the almost inactive mutant Y127A (10). Any values of k_off < 1 s⁻¹, with an association constant K_a, gives the same molar fraction of dsRNA. We constrained the binding reactions R2 and R3 of N-NTD to the sense (TRS) and antisense (cTRS) single-stranded RNA (ssRNA) (Fig. 6 A) based on the published experimental values for these association constants (10,42). For dsRNA (dsTRS) binding, there were no experimental data to constrain the simulation. However, simulations unambiguously showed that K_a for reaction R4 must be of the same order of that for ssRNAs, leading to the allowed ranges depicted in Fig. 6 A. We also determined k_on based on the simulations.

The simulated melting curves for model 1 resembled the near-exponential decay observed experimentally (Figs. 6 C, left, and S19). Remarkably, melting curves that either decayed to zero or reached a plateau were observed experimentally. There are no experimental data available to constrain reactions R5 and R6, but the simulations showed that they are tightly related to reactions R2 and R3, being both K_a and k_off of the same order of magnitude for reactions R2 and R3 (Fig. S19). Interestingly, when k_off of reactions R5 and R6 were larger than k_off for reactions R2 and R3, we observed a plateau in the exponential decay of the dsRNA melting curve (Fig. 6 C).

We also evaluated the kinetic model 2, in which a sandwich of 2 N-NTD and 1 dsRNA is necessary for the melting reaction. This stoichiometry for N-NTD melting activity should be considered, as the full-length N protein is a biologically functional dimer and recognition of the TRS duplex by the two N-NTD subunits for the melting activity is possible. In this model, a sandwich of two N-NTDs and one dsRNA is formed, and the final products are each N-NTD bound to TRS and cTRS ssRNA. To build a kinetic model that would exclusively produce ssRNA from the sandwiched dsRNA, we replaced reactions R5 and R6 of kinetic model 1. In this new model, reaction R5 forms the sandwiched dsRNA (C5; Fig. 6 A) and reaction R6 is the dissociation of C5 into the ssRNA-bound N-NTDs (C2 and C3; Fig. 6 A). To simulate N-NTD melting activity considering model 2, we used the same boundaries described earlier (B1, B2, B3, and B4), with reactions from R1 to R4 having almost the same constraints described for the model 1. We scanned all the kinetic space that led to the catalysis of melting activity and observed two contrasting situations. The first is when reaction R6 equilibrium is between 10⁻⁶ and 10⁷ M⁻¹, always having the dissociated forms C2 and C3 available and making the melting curve very stiff (model 2a). The second is the opposite situation, where equilibrium is skewed toward the sandwich state (C5) with K_a > 10⁷ M⁻¹ (model 2b). Fig. 6 C illustrates the melting curves obtained for the two situations.

Model 2a is characterized for the high efficiency in the dissociation of the dsRNA, k_on and k_off can assume any value (n and m, Fig. 6 A) as long as K_a is between 10⁻⁶ and 10⁷ M⁻¹. All simulated conditions led to the curve in red (Fig. 6 C), in which the minimal amount of N-NTD (10 nM) led to complete dissociation of the dsRNA (molar fraction of zero). Fig. S20 illustrates all the simulated boundaries. Note that for model 2a, there is never an accumulation of C5 (Fig. S20).

Model 2b corresponds to when the equilibrium of reaction R6 is shifted toward C5 (K_a > 10⁷ M⁻¹). Fig. S21 illustrates the reaction boundaries. In this situation, we were able to observe a melting curve (Fig. 6 C, blue) with a near-exponential decay at a low concentration of N-NTD and a near-exponential rise at higher concentrations of N-NTD. This behavior is explained by the accumulation of C5 and N-NTD concentration-dependent mutual compensation of C5 and dsRNA. None of the situations simulated for model 2 are parallel to the experimental observation.

Discussion

In this work, we used computational simulations to unravel the triggering event for the dsRNA melting activity of the isolated SARS-CoV-2 N-NTD. Our MD simulations showed the first steps that occurred in the nanosecond timescale. During interaction with dsRNA, protein dynamics drives the destabilization of hydrogen bonds involved in the WC dsRNA basepairing, probably in a 1:1 stoichiometry (N-NTD/dsRNA). We also showed that the capacity of the N-NTD to promote more permanent breaking events of the WC basepairing was sequence specific, being more efficient for dsTRS (5′-UCUAAAC-3′ and 5′-AGAUUUG-3′; sense and antisense) than for a nonspecific (dsNS) sequence (5′-CACUGAC-3′ and 5′-GUCAGUG-3′; sense and antisense). The MD simulation did not give information on the melting activity, which is an event that occurs in seconds. We probed the destabilization of the RNA duplex, which occurred in nanoseconds and only in the presence of N-NTD. To further explore the N-NTD/dsRNA stoichiometry, we constructed kinetic models based on the available experimental data (10). Remarkably, the model using a 1:1 stoichiometry greatly fits the experimental data, reinforcing the model we hypothesize here.

The strategy of performing 25 100 ns MD simulations with the same starting structure but different seeds of the random number generator provided a large sampling of conformational space of each molecular system (N-NTD, dsRNAs, and N-NTD/dsRNA complexes). This set of theoretical data ensured a significant result showing that N-NTD destabilizes the WC basepairing, especially for dsTRS. Specifically, for the dsTRS, we observed an increase in formation of hydrogen bonds between N-NTD and the nitrogenous bases of each RNA strand, followed by a decrease in RNA-RNA hydrogen bonds between the dsRNA strands. The results also revealed that the rigid-body geometric parameters of the dsTRS WC basepairing were significantly changed because of N-NTD binding.

To map the main protein-RNA hydrogen bonds and salt bridges, we counted the most prevalent protein-RNA hydrogen bonds. The mapped regions are consistent with available experimental data of NMR titration with dsRNA (16). The main protein-RNA interactions are mediated by arginine residues, mainly at the finger and the C-terminal region. Although these regions are flexible (as observed from PCA), many hydrogen bonds were persistent and displayed a high percentage of persistency. R92 (finger) and R177 (C-terminal) form hydrogen bonds with the RNA phosphates, which are also persistent salt bridges for both dsTRS and dsNS. For dsTRS, we observed persistent hydrogen bonds and salt bridges with the RNA phosphates involving R95 and persistent hydrogen bonds with E174. The presence of hydrogen bonds involving E174 is remarkable because it involves a negatively charged residue and an interaction with a nitrogenous base. E174 may be a key residue responsible for the difference in N-NTD-induced destabilization of dsTRS and dsNS.

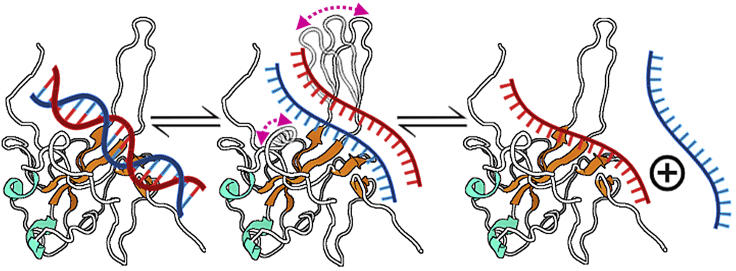
One notable N-NTD structural feature is the presence of a significant number of loops; only 32 out of 140 residues are involved in secondary structure (16,43). This is a typical feature of a dynamic protein. In fact, our results revealed that the N-NTD is a plastic protein, with the N- and C-termini and the β2-β3 loop (finger) as the most prominent dynamic regions. For the N-NTD/dsTRS interaction, a remarkable tweezer-like motion between the finger and the Δ2-β5 loop might be related to the sequence-specific WC basepairing destabilization. This information goes along with the observed transient protein-RNA hydrogen bonds within the timescale of tens of nanoseconds. Therefore, we hypothesized that after the formation of the N-NTD/dsTRS complex, the tweezer-like motion resulted from intrinsic protein dynamics might promote a steric effect causing a “compaction pressure” on the dsRNA strands. This might expose residues from the bottom of the palm (finger/Δ2-β5 cleft), allowing their interaction with the bases and leading to the destabilization of the WC basepairing (Fig. 7).

Figure 7.

Summary of the proposed mechanism for dsRNA melting activity of N-NTD. The binding of one N-NTD to one dsRNA triggers the destabilization of WC basepairing of the dsRNA and consequently exposes the nitrogenous bases for interacting directly with the N-NTD. We suggest that this activity is a consequence of intrinsic dynamics of N-NTD, especially because of the tweezer-like motion between β2-β3 (finger) and Δ2-β5 loops. The protein is denoted as cartoon with the helix-Δ and β-strand secondary structures colored in cyan and orange, respectively. The dsRNA is showed as a line model with the complementary strands colored in red and blue. The tweezer-like motion between the finger and Δ2-β5 loop is indicated by bidirectional arrows colored in magenta. To see this figure in color, go online.

The naturally occurring canonical RNA double helices are short (not larger than 12 nucleotides in length), possibly linked to the tendency of RNAs to form tertiary structures because of their intrinsic mechanic properties. The extra 2′ hydroxyl group provides many possibilities of noncanonical non-WC basepairs (37). dsRNA tends to unwind upon elongation in a sequence-dependent manner. Alternating purine-pyrimidine (AC, GC, AU, GU) and pyrimidine-purine (CA, CG, UA, UC) are softer than purine-purine (AA, GG) sequences (38). We may speculate that the TRS specific sequence used here (5′-UCUAAAC-3′) contains the AAA motif that is hard, and consequently, the force-induced unwinding is more difficult. The regions flanking the consensus TRS are softer and prompter to bend. Consequently, the biologically relevant dsRNA presented to the N-NTD is probably short.

To confirm the model that emerged from the MD simulations, in which the dynamics of only one molecule of N-NTD was enough to trigger the dsRNA destabilization, we constructed kinetic models considering two possible scenarios: a stoichiometry of 1:1 or 2:1 for N-NTD and dsRNA. The 2:1 stoichiometry is more intuitive because N protein is dimeric in solution (44). However, the 1:1 stoichiometry produced dsRNA melting curves compatible with the available experimental data (10). It is important to mention that the simulations of the kinetic models were only possible by constraining the kinetic space, as the number of degrees of freedom for six reactions is quite large. This constrained kinetic space was created by imposing boundaries to the system. These simulations brought two important conclusions: 1) the 1:1 stoichiometry is enough to explain the experimental data and 2) the sandwich model 2 is less likely to occur because simulations produced more complex melting curves, which are different from the experimental data.

Model 1 agrees with the previously proposed stoichiometry for the melting activity (10), which described that the formation of a sandwich (model 2) in diluted solution with the isolated domain is unlikely. Grossoehme et al. (10) modeled the system with four reactions (R1, R2, R3, and R4) and concluded that for the melting activity to occur, K_a for R4 would be <1 M⁻¹, which suggests an almost absent interaction of the dsRNA with the N-NTD. We showed here that model 1 describes the melting curves, considering the affinity of the dsRNA similar to the ssRNAs, which is more compatible with recent experiments (16). These authors reported a binding affinity for the N-NTD/dsRNA complex in the range of micromolar, similar to the simulated conditions showed in Fig. 6.

Altogether, the results presented here support the idea that two N-NTDs of dimeric N protein would not be necessary to act on one dsRNA motif (dsTRS). Each N-NTD of the same dimer would work independently, leading to a gain in efficiency of full-length N when compared to the sandwich model. The observation that one N-NTD could be able to melt dsRNA opens two new, to our knowledge, avenues for the understanding of the role played by the N protein in the viral replication cycle. First, the two N-NTD arms of full-length N could bind to two different RNA sites, which could either be spatially or closely separated in the viral genome, making it possible to bridge and induce melting on two different regions in a cooperative manner. Second, if monomeric full-length protein is active, a regulatory event involving the dissociation of the N protein dimer should be considered. Indeed, for the N protein of bovine betacoronavirus, studies suggested that it acts as a bridge between distant motifs in the genome (45).

Author contributions

Í.P.C. performed the MD simulations and analysis. K.S. and F.C.L.A. modeled the kinetics of RNA melting and analysis. A.S.P., A.T.D.P., F.C.L.A., and Í.P.C. participated in the experimental design and analysis. All authors contributed to the writing.

Editor: Chris Chipot.

Supporting citations

References (46, 47, 48) can be found in the Supporting material.