Abstract
Steel fiber reinforced concrete exhibits ductility. This ductility behavior enables redistribution of moment between the negative and positive moment zones in continuous SFRC beams. The sectional capacity of an SFRC continuous beam was determined using the moment-curvature response, the ductility of the member using the moment-rotation response, and the moment redistribution behavior using the moment-rotation response. The theoretical moment-curvature response was calculated from the stress-strain response for 0 % (control), 0.5 %, 0.75 %, and 1.5 % SFRC member which served the basis for the defined moment-rotation behavior and FEA. A five-point bending test was conducted on a two-span beam using a constitutive material model in the FEA software package, Abaqus/CAE. The concrete damage plasticity (CDP) model was used to conduct a displacement-controlled analysis on the fully integrated 3D hexahedral element (C3D8). The numerical study revealed that the flexural behavior, bending capacity, rotation capacity, and ductility of the 0.5 %, 0.75 %, and 1.5 % SFRC beams were significantly enhanced than the 0 % SFRC beam. However, as steel fiber volume increased, the quantity of moment redistribution in the SFRC beam decreased. The amount of moment redistribution obtained was 21.8 % for 0 %, 19 % for 0.5 %, 18.1 % for 0.75 %, and 13.9 % for 1.5 % SFRC.
Keywords: Steel fiber reinforced concrete, Moment redistribution, Flexural behavior, Ductility, FEA, Beam
Steel fiber reinforced concrete, Moment redistribution, Flexural behavior, Ductility, FEA, Beam.
1. Introduction
Steel fiber reinforced concrete is a category of reinforced concrete that has been reinforced with steel fiber [1, 2]. This process increases the tensile strength at the first crack and ultimate crack, which is regarded as a measure of fracture resistance and cracks propagation resistance [1].
Compared to normal concrete, the SFRC exhibits numerous exceptional dynamic properties, including increased explosion and penetrating resistance [3]. When employed in structural applications, SFRC advances resistance to impact loading and resists material disintegration [3].
The SFRC enhanced the elastic deformation [4], flexural toughness and energy absorption capacity [3, 4, 5, 6, 7], ductility [4, 6, 7, 8], post-cracking tensile resistance [3, 5, 6, 9, 10], shear and torsional strength [6], fatigue strength [6], and ultimate flexural strength capacity [4, 6, 10, 11] of the structural member.
According to [5] in the case of the SFRC, the contribution of fibers is most noticeable in the post-peak region, where a comparatively less steep decaying stress-strain response describes the response.
Redistribution of the moment is an essential feature in structural engineering and tests the section's ability to sustain a constant moment while rotating and redistributing moment to the adjacent zone of the member at the same period [12]. The basic principle for the moment redistribution, as an analysis in continuous reinforced concrete beams, is that the demand rotation needed for plastic hinges to develop at the ends and midspans should be smaller than the plastic hinge or hinges rotational potential that first yields [13]. Using the principle of plastic hinge length, the rotational capacity in members could easily be transferred to section curvature strength [13].
In the design of statically indeterminate elements, the principle of moment redistribution is used to minimize the absolute magnitudes of moments in critical areas, maximize the potential of non-critical cross-sections, and simplify detail by encouraging a reduction in reinforcement ratios [14].
The redistribution of moments in plastic hinge regions depends on sufficient ductility [15, 16]. At regions of the maximum positive or negative moment, these plastic hinge regions develop and create a change in the elastic moment diagram. The usual effect is a decline in the maximum negative moment values in the support regions and an increase in the positive moment values in the support regions from the determined elastic analysis values [16].
The addition of steel fibers to reinforce concrete enhances ductility, plastic hinge formation before failure in continuous flexural members (beams) to redistribute the moments by forming rotations around boundary conditions. Consequently, using the advantages of the moment redistribution behavior of continuous beams, the designer can design the member beyond the elastic region to minimize the reinforcement needed.
The allowable number of moment redistribution is indicated in structural design codes for traditional reinforced concrete structures but not for SFRCs. These phenomena may significantly impact the structural design process for SFRC and a circumstance in which conventional steel is used in conjunction with steel fibers.
Since recent years, research on the influence of steel fibers on reinforced concrete elements has included both adverse analysis and experimental examination. This entails examining the effect of steel fiber inclusion on the fresh concrete's workability, mechanical properties (compressive strength, tensile or splitting strength, toughness, flexural strength, stress-strain response, modulus of elasticity, ultrasonic pulse velocity, energy absorption, durability properties, and so on), and ductility properties. Numerous studies used laboratory testing and finite element modeling to investigate the effect and behavior of SFRC on the structure's compressive and tensile strength, flexural strength, shear strength behavior, and moment redistribution. While substantial research is being undertaken on SFRC material, its use in structural systems has been extremely limited due to a lack of specifics on design techniques and the absence of a code allowing for the benefit of tensile contribution in SFRC elements.
The study aims to specify the sectional capacity, ductility, and moment redistribution behavior of SFRC of a continuous beam using numerical and FEA investigation. This study predicted the amount and behavior of sectional capacity, ductility, and moment redistribution for varying steel fiber volume for 0 %, 0.5 %, 0.75 %, and 1.5 % steel fibers using the result obtained from the experimental test conducted by [17]. Due to the difficulty of casting the continuous SFRC beam in the laboratory and the lack of available resources, the study employed FEA software, Abaqus/CAE, using a constitutive material model. This research was studied for developing design models to develop a codified approach for the utilization of SFRC for moment redistribution. Additionally, it advised designers and code writers for SFRC materials on the appropriateness of steel fibers in various conditions. The study examined solely the theoretical moment-curvature response, moment-rotation response, and amount of moment redistribution of two spans SRFC beam subjected to concentrated loading using five-point bending.
2. Materials and methods
2.1. Material properties
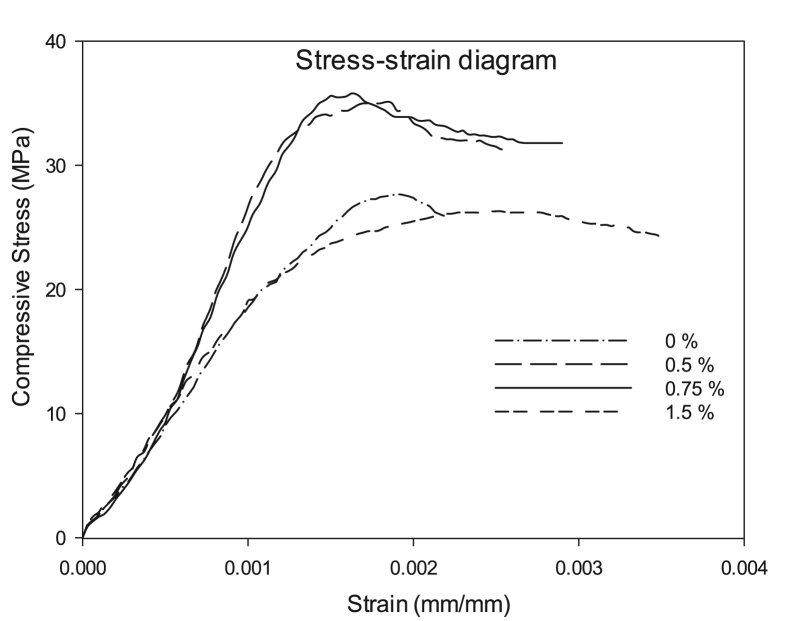
The experimental study result of stress-strain behavior (Figure 1) conducted by [17] on the effect of the addition of steel scrap to concrete on the mechanical properties was used to generate the moment-curvature response. The volume fraction (Vf) of steel scrap used as steel fiber considered by [17] was 0% (control), 0.5 %, 0.75 %, and 1.5 % in the analysis of sectional behavior and moment redistribution behavior. This volume fraction (Vf), which denotes the ratio of the volume of steel fibers in the section to the volume of concrete, has been used to express the quantity of steel fibers in the beam section. Hence, Vf is calculated as given in Eq. (1).
| (1) |
where Vf is the volume fraction, Vfiber is the volume of steel fiber, Vconcrete is the volume of concrete, wf is the weight of steel fiber, wc is the weight of concrete, ρf is the density of steel fiber, and ρf is the density of concrete.
Figure 1.
Compressive stress-strain response of SFRC under compressive [17].
It was crucial to develop a finite element model (FEM) of a statically indeterminate structural system that implements the generated moment-curvature response to determine the value of moment redistribution.
2.2. Moment-curvature response of SFRC beam
The objective of response determination for the moment-curvature of an SFRC beam was to measure its moment resistance capacity and curvature. The ratio of the compressive strain in the concrete extreme fiber, εcu, and the strain occurring at the centroid of the reinforcement rebars, εst or extreme tensile surface, εt of an SFRC member to the section depth was evaluated from the linear strain distribution behavior in the member section [5].
The moment-curvature gradient indicates the elastic flexural stiffness EI, which involves all the properties of the segment in a specific loading state [18].
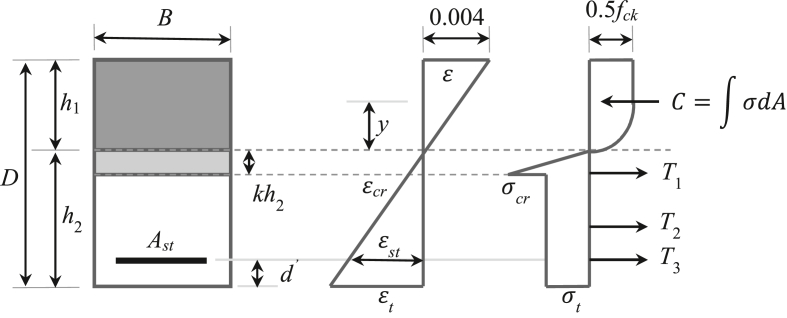
The section analysis empirical expressions and formulas were obtained from the stress-profile model in Figure 2 which shows a schematic illustration of an SFRC beam cross-section reinforced with the conventional flexural reinforcement by implementing the following assumptions and formulations given by [5]:
-
−
An SFRC rectangular beam section having a width (B) and depth (D) was considered.
-
−
In the whole section, steel fibers were assumed to be randomly scattered and displayed uniformly.
-
−
Conventional longitudinal reinforcement having a cross-sectional area (Ast) was provided at a distance () from its bottom face for the sake of completeness. The model of an SFRC beam section was analyzed by taking a zero value of reinforcement areas (Ast).
-
−
For a member having a span to depth ratio of greater than 2.5, the plane section normal to the beam longitudinal axis before bending remains plane after bending.
Figure 2.
Stress-profile model of SFRC [5].
The following expressions and formulas taken from [5] were used for analysis. The curvature (ϕ) denotes a change of the gradient that a member experiences when loaded. It is calculated as the ratio of strain in the extreme fiber to neutral axis depth. The expression in Eq. (2) taken from [5] was used to determine the curvature.
| (2) |
The neutral axis positions of the SFRC beam section in the balanced state shown in Figure 2 were evaluated using the similarity of the strain triangles that exist above and below the beam's section neutral axis [5].
| (3) |
The principle of statics was applied in the calculation of the actual neutral axis position and the corresponding moment capacity (Mu) in the SFRC beam section. By equating the compression force, and total tension force (T = T1+T2+T3) shown in Figure 2, the actual neutral axis position of the beam was obtained [5].
| (4) |
| (5) |
where Ast = ρBD
To determine the neutral axis positions, Eqs. (4) and (5) were simplified to Eqs. (6) and (7).
| (6) |
| (7) |
| (8) |
The ultimate moment capacity, Mu, of the SFRC beam section shown in Figure 2 was determined using the equation of statics, , that gives the general formula in Eq. (9).
| (9) |
Eq. (9) can be simplified to a non-dimensional moment capacity form as given in Eq. (10) by substituting the values of C, T1, T2, and T3.
| (10) |
where C is the total compressive force, T is the tensile forces, β is the fiber-index, ω is the reinforcement-index, fy is the yield strength, fck is the compressive strength, γ is the stress-mobilization factor for reinforcing rebar and ζ is the parameter that represents the effect of the steel fiber addition in the concrete on its crushing strain, ζ = 1.0 for SFRC and ζ = 0 for plain concrete.
The section flexural capacity (Mu) in Eq. (9) was determined using the limit values of strain for the SFRC in compression, εcu = 0.004 and for the steel rebars (fy = 415 N/mm2 grade), εst = 0.0038 [5].
General material properties and dimensions are given in Table 1.
Table 1.
Material properties and dimensions for moment-curvature response.
| Beam parameters | SFRC Beam | |||
|---|---|---|---|---|
| Steel fiber volume (%) | 0 | 0.5 | 0.75 | 1.5 |
| Cross-section () (mm2) | ||||
| Span of the beam (mm) | 1450 | 1450 | 1450 | 1450 |
| Fiber aspect ratio, l/d [17] | 50–60 | 50–60 | 50–60 | 50–60 |
| Conventional reinforcement, Ast (mm2) | 2φ16 | 2φ16 | 2φ16 | 2φ16 |
| Cracking strain value, εcr | 0.0001 | 0.0001 | 0.0001 | 0.0001 |
| Modulus of elasticity, E (MPa) [17] | 24370 | 26570 | 26870 | 23920 |
| Cracking tensile strength of the concrete, σcr= εcrE (MPa) |
2.44 | 2.66 | 2.69 | 2.39 |
| Compressive strength, fck (MPa) [17] | 27.69 | 35.10 | 36.18 | 26.92 |
| Yield strength of tensile rebar, fy (MPa) | 415 | 415 | 415 | 415 |
| Depth ratio (d’/D) | 0.1 | 0.1 | 0.1 | 0.1 |
2.3. Moment-rotation response of SFRC beam
The objective was to obtain the moment-rotation response that characterizes the structural behavior of a flexural element in the procedure of hinge development. It indicated the bending capacity and member ductility.
Plastic rotation capacity, θp at the center support (at the support B, θB = θp) of the beam shown in Figure 3(a) was quantified as the integral of curvatures after yielding of the steel reinforcement along the hinge (Figure 4(c)) using Eq. (12) based on the mechanical properties of materials from the principle offered by [15].
| (11) |
| (12) |
| (13) |
| (14) |
where ϕy and ϕu are the yield and ultimate curvatures at the critical section respectively, lp is the effective hinge length, ky is the compression zone depth at a yield that normalized to d, ρ and ρ′ are the reinforcement ratios of the tension and compression that normalized to bd respectively, εcu is the ultimate strain of concrete at extreme compression fiber, d is the beam section effective depth and h1 is the depth of the neutral axis.
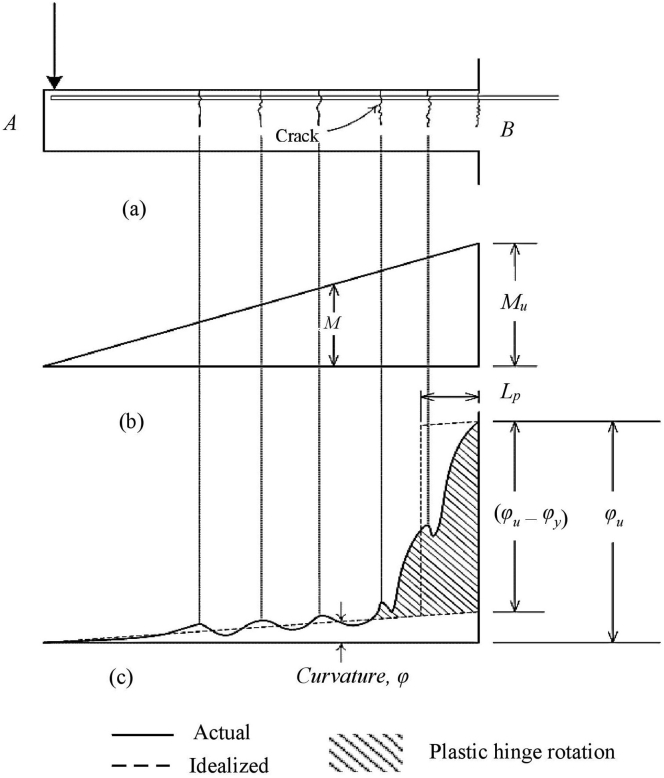
Figure 3.
Plastic hinge rotation for continuous beam (a) deflected shape when the ultimate load is reached. (b) idealized curvature distribution when the ultimate load is reached [15].
Figure 4.
Curvature distribution along the beam at ultimate bending moment (a) beam element, (b) bending moment diagram, (c) curvature diagram [15].
Equivalent plastic hinge length, lp to one side of the critical section, was obtained according to [19] from Eq. (15),
| (15) |
where z is the distance between the critical section and the point of contra flexure.
2.4. Modeling of SFRC beam using FEA
This section discussed the modeling of the statically indeterminate beam element using finite element modeling. A continuous beam with two spans was modeled using the FEA software Abaqus/CAE. The objective was to determine the amount of moment redistribution that occurred. To design complicated SFRC structural systems, it is essential to employ non-linear FEA [20]. According to [20] commercially available FEA packages (Abaqus/CAE) use the stress-strain relationship to describe the tension softening in the cracked region of concrete.
2.4.1. Failure mechanism
For a statically indeterminate beam to collapse, more than one plastic hinge should be developed, so the study assumed three plastic hinges were developed for a continuous beam to fail as shown in Figure 5(a).
Figure 5.
Failure mechanism (a) the failure mechanism of a continuous beam, (b) stress distribution in a symmetrical cross-section at a fully plastic stage.
The plastic hinge acted as a real hinge for further increase of load (until sufficient plastic hinges were developed for collapse). As the load increased, there was a redistribution of the moment, as the plastic hinge cannot carry any additional moment.
Plastic hinges developed at the center support first, then the span beam becomes a simple beam, finally after the plastic hinge developed at the center of the spans the beam collapsed.
The ultimate/collapse load, Pu was computed from the virtual-work method from the collapse mechanism of the beam. The virtual external work, We, by the plastic load, P, acting through the real external displacement, Δ, is equal to the virtual internal work, Wi, absorbed by the plastic hinges, that is We = Wi. From Figure 5(a), the virtual external work is equal to We = Σ(F×Δ). The virtual internal work is equal to Wi = Σ(Mp×θ). Thus Σ(F×Δ) = Σ(Mp×θ). Eq. (16) is obtained by solving P×Δ = Mp×(2θ+θ), θ = Δ/(L/2). The value of the plastic moment, Mp in Eq. (17) is calculated from the plastic stress distribution given in Figure 5(b). Hence Mp = σy×Zp, where Zp is the plastic section modulus, Zp = (BD2)/4.
| (16) |
| (17) |
where Pu is the collapse load, Mp is the plastic/ultimate moment, σy is the yield stress, B and D are the breadth and depth of the cross-section respectively.
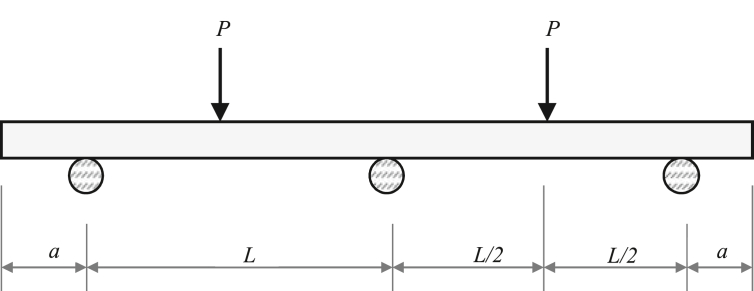
2.4.2. Geometry
The layout of the modeled structure is shown in Figure 6. The beam dimensions were chosen to be: span length, = 1450 mm, beamwidth, B = 150 mm, beam height, D = 250 mm, the total span length of the beam is 3100 mm with a span length to height ratio of 5.8. The section depth to width ratio is equal to 1.67 and over-hang length, a = 100 mm.
Figure 6.
The layout of the modeled beam.
2.4.3. Elements and meshing
Three-dimensional (3D) deformable elements capable of deforming under concentrated mechanical load (P) were employed to model continuous beams. The mesh module has several tools for specifying various mesh parameters, including element shape, mesh density, and element type. The eight-node linear brick element, commonly known as the fully integrated 3D hexahedral elements formulation (C3D8), was employed. Each node in this element type has three degrees of freedom, which represent x, y, and z displacements. Finer mesh provides reliable results for FE modeling of 3D elements, but the calculation time often becomes essential. A finite element model of 20 mm mesh size was used for all specimens as given in Figure 7.
Figure 7.
Mesh.
2.4.4. Boundary conditions
To stimulate symmetrical structural behavior, the boundary conditions were described as given in Figure 8. To improve the element's stability, the displacement at the node designating the midspan support is controlled in the x- and y-axis directions. To accommodate the member's horizontal movement, the side supports were restricted in the y-direction alone. Additionally, these nodes have been described as freely revolving. The nodes at the midspans were utilized to demonstrate the specified displacements.
Figure 8.
Boundary conditions.
2.4.5. Material properties
The representative moment-curvature relationships were used as the material properties for the beam elements to analyze the five-point bending test. It was previously considered that yielding happens initially at the center support via a collapse mechanism that creates a plastic hinge.
2.4.6. Analysis procedure
A procedure controlled by displacement has been carried out. The nodes at the midspans were specified with a vertical displacement of 20 mm. The initial crack was anticipated to occur at the center support. Following the initial phase, analysis was conducted in step-1 (static-general). The loading was achieved by designating a reference point at the top of the beam's midspans and associating it with a predetermined displacement. The necessary results were the bending moment distribution, the reaction forces, and the corresponding displacements. The input data and parameters for FEA are given in Table 2.
Table 2.
Input data and parameters for FEA, Abaqus/CAE.
| Input | The volume of steel fiber (%) |
|||
|---|---|---|---|---|
| 0 | 0.5 | 0.75 | 1.5 | |
| Cross-section () (mm2) | ||||
| Span of the beam (mm) | 1450 | 1450 | 1450 | 1450 |
| Number of spans | 2 | 2 | 2 | 2 |
| Modeling space | 3D | 3D | 3D | 3D |
| Modulus of elasticity, E (MPa) | 24370 | 26570 | 26870 | 23920 |
| Mass density (10−6 kg/mm3) | 2.472 | 2.438 | 2.517 | 2.433 |
| Concrete compressive strength, (MPa) | 27.69 | 35.10 | 36.18 | 26.92 |
| Mesh type | C3D8 | C3D8 | C3D8 | C3D8 |
2.4.7. Material constitutive relationship
The concrete damaged plasticity model's primary objective is to give a general capacity to analyze concrete structures subjected to various loads [21]. CDP model implements isotropic damaged elasticity concepts in conjunction with isotropic tensile and compressive plasticity to depict inelastic concrete behavior. The CDP model was used to characterize concrete with and without fiber in this study, with the fiber assumed to be uniformly distributed as it exists. As a result, in this simulation, the steel fiber is scattered in the concrete and integrates with it. Steel fiber reinforced concrete is described as a form of continuous homogenization, and it is represented in the material constitutive relationship to realize the model's establishment. As shown in Figure 9, the constitutive relationship of SFRC was categorized into compression and tensile constitutive relationships. The following default parameters of the CDP model used were taken from [22].
-
•
Dilation angle = 36°: Parameter characterizing the performance of concrete under compound stress
-
•
Eccentricity = 0.1: The ratio of tensile strength to compressive strength
-
•
: The ratio of the biaxial state compression strength to the strength in the uniaxial state
-
•
-
•
Viscous parameter = 0
-
•
Compressive stress data were stipulated as a tabular function of crushing or inelastic strain
| (18) |
where is the inelastic strain, is the total strain, and is the elastic strain associated with the undamaged material [21].
Figure 9.
CDP model material constitutive relationships of SFRC under uniaxial loading in (a) compression and (b) tension [21].
The stress-strain responses under uniaxial compression and taken were taken into account in Eqs. (19) and (20).
| (19) |
| (20) |
where σc and σt are the stresses under uniaxial tension and compression loading respectively, E0 refers to the material's initial (undamaged) elastic stiffness, and dc and dt are the uniaxial damage variables for compression and tension respectively.
Tension stiffening is utilized to simulate the post-failure behavior of direct straining, allowing the strain-softening behavior of cracked concrete to be described [21]. Additionally, this behavior enables a simple simulation of the effects of the steel fiber interaction with concrete. In the concrete damaged plasticity model, tension stiffening is required. A post-failure stress-strain relationship was used to specify tension stiffening.
2.5. Calculation of moment redistribution
The amount of moment redistribution is proportional to the difference between the ultimate and elastic bending moments. The amount of moment redistribution (MR) was calculated using Eq. (21) provided by [23, 24].
| (21) |
| (22) |
where Mred is the redistributed bending moment at the center support, Me is the elastic bending moment at the center support, and δ is the ratio of redistributed bending moment to elastic bending moment.
Figure 10 (a) shows at relatively low loads (P) the distribution of bending moment (Me) due to the concentrated loads is under the elastic theory. As applied loads increase, the ultimate moment of resistance (Mu) is attained at a critical section, the center support, before reaching the other sections, as seen in Figure 10(b). Due to the section's ductility resulting from the steel fiber addition, increasing the load results in plastic hinge rotations at the center support, maintaining ultimate moment resistance. Moment redistribution occurs until the maximum positive moment in the spans reaches Mu. At this instant, the collapse mechanism is formed as presented in Figure 10(c). Figure 10(d) depicts how the bending moment varies with the load on the beam at the critical sections, providing that the plastic hinge forms at the center support [15].
Figure 10.
Moment Redistribution and formation of collapse mechanism for a continuous beam. (a) elastic bending moment diagram, (b) ultimate moment at the formation of the first plastic hinge, (c) ultimate moment at the formation of collapse mechanism, (d) change of bending moment with load [15].
2.6. Validation of the finite element models
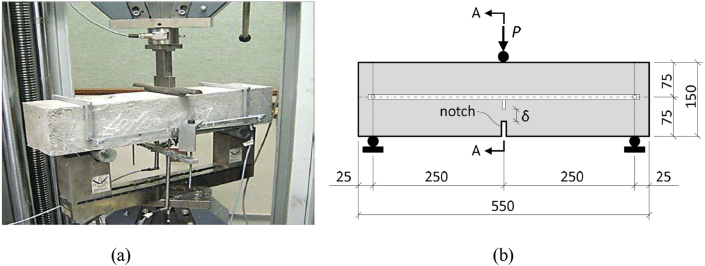
The researcher [25] performed experimental tests at Stellenbosch University, which were used to verify the FEA results. The experiments were carried out in conformity with RILEM standards [26]. For the flexural test, the specimen dimensions were 600 × 150 × 150 mm (L×b×h). The test setup was intended to stimulate a three-point bending mechanism. Figure 11 represents the test setup and configuration schematically. Steel fiber volumes of 0.5 % and 0.75 % were considered for the FE models. The experiment utilized hooked end steel fiber with an aspect ratio (L/d) of 80, 7850 kg/m3 density, 1050 MPa tensile strength, and 210 GPa young's modulus.
Figure 11.
Three-point bending test (a) setup [25], (b) schematic representation [26].
Figure 12 present a comparison load-displacement response of experimental and FE model results for SFRC beams of 0.5% and 0.75 % steel fiber, respectively. The two tests revealed that the experimental and FE models provide similar results with a nearly similar midspan load-displacement response which confirms the validity and the reliable use of the FEA.
Figure 12.
Midspan load-displacement response from experimental and FEA results for 0.5% and 0.75% SFRC beams.
The failure modes of the FE models were also compared to the results of experimental tests by [25]. The failure modes are represented in Figure 13 and it is confirmed that the failure modes show a similar pattern in bending.
Figure 13.
Failure modes (a) experimental, (b) FE models.
3. Results and discussions
The flexural action of each SFRC model was examined by deriving moment-curvature relationships and establishing a theoretical moment-rotation response that accurately reflects the rotational reaction of the plastic hinges. The numerical results were compared to the developed moment-curvature and moment-rotation models, and the possibility of moment redistribution was investigated. Additionally, the amount of moment redistribution is compared to the rotational values at the hinges. Finally, the behavior of the SFRC continuous beam's moment redistribution was examined and shown. The moment redistribution behavior of the SFRC continuous beam was analyzed and presented.
3.1. Section capacity from the moment-curvature response
The theoretical moment-curvature response for all SFRC sections is calculated and the result obtained is presented as dimensionless moment, Mu/fckBD2 versus curvature, ϕ (1/m) in Figure 14.
Figure 14.
The moment-curvature response of SFRC.
Figure 14 presents the results of the moment-curvature responses presented by the SFRC beams (for 0 %, 0.5 %, 0.75 % and 1.5 %). The result of moment-curvature responses indicates sectional ductility.
Table 3 indicates that the section analyzed with steel fiber of 1.5 %exhibits a slightly higher flexural capacity (15 %) when compared with a section having no steel fiber (0 %). Higher flexural capacity is observed with sections analyzed with 0.75 % and 0.5 % volume of steel fibers that flexural capacity increased by 57.3% and 52.7% respectively.
Table 3.
Sectional flexural capacity (Mu) of the SFRC beam.
| Volume of steel fiber (%) | B (mm) | D (mm) | fck (N/mm2) [17] | Mu/fckBD2 | Mu (kN-m) |
|---|---|---|---|---|---|
| 0 | 150 | 250 | 27.69 | 0.1756 | 45.59 |
| 0.5 | 150 | 250 | 35.10 | 0.2116 | 69.63 |
| 0.75 | 150 | 250 | 36.18 | 0.2114 | 71.70 |
| 1.5 | 150 | 250 | 26.92 | 0.2077 | 52.42 |
The corresponding value of the section curvature for the 1.5 % SFRC is reduced by 0.4 % in comparison to 0 % SFRC, determined corresponding to the strain value of 0.004. However, section curvature for 0.75 % and 0.5 % SFRC slightly increased by 2 %.
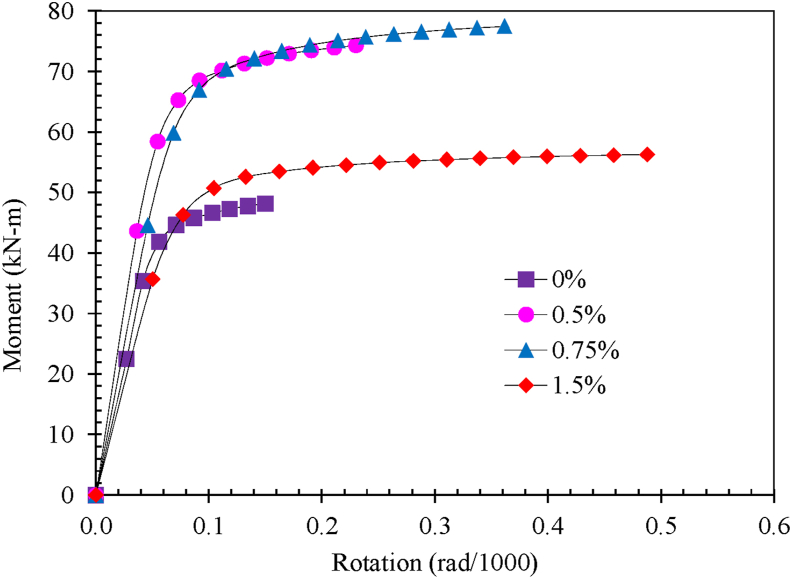
3.2. Ductility of the member from the moment-rotation response
The obtained moment-rotation results are presented in Figure 15. The first distinguishing feature that is found is that the curve forms are similar to those of the moment-curvature response. This is predictable given the concept of rotation as defined by the moment-area theorem, . It has been established that as the steel fiber volume increases, the SFRC beam's rotation capacity increases. As a result, increasing the volume of steel fiber in an SFRC beam allows it to rotate further. In comparison to concrete without steel fiber, Figure 15 shows that the bending moment capacity improves as the volume of steel fiber increases. The moment, on the other hand, declined as the percentage of steel fiber increased from 0.75 % to 1.5 %. Since the moment-rotation response is derived from the theoretical moment-curvature response, which is mainly based on the material strength of the SFRC section, an SFRC with 1.5 % steel fiber has lower compressive strength than one with 0.75 % steel fiber, as illustrated in Table 1.
Figure 15.
Moment-rotation response of SFRC.
The member ductility was calculated with the numerical results of plastic rotation experienced at the ultimate bending moment. Member ductility = θmax,i/θmax,0%., is calculated taking 0 % SFRC plastic rotation result as the base value and presented in Table 4.
Table 4.
Member ductility result.
| Member Ductility | The volume of Steel fiber (%) |
|||
|---|---|---|---|---|
| 0 | 0.5 | 0.75 | 1.5 | |
| θmax,i(rad) | 0.0015 | 0.0024 | 0.0036 | 0.0049 |
| θmax,i/θmax,0% | 1.0 | 1.59 | 2.41 | 3.25 |
The member ductility is increased 1.59 times, 2.41 times, and 3.25 for 0.5%, 0.75%, and 1.5% SFRC members respectively, compared to that of the 0 % SFRC member's rotation capability. The increasing volume of steel fiber increases member ductility. It is discovered that increasing the steel fiber volume improves the variance of the rotational value at the ultimate bending moment and the plastic rotation capability.
3.3. Moment redistribution behavior
This section discussed the calculated elastic bending moment and the result of redistributed moments for a modeled continuous beam. FEA software package, Abaqus/CAE, was used for modeling continuous SFRC beam for each steel fiber volume. Finally, the amount of moment redistribution is computed and provided in Figure 16.
Figure 16.
Elastic moment and redistributed moment diagram for a) 0 %, b) 0.5 %, c) 0.75 %, d) 1.5 % SFRC.
Table 5 summarizes the findings of the analysis of a continuous beam for SFRC using FEA, Abaqus/CAE.
Table 5.
Moment redistribution calculation.
| Stage | Result | The volume of steel fibers (%) |
|||
|---|---|---|---|---|---|
| 0 | 0.5 | 0.75 | 1.5 | ||
| Elastic [kN-m] | 29.6 | 38.4 | 39.5 | 43.5 | |
| 35.7 | 46.3 | 47.6 | 52.4 | ||
| Failure [kN-m] | 35.2 | 42.7 | 43.3 | 48.2 | |
| 27.9 | 37.5 | 39.0 | 45.1 | ||
| 130.9 | 169.7 | 174.6 | 192.1 | ||
| Moment | 0.782 | 0.810 | 0.819 | 0.861 | |
| Redistribution(%) | MR | 21.8 | 19 | 18.1 | 13.9 |
According to Table 5, the amount of moment redistribution obtained is 21.8 % for 0 %, 19 % for 0.5 %, 18.1 % for 0.75 %, and 13.9 % for 1.50% SFRC. The amount of moment redistribution decreases as the volume of the steel fiber increases, which is related to a more abrupt decrease in post-peak bending capacity. The maximum amount of moment redistribution 21.8 by percent is confirmed for 0 % SFRC.
4. Conclusion
The sectional flexural capacity, ductility, and moment redistribution behavior were studied by modeling a continuous SFRC beam using FEA software package, Abaqus/CAE after the moment-curvature and moment-rotation responses are analyzed from the available experimental result of stress-strain response of 0 %, 0.5 %, 0.75 %, and 1.5 % steel fiber by the volume of concrete. The CDP model was selected to model SFRC using material constitute relations. The FEA results were validated against the experimental tests, resulting in excellent alignment between the FEA and experimental test results. The moment-curvature response showed that increasing the volume of steel fibers increased bending capacity, while the moment-rotation response showed that increasing the volume of steel fibers enhanced member ductility. It can be concluded that the addition of steel fiber in concrete is effective in improving the bending capacity of the section and ductility of the member. The amount of moment redistribution shows a reduction due to the increased volume of steel fibers. In critical sections, SFRC members with an increased amount of steel fibers will rotate further, but a lower amount of moment redistribution has been experienced.
Declarations
Author contribution statement
Yohannes Werkina Shewalul: Conceived and designed the experiments; Performed the experiments; Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data; Wrote the paper.
Funding statement
This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.
Data availability statement
Data will be made available on request.
Declaration of interests statement
The authors declare no conflict of interest.
Additional information
No additional information is available for this paper.
References
- 1.Ali W.A., Ibrahim A.H., Ebead U. Flexural behavior of RC beams strengthened with steel fibers. Int. J. Appl. Eng. Res. 2020;15(5):468–480. http://www.ripublication.com [Internet] Available from: [Google Scholar]
- 2.Karadelis J.N., Zhang L. On the discrete numerical simulation of steel fiber reinforced concrete (SFRC) J. Civ. Eng. Res. 2015;5(6):151–157. http://article.sapub.org/10.5923.j.jce.20150506.04.html Available from: [Google Scholar]
- 3.Kumutha R., Vijai K. Effect of steel fibers on the properties of concrete. J. Reinf. Plast. Compos. 2010 Feb 23;29(4):531–538. http://journals.sagepub.com/doi/10.1177/0731684408100258 [Internet] Available from: [Google Scholar]
- 4.SS K., Rajamurugadoss J., GP G. Structural and other applications of steel fiber reinforced concrete – a review. Int. J. Sci. Technol. Res. 2019;8(10):2317–2322. www.ijstr.org [Internet] Available from: [Google Scholar]
- 5.Singh H. Springer Nature; Singabore: 2017. Steel Fiber Reinforced concrete Behavior, Modeling, and Design. [Google Scholar]
- 6.Islam M.M., Rahman M.S., Mitu S.M., Chowdhury M.A., Islam M.R., Siddique A. 2nd International Conference on Advances in Civil Engineering. 2014. Finite element modeling and analysis of RC beams made of steel fiber reinforced concrete (SFRC) pp. 978–984. [Google Scholar]
- 7.Luccioni B., Ruano G., Isla F., Zerbino R., Giaccio G. A simple approach to model sfrc. Construct. Build. Mater. 2012;37:111–124. [Internet] [Google Scholar]
- 8.Sun M., Zhu J., Li N., Fu C.C. Experimental research and finite element analysis on mechanical property of SFRC t-beam. Adv. Civ. Eng. 2017;2017:8. [Google Scholar]
- 9.Kooiman A.G. Optima Grasiche Communicatie; Rotterdam: 2000. Modeling Steel Fiber Reinforced concrete for Structural Design. [Google Scholar]
- 10.Kytinou V.K., Chalioris C.E., Karayannis C.G. Analysis of residual flexural stiffness of steel fiber-reinforced concrete beams with steel reinforcement. Materials (Basel) 2020 Jun 13;13(12):2698. doi: 10.3390/ma13122698. https://www.mdpi.com/1996-1944/13/12/2698/htm [Internet] [cited 2021 Jan 25];Available from: [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Abbass A., Abid S., Ozakça M. Experimental investigation on the effect of steel fibers on the flexural behavior and ductility of high-strength concrete. Adv. Civ. Eng. 2019;2019 [Google Scholar]
- 12.Haskett M., Oehlers D., Ali M. Design for moment redistribution in RC beams retrofitted with steel plates. Adv. Struct. Eng. 2010 Apr 1;13(2):379–392. [Google Scholar]
- 13.Baji H., Ronagh H.R. Reliability analysis of moment redistribution in reinforced concrete beams. Mag. Concr. Res. 2013;65(13):769–779. [Google Scholar]
- 14.Visintin P., Ali M., Xie T., Sturm A. Experimental investigation of moment redistribution in ultra-high performance fiber reinforced concrete beams. Construct. Build. Mater. 2018;(March) [Google Scholar]
- 15.Park T., Paulay R. John Wiley and Sons; 1974. Reinforced concrete Structures; pp. 1–783. [Google Scholar]
- 16.ACI 318R-14 A.C. American Concrete Institute; 2014. Building Code Requirements for Structural concrete.www.concrete.org [Internet] Available from: [Google Scholar]
- 17.Shewalul Y.W. Experimental study of the effect of waste steel scrap as reinforcing material on the mechanical properties of concrete. Case Stud. Constr. Mater. 2021;14 [Internet] [Google Scholar]
- 18.Kwak H.-G., Kim S.-P. Nonlinear analysis of RC beams based on the moment-curvature relation. Comput. Struct. 2002 Mar 1;80:615–628. [Google Scholar]
- 19.Mattock A.H. Discussion of rotational capacity of reinforced concrete beams. J. Struct. Div. 1967;93:519–522. [Google Scholar]
- 20.Tlemat H., Pilakoutas K., Neocleous K. Modelling of SFRC using inverse finite element analysis. Mater. Struct. 2006;39(286):221–233. [Google Scholar]
- 21.Abaqus/CAE . Dassault Systèmes Simulia Corp.; Providence: 2011. Abaqus/Cae User’s Manual. [Google Scholar]
- 22.Kmiecik P., Kamiński M. Modelling of reinforced concrete structures and composite structures with concrete strength degradation taken into consideration. Arch. Civ. Mech. Eng. 2011 Dec 31;11(3):623–636. [Google Scholar]
- 23.Oehlers D. Ductility of FRP plated flexural members. Cement Concr. Compos. 2006 Nov 1;28:898–905. [Google Scholar]
- 24.Liu I.S., Oehlers D.J., Seracino R. Moment redistribution in FRP and steel-plated reinforced concrete beams. J. Compos. Construct. 2006 Apr 1;10(2):115–124. [Google Scholar]
- 25.Möhr A.W. Stellenbosch University; 2012. Moment Redistribution Behavior of SFRC Members with Varying Fiber.http://scholar.sun.ac.za/handle/10019.1/20250?show=full [Internet] Available from: [Google Scholar]
- 26.RILEM TC 162-TDF Test and design methods for steel fiber reinforced concrete. Mater. Struct. 2003;36(October):560–567. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data will be made available on request.