Unexpected Diffusion Anisotropy of Carbon Dioxide in the Metal–Organic Framework Zn₂(dobpdc)

Abstract

Metal–organic frameworks are promising materials for energy-efficient gas separations, but little is known about the diffusion of adsorbates in materials featuring one-dimensional porosity at the nanoscale. An understanding of the interplay between framework structure and gas diffusion is crucial for the practical application of these materials as adsorbents or in mixed-matrix membranes, since the rate of gas diffusion within the adsorbent pores impacts the required size (and therefore cost) of the adsorbent column or membrane. Here, we investigate the diffusion of CO₂ within the pores of Zn₂(dobpdc) (dobpdc^4– = 4,4′-dioxidobiphenyl-3,3′-dicarboxylate) using pulsed field gradient (PFG) nuclear magnetic resonance (NMR) spectroscopy and molecular dynamics (MD) simulations. The residual chemical shift anisotropy for pore-confined CO₂ allows PFG NMR measurements of self-diffusion in different crystallographic directions, and our analysis of the entire NMR lineshape as a function of the applied field gradient provides a precise determination of the self-diffusion coefficients. In addition to observing CO₂ diffusion through the channels parallel to the crystallographic c axis (self-diffusion coefficient D_// = 5.8 ± 0.1 × 10⁻⁹ m²s⁻¹ at a pressure of 625 mbar CO₂), we unexpectedly find that CO₂ is also able to diffuse between the hexagonal channels in the crystallographic ab plane (D_⊥ = 1.9 ± 0.2 × 10⁻¹⁰ m²s⁻¹), despite the walls of these channels appearing impermeable by single crystal X-ray crystallography and flexible lattice MD simulations. Observation of such unexpected diffusion in the ab plane suggests the presence of defects that enable effective multi-dimensional CO₂ transport in a metal–organic framework with nominally one-dimensional porosity.

Graphical Abstract

INTRODUCTION

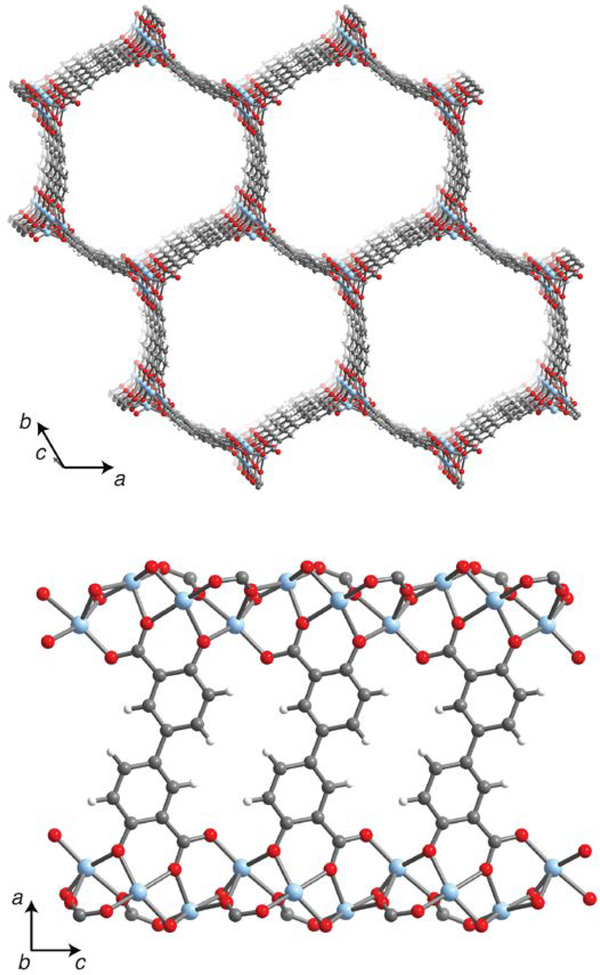
Synthetic porous materials such as metal–organic frameworks (MOFs) show great potential for energy-efficient gas separations. A key advantage of MOFs compared to traditional porous materials, such as carbons and zeolites, is their highly tunable chemistry, porosity, and topology, which allow the targeted design of materials for particular separations. Frameworks in the MOF-74 family,¹ such as M₂(dobdc) (dobdc^4– = 2,5-dioxido-1,4-benzenedicarboxylate; M = Mg, Mn, Fe, Co, Ni, Cu, Zn, Cd)^1–8 and the expanded variants M₂(dobpdc) (dobpdc^4– = 4,4′-dioxidobiphenyl-3,3′-dicarboxylate; M = Mg, Mn, Fe, Co, Ni, Zn),^9–11 in particular demonstrate promise for the separation of CO₂ from simulated fossil fuel flue gas mixtures^12–14 as well as for CO₂/CH₄ separations.¹⁵ These frameworks feature one-dimensional hexagonal channels lined with a high density of coordinatively-unsaturated metal centers (see Figure 1), and their CO₂ capture performance has been found to improve dramatically upon appending diamines to the metal sites. The diamine-appended frameworks cooperatively adsorb CO₂ via the formation of ammonium carbamate chains, resulting in a dramatically improved performance in the presence of water as well as low regeneration energies.^9,10,16–20

Figure 1.

A portion of the crystal structure of Zn₂(dobpdc) at 298 K shown from two different perspectives, as determined by single-crystal X-ray diffraction; light blue, red, gray, and white spheres represent Zn, O, C, and H atoms, respectively.

Despite the promise of MOF-74 materials for a variety of gas separations, an understanding of gas diffusion in this class of materials is lacking. The importance of strong CO₂–metal interactions in dictating local energy barriers for diffusive motion between different binding sites in Mg₂(dobdc) has previously been highlighted.²¹ Nuclear magnetic resonance (NMR) spectroscopy has also been used to probe the hopping dynamics and resulting average orientations of CO₂ molecules in the pores of Mg₂(dobdc) via the measurement of residual chemical shift anisotropies.^22,23 Despite this progress, little is known about the long-range diffusive motion of molecules within materials of this type. In particular, the magnitude and directionality of gas diffusion within the one-dimensional nano-sized pores of these adsorbents are poorly understood, even though such parameters have a substantial impact on their practical utility. By understanding gas diffusion in this class of MOFs, we hope to guide the design of new materials with improved gas transport properties.

Pulsed-field gradient (PFG) NMR spectroscopy allows the measurement of self-diffusion coefficients of pore-confined molecules,^24–30 and uses pulses of magnetic field gradients to encode and decode the positions of the molecules. In this technique, a series of NMR experiments are first carried out with magnetic field gradient pulses of increasing strength, and self-diffusion coefficients are subsequently obtained by fitting the decay of the NMR signal intensity as a function of the field gradient.³¹ PFG NMR spectroscopy is an attractive means of characterization, as it can also be used to measure diffusion anisotropy.^31–34 For example, aligning single crystals of a material at different orientations relative to the magnetic field gradient direction (the direction in which diffusion is measured) allows one to probe the diffusion of adsorbed molecules in different crystallographic directions.^35–37 An alternative approach that does not require oriented single crystals is to make use of residual anisotropic NMR interactions in static polycrystalline samples, wherein the resonance frequency is dependent on the crystallite orientation. Using the latter approach, residual quadrupole interactions (²H NMR) combined with PFG experiments have been used to measure the diffusion anisotropy of ²H₂O in a polycrystalline liquid crystal sample.³⁶ Later studies employed similar approaches based on residual chemical shift anisotropies.^37–39 In particular, the qualitative analysis of powder lineshapes for CO₂ adsorbed in a metal–organic framework can be used to determine the preferred crystallographic direction for self-diffusion.^39,40

Here, we utilize the residual chemical shift anisotropy of CO₂ confined in the nanopores of Zn₂(dobpdc) to extract the diffusion anisotropy as a function of gas pressure. The large single crystals of this material (up to ~750 μm in length) facilitate the measurement of diffusion of the pore-confined gas molecules, because exchange with the gas outside of the pores is negligible under the experimental conditions. Our quantitative analysis of the evolution of the entire spectral lineshape with increasing pulsed field gradient strength offers precise determination of self-diffusion coefficients parallel and perpendicular to the hexagonal channels. Molecular dynamics (MD) simulations and in situ single-crystal X-ray diffraction measurements are employed as aides in trying to understand the results.

RESULTS AND DISCUSSION

NMR Spectra of ¹³CO₂-Dosed Zn₂(dobpdc).

The reaction of Zn(NO₃)₂∙6H₂O and H₄dobpdc at 100 °C for two days¹⁷ yielded needle-like crystals of Zn₂(dobpdc) (Figure 2, see also Figure 1). Successively washing the crystals with N,N-dimethylacetamide, methanol, and toluene, followed by activation for 12 h at 250 °C under flowing Ar, yielded crystals with lengths of up to 750 μm and widths of up to 120 μm (Figure 2b, Figure S1), which were then used to prepare NMR samples.

Figure 2.

(a) Photograph of as-synthesized crystals of Zn₂(dobpdc) inside a sealed tube. (b) Microscope image of crystals in air following washing and activation.

The Zn₂(dobpdc) crystals were dosed ex situ with ¹³CO₂ using a custom-built gas dosing manifold (Figure 3a). Static ¹³C NMR spectra of these crystals exhibit a feature that can be assigned to CO₂ confined within the pores of the framework (Figure 3b). Measurements of the CO₂ adsorption isotherm and integrated NMR signal intensities from 0 to 2026 mbar of CO₂ (Figure S2) indicate occupancies of up to 0.9 CO₂ molecules per metal site at the highest studied pressure. An unusual powder pattern lineshape is apparent in the NMR spectra, with the overall width depending on the gas pressure. Previously reported ¹³C NMR spectra for solid CO₂ and our measured spectrum for gaseous CO₂ (Figure 3c) provide a useful reference here.⁴¹ In the gas phase, isotropic molecular rotation yields a narrow resonance at the isotropic chemical shift, δ_iso = 127.7 ppm. In the solid state, CO₂ exhibits a significant chemical shift anisotropy (Δ_CSA), arising from the highly anisotropic shape of the molecule. For solid CO₂, Δ_CSA = δ_// – δ_iso is approximately −210 ppm, where δ_iso = (2δ_⊥ + δ_//)/3, and intensity at δ_⊥ arises from CO₂ molecules that are oriented perpendicular to the applied magnetic field (B₀), while intensity at δ_// arises from CO₂ molecules oriented parallel to the applied field.

Figure 3.

(a) Custom-built gas dosing apparatus for preparing ¹³CO₂-dosed NMR samples. (b) Static ¹³C NMR (7.1 T) spectra of Zn₂(dobpdc) crystals (Sample 1) dosed with ¹³CO₂ at different pressures (T = 25 °C). Dashed blue line shows the predicted lineshape at 2026 mbar for randomly oriented crystals. Gray peaks indicate schematically the spectral contributions from crystals with different orientations. (c) Static ¹³C NMR spectra of gaseous (1 bar) and solid CO₂ (no adsorbent present), the latter is adapted from Ref. 41 with permission of Elsevier. (d) ¹³C NMR (18.8 T) spectrum of Zn₂(dobpdc) powder dosed with 1056 mbar ¹³CO₂ (T = 22 °C). (e) Pressure dependence of NMR parameters extracted from spectra on two independent samples, Samples 1 and Sample 2 (which were studied at different magnetic field strengths) and a powder sample, δ_iso = (2δ_⊥ + δ_//)/3 and Δ_CSA = δ_// – δ_iso.

Pore-confined CO₂ in Zn₂(dobpdc) crystals exhibits a residual chemical shift anisotropy. In this regime, crystals with different orientations relative to B₀ exhibit different chemical shifts for confined CO₂ molecules. This effect arises because the molecular reorientation inside the pores is not isotropic, and CO₂ has preferred average orientations relative to the crystal frame (Figure 3b). We stress that it is the different orientations of the crystals relative to B₀ that gives rise to the observed spread of chemical shifts in Figure 3b. While the metal is the primary binding site for CO₂ in these materials,¹⁴ CO₂ undergoes translations between different metal sites on the NMR timescale and a symmetric narrow line is thus expected for a single crystal (reflecting the average environment of pore-confined CO₂ on a millisecond timescale; see below for more details).^22,42 We note that similar lineshapes for confined CO₂ have previously been observed in other (non-cubic) MOFs,^{39,40,43–47} including the isoreticular framework Mg₂(dobdc).^22,42

We hypothesize that intensity at the left-hand edge of the spectrum arises from CO₂ inside the pores of crystals that are oriented perpendicular to the magnetic field (B₀) direction, and intensity at the right-hand edge arises from CO₂ in the pores of crystals that are oriented parallel to the field direction (Figure 3b). With this assumption, the calculated Δ_CSA (= δ_// – δ_iso) values are negative. The observed lineshapes deviate significantly from that expected for a randomly oriented polycrystalline powder sample (shown as a dashed blue line in Figure 3b). This deviation arises because the large crystal sizes result in a partial macroscopic alignment of their long axis with the long axis of the NMR tube, leading to additional intensity at δ_//. Consistent with this observation, we find that physical shaking of the crystal samples results in marked changes of intensity in different regions of the spectra (Figure S3).

Our assignments of δ_⊥ and δ_// are supported by four pieces of evidence. Firstly, magic angle spinning (MAS) spectra collected for gas-dosed single crystals (Figure S4) yield a negative chemical shift anisotropy, as well as an isotropic chemical shift consistent with our assignments. Secondly, measurements of Zn₂(dobpdc) powder dosed with ¹³CO₂ (Figure 3d, see Experimental Section for powder synthesis), yield a narrow resonance with an isotropic chemical shift consistent with our assignments (see Figure 3e). Interestingly, a residual chemical shift anisotropy is not visible in this spectrum, suggestive of either fast chemical exchange between different crystallites (typical crystallite lengths are < 15 μm, and widths are < 2 μm; see Figure S5), or that the preferred orientation of CO₂ relative to the crystal frame is slightly different in the powder and the crystal samples, which were synthesized via different routes. Thirdly, the sign of the assigned Δ_CSA agrees with that calculated by MD simulations (see below). Finally, the diffusion behavior observed below is consistent with our assignments, with D_// ≫ D_⊥ as anticipated. An alternative assignment of the spectra in Figure 3b would be that intensity at the left-hand edge arises from crystals that are parallel to B₀ and that intensity at the right-hand edge arises from crystals that are perpendicular to B₀ (i.e., positive Δ_CSA). However, we reject this alternative assignment, as it is inconsistent with the four observations above.

The graphs in Figure 3e show the variations of Δ_CSA and δ_iso with ¹³CO₂ pressure. These data are in agreement within error for two independent samples measured at different field strengths, which we call “Sample 1” and “Sample 2” (see Figure S6 for spectra of Sample 2, collected with in situ dosing). Notably, δ_iso shows small variations at lower pressures and then appears to plateau at higher pressures, while the magnitude of Δ_CSA increases continuously with pressure (see below for discussion of this).

Anisotropic Diffusion of CO₂.

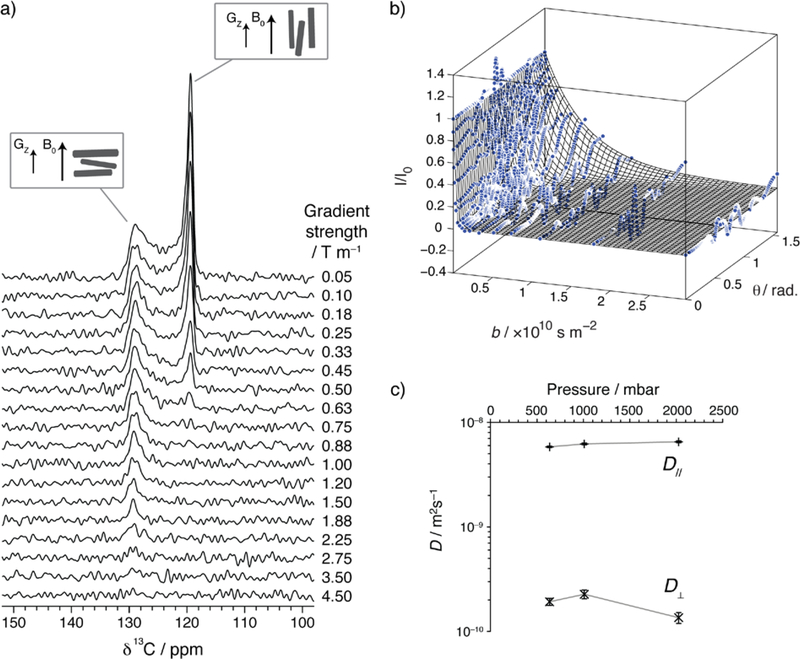
PFG NMR measurements of Sample 1 dosed ex situ with 625 mbar of ¹³CO₂ are shown in Figure 4a. In these measurements, magnetic field gradient pulses were applied along the laboratory z-direction (i.e., parallel to B₀; see Figure S7). Upon application of pulsed magnetic field gradients of increasing magnitude, the right-hand edge of the spectrum decays more rapidly than the left-hand edge. Face-indexing of a single crystal confirmed that the c-axis (and therefore the one-dimensional pores) runs along the long axis of the needle-like Zn₂(dobpdc) crystals. Using this observation and our prior assignments of the spectra (Figure 3b), we can obtain CO₂ self-diffusion coefficients both parallel (D_//) and perpendicular (D_⊥) to the hexagonal channels of Zn₂(dobpdc).

Figure 4.

(a) PFG NMR (7.1 T) spectra for Zn₂(dobpdc) crystals (sample 1) at a pressure of 625 mbar ¹³CO₂ with different applied gradient strengths (T = 25 °C). (b) Data and fit for results shown in (a) with PFG NMR signal decays shown as a function of crystal orientation, θ. The fit is represented as a meshed surface. Data points are shown as blue circles and are normalized to 1 for g = 0.05 T m⁻¹ for all crystal orientations (note that this normalization results in more noisy data at intermediate θ values where absolute signal intensities are weaker, due to the small number of crystals at these orientations). (c) Self-diffusion coefficients obtained at 25 °C for Zn₂(dobpdc) crystals (Sample 1) dosed with different pressures of ¹³CO₂. The errors in these values arise from uncertainty in the fitting procedure, and represent 95% confidence limits.

The observed chemical shift, δ, for pore-confined CO₂ in a crystal oriented at an angle (θ) relative to B₀ is given by:

$$\begin{gathered} \delta (\theta )={\delta }_{iso}+\frac{{\mathrm{\Delta }}_{CSA}}{2}(3\mathrm{c}\mathrm{o}{\mathrm{s}}^2\theta -1) \\ ={\delta }_{//}\mathrm{c}\mathrm{o}{\mathrm{s}}^2(\theta )+{\delta }_{\perp }\mathrm{s}\mathrm{i}{\mathrm{n}}^2(\theta ) \end{gathered}$$ (1)

The effective self-diffusion coefficient (D) measured using magnetic field gradients in the z-direction depends on θ in a similar way and is given by:³²

$$D(\theta )=D_{//}\mathrm{c}\mathrm{o}{\mathrm{s}}^2(\theta )+D_{\perp }\mathrm{s}\mathrm{i}{\mathrm{n}}^2(\theta )$$ (2)

Finally, the decay of signal intensity (I), normalized by the intensity for zero gradient (I₀), is given by:

$$\frac{I}{I_0}=\exp [-bD(\theta )]$$ (3)

The constant b is proportional to the square of the gradient strength (g) and also depends on the gyromagnetic ratio (γ) of the studied nucleus and a number of experimental constants (see Figure S8 for definitions of Δ, δ′, τ) and is given by:

$$b=g^2{(2{\delta }^{\prime }\gamma )}^2\left(\mathrm{\Delta }-\frac{{\delta }^{\prime }}{6}-\frac{\tau }{2}\right)$$ (4)

The self-diffusion coefficients D_// and D_⊥ are therefore the only free parameters in the fit to the data in Figure 4b using Equation 3. Here, we fit against all of the data (i.e., I/I₀ vs. b across all crystal orientations, θ) simultaneously to obtain diffusion coefficients with relatively small uncertainties. This analysis method is preferred to individual fits of integrated signal intensities across a small range of chemical shifts, which revealed similar results but with errors at least three times larger due to uncertainty in the fits. The dominant source of error in our analysis is most likely systematic error arising from the finite peak linewidths that arise from homogeneous broadening, such that for a given δ, crystals at a range of θ values contribute to the signal.^33,37 Indeed, this is evidenced by an apparent narrowing of the signal at δ_⊥ at the largest applied gradient strengths (Figure 4a). This arises from the signal decay for CO₂ in crystals with orientations, θ, close to, but unequal to, 90^o.³⁹ We note that it would be interesting to carry out PFG NMR with different gradient orientations.³⁹ Under such conditions the form of the PFG NMR decays would differ and could further improve the accuracy of our diffusion measurements.

A global fit to Equation 3 (Figure 4b) affords D_// = 5.8 ± 0.1 × 10⁻⁹ m²s⁻¹ and D_⊥ = 1.9 ± 0.2 × 10⁻¹⁰ m²s⁻¹. These values suggest that the self-diffusion of CO₂ is ~30 times faster along the hexagonal channels compared to diffusion between the channels at this pressure. It is surprising that gas diffusion perpendicular to the channels is possible at all, given the apparent lack of pore windows between neighboring channels in the ab plane, as judged from the crystal structure (see below). We note that the measured values are of similar order to self-diffusion values of bulk liquids, though they are more than three orders of magnitude smaller than the self-diffusion coefficient of gaseous CO₂ (1.1 × 10⁻⁵ m²s⁻¹ at 25 °C, 1 bar).⁴⁸ Our measured values are of similar order to the diffusion of CO₂ in other large-pore MOFs, such as HKUST-1 (D = 1.7 × 10⁻⁹ m²s⁻¹),⁴⁹ Zn₂(bdc)₂(dabco) (D_// = 1.1 × 10⁻⁸ m²s⁻¹ and D_⊥ = 3.7 × 10⁻⁹ m²s⁻¹),³⁹ and MIL-47(V) (D = 10⁻⁸–10⁻⁹ m²s⁻¹, depending on loading level).⁵⁰

Because these PFG NMR experiments probe diffusion on lengthscales on the order of tens of microns, D_⊥ is the effective self- diffusion coefficient as CO₂ moves between thousands of pores, rather than within a single pore (a length scale that is inaccessible by this technique). Furthermore, for the observation times (Δ) studied here, the experiments probe diffusion in the pore-confined phase. Indeed, the root mean square displacements (RMSDs) of confined CO₂ in our experiments are smaller than the typical crystal dimensions (Figure 2b, Figure S1). The RMSD is calculated using the expression (nDΔ)^0.5 (n = 2 for diffusion in the c-direction and n = 4 for diffusion in the ab plane). For example, given Δ = 80 ms, the RMSDs are 30 μm along the c axis, and 8 μm in the ab plane, values which are smaller than the typical crystal lengths (hundreds of μm) and widths (tens of μm), respectively (Figure S1). Furthermore, diffusion coefficients measured for different Δ in the range of 20–160 ms show minimal variation, indicating that exchange of pore-confined CO₂ with CO₂ outside of the pores is not significant at these timescales (Figure S9). Exchange spectroscopy additionally reveals that significant exchange of ¹³CO₂ between crystals occurs on timescales of hundreds of milliseconds, much longer than the timescales employed here (Figure S10). In contrast, PFG NMR measurements on the powdered sample (typical crystallite lengths up to 15 μm, widths up to 2 μm; Figure S5) yield much larger effective self-diffusion values, on the order of 10⁻⁷–10⁻⁸ m²s⁻¹, reflecting the more rapid exchange of CO₂ between different crystallites as well as rapid diffusion in the inter-crystallite space. Indeed, the probed RMSDs in this experiment are between ~100–300 μm for a relatively short observation time of 20 ms, highlighting the need for large crystals to reliably measure intra-crystalline diffusion coefficients.

Further PFG NMR experiments on samples dosed at different ¹³CO₂ gas pressures yielded similar results (see PFG NMR spectra and fits in Figures S11 and S12). The measured diffusion parameters at pressures of 635, 1010, and 2026 mbar are shown in Figure 4c and Table 1. The diffusion values appear relatively constant at these pressures, a result that is perhaps unsurprising given the relatively small variations in CO₂ loading in the pressure range investigated (see CO₂ adsorption isotherm in Figure S2a).

Table 1.

Self-Diffusion Coefficients of ¹³CO₂ in Zn₂(dobpdc) at 298 K.

Pressure / mbar	D∥ / m2s−1	D⟂ / m2s−1	D∥ / D⟂
635	5.8 (± 0.1) × 10−9	1.9 (± 0.2) × 10−10	30 ± 3
1010	6.2 (± 0.2) × 10−9	2.3 (± 0.3) × 10−10	27 ± 4
2026	6.5 (± 0.2) × 10−9	1.4 (± 0.2) × 10−10	48 ± 7

Molecular Dynamics Simulations.

To further probe CO₂ diffusion in Zn₂(dobpdc), we performed MD simulations using (i) a fully flexible MOF lattice model and (ii) a rigid MOF lattice. Figure 5a shows the time-evolution of the mean square displacement (MSD) of CO₂ molecules in the different crystallographic directions for the flexible lattice model with a CO₂ pressure of 1 bar. Since log(MSD) is given by log(nD) + log(t) in the diffusive regime, a slope of 1 and a y–intercept of log(nD) are anticipated on a log-log plot, provided that sufficiently long times are probed to reach this regime. Inspection of the plot in Figure 5a thus informs an assessment of the diffusion behavior of CO₂ in Zn₂(dobpdc).

Figure 5.

(a) MSDs in different crystallographic directions from flexible MOF MD simulations at 298, 400, and 500 K and a CO₂ pressure of 1 bar. Individual one-dimensional MSDs were calculated for the a and b directions, and the average is shown in the plot. (b) Self-diffusion coefficients (298 K) along the c axis (D_//) at a range of pressures. Values are shown for rigid and flexible lattice MD simulations as well as those obtained using PFG NMR. The amount of CO₂ adsorbed for the PFG NMR samples was estimated from Figure S2a. See Figure S13b for a plot of D_// against CO₂ pressure.

Long-range self-diffusion of CO₂ occurs along the c axis, as anticipated, with the diffusive regime (slope = 1) being reached at times longer than ~10 ps (Figure 5a). In contrast, diffusion of CO₂ in the ab plane is limited to displacements within a single pore, with no diffusive jumps occurring between different channels. This observation is reflected by the apparent plateauing of the MSD in the ab plane at long times, with the diffusive regime never being reached. At 298 K, the MSD climbs to ~160 Ų at a time of 10 ns, corresponding to a RMSD of ~13 Å, which, as expected, is less than the pore diameter of ~22 Å.

Similar behavior is apparent at all three studied temperatures of 298, 400, and 500 K, as well as at a lower pressure of 0.01 bar (Figure S13a), indicating the absence of a thermally activated diffusion mechanism that could allow CO₂ to move between pores. MD simulations with a rigid lattice also revealed the absence of long-range diffusion in the ab plane. This observation from MD simulations, which is based upon the assumption of perfect crystals, is in contrast to the results from PFG NMR experiments, where crystal defects may affect CO₂ diffusion (see below).

The self-diffusion coefficients along the c axis (D_//) determined from MD simulations are shown in Figure 5b and Figure S13b. These simulations allow access to pressures from 10 mbar to 100 bar (a much wider range of pressures, and therefore CO₂ loadings, than is accessible with our current NMR apparatus), and reveal loading-dependent diffusion behavior. A clear increase in D_// is observed at very low loadings, followed by decreases at higher loadings. We postulate that at the lowest loadings, the small D_// values result from the high density of open metal sites. Indeed, DFT calculations of CO₂ diffusion pathways in a similar MOF, Mg₂(dobdc), have shown that the energy barrier for CO₂ to move from a metal site to a neighboring unoccupied metal site is ~300 meV (~30 kJmol⁻¹).²¹ After some of the metal sites become occupied by CO₂, additional lower energy pathways may give rise to the observed increase in D_//, particularly diffusive motion of CO₂ through the pore center, which bypasses interaction with metal sites that are already occupied by other CO₂ molecules (for Mg₂(dobdc) barrier ~40 meV or ~4 kJmol⁻¹).²¹ The availability of these additional pathways is exemplified by the upturn in D_// between 750 and 1000 mbar, which also corresponds to the point at which a loading of 1 CO₂ per Zn²⁺ site is surpassed in the simulations. At higher CO₂ loadings, the observed decreases in D_// are due to CO₂–CO₂ interactions. We note that PFG NMR gives smaller self-diffusion values than MD by a factor of ~10, with such discrepancies not uncommon in the literature.^51,52 In the present case, differences in the experimental and simulated values may arise from both the presence of crystal defects in the experiment and small errors in the parameterization of the force field used for simulations.

The MD simulations also allow a prediction of the chemical shift anisotropy parameter Δ_CSA. We assume that the observed chemical shift is dependent only on the molecular orientation of CO₂ relative to the applied magnetic field and that framework-CO₂ interactions do not significantly perturb the chemical shift. This is a reasonable assumption given that our experimentally observed isotropic chemical shifts do not deviate significantly from that observed for free CO₂ gas (Figure 3e). Furthermore, we assume that CO₂ molecules exchange rapidly between different adsorption sites within the pores, such as primary sites (metal-bound) and secondary sites (not directly metal-bound) on the NMR timescale. Following a previously published procedure,^40,53 we first obtain probability distributions for the molecular orientations of CO₂ molecules in the crystal frame from the MD trajectories. We then obtain motionally averaged chemical shift tensors by performing a weighted average using the orientation probability distributions (see Supporting Information for details). Predicted Δ_CSA values are then obtained from these tensors, and are compared to the reported values for solid CO₂,⁴¹ Δ_CSA,solid, as the order parameter Δ_CSA/Δ_CSA,solid (Table 2).

Table 2.

Δ_CSA values for ¹³CO₂ in Zn₂(dobpdc) at 298 K from MD simulations and NMR spectroscopy (Sample 1).

Method	Pressure / mbar	ΔCSA / ppm	ΔCSA / ΔCSA,solid
MD	750	−51.4	0.24
	1000	−51.5	0.25
	7500	−54.9	0.26
NMR	625	−6.5	0.03
	1010	−8.7	0.04
	2026	−12.1	0.06

Consistent with the NMR experiments, negative Δ_CSA values are obtained that increase in magnitude with pressure (Table 2). The values show reasonable agreement, with the discrepancies similar to those in a related study.⁴⁰ The values from MD are systematically larger in magnitude than the NMR values. This disagreement likely arises from the presence of crystal defects that will affect the orientations of the CO₂ molecules in the pores. Our observed increases of the magnitude of Δ_CSA with pressure is consistent with recent NMR measurements on the related metal-organic framework Mg₂(dobdc).²³ The observed increases in |Δ_CSA| with pressure likely reflect a competition between two factors: (i) the preferred orientation of CO₂ strongly interacting with Zn²⁺ in primary adsorption sites and (ii) the occupation of secondary binding sites with a range of different orientations. At low pressures the majority of CO₂ is bound in primary binding sites (see X-ray measurements below) and factor (i) will tend to dominate. At higher CO₂ pressures, an increasingly large population of CO₂ in secondary sites is present in the pores, and factor (ii) becomes increasingly important.

X-ray Crystallography.

To further explore the observed CO₂ diffusion behavior and the non-zero value of D_⊥ from PFG NMR, we used in situ single-crystal X-ray diffraction to investigate the structure of Zn₂(dobpdc) before (Figures 1 and S14) and after (Figure 6) exposure to 1.01 bar CO₂ at 298 K. Activated Zn₂(dobpdc) is isostructural with previously reported solvated structures (Figure 1),^9,17 and no clear distortions of the framework are evident following the adsorption of CO₂ (Figure 6).

Figure 6.

Views of the structure of Zn₂(dobpdc) under 1.01 bar CO₂ obtained from single-crystal diffraction at 298 K; light blue, red, gray, and white ellipsoids represent Zn, O, C, and H atoms, respectively. Note that CO₂ was found to be disordered over two orientations with occupancies of 34% and 30%. Thermal ellipsoids are drawn at a 50% probability level. In (b), CO₂ atoms are omitted to enable a clear view of the pore walls.

We further examined the framework structure to determine if CO₂ can pass through the small space between dobpdc^4– linkers in the ab plane (Figure 6b). The H···H separations between adjacent linkers are 2.5436(3) Å (central H atoms) and 2.7781(3) Å (outer H atoms). Taking the H atom van der Waals radius to be 1.1 Å,⁵⁴ the maximum pore size of ~0.6 Å is much smaller than the diameter of a CO₂ molecule (estimated as 3.4 Å, twice the van der Waals radius of carbon⁵⁵), such that diffusion of CO₂ in the ab plane is not expected. There are thus two most likely causes of the unexpected diffusion in the ab plane: (i) dynamics, (ii) defects.

Thermal ellipsoids drawn at a 50% probability level are shown in Figure 6 to aid the visualization of framework dynamics. The ellipsoids of the framework atoms are relatively small under the experimental conditions at 298 K, suggesting that there is little movement of the framework atoms over the average of all unit cells. We note that coordination of three oxygen donors at each end of the (dobpdc)^4– to the metal chains (one bridging and one non-bridging carboxylate oxygen, and one bridging aryloxide oxygen) restrain the linker, limiting the motion of the phenyl rings. This contrasts to other common MOF linkers such as bpdc^2– (bpdc²⁻ = biphenyl-4,4′-dicarboxylate) that only bind through carboxylate groups. In these frameworks, the phenyl groups of the linker are often free to rotate about the phenyl–carboxylate C–C bond, which results in large thermal ellipsoids even at 100 K.⁵⁶ Note that our crystallographic data does not rule out an activated process in which the framework distorts to allow CO₂ to pass through a transient pore, which would not be discernable by crystallography. However, the flexible lattice MD simulations (Figure 5a) reveal no evidence for such an activated process, even at temperatures as high as 500 K. We therefore conclude that framework dynamics are unlikely to be responsible for the non-zero D_⊥ value observed by PFG NMR spectroscopy.

A second explanation for diffusion between channels in the ab plane is the presence of crystal defects. For example, missing linkers or missing Zn²⁺ ions could result in porosity in the ab plane that would otherwise be absent. Refinement of the occupancy of the Zn²⁺ site relative to a fixed occupancy of the dobpdc^4– linkers suggests a slight deficiency of zinc, with 94.8(4)% and 96.8(4)% of the anticipated electron density observed for activated and CO₂-dosed (1.01 bar) Zn₂(dobpdc), respectively. Inductively coupled plasma optical emission spectrometry (ICP-OES) also indicated a slight deficiency of zinc compared to the expected molecular formula. Although elemental analysis gave H and C mass ratios that agree with the expected values for Zn₂(dobpdc) within error (Table S2), we note that some types of defects may not lead to significant changes in the material stoichiometry. The nature of the possible defects in this class of frameworks remains an active area of investigation.

Returning to the X-ray diffraction experiments, the CO₂-loaded structure (Figure 6) allows two preferred binding sites for CO₂ to be resolved. The primary adsorption site lies at the open Zn²⁺ coordination sites of the framework. We find that the Zn–O_CO2 distance is 2.528(12) Å, which is slightly longer than the distance of 2.43(4) Å determined by powder neutron diffraction from an earlier study of CO₂-dosed Zn₂(dobdc) at 10 K.¹⁴ This disparity in the distances may arise from the large difference in data collection temperature for the two structures. By comparison, the most common Zn–O_CO2 distance from our MD simulations at similar conditions (1 bar CO₂, 298 K) is 2.8–2.9 Å. This is in reasonable agreement with the DFT calculations to which the MD force field was parameterized, though slightly longer than that from X-ray diffraction. From previous DFT calculations using a dispersion-corrected functional,^57,58 it was observed that the preferred Zn–O_CO2 distance in Zn₂(dobdc) is 2.7 Å, which is approximately 0.2 Å longer than the other equilibrium M–O_CO2 distances calculated (M = Mg, Co, Fe, and Ni) and also slightly longer than that observed experimentally by diffraction. A systematic overestimation of the M–O_CO2 distances from DFT calculations has been observed previously with the same dispersion-corrected functional.¹⁴ The longer distance obtained from MD may also be partly accounted for by the relatively large thermal ellipsoid of the metal-bound oxygen in the X-ray diffraction structure (Figure 6a), which will tend to lengthen the Zn–O_CO2 distance. The bound CO₂ molecule in our X-ray structure exhibits disorder over two orientations with Zn–O–C angles of 152(3)° and 122(3)° and occupancies of 34% and 30%, respectively (Figure 6a). These occupancies correspond to a total of 0.64 CO₂ molecules per Zn, which is similar to the value of 0.72 expected from the gas sorption isotherm (Figure S2). The discrepancy between the two values likely arises due to the presence of some CO₂ at secondary binding sites, which are not resolvable in the diffraction experiments carried out here, but can be seen in our MD simulations (Figure S15). In the future, variable-pressure crystallographic experiments may help us to further understand the nature of the different binding sites, as has been performed for the smaller pore M₂(dobdc) materials.^14,59–61

Conclusions

The foregoing results demonstrate how the residual chemical shift anisotropy for CO₂ confined in the pores of the metal–organic framework Zn₂(dobpdc) allows measurement of the diffusion anisotropy using PFG NMR spectroscopy. Surprisingly, we find that the pore-confined gas is able to diffuse between adjacent framework channels in the ab plane, with self-diffusion coefficients of D_// = 5.8 ± 0.1 × 10⁻⁹ m²s⁻¹ and D_⊥ = 1.9 ± 0.2 × 10⁻¹⁰ m²s⁻¹ at 298 K and a pressure of 625 mbar of CO₂. Measurements at gas pressures between 625 and 2026 mbar yielded very similar diffusion values, while MD simulations showed significant variations of self-diffusion at more extreme pressures. In situ single-crystal diffraction experiments revealed no obvious structural distortions upon the adsorption of CO₂, while flexible lattice MD simulations revealed no diffusion between different channels in the ab plane. These findings indicate that defects in the framework structure are likely responsible for the observed non-zero diffusion in the ab plane. The marked diffusion anisotropy opens considerable opportunities for crystal engineering for CO₂ capture as well as other gas storage and separation applications, both for adsorbents and mixed-matrix membranes. For example, one could tune the crystal shapes and sizes to optimize fast adsorption and desorption, while the possibility of orienting MOF crystals with anisotropic diffusion properties in membranes should also be explored. The approaches described herein should be readily applicable to other porous materials exhibiting anisotropic pore structures.

EXPERIMENTAL SECTION

Materials and Methods.

All manipulations were performed under an N₂ atmosphere in a VAC atmospheres glovebox or using standard Schlenk techniques. The ligand H₄dobpdc was purchased from Hangzhou Trylead Chemical Technology Co. N,N-dimethylacetamide (DMA) and methanol were dried over 3-Å molecular sieves and then degassed via three successive freeze-pump-thaw cycles. Toluene and N,N-dimethylformamide (DMF) were deoxygenated by purging with Ar for 1 h and dried using a commercial solvent purification system designed by JC Meyer Solvent Systems. All other reagents were purchased from commercial sources and used without further purification. Adsorption isotherms for CO₂ and N₂ were obtained by volumetric methods using a Micromeritics ASAP 2020 gas adsorption analyzer. All gases were 99.998% purity or higher. The CO₂ isotherm recorded at 25 °C was measured using a circulating water bath. The N₂ isotherm at 77 K was measured using a liquid nitrogen bath. Laboratory powder X-ray diffraction patterns were collected using a Bruker AXS D8 Advance diffractometer using CuKα radiation (λ = 1.5418 Å). Elemental analysis (H, C, and N) was conducted using a Perkin Elmer 2400 Series II combustion analyzer. Inductively Coupled Plasma Optical Emission Spectrometry (ICP-OES) was conducting using an ICP Optima 7000 DV instrument.

Preparation of Zn₂(dobpdc) Single Crystals.

A previously reported method was used to produce Zn₂(dobpdc) crystals.¹⁷ Briefly, H₄dobpdc (164.6 mg, 600.0 μmol) was dissolved in 20 mL of DMA, while Zn(NO₃)₂∙6H₂O (446.2 mg, 1500 μmol) was dissolved in 40 mL of a 1:1 (v/v) mixture of distilled water and ethanol. The two solutions were combined and ~10 mL aliquots were dispensed into 0.5 inch outer diameter borosilicate tubes. Each tube was subjected to three freeze-pump-thaw cycles and then flame-sealed. The sealed tubes were placed in an oven preheated to 100 °C and kept at that temperature for 2 days. The resulting pale yellow, needle-shaped crystals were collected and washed by soaking in excess dry DMA, dry methanol, and dry toluene (3 washes for each solvent, each wash for at least 2 h at room temperature) under an Ar atmosphere. The crystals for Sample 1 were activated at 250 °C under flowing Ar for 12 h. For Sample 2, a second 24-h activation period (at 250 °C under high vacuum) was carried out.

Synthesis of Zn₂(dobpdc) Powder.

A 1-L three-neck round-bottom flask was charged with H₄dobpdc (2.74 g, 10.0 mmol), ZnBr₂∙2H₂O (8.35 g, 32.0 mmol), ethanol (250 mL), and DMF (250 mL). The mixture was deoxygenated by purging with dry Ar for 1 h. The resulting solution was heated with magnetic stirring for 12 h at 120 °C under an Ar atmosphere. After allowing the reaction mixture to cool to room temperature, the solvent was decanted and the resulting off-white microcrystalline powder was washed by soaking three times in 500 mL of dry DMF at 120 °C for 24 h, then soaking three times in 500 mL of dry methanol at 120 °C for 24 h. The methanol-solvated powder was then filtered under Ar via cannula and desolvated by heating under dynamic vacuum at 180 °C for 24 h to give fully desolvated Zn₂(dobpdc). Yield: 1.94 g (48.4%). Langmuir surface area (N₂, 77 K): 3110 m²/g. The powder X-ray diffraction pattern of the material was found to match the pattern simulated from the single-crystal structure (see Figure S16).

Single-Crystal X-ray Diffraction Experiments.

Activation and gas dosing of single crystals were performed using a custom-designed environmental gas cell modified from a previous system.⁶¹ A single crystal was first mounted on a MiTeGen loop using a minimal amount of epoxy, taking care to avoid the ends of the rod-shaped crystals. The sample was then transferred to the environmental cell, which consists of a borosilicate capillary with a vacuum-tight O-ring seal and a Beswick ball valve for dosing. Within the cell, the crystal was desolvated for 1 h at an external temperature of 200 °C using an Oxford Cryosystems cryostream and a turbomolecular pump. After solving the structure to confirm the absence of residual solvent in the pores, the crystal was cooled to 298 K, and the activated structure was collected. The crystal was then dosed with 1.01 bar of CO₂ to obtain the structure of Zn₂(dobpdc)∙1.26CO₂.

Single-crystal X-ray diffraction data were collected at Beamline 11.3.1 at the Advanced Light Source, Lawrence Berkeley National Laboratory using synchrotron radiation (λ = 0.7749 Å) and a Bruker AXS D8 diffractometer equipped with a PHOTON100 CMOS detector. Both Zn₂(dobpdc) and Zn₂(dobpdc)∙1.26CO₂ were refined in space group P3₁21 as inversion twins based on Flack parameter values near 0.5. Raw data were corrected for Lorenz and polarization effects using Bruker AXS SAINT software⁶² and were corrected for absorption using SADABS.⁶³ The structures were solved using SHELXT⁶⁴ and refined using SHELXL⁶⁵ operated in the OLEX2⁶⁶ interface. Thermal parameters were refined anisotropically for all non-hydrogen atoms. All hydrogen atoms were placed geometrically and refined using a riding model. Disorder modeling of the CO₂ molecules bound to Zn²⁺ in Zn₂(dobpdc)∙1.26CO₂ required the use of displacement parameters (RIGU and SIMU) and distance (DFIX) restraints.

Face-indexing was performed at the CheXray Facility at UC Berkeley with a hexanes-solvated single crystal of Zn₂(dobpdc) exposed to air. The crystal was mounted on a Bruker QUAZAR diffractometer (Mo-Kα, λ = 0.71073 Å) equipped with a Bruker APEX II detector. Analysis of the crystal was performed using the Bruker APEX3 software.⁶²

Preparation of Samples for NMR Experiments.

Valved high-pressure 5-mm NMR tubes (Norell) were filled with activated crystals, and the tube was connected to a custom dosing apparatus (Figure 2a). Samples were first evacuated for at least 30 min before dosing with ¹³C-enriched CO₂ gas (Sigma Aldrich, 99 atom % ¹³C, <3 atom % ¹⁸O) for 30 min for equilibration. For ex situ dosing (as performed for Sample 1), the valve on the NMR tube was then closed before NMR measurements. For in situ dosing (Sample 2), measurements were made with the sample still attached to the custom dosing manifold. Here a long piece of copper tubing was used to connect the sample inside the NMR magnet to the dosing manifold.

NMR experiments.

Static NMR experiments were conducted using the magnetic field strengths indicated in the Figure captions. Liquid state probes and 5-mm sample tubes were used for all static measurements. MAS experiments (spectra are shown in the Supporting Information) were conducted using a DOTY 4-mm double resonance probe. For PFG NMR experiments, a Diff-30 probe and a 13-interval pulse sequence with bipolar magnetic field gradient pulses was employed (Figure S8).⁶⁷ Gradients were calibrated using the known self-diffusion coefficient of water at 25 °C (2.3 × 10⁻⁹ m²s⁻¹).⁶⁸ To test the system performance, diffusion coefficients were measured and verified against literature values for acetone, cyclohexane, toluene and glycerol at 24 °C,^68–70 covering a range of self-diffusion coefficients from 5 × 10⁻⁹ m²s⁻¹ (acetone) to 2 × 10⁻¹² m²s⁻¹ (glycerol). For experiments on MOF samples, the effective duration of the individual magnetic field gradient pulses (δ′) was 1 ms, and the maximum magnetic field gradient strength applied was 9 T m⁻¹, with sine-shaped gradient pulses used. Observation times (Δ) are stated in the text and were set to integer multiples of the period (20 ms) of the 50 Hz mains alternating current to mitigate potential issues from residual mains hum.³¹ The parameter τ was 3 ms (Figure S8). The PFG NMR decays were analyzed using Equations 3 and 4 and a fitting program written in Matlab software. ¹³C NMR chemical shifts are referenced to the ethylene carbon of neat ethanol at 57.4 ppm as a secondary reference relative to tetramethylysilane (1 vol. % in deuterated chloroform) at 0.0 ppm, except for MAS experiments that are referenced to the tertiary carbon atom in adamantane at 38.5 ppm.

Molecular Dynamics Simulations.

Molecular dynamics (MD) simulations were performed in the NVT ensemble with LAMMPS⁷¹ using a timestep of 1.0 fs and the Nosé-Hoover chain thermostat.^72,73 The dynamics of CO₂ were treated using a rigid-body time integrator.⁷⁴ The CO₂ molecules were modeled using the TraPPE force field,⁷⁵ and CO₂-framework interactions were modeled using a previously published force field.⁵⁸ The flexible lattice simulations required a molecular model for the framework atoms. Bond, angle, dihedral and torsion parameters for linker molecules were taken from the consistent valence force field,⁷⁶ while Zn²⁺ ions were modeled using a cationic dummy model.⁷⁷ Lorenz-Berthelot mixing rules were used to calculate cross-interactions between Zn²⁺ and linker atoms. For simulations at different pressures, the framework was loaded with a number of CO₂ molecules corresponding to previously published isotherms.⁵⁸ All MD simulations were equilibrated for 1 ns, and production runs lasted at least 10 ns to ensure that the mean-squared displacement (MSD) became linear as a function of time. The order-n algorithm^78,79 was used to calculate the MSD as a function of time, and the 1D self-diffusion coefficients were obtained by fitting the slope of the linear regime:

$$D=\frac{1}{2}{\text{lim}}_{t\to \infty }\frac{d}{dt}\langle [r(t)-r{(0)}^2]\rangle$$