In-Class Attention, Spatial Ability, and Mathematics Anxiety Predict Across-Grade Gains in Adolescents’ Mathematics Achievement

Abstract

Identifying meaningful cognitive and non-cognitive predictors of mathematical competence is critical for developing targeted interventions for students struggling with mathematics. Here, 317 students’ short-term verbal memory, verbal and visuospatial working memory, complex spatial abilities, intelligence, and mathematics attitudes and anxiety were assessed, and their teachers reported on their attentive-behavior in seventh-grade mathematics classrooms. Bayesian regression models revealed that complex spatial abilities and in-class attention were the most plausible predictors of seventh-grade mathematics, but not word reading, achievement, controlling for prior achievement. These results were confirmed with multilevel models that revealed interactions between these factors and prior achievement. The largest gains were among students with strong mathematical competencies in sixth-grade, and average or better in-class attention in seventh-grade as well as above average spatial abilities. High mathematics anxiety was associated with lower attention and through this indirectly influenced achievement gains. These results have implications for how to best target interventions for students at risk for long-term difficulties with mathematics.

There is consensus that students’ mathematical competence at school completion contributes to their preparation for and options in college, improves their wages in the labor market, and facilitates their decision making in many routine contexts, such as that related to their health care (Bynner, 1997; National Mathematics Advisory Panel, 2008; Reyna, Nelson, Han, & Dieckmann, 2009). There is also consensus that existing mathematical knowledge contributes to the learning of new knowledge, such that students who are behind in one grade will tend to remain behind in subsequent grades, controlling other factors (Duncan et al., 2007). At the same time, the mix of factors that contribute the most to growth in mathematical competencies remains uncertain. The proposed mechanisms include attitudes and beliefs about one’s mathematical competence and the long-term utility of mathematics (Eccles & Wigfield, 2002; Lauermann, Tsai, & Eccles, 2017), mathematics anxiety (Ashcraft & Kirk, 2001; Dowker, Sarkar, & Looi, 2016), domain-general cognitive abilities (Geary, Nicholas, Li, & Sun, 2017; Lee & Bull, 2016), specific cognitive abilities (e.g., spatial; Mix & Cheng, 2012), and in-class attention (Fuchs et al., 2006). The wide range of proposed mechanisms means it is unclear how to best focus interventions for students at risk for long-term difficulties. To narrow this focus, we conducted a broad assessment of functioning in these areas with the goal of identifying the most important contributors to gains in mathematics during middle school.

Cognitive Mechanisms

We were particularly interested in the relation between spatial abilities and mathematics outcomes, as there is a consistent relation between these abilities and accomplishment in science, technology, engineering, and mathematics (STEM) occupations in adults (Lubinski & Benbow 2006; Kell, Lubinski, Benbow, & Steiger, 2013), albeit this relation is not consistently found in children (Mix & Cheng 2012). One potential reason is that visuospatial abilities are less important for much of the mathematics encountered in early grades but become increasingly important for mathematics encountered in later grades (Li & Geary 2017), including some aspects of pre-algebra and algebra (Casey, Nuttall, & Pezaris, 1997; Casey, Nuttall, Pezaris, & Benbow, 1995; Kyttälä & Lehto 2008; Mix, 2019; Tolar, Lederberg, & Fletcher, 2009). Moreover, there are different types of spatial abilities that could be differentially related to gains in mathematics across grade levels or across different types of mathematical content (Gilligan, Hodgkiss, Thomas, & Farran, 2019; Hawes & Ansari, 2020; Uttal et al., 2013). The result is substantive ambiguity in whether and if so how and when various spatial abilities contribute to mathematics learning. We assessed students’ visuospatial working memory and two more complex spatial abilities to determine which aspects of spatial ability might be particularly important for mathematics achievement during middle school.

Intelligence and working memory (holding information in mind while engaged in other processes) are consistent predictors of longitudinal gains in mathematics achievement and thus were also included in our assessments (Bull & Lee, 2014; Deary, Strand, Smith, & Fernandes, 2007; Geary et al., 2017; Lee & Bull, 2016). Among other things, working memory processes contribute to the ease of engaging in any multi-step process, including performance on complex spatial tasks (Tolar et al., 2009). As with spatial abilities, the dynamic relations between various aspects of working memory and mathematics learning are not fully understood (Miller-Cotto & Byrnes, 2019; Paas & Ayres, 2014). Our inclusion of different types of working memory measures could help to clarify these relations. In addition to visuospatial working memory, we included measures of verbal short-term and working memory as these appear to contribute to basic number processing (Krajewski & Schneider, 2009), but may become less important as mathematics becomes more complex (Li & Geary, 2017). Moreover, correlations between spatial abilities and mathematics outcomes could emerge due to the influence of working memory on spatial-task performance and not spatial abilities per se. The simultaneous consideration of both working memory and spatial cognition measures helps to mitigate this potential confound.

Attitudes, Anxiety, and In-Class Attention

Various outcomes in mathematics, including grades, standardized achievement scores, and pursuit of math-intensive careers are correlated with confidence or efficacy about one’s abilities and to beliefs about the utility of mathematics (Eccles & Wang, 2016; Eccles, J. S., & Wigfield, 2002). For older students and adults there appear to be bidirectional influences between mathematical competence and these beliefs and attitudes (Talsma, Schüz, Schwarzer, & Norris, 2018; Valentine, DuBois, & Cooper, 2004), but the strength of these relations is less certain across elementary and middle school students (Geary et al., 2019; Gunderson, Park, Maloney, Beilock, & Levine, 2018). In any event, Lauermann et al. (2017) found reciprocal relations between mathematics self-efficacy and utility beliefs and math-intensive career plans throughout high school that in turn predicted employment in a mathematics-intensive profession 15 years later (controlling intelligence).

Casey et al. (1997) found that the combination of spatial ability and mathematics self-efficacy but not math anxiety predicted SAT-Mathematics scores. Despite Casey et al.’s (1997) null result, relation between mathematical competencies and mathematics anxiety are often found (Ashcraft & Kirk, 2001; Dowker et al., 2016; Ma & Xu, 2004). For instance, Byrnes and Miller-Cotto (2016) found that internalizing issues, including anxiety, were related to slower mathematics growth across the third- and eighth-grade academic years, controlling many other factors. Mathematics anxiety can also result in an avoidance of mathematics and through this an avoidance of career paths involving even basic mathematics (Hembree, 1990; Meece, Wigfield, & Eccles, 1990).

Moreover, higher mathematics anxiety is associated with poor spatial abilities and anxiety about spatial-related activities that in turn creates a confound if only anxiety or spatial abilities are assessed (Ferguson, Maloney, Fugelsang, & Risko, 2015). For instance, the correlation between math anxiety and mathematics outcomes might be more directly related to a reduced use of spatial strategies during mathematical problem solving than to anxiety per se. Consideration of both spatial and anxiety measures enables a more rigorous examination of their relative contributions to mathematics achievement.

It is not surprising that there is a consistent relation between teacher-ratings of students’ in-class attention and concurrent and longitudinal gains in mathematical competencies (Fuchs et al, 2006; Fuchs, Geary, Compton, Fuchs, &. Hamlett, 2014; Geary, Hoard, Nugent, & Bailey, 2013). These behaviors include sustained attention and attention to details during school-related activities, as well as distractibility in the classroom (J. M. Swanson et al., 2012), and are not fully captured by standard measures of attentional control and working memory. Indeed, many of these studies have found that working memory, intelligence, and in-class attention simultaneously predict gains in mathematics achievement, but these studies have not included measures of mathematics attitudes or anxiety.

In-class attention also provides a potential mechanism through which attitudes and anxiety might influence students’ mathematical development. Strong self-efficacy and belief in the utility of mathematics should, in theory, be related to greater engagement in mathematics classrooms. Experimental studies have shown that mathematics anxiety can disrupt the processing of mathematical information through disruption of the top-down ability to maintain attentional focus on problem solving (Ashcraft & Kirk, 2001; Hopko, McNeil, Gleason, & Rabalais, 2002; Suárez-Pellicioni, Núñez-Peña, & Colomé, 2014). The result is a reduction in functional working memory capacity and greater susceptibility to distraction by irrelevant information. It is not unreasonable to assume that mathematics anxiety might also result greater proneness to distraction in mathematics classrooms (Pekrun, 2006). If so, then mathematics anxiety might directly undermine performance on mathematical tasks and might indirectly reduce growth in mathematical competencies by reducing engagement in mathematics classrooms and thereby reducing the opportunity to learn (Byrnes & Miller-Cotto, 2016).

Current Study

Evidence can be marshalled in support of myriad cognitive, attitudinal, and emotional contributors to year-to-year gains in students’ mathematics achievement. Many of the associated studies have assessed traits in multiple domains, allowing for an estimation of the relative contributions of one trait (e.g., spatial abilities) or another (e.g., self-efficacy) to mathematics achievement (e.g., Byrnes & Miller-Cotto, 2016; Casey et al., 1997; Geary et al., 2017; Lauermann et al., 2017; Tolar et al., 2009). None of these studies, to our knowledge, has provided a broad simultaneous assessment of all the different cognitive and non-cognitive traits that have been proposed as influencing children’s mathematical development. Moreover, there are different competencies within specific domains, such as spatial abilities (Uttal et al., 2013), and the relative relation of these different competencies with mathematical development are not well understood (Gilligan et al., 2019).

As a result, it is not entirely clear which combination of factors are the most important for year-to-year gains in mathematics or whether this combination varies at different points in children’s schooling. We provide this broad assessment and focus on the middle school years. Mathematical competencies during these years are particularly important because any deficits at this time are likely to presage difficulties with high school algebra, which is the cornerstone for learning more complex mathematics (National Mathematics Advisory Panel, 2008).

Even for the studies that include the assessment of multiple traits, multi-collinearity among them results in potential confounds. To address these potential confounds, we used Bayesian methods that are better suited to identifying predictors among correlated variables than are standard methods. This approach allowed us to first identify the most plausible contributors to seventh-grade mathematics achievement within the broad non-cognitive (e.g., math anxiety) and cognitive (e.g., different types of spatial ability or working memory) domains. These contributors were then used in standard multilevel models of growth in mathematics achievement from sixth- to seventh-grade.

Method

Participants

The participants were 317 (154 boys) seventh-graders enrolled in an on-going longitudinal study conducted in collaboration with the Columbia Public Schools in Columbia, MO. They were recruited across two cohorts from a larger group of 2,027 students who were assessed on a battery of mathematical competencies along with mathematics and English attitudes and anxiety at the end of sixth grade. Of this larger group, data were missing (e.g., no information on student sex) for 101 students, leaving 1,926 of them for construction of a sixth-grade mathematical competence measure (below; Geary et al., 2019). All 1,926 students were invited to join the longitudinal component of the study and 342 of them and their parents did so. The 317 students included here completed all of the seventh-grade assessment sessions, and their mathematics teachers reported on their in-class attention. The mathematics teachers of the 25 students who were dropped did not report on their in-class attention; their sixth-grade mathematical competence did not differ from that of the 317 remaining students (p = .947). The sixth-grade mathematical competence of the current sample (M = 104.66, SD = 14.98) was higher than that of the students who did not enroll for the longitudinal component (M = 99.00, SD = 14.74), d = .38, p < .001.

For students in the longitudinal component, demographic information was obtained through a parent survey. As not all questions were answered on each survey, the n varied for the demographic variables (n = 259 to 278, depending on the particular item). For the group of 317 students, 88% of them were non-Hispanic, 6% were Hispanic or Latino, and the ethnic status of the remaining students was unknown. The racial composition was 70% White, 14% Black, 3% Asian, 1% Native American, 10% multiracial, with the remaining unknown. Self-reported annual household income was distributed as follows: $0–$24,999 (12%); $25,000–$49,999 (18%); $50,000–$74,999 (12%); $75,000–$99,999 (22%); $100,000–$149,999 (19%); and $150,000+ (17%). Sixty-three percent of the students had at least one parent with a college degree. Fifteen percent of the families received food assistance, and five percent received housing assistance.

Sixth-Grade Mathematics Competence

The tests and detailed instructions (https://osf.io/qwfk6/), as well as the raw data (https://osf.io/p7vzc/) for the key analyses are available at the Open Science Framework (OSF). The assessment included an Exponents and Radical Rules Test that is not reported here because of a high nonresponse rate. The remaining tests assess basic mathematics knowledge and skills typically expected for sixth graders. All of the tests were administered using paper-and-pencil for the first cohort, and the Equality Problems, Fractions Comparison Test, Fractions Number Line, Equal Sign items, and Academic Attitudes and Mathematics Anxiety tasks were assessed using iPads for the second cohort. There were only 2 significant cohort effects (all other ps > .07), whereby students in the first cohort scored higher on the arithmetic fluency (p = .002, d = .14) and fractions comparison test (p < .001, d = .17). Given the null effects for all other measures and the small difference for the arithmetic fluency and fractions comparison test, the two cohorts were combined.

Arithmetic fluency.

Students were allowed a total of 2 min to solve as many whole-number arithmetic problems as possible; addition (n = 24; e.g., 87 + 5), subtraction (n = 24; e.g., 35 − 8), and multiplication (n = 24; e.g., 48 × 2). The score was the number correct across the three operations (M = 18.94, SD = 6.25; α = .57).

Equality problems.

This 10-item multiple choice test assessed students’ understanding of equality in the context of problems presented in non-standard formats, such as 8 = __ + 2 – 3. Students did not answer 3.7% of the items and these were scored as incorrect. An equality composite was the percent correct for the 10 items (M = .80, SD = .24, α = .80).

Fractions arithmetic.

This test included sets of twelve addition (e.g., 1/3 + 1/6), twelve multiplication (e.g., 1/4 × 1/8), and 10 division (e.g., 2 ÷ 1/4) problems. Students had 1 min for each operation. The score was the sum of the number of addition (M = 5.86, SD = 3.80), multiplication (M = 2.98, SD = 3.04) and division (M = 1.49, SD = 2.38) problems that were solved correctly (α = .62).

Fractions comparison.

Students were presented with 48 pairs of fractions and were asked to circle the larger one within 90 sec. The 48 pairs were composed of four item types that reflect common problem-solving errors and strategies (Geary et al., 2013; Hecht, 1998; Hecht, Close, & Santisi, 2003). The first type assesses students’ understanding of the inverse relation between the value of the denominator and the quantity represented by the fraction; here, the numerator is constant but the denominator differs (e.g., 2/4 2/5). In the second type numerators have a ratio of 1.5 and denominators a ratio between 1.1 and 1.25 (e.g., 3/10 2/12), making identification of the larger magnitude easier using numerators (correct) than denominators (incorrect). Numerators and denominators in the third type are reversed (e.g., 5/6 6/5), which requires students to choose the fraction with the larger numerator and smaller denominator. The final type involves skill at using 1/2 as an anchor for estimating fraction values (e.g., 20/40 8/9). A composite was based on performance (correct – incorrect; M = 16.70, SD = 15.32) across the four item types (α = .87).

Fractions number line.

Following Siegler, Thompson, and Schneider (2011), students were asked to place (one at a time) 10 fractions on the 0 to 5 number line; 10/3, 1/19, 7/5, 9/2, 13/9, 4/7, 8/3, 7/2, 17/4, 11/4. Target fractions were in large font and centered above the line. Students were given 4 min to complete the 10 items, and 94.4% of the lines were completed. The data for the remaining 5.6% of lines were estimated using the average of five estimates derived from the multiple imputations procedure in SAS (2014). The score for each item was the absolute percent deviation between the placement and the correct location, and the overall score was the mean of the 10 items (M = 20, SD = 14, α = .85). The latter was multiplied by −1 so that higher scores represent more accurate placements.

Equal sign.

Two items focused explicitly on the ‘=’ (McNeil et al., 2011). The first asked students to identify the meaning of the symbol ‘=’ in ‘3 + 4 = 7’; the options were ‘add the numbers’, ‘solve the problem’, ‘same as’, and ‘the answer’. The second asked students to identify the symbol that indicated that five pennies were the same as one nickel; the options were ‘5 cents’, ‘=’, ‘+’, and ‘don’t know.’ Performance on the first (M = 28% correct) and second (M = 87% correct) items was only weakly correlated (r = .12, p < .001), but each was correlated with the other mathematics variables (rs = .16 to .30, ps < .001). Thus, we include both as separate items.

Mathematics competence.

The scores for all of the measures were submitted to a principle components analysis (SAS, 2014). The analysis yielded one factor with an eigenvalue greater than one that explained 45% of the covariance among the measures. Next, each individual variable was standardized (M = 0, SD = 1) and a composite was created based on their mean (α = .78). To make the scores comparable to the standardized measures (below), the composite was then rescaled (M = 100, SD = 15).

Academic Attitudes and Anxiety

The measures of mathematics and English attitudes were from the Michigan Study of Adolescent and Adult Transitions (http://garp.education.uci.edu/msalt.html) and are designed to assess students’ self-evaluated efficacy in and their beliefs about the long-term utility of these areas (Eccles & Wigfield, 2002; Meece et al., 1990). The mathematics measure included seven items on a 1-to-7 Likert scale; e.g., “How much do you like doing math?” rated from 1 (a little) to 7 (a lot), with the six English items being similar. Previous analyses using an exploratory principle components analysis, as well as parallel and MAP analyses (R Core Team, 2017), indicated that the mathematics items defined two factors and the English items one factor (Geary et al., 2019).

Mathematics attitudes.

The loadings of individual items on their respective factors were consistent with distinct utility (Items 1 to 4, inclusive) and self-efficacy (Items 5 to 7) dimensions. The scores were the sum of the corresponding items (α = .72 for utility, and .78 for self-efficacy).

English attitudes.

The score was the mean of the six items (α = .83).

Mathematics anxiety.

The 10 items were adapted from Hopko, Mahadevan, Bare, and Hunt (2003). Each item (e.g., “Taking an examination in a math course”) was rated on a 1 (low anxiety) to 5 (high anxiety) scale. All three analyses (i.e., EFA, MAP, parallel) indicated two factors. The first was defined by five items that involved learning mathematics (e.g., “Watching a teacher work an algebraic equation on the board”; items 1, 3, 6, 7, 9). The second factor was defined by four items that involved some type of evaluation (e.g., “Taking an examination in a math course”; items 2, 4, 5, 8), and the final item (i.e., “In general, how anxious are you about math?”). Composite scores were based on the mean of the five learning anxiety items (α = .76) and the five evaluation anxiety items (α =.86). The two core factors identified here are consistent with previous findings (Baloglu & Koçak, 2006).

In-Class Attention

We used the Strength and Weaknesses of ADHD-Symptoms and Normal-Behavior (SWAN) measure of in-class attention (J. M. Swanson et al., 2012). The measure includes items that assess attentional deficits and hyperactivity, with scores that are normally distributed and based on the behavior of a typical student in the classroom. The nine item (e.g., “Gives close attention to detail and avoids careless mistakes”) attention subscale was distributed to the students’ seventh-grade mathematics and language arts teachers who were asked to rate the behavior of the student relative to other students of the same age on a 1 (far below) to 7 (far above) scale. To keep the focus strictly on mathematics, the score was the mean across the nine items completed by their mathematics teachers (M = 4.83, SD = 1.45; α = .98)

Standardized Measures

Intelligence.

The Vocabulary and Matrix Reasoning subtests of the Wechsler Abbreviated Scale of Intelligence (WASI; Wechsler, 1999) were used to estimate full scale IQ, following procedures detailed in the manual. The intelligence of the sample was average (M = 104.52, SD = 12.83).

Achievement.

Mathematics and reading achievement were assessed using the Numerical Operations and Word Reading subtests from the Wechsler Individual Achievement Test–Third Edition (Wechsler, 2009), respectively. The mathematics (M = 99.68, SD = 18.36) and reading (M = 104.69, SD = 13.01) achievement of the students was average.

Cognitive Measures

Most of the cognitive tasks were administered on iPads using customized programs developed through Inquisit by Millisecond (https://www.millisecond.com). The verbal memory and proactive inhibition task was administered using a customized program developed in Qualtrics (https://www.qualtrics.com); manuals and detailed descriptions are available on OSF (https://osf.io/qwfk6/). All of the tasks are standard measures of short-term and working memory, verbal memory, and various aspects of spatial ability.

Digit span.

The administration of the forward and backward digit span measures followed Experiment 1 in Woods et al. (2011). The students heard a sequence of auditory digits, at 1 sec intervals starting with 3 digits for the forward assessment and 2 digits for the backward assessment. The task is to recall the digit list in order (in either a forward or backward manner, respectively) by tapping the digits on a circle of digits displayed on the screen. If the response is correct (in digits and presentation order), the student moves up to the next level. If the response is incorrect, the same level is presented a second time. If a consecutive error occurs, the student moves down to a lower level. Each direction (forward and then backward) ends after 14 trials. The student’s score was the highest digit span correctly recalled before making two consecutive errors at the same span length (M = 5.71, 4.59, SD = 1.12, 1.20 for forward and backward, respectively).

Verbal memory.

The verbal memory measure was taken from a longer proactive inhibition task. The student listens to a recording of a set of four animal words, presented in 1-sec intervals using the iPad speakers. To prevent rehearsal of the words, the student immediately names colors from a sheet with rows of different colors for 10 sec. After 10 sec, a tone prompts the student to recall the words, in order. Responses are recorded by the experimenter using Qualtrics on the iPad including options for recalling a word that was not presented (“other”) and “don’t know.” The process is repeated with two new sets of four animal words, and finally with a set of four fruit words. Items were taken from Gilhooly and Logie (1980) and Paivio, Yuille, and Madigan (1968). The words were chosen based on Imagery (I) and Concreteness (C) ratings (1 to 7 scale), with all scores > 6. The one exception was ‘lime’ (imagery of 5.7), which was included because it was the closest (to 6.0) available one-syllable fruit word. Each quartet included one moderate to high frequency word and three low frequency words (< 10/million), and three one syllable and one two-syllable words. All within-list words started with different letters and presentation orders were initially randomized, and subsequently presented in the same order to all students. We used percent correct on the first quartet of words as a measure of short-term verbal memory (M = .68, SD = .28).

n-back.

An adaptive version of a single n-back task with letters was administered following Jaeggi et al. (2010). The student is shown a “target” letter and then a sequence of 20 stimulus letters (all consonants; 6 are target; 14 are not; order determined randomly), and asked to indicate whether the currently presented letter is a target by tapping a key, or is not a target by not responding. The target letter could be the first stimuli presented (N = 0) or could be the same as the one that preceded it (N = 1) or the same as one presented in the two (N = 2) or three (N = 3) trials that preceded it.

Each trial presents a letter for 500 ms, followed by a 2,500 ms blank screen, and then by the next letter in the sequence. Students have the entire 3,000 ms to respond by tapping a key if they detect a target. After instructions and three 10-item practice blocks for levels N = 0 to N= 2, all participants start on level N = 0. Depending on performance, they move up, stay on the current level, or move down a level for five total blocks (<3 errors – move up; 3 – 5 errors – repeat level; >5 errors – move down). Performance feedback (percent correct) is displayed after each block. Hits (H), Misses, False Alarms (FA), and Correct Rejections are recorded and summarized by block. The score is (H – FA)/(total blocks); M = 3.80, SD = 0.76.

Spatial span.

The forward Corsi Block Tapping Task was administered following Kessels, van Zandvoort, Postma, Kappelle, and de Haan (2000). Students are presented with a display of nine squares that appear to be randomly arranged. The squares “light up” in a pre-determined sequence (constant across participants), and students are asked to tap on the squares in the same order they were lit. The sequence length starts at two squares (level = 2) and could increase to up to nine squares. Students have two attempts at each sequence length. If one of the sequences is recalled correctly, the next sequence level begins; if both sequences at a level are recalled incorrectly, the task is terminated. The score is the total number of correctly recalled sequences across the whole task (M = 8.34 SD = 1.83).

Spatial ability.

The first spatial measure was the Judgment of Line Angle and Position Test (JLAP), following Collaer, Reimers, and Manning (2007). The task requires students to match the angle of the single presented line to one of 15-line options in an array at the bottom center of the iPad screen. There are 20 test items presented one at a time, and the student uses the touch screen to select the matching angle. Each stimulus is presented for a maximum of 10 sec, and when a selection is made, a reaction time is recorded and the next stimulus is immediately presented. The outcome is the number correct (M = 13.33, SD = 3.03).

The second measure was Peters et al.’s (1995) Mental Rotation Task (MRT-A). On each trial, the student views images of 3D drawings of 10 connected cubes. For each trial, there is one target and four choice options, and the task is to select the two options that are the same figure as the target, only rotated to various degrees. After four self-paced practice problems, students are presented with 24 problems in two blocks of 12 problems each (3 min per block). The score is the number of problems on which the student chose both correct options (M = 8.75, SD = 4.13).

Procedure

The 45-min end of sixth-grade assessment was administered in mathematics classrooms to groups of 14 to 32 students. For the longitudinal component, students were administered the intelligence, achievement, attitudes, anxiety, and cognitive measures individually at a quiet location in their school across three 45-min assessments. As shown in Table 1, with the exception of the verbal memory task (due to time constraints), the cognitive measures were administered the first semester of seventh grade, and the remaining measures in the second semester. Parents provided informed written consent, and assent was obtained from adolescents for all assessments. The University of Missouri Institutional Review Board (IRB; Project 2002634, “Algebraic Learning and Cognition”) approved all methods included in this study.

Table 1.

Age of administration and timing of assessments

Task Name	Mean (SD)	6th Grade Spring	7th Grade Fall	7th Grade Spring
Mean Age at test		147	153	156
Mathematics Competence (6th grade)	104.66 (14.98)	x
Mathematics efficacy	5.00 (1.02)			x
Mathematics utility	5.27 (1.00)			x
Mathematics anxiety for learning	1.72 (0.66)			x
Mathematics anxiety for evaluations	2.63 (0.96)			x
Digit span forward	5.71 (1.12)		x
Digit span backward	4.59 (1.20)		x
N-back	3.80 (0.76)		x
Corsi	8.34 (1.83)		x
JLAP	13.33 (3.03)		x
Mental Rotations Test	8.75 (4.13)		x
Verbal Memory	0.68 (0.28)			x
Intelligence	104.52 (12.83)			x
Word Reading	104.69 (13.01)			x
Numerical Operations	99.68 (18.36)			x
In-class attention (math classroom)	4.83 (1.45)			x

Note: Age is in months, SDs range between 4.41 and 4.50 months. JLAP = Judgment of Line Angle and Position.

Analyses

We first used Bayesian regressions to provide a robust and transparent means for selecting the best set of cognitive and non-cognitive predictors for inclusion in the main analyses (Gallistel, 2009; Rouder & Morey, 2012), using the BayesFactor package in R (v0.9.12–4.2; Morey & Rouder, 2015). Default prior scales for standardized slopes were used, r_scale = ½. Bayes factors provide straightforward information regarding whether the inclusion of specific variables improves model fit above and beyond other specified variables. This model selection method is more robust than standard linear regression, especially with potential multi-collinearity, as with the current data. Bayes factors are higher when one of two highly correlated variables are included in relation to models containing both or none, providing the ability to compare the relative contribution of the predictors. In separate analyses, we selected the best combination of cognitive and then non-cognitive predictors of raw seventh-grade Numerical Operations scores. The variables identified from each of these analyses were subsequently used in a follow-up analysis to identify the best combination of cognitive and non-cognitive predictors of these scores. In a final model, sixth-grade mathematical competence scores were included with this combination to control for prior achievement. The sequence of analyses provides structured, step-by-step information on the best set of cognitive, non-cognitive, and combined predictors of seventh-grade mathematics achievement.

The first set of Bayes factors are noted as MC_m, where m = the specific set of cognitive (C) predictors in the model (M) and comparisons as BC_mn, with B representing the comparison ratio of Bayes factors between models m and n. BC_m0 represents a contrast of the selected model to a null model with no predictors. These analyses assess the likelihood of the data for alternative models. As an example, the full model MC₁ included the backward digit span, Corsi, JLAP, MRT, and IQ measures (below). Each of these predictors was then iteratively dropped one-by-one and change in the odds of the model was evaluated. For instance, dropping MRT resulted in model MC₃ and the comparison to the full model as BC₃₁. The latter resulted in a Bayes factor ratio of .0521, meaning the model without MRT was 5.21% as probable as the model with MRT, or the model including MRT was preferred 19 times to 1 (1/.0521). Dropping JLAP resulted in a model that was 57.43% as probable (MC₄₁), or with the model including JLAP only being preferred 1.74 times to 1. Here, lower Bayes factors indicate greater evidence for a predictor. As a rule of thumb, models that are less than 33% as probable without the variable provide evidence for retaining it, and models that are less than 10% as probable provide strong evidence for retaining it (Jeffreys, 1961; Raftery, 1995). We used the 33% criterion to retain variables, corresponding to a commonly used cutoff for positive evidence (e.g., Bayes factor of three, Kass & Raftery, 1995).

As described below, in-class attention and MRT were the only predictors to survive the Bayesian analyses. These variables were included with sixth-grade mathematical competence in the prediction of Numerical Operations scores. The model included interactions between sixth-grade mathematical competence and in-class attention and MRT scores, as well as the three-way interaction. To control for potential demographic confounds, we first used student ethnicity (Hispanic or not), race, family income, housing assistance (yes, no), food assistance (yes, no), and parental education as predictors of sixth-grade mathematical competence. Student race and family income were the only significant predictors (ps < .001). To control for these, we created dummy coded (0,1) variables for the six income categories and dummy coded race variables for Black, White, and Asian students. These were included in all models.

Participants were recruited from six schools and there were small but significant school effects for Numerical Operations scores, F(5, 311) = 3.94, p = .0018, R² = .06. To control for these effects, we used multilevel models with Proc Mixed (SAS, 2014), using students as level 1 units and 7^th-grade schools as level 2 units, allowing intercepts to vary randomly for schools. Seventh-grade Numerical Operations and predictor variables were centered (M = 0, SD = 1), but uncentered scores are shown in Table 1 and correlations among variables in Figure 1.

Figure 1.

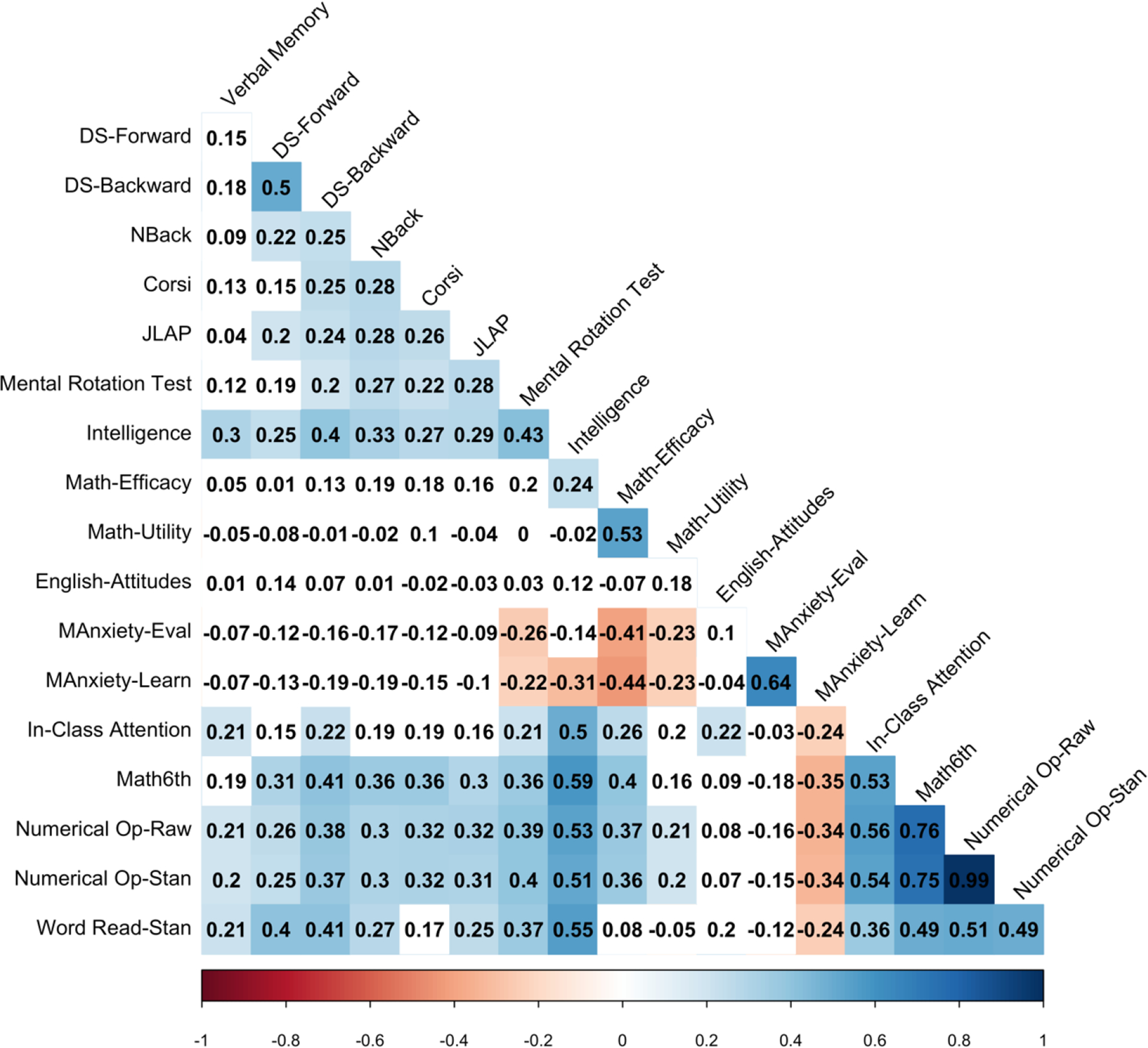
Correlations among key variables. Highlighted cells indicate significant (blue = positive; red = negative) correlations. JLAP = Judgment of Line Angle and Placement; Eval = Evaluation; Learn = Learning; Op = Operations.

Results

Bayesian Analyses

Mathematics achievement.

As shown in the top section of Table 2, the best Bayes model for the cognitive variables included digit span backward, Corsi, JLAP, MRT, and IQ. The BC_m0 is very large for this first model and all alternative models, providing strong evidence for some combination of cognitive predictors of Numerical Operations scores relative to the null. Dropping IQ resulted in a model that was < 1% as probable as the model with IQ. As noted, the model without MRT was 5.21% as probable as the model with it, while the model without JLAP was 57.43% as probable. The next two models indicated that dropping the Corsi and digit span backward variables resulted in models that were 35.45% and 4.59% as probable as the models with them, respectively. The results suggest that the inclusion of JLAP and Corsi does not substantively improve the prediction of Numerical Operations scores relative to the models without them. However, dropping both variables resulted in model that was only 8.5% as probable as the model with only digit span backward, MRT, and IQ (not shown in Table 2), suggesting that either Corsi or JLAP should be retained. The model with JLAP was only 62% as probable as the model with Corsi and thus we retained digit span backward, MRT, IQ, and Corsi for the combined analysis.

Table 2.

Bayes factor analyses of predictors of 7^th grade mathematics achievement

Model: Top Cognitive Predictors	BCm0	Excluded	BCm1
MC1 DSB + Corsi + JLAP + MRT + IQ	1.38 ×1027	---	1
MC2 DSB + Corsi + JLAP + MRT	1.28 × 1020	IQ	.0000
MC3 DSB + Corsi + JLAP + IQ	7.19 × 1025	MRT	.0521
MC4 DSB + Corsi + MRT + IQ	7.93 × 1026	JLAP	.5743
MC5 DSB + JLAP + MRT + IQ	4.90 × 1026	Corsi	.3545
MC6 Corsi + JLAP + MRT + IQ	6.34 × 1025	DSB	.0459
Model: Top Non-Cognitive Predictors	BNCm0	Excluded	BNCm1
MNC1 MEff + MAnxLearn + Atten	1.22 × 1026	---	1
MNC2 MEff + MAnxLearn	2.28 ×109	Atten	.0000
MNC3 MEff + Atten	4.74 × 1024	MAnxLrn	.0390
MNC4 MAnxLearn + Atten	9.20 × 1024	MEff	.0756
Model: Top Combined Predictors	BAm0	Excluded	BAm1
MA1 MEff + Atten + DSB + Corsi + MRT + IQ	5.21 × 1038	---	1
MA2 MEff + Atten + DSB + Corsi + MRT	1.07 ×1037	IQ	.0205
MA3 MEff + Atten + DSB + Corsi + IQ	1.08 ×1037	MRT	.0207
MA4 MEff + Atten + DSB + MRT + IQ	2.31 × 1038	Corsi	.4440
MA5 MEff + Atten + Corsi + MRT + IQ	3.30 × 1036	DSB	.0063
MA6 MEff + DSB + Corsi + MRT + IQ	1.34 × 1031	Atten	.0000
MA7 Atten + DSB + Corsi + MRT + IQ	5.78 ×1036	MEff	.0111
Model: Top Combined and 6th-Grade Mathematics	BASm0	Excluded	BASm1
MAS1 Atten + MRT + 6th-Grade Mathematics	1.43 × 1062	---	1
MAS2 Atten + MRT	1.89 × 1028	Math	.0000
MAS3 Atten + 6th-Grade Mathematics	5.33 × 1060	MRT	.0374
MAS4 MRT + 6th-Grade Mathematics	5.26 × 1058	Atten	.0004

Note. DSB = Digit Span Backward; Corsi = Corsi Block Tapping Task; JLAP = Judgment of Line Angle and Position Test; MRT = Mental Rotation Test; Meff = Mathematics Efficacy; MAnxLearn = Mathematics Anxiety for Learning; Atten = in-class attention in mathematics classrooms; MC = Models for cognitive variables; MNC = Models for non-cognitive variables; MA = Models for all, that is, top cognitive and non-cognitive variables; MAS = Top models from MA and 6^th-grade mathematics scores.

The second section of Table 2 indicates that the best set of non-cognitive predictors of Numerical Operations scores included in-class attention, mathematics anxiety for learning, and mathematics efficacy. Dropping each of these variables in succession resulted in models that were < 8% as probable as the models without them. Thus, all three variables were retained for the combined analysis.

The combined analysis included digit span backward, MRT, IQ, Corsi, in-class attention, mathematics anxiety for learning, and mathematics efficacy and the best model included all of them, except for mathematics anxiety for learning. As shown in the third section of Table 2, dropping each of these variables in succession suggested the elimination of Corsi but retention of the remaining variables.

The final set of models included the five retained variables from the combined analysis and sixth-grade mathematical competence. As shown in the last section of Table 2, the combination of mathematical competence, in-class attention, and MRT predicted Numerical Operations scores. Dropping any of these variables resulted in models that were < 4% as probable as the models with them. In other words, there is very strong evidence that in-class attention and MRT contribute to seventh-grade mathematics achievement above and beyond prior mathematics knowledge and thus all three were retained for the multilevel models.

Word reading achievement.

To assess the discriminant validity of the Bayes models that predict Numerical Operations scores, we ran the same models for Word Reading scores. As shown in the top section of Table 3, the best Bayes model for the cognitive variables included digit span forward, MRT, and IQ. The BC_m0 is very large for this first model and all alternative models, providing strong evidence for some combination of cognitive predictors of Word Reading scores relative to the null. Dropping IQ and digit span forward resulted in models that were < 1% as probable as the models with them, whereas dropping MRT resulted in a model that was 33.74% as probable. This suggests that the inclusion of MRT does not substantively improve the prediction of Word Reading scores. Follow-up assessments indicated that dropping either digit span forward or IQ resulted in models that were < 1% as probable as the model that included both of them. Thus, we retained digit span forward and IQ.

Table 3.

Bayes factor analyses of predictors of 7^th grade word reading achievement

Model: Top Cognitive Predictors	BCm0	Excluded	BCm1
MC1 DSF + MRT + IQ	7.09 × 1028	---	1
MC2 DSF + MRT	2.00 × 1016	IQ	.0000
MC3 DSF + IQ	2.39 × 1028	MRT	.3374
MC4 MRT + IQ	1.21 × 1023	DSF	.0000
Model: Top Non-Cognitive Predictors	BNCm0	Excluded	BNCm1
MNC1 MUtil + EnglishAtt + MAnxLearn + Atten	1.68 × 109	---	1
MNC2 MUtil + EnglishAtt + MAnxLearn	1.09 × 105	Atten	.0000
MNC3 MUtil + EnglishAtt + Atten	7.58 × 106	MAnxLrn	.0045
MNC4 MUtil + MAnxLearn + Atten	5.15 × 107	English	.0307
MNC4 EnglishAtt + MAnxLearn + Atten	1.81 × 107	MUtil	.0108
Model: Top Combined Predictors	BAm0	Excluded	BAm1
MA1 DSF + IQ	2.39 × 1028	---	1
MA2 DSF	1.94 × 1010	IQ	.0000
MA3 IQ	1.50 × 1022	DSF	.0000
Model: Top Combined and 6th-Grade Mathematics	BASm0	Excluded	BASm1
MAS1 DSF + IQ + 6th-Grade Mathematics	1.42 × 1030	---	1
MAS2 DSF + IQ	2.39 × 1028	Math	.0169
MAS3 DSF + 6th-Grade Mathematics	2.12 × 1022	IQ	.0000
MAS4 IQ + 6th-Grade Mathematics	3.46 × 1025	DSF	.0000

Note. DSF = Digit Span Forward; MRT = Mental Rotation Test; MUtil = Mathematics Utility; MAnxLearn = Mathematics Anxiety for Learning; Atten = in-class attention in mathematics classrooms; EnglishAtt = Attitudes about English; MC = Models for cognitive variables; MNC = Models for non-cognitive variables; MA = Models for all, that is, top cognitive and non-cognitive variables.

The second section of Table 3 indicates that the best set of non-cognitive predictors of Word Reading scores included mathematics utility, English attitudes, mathematics anxiety for learning, and in-class attention. Dropping each of these variables in succession resulted in models that were < 4% as probable as the models without them. Thus, all variables were retained for the combined analysis.

The combined analysis included digit span forward, IQ, mathematics utility, English attitudes, mathematics anxiety for learning, and in-class attention. The third section of Table 3 shows that only digit span forward and IQ were included in the top model, indicating that the non-cognitive variables did not add substantively to the prediction of Word Reading scores. The bottom section of the table indicates that these variables should be retained in a model that includes them and sixth-grade mathematical competence. The key finding here is that the core predictors of seventh-grade Word Reading achievement differ from those that predict seventh-grade mathematics achievement.

Multilevel Models

Preliminary analyses revealed no sex differences for Numerical Operations scores, F(1, 315) = 0.46, p = 0.499, and thus sex was not considered further. As noted, the initial model included sixth-grade mathematical competence, in-class attention, and MRT. We also included the interactions between the two latter variables and sixth-grade mathematical competence, and the three-way interaction; the income and race variables were included as controls. The interactions allowed us to explore, for instance, whether the benefits of strong spatial abilities or in-class attention varied depending on the prior level of mathematical knowledge. These types of interactions are sometimes found, but vary across grades and mathematical content (Gilligan et al., 2019) and we assessed whether this was the case for our sample.

The three-way interaction was not significant, F(1, 296) = 1.34, p = .248, and thus dropped. Table 4 shows the results for the model with only the two two-way interactions. The results confirm the Bayes factors regarding the importance of in-class attention and spatial ability in predicting seventh-grade mathematics achievement, controlling prior achievement (ps < .002).

Table 4.

Multi-level Model of Gains in Mathematics Achievement from Sixth- to Seventh-Grade

Variable	Estimate	se	t	p
Intercept	34.37	3.81	9.03	.001
Mathematics Competence (6th grade)	4.48	0.32	13.89	.001
In-class attention	1.35	0.29	4.72	.001
Mental Rotation Test	0.82	0.27	3.09	.002
Math × In-class attention	0.59	0.24	2.45	.015
Math × Mental Rotation Test	0.42	0.25	1.73	.085

Note. The income and race contrasts are not shown. The level 2 school effect was not significant (p = .159)

The sixth-grade mathematical competence by in-class attention interaction, F(1, 297) = 5.99, p = .015, is broken down in the upper panel of Figure 2. The high and low groups were defined by cutoffs 1 SD above or below the mean, respectively. The interaction was strongest in the high-attention group [b = 1.08, SE = 0.19], followed in turn by the middle- [b = 0.85, SE = 0.13] and low-attention [b = 0.63, SE = 0.11] groups (ps < .05). A contrast of these slopes indicated a significant difference across the high- and low-groups, t(307.57) = 2.38, p = .018, and a trend for the difference across the middle- and low-groups, t(307.99) = 1.67, p = .097; the difference across the high- and middle-groups was not significant, t(307.46) = 1.45, p = .148. The lower panel shows the overall relation between predicted scores derived from sixth-grade mathematical competence, in-class attention, and their interaction in the prediction of Numerical Operations scores.

Figure 2.

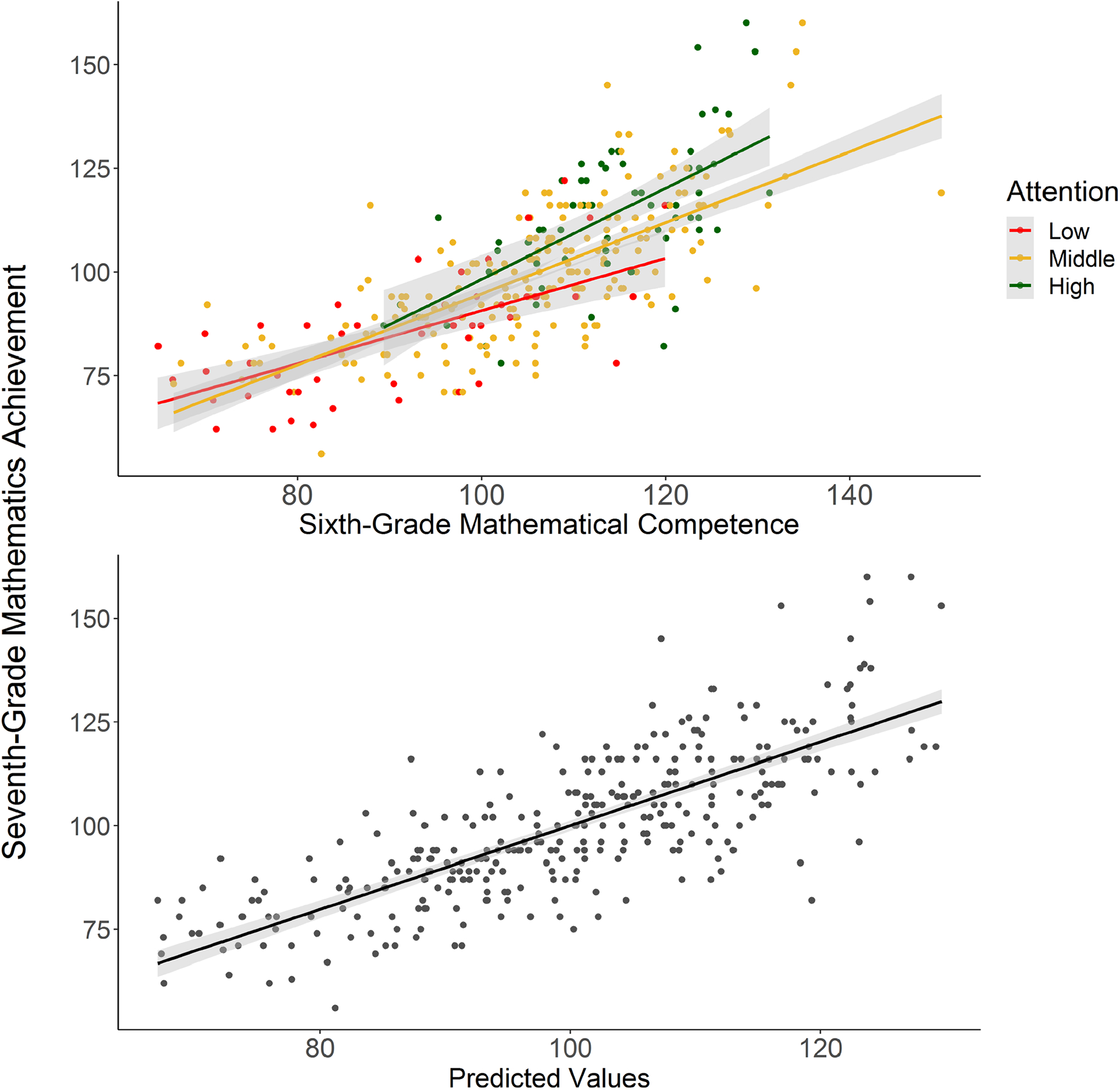
The upper panel shows the interaction between sixth-grade mathematical competence and in-class attention, with the high and low attention-groups including students 1 SD above and below the mean, respectively. The lower panel shows the relation between predicted scores derived from sixth-grade mathematical competence, in-class attention, their interaction and Numerical Operations scores.

As shown in Table 4, the sixth-grade mathematical competence by MRT interaction was only a trend, F(1, 297) = 3.00, p = .085, but given the potential importance of high spatial abilities for learning in some areas of mathematics, we broken the interaction down. The high and low groups were defined by cutoffs 1 SD above or below the mean, respectively, and are shown in Figure 3. The interaction was strongest in the high-MRT group [b = 1.23, SE = 0.19], followed in turn by the middle- [b = 0.83, SE = 0.15] and low-MRT [b = 0.67, SE = 0.14] groups (ps < .05). A contrast of these slopes indicated a significant difference across the high- and low-groups, t(309.23) = 2.93, p = .004, and the high- and middle-groups, t(309.92) = 2.89, p = .004; the difference across the middle- and low-groups was not significant, t(310.06) = 1.08, p = .282. The lower panel shows the overall relation between predicted scores derived from sixth-grade mathematical competence, MRT scores and their interaction in the prediction of Numerical Operations scores.

Figure 3.

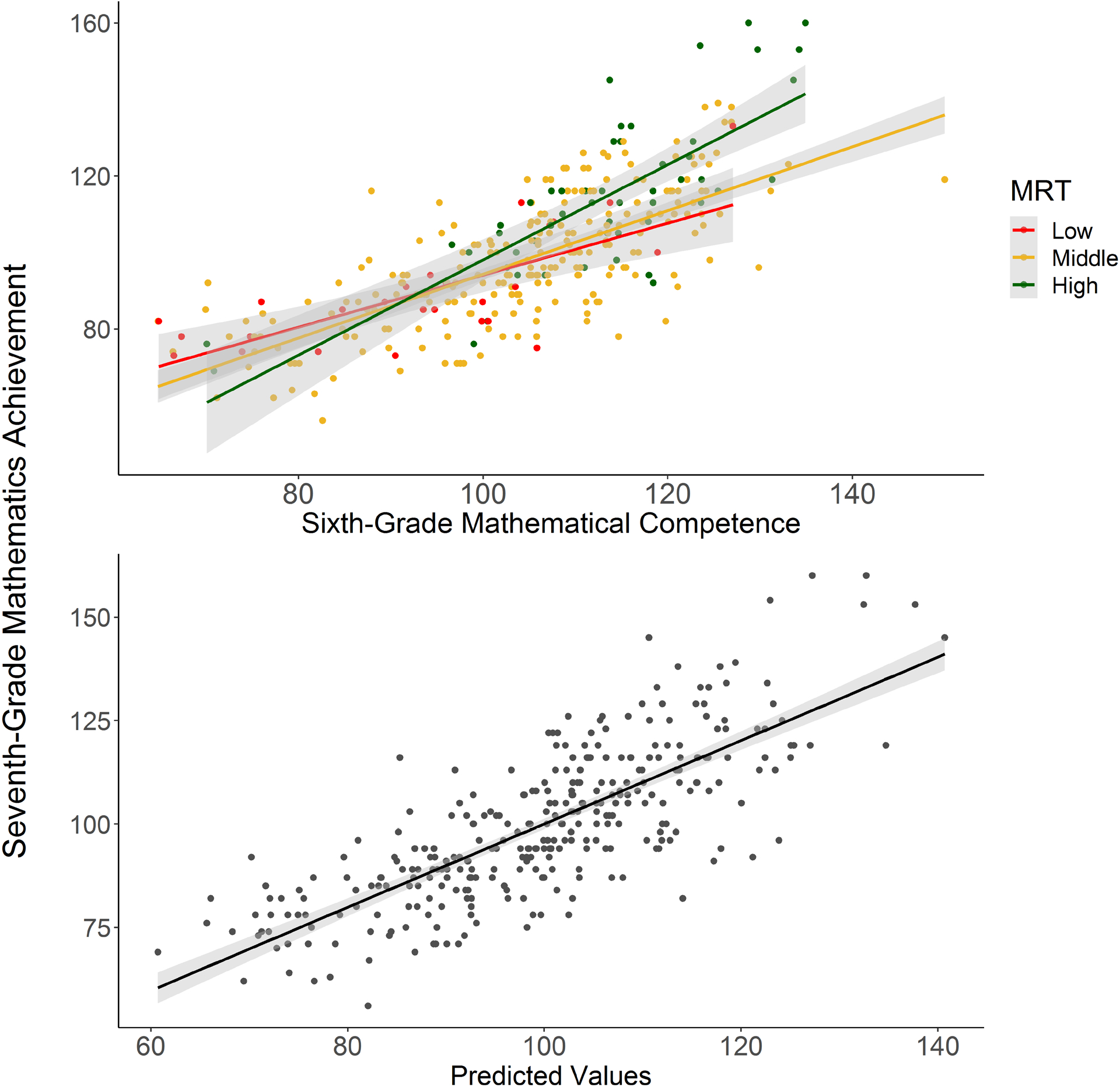
The upper panel shows the interaction between sixth-grade mathematical competence and Mental Rotation Test (MRT) scores, with the high and low MRT groups including students 1 SD above and below the mean, respectively. The lower panel shows the relation between predicted scores derived from sixth-grade mathematical competence, MRT, their interaction and Numerical Operations scores.

Sixth-Grade Mathematics Attitudes and In-Class Attention

The finding of no direct relations between the non-cognitive measures and Numerical Operations scores does not preclude indirect effects. As noted in the introduction, such effects could be related to attention in mathematics classrooms and through this indirectly influence mathematics achievement. To assess this, we conducted a series of analyses that examined the relation between the sixth-grade non-cognitive variables and in-class attention in seventh grade and assessed whether there were any indirect relations between these non-cognitive measures and Numerical Operations scores.

Among the sixth-grade attitudes variables only mathematics utility, mathematics efficacy, and mathematics anxiety for learning were correlated with both in-class attention and Numerical Operations scores (ps < .02). A Bayesian regression indicated that mathematics efficacy and mathematics anxiety for learning were the best set of predictors of in-class attention. Dropping mathematics anxiety resulted in a model that was 2.77% as probable as the model with it, whereas dropping mathematics efficacy resulted in a model that was 40.0% as probable as the model without it. These results indicate that among the sixth-grade non-cognitive measures, mathematics anxiety for learning is the most likely to have an indirect effect on Numerical Operations scores through in-class attention.

Indeed, Figure 4 shows a simple mediation model that only included mathematics anxiety for learning, in-class attention, and Numerical Operations. In this model, all of the paths are significant and the indirect relation between mathematics anxiety for learning and Numerical Operations scores is significant, b = −0.97 [95% CI = −1.45 to −0.49], z = −3.971, p < .001, and partially mediated by in-class attention.

Figure 4.

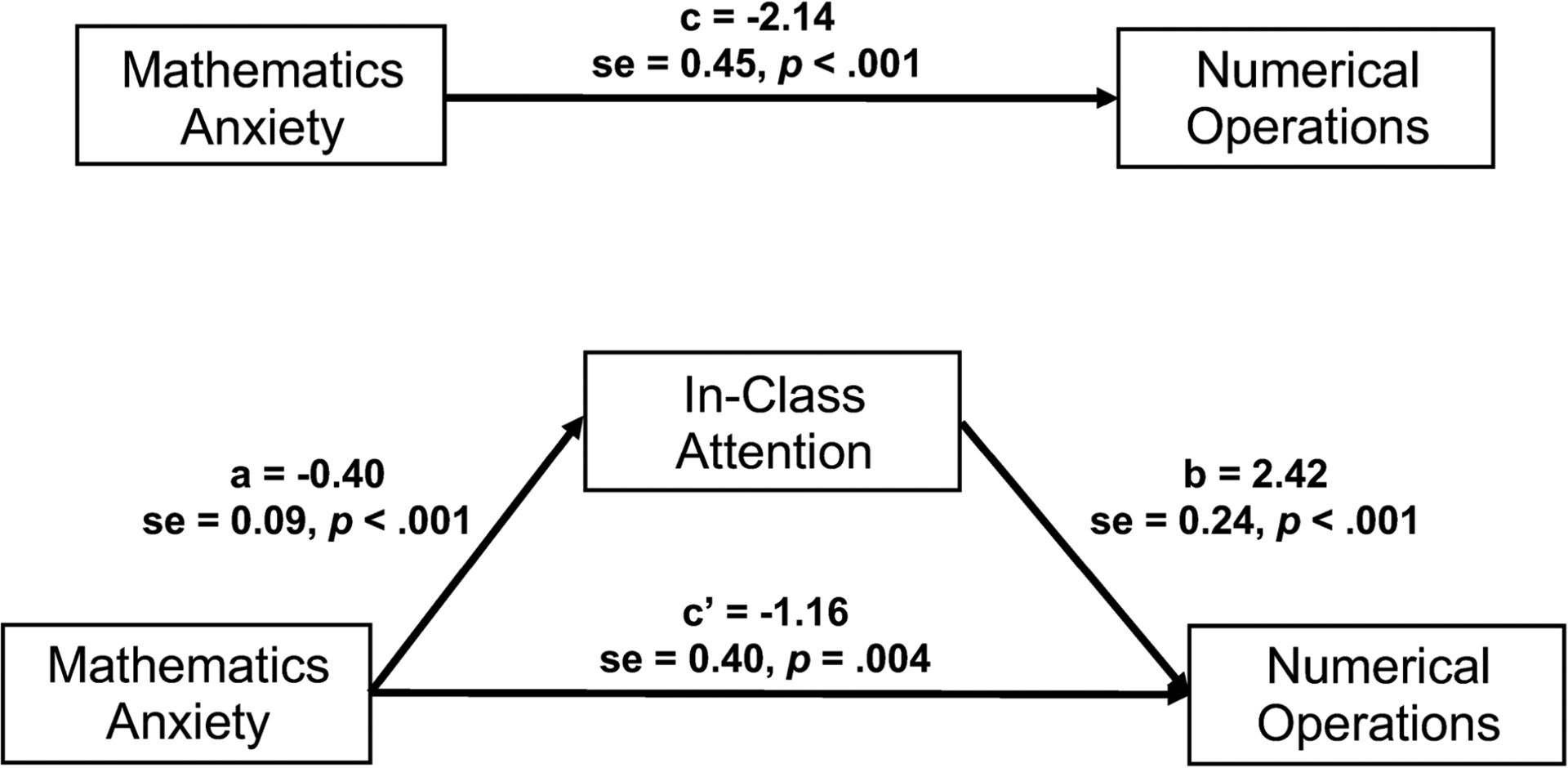
In-class attention is a partial mediator of seventh-grade Numerical Operations scores.

As shown in Figure 5, with control of sixth-grade mathematical competence, MRT scores, the covariances between them and with in-class attention and mathematics learning for anxiety, the c path is no longer significant; c = −.49, [95% CI = −1.11 to 0.14], z = −1.52, p = .127. Hayes (2009) argued that the significance of this path is not necessary to assess indirect effects, although in this situation the results are not typically called mediated effects. In any case, in this model there is a significant indirect relation between mathematics anxiety and Numerical Operations scores through in-class attention, b = −0.37 [95% CI = −0.60 to −.14], z = −3.16, p = .002, but now the direct relation between mathematics anxiety and Numerical Operations scores is not significant, b = −.12 [95% CI = −0.72 to 0.48], z = −0.39, p = .699.

Figure 5.

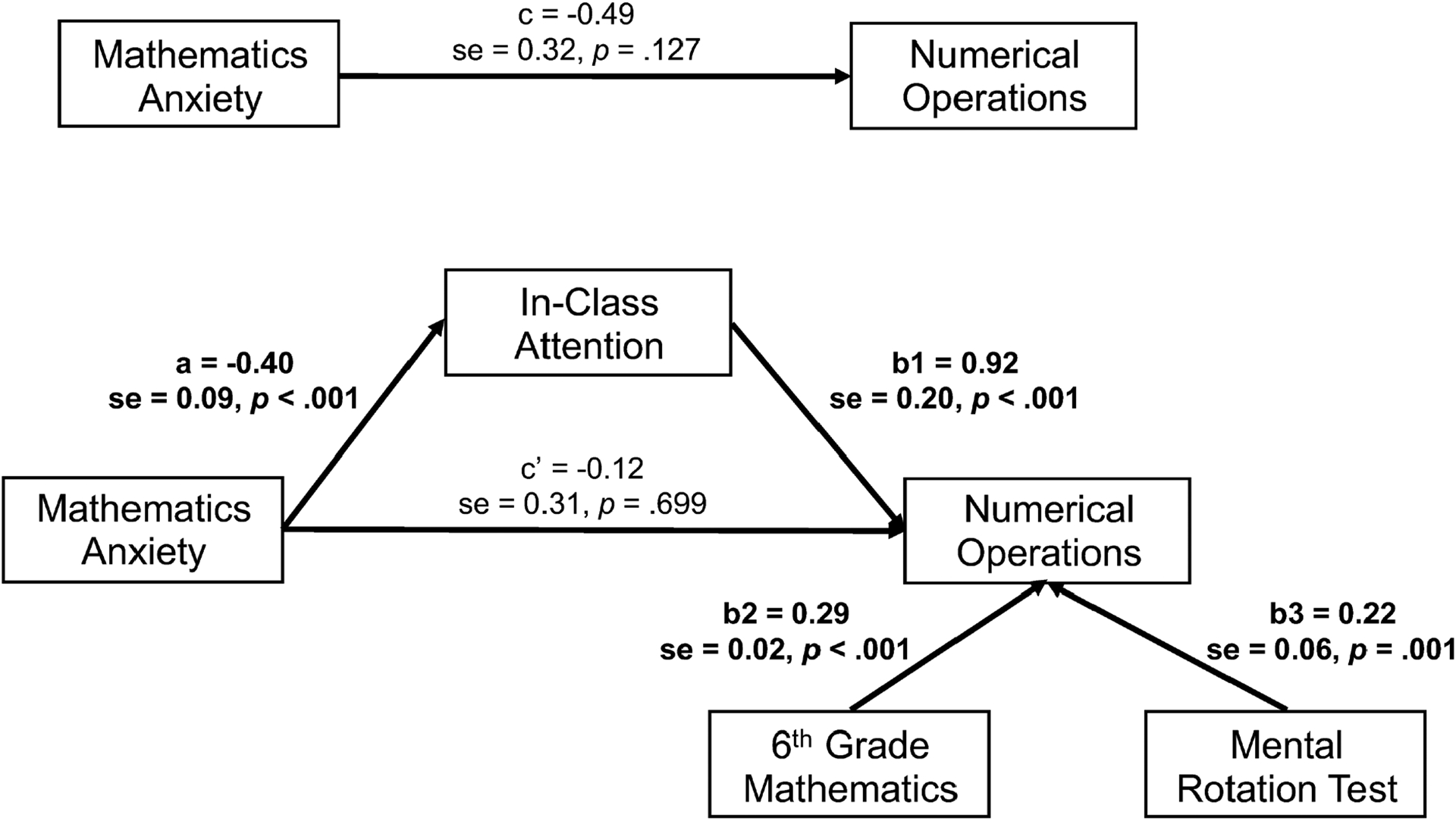
Mathematics anxiety is indirectly related to Numerical Operations scores though in-class attention, with control of prior achievement and Mental Rotation Test scores.

Discussion

Students who develop strong mathematical competencies have enhanced educational opportunities in college and a smoother path to well-paid employment and better long-term opportunities for career advancement than do their less-prepared peers (Bynner, 1997; National Mathematics Advisory Panel, 2008). Identifying the factors that contribute the most to this development is a critical step in the building of supportive educational environments. The myriad proposals regarding these factors might actually result in more confusion than direction for the building of such environments, because it is it not clear which factors should be prioritized, whether the most important ones vary from one grade to the next, and whether there are interactive or indirect effects among these factors.

Our very broad assessment of the associated theoretical terrain allowed for the identification of the most plausible factors, at least for middle school students. The overall results indicated that students with strong prior knowledge, average- to above-average in-class attention, and above average spatial abilities made stronger gains in mathematics during seventh grade than did other students, controlling student race and family income. Moreover, students with high levels of mathematics anxiety were less attentive in mathematics classrooms, and this in turn appeared to contribute to their relatively lower gains in mathematics during seventh grade. We discuss the implications with respect to the cognitive and non-cognitive factors that appear to contribute to the development of mathematical competencies.

Cognitive Mechanisms

The results of several prior studies are confirmed with the identification of complex spatial abilities as a robust predictor of seventh-grade mathematics achievement and by the finding that students with above-average spatial abilities and strong prior mathematical knowledge made the highest gains in seventh-grade mathematics (Casey et al., 1995, 1997; Li & Geary, 2017; Mix & Cheng, 2012). More precisely, the results are consistent with prior studies that have identified visuospatial abilities as contributing to mathematics learning in middle school and beyond. These results, however, do not indicate which aspects of mathematics learning are facilitated by spatial abilities, and we might speculate that it is the more complex or more novel mathematics at this grade level (Mix et al., 2016, 2017). This is because the best scores on the seventh-grade Numerical Operations test indicated successful students were correctly solving several spatially represented basic geometry problems. The problems that were successfully solved by average- and lower-achieving students were largely computational whole number and fractions arithmetic problems which should be familiar to most students and for which spatial abilities might not be as helpful (Geary & Widaman, 1987), but this is not certain (Hawes & Ansari, 2020; Xie, Zhang, Chen, & Xin, 2019).

Xie et al.’s (2019) meta-analysis revealed that spatial abilities (visuospatial memory and more complex abilities) are correlated with most mathematical competencies, including arithmetic, but these analyses do not typically control for potential confounds, such as working memory and intelligence. With control of these confounds, Li and Geary (2013, 2017) found that the relation between visuospatial working memory and performance on the Numerical Operations test grew stronger as students moved through elementary school and into middle school and high school. In other words, as the complexity of the mathematics increased, the importance of visuospatial abilities, or at least visuospatial working memory, appeared to increase. Our results suggest that any such relation is better captured by the Mental Rotation Test than by measures of visuospatial working memory (Casey et al., 1995, 1997), and that the contributions of spatial abilities to gains in mathematics learning may depend on pre-existing mathematical knowledge.

This conclusion is tentative because different aspects of visuospatial abilities might contribute to different aspects of mathematical learning (Gilligan et al., 2019; Hawes & Ansari, 2020) which is not captured by our composite measure, and any such specific relations could vary from one grade to the next (Mix et al., 2016, 2017). The results nonetheless indicate that more detailed studies of the relation between different spatial abilities and the learning of complex arithmetic and pre-algebraic competencies is warranted. The reason for the interaction between prior achievement and MRT scores in predicting seven-grade achievement needs follow-up studies as well. One prosaic possibility is that students with average or better mathematical competence in sixth grade solved more items on the Numerical Operations test and thus were exposed to more items that had a spatial component (e.g., geometry). Students with strong spatial abilities would, on average, be more successful than other students at solving such problems. It is also possible that strong prior knowledge facilitates the use of spatial strategies for solving more complex problems, but this remains to be determined.

At first blush, our results would appear to contradict many previous studies that have suggested that intelligence and working memory contribute to mathematical learning (Bull & Lee, 2014; Deary et al., 2007; Geary et al., 2017), but this is not the case. Prior to inclusion of sixth-grade mathematical competence, the Bayesian analyses indicated that intelligence and working memory (backward digit span) were strong independent predictors of seventh-grade mathematics achievement, in addition to spatial abilities. This means that there was considerable overlap in individual differences in working memory and intelligence and sixth-grade mathematical competencies. As might be expected based on prior studies and theory (Cattell, 1987), intelligent students with strong working memory skills acquired more mathematical knowledge by the end of sixth grade than did other students, masking the direct effect of intelligence and working memory. Nevertheless, the results do suggest that at this grade level, prior knowledge might be relatively more important or at least just as important as domain-general abilities in facilitating further learning (Geary et al., 2017; Lee & Bull, 2016).

Non-Cognitive Mechanisms

Our finding for attention in mathematics classrooms is consistent with studies of younger students, whereby teachers’ ratings of student engagement in these contexts predict gains in mathematics achievement above and beyond the contributions of various cognitive abilities (Fuchs et al., 2006, 2014; Geary et al., 2013). The finding of an interaction between prior knowledge and attention is more novel and revealed that the highest achievers at the end of seventh grade had strong prior mathematical competencies and at least average in-class attention (Figure 2), controlling spatial abilities. Most of the students with below average engagement in the classroom also performed poorly on the sixth-grade mathematics measure. Without information on their in-class attention in prior grades, we cannot determine whether their low attentive-behavior in seventh-grade classrooms is causing smaller gains in achievement, reflects a general disengagement with mathematics or schooling more generally, or some combination. Close inspection of Figure 2 reveals that even low-attentive students with average or better sixth-grade mathematical competencies gained less in seventh-grade than did their more attentive peers, suggesting a causal relation. One implication is that interventions for lower-achieving students might need to incorporate components on self-regulation (Wang et al., 2019) or enhancement of classroom management strategies (Korpershoek, Harms, de Boer, van Kuijk, & Doolaard, 2016).

In keeping with previous studies, a combination of mathematics attitudes and anxiety predicted seventh-grade mathematics achievement (Dowker et al., 2016; Eccles & Wang, 2016), but these did not survive the inclusion of prior mathematics achievement. As with working memory and intelligence, this does not necessarily mean that these factors do not affect mathematical development but rather they were not directly critical for gains from sixth- to seventh-grade. Indeed, our finding that mathematics anxiety for learning indirectly contributed to seventh-grade mathematics achievement through in-class attention suggests a nuanced relation between non-cognitive factors and achievement. The finding is consistent with Byrnes and Miller-Cotto’s (2016) finding of a relation between internalizing issues, including anxiety, and gains in mathematical knowledge across the academic year, and suggests that students’ engagement in the classroom–influencing their opportunity to learn–might contribute to this effect.

Over the longer term, attitudes and anxiety about mathematics contribute to future course and career choices (Lauermann et al., 2017), and these types of relations would not be detectable with our study design. Moreover, we assessed a fairly narrow slice of students’ mathematical development. As was noted earlier, meta-analyses of cross-lagged relations suggest that attitudes might be a more consistent influence on later achievement in students older than those assessed in our study (Talsma et al., 2018; Valentine et al., 2004).

Limitations and Conclusions

The primary limitation is the correlational nature of the data that precludes strong causal statements. Although we assessed a much broader array of cognitive and non-cognitive factors than in typical studies of students’ mathematical development, there may be other factors that we did not include. Although our findings for in-class attention and spatial abilities is consistent with many previous studies, this does not necessarily mean that they will emerge as key predictors of mathematical gains in earlier or later grades. Also, our sample had higher sixth-grade mathematical competencies scores than the full sixth-grade sample, was from relatively high-income families, and not ethnically diverse. Thus, the extent to which these findings generalize to other populations remains to be determined. Despite these limitations, the broad assessment of cognitive and non-cognitive factors enabled a more thorough assessment of individual differences in gains in mathematics achievement among middle school students than is typical in this literature and have implications for targeted interventions for students at-risk for long-term difficulties with mathematics.

Educational Impact and Implications Statement.

Students’ in-class attention and their spatial abilities emerged as predictors of gains in mathematics from sixth- to seventh-grade, with mathematics anxiety indirectly related to these gains through in-class attention. Strategies to enhance students’ engagement in the classroom, possibly by addressing anxiety for some of them, might facilitate the learning of at-risk students, and further study of the relation between spatial abilities and mathematics could result in the development of new interventions.