Challenges encountered applying equilibrium and non-equilibrium binding free energy calculations

Abstract

Binding free energy calculations have become increasingly valuable to drive decision making in drug discovery projects. However, among other issues, inadequate sampling can reduce accuracy, limiting the value of the technique. In this paper we apply absolute binding free energy calculations to ligands binding to T4 lysozyme L99A and HSP90 using equilibrium and non-equilibrium approaches. We highlight sampling problems encountered in these systems, such as slow side chain rearrangements and slow changes of water placement upon ligand binding. These same types of challenges are likely to show up in other protein-ligand systems as well and we propose some strategies to diagnose and test for such problems in alchemical free energy calculations. We also explore similarities and differences in how the equilibrium and the non-equilibrium approaches handle these problems. Our results show the large amount of work still to be done to make free energy calculations robust and reliable and provide insight for future research in this area.

Graphical Abstract

1. Introduction

In drug discovery, computational methods help navigate through a vast potential chemical space. There is often a trade-off between accuracy and speed of the methods which determines the value of each technique at different stages of the discovery process. A common goal in drug discovery is to search for molecules which bind to proteins with therapeutic potential.

In order to explore a binding site of interest and find putative binders, large chemical libraries like Enamine, with 1.36 billion molecules,¹ can be scanned.² Fast and less accurate methods, such as ligand-based approaches, molecular docking and physicochemical property prediction, are used to filter this large space. Promising compounds can then be purchased, tested and active compounds improved iteratively.

In lead optimization, experiments may require difficult synthesis and thus be costly and slow. Therefore, during optimization, more accurate, but also more computationally expensive methods, such as free energy calculations, are used to prioritize the synthesis of compounds based on the in silico predictions. Although all these methods are routinely applied in drug discovery projects, improvements in their accuracy are still needed to increase their impact.^3–6

The binding free energy, ΔG°, is defined as the difference between the free energy of the ligand in solution at a standard reference concentration, and the free energy of the ligand bound to the protein. This property can be calculated in a variety of ways, but two – which we consider here – are becoming relatively more common. In the so-called “absolute” approach, the ΔG° is calculated for each ligand independently. Alternatively, the “relative” approach determines the difference in binding free energy, ΔΔG°, between the binding of two ligands. In the latter case, commonly only atoms which differ between the two molecules are transformed, and the absolute binding free energy can be obtained if the binding free energy of one of the ligands is known. This relative approach, then, is most suitable for comparing or ranking binding of related ligands.

Absolute binding free energy (ABFE) calculations have some benefits over relative ones (RBFE),^5,7,8 but are thought to require more sampling because of the generally larger transformations involved compared to RBFE. In ABFE calculations, ligands of interest can be very chemically diverse since they need not share a common scaffold. In addition, different ligands need not share a common binding mode. The method can even be used for selectivity predictions, predicting binding of a ligand to multiple proteins.⁸ However, ABFE calculations are thought to require more sampling and simulations may take a long time to converge which can make them computationally expensive.⁵ ABFE calculations in some systems likely require additional sampling of slow protein motions relative to RBFE calculations, such as changes in protein conformation which occur on ligand binding (e.g. HIV protease flap opening/closing,⁹ kinase activation loop,¹⁰ etc.).

Alchemical free energy calculations employ an unphysical path that connects two physical end states in order to obtain free energy differences.^11–17 Let us consider for example the process of turning the interactions of a ligand off in the binding site. The initial state in this case is the fully interacting ligand bound to the protein and the final state is the decoupled ligand, not interacting with its surroundings, and a separate protein and solvent box. Here the unphysical path describes how the electrostatic and steric interactions between the ligand and the protein and surrounding solvent molecules are gradually turned off. The unphysical intermediates ensure sufficient overlap of phase space as the system is modified, allowing for calculation of accurate free energies. The Hamiltonian of the system is coupled to a parameter λ which controls the progress between the physical end states. λ can have discrete or continuous values between 0 (initial state) and 1 (final state) and the intermediate states are often referred to as λ windows. Different alchemical approaches have been developed, each having its strengths and weaknesses.

In equilibrium free energy calculations (EQ) a separate molecular dynamics (MD) simulation is performed for each of a set of discrete λ windows corresponding to different states of the system (Figure 1). This method often requires long simulation times since every state has to first reach equilibrium before data can be used for the analysis. If this is not achieved – and it can be difficult to ensure that it has been achieved – the approach can suffer from systematic errors.¹⁸

Figure 1.

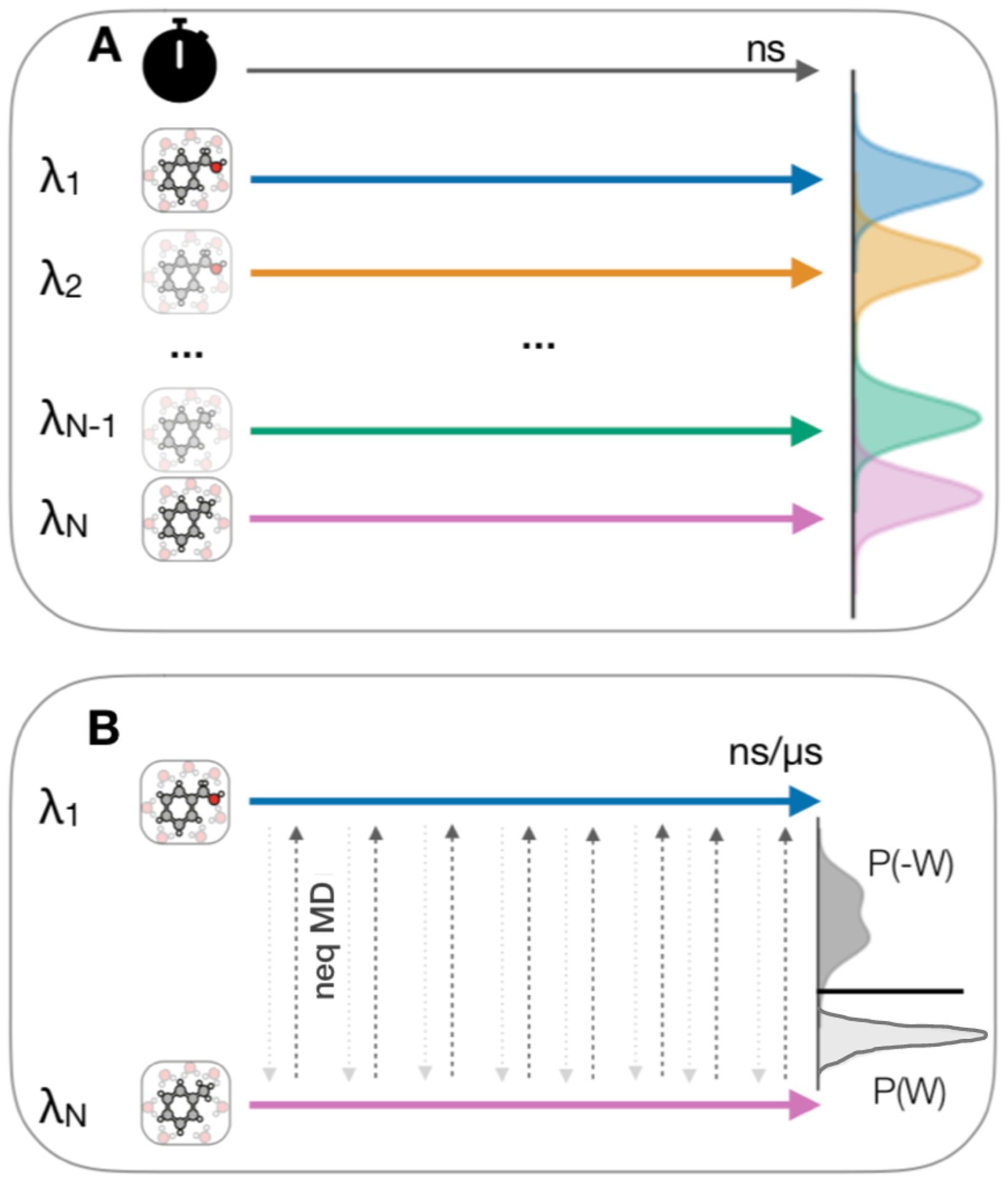
Protocols for the equilibrium (EQ) and nonequilibrium (NEQ) free energy calculations. (a) EQ sampling scheme. A separate molecular dynamics (MD) simulation (colored arrows) is performed for each of a set of discrete λ windows corresponding to different states of the system (λ₁−λ_N). (b) NEQ approach, where two equilibrium simulations at the physical end states are run (λ₁ and λ_N, blue and pink arrow). The alchemical path is explored in fast switching transitions in a single simulation (grey arrows). In the bidirectional approach, many trials are performed in both directions and the non-equilibrium work distributions of the forward and reverse direction (P(W) and P(−W)) are directly related to the free energy difference between the states (thick horizontal line between the distributions) by the Crooks fluctuation theorem. Figure was adapted from Mey et al.¹⁴ under the CC-BY 4.0 license.

In contrast, with a non-equilibrium approach (NEQ), only the physical end states (i.e. the interacting state and the noninteracting state) have to be sampled at equilibrium while the alchemical path is explored in fast switching transitions, as the ligand is switched from interacting to non-interacting (or vice versa) in a single simulation. The coupling parameter λ is continuous in this case. Multiple trials are performed, and the exponential average over the non-equilibrium work necessary to transform the ligand is related to the free energy difference of the process by the Jarzynski equality¹⁹ (or, better if transformations in both directions are possible, the Crooks formalism^18,20).

Another potential benefit of the NEQ approach is that it is highly parallelizable which can reduce wall clock time when distributed computing is available. In NEQ calculations, end state simulations can also benefit from enhanced sampling techniques²¹ to overcome energy barriers. Intuitively such strategies seem likely to be beneficial. However, recent literature²² using partial replica exchange MD (an enhanced sampling techique involving exchanges between replicas with modified Hamiltonians) showed no effect of the enhanced sampling. Work in preparation from Gapsys and de Groot also suggests that in some cases, enhancing the sampling of the apo/holo states can drive the system away from the starting crystallographic pose by accumulating force field artifacts and equilibrating in a new free energy minimum which may differ from the experimental one.

While most literature applications of free energy calculations have used EQ or NEQ approaches, a third possibility is expanded ensemble simulations and related approaches, such as λ dynamics.²³ Here, the parameter λ is a dynamic variable which is propagated throughout a single simulation. These calculations are not our focus here, but provide an interesting alternative.

In this paper, we test the non-equilibrium approach for absolute binding free energy calculations and compare it with equilibrium free energy calculations. We highlight challenges encountered applying the two methods and explore similarities and differences in handling these issues. Since the challenges we identify are likely to show up in other protein-ligand systems as well, we propose some strategies to assess sampling problems in alchemical free energy calculations (FEC). Although we find ways to work around some of the problems, our results highlight the large amount of work still to be done to make these calculations robust and to reliably detect problems in an automated way. Most literature studies report only successes, and calculations generally seem to work, though industry reports have highlighted the need for more careful analysis of failures.⁴ Here, we report on a relatively large number of “failures” with common protocols and highlight how they fail and why. We provide insights and directions for future method development and research in this area.

2. Theory

2.1. Alchemical free energy calculations are a physically rigorous approach to calculate binding free energies.

The strength of protein-ligand interactions can be measured by the binding affinity or the related quantity, the binding free energy, given by:

$$\Delta G^{°}=-k_{B}T\text{ ln}\left(c^{°}{K}_B\right)=-k_{B}T\text{ ln}(c^{°}\frac{[PL]}{[P][L]})$$ (1)

where k_B is the Boltzmann constant, T the temperature, K_B the binding affinity, c° the standard state concentration of 1 mol/l and [PL], [P], [L] the concentrations of the protein-ligand complex, the protein and the ligand, respectively.

Binding free energy calculations are based on the relationship between the free energy and the configurational integral (partition function).^24,25 This partition function cannot be calculated explicitly for complex systems, but can be approximated by an ensemble of conformations from the Boltzmann distribution. In practice, molecular dynamics or Monte Carlo simulations are used to sample the configurational space. Several approaches serve to analyze the resulting data and obtain the change in free energy.²⁶

2.2. Equilibrium free energy simulations require multiple separate intermediate states.

For the EQ approach, the Bennett Acceptance Ratio (BAR)²⁷ and its variant the Multistate BAR (MBAR)²⁸ are the most efficient estimators.

As input, BAR and MBAR take potential energy differences between adjacent alchemical states. These potential energy differences can be written (in “reduced”/dimensionless form) as Δu_ij where i and j denote the thermodynamic states in question. Particularly, these states correspond to different intermediate states or λ windows per the Introduction.

The potential energy differences Δu_ij are evaluated for samples taken from a single simulation and assess the work which would be required to move the system from one state (or one Hamiltonian) to the other. A simulation in state i can be said to have coordinates x_i, and from that simulation we evaluate Δu_ij(x_i), the energy difference to alter the energy function to that corresponding to state j. Like-wise, we also use snapshots from the simulation run in state j to compute Δu_ij(x_j). Here, Δu_ij(x) = u_j(x) − u_i(x).²⁶

In this notation, the potential energy u_i(x) refers to a dimensionless reduced potential function that includes the pressure-volume work; this allows easier accommodation of the equations to different choices of ensemble; here, calculations are performed in the isothermal-isobaric ensemble:²⁸

$$u_i(x)=\beta \left(U_i(x)+p_{i}V(x)\right)$$ (2)

where x is the configuration of the system, V (x) the volume and U_i(x) the potential energy function.

Overall in BAR, the free energy difference is obtained by numerically solving the following equation for ΔG:

$$\sum _{i=1}^{n_i}\frac{1}{1+e^{\left(M+\Delta u_{ij}\left(x_i\right)-\Delta G\right)}}=\sum _{j=1}^{n_j}\frac{1}{1+e^{-\left(M+\Delta u_{ij}\left(x_j\right)-\Delta G\right)}}$$ (3)

with $M=\text{ln}\frac{n_i}{n_j}$ and n_i and n_j being the number of samples at state i and j and β = 1/k_BT. MBAR generalizes this expression to multiple thermodynamic states rather than pairs of states as in BAR.

The sum of all free energy differences ΔG between the λ windows gives then the total free energy difference of the process.

In the case of BAR, only potential energy differences of adjacent states are computed while in the case of MBAR all states are considered and analyzed. MBAR provides a more generalized version of BAR which uses all available data to compute free energy estimates, rather than relying on information only from adjacent thermodynamic states.

It is important to mention that these estimators rely on phase space overlap between adjacent λ windows to obtain reliable free energy estimates (Figure 1).

Thermodynamic integration (TI) provides another common approach for EQ calculations.²⁹ Here, the free energy difference between two states is defined as

$$\Delta G={\int }_0^1{\langle \frac{\delta U(\lambda )}{\delta \lambda }\rangle }_{\lambda }d\lambda .$$ (4)

The alchemical path is sampled at a set of discrete λ values. Therefore, this integral has to be solved numerically which introduces a bias especially when there is (strong) curvature along the alchemical pathway.³⁰

Since sufficient sampling in all λ states is necessary to obtain reliable free energy estimates for both estimators, enhanced sampling techniques, such as Hamiltonian Replica Exchange (HREX),^31–33 are often used to improve the sampling of configuration space. Here, λ windows are run in parallel, so that the simulations can swap configurations of the system between the states. Energy barriers of the potential energy surface might be crossed more often and earlier since the energy landscape differs among the states of the alchemical pathway. The Metropolis acceptance criterion ensures that simulations in all states still converge towards the equilibrium distribution.³²

As mentioned in the introduction, all λ windows need to be simulated at equilibrium in EQ calculations, and some of these can require sampling unphysical states which might have even slower correlation times than the physical states,^34–36 necessitating very long sampling times despite the use of enhanced sampling techniques.

2.3. Non-equilibrium calculations drive rapid transitions between physical end states.

In contrast, non-equilibrium FEC sample only the physical end states at equilibrium while the alchemical path is explored in fast (non-equilibrium) transitions. After generating an ensemble of equilibrium conformations in the initial and final state, MD simulations are performed which rapidly switch the ligand from interacting to non-interacting and vise versa (Figure 1). By changing the parameter λ, the system is forced to quickly change to the other end state without reaching equilibrium at any intermediate state. Consequently, there is dissipated work along the path and the average work exceeds the free energy difference according to the second law of thermodynamics and the maximum work theorem

$$\langle W\rangle \ge \Delta G,$$ (5)

where W is the reduced work that includes the pressure-volume work similarly as described for the potential energy above. Jarzynski showed that this inequality becomes an equality when taking the exponential average of the irreversible work done in taking the system from one state to another:^19,37

$$\langle e^{-\beta W}\rangle =e^{-\beta \Delta G}.$$ (6)

Since this average over the work distribution is exponential, the tails of the distribution carry the most statistical weight.³⁸ The samples in these tails are rare, however. This introduces a bias when the tails are not sampled adequately, meaning that this estimator frequently performs poorly.

Convergence is in general expected to be worse in the “deletion” direction than the “insertion” direction,³⁹ unless the particular choice of restraints alters this balance. This may seem counter-intuitive since dissipation can be larger when inserting a ghost ligand with the protein in the apo conformation than when deleting the coupled ligand in the holo state (Figure 8, 11a). While dissipation is important, convergence is partly determined by how frequent important realizations are and Jarzynski showed³⁹ that important realizations are particularly infrequent in the deletion direction, so that approaches like Widom insertion are practical, though not Widom deletion. Wu and Kofke showed⁴⁰ that transitions in the direction that increases the entropy will not converge with a unidirectional estimator. However, as mentioned above, restraints can alter this balance.

Figure 8.

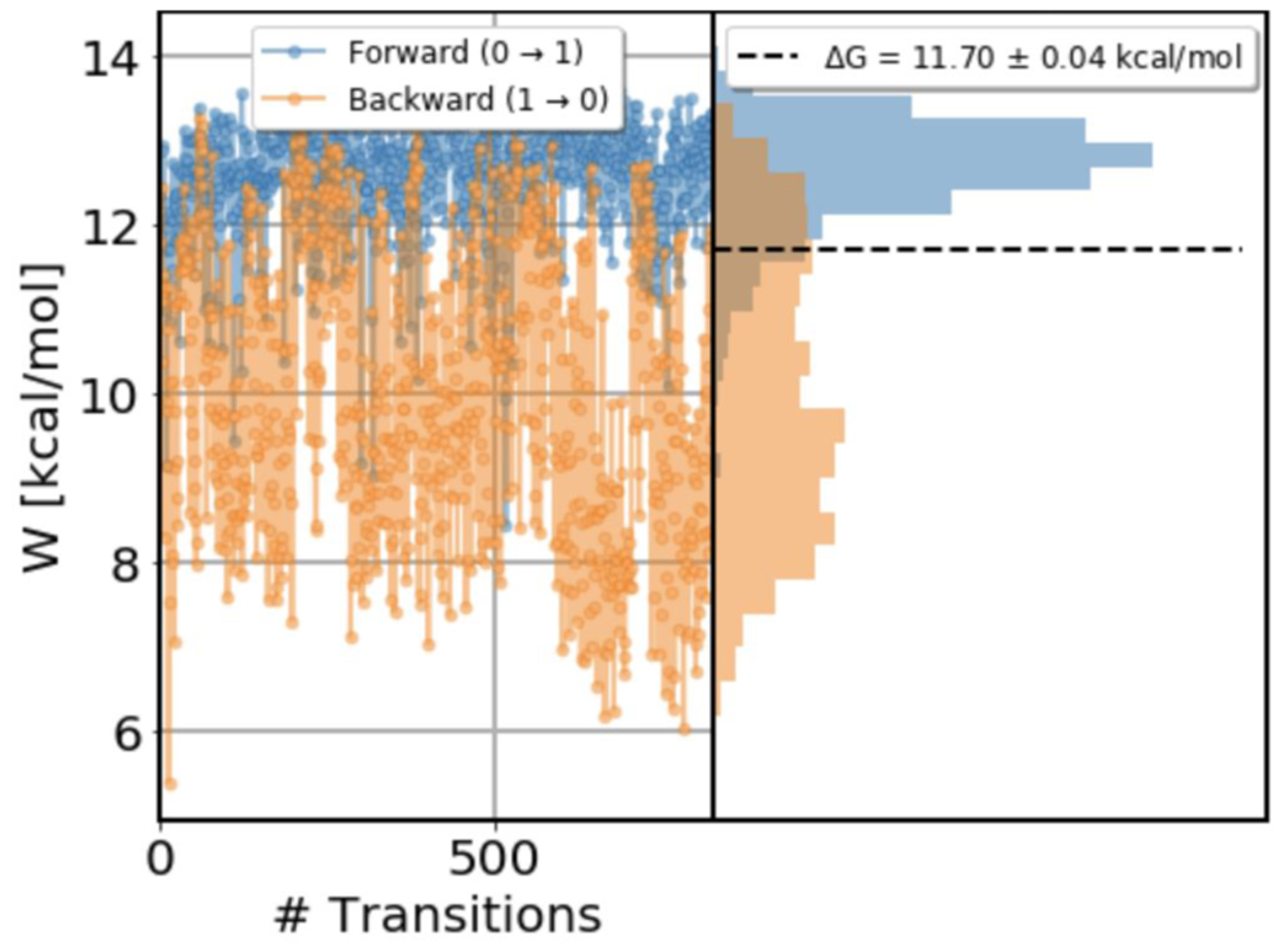
Work values for toluene binding to T4 lysozyme L99A, in forward (blue) and reverse (orange) direction. Shown are values measured for each attempted transition, as well as the distribution of the work values. The transition length for each transition was 200 ps. Data from trials in the reverse direction shows sudden changes in work values and the distribution of work values is bimodal indicating a slow degree of freedom in the system.

Figure 11.

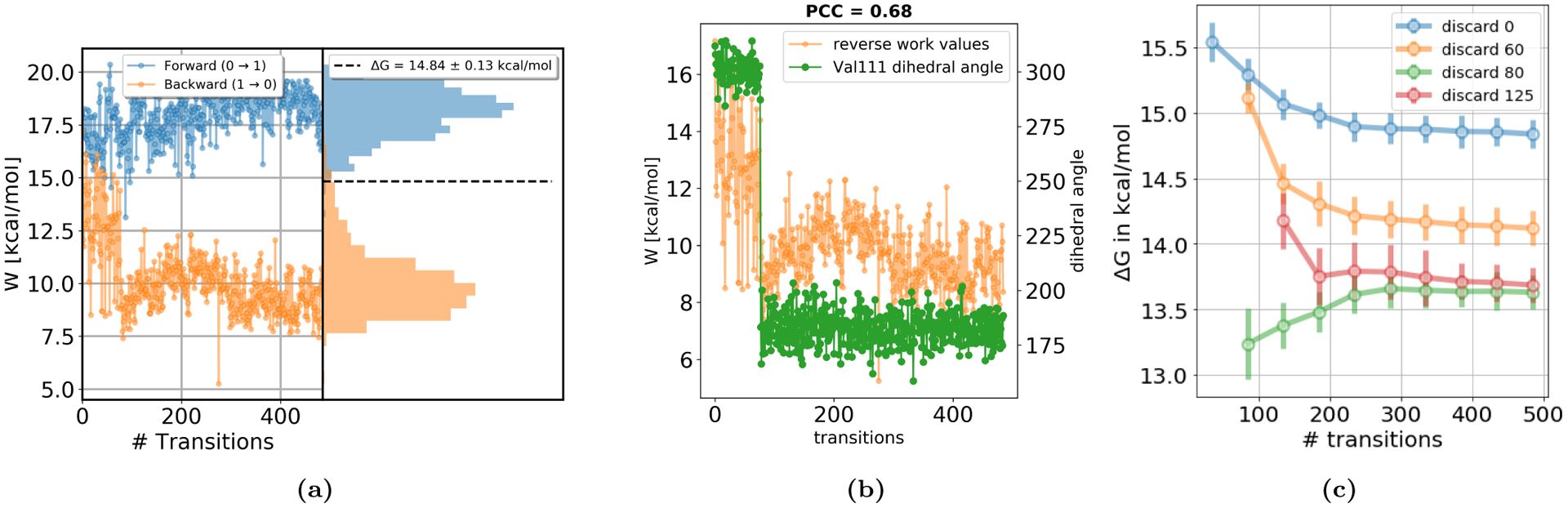
(a) Work values for 3-iodotoluene binding to T4 lysozyme L99A, in forward (blue) and reverse (orange) direction. Shown are values measured for each attempted transition, as well as the distribution of the work values. In contrast to the general protocol (Figure 10) where 5 ns of the end state simulation were discarded, here no data were discarded for equilibration. Data from trials in the reverse direction (coupling) shows a sudden change in work values at transition 77. This indicates sampling of a slow motion in the end state. (b) The reverse work values (orange) and the ξ1 dihedral angle of Val111 (green) as a function of transition number. The rotation of the Val111 side chain is correlated with the NEQ work (Pearson correlation coefficient PCC=0.68). The sudden change in work values is likely caused by the reorientation of Val111 in the end state simulation. (c) Free energy difference as a function of transition number. The analysis was performed for discarding 0, 60, 80 or 125 transitions to study the impact of the Val111 orientation on the final ΔG estimate. The final free energy estimate is highest when no frames were discarded for equilibration, underestimating the contribution of protein strain relaxation upon unbinding. When 17 transitions start from the wrong V111 rotamer (discard 60, reorientation at transition 77), the ΔG estimate did not converge to the same result as when starting all transitions in the dominant rotamer (discard 80 and 125). This shows the impact of the orientation of the Val111 side chain on the free energy difference.

In contrast to the unidirectional Jarzynski equality, the Crooks Fluctuation Theorem (CFT)^18,20,41 takes transformations in both directions (forward and reverse) into account. This bidirectional approach was shown to converge faster than exponential averaging.⁴² It relates the probability distribution of forward and reverse work values with the free energy difference

$$\frac{P_F(W)}{P_R(-W)}=e^{\beta (W-\Delta G)}.$$ (7)

If only unidirectional transformations are performed, the CFT reduces to the Jarzynski equality. The CFT can be solved for ΔG with the Bennett acceptance ratio method mentioned above (Sec. 2.2). Here, the summation is performed over the number of simulations in the forward (n_f) and reverse (n_r) direction:

$$\sum _{i=1}^{n_f}\frac{1}{1+\frac{n_f}{n_r}{e}^{\beta \left(W_f-\Delta G\right)}}=\sum _{j=1}^{n_r}\frac{1}{1+\frac{n_r}{n_f}{e}^{-\beta \left(W_r-\Delta G\right)}}$$ (8)

The work performed on the system is obtained by accumulating the energy changes as the coupling parameter is changed during the course of the switching transition.⁴³

$$W={\int }_0^1\frac{\delta H(\lambda )}{\delta \lambda }d\lambda .$$ (9)

Other uni- and bi-directional estimators are based on a Gaussian approximation of the probability distribution. However, these introduce significant errors even with large amounts of sampling, since the underlying work distributions are not always Gaussian, as demonstrated in the recent SAMPL6 SAMPLing challenge.⁴²

Non-equilibrium switching transition data must be collected from independent and uncorrelated trials in order for the average to converge to the true free energy. This is beneficial, in that switching transitions can be run in parallel and thus deploy extremely well in distributed computing environments. This can reduce the wall-clock time of these calculations relative to the EQ approach, at least when a large number of processors is available.

In order to obtain an unbiased estimate of the free energy change, the work distributions should overlap sufficiently (Figure 1). In the case of poor overlap, the CFT result becomes the mean of forward and reverse exponential averages individually computed by the Jarzynski equality. As mentioned above, the exponential average is highly sensitive to the tails of the distribution and therefore, depending on the amount of sampling, a biased estimate. Thus, when overlap is poor, computed free energies are likely incorrect.

3. Systems

We compared the performance of the EQ and NEQ methods on two different protein targets, examining two ligands binding to the T4 lysozyme mutant L99A and a ligand binding to HSP90. Each system has its own challenges which we will introduce in this section.

3.1. The T4 lysozyme mutant L99A is a simple test system, but still has sampling challenges.

The T4 lysozyme mutant L99A is a simple model binding site that has been extensively studied both experimentally and computationally.^11,44–49 The leucine to alanine mutation leads to the formation of an apolar cavity that binds small molecules. We chose this system for several reasons. First, the dry binding site and the simple, mostly rigid ligands make the system appropriate for the comparison of methods, as sampling times are not excessively long. Secondly, since it is a well studied binding site, it is possible to compare the results with other methods. Lastly, it poses some interesting challenges for alchemical FEC. Toluene is known to bind with two different binding modes (Figure 2a). If the population or free energy of each pose is assessed separately, the crystallographic pose should be the more favorable.

Figure 2.

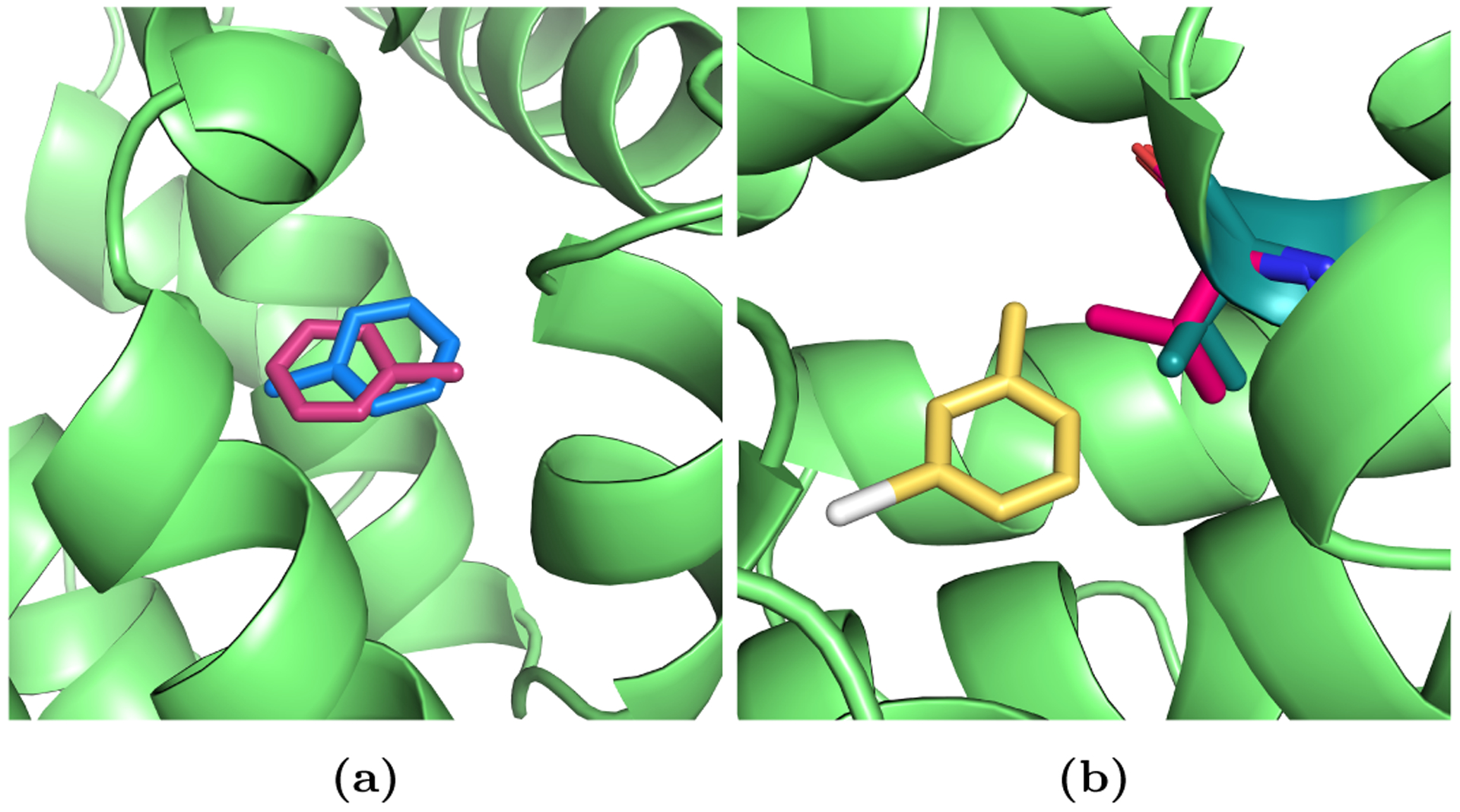
Toluene and 3-iodotoluene binding to T4 lysozyme mutant L99A. (a) Two binding poses of toluene in T4 lysozyme L99A (green). The crystallographic binding pose (pose I) is shown in blue and the alternative binding mode (pose II) is shown in magenta sticks. (b) Val111 side chain reorientation upon 3-iodotoluene binding. In the apo state, the Val111 side chain (magenta) points inside the binding pocket. It reorients upon binding (dark green sticks) to make room for 3-iodotoluene (yellow). PDB ID: 4W53

Other ligands, such as 3-iodotoluene and p-xylene, induce slow side chain rearrangements upon binding.⁴⁷ In particular, the valine 111 side chain rotates to make room for the slightly larger ligands (Figure 2b). Here, it will be interesting to see if this slow motion can be captured in the fast non-equilibrium transitions and whether correct binding free energies can be obtained.

3.2. HSP90 is a challenging, pharmaceutically relevant target.

Even though simple systems, for which convergence can be achieved on reasonable timescales, are highly valuable for method comparison, we are ultimately interested in how the methods perform on pharmaceutically relevant systems. HSP90 is an anticancer drug target, and multiple inhibitors of the protein have been developed.^50,51 Computationally, it is a more challenging system than the T4 lysozyme L99A mutant, though still regarded as relatively straightforward on the spectrum of potential pharmaceutical targets. The binding site is solvent exposed and, relative to T4 lysozyme L99A, the ligands are larger, more polar and flexible (Figure 3). While some ligands introduce larger protein conformational changes upon binding,⁵⁰ these are not observed for the ligand considered in this study.

Figure 3.

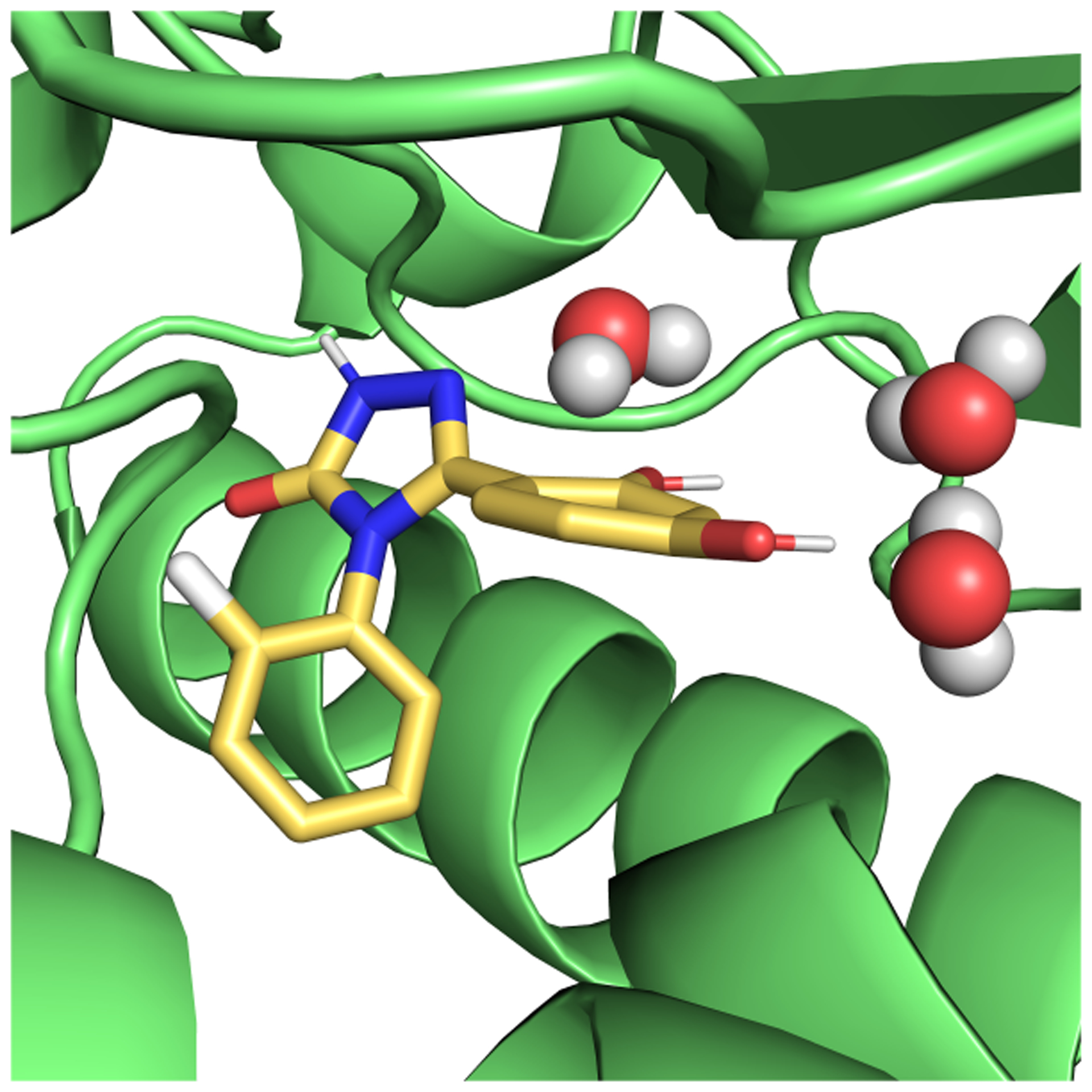
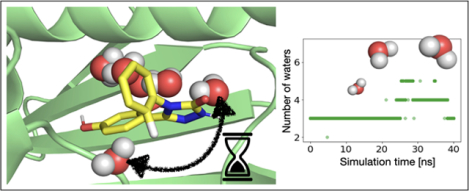
Ligand (yellow) binding to HSP90. Three buried binding side waters are represented as spheres. PDB ID: 5J64

Changes in water placement and occupancy on binding can lead to sampling problems in HSP90. In the unbound state, the solvent completely fills the binding site. In the presence of the ligand, three water molecules are deeply buried in a space between the ligand and the protein (Figure 3). In our MD simulations where these water molecules were not included in the starting structure, we found they do not enter the space even after 40 ns (Sec. 5.5.4). We ran calculations both with and without these bound water molecules to examine their contribution to the binding free energy. In the EQ approach, we studied whether the use of HREX alleviates the sampling of this slow motion.

4. Methods

4.1. We constructed a thermodynamic cycle to calculate the binding free energy.

Ligand binding/unbinding events (association-dissociation) are typically too slow for direct simulation. Therefore, it is more convenient to compute binding free energies via a thermodynamic cycle. Free energy is a state function, meaning that this allows us to construct artificial (more convenient) pathways to get between the states of interest. Figure 4 shows the thermodynamic cycle used in this paper. The binding free energy (panel F) is not simulated directly but obtained through summation along the cycle.

Figure 4.

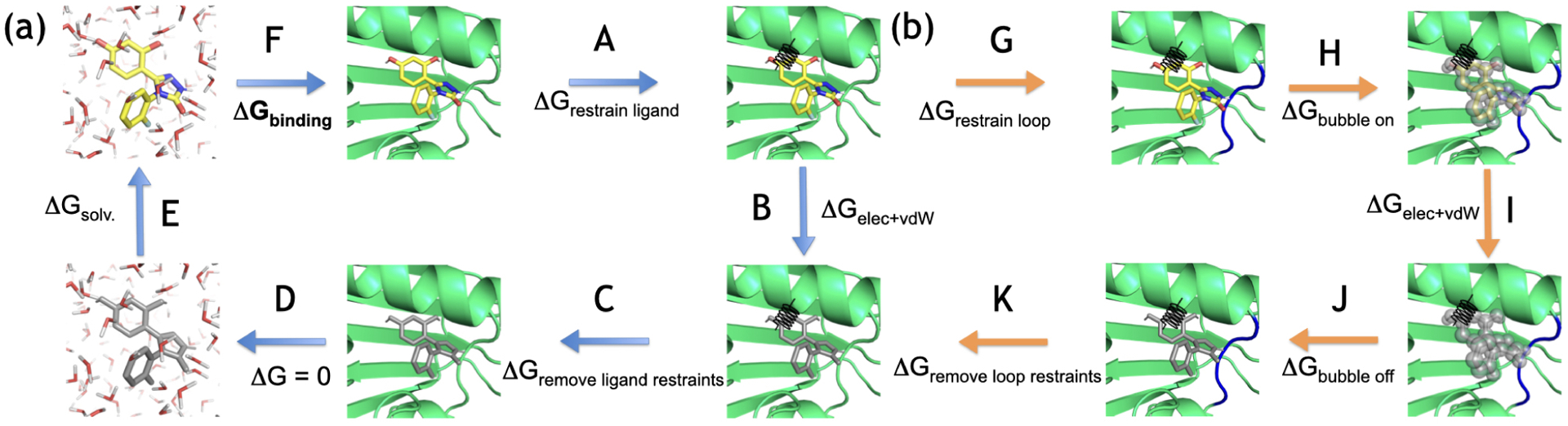
Thermodynamic cycle for computing binding free energies. The left part of the cycle (a) represents the standard cycle used in this paper, the right part (b) was only added for calculations including a bubble-ligand (Sec. 5.5.3). The ligand is restrained using orientational (Boresch-style)⁵² restraints (A) and then decoupled in the binding site, meaning that the intermolecular electrostatic and van der Waals (vdW) interactions of the ligand are turned off (B). The restraints are released analytically (C), the ligand is transferred from the complex into the solvent (D) and then coupled in the solvent (E). The next leg (F) represents the free energy difference upon ligand binding which is obtained through summation along the cycle. (b) For calculations that include a bubble-ligand to overcome insufficiencies in water sampling, a loop and three buried water molecules are restrained (G, Sec. 5.5.3), then the vdW interactions between the bubble-ligand and water are turned on (H). In the next step the ligand is decoupled in the binding site (I) and the bubble-ligand prevents water from entering the site. The bubble-ligand is then turned off again (J), the restraints on the loop and buried water molecules are released (K) which leads back to the regular cycle.

For the decoupling and recoupling of the ligand, we performed both NEQ and EQ calculations. Since these steps are most computationally challenging and expensive, we sought to investigate how NEQ performs compared to EQ.

Some of our simulations use a “bubble-ligand” that repels water to overcome water sampling problems during NEQ switching transitions. Below we show why and how it is used. To incorporate this bubble-ligand into the thermodynamic cycle (right part of Figure 4), we first have to restrain three buried water molecules and a protein loop close to the binding site. This is necessary because the bubble-ligand creates a vacuum in the empty binding site which some side chains of this loop try to fill resulting in conformational changes of the entire loop (Sec. 5.5.3). After restraining the loop, the bubble-ligand is turned on, so that in the next step, where the ligand is decoupled, water cannot enter the binding site. This separates the water sampling problems from the decoupling of the ligand in HSP90.

4.2. Simulation Details.

To prepare the structures for T4 lysozyme (PDB ID: 4W53) and HSP90 (N-terminal domain, PDB ID: 5J64), first, missing heavy atoms were added with PDBfixer⁵³ and protonation states were assigned at pH 7 using the PDB2PQR server.^54,55 ParmEd (http://parmed.github.io/ParmEd) was used to convert the pqr output to a pdb file. For the ligands, OpenEye toolkits⁵⁶ were used to add missing hydrogen atoms and to check the bond order and connectivities. For toluene and the HSP90 ligand the binding mode was extracted from the crystal structure. An alternative binding mode of toluene and the binding mode of 3-iodotoluene were obtained from the supporting information of the BLUES paper.⁵⁷

The systems of the protein-ligand complex and the ligand in solution were then generated using YANK.⁵⁸ The protein was parameterized with Amberff14SB⁵⁹ and the ligands with GAFF2⁶⁰ and AM1-BCC charges.⁶¹ The protein-ligand complex was solvated with TIP3P water⁶² in a cubic box and Na⁺ and Cl⁻ ions were added until a salt concentration of 50 mM (T4 lysozyme) or 150 mM (HSP90) was reached. The Amber output files of the system were then converted to GROMACS structure and topology files using ParmEd. For HSP90 two protein-ligand systems were prepared, one where all water molecules from the crystal structure were removed, while in the second crystallographic waters in the binding site were retained. The topology and coordinate files are available in the supporting information (SI).

Orientational (Boresch-style) restraints were applied by restraining 3 atoms in the protein and 3 atoms in the ligand through one distance, two angle and 3 dihedral restraints with a force constant of 20 kcal/(mol*Ų) for the bond and 20 kcal/(mol * rad²) for angles and dihedrals. A table of the protein and ligand atoms used to restrain the complex can be found in SI Table S2. The atoms were selected during the setup of the system with YANK. YANK’s selection process picked heavy atoms that are not co-linear and ensured that the distance restraint involved a protein-ligand atom pair within 1–4 Å. Previously, the calculated binding free energy was shown^52,63 to be independent of the atom selection and force constants. Here, the restraint contribution (Figure 4 panel A) was calculated by running two equilibrium states, one of the coupled, restrained ligand and one of the coupled ligand without restraints for 10 ns each. The free energy difference was estimated using BAR and three independent replicates were run to check for convergence and to estimate the uncertainty.

All MD simulations were performed using GROMACS 2018.3.^64,65 In the EQ approach, every λ window was energy minimized using steepest descent for 5000 steps, then equilibrated in the canonical ensemble for 10 ps at 298.15 K. Afterwards, the system was equilibrated in the isothermal-isobaric ensemble for 100 ps at a pressure of 1 bar. The production run was performed at constant NPT as well. All MD simulations were performed using the leap-frog integrator at a timestep of 2 fs. In the alchemical pathway, first the electrostatic interactions were decoupled, then the sterics, applying a soft-core potential.⁶⁶ The soft-core potential is used to avoid instabilities in intermediate lambda windows. Although new soft-core potential functions, including the smoothstep softcore potentials,⁶⁷ have been developed recently, the soft-core potential from Beutler et al.⁶⁶ was used in this work as this is widely available in GROMACS. EQ and NEQ methods were treated equivalently with respect to the soft-core potential, thus both approaches were evaluated at equivalent conditions. The intramolecular interactions of the ligand were not changed during the process. Complete settings can be found in the mdp files provided in the SI. Although the convergence rate can be different among λ windows,^34–36 we ran all alchemical states for an equal amount of time for convenience. The overall convergence of the free energy difference will therefore be determined by the slowest converging window.

For the NEQ approach, end state simulations were performed in the interacting state (state A) and the decoupled state (state B) using the same general procedure (minimization and equilibration) as in the EQ approach. Then, either the first nanosecond (in the case of toluene) or the first 5 ns of the production run was discarded for equilibration and frames extracted every 40 ps (T4 lysozyme) or every 50 ps (HSP90). Fast switching transitions from state A to B (A2B) and vice versa (B2A) were performed where the Δλ = 1/n_steps where n_steps is the number of steps. Since electrostatics and sterics were switched simultaneously, a softcore potential was applied for both non-bonded interactions with the soft-core parameter sc-alpha=0.5, sc-power=1 and sc-sigma=0.3, as is typical.

Some of the simulations included a bubble-ligand which overlaps with the normal ligand but interacts only with water molecules. The bubble-ligand interacts with the water (not including the three buried water molecules) through Lennard-Jones interactions while not interacting with any other molecules in the system, and is designed (Sec. 5.5.3) to alleviate water sampling problems in the binding site at intermediate lambda values. The Lennard-Jones parameters σ and ϵ of this bubble-ligand were set to 0.33 nm and 0.41 kJ/mol for all atoms of the bubble-ligand (see topology file SI).

We also introduced position restraints to prevent the side chains of a nearby protein loop from filling the vacuum of the empty binding site created by the bubble-ligand. The restraints were applied to the side chain backbone atoms using a force constant of 1000 kJ/(mol* nm²). The three buried water molecules which do not interact with the bubble-ligand were restrained with position restraints as well. The restraints were turned on and off using 15 λ windows with varying force constants.

4.3. We obtained uncertainty estimates by running independent repeats.

In order to obtain reliable error estimates, we performed independent replicates, both for the EQ and the NEQ approach. Given that MD simulations are sensitive to the initial conditions, two trajectories from the same system can diverge quickly. The divergence of an ensemble of independent simulations from various starting conditions provides insight into sensitivity to initial conditions. Although in the NEQ approach the fast-switching transitions are already independent of one another (at least to the extent that the equilibrium snapshots from which they are started are assumed uncorrelated), we also ran repeats of the end state simulations. Extracting snapshots from independent shorter MD simulations rather than one larger one can ensure better sampling of phase space. Bootstrapping of NEQ work values was used for the individual replicates but we found that it underestimated the uncertainty.

For the NEQ approach, analytical error estimates can help detect lack of overlap of the work distributions. For maximum likelihood methods, like BAR, the variance asymptotically converges to the inverse of the Fisher information of the joint distribution of, in this case, forward and reverse work values.⁶⁸ Using this variance estimate, the analytical uncertainty can be vastly overestimated when overlap is poor (Sec. 5.5 and especially Figure S15). We therefore only use this method as a diagnostic metric in the NEQ approach. A high uncertainly estimate indicates a potential overlap problem and that results cannot be trusted.

4.4. Overlapping work distributions don’t guarantee reliable free energy estimates.

Overlapping work distributions are a necessary but not sufficient requirement to obtain reliable free energy estimates. Consider for example a system where slow side chain rearrangements occur upon ligand binding. If this rearrangement is neither sampled in the equilibrium end state simulation nor in the fast switching transitions, the work distributions might overlap well. Computed free energies, however will not be correct, because the contribution of structural rearrangement in the binding site is not accounted for (Sec. 5.3.2, Figure 11). Running independent replicates helped assess these issues in this work. Phase space overlap measurements can serve as a diagnostic metric and have been examined fairly extensively for equilibrium calculations.^14,69 Even though sufficient overlap of the potential energy distributions of neighboring λ states is crucial to obtain an unbiased estimate, it is important to remember that overlap alone does not guarantee that sampling is adequate.

4.5. We compared the EQ and NEQ approaches based on convergence of computed free energy differences where possible.

Since the two approaches start their simulations from systems parameterized and prepared in the same way, the calculated free energy differences should converge to the same value when sampling is sufficient. In order to assess which method converges faster, we looked at how the cumulative ΔG, averaged over trials, changes over time.

A method can be considered efficient if it quickly reduces the standard deviation and bias. In the cases where convergence was achieved we therefore investigated how standard deviation and bias behave over the observed simulation time scale for the two methods. For the bias we used the converged final ΔG estimate as the true reference, although the supposedly converged free energy difference might not be correct if the most important conformations have not been sampled.

We had originally hoped to compare efficiency of EQ and NEQ approaches on all the systems considered here, but to assess efficiency, we must obtain well converged free energy estimates. However, in some of our simulations convergence is not achieved due to sampling problems we explain elsewhere (Sec. 5.), making it impossible to compare the efficiency of the two approaches.

In all systems, we used the MBAR estimator as implemented in alchemlyb/pymbar^28,70 to estimate free energy differences in the EQ approach and computed then the mean and standard deviation of three independent repeats.

For the NEQ approach we calculated free energy differences using the CFT/BAR method as implemented in pmx.^71,72 Instead of calculating the mean of three independent replicates, we pooled together all work values from the repeats to estimate one free energy difference. For the uncertainty estimate, we calculated the standard deviation obtained by treating the individual repeats separately. This analysis was performed for decoupling the ligand in the binding site as well as coupling it in the solvent.

4.6. We assessed potential sampling limitations.

To help assess sampling problems in this work, we find it helpful to examine several properties relating to free energies, as we will further discuss in Sec. 5. Particularly, we compute the Pearson correlation coefficient between the work values and all side chain (ξ) dihedral angles in the protein using the SciPy package in Python, with ξ angles calculated via GROMACS. Additionally, we examine dH/dλ values and their relationship to other degrees of freedom. Here, we do not use dH/dλ values for free energy estimates, but they can be used to do so via TI, and these dH/dλ values provide a view into the potential contributions of specific motions in specific trajectories to binding free energies (since they are measured for individual snapshots, allowing us to identify rearrangements/motions which lead to sudden changes in dH/dλ). We find (Sec. 5.3 and 5.5) that these are a helpful diagnostic.

5. Results

In this study we compare equilibrium and non-equilibrium approaches to calculating binding free energies of ligands to two protein targets, T4 lysozyme L99A and HSP90, and examine the different challenges these approaches encounter for the systems studied.

We first compare the performance of the two approaches for calculation of hydration free energies of the three ligands, which were computed as part of the thermodynamic cycle (Figure 4E). Those calculations converged well enough to compare the efficiency of the methods. After examining hydration free energies, we focus on protein-ligand systems.

5.1. Comparing the efficiency of EQ and NEQ on the hydration free energy.

The EQ and NEQ approach yielded similar results for the hydration free energy of toluene, 3-iodotoluene and the HSP90 ligand. In Supporting information (SI) Figure S1, we show how the cumulative free energy difference, the standard deviation and the bias converged for the two methods.

Using the same amount of sampling, the two approaches converged within uncertainty to the same values for toluene and 3-iodotoluene. The methods agreed to within 0.2 kcal/mol of each other fairly quickly (~40 ns total simulation time). In the case of the HSP90 compound, it took ~200 ns to agree within 0.2 kcal/mol, and EQ and NEQ free energy estimates did not converge to statistically the same result, but were very close (ΔΔG=0.14 kcal/mol). When running longer (500 ps) but fewer NEQ switching transitions the methods agreed, but the standard deviation was slightly higher (SI Figure S1). For these three ligands, the NEQ approach was able to reduce the standard deviation and the bias faster than the EQ approach, suggesting that it is more efficient. However, this needs investigation on a larger set of molecules.

5.2. Toluene binding to T4 lysozyme mutant L99A.

With the force field used here, toluene binds to the cavity in this T4 lysozyme mutant with two (non-symmetric) binding modes (Figure 2). The crystallographic binding pose (pose I) has a more favorable binding free energy than the other pose (pose II) and inter-conversion between these two binding modes is very slow compared to typical simulation timescales (e.g. 100 ns or more).⁵⁷ Therefore we ran separate calculations for each pose and applied restraints to keep the ligand from transitioning between binding modes (SI Figure S2).

While all the protocols we report used the same amount of overall sampling time, we investigated the effect of the transition length versus number of switching transitions on the ΔG estimate in the NEQ calculations. For both binding poses, the EQ and NEQ approaches converged to a statistically equivalent value of the free energy difference (Figure 6). The standard deviation in pose I, however, was higher with the non-equilibrium method for all three transition lengths.

Figure 6.

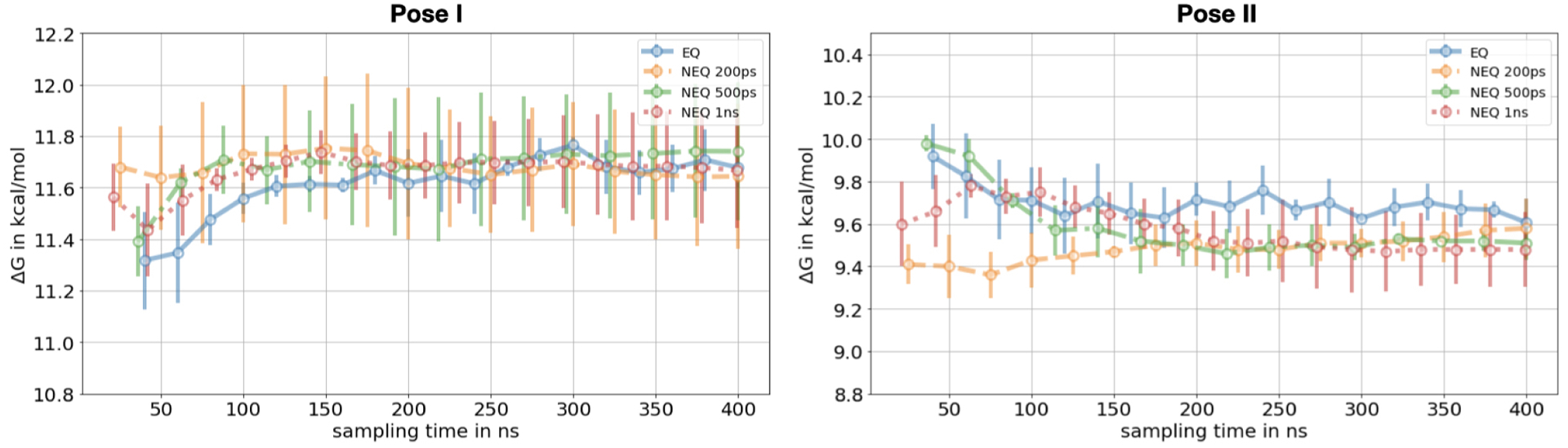
Decoupling of toluene in the binding site. The free energy difference for the EQ and NEQ approach for both poses is shown as a function of the sampling time. For the EQ approach we show the mean free energy difference across three replicates while for the NEQ approach the free energy estimate was obtained by pooling work values from three replicates and estimating one free energy difference using BAR (Sec. 4.5). The uncertainty estimate in both approaches is the standard deviation across three replicates. The NEQ protocols differ in the lengths of the NEQ switching transitions, which are 200 ps, 500 ps and 1 ns, respectively. The number of switching transitions differs among the protocols in such a way that the same amount of overall sampling time is used in all protocols. All protocols converged to the same free energy difference within uncertainty.

Finally, the overall binding free energy of toluene for both poses was obtained through the thermodynamic cycle (Table 1, results of individual legs of the cycle in SI Table S3). A symmetry correction of −k_BT ln 2 ≈ −0.4 kcal/mol was added to account for the symmetry-equivalent binding mode.⁶³ The crystallographic pose was correctly predicted with a more negative ΔG with both methods (Table 1). While the binding free energy for the non-crystallographic binding mode is not an experimental observable, when combined with the binding free energy for the crystallographic pose, it tells us the relative population of the two binding modes.

Table 1.

Binding free energy ΔG° for the toluene/T4 lysozyme system.

	EQ [kcal/mol]	NEQ [kcal/mol]	experimental [kcal/mol]
pose I (crystallographic pose)	−4.6±0.1	−4.7±0.3	−5.52 ± 0.04
pose II	−3.7±0.1	−3.7±0.1

5.2.1. Isoleucine 78 reorients upon binding of toluene.

The side chain of isoleucine 78 (Ile78) reorients upon binding of toluene, causing problems for both the EQ and NEQ approaches if this reorientation is not sampled adequately. While the side chain showed partial occupancy of both rotamers in the noninteracting state (state B), Ile78 had one preferred orientation in the bound state (state A, Figure 7).

Figure 7.

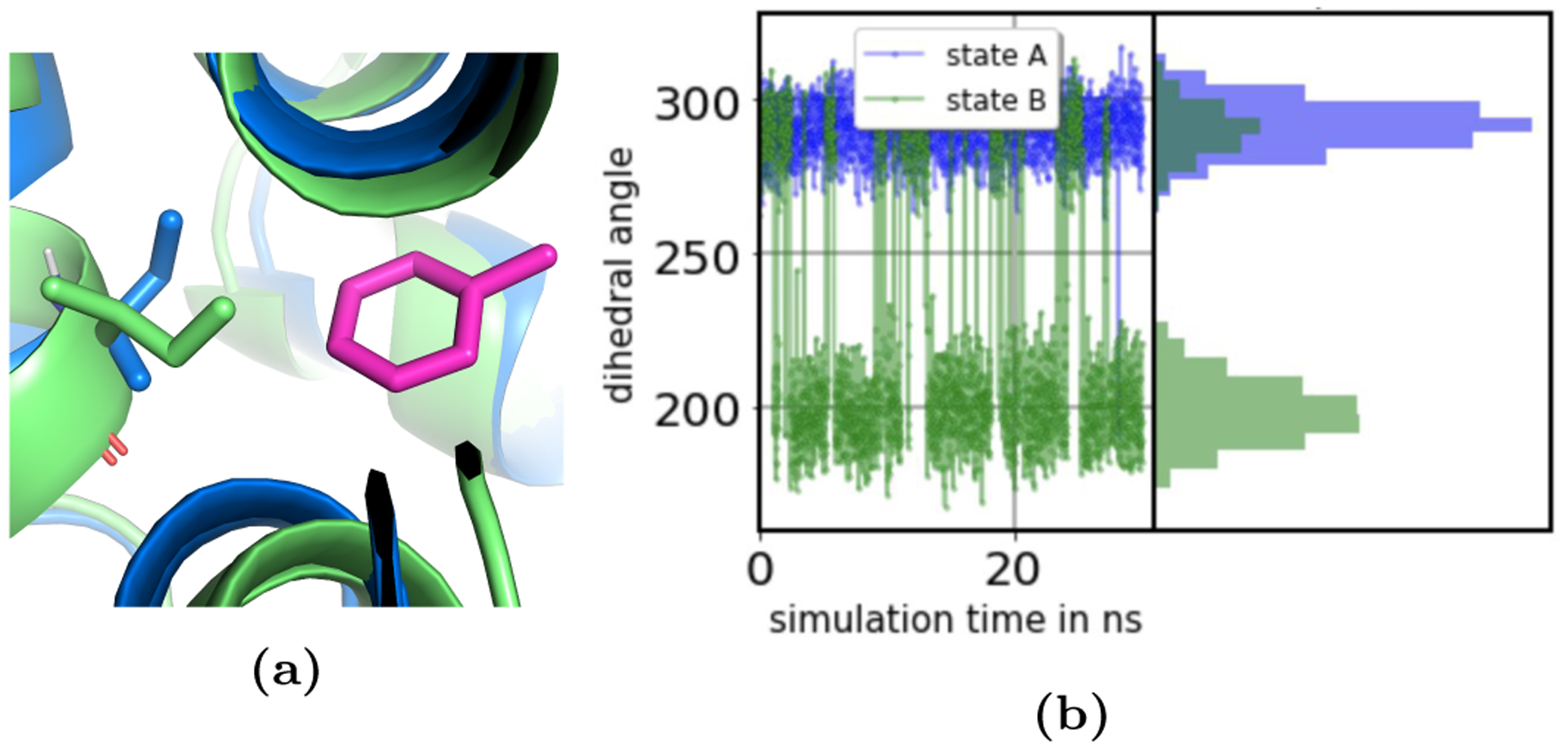
The side chain Ile78 reoriented upon binding of toluene to T4 lysozyme L99A. (a) In the bound state the Ile78 side chain occupied one rotamer state (blue sticks), while the side chain showed partial occupancy of two rotamers (blue and green sticks) in the unbound state. (b) The ξ1 dihedral angle of Ile78 as a function of simulation time in the simulation of the interacting (state A, blue) and the noninteracting state (state B, green) and its distribution. The non-interacting state had to be sampled long enough to observe multiple transitions between the rotamers.

The reorientation of the Ile78 dihedral angle occurred relatively fast on timescales of a few hundred ps – which is faster than simulation timescales and we seemed to be able to adequately sample the motion here (Figure 6 and S3). This helped us develop techniques to better assess important protein motion.

5.2.2. Side chain reorientation in NEQ switching transitions.

In the NEQ approach, end states have to be sampled long enough to start transitions from the correct distribution of dihedral angles and/or the transitions have to be slow enough to allow for reorientation (if needed) on ligand binding, otherwise the final distribution of dihedral angles will closely match the starting distribution.

According to the Crooks fluctuation theorem, provided that transitions are started from the correct distribution of conformational states in the end states and that a sufficient number of transitions are performed, the method will converge to the correct free energy difference. This is true even if the final distribution of dihedral angles after the transitions does not match the equilibrium distribution in that end state.

As can be seen in SI Figure S3, fast transitions (200 ps) can be long enough to allow for the side chain to reorient, however, the rotamer populations do not resemble those after the transition as observed in a long end state simulation. This does not mean that resulting values are necessarily wrong as they would be if the dominant rotamer were never sampled in the non-equilibrium switches (Sec. 5.3). Here, running shorter transitions, where we sampled the rotamer switching only sometimes, resulted in free energy estimates that were statistically equivalent to those obtained using longer transitions, in which the dominant rotamer was sampled most of the time, presumably because the free energy estimator gives the most weight to those transitions which discover the favorable rotamer. The standard deviation was also comparable among different NEQ protocols (Figure 6). This shows that sampling the side chain reorientation in some switching transitions is sufficient. The standard deviation between independent replicates for pose I is higher with the NEQ approach than with the EQ approach for all transitions lengths (0.2–0.3 kcal/mol vs. 0.1 kcal/mol), suggesting that the protein undergoes additional conformational changes.

In this system, sampling of different rotamers of Ile78 led to a bimodal work distribution in the direction of restoring the ligand-protein interactions (the direction we call B2A, as our B state is the noninteracting state), and this was especially common for fast transitions (Figure 8). While a bimodal distribution of work values itself does not necessarily pose a problem, it can pose a problem when it results from drawing from an incorrect or biased distribution of states at the end states – such as when a slow conformational transition is inadequately sampled for one or both end states – or when it results from transitions which are too fast to sample an important conformational change.

Concretely, for example, consider a situation where a minor rotameric state for a particular sidechain ought to be slightly populated in the bound state at equilibrium and becomes dominant in the unbound state. If the actual sampling of the bound state misses that minor conformer entirely and switching to the unbound state is so rapid as to miss rotameric transitions, there is a high likelihood that resulting free energy estimates will be biased (unless sampling of reverse transformations is somehow sufficient to recover). Here, then, we find it helpful to assess dihedral sampling in the end states and assess whether switching transitions ever sample rotamers appropriate for their target end state.

If the rotamer population is not sampled correctly in the end states, the results will be inaccurate or imprecise, and a bimodal distribution can in some cases be a warning sign that sampling might be complex or slow. Restraining the Ile78 side chain resulted in a unimodal work distribution (SI Figure S6) which further supports our findings that different rotamers of Ile78 in the B state led to a bimodal work distribution in the reverse transitions. The situation could have been worse if the noninteracting state did not already spend time sampling both rotamers and if the reorientation occurred on longer timescales. If a conformational transition is truly needed on binding then instead of having a bimodal distribution the final distribution might be unimodal, but wrong, as discussed in Sec. 4.4 and in Sec. 5.3.2.

There are generally two scenarios that can lead to dissipation and non-overlapping work distributions (SI Figure S9, S15) or bimodal work distributions (Figure 8): In the first scenario the system ends up in the correct end state but during NEQ switches was driven rapidly and accordingly heat was dissipated (friction). Secondly, the system does not end up in the equilibrium end state at the end of the short transition. An example for this second scenario is the Ile78 side chain orientation discussed above.

To investigate whether the Boresch-style restraints were a source for the large dissipation seen in the reverse process (orange work distribution Figure 8), we performed calculations applying a lower force constant on the orientational (Boresch-style) restraints (see SI Figure S4). The average dissipated work W_d, where W_d = W^R +ΔG = W^F − ΔG,³⁹ was the same for both protocols (1.7 kcal/mol in the reverse direction and 0.9 kcal/mol in the forward direction).

Center of mass (COM) – COM flat-bottom harmonic distance restraints are an alternative to orientational restraints and have been applied to binding free energy calculations.⁷³ We performed calculations restraining the distance between the COM of the ligand and the COM of a protein side chain and compared the results of the two restraint approaches (see SI Table S4). The dissipated work was higher in the COM-COM restraining protocol (3.8 kcal/mol in the reverse direction and 1.4 kcal/mol in the forward direction) compared to the one using Boresch-style restraints. With a single COM-COM distance restraint, the ligand can sample the sphere with the radius of that distance restraint which presumably caused the larger dissipation. These findings suggests that the Boresch-style restraints were not a major source for the dissipation seen in Figure 8.

5.2.3. The Ile78 orientation correlated with the work values as detected with the Pearson correlation coefficient.

In the NEQ approach, we detected slow protein motions by calculating the Pearson correlation coefficient (PCC) between the work values and all side chain dihedral angles in the protein. We calculated the dihedral angles from the set of first frames and the set of last frames of NEQ switching transitions. Then, we took the work values for the set of forward transitions and correlated it with the set of initial dihedral angles; we also did the same for the set of final dihedral angles. This gave two separate PCC for each dihedral angle (one using the dihedral angles from the first frames and one the dihedral angle of the set of last frames). We performed the calculation in both the forward and reverse direction (decoupling and coupling). When the ligand appeared in the binding site (backward direction), a high PCC was found between the ξ1 dihedral angle of Ile78 and the reverse work values in both poses. The correlation was highest in the NEQ protocol with 200 ps/transitions using the structure of the first frame of the switching transitions (PCC = 0.5–0.6), as can be seen in Figure 9a. The PCC was also high using the last frame of the transitions (0.5–0.6), suggesting that it is important to sample the side chain reorientation at least in some transitions. The PCC decreases as the transition length increases, especially the correlation between work and the starting orientation (first frame of transitions)(mostly PCC<0.5), since the side chain reorients more often in longer switching transitions. Figure 9b shows an example of a slow motion that is not correlated with work values. Asp127 is not close to the binding site and although the motion is slow, it does not seem to be important.

Figure 9.

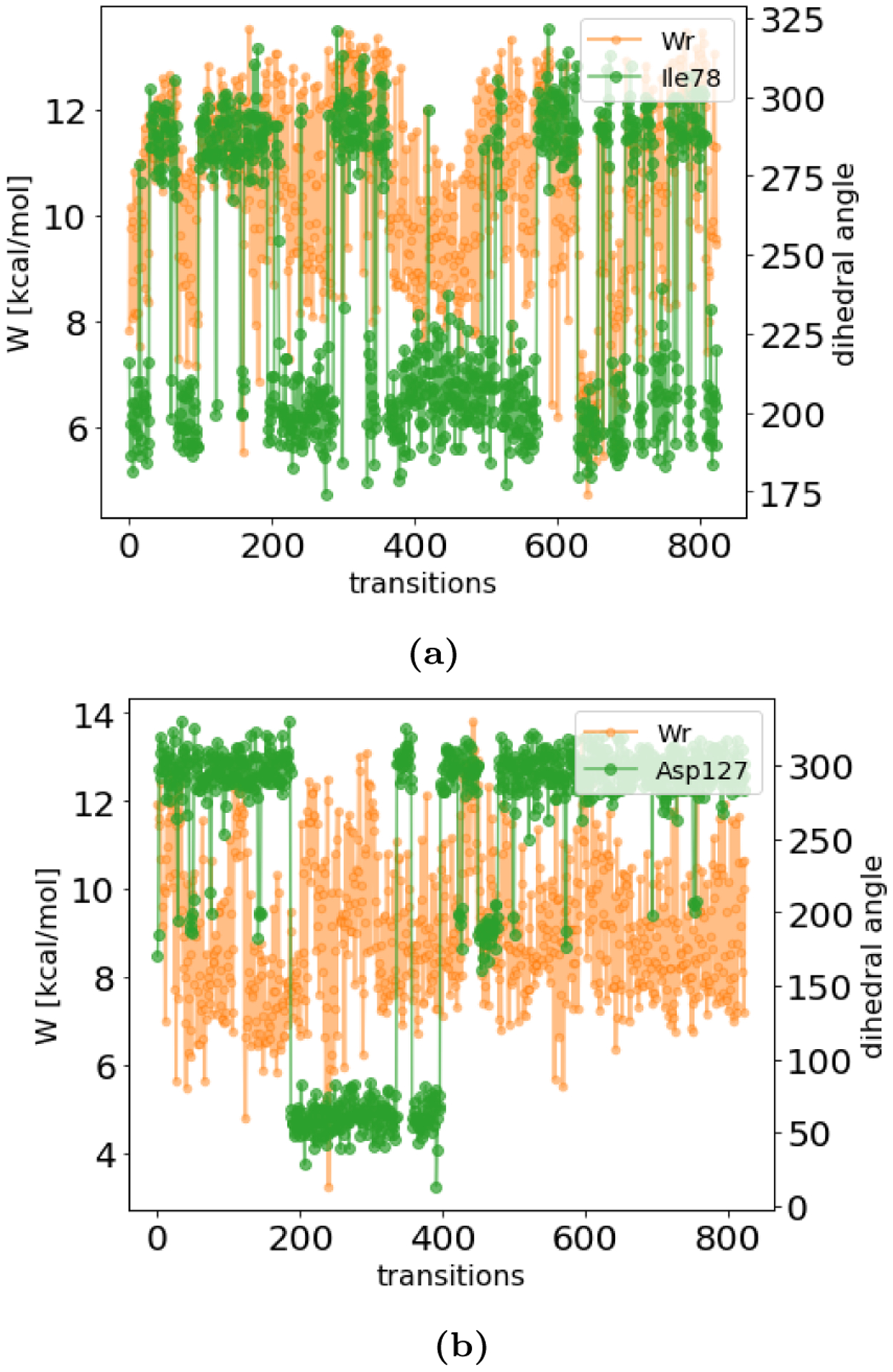
Correlation between reverse work values (Wr) and the dihedral angle of Ile78 (a) and Asp127 (b) for toluene binding to T4 lysozyme L99A. The work values (orange) and the dihedral angles (green) are plotted as a function of the transition number. The dihedral angle was calculated from the set of first frames of the NEQ transitions. (a) Work values are correlated with the dihedral angle of Ile78, which is supported by a high Pearson correlation coefficient (PCC=0.5). (b) A low PCC of 0.04 likely indicates no significant correlation between dihedral angle Asp127 and work values. Asp127 was included as an example of a motion that is not correlated with the free energy difference. Even though the motion is slow, it appears not to be important.

Calculating the correlation between work values and dihedral angles in the protein may be a useful general approach for identifying potentially problematic degrees of freedom. This approach will work best when the number of such degrees of freedom is low. If multiple side chains reorient upon binding, the correlation between the work and the orientation of each individual side chain will be reduced, making it more difficult to identify slow motions. Furthermore, the metric is prone to false positives due to accidental correlations that can cross significance testing thresholds, as illustrated in this comic.⁷⁴ If 200 residues are predicted not to correlate with the work values, a 5% false positive rate will mean that there are 10 false correlations. Careful inspection (e.g. considering proximity to the binding site) and cross-validation with replicates can help ensure apparent correlations are not spurious.

However, it is important to note that NEQ free energy calculations do not require switching transitions to sample all relevant conformational states; what is required is that end state sampling populate the correct equilibrium distribution of states, and switching transitions must be sufficiently numerous to provide an adequate average over possible work values. Thus, the presence of work values that correlate with a particular slow conformational degree of freedom does not necessarily indicate sampling problems; rather, it means that practitioners need to check that the end states in fact sample the correct equilibrium distribution of states. If they do not, results will be inaccurate or at least imprecise.

5.2.4. In the equilibrium FEC, the Ile78 orientation correlates with dH/dλ values.

In the EQ approach, sampling problems can in some cases be detected by examining sudden changes in the dH/dλ values and identifying related structural degrees of freedom. We plotted the running average of the dH/dλ values over the simulation time for every state, picked a λ window where there was an obvious jump in the dH/dλ value and looked at frames from the trajectory near that jump. Once any potential sampling problem – such as a motion which might be responsible for the sudden jump in dH/dλ – was identified we correlated the motion with the dH/dλ curves of all λ windows to assess correlations between that structural degree of freedom and dH/dλ values.

Here, we find that sampling problems primarily occurred in the alchemical intermediate states. In the EQ approach, each state has to be sampled at equilibrium, meaning that the correct equilibrium distribution of the Ile78 dihedral angle has to be sampled at every λ window. This can be especially challenging in intermediate states where energy barriers between the rotamers can be high. In SI Figure S5 we show an example of the correlation between the dH/dλ values in one λ window and the dihedral angle of Ile78. The three replicates did not sample the same rotamer distribution of the side chain indicating that sampling time was not sufficient to reach equilibrium.

This approach of correlating dH/dλ values with structural degrees of freedom can be a useful general strategy for identifying potentially problematic degrees of freedom in equilibrium FEC. This method is comparable to examining sudden changes in work values in the NEQ approach in that it helps to narrow down a large amount of trajectory data to a specific set of frames in which a slow but important rearrangement may occur.

Here, independent replicates converged well (Figure 6) suggesting that the motion of the Ile78 rearrangement, although not sampled adequately in every alchemical state, was overall sampled well enough to only have a minor impact on the free energy difference.

5.3. 3-Iodotoluene binding to T4 lysozyme mutant L99A.

For 3-iodotoluene binding to T4 lysozyme (L99A), in both EQ and NEQ calculations the independent replicates did not converge to the same result in 400 ns total simulation time, indicating inadequate sampling. In Figure 10 we show the mean and standard deviation for the independent repeats of the EQ, and different protocols of the NEQ approach; for details on the individual repeats see SI Figures S7 and S8. The standard deviation σ for the EQ approach was higher than in the toluene case (σ_{3−iodotoluene} = 0.4 kcal/mol, σ_toluene = 0.1 kcal/mol) suggesting that sampling problems were more severe. For the NEQ protocols, which all used the same total simulation time, the ΔG estimate depended on the length of the NEQ switching transitions. Since overlap of the work distributions was poor, even with 4 ns/transition (SI Figure S9), results are likely not to be trusted. The overall binding free energy of 3-iodotoluene, which was obtained through the thermodynamic cycle, varies between −4.8 and −5.7 kcal/mol among different protocols, as shown in SI Table S5. The experimental binding affinity of 3-iodotoluene to T4 lysozyme L99A was not found in the literature. Here our focus is not on agreement with experimental values, since this is also a function of the force field and other factors; rather, we focus on whether we have obtained converged values.

Figure 10.

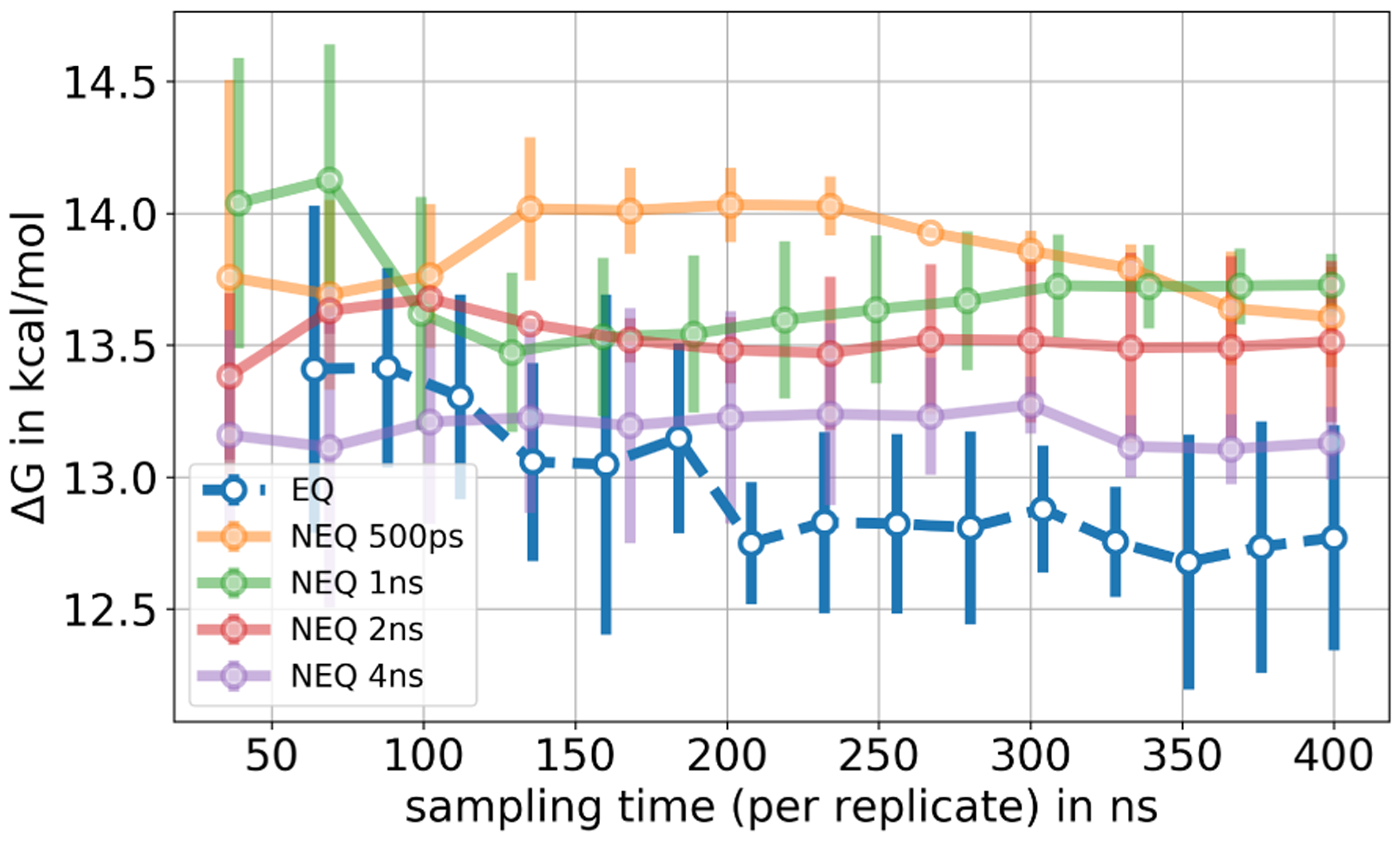
Free energy difference of decoupling 3-iodotoluene in the binding site as a function of sampling time. For the EQ approach we show the mean free energy difference across three replicates while for the NEQ approach the free energy estimate was obtained by pooling work values from three replicates and estimating one free energy difference using BAR (Sec. 4.5). The uncertainty estimate in both approaches is the standard deviation across three replicates. Same amount of total simulation time was used for the EQ and the four protocols of the NEQ approach. The different NEQ protocols differ in the length and the number of NEQ transitions. The standard deviation, especially for the EQ approach, was high and the ΔG estimate of the NEQ protocols depended on the transition length, suggesting insufficiencies in sampling.

5.3.1. Valine 111 reorients upon binding of 3-iodotoluene.

Slow conformational changes in the protein prevent convergence in both methods on the timescale of our simulation. 3-Iodotoluene, being more bulky than toluene, induces a rearrangement of the valine 111 (Val111) side chain upon binding (Figure 2b). The timescale for this reorientation is relatively slow (a couple of nanoseconds) and consequently results are highly sensitive to the initial protein conformation (Figure 11). The predicted free energy change is either too favorable or too unfavorable depending on which structure was used as a starting point. If this conformational change is not sampled properly in the free energy calculation, running simulations starting in the apo protein structure results in a predicted free energy which is too unfavorable. The contribution of protein rearrangement upon binding and potential steric clashes with the protein are not accounted for in this scenario. On the other hand, the free energy change is predicted as too favorable when simulations are started in the holo protein structure. The protein is deformed upon binding and the energetic cost of this protein strain energy is missing.⁴⁷

5.3.2. This side chain rearrangement is not sampled adequately in NEQ and EQ calculations.

In the NEQ approach it is important to sample the correct orientation of Val111 in the end states at equilibrium and to run the transitions between the end states slowly enough to allow for a rearrangement at least in some transitions (as discussed in Sec. 5.2.2). Although the free energy estimate should be independent of the switching rate, provided that a sufficient number of work values was collected, we found that the efficiency of a protocol can dependent on the switching rate. Performing the transitions at a slower rate increases the probability of observing the reorientation of a side chain, because the transition has less dissipation and follows closer the free energy gradient. Here, dissipation was large, and reducing the switching rate can be more efficient than running faster transitions (see Figure 10) which would require a longer total simulation time. Simulations were started in the bound protein conformation. The end state simulation of the decoupled state has therefore be run long enough so that the Val111 side chain can reorient adequately to obtain a correct equilibrium distribution of conformations. Here, the alternate rotamer (after reorientation) should be dominant in the unbound ensemble, so we discard all frames before reorientation to equilibration. This would not be necessary if the end state simulation was run long enough to capture the equilibrium distribution of conformations instead of being biased by the starting configuration of Val111.

Starting NEQ transitions from structures where Val111 had not reoriented yet led falsely to good overlap of the work distributions but a wrong estimate of the free energy difference (Figure 11). Only a few transitions starting from the “wrong” structure (the overpopulated minor rotamer) had a huge impact on the result since the tails of the distribution have a large statistical weight for the ΔG estimate. When as few as 17 transitions starting from the wrong Val111 rotamer were included (Figure 11c, discard 60), the free energy did not converge to the same result as when starting all transitions in the correct dominant rotamer (Figure 11c, discard 80). We attribute this to the fact that the alternate rotamer ought to be present to a vanishingly small degree at equilibrium.

Not only is it important to start the transitions with correctly populated orientations of the Val111 side chain, but the switching also has to be slow enough to allow for rearrangement towards the orientation in the other end state at least in some transitions. Note that it is also possible that, with sufficiently large end state ensembles which populate minor rotamers at exactly the right degree, such transitions during switching might not be necessary, but that was not observed here. Unfortunately, it is not obvious how the NEQ switching rate couples to the rate of side chain reorientation, making it difficult to know the required transition length a priori. As discussed in Sec. 5.2.2, although not all non-equilibrium switches have to sample this reorientation, it has to be sampled in some transitions to obtain overlapping work distributions and a reliable free energy estimate. Here, even with 4 ns/transition, the side chain reoriented only in 8 % of the transitions in the coupling direction (B2A) and 74 % during decoupling of the ligand (A2B), which results in too few transitions sampling the correct rotamer in the coupling direction. Since the conformational change was not sampled sufficiently in 400 ns total simulation time, we decided that it was better to restrain the side chain.

To support our findings that the large dissipation (SI Figure S9) was caused by a side chain rearrangement upon binding and not by the Boresch-style restraints, we performed calculations applying a lower force constant on the orientational (Boresch-style) restraints (see SI Figure S10). The average dissipated work W_d in the forward and reverse directions was similar for the protocols using weaker and stronger restraints (3.7 vs. 3.9 kcal/mol in the reverse direction and 3.4 vs. 4.1 kcal/mol in the forward direction). These findings suggests that the Boresch-style restraints were not a major source for the dissipation in this system.

Equilibrium FEC also suffered from sampling problems due to the rearrangement of the Val111 side chain. These issues were most severe in intermediate λ windows where the Val111 side chain showed partial occupancy of two rotamers and a slow rotation between them. In order to investigate this, we looked for sudden changes in dH/dλ values. Correlating these with the dihedral angle ξ1 of Val111 and comparing results among three independent replicates shows that the side chain was kinetically trapped in various intermediate states (Figure 12). Approaches to overcome these sampling problems include the use of enhanced sampling techniques, like HREX or incorporating BLUES-like side chain moves.^57,75

Figure 12.

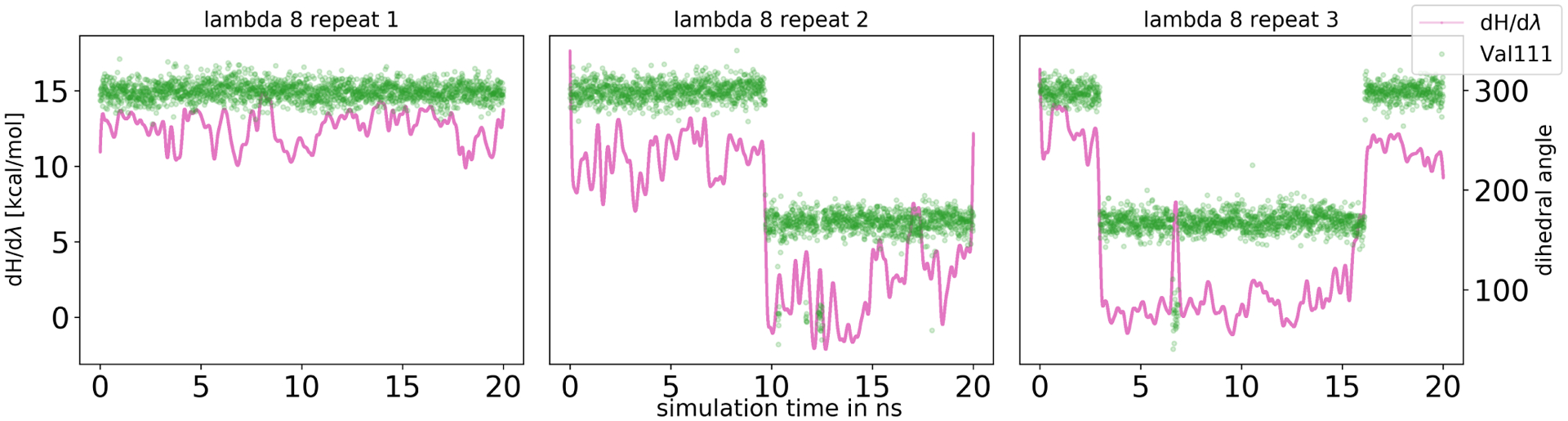
Correlation between dH/dλ values and the dihedral angle of Val111 for 3-iodotoluene binding to T4 lysozyme L99A. A running average of the dH/dλ values (pink, averaged across 2000 data points) and the dihedral angle of Val111 (green) is plotted as a function of simulation time. Here we only show λ 8 for the three independent replicates, additional λ windows can be found in the SI. Rotation of the Val111 side chain resulted in sudden changes of dH/dλ showing the impact of the side chain orientation on the free energy difference. The side chain did not rotate in repeat 1, while it did in the other two repeats indicating that the correct equilibrium distribution was not sampled adequately in 20 ns simulation time.

5.3.3. We restrained the Val111 side chain to avoid the sampling of slow DOF.

In this work, we decided to work around inadequate sampling of this motion by restraining the dihedral angle of the Val111 side chain for both EQ and NEQ approaches. We restrained the side chain to its preferred orientation in the bound and in the decoupled state and switched it during the alchemical path.

With this protocol, the work distributions in the NEQ case overlapped well already using 500 ps/transition (SI Figure S13), indicating that indeed the Val111 side chain sampling led to poor overlap in the unrestrained calculations. However, a lot of NEQ transitions (~ 320, SI Figure S12) were necessary in order to converge independent replicates which was probably due to additional slow DOF in the system (perhaps Ile78 rotamer sampling). The approach of switching the dihedral during the alchemical path was challenging using the EQ protocol. The standard deviation across replicates was higher (std=0.4 kcal/mol, SI Figure S11) than in the NEQ approach (std=0.07 kcal/mol) caused by insufficient sampling of the Val111 switching in some intermediate states.

Since we restrained the dihedral, to calculate binding free energies, we must account for the energetic costs of the dihedral restraints in the thermodynamic cycle. We did this by first turning the restraints on with the ligand interacting in the binding site, then decoupling the ligand while simultaneously switching the restraints to the orientation in the apo structure. Finally the restraints were then turned off again. The cost for restraining the side chain was very low (0.1 kcal/mol for restraining and −0.1 kcal/mol for unrestraining) since Val111 was restrained to its preferred orientation in both the holo and apo structure.

We also tested a different protocol, where we restrained the dihedral to the orientation in the holo structure both in the bound and unbound state and did not switch it upon decoupling of the ligand. This introduced new sampling problems: Other side chains in the binding site (methionine 102, valine 103, isoleucine 78) reoriented in response to the forced unfavorable orientation of Val111 in the unbound state (probably to fill the space which would otherwise be empty) making it necessary to restrain those as well. The Pearson correlation coefficient between the dihedral angles and the work values helped detect some of these DOF. This metric was however sometimes subject to noise since many dihedral angles correlated with work values. Correlations were also not always consistent across replicates because different side chain caused problems in different replicates. Restraining the dihedral angles of those side chains as well led to a low standard deviation (0.2 kcal/mol) in the NEQ approach already with short transitions (100 ps/transition).

With these additional restraints, it was more challenging to account for the restraining costs. More side chains were restrained and the costs for restraining those to an unfavorable rotameric state in the unbound state were high (~7.5 kcal/mol, see SI Figure S14).

Although we are aware that the use of restraints is not a good general solution to inadequate side chain rotamer sampling, we think that it helps illustrate a potential pitfall of these approaches. Particularly, restraining the side chains gives the same outcome one might get in a shorter simulation, or a simulation where the environment is more sterically constrained (in which the side chain might not switch rotamers at all). In such cases, one might see “good overlap” in the non-equilibrium work distributions but only because the simulations missed an important motion that needs to be sampled.

5.4. Summary of the T4 lysozyme system.

In the T4 lysozyme cases examined, convergence of the ΔG estimate was challenging due to side chain rotamer sampling. Slow side chain rearrangements, like Val111 in the 3-iodotoluene case, proved to be very challenging both in EQ and NEQ approaches. The length of NEQ transitions became very important here. Sufficient sampling of faster side chain-rearrangements upon binding, like Ile78 in the toluene system, was achieved by running longer/many NEQ transitions and long equilibration in the equilibrium FEC. In principle this could be true for slower rearrangements too, but in some cases the relevant motions can take nanoseconds to hundreds of nanoseconds for a single transition, making it less desirable to simply run longer simulations. In the NEQ approach, sampling problems were detectable from work value trends and their correlation with structural degrees of freedom in equilibrium snapshots they were derived from. Here, we restrain the dihedral angles of the side chains to work around the issues but our findings suggest that better and more robust methods are necessary to solve the problem.

5.5. Free energy calculations in the HSP90 system.

In the HSP90 system, in both EQ and NEQ calculations, independent replicates did not converge to the same free energy estimate within a standard deviation of 0.2 kcal/mol – even with ~1 μs sampling time per replicate – indicating inadequate sampling (Figure 13). In addition to the high standard deviation among replicates and convergence of the cumulative ΔG estimate, several additional factors suggest the presence of one or more slow degrees of freedom in the system.

Figure 13.

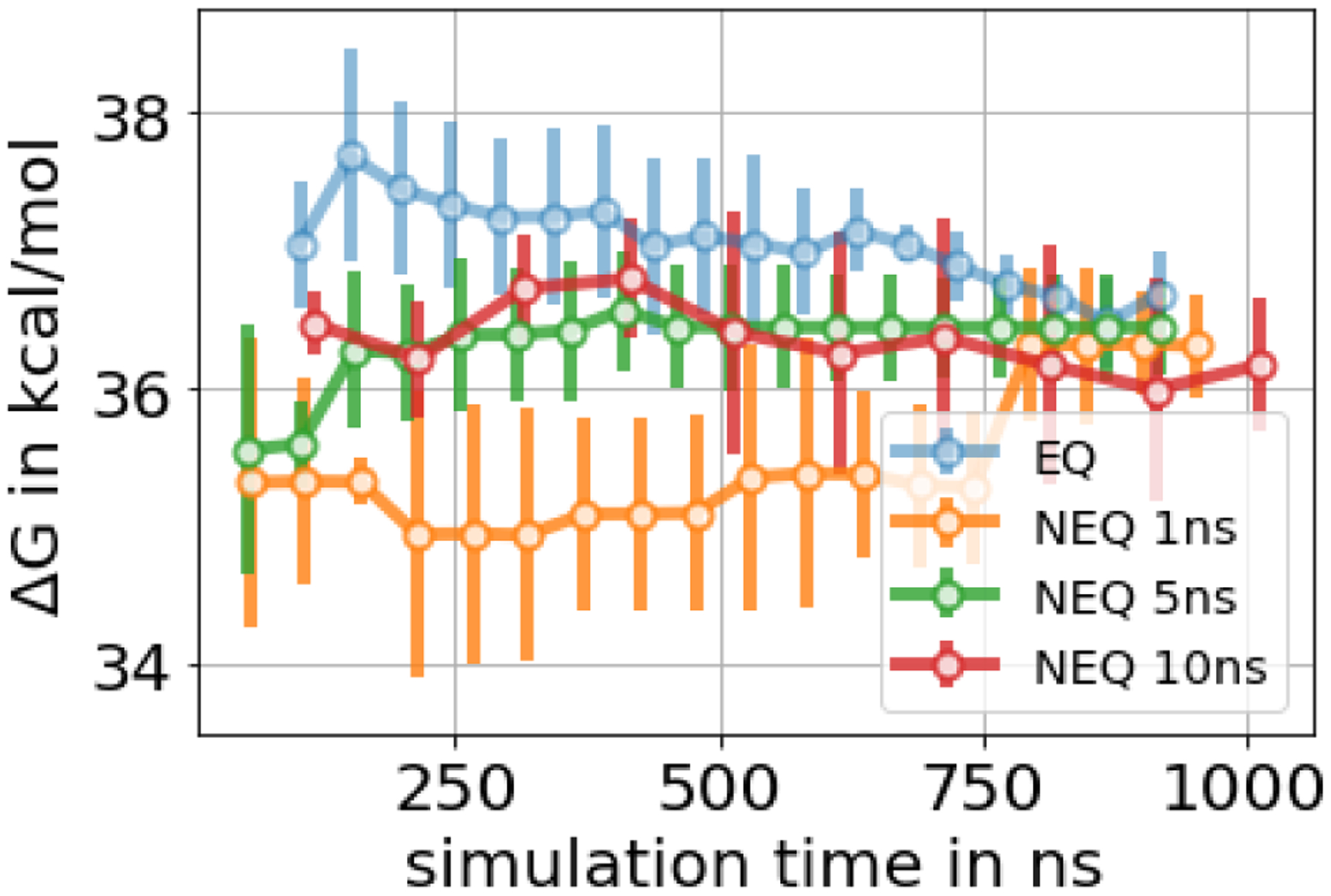
Free energy difference of decoupling the HSP90 ligand in the binding site as a function of total simulation time. For the EQ approach we show the mean free energy difference across three replicates while for the NEQ approach the free energy estimate was obtained by pooling work values from three replicates and estimating one free energy difference using BAR (Sec. 4.5). The uncertainty estimate in both approaches is the standard deviation across three replicates. The three NEQ protocols differ in the length and number of the switching transitions. A high standard deviation indicates inadequate sampling.

In the NEQ approach, the overlap of the work distributions was very poor, even with 10 ns/transition (SI Figure S15). Running 10 ns per transition requires considerable computational expense and removes much of the benefit of the NEQ approach. Given the same total simulation time for different NEQ protocols, the lengths of the switching transitions had a huge impact on the estimated free energy change and different protocols only converged to the same result within large uncertainty and after long simulation times. This suggests that the uncertainty of the ΔG estimates is larger when work distributions lack overlap.

On the other hand, for the EQ approach, the final ΔG estimate depended on the equilibration time (how much data were discarded to equilibration). Discarding more data (20 ns per λ window) made a difference of ~ 1 kcal/mol in all three replicates compared to not discarding any data to equilibration (SI Figure S16). This and a low number of uncorrelated samples in some λ windows can indicate a slow degree of freedom (DOF). Similar to the T4 lysozyme system, analyzing sudden changes in dH/dλ values helped identifying these slow DOF, as shown below.

The overall binding free energy of the HSP90 ligand, which was obtained through the thermodynamic cycle, varied between −11.0 and −11.8 kcal/mol among different protocols, as shown in SI Table S6. The binding free energy of the protocols, where three buried water molecules were not present in the starting structure (Sec. 5.5.4), differs from the other protocols by ~ 2 kcal/mol (−8.6 to −9.9 kcal/mol). These protocols agreed best with the experimental binding free energy of 9.34 +/− 0.07 kcal/mol, although inadequate sampling was most severe. This is possible since agreement with experimental values is not only a function of adequate sampling, but also of the force field and other factors. Therefore, we focus on whether we have obtained converged values rather than on agreement with experimental values.

5.5.1. Slow water sampling in the solvent exposed binding site of HSP90.

The first issue we identified was slow water sampling in this solvent exposed binding site. In the unbound state, water molecules completely fill the binding site. Upon binding the ligand displaces the solvent molecules except three buried water molecules between the ligand and the protein (Figure 3).

In equilibrium FEC, inadequate water sampling was mainly observed in the intermediate λ windows. As the interactions of the ligand were decoupled, more water molecules entered the space between the ligand and the protein, joining the three buried water molecules (Figure 14). However, since the ligand was still partly interacting and blocking or slowing solvent access to this space, this motion was slow to sample. For multiple λ windows, the number of water molecules in the binding site differed among the independent replicates, and 40 ns sampling time/λ window was not always sufficient to reach equilibrium. Jumps in dH/dλ curves correlated with water molecules entering the buried space (Figure 15). This suggests that sampling the correct number of waters in the binding site has an impact on the ΔG estimate. For the fully decoupled ligand, the timescales of the water molecules filling the empty binding site were relatively fast (roughly a few hundred ps).

Figure 14.

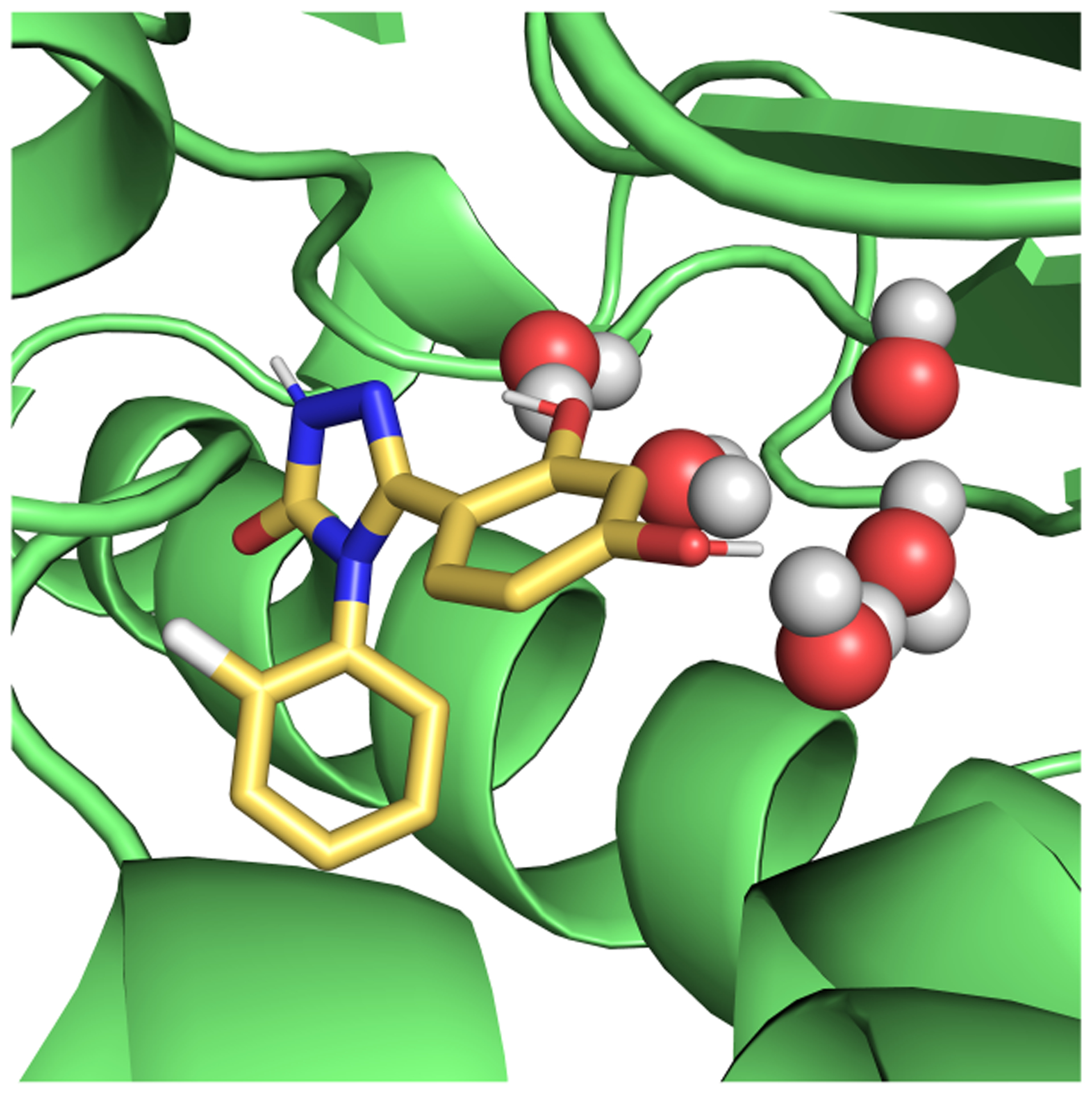
In the HSP90 system, water molecules got trapped in the binding site when the ligand appeared quickly during NEQ transitions as well as in intermediate λ windows in the EQ approach. HSP90 is shown in green, ligand in yellow sticks and water molecules are depicted as spheres.

Figure 15.

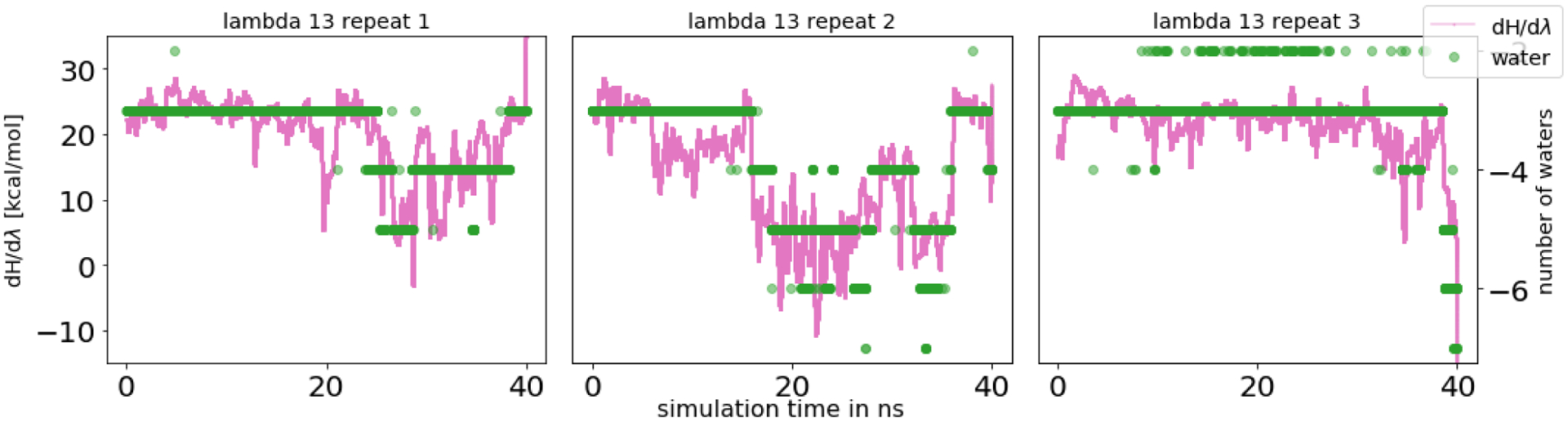
Correlation between dH/dλ values and the number of water molecules in the binding site fo HSP90. A running average of dH/dλ values (pink, averaged across 2000 data points) and number of water molecules (green, negative number to better show the correlation) as a function of simulation time per λ window. Here we show λ 13 across all three replicates as an example; additional data is in the SI. The entry of water molecules (more than the three that were already present in the starting structure) was a slow motion and had an impact on the potential energy of the system. Equilibrium was not reached at this particular λ window in any of the three repeats.

In the NEQ approach, water molecules got trapped in the same buried space that caused problems in the EQ approach (Figure 14). Particularly, when the ligand appeared in the solvent-filled binding site too quickly, water molecules were not displaced properly and got stuck between the ligand and the protein. This led to poor overlap of the probability distributions of forward and reverse work values and therefore an imprecise (and potentially biased) estimate of the free energy difference. Long transitions were necessary to properly displace the water molecules upon ligand binding. When running each transition for 10 ns, most transitions (63%) correctly ended up with the three buried water molecules in the binding site, for shorter transitions less did so (5 ns/transitions: 41% and 1 ns/transition 7%). But such transitions are computationally expensive and remove much of the benefit of the non-equilibrium approach.

5.5.2. We identified other slow DOF in this system.

A second sampling problem in this system was a binding mode flip that occurred when the ligand was decoupled or only weakly interacting (Figure 17). In this case, orientational restraints only included atoms from two of the three aromatic rings of the ligand (see spheres, Figure 17), hence the third ring was able to flip to a different location.

Figure 17.

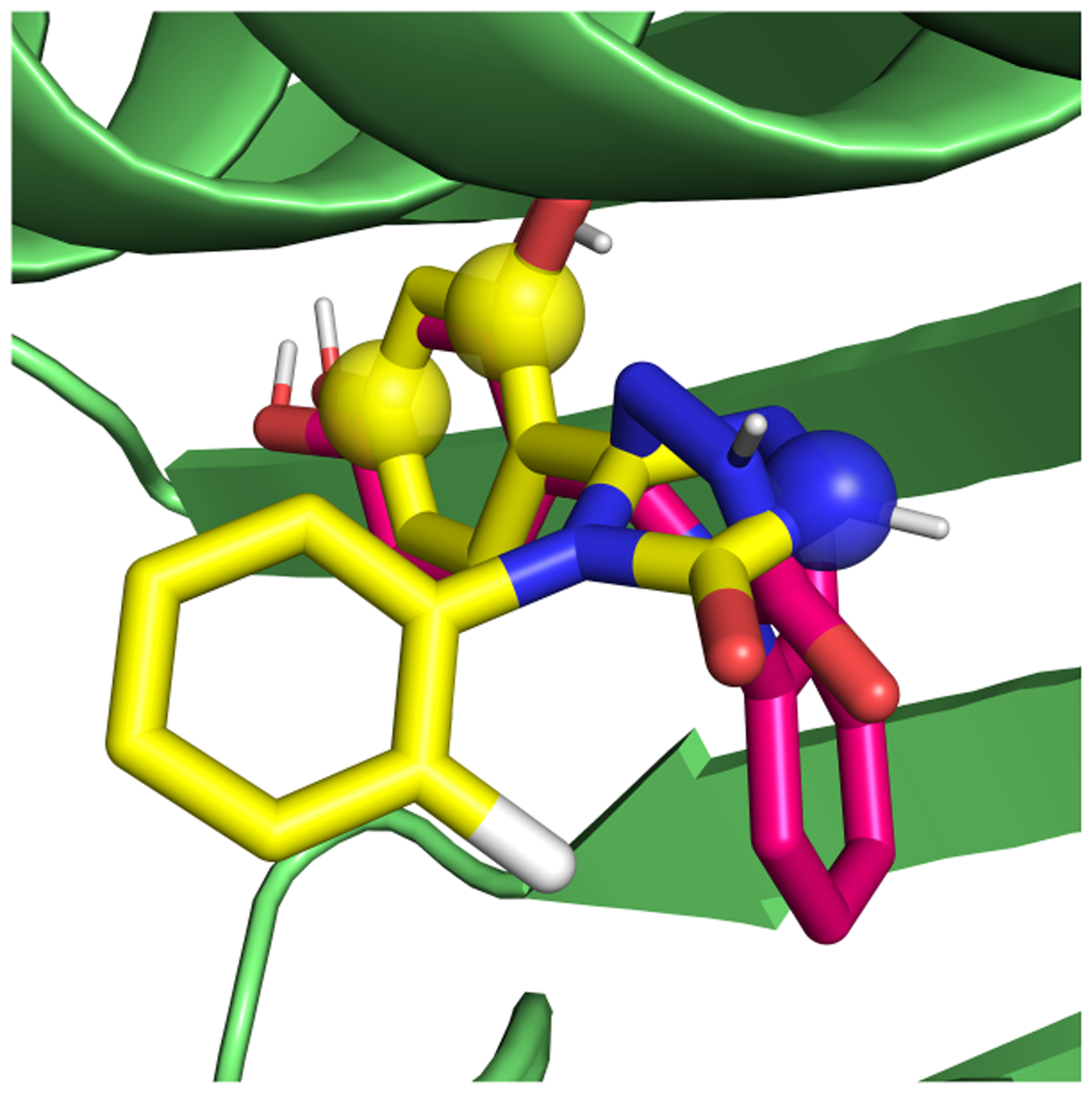
Binding mode flip of the weakly interacting ligand in HSP90. The crystallographic binding mode is shown in yellow, the flipped binding mode in pink and the protein in green. The three ligand atoms that are included in the orientational restraints are represented as spheres. The one aromatic ring that was not included in the restraints flipped into the binding pocket in the weakly and non-interacting alchemical states.

This only occurred in the weakly interacting states of the ligand, but affected the free energy difference as shown in the correlation between dH/dλ values and the RMSD of the ligand (Figure 18). The binding mode flip also had an impact in the NEQ approach as judged by a high PCC (PCC=0.61) between reverse work values and the ligand RMSD (SI Figure S17). To prevent this conformational change in the ligand, one could change the ligand atoms involved in the orientational restraints to also include the ring that flipped in the binding site in order to stabilize the binding mode better in the weakly-to non-interacting alchemical region. Another option would be the use of RMSD restraints.⁷⁶

Figure 18.

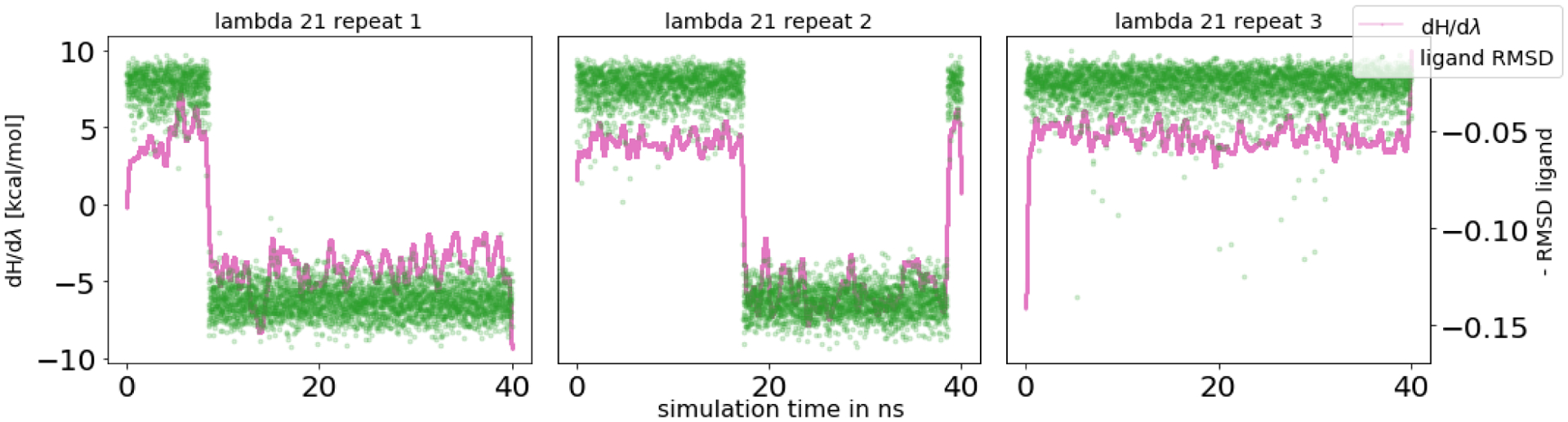
Running average of dH/dλ values (pink, averaged across 5000 data points) and the RMSD of the HSP90 ligand (green) as a function of the simulation time. We show data for λ 21 (second last state) for three independent replicates as an example, figures of all λ windows can be found in the SI. The correlation between dH/dλ values and the RMSD of the ligand indicates that the binding mode flip had an impact on the ΔG estimate, even though these only occurred when the ligand was weakly interacting.

Finally, minor problems were caused by side chain rearrangement of asparagine 36 (Asn36) upon binding. But since reorientation seemed not to be directly correlated with dH/dλ values nor to the work values in the NEQ approach, the impact of this DOF on the estimate of the free energy differences is not clear. However, this Asn36 rearrangement does have a huge impact on the ΔG estimate in the “bubble approach” as described in Section 5.5.3. It is not clear whether the sampling problem here is overshadowed by more severe problems in water and binding mode sampling, or whether it is directly linked to the bubble approach.

Similar to the T4 lysozyme systems, we checked the impact of the Boresch-style restraints on the dissipation by running calculations with a weaker force constant (1/4 of the original restraint strength). SI Figure S21 shows the comparison of these two protocols. We found that reducing the restraint strength did not have a huge impact on dissipation and the overlap of the work distributions. The average dissipated work W_d in the reverse process was 18.7 kcal/mol for the protocol with a weaker force constant and 15.2 kcal/mol for the original protocol and in the forward direction 11.5 vs. 13.9 kcal/mol, respectively.

5.5.3. Addressing inadequate water sampling.

The water sampling problem can be separated from the decoupling of the ligand by introducing a bubble-ligand that repels the water and keeps it out of the binding site. This bubble-ligand sits on top of the normal ligand but interacts only with the water molecules (Figure 5). The three buried water molecules were chosen not to interact with this bubble-ligand and were restrained with position restraints. This bubble-ligand reduces the dissipation in NEQ and overcomes sampling problems in the EQ approach. Even though the water problem should be accounted for in the NEQ theorem, we found that large dissipation required long transition times or a huge number of switching transitions which became computationally expensive. Our hope was that this approach might isolate some water sampling problems. However, we found that when the ligand was decoupled, the bubble-ligand created a vacuum in the binding site which created its own problems. Side chains of a loop close to the binding site moved in to this vacuum making it necessary to restrain their backbone atoms as well.

Figure 5.

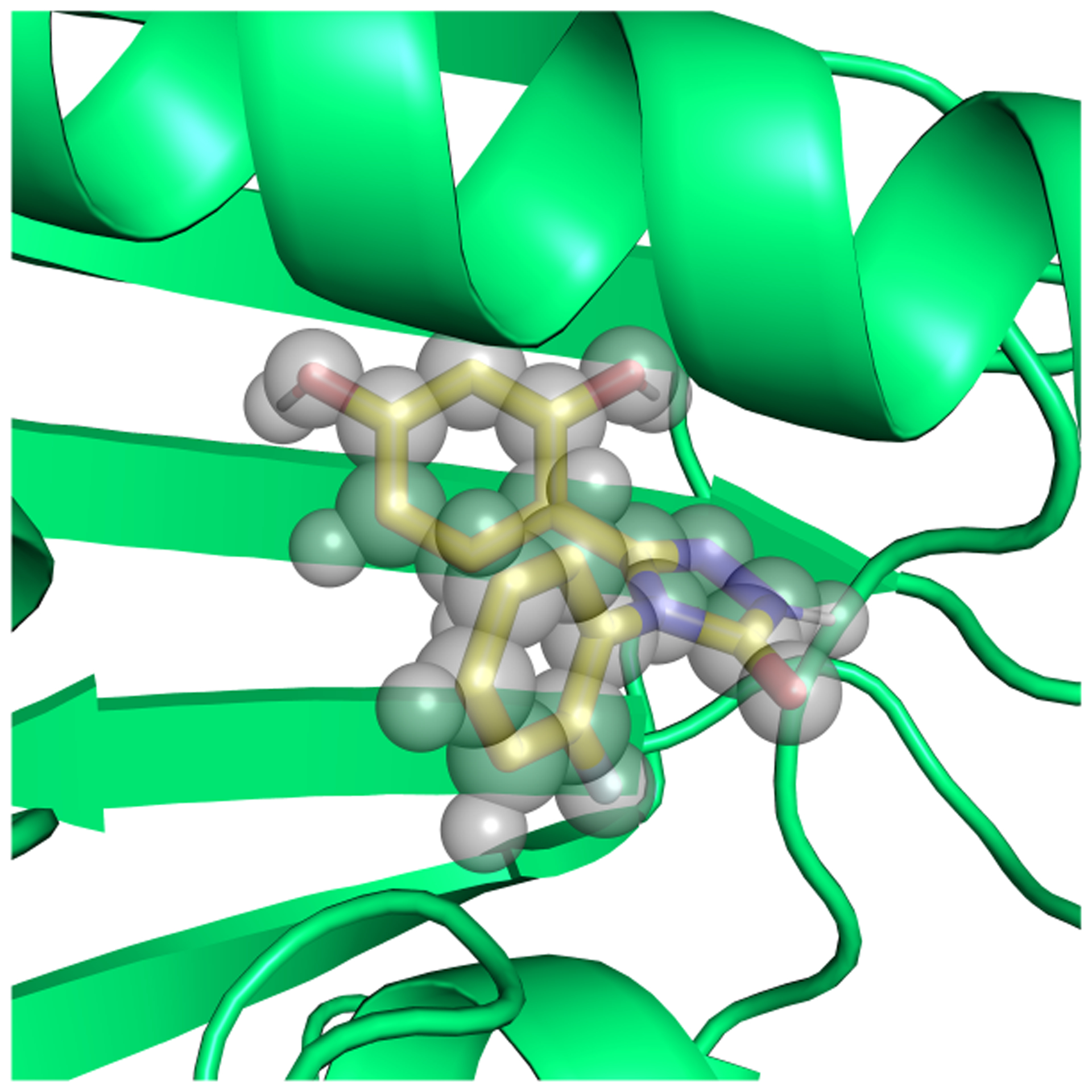
The bubble-ligand sits on top of the normal HSP90 ligand, but only interacts with water molecules in order to separate water sampling problems from the decoupling of the ligand. The bubble ligand is shown in grey spheres and the real ligand in colorized sticks.

Running NEQ with this bubble approach resulted in overlapping work distributions (already with 1 ns/transition, see SI Figure S18) which supports our hypothesis that water sampling was causing the overlap problems. However, in both the EQ and NEQ approaches the standard deviation across independent replicates was high (0.3–0.5 kcal/mol, SI Figure S19). This was due to slow side chain rearrangement of Asn36 (Section 5.5.2). Rotamer populations of this side chain in the unbound state differed among independent replicates which showed that sampling time was not sufficient to sample the correct Boltzmann weight of the rotamers (see SI). Both NEQ work values and dH/dλ values in the EQ approach correlated with the orientation of this side chain (SI).

In order to obtain the binding free energy, this bubble approach has to be included in the thermodynamic cycle (Figure 4, right). This makes the approach not only computationally demanding, but also difficult to generalize. The protocol had to be improved iteratively, gearing it towards this specific system. We had to optimize the van-der-Waals parameters of the bubble-ligand to sufficiently repel the water. We also had to restrain the loop that moved into the binding site to fill the vacuum created by the bubble (Sec. 4.). For a different system it would be difficult to predict such structural changes a priori. Additionally, water sampling problems, although less severe, were still present when turning the bubble-ligand off (SI Figure S20). The approach only separated the water sampling challenges from the decoupling of the ligand, but did not solve the problem directly. These factors suggest this approach is not a good general strategy but our results further support our hypothesis that water sampling caused issues in both EQ and NEQ calculations.

The overall binding free energy obtained with this bubble approach is statistically equivalent to the binding free energy obtained with the standard protocol (SI Table S7). The uncertainty, however, is slightly higher with the bubble approach, partly because four additional legs in the thermodynamic cycle (Figure 4) combine to increase the overall uncertainty.

5.5.4. The enhanced sampling technique HREX was not able to overcome inadequate sampling.

Enhancing sampling in the EQ approach using HREX did not lead to major improvements with respect to convergence and standard deviation. As shown in Figure 19, the standard deviation is actually higher using HREX (0.5 kcal/mol) than without enhanced sampling (0.3 kcal/mol), as we explore below.

Figure 19.

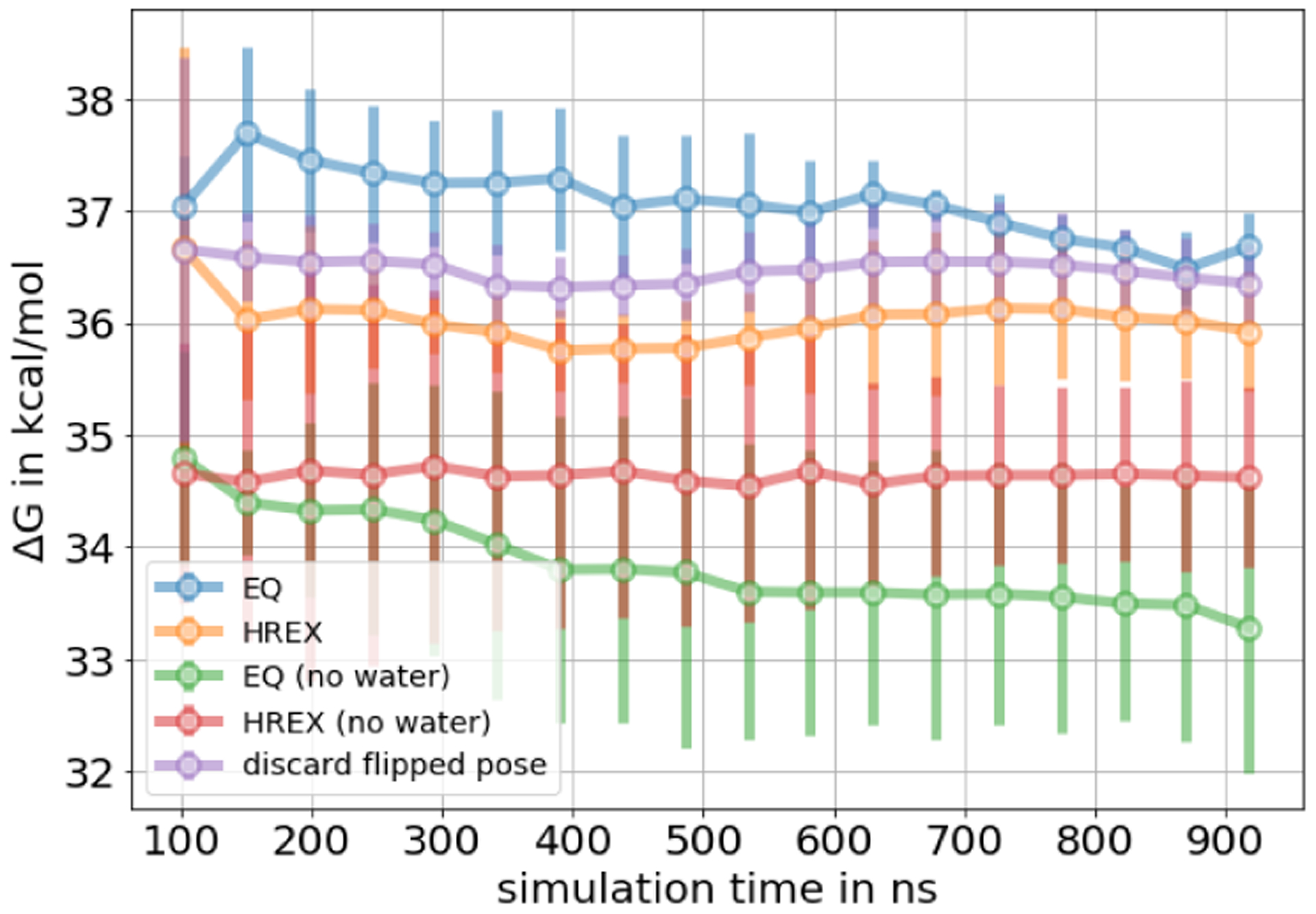
Mean free energy of the ligand binding to HSP90 as a function of total simulation time. We show the standard EQ approach (blue) and the same EQ protocol, but enhancing the sampling with HREX (orange). The purple line shows the free energy estimate of the HREX protocol after discarding all data that included the flipped binding mode. The flipped binding mode had an impact on the ΔG estimate. A high standard deviation on the HREX protocol indicates that the sampling enhancement here came with its own disadvantages. Green and red lines show simulations where the three buried water molecules were not present in the starting structure. The free energy differences from these calculations differs from the simulations where the buried waters were present (blue, orange, purple) which shows the impact of the binding site waters on the ΔG estimate.

Both water sampling and the rearrangement of the Asn36 side chain were improved by HREX mixing of replicates. Sampling of the correct binding mode, however, seemed to be more challenging, since unfavorable (flipped) binding modes were passed between different alchemical states through replica exchange swaps (SI). This was possible because some alternate binding modes were favorable enough to be swapped to alchemical states retaining significant interactions and became temporarily trapped, but not so favorable that they ought to be populated substantially at equilibrium. We reran the analysis after discarding all data that included the flipped binding mode. This changed the estimate of the free energy change by 0.4 kcal/mol and shows the impact of the binding mode flip (Figure 19).

In order to explore whether the NEQ approach benefits from enhanced sampling in the equilibrium end states, we performed NEQ switches using the structures from the EQ HREX run as input. As can be seen in SI Figure S22, using enhanced sampling in the end state did not improve results here. On the contrary, some simulations appearing the ligand crashed. NEQ switches starting from the flipped binding mode, which was sampled more frequently in the HREX protocol (as discussed above), sometimes sampled a binding mode where both phenyl rings switched position (SI Figure S23). This caused those simulation to crash as interaction of the ligand got stronger.

The presence of three buried water molecules in the binding site in the starting structure was crucial for both the EQ and NEQ approach. Indeed, not including these crystallographic waters in the starting structure had a great impact on the computed free energy difference as shown in Figure 19. Only when the ligand was already mostly decoupled, water molecules entered the binding site (SI). Using HREX in the EQ approach did not enhance the sampling sufficiently (Figure 19, red line), and other enhanced sampling methods, like GC/MC or MC/MD, are likely necessary here^77,78 unless far longer simulations are used, which would raise computational costs far beyond what is currently standard for these calculations.^5,6,79 Interestingly, inserting the ligand with NEQ transitions “found” these three water molecules in exactly the same positions as in the crystal structure.

Overall, it seems likely that the use of enhanced sampling methods like HREX impacts sampling in a complex way and will affect equilibrium and nonequlibrium free energy calculations differently. While it seems certain that HREX will help dramatically in some cases, in our tests here it does not provide dramatic benefits in terms of overall sampling quality and accuracy.

5.6. Summary of sampling problems in the HSP90 system.

In HSP90, water sampling in a solvent exposed binding site caused major problems in alchemical FEC. For the EQ approach, sampling of the correct number of waters in alchemical intermediate states was most challenging while in the NEQ calculations water molecules got trapped in the binding site when quickly coupling the ligand. We attempted to work around the water sampling problem by introducing a bubble-ligand that keeps the water from coming into the binding site. This approach worked to some extent and helped us understand the impact of the water sampling problem better, but is not a good general protocol and more robust methods are required to solve this issue. For both methods, it was crucial to start calculations from protein structures that had three buried binding site water molecules present. Besides the inadequate water sampling, ligand binding mode flips and slow side chain rearrangement caused sampling problems as well. These severe sampling problems highlight the limitation of both approaches in ABFE calculations and reveal clear directions for further investigation.

6. Discussion and Conclusions

In this work we highlight challenges encountered applying equilibrium and non-equilibrium binding free energy calculations. We provide insight into how to identify sampling problems and explore similarities and differences between these two methods in handling these issues.

Alchemical calculations frequently pose sampling problems for both the EQ and NEQ approach. We observed slow side chain rearrangements (T4 lysozyme), water sampling in a solvent exposed binding site (HSP90) and flips in ligand binding mode (HSP90). These problems are likely to show up in other protein-ligand systems and may also effect other techniques for binding free energy calculations.

6.1. Challenges encountered here in ABFE will probably effect RBFE as well.

Some of these challenges will probably affect relative binding free energy calculations (RBFE) as well. For instance, slow side chain rearrangements will pose challenges whenever different ligands induce slow side chain rotations, as in the case of toluene vs. 3-iodotoluene, here, which are not that dissimilar from R-groups that might be modified in RFBE calculations on a larger, drug-like ligand. Water sampling can also cause severe issues in relative binding free energy calculations when a buried water molecule is present with one ligand and displaced by another one.^77,80 If ligands have a similar shape or displace the same water molecules, RBFE will probably converge faster than the absolute protocol. Binding mode flips, on the other hand, are less likely to occur with RBFE since those happen mostly in the alchemical states where the ligand is only weakly interacting in the binding site. Still, the same issue can affect R-groups of drug-like ligands.

6.2. Strategies to assess sampling problems in alchemical FEC.

Sampling problems in these systems helped us to establish some general strategies on how to diagnose and test for problems in alchemical FEC. First, we found that in both EQ and NEQ, running independent replicates is important to identify inadequate sampling and to obtain uncertainty estimates. The analytical error – as well as bootstrapping in NEQ – underestimated the true error.

In the EQ approach, the impact of the equilibration time on the ΔG estimate and autocorrelation analysis can give a hint to the presence of slow DOF in the system (Sec. 5.5).

To identify slow motions in the system that can lead to inadequate sampling, we found it helpful to examine dH/dλ values and their relationship to other degrees of freedom. We do this by identifying sudden changes in dH/dλ values as simulations progress. These jumps then tell us when exactly to look for sudden/slow motions by analyzing frames near those jumps. Once a slow motion is identified, the correlation between the motion and the dH/dλ values across all alchemical states can be easily investigated. This method was successfully applied for the three ligands in this paper and helped identify sampling problems. The approach of detecting sampling issues affecting dH/dλ values could be automated in the future, including perhaps with machine learning, e.g. using functional mode analysis.

The overlap of forward and reverse work distributions provides a helpful further diagnostic for the NEQ approach. Having sufficient overlap of the distributions is necessary, but not sufficient for obtaining unbiased free energy estimates; as we found in Section 5.3.2, in some cases, inadequate sampling leads to a false appearance of good overlap. Slow degrees of freedom also often lead to poor overlap, which results in a high analytical error estimate. In addition, bimodal work distributions and sudden changes in work values can be a warning sign that sampling might be complex and slow. Calculating the cross-correlation between side chain dihedral angles in the protein and the non-equilibrium work values can help to diagnose problems. Instead of dihedral angles one could also choose other metrics for protein motion, such as side chain RMSD values. It is important to mention however, that analysis of correlations is prone to false positives – both for correlations between DOF and dH/dλ curves in the EQ approach and DOF with work values in the NEQ approach. It should therefore be applied with caution and the use of replicates for cross-correlation.

In a solvent exposed binding site, counting the number of water molecules in the binding pocket can help detect changes in water placement and occupancy on binding. We also found that it is crucial to include crystallographic water molecules, especially when coming from a high resolution structure with clear density showing ordered waters in the binding site. Here, this was important because the water molecules were buried in the binding site and the timescale for entering the buried space was very slow.

Although not exploited in this paper, it can be a good strategy to run simulations starting in apo and holo structures if both are available. Since both calculations should converge to the same answer this can help to determine when sampling is sufficient.^47,81

We attempted to address these sampling problems and discovered and found ways to work around some of them. We restrained side chains and introduced a bubble approach for water sampling. However, better solutions are needed to make alchemical FEC more general and robust. In the long-term, greater use of enhanced sampling techniques is likely needed, such as perhaps BLUES-like moves^57,75 to accelerate side chain sampling.

The sampling challenges in the systems we investigated made it difficult to directly compare the efficiency of the EQ and the NEQ approaches as we had originally hoped (and as some prior studies have attempted to do⁴²). For the hydration free energy of the three ligands however, calculations converged sufficiently and we were able to compare the efficiency of the EQ and NEQ approaches. Both methods performed very similar on these systems, but the NEQ approach was able to reduce the standard deviation and the bias faster than the EQ approach, suggesting that it is more efficient here, at least. However, differences were very small, and thus a larger data set is needed to investigate this more.

6.3. Similarities and differences of the EQ and NEQ approaches in handling slow DOF.

For the decoupling of the ligands in the binding site, we concentrated on providing some understanding as to why each method behaves the way it does.

First, we compared how the two methods handle side chain rearrangements upon binding. A benefit of the NEQ approach is that the equilibrium orientation of the side chain has to be sampled only in the physical end states and not in alchemical intermediates. Crystal structures can give insight here and help assess sufficient sampling.

A weakness, however, is that when end states differ and the conformational change is not sampled during NEQ switching, dissipation can be large and a slow switching rate or numerous transitions may be required to obtain a converged free energy difference. In the case of Val111 sampling in 3-iodotoluene, we saw that this can be very limiting. Possibly separation of states approaches can help with this issue,⁸² e.g. having the side chain restrained during the calculations and accounting for it later. This however, creates its own problems in some cases.

An advantage for EQ, on the other hand, is that every state is sampled for a long time, allowing for rearrangements. Every state has to be sampled at equilibrium. When there are slow side chain rotations upon binding it can be difficult to reach equilibrium as well as to detect when equilibrium has been reached. Experimental structures also do not indicate the preferred side chain orientation in the unphysical alchemical region.

Water sampling in a solvent exposed binding site caused problems for both methods. For the NEQ approach, very long transitions times (5 ns - 10 ns per transitions) were required to sample changes in water placement which removed much of the benefit of the non-equilibrium approach.

In our experience, a benefit of the NEQ approach is that it can be easier to do sanity checks. Only two long simulations are performed in the physical states which is easier than having to check all trajectories along the alchemical path in EQ. The long end state simulations also provide a point of reference to check that the transition simulations are capturing the right motions. Specifically, an A → B transition needs to (at least some fraction of the time) end up at snapshots that are representative of the same B state seen in the long equilibrium B simulation. This could be done in a systematic and automated way by ensemble comparison techniques.

In the NEQ approach, systematic errors can be introduced by starting NEQ transitions from local minima structures drawn from an incorrect or biased distribution (i.e. if the starting structures overpopulate some conformations and underpopulate others). In these cases, end state simulations can benefit from enhanced sampling techniques. In this work enhanced sampling methods were not investigated in detail in the NEQ approach, since we based this study on work of Gapsys et al. which has been successful without this.⁷⁹ In hindsight, given our results (e.g. Figure 9a), it is worth exploring if faster convergence can be achieved with such enhancements. We tested enhanced end state sampling in the HSP90 system, but starting transitions from structures of the EQ HREX calculations did not improve results in this case. We learned in this study that there is no “free lunch” switching from one alchemical approach to another. If a transition is challenging, the convergence issues will remain for both EQ and NEQ approaches. An advantage of using multiple protocols might be that sampling problems can manifest differently. This may be helpful in identifying where the main sampling issues are and therefore in devising ways to alleviate them.

Figure 16.

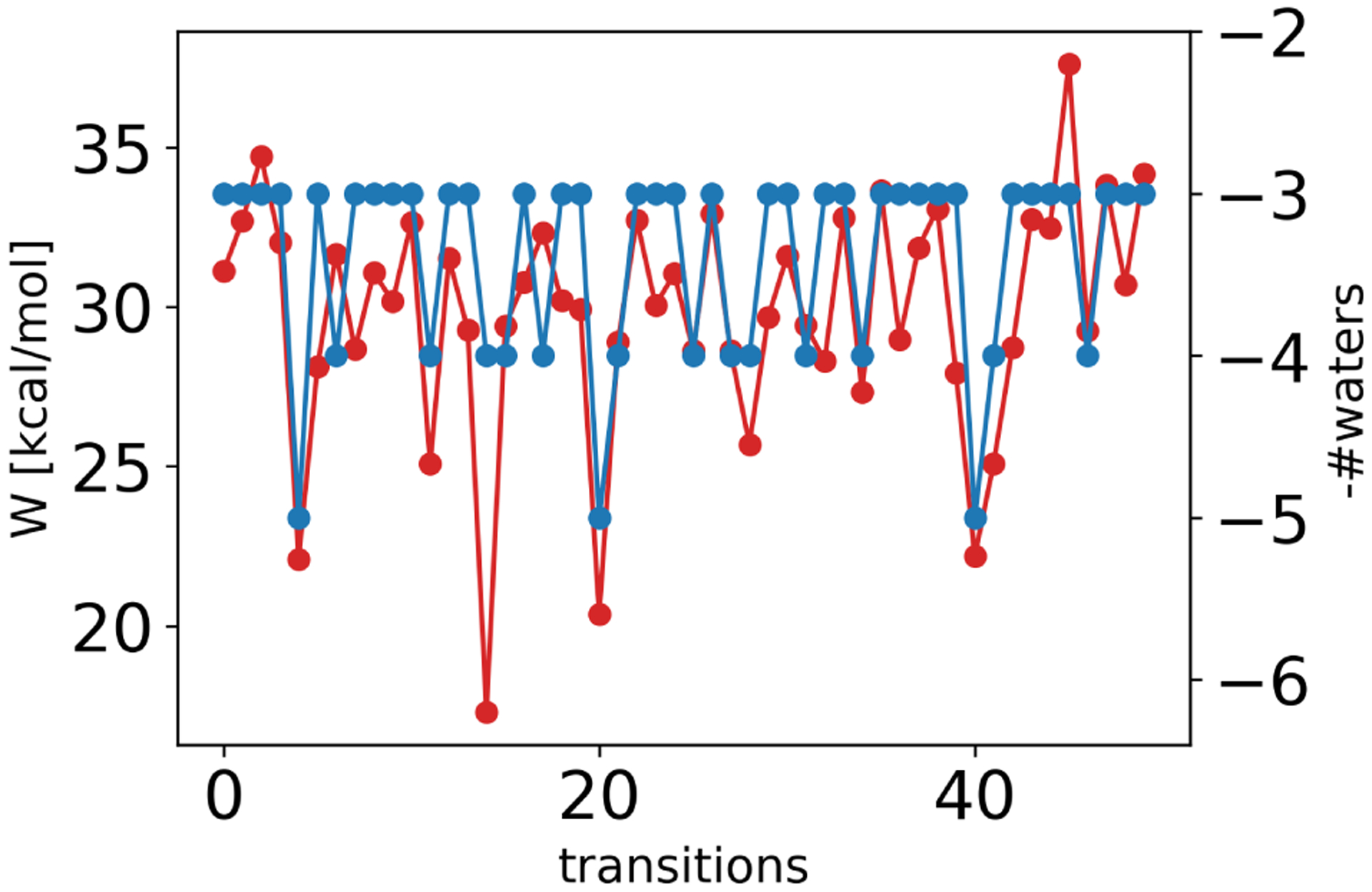
Correlation between NEQ work values (red) and the number of water molecules (blue, with negative numbers to better show the correlation) in the binding site of HSP90 as a function of transition number. Transitions – appearing the ligand in the binding site – were performed for 10 ns and the last frame of that switching transition was used for counting the number of water molecules. Most of the transitions ended up with three binding site waters, which is correct.